An Improved Iterated Greedy Algorithm for Solving Rescue Robot Path Planning Problem with Limited Survival Time

1  Introduction

In the modern world, natural disasters occur with increasing frequency [1]. These disasters present significant challenges to human society and pose major threats to human safety [2]. Recently, post-disaster rescue has emerged as a prominent research field garnering widespread attention [3]. In some severely affected scenarios, it is difficult for rescuers to enter the disaster area. Robot can assist humans in rescue missions [4]. The robot rescue path planning problem has become a current research hotspot.

Previous studies on rescue robot have mainly focused on structural design [5] and kinematics modeling [6], achieving some encouraging results. These research works enrich the methods and theories of robotic rescue, laying a good foundation for robots to efficiently complete rescue tasks. Although steady progress has been made in rescue path planning over the past decades, it remains an open problem [2,3]. One challenging aspect of this problem is that the life strength of survivors decreases over time [7]. Therefore, fast and effective path planning has become an urgent problem to be solved. In current research on rescue path planning, most studies model this problem as a variant of TSP, but rarely consider life strength constraints. In addition, the correlation information between the locations of survivors was not taken into account when dealing with rescue problem. Currently, the IG algorithm [8] has become a current research hotspot due to its advantages such as fewer parameters, strong local search ability, and fast convergence. It has achieved significant results in solving many problems, laying the foundation for its application in rescue path planning problems. Therefore, this paper proposes the IIG algorithm to solve the rescue path planning problem. The main contributions of this paper are as follows:

(1)   This study investigated and modeled the post-disaster rescue path planning problem. To the best of our knowledge, this study is the first attempt to address the rescue path planning problem using the improved IG algorithm.

(2)   A greedy-based insertion strategy is designed and used in the destruction and construction stage to enhance the global search ability of the algorithm.

(3)   Three problem-specific swap operators are developed to improve the proposed algorithm’s exploitation ability.

(4)   An improved acceptance criterion for evolutionary solution is designed.

The rest of this paper is organized as follows. Section 2 provides the literature review and Section 3 formalizes the rescue robot path planning problem. Next, we describe the proposed IIG algorithm and its detailed components in Section 4. Section 5 presents the simulation environments, parameter selection, results, and comparative analysis with the outstanding algorithms. Finally, conclusion is summarized in Section 6.

2  Literature Review

In this section, a concise overview of the relevant literature about both the rescue path planning problem and the state-of-the-art IG algorithms is provided.

The rescue path planning problem requires identifying the optimal or superior solution from feasible solutions while adhering to specific rescue constraints. For example, Zhang et al. [9] presented a heuristic crossing search and rescue optimization algorithm (HC-SAR) for rescue path planning that improves convergence speed and path efficiency. Cho et al. [10] proposed an effective two-stage path planning method for search area decomposition and rescue route optimization, which significantly shortens search time and improves rescue efficiency. In addition, Geng et al. [7] proposed a particle swarm optimization algorithm (PSO) based on integer coding to plan the route with the highest number of rescuers. Ding et al. [11] proposed a refined ant colony algorithm (ACO) tailored for rescue robot path planning in urban disaster scenarios. Moreover, Morin et al. [12] developed a variant of ACO for planning rescue paths, which maximizes the probability of finding moving search objects with Markov motion given a limited time range. Yang et al. [13] combined clustering and improved ACO to enhance urban emergency rescue by optimizing rescue station setup and the obtained path. To our best knowledge, most of current research on rescue path planning adopts swarm intelligence algorithms. These swarm intelligence algorithms usually require lots of computational resources and their efficiency rely on parameter adjustment, such as population size [14–16]. In addition, rescue path planning problem usually involve large-scale search spaces. Studies have shown that the random blind search that intelligent algorithms rely on is not suitable for solving path planning problem with correlated relationships between rescued individuals. To address these challenges, we attempted to use the IG algorithm and developed the local search operators based on the characteristics of the problem.

The IG algorithm was first proposed by Ruiz et al. [8] and was used to solve the permutation flow shop scheduling problem (PFSP). So far, the IG algorithm has been applied to many types of optimization problems. Similar to the above problem, Li et al. [17] improved the IG algorithm to solve the distributed permutation flow shop problem (DPFSP). Han et al. [18] proposed a simple and effective improved IG algorithm, namely NIG, to minimize makespan in DPFSPs. In addition, Li et al. [19] proposed a hybrid IG algorithm for the crane transportation flexible job shop problem (CFJSP). Zou et al. [20] proposed an efficient IG algorithm to solve a multi-compartment automated guided vehicle (AGV) scheduling problem in a matrix manufacturing workshop. Zhang et al. [21] combined the IG algorithm with the nearest-neighbor-based heuristic to optimize the cost of AGV problems. Moreover, Qin et al. [22] embedded the neighborhood probabilistic selection strategies for family and blocking-based jobs in the IG to solve the blocking hybrid flow shop group scheduling problem (BHFGSP). The rescue path planning problem has certain similarities with the above problems. They are essentially sorting problems. Inspired by the above problems, we applied IG to solve the rescue robot path planning problem and made improvements based on the characteristics of the problem.

3  Problem Description and Modeling

This section presents the description of the rescue robot path planning problem and provides mathematical models for this problem.

3.1 Problem Description

The objective of this study is to maximize the number of individuals receiving rescue within a limited time. Therefore, the following assumptions are made:

(1)   Before the survivors are rescued by robot, the locations of survivors are static and known in advance.

(2)   The rescue robot has enough power to complete rescue missions.

(3)   Each survivor is equipped with a vital signs detector that can provide real-time feedback before the disaster occurs.

(4)   During the rescue process, the robot maintains a constant operating speed, and the time required to perform a rescue at each survivor point remains uniform.

3.2 Mathematical Model

In a post-disaster scenario, the life strength of survivors decreases over time. When the life strength of a survivor is below the threshold, it indicates that the rescue of the survivor is failed. It is assumed that all survivors have equal initial life strength before the disaster, denoted as σ0. After the disaster, survivors closer to the disaster source have lower initial life strength, denoted as:

σsi0=σ0⋅min{dsiL,1}(1)

where dsi is the Euclidean distance between the survivor and the disaster center, and L is the maximum value of the distance between two points in the area of the indicated disaster wave. Life strength decreases over time, according to the existing research results [9], the life strength σsi at the current time can be calculated as follows:

σsi=σsi0⋅e−0.0037tsi(2)

tSi=d(si−1,si)v+ST(3)

where tsi denotes the time spent by the robot starting from the start location and arriving at the target location si. As shown in Eq. (3), it consists of two parts: the time spent by the robot in rescuing the target, equal to ST; and the time taken by the robot to move from its current location to the next survivor location si. The path between the two survivors is obtained by the A* algorithm [23]. To be more in line with the realities of post-disaster relief. Considering that some of the paths could not be traveled in both directions after the disaster, some of the relief paths were disturbed so that they could only be traveled in one direction. If path Eij can only pass in one direction, set its value to 1; otherwise, the value of Eij is set to 0.

The sequence of the rescue path is denoted as s1, s2,⋯, sn. F(S) represents the number of survivors rescued, it can be expressed as Eq. (4). When the robot arrives the location of a survivor, if the current life strength of the survivor σsi is greater than the threshold Δσ, it indicates that the survivor can be successfully rescued, f(si) equals to 1; otherwise, f(si) equals to 0.

F(S)=∑i=1Nf(si)(4)

The objective of rescue path planning can be formulated as follows:

maxF(S),s.t.S∈Rn(5)

where Rn denotes the solution space.

4  The Proposed IIG Algorithm

This section introduces the IIG algorithm designed for solving rescue path planning problems. It first outlines the framework of the algorithm, followed by a detailed explanation of the initialization strategy, destruction and construction strategies, local search strategy, and acceptance criterion.

4.1 Framework of the IIG

The proposed IIG algorithm includes four main components, i.e., PFIH strategy, greedy-based insertion strategy, three problem-specific swap operators, and an improved SA strategy. The framework of the proposed IIG algorithm is shown in Algorithm 1. Line 1 of Algorithm 1 describes the initialization strategy, line 3 describes the destruction-construction strategy, line 4 describes the local search strategy, and lines 5 to 9 describe the acceptance criterion.

4.2 Initialization Strategy

In general, an excellent initial solution can accelerate the convergence speed of the algorithm. This paper uses the PFIH strategy to generate a high-quality initial solution. The time complexity of the initialization strategy is O(n2). The initialization strategy works as follows:

Step 1: Select the point with the lowest life strength as the initial rescue point.

Step 2: Select the point closest to the current rescue point and attempt to insert it into each location of the rescue path.

Step 3: Calculate the number of survivors successfully rescued when inserting into each location.

Step 4: Insert the selected point into the location that maximizes the number of successfully rescued survivors.

Step 5: Return to step 2 until all rescue points have been inserted.

4.3 Encoding

For solving the rescue path planning problem, the solution in the algorithm is represented by an integer sequence. Each survivor in the scenario is assigned a unique integer number. Consequently, the path planned by IIG is represented as a sequence of integers, indicating the order of rescuing survivors. For example, we assume that 6 survivors are waiting for rescue. The robot starts from point 0 and first rescues survivor 1, then rescues survivors in order of 5, 4, 6, 3, and 2. Finally, return to the starting point. Hence, the rescue path is represented as [0, 1, 5, 4, 6, 3, 2, 0].

4.4 Destruction and Construction Strategies

Destruction and construction strategies are used to enhance the algorithm’s exploration ability and prevent the algorithm from falling into local optima. Algorithm 2 outlines the pseudocode for the destruction and construction strategies. As shown in Fig. 1a, during the destruction stage, random select points from the current path and save them to PSd. ‘d’ describes the number of points in the set PSd. The remainder of points are denoted as PSr. ‘r’ describes the number of points in the set PSr. The time complexity of the destruction strategy is O(n).

Figure 1: A graphical explanation of the destruction and construction strategies

The construction strategy is used to reinsert the points in the set PSd back into the set PSr. First, select one point from the set PSd, insert it into each location in the set PSr, and calculate the number of deaths. Then, select the location with the lowest number of deaths to insert. Next, repeat the above steps until all points in the set PSd are reinserted into the path. Finally, a new path is obtained. Fig. 1b provides a graphical explanation of the construction strategy, corresponding to lines 3 to 10 of Algorithm 2. The time complexity of the construction strategy is O(n2).

4.5 Local Search Strategy

Generally, compared to insertion operators, swap operators have lower time complexity. Therefore, this paper uses swap operators for local search. We consider the characteristics of the problem and develop three swap operators, i.e., random swap operator, complementary swap operator, and 2-opt swap operator. Fig. 2 provides a graphical illustration of these three swap operators, which work as follows.

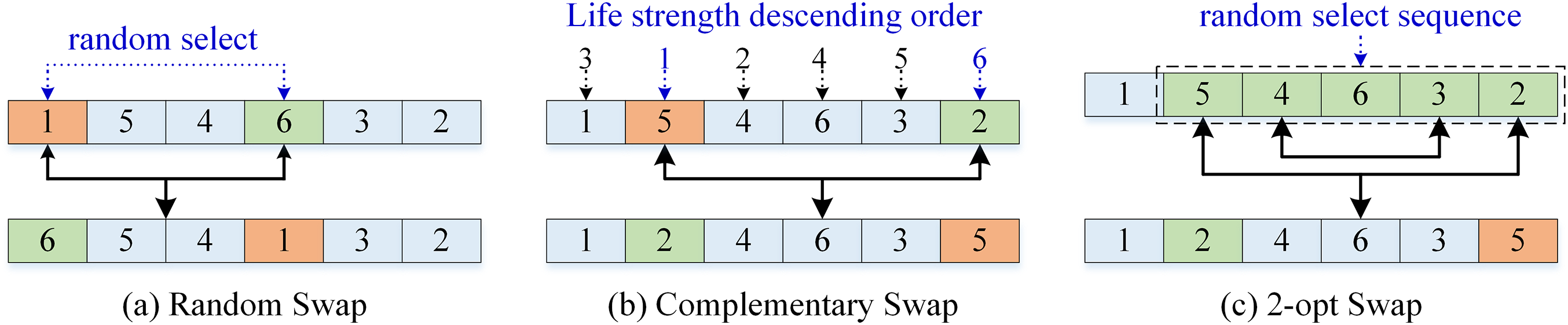
Figure 2: A graphical explanation of local search operators

Random swap: as shown in Fig. 2a, the specific steps of the operator are as follows. (1) Random select one point from the failed rescue sequence, denoted as P1. (2) Select the point closest to P1, such as P6. (3) Swap P1 and P6 to generate a new path. The time complexity of random swap is O(n).

Complementary swap: as shown in Fig. 2b, the specific steps of the operator are as follows. (1) Choose the point with the highest health intensity, such as P5, and choose the point with the lowest health intensity, such as P2. (2) Swap these two points, if the number of successful rescues increases, maintain the swap. (3) Otherwise, choose the point with the second highest life strength, such as P4, and choose the point with the second lowest life strength, such as P3, swap these two points. (4) And so on, until the number of successful rescues increases or all points are swapped. The time complexity of random swap is O(n).

2-opt swap: as shown in Fig. 2c, the specific steps of the operator are as follows. (1) Select a continuous sequence, such as 5, 4, 6, 3, 2. (2) If there are more than 2 failed rescue points in this sequence segment, perform a 2-opt swap. (3) Otherwise, select a new sequence segment. The time complexity of random swap is O(n).

This study adopts a probability dynamically changing roulette wheel strategy to select local search operators. When one of the operators is successfully used once, increase its probability of being selected and decrease the probability of the other two operators being selected. Meanwhile, to avoid the proposed algorithm overly relying on a specific operator during the evolution process, we set a maximum selection probability threshold for all three swap operators.

4.6 SA-Based Acceptance Criterion

The SA-based acceptance criterion is introduced to effectively prevent the algorithm from falling into local optima. The temperature of the acceptance criterion is shown in Eq. (6):

Temperature=F(S)10⋅N(6)

where F(S) represents the number of survivors rescued, the number of successful rescuers is relatively small in the early stages of the algorithm operation. The algorithm is highly likely to accept poor solutions to avoid falling into local optima. As the algorithm runs, the number of successful rescues increases. The algorithm accepts poor solutions with a lower probability to exploit the neighborhood of the current solution further.

4.7 Complexity of the IIG Algorithm

As described above, the time complexity of the initialization strategy is O(n2). The time complexity of the destruction strategy is O(n). The time complexity of the construction strategy is O(n2). The time complexity of the random swap operator is O(n). The time complexity of the complementary swap operator is O(n2). The time complexity of the 2-opt swap operator is O(n). In summary, the time complexity of the IIG algorithm is approximately O(n3).

5  Experimental Results

To verify the effectiveness of the proposed algorithm, we extended the Solomon dataset to generate 27 instances and conducted simulations on these instances. First, we conducted parameter analysis for the algorithm. Next, the effectiveness analysis of each component was verified one by one. Finally, the proposed IIG was compared with five state-of-the-art algorithms. All the algorithms are implemented in MATLAB R2020a on an Intel Core i7-12700 PC with 32 GB RAM. To ensure fairness for all comparison algorithms, the termination criterion is set to a maximum elapsed CPU time of 10 s.

5.1 Experimental Instances

In this section, we extended the Solomon dataset to generate 27 instances for simulation. The Solomon dataset was proposed by Solomon [24] in 1987 and was used to simulate many real-world problems, such as the vehicle routing problem (VRP). The problem studied in this paper has certain similarities with the VRP. Therefore, we added life-strength information to the Solomon dataset to simulate post-disaster rescue scenarios. Table 1 shows an example for instance c10, each instance consists of three parts, the title line is the survivor’s identification number, the first line is the coordinates of the survivor, and the second line gives the initial life strength of survivors.

5.2 Parameter Setting

In this study, two key parameters of the proposed algorithm are considered, including the iteration times of the local search operator ‘Ln’ and the selected length of the sequence in the destruction strategy ‘Ls’. The levels of each parameter are as follows: Ln = {5, 10, 15, 20} and Ls = {N/2, N/3, N/4, N/5}, N represents the number of survivors. The DOE Taguchi method [25] is used to construct an orthogonal matrix of L16. For each parameter combination, the proposed algorithm was run independently 30 times, with the average fitness value of the algorithm being recorded as a response variable. According to the factor-level trend of the parameters shown in Fig. 3, the proposed algorithm with the best performance is obtained by taking Ln = 10 and Ls = N/4. The simulation environment is a 100 × 100 grid map, and the coordinate of the disaster center is D (14, 11). The life strength threshold is equal to 2, the speed of the robot is equal to 20, the time ‘ST’ spent by the robot to rescue a survivor is 5, and the initial life strength is equal to 100. All compared algorithms adopted their parameter settings and have been tuned appropriately. The tuned parameters are shown in Table 2.

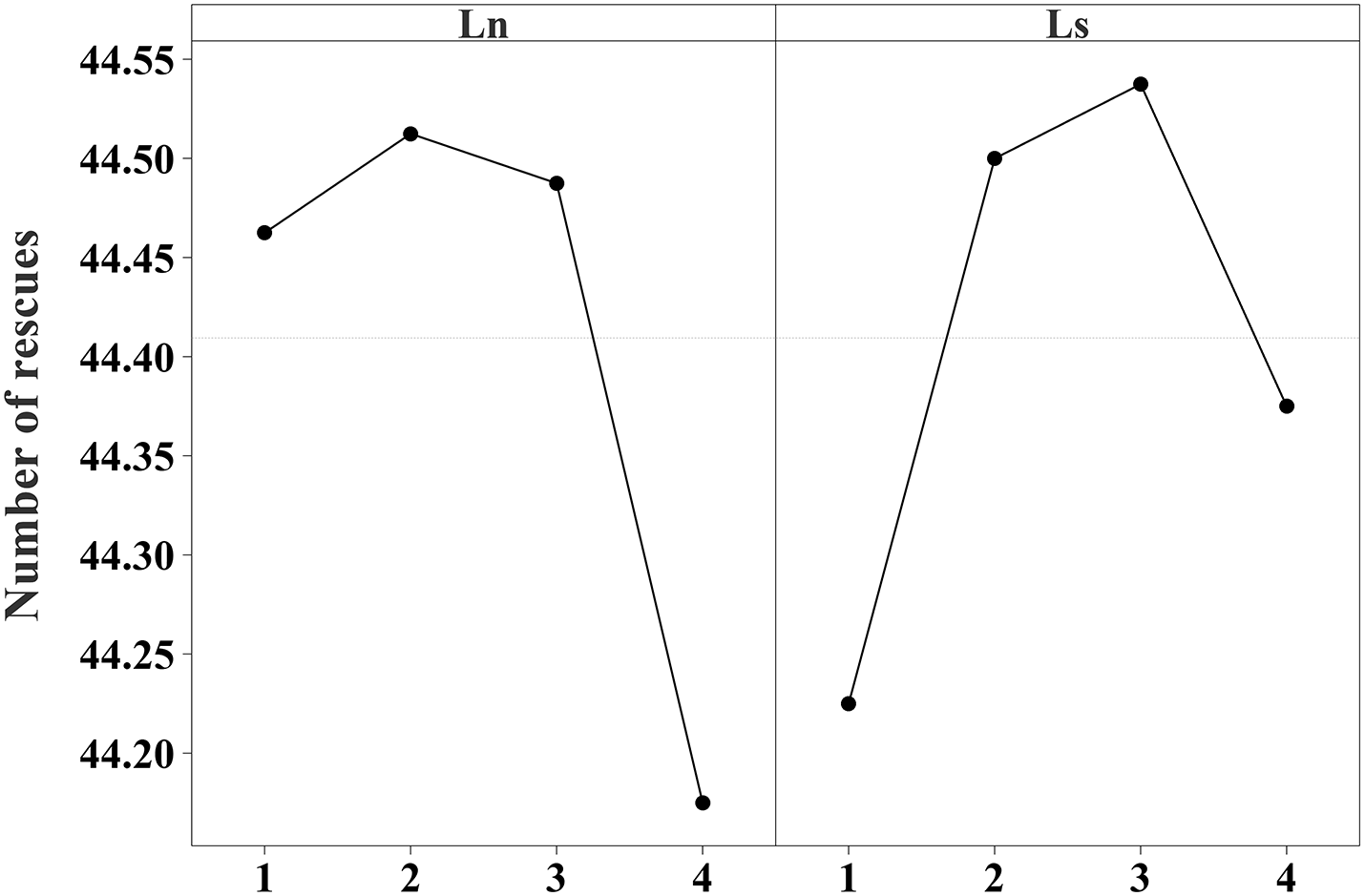
Figure 3: Factor-level trends of parameters

5.3 Efficiency of the Proposed Strategy

In IIG, three key strategies are proposed: a PFIH strategy, local search strategy, and reconstruction strategy. To investigate the effectiveness of the proposed three strategies, we designed four algorithms, the first one is the proposed IIG, the second one is the IIG without the PFIH strategy (IIG_NP), the third one is the IIG without the proposed local search strategy (IIG_NL), and the fourth one is the IIG without the proposed construction strategy (IIG_NC). All the four compared algorithms were run independently 30 times on 27 instances. The relative percentage increase (RPI) is employed to measure the algorithm’s performance.

RPI=fbest−fcfbest×100%(7)

where fbest is the best value found by all of the compared algorithms, and fc is the best value of the current algorithm.

Table 3 presents the comparison results for RPI values. From the comparison results, we can observe that: (1) All algorithms can obtain optimal solutions small-scale instances. (2) The IIG algorithm obtains 14 optimal solutions out of 18 large-scale instances while the remaining three algorithms obtained only 4 optimal solutions. (3) The average RPI value obtained by IIG is 0.001, which is significantly lower than the average RPI values obtained by the other three algorithms. Therefore, the results verify that the proposed strategy can significantly improve the efficiency of the algorithm. Fig. 4 shows the results of the analysis of variance (ANOVA) for the four algorithms, the p-value = 0.0087674 < 0.05, indicating the significant difference among the comparison algorithms.

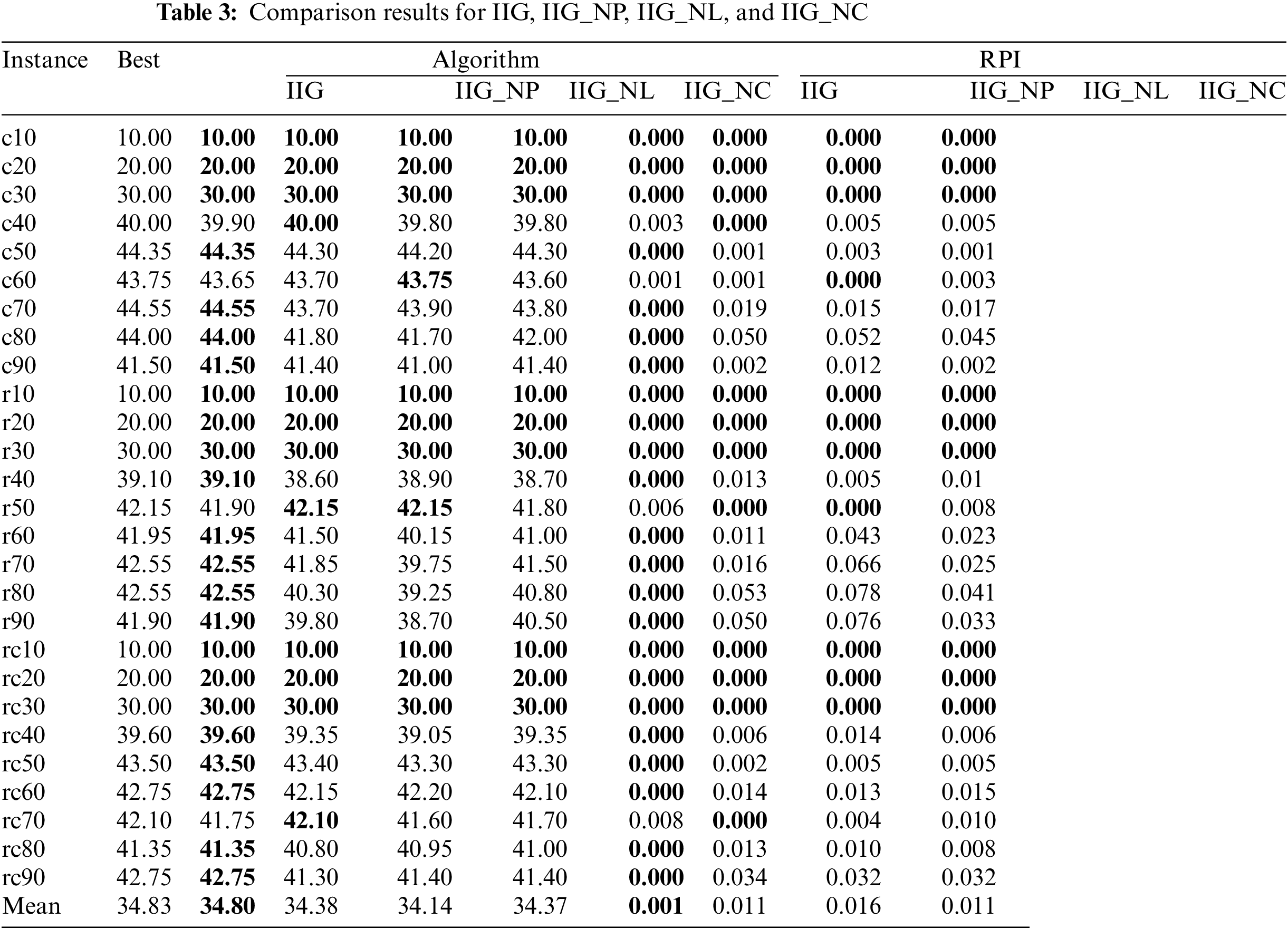
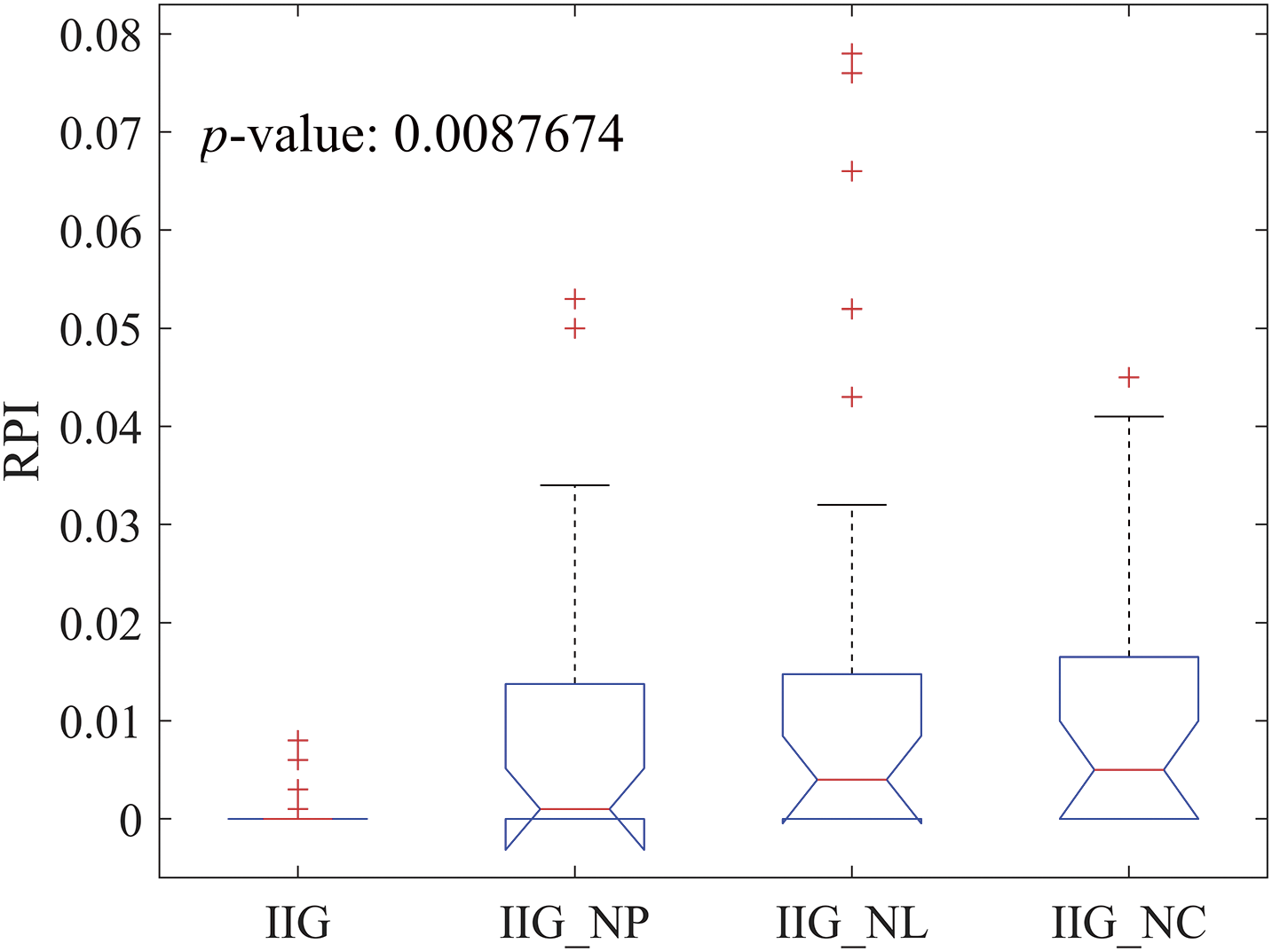
Figure 4: The ANOVA comparisons of IIG, IIG_NP, IIG_NL, and IIG_NC

5.4 Comparison of Several Efficient Algorithms

This section aims to evaluate the performance of the proposed IIG by comparing five algorithms: the NIG algorithm [18], the iterative greedy algorithm with double layer mutation strategy (IGDLM) [26], the improved artificial bee colony (IABC) algorithm [27], the improved iterated greedy (IIG) algorithm [28] (denoted IIG*) and the improved genetic algorithm IGA [29]. The IABC algorithm, as a typical swarm intelligence algorithm, shows good performance in solving the VRP problems. The other three IG based algorithms have achieved good results in solving flow shop scheduling problems which are similar to the path planning problems. The IGA algorithm has shown excellent performance in solving rescue path planning problems derived from VRP with time window. Therefore, these five algorithms are chosen to be compared with the proposed IIG.

Table 4 presents the comparison results of RPI values. It can be seen that: (1) Compared to other algorithms, the proposed IIG algorithm obtains 22 optimal results for the given 27 instances. (2) Both the IIG and the compared algorithms obtained the optimal results on small-scale instances. However, the IIG obtained 13 optimal results on large-scale instances, while the remaining algorithms only obtained 5 optimal results. (3) The average RPI of the IIG algorithm is only 0.002, which is 0.08, 0.25, 0.11, 0.14 and 0.25 times those of the IGDLM, NIG, IABC, IIG* and IGA, respectively. The ANOVA results shown in Fig. 5 indicate that the RPI value of IIG is significantly lower than the other five algorithms (p-value = 0.0017869 less than 0.05). Therefore, we can conclude that the IIG has better effectiveness and stability.

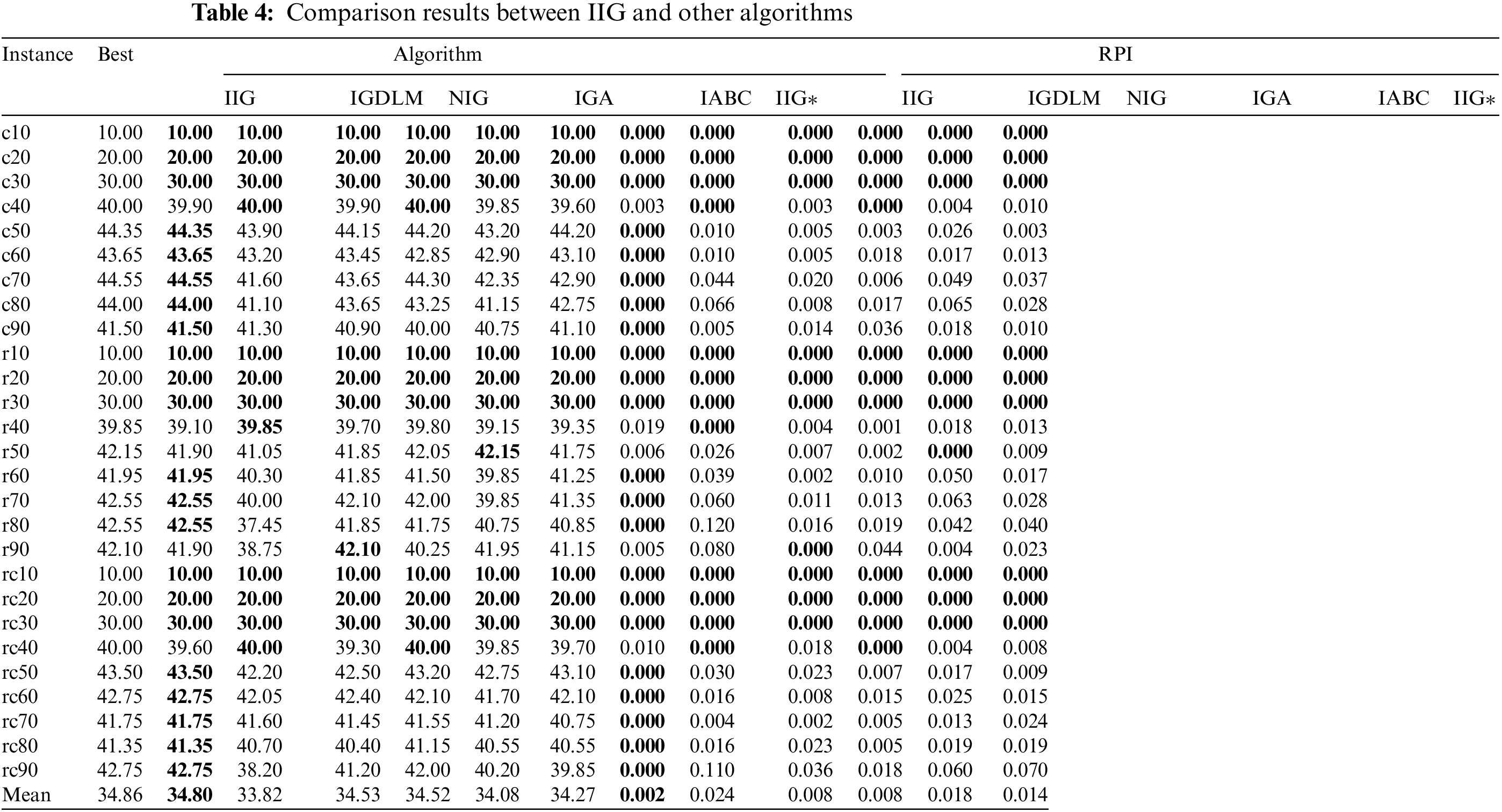
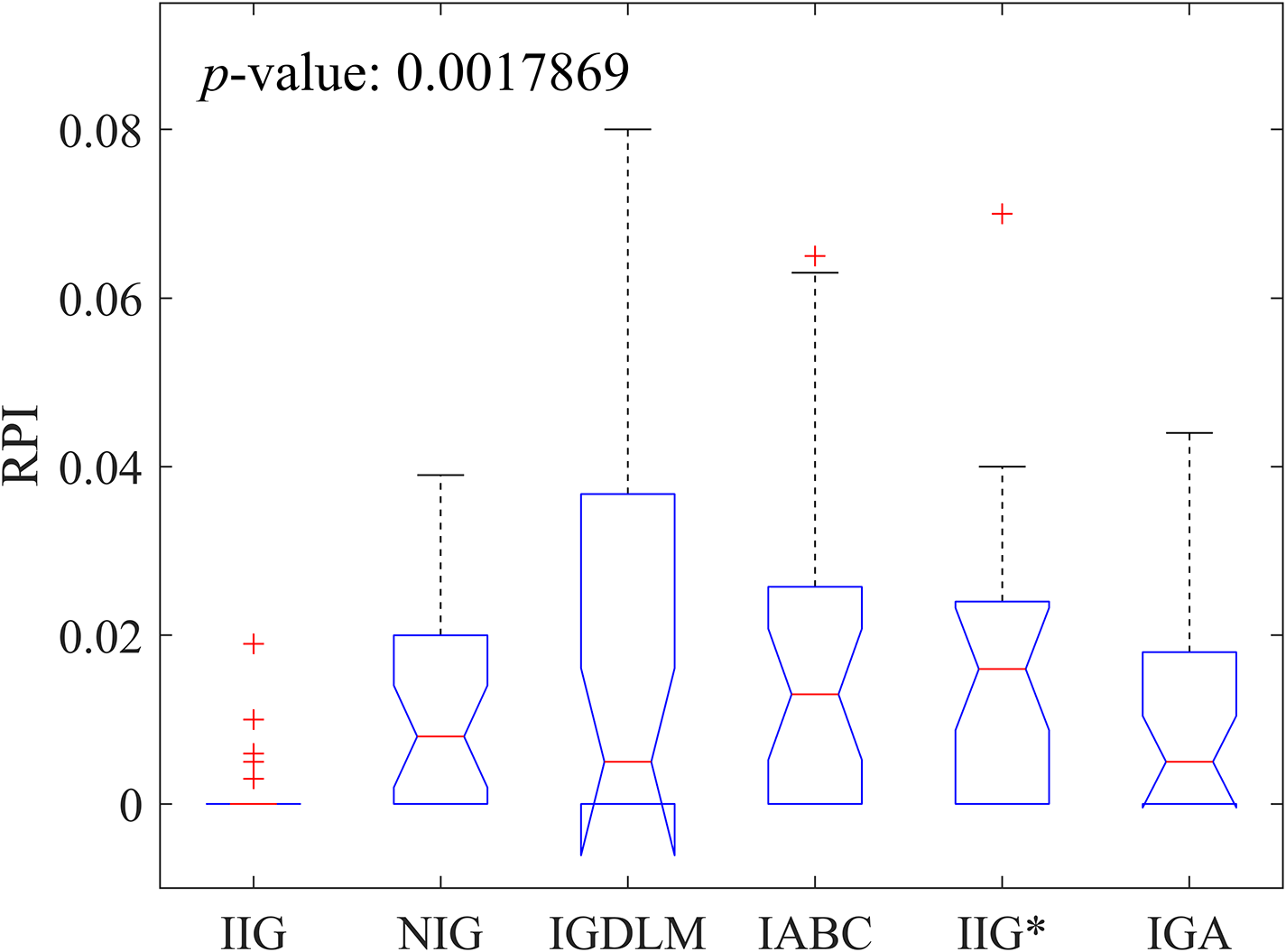
Figure 5: The ANOVA comparisons of IIG, NIG, IGDLM, IABC, IIG* and IGA

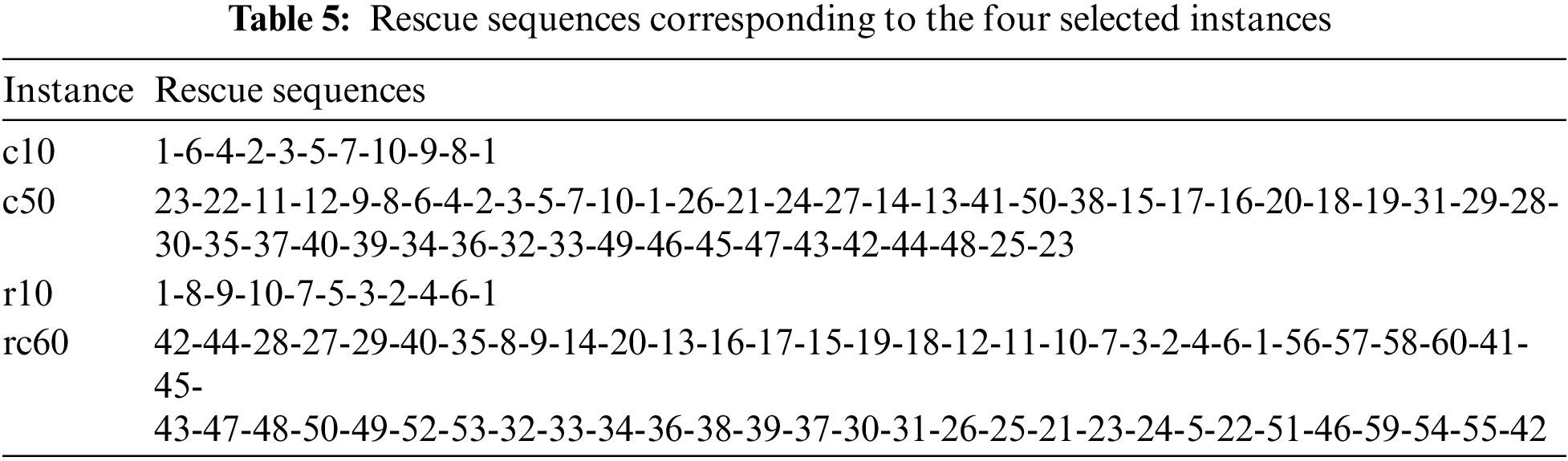
To intuitively reflect the evolution process of the algorithm, Fig. 6 shows the convergence curves of all comparison algorithms on four instances, i.e., c70, c80, r80, and rc90, where all compared algorithms are run for 10 s on the aforementioned PC. Furthermore, Fig. 7 shows the rescue path diagrams for the four selected instances. The flags in the figure represent the starting point, the red dots represent the survivors, the green path represents the rescue path, and the blue path represents the return path to the starting point after rescuing the last survivor. Table 5 provides the rescue sequence on the four instances of c10, c50, r10 and rc60.

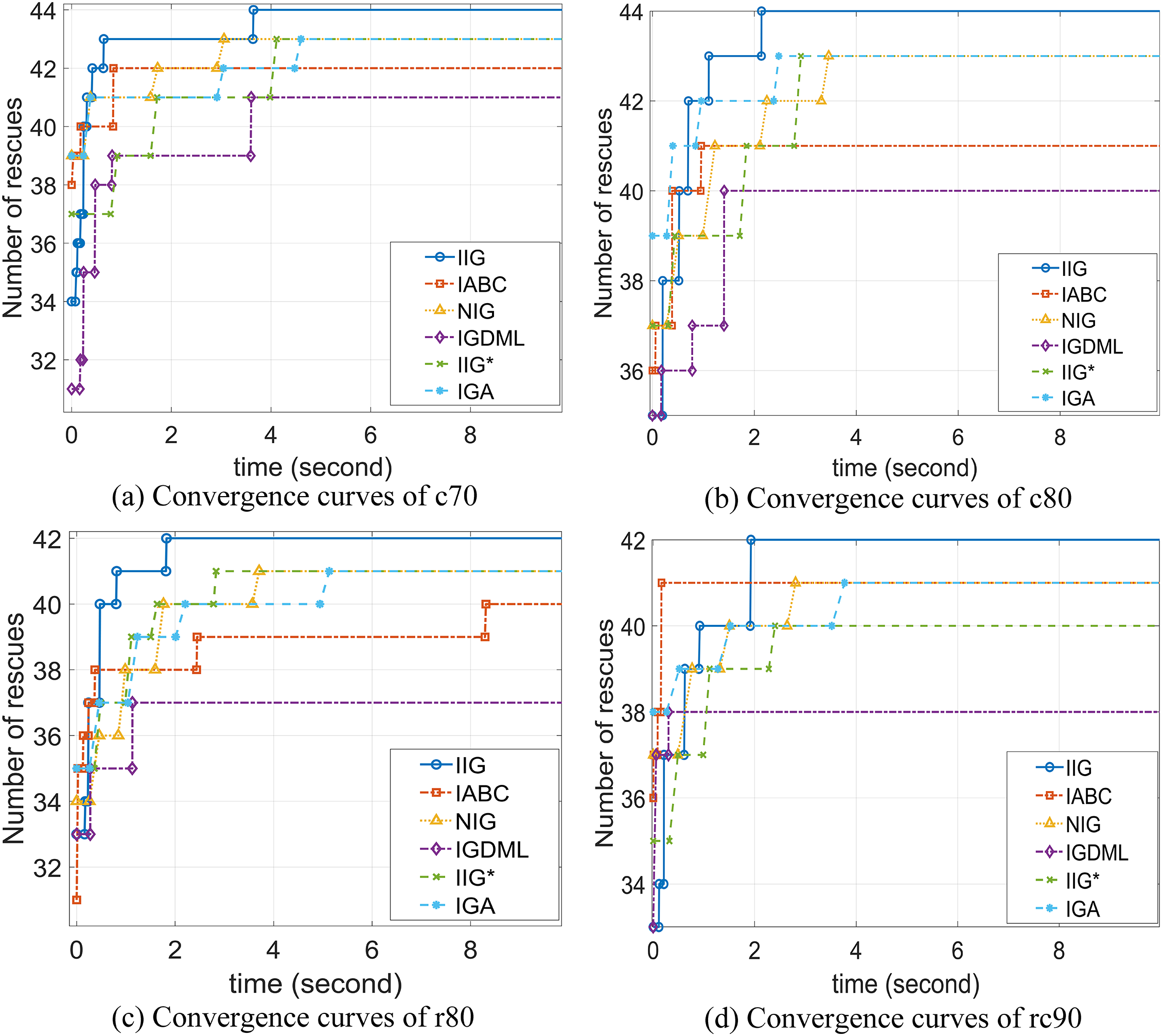
Figure 6: Convergence curves of the four different scale instances

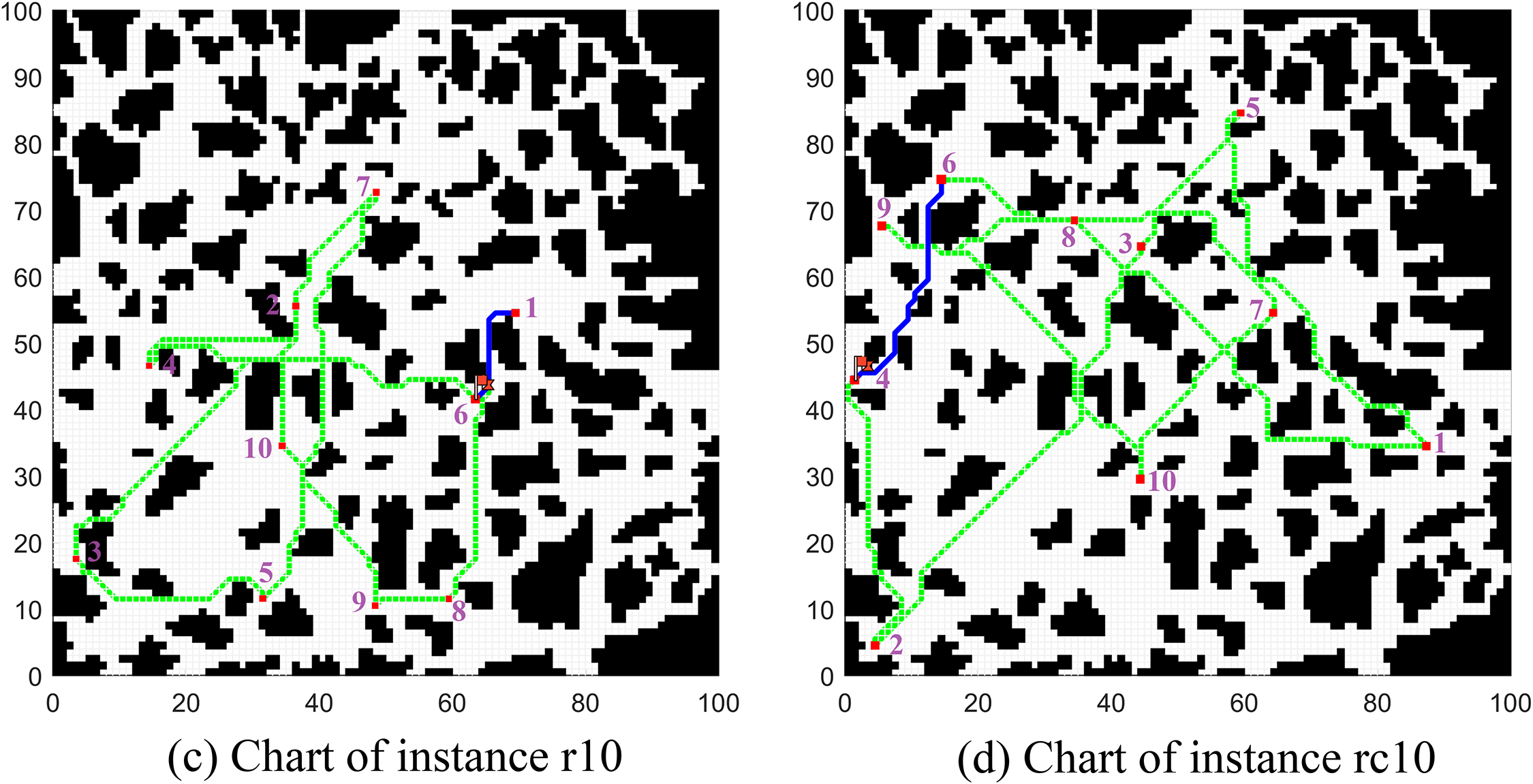
Figure 7: Chart of robotic rescue routes of the four instances

The analysis of the simulation results verified that the proposed IIG is competitive in solving rescue path planning problems. The main advantages of this algorithm are as follows. First, in the initialization stage, the generation of high-quality initial solutions accelerates the convergence of the algorithm. Second, the greedy-based insertion strategy is applied in the construction stage to increase the algorithm’s exploration ability. Additionally, three problem-specific swap operators are proposed to improve local search efficiency. Finally, the SA strategy is used as an acceptance criterion to effectively prevent the algorithm from falling into local optima.

6  Conclusions

In this paper, we proposed an improved IG to solve the rescue path planning problem. The PFIH strategy is applied to obtain a high-quality initial solution. In addition, we developed a construction operator based on greedy insertion and three problem-specific swap operators to reinforce the algorithm’s exploitation and exploration capabilities, respectively. Moreover, an improved SA strategy was used as an acceptance criterion to effectively prevent the algorithm from falling into local optima. We simulated 27 instances and validated the effectiveness analysis of each component of IIG. Finally, the IIG was compared with five state-of-the-art algorithms. The simulation results indicate that, the IIG algorithm obtained 14 optimal solutions from 18 larger instances. Meanwhile, the average RPI of the IIG algorithm is 0.068, 0.21, 0.087, 0.115, and 0.198 times that of IGDLM, NIG, IABC, IIG*, and IGA, respectively. Indeed, the proposed IIG algorithm is applicable to many types of rescue path planning problems, such as post-earthquake rescue path planning problems. The IIG achieves a rescue path based on the location coordinates of survivors and their life strength to maximize the rescue of survivors. The proposed algorithm is not only applicable to post-earthquake rescue. For example, at a fire scene, the IIG achieves a rescue path to avoid fire sources. For mountainous or hilly areas, IIG achieves a save path to avoid steep cliffs. In summary, the proposed IIG algorithm is suitable for solving rescue path planning problem.

The limitations of this study are as follows: 1) Single robot rescue is constrained by many factors, such as limited rescue supplies carried by robots and limited working time. 2) The IIG can be used to solve rescue path planning problems in static environments, but cannot adapt to real-time environmental changes.

In future work, the following directions can be explored: 1) We will consider the effect of economic and medical factors on rescue tasks. Expand more factors into the problem model. 2) The proposed algorithm will consider the effect of secondary disasters on rescue path planning. 3) We will focus on applying the IG algorithm to solve the multi robot rescue path planning problem.

Acknowledgement: The authors would like to express their gratitude to the editors and reviewers for their thorough review and valuable recommendations.

Funding Statement: This work was supported by the Opening Fund of Shandong Provincial Key Laboratory of Network based Intelligent Computing, the National Natural Science Foundation of China (52205529, 61803192), the Natural Science Foundation of Shandong Province (ZR2021QE195), the Youth Innovation Team Program of Shandong Higher Education Institution (2023KJ206), and the Guangyue Youth Scholar Innovation Talent Program support received from Liaocheng University (LCUGYTD2022-03).

Author Contributions: X.W.: Writing the original manuscript, methodology, and software. P.D.: Conceptualization, methodology, funding acquisition. L.M.: Formal analysis, software. K.Y.: Investigation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data will be available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Liu, S. Li, X. Xu, and J. Luo, “Integrated natural disasters urban resilience evaluation: The case of China,” Nat. Hazards, vol. 107, no. 3, pp. 2105–2122, 2021. doi: 10.1007/s11069-020-04478-8. [Google Scholar] [CrossRef]

2. F. Wex, G. Schryen, S. Feuerriegel, and D. Neumann, “Emergency response in natural disaster management: Allocation and scheduling of rescue units,” Eur. J. Oper. Res., vol. 235, no. 3, pp. 697–708, 2014. doi: 10.1016/j.ejor.2013.10.029. [Google Scholar] [CrossRef]

3. G. Tian, A. M. Fathollahi-Fard, Y. Ren, Z. Li, and X. Jiang, “Multi-objective scheduling of priority-based rescue vehicles to extinguish forest fires using a multi-objective discrete gravitational search algorithm,” Inf. Sci., vol. 608, no. 3, pp. 578–596, 2022. doi: 10.1016/j.ins.2022.06.052. [Google Scholar] [CrossRef]

4. X. Zhou, J. Yan, M. Yan, K. Mao, R. Yang and W. Liu, “Path planning of Rail-Mounted logistics robots based on the improved dijkstra algorithm,” Appl. Sci., vol. 13, no. 17, pp. 9955, 2023. doi: 10.3390/app13179955. [Google Scholar] [CrossRef]

5. S. Han et al., “Snake robot gripper module for search and rescue in narrow spaces,” IEEE Robot. Autom. Lett., vol. 7, no. 2, pp. 1667–1673, 2022. doi: 10.1109/LRA.2022.3140812. [Google Scholar] [CrossRef]

6. J. Peng, Y. Guo, D. Meng, and Y. Han, “Kinematics, statics modeling and workspace analysis of a cable-driven hybrid robot,” Multibody Syst. Dyn., vol. 27, no. 6, pp. 1–31, 2023. doi: 10.1007/s11044-023-09924-6. [Google Scholar] [CrossRef]

7. N. Geng, D. W. Gong, and Y. Zhang, “PSO-based robot path planning for multisurvivor rescue in limited survival time,” Math. Probl. Eng., vol. 2014, no. 2, pp. 1–10, 2014. doi: 10.1155/2014/187370. [Google Scholar] [CrossRef]

8. R. Ruiz and T. Stützle, “A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem,” Eur. J. Oper. Res., vol. 177, no. 3, pp. 2033–2049, 2007. doi: 10.1016/j.ejor.2005.12.009. [Google Scholar] [CrossRef]

9. C. Zhang, W. Zhou, W. Qin, and W. Tang, “A novel UAV path planning approach: Heuristic crossing search and rescue optimization algorithm,” Expert. Syst. Appl., vol. 215, no. 13, pp. 119243, 2023. doi: 10.1016/j.eswa.2022.119243. [Google Scholar] [CrossRef]

10. S. Cho, H. Park, H. Lee, D. Shim, and S. Kim, “Coverage path planning for multiple unmanned aerial vehicles in maritime search and rescue operations,” Comput. & Indust. Eng., vol. 161, no. 4, pp. 107612, 2021. doi: 10.1016/j.cie.2021.107612. [Google Scholar] [CrossRef]

11. Y. Ding and Q. Pan, “Path planning for mobile robot search and rescue based on improved ant colony optimization algorithm,” Appl. Mech. Mater., vol. 66, pp. 1039–1044, 2011. doi: 10.4028/www.scientific.net/AMM.66-68.1039. [Google Scholar] [CrossRef]

12. M. Morin, I. Abi-Zeid, and C. Quimper, “Ant colony optimization for path planning in search and rescue operations,” Eur. J. Oper. Res., vol. 305, no. 1, pp. 53–63, 2023. doi: 10.1016/j.ejor.2022.06.019. [Google Scholar] [CrossRef]

13. B. Yang, L. Wu, J. Xiong, Y. Zhang, and L. Chen, “Location and path planning for urban emergency rescue by a hybrid clustering and ant colony algorithm approach,” Appl. Soft Comput., vol. 147, no. 2, pp. 110783, 2023. doi: 10.1016/j.asoc.2023.110783. [Google Scholar] [CrossRef]

14. Y. Fu, X. Ma, K. Gao, Z. Li, and H. Dong, “Multi-objective home health care routing and scheduling with sharing service via a problem-specific knowledge based artificial bee colony algorithm,” IEEE Trans. Intell. Transp. Syst., vol. 25, no. 2, pp. 1706–1719, 2024. doi: 10.1109/TITS.2023.3315785. [Google Scholar] [CrossRef]

15. X. Ma, Y. Fu, K. Gao, L. Zhu, and A. Sadollah, “A multi-objective scheduling and routing problem for home health care services via brain storm optimization,” Complex Syst. Model. Simul., vol. 3, no. 1, pp. 32–46, 2023. doi: 10.23919/CSMS.2022.0025. [Google Scholar] [CrossRef]

16. L. Meng, C. Zhang, B. Zhang, K. Gao, Y. Ren and H. Sang, “MILP modeling and optimization of multi-objective flexible job shop scheduling problem with controllable processing times,” Swarm Evol. Comput., vol. 82, no. 5, pp. 101374, 2023. doi: 10.1016/j.swevo.2023.101374. [Google Scholar] [CrossRef]

17. W. Li, X. Chen, J. Li, H. Sang, Y. Han and S. Du, “An improved iterated greedy algorithm for distributed robotic flowshop scheduling with order constraints,” Comput. Ind. Eng., vol. 164, no. 2, pp. 107907, 2022. doi: 10.1016/j.cie.2021.107907. [Google Scholar] [CrossRef]

18. X. Han et al., “Distributed flow shop scheduling with sequence-dependent setup times using an improved iterated greedy algorithm,” Complex Syst. Model. Simul., vol. 1, no. 3, pp. 198–217, 2021. doi: 10.23919/CSMS.2021.0018. [Google Scholar] [CrossRef]

19. J. Li et al., “A hybrid iterated greedy algorithm for a crane transportation flexible job shop problem,” IEEE Trans. Autom. Sci. Eng., vol. 19, no. 3, pp. 2153–2170, 2021. doi: 10.1109/TASE.2021.3062979. [Google Scholar] [CrossRef]

20. W. Zou, Q. Pan, and M. F. Tasgetiren, “An effective iterated greedy algorithm for solving a multi-compartment AGV scheduling problem in a matrix manufacturing workshop,” Appl. Soft Comput., vol. 99, no. 3, pp. 106945, 2021. doi: 10.1016/j.asoc.2020.106945. [Google Scholar] [CrossRef]

21. X. Zhang, H. Sang, Z. Li, J. Li, and H. Guo, “An effective iterated greedy algorithm for multi-AGVs dispatching problem in material distribution,” presented at the J. Phys.: Conf. Ser., Dali, China, Jun. 18–20, 2021. [Google Scholar]

22. H. Qin, Y. Han, Y. Wang, Y. Liu, J. Li and Q. Pan, “Intelligent optimization under blocking constraints: A novel iterated greedy algorithm for the hybrid flow shop group scheduling problem,” Knowl. Based Syst., vol. 258, pp. 109962, 2022. doi: 10.1016/j.knosys.2022.109962. [Google Scholar] [CrossRef]

23. P. E. Hart, N. J. Nilsson, and B. Raphael, “A formal basis for the heuristic determination of minimum cost paths,” IEEE Trans. Syst. Sci. Cybern., vol. 4, no. 2, pp. 100–107, 1968. doi: 10.1109/TSSC.1968.300136. [Google Scholar] [CrossRef]

24. M. M. Solomon, “Algorithms for the vehicle routing and scheduling problems with time window constraints,” Oper. Res., vol. 35, no. 2, pp. 254–265, 1987. doi: 10.1287/opre.35.2.254 [Google Scholar] [CrossRef]

25. P. Duan, Z. Yu, K. Gao, L. Meng, Y. Han and F. Ye, “Solving the multi-objective path planning problem for mobile robot using an improved NSGA-II algorithm,” Swarm Evol. Comput., vol. 87, no. 2, pp. 101576, 2024. doi: 10.1016/j.swevo.2024.101576. [Google Scholar] [CrossRef]

26. H. Qin, Y. Han, Q. Chen, J. Li, and H. Sang, “A double level mutation iterated greedy algorithm for blocking hybrid flow shop scheduling,” Control Decis, vol. 37, no. 9, pp. 2323–2332, 2022. doi: 10.13195/j.kzyjc.2021.0607. [Google Scholar] [CrossRef]

27. Y. Han, J. Li, Z. Liu, C. Liu, and J. Tian, “Metaheuristic algorithm for solving the multi-objective vehicle routing problem with time window and drones,” Int. J. Adv. Robot. Syst., vol. 17, no. 2, pp. 1–14, 2020. doi: 10.1177/1729881420920031. [Google Scholar] [CrossRef]

28. C. Li, Y. Li, and L. Meng, “An improved iterated greedy algorithm for distributed mixed no-wait permutation flow shop problems with make span criterion,” Int. J. Ind. Eng. Comput., vol. 15, no. 2, pp. 553–568, 2024. doi: 10.5267/j.ijiec.2023.12.007. [Google Scholar] [CrossRef]

29. K. Yang, P. Duan, and H. Yu, “An improved genetic algorithm for solving the helicopter routing problem with time window in post-disaster rescue,” Math. Biosci. Eng., vol. 20, no. 9, pp. 15672–15707, 2023. doi: 10.3934/mbe.2023699. [Google Scholar] [PubMed] [CrossRef]