Frilled Lizard Optimization: A Novel Bio-Inspired Optimizer for Solving Engineering Applications

1  Introduction

In optimization, the aim is to determine a best solution from a set of options for a specific problem [1]. Mathematically, optimization problems consist of decision variables, constraints, and one or several objective functions. The objective is to assign appropriate values to the decision variables in order to maximize or minimize the objective function while adhering to the problem’s constraints [2]. Regarding such optimization problems, problem solving techniques can be partitioned into two main groups: deterministic and stochastic approaches [3]. Deterministic methods are particularly useful for solving linear, convex, low-dimensional, continuous, and differentiable problems [4]. However, as problems become more intricate and dimensions increase, deterministic approaches may struggle with being trapped in local optima and providing suboptimal solutions [5]. Conversely, within science, engineering, industry, technology, and practical applications, numerous intricate optimization problems exist that are characterized as non-convex, non-linear, discontinuous, non-differentiable, complex, and high-dimensional. Due to the inefficiencies and challenges associated with deterministic methods in addressing these optimization issues, scientists have turned to developing stochastic approaches [6].

Metaheuristic algorithms stand out as highly effective stochastic methods capable of offering viable solutions for optimization challenges, all without requiring derivative information. They rely on random exploration within the solution space, utilizing random operators and trial-and-error strategies. Their advantages include straightforward concepts, straightforward implementation, proficiency in tackling varied optimization problems, no matter how complex or high-dimensional they may be, as well as adaptability to nonlinear and unfamiliar search spaces. As a result, the popularity and extensive use of metaheuristic algorithms continue to grow [7]. In metaheuristic algorithms, the optimization process begins by randomly generating a set of candidate solutions at the start of the algorithm. These candidate solutions are then enhanced and modified by the algorithm during a certain number of iterations following its implementation steps. Upon completion of the algorithm, the best candidate solution found during its execution is put forward as the proposed solution to the problem [8]. This random search element in metaheuristic algorithms means that achieving a global optimum cannot be guaranteed using these methods. Nonetheless, the solutions derived from these algorithms, being near the global optimum, are deemed acceptable as quasi-optimal solutions [9].

For a metaheuristic algorithm to effectively carry out the optimization process, it needs to thoroughly explore the solution space on both a global and local scale. Global searching, through exploration, allows the algorithm to pinpoint the optimal area by extensively surveying all parts of the search space and avoiding narrow solutions. Local searching, through exploitation, helps the algorithm converge to solutions near a global optimum by carefully examining surrounding areas and promising solutions. Success in the optimization process hinges on striking a balance between exploration and exploitation during the search [10]. Researchers’ desire to improve optimization outcomes has resulted in the development of many metaheuristic algorithms. These metaheuristic algorithms are employed to deal with optimization tasks in various sciences and applications such as: engineering [11], data mining [12], wireless sensor networks [13], internet of things [14], etc.

The key question at hand is whether, based on the available metaheuristic algorithms, there remains a need in scientific research to develop new metaheuristic algorithms. The concept of No Free Lunch (NFL) [15] addresses this by highlighting that while a metaheuristic algorithm may perform well in solving a particular set of optimization problems, it might not guarantee the same solution quality for different optimization problems. The NFL theorem suggests that there is no one-size-fits-all optimal metaheuristic algorithm for all types of optimization problems. It is conceivable that an algorithm may efficiently reach a global optimum for one problem but struggle to do so for another, possibly getting stuck at a local optimum. As a result, the success or failure of employing a metaheuristic algorithm for an optimization problem cannot be definitively assumed.

The novelty of this paper is the introduction of a new innovative bio-metaheuristic algorithm called Frilled Lizard Optimization (FLO) to solve optimization problems in different research fields and real-world applications.

So far, several algorithms inspired by lizards have been introduced and designed. The strategy of Redheaded Agama lizards when hunting their prey has been the main idea of Artificial Lizard Search Optimization (ALSO). The concept originates from a recent study, where researchers observed that the lizards regulate the movement of their tails with precision, redirecting the angular momentum from their bodies to their tails. This action stabilizes their body position in the sagittal plane [16]. The Side-Blotched Lizard Algorithm (SBLA) is an algorithm inspired by lizards, the main idea in its design is derived from the mating process of these lizards as well as imitating their polymorphic population [17]. The Horned Lizard Optimization Algorithm (HLOA) is another algorithm inspired by lizards. The main source of inspiration in the HLOA design is derived from crypsis, skin darkening or lightening, blood-squirting, and move-to-escape defense methods [18]. As it is evident, although from the point of view of the type of living organism, all these algorithms are inspired by lizards, but they have major differences in the details and also in the mathematical model.

The proposed FLO approach is an algorithm derived from the frilled lizard. In order to design FLO, it is inspired by two characteristic behaviors among frilled lizards. The first behavior is related to the smart strategy of frilled lizards during hunting, which is called sit-and-wait hunting strategy. The second behavior is related to the strategy of frilled lizards when climbing trees after feeding. Based on the best knowledge obtained from the literature review, as well as the review of lizard-inspired algorithms, the originality of the proposed FLO approach is confirmed. This means that so far, no metaheuristic algorithm has been designed inspired by these intelligent behaviors of frilled lizards. Overall, it is confirmed that this is the first time that a new metaheuristic algorithm has been designed based on the modeling of frilled lizard’s intelligent behaviors including (i) sit-and-wait hunting strategy and (ii) climbing trees near the hunting site.

The main contributions of this investigation can be summarized as follows:

•   FLO is based on the imitation of the natural behavior of the frilled lizard in the wild.

•   The basic inspiration of FLO is taken from (i) the hunting strategy of the frilled lizard and (ii) the retreat of this animal to the top of the tree after feeding.

•   The concept behind FLO is outlined, and its procedural steps are mathematically formulated into two stages: (i) exploration, which replicates the frilled lizard’s predatory approach, and (ii) exploitation, which emulates the lizard’s withdrawal to safety atop the tree following a meal.

•   The performance of FLO has been tested on fifty-two standard benchmark functions of various types of unimodal, high-dimensional multimodal, fixed-dimensional multimodal as well as the CEC 2017 test suite.

•   FLO’s effectiveness has been tested on several practical challenges, including twenty-two constrained optimization issues from the CEC 2011 test suite and four engineering design tasks.

•   The outcomes produced by FLO are juxtaposed with those of alternative metaheuristic algorithms for performance comparison.

This paper is organized as follows: Section 2 contains a review of the relevant literature. Section 3 describes the proposed Frilled Lizard Optimization (FLO) and gives a mathematical model. Then Section 4 presents the results of our simulation studies. Section 5 investigates the effectiveness of FLO in solving real-world applications, and Section 6 provides some conclusions and suggestions for future research.

2  Literature Review

Metaheuristic algorithms are devised by drawing inspiration from a diverse array of sources, including natural phenomena, behaviors exhibited by living organisms in their natural habitats, principles from biological sciences, genetic mechanisms, physical laws, human behavior, and various evolutionary processes. These algorithms are typically classified into four distinct groups, each based on the specific inspiration behind its design. These categories include swarm-based approaches, evolutionary-based approaches, physics-based approaches, and human-based approaches, with each group leveraging different principles and mechanisms to guide the optimization process [19].

Swarm-based metaheuristic algorithms derive their principles from the collective behaviors and strategies observed in various natural systems, especially those exhibited by animals, aquatic creatures, and insects in their natural environments. These algorithms aim to mimic the efficient problem-solving strategies seen in nature to address complex optimization challenges. Among the most commonly used swarm-based metaheuristics are Particle Swarm Optimization (PSO) [20], Ant Colony Optimization (ACO) [21], Artificial Bee Colony (ABC) [22], and Firefly Algorithm (FA) [23]. PSO is inspired by the social behavior and collective movement patterns of birds flocking and fish schooling as they search for food. This algorithm simulates how individuals within a group adjust their positions based on personal experience and the success of their neighbors to find optimal solutions. ACO emulates the foraging behavior of ants, particularly how they find the shortest path between their nest and a food source by laying down and following pheromone trails. This method effectively models the way ants collectively solve complex routing problems through simple, local interactions. ABC is modeled after the foraging behavior of honey bees. It simulates how bees search for nectar, share information about food sources, and optimize their foraging strategies to maximize the efficiency of the colony. The Firefly Algorithm draws its inspiration from the bioluminescent communication of fireflies. It uses the concept of light intensity to simulate attraction among fireflies, guiding the search for optimal solutions through simulated social interactions. Furthermore, natural behaviors such as foraging, hunting, migration, digging, and chasing have inspired the development of various other metaheuristic algorithms. Examples include: Greylag Goose Optimization (GGO) [1], African Vultures Optimization Algorithm (AVOA) [24], Marine Predator Algorithm (MPA) [25], Gooseneck Barnacle Optimization Algorithm (GBOA) [26], Grey Wolf Optimizer (GWO) [27], Electric Eel Foraging Optimization (EEFO) [28], White Shark Optimizer (WSO) [29], Crested Porcupine Optimizer (CPO) [30], Tunicate Swarm Algorithm (TSA) [31], Orca Predation Algorithm (OPA) [32], Honey Badger Algorithm (HBA) [33], Reptile Search Algorithm (RSA) [34], Golden Jackal Optimization (GJO) [35], and Whale Optimization Algorithm (WOA) [36].

Evolutionary-based metaheuristic algorithms are inspired by fundamental principles from genetics, biology, natural selection, survival of the fittest, and Darwin’s theory of evolution. These algorithms model natural evolutionary processes to solve complex optimization problems effectively. Among the most notable examples in this category are Genetic Algorithm (GA) [37] and Differential Evolution (DE) [38], which have gained widespread popularity and adoption. Genetic Algorithms (GA) simulate the process of natural selection where the fittest individuals are selected for reproduction in order to produce the next generation. This algorithm involves mechanisms such as selection, crossover (recombination), and mutation to evolve solutions to optimization problems over successive generations. By mimicking biological evolution, GAs can efficiently explore and exploit the search space to find optimal or near-optimal solutions. Differential Evolution (DE) is another powerful evolutionary algorithm that optimizes a problem by iteratively trying to improve candidate solutions with regard to a given measure of quality. DE uses operations like mutation, crossover, and selection, drawing inspiration from the biological evolution and genetic variations observed in nature. The algorithm is particularly effective for continuous optimization problems due to its simple yet robust strategy. Additionally, Artificial Immune Systems (AIS) algorithms are inspired by the human immune system’s ability to defend against pathogens. AIS algorithms mimic the immune response process, learning and adapting to recognize and eliminate foreign elements. This approach provides robust mechanisms for optimization and anomaly detection [39]. Other prominent members of evolutionary-based metaheuristics include Genetic Programming (GP) [40], Cultural Algorithm (CA) [41], and Evolution Strategy (ES) [42]. These evolutionary-based metaheuristics emulate natural processes to harness the power of evolution, providing versatile and powerful tools for solving a wide range of optimization problems in various domains.

Physics-based metaheuristic algorithms are introduced, drawing inspiration from the modeling of forces, laws, phenomena, and other fundamental concepts in physics. Simulated Annealing (SA) [43], a widely employed physics-based metaheuristic algorithm, takes its design cues from the physical phenomenon of metal annealing. This process involves the melting of metals under heat, followed by a gradual cooling and freezing process to attain an ideal crystal structure. Gravitational Search Algorithm (GSA) [44] is crafted by modeling physical gravitational forces and applying Newton’s laws of motion. Concepts derived from cosmology and astronomy serve as the foundation for algorithms like Multi-Verse Optimizer (MVO) [45] and Black Hole Algorithm (BHA) [46]. Some other physics-based metaheuristic algorithms are: Thermal Exchange Optimization (TEO) [47], Prism Refraction Search (PRS) [48], Equilibrium Optimizer (EO) [49], Archimedes Optimization Algorithm (AOA) [50], Lichtenberg Algorithm (LA) [51], Water Cycle Algorithm (WCA) [52], and Henry Gas Optimization (HGO) [53].

Human-based metaheuristic algorithms draw inspiration from human behaviors, decisions, thoughts, and strategies observed in both individual and social contexts. These algorithms leverage the complexities and nuances of human actions to solve optimization problems effectively.

Teaching-Learning Based Optimization (TLBO) [54] is a prominent example of a human-based metaheuristic. TLBO simulates the teaching and learning processes in a classroom setting, modeling the interactions between teachers and students as well as peer learning among students. The algorithm improves solutions by mimicking the educational process where knowledge is imparted from teachers to students and shared among students, leading to enhanced performance and optimization outcomes. The Mother Optimization Algorithm (MOA) is inspired by the nurturing and caring behaviors exhibited by mothers, specifically modeled on Eshrat’s care for her children. This algorithm utilizes the principles of guidance, protection, and nurturing to iteratively improve solutions, reflecting the natural and effective strategies mothers use in raising their offspring [9]. War Strategy Optimization (WSO) takes its cue from the tactical and strategic movements of soldiers during ancient battles. By simulating various military strategies, formations, and maneuvers, WSO effectively explores and exploits the search space, providing robust solutions to complex problems [55]. Poor and Rich Optimization (PRO) [56] is designed based on the socioeconomic dynamics between the rich and the poor in society. This algorithm models the efforts of individuals to improve their financial and economic status, capturing the diverse strategies employed by different socioeconomic groups to achieve better outcomes. Some other human-based metaheuristic algorithms are: Coronavirus Herd Immunity Optimizer (CHIO) [57], Gaining Sharing Knowledge based Algorithm (GSK) [58], and Ali Baba and the Forty Thieves (AFT) [59].

The literature review highlights the absence of any metaheuristic algorithm that simulates the natural behavior of frilled lizards in their habitat. However, the strategic hunting and safety retreats employed by these lizards represent intelligent behaviors that hold potential for inspiring the development of a new optimizer. To fill this void, a novel metaheuristic algorithm has been created, drawing upon mathematical models of two primary behaviors exhibited by frilled lizards: predatory attacks and retreats to elevated positions, such as the top of a tree. This newly devised algorithm will be thoroughly discussed in the subsequent section.

3  Frilled Lizard Optimization

In this section, the source of inspiration used in the development and theory of Frilled Lizard Optimization (FLO) is stated. Then the corresponding implementation steps are mathematically modeled to be used for the solution of optimization problems.

3.1 Inspiration of FLO

The frilled lizard (Chlamydosaurus kingii) is a species of lizard from the family Agamidae, which is native to Southern New Guinea and Northern Australia [60]. The frilled lizard is an arboreal species and diurnal that spends more than 90% of each day up in the trees [61]. During the short time that this animal is on the ground, it is busy with feeding, socializing or traveling to a new tree [60]. A frilled lizard can move bipedally and do this when hunting or escaping from predators. To keep balanced, it leans its head far back enough, so it lines up behind the tail base [60,62]. The total length of the frilled lizard is about 90 centimeters, a head-body length of 27 centimeters, and weighs up to 600 grams [63]. The frilled lizard has a special wide and big head with a long neck to accommodate the frill. It has long legs for running and a tail that makes most of the total length of this animal [64]. The male species is larger than the female species and has proportionally bigger jaw, head, and frill [65]. A picture of a frilled lizard is shown in Fig. 1.

Figure 1: Frilled lizard taken from: free media wikimedia commons

The main diet of the frilled lizard are insects and other invertebrates, although it also rarely feeds on vertebrates. Prominent prey includes centipedes, ants, termites, and moth larvae [66]. The frilled lizard is a sit-and-wait predator that looks for potential prey. After seeing the prey, the frilled lizard runs fast on two legs and attacks the prey to catch it and feed on it. After feeding, the frilled lizard retreats back up a tree [60].

Among the frilled lizard’s natural behaviors, its sit-and-wait hunting strategy to catch prey and retreat to the top of the tree after feeding is much more prominent. These natural behaviors of frilled lizard are intelligent processes that are the fundamental inspiration in designing the proposed FLO approach.

3.2 Algorithm Initialization

The proposed FLO method is a metaheuristic algorithm that considers frilled lizards as its members. FLO efficiently discovers near-optimal solutions for optimization challenges by leveraging the search capabilities of its members within the problem-solving space. Each frilled lizard establishes value assignments for the decision variables according to its particular location in the problem-solving space. Consequently, every frilled lizard represents a potential solution that can be interpreted mathematically through a vector. Collectively, the frilled lizards constitute the FLO population, which can be mathematically described as a matrix using Eq. (1). The initial placements of the frilled lizards within the problem-solving space are established by a random initialization using Eq. (2):

X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,d⋯x1,m⋮⋱⋮⋰⋮xi,1⋯xi,d⋯xi,m⋮⋰⋮⋱⋮xN,1⋯xN,d⋯xN,m]N×m(1)

xi,d=lbd+r⋅(ubd−lbd)(2)

Here X denotes the FLO population matrix, Xi represents the ith frilled lizard (candidate solution), xi,d denotes its dth dimension in the search space (decision variable), N gives the number of frilled lizards, m denotes the number of decision variables, r represents a number randomly taken from the interval [0,1], lbd, and ubd are a lower bound as well as an upper bound on the dth decision variable, respectively.

Considering that each frilled lizard represents a candidate solution for the problem, corresponding to each candidate solution, the corresponding objective function value can be calculated for the problem. The set of determined objective function values can be represented mathematically using the vector given in Eq. (3):

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1(3)

Here F denotes the vector of the calculated objective function values and Fi gives the evaluated objective function value corresponding to the ith frilled lizard.

The determined objective function values are appropriate criteria for measuring the quality of the population individuals (i.e., the candidate solutions). In particular, the best evaluated value for the objective function corresponds to the best individual of the population (i.e., the best candidate solution) and similarly, the worst evaluated value for the objective function corresponds to the worst individual of the population (i.e., the worst candidate solution). Since in each iteration of FLO, the position of the frilled lizards is updated in the solution space, new values are also evaluated for the objective function under consideration. Consequently, in each iteration the position of the best individual (i.e., the best candidate solution) must also be updated. At the end of the implementation of Algorithm FLO, the best candidate solution obtained during the iterations of the algorithm is taken as the solution to the problem.

3.3 Mathematical Modelling of FLO

In each iteration of Algorithm FLO, the position of the frilled lizard in the problem-solving space undergoes updating in two distinct phases. Firstly, the exploration phase simulates the frilled lizard’s movement towards prey during hunting, aimed at diversifying the search space and exploring new potential solutions. This phase allows the algorithm to probe different areas of the problem space, facilitating the discovery of novel regions that may contain optimal solutions.

Secondly, the exploitation phase simulates the movement of the frilled lizard towards the top of a tree after feeding. In this phase, the algorithm capitalizes on the knowledge gained during exploration to exploit promising regions identified as potential optimal solutions. By focusing on refining these regions, the exploitation phase aims to improve the quality of solutions and converge towards the global optimum.

3.3.1 Phase 1: Hunting Strategy (Exploration)

One of the most characteristic natural behaviors of the frilled lizard is the hunting strategy of this animal. The frilled lizard is a sit-and-wait predator that attacks its prey after seeing it. The simulation of frilled lizard’s movement towards the prey leads to extensive changes in the position of the population members in the problem-solving space and as a result increases the exploration power of the algorithm for global search. In the first phase of FLO, the position of the population individuals in the solution space of the problem is updated based on the frilled lizard’s hunting strategy. In the design of FLO, for each frilled lizard, the position of other population members who have a better objective function value is considered as the prey position. According to this, the set of candidate preys’ positions for each frilled lizard is determined using Eq. (4):

CPi={Xk:Fk<Fiandk≠i},wherei=1,2,…,Nandk∈{1,2,…,N}(4)

Here CP is the candidate preys set for the ith frilled lizard, Xk is the population member with a better objective function value than the ith frilled lizard, and Fk is its objective function value.

In the FLO design, it is assumed that the frilled lizard randomly chooses one of these candidate preys and attacks it. Based on the modeling of the frilled lizard’s movement towards the chosen prey, a new position for each individual of the population has been calculated using Eq. (5). Then, if the objective function value is better, this new position replaces the previous position of the corresponding individual using Eq. (6):

xi,dP1=xi,d+r⋅(SPi,d−I⋅xi,d),i=1,2,…,N,andd=1,2,…,m(5)

Xi={XiP1,FiP1<FiXi,else(6)

Here XiP1 denotes the new suggested position of ith frilled lizard based on the first phase of FLO, xi,dP1 represents its dth dimension, FiP1 denotes its objective function value, r is a random number with a normal distribution from the interval [0,1], SPi,d denotes the dth dimension of the selected prey for the ith frilled lizard, I is a number randomly taken from the set {1,2}, N denotes the number of frilled lizards, and m gives the number of decision variables.

3.3.2 Phase 2: Moving Up the Tree (Exploitation)

After feeding, the frilled lizard retreats to the top of a tree near its position. Simulating the movement of the frilled lizard to the top of the tree leads to small changes in the position of the population individuals in the solution space of the problem and as a result, increasing the exploitation power of the algorithm for local search. In the second phase of FLO, the position of the population individuals in the solution space is updated based on the frilled lizard’s strategy when retreating to the top of the tree after feeding.

Based on modeling the movement of the frilled lizard to the top of the nearby tree, a new position for each population individual is calculated using Eq. (7). Then this new position, if it improves the objective function value, replaces the previous position of the corresponding individual using Eq. (8):

xi,dP2=xi,d+(1−2r)⋅(ubd−lbd)t,i=1,2,…,N,d=1,2,…,m,andt=1,2,…,T(7)

Xi={XiP2,FiP2<FiXi,else(8)

Here XiP2 denotes the new suggested position of the ith frilled lizard based on the second phase of FLO, xi,dP2 represents its dth dimension, FiP2 gives its objective function value, t represents the iteration counter of the algorithm, and T describes the maximum number of iterations of the algorithm.

3.4 Repetition Process, Pseudo-Code, and Flowchart of FLO

The initial iteration of the Frilled Lizard Optimization (FLO) algorithm concludes after updating the positions of all frilled lizards within the problem-solving space, following the execution of the first and second phases. Subsequently, armed with the newly updated values, the algorithm proceeds to commence the subsequent iteration, perpetuating the process of updating the frilled lizards’ positions until the algorithm reaches completion, guided by Eqs. (4) to (8). Throughout each iteration, the algorithm also maintains and updates the best candidate solution, storing it based on the comparison of obtained objective function values. Upon the algorithm’s full execution, the best candidate solution acquired throughout its iterations is presented as the ultimate FLO solution for the given problem. The implementation steps of FLO are visually depicted as a flowchart in Fig. 2, providing a comprehensive overview of its execution sequence. Additionally, the algorithm’s pseudocode is detailed in Algorithm 1, offering a structured representation of its operational logic and steps.

Figure 2: Flowchart of FLO

3.5 Computational Complexity of FLO

In this subsection, we delve into evaluating the computational complexity of the Frilled Lizard Optimization (FLO) algorithm. The computational complexity of FLO can be broken down into two main aspects: the preparation and initialization steps, and the position update process during each iteration. The preparation and initialization steps of FLO involve setting up the algorithm and initializing the positions of the frilled lizards. This process has a computational complexity denoted as O(Nm), where N represents the number of frilled lizards and m denotes the number of decision variables in the problem. During the execution of FLO, the positions of the frilled lizards are updated in each iteration, incorporating both exploration and exploitation phases. This update process contributes to the overall computational complexity of FLO, which is represented as O(2TNm), where T signifies the maximum number of iterations the algorithm will perform. Combining these aspects, the overall computational complexity of the FLO algorithm can be expressed as O(Nm(1+2T)). This analysis underscores the computational framework within which FLO operates, taking into account factors such as the number of lizards, decision variables, and iterations.

4  Simulation Studies and Results

In this section, we delve into evaluating the performance of the developed Frilled Lizard Optimization (FLO) algorithm in handling optimization problems. To this end, we utilize a diverse set of fifty-two standard benchmark functions encompassing unimodal, high-dimensional multimodal, fixed-dimensional multimodal types [67], alongside the CEC 2017 test suite [68]. To gauge the efficacy of FLO, we compare its performance against twelve well-known metaheuristic algorithms: GA [37], PSO [20], GSA [44], TLBO [54], MVO [45], GWO [27], WOA [36], MPA [25], TSA [31], RSA [34], AVOA [24], and WSO [29]. Fine-tuning control parameters significantly influences metaheuristic algorithm performance [69]. Therefore, the standard versions of MATLAB codes published by the main researchers are used. In addition, for GA and PSO, the standard MATLAB codes published by Professor Mirjalili are used. The links to the MATLAB codes of the mentioned metaheuristic algorithms are provided in Appendix. Control parameter values for each algorithm are detailed in Table 1.

For optimization of objective functions F1 to F23, FLO and competitive algorithms are executed in 30 independent runs. Each run comprises 30,000 function evaluations (FEs) with a population size of 30. For the CEC 2017 test suite, FLO and competitive algorithms undergo 51 independent runs, with each run incorporating 10,000m FEs (where m denotes the number of variables) and a population size of 30. Simulation results are presented using six statistical indicators: mean, best, worst, standard deviation (std), median, and rank. Ranking of metaheuristic algorithms for each benchmark function is established through comparison of mean index values, providing comprehensive insights into their relative performance.

4.1 Unimodal Functions

The unimodal functions F1 to F7, which do not have local optima, provide a suitable benchmark for evaluating the exploitation and local search capabilities of metaheuristic algorithms. These functions are particularly useful because they allow researchers to assess how well an algorithm can focus on finding the global optimum without being distracted by false peaks. The performance of FLO and several competitive algorithms on these functions is detailed in Table 2. The results indicate that FLO excels in exploitation and local search, successfully converging to the global optimum for functions F1 through F6. When it comes to the F7 function, FLO stands out as the leading optimizer, demonstrating its effectiveness. An in-depth comparison of the simulation results reveals that FLO’s high exploitation ability enables it to perform better than the competitive algorithms on the unimodal functions F1 to F7. This superior performance highlights FLO’s capability in focusing its search process effectively, ensuring it finds the optimal solutions for these unimodal benchmark functions.

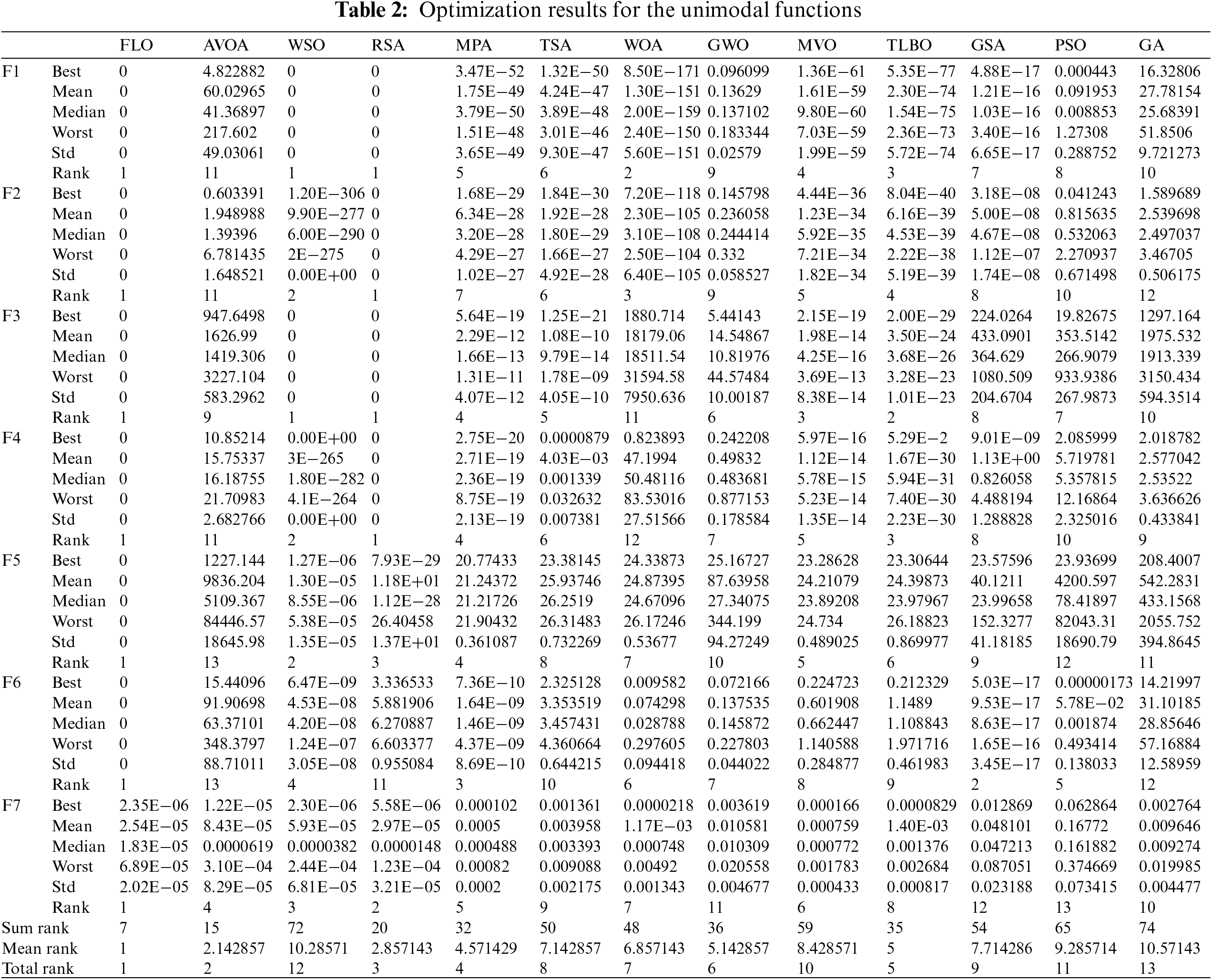
4.2 High-Dimensional Multimodal Functions

The high-dimensional multimodal functions F8 to F13, due to having multiple local optima, are suitable criteria for challenging the ability of the metaheuristic algorithms in exploration and global search. The optimization results for the functions F8 to F13 using FLO and the competitive algorithms are reported in Table 3. Based on the obtained results, FLO with its high ability in exploration has been able to provide a global optimum for these functions by discovering the main optimal region in dealing with the F9 and F11 functions. Also, in order to optimize the functions F8, F10, F12, and F13, FLO is the best optimizer for these functions. The analysis of the simulation results shows that FLO with high capability in exploration and global search in order to cross local optima and discover the main optimal area turned out to be superior in competition with the compared algorithms.

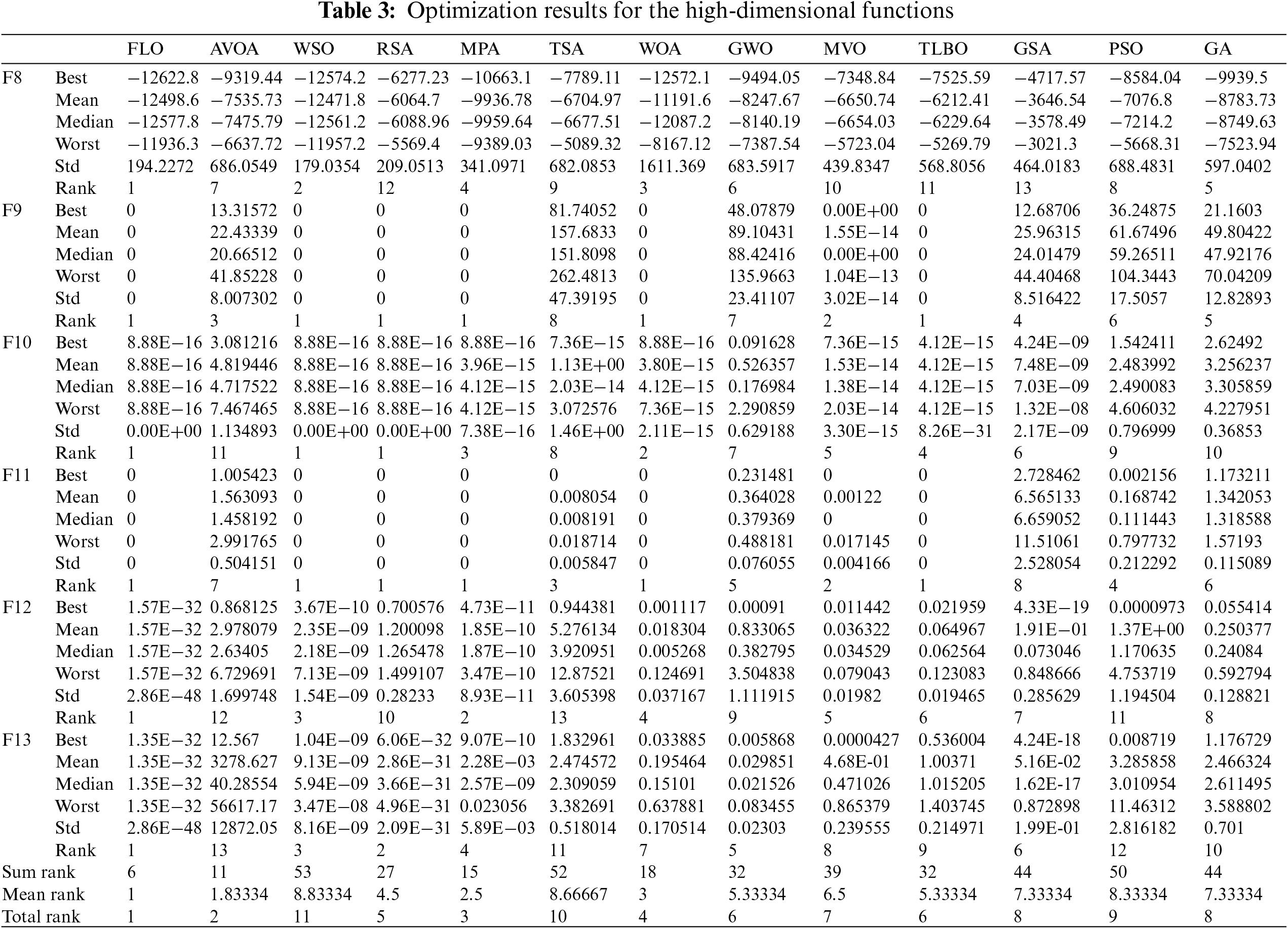
4.3 Results for Fixed-Dimensional Multimodal Functions

The fixed-dimension multimodal functions F14 to F23, having a smaller number of local optima compared to functions F8 to F13, are appropriate criteria for measuring the ability of the metaheuristic algorithms in balancing exploration and exploitation. The results of employing FLO and the competitive algorithms for the functions F14 to F23 are reported in Table 4. It turned out that FLO is the best optimizer for the functions F14 to F23. In the cases when FLO has the same value for the mean index as some competitive algorithms, it has provided a more effective performance by providing a better value for the std index. The simulation results show that FLO, with an appropriate ability to balance exploration and exploitation, has a better performance by providing superior results for the benchmark functions in comparison with the competitive algorithms.

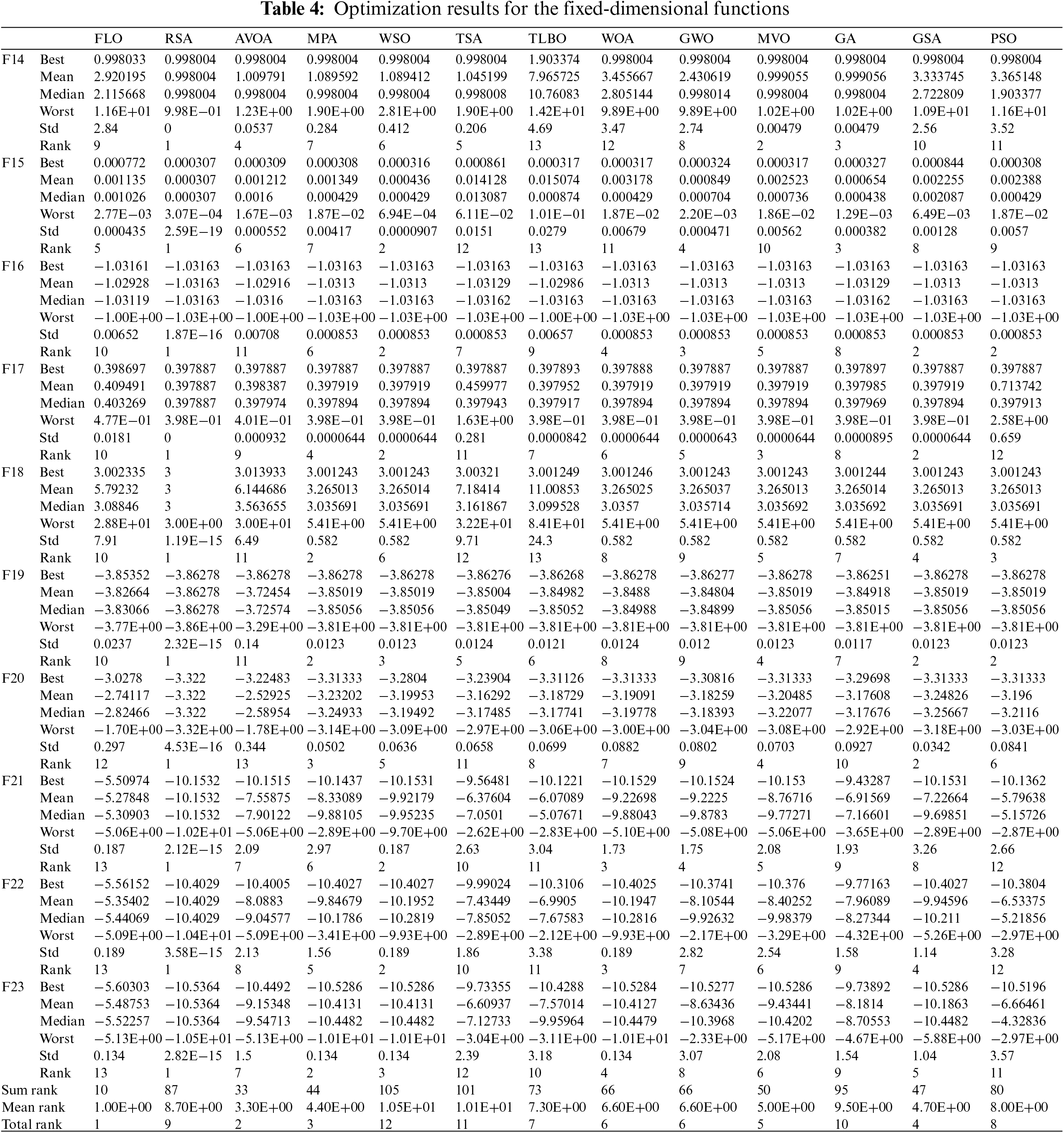
The convergence curves resulting from the execution of FLO and the competitive algorithms for the functions F1 to F23 are drawn in Fig. 3.

Figure 3: Convergence curves for FLO and the competitive algorithms on F1 to F23

4.4 CEC 2017 Test Suite

In this subsection, we conduct a comprehensive evaluation of the FLO algorithm’s efficiency in addressing the CEC 2017 test suite. The CEC 2017 test suite comprises thirty standard benchmark functions, which are divided into several categories: three unimodal functions (C17-F1 to C17-F3), seven multimodal functions (C17-F4 to C17-F10), ten hybrid functions (C17-F11 to C17-F20), and ten composite functions (C17-F21 to C17-F30). Due to instability in its behavior, the C17-F2 function was excluded from the simulation studies. For a full description and details of the CEC 2017 test suite, please refer to [68]. The results of optimizing the CEC 2017 test suite using FLO, in comparison with other competitive algorithms, are detailed in Table 5. Furthermore, the performance outcomes of these metaheuristic algorithms are visually represented through boxplot diagrams in Fig. 4. According to the obtained optimization results, FLO excels in several functions, specifically C17-F1, C17-F3 to C17-F21, C17-F23, C17-F24, and C17-F27 to C17-F30.

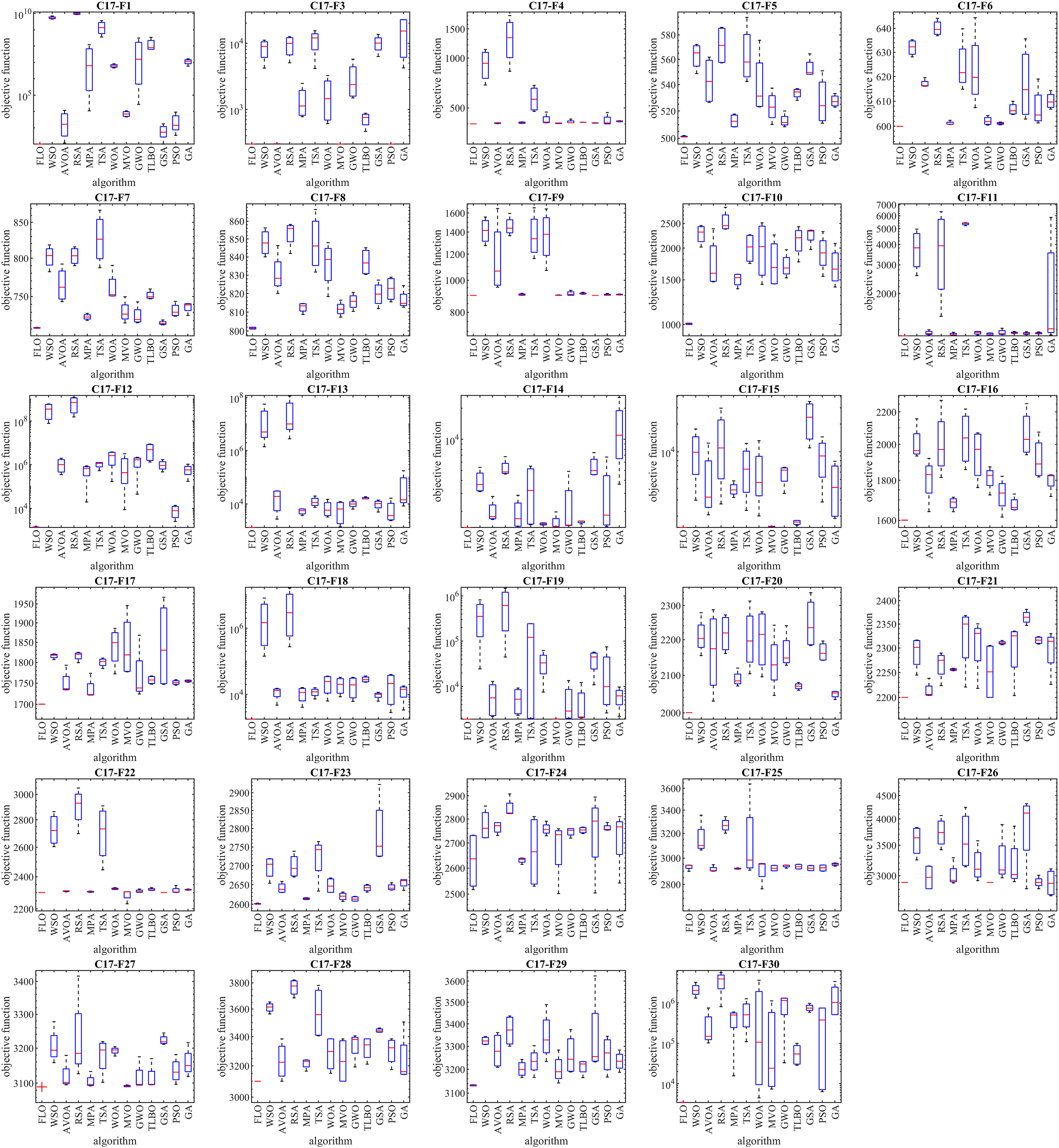
Figure 4: Boxplot diagrams of FLO and the performance of the competitive algorithms for the CEC 2017 test suite

These optimization outcomes indicate that FLO achieves favorable results for the benchmark functions, which can be attributed to its strong capabilities in both exploration and exploitation, as well as its effectiveness in balancing these two critical aspects throughout the search process. A comparative analysis of the simulation results clearly demonstrates that FLO outperforms the competitive algorithms for most of the benchmark functions. This establishes FLO as the premier optimizer overall, showcasing its superiority in handling the CEC 2017 test suite.

4.5 Statistical Analysis

A comprehensive statistical analysis has been undertaken to determine the significance of FLO’s superiority over competitive algorithms from a statistical perspective. To accomplish this, the non-parametric Wilcoxon rank sum test [70] has been employed, a widely recognized method for identifying substantial differences between the averages of two datasets. In the context of the Wilcoxon rank sum test, the primary aim is to assess whether there exists a noteworthy disparity in the performance of two algorithms, as indicated by the calculation of a key metric known as the p-value. The outcomes of conducting the Wilcoxon rank sum test on the performance of FLO compared to each of the competitive algorithms are meticulously presented in Table 6. These results play a pivotal role in elucidating the degree of FLO’s statistical advantage over alternative metaheuristic algorithms. Specifically, instances where the calculated p-value is below the threshold of 0.05 indicate a statistically significant advantage for FLO when pitted against its counterparts. In essence, the extensive statistical analysis underscores FLO’s significant statistical superiority across all benchmark functions examined in the study, reaffirming its efficacy as an optimization algorithm.

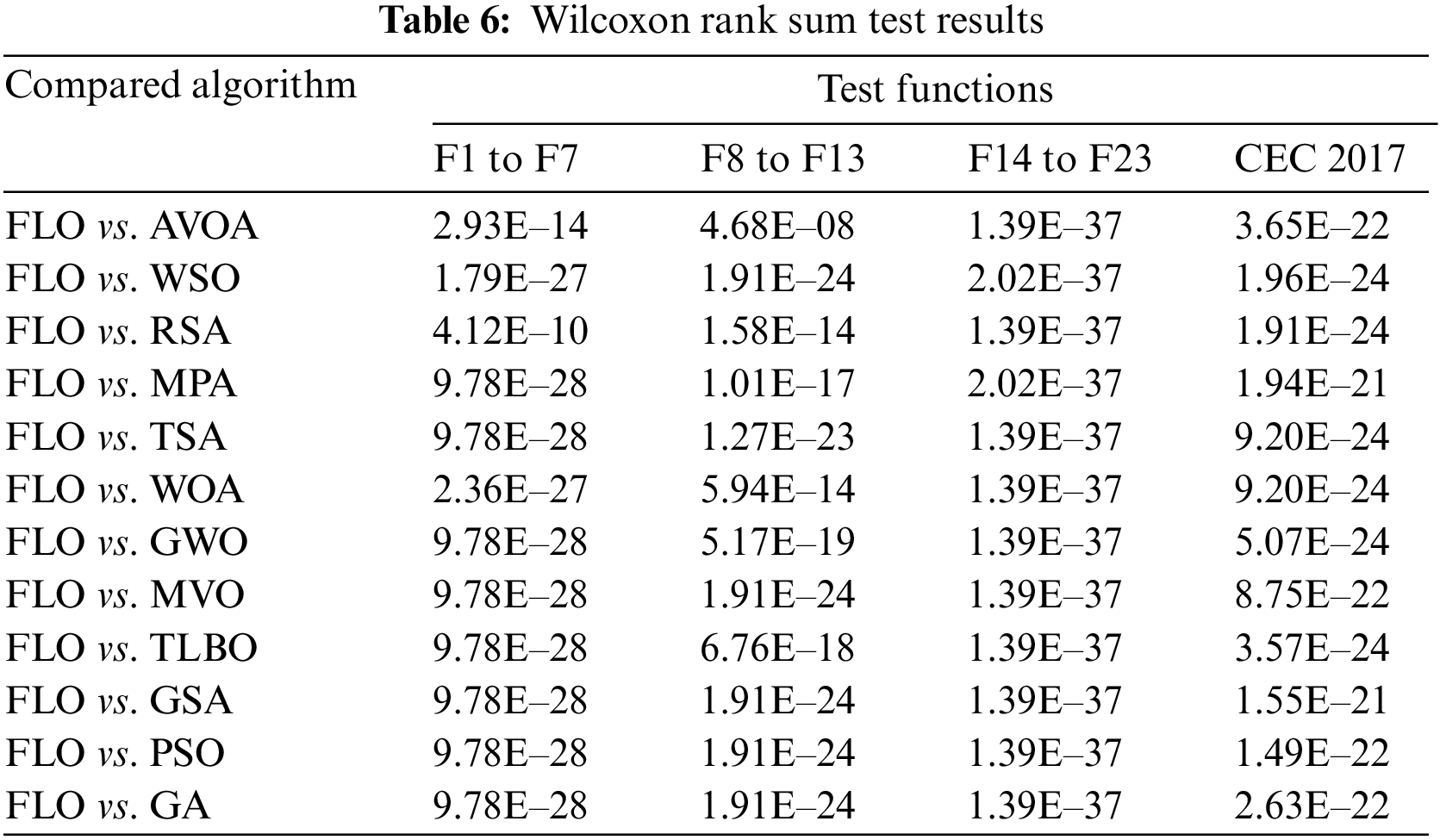
5  FLO for Real-World Engineering Applications

This segment delves into the exploration of FLO’s efficiency in tackling real-world optimization dilemmas. To assess its performance, we analyze its application across twenty-two constrained optimization problems sourced from the CEC 2011 test suite, in addition to evaluating its efficacy in solving four distinct engineering design problems.

5.1 Evaluation of the CEC 2011 Test Suite

In this subsection, we delve into evaluating the performance of FLO alongside competitive algorithms in addressing optimization tasks within real-world applications, focusing on the CEC 2011 test suite [71]. Comprising twenty-two constrained optimization problems, this test suite encompasses a diverse range of engineering challenges, making it a prime choice for assessing metaheuristic algorithms’ capabilities. Previous studies have often leveraged this suite due to its relevance in simulating real-world scenarios. To gauge FLO’s aptitude in handling such applications, we utilize the standard engineering problems from the CEC 2011 test suite. Employing a population size of 30, both FLO and competitive algorithms undergo rigorous testing across 25 independent runs, each spanning 150,000 function evaluations. The comprehensive results, as depicted in Table 7 and visually presented through boxplot diagrams in Fig. 5, offer insights into their comparative performances. Notably, FLO emerges as the top-performing algorithm across problems C11-F1 to C11-F22. Its superior performance is evident, outshining competitive algorithms in the majority of cases. Statistical analyses, including the p-values derived from the Wilcoxon rank sum test, further underscore FLO’s significant advantage over its counterparts in tackling the challenges posed by the CEC 2011 test suite.

Figure 5: Boxplot diagrams of FLO and the performance of the competitive algorithms for the CEC 2017 test suite

5.2 Pressure Vessel Design Problem

The optimization challenge of the pressure vessel design, illustrated schematically in Fig. 6, revolves around minimizing construction costs while meeting specified design requirements. This problem is encapsulated by a mathematical model outlined as follows [72]:

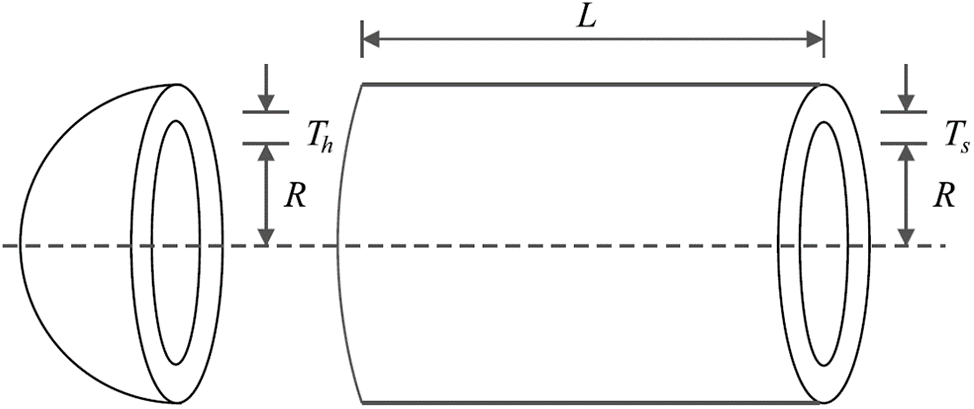
Figure 6: Schematic representation of the pressure vessel design

Consider: X=[x1,x2,x3,x4]=[Ts,Th,R,L].

Minimize: f(x)=0.6224x1x3x4+1.778x2x32+3.1661x12x4+19.84x12x3

subject to:

g1(x)=−x1+0.0193x3≤0,g2(x)=−x2+0.00954x3≤0,

g3(x)=−πx32x4−43πx33+1296000≤0,g4(x)=x4−240≤0,

with

0≤x1,x2≤100and10≤x3,x4≤200.

The optimization outcomes for pressure vessel design, utilizing FLO alongside competitive algorithms, are detailed in Tables 8 and 9. Additionally, the convergence trajectory of FLO, depicting its journey towards the solution across iterations, is illustrated in Fig. 7. Notably, FLO emerges triumphant, securing the optimal design with design variable values of (0.7780271, 0.3845792, 40.312284, 200) and an associated objective function value of 5882.9013. These results underscore FLO’s superior performance in pressure vessel design optimization, outshining competitive algorithms and delivering superior outcomes.

Figure 7: FLO’s performance convergence curve for the pressure vessel design

5.3 Speed Reducer Design Problem

The speed reducer design poses an optimization challenge, depicted schematically in Fig. 8, with the primary objective of minimizing the weight of the speed reducer. This mathematical model encapsulates the design as follows [73,74]:

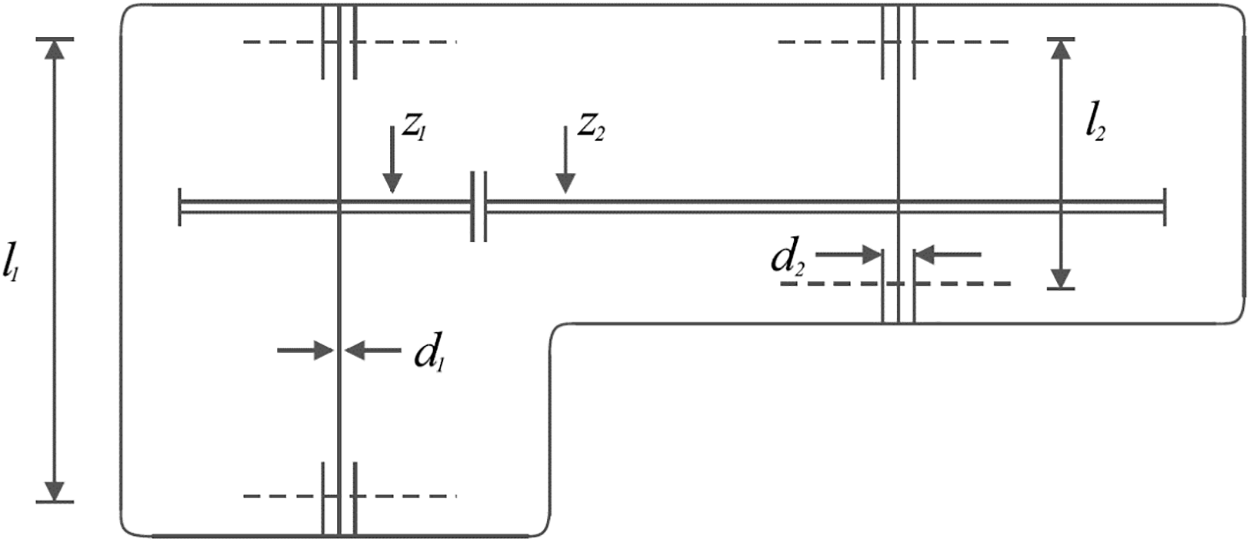
Figure 8: Schematic of the speed reducer design

Consider: X=[x1,x2,x3,x4,x5,x6,x7]=[b,m,p,l1,l2,d1,d2].

Minimize: f(x)=0.7854x1x22(3.3333x32+14.9334x3−43.0934)−1.508x1(x62+x72)+7.4777(x63+x73)+0.7854(x4x62+x5x72)

subject to:

g1(x)=27x1x22x3−1≤0,g2(x)=397.5x1x22x3−1≤0,

g3(x)=1.93x43x2x3x64−1≤0,g4(x)=1.93x53x2x3x74−1≤0,

g5(x)=1110x63(745x4x2x3)2+16.9×106−1≤0,

g6(x)=185x73(745x5x2x3)2+157.5×106−1≤0,

g7(x)=x2x340−1≤0,g8(x)=5x2x1−1≤0,

g9(x)=x112x2−1≤0,g10(x)=1.5x6+1.9x4−1≤0,

g11(x)=1.1x7+1.9x5−1≤0,

with

2.6≤x1≤3.6,0.7≤x2≤0.8,17≤x3≤28,7.3≤x4≤8.3,7.8≤x5≤8.3,2.9≤x6≤3.9, and 5≤x7≤5.5.

The outcomes of addressing the speed reducer design using FLO and the competitive algorithms are outlined in Tables 10 and 11. Additionally, the convergence trajectory of FLO is depicted in Fig. 9. Impressively, FLO achieves the best design, with the design variable values of (3.5, 0.7, 17, 7.3, 7.8, 3.3502147, 5.2866832) and an associated objective function value of 2996.3482. These results underscore FLO’s superior performance in speed reducer design optimization, surpassing competitive algorithms and delivering enhanced outcomes.

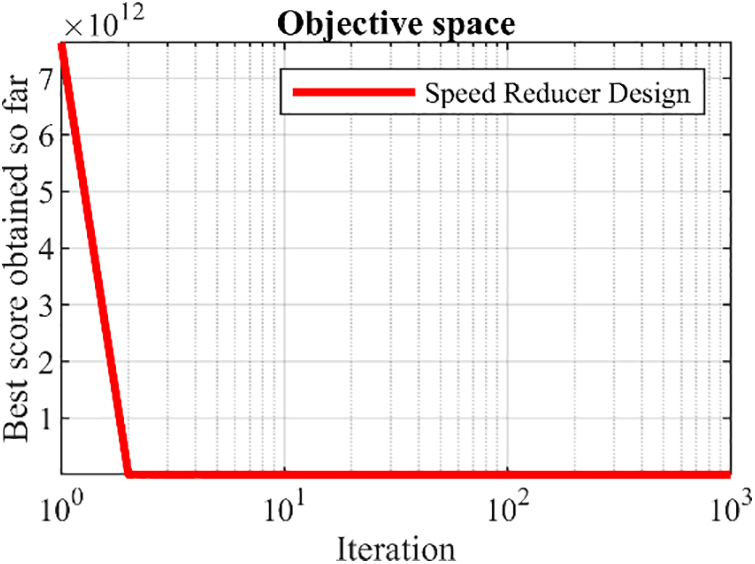
Figure 9: FLO’s performance convergence curve for the speed reducer design

5.4 Welded Beam Design

Welded beam design is an optimization problem of real-world applications with the schematic representation shown in Fig. 10, whose main design goal is the minimization of the fabrication cost of the welded beam. The mathematical model for this problem can be formulated as follows [36]:

Figure 10: Schematic of the welded beam design

Consider: X=[x1,x2,x3,x4]=[h,l,t,b].

Minimize: f(x)=1.10471x12x2+0.04811x3x4(14.0+x2)

subject to:

g1(x)=τ(x)−13600≤0,g2(x)=σ(x)−30000≤0,

g3(x)=x1−x4≤0,g4(x)=0.10471x12+0.04811x3x4(14+x2)−5.0≤0,

g5(x)=0.125−x1≤0,g6(x)=δ(x)−0.25≤0,

g7(x)=6000−pc(x)≤0,

where

τ(x)=(τ′)2+(2ττ′)x22R+(τ′′)2,τ′=60002x1x2,τ′′=MRJ,

M=6000(14+x22),R=x224+(x1+x32)2,

J=2{x1x22[x2212+(x1+x32)2]},σ(x)=504000x4x32,

δ(x)=65856000(30⋅106)x4x33,pc(x)=4.013(30⋅106)x32x4636196(1−x32830⋅1064(12⋅106)),

with

0.1≤x1,x4≤2 and 0.1≤x2,x3≤10.

The results comparing FLO with competitive algorithms for the welded beam design are summarized in Tables 12 and 13. Additionally, Fig. 11 illustrates the convergence curve of FLO towards the solution. Remarkably, FLO identifies the best design with the design variable values of (0.2057296, 3.4704887, 9.0366239, 0.2057296) and achieves an objective function value of 1.7246798. These findings underscore FLO’s superior performance in tackling the welded beam design optimization problem, showcasing its efficacy over competitive algorithms.

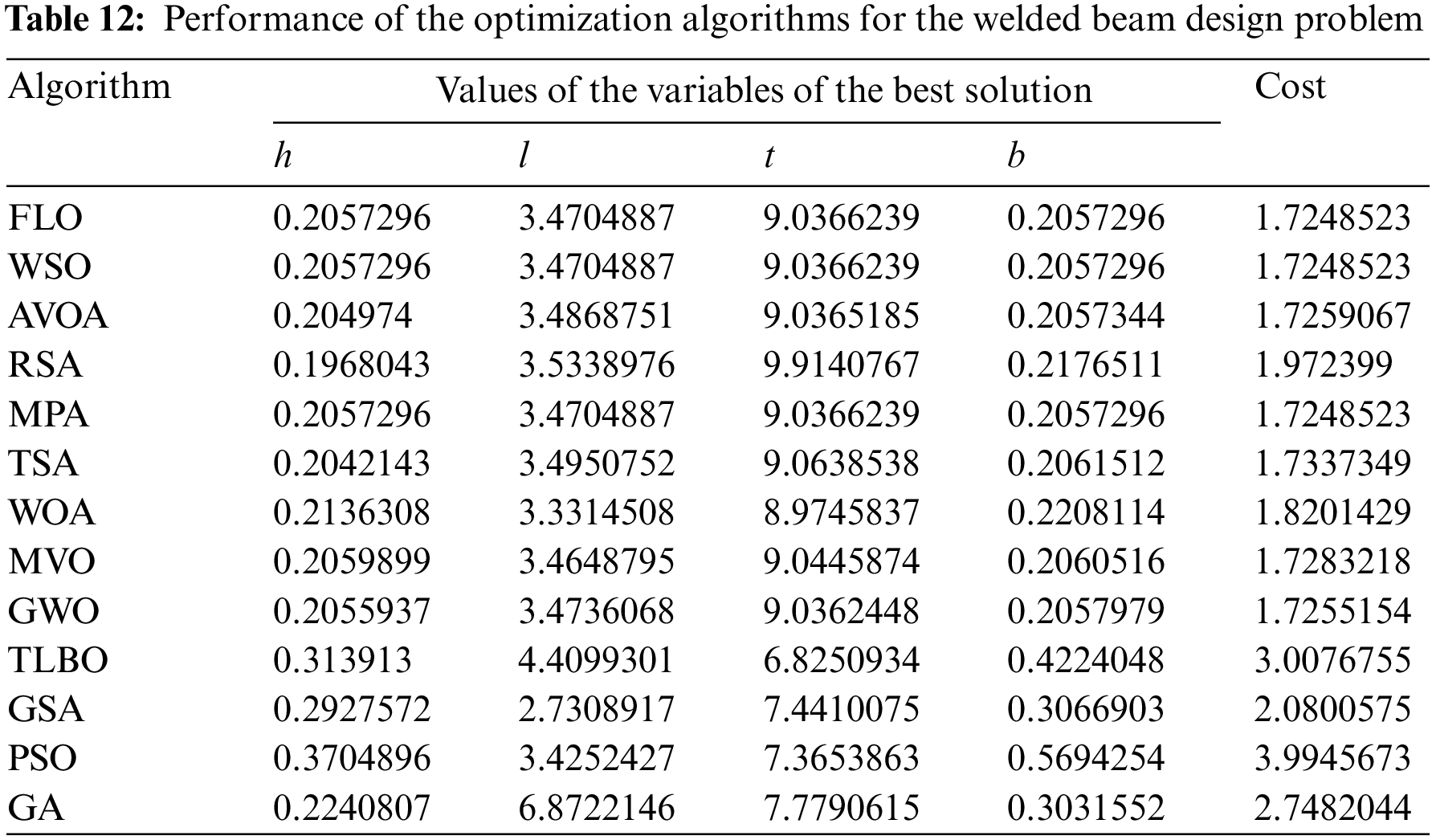
Figure 11: FLO’s performance convergence curve for the welded beam design

5.5 Tension/Compression Spring Design

The optimization task of tension/compression spring design stems from practical applications, featuring a schematic representation in Fig. 12. The primary design objective revolves around minimizing the weight of the tension/compression spring. Formulating this design challenge involves crafting a mathematical model as follows [36]:

Figure 12: FLO’s performance convergence curve for the welded beam design tension/compression spring design

Consider: X=[x1,x2,x3]=[d,D,P].

Minimize: f(x)=(x3+2)x2x12

subject to:

g1(x)=1−x23x371785x14≤0,g2(x)=4x22−x1x212566(x2x13)+15108x12−1≤0,

g3(x)=1−140.45x1x22x3≤0, g4(x)=x1+x21.5−1≤0

with

0.05≤x1≤2,0.25≤x2≤1.3and2≤x3≤15.

The outcomes of employing FLO alongside competitive algorithms for optimizing the tension/compression spring design are showcased in Tables 14 and 15. Additionally, Fig. 13 illustrates the convergence trajectory of FLO towards the solution. Notably, FLO achieves the optimal design with design variable values of (0.051689105, 0.356717704, 11.2889661) and an associated objective function value of 0.01260189. These findings unequivocally demonstrate FLO’s superior performance over competitive algorithms in addressing the tension/compression spring design problem.

Figure 13: FLO’s performance convergence curve for the welded beam design tension/compression spring design

6  Conclusions and Future Works

This paper introduces Frilled Lizard Optimization (FLO), a novel bio-metaheuristic algorithm inspired by the natural behaviors of frilled lizards. Drawing upon observations of these creatures in the wild, FLO is designed to emulate two key behaviors: the sit-and-wait hunting strategy and the post-feeding retreat behavior. The algorithm is intricately divided into two distinct phases, each aimed at replicating a specific aspect of the lizard’s behavior: exploration and exploitation. Through meticulous mathematical modeling, FLO seeks to capture the essence of these behaviors and apply them in the context of optimization problems. To assess its effectiveness, FLO undergoes rigorous testing on fifty-two standard benchmark functions, spanning a range of complexities and characteristics. The results of these evaluations reveal FLO’s remarkable aptitude in exploration, exploitation, and the delicate balance between these two aspects crucial in problem-solving environments. In comparative analyses against twelve well-established algorithms, FLO consistently emerges as the top-performing optimizer, showcasing its robustness and efficacy across various functions and problem domains. Furthermore, FLO’s capabilities extend beyond theoretical assessments, as it demonstrates remarkable performance when applied to practical scenarios. Testing on twenty-two constrained optimization problems sourced from the CEC 2011 test suite, as well as four engineering design challenges, underscores its versatility and applicability in real-world settings. Notably, FLO outperforms competitive algorithms in handling these challenges, highlighting its potential to address complex optimization tasks in diverse fields.

Despite its strengths, it is important to acknowledge the inherent limitations of FLO, common to many metaheuristic algorithms. The stochastic nature of these algorithms means that there is no guarantee of achieving the global optimum, and the No Free Lunch (NFL) theorem cautions against claims of universal superiority. Additionally, as with any evolving field, there is always the possibility of newer, more advanced algorithms being developed in the future.

Looking ahead, the introduction of FLO presents exciting opportunities for further research and exploration. Future endeavors may include the development of binary and multi-objective variants of the algorithm, as well as its application to a wider array of optimization problems across different disciplines. By continuing to refine and expand upon the principles underlying FLO, researchers can unlock new avenues for innovation and problem-solving in the realm of optimization.

Acknowledgement: The authors are grateful to editor and reviewers for their valuable comments.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: M.D., I.A.F., O.A.B., S.A., G.B., S.G.; data collection: F.W., G.B., O.P.M., S.G., I.L., S.A., O.A.B.; analysis and interpretation of results: O.A.B., I.A.F., F.W., O.P.M., S.A.; draft manuscript preparation: I.A.F., F.W., G.B., S.G., M,D., I.L. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. S. M. El-kenawy, N. Khodadadi, S. Mirjalili, A. A. Abdelhamid, M. M. Eid and A. Ibrahim, “Greylag goose optimization: Nature-inspired optimization algorithm,” Expert. Syst. Appl., vol. 238, no. 22, pp. 122–147, Mar. 2024. doi: 10.1016/j.eswa.2023.122147. [Google Scholar] [CrossRef]

2. N. Singh, X. Cao, S. Diggavi, and T. Başar, “Decentralized multi-task stochastic optimization with compressed communications,” Automatica, vol. 159, no. 3, pp. 111–363, Jan. 2024. doi: 10.1016/j.automatica.2023.111363. [Google Scholar] [CrossRef]

3. D. A. Liñán, G. Contreras-Zarazúa, E. Sánchez-Ramírez, J. G. Segovia-Hernández, and L. A. Ricardez-Sandoval, “A hybrid deterministic-stochastic algorithm for the optimal design of process flowsheets with ordered discrete decisions,” Comput. Chem. Eng., vol. 180, pp. 1085-01, Mar. 2024. [Google Scholar]

4. W. G. Alshanti, I. M. Batiha, M. M. A. Hammad, and R. Khalil, “A novel analytical approach for solving partial differential equations via a tensor product theory of Banach spaces.,” Partial Differ. Equ. Appl. Math., vol. 8, pp. 100531, Dec. 2023. [Google Scholar]

5. M. Dehghani, E. Trojovská, and P. Trojovský, “A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process,” Sci. Rep., vol. 12, no. 1, pp. 9924, Jun. 2022. doi: 10.1038/s41598-022-14225-7. [Google Scholar] [PubMed] [CrossRef]

6. Z. Montazeri, T. Niknam, J. Aghaei, O. P. Malik, M. Dehghani and G. Dhiman, “Golf optimization algorithm: A new game-based metaheuristic algorithm and its application to energy commitment problem considering resilience,” Biomimetics, vol. 8, no. 5, pp. 386, Sep. 2023. doi: 10.3390/biomimetics8050386. [Google Scholar] [PubMed] [CrossRef]

7. J. de Armas, E. Lalla-Ruiz, S. L. Tilahun, and S. Voß, “Similarity in metaheuristics: A gentle step towards a comparison methodology,” Nat. Comput., vol. 21, no. 2, pp. 265–287, Feb. 2022. doi: 10.1007/s11047-020-09837-9. [Google Scholar] [CrossRef]

8. M. Dehghani et al., “A spring search algorithm applied to engineering optimization problems,” Appl. Sci., vol. 10, no. 18, pp. 6173, Sep. 2020. doi: 10.3390/app10186173. [Google Scholar] [CrossRef]

9. I. Matoušová, P. Trojovský, M. Dehghani, E. Trojovská, and J. Kostra, “Mother optimization algorithm: A new human-based metaheuristic approach for solving engineering optimization,” Sci. Rep., vol. 13, no. 1, pp. 10312, Jun. 26, 2023. doi: 10.1038/s41598-023-37537-8. [Google Scholar] [PubMed] [CrossRef]

10. E. Trojovská, M. Dehghani, and P. Trojovský, “Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm,” IEEE Access, vol. 10, pp. 49445–49473, Nov. 2022. doi: 10.1109/ACCESS.2022.3172789. [Google Scholar] [CrossRef]

11. X. Sun, H. He, and L. Ma, “Harmony search meta-heuristic algorithm based on the optimal sizing of wind-battery hybrid micro-grid power system with different battery technologies,” J. Energy Storage, vol. 75, no. 14, pp. 109582, Jan. 2024. doi: 10.1016/j.est.2023.109582. [Google Scholar] [CrossRef]

12. S. S. Aljehani and Y. A. Alotaibi, “Preserving privacy in association rule mining using metaheuristic-based algorithms: A systematic literature review,” IEEE Access, vol. 12, no. 4, pp. 21217–21236, Feb. 2024. doi: 10.1109/ACCESS.2024.3362907. [Google Scholar] [CrossRef]

13. B. Saemi and F. Goodarzian, “Energy-efficient routing protocol for underwater wireless sensor networks using a hybrid metaheuristic algorithm,” Eng Appl. Artif. Intell., vol. 133, no. 1, pp. 108132, Jan. 2024. doi: 10.1016/j.engappai.2024.108132. [Google Scholar] [CrossRef]

14. M. Maashi et al., “Elevating survivability in Next-Gen IoT-Fog-Cloud networks: scheduling optimization with the metaheuristic mountain gazelle algorithm,” IEEE Trans. Consum. Electron., vol. 70, no. 1, pp. 3802–3809, Feb. 2024. doi: 10.1109/TCE.2024.3371774. [Google Scholar] [CrossRef]

15. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Trans. Evol. Comput., vol. 1, no. 1, pp. 67–82, Apr. 1997. doi: 10.1109/4235.585893. [Google Scholar] [CrossRef]

16. N. Kumar, N. Singh, and D. P. Vidyarthi, “Artificial lizard search optimization (ALSOA novel nature-inspired meta-heuristic algorithm,” Soft Comput., vol. 25, no. 8, pp. 6179–6201, Apr. 2021. doi: 10.1007/s00500-021-05606-7. [Google Scholar] [CrossRef]

17. O. Maciel C., E. Cuevas, M. A. Navarro, D. Zaldívar and S. Hinojosa, “Side-blotched lizard algorithm: A polymorphic population approach,” Appl. Soft Comput., vol. 88, no. 80, pp. 106039, Mar. 2020. doi: 10.1016/j.asoc.2019.106039. [Google Scholar] [CrossRef]

18. H. Peraza-Vázquez, A. Peña-Delgado, M. Merino-Treviño, A. B. Morales-Cepeda, and N. Sinha, “A novel metaheuristic inspired by horned lizard defense tactics,” Artif. Intell. Rev., vol. 57, no. 3, pp. 59, Feb. 2024. doi: 10.1007/s10462-023-10653-7. [Google Scholar] [CrossRef]

19. S. A. Omari et al., “Dollmaker optimization algorithm: A novel human-inspired optimizer for solving optimization problems,” Int. J. Intell. Eng. Syst., vol. 17, no. 3, pp. 816–828, Jan. 2024. [Google Scholar]

20. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. ICNN’95-Int. Conf. Neural Networks, IEEE, 1995, pp. 1942–1948. [Google Scholar]

21. M. Dorigo, V. Maniezzo, and A. Colorni, “Ant system: Optimization by a colony of cooperating agents,” IEEE Trans. Syst., Man, Cybern. Part B Cybern., vol. 26, no. 1, pp. 29–41, Jan. 1996. doi: 10.1109/3477.484436. [Google Scholar] [PubMed] [CrossRef]

22. D. Karaboga and B. Basturk, “Artificial bee colony (ABC) optimization algorithm for solving constrained optimization problems,” in Proc. IFSA World Congress, Berlin, Heidelberg, Springer Berlin, Heidelberg, Jun. 2007, pp. 789–798. [Google Scholar]

23. X. S. Yang, “Firefly algorithm, stochastic test functions and design optimisation,” Int. J. Bio-Inspired Comput., vol. 2, no. 2, pp. 78–84, Jan. 2010. doi: 10.1504/IJBIC.2010.032124. [Google Scholar] [CrossRef]

24. B. Abdollahzadeh, F. S. Gharehchopogh, and S. Mirjalili, “African vultures optimization algorithm: A new nature-inspired metaheuristic algorithm for global optimization problems,” Comput. Ind. Eng., vol. 158, no. 4, pp. 107408, Aug. 2021. doi: 10.1016/j.cie.2021.107408. [Google Scholar] [CrossRef]

25. A. Faramarzi, M. Heidarinejad, S. Mirjalili, and A. H. Gandomi, “Marine predators algorithm: A nature-inspired metaheuristic,” Expert Syst. Appl., vol. 152, pp. 113377, Aug. 2020. [Google Scholar]

26. M. Ahmed, M. H. Sulaiman, A. J. Mohamad, and M. Rahman, “Gooseneck barnacle optimization algorithm: A novel nature inspired optimization theory and application,” Math. Comput. Simul., vol. 218, no. 1, pp. 248–265, Apr. 2024. doi: 10.1016/j.matcom.2023.10.006. [Google Scholar] [CrossRef]

27. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, Mar. 2014. [Google Scholar]

28. W. Zhao et al., “Electric eel foraging optimization: A new bio-inspired optimizer for engineering applications,” Expert. Syst. Appl., vol. 238, no. 1, pp. 122200, Mar. 2024. doi: 10.1016/j.eswa.2023.122200. [Google Scholar] [CrossRef]

29. M. Braik, A. Hammouri, J. Atwan, M. A. Al-Betar, and M. A. Awadallah, “White shark optimizer: A novel bio-inspired meta-heuristic algorithm for global optimization problems,” Knowl.-Based Syst., vol. 243, no. 7, pp. 108457, May, 2022. doi: 10.1016/j.knosys.2022.108457. [Google Scholar] [CrossRef]

30. M. Abdel-Basset, R. Mohamed, and M. Abouhawwash, “Crested porcupine optimizer: A new nature-inspired metaheuristic,” Knowl.-Based Syst., vol. 284, no. 1, pp. 111257, Jan. 2024. doi: 10.1016/j.knosys.2023.111257. [Google Scholar] [CrossRef]

31. S. Kaur, L. K. Awasthi, A. L. Sangal, and G. Dhiman, “Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization,” Eng. Appl. Artif. Intell., vol. 90, no. 2, pp. 103541, Apr. 2020. doi: 10.1016/j.engappai.2020.103541. [Google Scholar] [CrossRef]

32. Y. Jiang, Q. Wu, S. Zhu, and L. Zhang, “Orca predation algorithm: A novel bio-inspired algorithm for global optimization problems,” Expert. Syst. Appl., vol. 188, no. 4, pp. 116026, Feb. 2022. doi: 10.1016/j.eswa.2021.116026. [Google Scholar] [CrossRef]

33. F. A. Hashim, E. H. Houssein, K. Hussain, M. S. Mabrouk, and W. Al-Atabany, “Honey badger algorithm: New metaheuristic algorithm for solving optimization problems,” Math. Comput. Simul., vol. 192, no. 2, pp. 84–110, Feb. 2022. doi: 10.1016/j.matcom.2021.08.013. [Google Scholar] [CrossRef]

34. L. Abualigah, M. Abd Elaziz, P. Sumari, Z. W. Geem, and A. H. Gandomi, “Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer,” Expert Syst. Appl., vol. 191, pp. 116158, Apr. 2022. [Google Scholar]

35. N. Chopra and M. M. Ansari, “Golden jackal optimization: A novel nature-inspired optimizer for engineering applications,” Expert Syst. Appl., vol. 198, pp. 116924, Jul. 15, 2022. [Google Scholar]

36. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 12, pp. 51–67, May, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

37. D. E. Goldberg and J. H. Holland, “Genetic algorithms and machine learning,” Mach. Learn., vol. 3, no. 2, pp. 95–99, Oct. 1988. doi: 10.1023/A:1022602019183. [Google Scholar] [CrossRef]

38. R. Storn and K. Price, “Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces,” J. Global Optim., vol. 11, no. 4, pp. 341–359, Dec. 1997. doi: 10.1023/A:1008202821328. [Google Scholar] [CrossRef]

39. L. N. De Castro and J. I. Timmis, “Artificial immune systems as a novel soft computing paradigm,” Soft Comput., vol. 7, no. 8, pp. 526–544, Aug. 2003. doi: 10.1007/s00500-002-0237-z. [Google Scholar] [CrossRef]

40. J. R. Koza, “Genetic programming as a means for programming computers by natural selection,” Stat. Comput., vol. 4, no. 2, pp. 87–112, Jun. 1994. doi: 10.1007/BF00175355. [Google Scholar] [CrossRef]

41. R. G. Reynolds, “An introduction to cultural algorithms,” in Proc. Third Annu. Conf. Evol. Program., River Edge, World Scientific, Feb. 24, 1994, pp. 131–139. [Google Scholar]

42. H. G. Beyer and H. P. Schwefel, “Evolution strategies-a comprehensive introduction,” Nat. Comput., vol. 1, no. 1, pp. 3–52, Mar. 2002. doi: 10.1023/A:1015059928466. [Google Scholar] [CrossRef]

43. S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, May, 1983. doi: 10.1126/science.220.4598.671. [Google Scholar] [PubMed] [CrossRef]

44. E. Rashedi, H. Nezamabadi-Pour, and S. Saryazdi, “GSA: a gravitational search algorithm,” Inf. Sci., vol. 179, no. 13, pp. 2232–2248, Jun. 2009. [Google Scholar]

45. S. Mirjalili, S. M. Mirjalili, and A. Hatamlou, “Multi-verse optimizer: A nature-inspired algorithm for global optimization,” Neural Comput. Appl., vol. 27, no. 2, pp. 495–513, 2016. [Google Scholar]

46. A. Hatamlou, “Black hole: A new heuristic optimization approach for data clustering,” Inf. Sci., vol. 222, pp. 175–184, 2013. doi: 10.1016/j.ins.2012.08.023. [Google Scholar] [CrossRef]

47. A. Kaveh and A. Dadras, “A novel meta-heuristic optimization algorithm: Thermal exchange optimization,” Adv. Eng. Softw., vol. 110, no. 4598, pp. 69–84, Aug. 2017. doi: 10.1016/j.advengsoft.2017.03.014. [Google Scholar] [CrossRef]

48. R. Kundu, S. Chattopadhyay, S. Nag, M. A. Navarro, and D. Oliva, “Prism refraction search: A novel physics-based metaheuristic algorithm,” J. Supercomput., vol. 80, no. 8, pp. 10746–10795, Jan. 2024. doi: 10.1007/s11227-023-05790-3. [Google Scholar] [CrossRef]

49. A. Faramarzi, M. Heidarinejad, B. Stephens, and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowl.-Based Syst., vol. 191, pp. 105190, Mar. 2020. doi: 10.1016/j.knosys.2019.105190. [Google Scholar] [CrossRef]

50. F. A. Hashim, K. Hussain, E. H. Houssein, M. S. Mabrouk, and W. Al-Atabany, “Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems,” Appl. Intell., vol. 51, no. 3, pp. 1531–1551, Mar. 2021. doi: 10.1007/s10489-020-01893-z. [Google Scholar] [CrossRef]

51. J. L. J. Pereira, M. B. Francisco, C. A. Diniz, G. A. Oliver, S. S. Cunha Jr and G. F. Gomes, “Lichtenberg algorithm: A novel hybrid physics-based meta-heuristic for global optimization,” Expert. Syst. Appl., vol. 170, no. 11, pp. 114522, May 2021. doi: 10.1016/j.eswa.2020.114522. [Google Scholar] [CrossRef]

52. H. Eskandar, A. Sadollah, A. Bahreininejad, and M. Hamdi, “Water cycle algorithm–A novel metaheuristic optimization method for solving constrained engineering optimization problems,” Comput. Struct., vol. 110, pp. 151–166, Nov. 2012. [Google Scholar]

53. F. A. Hashim, E. H. Houssein, M. S. Mabrouk, W. Al-Atabany, and S. Mirjalili, “Henry gas solubility optimization: A novel physics-based algorithm,” Future Gener. Comput. Syst., vol. 101, no. 4, pp. 646–667, Dec. 2019. doi: 10.1016/j.future.2019.07.015. [Google Scholar] [CrossRef]

54. R. V. Rao, V. J. Savsani, and D. Vakharia, “Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems,” Comput.-Aided Des., vol. 43, no. 3, pp. 303–315, Mar. 2011. doi: 10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]

55. T. S. L. V. Ayyarao et al., “War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization,” IEEE Access, vol. 10, no. 4, pp. 25073–25105, Feb. 2022. doi: 10.1109/ACCESS.2022.3153493. [Google Scholar] [CrossRef]

56. S. H. S. Moosavi and V. K. Bardsiri, “Poor and rich optimization algorithm: A new human-based and multi populations algorithm,” Eng. Appl. Artif. Intell., vol. 86, no. 12, pp. 165–181, Nov. 2019. doi: 10.1016/j.engappai.2019.08.025. [Google Scholar] [CrossRef]

57. M. A. Al-Betar et al., “Coronavirus herd immunity optimizer (CHIO),” Neural Comput. Appl., vol. 33, no. 10, pp. 5011–5042, May, 2021. [Google Scholar]

58. A. W. Mohamed, A. A. Hadi, and A. K. Mohamed, “Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm,” Int. J. Mach. Learn. Cyber., vol. 11, no. 7, pp. 1501–1529, Jul. 2020. doi: 10.1007/s13042-019-01053-x. [Google Scholar] [CrossRef]

59. M. Braik, M. H. Ryalat, and H. Al-Zoubi, “A novel meta-heuristic algorithm for solving numerical optimization problems: Ali Baba and the forty thieves,” Neural Comput. Appl., vol. 34, no. 1, pp. 409–455, Jan. 2022. doi: 10.1007/s00521-021-06392-x. [Google Scholar] [CrossRef]

60. R. Shine and R. Lambeck, “Ecology of frillneck lizards, Chlamydosaurus kingii (Agamidaein tropical Australia,” Wildl. Res., vol. 16, no. 5, pp. 491–500, 1989. doi: 10.1071/WR9890491. [Google Scholar] [CrossRef]

61. M. Pepper et al., “Phylogeographic structure across one of the largest intact tropical savannahs: Molecular and morphological analysis of Australia’s iconic frilled lizard Chlamydosaurus kingii,” Mol. Phylogenet. Evol., vol. 106, no. 2, pp. 217–227, Jan. 2017. doi: 10.1016/j.ympev.2016.09.002. [Google Scholar] [PubMed] [CrossRef]

62. C. A. Perez-Martinez, J. L. Riley, and M. J. Whiting, “Uncovering the function of an enigmatic display: Antipredator behaviour in the iconic Australian frillneck lizard,” Biol J. Linn. Soc., vol. 129, no. 2, pp. 425–438, Jan. 2020. doi: 10.1093/biolinnean/blz176. [Google Scholar] [CrossRef]

63. P. B. Frappell and J. P. Mortola, “Passive body movement and gas exchange in the frilled lizard (Chlamydosaurus kingii) and goanna (Varanus gouldii),” J. Exp. Biol., vol. 201, no. 15, pp. 2307–2311, Aug. 1998. doi: 10.1242/jeb.201.15.2307. [Google Scholar] [PubMed] [CrossRef]

64. G. Thompson and P. Withers, “Shape of western Australian dragon lizards (Agamidae),” Amphib. Reptilia, vol. 26, no. 1, pp. 73–85, Jan. 2005. doi: 10.1163/1568538053693369. [Google Scholar] [CrossRef]

65. K. Christian, G. Bedford, and A. Griffiths, “Frillneck lizard morphology: Comparisons between sexes and sites,” J. Herpetol., vol. 29, no. 4, pp. 576–583, Dec. 1995. doi: 10.2307/1564741. [Google Scholar] [CrossRef]

66. A. D. Griffiths and K. A. Christian, “Diet and habitat use of frillneck lizards in a seasonal tropical environment,” Oecologia, vol. 106, pp. 39–48, Apr. 1996. [Google Scholar] [PubMed]

67. X. Yao, Y. Liu, and G. Lin, “Evolutionary programming made faster,” IEEE Trans. Evol. Comput., vol. 3, no. 2, pp. 82–102, Jul. 1999. [Google Scholar]

68. N. H. Awad, M. Z. Ali, J. J. Liang, B. Y. Qu, and P. N. Suganthan, “Problem definitions and evaluation criteria for the cec 2017 special session and competition on single objective bound constrained real-parameter numerical optimization,” in Technical Report. Singapore: Nanyang Technological University, Nov. 2016. [Google Scholar]

69. H. A. Alsattar, A. Zaidan, and B. Zaidan, “Novel meta-heuristic bald eagle search optimisation algorithm,” Artif. Intell. Rev., vol. 53, no. 3, pp. 2237–2264, Mar. 2020. doi: 10.1007/s10462-019-09732-5. [Google Scholar] [CrossRef]

70. F. Wilcoxon, “Individual comparisons by ranking methods,” in Breakthroughs in Statistics. Springer, 1992, pp. 196–202. [Google Scholar]

71. S. Das and P. N. Suganthan, Problem Definitions and Evaluation Criteria for CEC, 2011 Competition on Testing Evolutionary Algorithms on Real World Optimization Problems. Kolkata: Jadavpur University, Nanyang Technological University, pp. 341–359, Dec. 2010. [Google Scholar]

72. B. Kannan and S. N. Kramer, “An augmented lagrange multiplier based method for mixed integer discrete continuous optimization and its applications to mechanical design,” J. Mech. Des., vol. 116, no. 2, pp. 405–411, Mar, 1994. doi: 10.1115/1.2919393. [Google Scholar] [CrossRef]

73. A. H. Gandomi and X. S. Yang, “Benchmark problems in structural optimization,” in Computational Optimization, Methods and Algorithms, Berlin, Heidelberg, Springer, 2011, vol. 356, pp. 259–281. doi: 10.1007/978-3-642-20859-1_12. [Google Scholar] [CrossRef]

74. E. Mezura-Montes and C. A. C. Coello, “Useful infeasible solutions in engineering optimization with evolutionary algorithms,” in Mexican Int. Conf. on Artif. Intell., Berlin, Heidelberg, Springer Berlin Heidelberg, Nov. 14, 2005, pp. 652–662. [Google Scholar]

Appendix MATLAB Codes of the Competitive Algorithms

The MATLAB codes of the competitive algorithms used in simulation and comparison studies are available as follows:

1- White Shark Optimizer (WSO): by Malik Braik

https://www.mathworks.com/matlabcentral/fileexchange/107365-white-shark-optimizer-wso?s_tid=srchtitle

2- African Vultures Optimization Algorithm (AVOA): by Benyamin Abdollahzadeh

https://www.mathworks.com/matlabcentral/fileexchange/94820-african-vultures-optimization-algorithm

3- Reptile Search Algorithm (RSA): by Laith Abualigah

https://www.mathworks.com/matlabcentral/fileexchange/101385-reptile-search-algorithm-rsa-a-nature-inspired-optimizer?s_tid=srchtitle

4- Tunicate Swarm Algorithm (TSA): by Gaurav Dhiman

https://www.mathworks.com/matlabcentral/fileexchange/75182-tunicate-swarm-algorithm-tsa?s_tid=srchtitle

5- Marine Predator Algorithm (MPA): by Afshin Faramarzi

https://www.mathworks.com/matlabcentral/fileexchange/74578-marine-predators-algorithm-mpa?s_tid=srchtitle

6- Whale Optimization Algorithm (WOA): by Seyedali Mirjalili

https://www.mathworks.com/matlabcentral/fileexchange/55667-the-whale-optimization-algorithm?s_tid=srchtitle

7- Grey Wolf Optimizer (GWO): by Seyedali Mirjalili

https://www.mathworks.com/matlabcentral/fileexchange/44974-grey-wolf-optimizer-gwo?s_tid=srchtitle

8- Multi-Verse Optimizer (MVO): by Seyedali Mirjalili

https://www.mathworks.com/matlabcentral/fileexchange/50113-multi-verse-optimizer-toolbox?s_tid=srchtitle

9- Teaching-Learning Based Optimization (TLBO): by SKS Labs

https://www.mathworks.com/matlabcentral/fileexchange/65628-teaching-learning-based-optimization?s_tid=srchtitle

10- Gravitational Search Algorithm (GSA): by Esmat Rashedi

https://www.mathworks.com/matlabcentral/fileexchange/27756-gravitational-search-algorithm-gsa?s_tid=srchtitle

11- Particle Swarm Optimization (PSO): by Seyedali Mirjalili

https://img1.wsimg.com/blobby/go/e8abc963-7b19-40d6-a270-eed55d317dba/downloads/PSO.zip?ver=1604036156826

12- Genetic Algorithm (GA): by Seyedali Mirjalili

https://www.mathworks.com/matlabcentral/fileexchange/67435-the-genetic-algorithm-ga-selection-crossover-mutation-elitism?s_tid=srchtitle