A Federated Learning Framework with Blockchain-Based Auditable Participant Selection

1  Introduction

Devices in IoT are continuously generating data, and Federated Learning (FL) as a distributed machine learning paradigm can securely and effectively exploit the value of these data. Therefore, FL is getting attention from all walks of life and is being applied in different scenarios, e.g., Google’s next-word prediction model [1], NVIDIA medical image AI [2]. Specifically, in each round of FL, the central server first selects a suitable set of participants. Next, the central server sends the latest model to these participants. Then the participants perform local training using private data to obtain local gradients and return them to the central server for rewards. Finally, the central server aggregates the local gradients to update the model. If this is not the last round of training, the above process is continued, otherwise the training is ended.

In reality, participants’ data are heterogeneous [3], which leads to buckets effect in federated learning, that is, participants with poorer training data limit the training efficiency and model accuracy growth of federated learning [4]. This is the reason for the participant selection before the start of each training round in the above federated learning process, and how to select a suitable subset of participants for model training has become a research topic for many scholars in the FL field. In the earliest federated learning scheme [5], scholars have introduced random selection to improve model accuracy. The central server randomly selects some participants for training before the start of each training round to improve the generalization performance of the model, and also avoids the problem of too many participants leading to high communication overhead of the central server. Recently, many scholars have found that random selection may also lead to degradation of model accuracy, so they have proposed schemes for participant selection based on information of participant. For example, in some schemes [6,7], the central server selects participants with faster computation and communication based on their device information to execute model training. In other schemes [8,9], the central server selects participants that are more useful for model optimization based on information about training data such as loss generated during training.

However, few scholars have noticed the following issues that can lead to a crisis of trust in the participant selection process. The first is that the central server may not truthfully select participants due to device limitations. Second, unselected participants may mislead the selection process and impersonate other participants to participate in the training. At last, privacy issues in the participant selection process are rarely noticed. Many scholars have ignored the reality that federated learning participants are reluctant to disclose training information to anyone outside of training. Once unauthorized others have access to a participant’s training loss and the model, they can compute local gradients and perform model updates. This is a violation of the interests of the participants in federated learning.

There are many challenges in designing a federated learning framework with a participant selection that addresses both of these issues. First, there is a conflict between achieving auditability and privacy. The former requires that information from the selection process can be utilized to support participants in conducting audits and verifying the correctness of the results, while the latter requires that the selection process does not disclose private information about the parties. For example, blockchain technology as a trustworthy enhancement technology can effectively achieve auditability [10]. However, the high transparency of blockchain and the high cost of invoking smart contracts are also challenges to security and efficiency. Second, resisting malicious participants compounds the design difficulty. The existence of malicious participants is unavoidable, so the behavior of misrepresenting information to mislead the selection process needs to be detected and excluded, but the detection process is prone to leaking private information.

The mainstream research topic in the field of auditable federated learning is still on achieving auditability of the aggregation process [11,12], and the design ideas of the relevant solutions cannot be directly applied to solve the difficulties faced by the auditable participant selection above. First, in most auditable federated learning, the most straightforward design idea is to utilize blockchain to achieve auditability. They protect privacy and ensure trustworthiness by introducing technologies such as blockchain committees or trusted execution environment (TEE), but these technologies currently have some unresolved issues of their own. There are also some solutions that do not require the use of blockchain to achieve the auditability, such as AP2FL [13] by introducing a trusted auditor to check the calculation and send the check results to the participants, but this is a special assumption. In [14], the author designed a general distributed protocol that supports public accountability, which can be used to achieve the auditability of calculations, but involves complex cryptographic algorithms and requires a large overhead. In terms of privacy, there are a number of privacy-preserving aggregation schemes [15–17] available. These schemes are mainly based on privacy computing techniques such as homomorphic encryption [18], differential privacy [19] and secure multiparty computation [20] to prevent the privacy of local gradients and the correctness of aggregated gradients. However, these privacy computation techniques still suffer from problems such as computational overhead and accuracy, and it is difficult to combine blockchain technology to achieve both auditability and privacy.

1.1 Our Contribution

In this paper, we design a federated learning framework with blockchain-based auditable participant selection for achieving auditable participant selection and secure model training. In the framework, we utilize smart contracts to achieve auditable participant selection while protecting participants’ private information based on the discrete logarithmic hard problem. In addition, we believe that it is possible for participants to misrepresent information and substitute for selected participants to disrupt the selection and training process. We introduce commitment schemes and zero-knowledge proof to defend against these malicious behaviors. In addition, The extra overhead of the framework is less to allow more time and power to be spent on model training. Overall, our contributions are as follows:

•   We design a federated learning framework with auditable and privacy-preserving participant selection that utilizes smart contracts for participant selection, thereby supporting participant auditing of the selection process and solving the trustworthiness problem. It also solves the privacy problem by ensuring that training losses submitted by participants are not leaked based on the discrete logarithm problem.

•   We then introduce commitment schemes and zero-knowledge proofs into the framework, thus ensuring that participants cannot fake training losses to compete maliciously or assume the identities of selected participants to disrupt the training process.

•   Finally, we discuss the security of the proposed framework, showing that the protocol does not disclose private information to anyone and ensures that participants cannot falsify the loss based on existing selection results. Also, we apply the framework to real federated learning and show that our protocol is beneficial to the training efficiency of federated learning and the overhead of implementing the protocol is small.

1.2 Paper Organization

We organize the remainder of the article as follows. In Section 2, we provide a brief overview of the state of the art of the relevant technologies. In Section 3, we first introduce the cryptographic primitives and define the model and design goals of the protocol. Then in Section 4, we describe in detail the execution flow of the framework with the associated algorithms. We analyze the security of the protocol in Section 5 and show the experimental results in Section 6. In Section 7, we summarize this work.

2  Related Works

In this section, we review the latest relevant work in the field of federated learning on participant selection, achieving auditability and privacy.

Not long after federated learning was proposed, McMahan et al. [5] noticed that a large number of training participants resulted in unbearable communication overhead and proposed the first federated learning participant selection scheme. Gradually, many scholars devoted themselves to this research topic. At a time when data and equipment are becoming increasingly heterogeneous, they found that the random selection method proposed by McMahan et al. sometimes causes participants with poor equipment performance and data quality to be selected to perform training. This makes the model accuracy tend to decrease and the time overhead increase under the same number of training rounds [4]. Therefore, they proposed evidence-based participant selection options. The first category is aimed at reducing model training time overhead. For example, in order to allow the central server to select a group of training participants to reduce training time overhead, Lee et al. [21] proposed the Adaptive Deadline Determination (ADD) algorithm to predict time overhead based on the participants’ device performance. Similarly, FedMCCS [6] and FedCS [7] comprehensively consider the computing and communication resources of participants to predict which participants can help federated learning achieve the best training cost. On the other hand, some participants chose solutions aimed at solving the problem of poor data leading to reduced model accuracy. In [8], the author proposed a federated learning framework that implements inference on the relationship between participant training data and model parameters based on a deep Q-learning model, thereby selecting a subset of participants to improve the performance of the federated learning trained model performance. ADACOMM [9] is an adaptive communication strategy designed to allow the central server to select appropriate participants to communicate and train the model, thereby achieving better model accuracy with fewer training rounds. Zhou et al. [22] used a clustering algorithm to cluster participants using social context data to obtain a group of participants that best contributed to model optimization. However, few people have paid attention to the auditability of participant selection schemes.

Blockchain is transparent and untamperable and can be used as a trusted distributed ledger that supports nodes to audit transactions. In recent years, blockchain has also been gradually used in the IoT to enable trusted data sharing [23–25]. Blockchain is now also being used to enable auditable federated learning. For example, existing solutions [11,13] support auditability by replacing the central server with a blockchain deployed with a TEE or committee to perform model aggregation and generate proof materials. At the same time, in these schemes, participants use encryption algorithms to encrypt and upload local gradients, and then the TEE or blockchain committee will decrypt and aggregate them to achieve privacy. However, trusted TEEs and blockchain committees are a strong assumption and have their own problems. Meanwhile, because blockchain supports trusted transactions with untamperable computations, it has been used by some scholars to implement incentives in federated learning [26–28]. Various privacy-preserving techniques have been proposed and used to solve practical problems [29–31]. In terms of privacy-preserving federated learning, Batchcrypt [15] implements privacy protection for local gradient ciphertext based on a homomorphic encryption scheme that can be calculated in batches, while supporting the central server to execute aggregation algorithms under ciphertext. At the same time, Hao et al. [16] introduced an additional server into the solution to assist the central server, and then implemented private and robust gradient aggregation and model update based on a secure two-party computing protocol. In [17], Wei et al. designed a privacy budget allocation scheme based on differential privacy to achieve privacy protection in model training while reducing the impact on model accuracy. In addition, various privacy protection technologies [32,33] are designed to solve different problems, and these works also have reference value. However, privacy protection for federated learning increases training overhead and harms model accuracy.

In summary, there is currently little research on the issue of trustworthiness in participant selection. And current auditable or privacy-preserving federated learning model training solutions have proven to be difficult to achieve auditability and privacy at the same time to improve the credibility of the solution.

3  Preliminaries and Models

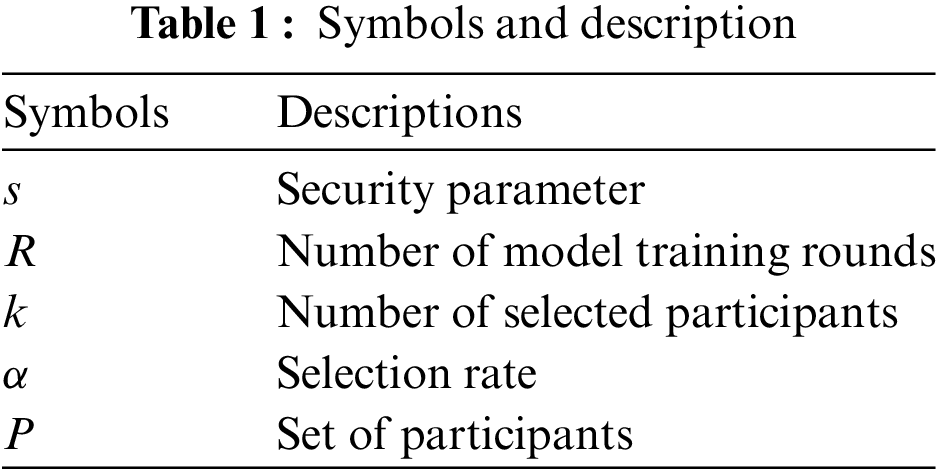
We begin this section by listing the cryptographic primitives and symbol definitions used by the framework (see Table 1), and then show the models and design goals.

3.1 Cryptographic Primitives

3.1.1 Blockchain and Smart Contract

In 2009, Satoshi Nakamoto first introduced Bitcoin, opening a new chapter in the study of blockchain technology. Blockchain technology is used to build decentralized systems where currencies can be issued and transactions conducted without trusting a third party. The security of the system is built on the backup chain stored by each node, and the information interaction between nodes is realized through P2P technology to keep the blockchain copy updated in real time. Due to the large number of nodes, it is difficult for an attacker to release a false block to obtain the recognition of most nodes, which ensures the security of the blockchain. Blockchain technology, with its advantages of openness, immutability and anonymity, has attracted the attention of various industries, which try to integrate it into their own systems to solve the security and trust problems. In order to enrich the functions of blockchain, people introduce the concept of smart contract.

In 1995, Nick Szabo proposed the concept of smart contracts [34], which is specifically defined as “A smart contract is a set of promises defined in digital form that includes protocols on which contract participants can execute those promises.” The decentralized nature of blockchain technology enables untrusted hosts to perform the same tasks honestly and according to rules, avoiding execution errors that may be caused by real-world factors and providing an environment for the implementation of smart contracts. Ether, as an example, smart contracts are executed in two phases: Contract deployment and invocation. Smart contracts are usually written in a computer programming language and are automatically executed based on preset conditions. The smart contract is compiled and deployed by the Ethernet Virtual Machine (EVM), after which each node receives a copy of the contract to enhance its distributed nature.

3.1.2 Commitment Scheme

Commitment schemes [35,36] are important cryptographic tools to ensure data integrity and uniqueness. A commitment scheme contains a committer and receiver, and two phases, the commitment phase and the opening phase.

Commit(m,r)→c: The commitment function receives a message m and a random number r as input, and then generates a commitment c. The committer then sends the promise to the receiver.

Decommit(c,m,r)→b: The committer sends message m with a random number r to the receiver. The receiver can then execute the decommitment algorithm to verify that the message is the one promised by the committer. If the verification fails, it outputs b=0, otherwise b=1.

A secure commitment scheme needs to satisfy hiding and binding:

Hiding: The commitment c does not display information about the message m. More precisely, based on the security of the pseudo-random generator (PRG) used, for the commitment c, the adversary cannot distinguish which message it is a promise about.

Binding: Two arbitrarily different messages m1,m2 cannot generate a single commitment. That is, for the committer, he cannot find different messages m1,m2 and r1,r2 to generate two equal commitment c1=c2.

A commitment scheme can be constructed by means of a hash function H. That is, the commitment function is made to be Commit(m,r)=H(m,r)=c. Then in the opening phase, the decommitment function can be realized as follows: The receiver computes the hash H(m,r)→c′ and then checks whether c and c′ are equal, if they are equal then the sender has sent the correct message.

3.1.3 Zero-Knowledge Proof

A zero-knowledge proof [37] is an interactive proof where the verifier gains no additional knowledge beyond the validity of the statement being proven. The theory of zero-knowledge proofs is not only elegant but also fundamental to the field of cryptography. In cryptographic protocols, zero-knowledge proofs play a crucial role in ensuring compliance by allowing parties to demonstrate adherence without revealing their private inputs, hence maintaining zero knowledge. While some may view zero-knowledge proofs as costly and simplistic for promoting honesty, they are essential for constructing efficient protocols. Although traditional zero-knowledge proofs for NP statements may be resource-intensive, there exist highly efficient zero-knowledge proofs tailored for specific languages of interest. In practice, leveraging an efficient zero-knowledge proof is often the most effective strategy to prevent fraudulent behavior by malicious actors.

Our framework uses a non-interactive zero-knowledge proof based on the discrete logarithm problem. Let p be a prime, q a prime divisor of p−1, and g an element of order q in zq. Suppose the prover holds a secret value v∈Zq as well as hv=gvmod p, and he wants to prove to the verifier that he holds v without revealing v to him. Then he can first sample a random number r∈Zq and compute hr=gr, e=H(hv,hr), then compute z=e⋅v+r and send (hv,hr,z) to the verifier. The verifier can then compute e=H(hv,hr) and check that gz=hr⋅hve holds, and if it does, then the verifier holds the correct v.

3.2 The Defined Model

3.2.1 System Model

Fig. 1 illustrates the system model of our designed framework, which contains three main actors.

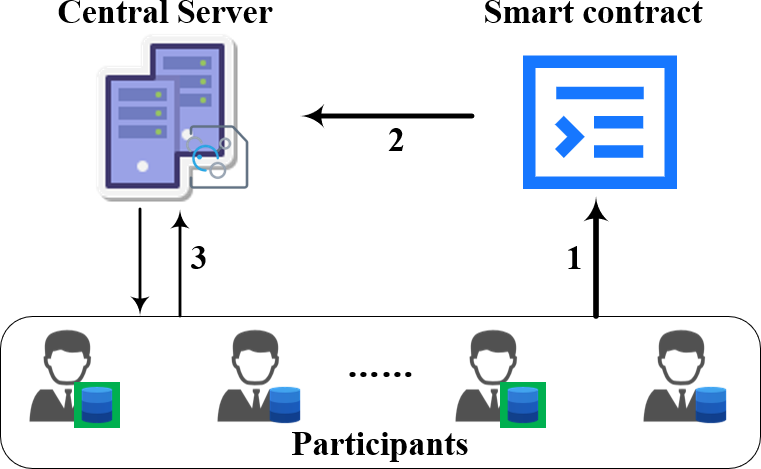
Figure 1: System model

Central Server: The central server (CS) holds the relevant configuration files for model training, containing information such as model structure, number of training rounds and participants, etc. He is responsible for scheduling the training participants to collaboratively execute the model training and determines the rewards that the participants receive at the end of the training.

Smart Contract: The smart contract is deployed on the blockchain to perform federated learning participant selection. It will accept the training loss uploaded by the participants and sort the participants accordingly and then output a set of participants with higher loss.

Participants: Here, we assume that there are IoT devices as participants, identified as p1,p2,⋯,pn. They hold rich data, but the data held by different participants are heterogeneous. Therefore, they have different roles in model optimization, and participant with a greater role in model optimization are selected to perform training and receive rewards.

The framework proposed in this paper is realized with the interaction of the above actors, specifically, the steps are as follows:

If it is the first round of training, the training loss of participants are not yet available, therefore, CS randomly selects some clients as participants to execute the first round of training. Otherwise, as shown in the system model figure, the first step is for the participants to anonymously upload the losses generated by the local model training to the smart contract, while the framework ensures that the loss are not leaked.

In the second step, the smart contract executes the participant selection algorithm and publishes the output participant set and then automatically issues rewards to the selected participants. CS will retrieve this participant set.

In the third step, CS sends the latest model to these selected participants who then perform local training and return the resulting local gradients to CS. At the same time, they send the loss to smart contract. Finally, CS will aggregate these local gradients to update the model and determine whether the preset number of training rounds has been reached, if so, end the training, otherwise perform the second step.

3.2.2 Threat Models

To make our framework more practical, we assume that CS is not to be trusted, and he does not always select FL participants correctly, and participants in the framework are allowed to be malicious but not collusive.

First, in order to be selected for a reward, they may want to know the training loss uploaded to the blockchain by others during the current selection process, so that they know what their own loss value is in order to be selected. They may also use the average of the training loss of the previously selected participants as their own loss. Of course, the most straightforward thing they can do is to choose a very large value as their training loss to pretend that they contributed a lot to the model training.

Second, they may take over the identity of a selected participant to perform federated learning model training and disrupt the training process. By assuming someone else’s identity, they can avoid being held accountable.

Finally, a malicious participant or adversary may be interested in the identities of other participants, which is not only a disclosure of the participant’s privacy, but may also be used by the adversary to commit illegal acts.

3.2.3 Design Goal

We work in this paper to design a federated learning framework with auditable and private blockchain-based participant selection that ensures private data of all parties as well as auditable participant selection in cases where all participants can be malicious. The design goals of the protocol can be categorized into the following four points:

Auditability: The execution process of the participant selection is auditable. This means that during the federated learning training process, the integrity of the execution process and results of the participant selection can be verified.

Privacy: Participants’ training loss and identifying information are not disclosed, and even information that can be inferred from the execution is not useful to the campaign. Thus, campaign violations are avoided and the privacy and personal safety of the participants are protected.

Resistance to malicious campaigning: The best campaign strategy for a participant is to honestly provide a training loss. A malicious participant cannot fake a valid loss by using other participants’ training loss, or presumably choose a very large value as their own.

Effectiveness: The participant selection we designed should help to improve the efficiency of federated learning. At the same time, equipment resources are valuable in the model training process of federated learning. Insufficient computational power can cause incorrect model training. Therefore, the framework we design should minimize the required overhead to avoid affecting model training.

4  Our FL Framework

Based on the above defined model with the introduced cryptographic primitives, we design a federated learning framework with auditable participant selection. In the framework, each round of federated learning model training except the first round can be categorized into a preparation phase, a selection phase and a model training phase.

•   Preparation Phase: Participants generate a pair of keys for encryption in the preparation phase, while the training loss is processed to mask private information.

•   Selection Phase: The smart contract selects α⋅k participants from those who performed training in the previous round based on the training loss, and also randomly selects (1−α)⋅k participants from those who did not participate in the previous round.

•   Training Phase: The central server performs a round of federated learning model training with the selected participants.

For the first round of training, the central server can select k participants that are the fastest to upload a local gradient. For the r-th (0<r≤R) training round, we assume that the set of participants who participated in the training in round r−1 is Pr−1, and the set of participants who did not participate in the training is P¯r−1,Pr−1∩P¯r−1=P. Also, it is assumed that the central server has already published the criteria for participant selection on the blockchain, as well as the security parameter s, the prime numbers p, q and the generating metrics of the ring Zp, g, have already been agreed upon by all nodes. We additionally assume that the smart contract recognizes the nodes submitting information as participants in P, and it is simple to do so, e.g., by the central server issuing identifiers to the participants as well as to the blockchain, respectively. Next, we move to the presentation of the framework execution flow, as show in the Fig. 2.

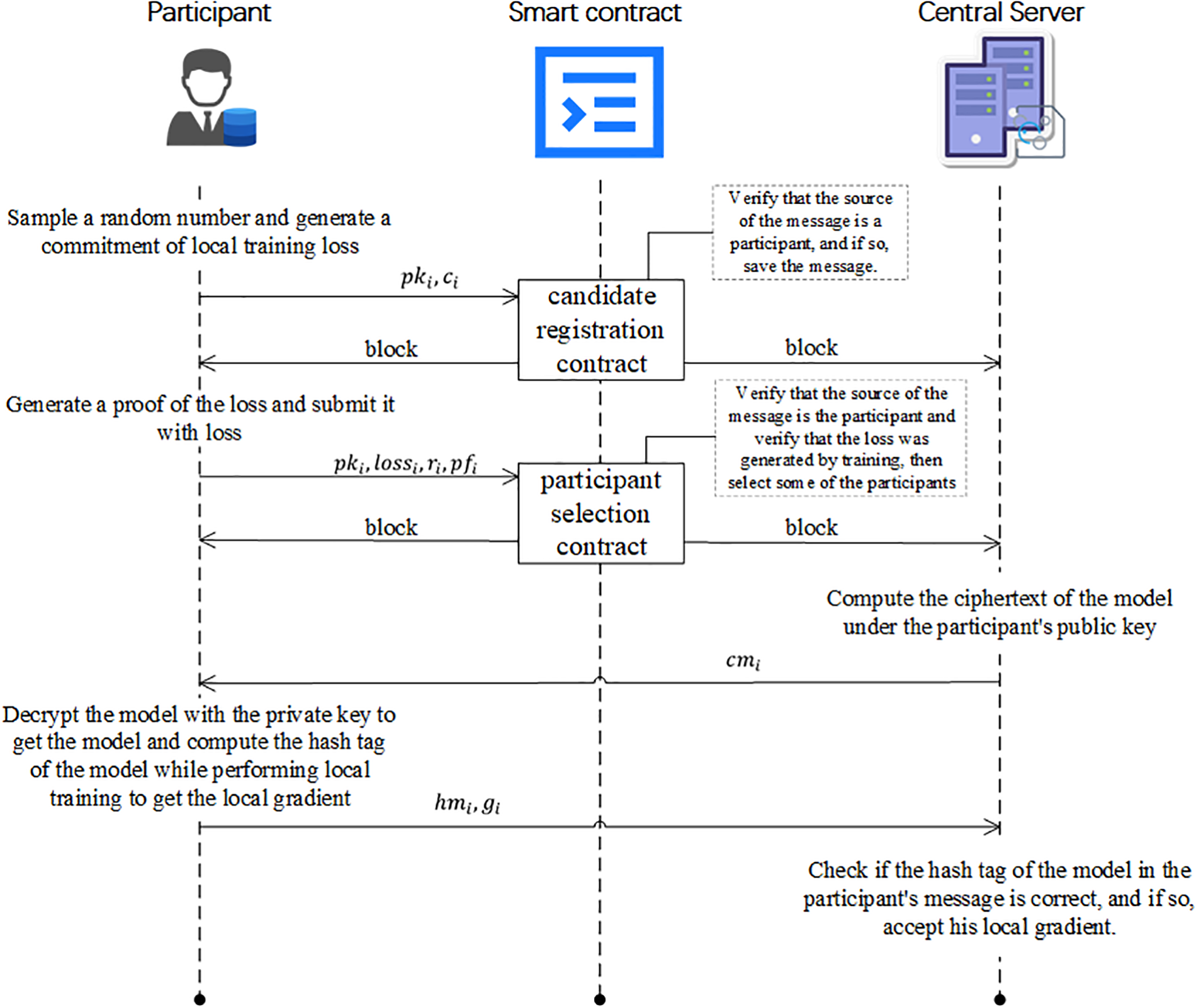
Figure 2: The execution flow of our framework

4.1 Preparation Phase

At this phase, each participant pi∈P generates a key pair (pki,ski), where the public key pki is used to encrypt the message and the private key ski is used to decrypt the ciphertext. Meanwhile, participants pi∈Pr−1 involved in the previous round of training process the training loss: In order not to compromise privacy, the participants first map the floating-point loss li to integer elements of the ring Zp, and then make lossi=gli. For the other participants pj∈P¯r−1, they will make the lossj=0.

4.2 Selection Phase

As shown in the Fig. 3, in the selection phase, participant pi∈Pr−1 samples the random numbers ri and ripf using PRG, and then computes the commitment ci=H(lossi,ri) and uploads (pki,ci) as the input to the candidate registration contract. The contract will confirm that the inputs all originate from real participants.

Figure 3: Participant selection contract

When participants have finished uploading their commitments, the contract packages public keys with the commitments into a block for publishing. Then, pi∈Pr−1 computes the proof pfi:

pfi=(hli,hri,zi)(1)

where hli=lossi, hri=gri and zi=H(hli,hri)⋅li+ri. pfi will be used to prove that pi holds li.

After that, pki,lossi,ri,pfi will be uploaded and used as input for the participant selection contract (Fig. 3). It is important to note here that the public key pki will also be used as the address of the participant.

As shown in the pseudo-code Fig. 3 of the contract, the contract will retrieve the candidate participant’s public key (i.e., address) previously uploaded to the blockchain with the commitment of training loss. Then, after the message has been received, the verifyParticipant function is called to verify that the participant who sent the message is a candidate participant who has already registered.

Next the getP function is executed to partition the candidate participants into two sets of participants, P_r1 and P_r2 (i.e., Pr−1 and P¯r−1). The participant in set Pr−1 holds the locally trained loss. The other set P¯r−1 holds the participants who did not perform the last round of training and they do not have the training loss.

In getP function, it first determines whether the loss uploaded by the participant is 0. If it is 0, it is added to the set P¯r−1. If it is not, the decommit function Decommit is called to verify that the loss is a value that the participant has previously committed to. If the verification passes, then the zero-knowledge proof function zkproof is then used to verify that the participant does indeed hold this loss. If the verification passes then this participant is added to the set Pr−1. After dividing all the candidate participants into sets Pr−1 and P¯r−1, the execution of the selection function selectParticipants is entered.

In function selectParticipants, the participants in Pr−1 are sorted based on their training loss. As shown in the function sortByLoss, we implement the function using bubble sort, where the comparison of the magnitude of the loss of participants pj∈Pr−1 and pj+1∈Pr−1 is realized by division, that is:

(lj<lj+1)=(lj−lj+1<0)=(glj−lj+1<1)=(gljglj+1<1)=(lossljlosslj+1<1)(2)

In the above equation, (ineq) represents a judgment function. If the inequality in the brackets holds, it outputs 1, otherwise it outputs 0.

Then the selecParticipants function calls the deleteSuspectparticipant function to remove some of the participants with higher ordering, and in the function, we take the loss of the top 5\% participants as the value that may be maliciously amplified. Finally, selecParticipants selects the top-ranked α⋅k participants from the ordered Pr−1 to be added to the set P_r (i.e., Pr), and (1−α)⋅k participants from P¯r−1 to be added to the set Pr. At this point, the contract outputs a set Pr containing k participants. Meanwhile, the contract automatically distributes rewards into the accounts of these participants.

4.3 Training Phase

In the model training phase, the central server will execute a round of model training with the participants selected by the participant selection contract. First, the central server encrypts the model Mr−1 to get the ciphertext cmi using the public key pki of participant pi∈Pr and broadcasts it. pi holding the private key ski can decrypt the cmi to obtain the model Mr−1. Then pi performs local training to obtain the local gradient gi and computes the hash label hmi=H(Mr−1,pki) of Mr−1 to send to the central server along with the gradient gi. Finally the central server verifies the correctness of hmi by checking hmi=H(Mr−1,pki). If the verification passes, the gradient gi is adopted. the central server aggregates the adopted local gradients to obtain the aggregated gradient agr to obtain the latest model Mr=Mr−1−η⋅agr, η is learning rate. At this point, if r=R, the federated learning model training ends, otherwise, the execution continues from the preparation phase.

4.4 Discussion

In this section, we discuss the ideas behind designing this framework. First, we achieve auditability of the process based on the blockchain and smart contracts automatically performing federated learning participant selection. Secondly, we achieve privacy protection for loss values based on the discrete logarithm problem. Finally, we utilize commitment and tailoring strategies to fend off malicious campaign participants, and in the execution part of the smart contract, we retain the freedom of design, so that people can define how to identify the participant’s messages and how to sort and select them themselves. The model training part is also extensible, and we do not specify how the training should be done and what cryptographic algorithms should be used.

5  Security Analysis

In this section, we analyze and discuss whether our framework achieves the security goals, including auditability, privacy and resistance to malicious campaigns.

Auditability: The framework achieves auditability based on blockchain. The distributed nature of the blockchain is such that computations and transactions performed through the blockchain are recorded and immutable. Therefore, blockchain-based federated learning participant selection makes the computation process transparent and immutable, that is, the values, lossi,ri, pfi, uploaded by participants cannot be tampered with. Based on the above discussion, we can know that any node on the blockchain can obtain the values, lossi,ri, pfi, and use these values to audit the selection process to verify the correctness of the process and results.

Privacy: In the framework, participants’ training loss are hidden by power operations, and their address is a randomly generated public key and therefore anonymous. Based on the discrete logarithm hard problem, the lossi of participant pi does not leak information about the loss li. Although losslilosslj may leak the training loss li to participant pj in sortByLoss function, it does not help the participant to be selected. In addition, the zero-knowledge proof scheme we use based on the hash function with the discrete logarithm hard problem ensures that the pfi does not leak any private information except for the fact that pi knows li.

Resistance to malicious campaigning: When campaigning for training participants, dishonest candidates may deliberately magnify their training losses. In the participant selection contract, cropping some of the participants with the highest loss values is used to guard against this behavior. Second, dishonest candidates may also calculate to get a loss′:

loss′=(∏pi∈Pr−1lossi)1‖Pr−1‖=g∑pi∈Pr−1li‖Pr−1‖(3)

‖Pr−1‖ denotes the number of participants in set Pr−1.

Since l′=∑pi∈Pr−1li‖Pr−1‖mod p is close to the median loss value, it is likely to be able to support dishonest candidates being selected. As a result, dishonest candidates may use this as their input to upload to the blockchain. To address this problem, the framework uses a zero-knowledge proof to solve it, where each participant pi must attach a proof that lossi is calculated from the training loss li he holds. Due to the discrete logarithmic difficulty problem, a dishonest candidate cannot obtain l′ through loss′. Finally, dishonest candidates may disrupt the training process by substituting for selected participants. In the framework, the central server encrypts the model with the public key of the selected participant and requires the participant to attach a hash tag of the model when uploading gradients. Thus, without the private key, dishonest candidates cannot obtain the hash tag of the model and upload a local gradient that can be adopted.

6  Experiments

We will next use our framework for federated learning model training. First, we implemented our framework on a server running Ubuntu 22.04 equipped with Intel Core CPU i7-12700F 2.10 GHz and NVIDIA RTX A6000 GPU, based on Python 3.10 and TensorFlow 2.15. We implement the contract and simulate the activities of each node on the Ethereum test network Remix [38], where we wrote our candidate registration contract and participant selection contract in java-style code and then deployed the contract to test the contract calls. In the framework, we will randomly divide the dataset into 20 subsets and assign them to 20 participants. Then, when the number of selected participants k = 6, 8, 10, 12, and 14, respectively, we trained the model on different data sets and compared it with [5]. The training parameters we set are as follows: The number of training rounds R is 500, the learning rate is 0.5, and the mini-batch is 64.

The structure of the model we use is as follows. The input layer size is (28,28,1), the first convolutional layer contains 30 convolution kernels with size (3,3), and the first pooling layer size is (2,2). The second convolutional layer contains 50 convolution kernels with size (3,3), and the second pooling layer has size (2,2). Then there is a flattening layer, a fully connected layer containing 100 neurons. The final output layer contains 10 neurons and uses the softmax activation function, while the previous convolutional layers and fully connected layers use the ReLU activation function.

First, in order to illustrate the effectiveness of the selection strategy adopted by our framework, we compared the accuracy and training loss changes of the models trained by our scheme and scheme of [5] in five instances. We represent the five cases where k is 6, 8, 10, 12, and 14 as instances I-6, I-8, I-10, I-12, and I-14. Each instance was then tested 10 times and averaged.

The accuracy of the model trained on the MNIST dataset [39] is shown in the left subplot of Fig. 4. Obviously, the accuracy of the model trained by our framework is higher because our framework selects participants with higher training loss to perform training in each round of training, while the scheme of [5] is to select randomly. Facts have shown that the higher the loss value, the greater the participant’s contribution to model optimization. And as the number of selected participants increases, the accuracy of the model also increases because more data is used for model training.

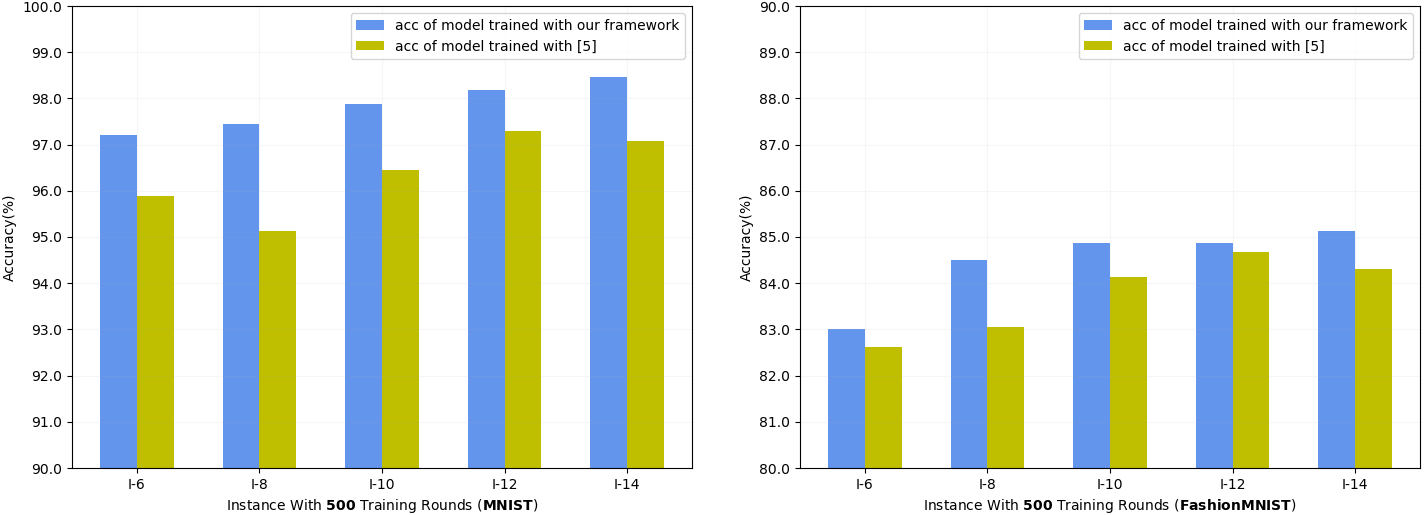
Figure 4: Comparison of acc of models trained under different participant selection

In the left subplot of Fig. 5, we show the changes in loss for model training on MNIST for the two schemes. To facilitate observation, we have reduced the amount of data displayed. It is obvious that our framework converges faster overall during model training. In addition, it can also be observed that the loss value of scheme in [5] fluctuates greatly. In comparison, our framework make model training more stable.

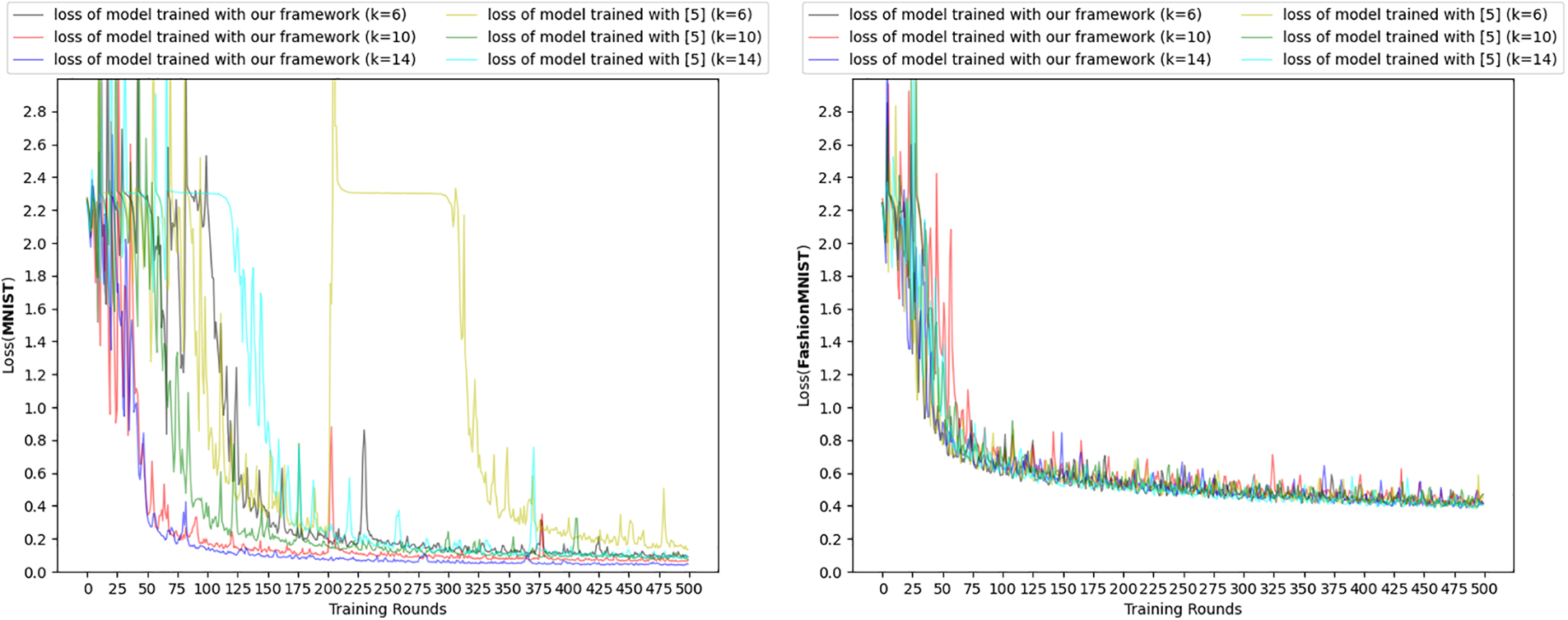
Figure 5: Comparison of convergence of training loss produced by different methods

We also conducted the same experimental comparison on the dataset FashionMNIST [40]. As shown in the left subplot of Figs. 4 and 5, the effect obtained by the experiment is similar to that on MNIST, except that the comparison between the loss convergence speed and the fluctuation is not so obvious, but it is enough to illustrate the effectiveness of our proposed framework. It is worth noting that as the data set becomes more complex, the accuracy of the model trained on FashionMNIST is lower under the same number of training rounds. This is understandable, and what can be further verified is that as the number of training rounds increases, the final accuracy of the model here can reach more than 95%.

The current other participant selection strategy [4–9] comprehensively considers the training data and device information of training participants, thereby contributing to model accuracy and training efficiency. We focus in this article on the auditability and privacy of the participant selection process. Our strategy only relies on training information to improve model accuracy, training efficiency can also be considered more to achieve a more effective participant screening strategy, but this is beyond the scope of this article.

Next, we conducted experiments on the accuracy of the framework’s calculations. Since in the framework, participants need to map the training loss of floating point type to the integer ring. This process may result in truncation of values, resulting in inaccurate comparison operations. Therefore, we experimentally compared the selection accuracy when using different numbers of bits to represent decimals.

As shown in the Fig. 6, we execute the smart contract to sort the participants multiple times and average the accuracy when the number of bits is 2 to 6. The experimental results show that as the number of bits representing decimals increases, the calculation accuracy of the framework also increases. When the bit count reaches 4, it has reached more than 99%. Of course, one fact that needs to be explained here is that such a calculation requires a large ring of prime numbers. In cryptography, it is acceptable to increase redundancy such as the representation length of data to ensure security. Excluding performing local model training, in our framework, the additional computational time overhead for each round of training for participants is 0.0281 s. The time cost required by the central server to perform additional calculations for each participant is 0.0442 s.

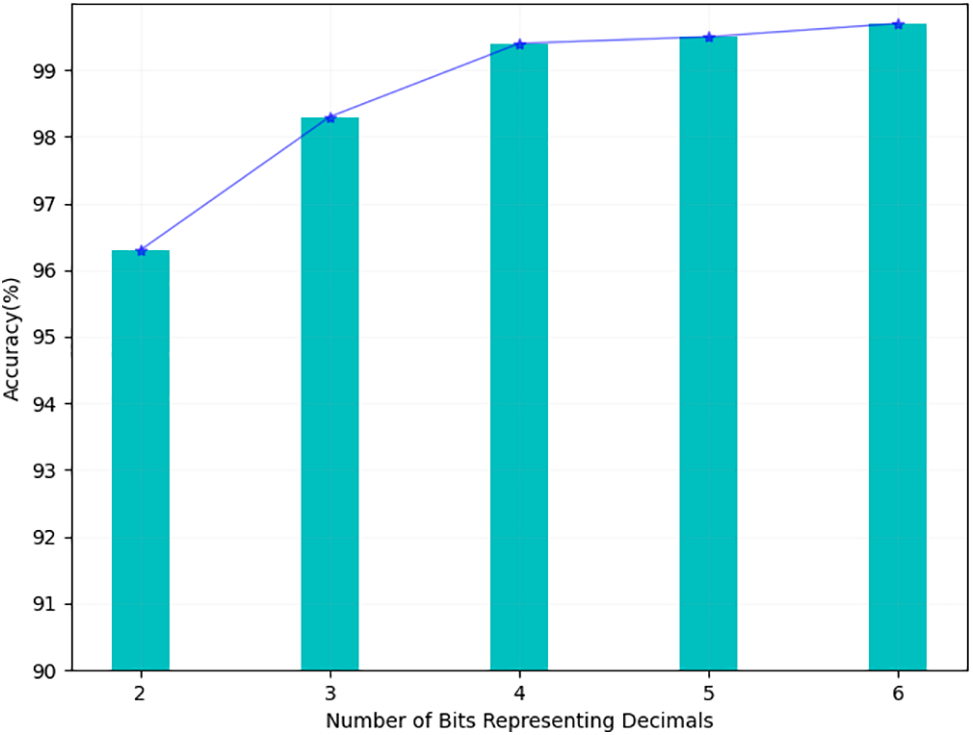
Figure 6: Comparison of calculation accuracy with different fixed point

Based on the above experimental results, we illustrate the effectiveness and accuracy of the federated learning framework proposed in this article in model training. This shows that the framework proposed in this paper is actually effective and has good application prospects.

7  Conclusion

In order to solve the problem of untrustworthy correctness and unguaranteed privacy of the participant selection process of federated learning, this paper designs a federated learning framework with auditable and private participant selection based on blockchain. The participant selection strategy adopted by this framework can resist malicious campaign behavior and support participants to audit the correctness of the execution. In addition, the framework is based on the discrete logarithm problem to prevent the training losses uploaded by participants to the blockchain from leaking to other nodes outside the participants. Security analysis shows that our framework achieves auditability, privacy and resistance to malicious campaign behavior. At the same time, experimental analysis also shows that the model trained using our framework can achieve higher accuracy and the training is more stable. Performing comparison operations on processed loss can also achieve higher accuracy. Therefore, experiments prove that our scheme is effective. In future work, we intend to study how more complex and effective participant selection strategies can be implemented in this framework.

Acknowledgement: The authors appreciate the valuable comments from the reviewers.

Funding Statement: This work was supported by the Key-Area Research and Development Program of Guangdong Province under Grant No. 2020B0101090004, the National Natural Science Foundation of China under Grant No. 62072215, the Guangzhou Basic Research Plan City-School Joint Funding Project under Grant No. 2024A03J0405, the Guangzhou Basic and Applied Basic Research Foundation under Grant No. 2024A04J3458, and the State Archives Administration Science and Technology Program Plan of China under Grant 2023-X-028.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: H. Zeng; data collection: H. Zeng; analysis and interpretation of results: H. Zeng, M. Zhang; draft manuscript preparation: H. Zeng, M. Zhang, T. Liu, A. Yang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The MNIST and FashionMNIST datasets used in this paper can be accessed at http://yann.lecun.com/exdb/mnist/ and https://github.com/zalandoresearch/fashion-mnist, respectively.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. Yang et al., “Applied federated learning: Improving google keyboard query suggestions,” arXiv preprint arXiv:1812.02903, 2018. [Google Scholar]

2. W. Li et al., “Privacy-preserving federated brain tumour segmentation,” in 10th Int. Workshop, MLMI 2019, Shenzhen, China, 2019, vol. 11861, pp. 133–141. [Google Scholar]

3. K. Hsieh, A. Phanishayee, O. Mutlu, and P. B. Gibbons, “The non-IID data quagmire of decentralized machine learning,” in Proc. 37th Int. Conf. Mach. Learn., Jul. 13–18, 2020, vol. 119, pp. 4387–4398. [Google Scholar]

4. L. Fu, H. Zhang, G. Gao, M. Zhang, and X. Liu, “Client selection in federated learning: Principles, challenges, and opportunities,” IEEE Internet Things J., vol. 10, no. 24, pp. 21811–21819, Dec. 15, 2023. doi: 10.1109/JIOT.2023.3299573. [Google Scholar] [CrossRef]

5. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Proc 20th Int Conf Artif. Intell. Stat., AISTATS 2017, Fort Lauderdale, FL, USA, Apr. 20–22, 2017, vol. 54, pp. 1273–1282. [Google Scholar]

6. S. Abdulrahman, H. Tout, A. Mourad, and C. Talhi, “FedMCCS: Multicriteria client selection model for optimal IoT federated learning,” IEEE Internet Things J., vol. 8, no. 6, pp. 4723–4735, Mar. 15, 2021. doi: 10.1109/JIOT.2020.3028742. [Google Scholar] [CrossRef]

7. T. Nishio and R. Yonetani, “Client selection for federated learning with heterogeneous resources in mobile edge,” in 2019 IEEE Int. Conf. Commun. (ICC), Shanghai, China, IEEE, May 20–24, 2019, pp. 1–7. [Google Scholar]

8. H. Wang, Z. Kaplan, D. Niu, and B. Li, “Optimizing federated learning on non-IID data with reinforcement learning,” in IEEE INFOCOM 2020-IEEE Conf. Comp. Commun., Toronto, ON, Canada, Jul. 6–9, 2020, pp. 1698–1707. doi: 10.1109/INFOCOM41043.2020.9155494. [Google Scholar] [CrossRef]

9. J. Wang and G. Joshi, “Adaptive communication strategies to achieve the best error-runtime trade-off in local-update SGD,” in Proc Mach. Learn Syst. (MLSys 2019), Stanford, CA, USA, Mar. 31–Apr. 2, 2019. [Google Scholar]

10. Y. Liu, J. Wang, Z. Yan, Z. Wan, and R. Jäntti, “A survey on blockchain-based trust management for internet of things,” IEEE Internet Things J., vol. 10, no. 7, pp. 5898–5922, Apr. 1, 2023. doi: 10.1109/JIOT.2023.3237893. [Google Scholar] [CrossRef]

11. J. Weng, J. Weng, J. Zhang, M. Li, Y. Zhang, and W. Luo, “DeepChain: Auditable and privacy-preserving deep learning with blockchain-based incentive,” IEEE Trans. Dependable Secur. Comput., vol. 18, no. 5, pp. 2438–2455, 2021. doi: 10.1109/TDSC.2019.2952332. [Google Scholar] [CrossRef]

12. Z. Peng et al., “VFChain: Enabling verifiable and auditable federated learning via blockchain systems,” IEEE Trans. Netw. Sci. Eng., vol. 9, no. 1, pp. 173–186, 2022. doi: 10.1109/TNSE.2021.3050781. [Google Scholar] [CrossRef]

13. A. Yazdinejad, A. Dehghantanha, and G. Srivastava, “AP2FL: Auditable privacy-preserving federated learning framework for electronics in healthcare,” IEEE Trans. Consum. Electron., vol. 70, no. 1, pp. 2527–2535, Feb. 2024. doi: 10.1109/TCE.2023.3318509. [Google Scholar] [CrossRef]

14. M. Rivinius, P. Reisert, D. Rausch, and R. Küsters, “Publicly accountable robust multi-party computation,” in 2022 IEEE Symp. Secur. Priv. (SP), San Francisco, CA, USA, May 22–26, 2022, pp. 2430–2449. doi: 10.1109/SP46214.2022.9833608. [Google Scholar] [CrossRef]

15. C. Zhang, S. Li, J. Xia, W. Wang, F. Yan and Y. Liu, “BatchCrypt: Efficient homomorphic encryption for cross-silo federated learning,” in 2020 USENIX Annu. Tech. Conf., Boston, MA, USA, Jul. 15–17, 2020, pp. 493–506. [Google Scholar]

16. M. Hao, H. Li, G. Xu, H. Chen, and T. Zhang, “Efficient, private and robust federated learning,” in ACSAC’21: Annu. Comput. Secur. Appl. Conf., USA, Dec. 6–10, pp. 45–60. [Google Scholar]

17. K. Wei et al., “Personalized federated learning with differential privacy and convergence guarantee,” IEEE Trans. Inf. Forensics Secur., vol. 18, pp. 4488–4503, 2023. doi: 10.1109/TIFS.2023.3293417. [Google Scholar] [CrossRef]

18. A. Acar, H. Aksu, A. S. Uluagac, and M. Conti, “A survey on homomorphic encryption schemes: Theory and implementation,” ACM Comput. Surv., vol. 51, no. 4, pp. 79:1–79:35, 2018. doi: 10.1145/3214303. [Google Scholar] [CrossRef]

19. C. Dwork, “Differential privacy: A survey of results,” in Theory App. Models Comput. 5th Int. Conf., TAMC 2008, Xi’an, China, Apr. 25–29, 2008, pp. 1–19. [Google Scholar]

20. Y. Lindell, “Secure multiparty computation (MPC),” Commun. ACM, vol. 64, no. 1, pp. 86–96, 2020. doi: 10.1145/3387108. [Google Scholar] [CrossRef]

21. J. Lee, H. Ko, and S. Pack, “Adaptive deadline determination for mobile device selection in federated learning,” IEEE Trans. Veh. Technol., vol. 71, no. 3, pp. 3367–3371, Mar. 2022. doi: 10.1109/TVT.2021.3136308. [Google Scholar] [CrossRef]

22. X. Zhou et al., “Hierarchical federated learning with social context clustering-based participant selection for internet of medical things applications,” IEEE Trans. Comput. Soc. Syst., vol. 10, no. 4, pp. 1742–1751, Aug. 2023. doi: 10.1109/TCSS.2023.3259431. [Google Scholar] [CrossRef]

23. J. Yu et al., “Robust and trustworthy data sharing framework leveraging on-chain and off-chain collaboration,” Comput. Mater. Contin., vol. 78, no. 2, pp. 2159–2179, 2024. doi: 10.32604/cmc.2024.047340 [Google Scholar] [CrossRef]

24. H. Tian and J. Tian, “A blockchain-based access control scheme for reputation value attributes of the internet of things,” Comput. Mater. Contin., vol. 78, no. 1, pp. 1297–1310, 2024. doi: 10.32604/cmc.2024.047058 [Google Scholar] [CrossRef]

25. C. Zhang, M. Zhao, J. Liang, Q. Fan, L. Zhu and S. Guo, “NANO: Cryptographic enforcement of readability and editability governance in blockchain databases,” IEEE Trans. Dependable Secur. Comput., pp. 1–14, 2023. doi: 10.1109/TDSC.2023.3330171. [Google Scholar] [CrossRef]

26. Z. Wang, Q. Hu, R. Li, M. Xu, and Z. Xiong, “Incentive mechanism design for joint resource allocation in blockchain-based federated learning,” IEEE Trans. Parallel Distrib. Syst., vol. 34, no. 5, pp. 1536–1547, May 2023. doi: 10.1109/TPDS.2023.3253604. [Google Scholar] [CrossRef]

27. M. Park and S. Chai, “BTIMFL: A blockchain-based trust incentive mechanism in federated learning,” in Comput. Sci. Appl.–ICCSA 2023 Workshops, Athens, Greece, Jul. 3–6, 2023, vol. 14106, pp. 175–185. [Google Scholar]

28. T. Li et al., “Enabling secure and flexible streaming media with blockchain incentive,” IEEE Internet Things J., vol. 11, no. 2, pp. 1966–1980, Jan. 15, 2024. doi: 10.1109/JIOT.2023.3305048. [Google Scholar] [CrossRef]

29. C. Zhang, C. Hu, T. Wu, L. Zhu, and X. Liu, “Achieving efficient and privacy-preserving neural network training and prediction in cloud environments,” IEEE Trans. Dependable Secure Comput., vol. 20, no. 5, pp. 4245–4257, 2023. doi: 10.1109/TDSC.2022.3208706. [Google Scholar] [CrossRef]

30. A. Yang, J. Xu, J. Weng, J. Zhou, and D. S. Wong, “Lightweight and privacy-preserving delegatable proofs of storage with data dynamics in cloud storage,” IEEE Trans. Cloud Comput., vol. 9, no. 1, pp. 212–225, Jan. 1–Mar. 2021. doi: 10.1109/TCC.2018.2851256. [Google Scholar] [CrossRef]

31. C. Dong et al., “Maliciously secure and efficient large-scale genome-wide association study with multi-party computation,” IEEE Trans. Dependable Secur. Comput., vol. 20, no. 2, pp. 1243–1257, Mar. 1–Apr. 2023. doi: 10.1109/TDSC.2022.3152498. [Google Scholar] [CrossRef]

32. C. Hu, C. Zhang, D. Lei, T. Wu, X. Liu and L. Zhu, “Achieving privacy-preserving and verifiable support vector machine training in the cloud,” IEEE Trans. Inf. Forensics Secur., vol. 18, pp. 3476–3491, 2023. doi: 10.1109/TIFS.2023.3283104. [Google Scholar] [CrossRef]

33. C. Zhang, X. Luo, J. Liang, X. Liu, L. Zhu and S. Guo, “POTA: Privacy-preserving online multi-task assignment with path planning,” IEEE Trans. Mobile Comput., vol. 23, no. 5, pp. 5999–6011, May 2024. doi: 10.1109/TMC.2023.3315324. [Google Scholar] [CrossRef]

34. N. Szabo, “Formalizing and securing relationships on public networks,” First Mon., vol. 2, no. 9, Sep. 1997. doi: 10.5210/fm.v2i9.548. [Google Scholar] [CrossRef]

35. T. P. Pedersen, “Non-interactive and information-theoretic secure verifiable secret sharing,” in Adv. Crypto.—CRYPTO’91, Santa Barbara, California, USA, Aug. 11–15, 1991, vol. 576, pp. 129–140. [Google Scholar]

36. A. Arun, C. Ganesh, S. Lokam, T. Mopuri, and S. Sridhar, “Dew: A transparent constant-sized polynomial commitment scheme,” in 26th IACR Int. Conf. Pract. Theor. Public-Key Crypto., Atlanta, GA, USA, May 7–10, 2023, vol. 13941, pp. 542–571. [Google Scholar]

37. L. Zhou, A. Diro, A. Saini, S. Kaisar, and P. C. Hiep, “Leveraging zero knowledge proofs for blockchain-based identity sharing: A survey of advancements, challenges and opportunities,” J. Inf. Secur. Appl., vol. 80, no. 6, pp. 103678, Feb. 2024. doi: 10.1016/j.jisa.2023.103678. [Google Scholar] [CrossRef]

38. Y. Levreau et al., “Remix online ethereum test network,” 2022. Accessed: Apr. 10, 2024. [Online]. Available: http://remix.ethereum.org [Google Scholar]

39. L. Deng, “The MNIST database of handwritten digit images for machine learning research [Best of the Web],” IEEE Signal Process. Mag., vol. 29, no. 6, pp. 141–142, Nov. 2012. doi: 10.1109/MSP.2012.2211477. [Google Scholar] [CrossRef]

40. H. Xiao, K. Rasul, and R. Vollgraf, “Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms,” arXiv preprint arXiv:1708.07747, 2017. [Google Scholar]