A Data Intrusion Tolerance Model Based on an Improved Evolutionary Game Theory for the Energy Internet

1  Introduction

The cross-fertilisation of the Internet and energy sector has given rise to a new form of industry-Energy Internet [1]. This complex network of interconnected energy systems, such as electricity, solar energy, natural gas, etc., integrates a variety of devices and systems for energy production, conversion, transmission, distribution and consumption. While this new form has great potential and value, it also poses unprecedented challenges, particularly regarding data protection [2].

In Energy Internet, data generation is extensive and complex. A plethora of information, including equipment status, consumer behavior patterns, and operational metrics, continuously traverses the network. Protecting this data, including its storage, transmission, and computational processing, requires a robust framework of security protocols [3]. In addition, the inherent complexity of the Energy Internet’s architecture presents formidable data security challenges. The complex web of interconnected devices, communication protocols, and software systems makes it difficult to implement effective security measures. Compounding this complexity, energy systems serve as vital components of national infrastructure, making them prime targets for malicious actors due to their strategic importance. Beyond traditional concerns such as data breaches and sabotage, these systems face heightened vulnerabilities to sophisticated cyber threats, including denial-of-service (DoS) attacks, network worms, ransomware, and other forms of digital aggression.

Data security is critical in the Energy Internet environment, where multiple actors are involved, including energy providers, consumers, operators, and regulators. These entities have different objectives, strategic preferences, and resources, and their decision-making behaviors regarding data management, sharing and protection are interdependent and influence each other. As a result, game theory provides a structured approach [4] to examining and optimizing data security strategies and mechanisms within the Energy Internet, helping to improve system security and the ability to adapt to evolving threats.

Existing methods for protecting energy Internet data security are mainly in the areas of encryption technology [5], access control [6], intrusion detection systems [7], and blockchain [8]. Encryption is an essential safeguard for the confidentiality, integrity, and availability of data. However, if encryption keys are misplaced or illegally obtained, data is at risk of becoming irretrievably inaccessible or compromised by unauthorized parties; access control prevents unauthorized users from accessing data through user authentication and rights management. Although access control improves security, it does not completely prevent all attacks, such as phishing attacks, social engineering attacks, etc.; IDSs require significant computing resources to process and analyze network traffic, which can impact network performance, especially when dealing with large volumes of traffic; Blockchain’s immutability prevents data from being maliciously altered, but blockchain has limited performance and capacity, which may limit its application in large-scale energy Internet environments. Therefore, the existing solutions cannot fully satisfy the data security protection in the energy Internet environment. Facing the problem of data security protection in the energy Internet, there is an urgent need for an adaptive intrusion tolerance model. There were three major challenges in constructing the model, as shown in Fig. 1.

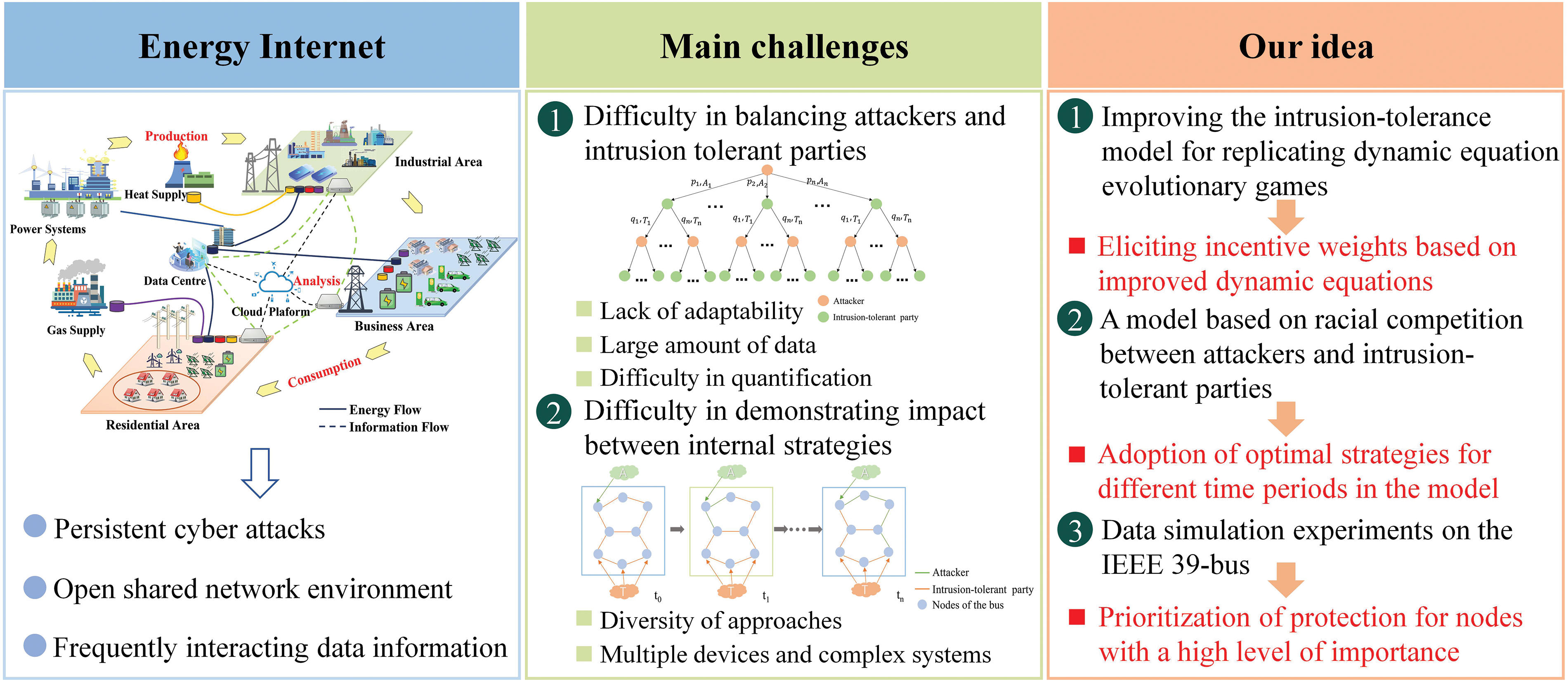
Figure 1: The framework of our model

In summary, the main contributions of this paper are summarized as follows:

•   We propose an improved intrusion-tolerance model based on replicator dynamics in evolutionary game theory, which establishes incentive weights through strategies of varying intensity, thereby deriving the optimal intrusion-tolerant strategy for different time periods based on the strength of each strategy.

•   By using optimal intrusion-tolerant strategies from different periods, we established a model based on competition between attackers and intrusion-tolerant entities, and numerically simulated the evolution of the intrusion-tolerant system.

•   By performing data simulation in the IEEE 39-bus system, the analysis of the initial and final node voltage values verifies the feasibility and effectiveness of the proposed data intrusion tolerance model (AITGM).

The rest of this paper is organized as follows. Section 2 introduces the related work. Section 3 establishes a model of attackers and intrusion-tolerant parties based on an improved evolutionary game theory (AT-IEG). Section 4 constructs a model of racial competition between attackers and intrusion-tolerant parties based on power distribution network attack scenarios (RACIT-PDN). Section 5 conducts data simulation in the IEEE 39-bus system. And, the conclusions are shown in Section 6.

2  Related Work

In this section, we first introduce the state of the art of research on evolutionary games and tolerating intrusions; then, we outline the existing techniques for data tolerating intrusions. Finally, we discuss and present our solution accordingly.

2.1 Evolutionary Game

Evolutionary game theory, first proposed in 1973 by John Maynard Smith and George R. Price [9] is an approach for analyzing and understanding the behavior of individuals with adaptive and strategic interactions. Currently, this theory is widely used in the fields of ecological and environmental sciences, economics, engineering, and network information security.

In recent years, the application of evolutionary game theory in the field of network information security has received widespread attention. Researchers use evolutionary game theory to study the dynamic evolutionary process of network attack and defense confrontation, their research can provide a theoretical basis for the formulation of network security defense strategies. Gothawal et al. [10] constructed a reliable and efficient anomaly based intrusion detection system model by using stochastic and evolutionary game models. Zhang et al. [11] constructed a model that combines an attack detection evolutionary game model and a Kalman filter algorithm to provide an optimized detection method by analyzing the evolution of equilibrium points. Jin et al. [12] constructed a network attack and defense evolution game decision model based on the RM algorithm; their decision model improves the convergence speed of the optimal defense strategy by optimizing the strategy learning mechanism through the RM algorithm. By using a case study of ransomware, Hu et al. [13] created a stochastic evolutionary game model to simulate the dynamics of network attack and defense, selected the optimal defense strategy and obtained the maximum defense benefit. Xu et al. [14] constructed a stochastic evolutionary game model based on stochastic differential equations for network attack and defense; their model achieves steady-state and optimal defense strategies under random perturbations. Liu et al. [15] incorporated a learning mechanism for the limited rationality and interaction range of players, which in turn created a more realistic offensive and defensive evolutionary game model.

Remark: The above researchers all propose new algorithmic models combined with evolutionary games to search for optimal game strategies from different perspectives. However, they do not consider the dependence between strategies in the same group, and there are not only incentives but also inhibitory relationships between the various strategies. Therefore, in this paper, we analyze the internal relationships between the aggressive and tolerant sides separately; moreover, we propose incentive weight coefficients.

2.2 Intrusion Tolerance

The concept of intrusion tolerance was first introduced by Fraga et al. [16]. The basic idea is that even if a system is partially infiltrated or a service is partially corrupted, the main functions of the system are guaranteed to operate normally. The intrusion tolerance includes network, application and data layers.

Network intrusion tolerance is a security policy that ensures that a system continues running services while under attack. di Giandomenico et al. [17] proposed a redundancy scheme for enhanced intrusion tolerance that improves the defense of the system against cyber attacks. Sanoussi et al. [18] used game theory to quantify cyberattacks and defense based on intrusion-tolerant systems to support the development of more effective cybersecurity strategies. Zhao et al. [19] proposed an adaptive neural network fault-tolerant control scheme for effective boundary control of flexible strings with uncertainties. Mehmood et al. [20] presented an energy-efficient fault-tolerant scheme for wireless LANs with improved reliability through cooperative communication and network coding. Application intrusion tolerance is used to maintain critical functionality for applications in the face of security threats through resilient design. Jadhav et al. [21] proposed an accuracy-based fault-tolerant two-phase intrusion detection system (TP-IDS) that improves the timeliness and fault-tolerance of malicious node identification. Flora [22] introduced an intrusion-tolerant microservice design approach that enhances the trustworthiness and resilience of IDSs. Zheng et al. [23] developed a quantitative security evaluation method for VM-based intrusion tolerance systems by using security downtime. Wang et al. [24] proposed an intrusion-tolerant scheduling algorithm to improve the security of cloud-based scientific workflows; their approach improves the success rate and efficiency through task replication and voting mechanisms.

Data intrusion tolerance is the maintenance of data integrity, availability and confidentiality in the event of unauthorized access or destruction. Hong et al. [25] presented a distributed fault-tolerant intrusion detection system to address the problems of a single point of failure and insufficient data processing of traditional IDSs. Kasu et al. [26] proposed a fault-tolerant framework for big data with parallel file transfers; they improved data transfer rates and managed failures in distributed environments. Khan et al. [27] developed a Byzantine fault-tolerant system designed to provide “as-a-service” intrusion tolerance that ensures local data confidentiality. Jarosz et al. [28] proposed a decentralized data management solution for institutional data autonomy by enhancing data availability and fault tolerance through peer sets and consensus mechanisms. Zhu et al. [29] presented a fault-tolerant PDP protocol for cloud storage that detects and repairs data by using cuckoo filters and Reed-Solomon codes to ensure security and utility. Li et al. [30] proposed closed-form equations based on the Weibull distribution to analyze and to optimize the reliability of active fault-tolerant cloud storage systems.

Remark: There have been some important advances in recent intrusion tolerance technology. However, there are still some shortcomings and challenges with current ITS technology. It is difficult for existing ITS techniques to adapt to evolving attack methods and diverse attack environments. Second, while intrusion-tolerant scheduling algorithms may improve task success and efficiency, their implementation can be hindered by complex system design challenges. In practice, correctly assessing the threats and vulnerabilities facing a system and developing an effective security strategy remain major challenges. Therefore, the intrusion tolerance system proposed in this paper addresses the above problems in depth.

2.3 Remarks and Our Thoughts

Given the intrinsic complexities of the Energy Internet, characterized by an extensive array of devices, intricate system architectures, and voluminous data, the requisite intrusion tolerance system for this domain demands exceptional accuracy and real-time responsiveness [31]. Existing methodologies may not adequately account for this multifaceted nature, which potentially falls short of offering effective protection. Moreover, as attack vectors evolve and become more sophisticated, recent intrusion detection and defense technologies may struggle to adapt promptly. Consequently, there is a risk that these technologies may fail to deliver enduring and efficient protection against such dynamic threats.

To address the above issues, in this paper, we address the shortcomings of existing approaches by synthesizing and analyzing real-time strategies for intrusion tolerance models:

•   We introduce tailored incentive weights for both the attacker and the intruder-tolerant entities to encourage strategic interactions.

•   We perform a thorough analysis and optimize the strategy in real time to ensure dynamic adaptability.

•   We utilize numerical analysis to simulate the evolution of the tolerant intrusion system model.

3  The Design of AT-IEG

The majority of recent research on data security has been focused on preemptive defense strategies that are implemented before an attack scenario. However, such measures cannot guarantee absolute system security. Therefore, systems must be designed with resilience in mind to maintain critical functionality and to avoid total incapacitation in the event of a breach. Existing game-theoretic models that represent the interactions between attackers and tolerant defenders tend to be biased in favor of one party over the other. This bias makes it difficult to accurately represent the interplay and the influence of each party’s internal strategies. Thus, these models often lack comprehensive gameplay and produce difficulties when attempting to apply them to real-world scenarios. In this section, we present the introduction of incentive weighting coefficients that articulate the strategic interdependence between attackers and defenders in the context of network attack scenarios. These coefficients are incorporated into attacker-defender tolerance models to refine replicator dynamic equations. The improved equations facilitate the determination of optimal strategies for both parties at each successive point in time.

3.1 Construction of the Evolutionary Game Model

The cyber-attacker and the intrusion-tolerant game model can be represented as a six-tuple ATEGM=(N,S,∂,θ,U,T).

1.    N=(NA,NT) is the total set of aggressors and aggressor-tolerant parties in the evolutionary game, where NA is the attacking party and NT is the tolerant party, both of which have multiple decision makers.

2.    S=(SA,ST) is the set of strategies of the attacker and the tolerant aggressor. Where SA={A1,A2,…,An} denotes the set of optional attacker strategies, ST={T1,T2,…,Tm} denotes the set of optional aggressor strategies, and n and m denote the number of attackers and aggressors, respectively.

3.    ∂=(P,Q) is the set of beliefs of the attacker and the tolerant aggressor, where pi∈P is the probability that the attacker chooses strategy Ai, and qj∈Q is the probability that the tolerant aggressor chooses strategy Tj.

4.    θ=(α,β) is the set of attacker and aggressor gains, where α denotes the incentive relationship between the strategies of the attacker and β denotes the incentive relationship between the strategies of the tolerant aggressor.

5.    U=(UA,UT) is the set of attacker and aggressor gains, where UA is the attacker’s gain and UT is the aggressor’s gain.

6.    T is the evolutionary game time. The attacker and aggressor game can be decomposed into several temporal subgame processes.

During the decision-making process of attacking and tolerating aggression, the attacker and the intrusion-tolerant party adjust and improve their curricula in real time according to their interests. This produces changes over time in the number of decision-makers choosing different strategies. As a result, the attack strategy set and the tolerance strategy set are constructed separately. Fig. 2 shows the game tree of the attacker and the intrusion-tolerant party.

Figure 2: The game tree of attackers and intrusion-tolerant parties

Table 1 shows the payoff matrix for attackers and intrusion-tolerant parties, Where V represents the original benefits derived from the information possessed by the intrusion-tolerant party itself. AC denotes the attack cost required by the attacker to adopt a certain attack strategy. TC denotes the tolerance cost required by the tolerant party to select a certain tolerance policy. AG denotes the gain from the attack. AGij represents the payoff obtained by the attacker choosing strategy SAi and the intrusion-tolerant party choosing strategy STj.

If the attackers choose a weak attack strategy and the intrusion-tolerant parties choose a strong intrusion-tolerant strategy, the resulting payoff for the attackers is denoted AG12, and AG12<AG11; When the attackers select a weak attack strategy and the intrusion-tolerant parties adopt a weak intrusion-tolerant strategy, the payoff obtained from the attack is denoted AG22 with AG22<AG21.

Based on the payoff matrix for attackers and intrusion-tolerant parties, the payoff UAi for different attack strategies and the average payoff U¯A are calculated.

UA1=q1(AG11−AC1)+q2(AG21−AC1)(1)

UA2=q1(AG12−AC2)+q2(AG22−AC2)(2)

U¯A=p1UA1+p2UA2=p1[q1(AG11−AC1)+q2(AG21−AC1)]+p2[q1(AG12−AC2)+q2(AG22−AC2)](3)

Fp=dp(t)dt=p1(1−p1)(UA1−U¯A)(4)

Similarly, the gains UTi and the average gains U¯T for the different defensive strategies of the intrusion-tolerant party against the attacks can be calculated.

UT1=p1(V−TC1−AG11)+p2(V−TC1−AG12)(5)

UT2=p1(V−TC2−AG21)+p2(V−TC2−AG22)(6)

U¯T=q1UT1+q2UT2==q1[p1(V−TC1−AG11)+p2(V−TC1−AG12)]+q2[p1(V−TC2−AG21)+p2(V−TC2−AG22)](7)

Fq=dq(t)dt=q1(1−q1)(UT1−U¯T)(8)

p1+p2=1q1+q2=1(9)

Due to the complex network environment of the power distribution system in actual power system attacks, the practical strategies of the attacker and the intruder-tolerant party can change, especially considering the dependency relationships between strategies within the attacker group and the intruder-tolerant party. Therefore, it is necessary to introduce incentive weights in the replication dynamic equations; this approach improves the accuracy of the replication dynamic rate. Then, we can obtain the optimal strategies for the attacker and the tolerant aggressor for each period.

3.2 Improved Replication Dynamic Build Strategy

The evolutionary game model of the attacker and the intrusion-tolerant part is established. We consider that there is a certain dependency between the attack strategy SAi and the defense strategy STj. The influence coefficients φi and γi are introduced for the attack strategy and the defense strategy respectively. φi represents the magnitude of the attacker’s strategy influence and is directly proportional to the attack payoff. Different strategies have different influence coefficients; a larger coefficient indicates stronger strategy intensity, while smaller coefficients indicate weaker strategy intensity. Similarly, γi represents the magnitude of the intrusion tolerant party’s strategy strength.

Let αij=φiφj. We define αij as the incentive weight between attack strategies SAi and SAj. When αij<1, strategy SAi has positive incentives for SAj; if αij>1, strategy SAi has positive incentives for SAj. Similarly, We define βij=γiγj as the incentive weight between the tolerant aggression strategies STi and STj. Combining Eqs. (4) and (8) further yields the improved replication dynamics equation.

{Fp′=dp(t)dt=φ1p1(1−p1){AG21−AC1−α(AG22−AC2)+q1[AG11−AG21+α(AG22−AG12)]}Fq′=dq(t)dt=γ1q1(1−q1){V−TC1−AG12−β(V−TC2−AG22)+p1[AG12−AG11+β(AG21−AG22)]}(10)

Letting Eq. (10) equal 0, the following five sets of equilibrium points can be obtained:

1){p1=0q1=0; 2){p1=1q1=0; 3){p1=0q1=1; 4){p1=1q1=1; 5){p1=TC1+AG12−V+β(V−TC2−AG22)AG12−AG11+β(AG21−AG22)q1=AC1−AG21+α(AG22−AC2)AG11−AG21+α(AG22−AG12)

3.3 Improved Replication Dynamic Build Strategy

For the improved replicated dynamic equations, the stability of the equilibrium points is analyzed based on the above five evolutionary game equilibrium points via local analysis. The Jacobi matrix of the improved replicated dynamics equations is obtained as follows:

Y=[∂FP′/∂p∂FP′/∂q∂Fq′/∂p∂Fq′/∂q](11)

In Eq. (11), ∂FP′/∂p=γ(1−2q1){V−TC1−AG12−β(V−TC2−AG22)+p1[AG12−AG11+β(AG21−AG22)]}; ∂FP′/∂q=γ1q1(1−q1)[AG12−AG11+β(AG21−AG22)]; ∂Fq′/∂p=φ1p1(1−p1)[AG11−AG21+α(AG22−AG12)]; ∂Fq′/∂q=φ1(1−2p1){AG21−AC1−α(AG22−AC2)+q1[AG11−AG21+α(AG22−AG12)]}.

According to Table 2:

DetJ(0,0)=γ1φ1[V−TC1−AG12−β(V−TC2−AG22)][AG21−AC1−α(AG22−AC2)]TrJ(0,0)=γ1[V−TC1−AG12−β(V−TC2−AG22)]+φ1[AG21−AC1−α(AG22−AC2)](12)

DetJ(0,1)=−γ1φ1[V−TC1−AG11−β(V−TC2−AG21)][AG21−AC1−α(AG22−AC2)]Tr J(0,1)=γ1[V−TC1−AG11−β(V−TC2−AG21)]−φ1[AG21−AC1−α(AG22−AC2)](13)

DetJ(1,0)=−γ1φ1[V−TC1−AG12−β(V−TC2−AG22)][AG11−AC1−α(AG12−AC2)]TrJ(1,0)=−γ1[V−TC1−AG12−β(V−TC2−AG22)]+φ1[AG11−AC1−α(AG12−AC2)](14)

DetJ(1,1)=γ1φ1[V−TC1−AG11−β(V−TC2−AG21)][AG11−AC1−α(AG12−AC2)]DetJ(1,1)=−γ1[V−TC1−AG11−β(V−TC2−AG21)]−φ1[AG11−AC1−α(AG12−AC2)](15)

The numerical expression for the stabilization point is shown. Let m=V−TC1−AG11−β(V−TC2−AG21), n=AG11−AC1−α(AG12−AC2), We break it into the following four cases:

•   m<0, n<0, Point A(0,0) behaves as an ESS equilibrium point, indicating that both the attacker and the intrusion tolerant party choose weak attack and weak intrusion tolerant strategies; B(0,1) and C(1,0) are saddle points and D(1,1) is unstable.

•   m<0, n>0, Point B(0,1) represents an ESS equilibrium point, indicating that the attacker and the intrusion-tolerant party choose a weak attack strategy and a strong intrusion tolerant strategy, respectively. Points A(0,0) and D(1,1) are saddle points, and C(1,0) is an unstable point.

•   m>0, n<0, Point C(1,0) acts as an ESS equilibrium point, indicating that the attacker and the intrusion-tolerant party choose a strong attack strategy and a weak intrusion tolerant strategy, respectively. Points A(0,0) and D(1,1) are saddle points, and B(0,1) is an unstable point

•   m>0, n>0, Point D(1,1) acts as an ESS equilibrium point, indicating that both the attacker and the intrusion-tolerant party choose strong attack strategies and strong intrusion-tolerant strategies, respectively. B(0,1) and C(1,0) are saddle points, and A(0,0) is an unstable point.

4  The RACIT-PDN Model

In this section, we combine the game processes of the attacker and the intrusion-tolerant party with a model of racial competition to construct a dynamic model that describes the behavior of the game between the attacker and the intrusion-tolerant party. The goal of an attacker is to destabilize the power system by consuming or by controlling critical resources through various means. A tolerant party implements a strategy to protect these resources as much as possible while tolerating the attacker’s attacks and maintaining the normal operation of the system.

The model places resource competition at the center of the dispute between the two parties, simulating the allocation and the occupation of key resources such as bandwidth, processing power, and power supply in the network. The adaptive strategy of the intrusion-tolerant party mirrors the evolutionary mechanism of the biological species, which responds to the evolution of the means of attack by constantly updating and by improving security measures. The dynamic equilibrium between the attacker and the intrusion-tolerant party is achieved through the iterative evolution of the strategies of both parties.

For the attacking and tolerating parties in the power system, the process of the game can be specifically simulated by the racial competition model. With the attacking and tolerating parties as the two populations, Eq. (16) is obtained by assuming that the change in quantity in the normal state of both parties conforms to a logistic law:

dPdt=μ1P(1−PM)dQdt=μ2Q(1−QN)(16)

where P denotes the number of attacking parties, Q denotes the number of tolerating parties, μ1 and μ2 denote the diffusion rate of attacking parties and the repair rate of tolerating parties, respectively, and t denotes the time of the game. However, when attackers and intrusion-tolerant parties compete, the deterrent effect of attackers on the growth of tolerant aggressors is proportional to the number of attackers. Similarly, intrusion-tolerant parties have the same deterrent effect on attackers. This leads to Eq. (17):

dPdt=μ1P(1−PM−SiQN)dQdt=μ2Q(1−QN−DiPM)(17)

In Eq. (17), Si and Di denote the strength of the attacker’s strategy and the strength of the intrusion-tolerant party’s strategy, respectively, with smaller values indicating greater strength. This is further combined with the incentive weights to obtain α=SiSj and β=DiDj.

5  Experimental Analysis

In this section, experimental simulations and analyses of the game process between the attacking party and the aggressor-tolerant party under cyber attacks based on the IEEE 39-bus system are conducted to demonstrate the validity and the feasibility of the method proposed in this paper. First, the experimental environment and the parameter settings are presented; second, the feasibility of improving the incentive weights of the replicated dynamic equations is verified and analyzed. Finally, experimental simulations and analyses are conducted based on the voltage values on the IEEE 39-bus system for the attacker and the intrusion-tolerant party race competition models.

5.1 Experimental Setting

This paper is implemented in MATLAB 2019a, the experimental simulation is conducted with the IEEE 39-bus system, and the network topology is shown in Fig. 3. The relevant parameters are shown in Table 3.

Figure 3: IEEE 39-bus system topology diagram

First, 39 nodes with 46 branches were analyzed and divided into 39 nodes based on the correlation between the nodes: Minor nodes, comparatively important nodes, moderate nodes, important nodes, and very important nodes. There are 12 minor nodes, 10 more important nodes, 13 moderately important nodes, 3 important nodes, and 1 very important node.

The more connected the nodes are, the greater the importance level of the node. A node with a high importance level indicates that the node is in the core part of the system, and it must adopt the strategy of incremental strength of tolerance intrusion in the game model to ensure that the function of the node is complete. In contrast, nodes with lower importance levels use a strategy of decreasing the strength of tolerance intrusion to ensure that the nodes can perform the most basic functions.

5.2 Feasibility Analysis of the Incentive Weights

In this section, feasibility simulation experiments are conducted on the incentive weights proposed in the network attacker and intrusion-tolerant party model based on the evolutionary game model. By varying the values of the incentive weights, the simulation explores the impact of different strategies between the attacker and the intrusion-tolerant party on the changes in the evolutionary model.

Due to the particularity of the intrusion tolerant party, the costs and the benefits of weak intrusion tolerance strategies and weak attack strategies are much lower than those of strong intrusion tolerance strategies and strong attack strategies. Therefore, we set V=12, TC1=1, TC2=1, AC1=1, AC2=0.1, AG11=11, AG12=0.1, AG21=9, AG22=0.1, φ1=1, and γ1=1. The initial states of the attacker and the intrusion-tolerant party are set to (p1,q1)=(0.6,0.2) and (p1,q1)=(0.8,0.4), respectively. Based on this fact, the incentive weights for the attacker and the intrusion-tolerant party are assigned values for simulation to obtain the game evolution process under different incentive weights.

•   Set α21=1, β21=1. At this point, there is no incentive relationship between strategy ST1 and strategy ST2 of the intrusion-tolerant party. This is consistent with the traditional replicator dynamics equation. As shown in Fig. 4, when the initial state is (p1,q1)=(0.6,0.2), the strong aggressive strategy reaches a steady state after 1.25-time units of simulation, and the strong intrusion tolerant strategy reaches a steady state after 2.7-time units of simulation, When the initial state is (p1,q1)=(0.8,0.4), the strong attack strategy reaches stability after 1.35-time units of simulation, and the strong intrusion tolerant strategy reaches stability after 3-time units of simulation.

•   Set α21=2, β21=2. This time, the attacker’s strategy SA2 has an inhibitory effect on strategy SA1, and the strategy ST2 of the intrusion tolerant party has a facilitating effect on strategy ST1. Compared to scenario 1, scenario 2 slowed the convergence speed of the attacker and accelerated the convergence speed of the intrusion-tolerant party. As shown in Fig. 4, when the initial state is (p1,q1)=(0.6,0.2), the strong attack strategy reaches a steady state after 1.31-time units of simulation, and the strong intrusion tolerance strategy reaches a steady state after 1.08-time units of simulation. When the initial state is (p1,q1)=(0.8,0.4), the strong attack strategy reaches stability after 1.46-time units of simulation, and the strong intrusion tolerance strategy reaches stability after 1.35-time units of simulation.

•   Set α21=0.5, β21=0.5. At this point, the attacker’s strategy SA2 promotes strategy SA1, while the intrusion-tolerant party’s strategy ST2 inhibits strategy ST1. Facilitates the convergence of the attacking side and slows the convergence of the intrusion tolerant-party compared to that of case 1. As shown in Fig. 4, when the initial state is (p1,q1)=(0.6,0.2), the strong attack strategy reaches a steady state after 0.94-time units of simulation, and the strong intrusion tolerance strategy reaches a steady state after 4.3-time units of simulation; When the initial state is (p1,q1)=(0.8,0.4), the strong attack strategy reaches stability after 1.25-time units of simulation, and the strong intrusion tolerance strategy reaches stability after 4.8-time units of simulation.

Figure 4: Evolutionary trend of the attacker and the intrusion tolerant party

In summary, after simulation for the given parameter values, the attacker and the intrusion-tolerant party reach a steady state after many evaluations to calculate their respective optimal strategies. For the intrusion-tolerant party, convergence is faster when the incentive weights are larger and when the strategy is more favorable to the intrusion-tolerant party. However, for the attacker, convergence is faster when the incentive weights are smaller. The faster the convergence rate is, the more favorable the strategy is for the attacker at this point. The simulation results of the experiment are consistent with the theoretical part described in this paper. The results verify the feasibility of the incentive weights of the improved replicated dynamic equations, and they provide strategy support for the experiments of the game model based on racial competition in the next section.

5.3 Nodal Voltage Influence Experiment

For the attacker’s strategy set SA, we divide the attacker’s strategy into five categories based on the attack strength SA={A1,A2,A3,A4,A5}, where the smaller value represents a higher strategy strength, i.e., a higher attack threat level, specifically as shown in Table 4.

For the strategy set ST of the intrusion-tolerant party, we divide the strategies of the intrusion tolerant party into five categories ST={T1,T2,T3,T4,T5} according to the aggression tolerance strength, where a smaller value represents greater strategy strength, i.e., greater intrusion tolerance strength. The details are shown in Table 5.

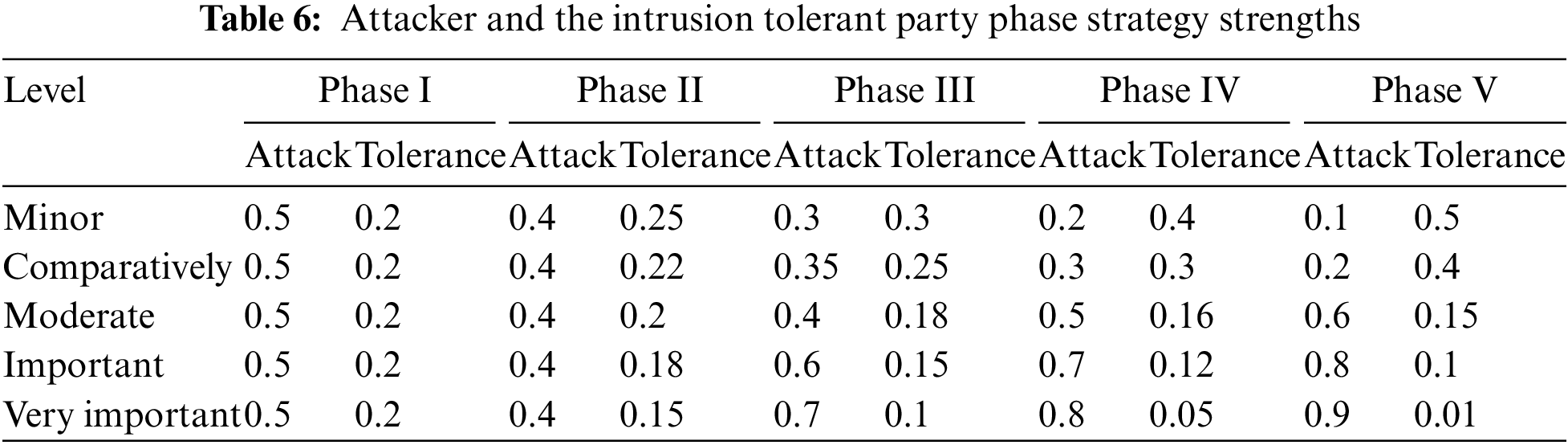
In this paper, we divide the racial competition game process between the attacker and the intrusion-tolerant party into five stages. In each stage, the optimal strategies of both sides are derived according to the current situation. Simulation experiments are conducted based on the current strategies at each node voltage of the IEEE 39-bus system. The feasibility and the usability of the presented model are analyzed through the final voltage of each node. The specific strategy strength is shown in Table 6.

•   As shown in Table 6, it is assumed that the attacker achieves greater gains by attacking the nodes with lower strategy strengths during the attack process; this increases the attack strength on the nodes with lower strategy strengths and weakens the attack strength on the nodes with lower gains in the next phase. Similarly, when the intrusion-tolerant party receives an attack, it adopts different intrusion tolerance strategies according to the importance of different nodes. The more important nodes adopt higher strength intrusion tolerance strategies to ensure that such nodes can complete the required functions; less important nodes adopt lower strength intrusion tolerance strategies to ensure that such nodes can complete the most basic functions.

•   In the first phase, since the attacker and the intrusion-tolerant party do not know each other’s policy strengths, the intrusion-tolerant party chooses a policy strength of 0.2 for all nodes. The attacker chooses a policy strength of 0.5. In the second phase, the attacker adjusts the policy strength to 0.4 after gaining the attack gain; then, the intrusion-tolerant party adjusts the tolerance policy after being compromised by the attacker by adopting policy strengths of 0.25, 0.22, 0.2, 0.18, and 0.15 for nodes of different importance. Phase III and so on continue with different strengths of attack and intrusion tolerance strategies in real time.

•   The residual voltage of each node is finally obtained, and the secondary node can fulfill the most basic function if it reaches 30% of the starting voltage. The comparatively important nodes can fulfill the required function if they reach 40% of the starting voltage. Moderately important nodes can perform the required function if they reach 60% of the starting voltage. Important nodes can complete the step-down function if they reach 80% of the starting voltage. Very important nodes are the core of the system, and the integrity of the function of this node must be ensured. This requires that the residual voltage reaches 90% of the starting voltage.

Based on Table 6, the attacker and the intrusion-tolerant party adopted different policy strengths for the IEEE 39-bus system. Fig. 5 shows the voltage values of the minor, comparatively important, moderately important, important and critical nodes at the initial moment, the first stage and the final moment.

•   Figs. 5a and 5b show that less voltage is lost after the first phase. The strength of the tolerant intrusion strategy chosen by the minor and comparatively important nodes in the first phase is 0.2.

•   Fig. 5c shows that the moderately important nodes adopted an incremental strategy intensity of the intrusion-tolerant party from the first stage onward. At this point, since the attacker achieves less attack gain on the medium important nodes compared to that of the secondary and more important nodes, the attacker chooses a decreasing strategy strength. Eventually, the moderately important nodes maintain most of the tension.

•   Fig. 5d shows the voltage variations at important and critical nodes. Important and very important nodes are the core of the whole system. Most of the work must be done by these two types of nodes. When the attacker is detected by the intrusion-tolerant party, the strategy is adjusted after the first phase, and the intrusion-tolerant party adopts an increasing strategy strength; then, the attacker wins fewer attacks on these two types of nodes and adjusts to a decreasing strategy strength. Finally, important and very important nodes lose the least tension.

Figure 5: Voltage variation of IEEE 39-bus

For the IEEE 39-bus system, the same level of node voltage change is not obvious. To simplify the analysis, in the experiments, the most obvious nodes at different levels are selected for comparison. For minor nodes, comparatively important nodes, moderately important nodes, important nodes and very important nodes, nodes 30, 9, 17, 2, and 16, respectively, were selected. as shown in Fig. 6.

Figure 6: Voltage variation of IEEE 39-bus

In a normal attack scenario, the attacker randomly and indiscriminately attacks all nodes. This can result in the paralysis of critical nodes and the inability of the required functions of the system to be performed. Therefore, the AITGM is used to protect nodes of high importance as much as possible by adopting an intrusion-tolerant strategy at certain nodes that cannot withstand the strength of the attack. To ensure the proper operation of the entire system, it is necessary to maintain only the minimum voltage for each node to perform its required function.

•   As shown in Fig. 6, the voltage of node 30 in the minor nodes decreases from 1.05 to 0.378 V after five stages of the strategy. As such, nodes are required to perform only the most basic functions in the system, a voltage of 30 percent of the starting voltage is sufficient. The comparatively important node 9 goes from an initial value of 1.038 to 0.447 V, reaching 40 percent of the starting voltage. Moderately important node 17 went from 1.034 to 0.699 V, reaching 60 percent of the starting voltage. Important and very important nodes, which are the core part of the whole system, have higher voltage requirements than do other classes of nodes. Important node 2 went from 1.048 to 0.844 V, meeting 80% of the requirement, and very important node 16 went from 1.033 to 0.932 V, meeting 90% of the residual voltage to the starting voltage.

•   We consider, for example, minor nodes and very important nodes. In the first stage, the attack intensity and intrusion tolerance for minor nodes and very important nodes are 0.5 and 0.2, respectively. In this stage α15=S1S5=1, β15=D1D5=1. There is no incentive relationship between intrusion strategies for minor nodes and highly important nodes, likewise, there is no incentive relationship between attack strategies.

•   Due to the system detecting an attack, in the second stage, the system adjusts the strategy intensities for each node. The attack intensity and intrusion tolerance for minor nodes are adjusted to 0.4 and 0.25, respectively, while for very important nodes, the attack intensity and intrusion tolerance are adjusted to 0.4 and 0.15, respectively. In this stage α15=S1S5=1, β15=D1D5=1.6. Therefore, there is no incentive relationship between attack strategies for minor nodes and very important nodes. The intrusion tolerance strategy of minor nodes promotes the intrusion tolerance strategy of very important nodes. As a result, minor nodes endure more attacks compared to very important nodes, thereby safeguarding the very important nodes.

•   In the third stage, to safeguard nodes of very important levels, the attack intensity and intrusion tolerance for minor nodes are adjusted to 0.3 each, while for very important nodes, the attack intensity and intrusion tolerance are adjusted to 0.7 and 0.1, respectively. In this stage α15=S1S5=0.428, β15=D1D5=3. Minor nodes’ intrusion tolerance strategy promotes the intrusion tolerance strategy of very important nodes. However, attackers gain more benefits from attacking minor nodes compared to very important nodes, which leads to an increase in the attack intensity on minor nodes and a decrease in the attack intensity on highly important nodes. At the same time, the intrusion side further intensifies its intrusion tolerance strategy against very important nodes while reducing the intrusion tolerance intensity against minor nodes. Following this pattern, similar methods are employed in subsequent stages to achieve the protection of nodes with higher importance levels while ensuring that nodes with lower levels can maintain the voltage required to perform basic functions.

Through the experimental simulation, all five types of nodes satisfy the required voltage for the normal operation of the system, which again verifies the feasibility of the incentive weights and proves the effectiveness of the AITGM proposed in this paper. The core idea is to reduce the voltage of nodes with low importance levels, while preserving the voltage of nodes with higher importance levels as much as possible, ensuring that each node can still perform its required functions even when under attack, ultimately guaranteeing the normal operation of the entire system in network attack scenarios.

6  Conclusions

This paper proposes an Adaptive Intrusion Tolerance Game Model for network attacks. Firstly, a tolerant intrusion model with improved replication of the dynamic equation evolution game is constructed to elicit the incentive weights. Secondly combining incentive weights to model the attacker and the intrusion tolerant party based on racial competition. Finally, the incentive weights are verified by experimental simulation to motivate the strategies in the game between the attacker and the intrusion tolerant party, and the residual voltages of the nodes with different importance levels are obtained by simulating the game process between the attacker and the intrusion tolerant party at the IEEE 39-bus system. Experiments demonstrate the feasibility and effectiveness of the Adaptive Tolerance Intrusion Game Model proposed in this paper. In the future, based on the research in this paper, the dynamic adaptability and tolerance level accuracy of the model will be further optimized by considering factors such as the actual operating mode of the power equipment, multiple nodes or branches.

Acknowledgement: The authors would like to thank all the reviewers for their comments and suggestions on this paper.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 51977113, 62293500, 62293501 and 62293505).

Author Contributions: Study conception and design: Song Deng and Yiming Yuan; data collection: Song Deng and Yiming Yuan; analysis and interpretation of results: Song Deng and Yiming Yuan; draft manuscript preparation: Song Deng and Yiming Yuan. Both authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. Yue and Q. L. Han, “Guest editorial special issue on new trends in energy internet: Artificial intelligence-based control, network security, and management,” IEEE Trans. Syst., Man, Cybern.: Syst., vol. 49, no. 8, pp. 1551–1553, 2019. doi: 10.1109/TSMC.2019.2923034. [Google Scholar] [CrossRef]

2. A. K. Sandhu, “Big data with cloud computing: Discussions and challenges,” Big Data Min. Anal., vol. 5, no. 1, pp. 32–40, 2021. doi: 10.26599/BDMA.2021.9020016. [Google Scholar] [CrossRef]

3. H. Lu, M. Zhang, X. Xu, Y. Li, and H. T. Shen, “Deep fuzzy hashing network for efficient image retrieval,” IEEE Trans. Fuzzy Syst., vol. 29, no. 1, pp. 166–176, 2020. doi: 10.1109/TFUZZ.2020.2984991. [Google Scholar] [CrossRef]

4. H. Lu, Y. Teng, and Y. Li, “Learning latent dynamics for autonomous shape control of deformable object,” IEEE Trans. Intell. Transp. Syst., vol. 24, no. 11, pp. 13133–13140, Nov. 2023. doi: 10.1109/TITS.2022.3225322. [Google Scholar] [CrossRef]

5. H. Song, J. Li, and H. Li, “A cloud secure storage mechanism based on data dispersion and encryption,” IEEE Access, vol. 9, pp. 63745–63751, 2021. doi: 10.1109/ACCESS.2021.3075340. [Google Scholar] [CrossRef]

6. M. Tanveer, A. U. Khan, N. Kumar, A. Naushad, and S. A. Chaudhry, “A robust access control protocol for the smart grid systems,” IEEE Internet Things J., vol. 9, no. 9, pp. 6855–6865, 2021. doi: 10.1109/JIOT.2021.3113469. [Google Scholar] [CrossRef]

7. A. Thakkar and R. Lohiya, “A survey on intrusion detection system: Feature selection, model, performance measures, application perspective, challenges, and future research directions,” Artif. Intell. Rev., vol. 55, no. 1, pp. 453–563, 2022. doi: 10.1007/s10462-021-10037-9. [Google Scholar] [CrossRef]

8. S. Deng, Q. Hu, D. Wu, and Y. He, “BCTC-KSM: A blockchain-assisted threshold cryptography for key security management in power IoT data sharing,” Comput. Electr. Eng., vol. 108, no. 1, pp. 108666, 2023. doi: 10.1016/j.compeleceng.2023.108666. [Google Scholar] [CrossRef]

9. G. Wang, Y. Chao, Y. Cao, T. Jiang, W. Han, and Z. Chen, “A comprehensive review of research works based on evolutionary game theory for sustainable energy development,” Energy Rep., vol. 8, pp. 114–136, 2022. doi: 10.1016/j.egyr.2021.11.231. [Google Scholar] [CrossRef]

10. D. B. Gothawal and S. Nagaraj, “Anomaly-based intrusion detection system in rpl by applying stochastic and evolutionary game models over IoT environment,” Wirel. Pers. Commun., vol. 110, no. 3, pp. 1323–1344, 2020. doi: 10.1007/s11277-019-06789-x. [Google Scholar] [CrossRef]

11. Z. Zhang, J. Hu, J. Lu, J. Cao, and F. E. Alsaadi, “Preventing false data injection attacks in lfc system via the attack-detection evolutionary game model and KF algorithm,” IEEE Trans. Netw. Sci. Eng., vol. 9, no. 6, pp. 4349–4362, 2022. doi: 10.1109/TNSE.2022.3199881. [Google Scholar] [CrossRef]

12. H. Jin et al., “Evolutionary game decision-making method for network attack and defense based on regret minimization algorithm,” J. King Saud Univ.-Comput. Inf. Sci., vol. 35, no. 3, pp. 292–302, 2023. doi: 10.1016/j.jksuci.2023.01.018. [Google Scholar] [CrossRef]

13. H. Hu, Y. Liu, C. Chen, H. Zhang, and Y. Liu, “Optimal decision making approach for cyber security defense using evolutionary game,” IEEE Trans. Netw. Serv. Manag., vol. 17, no. 3, pp. 1683–1700, 2020. doi: 10.1109/TNSM.2020.2995713. [Google Scholar] [CrossRef]

14. X. Xu, G. Wang, J. Hu, and Y. Lu, “Study on stochastic differential game model in network attack and defense,” Secur. Commun. Netw., vol. 2020, no. 6, pp. 1–15, 2020. doi: 10.1155/2020/3417039. [Google Scholar] [CrossRef]

15. X. Liu, H. Zhang, Y. Zhang, and L. Shao, “Optimal network defense strategy selection method based on evolutionary network game,” Secur. Commun. Netw., vol. 2020, no. 6, pp. 1–11, 2020. doi: 10.1155/2020/8856592. [Google Scholar] [CrossRef]

16. J. Fraga and D. Powell, “A fault-and intrusion-tolerant file system,” in Proc. 3rd Int. Conf. Comput. Secur., vol. 203, no. 218, 1985. [Google Scholar]

17. F. Di Giandomenico, G. Masetti, and S. Chiaradonna, “Redundancy-based intrusion tolerance approaches moving from classical fault tolerance methods,” Int. J. Appl. Math. Comput. Sci., vol. 32, no. 4, pp. 701–719, 2022. [Google Scholar]

18. N. Sanoussi, G. Orhanou, and S. E. Hajji, “A game theoretic approach based on intrusion tolerant systems,” Int. J. Secur. Netw., vol. 15, no. 3, pp. 175–181, 2020. doi: 10.1504/IJSN.2020.109698. [Google Scholar] [CrossRef]

19. Z. Zhao, Y. Ren, C. Mu, T. Zou, and K. S. Hong, “Adaptive neural-network-based fault-tolerant control for a flexible string with composite disturbance observer and input constraints,” IEEE Trans. Cybern., vol. 52, no. 12, pp. 12843–12853, 2021. doi: 10.1109/TCYB.2021.3090417. [Google Scholar] [PubMed] [CrossRef]

20. G. Mehmood, M. Z. Khan, S. Abbas, M. Faisal, and H. U. Rahman, “An energy-efficient and cooperative fault-tolerant communication approach for wireless body area network,” IEEE Access, vol. 8, pp. 69134–69147, 2020. doi: 10.1109/ACCESS.2020.2986268. [Google Scholar] [CrossRef]

21. A. D. Jadhav and V. Pellakuri, “Accuracy based fault tolerant two phase-intrusion detection system (TP-IDS) using machine learning and HDFS,” Rev. Intell. Artif., vol. 35, no. 5, pp. 359–366, 2021. [Google Scholar]

22. J. Flora, “Improving the security of microservice systems by detecting and tolerating intrusions,” in 2020 IEEE Int. Symp. Softw. Reliab. Eng. Workshops (ISSREW), Coimbra, Portugal, 2020, pp. 131–134. [Google Scholar]

23. J. Zheng, H. Okamura, T. Dohi, and K. S. Trivedi, “Quantitative security evaluation of intrusion tolerant systems with markovian arrivals,” IEEE Trans. Reliab., vol. 70, no. 2, pp. 547–562, 2020. doi: 10.1109/TR.2020.3026570. [Google Scholar] [CrossRef]

24. Y. Wang, Y. Guo, W. Wang, H. Liang, and S. Huo, “INHIBITOR: An intrusion tolerant scheduling algorithm in cloud-based scientific workflow system,” Future Gener. Comput. Syst., vol. 114, no. 9, pp. 272–284, 2021. doi: 10.1016/j.future.2020.08.004. [Google Scholar] [CrossRef]

25. B. Hong, H. Wang, and Z. Cao, “An effective fault-tolerant intrusion de-tection system under distributed environment,” Wirel. Commun. Mob. Comput., vol. 2021, pp. 1–9, 2021. [Google Scholar]

26. P. Kasu, P. Hamandawana, and T. S. Chung, “DLFT: Data and layout aware fault tolerance framework for big data transfer systems,” IEEE Access, vol. 9, pp. 22939–22954, 2021. doi: 10.1109/ACCESS.2021.3055731. [Google Scholar] [CrossRef]

27. M. Khan and A. Babay, “Toward intrusion tolerance as a service: Confidentiality in partially cloud-based bft systems,” in 2021 51st Annual IEEE/IFIP Int. Conf. Dependable Syst. Netw. (DSN), Taipei, Taiwan, 2021, pp. 14–25. [Google Scholar]

28. K. Jarosz, Ł. Opioła, Ł. Dutka, R. G. Słota, and J. Kitowski, “Increasing data availability and fault tolerance for decentralized collaborative data-sharing systems,” in 2022 17th Conf. Comput. Sci. Intell. Syst. (FedCSIS), Sofia, Bulgaria, 2022, pp. 563–566. [Google Scholar]

29. K. Zhu, Y. Ren, and Q. Zhu, “A provable data possession protocol in cloud storage systems with fault tolerance,” in 2021 IEEE Conf. Dependable Secur. Comput. (DSC), Aizuwakamatsu, Fukushima, 2021, pp. 1–6. [Google Scholar]

30. J. Li, P. Li, R. J. Stones, G. Wang, Z. Li and X. Liu, “Reliability equations for cloud storage systems with proactive fault tolerance,” IEEE Trans. Dependable Secure Comput., vol. 17, no. 4, pp. 782–794, 2018. doi: 10.1109/TDSC.2018.2882512. [Google Scholar] [CrossRef]

31. Y. Li, M. Wang, X. Xie, W. Chai, and X. Chen, “Brain-inspired perception feature and cognition model applied to safety patrol robot,” IEEE Trans. Ind. Inform., vol. 20, no. 4, pp. 5683–5691, 2023. doi: 10.1109/TII.2023.3337971. [Google Scholar] [CrossRef]