SFGA-CPA: A Novel Screening Correlation Power Analysis Framework Based on Genetic Algorithm

1  Introduction

Cryptographic devices are widely used in modern life with the rapid development of information technology. However, the security problems of the device are also more serious when people enjoy the convenience. In particular, encryption algorithms are the key to cryptographic devices, and their security also directly affects the operation of the devices [1]. Therefore, encryption algorithms have aroused increasingly more attention. In fact, their security depends not only on mathematical security but is closely related to the operation of the device during operation. Moreover, side-channel analysis (SCA) is a very important role in evaluating encryption algorithms. It is based on the assumption that an attacker can obtain some intermediate state information to break the key. This information is related to the operation of the device to save the secret key or subkey in running the encryption algorithm [2]. It includes time [3], power consumption [4–6], electromagnetic energy [7,8], and some other ones. After that, many effective methods have been proposed along with the development of SCA, such as correlation power analysis (CPA) [9], template attack [10], collision attack [11], mutual information analysis [12], and other methods. Among them, CPA is one of the most commonly used attack methods in SCA [13–15]. It is able to recover the key very quickly by the divide and conquer method. However, CPA disregards the information generated by other modules as noise when analyzing only one module. Consequently, valuable information contained in those modules goes to waste.

Recently, a lot of attack methods that combine artificial intelligence (AI) with CPA have continued to emerge. This includes machine learning-based CPA, which incorporates support vector machines (SVM) [16,17], neural networks [18,19], decision trees [20,21], rotation forests [22,23], and more. Meanwhile, heuristic algorithm are now being utilized to tackle complex problems arising in various fields, such as economics, engineering, politics, and management [24]. Therefore, the SCA community has also developed a strong interest in Genetic Algorithms (GA) within heuristic algorithms and is attempting to integrate CPA with GA [25]. GA is chosen to combine with CPA because it can handle discrete variable effectively. Ant colony optimization is not suitable for CPA even though it can also handle discrete variable. Because its focus leans more towards finding the optimal path for the solution combination. However, the individual key should be given more attention when recovering the key. For these reasons and the advantages that GA is easy to implement, GA has been widely used in CPA. Moreover, the SCA community is continuously working to enhance the performance of CPA based on GA.

More recently, a CPA method based on a simple genetic algorithm (SGA-CPA) was proposed by Zhang et al., and it is capable of recovering all subkeys [26]. Therefore, SGA-CPA addresses the issue of inadequate utilization of key information present in CPA and achieves a superior attack effectiveness compared to CPA. Because its target is to recover a key rather than individual bytes, it does not ignore the power consumption information generated by other bytes. In 2021, Ding et al. optimized the algorithmic structure of SGA-CPA and introduced multi-screening method (MS-CPA) [27]. Thus, the issues of insufficient search capability and premature convergence in SGA-CPA have been addressed. Unfortunately, these methods still face some challenges, even though researchers in the field of SCA have been consistently working to improve the performance of CPA based on GA. These issues include: (1) the population evolution rate in the GA-based CPA method is too slow, (2) the key population may exhibit a phenomenon of reverse evolution, and we refer to this as key degradation and (3) how to choose better parameters. These issues severely limit the speed of subkeys recovery.

It is believed that addressing these issues can bring several advantages, such as more powerful attacks can be launched and more secure cryptographic algorithms are designed and implemented in chips. While this sounds like an intuitive approach to enhance the speed of key recovery, it is not a simple problem. Firstly, the evolution speed of the key population needs to be increased by carefully balancing multiple aspects. If the evolutionary speed is too fast, the key population is prone to getting stuck in local optima and finding incorrect keys. Secondly, the three issues mentioned above will collectively influence the evolutionary speed. If only two of these issues are addressed, the speed of key recovery will still decrease due to the remaining problem. Therefore, it is necessary to propose a suitable solution for each of these three issues based on the characteristics of CPA.

A correlation power analysis screening framework combined with the genetic algorithm (SFGA-CPA) has been proposed which effectively addresses the aforementioned issues. The propagation operation has been integrated into SFGA-CPA, combining the characteristics of CPA and possessing the advantage of promoting the secondary evolution of the key population. At the same time, the crossover and mutation operations in the genetic algorithm (GA) have been reconstructed and optimized into constrained crossover and constrained mutation operations. These two operations can overcome the issue of key degradation. Finally, parameters are also one of the important factors influencing key recovery. However, determining the parameters is a complex task. Therefore, an intelligent search method is proposed to find optimal parameters to enhance the speed of key recovery.

The contribution of this paper is as follows:

•   The theoretical proof that SFGA-CPA can accelerate population evolution has been provided. This theoretical proof may have a positive impact on the research and practice of GA-based CPA, providing strong support for further algorithm optimization and improvement.

•   We provide experimental results on publicly available datasets. The results consistently indicate that SFGA-CPA surpasses other methods in both the speed of key recovery and the number of power traces employed. Then, the process of recovering the key proves that there is no degradation in the key population.

•   This article also proposes an intelligent search method to find better solutions. It can overcome the complexity of parameter selection and explore the parameter space more effectively.

The remaining parts of this paper are constructed as follows: Chapter 2 introduces the related technical theory of GA and CPA; Chapter 3 is divided into two sections. The first section describes the methods and issues of SGA-CPA and MS-CPA, while the second section describes the theory and process of SFGA-CPA; Chapter 4 describes the methods of constrained crossover, constrained mutation, and obtaining optimal parameters; Chapter 5 compares our method with other methods through simulation experiments and real experiments; Chapter 6 concludes the paper.

2  Basic Principle

2.1 Genetic Algorithm

GA is a random search method by imitates the evolutionary rule of nature. It was proposed by American scholar J. Holland in 1975. GA has the capability to directly operate on the target and dynamically adjust the search direction [25]. The characteristics of the algorithm are random, adaptive, and highly parallel, so it has a good ability to search for the optimal solution. GA involves the following concepts:

•   Individuals refer to potential solutions to problems. It needs to be represented by a code, whereas a common representation is a binary code.

•   Populations are composed of multiple individuals. The population size refers to the number of individuals within the population. If a population consists of N individuals, it is referred to as having a population size of N.

•   Fitness reflects the degree of goodness of the individual. It is calculated by the fitness function. In this paper, the fitness function is chosen from the correlation coefficient formula.

•   Selection operation can choose excellent individuals for the new population. It not only enhances the fitness of the population but also facilitates its advancement in a favorable direction.

•   Crossover operations usually allow two individuals (parents) to swap genes with pc probability. Therefore, two new individuals are generated.

•   Mutation operations can randomly change one or several bits in an individual with pm probability to generate a new bit string.

First, an initial population is generated at random, and the fitness of individuals is calculated through the fitness function within the GA. Subsequently, it is determined whether the desired outcome is included in the population. If a desired outcome is found, it is outputted and the algorithm terminates; otherwise, the selection process is initiated. Then, some excellent individuals are selected through fitness to enter the next generation and form a new population. Afterwards, individuals in the new population undergo crossover and mutation operations to produce new offspring. These two operations can effectively ensure the diversity of the population and help the population find results more quickly. Finally, the fitness of each individual is calculated again to determine whether there is a correct solution. If a correct result is found, the algorithm terminates and outputs the result. Otherwise, the aforementioned process is repeated.

2.2 Correlation Power Analysis

All symbols appearing in this article are elaborately defined in Table 1.

CPA is widely used because of its efficiency and simplicity. It is a statistical method used to reveal the secret key K by analyzing a large number of power traces T generated by a cryptographic device encrypting plaintext P. The power consumption model can be regarded as a method that maps the intermediate value f(P,K) to the power traces T. The Hamming weight model is a commonly used power consumption model in the SCA community. It assumes that power consumption T is correlated with the number of 1’s in the binary representation of the intermediate value f(P,K). Therefore, the Hamming weight of x is HW(x)=∑i=07xi when data x={x7x6⋯x0} is stored in an 8-bit register. The power consumption W is shown in Eq. (1).

W=α×HW(f(P,K))+Pnoise(1)

The CPA differs from traditional attack methods as it can recover only one byte Ki of the secret key K at a time. Therefore, it employs a divide-and-conquer approach to recover the secret key K. The attacker will calculate the Hamming weight of intermediate values HW(f(P,G_K)). If G_K=K, then there will be a strong correlation between the Hamming weight and T. Therefore, the Pearson correlation coefficient can be used to assess whether the guessed key G_K is correct. The pearson correlation coefficient equation is shown in Eq. (2).

ρ=cov(W,HW(f(P,G_K)))σWσHW(f(P,G_K))(2)

3  A Correlation Power Analysis Screening Framework

3.1 Introduction of SGA-CPA and MS-CPA

SGA-CPA was proposed by Zhang et al. in 2015 to improve CPA efficiency [26]. In SGA-CPA, candidate keys are defined as individuals. Correlation coefficients are regarded as individual fitness, which is obtained by calculating the relationship between assumed power traces and real power traces. This method produces a population by initializing multiple candidate keys and subsequently calculates the fitness of individuals. Then new individuals are obtained by selecting individuals with high fitness for crossover and mutation. These new individuals enter the next generation to form new populations. Finally, the fitness of the new individual is calculated. If the correct result exists in the new individual, the algorithm terminates; otherwise, it proceeds with the previous process. This approach solves the problem of underutilization of information in traditional CPA because it operates on keys rather than bytes. However, Ding et al. found the problems of premature convergence and insufficient local search capability of SGA-CPA [27]. Therefore, MS-CPA was proposed. The method uses a multi-population strategy. Therefore, MS-CPA can obtain multiple excellent individuals. Then these best individuals are combined again to produce the best result. Although MS-CPA has solved the problem of SGA-CPA and improved the efficiency of the attack, there are still some problems with the above two methods.

Firstly, the essence of the GA lies in the evolution of the population to search for optimal results. However, only the selection operation in GA can meet this requirement among all its operations. As a result, it is not enough to sufficiently improve the evolutionary speed of the population.

Second, crossover and mutation may decrease the fitness of individuals even though these are designed to increase the diversity of populations. The reason is that the correct byte can deteriorate further after undergoing crossover and mutation. This can interfere with the evolution of the population and increase the difficulty of attack.

Thirdly, the approach used to determine the parameters in these methods is unreasonable. They cannot be determined individually because parameters are interdependent rather than independent and mutually affect each other in experiments. So, determining excellent parameters is also important for improving attack efficiency.

3.2 A Correlation Power Analysis Screening Framework

Recovering the key should not solely rely on the number of GA iterations, but rather should be optimized in terms of its structure and operations. At the same time, some conditions can be known and utilized when executing the algorithm. First, the candidate key is always given some correct bytes in a round of GA. In addition, the number of correct bytes in the candidate key is proportional to the degree of fitness [26]. Therefore, a method should be proposed according to this situation to solve the problem in Section 3.1.

First, the set Aj={ki|i=0,1,2,⋯,n}(j=1,2,3,⋯,N) is used to record the recovered bytes during the execution of GA with the key, where i and j represent the positions of the recovered bytes and the key individuals, respectively. Meanwhile, aj(j=1,2,3,⋯,N) is used to represent the count of elements in set Aj, which corresponds to the number of correct bytes recovered for an individual. The relationship between the set Aj and aj is as follows, where the purpose of Card is to find the number of elements contained in Aj.

{a1=Card(A1)a2=Card(A2)a3=Card(A3)⋮aN=Card(AN)(3)

At the same time, the key requires a minimum of mj(mj≥naj) iterations of GA for recovery when it consists of n bytes. The probability P that each key can be recovered is:

{P1≈1−(Cn−1a1Cna1)m1P2≈1−(Cn−1a2Cna2)m2P3≈1−(Cn−1a3Cna3)m3⋮PN≈1−(Cn−1ajCnaj)mj(4)

If ncorrect=1n∑i=1nai, the success rate of key recovery can be represented by Eq. (5) when the key undergoes m(m≥nncorrect) iterations of a GA.

Psuccess≈1−(Cn−1ncorrectCnncorrect)m≈1−(n−ncorrectn)m(5)

According to Eq. (5), it is clear that choosing the maximum value of ncorrect can maximize the success rate Psuccess for key recovery. At this stage, set Bj(j=1,2,3,⋯,N) is redefined and ensuring that it satisfies the following relationship with set Aj:

{B1=A1B2=(B1∪A2)B3=(B2∪A3)⋮BN=(BN−1∪AN)(6)

The number of elements in the sets Bj is denoted by bj(j=1,2,3,⋯,N), and the relationships between bj and set Bj are as follows:

{b1=Card(B1)b2=Card(B2)b3=Card(B3)⋮bN=Card(BN)(7)

Eq. (8) can also be obtained based on b3=Card(B3)=Card(B2∪A3).

b3=Card(B2∪A3)≥max(b2,a3)(8)

Eq. (9) can be obtained by analogy to Eq. (8). The results are as follows:

{b1=a1b2≥(b1,a2)b3≥(b2,a3)⋮bn≥(bn−1,an)(9)

The probability Psuccess of key recovery is maximized when ncorrect equals bn. So a correlation power analysis screening framework (SFGA-CPA) is proposed based on the above theory. Fig. 1 illustrates the specific solution proposed in this paper. The red squares represent the correct bytes at those positions, while the white squares represent the incorrect bytes.

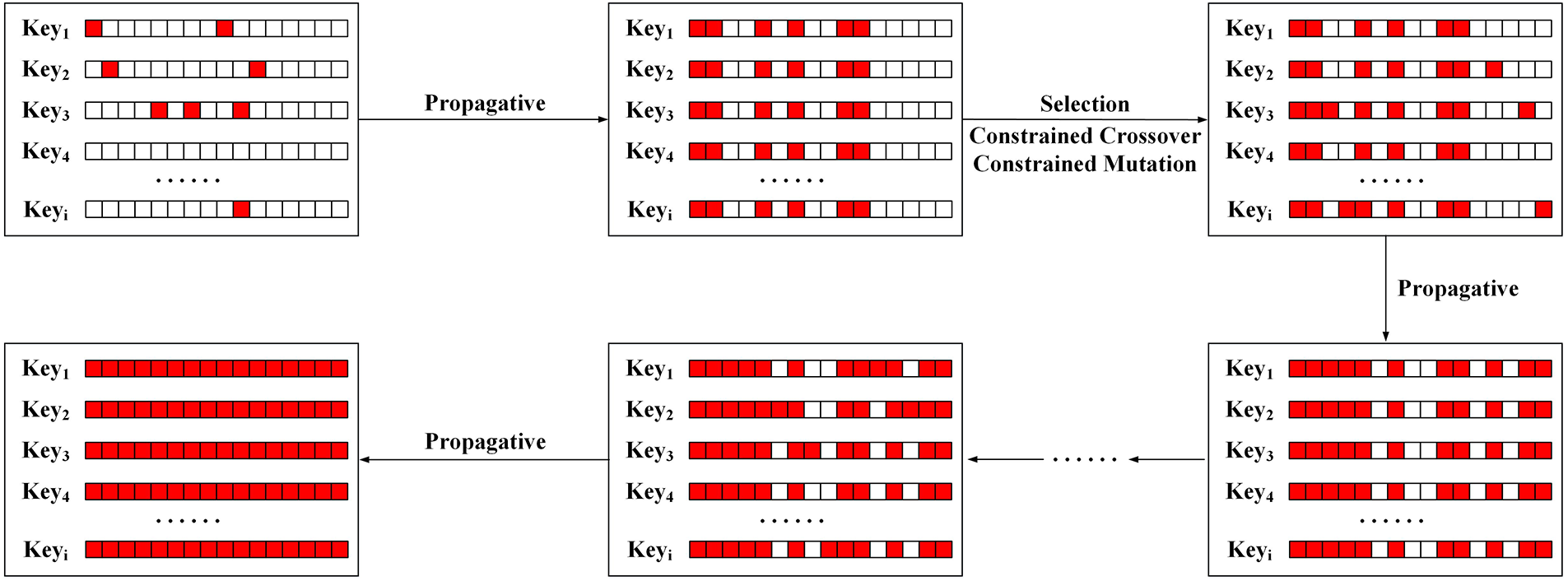
Figure 1: Schematic diagram of SFGA-CPA

SFGA-CPA pays more attention to whether the correct bytes will be filtered out compared to MS-CPA and SGA-CPA. The correct bytes refer to the bytes with the highest correlation coefficient to the guessed key. This means that MS-CPA and SGA-CPA lack structural protective mechanisms addressing this aspect. Therefore, SFGA-CPA has been structurally optimized to avoid this scenario. It not only possesses protective capabilities but also has the advantage of accelerating population evolution compared to MS-CPA and SGA-CPA. Fig. 2 depicts the flow chart of SFGA-CPA.

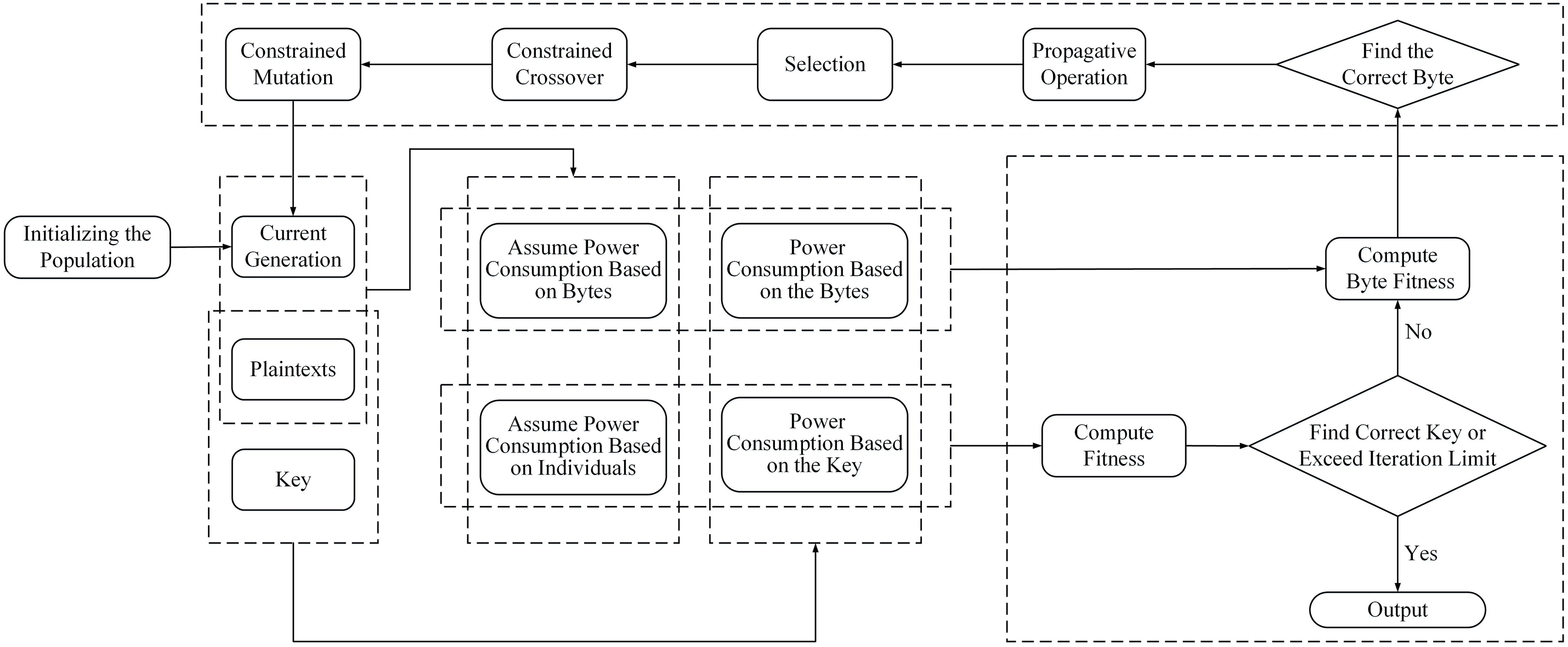
Figure 2: Flow chart of SFGA-CPA

First, multiple candidate keys are initialized to form a population. Then the candidate key and byte fitness are calculated separately. If the correct key exists, output the result; otherwise, determine if the correct byte exists. The right bytes are propagated to other candidate keys. The process ensures that the number of right bytes in the candidate key is maximized. Because the candidate key is capable of obtaining the correct bytes from other candidate keys. Then, the good individuals are selected for constrained crossover and constrained mutation. Among them, the correct bytes in individuals will not be altered. This ensures the maximization of the number of correct bytes in the candidate key and addresses the issue of degradation in the GA. Finally, this process is repeated until the correct key is recovered. The pseudo-code of this method is shown in Algorithm 1.

Init_Population(N) randomly generates N candidate keys as a group Pop. Compute_Fitness(Pop) calculates the fitness of individuals in Pop. Compute_byte(Pop) is to calculate the fitness of bytes of individuals in Pop. Propagative_operations(Pop) copies the correct bytes of the individual in Pop to other ones. Selection(Pop) selects good individuals in Pop to form a new population Child_Pop. Constrained_Crossover(Child_Pop, pc) recombines the individuals in Child_Pop with probability pc, and Constrained_Mutations(Child_Pop, pm) mutates individuals in Child_Pop with pm. Meanwhile, the right byte will not be changed with Better_Crossover(Child_Pop, pc) and Better_Mutations(Child_Pop, pm). MaxFitness(Pop) will select the individual with the largest fitness in Pop as the result Best_key.

4  Operator and Parameters of SFGA-CPA

Operators are essential prerequisites for guiding GA to solve problems, as they generate and maintain the diversity of individuals. GA contains three operators, namely selection, crossover, and mutation, each of which includes various strategies. These operators need to collaborate with each other in order to effectively achieve optimal results, despite being employed to enhance individuals within the GA. In this context,the crossover and mutation operations are discussed and improved. At the same time, the determination of parameters is also important in GA. Therefore, the parameters of the algorithm will also be determined in 4.2 of this chapter.

4.1 Constrained Crossover and Constrained Mutation of SFGA-CPA

In traditional GA, the crossover operation involves exchanging chromosomes between two or more parent individuals to generate new offspring. It can uncover the excellent genes of an individual and prevent premature convergence to local optima. The mutation operation plays a crucial role in preserving population diversity and exploring the search space.

However, the individuals generated by crossover and mutation operations may not always be better than the previous generation, as the outcomes of crossover and mutation are random. Moreover, individuals have the possibility to become worse after crossover or mutation. This phenomenon is key degradation. The situation increases the time and difficulty of recovering the key. Meanwhile, the outcomes of individuals after crossover and mutation are difficult to control. Although guiding the offspring resulting from crossover and mutation is challenging, key degradation issues can be addressed by preserving the exceptional individuals from the previous generation. The degradation of the key is caused by the alteration or transfer of exceptional genes, and thus safeguarding these genes offers a solution to this problem. Consequently, constrained crossover and constrained mutation strategies have been proposed.

The basic idea of this process is to prevent the correct bytes from changing during crossover and mutation operations. This means that the crossover and mutation operations are constrained to be performed on the unmarked bytes. The key degradation problem can be solved by making the right bytes unaffected in crossover and mutation operations. Firstly, the fitness of the byte should also be taken into consideration when calculating the fitness of the individual, and the presence of the correct byte should be determined. If it exists, mark the correct byte accordingly. After that, the marked bytes will not be executed for crossover and mutation operations. This process is effective in protecting the right bytes and solving the key degradation problem. At the same time, the problem that populations fall into locally optimal solutions does not follow by the presence of constrained crossovers and mutation. Because the key individuals can escape from local optima and move closer to the global optimum when they contain more correct bytes than before. The presence of this condition is caused by the characteristics of CPA, where the fitness value increases as the number of correct bytes in the key increases.

The pseudo-code of the crossover operator is shown by Algorithm 2.

Pop is the population produced after the selection operation. w[j] is used to record the position of the right byte. Random_select(Pop) selects two random candidate keys pop1 and pop2 in Pop. Random(size(pop1)) randomly selects a position nbit for crossover, where size(pop1) is the length of pop1. Belong_byte(nbit) will find the byte j that contains the bit at position nbit. Exchange(pop1_ nbit, pop2_ nbit) is to exchange the bits of nbitpositions in pop1 and pop2.

The pseudo-code of the mutation operator is shown by Algorithm 3.

Pop is the population generated after crossover.

4.2 Intelligent Search Method of SFGA-CPA

There are four parameters to be determined in the GA, which are the number of individuals N, the number of competition individuals x, the crossover probability pc, and the mutation probability pm. However, these four parameters cannot be determined separately because their effects on attack efficiency are not independent. Therefore, intelligent search methods are proposed to obtain the best combination of parameters. Its process of searching for the optimal parameters is shown in Fig. 3.

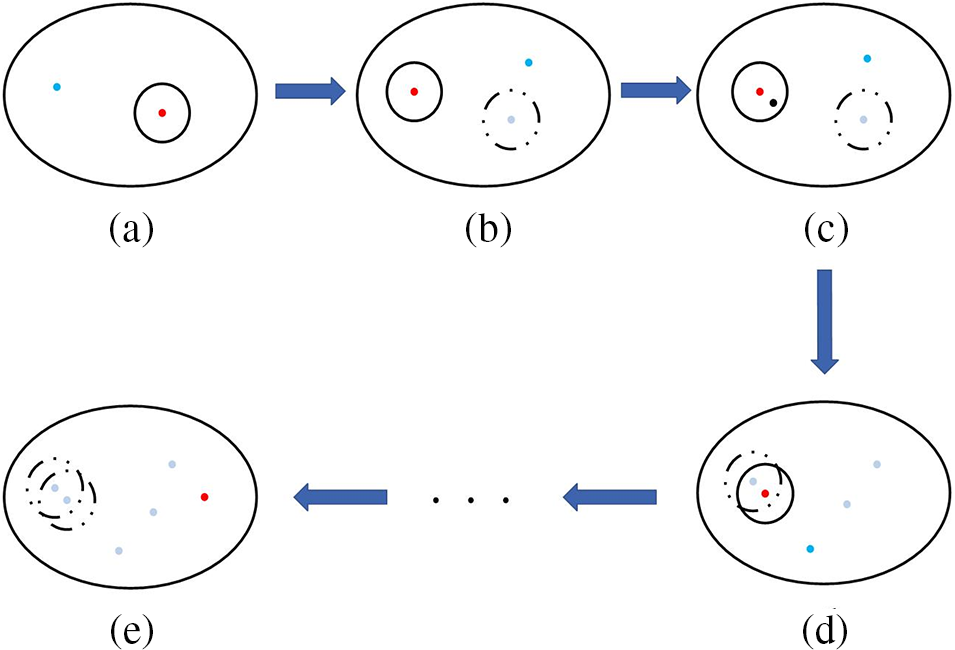
Figure 3: The process of searching for the optimal parameters

In Fig. 3, each point represents a combination of parameters N, x, pc, and pm. The interior of the ellipse represents all possible combinations of these four parameters. Meanwhile, the gray dots and the range enclosed by the dashed lines represent the discarded parameter combinations. Firstly, a set of initial parameters is determined based on experience, as shown in Fig. 3a. It is also known as the central data, represented by a red dot. Then search for combinations of parameters around the center data. At the same time, a group of parameters is randomly selected among all parameter combinations and represented by the blue dot. Finally, these selected combinations of parameters were subjected to experiments. The set of parameters with the best experimental results is considered the central data for the next operation. As shown in the process from Figs. 3a to 3b, the combination represented by the blue dot in Fig. 3a becomes the center data in Fig. 3b and is represented by a red dot. Because its experimental performance is the best among all the combinations. In addition, the central data in Figure a is represented by a gray dot in Fig. 3b, representing that it is discarded, and the solid circle drawn with it as the center becomes a dashed circle. It indicates that all parameter combinations within the dotted circle have been discarded. The next operation is the same as the one in Fig. 3a, but the experimental data are different. In Fig. 3b, the parameter combinations around the central data point were selected, and another set of parameters was chosen randomly. Then, these parameter combinations were experimented with again. In Fig. 3c, a black dot will be used temporarily to represent the combination with the best experimental result if it is around the central data. After that, it is considered as the central data for the next operation (Fig. 3d), and represented by a red dot. This operation is repeated 100 times until the best set of parameters is found. This method not only takes into account the local optimal solution, but also considers the global optimal solution.

In this paper, the initial parameters (N, x, pc, pm) = (60,24,0.6,0.02)are first determined empirically, where the parameter range is N∈[30,150], x={N×j|j=0.2,0.4,0.6,0.8}, pc∈{0.25,0.75}, pc∈{0.01,0.2}. The step sizes of N, x, pc, and pm are set to 5, 0.2, 0.1, and 0.01, respectively. These four parameters are moved only in one step and combined for them. Then, these four parameters are randomly selected and combined together. Experiments are performed on all parameter combinations. The best combination of parameters is found experimentally and identified as the central data. After that, the center data is performed the same operation as the start. Finally, the best combination of parameters is output if the number of executions exceeds a set threshold. The experimental results are shown in Fig. 4.

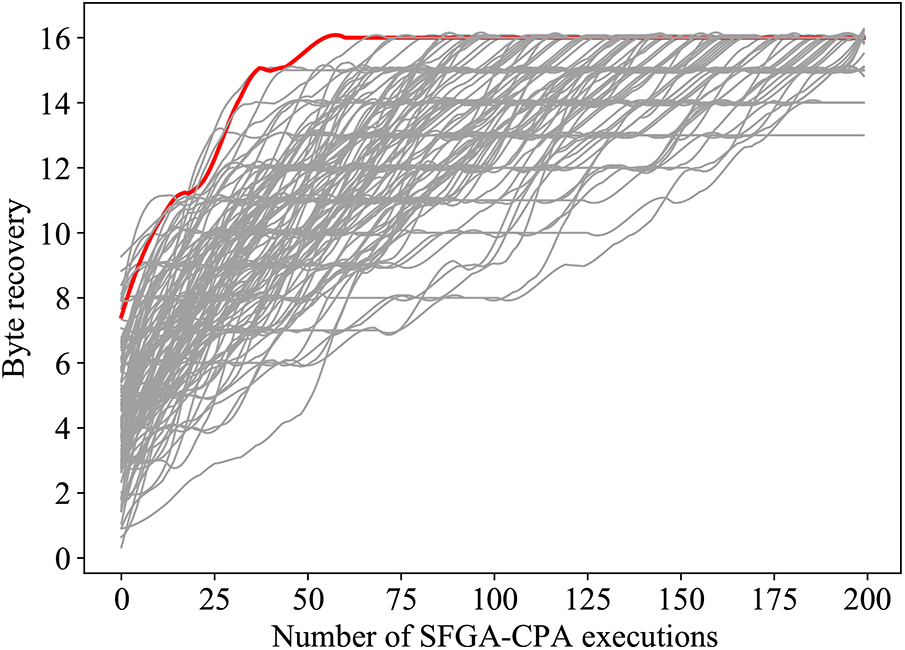
Figure 4: Comparison of simulation experiments

The combination of parameters represented by the red line in Fig. 4 can recover all bytes with just 53 times of SFGA-CPA, which is faster than other combinations. It represents the parameter combination of (N, x, pc, pm) = (75,45,0.6,0.1).

This approach is different from grid search and random search methods. Firstly, although grid search results are highly reliable, it is only suitable for small sample parameters. Secondly, random search is prone to miss the optimal solution, although it is suitable for parameters with large samples. This method reduces the difficulty as well as increases the accuracy in searching for the optimal solution to some extent.

5  Experimental Comparison and Analysis

5.1 Simulation Experiments

In the simulation experiments, the power consumption of the S-box operation is simulated by adding noise with a standard deviation of ∂=3. Meanwhile, SFGA-CPA, MS-CPA, and SGA-CPA were experimentally compared at the same power traces, which was sized from 60 to 500 in steps of 20. The success rate was used to assess the effectiveness of the three methods. For SFGA-CPA, the parameter are (N, x, pc, pm) = (75,45,0.6,0.1). The parameter used is (N, pt, pc, pt, Thgen, Thpop) = (500,0.4,0.5,0.12,150,30) in the execution of MS-CPA [27]. The parameter is (N, pt, pc, gen) = (30,0.6,0.01,100) when experimenting with SGA-CPA [26]. Fig. 5 shows the success rates of the three methods. The blue line represents SFGA-CPA, the orange line represents MS-CPA, and the green line represents SGA-CPA.

Figure 5: Comparison of simulation experiments

The experimental results demonstrate that our method is superior to the other two methods. SFGA-CPA achieves a success rate of 90% when using the 160 traces, while MS-CPA and SGA-CPA only achieve success rates of 65% and 30%, respectively. The MS-CPA and SGA-CPA require 220 and 380 power consumption curves respectively to achieve a success rate of 90%.

5.2 Real Experiments of SAKURA-G

In this section, we also conducted real experiments by encrypting random plaintexts on SAKURA-G using a fixed key in AES-128. The core of AES-128 is designed with a round-based structure, requiring 11 clock cycles for each encryption. The power traces during AES-128 encryption can be collected using the oscilloscope. Our attack is primarily focused on the intermediate state before the last round of S-box operation and the ciphertext, due to the fact that the registers in this hardware are implemented before the S-box operation.

In Fig. 6, 3000 power traces are acquired and stored with corresponding plaintexts and ciphertexts. These three methods, SFGA-CPA, ME-CPA, and SGA-CPA, were experimented on the same power traces, respectively. The range of power traces number used is from 100 to 400 with a step size of 10. The same parameters from the simulation experiments will be used in the real experiments, as AES-128 will still be used as an example in this section.

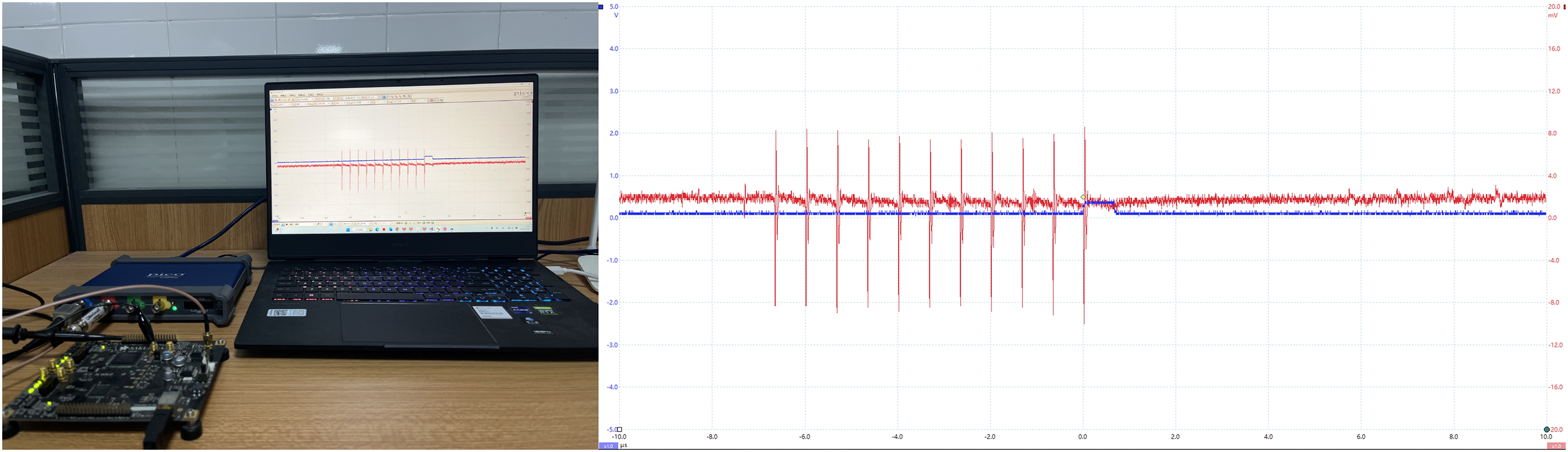
Figure 6: Power traces acquisiton

Fig. 7 illustrates the success rates for the number of recovered bytes. They show the relationship between the number of bytes recovered and the power traces. The success rate of byte recovery using SFGA-CPA is depicted in Fig. 7a. It is able to recover 16 bytes with only 290 power traces, which means that the correct key has been successfully recovered at this point. At the same time, the success rate of recovering 16 bytes can reach 90% when using 260 power traces. The MS-CPA byte recovery success rate is shown in Fig. 7b. This method requires 340 power traces to recover 16 bytes, an increase of 17.2% over SFGA-CPA. Meanwhile, the success rate of recovering 16 bytes to 90% requires 300 power consumption curves, which is 15.3% more than SFGA-CPA. The experimental results for SGA-CPA are shown in Fig. 7c. However, the attack success rate of SGA-CPA was not very high when using 400 power traces. At this point, the success rate is only 51%, which is 49% lower than that of SFGA-CPA and MS-CPA. It can be seen that SFGA-CPA has a better effect compared with MS-CPA and SGA-CPA.

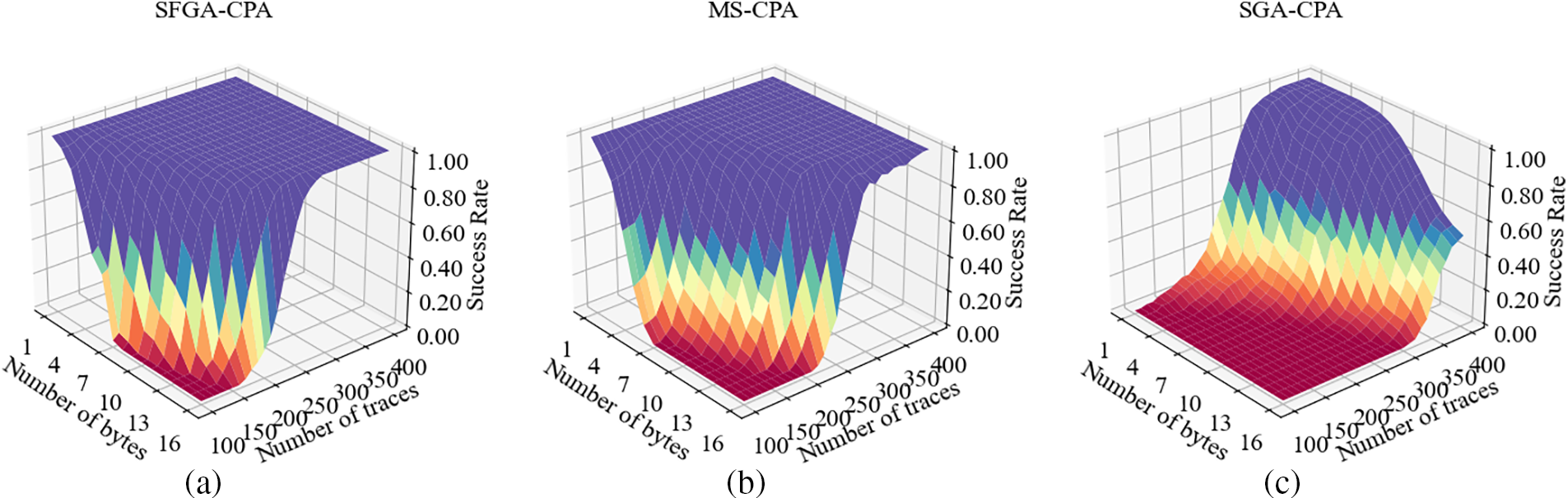
Figure 7: The success rate of recovering bytes by SFGA-CPA, MS-CPA and SGA-CPA

It has also been studied whether SFGA-CPA is subject to key degradation. The count of correct bytes present in the best individuals of each generation was recorded. Fig. 8 shows the exact process of recovering the key using the SFGA-CPA, MS-CPA and SGA-CPA method. SFGA-CPA, MS-CPA, and SGA-CPA are represented by the orange, blue, and green curves, respectively.

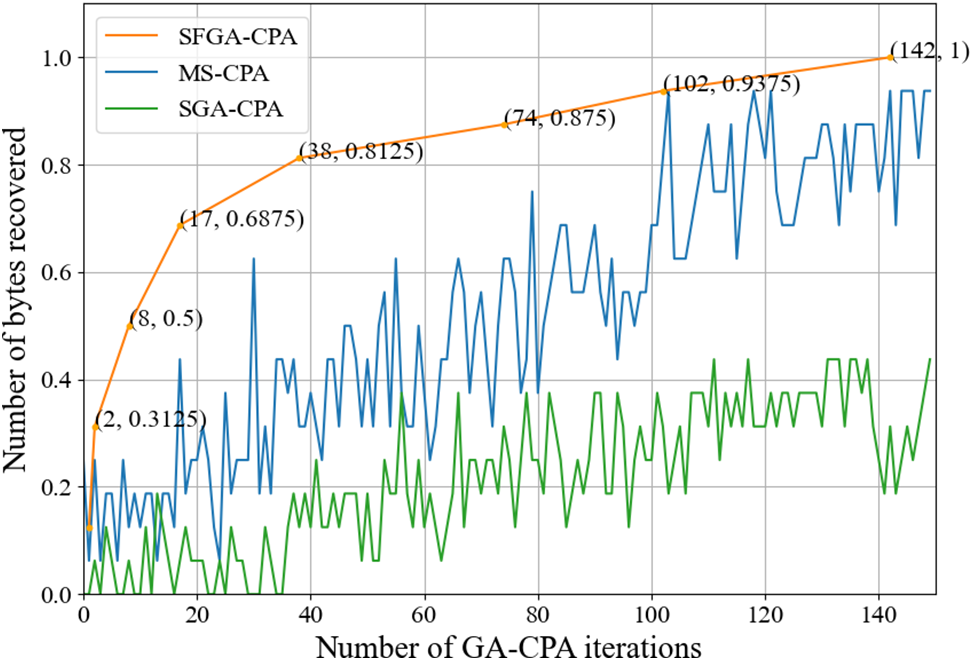
Figure 8: The number of correct bytes contained in the best individual of SFGA-CPA, MS-CPA and SGA-CPA

At the same time, the orange curve consistently remains above the blue curve, and only 142 executions are required to recover the key. Furthermore, comparing the results of the two experiments, it can be observed that the orange curve does not show any fluctuations, whereas the blue curve does. This means that in the SFGA-CPA method, the number of correct bytes contained in the best individuals is gradually increasing. Therefore, the key degradation issue can be addressed by SFGA-CPA, ensuring that the recovered correct bytes do not turn into erroneous ones. Meanwhile, these three methods underwent Friedman testing when the number of occurrences of key degradation in the population was used as the metric [28,29]. The test results are presented in Table 2.

The rejection of Hθ indicates significant differences among the three models. This also implies that the performance of the three methods differs in addressing the key degradation issue. Therefore, the advantage of SFGA-CPA can be acknowledged.

6  Conclusion

The significance of this article is to address the issues of key degradation and slow population evolution in GA-based CPA. Therefore, the SFGA-CPA method is proposed, derived through theoretical analysis of the characteristics of CPA. Firstly, the issue of slow population evolution is addressed by collecting the correct bytes in the key, as the number of correct bytes in the secret key is directly proportional to individual fitness (correlation coefficient). So, the fitness of a key individual is improved by including correct bytes from other individuals. Subsequently, the application of this operation to all individuals effectively increases the evolutionary speed of the population. Furthermore, the issue of key degradation significantly impacts the evolutionary speed of the key population. The constrained crossover and constrained mutation of SFGA-CPA can address this issue by preventing the alteration of correct bytes. Finally, parameters are also crucial factors influencing the effectiveness of the attack. The paper also introduces an intelligent search method to find optimal parameters for application in SFGA-CPA. Our simulation and real experimental results indicate that SFGA-CPA can quickly recover the key and achieve successful attacks with fewer power consumption curves. This is consistent with the conclusions in this paper. At the same time, it can be observed from the experimental process that the issues associated with GA-based CPA have also been addressed. The situation of key degradation did not occur during the key recovery process. These techniques are also expected to help address the issues present in heuristic algorithm-based CPA. Furthermore, these methods and experiments indicate that we still have a long way to go, as they cannot recover masked keys. This will also be a direction for our future research.

Acknowledgement: The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers and editors, which have improved the presentation.

Funding Statement: This research is supported by the Hunan Provincial Natrual Science Foundation of China (2022JJ30103), “the 14th Five-Year” Key Disciplines and Application Oriented Special Disciplines of Hunan Province (Xiangjiaotong [2022], 351), the Science and Technology Innovation Program of Hunan Province (2016TP1020).

Author Contributions: Jiahui Liu: Conceptualization, Writing-Original Draft; Lang Li: Writing-Review and Editing, Supervision; Di Li: Formal Analysis; Yu Ou: Term, Project Administration. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not available.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Feng and L. Li, “SCENERY: A lightweight block cipher based on Feistel structure,” Front. Comput. Sci., vol. 16, no. 3, pp. 1–10, 2022. [Google Scholar]

2. K. F. Jasim et al., “Analysis the structures of some symmetric cipher algorithms suitable for the security of IoT devices,” Cihan Univ.-Erbil Sci. J., vol. 5, no. 2, pp. 13–19, 2021. doi: 10.24086/cuesj.v5n2y2021.pp13-19. [Google Scholar] [CrossRef]

3. A. Singh et al., “Energy efficient and side-channel secure cryptographic hardware for IoT-edge nodes,” IEEE Internet Things J., vol. 6, no. 1, pp. 421–434, 2018. doi: 10.1109/JIOT.2018.2861324. [Google Scholar] [CrossRef]

4. K. Ramezanpour, P. Ampadu, and W. Diehl, “SCAUL: Power side-channel analysis with unsupervised learning,” IEEE Trans. Comput., vol. 69, no. 11, pp. 1626–1638, 2020. doi: 10.1109/TC.2020.3013196. [Google Scholar] [CrossRef]

5. M. Randolph and W. Diehl, “Power side-channel attack analysis: A review of 20 years of study for the layman,” Cryptography, vol. 4, no. 2, pp. 15, 2020. doi: 10.3390/cryptography4020015. [Google Scholar] [CrossRef]

6. Y. Ou and L. Li, “Side-channel analysis attacks based on deep learning network,” Front. Comput. Sci., vol. 16, pp. 1–11, 2022. [Google Scholar]

7. A. Ghosh et al., “Electromagnetic analysis of integrated on-chip sensing loop for side-channel and fault-injection attack detection,” IEEE Microw. Wirel. Compon. Lett., vol. 32, no. 6, pp. 784–787, 2022. doi: 10.1109/LMWC.2022.3161001. [Google Scholar] [CrossRef]

8. D. Kamel et al., “Side-channel analysis of a learning parity with physical noise processor,” J. Cryptogr. Eng., vol. 11, no. 2, pp. 171–179, 2021. doi: 10.1007/s13389-020-00238-3. [Google Scholar] [CrossRef]

9. D. Li, L. Li, and Y. Ou, “CKGS: A way of compressed key guessing space to reduce ghost peaks,” KSII Trans. Internet Inf. Syst., vol. 16, no. 3, pp. 1047–1062, 2022. [Google Scholar]

10. F. Kordi, H. Hosseintalaee, and A. Jahanian, “A time randomization-based countermeasure against the template side-channel attack,” ISeCure, vol. 14, no. 1, pp. 47–55, 2022. [Google Scholar]

11. R. Wang et al., “Cryptanalysis of a white-box SM4 implementation based on collision attack,” IET Inf. Secur., vol. 16, no. 1, pp. 18–27, 2022. doi: 10.1049/ise2.12045. [Google Scholar] [CrossRef]

12. G. Zaid et al., “Ranking loss: Maximizing the success rate in deep learning side-channel analysis,” IACR Trans. Cryptogr. Hardware Embed. Syst., vol. 2021, pp. 25–55, 2020. doi: 10.46586/tches.v2021.i1.25-55. [Google Scholar] [CrossRef]

13. Y. Zhou and F. X. Standaert, “Deep learning mitigates but does not annihilate the need of aligned traces and a generalized resnet model for side-channel attacks,” J. Cryptogr. Eng., vol. 10, no. 1, pp. 85–95, 2020. doi: 10.1007/s13389-019-00209-3. [Google Scholar] [CrossRef]

14. M. Lipp et al., “PLATYPUS: Software-based power side-channel attacks on x86,” in 2021 IEEE Symp. Secur. Priv., IEEE, 2021, pp. 355–371. [Google Scholar]

15. J. Kim et al., “Make some noise. Unleashing the power of convolutional neural networks for profiled side-channel analysis,” IACR Trans. Cryptogr. Hardware Embed. Syst., vol. 2019, no.3, pp. 148–179, 2019. doi: 10.46586/tches.v2019.i3.148-179. [Google Scholar] [CrossRef]

16. C. Zhang, P. Patras, and H. Haddadi, “Deep learning in mobile and wireless networking: A survey,” IEEE Commun. Surv. Tutorials, vol. 21, no. 3, pp. 2224–2287, 2019. doi: 10.1109/COMST.2019.2904897. [Google Scholar] [CrossRef]

17. M. A. Al-Garad et al., “A survey of machine and deep learning methods for internet of things security,” IEEE Commun. Surv. Tutorials, vol. 22, no. 3, pp. 1646–1685, 2020. doi: 10.1109/COMST.2020.2988293. [Google Scholar] [CrossRef]

18. R. Benadjila et al., “Deep learning for side-channel analysis and introduction to ASCAD database,” J. Cryptogr. Eng., vol. 10, no. 2, pp. 163–188, 2020. doi: 10.1007/s13389-019-00220-8. [Google Scholar] [CrossRef]

19. G. Zaid et al., “Methodology for efficient CNN architectures in profiling attacks,” IACR Trans. Cryptogr. Hardware Embed. Syst., vol. 2020, no.1, pp. 1–36, 2020. [Google Scholar]

20. R. Y. Acharya, F. Ganji, and D. Forte, “Information theory-based evolution of neural networks for side-channel analysis,” IACR Trans. Cryptogr. Hardware Embed. Syst., vol. 2023, no. 1, pp. 401–437, 2023. [Google Scholar]

21. S. Picek et al., “SoK: Deep learning-based physical side-channel analysis,” ACM Comput. Surv., vol. 55, no. 11, pp. 1–35, 2023. doi: 10.1145/3569577. [Google Scholar] [CrossRef]

22. S. Picek et al., “The curse of class imbalance and conflicting metrics with machine learning for side-channel evaluations,” IACR Trans. Cryptogr. Hardware Embed. Syst., vol. 2019, no. 1, pp. 1–29, 2019. [Google Scholar]

23. P. Kashyap et al., “2Deep: Enhancing side-channel attacks on lattice-based key-exchange via 2-D deep learning,” IEEE Trans. Comput. Aided Des. Integr. Circuits Syst., vol. 40, no. 6, pp. 1217–1229, 2020. doi: 10.1109/TCAD.2020.3038701. [Google Scholar] [CrossRef]

24. X. Duan et al., “Research of CPA attack methods based on ant colony algorithm,” in Secur. Privacy in Commun. Netw.: 17th EAI Int. Conf., Berlin Heidelberg, Springer, 2021, pp. 270–286. [Google Scholar]

25. F. Chicano et al., “Dynastic potential crossover operator,” Evol. Comput., vol. 30, no. 3, pp. 409–446, 2022. doi: 10.1162/evco_a_00305. [Google Scholar] [PubMed] [CrossRef]

26. Z. Zhang et al., “A novel bit scalable leakage model based on genetic algorithm,” Secur. Commun. Netw., vol. 8, no. 18, pp. 3896–3905, 2015. doi: 10.1002/sec.1308. [Google Scholar] [CrossRef]

27. Y. Ding et al., “A multiple sieve approach based on artificial intelligent techniques and correlation power analysis,” ACM Trans. Multimed. Comput. Commun. Appl., vol. 17, no. 2s, pp. 1–21, 2021. doi: 10.1145/3433165. [Google Scholar] [CrossRef]

28. N. E. Zamri et al., “A modified reverse-based analysis logic mining model with weighted random 2 satisfiability logic in discrete hopfield neural network and multi-objective training of modified niched genetic algorithm,” Expert Syst. Appl., vol. 240, no. 6, pp. 122307, 2024. doi: 10.1016/j.eswa.2023.122307. [Google Scholar] [CrossRef]

29. N. E. Zamri et al., “Weighted random k satisfiability for k = 1, 2 (r2SAT) in discrete Hopfield neural network,” Appl. Soft Comput., vol. 126, no. 6, pp. 109312, 2022. doi: 10.1016/j.asoc.2022.109312. [Google Scholar] [CrossRef]