Weak Fault Feature Extraction of the Rotating Machinery Using Flexible Analytic Wavelet Transform and Nonlinear Quantum Permutation Entropy

1  Introduction

The diagnosis of faults in rotating machinery, especially in their initial stages, has gained considerable attention due to its critical importance in averting potential catastrophic incidents and allowing for adequate maintenance time [1–3]. Vibration-based analysis has been widely applied because of its inherent advantages in revealing the characteristic features of mechanical faults [4–6].

From the perspective of mechanical fault mechanisms, when critical rotating components such as rolling bearings, rotors, and gearboxes exhibit localized defects, the transmission path from the damaged meshing position to the fixed accelerometer undergoes changes in its evolution process [7,8]. Simultaneously, strong vibration responses from other mechanical components and significant background noise can render these fault impacts extremely weak. Therefore, appropriate signal processing techniques are essential prerequisites for identifying fault features [9].

Most signal processing techniques, particularly methods such as Discrete Wavelet Transform (DWT) and Wavelet Packet Transform (WPT) [10], hold great promise for identifying faults in rotating machinery. When diagnosing gear faults, DWT’s inherent limitations lead to low precision in diagnosing transient frequencies [11–13]. To address these limitations, Wavelet Packet Transform (WPT) is commonly utilized to reveal high-frequency regions of transient components [14]. However, both WPT and DWT are plagued by sub-sampling, which reduces time-based resolution. In a study by Hong et al. [15], the combination of Hilbert spectrum with Maximum Overlap Discrete WPT was used to analyze vibration signals from gear faults. Wang et al. [16] proposed a denoising method based on Dual-Tree Complex Wavelet Transform (DTCWT) for fault diagnosis in rotating machinery. Subsequently, DTCWT has been applied to analyze vibration signals from gearboxes [17,18] and biomedical signals [19]. Cai et al. [20] introduced a new method for sparse signal decomposition using Time-Frequency Hermite Transform (TQWT). However, traditional wavelet filters designed for linear systems perform poorly on nonlinear systems, especially in detecting transient components with high-frequency characteristics, due to low resolution and poor shift invariance.

Flexible Analytical Wavelet Transform (FAWT) is a relatively recent concept initially explored by Bayram [21]. FAWT offers several advantages over traditional binary wavelet filters, including flexible selection of time-frequency windows, effective shift invariance, the capability to decompose complex signals based on oscillatory behavior, and the ability to capture weak fault features. FAWT allows for arbitrary sampling rates in both low-pass and high-pass channels, providing a flexible partitioning scheme where scaling and translation factors can be easily adjusted. Additionally, by fine-tuning the width of the frequency transition band, FAWT can achieve optimal oscillatory bases for detecting various oscillatory pulses. Therefore, the application of the FAWT method in fault diagnosis for rotating machinery proves advantageous in improving the detection performance of subtle fault features [22–24].

Although FAWT holds great potential for signal decomposition, signals obtained from rotating machinery often exhibit nonlinear and non-stationary characteristics, posing challenges for the extraction of fault-related features. Entropy serves as a widely used metric for quantifying the randomness and dynamic changes in real dynamic systems, and it finds extensive application in fault diagnosis for rotating machinery [25]. Specifically, Permutation Entropy (PE), as a nonlinear parameter measuring the randomness and dynamic changes in time series, has been proven highly effective in detecting the dynamic characteristics of vibration signal time series. PE boasts advantages such as simplicity in calculation, rapid computation, robustness to nonlinear monotonic transformations, and stability, making it efficient for detecting and amplifying dynamic changes in vibration signals. When employing PE for feature extraction, defining events and comparing the complexity of time-domain data are crucial for its effective application [26,27].

In recent years, quantum theory has experienced rapid development, emerging as a revolutionary and enigmatic theoretical framework. Diverging significantly from traditional modes of information representation, quantum theory, with its principles of superposition, coherence, and entanglement, accurately captures many objective regularities [28]. In this paper, quantum theory is introduced into permutation entropy to form Nonlinear Quantum Permutation Entropy, serving as a fault feature parameter for rotating machinery. Leveraging the advantages of the novel expression offered by quantum theory and the dynamic characteristics of permutation entropy, Nonlinear Quantum Permutation Entropy (QPE) enables more sensitive and accurate characterization of subtle faults in rotating machinery.

In conclusion, this paper presents a novel method for extracting weak features in rotating machinery. The approach first utilizes the FAWT to decompose vibration signals collected from rotating machinery, obtaining several sub-band signals. Nonlinear Quantum Permutation Entropy of each sub-band signal is then extracted as fault characterization feature vectors. As the Multiclass Extreme Learning Machine (ELM) is a fast, simple, and efficient artificial neural network algorithm known for its quick training speed and strong generalization capability, it is employed in this study for classification. This intuitively demonstrates the effectiveness of the proposed method. Finally, the superiority of the proposed method is validated through comparative experiments.

The organization of the remaining sections of this paper is as follows. Section 2 provides a brief overview of the theoretical background of FAWT. In Section 3, the Nonlinear Quantum Permutation Entropy algorithm is elucidated. Building on this, Section 4 proposes a fault feature extraction method based on FAWT and Nonlinear Quantum Permutation Entropy. Section 5 introduces the experimental setup and comparative study. Additionally, discussions follow each application case. Finally, Section 6 summarizes the conclusions.

2  Flexible Analytic Wavelet Transform (FAWT)

FAWT achieves signal decomposition by using an Iterated Filter Bank (FB). The filter bank comprises a low-pass filter H(w) and two high-pass channels G(w) and G(-w). Here, G(w) analyzes the “positive frequency,” while G(-w) analyzes the “negative frequency” [29]. Due to this significant positive and negative frequency separation characteristic, FAWT facilitates arbitrary selection of sampling rates in the high-pass channels. Consequently, by employing the Hilbert transform, one can flexibly control redundancy, scaling factors, and Q factors. The frequency responses of the low-pass and high-pass channels in FAWT can be defined by Eq. (1), where H(w) represents the frequency response of the scaling function, and G(w) represents the frequency response of the analytic wavelet function [30,31].

H(w)={pq,|w|<wppqθ(w−wpws−wp),wp≤w≤wspqθ(π−w+wpws−wp),−ws≤w≤−wp0,|w|>wsG(w)={2rsθ(π−w−w0w1−w0),w0≤w≤w12rs,w1<w<w22rsθ(w−w2w3−w2),w2≤w≤w30,w∈[0,w0]∪[w3,2π](1)

where, p and q regulate the sampling rate of the low-pass channel, while r and s are parameters controlling the sampling rate of the high-pass channel. Additionally, ws and wp represent the stopband and passband frequencies of the low-pass filter, respectively. The definitions of other parameters are as follows:

wp=1−βpπ+εp,ws=πq,w0=1−βrπ+εr,w1=pqrπ,w2=πr−εr,w3=πr+εr,ε=132(p−q+βqp+q)π,θ(w)=12(1+cos⁡w)2−cos⁡w for w∈[0,π](2)

where, the constants β and ε are non-negative constants satisfying β<1. The transition band θ(w) is constructed using Daubechies wavelets with 2 vanishing moments, forming an orthogonal wavelet filter in FAWT.

The reconstruction of the filter bank in FAWT must adhere to the following two conditions, as expressed in Eqs. (3) and (4):

|θ(π−w)|2+|θ(w)|2=1(3)

(1−pq)≤β≤rs(4)

The redundancy and the Q factor is expressed by Eqs. (5) and (6), respectively.

R=r/s1−p/q(5)

Q=2−ββ(6)

For the analysis of gearbox vibration signals, FAWT provides adjustable parameters to control the quality factor, scaling factor, and redundancy. Based on the advantages of Genetic Algorithm optimization such as strong global search capability, high parallelism, wide applicability, and robustness, we have chosen Genetic Algorithm as the method for optimizing the parameters of FAWT. The Genetic Algorithm effectively explores the parameter space to find the optimal parameter combination, thereby enhancing the performance of FAWT and improving the accuracy and reliability of fault diagnosis. Its strong global search capability and robustness enable Genetic Algorithm to handle complex parameter optimization problems and achieve good results in various application scenarios.

3  Nonlinear Quantum Permutation Entropy

Quantum theory, as an emerging science, has experienced rapid development across various disciplines. Permutation entropy, as an algorithm quantifying the state of time series signals, plays a crucial role. The focal point of this study is how to incorporate quantum theory into permutation entropy, offering broader avenues for development. Quantum theory, as a powerful tool for information processing, continuously propels rapid advancements in related fields. Leveraging the novel concepts and distinctive state representations used to describe the microscopic world, quantum theory has also found effective applications in the processing of vibration signals [32,33].

Quantum bits, or qubits, are the fundamental units describing the quantum world in quantum theory. The states they represent are a form of superposition. The mathematical expression for this is:

|φ⟩=a|0⟩+b|1⟩(7)

where, |0⟩ and |1⟩ are the quantum basis states for a quantum bit, with coefficients a and b representing the probability amplitudes of the quantum state. These coefficients can be real or complex numbers, and the square of the modulus of the probability amplitude defined as the quantum probability. |a|2 and |b|2 represent the probabilities of the quantum basis states |0⟩ and |1⟩ occurring, respectively. The quantum probability amplitudes adhere to the normalization condition:

|a|2+|b|2=1(8)

From Eqs. (7) and (8), it is evident that a quantum bit can describe various states composed of different combinations of two basic states with different probabilities.

Assuming a one-dimensional vibration signal X={x(i),i=1,2,…,N} composed of N sampling points, each element x(i) of the signal X is normalized using the following equation:

y(i)=x(i)−min(X)max(X)−min(X)y(i)∈[ 0,1 ](9)

Here, min(X) and max(X) represent the minimum and maximum values of the signal X, respectively.

The quantum representation of vibration signals is a crucial aspect for further data processing. According to reference [34], a mathematical expression for the nonlinear quantum representation of vibration signals is proposed, mapping the vibration signal from the time domain space to the quantum space for the analysis of its states. After normalizing the vibration signal, its nonlinear quantum expression is given by:

|y(i)⟩=cos⁡(y(i)×π/2)|0⟩+sin⁡(y(i)×π/2)|1⟩(10)

where, cos⁡(y(i)×π/2) and sin⁡(y(i)×π/2) represent the probability amplitudes of the two basis states, |0⟩ and |1⟩, respectively. Additionally, cos2⁡(y(i)×π/2) and sin2⁡(y(i)×π/2) represent the probabilities of the two basis states, |0⟩ and |1⟩. Due to the normalization condition cos2(y(i)×π/2)+sin2(y(i)×π/2)=1, which satisfies the criteria for quantum bits, this can be applied for the quantization of vibration signals. Since the probabilities cos2⁡(y(i)×π/2) and sin2⁡(y(i)×π/2) undergo nonlinear variations, Eq. (9) is termed the nonlinear quantization of vibration signals.

If each sampling point of the vibration signal undergoes nonlinear quantization using quantum bits, then a vibration signal composed of adjacent k sampling points can be described by k quantum bits. Here, the state of the i-th quantum bit is represented as |ϕi⟩=ai|0⟩+bi|1⟩. In a multi-qubit system, the ground state, composed of multiple symbols, is often referred to as a state vector. Therefore, the state vector of the vibration signal can be expressed as the tensor product of k quantum bits:

|Yk⟩=|y(1)⟩⊗|y(2)⟩⊗⋯⊗|y(k)⟩=a1a2⋯ak|00⋯0⟩+a1a2⋯ak−1bk|00⋯01⟩+⋯+b1b2⋯bk|11⋯1⟩=∑i=12kwi|ib⟩(11)

where, for the quantum system (vibration signal) |Yk⟩, the i-th state vector is denoted as |ib⟩. The state vector is expressed in binary form, where wi is the probability amplitude of the state vector |ib⟩ and |wi|2 is the probability of the state vector |ib⟩. According to the normalization condition in quantum theory, the probabilities should satisfy:

∑i=02i−1|wi|2=1(12)

Permutation entropy, as a nonlinear parameter for quantifying the randomness and dynamic variations of time series signals, has found widespread applications in various fields. Inspired by the resemblance between permutation entropy and the representation of information states in quantum theory, which involves various quantum basis states or state vectors and their associated probabilities, the integration of quantum theory with permutation entropy has been proposed to describe the operational state of vibration signals. This combination is utilized to extract and characterize feature parameters related to the system’s operational state [26].

During the operation of a gearbox, its vibration signals are associated with its operational state. Different vibration time series correspond to different probabilities or probability amplitudes of various basis states or state vectors in their quantum representation. The entropy values of these basis states or state vectors are calculated using the permutation entropy method, and these are utilized as features to characterize the gearbox’s operation.

Combining the concepts of quantum theory and permutation entropy, the basic principles of nonlinear quantum permutation entropy are outlined as follows:

(1) Normalization of Vibration Signals. Let the time series of the vibration signal be denoted as X = {x(i), i = 1, 2, …, N}. Applying Eq. (9) to normalize the time series of the vibration signal, resulting in the normalized time series Y = {y(i), i = 1, 2, …, N}.

(2) Phase space reconstruction. Conducting phase space reconstruction on the time series Y, a matrix Y0 is obtained.

Y0=[Y0(1)Y0(2)⋯Y0(j)⋯Y0(K)]=[y(1)y(1+τ)⋯y(1+(m−1)τ)y(2)y(2+τ)⋯y(2+(m−1)τ)⋯⋯⋯⋯y(j)y(j+τ)⋯y(j+(m−1)τ)⋯⋯⋯⋯y(K)y(K+τ)⋯y(K+(m−1)τ)](13)

where, j = 1, 2, 3, …, K. m is the embedding dimension, τ is the time delay, and K = N −(m −1) τ. Each row Y0 (j) in the reconstruction matrix represents a reconstruction component, and there are total of K reconstruction components in the reconstruction matrix.

(3) Nonlinear quantization of reconstruction components. Each reconstruction component in the reconstruction matrix undergoes nonlinear quantization. A multi-qubit system is employed to form quantum bit state vectors composed of m qubits. The total number of state vectors is n = 2m, namely:

|Y0(j)⟩=wj,1|00⋯0⟩+wj,2|00⋯01⟩+⋯+wk,n|11⋯1⟩=∑k=1nwj,k|ib⟩(14)

where, |ib⟩ represents the i-th state vector of the quantum system, wj,k is the probability amplitude of the state vector |ib⟩, and |wj,k|2 is the probability of the state vector |ib⟩. These probabilities satisfy the normalization condition:

∑k=1n|wj,k|2=1(15)

(4) Each row in the matrix is regarded as a component. By sorting the reconstruction components |Y0(j)⟩ in ascending order based on the probability amplitudes of each state vector, we obtain: |Y0[j+(j1−1)τ]⟩≤|Y0[j+(j2−1)τ]⟩≤…≤|Y0[j+(jm−1)τ]⟩, where, j1,j2,…,jm represent the index numbers of the columns in which each element is located. Therefore, for each row in the matrix |Y0⟩, a set of symbol sequences S(g)=(j1,j2,…,jm), namely ordinal pattern, can be obtained., where g=1,2,…,l. Then, calculate the probability distribution pk of the ordinal patterns, where k = 1, 2, 3, …, n.

(5) Calculate nonlinear quantum permutation entropy by estimating the Shannon entropy of the ordinal probability distribution of each state vector.

Hq∗(X)=−∑i=1npkln⁡pk(16)

(6) Normalization of nonlinear quantum permutation entropy. The maximum value ln(m!) of nonlinear quantum permutation entropy Hq(X) is obtained when Pk = 1/m!. For convenience, Hq(m) is typically normalized, namely:

Hq(X)=Hq∗(X)ln⁡(m!)(17)

The nonlinear quantum permutation entropy Hq(X) represents the probability distribution of the state vectors in the ascending order after quantizing the time series X. A larger Hq(X) indicates a more regular probability distribution of the state vectors’ arrangement, while a smaller Hq(X) suggests greater differences in the probability of state vectors’ arrangement. For a gear transmission system, a larger Hq(X) implies a more stable operational state, closer to the normal condition, while a smaller Hq(X) indicates an unstable gearbox operational state, deviating from the normal condition and exhibiting anomalies. The variation of Hq(X) can reflect and amplify subtle changes in the time series. The workflow of the nonlinear quantum permutation entropy algorithm is illustrated in Fig. 1.

Figure 1: Algorithm flow chart of nonlinear quantum permutation entropy

In a gearbox, the occurrence of faults in gears can lead to changes in the frequency components and amplitudes of the corresponding vibration signals. Moreover, the presence of noise interference in the vibration signals complicates the analysis. Taking a planetary gearbox as an example, the nonlinear quantum permutation entropy is analyzed for three types of simulated vibration signals: Normal operation, local fault in the sun gear, and local fault in the planetary gear. This analysis aims to demonstrate the feasibility of using nonlinear quantum permutation entropy as a characteristic feature for gearbox condition monitoring.

According to the reference [35], the vibration simulation signal for a single-stage planetary gearbox with normal gear conditions is given by:

x(t)=[1−cos⁡(2πfct)]⋅cos⁡(2πfmt+θ)(18)

where, fc represents the rotation frequency of the planetary carrier, fm is the meshing frequency of the planetary gearbox, and θ is the initial phase of the meshing vibration.

The vibration simulation signal for local fault in the sun gear is:

x(t)=[1−cos⁡(2πfs(r)t)][1+0.5cos⁡(2πfst)]⋅cos⁡[2πfmt+0.5sin⁡(2πfst)+θ](19)

where, fs(r) is the absolute rotation frequency of the sun gear, and fs is the characteristic frequency of the local fault in the sun gear.

The vibration simulation signal for local fault in the planetary gear is:

x(t)=[1−cos⁡(2πfct)][1+0.5cos⁡(2πfpt)]⋅cos⁡[2πfmt+0.5sin⁡(2πfpt)+θ](20)

where, fp is the characteristic frequency of the local fault in the planetary gear.

According to the reference [35], the parameters for the simulation signals are set as shown in Table 1.

Setting θ = 0 and all initial phases to zero, Gaussian white noise with a signal-to-noise ratio of 10 dB is added to the time-domain signals for the three states. The sampling frequency is set to 5120 Hz, and the simulation time is 10 s. The vibration time-domain simulation signals for the three states are shown in Fig. 2.

Figure 2: Time domain waveforms of signals

During the phase space reconstruction, for the vibration simulation signals corresponding to the three states, the delay time is determined to be τ = 2 using the mutual information method, and the embedding dimension is determined to be m = 6 using the false nearest neighbor method. Nonlinear quantum permutation entropy is calculated every 1 s, and a total of 20 simulation signal samples are computed. The results are shown in Fig. 3. From Fig. 3, it can be observed that the QPE values of the normal gears are higher than those of the faulty gears. Additionally, the vibration signals for the three states in the planetary gearbox exhibit significant differences in nonlinear quantum permutation entropy, providing preliminary evidence for the effectiveness of nonlinear quantum permutation entropy as a feature for monitoring the operational state of a single-stage planetary gearbox. Moreover, the relatively small fluctuations in the nonlinear quantum permutation entropy values for the vibration signals in each state indicate a certain level of noise resistance.

Figure 3: The QPE of three signals

4  Weak Fault Feature Extraction Method

Previous studies have demonstrated the superiority of nonlinear quantum entropy as a feature parameter for faults. However, the time-domain representation of vibration signals in actual rotating machinery often conceals a significant amount of useful information, making fault feature extraction challenging. In order to effectively reveal potential fault information, it is necessary to decompose the vibration signals first and expose the fault information sufficiently in the decomposed sub-signals. Therefore, this study proposes a novel method for extracting weak fault features based on Flexible Analytical Wavelet Transform (FAWT) and Nonlinear Quantum Permutation Entropy. FAWT overcomes many inherent limitations of Wavelet Transform (WT) by adaptively selecting suitable wavelet bases and sensitive sub-bands using arbitrary scaling and translation factors, thereby maximizing the revelation of hidden fault features. Then, by extracting the nonlinear quantum permutation entropy of each sub-signal, a feature matrix is obtained. Finally, the feature matrix is divided into training and testing sets, which are input into ELM for classification and identification.

However, due to the extreme sensitivity of FAWT results to parameter settings, this study employs a Genetic Algorithm (GAs) to select the optimal control parameters, using the maximization of the feature kurtosis spectrum entropy as its fitness function. To obtain appropriate FAWT parameters, a Genetic Algorithm (GAs) is employed to optimize the wavelet basis function factors p, q, r, s, and β for FAWT. The feature kurtosis spectrum entropy indicator is used to evaluate the pulse and periodic behavior of each sub-band signal. By optimizing the FAWT parameters to maximize kurtosis spectrum entropy, the optimal FAWT basis functions can be obtained. The determined basis function factors can better decompose vibration signals, thereby having a greater potential to reveal weak fault features.

The kurtosis indicator is one of the commonly used features in the field of fault diagnosis, particularly sensitive to transient impulses. For an input signal x(n), its kurtosis is defined as follows:

Kurt[x]=E[(x(n)−u)4]σ4(21)

where, μ and σ are the mean and standard deviation of x(n), respectively.

Given that vibration signals in gearboxes often exhibit characteristics of periodic fault impulses, selecting the kurtosis spectrum entropy as the adaptability function for FAWT parameter selection is considered. Let S (ω) be the envelope spectrum of the input signal xn(t), and Es be the entropy of the envelope spectrum. Assume J represents the number of layers in the FAWT decomposition. Then, the envelope spectrum is segmented into J frequency intervals across the frequency axis. The portion of the spectrum sampled within the i-th interval is referred to as the probability distribution Pi. The kurtosis spectrum entropy CKSE defined using this probability distribution satisfies the following conditions:

CKSE=Kurt[x]/(−∑i=1JPilog2⁡(Pi)),∑i=1JPi=1(22)

Using the maximum value of the kurtosis spectrum entropy as the fitness function in the genetic algorithm to optimize the parameters of FAWT aims to maximize the optimization of FAWT decomposition sub-bands. This ensures that the sub-band signals contain the most fault feature information.

Hence, this study employs the constructed optimal FAWT basis to decompose the input signal into various scales. Subsequently, it captures the nonlinear quantum permutation entropy of wavelet sub-bands to unveil potential fault characteristics. Based on the advantages of faster training speed and simpler parameter adjustment, Extreme Learning Machine (ELM) is selected for the final classification and recognition. In summary, the process of extracting weak fault features in rotating machinery can be summarized as follows: (1) Collect vibration signals from gears or bearings in rotating machinery. (2) Use the FAWT method to decompose the vibration signals, maximizing the kurtosis spectrum entropy as the fitness function in the decomposition. Utilize a Genetic Algorithm to select suitable parameters for the FAWT basis. (3) Calculate the nonlinear quantum permutation entropy of each decomposed sub-band signal, forming a multidimensional feature matrix. (4) Input the feature matrix into ELM, using part of it for model training and the other part for classification and recognition. (5) Output the final fault type and severity. The overall flowchart is shown in Fig. 4.

Figure 4: Procedures of the proposed method

5  Application of the Proposed Method in Rotating Machinery Fault Diagnosis

5.1 Case 1: Detection Bearing Fault of Case Western Reserve University

To authenticate the proposed methodology and evaluate its efficacy, researchers utilized data from a rolling bearing experiment conducted by Case Western Reserve University. The experiment focused on the 6205-2RS deep groove ball bearing, where single-point failures were induced using electro-discharge machining, resulting in faults ranging from 0.007 in to 0.021 in in diameter. Vibrational acceleration signals were gathered under various conditions, including the normal state of the rolling bearing (referred to as “Norm”) and faults such as ball element fault (denoted as “B”), outer raceway fault (“OR”), and inner raceway fault (“IR”). The study encompassed data from the 12 k drive end bearing, 24 k drive end bearing, and fan-end bearing, with a sampling frequency of 12 kHz. For detailed classification information, please refer to Table 2.

When any fault occurs in the bearing components, the vibration signals are manifested in pulses. These pulses result from variations in the inherent oscillations. Due to the superimposition of signal amplitudes and their modulated vibrational signals, time-domain signals do not intuitively display the fault type and severity. In this study, 150 segments were selected for each fault signal under different conditions. These segments represent various fault conditions of the bearing, which were decomposed into 10 sub-band signals using FAWT. Genetic Algorithms were employed for selecting FAWT parameters, utilizing arithmetic crossover and non-uniform mutation operators. The parameters of the genetic algorithm were set as follows: A population size of 20, 30 iterations, a crossover probability of 0.7, and a mutation probability of 0.05, which are commonly used values in parameter optimization. The fitness function was defined based on the maximization of feature kurtosis spectrum entropy (CKE), yielding optimal values for the FAWT base parameters (p, q, r, s, β) as 4, 5, 2, 3, 0.53, respectively. Subsequently, the nonlinear quantum permutation entropy of the decomposed sub-band signals was computed, resulting in a feature matrix of size 1500 × 10. The three-dimensional scatter plot formed by this feature matrix is shown in Fig. 5, where samples of different fault conditions tend to cluster. Since the three-dimensional scatter plot only displays the nonlinear quantum permutation entropy of the first three sub-bands, the entire feature matrix was further classified and recognized using the ELM classifier. The first 60 samples of each type were used for training the model, and the remaining 90 samples were used for testing. The testing accuracy was found to be 98.8889%, as illustrated in Fig. 6.

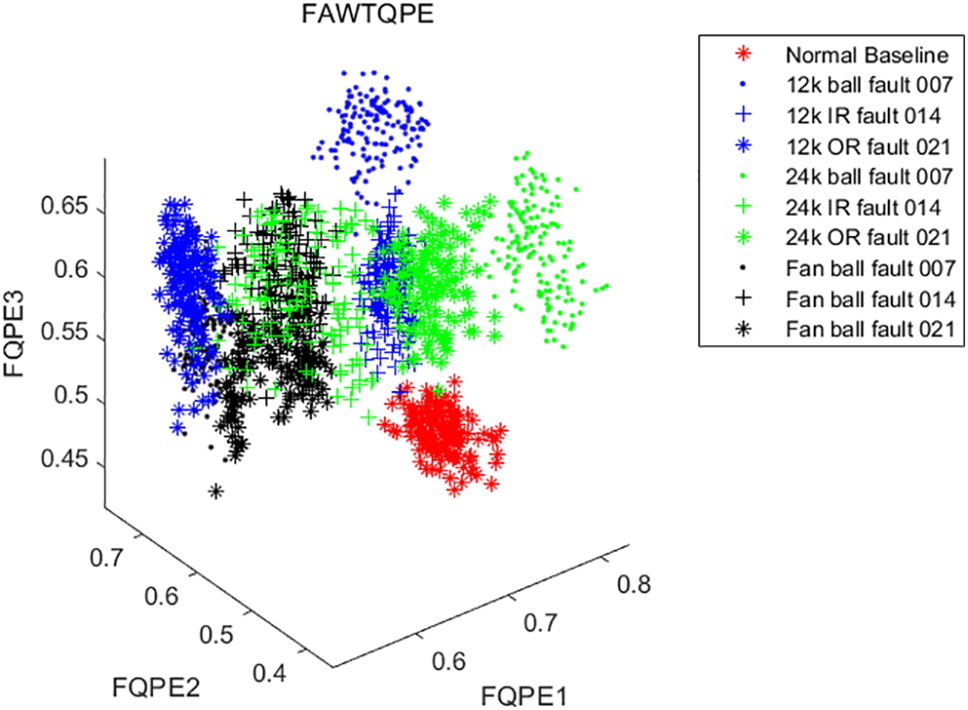
Figure 5: Scatter plot of the first three elements

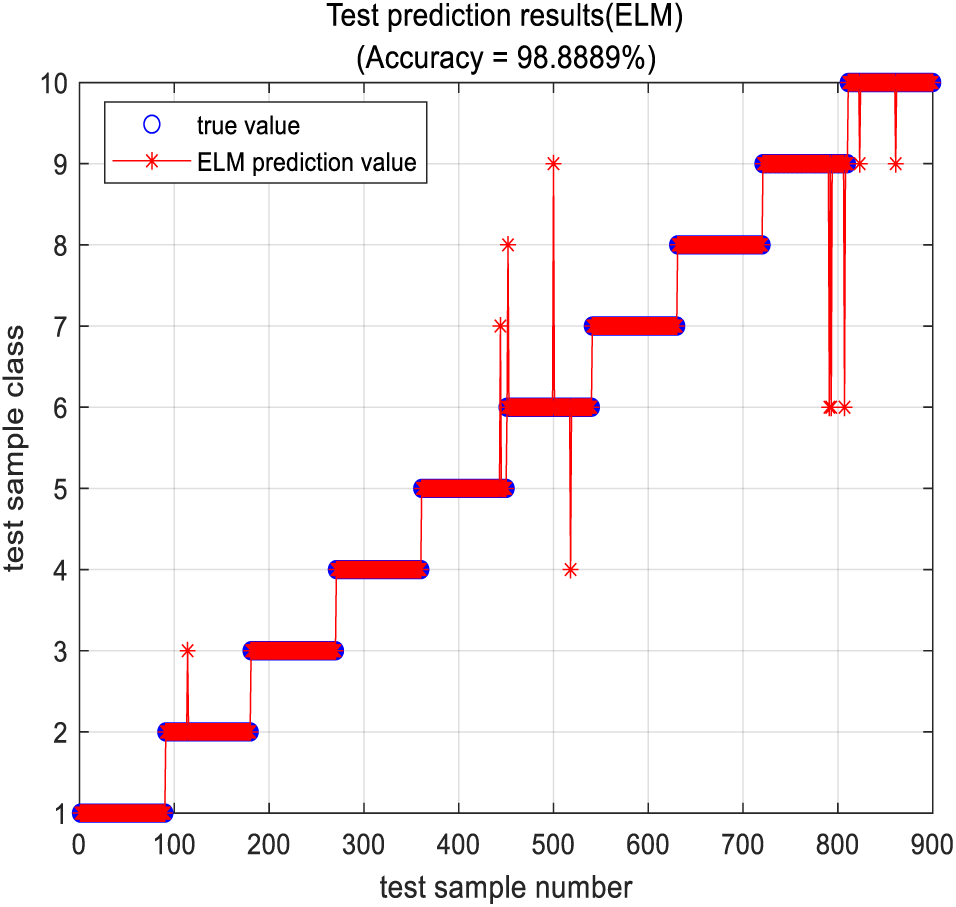
Figure 6: Test set prediction result comparison

5.2 Case 2: Detection Gear Fault of the One-Stage Spur Gearbox

In this segment, we employ the proposed technique for feature extraction to validate the gear data based on experimental results. Illustrated in Fig. 7 is the testing apparatus for the single-stage gearbox utilized in this study. It includes the primary test gearbox, an auxiliary test gearbox, accelerometers, speed and torque sensors, and a torsion bar. The entire transmission system is driven by a motor, establishing a closed power flow circuit by applying load to the torsion bar. Four accelerometers are strategically positioned at the base of the bearings of the driving and driven gears. The vibration signals captured by these sensors are gathered using the dynamic data acquisition and analysis system.

Figure 7: The gear transmission test rig system

Table 3 displays the parameters for the one-stage spur gearbox. In consideration of experimental limitations, gear cracks were deliberately induced near the tooth root of the driven gear. The crack depths ranged from 2 to 4 mm, accomplished via wire-electrode cutting. Furthermore, data collected during normal gear operation and gear operation with pitting were examined and interpreted as indicative of normal and pitting states, respectively. Subsequently, the data pertaining to each fault type at various speeds were scrutinized. The precise classification particulars of the gear fault types are delineated in Table 4.

Similarly, the proposed feature extraction method is applied to analyze eight datasets from this experimental data, with each class consisting of 150 samples. The Nonlinear Quantum Permutation Entropy (QPE) values obtained directly without undergoing FAWT decomposition are shown in Fig. 8. In the process of phase space reconstruction, the delay time is determined using mutual information with τ = 2, and the embedding dimension is determined using the false nearest neighbor method with m = 6. The non-linear quantum permutation entropy is computed for each sample (L = 15,000). It can be observed that the non-linear quantum permutation entropy for various states exhibits relatively stable behavior. However, there are subtle differences in some numerical values, which may lead to misjudgments in determining the operating states of certain gearboxes.

Figure 8: QPE obtained without decomposition

Comparisons between Permutation Entropy (PE), Sample Entropy (SE), Approximate Entropy (AE), and Fuzzy Entropy (FE) are illustrated in Fig. 9. It can be observed that the results of fuzzy entropy are more chaotic and exhibit larger fluctuations, while permutation entropy, sample entropy, and approximate entropy show relatively smooth patterns. However, there is a considerable overlap among them, indicating that they may not serve as effective features for determining the operational states. This further underscores the superiority of non-linear quantum permutation entropy in gearbox feature extraction.

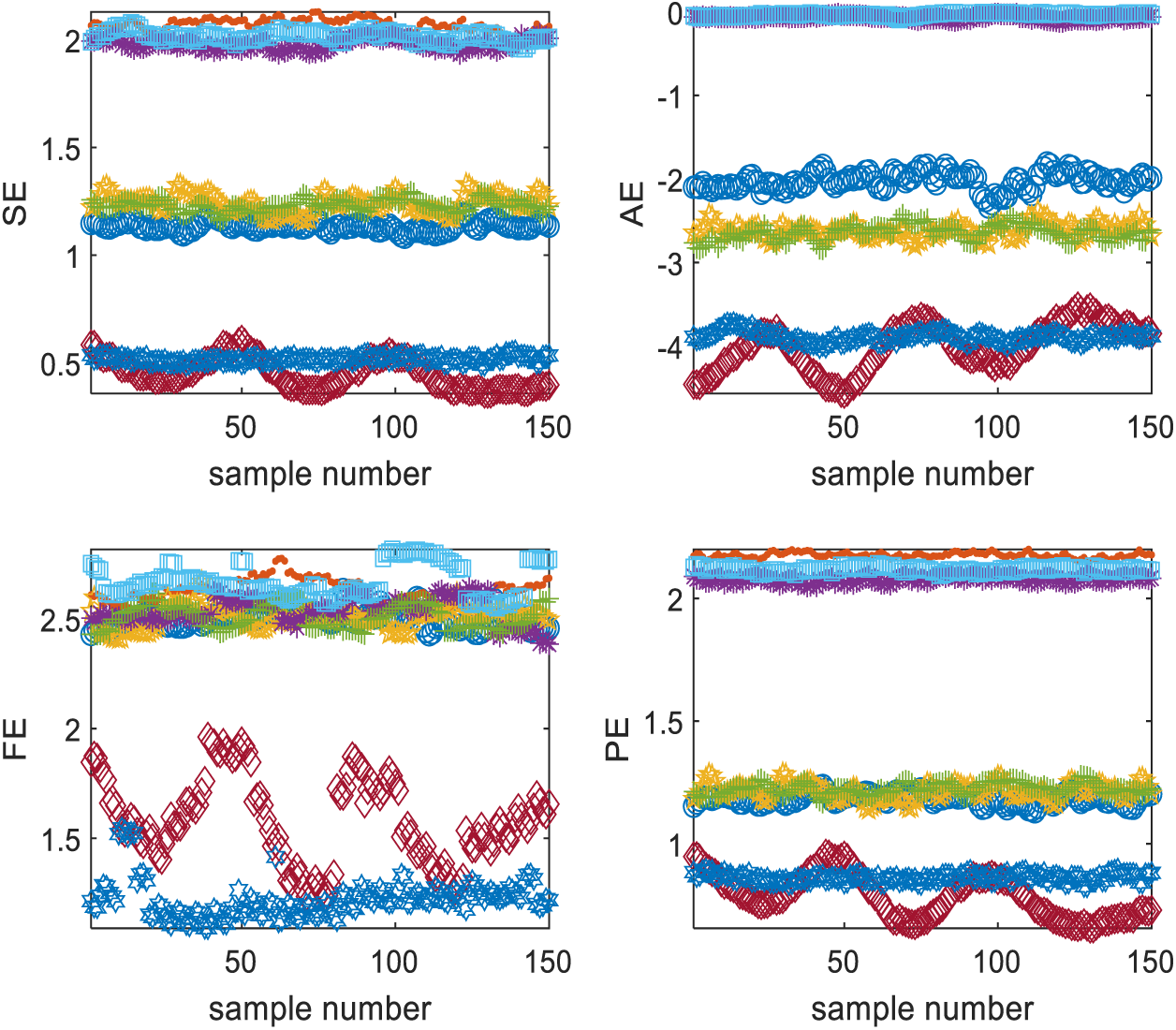
Figure 9: Comparison of various entropy features

While nonlinear quantum permutation entropy exhibits certain advantages in directly characterizing gearbox operational states, for more accurate identification of fault patterns, this study first decomposes the original vibration signals using FAWT to obtain eight distinct sub-band signals, and the sub-band signals after decomposition are more regular compared to the original signal, with a certain reduction in the superposition and harmonic characteristics of the signal. This separates some weak fault information into different sub-band signals, which is more conducive for subsequent characterization. Subsequently, the non-linear quantum entropy of these sub-band signals is employed as a discriminatory criterion for classifying and recognizing gearbox fault features. Similarly, the first 60 samples of each category are chosen as training samples for ELM model training, and the remaining 90 samples are utilized to test the model’s classification performance. The testing results show a recognition rate of 98.7836%. This is because, after FAWT decomposition of vibration signals during gearbox operation, the non-linear quantum permutation entropy of sub-band signals under various states exhibits a certain statistical regularity, providing better analytical capabilities post-decomposition.

To further underscore the effectiveness of the proposed approach, supplementary comparative experiments were conducted. The original vibration signals were decomposed using wavelet transform (WT) and empirical mode decomposition (EMD), respectively. Following this, classification recognition was carried out utilizing selected features spanning the time domain, frequency domain, time-frequency domain, and entropy features. The specific feature selections are outlined in Table 5. The comparative results are presented in Table 6, revealing that the overall recognition rate after FAWT decomposition surpasses that of wavelet transform and EMD. This improvement is attributed to the flexible time-frequency coverage employed by FAWT, enhancing the representation of fault features. Furthermore, the recognition rate using time-domain signals as feature parameters was the lowest, with slightly increased rates observed for frequency and time-frequency domains. Entropy, as a fault feature, exhibited unique advantages in characterizing faults in rotating machinery, resulting in a significant improvement in recognition rates. The proposed non-linear quantum permutation entropy demonstrated outstanding performance in capturing hidden fault types and severity in vibration signals.

6  Conclusions

This study presents an innovative approach for extracting fault features by integrating nonlinear quantum permutation entropy with Flexible Analytical Wavelet Transform (FAWT). The developed method is utilized to capture subtle characteristics in rolling bearings and gearboxes, effectively recognizing fault signatures in rotating machinery across diverse operational scenarios. The key contributions of this investigation are outlined as follows:

(1) The application of FAWT offers a more adaptable time-frequency coverage. By employing arbitrary scaling and translation factors, FAWT’s oscillatory properties become adjustable, providing additional time-frequency information for detecting fault components. Utilizing a Genetic Algorithm and adhering to the maximization principle of the kurtosis spectrum entropy, an adaptive and dynamically designed optimal basis for the input signal is achieved. This facilitates the revelation of subtle fault features in the decomposed wavelet sub-bands.

(2) Quantum theory, as a profoundly transformative framework, holds enormous potential when introduced into the analysis of vibration signals. Its integration into vibration signal analysis is poised to offer novel perspectives to the field. The utilization of nonlinear quantum permutation entropy in the process of nonlinear quantization takes into account the actual values of the time series and ensures highly accurate calculations of the probability distribution of the arrangement of various states. Therefore, leveraging nonlinear quantum permutation entropy allows for a more precise reflection of the system’s operational state. Comparisons with conventional entropy values such as sample entropy indicate that nonlinear quantum permutation entropy proves to be more effective for feature extraction from vibration signals in complex structured rotating machinery.

(3) The feature extraction algorithm proposed, based on FAWT and nonlinear quantum permutation entropy, is employed on both rolling bearing and experimental gear data. Experimental findings indicate that the proposed method effectively discerns various fault types and severity levels with accuracy. Comparative analysis with existing techniques highlights the effectiveness and practicality of the proposed model.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported financially by Fundamental Research Program of Shanxi Province (No. 202103021223056).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Bai L., Li W. and Ren H.; data collection: Li F. and Yan T.; analysis and interpretation of results: Bai L., Chen L., Li W.; draft manuscript preparation: Bai L., Yan T. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. Han et al., “Parallel network using intrinsic component filtering for rotating machinery fault diagnosis,” Meas. Sci. Technol., vol. 34, no. 3, pp. 035108, 2023. doi: 10.1088/1361-6501/aca705. [Google Scholar] [CrossRef]

2. Y. Miao, B. Zhang, C. Li, J. Lin, and D. Zhang, “Feature mode decomposition: New decomposition theory for rotating machinery fault diagnosis,” IEEE Trans. Ind. Electron., vol. 70, no. 2, pp. 1949–1960, 2023. doi: 10.1109/TIE.2022.3156156. [Google Scholar] [CrossRef]

3. P. Liang, L. Xu, H. Shuai, X. Yuan, B. Wang and L. Zhang, “Semisupervised subdomain adaptation graph convolutional network for fault transfer diagnosis of rotating machinery under time-varying speeds,” IEEE/ASME Trans. Mechatron., vol. 29, no. 1, pp. 730–741, 2024. doi: 10.1109/TMECH.2023.3292969. [Google Scholar] [CrossRef]

4. X. Xu, B. Li, Z. Qiao, P. Shi, H. Shao and R. Li, “Caputo-Fabrizio fractional order derivative stochastic resonance enhanced by ADOF and its application in fault diagnosis of wind turbine drivetrain,” Renew. Energy, vol. 219, pp. 119398, 2023. doi: 10.1016/j.renene.2023.119398. [Google Scholar] [CrossRef]

5. L. Jing, M. Zhao, P. Li, and X. Xu, “A convolutional neural network-based feature learning and fault diagnosis method for the condition monitoring of gearbox,” Measurement, vol. 111, pp. 1–10, 2017. doi: 10.1016/j.measurement.2017.07.017. [Google Scholar] [CrossRef]

6. S. Wang et al., “Single and simultaneous fault diagnosis of gearbox via wavelet transform and improved deep residual network under imbalanced data,” Eng. Appl. Artif. Intell., vol. 133, no. 18, pp. 108146, 2024. doi: 10.1016/j.engappai.2024.108146. [Google Scholar] [CrossRef]

7. X. Xu, S. Bao, P. Liang, Z. Qiao, C. He, and P. Shi, “A broad learning model guided by global and local receptive causal features for online incremental machinery fault diagnosis,” Expert. Syst. Appl., vol. 246, no. 6, pp. 123124, 2024. doi: 10.1016/j.eswa.2023.123124. [Google Scholar] [CrossRef]

8. J. Lee, F. Wu, W. Zhao, M. Ghaffari, L. Liao and D. Siegel, “Prognostics and health management design for rotary machinery systems—Reviews, methodology and applications,” Mech. Syst. Signal Process., vol. 42, no. 1–2, pp. 314–334, 2014. doi: 10.1016/j.ymssp.2013.06.004. [Google Scholar] [CrossRef]

9. X. Xu, S. Bao, H. Shao, and P. Shi, “A multi-sensor fused incremental broad learning with D-S theory for online fault diagnosis of rotating machinery,” Adv. Eng. Inform., vol. 60, no. 12, pp. 102419, 2024. doi: 10.1016/j.aei.2024.102419. [Google Scholar] [CrossRef]

10. W. He, Y. Zi, B. Chen, F. Wu, and Z. He, “Automatic fault feature extraction of mechanical anomaly on induction motor bearing using ensemble super-wavelet transform,” Mech. Syst. Signal Process., vol. 54, no. 4, pp. 457–480, 2015. doi: 10.1016/j.ymssp.2014.09.007. [Google Scholar] [CrossRef]

11. F. Dao, Y. Zeng, and J. Qian, “A novel denoising method of the hydro-turbine runner for fault signal based on WT-EEMD,” Measurement, vol. 219, pp. 113306, 2023. doi: 10.1016/j.measurement.2023.113306. [Google Scholar] [CrossRef]

12. R. Yan, R. Gao, and X. Chen, “Wavelets for fault diagnosis of rotary machines: A review with applications,” Signal Process., vol. 96, no. 4, pp. 1–15, 2014. doi: 10.1016/j.sigpro.2013.04.015. [Google Scholar] [CrossRef]

13. C. Li, R. Sanchez, G. Zurita, M. Cerrada, D. Cabrera and R. Vásquez, “Gearbox fault diagnosis based on deep random forest fusion of acoustic and vibratory signals,” Mech. Syst. Signal Process., vol. 76–77, pp. 283–293, 2016. doi: 10.1016/j.ymssp.2016.02.007. [Google Scholar] [CrossRef]

14. R. Yan et al., “Wavelet transform for rotary machine fault diagnosis: 10 years revisited,” Mech Syst. Signal Process., vol. 200, no. 5, pp. 110545, 2023. doi: 10.1016/j.ymssp.2023.110545. [Google Scholar] [CrossRef]

15. Y. Hong, S. Ahn, C. Song, and Y. Cho, “Component-level fault diagnostics of a bevel gear using a wavelet packet transform,” Proc. IMechE Part E: J. Process Mech. Eng., vol. 225, no. 1, pp. 1–12, 2011. doi: 10.1177/2041300910393428. [Google Scholar] [CrossRef]

16. N. Wang, D. Jiang, and W. Yang, “Dual-tree complex wavelet transform and SVD-based acceleration signals denoising and its application in fault features enhancement for wind turbine,” J. Vib. Eng. Technol., vol. 7, no. 4, pp. 311–320, 2019. doi: 10.1007/s42417-019-00126-z. [Google Scholar] [CrossRef]

17. B. Chen, Z. Zhang, and C. Sun, “Fault feature extraction of the gearbox by using overcomplete rational dilation discrete wavelet transform on signals measured from vibration sensors,” Mech Syst. Signal Process., vol. 33, no. 3, pp. 275–298, 2012. doi: 10.1016/j.ymssp.2012.07.007. [Google Scholar] [CrossRef]

18. H. Jin, A. Titus, Y. Liu, Y. Wang, and Z. Han, “Fault diagnosis of rotary parts of a heavy-duty horizontal lathe based on wavelet packet transform and support vector machine,” Sensors, vol. 19, no. 19, pp. 4069, 2019. doi: 10.3390/s19194069. [Google Scholar] [PubMed] [CrossRef]

19. M. Sharma, P. Sharma, R. Pachori, and U. Acharya, “Dual-tree complex wavelet transform-based features for automated alcoholism identification,” Int. J. Fuzzy Syst., vol. 20, no. 4, pp. 1297–1308, 2018. doi: 10.1007/s40815-018-0455-x. [Google Scholar] [CrossRef]

20. G. Cai, X. Chen, and Z. He, “Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of a gearbox,” Mech. Syst. Signal Process., vol. 41, no. 1–2, pp. 34–53, 2013. doi: 10.1016/j.ymssp.2013.06.035. [Google Scholar] [CrossRef]

21. I. Bayram, “An analytic wavelet transform with a flexible time-frequency covering,” IEEE Trans. Signal Process., vol. 61, no. 5, pp. 1131–1142, 2013. doi: 10.1109/TSP.2012.2232655. [Google Scholar] [CrossRef]

22. C. Zhang, B. Li, B. Chen, H. Cao, Y. Zi and Z. He, “Weak fault signature extraction of rotating machinery using flexible analytic wavelet transform,” Mech. Syst. Signal Process., vol. 64, pp. 162–187, 2015. doi: 10.1016/j.ymssp.2015.03.030. [Google Scholar] [CrossRef]

23. S. Sharma, S. Tiwari, and S. Singh, “Integrated approach based on flexible analytical wavelet transform and permutation entropy for fault detection in rotary machines,” Measurement, vol. 169, pp. 108389, 2021. doi: 10.1016/j.measurement.2020.108389. [Google Scholar] [CrossRef]

24. A. Glowacz, W. Glowacz, Z. Glowacz, and J. Kozik, “Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals,” Measurement, vol. 113, pp. 1–9, 2018. doi: 10.1016/j.measurement.2017.08.036. [Google Scholar] [CrossRef]

25. L. Bai, Z. Han, J. Ren, and X. Qin, “Research on feature selection for rotating machinery based on supervision kernel entropy component analysis with whale optimization algorithm,” Appl. Soft Comput., vol. 92, no. 1, pp. 106245, 2020. doi: 10.1016/j.asoc.2020.106245. [Google Scholar] [CrossRef]

26. R. Yan, Y. Liu, and R. Gao, “Permutation entropy: A nonlinear statistical measure for status characterization of rotary machines,” Mech. Syst. Signal Process., vol. 29, pp. 474–484, 2012. doi: 10.1016/j.ymssp.2011.11.022. [Google Scholar] [CrossRef]

27. X. Zhang, Y. Liang, J. Zhou, and Y. zang, “A novel bearing fault diagnosis model integrated permutation entropy, ensemble empirical mode decomposition and optimized SVM,” Measurement, vol. 69, pp. 164–179, 2015. doi: 10.1016/j.measurement.2015.03.017. [Google Scholar] [CrossRef]

28. J. Tsai, F. Hsiao, Y. Li, and J. Shen, “A quantum search algorithm for future spacecraft attitude determination,” Acta Astronaut., vol. 68, no. 7–8, pp. 1208–1218, 2011. doi: 10.1016/j.actaastro.2010.10.023. [Google Scholar] [CrossRef]

29. A. Malhotra, A. Minhas, S. Singh, M. Zuo, R. Kumar and P. Kankar, “Bearing fault diagnosis based on flexible analytical wavelet transform and fuzzy entropy approach,” Mater. Today Proc., vol. 43, no. 7, pp. 629–635, 2021. doi: 10.1016/j.matpr.2020.12.160. [Google Scholar] [CrossRef]

30. M. Kumar, R. Pachori, and R. Acharya, “An efficient automated technique for CAD diagnosis using flexible analytic wavelet transform and entropy features extracted from HRV signals,” Expert. Syst. Appl., vol. 63, no. 1, pp. 165–172, 2016. doi: 10.1016/j.eswa.2016.06.038. [Google Scholar] [CrossRef]

31. D. Ramteke, R. Pachori, and A. Parey, “Automated gearbox fault diagnosis using entropy‐based features in flexible analytic wavelet transform (FAWT) domain,” J. Vib. Eng. Technol., vol. 9, no. 7, pp. 1703–1713, 2021. doi: 10.1007/s42417-021-00322-w. [Google Scholar] [CrossRef]

32. Y. Chen, P. Zhang, Z. Wang, W. Yang, and Y. Yang, “Denoising algorithm for mechanical vibration signal using quantum Hadamard transformation,” Measurement, vol. 66, pp. 168–175, 2015. doi: 10.1016/j.measurement.2015.02.005. [Google Scholar] [CrossRef]

33. Y. Chen, “Morphological filtering using nonlinear quantum bit and its application,” J. Mech. Eng., vol. 51, no. 2, pp. 127–133, 2015. doi: 10.3901/JME.2015.02.127. [Google Scholar] [CrossRef]

34. C. Ding, B. Zhang, F. Feng, and S. Wu, “Nonlinear quantum entropy and its application in feature extraction for planetary gearboxes,” J. Vib. Shock., vol. 37, no. 23, pp. 120–148, 2018. [Google Scholar]

35. Z. Feng, L. Zhao, and F. Chu, “Vibration spectral characteristics of localized gear fault of planetary gearboxes,” (in ChineseProc. CSEE, vol. 33, no. 5, pp. 119–127, 2013. [Google Scholar]