 Open Access
Open Access
ARTICLE
Vector Dominance with Threshold Searchable Encryption (VDTSE) for the Internet of Things
1 College of Safety Science and Engineering, Xi’an University of Science and Technology, Xi’an, 710054, China
2 College of Computer Science and Technology, Xi’an University of Science and Technology, Xi’an, 710054, China
* Corresponding Author: Jingjing Nie. Email:
Computers, Materials & Continua 2024, 79(3), 4763-4779. https://doi.org/10.32604/cmc.2024.051181
Received 28 February 2024; Accepted 19 April 2024; Issue published 20 June 2024
Abstract
The Internet of Medical Things (IoMT) is an application of the Internet of Things (IoT) in the medical field. It is a cutting-edge technique that connects medical sensors and their applications to healthcare systems, which is essential in smart healthcare. However, Personal Health Records (PHRs) are normally kept in public cloud servers controlled by IoMT service providers, so privacy and security incidents may be frequent. Fortunately, Searchable Encryption (SE), which can be used to execute queries on encrypted data, can address the issue above. Nevertheless, most existing SE schemes cannot solve the vector dominance threshold problem. In response to this, we present a SE scheme called Vector Dominance with Threshold Searchable Encryption (VDTSE) in this study. We use a Lagrangian polynomial technique and convert the vector dominance threshold problem into a constraint that the number of two equal-length vectors’ corresponding bits excluding wildcards is not less than a threshold t. Then, we solve the problem using the proposed technique modified in Hidden Vector Encryption (HVE). This technique makes the trapdoor size linear to the number of attributes and thus much smaller than that of other similar SE schemes. A rigorous experimental analysis of a specific application for privacy-preserving diabetes demonstrates the feasibility of the proposed VDTSE scheme.Keywords
The Internet of Things (IoT) [1] provides safe and controllable real-time online monitoring, positioning, and other service functions. As an important IoT application in the medical field, the Internet of Medical Things (IoMT) can realize efficient and inexpensive healthcare and enhance patient comfort. However, the data involved in continuous monitoring can be massive, and the devices used to collect the data are resource-constrained. As a result, the data is often stored in the cloud, which may seriously violate patient privacy during data collection, storage, and computation. Suspecting the infringement of their healthcare privacy, patients may become reluctant to participate or encrypt their medical data before uploading it to service providers. This raises another question: how to perform a user search about this encrypted private data. In this context, Searchable Encryption (SE) is desirable as a prominent encryption tool for privacy-preserving IoMT [2,3].
Consider a specific example of privacy-preserving diabetes screening (see Fig. 1) in IoMT. In this example, a nurse tries to screen out diabetics from Personal Health Records (PHRs). However, PHRs contain private information, and the patient is unwilling to share them with anyone. Therefore, the patient in this example encrypts the medical record →X (random blood glucose = 4, fasting blood glucose = 3, 2-h post-load glucose = 5, glycated hemoglobin = 4) and the personal information M before uploading them to the service provider. In this case, the nurse sends a search request (→Δ, t) (random blood glucose = 3, fasting blood glucose = 2, 2-h post-load glucose = 3, glycated hemoglobin = 5, t = 2 (1≤t≤4)) to the service provider using a handheld Personal Digital Assistant (PDA). When the service provider detects number(→X≻→Δ)≥t (→X≻→Δ means that →X dominates →Δ [4]), it will send the encrypted M to the nurse. In this process, the service provider has no prior knowledge of →X and M.
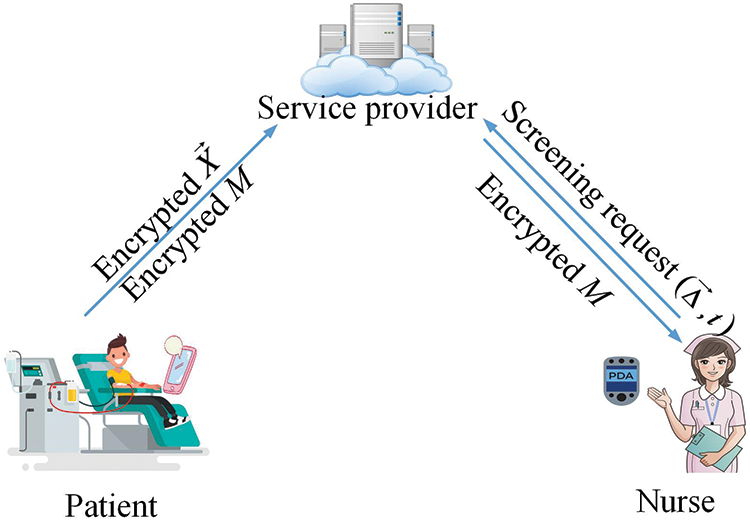
Figure 1: Privacy-preserving diabetes screening
For the application above, it is necessary to solve number(→X≻→Δ)≥t in SE. It is very helpful when we need to compare multiple attributes while counting the number of matches. We call the proposed scheme Vector Dominance [4] with Threshold Searchable Encryption (VDTSE). The vector dominance with threshold problem determines whether the number of components in vectors →X=(X1,…,Xn) and →Δ=(Δ1,…,Δn) (Xi>Δi, i∈[1,n]) reaches a certain threshold t.
Therefore, the proposed VDTSE scheme is favorable for threshold comparison queries in a public-key SE system. When number (→X≻→Δ)≥t holds, the encrypted M will be sent to the requester. Besides, our algorithm can solve the problem of existing SE schemes by controlling the threshold t, which is adaptive and can support additional functionalities such as range queries (t = 0) or similarity searches (Xi=Δi).
The main contributions of this study are outlined below:
• We design a VDTSE scheme supporting comparable attributes that can function for the (t, n)-threshold policy. Although existing schemes [5–8] also support this feature, they are restricted to AND-gates (or (t, t)-threshold). We implement the threshold using a Lagrangian polynomial technique.
• The VDTSE scheme has a shorter trapdoor that makes it more suitable for data storage on mobile devices (such as PDAs). To achieve this, we solve it using our technique modified in Hidden Vector Encryption (HVE) [7], which makes the trapdoor size linear.
• We prove the security, flexibility, and effectiveness of the proposed scheme through theoretical comparison with other schemes. Finally, the experiment shows that the trapdoor size of our method is much smaller than that of other similar SE schemes.
The rest of this paper is structured as below. Section 2 describes the related work of VDTSE. Section 3 contains the preliminaries, while Section 4 presents the scheme construction. Section 5 discusses the security proof for our scheme, Section 6 describes the performance of the proposed scheme, and Section 7 concludes the article and suggests possible future work.
Song et al. popularized the SE scheme [9] that enabled a user to generate both ciphertexts and trapdoors under a symmetric system, so service providers could perform a match search on encrypted information. Under the symmetric system, SE was further improved in [10–12]. In 2004, Boneh et al. [13] considered the first asymmetric SE scheme, Public-key Encryption with Keyword Search (PEKS). The initial public-key SE schemes, however, were limited to test keyword equality. Among these developments, comparative searches received little attention.
To address the aforementioned issue, Boneh et al. [5] created a searchable public-key system called HVE in 2007, which allowed for conjunctive range queries over encrypted data. That same year, Shi et al. [6] proposed a multi-dimensional range SE scheme. However, the aforementioned methods were inefficient and disadvantageous from an operational standpoint. As a result, Park [7] proposed a novel HVE that was effective in prime-order groups significantly smaller than the composite-order groups on the identical level. Later, Park et al. [8] realized a more effective HVE scheme. Although the schemes above supported the AND gate of attribute comparison, they could not apply to arbitrary threshold gates. Fortunately, Sun et al. [14] extended the technique by combining HVE and predicate encryption (PE) for the inner product (called IPE) to achieve threshold comparison queries.
In addition to these references, other scholars addressed the threshold comparison. In 2007, Bethencourt et al. [15] presented a threshold comparison scheme to realize numeric ranges search. In 2018, Attrapadung et al. [16] developed a numeric comparison scheme under the Attribute-Based Encryption (ABE) system. In 2017, Xue et al. [17] constructed a comparable ABE scheme that was more efficient. Although these schemes [15–17] were under the public key system, they could not protect the privacy of →X.
To the best of our knowledge, the only scheme that supported the threshold comparison was [14], but their ciphertext and private key size increased quadratically, posing potential challenges in resource-constrained IoT devices. Therefore, we need to design a more efficient SE scheme.
Assume g is a generator in G, while G and GT are two multiplicative cyclic groups whose order is prime p. e:G×G→GT is a function with these attributes:
1. Bilinear. We have e(uc,vd)=e(u,v)cd, where u,v∈G, c,d∈Zp.
2. Nondegenerate. e(g,g)≠1.
3. Computable. e is a computable map algorithm.
Therefore, we state that e is a bilinear pairing map within G. It is worth noting that e(,) is symmetric because e(gc,gd)=e(g,g)cd=e(gd,gc).
Decisional Bilinear Diffie-Hellman (DBDH) Assumption. The following describes the DBDH problem: Provided (g,ga,gb,gc,Z)∈G4×GT, identify Z=e(g,g)abc or Z is random in GT.
Augmented Decision Linear (ADLIN) Assumption. Provided (g,gz1,gz2,gz22,gz2/z1,gz22z3,gz4,Z) ∈G8, find Z=gz1(z3+z4) or Z is random in G.
Definition 1. The {DBDH, ADLIN} assumption holds in G when the advantage of any polynomial time algorithm in dealing with the {DBDH, ADLIN} problem is negligible.
Our scheme is characterized by a chosen plaintext security, and ciphertext CT offers no information about the vector →X and the message M, which is proved in a security proof that relies on the difficulty of DBDH and ADLIN. The following games are played between an adversary 𝒜 and a challenger 𝒞. Besides, U and ℓ are given to 𝒜, where U is the attribute universal set and ℓ is the length of vector.
• Initialization (Init). 𝒜 commits →X∗0, →X∗1∈Σℓ/U to 𝒞.
• Setup. 𝒞 runs the KeyGen algorithm to get a public key PK and a secret key SK, offers PK to 𝒜.
• Query Phase 1. 𝒜 performs a series of trapdoor queries adaptively. To any trapdoor T→Δi from queried vectors →Δ1,…,→Δqη∈(Σ)ℓ/U and thresholds t1,…,tqη, there is a restriction of f→Δi,ti(→X∗0)=f→Δi,ti(→X∗1) for all i=1,…,qη. 𝒞 uses trapdoors TK→Δi,ti←Trapdoor(SK,→Δi,ti) to respond to 𝒜.
• Challenge. 𝒜 offers M0,M1∈ℳ. If f→Δi,ti(→X∗0)=f→Δi,ti(→X∗1)=1, then M0=M1. 𝒞 responds CT∗ ← PEKS(PK,→X∗β,Mβ) to 𝒜, where β∈{0,1}.
• Query Phase 2. 𝒜 makes other trapdoor queries adaptively for vectors →Δqn+1,…,→ΔqTK and thresholds tqn+1,…,tqTK. The restrictions are the same as those in Query Phase 1 and Challenge.
• Guess. 𝒜 guesses β′. 𝒜 wins the game when β′=β, where β′∈{0,1}.
We define AdvVDTSE𝒜=|Pr[β′=β]−1/2| as the advantage that 𝒜 has in breaking the VDTSE scheme.
Definition 2. If the advantage AdvVDTSE𝒜 is negligible, the VDTSE scheme is selectively secure.
This section presents the techniques for solving number(→X≻→Δ)≥t in the form of a novel encoding. We set a universal set U={1,2,…,|U|}. Every bit xj of a |→Δ|×|U|-dimension vector →x converted from vector →X is chosen from {0,1} following Eq. (1). In a similar way, every bit σj of another |→Δ|×|U|-dimension vector →σ transformed from vector →Δ is selected from {1,∗} according to Eq. (2).
x(i−1)×|U|+j={1,Xi<j,0,otherwise,(1)
where 1≤j≤|U|, 1≤i≤|→X|.
σ(i−1)×|U|+j={1,Δi=j,∗,otherwise,(2)
where 1≤j≤|U|, 1≤i≤|→Δ|.
When the VDTSE scheme is used in multi-user scenarios, a trusted private service provider needs to be added to receive trapdoors from users and then send the trapdoors to an untrusted public service provider. Therefore, only single-user scenarios are considered in this paper.
Applying the example of privacy-preserving diabetes screening in the Introduction, set →X=(X1, X2, X3, X4)=(4, 3, 5, 4), →Δ=(Δ1,Δ2,Δ3,Δ4)=(3,2,3,5), t = 2, ℓ=|→X|×|U|=20, where U={1, 2, 3, 4, 5} and |→X|=|→Δ|=4. Two 20-dimension vectors →x and →σ are transformed from →X and →Δ following Eqs. (1) and (2), respectively.
For →X, the 20-dimension vector →x is represented by
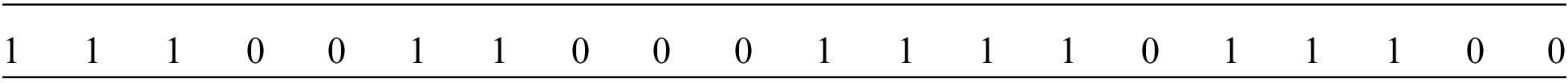
For →Δ, the 20-dimension vector →σ is represented by

Since there are 3 (>t) equal corresponding bits of →x and →σ excluding * bits, number(→X≻→Δ)≥t holds. The detailed scheme is as follows.
• KeyGen(k, ℓ, U). The KeyGen algorithm uses a security parameter k = 1024 bit and a type-A elliptic curve that has as input a 160-bit group order, a vector length ℓ, a universe U, and a random generator g ∈ G to generate our scheme parameters. It selects random exponents y1,v1,…,vℓ, t1,…,tℓ∈Zp as well as random elements α, (h1, u1, w1) ,…, (hℓ, uℓ, wℓ)∈G. It defines g1=gα, Y1=gy1, Vi=gvi, Ti=gti for i=1,…,ℓ. Furthermore, it establishes Ω=e(g1,Y1) ∈ GT. The public key PK and the secret key SK are
PK=(g,Y1,(h1,u1,w1,V1,T1),…,(hℓ,uℓ,wℓ,Vℓ,Tℓ),Ω)∈G5ℓ+2×GT,SK=(α,g1=gα,y1,v1,…,vℓ,t1,…,tℓ)∈Z2ℓ+2p×G.
• PEKS(PK, →X). With PK and vector →X=(X1,…,Xℓ/U) as input, this algorithm initially converts →X into →x=(x1,…,xℓ) based on Eq. (1). It chooses two random parameters s1, s2∈Zp, then uses them to encrypt message M∈GT and vector →x for generating ciphertext:
CT=(Ys11,gs2,(h1ux11)s1Vs21,…,(hℓuxℓℓ)s1Vs2ℓ,ws11Ts21,…,ws1ℓTs2ℓ,Ωs1M)∈G2ℓ+2×GT.
This encryption algorithm ensures the confidentiality of M and →x. Their integrity can be recognized by the Message Authentication Code (MAC), public key-based Homomorphic Linear Authentication (HLA), Hash-based Message Authentication Code (HMAC), etc.
• Trapdoor(SK, →Δ, t). This algorithm uses SK and vector →Δ=(Δ1,…,ΔJ,…,Δℓ/U) as input, then chooses at random a t-1 degree polynomial q(x) where q(0)=α. It first transforms →Δ into →σ = (σ1,…,σℓ) ∈ (Σ∗)ℓ based on Eq. (2). To generate a trapdoor T→σ for i∈S(→σ), where S(→σ) is the set of all indexes i that satisfies σi≠∗, it computes T→σ as
T→σ=(σ∗,∀i∈S(→σ):{gq(J)(hiuσii)rJwηJi,YrJ1,YηJ1,Y−(virJ+tiηJ)1,Vy1ZJi,YZJ1,(hiuσii)ZJ}ℓ/UJ=1)∈G7(ℓ/U),i=(J−1)U+ΔJ.
• Test (CT,T→σ). Let CT = (C1, C2, C3,1, …, C3,i, …, C3,ℓ, C4,1, …, C4,i, …, C4,ℓ, C5) and T→σ=(K1,J,K2,J,K3,J,K4,J,K5,J,K6,J,K7,J) for 1≤J≤ℓ/U. The Test algorithm computes the following:
Step 1.
e(K7,J,C1)⋅e(K5,J,C2)e(K6,J,C3,i)=e((hiuσii)ZJ,Ys11)⋅e(Vy1ZJi,gs2)e((hiuxii)s1Vs2i,YZJ1)=e(ui,g)y1s1ZJ(σi−xi)=1, when σi=xi.
Step 2.
When number(xi=σi)≥t holds except for * bits, chooses t elements of S satisfying xi=σi. So we have
C5/∏i∈S[e(C1,K1,J)e(C3,i,K2,J)⋅e(C4,i,K3,J)⋅e(C2,K4,J)]AJ→M,
where AJ is the Lagrange coefficient for i and S: AJ(x)=∏j∈S,j≠i[(x−j)/(i−j)].
If the DBDH and ADLIN assumptions are met, the VDTSE scheme is selectively secure. The adversary chooses two vectors →x∗0=(x∗0,1,…,x∗0,ℓ) and →x∗1=(x∗1,1,…,x∗1,ℓ)∈Σℓ that are transformed from vectors →X∗0,→X∗1 at the beginning of this security game. We assume that A={1,2,…,|A|}, where A is the set of indexes i that satisfies A={i∈{1,…,ℓ}∣x∗0,i≠x∗1,i}. We continue to choose random elements (R3,1,…,R3,∣A∣, R4,1,…,R4,∣A∣) from G and R5 from GT. We assume the following games:
Game0:CT0=(C1,C2,C3,1,…,C3,∣A∣,C3,∣A∣+1,…,C3,ℓ,C4,1,…,C4,∣A∣,C4,∣A∣+1,…,C4,ℓ,C5),
Game1:CT1=(C1,C2,C3,1,…,C3,∣A∣,C3,∣A∣+1,…,C3,ℓ,C4,1,…,C4,∣A∣,C4,∣A∣+1,…,C4,ℓ,R5),
Game2,1:CT2,1=(C1,C2,R3,1,…,C3,∣A∣,C3,∣A∣+1,…,C3,ℓ,R4,1,…,C4,∣A∣,C4,∣A∣+1,…,C4,ℓ,R5),
⋮,
Game2,∣A∣:CT2,∣A∣=(C1,C2,R3,1,…,R3,∣A∣,C3,∣A∣+1,…,C3,ℓ,R4,1,…,R4,∣A∣,C4,∣A∣+1,…,C4,ℓ,R5).
When the adversary sends M0,M1, the challenger provides the ciphertext about (→x∗β,Mβ) to the adversary, where β∈{0,1}. If the adversary guesses β correctly, he will win the game. Game0 is the real security game that is given to the adversary. In this game, C3,1,…,C3,ℓ,C4,1,…,C4,ℓ are the ciphertext about →x∗β, and C5 is the ciphertext about Mβ. CT2,∣A∣ is the challenge ciphertext of Game2,∣A∣, which reveals nothing about the attributes associated with A or message Mβ. We show this in the following games, which are all computationally indistinguishable.
In our model (the selective security), the adversary performs trapdoor queries for any vector →Δ=(Δ1, …,ΔJ,…,Δℓ/U) and a threshold t transformed to vector →σ=(σ1,…,σℓ)∈(Σ∗)ℓ and t, under the constraint that f→Δ,t(→X∗0)=f→Δ,t(→X∗1) (i.e., f→σ,t(→x∗0)=f→σ,t(→x∗1)). We assume S is the set of i for which σi is not a wildcard. We divide the queries into two types:
• Type 1. [number(X0,J>ΔJ)≥t]∧[number(X1,J>ΔJ)≥t] (i.e., [number(σi=x∗0,i)≥t]∧ [number (σi=x∗1,i)≥t]). If the challenge message meets M0=M1, this type of query can be performed.
• Type 2. [number(X0,J>ΔJ<t]∧[number(X1,J>ΔJ)<t] (i.e., [number(σi=x∗0,i)<t]∧ [number(σi) =x∗1,i)<t].
Case 1. Type 1 does not match. Additionally, there is an index i∈S∩A for which σi≠x∗β,i.
Case 2. Type 1 and Case 1 fail to hold, and there exist i∈S∩A for which σi=x∗β,i, while there exists j∈S for which σi≠x∗β,i.
Lemma 1. Suppose that the DBDH assumption holds. In other words, the distinct difference in the advantage of 𝒜 who is an adversary of any polynomial time in Game0 and Game1 is negligible.
Proof. Suppose 𝒜 has a non-negligible difference about the advantage of G. If Z=e(g,g)abc holds for a random instance (g,ga,gb,gc,Z), ℬ returns 1, otherwise, ℬ returns 0. ℬ communicates with 𝒜 in the following ways:
• Init. At the start of the game, 𝒜 produces two vectors →X∗0,→X∗1 that have been converted to →x∗0,→x∗1∈Σℓ. ℬ internally changes β∈{0,1}.
• Setup. ℬ selects exponents at random γ, y1,v1,…,vℓ, t1,…, tℓ, θ1,…,θℓ, ϕ1,…,ϕℓ, λ1,…,λℓ\break∈Zp. It sets Y1=gy1, hi=gθi(gb)−ϕi⋅x∗β,i,ui=(gb)ϕi,wi=gλi,Vi=gvi,Ti=gti. Besides, ℬ establishes Ω = e(g1,Y1) =e(ga, gb)y1e(g, g)γy1. Take note that g1=gabgγ, and this is secret to ℬ. 𝒜 is handed the public key PK=(g, Y1, (h1, u1, w1, V1, T1),…,(hℓ, uℓ, wℓ, Vℓ, Tℓ), Ω).
• Query Phase 1. 𝒜 triggers the trapdoor queries. Assume 𝒜 searches for →Δ that has been changed to →σ=(σ1,…,σℓ)∈(Σ∗)ℓ. Let S={i|σi≠∗}, where * is a wildcard. The queries of 𝒜 are divided into the following two types.
Type 1. 𝒜 sends a Type 1 query, and ℬ answers an arbitrary guess. The query above shows that M0=M1, and ℬ provides the message’s encryption. Since in this circumstance the two games, Game0 and Game1, are identical, there ought to be no difference in 𝒜’s advantage.
Type 2. These two scenarios imply that there exists at least one index j∈S that satisfies σj≠x∗β,j. ℬ initially defines the three sets, Γ, Γ′, S, as follows: Γ={i∣σi=x∗β,i}, Γ′ is any set such that Γ⊆Γ′⊆S and |Γ′|=t−1, and S=Γ′∪{0}. Following that, ℬ specifies the trapdoor KJ, where J=(i−ΔJ)/U+1. ℬ selects a random t-1 degree polynomial q(x) by randomly selecting its value for the t-1 points and having q(0)=ab+γ.
If i∈Γ′, ℬ chooses a random rJ,ηJ∈Zp,q(J)=τJ.
K1,J=gq(J)(hiuσii)rJwηJi=(g)τJ+θi+λiηJ(gb)rJ(σi−x∗β, i)ϕi,
K2,J=YrJ1=(g)y1rJ,
K3,J=YηJ1=(g)y1ηJ,
K4,J=Y−(rJvi+ηJti)1=(g)−y1(rJvi+ηJti),
K5,J=Vy1ZJi=(g)y1viZJ,
K6,J=YZJ1=(g)y1ZJ,
K7,J=(hiuσii)ZJ=((g)θi(gb)(σi−x∗β,i)ϕi)ZJ
If i∈S−Γ′:σi−x∗β,i≠0, q(J)=Σi∈Γ′q(J)ΔJ+q(0)Δ0,rJ=(˜rJ−a/[(σi−x∗β,i)ϕi])Δ0.
K1,J=gq(J)(hiuσii)rJwiηJ=gΣi∈Γ′q(J)ΔJ+q(0)Δ0((g)θi(gb)(σi−x∗β,i)ϕi)rJ(gλi)ηJ
=(g)Σi∈Γ′q(J)ΔJg(ab+γ)Δ0((g)θi(gb)(σi−x∗β,i)ϕi)(˜rJ−a/[(σi−x∗β,i)ϕi])Δ0(gλi)ηJ
=(g)Σi∈Γ′q(J)ΔJ+γΔ0gabΔ0(g)θi˜rJΔ0(ga)(θi/[(σi−x∗β,i)ϕj])Δ0(gb)(σi−x∗β,i)ϕi˜rJΔ0(g−abΔ0)(gλi)ηJ
=(g)Σi∈Γ′q(J)ΔJ+γΔ0+θi˜rJΔ0+λiηJ(ga)(θi/[(σi−x∗β,i)ϕj])Δ0(gb)(σi−x∗β,i)ϕi˜rJΔ0,
K2,J=YrJ1=(gy1)(˜rJ−a/[(σi−x∗β,i)ϕi])Δ0=(g)y1˜rJΔ0(ga)−(y1Δ0)/[(σi−x∗β,i)ϕi],
K3,J=YηJ1=(g)y1ηJ,
K4,J=Y−(rJvi+ηJti)1=(gy1)−((˜rJ−a/[(σi−x∗β,i)ϕi])Δ0vi+ηJti)=(g)−y1(˜rJΔ0vi+ηJti)(ga)(y1Δ0vi)/(σi−x∗β,i)ϕi,
K5,J=Vy1ZJi=(g)y1viZJ,
K6,J=YZJ1=(g)y1ZJ,
K7,J=(hiuσii)ZJ=((g)θi(gb)(σi−x∗β,i)ϕi)ZJ=(g)θiZJ(gb)(σi−x∗β,i)ϕiZJ.
• Challenge. 𝒜 sends M0 and M1 to ℬ. If M0=M1, ℬ finishes the game and guesses β′∈{0,1}. Otherwise, ℬ chooses s1,s2∈Zp randomly and generates the challenge ciphertext CT∗, where s1=c.
C∗1=Ys11=(gy1)c=(gc)y1,
C∗2=gs2=(g)s2,
C∗3,1=(h1ux∗β,11)s1Vs21=((g)θ1(gb)(x∗β,1−x∗β,1)ϕ1)cgv1s2=(gc)θ1(gv1)s2,…,
C∗3,i=(hiux∗β,ii)s1Vs2i=(gc)θi(g)vis2,…,
C∗3,ℓ=(hℓux∗β,ℓℓ)s1Vs2ℓ=(gc)θℓ(g)vℓs2,
C∗4,1=ws11Ts21=(gλ1)c(gt1)s2=(gc)λ1(g)t1s2,…,
C∗4,i=ws1iTs2i=(gc)λi(g)tis2,…,
C∗4,ℓ=ws1ℓTs2ℓ=(gc)λℓ(g)tℓs2,
C∗5=e(g1,Y1)s1Mβ=e(gab+γ,gy1)cMβ=Ze(gc,g)y1γMβ,
where Z=e(g,g)abc.
• Query Phase 2. 𝒜 carries on issuing questions that were not asked in Query Phase 1. ℬ reacts the same way as previously.
• Guess. For the challenge ciphertext, 𝒜 provides a guess β′∈{0,1}. If β′=β, ℬ returns 1, else ℬ returns 0.
ℬ’s advantage in solving the DBDH problem is related to 𝒜’s advantage of distinguishing Game0 and Game1. Allow Game1 = Game2, 0, and the following lemma is true for j=0,1,…,|A|−1.
Lemma 2. Suppose that the ADLIN assumption is true. In other words, the difference in the advantage of 𝒜 in Game2, j and Game2, j + 1 is negligible for every polynomial time adversary 𝒜.
Proof. Consider 𝒜 with a non-negligible difference ε about its advantage between Game2, j and Game2, j + 1. We hope to create an algorithm in which ℬ employs 𝒜’s ability to work out the ADLIN issue in G. Given (g,gz1,gz2,gz22,gz2/z1,gz22z3,gz4,Z)∈G8, ℬ outputs 1 when Z=gz1(z3+z4), otherwise ℬ generates 0. ℬ communicates with 𝒜 using the subsequent process:
• Init. At the start of the game, 𝒜 commits two vectors →X∗0,→X∗1 converted to →x∗0,→x∗1∈Σℓ. ℬ internally throws a coin β∈{0,1}.
• Setup. δ denotes the (j + 1)-th index in A. ℬ randomly selects γ,y1, v1,…,vℓ, t1,…,tℓ, θ1,…,θℓ, ϕ1,…,ϕℓ, λ1,…,λℓ, then places g1=gγ, Y1=(gz22)y1, and Ω=e(g1,Y1). Take note that ˜y1 =y1z22. Following that, ℬ sets hδ=(gz1)θδ(gz2)−ϕδ⋅x∗β,δ, uδ=(gz2)ϕδ,wδ=(gz1)λδ,Vδ=(gz1)θδgvδ, Tδ=(gz1)λδgtδ. For all i≠δ, ℬ sets hi=(gz22)θi(gz2)−ϕi⋅x∗β,i, ui=(gz2)ϕi, wi=(gz22)λi, Vi=gvi, and Ti=gti. ℬ sends the public key PK=(g,Y1,(h1,u1,w1,V1,T1),…,(hℓ,uℓ,wℓ,Vℓ,Tℓ),Ω) to 𝒜. Because g and all exponents are chosen at random, the public key PK has the same distribution as the original construction.
• Query Phase 1. 𝒜 offers trapdoor queries, where a trapdoor vector →Δ from 𝒜 is changed to →σ=(σ1,…,σℓ)∈(Σ∗)ℓ and S is the set of indexes i such that σi≠∗. We consider the two types of trapdoor queries stated previously.
Type 1. This describes the situation with δ∉S. ℬ then selects at random r1,…,rJ, η1,…,ηJ, Z1,…,ZJ ∈ ZJ for all i∈S, and makes rJ=˜rJ,ηJ=˜ηJ,ZJ=˜ZJ. Next, ℬ calculates i∉S,q(J)=γ.
K1,J=gq(J)(hiuσii)rJwηJi=gγ((gz22)θi(gz2)(σi−x∗β,i)ϕi)˜rJ(gz22)λi˜ηJ=gγ(gz22)θi˜rJ+λi˜ηJ(gz2)(σi−x∗β,i)ϕi˜rJ,
K2,J=YrJ1=(gz22)y1˜rJ,
K3,J=YηJ1=(gz22)y1˜ηJ,
K4,J=Y1−(rJvi+ηJti)=(gz22)−y1(rJvi+ηJti),
K5,J=Vy1ZJi=(g)y1vi˜ZJ,
K6,J=Y1ZJ=(gz22)y1˜ZJ,
K7,J=(hiuσii)ZJ=((gz22)θi˜ZJ(gz2)(σi−x∗β,i)ϕi˜ZJ).
Type 2. Case 1. Assume δ∈S and σδ≠x∗β,δ. Then, for each i(≠δ)∈S, ℬ chooses random r1,…,rJ, η1,…,ηJ,Z1,…,ZJ∈Zp. K1,J,…,K7,J are identical as those in Type 1. When i=δ, ℬ then calculates q(J)=γ, rJ=(˜rJ/z2+˜ηJ/z22)λδ, ηJ=−(˜rJ/z2+˜ηJ/z22)θδ−[ϕδ˜ηJ(σδ−x∗β,δ)]/(z1z2), and ZJ=˜ZJ.
K1,J=gq(J)(hδuσδδ)rJwηJδ=gγ((gz1)θδ(gz2)(σδ−x∗β,δ)ϕδ)(˜rJ/z2+˜ηJ/z22)λδ(gz1λδ)−(˜rJ/z2+˜ηJ/z22)θδ−[ϕδ˜ηJ(σδ−x∗β,δ)]/z1z2=gγ(g)(σδ−x∗β,δ)ϕδλδ˜rJ,
K2,J=YrJ1=(gz22y1)(˜rJ/z2+˜ηJ/z22)λδ=(gz2)y1˜rJλδ(g)y1˜ηJλδ,
K3,J=YηJ1=(gz22y1)−(˜rJ/z2+˜ηJ/z22)θδ−[ϕδ˜ηJ(σδ−x∗β,δ)]/(z1z2)=(gz2)−y1˜rJθδ(g)−y1˜ηJθδ(gz2/z1)−y1ϕδ˜ηJ(σδ−x∗β,δ),
K4,J=Y−(rJvδ+ηJtδ)1=(gz22y1)−((˜rJ/z2+˜ηJ/z22)λδvδ+[−(˜rJ/z2+˜ηJ/z22)θδ−[ϕδ˜ηJ(σδ−x∗β,δ)]/(z1z2)]tδ)
=(gz2)−y1˜rJ(vδλδ−tδθδ)(g)−y1˜ηJ(λδvδ−tδθδ)(gz2/z1)y1˜ηJϕδtδ(σδ−x∗β,δ),
K5,J=Vy1ZJδ=(g)y1vδ˜ZJ,
K6,J=YZJ1=(gz22)y1˜ZJ,
K7,J=(hδuσiδ)ZJ=(gz1)θδ˜ZJ(gz2)(σδ−x∗β,δ)ϕδ˜ZJ.
Case 2. Assume δ∈S and σδ=x∗β,δ, yet there exists an index j∈S such that σj≠x∗β,j. As in Case 1, ℬ chooses at random r1,…,rJ,η1,…,ηJ,Z1,…,ZJ∈Zp for each i(≠δ)∈S. K1,J,…,K7,J are identical to those in Type 1. Otherwise (i.e., i(=δ)∈S), ℬ generates q(J)=γ, rJ=(˜rJ/z22+ ˜ηJ/z2)λδ, ηJ= −(˜rJ/z22+˜ηJ/z2)θδ −ϕj˜ηJ(σj−x∗β,j), ZJ=˜ZJ.
K1,J=gq(J)(hδuσδδ)rJwηJδ=gγ((gz1)θδ(gz2)(σδ−x∗β,δ)ϕδ)rJ(gz1λδ)ηJ=gγ((gz1)θδ(gz2)(σδ−x∗β,δ)ϕδ)(˜rJ/z22+˜ηJ/z2)λδ(gz1λδ)−(˜rJ/z22+˜ηJ/z2)θδ−ϕj˜ηJ(σj−x∗β,j)=gγ(gz1)−λδϕj˜ηJ(σj−x∗β,j),
K2,J=YrJ1=(gz22y1)(˜rJ/z22+˜ηJ/z2)λδ=(g)y1˜rJλδ(gz2)y1˜ηJλδ,
K3,J=YηJ1=(gz22y1)−(˜rJ/z22+˜ηJ/z2)θδ−ϕj˜ηJ(σj−x∗β,j)=(g)−y1˜rJθδ(gz2)−y1˜ηJθδ(gz22)−y1ϕj˜ηJ(σj−x∗β,j),
K4,J=Y−(rJvδ+ηJtδ)1=(gz22y1)−((˜rJ/z22+˜ηJ/z2)λδvδ+[−(˜rJ/z22+˜ηJ/z2)θδ−ϕj˜ηJ(σj−x∗β,j)]tδ)
=(g)−y1˜rJ(λδvδ−tδθδ)(gz2)−y1˜ηJ(λδvδ−tδθδ)(gz22)y1tδϕj˜ηJ(σj−x∗β,j),
K5,J=Vy1ZJδ=(g)y1vδZJ,
K6,J=YZJ1=(gz22)y1˜ZJ,
K7,J=(hiuσii)ZJ=(gz1)θδ˜ZJ(gz2)(σδ−x∗β,δ)ϕδ˜ZJ.
We verify that it is a well-formed trapdoor via random exponents i∈S (including δ). Based on the exponents above, the subsequent formulas hold for every i∈S as in the actual construction.
• Challenge. 𝒜 sends ℬ with M0 and M1. ℬ chooses random R6∈GT, R3,1,…, R3,δ−1, R4,1,…, R4,δ−1 ∈G. If s1=z3, s2=z4, ℬ gives the challenge ciphertext CT∗ as
C∗1=Ys11=(gz22)y1z3=(gz22z3)y1,
C∗2=gs2=gz4,
C∗3,1=R3,1,⋯,
C∗3,δ=(hδux∗β,δδ)s1Vs2δ=((gz1)θδ(gz2)(x∗β,i−x∗β,δ)ϕδ)z3((gz1)θδ(gvδ))z4=(gz1(z3+z4))θδ(gz4)vδ=(Z)θδ(gz4)vδ,
C∗3,δ−1=R3,δ−1,
C∗3,δ+1=(hδ+1ux∗β,δ+1δ+1)s1Vs2δ+1=((gz22)θδ+1z3(gz2)(x∗β,δ+1−x∗β,δ+1)ϕδ+1z3)(gvδ+1z4)=(gz22z3)θδ+1(gz4)vδ+1,⋯,
C∗3,ℓ=(hℓux∗β,ℓℓ)s1Vs2ℓ=(gz22z3)θℓ(gz4)vℓ,
C∗4,δ−1=R4,δ−1,
C∗4,1=R4,1,⋯,
C∗4,δ=ws1δTs2δ=(gz1)λδz3(gz1λδgtδ)z4=(gz1(z3+z4))λδ(gz4)tδ=(Z)λδ(gz4)tδ,
C∗4,δ+1=ws1δ+1Ts2δ+1=(gz22)λδ+1z3(gtδ+1)z4=(gz22z3)λδ+1(gz4)tδ+1,⋯,
C∗4,ℓ=ws1ℓTs2ℓ=(gz22z3)λℓ(gz4)tℓ,
C∗5=e(g1,Y1)s1Mβ=R6,
where s1=c and Z=e(g,g)abc.
If M0=M1, ℬ substitutes R6 with e(g,gz22z3)γy1M0; otherwise, it follows the preceding procedure. If Z=gz1(z3+z4), we can deduce that Zθδ(gz4)vδ=(gz1(z3+z4))θδ(gz4)vδ =((gz1)θδ(gz2)−ϕδx∗β,δ(gz2)ϕδx∗β,δ)z3 ((gz1)θδgvδ)z4=(hδux∗β,δδ)s1Vs2δ. In this case, ℬ plays Game2,j. Otherwise, Z is chosen at random and ℬ performs Game2, j + 1.
• Query Phase 2. 𝒜 keeps asking queries that were not asked in Query Phase 1. ℬ responds in the same manner as before.
• Guess. 𝒜 returns a guess β′∈{0,1} to the challenge ciphertext. If β′=β, ℬ offers 1, else 0.
If 𝒜 guesses properly, ℬ also guesses correctly, implying that Z=gz1(z3+z4) holds in the ADLIN problem. In addition, ℬ considers that Z≠gz1(z3+z4). Consequently, any advantage obtained by 𝒜 in distinguishing between Game2, j and Game2, j + 1 is transferred to ℬ’s advantage when dealing with the ADLIN problem.
To analyze the vector dominance threshold problem in a public key system, we compare the proposed scheme with the schemes in [5–8] and [14–17] and show the results in Table 1. In [5–8], the authors create searchable public-key systems that support comparison. Unfortunately, these schemes cannot conduct threshold comparisons, which means some of their search results are not flexible. Although the schemes in [14–17] can perform it, the schemes in [15–17] are not attribute-hiding. Besides, the scheme in [14] is not efficient. Our scheme requires a ciphertext size of O(wn) and merely a trapdoor size of O(w) when any threshold comparison queries are constructed. Overall, our scheme performs better than the other SE methods in terms of computational efficiency and resource utilization.

Since the scheme in [14] deals with the same problem and system as our scheme, we make a further comparison between the two in Table 2. The computation tasks involve pairing and exponentiation operations where pairing operations cost the most time.

For [14], its PK size expands exponentially with w, while the PK size of our scheme only increases linearly. The ciphertext size (CT size) of [14] requires (nw+3)G+GT actions, and ours is (2nw)G+GT. Furthermore, to compute a trapdoor, reference [14] requires (nw+2)G group operations, whereas our scheme requires just 7wG group operations. Finally, reference [14] requires (nw+4)p1 operations and our scheme needs (w)p1+(w)e. Because p1 requires more processing resources than e in general, our technique outperforms the scheme in [14]. Overall, it is clear that our system outperforms the scheme of [14] in terms of computation efficiency.
To compute the storage overhead, we set |G|=1024 and |ZP|=160 in the simulation. We assume that the number of our query keywords ranges from 0 to 50, then count the storage overhead of the parameters in the algorithm. Fig. 2 compares the results between our scheme and [14]. According to Fig. 2a, our PK size is smaller than that of [14]. In Fig. 2b, the CT size of our scheme grows linearly with the number of query keywords while the CT size of the scheme in [14] increases exponentially and is larger than ours. From Fig. 2c, the storage overheads of our method and the scheme in [14] also grow linearly and exponentially, respectively. The simulation results show that the overheads of the proposed scheme are much smaller than those of [14], indicating higher efficiency of our scheme.
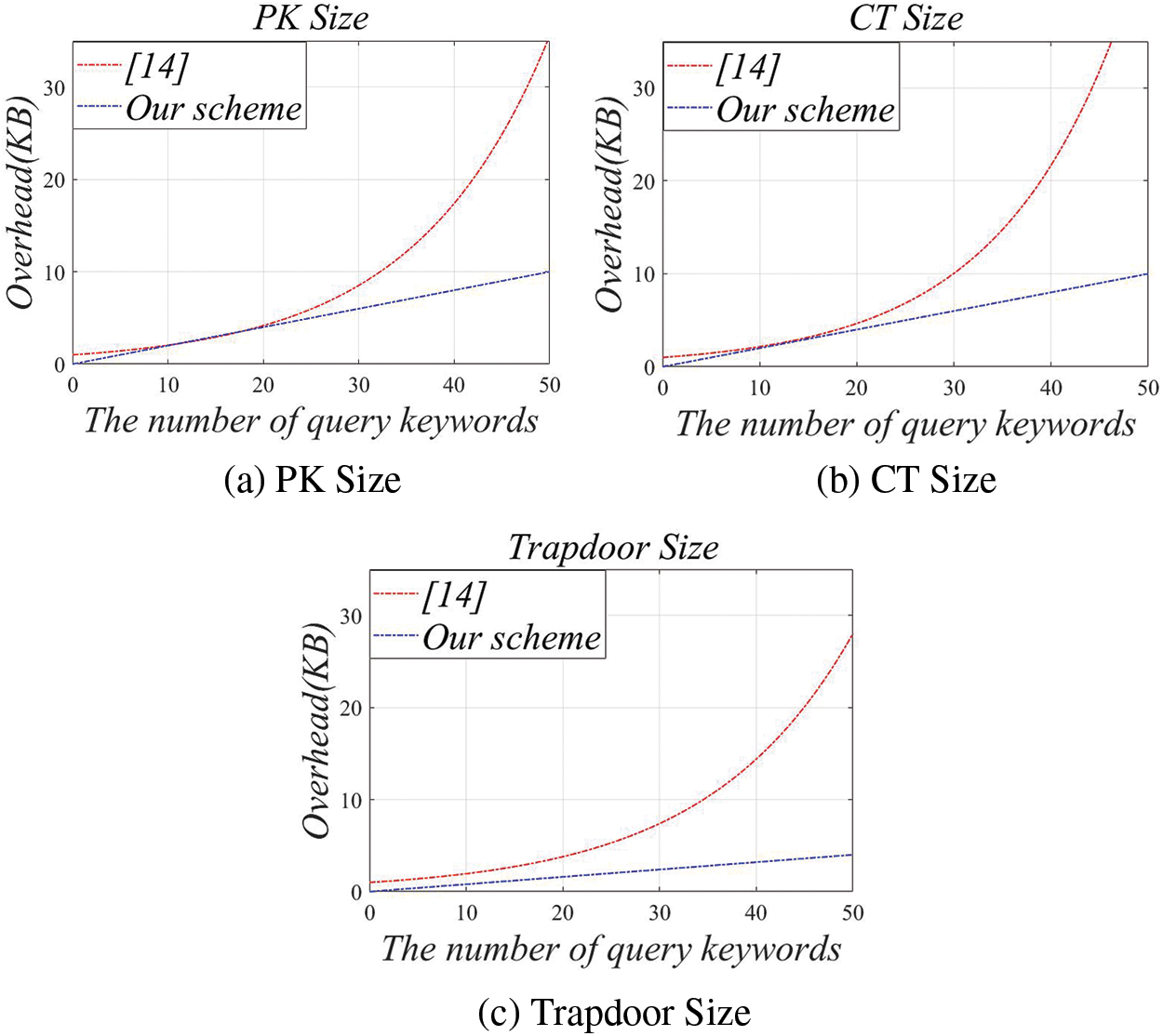
Figure 2: Storage overhead of each parameter as a function of the number of query keywords
We implement the algorithm with C language employing the GNU Multiple Precision Arithmetic (GMP) and Pairing-Based Cryptographic (PBC) libraries. Furthermore, this experiment makes use of the Pima Indians Diabetes Dataset at https://www.kaggle.com/uciml/pima-indians-diabetes-database.
The execution time of the scheme of [14] and our scheme for the KeyGen, PEKS, Trapdoor, and Test algorithms is displayed in Figs. 3a–3d, respectively. The universal set is set to 100. According to [14], as the number of query keywords grows from 0 to 100, the cost time required for KeyGen creation rises from 0.024 to 50 s and the cost time for PEKS generation increases from 0.37 to 300 s. Considering that the generation time of the Trapdoor and Test algorithms is excessive, we change the number of query keywords to 0–50. In [14], the cost time required for trapdoor generation climbs from 0.24 to 500 ms, while the test generation time rises from 0.37 to 600 ms. Our algorithm, however, takes almost no time. The execution time for KeyGen represents the time for PK and SK to be generated, and the PEKS time indicates the ciphertext generation time. The Trapdoor and Test algorithms involve the time of trapdoor generation and the time of cloud server search, respectively.
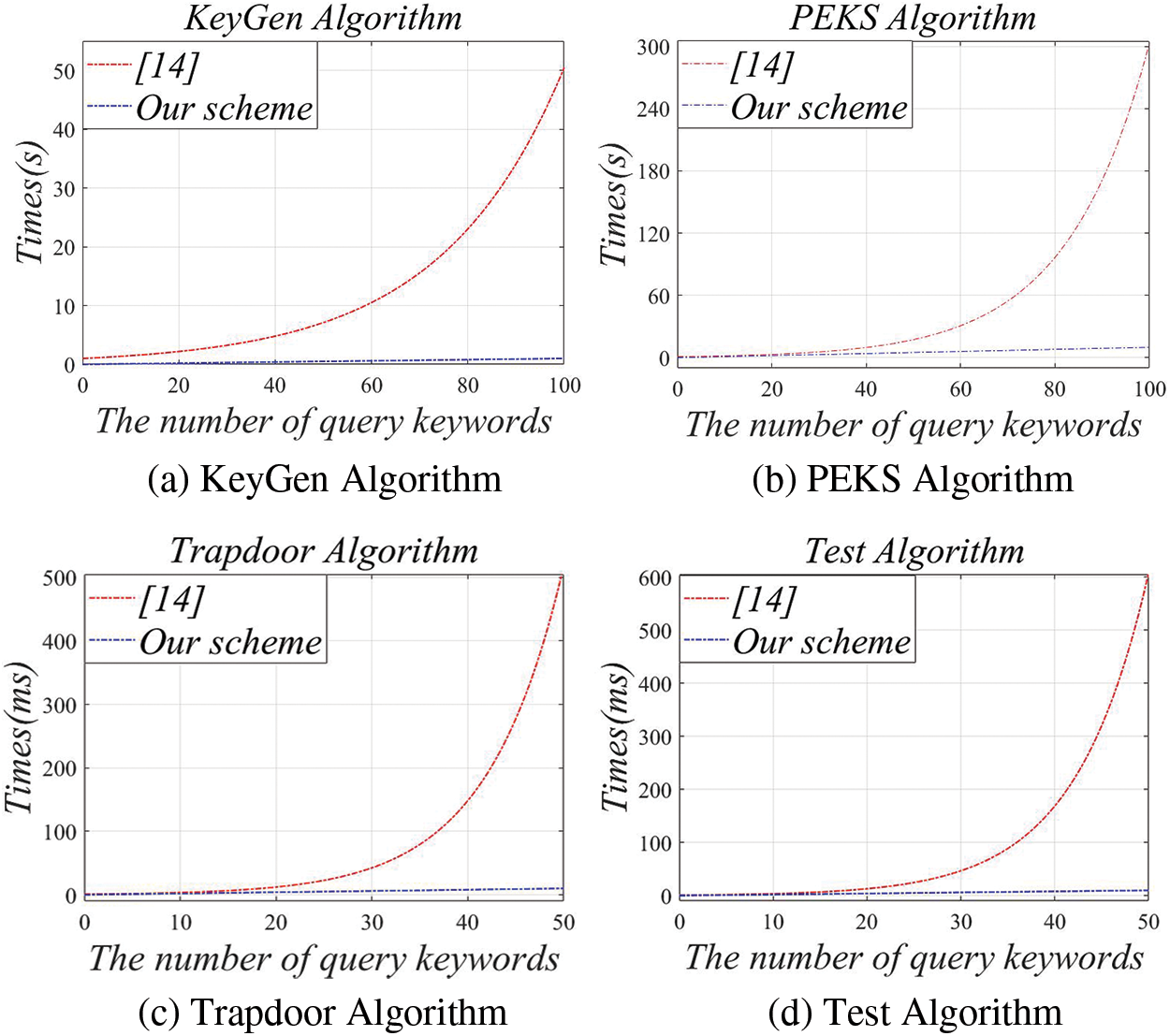
Figure 3: Time cost of each algorithm as a function of the number of query keywords
It can be seen from Fig. 3 that the runtime of our algorithm increases slowly with the increase of query keywords, while the runtime of [14] increases exponentially. The experiment shows that our scheme is more efficient. In addition, our scheme uses real data sets and is carried out on a cloud outsourcing platform, therefore it will be feasible and effective in real-world scenarios.
In addition to the number of query keywords, the varying size of encrypted diabetes data also has a great effect on algorithm performance. As the encrypted data increases, the service provider will continuously run the VDTSE scheme to search until it finds all matched ciphertexts. Therefore, the performance of VDTSE degrades linearly with the increase of encrypted data. Note that although the threshold t has a range, it takes a fixed value every time the algorithm runs so it has no impact on the performance of the scheme.
In theoretical comparison to existing schemes, the proposed VDTSE scheme obtains a shorter trapdoor that makes it more suitable for storage on mobile devices. It supports comparable attributes that can work for the (t, n)-threshold policy. Then, its security, flexibility, and effectiveness are proved through comparison with other SE schemes.
However, there are also some limitations in this research. Although our scheme is more efficient than other existing SE schemes, it does not work well on large real-world datasets. The larger data is transformed into a longer vector, lowering the efficiency. Besides, when dealing with floating data, the scheme converts the floating data to integer data through multiple expansions. For example, 0.1 is expanded 10 times and converted to 1. In addition, the Lagrangian polynomial technique is not efficient in dealing with the vector dominance threshold problem, but it is currently the most suitable technique. We will look for a better technique to solve these issues.
More fascinating, this work inspires some excellent open problems. Firstly, our research does not address video encryption [18,19], which is an engaging research direction. In the future, we will apply SE algorithms to more scenarios, such as images [20] and other situations [21–23]. Secondly, it will be an intriguing path to demonstrate how to reduce the ciphertext size, which appears difficult to achieve at the moment.
Acknowledgement: Not applicable.
Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant Nos. 61872289 and 62172266, and in part by the Henan Key Laboratory of Network Cryptography Technology LNCT2020-A07 and the Guangxi Key Laboratory of Trusted Software under Grant No. KX202308.
Author Contributions: The authors confirm that the contributions to the paper are as follows: Study conception and design: Jingjing Nie, Zhenhua Chen; draft manuscript preparation: Jingjing Nie. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are openly available at https://www.kaggle.com/uciml/pima-indians-diabetes-database.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Z. Zhou et al., “Blockchain-based secure and efficient secret image sharing with outsourcing computation in wireless networks,” IEEE Trans. Wirel. Commun., vol. 23, no. 1, pp. 423–435, Jan. 2024. doi: 10.1109/TWC.2023.3278108. [Google Scholar] [CrossRef]
2. Z. Shen, F. Ding, Y. Yao, A. Bhardwaj, Z. Guo and K. Yu, “A privacy-preserving social computing framework for health management using federated learning,” IEEE Trans. Comput. Soc. Syst., vol. 10, no. 4, pp. 1666–1678, Aug. 2023. doi: 10.1109/TCSS.2022.3222682. [Google Scholar] [CrossRef]
3. Z. Shen, F. Ding, A. Jolfaei, K. Yadav, S. Vashisht and K. Yu, “DeformableGAN: Generating medical images with improved integrity for healthcare cyber physical systems,” IEEE Trans. Netw. Sci. Eng., vol. 10, no. 5, pp. 2584–2596, Jul. 2022. doi: 10.1109/TNSE.2022.3190765. [Google Scholar] [CrossRef]
4. M. J. Atallah and W. Du, “Secure multi-party computational geometry,” in Proc. 7th Int. Workshop Algorithms Data Struct. (WADS), Providence, RI, USA, Aug. 2001, pp. 165–179. [Google Scholar]
5. D. Boneh and B. Waters, “Conjunctive, subset, and range queries on encrypted data,” in Proc. 4th Theory Cryptogr. Conf. (TCC), Amsterdam, The Netherlands, Feb. 2007, pp. 535–554. [Google Scholar]
6. E. Shi, J. Bethencourt, T. H. Chan, D. Song, and A. Perrig, “Multi-dimensional range query over encrypted data,” in Proc. IEEE Symp. Secur. Priv. (SSP), Berkeley, CA, USA, May 2007, pp. 350–364. [Google Scholar]
7. H. Park, “Efficient hidden vector encryption for conjunctive queries on encrypted data,” IEEE Trans. Knowl. Data Eng., vol. 23, no. 10, pp. 1483–1497, Oct. 2011. doi: 10.1109/TKDE.2010.206. [Google Scholar] [CrossRef]
8. J. H. Park, K. Lee, W. Susilo, and D. H. Lee, “Fully secure hidden vector encryption under standard assumptions,” Inf. Sci., vol. 232, pp. 188–207, May 2013. doi: 10.1016/j.ins.2012.12.034. [Google Scholar] [CrossRef]
9. D. X. Song, D. Wagner, and A. Perrig, “Practical techniques for searches on encrypted data,” in Proc. IEEE Symp. Secur. Priv. (SSP), Berkeley, CA, USA, May 2000, pp. 44–55. [Google Scholar]
10. Y. Zheng, R. Lu, J. Shao, F. Yin, and H. Zhu, “Achieving practical symmetric searchable encryption with search pattern privacy over cloud,” IEEE Trans. Serv. Comput., vol. 15, no. 3, pp. 1358–1370, May 2020. doi: 10.1109/TSC.2020.2992303. [Google Scholar] [CrossRef]
11. Z. Gui, K. G. Paterson, and S. Patranabis, “Rethinking searchable symmetric encryption,” in Proc. IEEE Symp. Secur. Priv. (SSP), San Francisco, CA, USA, May 2023, pp. 1401–1418. [Google Scholar]
12. E. Molla, P. Rizomiliotis, and S. Gritzalis, “Efficient searchable symmetric encryption supporting range queries,” Int. J. Inf. Secur., vol. 22, no. 4, pp. 785–798, Feb. 2023. doi: 10.1007/s10207-023-00667-1. [Google Scholar] [CrossRef]
13. D. Boneh, D. G. Crescenzo, R. Ostrovsky, and G. Persiano, “Public key encryption with keyword search,” in Proc. Int. Conf. Theory Appl. Cryptogr. Tech., Interlaken, Switzerland, May 2004, pp. 506–522. [Google Scholar]
14. D. Sun, C. Boyd, and J. M. G. Nieto, “Predicate encryption for multi-inner-products,” Secur. Commun. Netw., vol. 6, no. 3, pp. 325–339, Mar. 2013. doi: 10.1002/sec.566. [Google Scholar] [CrossRef]
15. J. Bethencourt, A. Sahai, and B. Waters, “Ciphertext–policy attribute-based encryption,” in Proc. IEEE Symp. Secur. Priv. (SSP), Berkeley, CA, USA, May 2007, pp. 321–334. [Google Scholar]
16. N. Attrapadung, G. Hanaoka, K. Ogawa, G. Ohtake, H. Watanabe and S. Yamada, “Attribute based encryption for range attributes,” IEICE Trans. Fundam. Electron., Commun. Comput., vol. 101, no. 9, pp. 1440–1455, Sep. 2018. doi: 10.1587/transfun.E101.A.1440 [Google Scholar] [CrossRef]
17. K. Xue, J. Hong, Y. Xue, D. S. Wei, N. Yu and P. Hong, “CABE: A new comparable attribute-based encryption construction with 0-encoding and 1-encoding,” IEEE Trans. Comput., vol. 66, no. 9, pp. 1491–1503, Sep. 2017. doi: 10.1109/TC.2017.2693265. [Google Scholar] [CrossRef]
18. H. Li, Z. Gu, L. Deng, Y. Han, C. Yang and Z. Tian, “A fine-grained video encryption service based on the cloud-fog-local architecture for public and private videos,” Sensors, vol. 19, no. 24, pp. 5366, Dec. 2019. doi: 10.3390/s19245366. [Google Scholar] [PubMed] [CrossRef]
19. K. M. Hosny, M. A. Zaki, N. A. Lashin, and H. M. Hamza, “Fast colored video encryption using block scrambling and multi-key generation,” Vis. Comput., vol. 39, no. 12, pp. 6041–6072, Dec. 2023. doi: 10.1007/s00371-022-02711-y. [Google Scholar] [CrossRef]
20. M. Liu, J. Fan, and Q. Liu, “Biomedical image segmentation algorithm based on dense atrous convolution,” Math. Biosci. Eng., vol. 21, no. 3, pp. 4351–4369, Feb. 2024. doi: 10.3934/mbe.2024192. [Google Scholar] [PubMed] [CrossRef]
21. H. A. Li, L. Wang, and J. Liu, “Application of multi-level adaptive neural network based on optimization algorithm in image style transfer,” Multimed. Tools Appl., vol. 23, pp. 1–23, Feb. 2024. doi: 10.1007/s11042-024-18451-1. [Google Scholar] [CrossRef]
22. Y. Ju et al., “Reliability-security tradeoff analysis in mmWave ad hoc-based CPS,” ACM Trans. Sens. Netw., vol. 20, no. 2, pp. 1–23, Jan. 2024. doi: 10.1145/3582556. [Google Scholar] [CrossRef]
23. Z. Zhou et al., “Generative steganography via auto-generation of semantic object contours,” IEEE Trans. Inf. Forensics Secur., vol. 18, pp. 2751–2765, Apr. 2023. doi: 10.1109/TIFS.2023.3268843. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools
