GCAGA: A Gini Coefficient-Based Optimization Strategy for Computation Offloading in Multi-User-Multi-Edge MEC System

1  Introduction

With the proliferation of various smart devices (e.g., smart homes, wearables, smartphones), the mobile data traffic generated by these emerging services has exploded [1] while also posing more demanding challenges to both data transmission networks and core networks [2]. Moreover, new services or applications (e.g., real-time entertainment, artificial reality (AR), virtual reality (VR), and other technologies) are typically latency-sensitive and compute-intensive. But paradoxically, end devices are generally pursuing miniaturization and lightweight again, resulting in limited resources (e.g., battery capacity, size) to meet users’ expectations. Taking intelligent driving as an example, sensors and cameras mounted on autonomous vehicles capture real-time road condition information, generating approximately 1 GB of data per second. However, the main frequency of onboard processors often ranges from 500 to 900 MHz (e.g., Qualcomm 8155 700 MHz), which is far from meeting the requirements for real-time road analysis. Therefore, to cope with the increasing traffic demand and more stringent quality of service, it is crucial to further break through the physical limitations of end devices and expand the computing capacity of end devices.

Mobile-edge Computing (MEC) is one of the most promising solutions [3]. As one of the key technologies in the information age, MEC allows users to offload latency-sensitive and computation-intensive tasks to edge cloud servers for execution through wireless networks by deploying small edge cloud servers around the user. Thus, the MEC system has made a breakthrough in the hardware limitation of mobile terminals [4]. Compared with the traditional central cloud model, edge clouds can reduce response time, relieve network congestion on backhaul links, and significantly reduce network upgrade costs. Edge cloud servers inevitably have problems, i.e., small coverage and limited resources. They are solved or studied in different ways.

For the limited coverage of edge servers, unmanned aerial vehicles (UAVs) have been employed to improve the connectivity of ground Internet of Things (IoT) devices due to their high altitude [5]. The UAV moves above the users and provides computing service in an orthogonal multiple-access manner over time [6]. Because of the mobility of user equipment (UEs), the essential part of UAVs in the MEC system is to design an algorithm for calculating the trajectory. Wang et al. [7] proposed a multi-agent deep reinforcement learning algorithm for managing the course of each UAV independently. Hu et al. [8] proposed an alternating optimization algorithm to jointly optimize the computation resource scheduling, bandwidth allocation, and the UAV’s trajectory in an iterative fashion. Zhang et al. [9] applied a Lyapunov-based approach to analyze the task queue, and the energy consumption minimization problem is decomposed into three manageable subproblems.

For the limited computing and communication resources, many scholars have started to study and design suitable offloading decisions and resource allocation schemes. This optimization problem is usually abstracted as a Mixed Integer Nonlinear Program (MINLP), a nonconvex NP-hard problem. Since solving the optimal solution of this type of problem directly is difficult and impractical when the number of offloading tasks is too large, a large amount of literature has been devoted to this study. The typical approach is to decouple the problem into two subproblems, i.e., resource allocation and offloading decision, and then solve them using different algorithms. The most used algorithms are heuristics. However, these algorithms are often faced with a lack of convergence speed and stability. Zhao et al. [10] first applied the Gini coefficient to estimate the server energy load pressure, which demonstrated the ability to utilize prior conditions. Inspired by the unique function, we believe that the offloading limit of each MEC server can be estimated in the same way. Thus, the dilemma of heuristic algorithms can be alleviated.

This paper will study the problem of resource allocation and offloading decisions. We jointly considered the time delay and energy consumption to improve the users’ experience. Then an EoU reward function maximization problem is proposed for optimization. To solve the challenges of heuristic algorithms, we propose the Gini coefficient-based adaptive genetic algorithm (GCAGA). The Gini coefficient can fully utilize the priori conditions to estimate the offloading limit of each MEC server, and the adaptively changing genetic operators can accelerate the convergence speed of the algorithm. The main contributions are summarized as follows:

•   We characterize the EoU by energy consumption and computation time in local computing and collaborative cloud computing, respectively. Then, an EoU minimization problem is formulated by jointly optimizing the offloading decision, communication, computation resources, and mobile-edge matching strategies under hard constraints. Since the formulated problem is a MINLP and optimization variables are coupled, we decompose the original one and propose the heuristic offloading algorithm, namely GCAGA, to solve it.

•   The proposed GCAGA runs in three stages. First, the transmission power and computation resource for each possible matching strategy under the current offloading decisions is optimized. Then, the capacity bound of each server is calculated with the Gini coefficient. Finally, AGA is used to find the offloading decisions by iterative updating resource allocation and matching strategies to minimize system EoU.

2  Related Work

Recently, scholars have carried out much research on optimizing the factors involved in the task offloading and resource allocation problem. In this section, some typical works will be reviewed and compared with the proposed scheme.

Rahimi et al. [11] focused on optimizing offloading decisions without considering the resource allocations, and thus, the full benefit of offloading cannot be reached. Yu et al. [12] minimized the total cost by optimizing offloading decisions and resource allocation in the MEC system with the assistance of the central cloud. However, they only considered the single-user-single-edge cloud scenario, which simplifies the problem analysis and system model. The joint optimization of the offloading decisions and the resource allocation for a general multi-user-multi-edge computation offloading system had yet to be investigated. A low-complexity iterative suboptimal algorithm called FAJORA was proposed by Du et al. [13], which jointly optimizes the offloading decision and resource allocation in a multi-user-multi-edge system. Still, the algorithm does not achieve an optimal convergence result when the number of tasks increases. Cong et al. [14] employed the Gray Wolf algorithm to approximate the optimal point. Their results indicate that the algorithm performs well when tasks increase.

The latter literature is written based on a multi-user-multi-edge system, but some fail to consider the time delay and energy consumption jointly. A socially aware dynamic computation offloading scheme was proposed by Liu et al. [15] to use a game theoretic approach to minimize the social group execution cost with energy harvesting devices, but the time delay was not considered. Huang et al. [16] proposed a novel protocol for the MEC system and saved at most 80% of energy consumption compared to other schemes. By using lexicographic max-min fairness, delay-aware task offloading was studied by Jiang et al. [17], but the energy consumption was not analyzed. Zhang et al. [18] considered energy consumption and time delay. They proposed a two-step fair task offloading (FTO) scheme aiming at decreasing energy consumption but just with a fixed time delay upper limit. Several delay-minimizing collaboration and offloading policies were proposed in [19–23] without optimizing energy consumption.

Other studies have taken both the time delay and energy consumption into consideration. They addressed the problem in different ways. However, only a few could consider the users’ experience, while others added the time delay and the energy consumption directly with two weight factors. However, the time delay and energy consumption may not necessarily have the same unit or even magnitude. Xu et al. [24] used a combination of Deep Reinforcement Learning (DLR) and Genetic Algorithm (GA) algorithm to obtain an approximate optimal solution that minimizes the system cost. Some research work [25–27] relaxed this MINLP problem into a convex problem and then constructed a suboptimal task assignment solution based on the obtained optimal solution, effectively reducing the user’s computational latency. Ning et al. [28] considered the channel allocation problem. The task offloading and resource allocation problem in the telematics system is studied. The problem is decomposed into three subproblems, task allocation, sub-channel allocation, and power allocation, to maximize the total offloading rate, and each subproblem is solved by iteration. In the research of Xu et al. [29], a non-dominated ranking GA (NSGA-III) was proposed to solve the multi-objective optimization problem. Wu et al. [30] designed a memory algorithm based on GA and a local search method. Besides, in [31–35], the deep learning approach was employed to obtain the optimal offloading policy. Still, some problems can be found in these approaches, such as poor adaptability to new environments. Attention mechanism is employed in [36–38] to improve the convergence stability but the convergence speed is slowed down. Zhang et al. [39] designed a novel hybrid many-objective optimization algorithm by cascading clustering and incremental learning to solve the offloading decision. Based on the optimal offload decision solution, they solve the resource allocation problem with a low-complexity heuristic method. Liu et al. [40] partitioned the offloaded application into a directed acyclic graph with multiple collaborative sub-tasks and then proposed a cooperative resource allocation approach to optimize the problem.

The review of previous research shows that heuristic algorithms have received much attention in the performance optimization of MEC systems. It can find the approximate optimal solution to the problem in a reasonable time. However, such algorithms also have some inherent defects: One is easy to fall into the dilemma of locally optimal solutions, and the other is due to the randomness of initial solution generation, which can lead to a long iteration time of the system. These two drawbacks may cause the slow convergence speed and poor stability of convergence results. The GA algorithm has a fast convergence speed and stability, but it often eliminates the current lowest fitness individual (even if the individual has a good genetic pattern), leading to getting stuck in a locally optimal solution. The simulated annealing algorithm (SAA) can dynamically adjust its search space with the iteration process, and escape the local optimal solution by increasing system entropy, which has strong optimization performance. However, due to the difficulty in grasping the downward trend of system entropy, it is difficult to ensure the convergence stability of SAA.

After reviewing the recent work, Table 1 is made to show the categorized list of the research content, in which ‘—’ means that the corresponding factor was not mentioned in these articles.

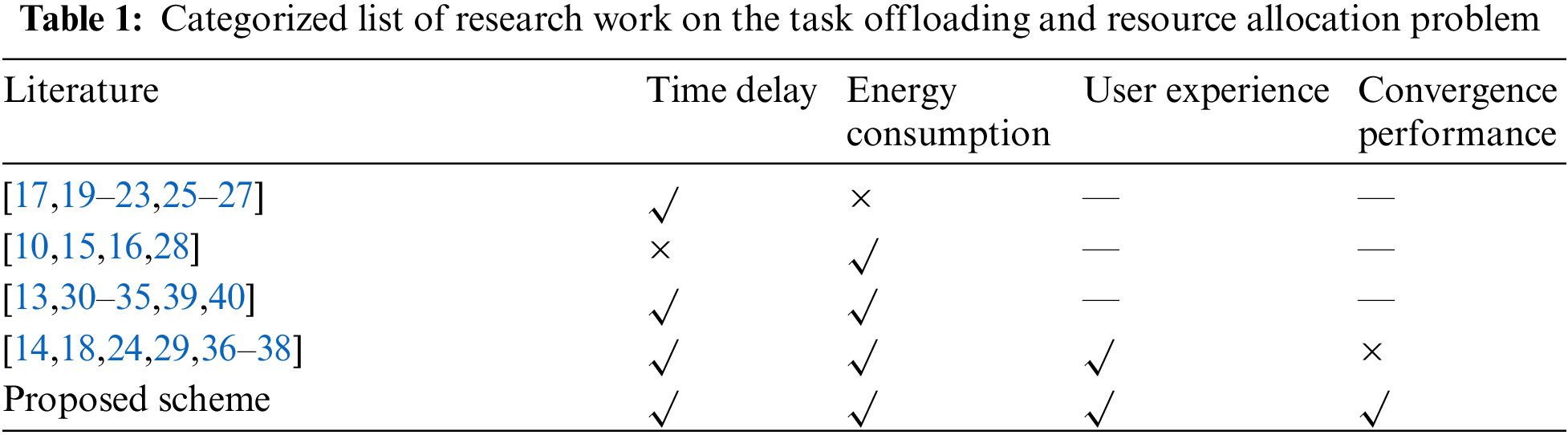
Unlike the above research work, we propose a user-benefit function EoU, which includes both the time delay and energy consumption. Then, the prior conditions are fully utilized by the Gini coefficient to estimate the offloading limit of each MEC server. Finally, the AGA is employed to optimize the offloading decision. Experiment results indicate that the proposed GCAGA performs well on users’ experience and convergence. The specific model-building process will be described in the following text.

3  System Model

Consider a multi-user, multi-server MEC system, as shown in Fig. 1, where each base station (BS) is equipped with an MEC server to provide high-bandwidth, low-latency cloud-based services to surrounding user devices in proximity. Each mobile user can also choose to offload computationally intensive program tasks to the MEC server from the nearby BSs. A program task is typically offloaded at only one MEC server of choice. The users and MEC servers in the MEC system are denoted as U={1,2,⋯,u,⋯,U} and 𝒮={1,2,⋯,s,⋯,S}. It is assumed that the computational tasks generated by each user can be represented by a tuple consisting of two parameters, i.e., Tu=⟨du,cu⟩, where du [bits] refers to the amount of input data that needs to be transferred from the local device to the MEC server, and cu [cycles] refers to the workload, i.e., the total amount of computation required to complete the task program. Each program task can be executed locally or on one of the MEC servers. In this section, the models of local computing, task transfer, and edge computing for mobile users are presented separately. The meanings of the symbols in this paper are listed in Table 2.

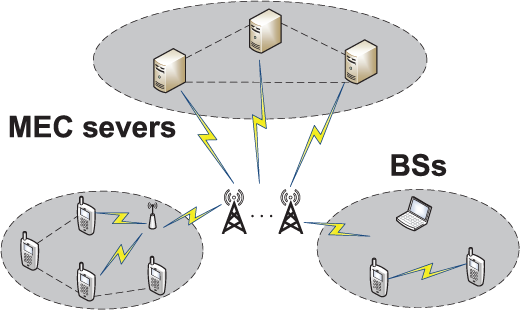
Figure 1: The structure of the MEC system

3.1 Local Computing Model

Assuming that each user u∈𝒰 can only generate one task Tu at a time, it will be selected as a whole whether to offload to the MEC server for execution. For this purpose, the offloading decision variable xus,u∈𝒰,s∈𝒮 is introduced, in which xus=1 denotes that task Tu will be offloaded to the MEC server for execution. Otherwise, Tu will be executed locally. Then we have

C1:xus∈{0,1},∀u∈𝒰,s∈𝒮.(1)

The local computing power of user u is expressed in ful [CPU cycles/s], i.e., the local CPU frequency size on the end device. Therefore, when xus=0, the completion time of Tu can be defined as

tul=cuful.(2)

Meanwhile, the energy consumption of Tu can be expressed as

Eul=kfulcu(3)

in which k is the energy factor depending on the chip architecture.

3.2 Task Transmission Model

Orthogonal Frequency Division Multiple Access (OFDMA) is used as a multiple access scheme in the uplink [41], where each channel in a cell is orthogonal to the other channels. The operational band A is divided into N equal subbands of size W=B/N[Hz]. This also implies that the MEC server can serve at most N users simultaneously, which gives the following constraints:

C2:∑s∈𝒮xus≤1∀u∈𝒰(4)

C3:∑u∈𝒰xus≤N,∀s∈𝒮.(5)

Define Us={u∈𝒰|xus=1} as the set of users who offload the task program to the MEC server s. The total set of users who perform task offloading is Uoff=∪s∈𝒮Us. Denote the transmit power of user u by 𝒫={0<pu≤Pu,u∈Uoff} [W], where Pu is the maximum transmission power of user u. Then we have

C4:0<pu≤Pu,∀u∈Uoff.(6)

Obviously, if the task of user u is executed locally, i.e., u∉Uoff, then pu=0. At this point, the signal-to-noise from user u to MEC server s can be expressed as

⋎us=puhusBρs/N+σ2,u∈𝒰,s∈𝒮(7)

where σ2 is the background noise variance, ρs is the co-band interference density of server s, and hus denotes the uplink channel gain between user u and MEC server s.

Thus, by Shannon’s theorem, the rate at which the user can send data to the MEC server is limited to

Rus(𝒫)=Wlog2(1+Υus),u∈𝒰,s∈𝒮.(8)

Therefore, the transmission time when the user sends its task input data in the uplink is

tuup=∑s∈𝒮xusduRus(𝒫),u∈𝒰.(9)

At this point, the energy the corresponding user consumes to send data is denoted by Eu.

Eu=putuup=pudu∑s∈SxusRus(𝒫),u∈𝒰(10)

where Eu is a variable that only related to u. If user u decides to offload its task to an MEC server, then Eu≠0, otherwise, if user u decides to perform local computation, then Eu=0.

3.3 Edge Computing Model

Define ℱ={fus|u∈𝒰,s∈𝒮} as the computational resource allocation decision where fus indicates the computing resources that server s allocates to user u. Obviously, the computational resources allocated to the offloaded task should not exceed the total computational resources of the MEC server, so there is a constraint

C5:fus≥0,∀u∈U,s∈𝒮C6:∑u∈Ufus≤fs,∀s∈𝒮(11)

where fs denotes the total computing resources of server s.

When the computational resource allocation decision is known, the execution time of task Tu at the MEC server can be denoted by

tuexe=∑s∈Sxuscufus,∀u∈𝒰.(12)

where tuexe is the task computation time on the MEC server only related to the offloading decision performed by user u. If user u decides to offload its task to an MEC server, then tuexe≠0, otherwise, if user u decides to perform local computation, then tuexe=0.

4  Problem Formulation

In this section, the problem is described formally based on the above system model. Then the problem is decoupled into two continuous-type extreme value problems and a discrete integer programming problem. Finally, we will give the complete offloading strategy.

4.1 Formulaic Description

The user experience is used as the benefit evaluation criterion for resource allocation and offloading decisions. Since the time delay and energy consumption may not necessarily have the same unit or even magnitude, it is more reasonable that the experience of users is mainly characterized by the relative improvement in task completion time and energy consumption in a mobile cloud computing system [42]. Therefore, we defined the relative improvement in energy consumption and latency by comparing the offloaded computing model with the local computing model. The relative improvement of energy consumption and time delay is defined as Eul−EuEul and tul−tutul, respectively. The lower the latency and energy consumption of offloading computation compared to local computation, the better the user experience of offloading computation. From this, we give the gain function of users, i.e., EoU (Experience of User).

EoUu=∑s∈Sxus(αuttul−tutul+αueEul−EuEul),u∈𝒰(13)

where tu=tuup+tuexe and αut,αue∈[0,1],αut+αue=1. Obviously, we have EoUu>0. If EoUu<0 then it means that the task is offloaded to the MEC server with a negative gain, and it is better to execute the task locally. At this point, we should set EoUu=0, i.e., task A will not be offloaded.

The target is to maximize EoU through the joint optimization of resource allocation and offloading decisions, so the problem can be described by J, i.e.,

J: 𝒳,𝒫,ℱmaxEoU(𝒳,𝒫,ℱ)=∑u∈𝒰EoUus.t.C1,C2,C3,C4,C5,C6.(14)

In problem J, there are three variables to be optimized, i.e., 𝒳,𝒫,ℱ, where 𝒳 is a discrete decision matrix, 𝒫 and ℱ represent continuous interval variables. Obviously, J is a MINLP, which cannot be directly solved. Therefore, it is necessary to decompose problem J.

4.2 Decomposition

In this section, we transform the high-complexity joint optimization problem into an equivalent master problem and a set of low-complexity subproblems.

First, the constraints on the resource allocation and offloading decisions are decoupled from each other, so with the offloading decision 𝒳 fixed, problem J can be transformed into maximizing the function EoU by optimizing the transmit power 𝒫, the resource allocation ℱ on the MEC server, and the new problem formulation can be expressed as J1, i.e.,

J1: 𝒫,ℱmax∑u∈Uoff(αuttul−tutul+αueEul−EuEul)s.t.C4,C5,C6.(15)

After replacing the corresponding parts of Eq. (13) with Eqs. (1), (2), and (10), J1 is transformed into

J1: 𝒫min∑s∈𝒮∑u∈Usdu(αuttul+αuepuEul)Wlog2⁡(1+puhusBρs/N+σ2)+ℱmin∑s∈𝒮∑u∈Usαuttulcufuss.t.C4,C5,C6.(16)

Observing Eq. (16), we can see that the first term on the left side is only related to the transmission power 𝒫 and the second term is only related to the computational resource allocation ℱ, so J1 can be decoupled into two independent problems, i.e., the transmission power allocation problem and the MEC server computational resource allocation problem.

As a result, the optimal resource allocation scheme 𝒫∗ and ℱ∗ will become a function associated with the offloading decision 𝒳, i.e., 𝒫∗=𝒫∗(𝒳) and ℱ∗=ℱ∗(𝒳), so problem J is equivalent to an offloading problem, which can be denoted by

 𝒳maxJ∗(𝒳)=EoU(𝒳,𝒫∗,ℱ∗).(17)

4.3 Resources Allocation

4.3.1 Transmission Power Allocation

The first term on the left-hand side in J1 is used as the objective function of the power allocation strategy in the MEC system, denoted by J2

J2: 𝒫minΓ(𝒳,𝒫)=∑s∈S∑u∈Usdu(αuttul+αuepuEul)Wlog2⁡(1+puhusBρs/N+σ2)s.t.C4.(18)

However, since the transmit power of different users in the MEC system is independent, the above equation can also be decomposed into an optimal transmit power problem for each user. The function of J2 can be rewritten as

f(pu)=θu+λupuWlog2⁡(1+μuspu),0<pu≤Pu,u∈Us(19)

where θu=αutdutul, λu=αueduEul, μus=husBρs/N+σ2, are given in the task program, and the channel environment of the uplink is known and fixed. The derivation of the function is given by

f′(pu)=λuWlog2⁡(1+μuspu)−μus(θu+λupu)ln⁡2W(1+μuspu)ln2⁡(1+μuspu).(20)

It is easy to see that when pu>0, the denominator of the above equation is positive. The numerator is then taken to be q(pu).

q(pu)=λu(1+μuspu)ln⁡(1+μuspu)−μus(θu+λupu)(21)

The derivative for q(pu) is given by

q′(pu)=λuμusln⁡(1+μuspu).(22)

For pu>0, we have q′(pu)>0, i.e., q(pu) is monotonically increasing. There is also q(0)=−μusθu<0, so the zero point of q(pu) is the minimal value point of f(pu). Let that extreme point be pumin and pumin>0. When pumin>Pu, there is no extreme point within 0<pu≤Pu. When pumin>Pu, there is only a single extreme value point in 0<pu≤Pu. In summary, it can be found that the function f(pu) has at most one extreme value point in its definition domain, so it can be solved by the dichotomy method.

4.3.2 Computational Resource Allocation

The second term of J1 is used to optimize the computational resource allocation problem, and the objective function of this problem can be expressed by J3.

J3:ℱminΛ(X,ℱ)=∑s∈S∑u∈Usηufus     s.t.C5,C6(23)

where ηu=cuαuttul. Since the constraints C5, C6 form a closed region, there is a minimum value in this region.

Ref. [43] gives the solution to J3, i.e.,

fus∗=fsηu∑u∈𝒰sηu,∀s∈𝒮,u∈UsΛ(𝒳,ℱ∗)=∑s∈S1fs(∑u∈Usηu)2.(24)

4.4 Offloading Strategy

For a fixed task offloading strategy, it is possible to determine the resource allocation strategy 𝒫∗ and ℱ∗. Now we can rewrite J1 to

J1: 𝒳min∑s∈𝒮∑u∈Us(Γ(𝒳,𝒫∗)+Λ(𝒳,ℱ∗))s.t.C4,C5,C6.(25)

Since there is only one optimization variable 𝒳 in J1, we propose the Gini coefficient-based adaptive genetic algorithm (GCAGA). The algorithm is divided into three steps.

Step 1 Pre-offloading

We define EoUusONE=EoU(𝒳usONE,𝒫∗,ℱ∗), where 𝒳usONE={xus=1} indicates the offloading decision consists only of offloading Tu to s. It is easy to see that only when EoUusONE>0, we can offload Tu to server s. After pre-offloading, the pre-offloading user set is achieved, i.e., Bs={u∈𝒰|EOUusONE>0}.

Step 2 Estimating the server capacity bound

Define the revenue function for server s, i.e., Ys=∑u∈BsEoUu,∀s∈𝒮. Then we have the cumulative income ratio, i.e., yis=1Ys∑j=1iEoUsj∀s∈𝒮,i=1,2,…,|Bs|,sj∈Bs,j=1,2,…,|Bs|,sj≠sk,j≠k. From this, the Gini coefficient Gs corresponding to server s can be calculated [44].

Gs=1−1|Bs|(1+2∑i=1|Bs|−1yis),∀s∈𝒮(26)

Thus, we obtain the capacity bound Is corresponding to server s.

Is=min{⌈1Gs⌉+⌈Ls|Bs|(|Bs|−⌈1Gs⌉)⌉,|Bs|}(27)

where Ls=min{⌊fsfsmid⌋,|Bs|,N},  fsmid is the median value of set {fus|u∈Bs}, ⌈1Gs⌉ indicates the number of users who contribute most of the revenue, and ⌈Ls|Bs|(|Bs|−⌈1Gs⌉)⌉ is the correction factor of ⌈1Gs⌉. Ls shows the capacity of server s. Define the average value of set {fus|u∈Bs} as fsavg, there is fsavg=fs|Bs|. If fsmid≤fsavg, we have ⌊fsfsmid⌋≥|Bs|, then there is Ls=|Bs|. If fsmid≥fsavg, we have ⌊fsfsmid⌋≤|Bs|. It means half of the pre-offloaded tasks have taken over more than half of the resources on MEC server s, and server s is not supposed to provide computing resources for all of them to achieve a better EoU result. Thus, ⌊fsfsmid⌋ can be the up limit of Ls. Ls|Bs| can represent the portion of tasks that might contribute to EoU in Bs. Therefore, there are ⌊Ls|Bs|(|Bs|−⌈1Gs⌉)⌋ tasks that should be considered aside from the ⌈1Gs⌉ tasks contributing most of the EoU.

The detailed procedure of the pre-offloading and capacity estimation is shown in Algorithm 1. The pre-offloading part requires all possible binary groups ⟨u,s⟩ to be traversed, so the time complexity is O(|𝒰|⋅|𝒮|). The time complexity of the capacity estimation part is lower than the pre-offloading part, because Bs<|𝒰|. Thus, the time complexity of Algorithm 1 is O(|𝒰|⋅|𝒮|).

In the practical application scenarios of MEC networks, the number of servers |𝒮| is usually a constant value. From the above analysis, it can be seen that the time complexity of Algorithm 1 is only related to the number of users |𝒰| and increases linearly. Therefore, Algorithm 1 has good scalability. Besides, Algorithm 1 can be applied to other heuristic algorithms in addition to combining with GA, thereby reducing the solution space size and improving the convergence speed of the heuristic algorithm.

To evaluate the generalizability of the algorithm, we need to consider whether the algorithm depends on specific data distributions or assumptions. In Algorithm 1, we utilize the pre-offloading operation to obtain the load capacity of each server, which indicates that Algorithm 1 relies on certain prior knowledge. Therefore, Algorithm 1 is only applicable to MEC networks with global controllers.

Step 3 Solving offloading strategies by AGA

With Is, J can be transformed into J3, i.e.,

J3:s.t.C1,C2,C3*:∑xus≤Is,∀s∈Su∈U XmaxEoU(X,P*,ℱ*)(28)

where C3∗ is an improvement of C3 based on Is.

For J3, the chromosome code is denoted by

g=[g1,g2,…,g|𝒰|](29)

where gu∈𝒮,u∈𝒰 indicates that Tu is offloaded to server s. Each chromosome is equivalent to an offloading strategy 𝒳.

The fitness function is given by

F=∑u∈𝒰EoUu−penalty(30)

where penalty is a punishment for violations of C1 and C2.

The penalty is not applied to C3, because we believe that a little bit of relaxation for J3 may benefit searching for the extreme point. C3 is mainly used in the generation of the initial population. We randomly generate chromosomes but select only those that satisfy |Is−∑u∈𝒰xus|≤Is3 into the initial population.

The parameters include the crossover probability Pc and the mutation probability Pm. In AGA, genetic operators can be dynamically adjusted after natural selection.

Pc=P+ΔcPm=P+ΔmΔc=Pc(Favg−Fmid)/2(Fmax−Favg)Δm=Pm(Favg−Fmid)/2(Fmax−Favg)(31)

where Fmid and Favg are the median and average values of parental fitness, respectively.

The detailed procedure of GCAGA is shown as Algorithm 2. The time complexity of the external circulation of GCAGA is O(MAXV⋅iterMax), which is fixed. The internal circulation consists of the dichotomy method and the fitness function calculation. The time complexity of fitness function calculation is O(|𝒮|). Take ε as the error tolerance, the time complexity of dichotomy is O(⌈lg⁡Puε⌉). Algorithm 1 provides the total number of users that can be uploaded to each MEC server, i.e., Is, thereby reducing the size of the solution space and accelerating the convergence speed of the algorithm. However, AGA must search all the users, i.e., |𝒰|, to perform offloading. Thus, the time complexity of AGA is O(MAXV⋅iterMax⋅|𝒰|⋅(|𝒮|+⌈lg⁡Puε⌉)), while GCAGA is O(MAXV⋅iterMax⋅∑s∈𝒮Is⋅(|𝒮|+⌈lg⁡Puε⌉)), which is lower than AGA. Since Algorithm 1 can accelerate the convergence of AGA, the iterMax is not set to be a fixed value in practical scenarios. The termination condition can be set as the unchanging of optimal individual fitness.

5  Experiments

In this section, appropriate data are provided for the experiment. To prove the effectiveness of adaptive heuristic operators and the Gini coefficient-based optimization strategy, an ablation study is employed and the comparison groups are set in Table 3. In Table 3, ‘GA’ means applying the genetic algorithm; ‘Gini coefficient’ means applying Algorithm 1; ‘Adaptive operators’ means combining GA with Eq. (31) to form AGA.

We will verify the effectiveness of Algorithms 1 and 2 from three aspects, i.e., convergence behavior, convergence results, and convergence speed. We will triple mean filter the data to make the experimental curves easier to analyze.

5.1 Experiment Environment

The parameters are set as shown in Table 4. The parameters of the MEC system and GA are all verified [44,45]. The experimental program is written based on Python. The simulation runs on the PyCUDA 2021.1 framework, and one NVIDIA RTX3070 is used for accelerating the calculation. In the simulation, each user in this article can freely choose MEC servers for computation offloading. We use the convergence epoch to evaluate the convergence speed of each comparison group. We use EoU as the evaluation metric for convergence results, which is equal to the fitness value of GA. In the following text, we will not differentiate between Fitness and EoU.

5.2 Convergence Behavior

To evaluate the convergence behavior of the three algorithms, we conducted 100 repeated experiments for each of them, with 95% Confidence Interval (CI). The corresponding parameters are set as 𝒰=20,𝒮=5,N=10,αut=0.7,fs=25 MHz. The uplink channel gain matrix {hus} is randomly generated in (0, 2] for a more general situation. The comparison results are reported in Fig. 2.

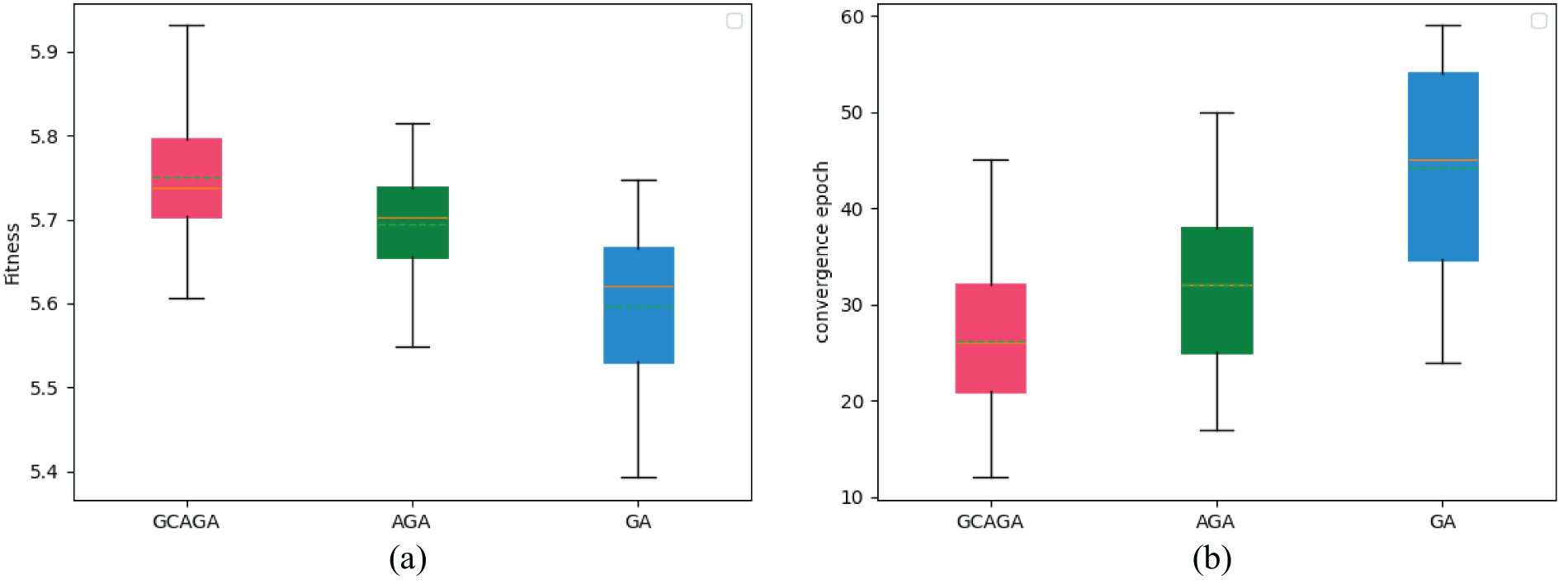
Figure 2: Convergence behavior comparison of three algorithms with 95% CI. (a) Fitness distribution comparison. (b) Earliest convergence distribution comparison

As can be seen from Fig. 2a, all three algorithms have completed convergence. Among them, GCAGA obtained 1% more EoU compared to AGA, while GCAGA obtained nearly 2% more EoU compared to GA. We also observed that GCAGA and AGA had higher convergence stability compared to GA according to the width of the distribution.

As shown in Fig. 2b, GCAGA has an obvious convergence speed advantage compared to the other two algorithms. Compared to AGA, GCAGA achieved nearly 25% speed improvement. Compared to GA, GCAGA achieved nearly 67% speed improvement. The distribution also shows that GCAGA and AGA have higher stability compared to GA, indicating the effectiveness of the Gini coefficient and adaptive changing genetic operators.

5.3 Convergence Results

Notice that in Fig. 3a, GCAGA does not have a significant advantage over AGA and GA when the computational resources are insufficient or too sufficient (corresponding to both ends of the curve). This is because when computational resources are insufficient, users prefer local computation, and there is no need for computational offloading. When the computational resources are too sufficient, the capacity bound Is, which is calculated by the Gini coefficient, reaches the upper limit, and GCAGA degrades to AGA. In the middle of the curve, we can see that GCAGA outperforms other algorithms when the computational resources are sufficient to support part of the tasks for offloading but not very abundant, which indicates that the capacity boundary calculated by the Gini coefficient plays a crucial role.

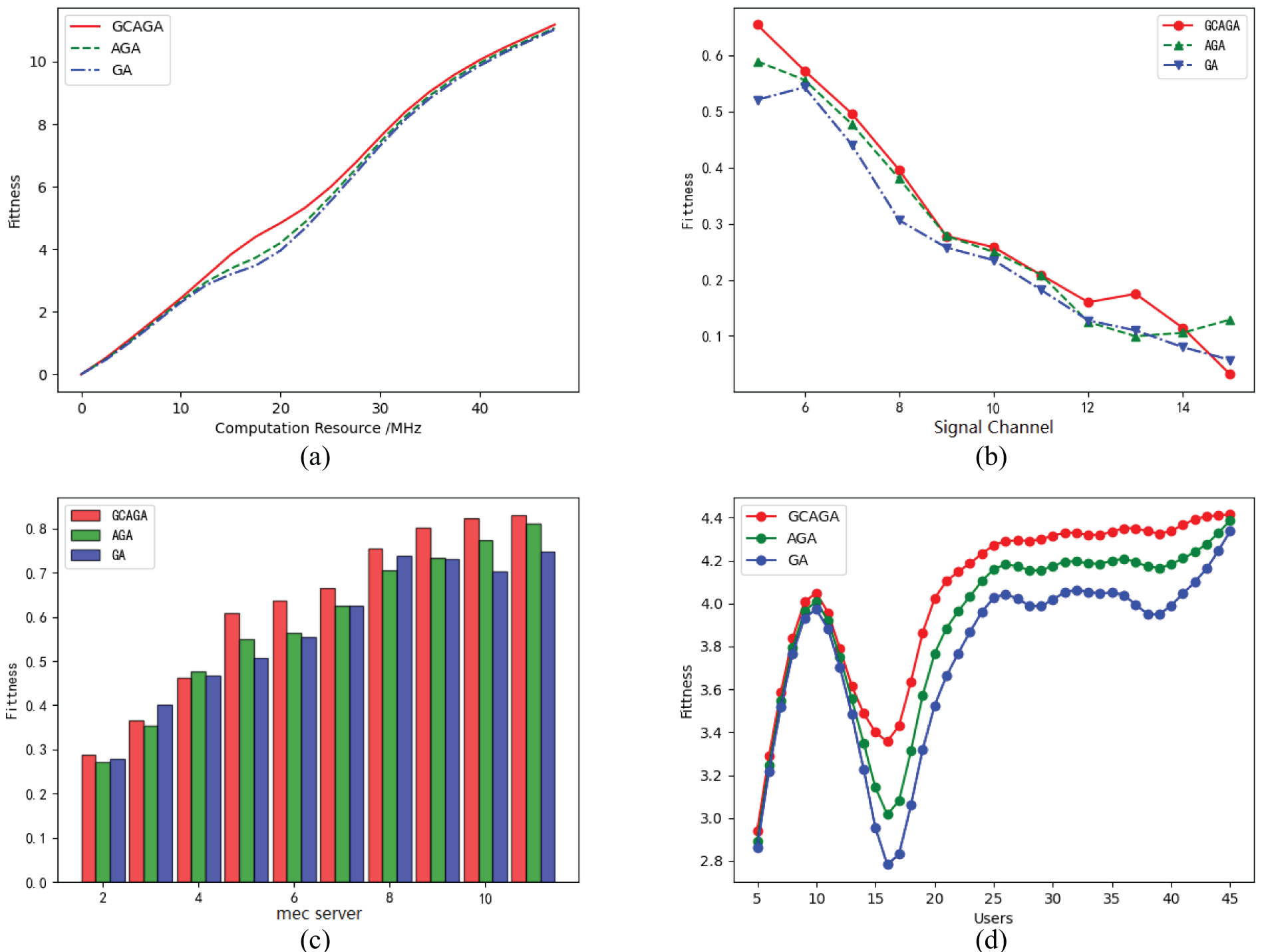
Figure 3: Optimal points of convergence results. (a) 𝒰=20,𝒮=5,N=10,αut=0.7 Fitness varies as the increasing of computation resources with a step of 2.5 MHz. (b) 𝒰=20,𝒮=5,αut=0.7,fs=6 MHz Fitness varies as the increasing of signal channels. (c) 𝒰=20,N=10,αut=0.7,fs=6 MHz Fitness varies as the increasing of MEC servers. (d) 𝒮=5,N=10,αut=0.7,fs=25 MHz Fitness varies as the increasing of users

As shown in Fig. 3b, the total revenue gradually decreases as the number of channel divisions increases. This is because the total bandwidth is limited. As the number of channel divisions increases, the bandwidth allocated to each channel decreases, which leads to an increase in the offloading delay of the uplink, i.e., the communication cost becomes larger, and the total revenue decreases.

As shown in Fig. 3c, the revenue increases while tending to be flat. When the number of servers is smaller than the number of users, the average computing resources per user increases as the number of servers increases. However, when the number of servers is larger than the number of users, the average computing resources per user tends to be constant as each user offloads to at most one server, and the revenue tends to be constant.

In Fig. 3d, the revenue curve roughly follows an increasing trend and converges when the number of users exceeds 25. This is because the capacity of the servers is limited. If the user number has reached the upper bound of the servers, only a fixed number of users can perform offloading. However, it is essential to note that there is a minimal point when the number of users is around 15. Before 10, the server load is light, and users can offload their tasks. When the user number is greater than 10, some users cannot offload. At this time, the extreme point region of the solution space becomes narrow, and the algorithm searches less efficiently. When the number of users exceeds 15, the extreme value point area becomes wider with the increase of users, and the algorithm starts to function normally.

In summary, in the simulation experiments in Figs. 3a and 3b, the two factors of edge server computing frequency and channel partition number directly relate to edge server computing and communication resources. In the simulation experiments in Figs. 3c and 3d, the two factors, i.e., the number of users and the number of MEC servers, directly relate to the computing complexity of the resource allocation and task offloading problem. The experimental results of Figs. 3a and 3b indicate that GCAGA can work effectively and stably when the resources of MEC servers are limited. The experimental results of Figs. 3c and 3d indicate that GCAGA can achieve a better convergence result while increasing problem complexity.

5.4 Convergence Speed

Fig. 4a shows that the curve gradually converges with the increase of compute resources. As computational resources increase, users are more inclined to offload tasks to edge servers, and eventually, all users will decide to perform task offloading. This means that the calculation of the Gini coefficient for the server capacity bound will fail, and GCAGA degenerates to AGA. The experimental curve also confirms this, and eventually, GCAGA needs the same epochs as AGA, which still has a speed advantage compared to GA.

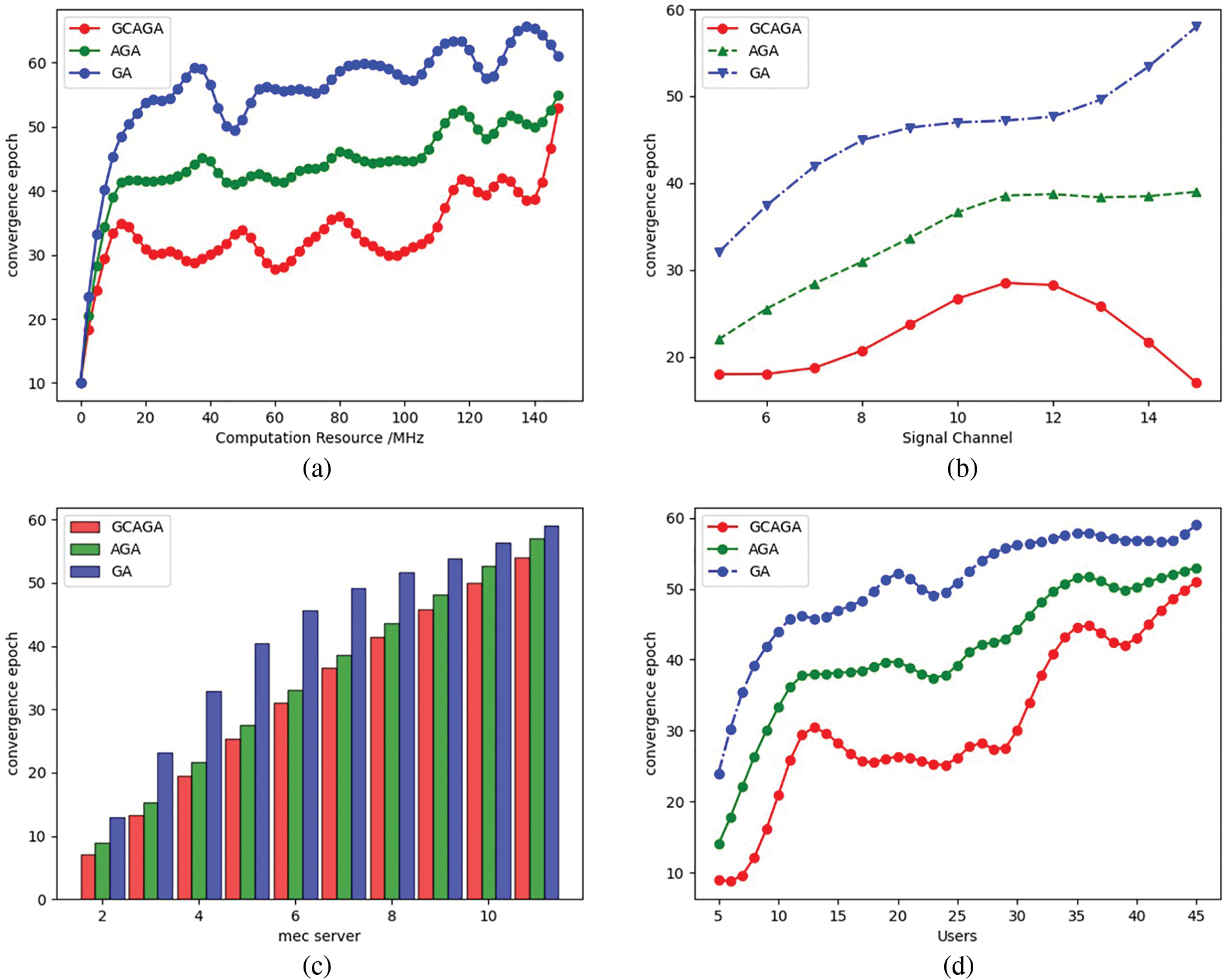
Figure 4: Experiment results of earliest convergence epochs. (a) 𝒰=20,𝒮=5,N=10,αut=0.7 Earliest convergence epochs vary as the increasing of computation resources with a step of 2.5 MHz. (b) 𝒰=20,𝒮=5,αut=0.7,fs=6 MHz Earliest convergence epochs vary as the increasing of signal channels. (c) 𝒰=20,N=10,αut=0.7,fs=6 MHz Earliest convergence epochs vary as the increasing of MEC servers. (d) 𝒮=5,N=10,αut=0.7,fs=25 MHz Earliest convergence epochs vary as the increasing of users

From Fig. 4b, the curve of GCAGA rises and falls as the number of channels increases. This is because as the number of channels increases, the upper limit of server capacity increases, users can use more channels for offloading, the number of users who can choose to perform offloading increases, and the algorithms need more epochs to converge. However, as the number of channels increases further, the number of computational resources allocated to each channel decreases, the server capacity limit decreases, and the server capacity bound calculated by the Gini coefficient comes into play at this time. Fewer epochs are required for GCAGA to converge.

In Fig. 4c, the epochs required for the convergence of the algorithms increase linearly as the number of servers increases. This is because the solution space size is linearly related to the number of servers. More servers mean more abundant computational resources and more users for offloading computations. However, due to the limited resources set per server, the server capacity bound calculated by the Gini coefficient still functions normally, as can be seen from the speed advantage of GCAGA in the figure.

In Fig. 4d, the curve rises as the number of users increases. The increased number of users means the solution space expands, and the algorithms need more epochs to converge. Due to the limited resources in the cloud, the optimal number of users that each edge server can accommodate is constant, in which case GCAGA has a significant advantage over AGA and GA.

To conclude, Figs. 4a and 4b show the relationship between the algorithms’ convergence speed and the resources provided by MEC servers. The experimental results of Figs. 4a and 4b indicate that GCAGA can accelerate convergence in the situation of insufficient resources. In Figs. 4c and 4d , the computing and communication resources on MEC servers are set limited deliberately. Experiment results show that the adaptive genetic operators and capacity bound calculated by the Gini coefficient indeed accelerate the convergence of GA.

Experimental analysis shows that the proposed Gini coefficient-based offloading strategy can reduce the size of the solution space and adaptively converge, making it effective for real-world MEC networks. Taking the widely used MQTT (Message Queuing Telemetry Transport) protocol of IoT as an example, both QoS 1 and QoS 2 services have reply messages from MEC servers, ensuring that EoUusONE can be accurately obtained by the global controller. Then, Algorithm 1 is employed to estimate the servers’ capacity. After that, Algorithm 2 can converge stably and quickly to optimize EoU. Therefore, the proposed algorithm can be effectively applied to improve the experience of users.

6  Conclusion

This paper studies the resource allocation and computational offloading problem in a multi-user multi-server MEC system. First, the offloading benefit of each user is modeled as a weighted sum of latency and energy improvement ratios. Then the total sum of offloading benefits EoU for all users in the system is maximized by jointly optimizing the resource allocation and offloading strategy. To solve this optimization problem in a feasible time, we decompose the problem into two parts: The optimization of the resource allocation problem when it has a fixed offloading decision and the optimization of the resource allocation. For problem one, it is further shown that the resource allocation problem can be decomposed into two independent problems, i.e., the transmission power allocation problem and the computational resource allocation problem. They can be solved by convex optimization and proposed quasi-convex optimization techniques, respectively. For problem two, a low-complexity algorithm is proposed to solve it. GCAGA is designed by combining the Gini coefficient with AGA. Experiment results show that the proposed algorithm can significantly improve the total users’ experience with an accelerated convergence speed when the resources on MEC servers are limited.

Acknowledgement: The resources and computing environment was provided by the Xi’an Shiyou University, Xi’an, China. We are thankful for their support.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Qiuchao Dai, Junqing Bai; data collection: Yingying Li; analysis and interpretation of results: Qiuchao Dai, Yingying Li; draft manuscript preparation: Qiuchao Dai, Junqing Bai. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. He, L. Ma, and R. Zhou, “Online task allocation in mobile cloud computing with budget constraints,” Comput. Netw., vol. 151, no. 3, pp. 42–51, Jan. 2019. doi: 10.1016/j.comnet.2019.01.003. [Google Scholar] [CrossRef]

2. Y. M. Saputra, D. Hoang, and D. N. Nguyen, “JOCAR: A jointly optimal caching and routing framework for cooperative edge caching networks,” in Proc. GLOBECOM, Waikoloa, HI, USA, 2019, pp. 1–6. doi: 10.1109/GLOBECOM38437.2019.9013745. [Google Scholar] [CrossRef]

3. Y. Mao, C. You, J. Zhang, K. Huang, and K. B. Letaief, “A survey on mobile edge computing: The communication perspective,” IEEE Commun. Surv. Tutorials, vol. 19, no. 4, pp. 2322–2358, Aug. 2017. doi: 10.1109/COMST.2017.2745201. [Google Scholar] [CrossRef]

4. N. Fernando, S. W. Loke, and W. Rahayu, “Computing with nearby mobile devices: A work sharing algorithm for mobile edge-Clouds,” IEEE Trans. Cloud Comput., vol. 7, no. 2, pp. 329–343, Apr. 2019. doi: 10.1109/TCC.2016.2560163. [Google Scholar] [CrossRef]

5. Z. Yu, Y. Gong, S. Gong, and Y. Guo, “Joint task offloading and resource allocation in UAV-enabled mobile edge computing,” IEEE Internet Things J., vol. 7, no. 4, pp. 3147–3159, Apr. 2020. doi: 10.1109/JIOT.2020.2965898. [Google Scholar] [CrossRef]

6. Q. Hu, Y. Cai, G. Yu, Z. Qin, M. Zhao and G. Y. Li, “Joint offloading and trajectory design for UAV-enabled mobile edge computing systems,” IEEE Internet Things J., vol. 6, no. 2, pp. 1879–1892, Apr. 2019. doi: 10.1109/JIOT.2018.2878876. [Google Scholar] [CrossRef]

7. L. Wang, K. Wang, C. Pan, W. Xu, N. Aslam and L. Hanzo, “Multi-agent deep reinforcement learning-based trajectory planning for multi-UAV assisted mobile edge computing,” IEEE Trans. Cogn. Commun. Netw., vol. 7, no. 1, pp. 73–84, Mar. 2021. doi: 10.1109/TCCN.2020.3027695. [Google Scholar] [CrossRef]

8. X. Hu, K. K. Wong, K. Yang, and Z. Zheng, “UAV-assisted relaying and edge computing: Scheduling and trajectory optimization,” IEEE Trans. Wirel. Commun., vol. 18, no. 10, pp. 4738–4752, Oct. 2019. doi: 10.1109/TWC.2019.2928539. [Google Scholar] [CrossRef]

9. J. Zhang, “Stochastic computation offloading and trajectory scheduling for UAV-assisted mobile edge computing,” IEEE Internet Things J., vol. 6, no. 2, pp. 3688–3699, Apr. 2019. doi: 10.1109/JIOT.2018.2890133. [Google Scholar] [CrossRef]

10. P. Zhao, H. Tian, C. Qin, and G. Nie, “Energy-saving offloading by jointly allocating radio and computational resources for mobile edge computing,” IEEE Access, vol. 5, pp. 11255–11268, Jun. 2017. doi: 10.1109/ACCESS.2017.2710056. [Google Scholar] [CrossRef]

11. M. R. Rahimi, N. Venkatasubramanian, S. Mehrotra, and A. V. Vasilakos, “MAPCloud: Mobile applications on an elastic and scalable 2-tier cloud architecture,” in Proc. UCC, Chicago, IL, USA, 2012, pp. 83–90. doi: 10.1109/UCC.2012.25. [Google Scholar] [CrossRef]

12. H. Yu, Q. Wang, and S. Guo, “Energy-efficient task offloading and resource scheduling for mobile edge computing,” in Proc. NAS, Chongqing, China, 2018, pp. 1–4. doi: 10.1109/NAS.2018.8515731. [Google Scholar] [CrossRef]

13. J. Du, L. Zhao, X. Chu, F. R. Yu, J. Feng and I. Chih-Lin, “Enabling low-latency applications in LTE–A based mixed fog/cloud computing systems,” IEEE Trans. Vehicular Technol., vol. 68, no. 2, pp. 1757–1771, Feb. 2019. doi: 10.1109/TVT.2018.2882991. [Google Scholar] [CrossRef]

14. Y. Cong, K. Xue, C. Wang, W. Sun, S. Sun and F. Hu, “Latency-energy joint optimization for task offloading and resource allocation in MEC-assisted vehicular networks,” IEEE Trans. Vehicular Technol., vol. 72, no. 12, pp. 16369–16381, Dec. 2023. doi: 10.1109/TVT.2023.3289236. [Google Scholar] [CrossRef]

15. L. Liu, Z. Chang, and X. Guo, “Socially aware dynamic computation offloading scheme for fog computing system with energy harvesting devices,” IEEE Internet Things J., vol. 5, no. 3, pp. 1869–1879, Jun. 2018. doi: 10.1109/JIOT.2018.2816682. [Google Scholar] [CrossRef]

16. X. Huang, X. Bao, S. Feng, Z. Luo, and G. Huang, “Optimal offline energy and task scheduling algorithm design for wireless-powered IRS-assisted mobile edge computing systems,” in Proc. ICCCS, Guangzhou, China, 2023, pp. 337–344. doi: 10.1109/ICCCS57501.2023.10151260. [Google Scholar] [CrossRef]

17. Y. Jiang and D. H. K. Tsang, “Delay-aware task offloading in shared fog networks,” IEEE Internet Things J., vol. 5, no. 6, pp. 4945–4956, Dec. 2018. doi: 10.1109/JIOT.2018.2880250. [Google Scholar] [CrossRef]

18. G. Zhang, F. Shen, Y. Yang, H. Qian, and W. Yao, “Fair task offloading among fog nodes in fog computing networks,” in Proc. ICC, Kansas City, MO, USA, Jul. 2018, pp. 1–6. doi: 10.1109/ICC.2018.8422316. [Google Scholar] [CrossRef]

19. A. Yousefpour, G. Ishigaki, R. Gour, and J. P. Jue, “On reducing IoT service delay via fog offloading,” IEEE Internet Things J., vol. 5, no. 2, pp. 998–1010, Apr. 2018. doi: 10.1109/JIOT.2017.2788802. [Google Scholar] [CrossRef]

20. H. Shah-Mansouri and V. W. S. Wong, “Hierarchical fog-cloud computing for IoT systems: A computation offloading game,” IEEE Internet Things J., vol. 5, no. 4, pp. 3246–3257, Aug. 2018. doi: 10.1109/JIOT.2018.2838022. [Google Scholar] [CrossRef]

21. J. Xin, X. Li, L. Zhang, Y. Zhang, and S. Huang, “Joint computation and traffic loads balancing task offloading in multi-access edge computing systems interconnected by elastic optical networks,” IEEE Commun. Lett., vol. 27, no. 9, pp. 2378–2382, Sep. 2023. doi: 10.1109/LCOMM.2023.3292364. [Google Scholar] [CrossRef]

22. L. Liu and Z. Chen, “Joint optimization of multi-user computation offloading and wireless-caching resource allocation with linearly related requests in vehicular edge computing system,” IEEE Internet Things J., vol. 11, no. 1, pp. 1534–1547, Jan. 01, 2024. doi: 10.1109/JIOT.2023.3289994. [Google Scholar] [CrossRef]

23. Z. Xu, Y. Xie, F. Dong, S. Fu, and J. Hao, “Joint optimization of task offloading and resource allocation for edge video analytics,” in Proc. CSCWD, Rio de Janeiro, Brazil, 2023, pp. 636–641. doi: 10.1109/CSCWD57460.2023.10152681. [Google Scholar] [CrossRef]

24. J. Xu, X. Liu, and X. Zhu, “Deep reinforcement learning based computing offloading and resource allocation algorithm for mobile edge networks,” in Proc. ICCC, Chengdu, China, 2020, pp. 1542–1547. doi: 10.1109/ICCC51575.2020.9345089. [Google Scholar] [CrossRef]

25. H. Chen, D. Zhao, Q. Chen, and R. Chai, “Joint computation offloading and radio resource allocations in wireless cellular networks,” in Proc. WCSP, Hangzhou, China, 2018, pp. 1–6. doi: 10.1109/WCSP.2018.8555588. [Google Scholar] [CrossRef]

26. H. Xing, L. Liu, J. Xu, and A. Nallanathan, “Joint task assignment and resource allocation for D2D-enabled mobile-edge computing,” IEEE Trans. Commun., vol. 67, no. 6, pp. 4193–4207, Jun. 2019. doi: 10.1109/TCOMM.2019.2903088. [Google Scholar] [CrossRef]

27. J. Ren, G. Yu, Y. He, and G. Y. Li, “Collaborative cloud and edge computing for latency minimization,” IEEE Trans. Veh. Technol., vol. 68, no. 5, pp. 5031–5044, May 2019. doi: 10.1109/TVT.2019.2904244. [Google Scholar] [CrossRef]

28. Z. Ning, X. Wang, J. J. P. C. Rodrigues, and F. Xia, “Joint computation offloading, power allocation, and channel assignment for 5G-enabled traffic management systems,” IEEE Trans. Ind. Inform., vol. 15, no. 5, pp. 3058–3067, May 2019. doi: 10.1109/TII.2019.2892767. [Google Scholar] [CrossRef]

29. X. Xu, Q. Liu, and X. Zhang, “A computation offloading method over big data for IoT-enabled cloud-edge computing,” Future Gener. Comput. Syst., vol. 95, no. 6, pp. 522–533, Jan. 2019. doi: 10.1016/j.future.2018.12.055. [Google Scholar] [CrossRef]

30. Y. Wu, L. P. Qian, K. Ni, C. Zhang, and X. Shen, “Delay-minimization nonorthogonal multiple access enabled multi-user mobile edge computation offloading,” IEEE J. Sel. Top. Signal Process., vol. 13, no. 3, pp. 392–407, Jun. 2019. doi: 10.1109/JSTSP.2019.2893057. [Google Scholar] [CrossRef]

31. F. Wang, M. Zhang, X. Wang, X. Ma, and J. Liu, “Deep learning for edge computing applications: A state-of-the-art survey,” IEEE Access, vol. 8, pp. 58322–58336, Aug. 2020. doi: 10.1109/ACCESS.2020.2982411. [Google Scholar] [CrossRef]

32. Z. Zhou, X. Chen, E. Li, L. Zeng, K. Luo and J. Zhang, “Edge intelligence: Paving the last mile of artificial intelligence with edge computing,” Proc. IEEE, vol. 107, no. 8, pp. 1738–1762, Aug. 2019. doi: 10.1109/JPROC.2019.2918951. [Google Scholar] [CrossRef]

33. X. Wang, Y. Han, V. C. M. Leung, D. Niyato, X. Yan and X. Chen, “Convergence of edge computing and deep learning: A comprehensive survey,” IEEE Commun. Surv. Tutorials, vol. 22, no. 2, pp. 869–904, Jan. 2020. doi: 10.1109/COMST.2020.2970550. [Google Scholar] [CrossRef]

34. G. Qu, H. Wu, R. Li, and P. Jiao, “DMRO: A deep meta reinforcement learning-based task offloading framework for edge-cloud computing,” IEEE Trans. Netw. Serv. Manag., vol. 18, no. 3, pp. 3448–3459, Sep. 2021. doi: 10.1109/TNSM.2021.3087258. [Google Scholar] [CrossRef]

35. X. Chen and G. Liu, “Energy-efficient task offloading and resource allocation via deep reinforcement learning for augmented reality in mobile edge networks,” IEEE Internet Things J., vol. 8, no. 13, pp. 10843–10856, Jul. 2021. doi: 10.1109/JIOT.2021.3050804. [Google Scholar] [CrossRef]

36. Z. Gao, L. Yang, and Y. Dai, “Large-scale cooperative task offloading and resource allocation in heterogeneous MEC systems via multi-agent reinforcement learning,” IEEE Internet Things J., vol. 11, no. 2, pp. 2303–2321, Jan. 15, 2024. doi: 10.1109/JIOT.2023.3292387. [Google Scholar] [CrossRef]

37. J. A. Ansere, “Optimal computation resource allocation in energy-efficient edge IoT systems with deep reinforcement learning,” IEEE Trans. Green Commun. Netw., vol. 7, no. 4, pp. 2130–2142, Dec. 2023. doi: 10.1109/TGCN.2023.3286914. [Google Scholar] [CrossRef]

38. Z. Gao, L. Yang, and Y. Dai, “Fast adaptive task offloading and resource allocation in large-scale MEC systems via multi-agent graph reinforcement learning,” IEEE Internet Things J., vol. 11, no. 1, pp. 758–776, Jan. 2024. doi: 10.1109/JIOT.2023.3285950. [Google Scholar] [CrossRef]

39. J. Zhang, B. Gong, M. Waqas, S. Tu, and Z. Han, “A hybrid many-objective optimization algorithm for task offloading and resource allocation in multi-server mobile edge computing networks,” IEEE Trans. Serv. Comput., vol. 16, no. 5, pp. 3101–3114, Sep. 2023. doi: 10.1109/TSC.2023.3268990. [Google Scholar] [CrossRef]

40. J. Liu, G. Li, Q. Huang, M. Bilal, X. Xu and H. Song, “Cooperative resource allocation for computation-intensive IIoT applications in aerial computing,” IEEE Internet Things J., vol. 10, no. 11, pp. 9295–9307, Jun. 2023. doi: 10.1109/JIOT.2022.3222340. [Google Scholar] [CrossRef]

41. E. Dahlman, S. Parkvall, and J. Skold, “Chapter 3–OFDM transmission,” in 4G: LTE/LTE-Advanced for Mobile Broadband, 2nd ed. NY, USA: Academic Press, 2014, pp. 29–48. [Google Scholar]

42. W. Zhan, C. Luo, G. Min, C. Wang, Q. Zhu and H. Duan, “Mobility-aware multi-user offloading optimization for mobile edge computing,” IEEE Trans. Veh. Technol., vol. 69, no. 3, pp. 3341–3356, Mar. 2020. doi: 10.1109/TVT.2020.2966500. [Google Scholar] [CrossRef]

43. T. X. Tran and D. Pompili, “Joint task offloading and resource allocation for multi-server mobile-edge computing networks,” IEEE Trans. Veh. Technol., vol. 68, no. 1, pp. 856–868, Jan. 2019. doi: 10.1109/TVT.2018.2881191. [Google Scholar] [CrossRef]

44. D. Wang, Z. Liu, X. Wang, and Y. Lan, “Mobility-aware task offloading and migration schemes in fog computing networks,” IEEE Access, vol. 7, pp. 43356–43368, Mar. 2019. doi: 10.1109/ACCESS.2019.2908263. [Google Scholar] [CrossRef]

45. F. Guo, H. Zhang, H. Ji, X. Li, and V. C. M. Leung, “An efficient computation offloading management scheme in the densely deployed small cell networks with mobile edge computing,” IEEE/ACM Trans. Netw., vol. 26, no. 6, pp. 2651–2664, Dec. 2018. doi: 10.1109/TNET.2018.2873002. [Google Scholar] [CrossRef]