 Open Access
Open Access
ARTICLE
Multiscale and Auto-Tuned Semi-Supervised Deep Subspace Clustering and Its Application in Brain Tumor Clustering
1 School of Artificial Intelligence and Computer Science, Jiangnan University, Wuxi, 214122, China
2 Department of Medical Imaging, The Changshu Affiliated Hospital of Soochow University, Suzhou, 215500, China
3 Department of Neurosurgery, The Changshu Affiliated Hospital of Soochow University, Changshu, 215500, China
4 Department of Scientific Research, The Changshu Affiliated Hospital of Soochow University, Suzhou, 215500, China
5 Changshu Key Laboratory of Medical Artificial Intelligence and Big Data, Suzhou, 215500, China
6 Department of Biomedical Engineering, Faculty of Engineering, University of Malaya, Kuala Lumpur, 50603, Malaysia
* Corresponding Author: Kaijian Xia. Email:
(This article belongs to the Special Issue: Advanced Artificial Intelligence and Machine Learning Frameworks for Signal and Image Processing Applications)
Computers, Materials & Continua 2024, 79(3), 4741-4762. https://doi.org/10.32604/cmc.2024.050920
Received 22 February 2024; Accepted 28 April 2024; Issue published 20 June 2024
Abstract
In this paper, we introduce a novel Multi-scale and Auto-tuned Semi-supervised Deep Subspace Clustering (MAS-DSC) algorithm, aimed at addressing the challenges of deep subspace clustering in high-dimensional real-world data, particularly in the field of medical imaging. Traditional deep subspace clustering algorithms, which are mostly unsupervised, are limited in their ability to effectively utilize the inherent prior knowledge in medical images. Our MAS-DSC algorithm incorporates a semi-supervised learning framework that uses a small amount of labeled data to guide the clustering process, thereby enhancing the discriminative power of the feature representations. Additionally, the multi-scale feature extraction mechanism is designed to adapt to the complexity of medical imaging data, resulting in more accurate clustering performance. To address the difficulty of hyperparameter selection in deep subspace clustering, this paper employs a Bayesian optimization algorithm for adaptive tuning of hyperparameters related to subspace clustering, prior knowledge constraints, and model loss weights. Extensive experiments on standard clustering datasets, including ORL, Coil20, and Coil100, validate the effectiveness of the MAS-DSC algorithm. The results show that with its multi-scale network structure and Bayesian hyperparameter optimization, MAS-DSC achieves excellent clustering results on these datasets. Furthermore, tests on a brain tumor dataset demonstrate the robustness of the algorithm and its ability to leverage prior knowledge for efficient feature extraction and enhanced clustering performance within a semi-supervised learning framework.Graphic Abstract
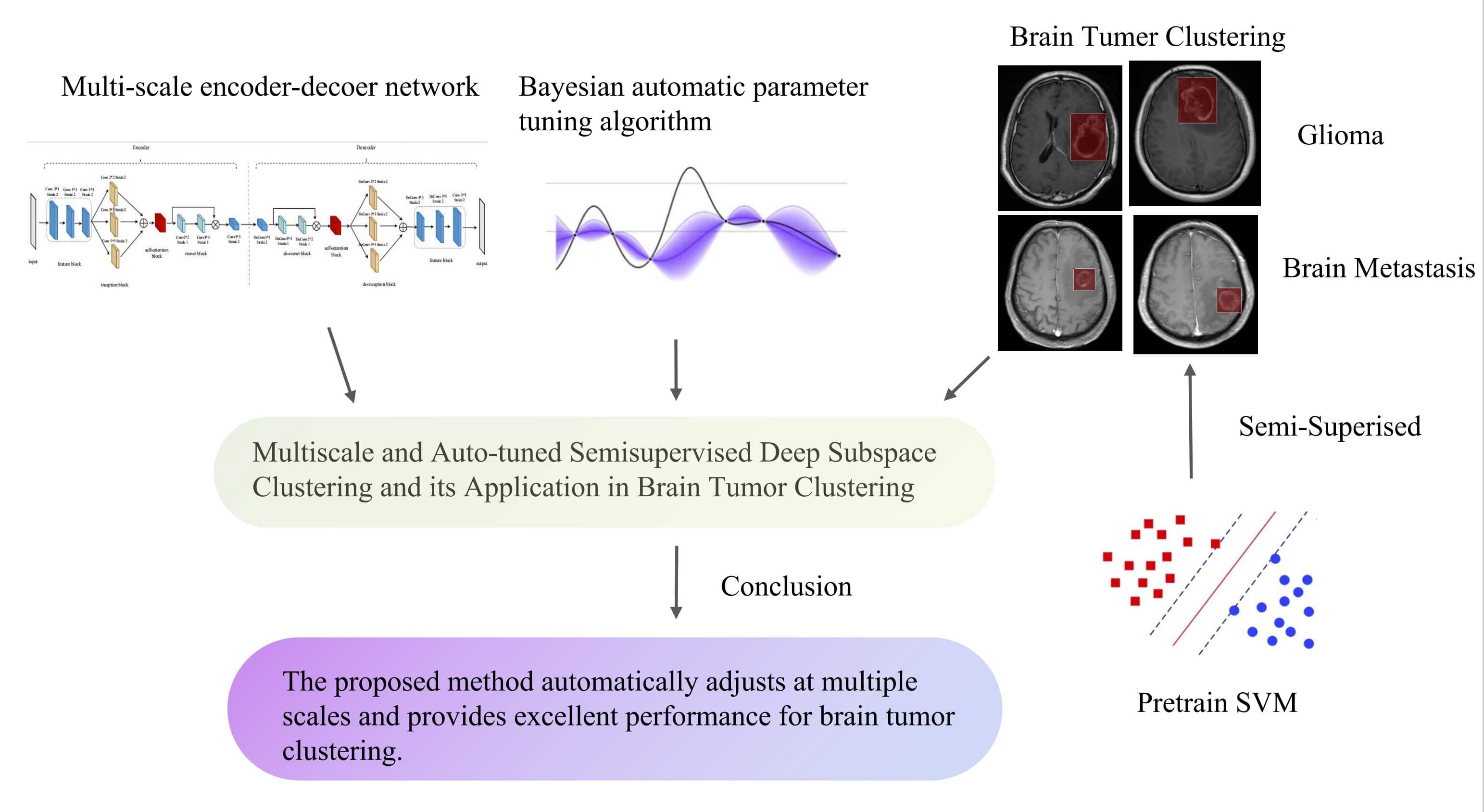
Keywords
In the field of machine learning, classification [1] and clustering are two core tasks. Classification is widely used in people’s daily lives, such as face recognition [2,3], sentiment analysis [4], etc. Compared to classification, clustering does not require the introduction of labels, making it more flexible and user-friendly. Among existing clustering algorithms, subspace clustering, as a significant branch of unsupervised learning, aims to cluster data points from the union of low-dimensional subspaces in an unsupervised manner. With the widespread application of clustering in areas such as image segmentation [5,6], motion segmentation [7,8], and image clustering [9,10], the importance of subspace clustering in practical applications has become increasingly evident.
Despite the prevalence of linear subspace clustering algorithms, they often fall short when applied to real-world data, which may not strictly adhere to linear models. This is particularly true for nonlinear data structures, such as those found in facial recognition tasks. To bridge this gap, recent efforts have seen the integration of deep convolutional neural networks with subspace clustering algorithms [11–14], exemplified by the Deep Subspace Clustering Network (DSC-Net) [15] algorithm. This approach utilizes deep convolutional autoencoders to unearth nonlinear features for subspace clustering, thereby bolstering clustering outcomes. Nevertheless, the potential of these deep subspace clustering algorithms to extract nonlinear features is not fully realized, as evidenced by the simplistic convolutional layers used in the DSC-Net [15] algorithm, which limit the efficacy of the clustering process.
Especially noteworthy is the heightened performance challenges of deep subspace clustering algorithms when dealing with more complex and high-dimensional medical images. This paper focuses on the classification of intracranial solitary metastases and gliomas, which is one of the challenging issues in medical imaging [16]. Given the stark differences in treatment approaches and prognoses between these two tumor types, precise pre-surgical differentiation and diagnosis hold immense importance [17]. Yet, the autoencoder structures in current deep subspace clustering algorithms, with their fixed convolutional kernels and pooling layers, struggle to effectively capture the diverse features of brain tumors. The complexity of brain tumors, with their variable cross-sectional positions and intricate topological structures, underscores the significance of the receptive field’s size. A field too small captures merely local features, while one too large may gather irrelevant features. Thus, optimizing the receptive field within the network is key to improving feature extraction efficiency. With the development of convolutional neural network architectures, deep network structures like Residual Network (ResNet) [18] and wide network structures like Inception [19] have been proposed, enabling the fusion of multi-scale features in terms of width and depth.
Simultaneously, related studies indicate that the introduction of prior knowledge can effectively enhance clustering performance for medical image data [20]. For example, in brain tumor analysis, the lesion’s location is critical; brain metastases typically reside just below the cortex, whereas gliomas are more commonly located in the deep white matter [21,22]. By converting this diagnostic insight into a prior regularization term within the model, one can markedly enhance the clustering impact on medical images and improve the model’s interpretability. However, despite some deep subspace clustering algorithms being applied to medical imaging for clustering purposes, they have not yet utilized the prior knowledge inherent in medical images to enhance clustering performance, thereby limiting their overall effectiveness. Furthermore, in the realm of current mainstream deep convolutional network training, the optimization of hyperparameters has become crucial. An appropriate hyperparameter tuning algorithm can significantly enhance the effectiveness of deep subspace clustering.
To address these common issues in existing deep subspace clustering algorithms, this paper introduces a semi-supervised deep subspace clustering algorithm that leverages multi-scale network structures and automatic hyperparameter tuning (MAS-DSC). The key contributions of this paper are summarized as follows:
1. Addressing the limitation of current deep subspace clustering algorithms, which rely solely on simple convolutional neural network layers and consequently restrict clustering effectiveness, this paper innovatively designs structures based on ResNet deep network and Inception wide network, along with corresponding reverse ResNet and reverse Inception autoencoder structures. This design integrates multi-scale feature information from depth and width, achieving dimensionality reduction for complex image data and successfully extracting crucial features. Additionally, this paper introduces a self-attention mechanism between each layer of the multi-scale encoder to further enhance the feature representation capability of the autoencoder.
2. Targeting the limitations of deep subspace clustering in medical images, this paper transforms prior knowledge about medical tumors into a regularization term in the decision loss function, thereby enhancing the robustness and interpretability of the model.
3. In response to the hyperparameter tuning challenge, this paper introduces an optimization method based on Bayesian algorithms, automating the selection of hyperparameters and effectively improving clustering performance.
4. To validate the effectiveness of the proposed algorithm, extensive experiments were conducted on standard clustering datasets, including ORL, COIL20, and COIL100. The results indicate a significant performance improvement of the proposed algorithm, especially on the COI100 dataset, showcasing its robust learning ability for complex structures. Additionally, the paper annotated a BrainTumor dataset provided by a collaborating hospital to verify the achievements in medical image clustering. Experimental results on the BrainTumor dataset demonstrate that the multi-scale autoencoder structure proposed in this paper has excellent learning capabilities for medical image features. Moreover, the introduction of a semi-supervised medical prior knowledge regularization term further enhances clustering performance.
The organization of the remaining sections in this paper is as follows. Section 2 provides a comprehensive review of related work and introduces the concepts of deep subspace clustering, semi-supervised deep subspace clustering, multi-scale network structures, residual network structures, and hyperparameter auto-search algorithms. Section 3 provides a detailed exposition of the proposed semi-supervised deep subspace clustering algorithm based on multi-scale network structures and hyperparameter auto-search. This chapter also explores its specific implementation in brain tumor clustering research. Section 4 starts by introducing the datasets, followed by an explanation of the algorithm’s performance on different datasets. Finally, this chapter conducts ablation experiments, analyzing the impact of different loss terms on the algorithm and discussing the influence of various parameters in the Bayesian algorithm on algorithm performance, along with experiments on convergence analysis. Section 5 concludes the work done in this paper and offers prospects for future research.
In the current field of machine learning, Subspace Clustering (SC) [10] has garnered considerable attention as an effective method for clustering high-dimensional data. Traditional Subspace Clustering algorithms [23,24] are dedicated to partitioning a dataset into multiple low-dimensional subspaces, assigning corresponding samples to each subspace. Subspace Clustering assumes that any sample can be linearly represented by other samples from the same category, emphasizing the self-expressive nature of the data. Therefore, Subspace Clustering typically employs the following loss function [25]:
where
The advent of deep learning has led to the development of Deep Subspace Clustering (DSC) [26], which offers a novel solution for analyzing high-dimensional and nonlinear data. DSC leverages deep neural networks to learn detailed feature representations, enhancing the ability to model data subspaces. Its effectiveness in learning complex, nonlinear features make it superior for processing intricate datasets, including images and medical data. DSC has shown to outperform traditional methods like Sparse Subspace Clustering (SSC) [10] and Low-Rank Representation (LRR) [23] in image data analysis. The clustering loss function in Deep Subspace Clustering algorithms (DSC-Net) not only determines the coefficients matrix C but also improves the embedded features Z, resulting in more accurate clustering.
The clustering loss used in DSC-Net is given by:
To optimize this loss, Ji et al. [15] ingeniously designed a self-expression layer that performs the operation
The autoencoder (AE) [27] is the most commonly used neural network trained in an unsupervised manner and has been widely employed for clustering tasks. Specifically, an autoencoder typically consists of two sub-networks, an encoder
Ji et al. [15] proposed training the clustering loss
Recently, some scholars [28] have also optimized clustering effects from the perspective of the representation learning layer. For instance, Lv et al. [29] employed pseudo-label supervised similarity learning to enhance clustering performance, while Li et al. [30] optimized clustering effects using a multi-view approach. Unlike their work, which improves performance by refining the downstream clustering task, our paper focuses on enhancing the feature extraction capabilities of autoencoders in the upstream task to subsequently improve the downstream clustering task. Moreover, the application of deep clustering problems to medical images is feasible; for example, researchers [31] have achieved commendable results by performing deep embedding clustering on large-scale medical images using deep variational autoencoders. However, their method is based on unsupervised clustering, which lacks emphasis on the distinctive features and interpretability of medical images. Our paper, through a semi-supervised mechanism, utilizes a small portion of labeled medical image data to extract key prior knowledge, which is then integrated into a traditional classification framework as a regularized loss term, guiding the process towards more accurate clustering.
2.2 Semi-Supervised Deep Subspace Clustering
Most semi-supervised clustering frameworks integrate an unsupervised clustering loss with a constraint-based loss. In recent advancements, Guan et al. [32] introduced a model for feature space learning within a semi-supervised paradigm to enhance the comprehension and learning of feature representations. Similarly, Kang et al. [33] amalgamated multi-kernel learning with semi-supervised approaches to tackle clustering challenges. When juxtaposed with conventional unsupervised deep clustering methods, semi-supervised deep subspace clustering algorithms exhibit a superior capacity to extract more meaningful and discriminative features, thereby bolstering clustering outcomes. Empirical research underscores the pivotal importance of incorporating prior knowledge into semi-supervised medical image clustering to significantly refine the clustering process [20]. This paper zeroes in on the clustering of brain tumors, revealing that the incorporation of prior knowledge regarding the morphology and spatial distribution of brain tumors as clustering constraints exerts a beneficial influence on the enhancement of clustering accuracy.
2.3 Multiscale Network Architecture
Drawing inspiration from image processing architectures like Visual Geometry Group (VGG) Net [34] and Google Inception Net (GoogleNet) [19], the Inception Architecture Version 3 (InceptionV3) module [35] has been employed for its efficacy in feature extraction and image reconstruction, yielding commendable results. The Inception module enhances the conventional convolutional layers by reducing the number of parameters while simultaneously expanding the network’s depth and breadth. It executes parallel computations on various transformations of the same input and amalgamates their outcomes into a unified output. The utilization of the Inception module is advantageous for distilling feature information from images laden with noise through convolutional kernels of differing sizes, thereby endowing the model with improved generalization capabilities. Some multi-scale neural network models have also been utilized to address the classification of medical images, such as [36,37] which employs multimodal and multi-scale deep neural networks for the early diagnosis of Alzheimer’s disease. However, these models use supervised methods. This paper, through a combination of semi-supervised and unsupervised clustering methods, reduces the reliance on semantic labels and effectively leverages the potential value of unlabeled data.
In 2016, He et al. proposed a deep residual network (ResNet) for image recognition in the paper [18]. ResNet is a type of convolutional neural network (CNN) that introduces the concept of shortcut connections, adding the input from the previous layer to the output of the current layer. These connections facilitate easier training of the network and have been shown to improve performance [38], as well as mitigate the issue of vanishing gradients, thereby accelerating the convergence of deep networks. The innovative architecture of ResNet has been widely adopted in medical image processing, demonstrating remarkable capabilities in tasks [39] such as image classification, lesion detection, and tissue segmentation. In a different approach, the Dense Convolutional Network (DenseNet) [40] utilizes cross-layer connections, which strengthens feature propagation and reuse, leading to more efficient feature extraction [41,42].
2.4 Automatic Hyperparameter Search
Fine-tuning hyperparameters is essential for deep learning models to achieve peak performance. Traditionally, this optimization has been a manual, iterative process performed by experienced practitioners, which is inefficient and may not yield the best results. Automated hyperparameter adjustment is now being explored to enhance both efficiency and model performance.
In response to the drawbacks of manual tuning, a spectrum of automatic hyperparameter search algorithms has been introduced, including grid search [43], random search [44], evolutionary algorithms [45], reinforcement learning-based methods [46], and notably, Bayesian optimization [47,48]. Bayesian optimization stands out as a particularly efficient automated method. Unlike grid search, which methodically probes a set parameter grid, or random search, which selects parameters unpredictably, Bayesian optimization smartly navigates the parameter space by learning from past outcomes, thus reducing the number of trials and accelerating the discovery of superior solutions. When compared to evolutionary algorithms, Bayesian optimization is more evaluation-efficient, as it constructs a probabilistic model to forecast which parameters are likely to perform better. Evolutionary algorithms, in contrast, require extensive computation to generate and test multiple candidate solutions. Bayesian optimization also offers a more direct approach than reinforcement learning, which is generally applied to strategy learning in complex scenarios. Specifically tailored for hyperparameter optimization, Bayesian optimization uses probability models, such as Gaussian processes, to estimate the performance of untested parameters, guiding the selection of new candidates more effectively.
3 Our Proposal: Multiscale and Auto-Tuned Semi-Supervised Deep Subspace Clustering, MAS-DSC
In exploring Deep Subspace Clustering algorithms (DSC-Net), we identified a limitation in feature extraction due to the simplistic layering of convolutional neural networks within its autoencoder architecture, which hampers the effective extraction of multiscale features. Moreover, the DSC-Net algorithm’s performance is compromised by the need for manual adjustment of weights for clustering loss, autoencoder reconstruction loss coefficients, and various hyperparameters within the subspace clustering framework. To overcome these challenges, our paper introduces an advanced convolution and deconvolution architecture inspired by Resnet and Inception models. We have optimized the network’s architecture both horizontally and vertically, and have incorporated attention mechanisms to further refine the feature extraction capabilities of the autoencoder. This enhancement significantly boosts the deep subspace clustering performance. Additionally, we have integrated a Bayesian-based hyperparameter optimization algorithm that autonomously navigates the hyperparameter space, thereby markedly improving the model’s clustering efficacy.
In the context of brain tumor datasets, our paper adopts a semi-supervised methodology that leverages existing clinical knowledge about brain tumors. The subsequent sections will delve into a comprehensive discussion of these innovations.
3.1 Multiscale Autoencoder Structure
This paper proposes a convolutional and deconvolutional autoencoder structure based on the Resnet and Inception architectures. Simultaneously, an attention mechanism is introduced to enhance the feature extraction effectiveness. The structure of the proposed autoencoder is illustrated in Fig. 1.

Figure 1: This is the autoencoder framework during the pretraining part of the pretraining and fine-tuning process, where we first pretrain a deep autoencoder without the self-expression layer using the autoencoder; then, we use this pretrained model for initialization to fine-tune the entire network
3.1.1 Feature Block and Decode Feature Block
As shown in Table 1, the Feature Block consists of three convolutional layers. Each convolutional layer has a kernel size of 3 * 3, a stride of 2, and employs the “same” padding. Each layer of the Feature Block reduces the size of the original image by half. The corresponding Decode Feature Block performs the operation of doubling the size of the feature maps.

3.1.2 Inception Block and Decode Inception Block
As shown in Table 2, the Inception Block consists of three convolutional branches. The first branch has a kernel size of 2 * 2, a stride of 2, the second branch has a kernel size of 3 * 3, a stride of 2, and the third branch has a kernel size of 5 * 5, a stride of 2. The padding for all three branches is “same.” Each branch of Inception reduces the size of the original image by half while employing different-sized convolutional kernels to aggregate features of varying scales, enhancing the feature extraction effect. The corresponding Decode Inception Block doubles the size of the feature maps.

3.1.3 Resnet Block and Decode Resnet Block
As shown in Table 3, the Resnet Block consists of 2 convolutional layers. The first layer has a kernel size of 2 * 2, a stride of 1, and the second layer has a kernel size of 3 * 3, a stride of 1. Both layers use “same” padding. The Resnet Block does not change the size of the input feature map, and it is introduced to enhance feature extraction while speeding up the network training process. Similarly, the Decode Resnet Block does not alter the size of the input feature map.

The Self-Attention Block used in this paper is based on the attention module of Efficient Channel Attention for Deep Convolutional Neural Networks (ECA-Net), as illustrated in Fig. 2. Compared to Squeeze Excitation Network (SE-Net), ECA-Net removes the fully connected layer after global average pooling and replaces it with a 1 * 1 convolution after channel-wise global average pooling without dimension reduction. ECA-Net utilizes a one-dimensional convolution for inter-channel information interaction, and the size of the convolution kernel k is adaptive through a function.

Figure 2: The architecture of self-attention block
3.2 Semi-Supervised Deep Subspace Clustering with Prior Knowledge
3.2.1 Prior Knowledge Constraints
In this paper, a semi-supervised algorithm based on prior knowledge is proposed for the brain tumor dataset. The focus is on the classification of gliomas and brain metastases, and the relevant medical knowledge provides the following prior information:
1. Gliomas often exhibit irregular shapes, while brain metastases tend to be relatively regular.
2. In terms of lesion locations, brain metastases are more likely to be located below the cortex, while gliomas are often found in the deep white matter.
To capitalize on this prior knowledge, we initially process Computed Tomography (CT) images using the You Only Look Once version 5 (YOLOv5) algorithm to segment the tumor regions. The tumor coordinates
A subset comprising 25% of the dataset, as delineated by YOLOv5, is employed to train the SVM model. The SVM takes the aspect ratio and the distance to the mass center as input, producing probabilities corresponding to gliomas and metastases. The output probabilities, ranging from 0 to 1, are adjusted using hyperparameters
3.2.2 The Algorithm Workflow of MAS-DSC
By initiating the process with the pre-training of an SVM classification model using a select proportion of samples, our novel MAS-DSC algorithm harmoniously blends this pre-training phase with the fine-tuning stages inherent to the DSC-Net algorithm. The procedural flow of the MAS-DSC algorithm is depicted in Fig. 3.

Figure 3: The algorithm flowchart of MAS-DSC
As illustrated in Fig. 3, we commence with the BrainTumor dataset, where 25% of the data is employed to train an SVM classifier, guided by predefined knowledge-based rules. This step is omitted for the standard dataset. Subsequently, we proceed to train the proposed multi-scale autoencoder. During this phase, a self-expression layer is integrated, which is then followed by a meticulous fine-tuning of the deep autoencoder. The culmination of this process involves the refinement of the hyperparameters within the deep clustering model, achieved through the application of a Bayesian optimization algorithm.
The loss function of MAS-DSC is as follows:
In the loss function, the autoencoder’s reconstruction loss is denoted by the first term, while the second and third terms encapsulate the loss associated with the self-expression layer. The fourth term represents the clustering loss function, which is introduced and informed by the SVM classifier. Given that deep subspace clustering algorithms do not inherently preserve the order relationship between the output clusters and the corresponding input images—since clustering is inherently a self-optimizing process—the semi-supervised approach employed in this study utilizes an SVM to infer the category probability based on the input images. We set hyperparameters
3.2.3 Bayesian Hyperparameter Optimization
The core of the MAS-DSC algorithm’s Bayesian optimization consists of two parts:
1. Gaussian Process Regression: It calculates the mean and variance of the function value at each point.
2. Acquisition Function Construction: Based on the mean and variance, it constructs an acquisition function to determine where to sample during this iteration.
The specific algorithm flow is shown in Algorithm 1.

3.2.4 Hyperparameter Descriptions
In response to the issue of manually setting hyperparameters in the DSC-Net algorithm, the MAS-DSC algorithm proposed in this paper introduces Bayesian optimization for hyperparameter tuning. The hyperparameters in this study are categorized into three types: hyperparameters for the loss function during model fine-tuning, hyperparameters for subspace clustering, and hyperparameters related to prior knowledge, as shown in Table 4.

In Table 4, in the loss function, the hyperparameters
As shown in Table 5, the hyperparameter ro represents the regularization term for subspace clustering. The parameter alpha is typically used to adjust or threshold the similarity matrix. The variable dim_space represents the dimensionality of the subspace after reduction, indicating the dimensionality of the subspace to which the data is reduced before performing spectral clustering.

As shown in Table 6, this paper sets the hyperparameters

To evaluate the clustering performance of the proposed method, experiments were conducted on three subspace tasks: a) Face Recognition (ORL), b) Object Clustering (COIL20 and COIL100), and c) Medical Image Clustering (a brain tumor classification dataset collected from a collaborative hospital). Among these, the clustering task on the face recognition dataset is relatively straightforward, as facial images approximately lie on the union of linear subspaces. However, the latter two tasks are more challenging due to their complex shapes, noise interference, and the presence of nonlinear relationships, making accurate representation in nonlinear subspaces more challenging.
The ORL dataset [49] consists of facial images from 40 different subjects, with 10 facial images per subject under different lighting conditions. Each subject’s facial images exhibit various facial expressions (open/closed eyes, smiling/non-smiling) and facial details (with/without glasses) [49]. The COIL-20 [50] dataset comprises 1440 toy images from 20 categories, while COIL-100 [50] includes 7200 images of 100 objects. In both databases, the shooting pose of each object varies at intervals of 5 degrees, resulting in a total of 72 images per object. As shown in Fig. 4.

Figure 4: Sample images from ORL, COIL20 and COIL100, BrainTumor
For medical image clustering, this paper utilized a brain tumor dataset collected from the Affiliated Changshu Hospital of Soochow University, which includes gliomas and brain metastases, as illustrated in Fig. 4. These two types of tumor diseases constitute approximately 70% of patients with brain tumors in the hospital. Due to the limited availability of datasets for other brain tumor diseases, we chose to concentrate on this larger and representative subset of data.
In this research, we acquired compressed T1-weighted Magnetic Resonance Imaging (MRI) images from 233 patients at our partner hospital, with the ethical committee’s approval. These images are saved in the Neuroimaging Informatics Technology Initiative (NII) format, where each file comprises 18 2D cross-sectional slices. To maintain data integrity, a manual screening was initially performed. Two seasoned neuroimaging specialists preliminarily examined the images, discarding any with motion or metal artifacts, or inconsistent signal intensities. Given that not all slices in a patient’s MRI sequence may exhibit tumor characteristics, we utilized Python’s nibabel library to access the 18 2D slices. We then meticulously selected the most diagnostically valuable slice for each patient, focusing on tumor clarity and contrast. This process, conducted by professional radiologists, resulted in a refined dataset of 140 2D slices each for gliomas and brain metastases.
These selected slices were then processed through YOLOv5 for precise extraction of the Regions of Interest (ROI). We meticulously documented the coordinate details of each tumor’s bounding box during detection and executed the necessary cropping. This meticulous curation culminated in the creation of the “BrainTumor” dataset, which is distinguished by its precise tumor localization and serves as a robust experimental basis for our study.
We use Clustering Accuracy (ACC) and Normalized Mutual Information (NMI) to evaluate the performance of the clustering algorithm. ACC is defined as the best match between true labels
where
NMI is defined as:
where
The MAS-DSC model is implemented in Python 3.7 using PyTorch 1.13, and the optimizer used is Adam [52]. For all experiments, the learning rate is initially set to
To validate the effectiveness of our proposed algorithm, we conducted ablation experiments on the ORL, COIL20, COIL100, and BrainTumor datasets to assess the impact of the three innovations in our approach: the multi-scale autoencoder network structure, the semi-supervised mechanism based on prior knowledge, and the Bayesian hyperparameter optimization algorithm. The results of the ablation study are shown in Table 7, with the best results highlighted in bold.

From the experimental results, we can draw the following conclusions: Using only the multi-scale autoencoder structure shows a significant improvement compared to the DSC-Net structure on each dataset, especially on the COIL100 dataset, where the clustering accuracy improves by approximately 5.67%. This indicates that the feature extraction capability of the multi-scale autoencoder network structure is stronger, leading to a significant enhancement in the performance of deep subspace clustering, especially on relatively complex datasets. After introducing the Bayesian hyperparameter optimization algorithm, our algorithm further improves accuracy (ACC) on the respective datasets, essentially reaching optimal results. For the BrainTumor dataset, our algorithm introduces a semi-supervised mechanism based on prior knowledge on top of the multi-scale autoencoder. The ACC metric improves by approximately 3.02%. This suggests that leveraging prior knowledge from medical experts can help the model obtain more discriminative feature representations.
As shown in Fig. 5, where NULL represents adopting DSC-Net, Multi-scale Deep Encoder-Decoder Architecture (MDEA) uses the multi-scale autoencoder structure, Semi-Supervised Prior Knowledge (SSPK) represents using the semi-supervised mechanism based on prior knowledge, and Bayesian Search (BS) indicates the use of Bayesian hyperparameter optimization. The figure intuitively reflects that the three innovations proposed in this work, namely the multi-scale autoencoder structure, Bayesian hyperparameter optimization, and the semi-supervised mechanism based on prior knowledge, have significantly improved the model accuracy on various datasets. This demonstrates the effectiveness of our work. This series of ablation experiments provides strong support for the innovations in our algorithm and offers important insights into enhancing the performance of deep clustering methods.
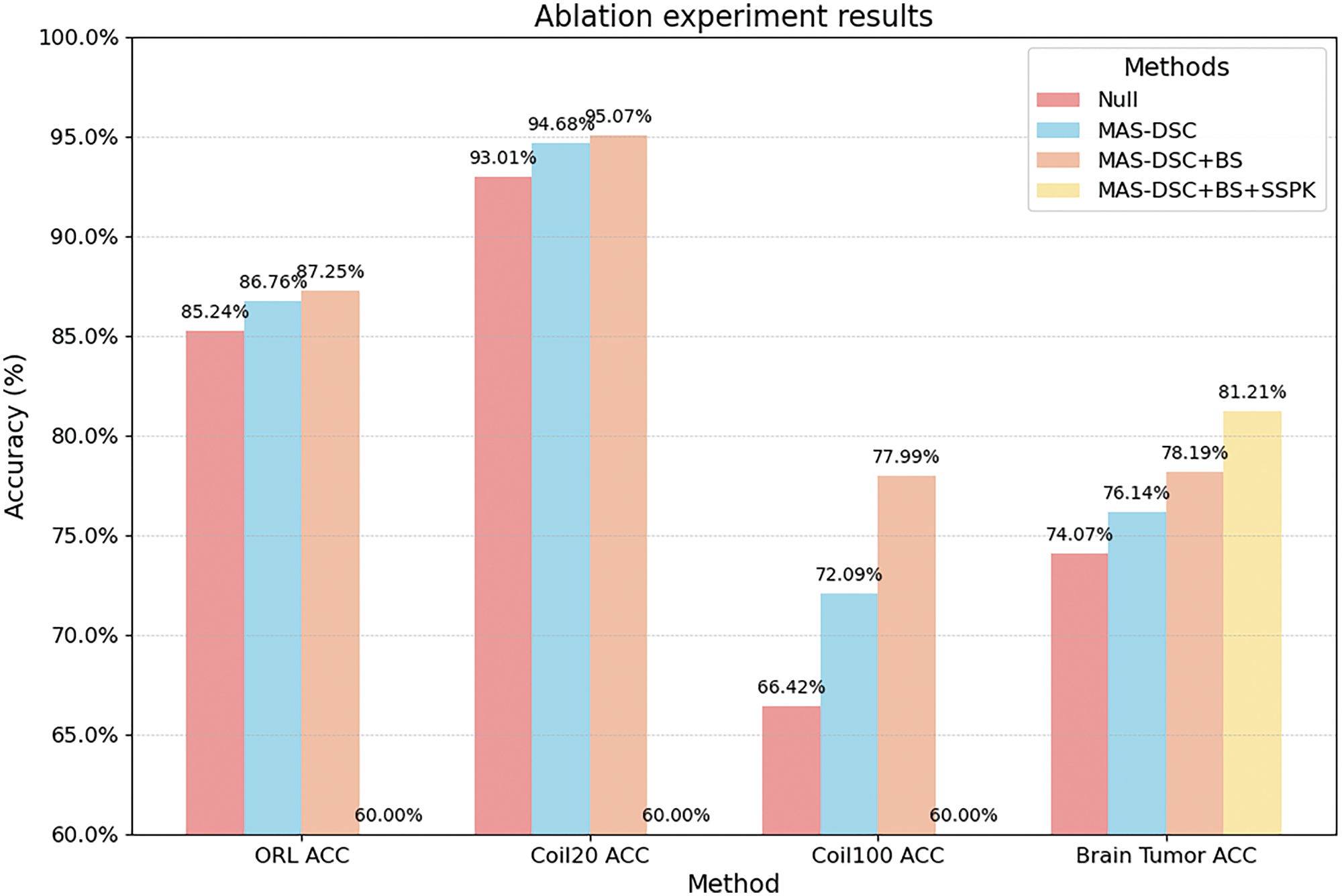
Figure 5: The ablation experiment result of MAS-DSC
We compared our method with both shallow and deep clustering techniques, including Low-Rank Representation (LRR) [23], Low-Rank Subspace Clustering (LRSC) [53], Sparse Subspace Clustering (SSC) [10], Kernel Sparse Subspace Clustering (KSSC) [54], Orthogonal Matching Pursuit for SSC (SSCOMP) [55], Efficient Dense Subspace Clustering (EDSC) [56], Deep Subspace Clustering Networks (DSCNet) [15], SSC with Pre-trained Convolutional Auto-Encoder (AE + SSC), EDSC with Pre-trained Convolutional Auto-Encoder (AE + EDSC), Deep Subspace Clustering Algorithm (DSCNet), and Deep Adversarial Subspace Clustering Algorithm (DASC) for EDSC, Synchronous Data Representation Learning and Subspace Clustering (DSC-L1) [57], Deep Self-Representative Subspace Clustering Network (DSRSC) [58], Pseudo-Supervised Deep Subspace Clustering (PSSC) [31], and Adaptive Attribute and Structure Subspace Clustering Network (AASSC-Net) [59]. The experimental results of the error rates for each algorithm on the respective datasets are presented in Table 8, with the best results highlighted in bold.

As shown in Table 8, our proposed algorithm achieves clustering error rates of 12.75% on the ORL dataset and 4.93% on the COIL20 dataset, performing well compared to the majority of algorithms. On the more challenging COIL100 dataset, our algorithm excels with an error rate of 22.91%, which stands as the best result among all the evaluated clustering algorithms. This indicates that our algorithm has an advantage in clustering complex datasets, primarily because the proposed multi-scale autoencoder can effectively extract features from complex datasets, thereby improving clustering performance.
Additionally, we have replicated the DSC-Net and DASC algorithms on the BrainTumor dataset, with their respective clustering error rates being 25.6%, 23.7%, and 21.3%. In contrast, our algorithm achieved the best result on the BrainTumor dataset with an error rate of 18.79%. These experimental results suggest that our structural advantages and the semi-supervised mechanism based on prior knowledge can effectively enhance clustering performance when dealing with medical image datasets.
4.6.1 MAS-DSC Convergence Analysis
To validate the convergence of the proposed method, a series of experiments were conducted on the ORL, COIL20, COIL100, and BrainTumor datasets. The experimental results are depicted in Fig. 6. On the ORL dataset, our model reaches convergence after 100 fine-tuning iterations, achieving a clustering accuracy of approximately 87%. On the COIL20 dataset, the model attains a 95% accuracy after 50 fine-tuning iterations. For the COIL100 dataset, the model converges around 80 iterations during the fine-tuning phase, reaching an accuracy of about 77%. These results collectively demonstrate the excellent convergence of the proposed multi-scale network structure. To verify the convergence of the proposed semi-supervised method based on prior knowledge, validation experiments were conducted on the BrainTumor dataset. The experimental results indicate that the model reaches convergence after approximately 120 fine-tuning iterations, stabilizing at a clustering accuracy of around 81%. Thus, experimental evidence confirms that the proposed semi-supervised method based on prior knowledge exhibits good convergence.

Figure 6: Convergence analysis on ORL, COIL20, COIL100, BrainTumor
4.6.2 Convergence Analysis of Bayesian Hyperparameter Tuning
In this study, Bayesian optimization is employed for hyperparameter optimization. To demonstrate the convergence of the Bayesian optimization algorithm, we conducted five independent random experiments on the BrainTumor dataset. The experimental results are illustrated in Fig. 7. At the beginning of the model fine-tuning phase, the model’s clustering accuracy from random search is relatively poor. However, as the Bayesian optimization algorithm iterates, the corresponding model’s clustering accuracy continuously improves, and the model converges around 20 iterations of the Bayesian algorithm. Due to limitations in Graphics Processing Unit (GPU) resources, the optimal parameters obtained by the Bayesian algorithm might be a local optimum. Nevertheless, compared to the manually designed hyperparameters in DSC-Net, the corresponding results have shown a significant improvement. The optimal hyperparameter results obtained using Bayesian hyperparameter optimization algorithm are presented in Table 9.

Figure 7: Convergence analysis of MAS-DSC algorithm based on bayesian optimization algorithm

This study introduces a semi-supervised deep subspace clustering algorithm that improves upon the feature extraction limitations of existing deep clustering methods, particularly in the context of brain tumor differentiation. By integrating a multi-scale network structure with automated hyperparameter tuning through Bayesian optimization, the algorithm enhances feature representation and learning robustness. The model incorporates expert medical knowledge as constraint losses, which proves beneficial for the accuracy of medical image clustering. The effectiveness of the proposed method is confirmed through experiments on standard datasets and a brain tumor dataset from a partner hospital. The results, supported by ablation studies and comparative analyses, demonstrate the superior performance of our algorithm in accurately clustering brain tumors.
Acknowledgement: None.
Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant 62171203; in part by the Jiangsu Province “333 Project” High-Level Talent Cultivation Subsidized Project; in part by the Suzhou Key Supporting Subjects for Health Informatics under Grant SZFCXK202147; in part by the Changshu Science and Technology Program under Grants CS202015 and CS202246; and in part by Changshu Key Laboratory of Medical Artificial Intelligence and Big Data under Grants CYZ202301 and CS202314.
Author Contributions: Zhenyu Qian: Contributed to the writing of the paper, performed results analysis, and implemented the code. Yizhang Jiang: Formulated the research problem, designed the experimental plan, and provided guidance throughout the study. Zhou Hong: Executed experiments and implemented the code for the experimental part. Lijun Huang: Collected and organized experimental data and data annotation. Fengda Li: Contributed to the collection and organization of experimental data and data annotation. KhinWee Lai: Provided experimental guidance for the paper and contributed to the refinement of the manuscript. Kaijian Xia: Offered guidance in the experiments and contributed to the refinement of the manuscript. All authors reviewed the manuscript.
Availability of Data and Materials: If need the data in the paper, please contact the corresponding author, KhinWee Lai.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. W. Liu, I. W. Tsang, and M. Klaus-Robert, “An easy-to-hard learning paradigm for multiple classes and multiple labels,” J. Mach. Learn. Res., vol. 18, no. 94, pp. 1–38, Sep. 2017. [Google Scholar]
2. Z. Wang, B. Huang, G. Wang, P. Yi, and K. Jiang, “Masked face recognition dataset and application,” IEEE Trans. Biom. Behav. Identity Sci., vol. 5, no. 2, pp. 298–304, Apr. 2023. doi: 10.1109/TBIOM.2023.3242085. [Google Scholar] [CrossRef]
3. J. Guo, X. Zhu, C. Zhao, D. Cao, Z. Lei and S. Z. Li, “Learning meta face recognition in unseen domains,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, Jun. 13–19, 2020, pp. 6163–6172. [Google Scholar]
4. G. Xu, Y. Meng, X. Qiu, Z. Yu, and X. Wu, “Sentiment analysis of comment texts based on BiLSTM,” IEEE Access, vol. 7, pp. 51522–51532, Apr. 2019. doi: 10.1109/ACCESS.2019.2909919. [Google Scholar] [CrossRef]
5. A. Y. Yang, J. Wright, Y. Ma, and S. S. Sastry, “Unsupervised segmentation of natural images via lossy data compression,” Comput. Vis. Image Und., vol. 110, no. 2, pp. 212–225, May 2008. doi: 10.1016/j.cviu.2007.07.005. [Google Scholar] [CrossRef]
6. Y. Ma, H. Derksen, W. Hong, and J. Wright, “Segmentation of multivariate mixed data via lossy data coding and compression,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 29, no. 9, pp. 1546–1562, Sep. 2007. doi: 10.1109/TPAMI.2007.1085. [Google Scholar] [PubMed] [CrossRef]
7. K. Kanatani, “Motion segmentation by subspace separation and model selection,” in Proc. 8th IEEE Int. Conf. Comput. Vis., Vancouver, BC, Canada, Jul. 7–14, 2001, pp. 586–591. [Google Scholar]
8. E. E. R. Vidal, “Sparse subspace clustering,” in Proc. 2009 IEEE Conf. Comput. Vis. Pattern Recognit., Miami, FL, USA, Jun. 20–25, 2009, pp. 2790–2797. [Google Scholar]
9. J. Ho, M. H. Yang, J. Lim, K. C. Lee, and D. Kriegman, “Clustering appearances of objects under varying illumination conditions,” in Proc. 2003 IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Madison, WI, USA, Jun. 18–20, 2003, pp. 11–18. [Google Scholar]
10. E. Elhamifar and R. Vidal, “Sparse subspace clustering: Algorithm, theory, and applications,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 35, no. 11, pp. 2765–2781, Nov. 2013. doi: 10.1109/TPAMI.2013.57. [Google Scholar] [PubMed] [CrossRef]
11. J. Xie, R. Girshick, and A. Farhadi, “Unsupervised deep embedding for clustering analysis,” in Proc. 33rd Int. Conf. Mach. Learn., New York, NY, USA, Jun. 19–24, 2016, pp. 478–487. [Google Scholar]
12. F. Li, H. Qiao, and B. Zhang, “Discriminatively boosted image clustering with fully convolutional auto-encoders,” Pattern Recogn., vol. 83, no. 8, pp. 161–173, Nov. 2018. doi: 10.1016/j.patcog.2018.05.019. [Google Scholar] [CrossRef]
13. K. G. Dizaji, A. Herandi, C. Deng, W. Cai, and H. Huang, “Deep clustering via joint convolutional autoencoder embedding and relative entropy minimization,” in Proc. 2017 IEEE Int. Conf. Comput. Vis., Venice, Italy, Oct. 22–29, 2017, pp. 5736–5745. [Google Scholar]
14. C. C. Hsu and C. W. Lin, “CNN-based joint clustering and representation learning with feature drift compensation for large-scale image data,” IEEE Trans. Multimedia., vol. 20, no. 2, pp. 421–429, Feb. 2018. doi: 10.1109/TMM.2017.2745702. [Google Scholar] [CrossRef]
15. P. Ji, T. Zhang, H. Li, M. Salzmann, and I. Reid, “Deep subspace clustering networks,” in Proc. 31st Int. Conf. Neural Inf. Process. Syst., Long Beach, CA, USA, Dec. 4–9, 2017, pp. 23–32. [Google Scholar]
16. Q. T. Ostrom, G. Cioffi, K. Waite, C. Kruchko, and J. S. Barnholtz-Sloan, “CBTRUS statistical report: Primary brain and other central nervous system tumors diagnosed in the United States in 2014–2018,” Neuro. Oncol., vol. 23, no. Suppl 3, pp. iii1–iii105, Oct. 2021. doi: 10.1093/neuonc/noab200. [Google Scholar] [PubMed] [CrossRef]
17. S. Bijari, A. Jahanbakhshi, P. Hajishafiezahramini, and P. Abdolmaleki, “Differentiating glioblastoma multiforme from brain metastases using multidimensional radiomics features derived from MRI and multiple machine learning models,” Biomed Res. Int., vol. 2022, pp. 2016006, Sep. 2022. doi: 10.1155/2022/2016006. [Google Scholar] [PubMed] [CrossRef]
18. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proc. 2016 IEEE Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, Jun. 27–30, 2016, pp. 770–778. [Google Scholar]
19. C. Szegedy et al., “Going deeper with convolutions,” in Proc. 2015 IEEE Conf. Comput. Vis. Pattern Recognit., Boston, MA, USA, Jun. 7–12, 2015, pp. 1–9. [Google Scholar]
20. Y. Ren et al., “Deep clustering: A comprehensive survey,” 2022. Accessed: April 17, 2024. [Online]. Available: https://arxiv.org/pdf/2210.04142.pdf [Google Scholar]
21. X. Lin and L. M. DeAngelis, “Treatment of brain metastases,” J. Clin. Oncol., vol. 33, no. 30, pp. 3475–3484, Oct. 2015. doi: 10.1200/JCO.2015.60.9503. [Google Scholar] [PubMed] [CrossRef]
22. M. Weller et al., “European Association for Neuro-Oncology (EANO) guideline on the diagnosis and treatment of adult astrocytic and oligodendroglial gliomas,” Lancet Oncol., vol. 18, no. 6, pp. e315–e329, Jun. 2017. doi: 10.1016/S1470-2045(17)30194-8. [Google Scholar] [PubMed] [CrossRef]
23. G. Liu, Z. Lin, S. Yan, J. Sun, Y. Yu and Y. Ma, “Robust recovery of subspace structures by low-rank representation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 35, no. 1, pp. 171–184, Jan. 2013. doi: 10.1109/TPAMI.2012.88. [Google Scholar] [PubMed] [CrossRef]
24. C. G. Li and R. Vidal, “Structured sparse subspace clustering: A unified optimization framework,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Boston, MA, USA, Jun. 7–12, 2015, pp. 277–286. [Google Scholar]
25. L. Parsons, E. Haque, and H. Liu, “Subspace clustering for high dimensional data: A review,” ACM SIGKDD Explor. Newsl., vol. 6, no. 1, pp. 90–105, Jun. 2004. doi: 10.1145/1007730.1007731. [Google Scholar] [CrossRef]
26. B. Yang, X. Fu, N. D. Sidiropoulos, and M. Hong, “Towards K-means-friendly spaces: Simultaneous deep learning and clustering,” in Proc. 34th Int. Conf. Mach. Learn., Sydney, NSW, Australia, Aug. 6–11, 2017, pp. 3861–3870. [Google Scholar]
27. C. Song, Y. Huang, F. Liu, Z. Wang, and L. Wang, “Deep auto-encoder based clustering,” Intell. Data Anal., vol. 18, no. 6S, pp. S65–S76, Jan. 2014. doi: 10.3233/IDA-140709. [Google Scholar] [CrossRef]
28. Y. Sun, X. Wang, D. Peng, Z. Ren, and X. Shen, “Hierarchical hashing learning for image set classification,” IEEE Trans. Image Process., vol. 32, pp. 1732–1744, Mar. 2023. doi: 10.1109/TIP.2023.3251025. [Google Scholar] [PubMed] [CrossRef]
29. J. Lv, Z. Kang, X. Lu, and Z. Xu, “Pseudo-supervised deep subspace clustering,” IEEE Trans. Image Process., vol. 30, pp. 5252–5263, May 2021. doi: 10.1109/TIP.2021.3079800. [Google Scholar] [PubMed] [CrossRef]
30. X. Li, Y. Sun, Q. Sun, Z. Ren, and Y. Sun, “Cross-view graph matching guided anchor alignment for incomplete multi-view clustering,” Inform. Fusion., vol. 100, no. 1, pp. 101941, Dec. 2023. doi: 10.1016/j.inffus.2023.101941. [Google Scholar] [CrossRef]
31. F. Soleymani, M. Eslami, T. Elze, B. Bischl, and M. Rezaei, “Deep variational clustering framework for self-labeling large-scale medical images,” in Proc. SPIE Med. Imaging 2022: Image Process., San Diego, CA, USA, Feb. 20–24, 2022, pp. 68–76. [Google Scholar]
32. R. Guan, X. Wang, M. Marchese, Y. Liang, and C. Yang, “A feature space learning model based on semi-supervised clustering,” in Proc. 2017 IEEE Int. Conf. Comput. Sci. Eng. (CSE) IEEE Int. Conf. Embed. Ubiquit. Comput. (EUC), Guangzhou, China, Jul. 21–24, 2017, pp. 403–409. [Google Scholar]
33. Z. Kang, X. Lu, J. Yi, and Z. Xu, “Self-weighted multiple kernel learning for graph-based clustering and semi-supervised classification,” in Proc. 27th Int. Joint Conf. Artif. Intell., Stockholm, Sweden, Jul. 13–19, 2018, pp. 2312–2318. [Google Scholar]
34. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Proc. 3rd Int. Conf. Learn. Represent, San Diego, CA, USA, May 7–9, 2015, pp. 1–14. [Google Scholar]
35. C. Szegedy, V. Vanhoucke, S. Ioffe, J. Shlens, and Z. Wojna, “Rethinking the inception architecture for computer vision,” in Proc. 2016 IEEE Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, Jun. 27–30, 2016, pp. 2818–2826. [Google Scholar]
36. H. E. Kim, A. Cosa-Linan, N. Santhanam, M. Jannesari, M. E. Maros and T. Ganslandt, “Transfer learning for medical image classification: A literature review,” BMC Med. Imag., vol. 22, no. 1, pp. 69, Apr. 2022. doi: 10.1186/s12880-022-00793-7. [Google Scholar] [PubMed] [CrossRef]
37. D. Lu, K. Popuri, G. W. Ding, R. Balachandar, and M. F. Beg, “Multimodal and multiscale deep neural networks for the early diagnosis of Alzheimer’s disease using structural MR and FDG-PET images,” Sci. Rep., vol. 8, no. 1, pp. 5697, Apr. 2018. doi: 10.1038/s41598-018-22871-z. [Google Scholar] [PubMed] [CrossRef]
38. R. K. Srivastava, K. Greff, and J. Schmidhuber, “Highway networks,” 2015. Accessed: Apr. 18, 2024. [Online]. Available: https://arxiv.org/pdf/1505.00387.pdf [Google Scholar]
39. W. Xu, Y. L. Fu, and D. Zhu, “ResNet and its application to medical image processing: Research progress and challenges,” Comput. Methods Programs Biomed., vol. 240, no. 9, pp. 107660, Oct. 2023. doi: 10.1016/j.cmpb.2023.107660. [Google Scholar] [PubMed] [CrossRef]
40. G. Huang, Z. Liu, L. van der Maaten, and K. Q. Weinberger, “Densely connected convolutional networks,” in Proc. 2017 IEEE Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, Jul. 21–26, 2017, pp. 4700–4708. [Google Scholar]
41. J. Rubin, S. Parvaneh, A. Rahman, B. Conroy, and S. Babaeizadeh, “Densely connected convolutional networks for detection of atrial fibrillation from short single-lead ECG recordings,” J. Electrocardiol., vol. 51, no. 6S, pp. S18–S21, Nov.–Dec. 2018. doi: 10.1016/j.jelectrocard.2018.08.008. [Google Scholar] [PubMed] [CrossRef]
42. P. Kuang, T. Ma, Z. Chen, and F. Li, “Image super-resolution with densely connected convolutional networks,” Appl. Intell., vol. 49, no. 1, pp. 125–136, Jan. 2019. doi: 10.1007/s10489-018-1234-y. [Google Scholar] [CrossRef]
43. Y. Bao and Z. Liu, “A fast grid search method in support vector regression forecasting time series,” in Proc. 7th Int. Conf. Intell. Data Eng. Autom. Learn., Burgos, Spain, Sept. 20–23, 2006, pp. 504–511. [Google Scholar]
44. J. Bergstra and Y. Bengio, “Random search for hyper-parameter optimization,” J. Mach. Learn. Res., vol. 13, pp. 281–305, Feb. 2012. doi: 10.5555/2503308.2188395. [Google Scholar] [CrossRef]
45. Y. Liu, X. Yao, and T. Higuchi, “Evolutionary ensembles with negative correlation learning,” IEEE Trans. Evol. Comput., vol. 4, no. 4, pp. 380–387, Nov. 2000. doi: 10.1109/4235.887237. [Google Scholar] [CrossRef]
46. S. Hansen, “Using deep Q-learning to control optimization hyperparameters,” 2016. Accessed: Apr. 18, 2024. [Online]. Available: https://arxiv.org/pdf/1602.04062.pdf [Google Scholar]
47. J. Bergstra, R. Bardenet, Y. Bengio, and B. Kégl, “Algorithms for hyper-parameter optimization,” in Proc. 24th Int. Conf. Neural Inf. Process. Syst., Granada, Spain, Dec. 12–15, 2011, pp. 2546–2554. [Google Scholar]
48. S. Toscano-Palmerin and P. I. Frazier, “Bayesian optimization with expensive integrands,” SIAM J. Optim., vol. 32, no. 2, pp. 417–444, Jan. 2022. doi: 10.1137/19M1303125. [Google Scholar] [CrossRef]
49. F. S. Samaria and A. C. Harter, “Parameterisation of a stochastic model for human face identification,” in Proc. 1994 IEEE Workshop Appl. Comput. Vis., Sarasota, FL, USA, Dec. 5–7, 1994, pp. 138–142. [Google Scholar]
50. S. A. Nene, S. K. Nayar, and H. Murase, “Columbia object image library (COIL-20),” Technical Report No. CUCS-006-96, New York, NY, USA: Columbia Univ, 1996. [Google Scholar]
51. H. W. Kuhn, “The Hungarian method for the assignment problem,” Nav. Res. Logist. Quart., vol. 2, no. 1–2, pp. 83–97, Mar. 1955. doi: 10.1002/nav.3800020109. [Google Scholar] [CrossRef]
52. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” 2014. Accessed: April 18, 2024. [Online]. Available: https://arxiv.org/pdf/1412.6980.pdf [Google Scholar]
53. R. Vidal and P. Favaro, “Low rank subspace clustering (LRSC),” Pattern Recognit. Lett., vol. 43, no. 3, pp. 47–61, Jul. 2014. doi: 10.1016/j.patrec.2013.08.006. [Google Scholar] [CrossRef]
54. V. M. Patel and R. Vidal, “Kernel sparse subspace clustering,” in Proc. 2014 IEEE Int. Conf. Image Process., Paris, France, Oct. 27–30, 2014, pp. 2849–2853. [Google Scholar]
55. C. You, D. Robinson, and R. Vidal, “Scalable sparse subspace clustering by orthogonal matching pursuit,” in Proc. 2016 IEEE Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, Jun. 27–30, 2016, pp. 3918–3927. [Google Scholar]
56. P. Ji, M. Salzmann, and H. Li, “Efficient dense subspace clustering,” in Proc. 2014 IEEE Winter Conf. Appl. Comput. Vis., Steamboat Springs, CO, USA, Mar. 24–26, 2014, pp. 461–468. [Google Scholar]
57. X. Peng, J. Feng, J. T. Zhou, Y. Lei, and S. Yan, “Deep subspace clustering,” IEEE Trans. Neural Netw. Learn. Syst., vol. 31, no. 12, pp. 5509–5521, Dec. 2020. doi: 10.1109/TNNLS.2020.2968848. [Google Scholar] [PubMed] [CrossRef]
58. S. Baek, G. Yoon, J. Song, and S. M. Yoon, “Deep self-representative subspace clustering network,” Pattern Recognit., vol. 118, no. 490, pp. 108041, Oct. 2021. doi: 10.1016/j.patcog.2021.108041. [Google Scholar] [CrossRef]
59. Z. Peng, H. Liu, Y. Jia, and J. Hou, “Adaptive attribute and structure subspace clustering network,” IEEE Trans. Image Process., vol. 31, pp. 3430–3439, May 2022. doi: 10.1109/TIP.2022.3171421. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools