Modeling and Analysis of OFDMA-NOMA-RA Protocol Considering Imperfect SIC in Multi-User Uplink WLANs

1  Introduction

With the growth of the internet of things (IoT), many wireless devices access the network. Each device initializes the uplink through random access (RA) to establish communication with the base station, as in the work of Hasan et al. [1,2]. However, as the number of access users in the network continues to increase, a large number of devices try to access the base station in a relatively short time. This results in the probability of collision in the whole system becomes larger, and the probability of successfully accessing the channel decreases dramatically, ultimately leading to a decrease in spectrum utilization efficiency, as described by Zhen et al. [3]. Today, improving spectrum utilization efficiency and alleviating congestion are considered to be some of the most urgent requirements in large-scale 5G networks, as noted by Xu et al. [4]. Thus, it is necessary to break the traditional RA model and design a new large-scale RA scheme.

In large-scale communication scenarios, orthogonal frequency division multiple access (OFDMA) technology is currently widely used. By dividing the spectrum resources into multiple orthogonal and non-overlapping subcarrier blocks, these subcarrier blocks are then dynamically allocated to users, achieving multiple users to access and transmit data on the channel simultaneously. For example, Chen et al. [5] improve the throughput in density scenarios by using the characteristics of multi-user uplink OFDMA random access (UORA). Zhou et al. [6,7] propose a DRA-OFDMA protocol which allows users who failed to compete to re-access the unused free spectrum, thus the spectrum resources are utilized and the collision probability is reduced. Fan et al. [8] propose a new UORA access protocol based on IEEE 802.11ax. This protocol improves throughput and reduces packet delay by considering the number of retransmissions, the number of RUs, and the number of STAs to decide whether to double its OCW size. However, OFDMA technology also faces some challenges, as Anand et al. [9] described. For example, with the rapid development of mobile internet and wireless communication, the current communication environment is becoming increasingly complex, and the number of users needing to access the wireless communication network is increasing. However, the number of users cannot exceed the number of available orthogonal channels in the OFDMA scheme, which restricts the improvement of communication quality.

Unlike OFDMA, non-orthogonal multiple access (NOMA) can allocate the same resource to multiple users, like in the work of Li et al. [10,11]. The transmitter employs superposition coding and allocates different power to the users. The receiver then decodes the strong user signal using successive interference cancellation (SIC) technology (other user’s signals are considered interference), as noted by Anand et al. [12]. The decoded user’s signal is removed from the aliasing signal and the weak user’s signal is decoded, which enables more users to access the spectrum resources. Due to the possibility of decoding errors, Luo et al. [13] analyze the performance of the NOMA system in the case of imperfect SIC and evaluate the influence of imperfect SIC coefficients on outage probability and throughput. However, multiple users sharing the same spectrum resource in the system will increase decoding complexity at the receiving end. This is because when the receiver decodes the information of one user, it must first decode the information of the user who has a higher power than the user. In addition, with NOMA superposition coding, there is interference between the signals of different users, which will significantly degrade the outage performance of the system when the number of users is too high. The combination of NOMA and OFDMA technology provides the possibility to overcome the complexity of SIC decoding at the receiver and improve the interrupt performance, which is conducted by Bany Salameh et al. [14]. This is because the available transmission bandwidth provided by OFDMA is divided into multiple orthogonal subchannels to avoid co-channel interference in hybrid OFDMA-NOMA systems. Within the subchannels, more than one user can be served on each channel. This is achieved using the power domain multiplexing provided by NOMA. Therefore, the combination of OFDMA and NOMA enables the multiplexing of both the power domain and the frequency domain, which is expected to further improve the spectrum utilization efficiency and support large-scale transmission, as described by Tang et al. [15,16].

Recently, some literature has studied the potential capability of hybrid OFDMA-NOMA. For example, Rezvani et al. [17] propose a globally optimal power allocation strategy for downlink OFDMA-NOMA systems to maximize the sum rate of the users and the system’s energy efficiency. In this system, users are divided into NOMA clusters, and users within each cluster adopt superposition coding and SIC technology, while users between different clusters transmit on orthogonal subcarriers. A hybrid OFDMA/NOMA transmission scheme is proposed by Guo et al. [18]. The scheme multiplexes multiple subunits through OFDMA to avoid performance degradation due to cochannel interference in NOMA systems. In addition, NOMA significantly improves spectrum efficiency by allowing multiple users to share the spectrum within the same cell. In order to alleviate random access congestion for machine-based communication and to support massive connectivity with lower energy consumption in 5G cellular networks, a massive resource allocation scheme based on NOMA-OFDMA has been proposed by Wu et al. [19]. Tseng et al. [20] add NOMA to the downlink OFDMA video transmission system, and it is proposed to allocate the power to the users on each subcarrier to minimize the sum of the mean square errors, thus improving the peak signal-to-noise ratio and ultimately improve the video quality. A resource allocation scheme based on OFDMA-NOMA is proposed by Hadi et al. [21]. The resource allocation problem is formulated as a non-convex NP-hard optimization problem, which jointly designs subchannel allocation and power allocation to maximize the sum rate. Tutelian et al. [22] consider the joint use of OFDMA and NOMA for uplink transmission in Wi-Fi 6 networks, and the problem of optimal allocation of radio resources among users is posed to maximize some utility functions (such as geometric mean throughput). Promponas et al. [23] design three resource allocation schemes based on game theory principles using OFDMA and NOMA technologies to maximize individual user utility, maximize system utility, and guarantee minimum quality of service (QoS) for users, respectively.

1.1 Motivation and Contribution

Most of the above studies of hybrid OFDMA-NOMA systems were analyzed in the case of perfect SIC. However, hardware damage and decoding errors exist in the communication environment. It motivates the necessity to analyze the performance of OFDMA-NOMA in imperfect SIC. In addition, the research on hybrid OFDMA-NOMA systems mainly focus on the theoretical analysis of resource allocation schemes and power allocation strategies during data transmission, and few studies consider the problems of network congestion and low utilization of spectrum resources. Inspired by Zhou et al. [6], this paper proposes a random access (OFDMA-NOMA-RA) protocol combining OFDMA and NOMA to alleviate access congestion and low spectrum utilization. Different from Zhou et al. [6], we not only let the collision users compete again for the remaining subchannels but also combine OFDMA and NOMA, which breaks the limitation that a subchannel can serve only one user in the work of Zhou et al. [6]. The key idea of the protocol in this paper is: OFDMA divides the entire bandwidth into multiple subchannels, and multiple users can access and transmit data on the same subchannels through the NOMA scheme. In addition, the users who fail to compete can compete again for the remaining subchannels to get a transmission opportunity. Thereby, this paper achieves the research objectives of reducing network congestion and improving spectrum resource utilization under imperfect SIC cases in multi-user networks. The main contributions of this paper are as follows:

•   A new OFDMA-NOMA-RA protocol is proposed for multi-user uplink WLAN. The protocol alleviates access congestion and wastage of spectrum resources by allowing users to compete for the remaining subchannels. In addition, the subchannels are orthogonal to avoid cochannel interference, and the NOMA principle is used to superimpose the signals within the subchannels, which enables multiple users to share the same spectrum resource and improves spectrum efficiency.

•   Based on the proposed protocol and system, the probability of successfully competing subchannels is derived in the cases of users occupying the subchannel individually and users sharing the subchannel, and the outage probability and throughput are derived in the case of imperfect SIC. In addition, an optimal power allocation algorithm is proposed based on a closed expression for the outage probability, which provides a power allocation scheme to minimize the outage probability.

•   To illustrate the superiority of OFDMA-NOMA-RA, this paper derives the probability of successfully competing subchannels and the outage probability of pure OFDMA and NOMA systems respectively. Thus, the system throughput expressions for pure OFDMA and NOMA are obtained.

•   We verify the performance of OFDMA-NOMA-RA by numerical analysis. The influence of transmission power on the outage probability and the optimal power for the different users are shown. The effect of imperfect SIC coefficients on interrupt performance is revealed, and numerical results show that OFDMA-NOMA-RA consistently outperforms ODFMA and NOMA when the imperfect SIC coefficients are less than a specific value.

1.2 Organization

The rest of this paper is organized as follows: Section 2 introduces the system model and describes the details of the designed protocol. Section 3 derives the probability of successfully competing subchannels, outage probability, and system throughput based on the designed protocol and system. Furthermore, the optimal power allocation algorithm is provided. The system throughput expressions of pure OFDMA and NOMA are given in Section 4. In Section 5, we present numerical results to verify the performance analysis. Finally, we conclude the work of this paper in Section 6.

2  System Model and Protocol Design

To overcome the shortcomings of OFDMA and NOMA, this paper combines OFDMA and NOMA, using OFDMA between subchannels and NOMA within subchannels. This allows multiple users to share the same subchannel and avoids outage performance degradation due to cochannel interference and SIC complexity, as shown in Fig. 1. In addition, the combination of OFDMA and NOMA not only increases the number of users who access subchannel, but also alleviates the scarcity of spectrum resources.

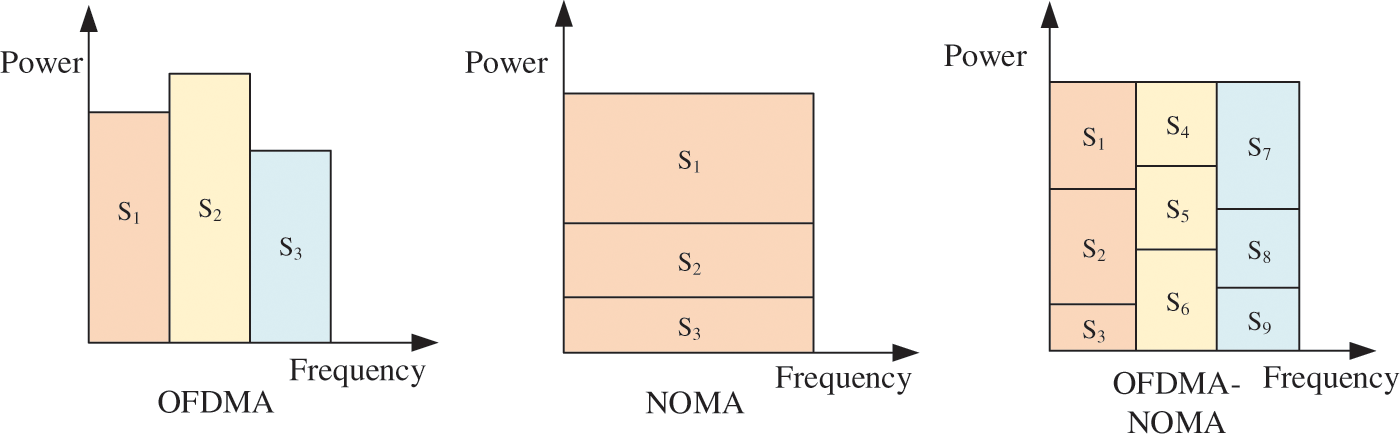
Figure 1: Comparison of the spectrum utilization of OFDMA, NOMA, OFDMA-NOMA

This paper considers the uplink OFDMA-NOMA system in a Basic Service Set (BSS) to analyze and optimize system performance. As shown in Fig. 2, the system consists of a receiver AP and K users, and the set of users is denoted by 𝒦={1,⋯,K}. Each user is equipped with an antenna and operates in half-duplex mode. The total bandwidth W(Hz) is divided into N orthogonal subchannels, and the set of subchannels is denoted by 𝒩={1,⋯,N}, where the bandwidth of each subchannel is Ws=WN. The NOMA is used within each subchannel to transmit signals and the maximum number of multiplexed users is Umax. The set of multiplexed users on subchannel n is denoted by 𝒦n={k∈𝒦|ξnk=1}, where ξnk is the subchannel assignment indication symbol, and we set ξnk=1 if user k occupies subchannel n, otherwise, ξnk=0. To analysis easier, we assume that each subchannel is used by at most two users simultaneously, i.e., Umax=2. Thus, we have |𝒦n|≤2.

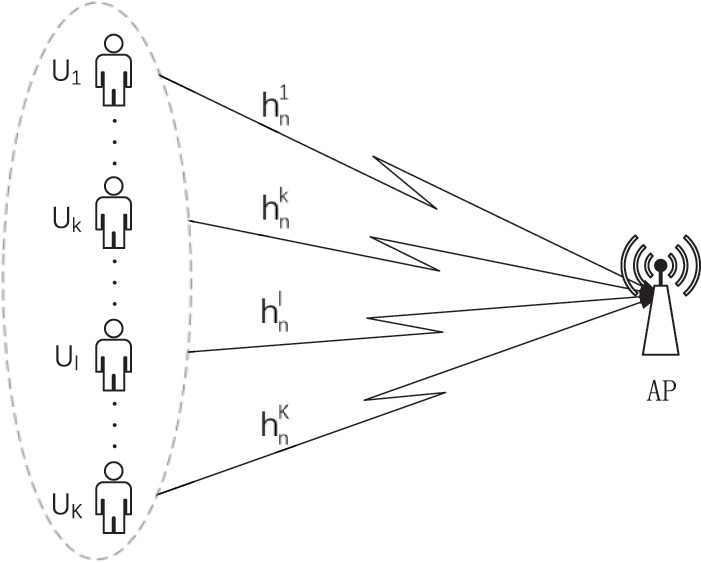
Figure 2: System model for multi-user uplink transmission

Assuming that all subchannels have additive Gaussian white noise (AWGN) with mean 0 and variance σnk. Let hnk denotes the channel coefficients from user k to the AP on subchannel n, n∈𝒩 and k∈𝒦. Then hnk is modeled as a circularly symmetric complex Gaussian random variable with mean 0 and variance λnk. Therefore, the channel gain |hnk|2 follows an exponential distribution with parameter 1/λnk. Without loss of generality, the channel gain for each user is ordered as |hn1|2≤⋯≤|hnk|2≤⋯|hnl|2≤⋯≤|hnK|2, where n∈𝒩.

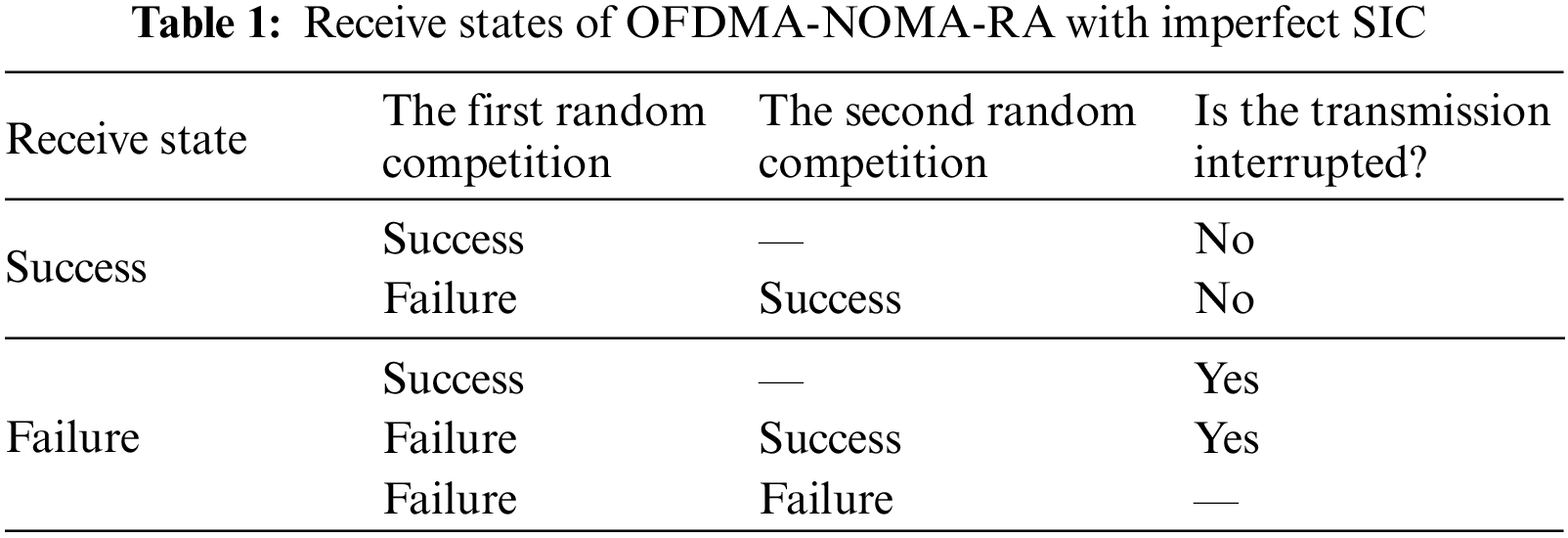
Based on the ideas of Zhou et al. [6], this paper proposes an OFDMA-NOMA-RA protocol in the uplink for the considering system. The protocol adopts two random accesses to compete for the subchannels. The first random access is a fair competition for the subchannels to get the transmission opportunity. Due to the combination of NOMA and OFDMA, a subchannel can be used by two users simultaneously. If the number of users competing for the same subchannel is less than or equal to two, the users compete successfully. Then, the users transmit according to the power and subchannel indicated by the controlling information. When the number of users exceeds 2, the users fail to compete in the subchannel. Therefore, some subchannels may not be used. To fully utilize these remaining subchannels, we allow the users who failed in completion to compete again for these remaining subchannels. Similarly, these remaining subchannels can serve two users at the same time. In addition, users who have successfully competed may be unable to transmit data due to factors such as damaged hardware or decoding errors. Table 1 shows the possible cases of the whole transmission process. If at least one of the two random contentions succeeds and the transmission is not interrupted, the receiver can receive the user’s message correctly.

3  Performance Modeling Analysis

Since the competition is random and the subchannel may be used by one user or shared by two users, this section derives the probability of successfully competing and the outage probability in two random competitions under two conditions of |𝒦n|=1 and |𝒦n|=2. In addition, optimal power allocation and throughput analysis are also considered.

3.1 The First Random Competition

Since the backoff period is required before random competition, and the backoff mechanism is not the focus of this paper, the OBF backoff mechanism is adopted directly, and the specific details are obtained from Xie et al. [24]. We can obtain the probability of data transmission by Eq. (7) from Xie et al. [24].

τ=[∑i=0m−1pi(∑r=1Wi−1Wi−rNWi+1)+pm1−p(∑r=1Wm−1Wi−rNWi+1)]−11−p,(1)

where p is the collision probability, Wi is the value of the competition window, and m is the maximum backoff state.

We can find that τ is dependent on p, which is also uncertain. To find the value of τ, we derive the expression of p. From the protocol designed in Section 2, the collision occurs when the number of users competing for the same subchannel exceeds 2, thus we have:

p=1−(1−τN)K−2.(2)

The probability that a subchannel is selected by at least one of users is as follows:

ptr,1=1−(1−τN)K.(3)

The probability that a subchannel is selected by only one user is pc1=KτN(1−τN)K−1. The probability that a subchannel is selected by two users at the same time is pc2=K(K−1)2(τN)2(1−τN)K−2. Thus, the probability that the user succeeds in competing for the subchannel in the first access and exclusively uses the whole subchannel can be obtained as:

ps,11=pc1ptr,1=KτN(1−τN)K−11−(1−τN)K.(4)

The probability that the user succeeds in competing for the subchannel in the first access, but the user shares the subchannel with another user is:

ps,21=pc2ptr,1=K(K−1)2(τN)2(1−τN)K−21−(1−τN)K.(5)

3.2 The Second Random Competition

The number of users who failed in the first competition is Kf=Kτp, and the number of remaining subchannels is Nf=N−Kτps,11−12Kτps,21. Thus, we can get the probability that a remaining subchannel is selected by at least one user.

ptr,2=1−(1−1N−Kps,11−12Kps,21)Kτp.(6)

The probability that a remaining subchannel is selected by only one user is psc1=Kf1Nf(1−1Nf)Kf−1. The probability that a remaining subchannel is selected by exactly two users at the same time is psc2=Kf(Kf−1)2(1Nf)2(1−1Nf)K−2. Thus, the probability that the user succeeds in competing for the subchannel at the second competition and uses the entire subchannel exclusively can be obtained.

ps,12=psc1ptr,2=KτpN−Kps,11−12Kps,21(1−1N−Kps,11−12Kps,21)Kτp−11−(1−1N−Kps,11−12Kps,21)Kτp.(7)

The probability that the second competition is successful but the user shares the subchannel with another user is:

ps,22=psc2ptr,2=Kτp(Kτp−1)2(1N−Kps,11−12Kps,21)2(1−1N−Kps,11−12Kps,21)Kτp−21−(1−1N−Kps,11−12Kps,21)Kτp.(8)

Combining the results of the two competitions, we can get the probability that the user competes for subchannel n successfully and |𝒦n|=1.

ps,1=ps,11+(1−p)ps,12=KτN(1−τN)K−11−(1−τN)K+(1−p)Kτp1N−Kps,11−12Kps,21(1−1N−Kps,11−12Kps,21)Kτp−11−(1−1N−Kps,11−12Kps,21)Kτp.(9)

The probability that the user competes successfully for subchannel n with |𝒦n|=2 is:

ps,2=ps,21+(1−p)ps,22=K(K−1)2(τN)2(1−τN)K−21−(1−τN)K+(1−p)Kτp(Kτp−1)2(1N−Kps,11−12Kps,21)2(1−1N−Kps,11−12Kps,21)K−21−(1−1N−Kps,11−12Kps,21)Kτp.(10)

3.3 Outage Probability

Let xnk denote the signal of user k on subchannel n and E{|xnk|2}=1. Let Pnk denote the transmission power of user k on subchannel n. Then the signal received by AP on subchannel n is:

ynk=∑k∈𝒦nPnkhnkxnk+zn,(11)

where zn denotes the AWGN with mean 0 and variance σn, which is the superposition of the respective uplink channel noise of the individual users on subchannel n.

When |𝒦n|=1, AP receives only one user’s signal on subchannel n and decodes it directly. At this time, the reachable rate of AP decoding signal of user k is:

Rn,1k=1Nlog2⁡(1+ρnk|hnk|2),(12)

where ρnk=Pnkσn.

When |𝒦n|=2, the AP receives the superimposed signals of two users on subchannel n. Assuming that;𝒦n={k,l},k,l∈𝒦. The AP uses the SIC technique to decode the user’s signal in the reduced power order. As shown in Fig. 3, in the uplink, the AP first decodes the strong user’s signal with the highest received power during the decoding process.

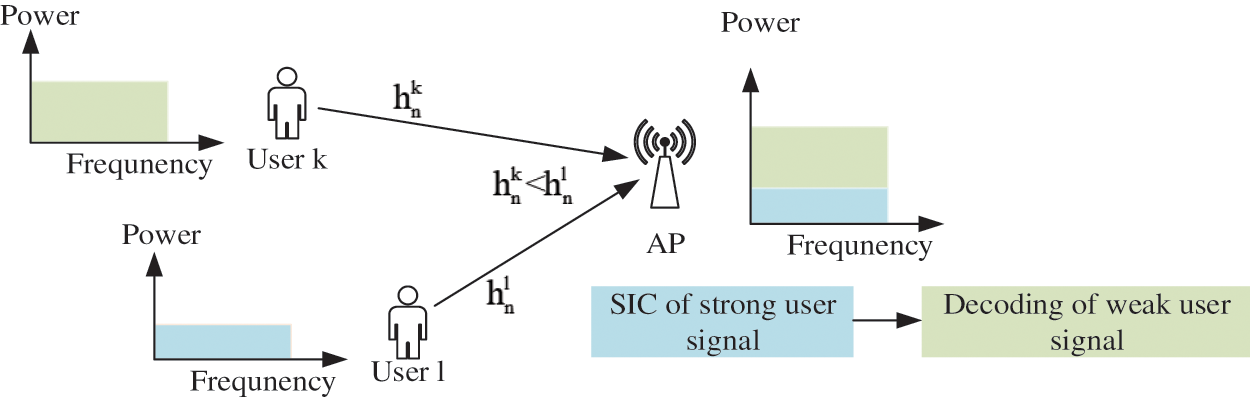
Figure 3: Base station side decoding order in NOMA uplink scenario

Assuming that the signal with higher power at the receiver is the signal of α, α∈{k,l}, then the reachable rate of the stronger user can be obtained by Shannon’s theorem.

Rn,2α=1Nlog2⁡(1+ρnα|hnα|2ρnβ|hnβ|2+1),α∈{k,l},β∈{k,l}∖α.(13)

Imperfect SIC is considered in realistic scenarios due to decoding errors and hardware damage. We model the imperfect SIC errors using Gaussian distribution, inspired by Luo et al. [13], i.e., gni∼CN(0,ελni), 0≤ε≤1, ε is the level of residual interference caused by the imperfect SIC, and ε=0 indicates the perfect SIC. Under imperfect SIC, the reachable data rate for AP decoding the signal of low power user β is denoted as follows:

Rn,2β=1Nlog2⁡(1+ρnβ|hnβ|2ρnα|gnα|2+1),α∈{k,l},β∈{k,l}∖α.(14)

We derive the outage probability due to the channel noise and user’s interference. The probability density functions of |hnk|2 and |hnl|2 are given before deriving the outage probability, and the details can be obtained from Men et al. [25].

f|hnk|2(x)=K!(K−k)!(k−1)!1λ∑a=0k−1(k−1a)(−1)ae−x(K−k+a+1)λ.(15)

To keep the formula brief, Ωk is used subsequently to denote K!(K−k)!(k−1)!, and;δk,a denotes K−k+a+1.

f|hnl|2(y)=K!(K−l)!(l−1)!1λ∑b=0l−1(l−1b)(−1)be−y(K−l+b+1)λ.(16)

Similarly, let Ωl denotes K!(K−l)!(l−1)!, δl,b denotes K−l+b+1 subsequently.

When |𝒦n|=1, OFDMA is used to transmit data and there is no inter-user’s interference. In this case, the outage probability of user k on subchannel n is:

pout,1k=Pr[Rn,1k<Rk]=Pr[1Nlog2⁡(1+ρnk|hnk|2)<Rk]=Pr[|hnk|2<φkρnk]=Ωkλ∑a=0k−1(k−1a)(−1)a∫0φkρnke−xδk,aλdx=∑a=0k−1(k−1a)(−1)aΩkδk,a(1−e−φkδk,aρnkλ),(17)

where φk=2NRk−1.

When |𝒦n|=2, NOMA is used to transmit the signals within the subchannel, and the AP decodes the signals according to the SIC. Assuming that the AP can accurately obtain the user’s channel status information and decode the user’s signals in reduced order based on the user’s instantaneous power. Since the decoding order of a specific user’s signals at the AP is not fixed, and the user k may be a strong or weak power user, we discuss the decoding order of user k and the corresponding probability. The base station has two decoding orders, i.e., H1: AP first decodes the signals of user k, and then decodes the signals of user l; H2: AP first decodes the signals of user l, and then decodes the signals of user k.

The power of user at AP is the product of transmission power and channel gain, i.e., Pk=Pnk|hnk|2, Pl=Pnl|hnl|2. According to the probability theory, the distribution function of Pk can be obtained.

FPk(Pk)=P(Pnk|hnk|2≤Pk)=Ωkλ∑a=0k−1(k−1a)(−1)a∫0PkPnke−xδk,aλdx=∑a=0k−1(k−1a)(−1)aΩkδk,a(1−e−Pkδk,aPnkλ).(18)

Derivation of FPk(Pk) obtains the probability density function of Pk as fPk(Pk)=∑a=0k−1(k−1a)(−1)aΩkλPnke−Pkδk,aλPnk, and similarly, fPl(Pl)=∑b=0l−1(k−1b)(−1)bΩlλPnle−Plδl,bλPnl.

The probability of H1 occurring, which is the probability of Pk>Pl, thus we have:

p(H1)=∫0∞∫Pl∞fPk(Pk)fPl(Pl)dPkdPl=ΩkΩl∑a=0k−1(k−1a)∑b=0l−1(k−1b)(−1)a+b∫0∞∫Pl∞1λPnke−Pkδk,aλPnk1λPnle−Plδl,bλPnldPkdPl=ΩkΩl∑a=0k−1(k−1a)∑b=0l−1(k−1b)(−1)a+bδk,aPnkPnkδk,a+Pnlδl,b.(19)

The probability of H2 occurring is given by 1−p(H1).

Theorem 1: When H1 occurs, k is a strong user, directly decoding the signal of user k at AP. In this case, the outage probability of AP decoding the signal is:

pout,highk=Ωk∑a=0k−1(k−1a)(−1)aδk,a(1−e−φkδk,aλρnk)+ΩkΩl∑a=0k−1(k−1a)∑b=0l−1(l−1b)(−1)a+b1δl,bφkρnlφkρnlδk,a+ρnkδl,be−φkδk,aλρnk.(20)

The proof of Theorem 1 is given in Appendix A.

When H2 occurs, k is weak user, so the AP decodes the signal of user l with stronger power first, and after successfully decoding the signal of user l, the signal of user k can be decoded by eliminating the signal of user l from the received signals. Because we consider the imperfect SIC, there exists a part of the residual interference. The probability density function of the imperfect error |gnj|2 can be expressed as:

f|gnj|2(z)=Ωl∑b=0l−1⁡(l−1b)(−1)b1ελe−zδl,bελ.(21)

When user k is a weak power user, the outage probability of the AP decoding signal can be expressed as:

pout,lowk=1−Pr[Rn,2l≥Rl,Rn,2k≥Rk]=1−Pr[1Nlog2⁡(1+ρnl|hnl|2ρnk|hnk|2+1)≥Rl]×Pr[1Nlog2⁡(1+ρnk|hnk|2ρnl|gnl|2+1)≥Rk]=1−T1T2.(22)

where T1≜Pr[1Nlog2⁡(1+ρnl|hnl|2ρnk|hnk|2+1)≥Rl],T2≜Pr[1Nlog2⁡(1+ρnk|hnk|2ρnl|gnl|2+1)≥Rk]. The expressions for T1 and T2 are given in Theorem 2.

Theorem 2: The expression of T1 is as follows:

T1=1−Ωl∑b=0l−1(l−1b)(−1)bδl,b(1−e−φlδl,bλρnl)−ΩkΩl∑a=0k−1(k−1a)∑b=0l−1(l−1b)(−1)a+b1δk,ae−φlδl,bλρnlφlρnkφlρnkδl,b+ρnlδk,a.(23)

The expression of T2 is as follows:

T2=ΩkΩl∑a=0k−1(k−1a)∑b=0l−1(k−1a)(−1)a+b1δl,be−φkδk,aλρnk(1δk,a−φkερnlεφkρnlδk,a+ρnkδl,b).(24)

The proof of Theorem 2 is given in Appendix B.

3.4 Throughput Analysis

The user’s signal can be successfully received when the user successfully competes for the subchannel and the AP decodes the user’s signal successfully. Thus, the probability of successful reception of the user’s signal can be obtained.

psucck=ps,1(1−pout,1k)+ps,2[p(H1)(1−pout,highk)+(1−p(H1))(1−pout,lowk)],(25)

The first term indicates the probability that the user has exclusive access to the subchannel and the transmission is successful. The second term indicates the probability that a strong power user shares a subchannel with another user and the transmission is successful. The third term is the probability of successful transmission when a weak power user shares a subchannel with another user.

In this model, each user transmits signals at a fixed rate, and the throughput depends on the probability of successful competition and the outage probability. Based on the results of the previous analysis, the expression for the system throughput is as follows:

η=∑k=1KpsucckRk=∑k=1K{ps,1(1−pout,1k)+ps,2[p(H1)(1−pout,highk)+(1−p(H1))(1−pout,lowk)]}Rk.(26)

3.5 Optimal Power Allocation Scheme

This section provides an optimization problem that is solved to find the optimal power allocation strategy that minimizes the probability of interruption in order to optimize the system’s performance. Due to the combination of OFDMA and NOMA, users may exclusively access the subchannels or share the subchannels with other users. Therefore, the optimal power allocation strategy is discussed separately in both cases.

3.5.1 User Access to Subchannel Individually

This section presents the power allocation optimization problem in the case of the user exclusive access to the subchannel. The objective is to minimize the outage probability for user k. The outage probability Pout,1k is given by Eq. (17). The constraints are as follows: (i) The transmission power of user k cannot exceed the maximum amount of the transmitter Pmaxk, which depends on the user’s hardware equipment. (ii) The user’s transmission power cannot exceed the total subchannel power threshold Pmaskn, which is set by the Federal Communications Commission (FCC). The mathematical description is as follows:

minimizePout,1k(Pnk)(27a)

subject to   0<Pnk≤Pmaxk,0<k<K,∀n∈𝒩,(27b)

0<Pnk≤Pmaskn,0<k<K,∀n∈𝒩,(27c)

where Pout,1k(Pnk)≜Pout,1k, just to show Pout,1k(Pnk) is a function about Pnk. According to Eq. (17), the higher the transmission power, the lower the outage probability in the case of the channel being shared only by one user, so the user transmits the signal with the highest power to achieve the optimum outage performance.

3.5.2 Two Users Sharing a Subchannel

This section presents the power allocation optimization problem in the case of users sharing subchannels, assuming k is a weak user and l is a strong user. The objective is to minimize the sum of the outage probabilities of user k and user l, where the outage probabilities pout,highl and pout,lowk are given by Eqs. (20) and (22). The constraints are as follows: (i) The transmission power of user k cannot exceed the maximum transmission power of transmitter Pmaxk. (ii) The transmission power of user l cannot exceed the maximum transmission power of the transmitter Pmaxl. (iii) The power of user k should be greater than the power of user l. (iv) The total transmission power of user k and user l must not exceed the total power threshold Pmaskn of the subchannel. The mathematical description is as follows:

minimizepout,highl(Pnk,Pnl)+pout,lowk(Pnk,Pnl)(28a)

subject to   0<Pnk≤Pmaxk,0<k<K,∀n∈𝒩,(28b)

0<Pnl≤Pmaxl,k<l<K,∀n∈𝒩,(28c)

0<Pnk+Pnl≤Pmaskn,0<k<l<K,∀n∈𝒩,(28d)

Pnk<Pnl,0<k<l<K,∀n∈𝒩,(28e)

where pout,highl(Pnk,Pnl)≜pout,highl, pout,lowk(Pnk,Pnl)≜pout,lowk, just to show that they are function about Pnk and Pnl. When user k is a strong user and user l is a weak user, the optimal power allocation scheme can be obtained by simply exchanging the positions of k and l in Eq. (28).

In summary, Algorithm 1 demonstrates the power allocation scheme for multiuser OFDMA-NOMA-RA systems. This algorithm rationally allocates power to users based on the number of users competing for the subchannel. If the number of users exceeds 2, the user cannot access the channel and no power is allocated. When the number of users is 2, the power is allocated to the users according to Eq. (28). When only one user accesses the channel, the maximum power within the allowed range is allocated to the user to ensure successful data transmission.

4  Comparative Analysis

To demonstrate the superiority of OFDMA-NOMA-RA, the throughput of pure OFDMA and pure NOMA are analyzed in this section.

4.1 OFDMA Throughput Analysis

Different from OFDMA-NOMA-RA system, at most one user is allowed to access the subchannel in OFDMA mode, so the collision probability changes in OFDMA mode. Notably, the transmission probability also varies from the collision probability.

τOF=[∑i=0m−1(pOF)i(∑r=1Wi−1Wi−rNWi+1)+(pOF)m1−pOF(∑r=1Wm−1Wm−rNWm+1)]−11−pOF.(29)

pOF=1−(1−τOFN)K−1.(30)

The OFDMA mode is similar to the OFDMA-NOMA-RA mode with |𝒦n|=1 in the first random contention. Thus, the probability of successfully competing subchannels in OFDMA mode is:

ps,1OF=KτOFN(1−τOFN)K−11−(1−τOFN)K.(31)

The outage probability of the user in OFDMA mode is the same as the outage probability in the case of OFDMA-NOMA-RA mode with |𝒦n|=1. Thus, the system throughput expression is given by:

ηOF=∑k=1Kps,1OF(1−pout,1k)Rk.(32)

4.2 NOMA Throughput Analysis

Compared to OFDMA-NOMA-RA scheme, NOMA allows multiple users to access the entire spectrum simultaneously, so OFDMA-NOMA-RA is synonymous with NOMA when N=1. The transmission probability and collision probability of the NOMA model can be obtained by substituting N=1 into Eq. (1).

τNO=[∑i=0m−1(pNO)i(∑r=1Wi−1Wi−rWi+1)+(pNO)m1−pNO(∑r=1Wm−1Wi−rWm+1)]−11−p.(33)

pNO=1−(1−τNO)K−2.(34)

Similarly, we assume that the maximum number of user accesses is 2. The probability that a user successfully competes for the channel and |𝒦n|=1 can be obtained.

ps,1NO=KτNO(1−τNO)K−11−(1−τNO)K.(35)

Similarly, the probability that a user successfully competes for the channel with |𝒦n|=2 is given by:

ps,2NO=K(K−1)2(τNO)2(1−τNO)K−21−(1−τNO)K.(36)

Since the user utilizes the entire spectrum in NOMA mode, the data rate becomes N times that of OFDMA-NOMA-RA, i.e., RkNO=NRk. Thus, φkNO=φk=2NRk−1. Thereby the outage probability does not change and the expression for throughput is as follows:

ηNO=∑k=1K{ps,1NO(1−pout,1k)+ps,2NO[p(H1)(1−pout,highk)+(1−p(H1))(1−pout,lowk)]}Rk.(37)

5  Numerical Analysis

In this section, numerical results of outage probability and throughput are given by Matlab to validate the performance analysis. Without loss of generality, this section assumes that the number of users K=10, the maximum backoff phase m=8, the number of subchannels N=5, σn=1,∀n∈𝒩, λ=0.5, Pmaxk=20 dBm,Pmaskn=30 dBm.

Fig. 4 shows the relationship between the transmission SNR ρnk and the outage probability with different k in the case of a single user exclusive access to the subchannel. It is observed that the outage probability decreases with the increase of ρnk. This is because increasing ρnk means increasing transition power, which benefits user decoding. Meanwhile, the outage probability also decreases with the increase of k, because a larger k means better channel conditions and great channel condition is advantageous for successful decoding.

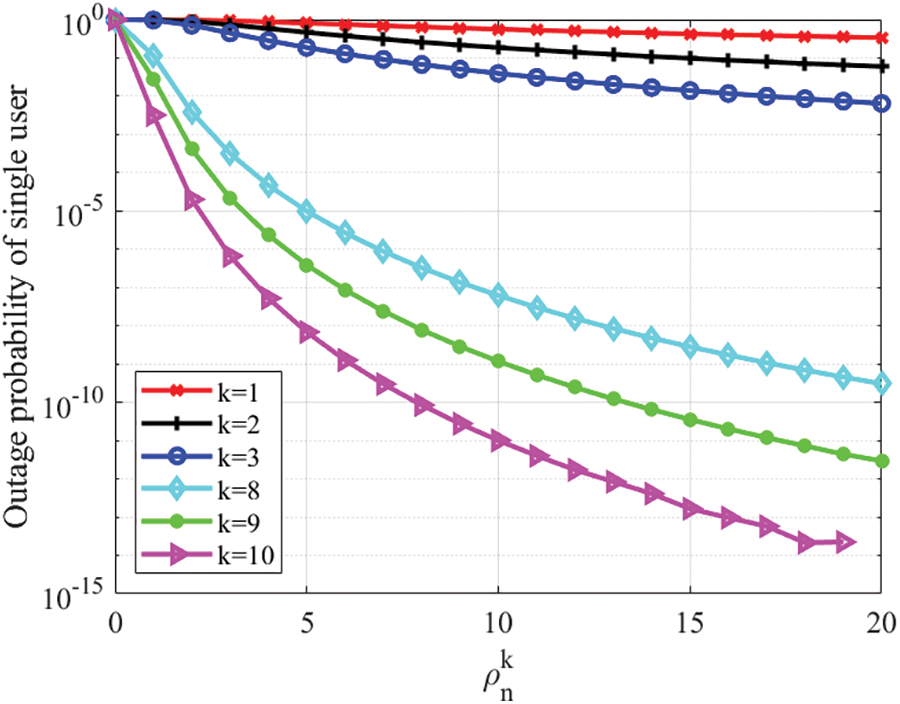
Figure 4: Outage probability vs. ρnk with |𝒦n|=1, Rk=0.2 bps/Hz

Fig. 5 reveals the relationship between ρnk and the outage probability of a strong user in the case of two users sharing the same subchannel with k=5. We can observe that the strong user outage probability decreases with the increase of ρnk. This is because the AP treats the weak user’s signal as interference and decodes the strong user’s signal directly. Therefore, the signal-to-noise ratio decreases as ρnk increases, and thus the outage probability decreases. In addition, it is observed that the outage probability of strong user k increases with is decreasing l. This is because the smaller l, the worse the channel conditions for the weak user, resulting in a higher signal-to-noise ratio, which is more favorable for decoding the strong user’s signal.

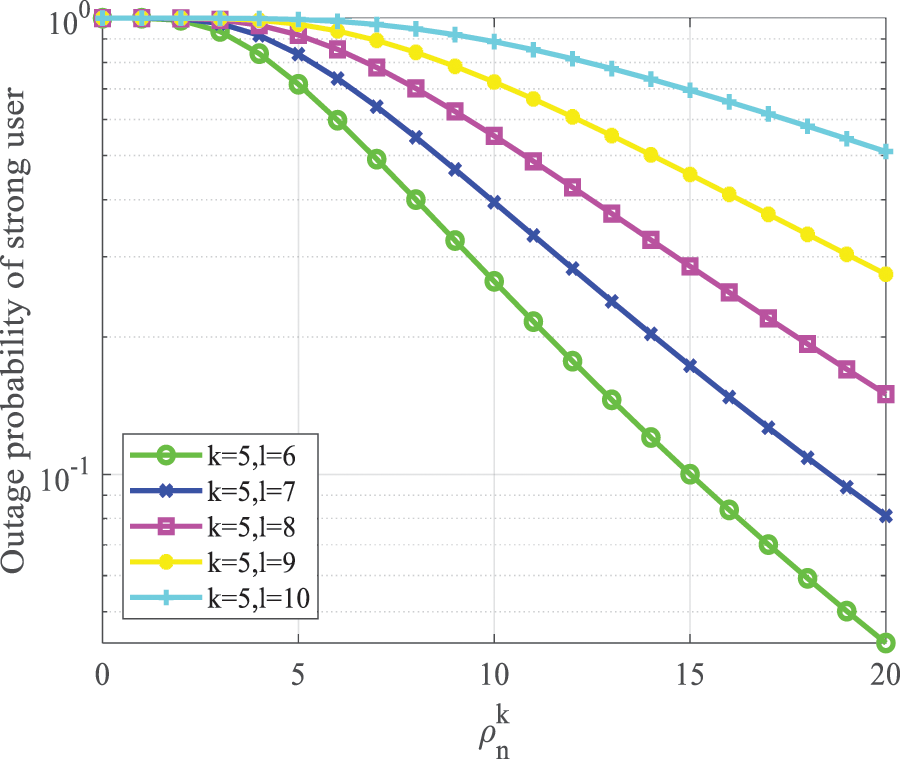
Figure 5: Strong user outage probability vs. ρnk with |𝒦n|=2, ρnl=10 dB

In Fig. 6, the relationship between the interruption probability of weak users and ρnk is revealed, with k=5 again. Different from Fig. 2, as ρnk increases, the outage probability of the weak user first increases and then decreases. The reason is that according to the SIC principle, the AP decodes the strong user’s signals first and decodes the weak user’s signals after eliminating the strong user’s signals. Thus, whether the strong user’s signals are successfully decoded or not also affects the outage probability of the weak user’s signals. When ρnk is small, the outage probability for weak users decreases as ρnk increases. However, when ρnk is too large, strong user’s signals are difficult to be successfully decoded, leading to decrease in the probability of successfully decoding weak user’s signals.

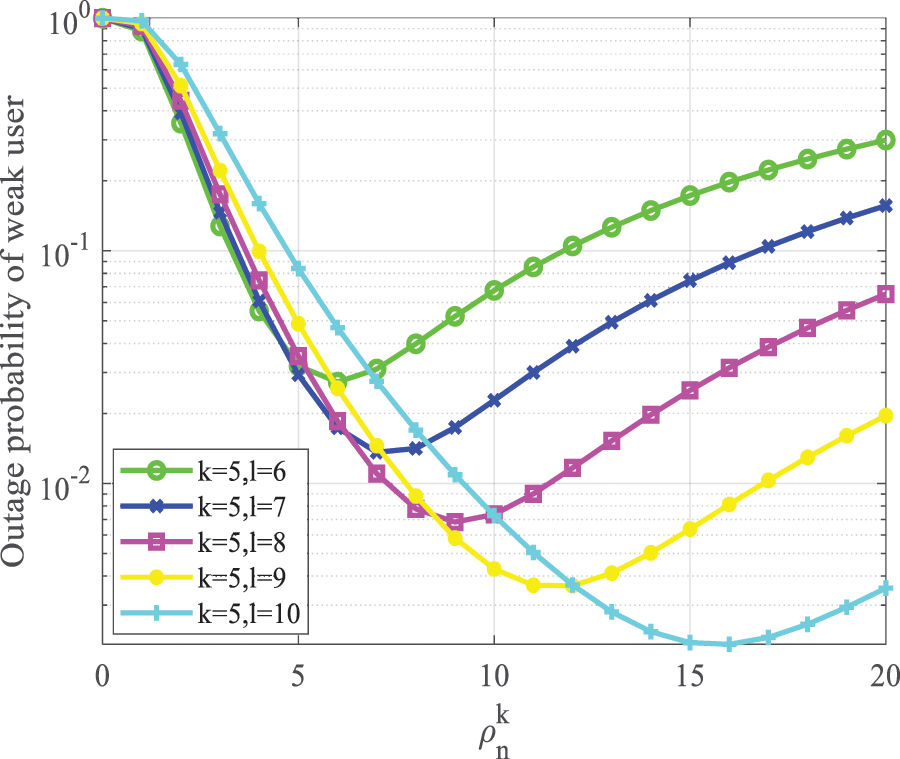
Figure 6: Weak user outage probability vs. ρnk with |𝒦n|=2, ρnl=10 dB, ℰ=0.05

In Fig. 7, the effect of ρnl on the outage probability of a weak user is shown for the case of k=6, l=8 with different ℰ. We can observe that the best outage performance is obtained at ℰ=0, and the weak user’s outage probability increases as ℰ increases. This is because imperfect SCI can cause serious interference to the weak users, which leads to a degradation of the weak user’s outage performance. Thus, imperfect SIC must be considered in real communication as it can seriously degrade the quality of communication if ℰ becomes too large.

Figure 7: Weak user outage probability vs. ρnl, ρnk=10 dB

To reveal the optimal power allocation scheme, Fig. 8 shows the effect of ρnk and ρnl on the sum of outage probabilities for user k and user l for example with k=4, l=6. The optimal value point derived from the power allocation algorithm in Section 3 is shown at the pentagram marking in the figure, which achieves the minimum value of the outage probability, and this means that ρnk and ρnl corresponding to this point are the optimal power for user k and user l, respectively. Furthermore, the figure illustrates that when ρnl is less than 5, the sum of the interruption probabilities of user k and user l is close to 2. This shows the importance of rational power allocation.

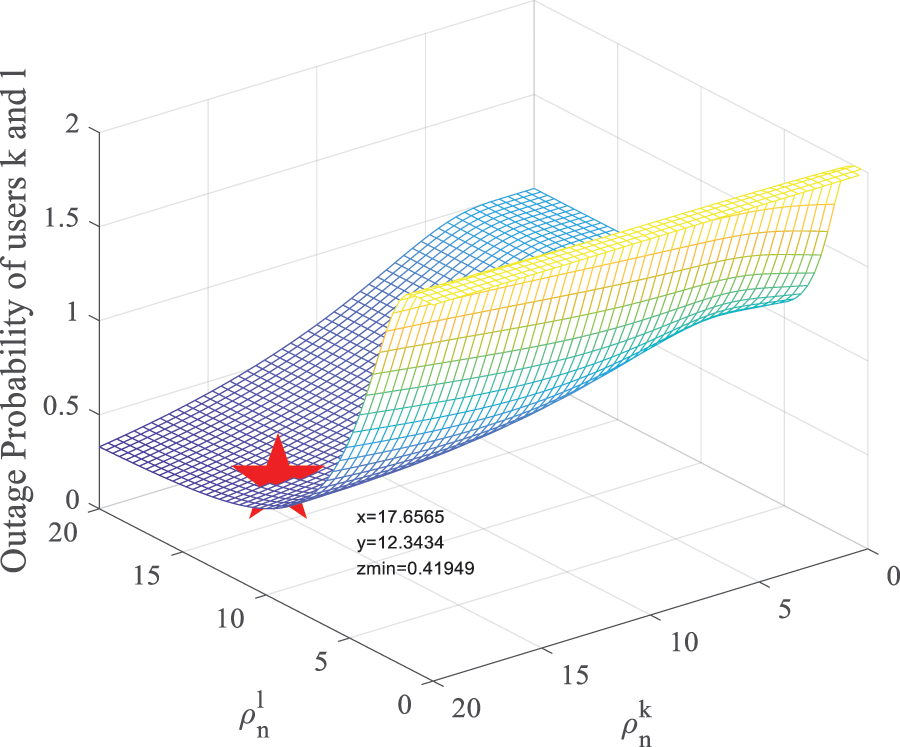
Figure 8: Outage probability vs. ρnk, ρnl

Fig. 9 illustrates the relationship between system throughput and ρnk. It can be seen that the system throughput increases with the increase of ρnk. After ρnk=15, the system throughput of both NOMA and OFDMA-NOMA-RA decreases in some extent. This is because multiple users in the system are accessing the channel simultaneously. When the power of a particular user is too high, it will be difficult for the weak user to decode correctly, the interruption probability of weak user becomes large, and thus the system throughput tends to decrease. In OFDMA systems, a user accesses the channel individually, so the system throughput is not degraded. In addition, we can observe that the OFDMA-NOMA-RA proposed in this paper obtains better throughput performance compared to OFDMA and NOMA, which validates the superiority of the protocol in this paper.

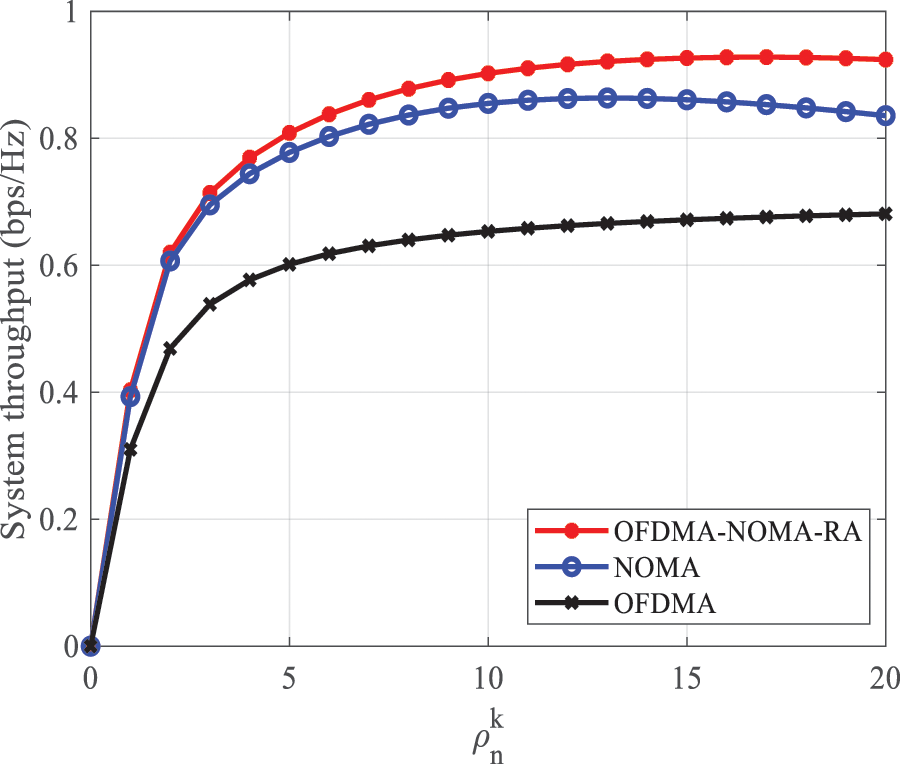
Figure 9: System throughput vs. ρnk, ρnl=10 dB

Fig. 10 reveals the relationship between the imperfect factor ε and the system throughput with different Rk. We can see that the system throughput tends to decrease as ε increases, which is more evident when Rk is larger. In addition, when Rk=0.5 bps/Hz and ε is larger, the throughput of OFDMA-NOMA-RA proposed in this paper and NOMA is lower than OFDMA, that is because there is no inter-user interference in OFDMA, therefore it is not affected by ε. This also reveals the need to suppress ε to a lower level when OFDMA-NOMA-RA is employed.

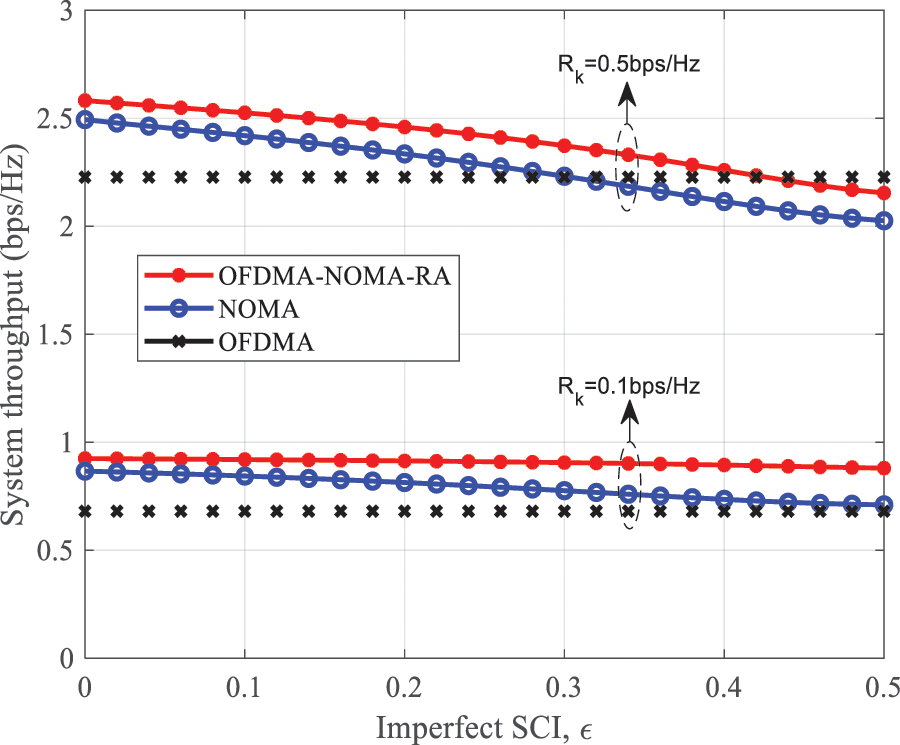
Figure 10: System throughput vs. imperfect SIC factor ε, ρnk=20, ρnl=10 dB

6  Conclusions

To address the issues of network congestion and spectrum wastage in large-scale multi-user scenarios, this paper proposes a new OFDMA-NOMA-RA protocol with two random accesses that combines the advantages of OFDMA and NOMA. The protocol utilizes OFDMA to divide the frequency band into multiple orthogonal subchannels, and NOMA superposition coding is adopted in the subchannels, which realizes multiple users accessing the channel simultaneously and overcomes the SIC decoding complexity in the NOMA multi-user scenario. Based on the proposed protocol, in the case of imperfect SIC, we derive the probability of successfully competing subchannels and the outage probability considering both the user dominates subchannel and the users share subchannel. The decoding order of the users is not fixed when two users share the subchannel. Thus, we consider the decoding order of the users and the corresponding probabilities. Then, the expression of system throughput is derived based on the probability of successful contention for subchannels and the outage probability. In addition, we propose an optimization problem, the optimal power allocation scheme can be obtained by solving the problem to minimize the outage probability. The numerical results demonstrate the superiority of OFDMA-NOMA-RA proposed in this paper compared to pure OFDMA and NOMA when the imperfect SIC factor ε is suppressed in a small range. For further work, we attempt to combine multi-antenna MIMO to further alleviate congestion and improve spectrum resource utilization from the space dimension.

Acknowledgement: The authors are thankful to the National Natural Science Foundation of China and Lanzhou University of Technology for funding this work.

Funding Statement: This study was funded in part by the National Natural Science Foundation of China under Grant 61663024 and in part by the Hongliu First Class Discipline Development Project of Lanzhou University of Technology (25-225305).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Suoping Li, Hailing Yang; data collection: Hailing Yang, Suoping Li, Duo Peng; analysis and interpretation of results: Hailing Yang, Suoping Li; draft manuscript preparation: Hailing Yang, Suoping Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting this article are from previously reported studies and datasets, which have been cited.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Hasan, E. Hossain, and D. Niyato, “Random access for machine-to-machine communication in LTE-advanced networks: Issues and approaches,” IEEE Commun. Mag., vol. 56, no. 6, pp. 86–93, Jun. 2013. doi: 10.1109/MCOM.2013.6525600. [Google Scholar] [CrossRef]

2. L. Zhen, H. Qin, B. Song, R. Ding, and X. Du, “Random access preamble design and detection for mobile satellite communication systems,” IEEE J. Sel. Areas. Commun., vol. 36, no. 2, pp. 280–291, Feb. 2018. doi: 10.1109/JSAC.2018.2804138. [Google Scholar] [CrossRef]

3. L. Zhen, Y. Zhang, K. Yu, N. Kumar, and A. Barnawi, “Early collision detection for massive random access in satellite-based internet of things,” IEEE Trans. Veh. Technol., vol. 70, no. 5, pp. 5184–5189, May 2021. doi: 10.1109/TVT.2021.3076015. [Google Scholar] [CrossRef]

4. Y. Xu, G. Gui, H. Gacanin, and F. Adachi, “A survey on resource allocation for 5G heterogeneous networks: Current research, future trends, and challenges,” IEEE Commun. Surv. Tutor., vol. 523, no. 2, pp. 668–695, Feb. 2021. doi: 10.1109/COMST.2021.3059896. [Google Scholar] [CrossRef]

5. Q. Chen, Z. Weng, X. Xu, and G. Chen, “A target wake time scheduling scheme for uplink multiuser transmission in IEEE 802.11ax-based next generation WLANs,” IEEE Access, vol. 7, pp. 158207–158222, Oct. 2019. doi: 10.1109/ACCESS.2019.2950464. [Google Scholar] [CrossRef]

6. R. Zhou, B. Li, M. Yang, Z. Yan, and A. Yang, “DRA-OFDMA: Double random access based QoS oriented OFDMA MAC protocol for the next generation WLAN,” Mobile Netw. Appl., vol. 24, no. 5, pp. 1425–1436, May 2019. doi: 10.1007/s11036-019-01268-w. [Google Scholar] [CrossRef]

7. S. P. Li, H. L. Yang, R. M. Gao, T. T. Jia, and H. L. Li, “Performance analysis of QoS-oriented OFDMA protocol based on IEEE 802.11 ax for cognitive radio network,” Appl. Sci., vol. 513, no. 12, pp. 7163, May. 2023. doi: 10.3390/app13127163. [Google Scholar] [CrossRef]

8. P. Z. Fan, L. Li, H. Chen, G. Cheng, and L. Yang, “Random access for massive internet of things: Current status, challenges and opportunities,” J. Commun., vol. 42, no. 4, pp. 1–21, Jul. 2021. doi: 10.11959/j.issn.1000-436x.2021098. [Google Scholar] [CrossRef]

9. S. Anand, S. Sabud, A. K. Singh, and P. Kumar, “A use-case efficient DFrFT-based index modulated-OFDM system in the presence of CFO,” Int. J. Electron. Commun., vol. 170, no. 4, pp. 154756, Oct. 2023. doi: 10.1016/j.aeue.2023.154756. [Google Scholar] [CrossRef]

10. S. P. Li, W. W. Liang, V. Pla, N. N. Yang, and S. Yang, “Two-stage adaptive relay selection and power allocation strategy for cooperative CR-NOMA networks in underlay spectrum sharing,” Appl. Sci., vol. 11, no. 21, pp. 10433, Nov. 2021. doi: 10.3390/app112110433. [Google Scholar] [CrossRef]

11. Y. Tian, “A non-orthogonal multiple access and interference mitigation combined strategy in multi-user networks,” Wirel. Pers. Commun., vol. 104, no. 1, pp. 111–128, Oct. 2018. doi: 10.1007/s11277-018-6011-z. [Google Scholar] [CrossRef]

12. S. Anand and P. Kumar, “Low complexity successive interference cancellation receiver for DCT-NOMA-OFDM system with CFO,” Phys. Commun., vol. 58, no. 4, pp. 102053, Jun. 2023. doi: 10.1016/j.phycom.2023.102053. [Google Scholar] [CrossRef]

13. L. P. Luo, Q. Z. Li, and J. L. Cheng, “Performance analysis of overlay cognitive NOMA systems with imperfect successive interference cancellation,” IEEE Trans. Commun., vol. 68, no. 8, pp. 4709–4722, Aug. 2020. doi: 10.1109/TCOMM.2020.2992471. [Google Scholar] [CrossRef]

14. H. Bany Salameh, R. Tashtoush, H. Al-Obiedollah, A. Alajlouni, and Y. Jararweh, “Power allocation technique with soft performance guarantees in hybrid OFDMA-NOMA cognitive radio systems: Modeling and simulation,” Simul. Model. Pract. Theory, vol. 112, no. 4, pp. 102370, Nov. 2021. doi: 10.1016/j.simpat.2021.102370. [Google Scholar] [CrossRef]

15. T. Tang, Y. L. Mao, and G. M. Hu, “A fair power allocation approach to OFDM-based NOMA with consideration of clipping,” Electronics, vol. 9, no. 10, pp. 1743, Oct. 2020. doi: 10.3390/electronics9101743. [Google Scholar] [CrossRef]

16. A. R. Sharief, A. O. Haitham, and B. S. Haythem, “Efficient user-channel pairing with power-domain sum-rate maximization in opportunistic hybrid OFDMA-NOMA IoT systems,” Cluster Comput., vol. 25, no. 4, pp. 2501–2514, Jul. 2021. doi: 10.1007/s10586-021-03365-6. [Google Scholar] [CrossRef]

17. S. Rezvani, E. A. Jorswieck, R. Joda, and H. Yanikomeroglu, “Optimal power allocation in downlink multicarrier NOMA systems: Theory and fast algorithms,” IEEE J. Sel. Areas. Commun., vol. 40, no. 4, pp. 1162–1189, Apr. 2022. doi: 10.1109/JSAC.2022.3143237. [Google Scholar] [CrossRef]

18. X. Y. Guo and Y. Luo, “Hybrid NOMA/OFDMA visible light communication system with coordinated multiple point transmission,” Opt. Express, vol. 30, no. 26, pp. 47404–47420, Dec. 2022. doi: 10.1364/OE.477769. [Google Scholar] [PubMed] [CrossRef]

19. Y. L. Wu, S. Zhang, Z. X. Liu, X. S. Liu, and J. F. Li, “An efficient resource allocation for massive MTC in NOMA-OFDMA based cellular networks,” Electronics, vol. 9, no. 5, pp. 705, Apr. 2020. doi: 10.3390/electronics9050705. [Google Scholar] [CrossRef]

20. S. M. Tseng, W. D. Tsai, and H. S. Suo, “Cross-layer 1 and 5 user grouping/power allocation/subcarrier allocations for downlink OFDMA/NOMA video communications,” Int. J. Commun. Syst., vol. 32, no. 14, pp. e4084, Jul. 2019. doi: 10.1002/dac.4084. [Google Scholar] [CrossRef]

21. M. Hadi and R. Ghazizadeh, “Sub-channel assignment and power allocation in OFDMA-NOMA based heterogeneous cellular networks,” Int. J. Electron. Commun., vol. 120, no. 3, pp. 153195, Jun. 2020. doi: 10.1016/j.aeue.2020.153195. [Google Scholar] [CrossRef]

22. S. A. Tutelian and E. M. Khorov, “Joint usage of OFDMA and NOMA for uplink transmissions in Wi-Fi networks,” J. Commun. Technol. Electron., vol. 67, no. 2, pp. S222–S232, Mar. 2023. doi: 10.1134/S1064226922140108. [Google Scholar] [CrossRef]

23. P. Promponas, C. Pelekis, E. E. Tsiropoulou, and S. Papavassiliou, “Games in normal and satisfaction form for efficient transmission power allocation under dual 5G wireless multiple access paradigm,” IEEE ACM Trans. Netw., vol. 29, no. 6, pp. 2574–2587, Dec. 2021. doi: 10.1109/TNET.2021.3095351. [Google Scholar] [CrossRef]

24. D. H. Xie, J. W. Zhang, A. M. Tang, and X. D. Wang, “Multi-dimensional busy-tone arbitration for OFDMA random access in IEEE 802.11ax,” IEEE Trans. Wirel. Commun., vol. 19, no. 6, pp. 4080–4094, Jun. 2020. doi: 10.1109/TWC.2020.2979852. [Google Scholar] [CrossRef]

25. J. J. Men and J. H. Ge, “Performance analysis of non-orthogonal multiple access in downlink cooperative network,” IET Commun., vol. 9, no. 18, pp. 2267–2273, Dec. 2015. doi: 10.1049/iet-com.2015.0203 [Google Scholar] [CrossRef]

Appendix A

pout,highk=Pr[Rnk<Rk]=Pr[1Nlog2⁡(1+Pnk|hnk|2Pnl|hnl|2+σn)<Rk]=Pr[ρnk|hnk|2ρnl|hnl|2+1<φk]=Pr[|hnl|2>ρnk|hnk|2−φkρnlφk]=Ωkλ∑a=0k−1(k−1a)(−1)a∫0φkρnke−δk,axλdx+ΩkΩl∑a=0k−1(k−1a)∑b=0l−1(k−1a)(−1)a+b∫φkρnk∞∫ρnkx−φkρnlφk∞1λe−δk,axλ1λe−δl,byλdydx=Ωkδk,a∑a=0k−1(k−1a)(−1)a(1−e−φkδk,aλρnk)+ΩkΩl∑a=0k−1(k−1a)∑b=0l−1(l−1b)(−1)a+b1δl,bφkρnlφkρnlδk,a+ρnkδl,be−φkδk,aλρnk.(38)

where x=|hnk|2, y=|hnl|2.