An Opposition-Based Learning-Based Search Mechanism for Flying Foxes Optimization Algorithm

1  Introduction

As an effective method for solving single-objective problems (SOPs), the metaheuristic algorithm uses some random strategies during the execution process. These strategies help guide the algorithm through various regions within the search domain, facilitating the elimination of local optima and the discovery of an optimal solution. In addition, without the need for further intricate mathematical procedures (such as derivatives), they are easily applicable to solving continuous, binary and discrete SOPs [1], which are commonly employed in multiple practical domains such as engineering, economics, logistics, planning and beyond [2]. Typically, a minimized SOP can be formally expressed as formula (1).

minimize f(X),X=[x1,x2,⋯,xd](1)

where f refers to the objective function of the given solution, xi represents the variable and d signifies the dimension.

Metaheuristic algorithm is one of the effective approaches for solving SOPs. Classical metaheuristic algorithms consist of genetic algorithm (GA) [3], particle swarm optimization (PSO) [4], differential evolution (DE) [5], simulated annealing (SA) [6], tabu search (TS) [7] and others. Although the classical algorithms perform very well, the no free lunch theorem shows that no single metaheuristic algorithm can address every type of optimization problem. This theory has promoted the emergence of a substantial amount of novel metaheuristic algorithms [8–11]. And researchers have also investigated ways to enhance their performance [12–15]. Among these innovations, Flying Foxes Optimization (FFO) [16] stands out, a metaheuristic algorithm devised by Zervoudakis et al., inspired by the survival tactics of flying foxes in a heat wave environment. It provides an efficient solution to SOPs. Compared with other metaheuristic algorithms, FFO exploits fuzzy logic for individual parameter determination across solutions, leading to an algorithm that operates without predefined parameters. And it also presents a potent hybrid algorithmic framework that merges operators from current algorithms, deploying these operators as dictated by the requirements of the specific problem. Its convergence ability is very competitive, usually faster in reaching the optimum point. And it provides an effective and appealing substitute for conventional global optimization.

FFO performs well in SOPs, but it also has some problems. FFO uses the survival list method to replace dead individuals, that is, it selects outstanding individuals to enter the survival list, and updates the dead individuals through the information of individuals in the survival list. This method has major flaws in the issue of population diversity. Using the survival list method to replace dead flying fox individuals does not always help the algorithm get rid of the solution that best fits the local context. Most excellent individuals in the survival list in the later stage of the algorithm are gathered together, and the newly created solution is also very likely to still be located in the same area in the search area. It exposes the issue of population diversity in FFO, which will significantly influence the algorithm’s optimization efficiency. Furthermore, relevant papers [17,18] have shown that the initial population’s quality plays a crucial role in the algorithm’s efficacy in achieving convergence. FFO uses a randomized initial strategy to generate the population, potentially leading to converging slowly or even failing to find the best solution globally.

In addressing the aforementioned issues, this paper proposes an opposition-based learning-based search mechanism for the FFO algorithm, which combines opposition-based learning and niching techniques with FFO and is called the Improved FFO (IFFO) algorithm. The motivation behind IFFO stems from the imperative for enhanced navigation through search domains, especially in scenarios where FFO may encounter difficulties in maintaining diversity and achieving global optimum. The main research works outlined in this paper include:

(1) In light of the diversity problem of the original algorithm, IFFO uses niching techniques to improve the selection strategy of the survival list method. In addition to considering the objective function value used by the original strategy, the new selection strategy is further based on the population’s flying fox individuals’ crowding degree. The new selection strategy. Most of the flying fox individuals selected by the new method have good objective functions and low crowding, which helps the newly generated solution to jump out of the nearby area of the search space, thereby getting rid of the local optimal solution.

(2) A better initial population can explore the search space through a larger range, expediting the algorithm’s journey toward local optimum. In response to the concerns that the initial population may be of poor quality, IFFO adopts an opposition-based learning approach to abandon areas with low search value, thus aligning the initialized population closer to optimal solutions and accelerating convergence. Opposition-based learning and niching techniques allow IFFO to enhance its capability to more effectively equilibrate the processes of search and utilization.

(3) To verify the superiority of IFFO, experiments are performed on IFFO, FFO and the metaheuristic algorithms using the CEC2017 test function set. These experiments confirm IFFO’s optimization prowess and convergence velocity. In addition, the effectiveness of two improvement strategies used in IFFO is analyzed to verify their impact on algorithm improvement.

The subsequent sections of this paper are organized as follows: Section 2 offers a concise introduction to FFO. In Section 3, the improvements to FFO are elaborated in detail. Section 4 displays experimental outcomes of IFFO and other enhanced single-objective optimization algorithms on benchmark tests. Finally, Section 5 summarizes the primary research findings.

2  Related Work

2.1 FFO Algorithm

This section concisely presents FFO and analyzes the defects of the algorithm. FFO is mainly composed of three parts, namely movement of flying foxes, the handling of mortality and replacement within the flying fox population, and a fuzzy self-tuning method. Algorithm 1 presents the pseudo code outlining the FFO methodology.

The movement of flying foxes is to look for the best way to avoid the attack of the heat wave (lines 8–10). Similar to most swarm intelligence algorithms, the flying fox (candidate solution) searches nearby locations based on information from other candidate solutions or the optimal solution, moving to a cooler (better) location to avoid the heat wave. The movement of flying foxes can help the flying fox (candidate solution) avoid the heat wave attack of the environment, ensuring that the flying fox (candidate solution) can continue to go to the current coldest (the best solution) position and stay near the current coldest (optimal solution) position to search for better solutions.

Death and replacement of flying foxes control the death conditions and replacement methods of flying fox individuals (candidate solutions) within the population. There are two main reasons for the death of the flying fox (candidate solution). One is that the flying fox is located in a very poor (hot) position in the search area, positioned unfavorably far from the coldest position found so far (line 12). The other is that many flying foxes gather in the same place, even if the place is very cold, it will cause the flying foxes to suffocate and die (line 18). In order to keep the number of flying foxes unchanged, the death of a flying fox (candidate solution) must regenerate a new flying fox (candidate solution) as a replacement. There are two methods to generate replacement flying foxes, namely the survival list method and the offspring of flying foxes method. In different death situations, the algorithm uses different methods of generating alternatives (lines 13 and 18).

The fuzzy self-tuning method is an automatic parameter adjustment method for FFO, which automatically adjusts parameter changes in the algorithm (line 7). There are two types of parameters in the fuzzy self-tuning method: one is a fixed parameter. It mainly includes the population number N of FFO and the size of the survival list NL = N/4. The other is variable parameters, which change according to the situation. They mainly include parameters a and pa used in the movement of flying foxes part.

After initializing the population, the algorithm enters the main iteration process: the movement, death and regeneration of the flying fox population. During each cycle, the globally best solution of the function is approximated. Here is how the iteration unfolds: by utilizing the fuzzy self-tuning approach to determine the parameters a and pa used in the movement of flying foxes part based on their current situation within the population (line 7). After the parameters are determined, the flying foxes engage in movement to evade the menace of heat waves (line 8). When the movement of flying foxes is completed, start to evaluate the flying fox individuals in the population to check whether there are any flying fox individuals that have moved to the heat wave area (a search space far away from the historical optimal point) (line 9). If it exists, enter death and replacement of flying foxes through SL. The algorithm uses the survival list method to generate a new individual to replace the dead flying fox (lines 12 and 13). After determining that all flying foxes in the population are in the appropriate area in the search space, the algorithm begins to check whether there are multiple flying fox individuals gathered together (Suffocate) (line 18). If it exists, enter death and replacement of flying foxes through SL and crossover. The algorithm causes some of the gathered individuals to die, and the algorithm will randomly use a method in the survival list or crossover to generate new individuals to replace the dead flying foxes. The aforementioned describes the algorithm’s repetitive procedure. If the termination criteria remain unfulfilled, the algorithm will iterate one by one and gradually approach the best approach globally of the function. After the end condition is satisfied, the algorithm exits the iterative process and outputs the recorded historical optimal solution, which is the output result of FFO.

2.2 Motivation

FFO has a good performance in SOPs, but there are some problems. FFO has a certain defect in the problem of population diversity. Replacing dead flying fox individuals using the survival list method may not consistently help steer the algorithm away from local optima. Toward the end of the algorithm’s run, most of the excellent candidate solutions within the population tend to cluster in a certain local area, resulting in the newly generated solution possibly still being located within the identical zone of the exploration domain. This exposes the problem of population diversity in FFO, which will significantly impact the algorithm’s capability in optimizing performance. In addition, the randomization initialization strategy of FFO will also affect the convergence effect of the algorithm. The random initial strategy may generate a poor initial population, which will greatly affect the subsequent optimization process of the algorithm.

This paper introduces IFFO to improve the above problems. Concerning diversity, IFFO improves the survival list method mentioned in the paper to ensure that its newly generated solution can jump out of the nearby area of the search space. Furthermore, to enhance the initial population’s quality and expedite algorithm convergence, IFFO uses an initialization strategy based on opposition-based learning.

3  The Proposed Search Mechanism

As shown in Fig. 1, in response to the lack of population diversity, IFFO uses opposition-based learning and niching techniques to enhance the survival list method. The main concept for improvement involves modifying the selection strategy of the survival list. Selecting flying fox individuals into the survival list only based on the objective function’s value often causes the aggregation of individuals around a local optimal point within the internal population of the list. Therefore, it is difficult for the generated flying fox to break free from the locally best solution. The optimized selection strategy will select some distant individuals, so that the newly generated solution is more likely to escape the local optimum, thus ensuring the population diversity of the algorithm.

Figure 1: The framework of IFFO (The dotted line box is the original algorithm, the green solid line boxes are the improvements proposed in this paper)

Enhancing the algorithm’s population diversity may also bring about the problem of a reduction in its convergence rate. The rise in population diversity broadens the algorithm’s scope, enabling it to delve into numerous local optimal solutions across the search space in pursuit of the ultimate global solution. However, it will also diminish the number of populations exploring a specific local optimal solution, potentially slowing down convergence. To maintain the convergence speed, IFFO modifies the random initialization strategy of the original algorithm, opting instead for a population initialization approach rooted in opposition-based learning.

3.1 Initialization Strategy Based on Opposition-Based Learning

Opposition-based learning [19–22] introduces a unique approach: For a candidate method, calculate and evaluate its opposite solution, and select the better solution as the next generation individual. A large number of classical algorithms (e.g., PSO, DE, GA, GWO, etc.) [23–26] rely on this method for enhancing performance. The initialization strategy rooted in opposition-based learning leverages fitness value information to choose superior individuals for creating the initial group.

IFFO employs an innovative approach to initialization, drawing on opposition-based learning to enhance algorithm convergence. The proximity between each initial population member and the optimal candidate greatly influences convergence speed. When individuals are born close to the optimal value, then rapid convergence will occur for all its members. The convergence speed of randomly generated initial populations remains unknown. However, if the opposite individual of each individual is simultaneously accounted for, then there exists a 50% likelihood that either the member or its opposite individual will be nearer to the optimal individual. Selecting the nearer individual as the initial member of the population results in each individual being nearer to the best one, advancing convergence by a step. Therefore, compared with the random initialization strategy, opposition-based learning significantly boosts algorithm convergence speed.

xi′=li+ui−xi(2)

Population initialization utilizes opposition-based learning, employing the concept of the opposite solution. Eq. (2) gives the definition of the inverse solution X′=(x1′,x2′,⋯,xD′). Suppose X=(x1,x2,⋯,xD) is a candidate solution in a D-dimensional search area, xi∈[li,ui], and D denotes the optimization problem’s dimensionality.

The pseudo code of the initialization strategy based on opposition-based learning in IFFO is shown in Algorithm 2.

This strategy uses a random initialization strategy to generate an initial population Q, comprising N individuals, each with D dimensions. Then, according to each individual X within the population Q, use Eq. (2) to generate the opposite solution X’, compare the objective function values of the original individual X and the opposite solution X’, and select the smaller one to put into the population P. Finally, the initialization population is P.

3.2 Niching Techniques-Based Survival List Method

The original flying fox algorithm incorporated a vital component known as the survival list, aimed at managing the replacement of deceased flying foxes. The survival list contains the best NL candidate solutions within the population (selecting the NL candidate solutions with the smallest objective function values). The generation of flying fox (candidate solution) is determined by the candidate solution information in the survival list. The Eq. (3) for generating flying fox is as follows:

xi,jt+1=∑k=1nSLk,jtn(3)

where SLk,jt represents the k-th candidate solution in the survival list under t iterations and n is an integer generated at random with a range of [2, NL].

In the later stage of FFO, many flying fox members within the population tend to cluster around the current optimal point. Since the survival list’s selection criteria rely on the magnitude of the objective function, candidate solutions in the survival list are clustered near the same area of the search space. Therefore, replacing dead flying fox individuals using the survival list method may not consistently help steer the algorithm away from local optima, since the newly generated solution might occupy the same area of the search area.

To enhance the selection process of the survival list and mitigate the dominance of local optimal solutions, IFFO has refined its approach, and no longer selects based solely on the size of objective function values. In addition to considering the objective function value used by the original strategy, the new selection strategy is further based on the individual flying fox’s crowding degree within the population. In this case, the survival list will select a group of flying fox individuals with higher quality and less congestion, which can simultaneously ensure the diversity and high quality of flying fox individuals in the survival list.

To measure individual crowding degrees, IFFO uses niching techniques [27]. Niching techniques are based on the idea of shared resources and aim to promote the exploration of multiple optimal solutions or suboptimal solutions in the search space effectively gauging population diversity. Widely utilized in evolutionary algorithms, niching techniques play a pivotal role in addressing diversity concerns within populations.

The niching techniques process is introduced in detail below:

The shared function between two candidate solutions p and q within the population is shown in Eq. (4).

sh(p,q)={(1−d(p,q)r)2,ifd(p,q)<r0,otherwise(4)

Among them, d(p, q) measures the normalized distance between candidate solutions p and q relative to the existing population within the target domain. Furthermore, r, representing the scope of the ecological niche, is determined by the prescribed population size N and the target quantity m. The calculation method of r is shown in Eq. (5).

r=1Nm(5)

Using the shared function of Eq. (4), the crowding degree estimate cd of the candidate solution p in the current population P can be calculated. The method for calculating cd is presented in Eq. (6).

cd(p)=(∑q∈P,q≠Psh(p,q))12(6)

The crowding degree of each candidate solution within the population can be calculated using Eqs. (4)–(6). However, there is a problem with this calculation method. If there are multiple candidate solutions within a niche, and the distances between these candidate solutions are very close, then the crowding degree estimate cd of the candidate solutions within the niche will be high, and very near. In the next step of the selection process, because the crowding degree estimate cd is high (the crowding degree performance is poor), all candidate solutions in this niche are eliminated. Niching techniques aim to guide individuals to disperse across various areas within the search domain, discouraging them from clustering around a single solution. This facilitates comprehensive exploration of the problem space and allows the algorithm to discover diverse and non-dominated solutions. A niche is eliminated as a whole, which is obviously not in line with the design ideas of niching techniques.

The work of Li et al. [28] modified Eq. (4) to avoid the above problems. To calculate the shared function value of two candidate solutions within a specific domain, give them a weight based on their respective objective function values. Candidate sets with smaller objective function values are given a weight of 0.5, and candidate solutions with larger objective function values are given a weight of 1.5. The calculation method is shown in Eq. (7).

sh(p,q)={(0.5(1−d(p,q)r))2,if d(p,q)<r,  f(p)<f(q)(1.5(1−d(p,q)r))2,if d(p,q)<r,  f(p)<f(q)rand(),if d(p,q)<r,  f(p)<f(q)0,otherwise(7)

Shared functions affect how densely populated a space becomes. Individuals who are closer together will achieve lower crowding levels than their neighbors. For two individuals in a population that are uniquely adjacent to each other, their initial crowding level might be the same. However, the individual with a more advantageous position experiences a reduction of half the original crowding, while the other retains half of the original level.

Using improved niching techniques, IFFO modifies the survival list generation strategy. The specific generation strategy is shown in Algorithm 3. First, it will select NL/2 different optimal solutions within the population into the survival list. Within the remaining population Q, calculate its objective function fob(X) and crowding degree fcd(X) for each individual X. Sort the population Q in a non-dominated manner based on these values, and NL/2 is entered into the survival list before selection. Then, use Eqs. (2) and (3) to generate new flying foxes to replace the dead individuals.

IFFO uses the opposite solution at the end to expand population diversity and facilitate the algorithm’s escape from local optima in pursuit of the global optimum. By incorporating opposing solutions, IFFO effectively broadens the algorithm’s exploration scope. However, it is essential to reinforce domain-specific search efforts, especially for individuals whose initial solution outperforms its counterpart. In such cases, prioritizing domain search over exploration of opposing solutions proves more beneficial for overall development.

4  Experimental Studies

This section compares the performance of IFFO, the initial algorithm and additional algorithms, using a Benchmark Set, namely CEC 2017 [29]. All algorithms are coded using MATLAB. Algorithm experiments have been performed on an AMD, 3.30 GHz computer with 16 GB of onboard RAM. The experimentation involves each algorithm running until a predetermined number of function evaluations is reached, set at 100,000. Independent runs of each algorithm are conducted for 30 iterations, from which minimum, average, and variance values are derived.

4.1 Benchmark and Comparative Algorithms

The experiment employs the CEC 2017 benchmark, comprising 30 distinct functions categorized into Unimodal (F1–F3), Simple Multimodal (F4–F10), Hybrid (F11–F20), and Composition (F21–F30) functions. Since its development, CEC 2017 serves as a reliable yardstick for assessing the efficacy of single-objective optimization algorithms.

In addition to IFFO and the original algorithm, this paper also selects excellent metaheuristic algorithms in recent years for comparison to more comprehensively demonstrate the performance of IFFO. SOGWO [30], AOA [31], and JOSHHO [32] were selected.

Florentina et al. leveraged the approach of opposition-based learning to improve the HHO algorithm to address the issue of local optimal solution stagnation and premature convergence. GWO incorporates parameter adaptation to balance exploration and optimization, but Souvik and his team pushed its exploration capabilities further by integrating opposition-based learning and introducing SOGWO. Fatma and his team proposed a novel metaheuristic algorithm called Archimedes Optimization Algorithm (AOA) to address the problems. The design of the AOA draws inspiration from the fascinating physical law, Archimedes’ Principle. This principle mimics the buoyancy effect, where an object immersed in a fluid experiences an upward force proportional to the displaced fluid’s mass.

In this study, the initial parameters were taken from the default settings given in the original paper. Table 1 displays the distinct specifications for the three enhanced algorithms mentioned earlier. Among them, maxFE is the maximum function evaluation count, population size denotes the quantity of populations, C1–C4 are parameters involved in position update in the AOA algorithm, and jr is the parameter jumping rate in the JOSHHO algorithm. The original algorithms are all set according to their default parameters.

4.2 Strategy Effectiveness Analysis of IFFO

In validating the efficacy of the enhancement strategy, we set up the FFO1 algorithm to add the niching techniques, and the FFO2 algorithm to add the opposition-based learning initialization strategy. The CEC 2017 test set was optimized, including 10 dimensions and 30 dimensions. Other parameters were the same as in Section 4.1. Some experimental findings are summarized in Table 2 where mean and standard deviation metrics serve as benchmarks for performance evaluation.

Owing to spatial constraints, only a selection of indicative experimental outcomes from the test functions is showcased.

In the experimental results of 10-dimensional CEC 2017, both the FFO1 and FFO2 algorithms perform superior to the initial algorithm, and IFFO surpasses the other three algorithms with regard to performance generally. However, IFFO’s improvement strategy is not always effective. On the F20, the FFO1 algorithm performs better than FFO. This may be because on F20, IFFO’s population initialization strategy places the initial population in a poor search space. And its strategy has a certain degree of randomness and cannot guarantee a positive effect on all problems. In addition, in terms of stability, the results of the standard deviation show that although the algorithm with added niching techniques works slightly worse, in most cases opposition-based learning has a significant promotion effect. Therefore, the stability of IFFO is overall better than that of the original algorithm.

In the findings from the 30-dimensional CEC 2017, IFFO outperforms the other three algorithms. The FFO2 algorithm exhibits notably enhanced (or on par) capabilities compared to the original algorithm, whereas the FFO1 algorithm does not consistently outperform the original. The complexity of higher dimensions often hampers a single approach from universally enhancing the original algorithm’s efficacy across all scenarios. In the realm of local optimum, the opposite solution generated by opposition-based learning is always repeatedly explored within a certain search area, which wastes the number of evaluations and prevents the exploration of more meaningful areas. The niching techniques strategy maintains population diversity, while concurrently steering the algorithm towards a closer approximation of the optimal solution. This convergence may lead to a shift in the population towards the current optimum. When the two strategies are combined, niching techniques can select individuals with larger crowding distances, and the opposite solution generated by opposition-based learning may be selected by niching techniques. Consequently, this broadens the exploration scope, facilitating faster escape from local optima. In addition, in terms of stability, the results of the standard deviation show that due to the impact of the increase in dimension, the improved algorithm using niching techniques performs poorly, but opposition-based learning can play a role in promoting stability. Therefore, in high-dimensional cases, the stability of IFFO is not significantly different from that of the original algorithm.

4.3 Analysis of Comparison Results of Related Algorithms

The section presents a comprehensive examination of the experimental results for IFFO and comparative algorithms using both 10-dimensional and 30-dimensional test function sets, as depicted in Tables 3 and 4, respectively. Noteworthy results are highlighted within the tables. Among them, the rank sum represents the outcomes from the Wilcoxon rank sum test [33,34] comparing this algorithm with others at a 5% significance level. On 10-dimensional CEC 2017, compared alongside the initial algorithm and various benchmark algorithms, IFFO performed very well, showing strong optimization capabilities. On 30-dimensional CEC 2017, IFFO performed better, surpassing the original one.

According to the analysis of the Wilxcon hypothesis test results in Table 3, on 10-dimensional CEC 2017, IFFO performed significantly better than SOGWO on 21 test functions, performed markedly superior to AOA on 19 test functions, with a particularly strong advantage over AOA on 26 test functions. Furthermore, IFFO’s performance surpassed that of JOSHHO. Compared to the original algorithm, IFFO demonstrated significant enhancements across 7 test functions. The test functions markedly superior to the original algorithm are F6, F9, F10, F14, F18, F20, and F22.

To analyze the effectiveness of the improved strategy, we generated convergence curves for all algorithms across four distinct test functions: F6, F9, F10, and F20. The results are shown in Fig. 2. It can be concluded from F6, F9, and F20 that the utilization of opposition-based learning for initialization appears to significantly refine the initial population of IFFO, fostering proximity to optimal solutions. This strategic adjustment prompts the algorithm to abandon some search areas that have no exploration value in advance, so that the algorithm converges in advance. It can be concluded from F9, F10, and F20 that FFO has tended to converge after 1000 function evaluations and cannot get rid of the best solution locally and is trapped in the current position until the end of the algorithm. However, the integration of niching techniques within IFFO presents an alternative advantage, affording opportunities to break free from the best solution locally in the later stage (after 1000 function evaluations) and continue to explore the global optimal solution.

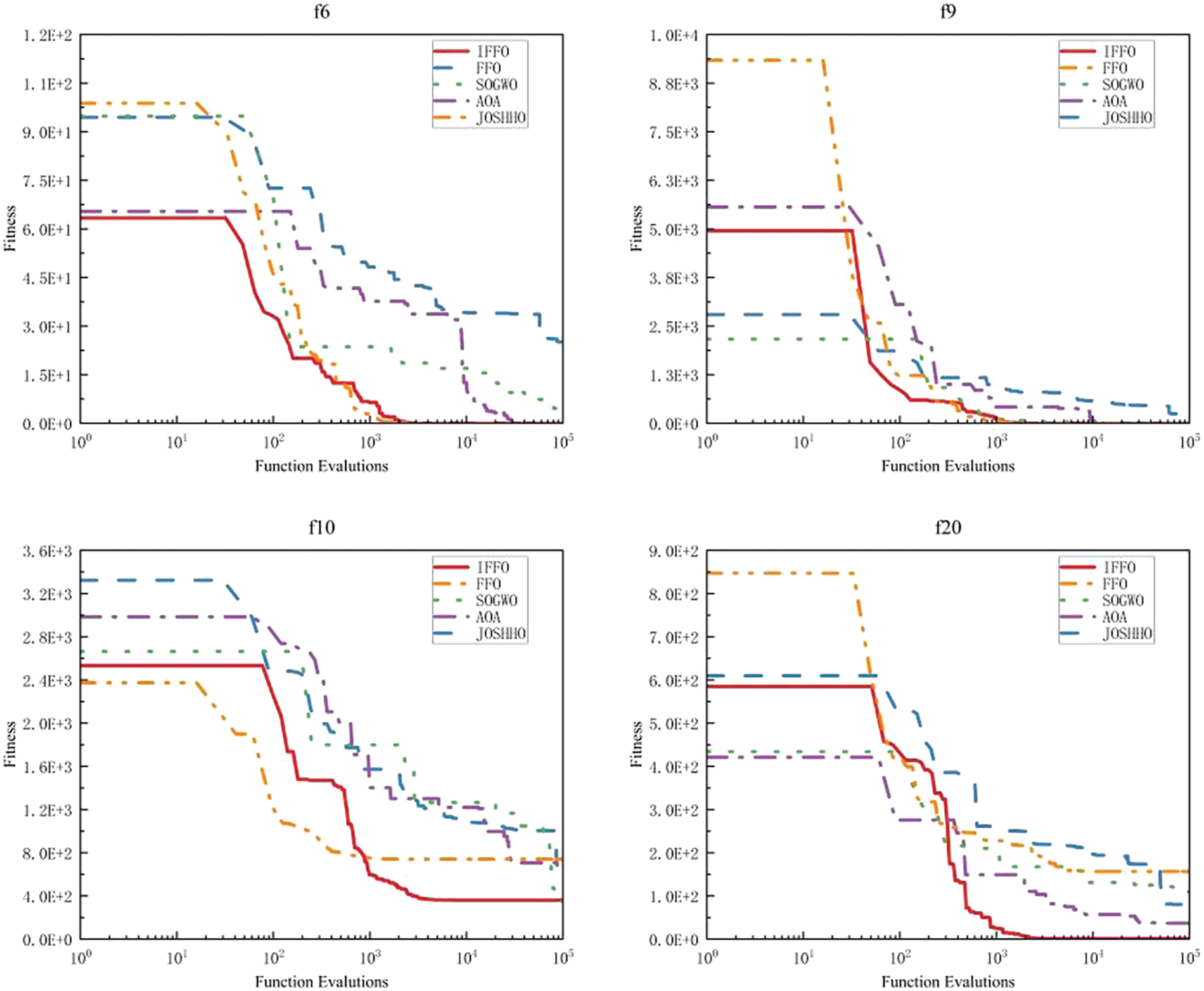
Figure 2: Convergence characteristic curves when performing some test functions on 10D CEC 2017

As shown in Table 3 on 10-dimensional CEC 2017, IFFO performed very well. When evaluating algorithm efficacy based on output averages, IFFO outperformed others on 17 test functions, while on the remaining 12 functions, its performance is equivalent or slightly worse than other algorithms. At the same time, viewed from the standpoint of minimum values, IFFO achieved the minimum value across 23 test functions, which shows that IFFO has strong optimization capabilities. In direct comparison with the base algorithm, the IFFO performs better than the original algorithm on 22 test functions, and is equivalent to or slightly worse than the original algorithm on the remaining 7 functions. At the same time, from the perspective of minimum values, the IFFO performed better than the original algorithm in 18 test functions, was on par with the original algorithm in 7 test functions, and showed slightly inferior results on the remaining four test functions. Furthermore, to assess the variance in stability between the enhanced and the original algorithm, an analysis of their standard deviation metrics is also conducted. The results show that IFFO is more stable than the original algorithm on 22 test functions. The stability on the other 8 test functions is slightly worse. This shows that IFFO achieves its results with minimal deviation.

According to the analysis of the Wilxcon hypothesis test results in Table 4, on 30-dimensional CEC 2017, IFFO markedly outperforms SOGWO on 17 test functions, markedly outperforms AOA on 21 test functions, and markedly outperforms AOA on 25 test functions. The performance markedly outperforms JOSHHO. Compared with the original algorithm, IFFO markedly outperforms the original algorithm on six test functions, which are: F10, F14, F18, F20, F22, and F24.

To analyze the effectiveness of the improved strategy, we generated convergence curves for all algorithms across four distinct test functions: F10, F20, F22, and F24. The results are shown in Fig. 3. It can be concluded from the four figures that the initial population of IFFO has no advantage compared with other algorithms. This limitation stems from the inherent complexity of implementing opposition-based learning in expansive search spaces, hindering its ability to effectively probe regions closer to the global optimum. Consequently, the initialized population after using the opposition-based learning initialization strategy is about one-third lower than the initial optimal solution of other populations. However, niching techniques can still help the IFFO convergence curve to decline rapidly in the early stage (10–100 function evaluations), and overcome local optima to explore the global optimum in later stages (after 1000 function evaluations).

Figure 3: Convergence characteristic curves when performing on some test functions on 30D CEC 2017

As shown in Table 4, on 30-dimensional CEC 2017, overall, IFFO performed better. When evaluating algorithm efficacy based on output averages, IFFO outperformed others on the 13 test functions. At the same time, from the perspective of minimum values, IFFO obtained the minimum value on the 15 test functions. When measured against the baseline algorithm solely based on average output performance across various tests, the IFFO performs better than the original algorithm on 22 test functions, and is equivalent to or slightly worse than the original algorithm on the remaining 7 functions. At the same time, from the perspective of minimum values, the IFFO performed better than the original algorithm on 22 test functions, and performed slightly worse on 7 test functions. In addition, to contrast the stability differences between the improved algorithm and the original one, the standard deviation indicators of the two algorithms were also analyzed. The results showed that IFFO was more stable than the original algorithm on 17 test functions.

In addition, to delve deeper into assessing IFFO’s efficacy, the experiment employs the Friedman test for statistical analysis to verify whether notable disparities exist between the algorithms. The Friedman hypothesis test uses the above experimental data to obtain the results. The hypothesis test results of IFFO and other algorithm experimental results are as follows. A lower rank value indicates superior algorithm performance.

It can be concluded from Table 5 that, on 10-dimensional and 30-dimensional CEC 2017, IFFO rejects the null hypothesis with a 95% level of statistical significance, indicating that a notable disparity in performance exists among the algorithms under comparison. Among them, IFFO not only performed better than the original algorithm but also ranked first among the five algorithms, further verifying the effectiveness of the improved strategy.

5  Conclusion and Future Work

The lack of population diversity is one of the key issues that metaheuristic algorithms currently face. A good search mechanism can provide effective solutions to the algorithm’s population diversity problem and improve its worldwide search abilities. This study introduces a search mechanism of opposition-based learning to enhance FFO. The mechanism not only accelerates the algorithm’s convergence but also enhances its population diversity. The proposed search mechanism mainly consists of two parts, namely niching techniques-based survival list method and initialization strategy based on opposition-based learning. In the death and replacement of flying foxes part of the original algorithm, IFFO uses niching techniques to assess the population’s crowding levels. By improving the selection strategy of the survival list method, not only the objective function value used by the original strategy is considered, but also flying fox individuals are selected based on the crowding degree obtained by niching techniques. This prevents the flying fox individuals in the survival list from gathering in a certain area in the search space, so that the newly generated flying fox individuals can get rid of the locally best solution. The new selection strategy enhances algorithmic diversity, encouraging exploration across diverse areas. However, it may impede convergence during the optimization process, thereby obstructing the attainment of the ultimate global optimum. To counter this, in the original algorithm’s population initialization phase, IFFO introduces an opposition-based learning strategy. In verification part, we conducted experiments on CEC 2017, compared and analyzed IFFO, FFO and the improved metaheuristic algorithms proposed in recent years, and analyzed the efficacy of the two improvement strategies used in the study within IFFO. The results demonstrate that IFFO outperforms and holds notable benefits against competing algorithms.

In addition, this paper has some limitations that may point the way to future research directions. The backward learning initialization strategy has its own shortcomings. When generating the initial population, it consumes more evaluation times than other initialization strategies, and there is also a situation where information is lost. When the selection mechanism of the initialization population is too greedy, some promising solutions and regional information will be discarded. In addition, IFFO requires overall information of the population when calculating individual crowding using niching techniques, which consumes a lot of time. This also points out the direction of future research. It is necessary to avoid the limitations of the search mechanism through more in-depth research to further improve IFFO’s optimization capabilities. In terms of algorithm structure, future research can pay more attention to the update mechanism of flying fox position, such as using a two-way local search strategy. In terms of algorithm application, it finds relevance in the efficient management of structural dynamics and the analysis of clustering, effectively tackling practical obstacles in engineering and industrial sectors across the globe.

Acknowledgement: The authors thank the anonymous reviewers and journal editors for their valuable insights and feedback.

Funding Statement: This research received support from the Ningxia Natural Science Foundation Project (2023AAC03361).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Chen Zhang, Liming Liu, Changsheng Zhang; data collection: Yu Sun, Jiaxu Ning, Yu Zhang; analysis and interpretation of results: Chen Zhang, Liming Liu, Yufei Yang, Ying Guo; draft manuscript preparation: Chen Zhang, Liming Liu, Yufei Yang, Yu Sun, Changsheng Zhang. All authors contributed equally to this work, reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in codes.rar at https://github.com/P-N-Suganthan/CEC2017-BoundContrained.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Ma, Z. Huang, X. Li, Y. Qi, L. Wang and Z. Zhu, “Multiobjectivization of single-objective optimization in evolutionary computation: A survey,” IEEE Trans. Cybern., vol. 53, no. 6, pp. 3702–3715, Jun. 2023. doi: 10.1109/TCYB.2021.3120788. [Google Scholar] [PubMed] [CrossRef]

2. A. Slowik and H. Kwasnicka, “Nature inspired methods and their industry applications—swarm intelligence algorithms,” IEEE Trans. Ind. Inform., vol. 14, no. 3, pp. 1004–1015, Mar. 2018. doi: 10.1109/TII.2017.2786782. [Google Scholar] [CrossRef]

3. C. Zhou, G. Liu, and S. Liao, “Probing dominant flow paths in enhanced geothermal systems with a genetic algorithm inversion model,” Appl. Energy, vol. 360, no. 1, pp. 122841, 2024. doi: 10.1016/j.apenergy.2024.122841. [Google Scholar] [CrossRef]

4. T. M. Shami, A. A. El-Saleh, M. Alswaitti, Q. Al-Tashi, M. A. Summakieh and S. Mirjalili, “Particle swarm optimization: A comprehensive survey,” IEEE Access, vol. 10, no. 4, pp. 10031–10061, 2022. doi: 10.1109/ACCESS.2022.3142859. [Google Scholar] [CrossRef]

5. M. P. Bilal, H. Zaheer, L. Garcia-Hernandez, and A. Abraham, “Differential evolution: A review of more than two decades of research,” Eng. Appl. Artif. Intell., vol. 90, no. 1, pp. 103479, 2020. doi: 10.1016/j.engappai.2020.103479. [Google Scholar] [CrossRef]

6. M. Abdel-Basset, W. Ding, and D. El-Shahat, “A hybrid harris hawks optimization algorithm with simulated annealing for feature selection,” Artif. Intell. Rev., vol. 54, no. 1, pp. 593–637, 2021. doi: 10.1007/s10462-020-09860-3. [Google Scholar] [CrossRef]

7. M. Gmira, M. Gendreau, A. Lodi, and J. Y. Potvin, “Tabu search for the time-dependent vehicle routing problem with time windows on a road network,” Eur. J. Oper. Res., vol. 288, no. 1, pp. 129–140, 2021. doi: 10.1016/j.ejor.2020.05.041. [Google Scholar] [CrossRef]

8. W. Zhao, Z. Zhang, and L. Wang, “Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications,” Eng. Appl. Artif. Intell., vol. 87, no. 5, pp. 103300, 2020. doi: 10.1016/j.engappai.2019.103300. [Google Scholar] [CrossRef]

9. W. Zhao, L. Wang, and Z. Zhang, “Artificial ecosystem-based optimization: A novel nature-inspired meta-heuristic algorithm,” Neural Comput. Appl., vol. 32, no. 13, pp. 9383–9425, 2020. doi: 10.1007/s00521-019-04452-x. [Google Scholar] [CrossRef]

10. Z. Wang and J. Liu, “Flamingo search algorithm: A new swarm intelligence optimization algorithm,” IEEE Access, vol. 9, pp. 88564–88582, 2021. doi: 10.1109/ACCESS.2021.3090512. [Google Scholar] [CrossRef]

11. J. Xue and B. Shen, “A novel swarm intelligence optimization approach: Sparrow search algorithm,” Syst. Sci. Control Eng., vol. 8, no. 1, pp. 22–34, 2020. doi: 10.1080/21642583.2019.1708830. [Google Scholar] [CrossRef]

12. S. Liao, Y. Wu, K. Ma, and Y. Niu, “Ant colony optimization with look-ahead mechanism for dynamic traffic signal control of IoV systems,” IEEE Internet Things J., vol. 11, no. 1, pp. 366–377, 2024. doi: 10.1109/JIOT.2023.3286799. [Google Scholar] [CrossRef]

13. S. S. Reddy and C. S. Rathnam, “Optimal power flow using glowworm swarm optimization,” Int. J. Electr. Power Energy Syst., vol. 80, no. 8, pp. 128–139, 2016. doi: 10.1016/j.ijepes.2016.01.036. [Google Scholar] [CrossRef]

14. M. Liu, K. Luo, J. Zhang, and S. Chen, “A stock selection algorithm hybridizing grey wolf optimizer and support vector regression,” Expert. Syst. Appl., vol. 179, pp. 115078, 2021. doi: 10.1016/j.eswa.2021.115078. [Google Scholar] [CrossRef]

15. M. Premkumar et al., “Augmented weighted K-means grey wolf optimizer: An enhanced metaheuristic algorithm for data clustering problems,” Sci. Rep., vol. 14, no. 1, pp. 5434, 2024. doi: 10.1038/s41598-024-55619-z. [Google Scholar] [PubMed] [CrossRef]

16. K. Zervoudakis and S. Tsafarakis, “A global optimizer inspired from the survival strategies of flying foxes,” Eng. Comput., vol. 39, no. 2, pp. 1583–1616, 2023. doi: 10.1007/s00366-021-01554-w. [Google Scholar] [CrossRef]

17. K. Borhan, X. D. Li, and A. K. Qin, “A review of population initialization techniques for evolutionary algorithms,” in 2014 IEEE Congress Evol. Comput. (CEC), Beijing, China, Jul. 2014, pp. 2585–2592. [Google Scholar]

18. E. K. Burke, J. P. Newall, and R. F. Weare, “Initialization strategies and diversity in evolutionary timetabling,” Evol. Comput., vol. 6, no. 1, pp. 81–103, 1998. doi: 10.1162/evco.1998.6.1.81. [Google Scholar] [PubMed] [CrossRef]

19. S. Mahdavi, S. Rahnamayan, and K. Deb, “Opposition based learning: A literature review,” Swarm Evol. Comput., vol. 39, no. 8, pp. 1–23, 2018. doi: 10.1016/j.swevo.2017.09.010. [Google Scholar] [CrossRef]

20. C. Zhong, G. Li, Z. Meng, and W. He, “Opposition-based learning equilibrium optimizer with Levy flight and evolutionary population dynamics for high-dimensional global optimization problems,” Expert. Syst. Appl., vol. 215, no. 4, pp. 119303, 2023. doi: 10.1016/j.eswa.2022.119303. [Google Scholar] [CrossRef]

21. S. K. Joshi, “Chaos embedded opposition based learning for gravitational search algorithm,” Appl. Intell., vol. 53, pp. 5567–5586, 2023. doi: 10.1007/s10489-022-03786-9. [Google Scholar] [CrossRef]

22. F. H. Shajin, B. A. Devi, N. B. Prakash, G. R. Sreekanth, and P. Rajesh, “Sailfish optimizer with Levy flight, chaotic and opposition-based multi-level thresholding for medical image segmentation,” Soft Comput., vol. 27, no. 17, pp. 12457–12482, 2023. doi: 10.1007/s00500-023-07891-w. [Google Scholar] [CrossRef]

23. M. Agarwal and G. M. S. Srivastava, “Opposition-based learning inspired particle swarm optimization (OPSO) scheme for task scheduling problem in cloud computing,” J. Ambient Intell. Humaniz. Comput., vol. 12, no. 10, pp. 9855–9875, 2021. doi: 10.1007/s12652-020-02730-4. [Google Scholar] [CrossRef]

24. F. Yu, J. Guan, H. Wu, Y. Chen, and X. Xia, “Lens imaging opposition-based learning for differential evolution with cauchy perturbation,” Appl. Soft Comput., vol. 152, no. 1, pp. 111211, 2024. doi: 10.1016/j.asoc.2023.111211. [Google Scholar] [CrossRef]

25. W. Ding, S. Chang, X. Yang, S. D. Bao, and M. Chen, “Genetic algorithm with opposition-based learning and redirection for secure localization using ToA measurements in wireless networks,” IEEE Internet Things J., vol. 10, no. 24, pp. 22294–22304, Dec. 2023. doi: 10.1109/JIOT.2023.3303353. [Google Scholar] [CrossRef]

26. X. Yu, W. Xu, and C. Li, “Opposition-based learning grey wolf optimizer for global optimization,” Knowl.-Based Syst., vol. 226, pp. 107139, 2021. doi: 10.1016/j.knosys.2021.107139. [Google Scholar] [CrossRef]

27. X. Li, H. Zhao, and J. Liu, “Minimum spanning tree niching-based differential evolution with knowledge-driven update strategy for multimodal optimization problems,” Appl. Soft Comput., vol. 145, no. 5, pp. 110589, 2023. doi: 10.1016/j.asoc.2023.110589. [Google Scholar] [CrossRef]

28. M. Li, S. Yang, and X. Liu, “Bi-goal evolution for many-objective optimization problems,” Artif. Intell., vol. 228, pp. 45–65, 2015. doi: 10.1016/j.artint.2015.06.007. [Google Scholar] [CrossRef]

29. N. H. Awad, M. Z. Ali, J. J. Liang, B. Y. Qu, and P. N. Suganthan, “Problem definitions and evaluation criteria for the CEC 2017 special session and competition on single objective bound constrained real-parameter numerical optimization,” in Technical Report. Singapore: Nanyang Technological University, Nov. 2016. [Google Scholar]

30. S. Dhargupta, M. Ghosh, S. Mirjalili, and R. Sarkar, “Selective opposition based grey wolf optimization,” Expert. Syst. Appl., vol. 151, no. 11, pp. 113389, 2020. doi: 10.1016/j.eswa.2020.113389. [Google Scholar] [CrossRef]

31. F. A. Hashim, K. Hussain, E. H. Houssein, M. S. Mabrouk, and W. Al-Atabany, “Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems,” Appl. Intell., vol. 51, no. 3, pp. 1531–1551, 2021. doi: 10.1007/s10489-020-01893-z. [Google Scholar] [CrossRef]

32. F. Y. Arini, S. Chiewchanwattana, C. Soomlek, and K. Sunat, “Joint Opposite Selection (JOSA premiere joint of selective leading opposition and dynamic opposite enhanced Harris’ hawks optimization for solving single-objective problems,” Expert. Syst. Appl., vol. 188, no. 2, pp. 116001, 2022. doi: 10.1016/j.eswa.2021.116001. [Google Scholar] [CrossRef]

33. J. Xue and B. Shen, “Dung beetle optimizer: A new meta-heuristic algorithm for global optimization,” J. Supercomput., vol. 79, no. 7, pp. 7305–7336, 2023. doi: 10.1007/s11227-022-04959-6. [Google Scholar] [CrossRef]

34. B. Irmak, M. Karakoyun, and Ş Gülcü, “An improved butterfly optimization algorithm for training the feed-forward artificial neural networks,” Soft Comput., vol. 27, no. 7, pp. 3887–3905, 2023. doi: 10.1007/s00500-022-07592-w. [Google Scholar] [PubMed] [CrossRef]