 Open Access
Open Access
ARTICLE
An Immune-Inspired Approach with Interval Allocation in Solving Multimodal Multi-Objective Optimization Problems with Local Pareto Sets
1 College of Computer Science and Technology, Zhengzhou University of Light Industry, Zhengzhou, 450001, China
2 Technology Research and Development Center, Jilin Tobacco Industry Company Limited, Changchun, 130031, China
3 College of Tobacco Science and Engineering, Zhengzhou University of Light Industry, Zhengzhou, 450001, China
4 Raw Material Department, Hongyun Honghe Tobacco (Group) Company, Kunming, 650202, China
* Corresponding Author: Zhi Rao. Email:
(This article belongs to the Special Issue: Recent Advances in Ensemble Framework of Meta-heuristics and Machine Learning: Methods and Applications)
Computers, Materials & Continua 2024, 79(3), 4237-4257. https://doi.org/10.32604/cmc.2024.050430
Received 06 February 2024; Accepted 12 April 2024; Issue published 20 June 2024
Abstract
In practical engineering, multi-objective optimization often encounters situations where multiple Pareto sets (PS) in the decision space correspond to the same Pareto front (PF) in the objective space, known as Multi-Modal Multi-Objective Optimization Problems (MMOP). Locating multiple equivalent global PSs poses a significant challenge in real-world applications, especially considering the existence of local PSs. Effectively identifying and locating both global and local PSs is a major challenge. To tackle this issue, we introduce an immune-inspired reproduction strategy designed to produce more offspring in less crowded, promising regions and regulate the number of offspring in areas that have been thoroughly explored. This approach achieves a balanced trade-off between exploration and exploitation. Furthermore, we present an interval allocation strategy that adaptively assigns fitness levels to each antibody. This strategy ensures a broader survival margin for solutions in their initial stages and progressively amplifies the differences in individual fitness values as the population matures, thus fostering better population convergence. Additionally, we incorporate a multi-population mechanism that precisely manages each subpopulation through the interval allocation strategy, ensuring the preservation of both global and local PSs. Experimental results on 21 test problems, encompassing both global and local PSs, are compared with eight state-of-the-art multimodal multi-objective optimization algorithms. The results demonstrate the effectiveness of our proposed algorithm in simultaneously identifying global Pareto sets and locally high-quality PSs.Keywords
Nomenclature
| NP | Population size |
| G | Evolutionary generations |
| Ci; | Cloning quantity of abi |
| Ri | Nondominated rank of abi |
| m | The number of objectives |
| L | The number of intervals |
| abi | ith antibody |
| CDi | Special crowding distance |
| Hypermutation operation | |
| Ns | Number of non-dominated solutions |
| Nc | Initial number of intervals |
| K | Number of clusters |
In many practical optimization problems, the consideration of multiple objectives is often necessary. Taking feature selection problems [1] as an example, one typically needs to optimize not only for the highest classification performance but also for minimizing the number of selected features to reduce computational complexity. Such optimization problems involving the simultaneous optimization of two or more objectives are well-known as multi-objective optimization problems (MOPs). Due to the potential conflicts between objectives, finding a solution in MOPs that outperforms another solution across all objectives is challenging. This leads to the establishment of a non-dominated relationship [2] between solutions, where one solution is not consistently superior to another. The optimal solutions, characterized by these non-dominated trade-off solutions in the decision space, are referred to as Pareto sets (PS). In the objective space, these solutions form the Pareto front (PF).
In certain MOPs, such as flow-shop scheduling [3], fighter vehicle control [4] and space mission design [5], it is common to encounter scenarios where multiple PSs correspond to the same PF, or even situations where there are both local PSs and global PSs. This type of problem is defined as a Multimodal Multi-Objective Optimization Problem (MMOP) with local PSs. The existence of multiple PSs corresponding to a global PF and local PSs associated with superior local PFs proves to be highly valuable in practical applications. Due to the complexity of real-world problems, they are often influenced by uncertain factors, such as constraints or environ-mental changes, leading to some optimal solutions becoming infeasible. Rapidly providing equivalent global optimal alternatives or locally optimal solutions of acceptable quality can offer decision-makers more choices and reduce the risks associated with uncertain factors. On the other hand, having multiple global PSs and local PSs can present a more comprehensive fitness landscape for the problem, providing valuable information for exploring the nature of practical optimization problems.
Recently, a notable focus has been on developing effective solutions for MMOPs. To solve these complex problems, several Multi-modal Multi-Objective Evolutionary Algorithms (MMEAs) have been introduced. A prevalent approach in this domain is the integration of techniques tailored for multimodal problem, such as niching based technique, with well-established multi-objective algorithms like Pareto-dominated based algorithms [2] and decomposition-based algorithms [6]. This integration aims to enhance the algorithms’ ability to handle both the multimodality and multi-objective aspects of the optimization problems effectively. For example, Liang et al. [7] introduced a niching strategy in the decision space within Non-dominated Sorting Genetic Algorithm-II (NSGA-II) [2], effectively enhancing the diversity of solutions in the decision space. Yue et al. [8] utilized an index-based ring topology to establish stable niches and proposes a special crowding distance to promote distribution of solutions. The quality of solutions is evaluated by combining the special crowding distance with non-dominated ranking.
While the previously mentioned MMEAs excel at discovering equivalent global PSs in the decision space, the exploration of high-quality local PSs presents a significant challenge. Approaches like the Multimodal Multi-objective Genetic Algorithm (MMOGA) [9] and the MMEA with dual clustering (MMOEA/DC) [10] leverage neighborhood and clustering techniques to partition niches, limiting competition among individuals to local regions and enhancing the preservation of local PSs. However, these algorithms often struggle with balancing the number and distribution of individuals across different niches. To tackle this issue, innovative strategies such as the MMEA based on weighted indicator (MMEA-WI) [11] and the MMEA with hierarchy ranking method (HREA) [12] introduce metrics to assess the local convergence performance of solutions. By incorporating local convergence quality, these methods restrict dominance relationships among individuals from the entire search space to local regions, effectively preserving local PSs. However, the inclusion of local convergence quality may come at the expense of global convergence capability. In situations where local PSs are distant from global PSs, this may lead the population to converge locally, creating challenges in simultaneously identifying both global and local PSs.
Compared to the introduced niching-based mechanism, an artificial immune system inherently possesses the capability to handle both multimodality and multi-objectives. Through antibody affinity maturation and variation [13], the immune system can concurrently recognize multiple antigens and adaptively adjust antibody concentrations through immunoregulation mechanisms. This is particularly advantageous for addressing MMOP with local PSs. Therefore, this paper proposes an immune-inspired algorithm to simultaneously address the challenges of multimodality and multi-objectivity in the problem. Moreover, we introduce an interval allocation based environmental selection to concurrently locate local PSs. The main contributions of this paper are as follows:
1. To achieve comprehensive coverage of both global and local PSs, we propose an Immune-based Reproduction Mechanism. This mechanism generates more offspring in sparse, promising regions while reducing the number of offspring in crowded and already explored regions by controlling the cloning size. Through adaptive allocation of computational resources, the exploration and exploitation are balanced effectively.
2. Instead of using the objective value directly as fitness, an interval allocation strategy is proposed to assign fitness. This strategy dynamically adjusts the relaxation of objective values through grid scaling. In the early stages, it permits the coexistence of more similar objective values, thereby enhancing diversity and providing survival space for multiple solutions. As the algorithm evolves, it incrementally increases the differentiation of fitness values among individuals, complementing environment selection to improve population convergence and facilitate exploitation capabilities.
3. A multi-population mechanism is introduced, wherein the interval allocation (IA) strategy is applied to each subpopulation for environment selection. Through precise control over subpopulations, it enables the algorithm to effectively locate and cover multiple global and local PSs.
4. Comparative experiments were carried out on 21 test problems encompassing both local and global PSs, wherein the proposed algorithm was compared against seven representative algorithms. The results of these experiments convincingly showcase the superior performance of our proposed algorithm in effectively identifying both local and global PSs.
The remainder of this paper is organized as follows. Section 2 provides an overview of related work on MMOP and immune-inspired algorithms. Section 3 elaborates on the specific strategies of the proposed algorithm MMIA_IA. Section 4 presents the experimental setup, results analysis, and discussions. Section 5 offers a summary and prospects for MMIA_IA.
2.1 Multimodal Multi-Objective Optimization
In recent years, MMOPs have gained attention, leading to the development of various MMEAs targeting global PS acquisition. Initially, Deb and Tiwari [14] identified multimodal characteristics in MOPs, introducing the first MMOP test problem, the omni-test problem. Subsequently, the SYM-PART [15] test problem was proposed. To advance MMOP research, Yue et al. [16] designed more complex MMOPs, the MMF benchmark test problems, with both local and global PSs. Numerous MMEAs followed, with Liang et al. [7] introducing a decision space niche mechanism for enhanced diversity, and Yue et al. [8] establishing a circular topology for stability and introducing a special crowding distance. Guided by the special crowding distance, Yue et al. [17] proposed MMODE_ICD, and Zhang et al. [18] employed K-means clustering for enhanced diversity. Liang et al. [19] used a clustering mechanism, and Qu et al. [20] introduced a grid-based mechanism. Li et al. [21] integrated a multi-population mechanism with grid techniques, and Qu et al. [22] utilized a species formation mechanism. Wu et al. [23] presented a multi-stage strategy, while Wang et al. [24] introduced a modified maximum extension distance metric. Hu et al. [25] and Liu et al. [26] segregated individuals into diversity and convergence archives, and decomposition-based and indicator-based approaches were employed, e.g., Tanabe et al. [27] proposed a decomposition-based multi-modal multi-objective algorithm framework, which assigns one or more individuals to the same subproblem to handle equivalent solutions. Similarly, Peng et al. [28] employed a decomposition-based framework, utilizing a clearing mechanism and greedy removal strategy to preserve equivalent global PSs. Additionally, Tanabe et al. [29] also introduced an indicator-based algorithm framework with a niche mechanism to locate multiple PSs in the problem.
Liu et al. [30], considering practical applications, devised an imbalanced test problem set of PFs with varying levels of search difficulty. Due to the predominant focus of many existing algorithms on population convergence, these algorithms often swiftly converge to PF that are easier to explore within the MMOP with the imbalance between convergence and diversity in the decision space (MMOP_ICDs). They struggle to escape local search regions, resulting in the algorithms ultimately identifying only one PS. In response to this challenge, Liu et al. [30] proposed a convergence-penalized density method to prevent premature convergence of the population. Based on this method, they proposed an evolutionary algorithm with convergence-penalized density method (CPDEA). Recently, Tanabe et al. [31] conducted a notable review, emphasizing the significance of seeking both global and local PSs. In practical applications, certain challenging to model uncertainties may render solutions on the global PS practically infeasible. Consequently, locally acceptable PSs can offer decision-makers a broader array of choices. However, within the existing landscape of MMEAs, only a handful of algorithms can effectively handle MMOPs with both local and global PSs. To address this research gap, Liang et al. [32] introduced the IEEE Congress on Evolutionary Computation (CEC) 2020 test problem set, comprising nine MMOPs featuring both local and global PSs. In a bid to simultaneously locate local and global PSs, Lin et al. [10] proposed an algorithm employing dual clustering in both decision and objective spaces, referred to as MMOEA/DC. Li et al. [12] employed hierarchical ranking methods to acquire both global and local PSs. Wang et al. [33] introduced a layer-to-layer evolution strategy and a clearing-based niche method to preserve some locally acceptable solution sets. Yue et al. [9] utilized a neighborhood mechanism to restrict competition among individuals, thereby maintaining local solutions. Liu et al. [34] introduced a dual niche strategy to enhance diversity and an additional archive set to preserve both global and local PSs.
The biological immune system has the ability to protect the body from antibody invasion and possesses an adaptive immune regulation mechanism. Inspired by this, numerous immune algorithms have been proposed. The primary concept derives from B lymphocytes, which can generate antibodies matching antigens through cloning and hypermutation. Immune-inspired algorithms typically involve five main operations: Initializing antibodies, evaluating antibody-antigen affinity, antibody cloning, mutation, and selection, as depicted in Algorithm 1.
Cloning: In the immune algorithm, each feasible solution is considered an antibody, and antibodies are replicated through a proportional cloning operation. The number of clones for each antibody is determined by its affinity, usually assigning more clones to individuals with higher fitness values.
Hypermutation: Unlike traditional genetic algorithms, the immune-inspired algorithm does not involve crossover operations. Instead, each antibody undergoes a hypermutation operation after cloning. This operation enhances the diversity of antibodies, facilitating a more comprehensive exploration of the solution space.
Selection: The selection strategy focuses on choosing antibodies with promising prospects to enter the next generation.

3.1 General Framework of MMIA_IA
In order to simultaneously locate global and local PSs in MMOPs, a multimodal multi-objective immune algorithm based on the interval allocation strategy (MMIA_IA) is proposed. The framework of MMIA_IA is illustrated in Algorithm 2. The antibody population is initialized and evaluated at first. Then, an immune-based recombination mechanism is introduced to generate offspring for each antibody in the population. After merging the offspring with the parent populations, the population is then partitioned into multiple subpopulations by using K-means clustering. Following this, the interval allocation-based environmental selection is applied to each subpopulation to select the well-converged and well-distributed antibodies to survive to the next generation. This process is repeated until the termination condition is satisfied. Finally, the nondominated solutions in the population P are output.

3.2 Immune-Based Reproduction Mechanism
To meet the requirement of concurrently locating both global and local PSs in MMOPs with local PSs, the algorithm must possess both global and local search capabilities. To address these challenges, we designed an immune-based reproduction mechanism, which includes two methods for implementation cloning. The pseudocode for immune-based recombination mechanism is shown in Algorithm 3.

Firstly, the number of non-dominated antibodies in population P is calculated and denoted as Nd. If Nd is less than half of the total population size NP, indicating insufficient convergence capability in the population, it is necessary to enhance the ability to explore local and global PF. In this case, the cloning size of each antibody is evaluated using Eq. (1).
where
It can be observed from Eq. (1) that antibodies with stronger convergence will generate more clones. When the number of non-dominated antibodies in the population exceeds half of the total population size NP, we encourage the population to learn around individuals with better diversity to enhance the uniformity of population distribution. In this situation, Eq. (2) is used to evaluate the cloning quantity for each antibody, where antibodies with larger crowding distances will produce more clones.
where
For each
Subsequently, the static hypermutation [18] is applied on each of the clones as Eq. (4).
Finally, all mutated clones are output as offspring Q. By adjusting the number of cloned individuals, this mechanism achieves a balance between exploration and exploitation of the population at different stages.
3.3 Interval Allocation Based Environmental Selection
To address the issue that local PSs are prone to domination by global PSs, an interval allocation strategy is proposed. In the proposed strategy, the objective space is partitioned into distinct intervals, where individuals within the same interval are assumed to possess identical fitness values. During the early stages of evolution, larger intervals are employed, where the fitness values exhibit minimal differentiation among individuals. This approach is conducive to retaining a diverse set of solutions, steering the exploration towards both global and local PF. As the iterative process unfolds, the intervals progressively shrink, leading to a gradual differentiation in fitness values among individuals. This meticulous adjustment ensures precise exploration, allowing the algorithm to adapt to the changing landscape of the optimization problem. The detailed implementation is outlined below:
Firstly, each dimension of the objective space is partitioned into intervals of size
where
Subsequently, the objective value of each individual is evaluated based on the determined intervals. The objective value is then adjusted according to the corresponding interval number. Individuals falling into the same interval are assigned identical fitness values. The fitness value of each individual is evaluated as Eq. (6).
where
The size of the grid cells is inversely proportional to the number of generations during the evolutionary process, as indicated by Eq. (5). In the initial stages, the grid has larger intervals, facilitating the coexistence of individuals in the same grid cell. This results in a weakened impact of differences in objective values between individuals, making it less likely for solutions to dominate each other. Consequently, this encourages the preservation of solutions with favorable convergence traits, promoting effective exploration in the early stage of evolution. As the algorithm progresses and the population becomes diverse with numerous non-dominated solutions, the grid intervals decrease, leading to a continuous increase in the number of grids. This dynamic adjustment enhances the discriminative capability of the grids, allowing for a more nuanced exploration of the solution space.

Fig. 1 provides an illustrative example to enhance the understanding of the interval allocation strategy. Assuming current iteration G = 1, with a predefined number of Nc set to 5. The range of the objectives
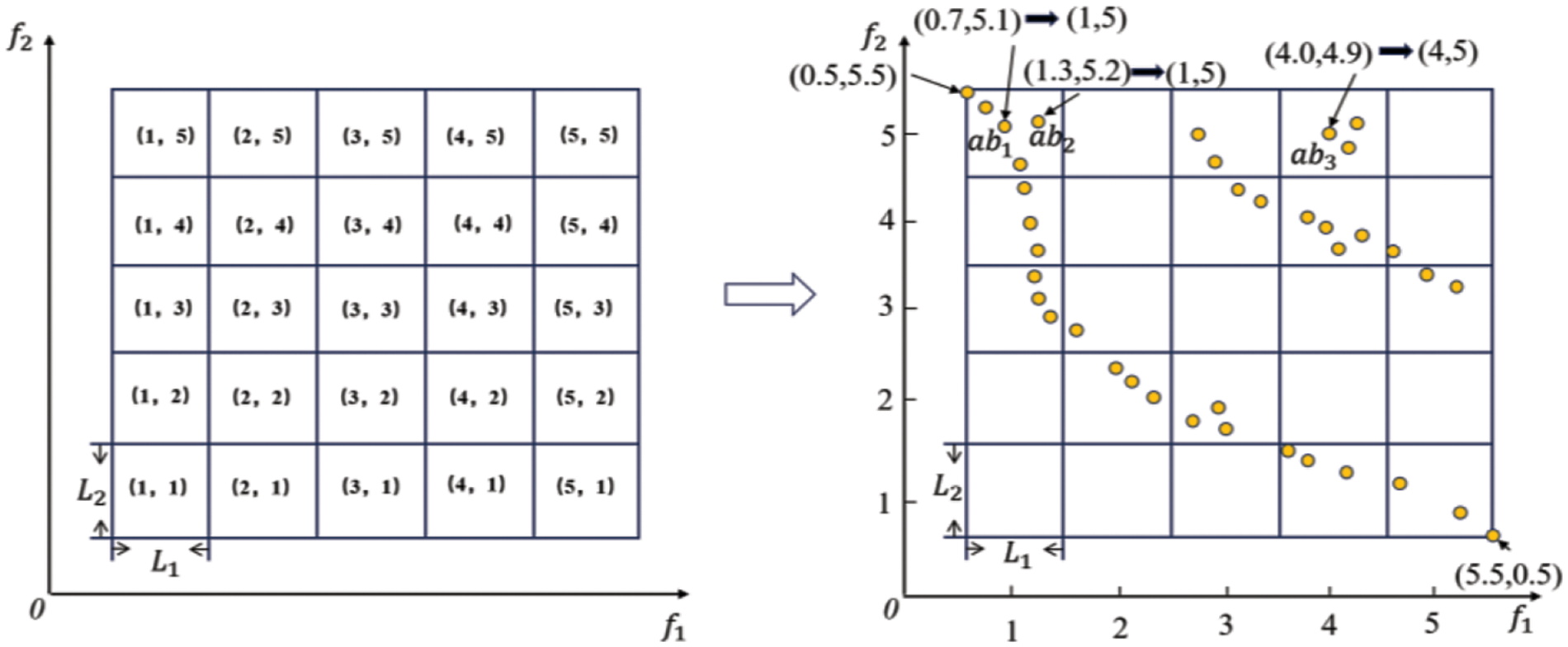
Figure 1: Illustration of interval allocation strategy, where
Algorithm 4 describes the environmental selection process based on the interval allocation strategy. Firstly, the size of each subpopulation is calculated. Then, the size of intervals
4 Experimental Results and Analysis
To evaluate the performance of the proposed algorithm in tackling MMOPs with local PSs, three test suites were utilized: The CEC 2020 MMOPs benchmark [32], the imbalanced distance minimization benchmark problems with epsilon-efficient solutions (IDMP_e) [12], and the Polygon-based MMOPs [34]. In the CEC 2020 MMOPs benchmark, 9 test problems feature local PSs, namely MMF10_l, MMF11_l, MMF12_l, MMF13_l, MMF15_l, MMF15_a_l, MMF16_l1, MMF16_l2, and MMF16_l3, respectively. These problems exhibit diverse PS shapes and various PF shapes, including convex PS, concave PS, nonlinear PF, and linear PF. Importantly, they demonstrate varying numbers of global PSs and local PSs. In the IDMP_e test suite, 8 test problems feature local PSs, including IDMPM2T1_e, IDMPM2T2_e, IDMPM2T3_e, IDMPM2T4_e, IDMPM3T1_e, IDMPM3T2_e, IDMPM3T3_e, and IDMPM3T4_e. These test functions possess multiple global PSs and concurrent local PSs. For instance, IDMPM2T4_e-e and IDMPM3T4_e-e feature 2 global PSs and 6 local PSs. These test functions present additional challenges as they are unbalanced, i.e., the computational resources required for solving different PSs differ.
Additionally, four Polygon-based MMOP test problems, denoted as Polygon1-4, were designed. These problems involve a variable number of global PSs and local PSs, along with variable radius and vertices of the polygon. Table 1 outlines the characteristics of these four polygonal test problems. In Table 1, M denotes the number of objectives, Radius signifies the size of the four PSs, and Global PS and Local PS indicate the quantity of global and local PSs, respectively. In Fig. 2, Polygon1-4 are illustrated to demonstrate the polygon-based MMOPs. Specifically, for Polygon1, Polygon3, and Polygon4, there are four equivalent PSs, consisting of a global PSs and three equivalent local PSs, respectively. For Polygon2, there are 2 global PSs and 2 inequivalent local PSs.

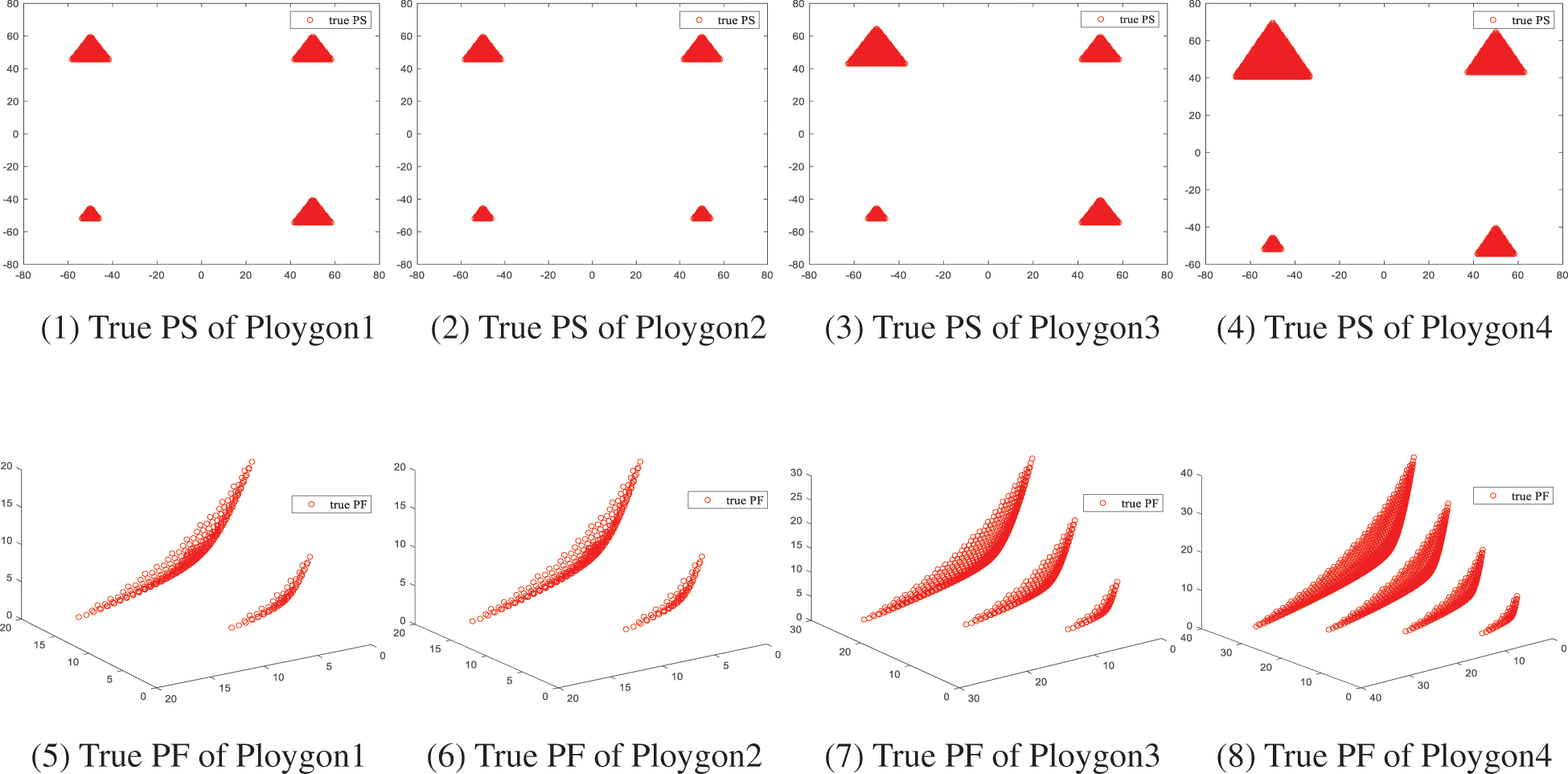
Figure 2: The true PS and true PF of three Polygon-based MMOPs
To assess the performance of algorithms in searching for global and local PSs, we employ the Inverted Generation Distance (IGD) [35] for both decision space and objective space. The IGDx indicator reflects the average Euclidean distance between the solutions obtained by the algorithm in the decision space and the true PS of the test problem. The IGDf indicator reflects the difference between the objective values of the solutions obtained by the algorithm and the true PF of the test problem. The calculation of these indicators is given by Eqs. (7) and (8).
where ps represents the obtained PS by the MMEA, pf represents the obtained PF by the MMEA. PS represents the true PS. PF represents the true PF. v represents the solution values in the true PS and PF,
To ensure fair comparisons, the population size (NP) is set to 100 times the number of decision variables (d), and the maximum function evaluation count (FES) is set to 5000 * d. All the experiments are 30 independent runs. Parameter settings for all comparative algorithms are maintained in line with the original literature. In MMIA_IA, the parameters
4.2 Comparison with the State-of-the-Art Algorithms
To evaluate the performance of MMIA_IA, this study conducts a comparative analysis with seven representative MMEAs: Omni-optimizer [14], MO-Ring-PSO-SCD (MRPS) [8], MMOHEA [25], CPDEA [30], MMEA_WI [11], MMOGA [9], MMOEA/DC [10] and CEA-LES [33]. These algorithms were chosen based on their prominence in solving MMOPs, and their performance has been widely validated. Omni-optimizer and MRPS are notable algorithms for MMOPs, while MMOHEA is a hybrid evolutionary algorithm incorporating a dual-archive approach. CPDEA and MMEA_WI are specifically designed to address imbalanced test problems. MMOGA, MMOEA/DC and CEA-LES are tailored for MMOPs featuring local PSs.
Table 2 displays the experimental results of average and variance in IGDx values for all compared algorithms. From the results of the rank-sum test, it is evident that MMIA_IA outperforms Omni-optimizer, MRPS, MMOHEA, CPDEA, and MMEAWI algorithms on almost every test problem, with a considerable advantage in terms of p-values. Furthermore, MMIA_IA exhibits superior performance compared to MMOGA, MMOEAD/C, and CEA-LES, which are state-of-the-art algorithms designed for MMOP with local PS. Although MMOEAD/C and CEA-LES achieve comparable performance to MMIA_IA on some problems, the calculated p-values demonstrate that MMIA_IA outperforms them significantly. Notably, MMIA_IA consistently emerges as the top-performing algorithm across 14 test problems: MMF10_l, MMF11_l, MMF13_l, MMF15_l, MMF16_l1, MMF16_l2, IDMPM2T4_e, IDMPM3T1_e, IDMPM3T3_e, IDMPM3T4_e, and Polygon1~4. In contrast, Omni-optimizer, MRPS, MMOHEA, MMOGA, CPDEA, MMEAWI, and MMOEA/DC secure the best IGDx values on 0, 0, 0, 0, 0, 0, and 7 test problems, respectively. MMOEA/DC ranks second, slightly behind MMIA_IA. MMOGA, designed for local PS localization, outperforms algorithms like Omni-optimizer, MRPS, and MMOHEA, which are tailored for global PS localization.
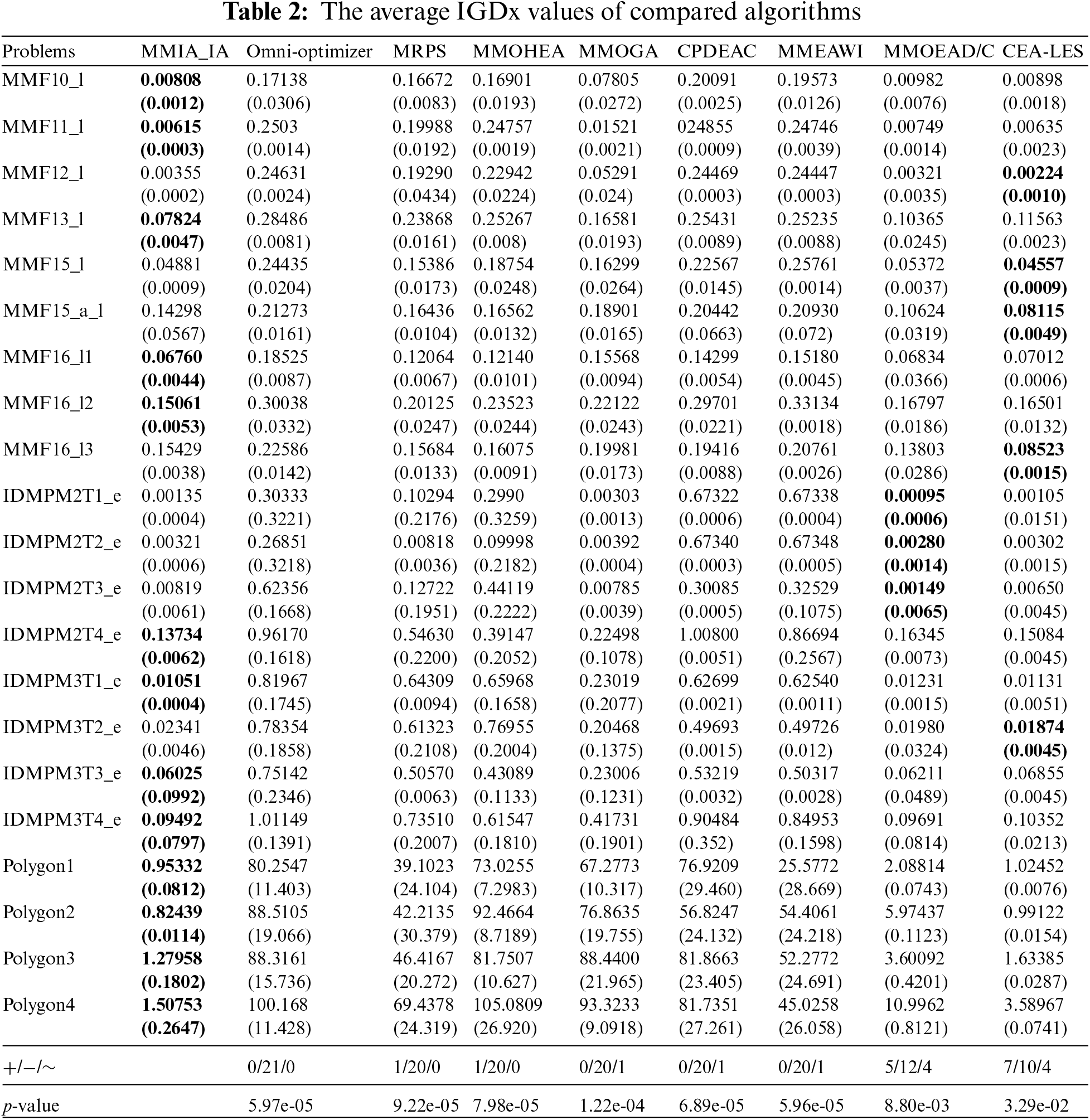
Among these comparative algorithms, Omni-optimizer, MRPS, and MMOHEA guide offspring generation through individuals with good convergence, while using a combination of crowding distance and non-dominance sorting for environment selection to locate equivalent global PSs effectively. However, the mechanism to maintain diversity in these algorithms fails to prevent local PSs from being dominated, resulting in only global PSs being located ultimately. MMOGA employs individual neighborhood information to guide offspring generation, using a predefined fixed neighborhood radius to partition individual neighborhoods. However, this neighborhood construction method performs poorly on test problems with complex PS shapes and numerous PSs. CPDEA and MMEAWI are designed for test problems with imbalanced PSs, introducing different local convergence qualities to judge the superiority of individuals. This approach limits competition among individuals to local regions, effectively preventing the population from clustering around a single PS. However, this method also fails to avoid local PSs being dominated by global PSs in MMOPs with local PSs, resulting in some PSs not being preserved. MMOEA/DC adopts a dual-clustering approach in decision space and objective space to enhance diversity in both spaces. The combination of these clustering methods can distinguish all PSs, and in environment selection, individuals from the most crowded clusters in the objective space are removed each time, preventing local PSs from being discarded when using non-dominance sorting for environment selection. Thanks to dual-space clustering in decision space and objective space, MMOEA/DC slightly outperforms MMIA_IA in handling MMF12_l, IDMPM2T2_e, and IDMPM2T3_e, which have more PSs. However, as the number of objectives increases, such as in IDMPM3T1_e, IDMPM3T3_e, IDMPM3T4_e, and the 4 Polygon test problems, MMIA_IA outperforms MMOEA/DC. This is because the effectiveness of objective space clustering decreases as the number of objectives increases. MMIA_IA effectively balances population diversity and convergence by adopting different cloning strategies in different convergence stages. The clustering method controls environmental selection pressure within local regions, allowing the algorithm to effectively handle complex problems with numerous and widely dispersed PSs in the decision space. Moreover, the interval allocation strategy relaxes dominance relationships in the early stages, allowing more potential solutions to be preserved, and conducts refined local search in the later stages. This interval allocation strategy maintains good performance even as the number of objectives increases, as demonstrated in IDMPM3T1_e, IDMPM3T3_e, IDMPM3T4_e, and Polygon1~4 test problems. CEA-LES employs a layer-to-layer evolutionary strategy and selection operation based on a clearing radius, effectively confining the search space to local regions. However, when the number of PSs is high and they are widely dispersed, the efficiency of the distance-based clearing strategy decreases. Additionally, interactions among individuals in adjacent layers with lower non-dominance ranks may lack elite guidance, leading to excessive local search. MMIA_IA effectively balances diversity and convergence by adopting different cloning strategies in different convergence stages. The clustering method controls environmental selection pressure within local regions, and the interval allocation strategy relaxes dominance strength in local regions. Consequently, MMIA_IA preserves well-distributed global and local PSs in MMOPs with local PSs. According to p-values, MMIA_IA significantly outperforms other comparative algorithms.
To visually illustrate the exceptional performance of MMIA_IA in the decision space, Fig. 3 show the experimental results for four algorithms (CPDEA, MMOHEA, MMOGA, and MMIA_IA) across test problems MMF12_l, IDMPM2T3_e, IDMPM3T2_e and Polygon4. Figs. 3(1) to 3(4) depict the results for MMF12. MMF11 features one global PS and one local PS, whereas MMF12 exhibits four global PSs and four local PSs. Notably, CPDEA and MMOHEA converge solely to global PSs on both test problems, neglecting local PSs.
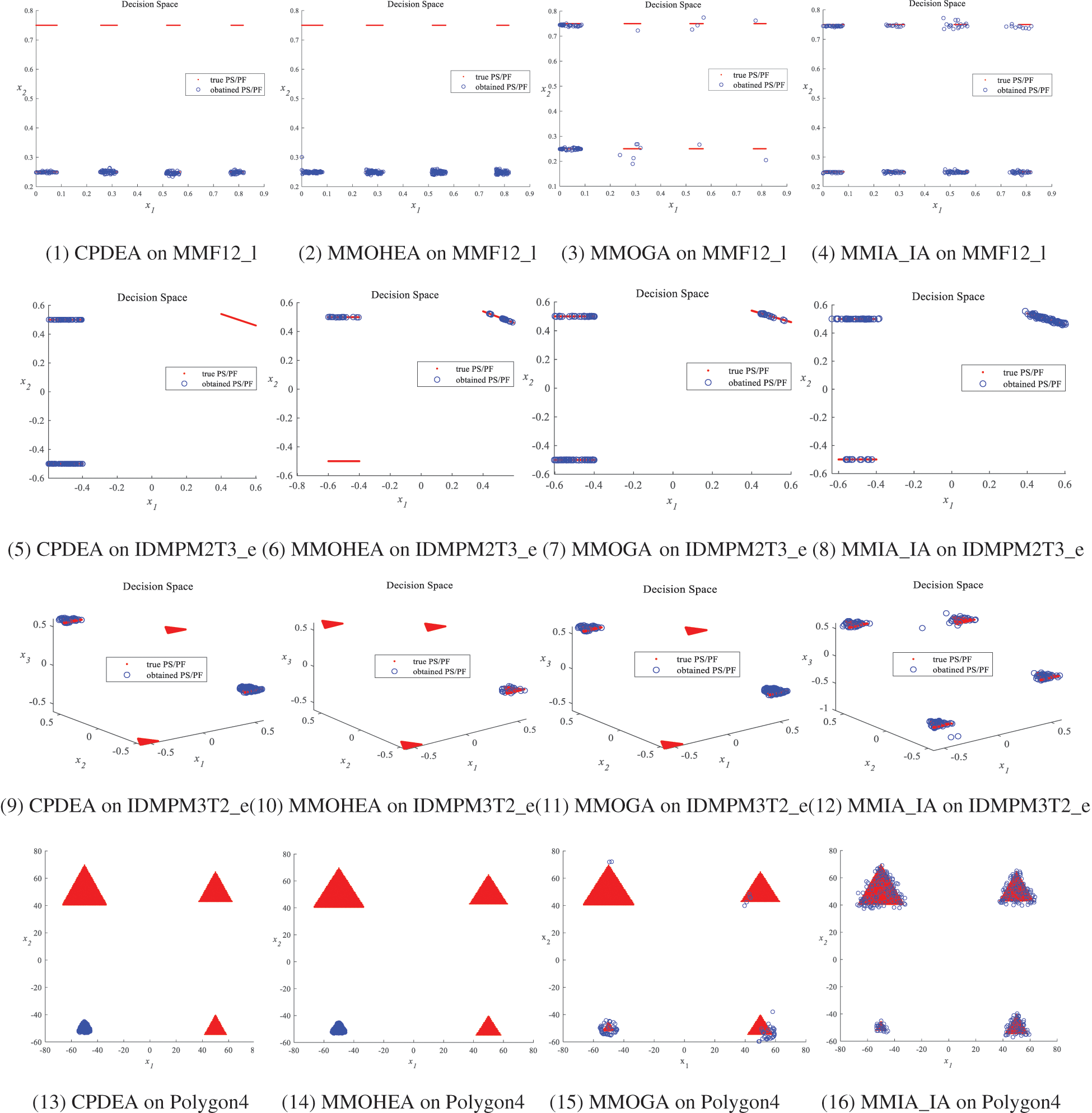
Figure 3: Distribution of PS obtained by several competing algorithms
While MMOGA captures global and local PSs on MMF11, it exhibits poor convergence and fails to locate all global and local PSs on MMF12. In stark contrast, MMIA_IA successfully identifies all global and local PSs on these test problems, achieving a uniformly distributed and well-converging solution set. Figs. 3(5) to 3(12) present the results for IDMPM2T3_e and IDMPM3T2_e. CPDEA converges effectively on multiple global PSs but falls short in locating any local PSs. MMOHEA, on both test problems, fails to identify all global and local PSs. MMOGA successfully captures all global and local PSs on IDMPM2T3_e but exhibits uneven distribution on local PSs. Additionally, on IDMPM3T2_e, MMOGA completely neglects local PSs, capturing only global PSs. In contrast, MMIA_IA excels in locating all global and local PSs on both problems, yielding a well-converging solution set. Figs. 3(13) to 3(16) depict the decision space performance of MMIA and the comparative algorithms on the Polygon4 test problem. It can be observed that MMIA_IA is capable of identifying all four PSs, despite variations in the size and considerable distances between them. Furthermore, MMIA_IA exhibits a well-distributed presence on each PS.
Fig. 4 presents the boxplots of IGDf results for different algorithms. It can be observed that the MMIA_IA algorithm achieves the best IGDf in 13 test functions: MMF10_l, MMF11_l, MMF12_l, MMF13_l, MMF15_l, MMF16_l1, MMF16_l2, IDMPM2T4_e, MMFM3T3_e and Polygon1~Polygon4. Moreover, the variance is very small in almost all test problems, indicating the high robustness of MMIA_IA. Additionally, MMOEAD/C performs exceptionally well, ranking second to MMIA_IA and demonstrating excellent performance on the IDMP_e test problem. However, several other algorithms fail to achieve the best IGDf values in any of the test problems.
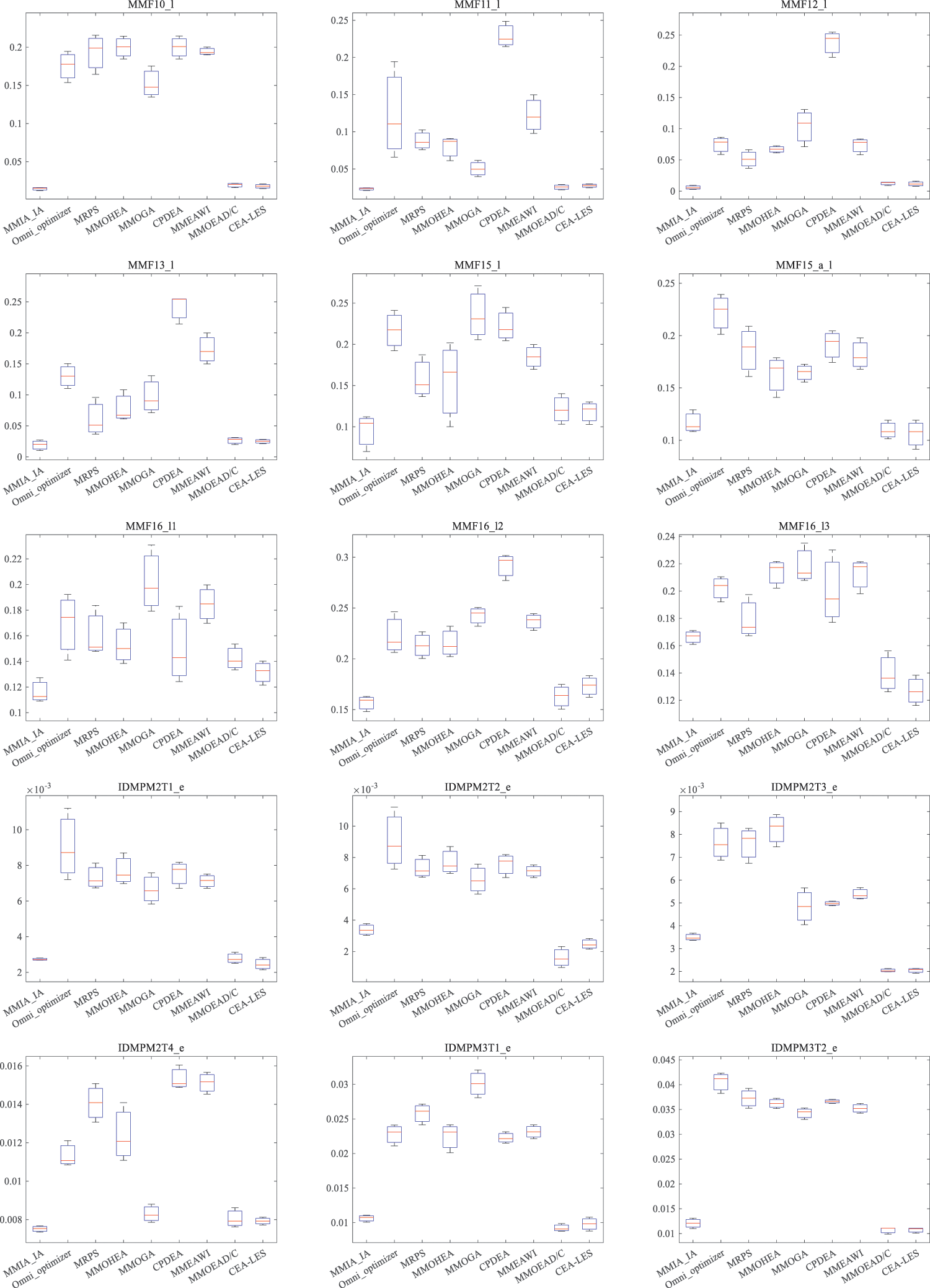
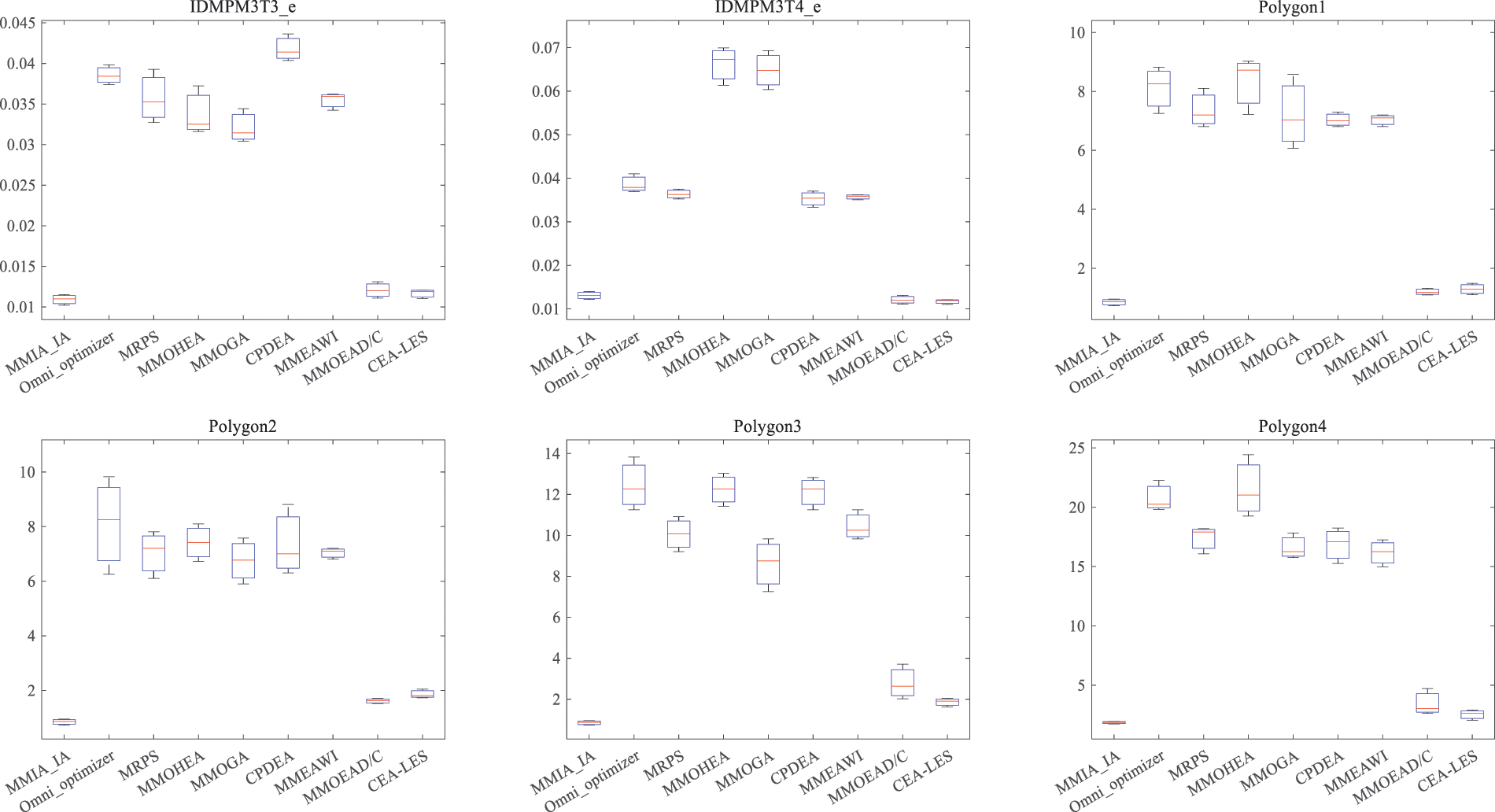
Figure 4: The boxplot of IGDf values for the comparative algorithms
The analysis of experimental figures in this section suggests that MMIA_IA excels in handling MMOPs with local PSs, showing outstanding performance in both decision space and objective space simultaneously.
4.3 Analysis of the Parameters
In our proposed algorithm, we introduce two main mechanisms: The immune-inspired recombination operation and the interval allocation-based environmental selection strategy. The parameters involved in the immune-inspired recombination operation, such as
Fig. 5 presents a bar chart of IGDx results for MMIA_IA using Nc values of 50, 100, 150, and 200, respectively. The optimal performance is observed when Nc is set to 100. A low number of intervals leads to slow population convergence and a small number of elite individuals, potentially causing the algorithm to converge only to local PSs within limited computational resources. Conversely, an excessively large number of intervals results in rapid convergence to global PSs, leading to an over-aggregation of the population towards global PSs, reducing search efficiency, and possibly neglecting local PSs. Fig. 6 displays the IGDx bar chart for MMIA_IA using different K on CEC 2020 MMOPs benchmark and IDMP_e test functions. The optimal performance is observed when the K is set to 10. The environmental selection strategy in MMIA_IA operates within clusters, and a too small K might lead to the neglect of certain local and global PSs in test functions with a significant number of PSs, resulting in inferior final results. On the other hand, when K is too large, some clusters may be placed in search regions without potential, reducing the search efficiency of the population.
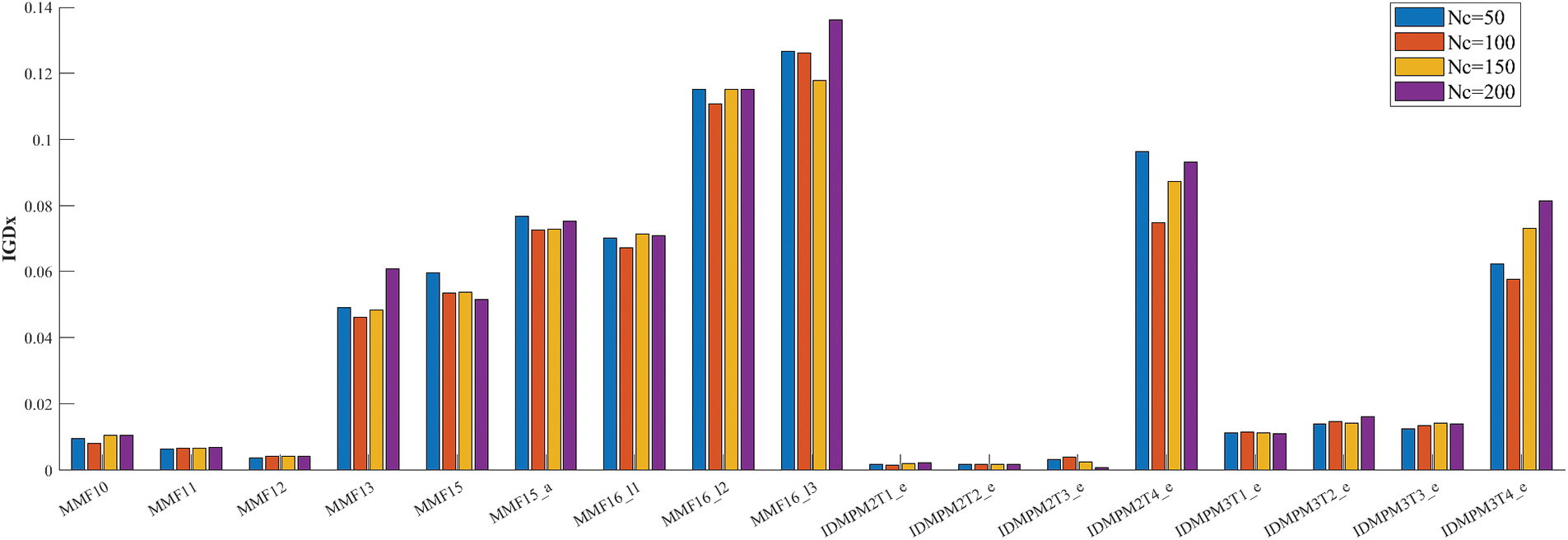
Figure 5: IGDx values obtained by MMIA_IA with different Nc
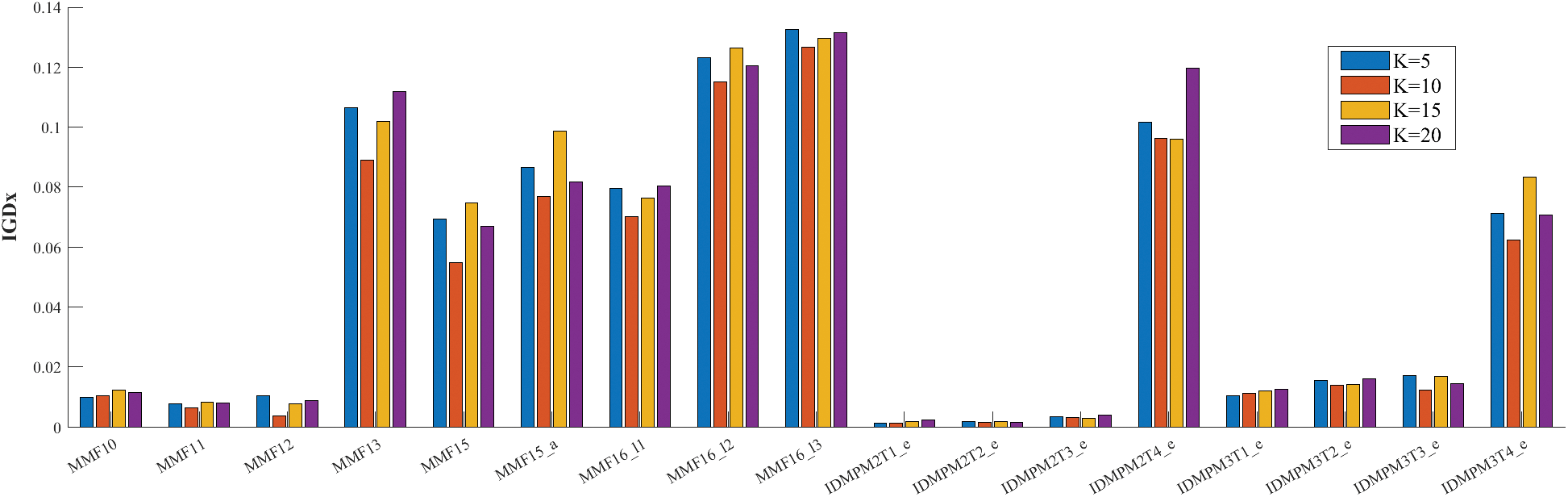
Figure 6: IGDx values obtained by MMIA_IA with different K
From Figs. 5 and 6, it is evident that the algorithm demonstrates overall insensitivity to the parameters K and Nc. Although some fluctuations are observed in individual test cases when K and Nc reach their maximum and minimum values, the overall range of variation in the experimental results (as indicated by the y-axis representing IGDx) is minimal (within the range of 0 to 0.14). This indicates the algorithm’s robustness to variations in these parameters.
In summary, the experimental results suggest that configuring K to 10 and Nc to 100 optimizes the search efficiency for both global and local PSs within the population. This configuration ultimately results in the best overall performance.
4.4 Analysis of the Effectiveness of Interval Allocation Strategy
To evaluate the effectiveness of the proposed Interval Allocation (IA) Strategy in handling MMOPs with local PSs, we conducted a comparative experiment. In this experiment, MMIA_without_IA does not incorporate target space interval allocation during environmental selection, utilizing actual objective values as its fitness. The performance of the proposed MMIA_IA and MMIA_without_IA is compared across 21 test functions. Table 3 presents the IGDx and IGDf metrics for both algorithms.
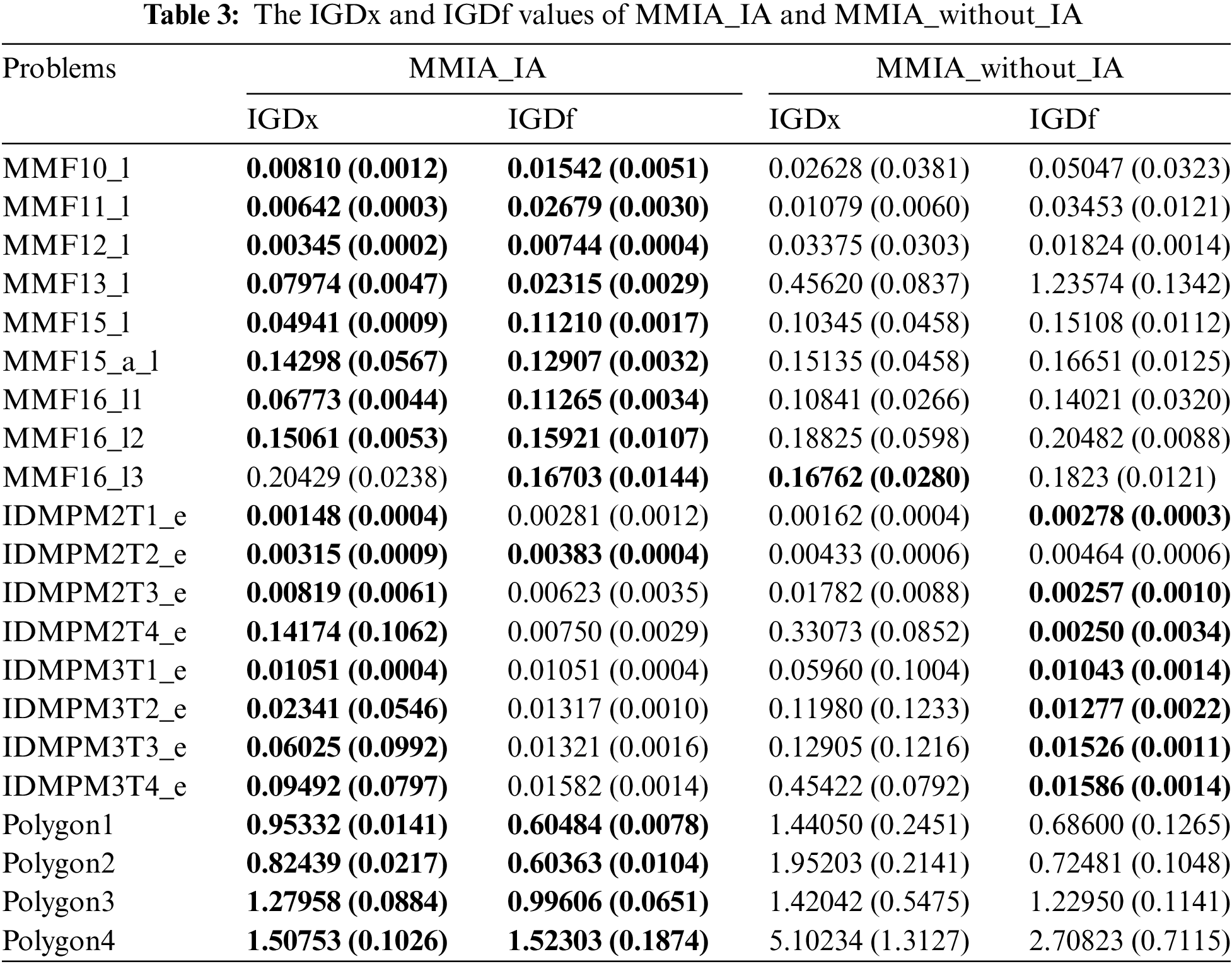
In summary, MMIA_IA exhibits better performance on MMOPs with local PSs, showcasing the effectiveness of the Interval Allocation strategy.
This paper introduces MMIA_IA, a novel immune-inspired algorithm. The paper proposes an innovative strategy that combines clustering technology with interval allocation, enhancing the capability of the immune algorithm to address MMOPs characterized by local PFs. Unlike existing algorithms that primarily tackle scenarios with multiple equivalent global PSs, MMIA_IA is specifically tailored to situations where local PSs offer decision-makers diverse solution options, potentially enhancing the effectiveness of addressing real-world problems. Through experimental comparisons with state-of-the-art algorithms, MMIA_IA demonstrates the ability to obtain a set of solutions with both good convergence and diversity in MMOP with local PFs. In future applications, our goal is to utilize this algorithm to optimize process parameters, ensuring efficient fermentation, and maintaining consistent high-quality tobacco leaf production, particularly in the context of cigar fermentation.
Acknowledgement: Not applicable.
Funding Statement: This work was supported in part by the Science and Technology Project of Yunnan Tobacco Industrial Company under Grant JB2022YL02, in part by the Natural Science Foundation of Henan Province of China under Grant 242300421413, and in part by the Henan Province Science and Technology Research Projects under Grants 242102110334 and 242102110375.
Author Contributions: Conceptualization, W.Z., J.L., M.L. and Z.R.; Methodology, W.Z., J.L. and Z.R.; Software, W.Z., J.L.; Validation, Z.R.; Investigation, W.Z., J.L., M.L., C.W. and Z.R.; Resources, C.W. and Z.R.; Writing—original draft, W.Z., J.L.; Writing—review & editing, W.Z., J.L., M.L. and Z.R.; Supervision, C.W. and Z.R.; Project administration, C.W. and Z.R.; Funding acquisition, M.L., C.W. and Z.R. All authors have read and agreed to the published version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare no conflict of interest to report regarding the present study.
References
1. C. T. Yue, J. J. Liang, B. Y. Qu, K. J. Yu, and H. Song, “Multimodal multiobjective optimization in feature selection,” in 2019 IEEE Congr. Evol. Comput. (CEC), Wellington, New Zealand, 2019, pp. 302–309. doi: 10.1109/cec.2019.8790329. [Google Scholar] [CrossRef]
2. K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. Evol. Comput., vol. 6, no. 2, pp. 182–197, Apr. 2002. doi: 10.1109/4235.996017. [Google Scholar] [CrossRef]
3. S. Janis Neufeld, S. Sven, and U. Buscher, “A systematic review of multi-objective hybrid flow shop scheduling,” Eur. J. Oper. Res., vol. 309, no. 1, pp. 1–23, Aug. 2023. doi: 10.1016/j.ejor.2022.08.009. [Google Scholar] [CrossRef]
4. Z. Taj, A. Bilal, M. Awais, S. Salamat, M. Abbas and A. Maqsood, “Design exploration and optimization of aerodynamics and radar cross section for a fighter aircraft,” Aerosp. Sci. Technol., vol. 133, pp. 108114, Feb. 2023. doi: 10.1016/j.ast.2023.108114. [Google Scholar] [CrossRef]
5. B. Sawik, “Space mission risk, sustainability and supply chain: Review, multi-objective optimization model and practical approach,” Sustainability, vol. 15, no. 14, pp. 11002, Jul. 2023. doi: 10.3390/su151411002. [Google Scholar] [CrossRef]
6. Q. F. Zhang and H. Li, “MOEA/D: A multiobjective evolutionary algorithm based on decomposition,” IEEE Trans. Evol. Comput., vol. 11, no. 6, pp. 712–731, Dec. 2007. doi: 10.1109/TEVC.2007.892759. [Google Scholar] [CrossRef]
7. J. J. Liang, C. T. Yue, and B. Y. Qu, “Multimodal multi-objective optimization: A preliminary study,” in 2016 IEEE Congr. Evol. Comput. (CEC), Vancouver, BC, Canada, Jul. 2016, pp. 2454–2461. doi: 10.1109/CEC.2016.7744093. [Google Scholar] [CrossRef]
8. C. T. Yue, B. Y. Qu, and J. J. Liang, “A multiobjective particle swarm optimizer using ring topology for solving multimodal multiobjective problems,” IEEE Trans. Evol. Comput., vol. 22, no. 5, pp. 805–817, Sep. 2017. doi: 10.1109/TEVC.2017.2754271. [Google Scholar] [CrossRef]
9. C. T. Yue, J. J. Liang, P. N. Suganthan, B. Y. Qu, K. J. Yu and S. Liu, “MMOGA for solving multimodal multiobjective optimization problems with local Pareto Sets,” in 2020 IEEE Congr. Evol. Comput. (CEC), Glasgow, UK, Jul. 2020, pp. 1–8. doi: 10.1109/CEC48606.2020.9185886. [Google Scholar] [CrossRef]
10. Q. Lin, W. Lin, Z. Zhu, M. Gong, J. Li and C. Coello, “Multimodal multiobjective evolutionary optimization with dual clustering in decision and objective spaces,” IEEE Trans. Evol. Comput., vol. 25, no. 1, pp. 130–144, Jul. 2020. doi: 10.1109/TEVC.2020.3008822. [Google Scholar] [CrossRef]
11. W. Li, T. Zhang, R. Wang, and H. Ishibuchi, “Weighted indicator-based evolutionary algorithm for multimodal multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 25, no. 6, pp. 1064–1078, May 2021. doi: 10.1109/TEVC.2021.3078441. [Google Scholar] [CrossRef]
12. W. Li, X. Yao, T. Zhang, R. Wang, and L. Wang, “Hierarchy ranking method for multimodal multiobjective optimization with local pareto fronts,” IEEE Trans. Evol. Comput., vol. 27, no. 1, pp. 98–110, Mar. 2022. doi: 10.1109/TEVC.2022.3155757. [Google Scholar] [CrossRef]
13. L. J. Li, Q. Z. Lin, and Z. Ming, “A survey of artificial immune algorithms for multi-objective optimization,” Neurocomputing, vol. 489, pp. 211–229, Jun. 2022. doi: 10.1016/j.neucom.2021.08.154. [Google Scholar] [CrossRef]
14. K. Deb and S. Tiwari, “Omni-optimizer: A procedure for single and multi-objective optimization,” in Third Int. Conf. Evol. Multi-Criterion Optim., Guanajuato, Mexico, Mar. 2005, vol. 3410, pp. 47–61. doi: 10.1007/978-3-540-31880-4_4. [Google Scholar] [CrossRef]
15. G. Rudolph, B. Naujoks, and M. Preuss, “Capabilities of EMOA to detect and preserve equivalent pareto subsets,” in 4th Int. Conf. Evol. Multi-Criterion Optim., Matsushima, Japan, Mar. 2007, vol. 4403, pp. 36–50. doi: 10.1007/978-3-540-70928-2_7. [Google Scholar] [CrossRef]
16. C. T. Yue, B. Y. Qu, K. J. Yu, J. J. Liang, and X. Li, “A novel scalable test problem suite for multimodal multiobjective optimization,” Swarm Evol. Comput., vol. 48, pp. 62–71, Mar. 2019. doi: 10.1016/j.swevo.2019.03.011. [Google Scholar] [CrossRef]
17. C. T. Yue et al., “Differential evolution using improved crowding distance for multimodal multiobjective optimization,” Swarm Evol. Comput., vol. 62, pp. 100849, Apr. 2021. doi: 10.1016/j.swevo.2021.100849. [Google Scholar] [CrossRef]
18. W. Z. Zhang, G. Q. Li, W. W. Zhang, J. Liang, and G. G. Yen, “A cluster based PSO with leader updating mechanism and ring-topology for multimodal multi-objective optimization,” Swarm Evol. Comput., vol. 50, pp. 100569, Nov. 2019. doi: 10.1016/j.swevo.2019.100569. [Google Scholar] [CrossRef]
19. J. J. Liang et al., “A clustering-based differential evolution algorithm for solving multimodal multi-objective optimization problems,” Swarm Evol. Comput., vol. 60, pp. 100788, Feb. 2021. doi: 10.1016/j.swevo.2020.100788. [Google Scholar] [CrossRef]
20. B. Y. Qu et al., “A grid-guided particle swarm optimizer for multimodal multi-objective problems,” Appl. Soft Comput., vol. 117, pp. 108381, Mar. 2022. doi: 10.1016/j.asoc.2021.108381. [Google Scholar] [CrossRef]
21. G. Q. Li, W. L. Wang, W. W. Zhang, Z. Wang, H. Y. Tu and W. You, “Grid search based multi-population particle swarm optimization algorithm for multimodal multi-objective optimization,” Swarm Evol. Comput., vol. 62, pp. 100843, Apr. 2022. doi: 10.1016/j.swevo.2021.100843. [Google Scholar] [CrossRef]
22. B. Y. Qu, C. Li, J. J. Liang, L. Yan, K. J. Yu and Y. Zhu, “A self-organized speciation based multi-objective particle swarm optimizer for multimodal multi-objective problems,” Appl. Soft Comput., vol. 86, pp. 105886, Jan. 2020. doi: 10.1016/j.asoc.2019.105886. [Google Scholar] [CrossRef]
23. T. Wu, F. Ming, H. Zhang, Q. Yang, and W. Gong, “Multimodal multi-objective optimization with multi-stage-based evolutionary algorithm,” Memetic Comput., vol. 15, pp. 377–389, Sep. 2023. doi: 10.1007/s12293-023-00399-8. [Google Scholar] [CrossRef]
24. Y. Wang, Z. Liu, and G. G. Wang, “Improved differential evolution using two-stage mutation strategy for multimodal multi-objective optimization,” Swarm Evol. Comput., vol. 78, pp. 101232, Apr. 2023. doi: 10.1016/j.swevo.2023.101232. [Google Scholar] [CrossRef]
25. Y. Hu et al., “A two-archive model based evolutionary algorithm for multimodal multi-objective optimization problems,” Appl. Soft Comput., vol. 119, pp. 108606, Apr. 2022. doi: 10.1016/j.asoc.2022.108606. [Google Scholar] [CrossRef]
26. Y. P. Liu, G. G. Yen, and D. W. Gong, “A multimodal multiobjective evolutionary algorithm using two-archive and recombination strategies,” IEEE Trans. Evol. Comput., vol. 23, no. 4, pp. 660–674, Nov. 2018. doi: 10.1109/TEVC.2018.2879406. [Google Scholar] [CrossRef]
27. R. Tanabe and H. Ishibuchi, “A framework to handle multimodal multiobjective optimization in decomposition-based evolutionary algorithms,” IEEE Trans. Evol. Comput., vol. 24, no. 4, pp. 720–734, Oct. 2019. doi: 10.1109/TEVC.2019.2949841. [Google Scholar] [CrossRef]
28. Y. M. Peng and H. Ishibuchi, “A decomposition-based large-scale multi-modal multi-objective optimization algorithm,” in 2020 IEEE Congr. Evol. Comput. (CEC), Glasgow, UK, Sep. 2020, pp. 1–8. doi: 10.1109/CEC48606.2020.9185674. [Google Scholar] [CrossRef]
29. R. Tanabe and H. Ishibuchi, “A niching indicator-based multi-modal many-objective optimizer,” Swarm Evol. Comput., vol. 49, pp. 134–146, Sep. 2019. doi: 10.1016/j.swevo.2019.06.001. [Google Scholar] [CrossRef]
30. Y. P. Liu, H. Ishibuchi, G. G. Yen, Y. Nojima, and N. Masuyama, “Handling imbalance between convergence and diversity in the decision space in evolutionary multi-modal multi-objective optimization,” IEEE Trans. Evol. Comput., vol. 24, no. 3, pp. 551– 565, Jun. 2020. doi: 10.1109/TEVC.2019.2938557. [Google Scholar] [CrossRef]
31. R. Tanabe and H. Ishibuchi, “A review of evolutionary multimodal multiobjective optimization,” IEEE Trans. Evol. Comput., vol. 24, no. 1, pp. 193–200, Apr. 2019. doi: 10.1109/TEVC.2019.2909744. [Google Scholar] [CrossRef]
32. J. J. Liang, P. N. Suganthan, C. T. Yue, B. Y. Qu, and D. W. Gong, “Problem definitions and evaluation criteria for the CEC, 2020 special session on multimodal multiobjective optimization,” Zhengzhou Univ., China, Apr. 2019. doi: 10.13140/RG.2.2.31746.02247. [Google Scholar] [CrossRef]
33. W. L. Wang, G. Q. Li, Y. L. Wang, F. Wu, W. W. Zhang, and L. Li, “Clearing-based multimodal multi-objective evolutionary optimization with layer-to-layer strategy,” Swarm Evol. Comput., vol. 68, pp. 100976, Feb. 2022. doi: 10.1016/j.swevo.2021.100976. [Google Scholar] [CrossRef]
34. Y. P. Liu, H. Ishibuchi, Y. Nojima, N. Masuyama and Y. Y. Han, “Searching for local Pareto optimal solutions: A case study on polygon-based problems,” in 2019 IEEE Congr. Evol. Comput. (CEC), Wellington, New Zealand, Aug. 2019, pp. 896–903. doi: 10.1109/CEC.2019.8790066. [Google Scholar] [CrossRef]
35. F. Li, Z. K. Shang, H. Shen, Y. P. Liu, and P. Q. Huang, “Combining modified inverted generational distance indicator with reference-vector-guided selection for many-objective optimization,” Appl. Intell., vol. 53, no. 10, pp. 12149–12162, Sep. 2022. doi: 10.1007/s10489-022-04115-w. [Google Scholar] [CrossRef]
36. L. De Capitani and D. de Martini, “Reproducibility probability estimation and testing for the Wilcoxon rank-sum test,” J. Stat. Comput. Simul., vol. 85, no. 3, pp. 468–493, Dec. 2013. doi: 10.1080/00949655.2013.825721. [Google Scholar] [CrossRef]
37. G. P. Coelho, F. O. de Franca, and F. J. Von Zuben, “A concentration-based artificial immune network for continuous optimization,” in 2011 IEEE Congr. Evol. Comput., Orleans, LA, USA, Jul. 2011, pp. 1242–1249. doi: 10.1109/CEC.2011.5949758. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools