Joint Modeling of Citation Networks and User Preferences for Academic Tagging Recommender System

1  Introduction

Tag recommendations help to limit the tagging vocabulary, thus improving annotation efficiency. Users can complete the tag attachment process with just a few clicks using the tag recommendation system. A tagging system is a crucial tool that helps users organize large quantities of academic information efficiently. Users can efficiently manage information and locate relevant resources using a tagging system. Users can tag articles individually in RefWorks (www.refworks.com), Connotea (www.connotea.org), CiteULike (www.citeulike.org) and Zotero (www.zotero.org). Zotero provides a free tagging system, as illustrated in Fig. 1. Tags selected by various individuals may be idiosyncratic and unpredictable. Moreover, different user actions can cause issues with entity recognition [1]. Tag recommendations enhance annotation efficiency by restricting the tagging vocabulary. Users can finish the tag attachment procedure efficiently using the tag recommendation system with minimal effort.

Figure 1: Zotero’s personalized tagging system allows users to customize article tags. Personalized labelling service is provided on the right side to facilitate literature management

Based on the realized methods, the current label recommendation can be broadly classified into three categories: Content-based methods, co-occurrence-based methods, and user preference-based methods. Content-based methods directly utilize item content for label recommendation. Content-based label recommendation generally does not consider user information but only the association between content information and item labels, such as term frequency–inverse document frequency (TF-IDF) [2]. Later on, the industry has developed methods that consider the order of words, e.g., reference [3] uses a capsule network to encode the intrinsic spatial relationships between the parts and the whole that make up the viewpoint-invariant knowledge, and another example in [4] builds a convolutional neural network considering the document topic and global semantics and inputs textual and word-vector features to predict the most relevant labels for unlabeled or few-labeled assigned items. The content-based approach is mainly used in the cold-start phase. Co-occurrence-based methods primarily utilize the co-occurrence of tags between items (i.e., the item-pagination matrix) for tagging. The fundamentals of co-occurrence-based and user preference-based approaches are similar to Collaborative Filtering (CF) approaches. As in [5], deep latent embeddings are learned from different item auxiliary information using a Variational Autoencoder (VAE), and generative distributions can be formed on each auxiliary information by introducing latent variables parameterized by a deep neural network. As in [6], correlations between user attribute labels and concepts extracted from usable parts of scientific papers are defined based on statistical, structural and semantic aspects.

However, the object of study of tag recommendation is the three subjects of users, items and tags, as well as the interaction between the subjects. Users may pay attention to items in various fields and have different paging habits. Therefore, ignoring user preferences will simplify the model, but at the same time, it will inevitably cause some critical information to be missing, which affects the recommendation ability of the model, so some studies have begun to consider the interaction between the three subjects. For example, Huang et al. [7] used a Tag-aware Attentional Graph Neural Network (TA-GNN) to extract user-label interaction and item-label interaction from the user-label-item graph structure. Another example is [8], which uses an autoencoder network of learned hidden representations to encode multiple types of relationships between entities, i.e., between users and labels, between items and labels, and between labels, and uses a decoder component to reconstruct the original inputs based on the learned latent representations. Literature [9] uses a metric learning approach to explore the distance relationships between user × item × label triples and applies existing metric learning-based approaches (i.e., latent relational metric learning (LRML), collaborative metric learning (CML), symmetric metric learning (SML)) to label recommendation.

However, users are accustomed to choosing their preferred labels for academic labelling recommendations, so papers read by similar users may be given the same label. For example, a mathematician may label the paper “Stochastic Variational Reasoning” [10] as “Statistics”, while a computer scientist may label the paper as “Machine Learning”. In addition, there is a citation relationship between articles, and usually, two articles with a citation relationship may be about the same topic, so that they may have the same label. Therefore, finding an effective way to combine citation networks, paper labelling and user paper matrices, remains challenging. This paper proposes new approaches to solve the multi-label recommendation problem for systems that provide closed-label recommendations. The main contributions of this paper are as follows:

To the best of our knowledge, this is the very first work to study multifactor Poisson factorization for tag-oriented recommender systems.

By extending the Poisson Factorization model, we propose to exploit the additivity of the gamma distribution to seamlessly integrate the three networks, namely, the paper labelling matrix, the citation network, and the user paper interaction matrix, into the same principle model.

Extensive experiments on real-world datasets have shown that the model significantly outperforms baseline models based on the paper label or user paper matrix. Furthermore, the computational complexity of the model is low.

Section 2 of this paper describes the related work on tagging recommendation, Poisson factorization recommendation, etc. Section 3 describes our Poisson Decomposition recommendation model with social regularization. Section 4 describes using the coordinate ascent algorithm to infer the model parameters. Finally, Section 5 validates the experimental performance of the model on the CiteULike dataset.

2  Related Works

This section provides an overview of the current research on tag recommendation and the Poisson factorization-based recommender system closely associated with this work.

2.1 Tag Recommendation

The article emphasizes the importance of tag recommendation systems in academic resources to alleviate information overload and improve user tagging experience [11]. It outlines three primary tag recommendation methods: Content-based, co-occurrence-based, and user preference-based approaches [1].

2.1.1 Content-Based Tag Recommendation

Content-based tag recommendation methods primarily focus on the association between an item’s content and its labels, often ignoring user information and behaviors patterns [12–14]. Initially, these methods treated the text as a “Bag of Words” (BoW) [15], using word frequency [16] for feature extraction and feeding these features into multi-label classifiers. However, this approach did not accurately capture the importance of each word, leading to the adoption of Term Frequency–Inverse Document Frequency (TF-IDF) [2] for more effective text representation. Despite advancements, these methods still overlooked the sequential structure of text, neglecting sentence-level information. To address this, deep learning techniques, such as capsule networks [3] and convolutional neural networks [4], have been employed to consider both word-level and sentence-level information, enhancing the model’s ability to predict relevant tags [13]. Additionally, external knowledge bases like knowledge graphs [17] and pre-trained models [18] have been integrated to improve the recognition of new concepts and to capture richer semantic information. However, these additions can introduce complexity and noise. Despite these efforts, content-based methods still struggle to reflect personalized user preferences and group intelligence.

2.1.2 Co-Occurrence-Based Tag Recommendation

Co-occurrence-based methods enhance tag recommendation by exploring correlations between tags, leveraging conditional probabilities and deep learning techniques like Variational AutoEncoders (VAE) [5] to learn latent embeddings and predict label recommendations [6]. These methods also consider tag structures, as seen in [14], which uses graph diffusion mechanisms and hierarchical tag structures [19] for better performance. Furthermore, label semantic-based approaches, such as those using Graph Convolutional Networks (GCNs) [20] and pre-trained word vectors like Global Vectors for Word Representation (GloVe), enrich the semantic information of labels [21], guiding the content representation for improved classification. To capture the complex interactions in tag recommendation, Neural Graph for Personalized Tag Recommendation (NGTR) [22] employs graph neural networks within a tensor decomposition model, integrating neighborhood representations to enhance the encoding of entity relationships.

2.1.3 Tag Recommendation Based on User Preferences

User preference-based methods in tag recommendation systems address the multi-label classification problem by considering the interactions among users, items, and tags. These methods often combine user and item representations, from user-to-user, user-to-item, and item-to-item interactions, to capture individual preferences and enhance model accuracy [23]. Techniques such as hierarchical attention models and graph neural networks integrate collaboration signals and generate richer entity representations [24]. Additionally, some works explore different vector spaces to learn entity representations and measure semantic correlations [25], such as using hyperbolic spaces and tangent space optimization [26]. To directly capture the interactions between users, items, and tags, methods like the Tag-aware Attentional Graph Neural Network (TA-GNN) [7] and variational self-encoders [8] have been proposed, which utilize attention mechanisms and metric learning to understand better and leverage these interactions [9]. This paper contributes to the field by proposing a collaborative filtering model that integrates tag co-occurrence and user preference, aiming to optimize the utilization of interaction data in academic tagging.

2.2 Poisson Factorization for Recommendation System

Poisson factorization is a matrix decomposition technique applied in recommender systems, notably for its effectiveness in handling sparse datasets. It has been utilized in models like Collaborative Topic Poisson Factorization (CTPF) [27] and Collaborative Topic Regression (CTR) [28] to integrate topic distributions with item representations and alleviate data sparsity. The multilayer Poisson decomposition model [29] is introduced to describe the combination of users’ purchase budgets and preferences for items. The method reduces computational complexity and capitalizes on the value of long-tail items. Poisson factorization excels in sparsity modelling, diminishing the impact of unvisited items on predictions, and demonstrates flexibility, scalability, and robustness in the presence of noisy or missing data. These attributes make Poisson factorization a powerful tool for various applications, including recommender systems, text mining, and image processing. This paper proposes a novel approach that regularizes the Poisson factorization of the paper-tag matrix using citation networks and user-paper interactions, offering improvements over existing methods that do not consider citation networks. It can fuse multiple contexts using the additivity property of the Poisson distribution.

3  Problem Description and Preparatory Knowledge

The two tasks closely related to tag recommendation are item recommendation and multi-tag classification, and part of the tag recommendation also draws on the idea of these two. As shown in Fig. 2a, the general item recommendation recommends a collection of items I={i1,i2,⋯,in} for the current user ui based on the user’s behavior and other information.

Figure 2: Paper recommendation, tag classification for papers and tag recommendation

The multi-tag classification problem generally refers to tagging a set of tags V={v1,v2,⋯,vm} for the current item ij based on its content information, as shown in Fig. 2b.

Tag recommendation refers to the process that when the current user ui wants to tag the target item ij (which often contains content information such as text, images or videos), the system automatically recommends a tag set V={v1,v2,⋯,vm} to the user for paper tagging. This tagging process is affected by the habit of user and project information. The relationship between user ui and project ij, tag vm is shown in Fig. 2c.

We base our study on the CiteULike dataset, which is collected from the CiteULike website. CiteULike provides three entities: Users, papers, tags, and their multidimensional relationships. To describe the formal model of CiteULike, we first give the relevant definitions:

Definition 1. User paper interaction network, the network formed by the user’s clicks, favorites and evaluation records of papers, can be expressed as an undirected graph structure, denoted as R=(U,I,S), where U denotes the set of users, I denotes the set of papers, and S denotes the set of user behaviors such as clicks, favorites, evaluations, etc. The CiteULike does not differentiate between multiple behaviors, and thus can be taken as R=(U,I).

Definition 2. Citation network, a directed graph network formed by paper-to-paper citation relationships, denoted as G=(I,E), where I denotes the set of papers and E denotes the set of edges of citation relationships between papers, i.e., E={(ik,ij)|ik,ij∈I}.

Definition 3. Paper-tag network, an undirected graph network formed by the relations between papers and tags, it denoted as C=(I,V), where I denotes the set of papers and V denotes the set of paper tags.

This paper further gives a heterogeneous data utilization model that fuses the three relationships of definitions 1∼3. This model can also be generalized to similar industry data.

Gopalan et al. [27] proposed the Bayesian Poisson Factorization (BPF) model. The BPF model assumes that the user’s responses to items (e.g., clicks, favorites, purchases, follows, ratings, comments, retweets, etc.), yui, follow a Poisson distribution:

yui∼Poisson(ηuTθi)(1)

where ηu and θi are K-dimensional non-negative vectors following a Gamma distribution, i.e.,

ηu∼Gamma(λua,λub)(2)

θi∼Gamma(λia,λib)(3)

where λua, λub is the shape parameter of the Gamma distribution and λia, λib is the scale parameter of the Gamma distribution. We can infer the values of ηu and θi by Gibbs sampling or variational inference.

4  Joint Modeling of Citation Networks and User Preferences

4.1 Context-Enhanced Poisson Factorization Models

We take advantage of the additivity of the gamma distribution and use the Poisson factorization model as a general framework, as modelled in the following equation:

yvi|y¬vi∼Poisson(ηvTθi+∑j=1|J|δvjsijyji+∑w=1|W|τvwsiw′ywi)(4)

where ηv is the hidden feature vector of the tag, θi is the hidden feature vector of the paper, sij is the user preference-based similarity between paper j and paper i, δvj is the attenuation coefficient of the user preference-based similarity, siw′ is the citation network-based similarity between paper w and paper i, and τvw is the decay coefficient of citation network similarity. yji is the set of papers that have been labelled i, and ywi is the set of papers that have been labelled i as well. In fact, the two sets are consistent. However, due to the different semantics of the two summation terms ∑j=1|J|δvjsijyji and ∑w=1|W|τvwsiw′ywi, to semantically distinguish these two terms, we take the middle variable of these two terms to be different. The probability plot of the model is shown in Fig. 3. From the above equation, we can see that when the value of yji or ywi in the matrix is 0, there is no need to calculate ∑j=1|J|δvjsijyji or ∑w=1|W|τvwsiw′ywi. For sparse matrices, this feature of Poisson factorization can save a large part of the computation. In the massive paper queue, the model call data is often only a few of them, so for the academic platform-oriented tagging recommendation, the Poisson factorization algorithm is a very suitable method.

Figure 3: Probabilistic graphical models

4.2 Article Similarity Metrics Based on User Preferences

This section introduces symmetric metapaths and computes the path similarity of the head and tail nodes (PathSim). The task can be described as, for example, finding the path similarity in the meta-path ‘paper → reader → paper’. The formula for path similarity is as follows:

s(x,y)=2×|px→y||px→x|+|py→y|(5)

where s(x,y) is the path similarity between node x and node y. |px→y| represents the number of paths between node x and node y in the case of a meta-path P. Intuitively, when there are more paths between nodes, the two nodes are more similar. The denominator in the formula is the number of total paths of the two nodes back to themselves as a normalization term.

Take the meta-path ‘paper → reader → paper’ as an example. The goal is to find the similarity of the paper. Suppose there are readers A1, A2, A3, A4, and papers B1, B2, B3, and their interaction matrices are shown in the following Table 1:

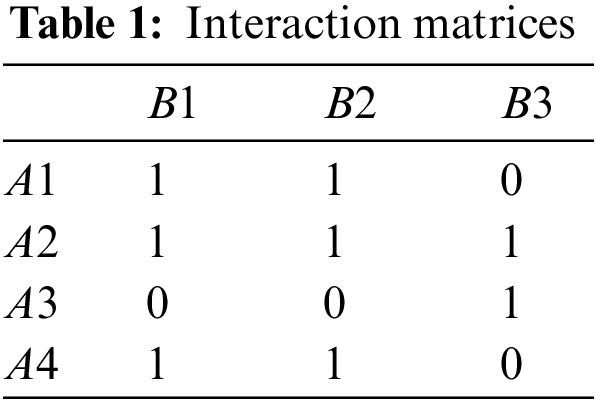
The data in the table can be represented as a bipartite graph as shown in Fig. 4. From Fig. 4, it can be easily noticed that B1 has 3 paths to B2, B1→A1→B2 and B1→A2→B2 and B1→A4→B2. It can be obtained that |pB1→B2|=3.

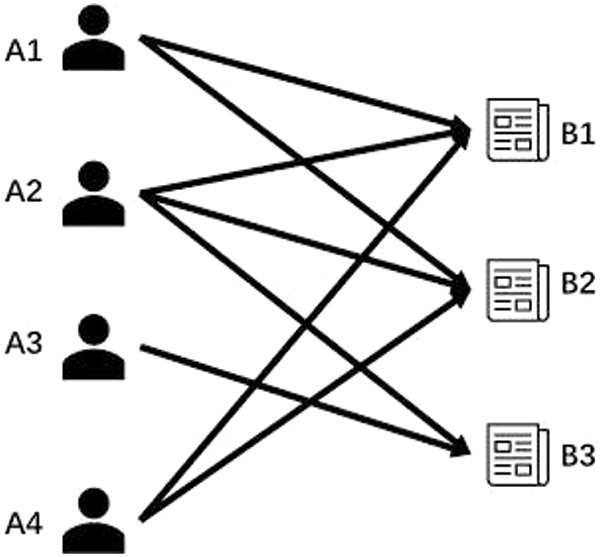
Figure 4: Bipartite graph for interaction matrices

B1 has three paths back to B1, B1→A1→B1 and B1→A2→B1 and B1→A4→B1. Then |pB1→B1|=3. B2 has 3 paths back to B2 as B2→A1→B2, B2→A2→B2 and B2→A4→B2. Then |pB2→B2|=3. Then we can get:

s(B1,B2)=2×33+3=1(6)

We use matrices cash skill to speed up the computation. The user-paper matrix is R. We use the Commuting Matrix (CM) to simplify the calculation process. Commuting Matrix (CM) M=RTR. Then, the meta-path similarity of the papers in the interaction matrix is:

sij=2MijMii+Mjj(7)

where Mij is the element of the corner scale i, j in the commuting matrix. Then the procedure of adopting matrix for s(B1,B2) is as follows:

M=RTR=[110111010110][110111001110]=[331331112](8)

s12=2M12M11+M22=2×33+3=1(9)

In the specific implementation, the Gamma distribution can fit the decay process well and can be introduced as a decay factor to learn the representation of user preferences. Take δvj∼Gamma(γvjshp,γvjrte) to denote the user’s interest to thesis j decays according to the Gamma distribution. Then the likelihood of a tag v reaching a new paper i through paper j is:

zvji=δvjsij(10)

Then, the likelihood of a tag v reaching a new paper i through a collection of papers J can be calculated as follows:

zvji=∑j=1|J|δvjsij(11)

4.3 Spatial Similarity Measures Based on Citation Networks

Even if the papers have significant textual gaps, they may still have intrinsic theoretical similarities that cannot be obtained by computing textual representation vectors. Given a citation network, it is necessary to utilize as much of the citation network as possible to obtain a low-dimensional vector representation of the papers. Utilizing only neighboring nodes may prevent the model from losing much information about the structure. Once too many layers of network node information are utilized, too much noise may be introduced into the model. Therefore, we utilize a node’s neighboring edges and adjacent nodes as the contextual information of the current node. Intuitively, two nodes are more similar if two nodes have more neighboring nodes.

Let the meta-path similarity of the paper i and j in the interaction matrix is sij′. In the specific implementation, Gamma is similarly introduced as a decay factor in the representation learning of citation networks. Take τvw∼Gamma(γvwshp,γvwrte). Then, the likelihood of a tagged v pair reaching the citation network of a new paper i through paper w can be expressed by the following equation:

zvwi=τvwsiw′(12)

Then, the spatial similarity of the citation network for a user to reach a new paper i node on the citation network through the cluster of paper set J is described as:

zvwi=∑j=1|J|τvwsiw′(13)

Suppose there are nine papers B1, B2, B3, B4, B5, B6, B7, B8, B9. The citation network is shown in Fig. 5 and its adjacency matrices is shown in Table 2. As we can see, the adjacency matrix G of the directed graph is an asymmetric matrix. We take its Commuting Matrix (CM) as:

Figure 5: Citation networks

M′=(G+GT)(G+GT)T(14)

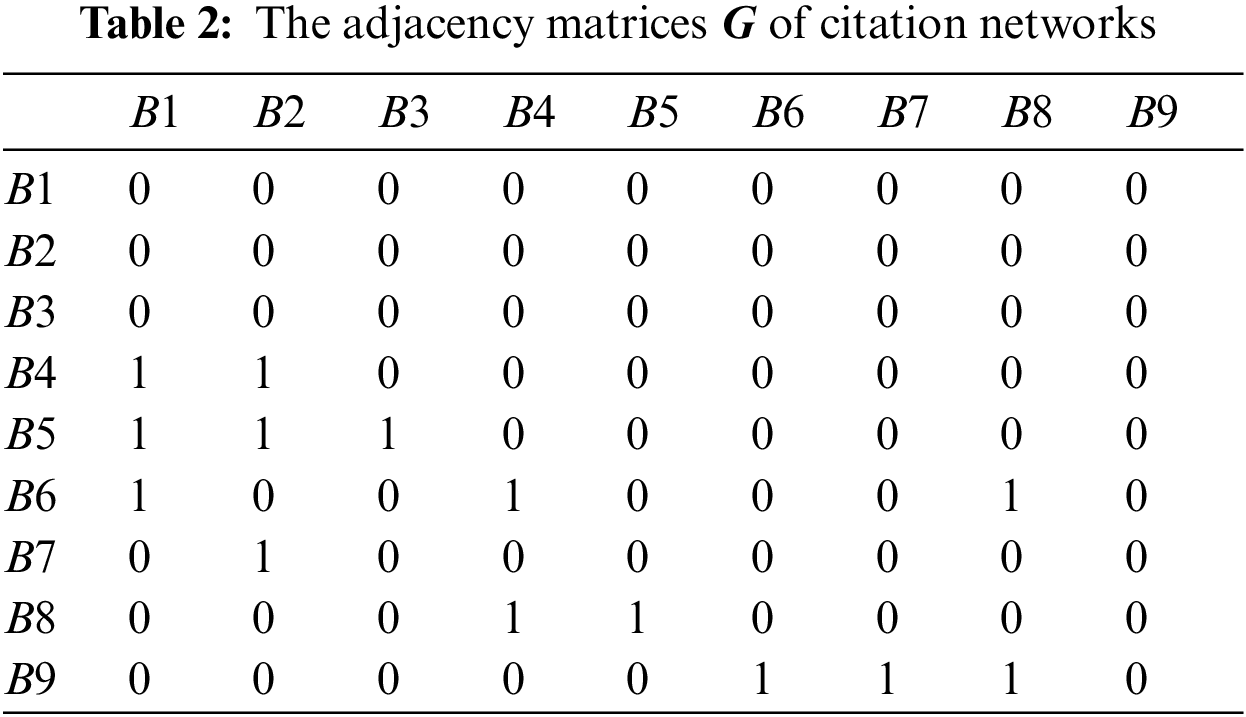
Let us take the meta-path ‘paper →paper → paper’ as an example. The goal is to find the paper’s similarity in citation. We simplify the citations network to an undirected graph so their adjacency matrices became symmetric. We use matrices cash skill to speed up the computation. The adjacency matrices are G, we take the Commuting Matrix (CM) M′=(G+GT)(G+GT)T, then the meta-path similarity of the papers in the interaction matrix is:

sij′=2Mij′Mii′+Mjj′(15)

where Mij′ is the element of the corner scale i, j in the commuting matrix.

M′=(G+GT)(G+GT)T=[321101031231001021111000010100432112000342101110224121000111210321102141110211013](16)

s56′=2M56′M55′+M66′=2×34+4=0.75(17)

s57′=2M57′M55′+M77′=2×14+2=0.33(18)

So paper 5 is more similar to paper 6 than to paper 7.

4.4 Approximate Posterior Inference

We use variational inference to solve the model, and the details of the solution process are described below. δvj and τvw obey a gamma distribution, δvj∼Gamma(γvjshp,γvjrte), τvw∼Gamma(γvwshp,γvwrte), let zvikM∼Poisson(ηvkTθik), zvji∼Poisson(δvjsijyji), zvwi∼Poisson(τvwsiw′ywi), then Eq. (13) can be reduced to:

yvi|y¬vi=∑k=1KzvikM+∑j=1|J|zvji+∑w=1|W|zvwi(19)

Due to the additivity of Poisson distribution, the sum of multiple Poisson distributions yvi still obeys Poisson distribution. We can obtain the Variational family of the above model as follows:

q(zvikM,zvji,zvwi,δvj,τvw,ηv,θi)=∏v,i,k⁡zvikM∏v,j,i⁡zvji∏v,w,i⁡zvwi∏v,j⁡δvj∏v,w⁡τvw∏v⁡ηv∏i⁡θi(20)

According to the conditional conjugate model, each variational parameter equals the expectation of the other corresponding parameters in the complete condition. Detailed proofs are shown in Appendix (including Table A1). In summary, the parameters are updated as follows:

(γvkshp,γvkrte)←(λva+∑i⁡yviϕvikM,λvb+∑i⁡γikshpγikrte)(21)

(γikshp,γikrte)←(λia+∑v⁡yviϕvikM,λib+∑v⁡γvkshpγvkrte)(22)

(γvjshp,γvjrte)←(λja+∑i⁡yviϕvji,λjb+∑i⁡sijyji)(23)

(γvwshp,γvwrte)←(λha+∑i⁡yviϕvwi,λhb+∑i⁡siw′ywi)(24)

ϕviM∝⟨ϕvi1M,…,ϕvikM,…,ϕviKM⟩(25)

We expect the latent variable as following:

ϕvikM=Gq[ηvkTθik]=exp⁡{Eq[log⁡ηvkT+log⁡θik]}=exp⁡{Ψ(γvkshp)−log⁡γvkrte+Ψ(γikshp)−log⁡γikrte}(26)

By the same reasoning, it is easy to obtain the following equation:

ϕvji=exp⁡{Ψ(γvjshp)−log⁡γvjrte+log⁡sijyji}(27)

ϕuwi=exp⁡{Ψ(γvwshp)−log⁡γvwrte+log⁡siw′ywi}(28)

4.5 Optimization and Complexity Analysis

Algorithm 1 shows the entire optimization of our proposed method. The coordinate ascent method is more efficient than the batch algorithm. The computational complexity per iteration of the batch algorithm is O((W+R)K), where R and W are the total number of non-zero observations in the document-user and document-word matrices, respectively. For the coordinate ascent method, this is O((wd+rd)K), where rd is the number of users who rated the sampled document d and wd is the number of unique words in it. We assume that only one document is sampled in each iteration. In Fig. 3, sums involving polynomial parameters can be tracked for efficient memory usage. The constraint on memory usage is O((D+V+U)K). As in Table 3, the update algorithm is of the same order of magnitude of complexity as the Bayesian Personalized Ranking (BPR), which does not introduce relational contexts. Therefore, on the premise of pre-processing contextual content and not increasing the arithmetic burden of the online model, the computational complexity of the model proposed in this paper remains the same as that of the BPR algorithm without fusing content information. Therefore, it is currently a more advanced algorithm regarding computational efficiency.

5  Experimental Results and Analysis

We examine the algorithm’s efficacy using the citeulike-a and citeulike-t datasets [30]. The two datasets both contain the tags corresponding to the papers, records of user interactions with the articles, citation networks, and the bag of words for the articles. The statistical information of the dataset is shown in Table 4.

5.1 Evaluation Metric

We use implicit feedback for the computation, where we recommend K tags to papers based on the ranking of the predicted values and evaluate them based on the articles that users have checked in. We use two metrics to evaluate the quality of the sorted list of tags: The Area Under Curve (AUC) and Mean Average Precision (MAP), which are defined as follows:

AUC=∑i=1Pranki−P(P+1)2P×N(29)

where ranki denotes the predicted ranking of the ith positive sample, P denotes the number of positive samples, and N denotes the number of negative samples.

In the actual calculation process, the samples are usually ranked according to the predicted probability value. Then the ranked samples are taken as positive samples one by one, and the corresponding ranki values are calculated. Then these values are brought into the AUC calculation formula to obtain the final AUC value.

MAP=1I∑i∈I⁡1ni∑k=1NP(Rik)(30)

Average precision (AP) is the average of precision values at all ranks where relevant research papers are found and Mean Average Precision (MAP) given by Eq. (30), is the average of all APs. Where P(Rik) denotes the precision of returned papers from the top until paper k is reached, N represents the length of the recommendation list, ni is the number of relevant papers in the recommendation list and I is the set of papers.

5.2 Baselines

In order to validate the effectiveness of introducing contextual information and optimization methods, we have chosen the following recommended techniques to compare with our approach:

PF [27]. Poisson Factorization (PF) is a method that estimates the parameters of a variable by variational inference, using the Poisson distribution as a prior for the variable.

CTR [30]. Collaborative Topic Regression (CTR). Collaborative Topic Regression method that combines Poisson decomposition and topic distribution can mitigate data sparsity and cold-start problems of articles.

mostPop [31]. mostPop is a tag-popularity-based ranking method.

userKNN [32]. User-based K-Nearest Neighbors (userKNN) is the user-based near-neighbor method which calculates the similarity between users based on their reading history using similarity metrics. Here, the paper is considered a user and the tag is an item.

itemKNN [32]. Item-based K-Nearest Neighbors (itemKNN) is the item-based nearest neighbor method, based on the reading records of papers, using similarity metrics to calculate the similarity between items. Here, the paper is considered a user and the tag is an item.

BPR [33]. Bayesian Personalized Ranking (BPR) is the classical ranking learning algorithm based on the principle that positive samples should be ranked before negative samples, and the recommendation model is trained by learning the ranking loss function.

CDR [34]. Collaborative Deep Ranking (CDR) is a hierarchical Bayesian deep learning framework combining a deep feature representation of the paper’s content and implicit user preferences to reduce sparsity.

ALS [35]. Alternating Least Squares (ALS) is an implicit feedback-based matrix decomposition method that employs negative sample complete sampling.

We randomly draw 80% of the data from the thesis-tag matrix as training data and the remaining 20% as test data. For a fair comparison, we set the parameters of different algorithms concerning the corresponding literature or experimental results of the compared algorithms.

5.3 Result

5.3.1 Performance Comparison

The experimental results obtained by baselines on the citeulike-a and citeulike-t datasets are shown in Fig. 6. We can find following:

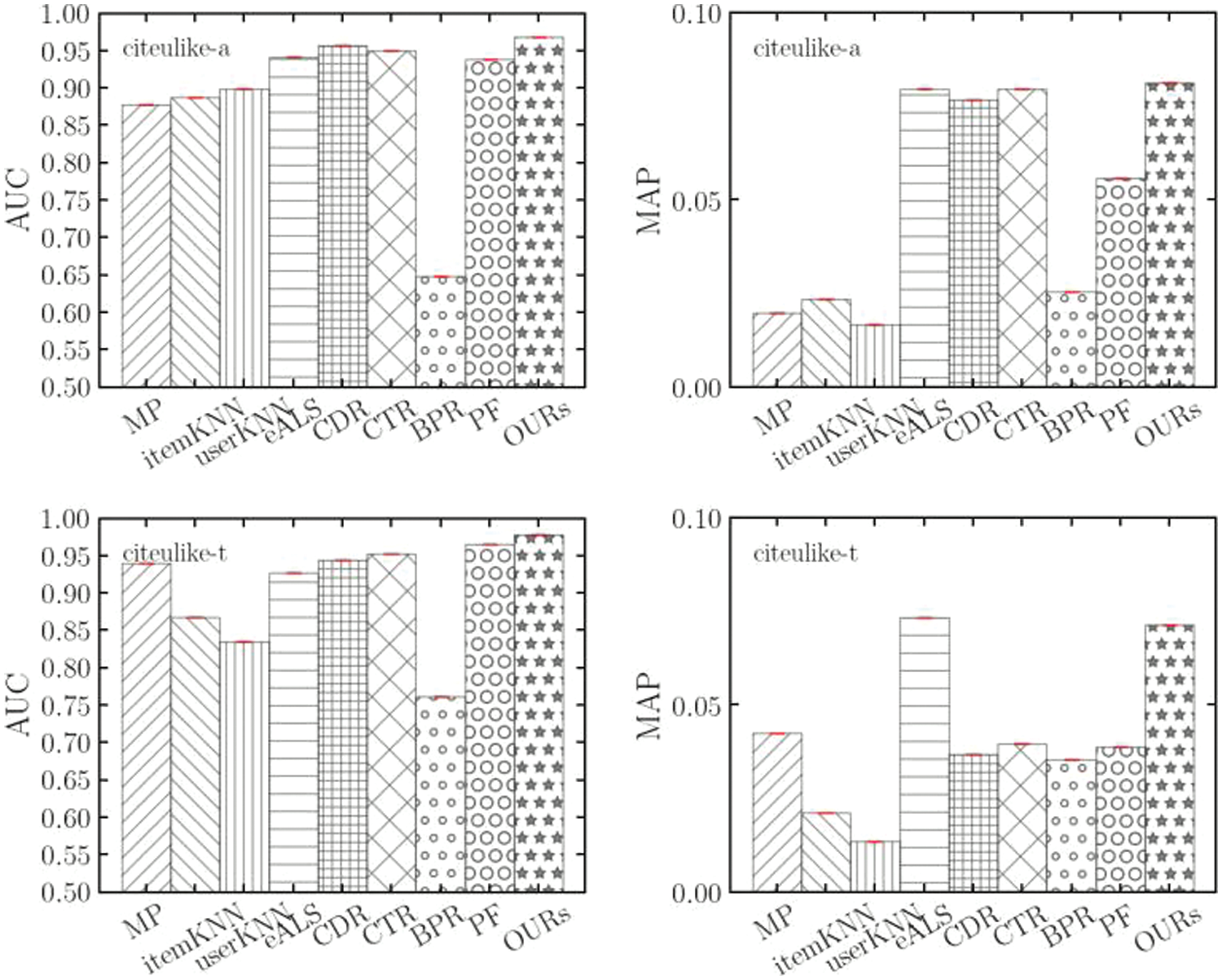
Figure 6: Performance comparison (Kd=50)

1) The algorithm proposed in this paper has greatly improved over the Poisson decomposition algorithm that does not introduce context, proving that it is feasible to introduce context through the additivity of the gamma distribution. This finding is consistent with the conclusion of the paper [1].

2) Our method shows more than 3% improvement over the alternating element least square method, we believe it is because our model uses a more rational approach to compute the trust strength, and our model successfully combines two contexts to mitigate the data sparsity problem. The eALS models do not model users’ implicit feedback well due to the extremely sparse data in tag recommendations.

3) The recommendation performance of the model introducing contextual information is similar to that of the collaborative filtering-based model, suggesting that introducing contextual information requires an appropriate approach.

4) The performance of BPR based on negative sample sampling is worse than the ALS method based on complete negative sample sampling, which suggests that random negative sample sampling affects the model.

5) the recommendation accuracy of userKNN is higher than itemKNN in memory-based tagging recommendation algorithms. The reason is that many papers share fewer tagged, which leads to the fact that item-based paper similarity calculation is less accurate than user-based user similarity calculation. This observation is consistent with that of literature [36]. ItemKNN has the lowest accuracy and MAP, and collaborative filtering based solely on paper similarity computation cannot adequately characterize the reading preference of users.

5.3.2 The Effect of the Dimension of the Latent Vector

For the tag recommendation algorithm proposed in this paper, the dimension Kd of the latent feature vector is also an important parameter that affects the algorithm’s performance. In incremental steps, we vary the value of Kd, from 10 to 150 and observe the variation of AUC and MAP on the citeulike-a dataset.

The experimental results are shown in Fig. 7. It can be observed that the values of AUC and MAP increase first with the increment of Kd. After reaching the optimal value, AUC and MAP decrease with the increment of Kd. On the citeulike-t dataset, the effect of parameter Kd on AUC and MAP shows a similar trend. This observation suggests that over-increasing the value of Kd may introduce some noise to reduce the accuracy of the recommendation algorithm.

Figure 7: Prediction accuracy of four implicit feedback methods vs. Kd

5.3.3 Ablation Experiments

In this paper, we propose a tag recommendation algorithm that fuses context regularization through the additivity of the gamma distribution. We implement regularization of the article-tag interaction model with the citation and user-article networks. In this section, we exclude the citation and user-article network, respectively, and compare the changes of AUC and MAP with one missing term and without regularization.

•   PF. This model removes items representing user-profiles and citation networks in Eq. (4).

•   PF+ citation. This model removes items representing user profiles.

•   PF+ profile. This model removes items representing citation networks.

•   This is the full context-augmented Poisson factorization model with user profiles and citation network as context.

Fig. 8 shows the results evaluated on two datasets regarding AUC and MAP. There are several interesting observations:

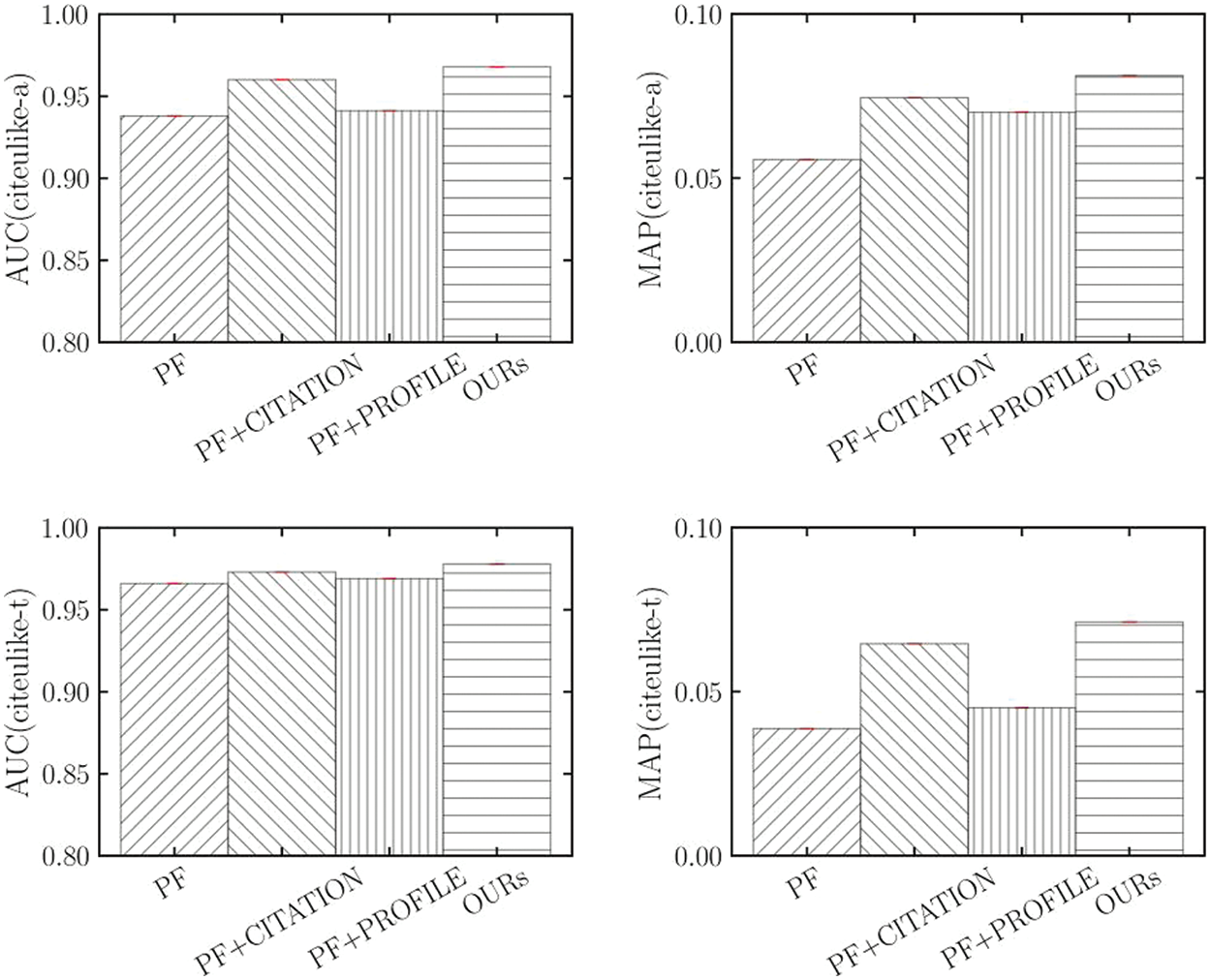
Figure 8: Ablation tests (Kd=50)

•   Jointly training mode is crucial. Compared with the Poisson decomposition without context, our model improves the AUC by 3.1% and 1.2% and the MAP by 46.1% and 84.0% on the two datasets, respectively. This demonstrates the effectiveness of gamma distribution additivity for feature extraction. This mechanism enables our model to capture various features in context for each tag by dynamically adjusting the feature weights for better tag recommendation.

•   Effectiveness of context-sensitive modelling. By comparing PF with citation and PF with profile, it can be found that the model using citation as context performs relatively better (AUC improves by about 2.0% on citeulike-a dataset and 0.4% on citeulike-t dataset, MAP improves by about 19.1% on citeulike-a dataset and 50.4% on citeulike-t dataset). This suggests that citation network have a larger impact than user preference in labelling recommendations. Furthermore, the model is slightly better in citeulike-a than citeulike-t datasets. This is reasonable because of the different data sparsity.

6  Conclusion and Future Work

With the rapid growth of academic resources, the reading and organizing academic resources become more and more time-consuming. Tag recommendation is an integral part of the academic resource platform, which can help users personalize the classification of papers, facilitate users’ finding papers, and reduce information overload. In order to fully utilize the three kinds of relational data in tag recommendation, this paper proposes a context-aware tag recommendation model based on Poisson decomposition. We explicitly integrate user preferences and citation networks into the model and solve it with gradient climbing method, which significantly reduces the complexity. Experimental results on two real tagging recommendation datasets show that the method in this paper outperforms current methods in terms of tag recommendation accuracy and computational efficiency.

However, academic tag recommendation systems may exacerbate the phenomenon of hot and cold areas or topics of academic research, leading to over-attention to certain areas of research and neglect of others. This is not conducive to the diversity and balanced development of academic research. We will look into this issue in our follow-up work.

Acknowledgement: Not applicable.

Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 62271274).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Weiming Huang; data collection: Weiming Huang, Zhaoliang Wang; analysis and interpretation of results: Weiming Huang, Baisong Liu; draft manuscript preparation: Weiming Huang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data supporting this study’s findings are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. P. Xu, H. Liu, B. Liu, L. Jing, and J. Yu, “Survey of tag recommendation methods,” J. Softw., vol. 33, no. 4, pp. 1244–1266, 2022. doi: 10.13328/j.cnki.jos.006481. [Google Scholar] [CrossRef]

2. R. Ashvanth, G. Deepak, J. Sheeba Priyadarshini, and A. Santhanavijayan, “KMetaTagger: A knowledge centric metadata driven hybrid tag recommendation model encompassing machine intelligence,” in Intelligent Systems Design and Applications, Springer, Cham, pp. 1–11, 2023. [Google Scholar]

3. K. Lei, Q. Fu, M. Yang, and Y. Liang, “Tag recommendation by text classification with attention-based capsule network,” Neurocomputing, vol. 391, pp. 65–73, 2020. doi: 10.1016/j.neucom.2020.01.091. [Google Scholar] [CrossRef]

4. L. Yang, R. Yang, T. Chen, H. Fei, and J. Tang, “MF-TagRec: Multi-feature fused tag recommendation for GitHub,” in Proc. PRICAI, Shanghai, China, 2022, pp. 17–31. doi: 10.1007/978-3-031-20868-3_2. [Google Scholar] [CrossRef]

5. J. Yi, X. Ren, and Z. Chen, “Multi-auxiliary augmented collaborative variational auto-encoder for tag recommendation,” ACM Trans. Inf. Syst., vol. 41, no. 4, pp. 1–25, 2023. doi: 10.1145/3578932. [Google Scholar] [CrossRef]

6. D. Boughareb, A. Khobizi, R. Boughareb, N. Farah, and H. Seridi, “A graph-based tag recommendation for just abstracted scientific articles tagging,” Int. J. Coop. Inf. Syst., vol. 29, no. 3, pp. 2050004, 2020. doi: 10.1142/S0218843020500045. [Google Scholar] [CrossRef]

7. R. Huang, C. Han, and L. Cui, “Tag-aware attentional graph neural networks for personalized tag recommendation,” in Proc. IJCNN, Shenzhen, China, 2021, pp. 1–8. doi: 10.1109/IJCNN52387.2021.9533380. [Google Scholar] [CrossRef]

8. W. Zhao, L. Shang, Y. Yu, L. Zhang, C. Wang and J. Chen, “Personalized tag recommendation via denoising auto-encoder,” in Proc. WWW., vol. 26, no. 1, pp. 95–114, 2023. doi: 10.1007/s11280-021-00967-3. [Google Scholar] [CrossRef]

9. Z. Fei, J. Wang, B. Huang, and X. Xiang, “Pairwise metric learning with angular margin for tag recommendation,” IEEE Access, vol. 11, pp. 27020–27033, 2023. doi: 10.1109/ACCESS.2023.3246090. [Google Scholar] [CrossRef]

10. M. D. Hoffman, D. M. Blei, C. Wang, and J. W. Paisley, “Stochastic variational inference,” J. Mach. Learn. Res., vol. 14, pp. 1303–1347, 2012. [Google Scholar]

11. Y. Wu, Y. Yao, F. Xu, H. Tong, and J. Lu, “Tag2Word: Using tags to generate words for content based tag recommendation,” in Proc. CIKM, Indianapolis, Indiana, USA, 2016, pp. 2287–2292. Accessed: Jan. 01, 2024. [Online]. Available: https://api.semanticscholar.org/CorpusID:14840323. [Google Scholar]

12. R. Tang, C. Yang, and Y. Wang, “A cross-domain multimodal supervised latent topic model for item tagging and cold-start recommendation,” IEEE Multimed., vol. 30, no. 3, pp. 48–62, 2023. doi: 10.1109/MMUL.2023.3242455. [Google Scholar] [CrossRef]

13. L. Wang, Y. Li, and W. Jing, “KEIC: A tag recommendation framework with knowledge enhancement and interclass correlation,” Inf. Sci., vol. 645, pp. 119330, 2023. doi: 10.1016/j.ins.2023.119330. [Google Scholar] [CrossRef]

14. S. Yu, Q. Li, M. Liu, and Z. Wang, “Observation is reality? A graph diffusion-based approach for service tags recommendation,” in Proc. ICSOC., vol. 14420, pp. 100–114, 2023. doi: 10.1007/978-3-031-48424-7. [Google Scholar] [CrossRef]

15. L. Li, P. Wang, X. Zheng, Q. Xie, X. Tao and J. D. Velásquez, “Dual-interactive fusion for code-mixed deep representation learning in tag recommendation,” Inf. Fusion, vol. 99, pp. 101862, 2023. doi: 10.1016/j.inffus.2023.101862. [Google Scholar] [CrossRef]

16. R. Gharibi, A. Safdel, S. M. Fakhrahmad, and M. H. Sadreddini, “A content-based model for tag recommendation in software information sites,” Comput. J., vol. 64, no. 11, pp. 1680–1691, 2019. doi: 10.1093/comjnl/bxz144. [Google Scholar] [CrossRef]

17. N. Engleitner, W. Kreiner, N. Schwarz, T. Kopetzky, and L. Ehrlinger, “Knowledge graph embeddings for news article tag recommendation,” in Proc. ICSS, Amsterdam, Netherlands, 2021. Accessed: Jan. 01, 2024. [Online]. Available: Https://api.semanticscholar.org/CorpusID:238207994. [Google Scholar]

18. X. Wang, P. Zhou, Y. Wang, X. Liu, J. Liu and H. Wu, “ServiceBERT: A pre-trained model for web service tagging and recommendation,” in Proc. ICSOC, Dubai, UAE, 2021, pp. 464–478. doi: 10.1007/978-3-030-91431-8_29. [Google Scholar] [CrossRef]

19. J. Gao et al., “STAR: Spatio-temporal taxonomy-aware tag recommendation for citizen complaints,” in Proc. CIKM, Beijing, China, 2019. Accessed: Jan. 01, 2024. [Online]. Available: https://api.semanticscholar.org/CorpusID:207757333. [Google Scholar]

20. L. Xiao, X. Huang, B. Chen, and L. Jing, “Label-specific document representation for multi-label text classification,” in Proc. EMNLP-IJCNLP, Hong Kong, China, 2019. Accessed: Jan. 01, 2024. [Online]. Available: https://api.semanticscholar.org/CorpusID:202771535. [Google Scholar]

21. Y. Wei, Z. Cheng, X. Yu, Z. Zhao, L. Zhu and L. Nie, “Personalized hashtag recommendation for micro-videos,” in Proc. MM, Nice, France, 2019, pp. 1446–1454. doi: 10.1145/3343031.3350858. [Google Scholar] [CrossRef]

22. Y. Yu, X. Chen, L. Zhang, R. Gao, and H. Gao, “Neural graph for personalized tag recommendation,” IEEE Intell. Syst., vol. 37, no. 1, pp. 51–59, 2022. doi: 10.1109/MIS.2020.3040046. [Google Scholar] [CrossRef]

23. J. Sun, M. Zhu, Y. Jiang, Y. Liu, and L. Wu, “Hierarchical attention model for personalized tag recommendation,” J. Assoc. Inf. Sci. Technol., vol. 72, no. 2, pp. 173–189, 2021. doi: 10.1002/asi.24400. [Google Scholar] [CrossRef]

24. X. Chen, Y. Yu, F. Jiang, L. Zhang, R. Gao and H. Gao, “Graph neural networks boosted personalized tag recommendation algorithm,” in Proc. IJCNN, Glasgow, UK, 2020, pp. 1–8. doi: 10.1109/IJCNN48605.2020.9207610. [Google Scholar] [CrossRef]

25. J. Zhao, Q. Zhang, Q. Sun, H. Huo, Y. Xiao, and M. G., “FolkRank++: An optimization of FolkRank Tag recommendation algorithm integrating user and item information,” KSII Trans. Internet Inf. Syst., vol. 15, no. 1, pp. 1–19, 2021. doi: 10.3837/tiis.2021.01.001. [Google Scholar] [CrossRef]

26. W. Zhao, A. Zhang, L. Shang, Y. Yu, and L. Zhang, “Hyperbolic personalized tag recommendation,” in Proc. DASFAA, vol. 13246, pp. 216–231, 2022. doi: 10.1007/978-3-031-00126-0. [Google Scholar] [CrossRef]

27. P. Gopalan, J. M. Hofman, and D. M. Blei, “Scalable recommendation with hierarchical poisson factorization,” in Proc. UAI, Amsterdam, Netherlands, 2015, pp. 326–335. Accessed: Jan. 01, 2024. [Online]. Available: https://api.semanticscholar.org/CorpusID:1723648. [Google Scholar]

28. C. Wang and D. M. Blei, “Collaborative topic modeling for recommending scientific articles,” in Proc. SIGKDD, San Diego, California, USA, 2011, pp. 448. doi: 10.1145/2020408.2020480. [Google Scholar] [CrossRef]

29. Y. Guo, C. Xu, H. Song, and X. Wang, “Understanding users’ budgets for recommendation with hierarchical poisson factorization,” in Proc. IJCNN, Melbourne, Australia, 2017, pp. 1781–1787. doi: 10.24963/ijcai.2017/247. [Google Scholar] [CrossRef]

30. H. Wang, B. Chen, and W. J. Li, “Collaborative topic regression with social regularization for tag recommendation,” in Proc. IJCAI 2013, Beijing, China, 2013, pp. 2719–2725. Accessed: Jan. 01, 2024. [Online]. Available: http://www.aaai.org/ocs/index.php/IJCAI/IJCAI13/paper/view/7006. [Google Scholar]

31. Y. Zhang, J. Hu, S. Sano, T. Yamasaki, and K. Aizawa, “A tag recommendation system for popularity boosting,” in Proc. MM, California, USA, 2017, pp. 1227–1228. doi: 10.1145/3123266.3127913. [Google Scholar] [CrossRef]

32. J. Wang, A. P. de Vries, and M. J. T. Reinders, “Unifying user-based and item-based collaborative filtering approaches by similarity fusion,” in Proc. SIGIR, Seattle, Washington, USA, 2006, pp. 501. doi: 10.1145/1148170.1148257. [Google Scholar] [CrossRef]

33. S. Rendle, C. Freudenthaler, Z. Gantner, and L. Schmidt-Thieme, “BPR: Bayesian personalized ranking from implicit feedback,” in Proc. UAI'09, Arlington, Virginia, USA, 2009, pp. 452–461. [Google Scholar]

34. H. Ying, L. Chen, Y. Xiong, and J. Wu, “Collaborative deep ranking: A hybrid pair-wise recommendation algorithm with implicit feedback,” in Proc. PAKDD 2016, Auckland, New Zealand, 2016, pp. 555–567. doi: 10.1007/978-3-319-31750-2_44. [Google Scholar] [CrossRef]

35. Y. Hu, Y. Koren, and C. Volinsky, “Collaborative filtering for implicit feedback datasets,” in Proc. ICDM, Pisa, Italy, 2008, pp. 263–272. doi: 10.1109/ICDM.2008.22. [Google Scholar] [CrossRef]

36. T. Bogers and A. van den Bosch, “Recommending scientific articles using citeulike,” in Proc. RecSys 2008, Lausanne, Switzerland, 2008, pp. 287–290. doi: 10.1145/1454008.1454053. [Google Scholar] [CrossRef]

Appendix

Details of Variational Inference

The Poisson decomposition employs variational inference as an optimization objective function to solve for the parameters. A hidden variable factor k is added to the model, and for the observation yvi, We add k intermediate variables yvik, such that yvik∼Poisson(ηvkTθvi) and yvi=∑kyvik, yui is converted to a polynomial by the transformation ∑kyvik, while yvi still satisfies the Poisson distribution, due to the principle of additivity, the sum of multiple Poisson distributions obeys a Poisson distribution.

We use variational inference to solve the model, and the details of the solution process are described below. δuj and τuw obey a gamma distribution, ηvk∼Gamma(γvkshp,γvkrte), θik∼Gamma(γikshp,γikrte), δvj∼Gamma(γvjshp,γvjrte), τvw∼Gamma(γvwshp,γvwrte), let zvikM∼Poisson(ηvkTθik), zvij∼Poisson(δvjsijyji), zviw∼Poisson(τvwsiw′ywi), then Eq. (19) can be reduced to:

yvi|y¬vi=∑k=1KzvikM+∑j=1|J|zvij+∑w=1|W|zviw(31)

Due to the additivity of Poisson distribution, the sum of multiple Poisson distributions yvi still obeys Poisson distribution. We can obtain the Variational family of the above model as follows:

q(zvikM,zvji,zvwi,δvj,τvw,ηv,θi)=∏v,i,k⁡zvikM∏v,j,i⁡zvji∏v,w,i⁡zvwi∏v,j⁡δvj∏v,w⁡τvw∏v⁡ηv∏i⁡θi(32)

For Eq. (31), we extracting the portion associated with ηvk yields

p(ηvk|yvi,λva,λvb)∝ηvkλva−1exp⁡(−λvbηvk)∏i⁡[(ηvkTθik)yuikexp⁡(−ηvkTθik)]∝ηvkλva+∑iyuik−1exp⁡[−(λvb+∑i⁡θik)ηvk]=Gamma(λva+∑i⁡yuik,λvb+∑i⁡θik)(33)

For yvik, according to Lagrange’s median theorem, we can get there must exists yvi=∑kyvik and ∑kϕvikM=1, make yvik=yviϕvikM. Since θik obeys the Gamma distribution, its expectation is γikshpγikrte. So the iterative formula for (γvkshp,γvkrte) can be rewritten as (γvkshp,γvkrte)←(λva+∑iyviϕvikM,λvb+∑iγikshpγikrte).

By the same reasoning, it is easy to obtain the following equation:

(γikshp,γikrte)←(λia+∑v⁡yviϕvikM,λib+∑v⁡γvkshpγvkrte)(34)

(γvjshp,γvjrte)←(λja+∑i⁡yviϕvji,λjb∑i⁡sijyji)(35)

(γvwshp,γvwrte)←(λha+∑i⁡yviϕvwi,λhb+∑i⁡siw′ywi)(36)

ϕviM∝⟨ϕvi1M,…,ϕvikM,…,ϕviKM⟩(37)

The variational inference method assumes at this point that there exists a Poisson distribution q. The iterative method makes the distribution q move closer and closer to the target distribution p, which we need to solve for, and thus makes the following transformations:

ϕvikM=ηvkTθikyvi∝exp⁡(log⁡(Eq[ηvkTθik]))=exp⁡(Eq[log⁡(ηvkTθik)])=exp⁡{Eq[log⁡ηvkT+log⁡θik]}(38)

where Eq(⋅) represents the expectation under the distribution q. Since there exists log⁡ηvkT=Ψ(γvkshp)−log⁡γvkrte, the final iterative formula for ϕvikM is given as:

ϕvikM=Gq[ηvkTθik]=exp⁡{Eq[log⁡ηvkT+log⁡θik]}=exp⁡{Ψ(γvkshp)−log⁡γvkrte+Ψ(γikshp)−log⁡γikrte}(39)

By the same reasoning, it is easy to obtain the following equation:

ϕvji=exp⁡{Ψ(γvjshp)−log⁡γvjrte+log⁡sijyji}(40)

ϕuwi=exp⁡{Ψ(γvwshp)−log⁡γvwrte+log⁡siw′ywi}(41)

Then we can derive and obtain the update equations are summarize in Table A1: