Distributed Graph Database Load Balancing Method Based on Deep Reinforcement Learning

1  Introduction

In recent years, the continuous growth in data volume and the expansion of application scenarios have progressively exposed the limitations of traditional database technologies in handling ultra-large scale data. Traditional databases encounter bottlenecks in data storage, diminished query efficiency, and performance constraints in scenarios that demand high real-time responsiveness, low latency, and high computational efficiency [1]. These limitations become particularly pronounced when processing complex topological structures and relational queries.

To address such challenges, graph database technology has emerged as a promising solution for managing large-scale data [2]. Graph databases, with their intuitive and efficient data structuring, excel at handling and querying complex relationships. They are especially advantageous when dealing with intricate topological structures and relational queries. To cater to the needs of large-scale data processing, distributed graph databases have been developed. These databases not only inherit the advantages of graph databases in processing complex relational queries but also offer scalability, performance optimization, high availability, and fault tolerance [3].

However, distributed graph databases still face challenges when tasked with handling very large-scale data and tasks [4]. A significant issue among these is achieving load balancing in a distributed graph database [5]. Load balancing requires optimizing data storage and queries, rational allocation of server resources, effective task scheduling in distributed graph databases, and ensuring high system availability and stability. To resolve this issue, the present study proposes a load balancing method for distributed graph databases based on deep reinforcement learning (DRL). Owing to the unique characteristics of graph data structures and their intricate interconnections, distributed graph databases face challenges in optimizing load balancing effectiveness and enhancing the efficiency of task scheduling. DRL can effectively meet these challenges through the following avenues:

•   Dynamic Adaptation: By continuously assimilating feedback on system performance, DRL is capable of real-time adjustments to scheduling strategies, thereby improving the balance among query workloads.

•   Strategic Resource Allocation: Utilizing predictive analytics to anticipate load demands and identify task dependencies, DRL skillfully allocates server resources to enhance system performance.

•   Dependency-Aware Scheduling: The reward function within the DRL framework is meticulously crafted to account for task dependencies, promoting the scheduling of tasks that respect these constraints while striving to achieve efficiency optimization.

The primary goal of this paper is to develop and present a sophisticated, precise, and robust load balancing framework, namely Q-learning Deep Reinforcement Learning (Q-DRL), tailored for distributed graph databases, thereby enabling enhanced system performance. In formulating this framework, the authors have rigorously analyzed various critical factors, including query optimization techniques, advanced distributed computing technologies, and overall system stability. The resultant product is an innovative, adaptive load balancing algorithm that incorporates the principles of DRL. This algorithm is designed to dynamically modulate the distribution of workload in accordance with the real-time system dynamics and specific task demands, with the ultimate aim of maximizing system throughput and optimizing response speed.

This research endeavors to make a significant contribution to the evolution of load balancing methodologies within the sphere of distributed graph databases. It offers more streamlined and resilient solutions for handling large-scale data processing challenges. This is particularly pertinent in addressing the burgeoning requirements of big data processing and intelligent analytical applications in contemporary settings. To validate the efficacy of the proposed methodology, comprehensive experimental evaluations were conducted within an actual distributed graph database environment. The findings from these experiments demonstrably show that the proposed DRL-based load balancing approach substantially improves system performance and efficiency, especially in scenarios involving the management of ultra-large scale datasets. Furthermore, it ensures the maintenance of system stability and reliability, underscoring its practical applicability and potential for widespread adoption in relevant fields.

The main contributions of this paper are highlighted as follows:

•   Parallelized multi-workflow task stage division: The paper emphasizes the strategic division of workflow subtasks into parallel stages. This segmentation is informed by a detailed analysis of task dependencies and temporal considerations within the workflow, enabling optimized task execution.

•   Reward function with time optimization and load nalancing: A sophisticated reward function for the DRL agent is meticulously crafted, featuring constraints designed for time optimization and load balancing. This function is pivotal to the agent’s learning process, guiding it towards scheduling decisions that not only minimize the maximum completion time (makespan) but also improve the average response speed of the workflow tasks.

2  Related Works

2.1 Task Scheduling Based on Heuristic Algorithm

Task scheduling methods based on heuristic algorithms are known for their simplicity in rules and implementation. For instance, the First Come First Service (FCFS) scheduling algorithm schedules tasks purely based on the order of submission. While this approach is straightforward to implement, it lacks flexibility, failing to account for task characteristics and machine load status. The Shortest Job First (SJF) scheduling algorithm prefers shorter tasks, which can lead to a bottleneck for longer tasks, thus performing poorly when handling complex task scheduling issues.

Hyytiä et al. combined the Round-Robin scheduling algorithm with FCFS to study routing to parallel queue systems, which can serve jobs through either FCFS or a preemptive Last Come First Served (LCFS) scheduling rule [6]. Seth et al. introduced a scheduling method based on a dynamic heterogeneous SJF model, aimed at minimizing actual CPU time and the overall system execution time, thereby improving resource utilization [7]. Békési et al. addressed the job scheduling problem involving tasks with two subtasks, proposing a First-fit based scheduling approach to optimize both task scheduling delay and makespan [8]. Gao et al. devised a distributed scheduling approach for data center networks, named Shortest Remaining Time First. Estimations of the remaining size of the workflow and the available bandwidth are utilized to calculate the residual time for each data flow, which in turn aids in setting the workflow priorities [9]. Ajayi et al. designed a weighted round-robin approach for task scheduling. This method aims to minimize latency and total completion time, taking into account various classes of workloads but not prioritizing service levels or considering the diversity in cloud environments [10]. Shirvani et al. proposed a novel hybrid heuristic list scheduling algorithm specifically designed for use in heterogeneous cloud computing environments. The primary objective of this algorithm is to optimize the makespan of tasks [11].

However, with the expanding scale of cloud computing and the escalating complexity of task scheduling, traditional heuristic scheduling methods, which rely on simplistic rule sets, are increasingly challenged to keep pace with the dynamic and complex requirements of cloud environments. This mismatch can result in diminished resource utilization and a decline in the quality of service, particularly in distributed graph database contexts.

2.2 Task Scheduling Based on Metaheuristic Algorithm

Metaheuristic algorithms represent a sophisticated advancement over heuristic algorithms, emerging through an amalgamation of random and local search techniques. Notable examples include genetic algorithms and Particle Swarm Optimization (PSO). Specifically, PSO exemplifies this approach by dividing a single problem set into numerous smaller particles, each contributing to a collective search for optimal or near-optimal solutions to NP-hard problems.

Zhao developed a scheduling approach utilizing the PSO method. This approach focuses on assigning computational resources to independent tasks to reduce the overall time required for processing requests [12]. Mansouri et al. introduced FMPSO, a hybrid scheduling algorithm that fuses fuzzy systems with an enhanced PSO technique to improve load balancing and throughput [13]. Wu et al. refined the standard particle swarm algorithm by integrating a selection operator, addressing efficiency gaps in existing models [14]. Kumar et al. proposed an efficient resource allocation model paired with a PSO-based scheduling algorithm, aiming to optimize execution costs and timing during task scheduling [15]. Dubey et al. advanced a novel multi-objective CR-PSO task scheduling algorithm. This algorithm, which integrates features of traditional chemical reaction optimization with PSO, aims to meet specific demands and deadlines, thus reducing costs, energy consumption, and the makespan of tasks [16]. Meziani et al. formulated a metaheuristic hybrid algorithm that combines PSO with Simulated Annealing (SA-PSO). This algorithm addresses the challenges encountered in two-machine flow shop scheduling with coupled operations [17]. Mangalampalli et al. designed a new workflow task scheduling mechanism based on the whale swarm algorithm, effectively prioritizing subtasks within a workflow and scheduling them to appropriate virtual resources [18]. Alsaidy et al. improved upon the standard PSO algorithm by incorporating heuristic methods such as ‘longest task to the fastest processor’ and ‘minimum completion time’, with the objective of curtailing the makespan in task scheduling [19]. Qi suggested a task scheduling methodology based on an Improved PSO algorithm (IPSO), designed to decrease task execution time and enhance service quality [20]. Shokouhifar proposed the FH-ACO algorithm, a fuzzy logic-enhanced ant colony optimization approach that synergized the rapid convergence characteristic of heuristic algorithms with the high-quality solutions typical of metaheuristic algorithms. This method effectively addressed the placement and routing problems of virtual network function (VNF) within network function virtualization (NFV) environments. Simulation results demonstrated its superiority over existing technologies [21].

While metaheuristic algorithms have advanced beyond the capabilities of heuristic methods, providing a promising avenue for exploring optimal solutions, they also display inherent instability. The random nature of the initialization process can lead to significant variations in solution quality for different instances of the same problem. It is noted that the quality of the initial population significantly impacts the final outcome achieved by the particles in the system; suboptimal initial solutions may cause the particles to converge around local optima. Despite their ability to explore solutions under predefined rules, metaheuristic methods such as particle swarm optimization lack self-learning capabilities. As artificial intelligence technology rapidly evolves, particularly in managing complex applications, reinforcement learning, with its enhanced self-learning capacities through environmental interaction, is increasingly being incorporated into task scheduling technologies.

2.3 Task Scheduling Based on Reinforcement Learning Algorithm

In the realm of machine learning, recent advancements have demonstrated significant efficacy in addressing complex challenges. One notable area is the allocation of tasks to resources in dynamic cloud environments, a process increasingly being addressed through machine learning techniques. Khan et al. conducted a comprehensive survey and identified seven adaptive methods driven by performance and supported by queuing networks. The study underscores the potential role of machine learning, exploration of the search space, and mixed-integer programming in optimizing fitness functions, which encompass key performance indicators [22]. Typically, the dynamic and complex nature of distributed graph databases eludes predefined modeling. Yet, task scheduling approaches employing Q-learning, a branch of reinforcement learning, circumvent the need for such predefined cloud environment models. These approaches interact with their environment via agents, continuously enhancing their understanding of situational contexts and decision-making abilities. Consequently, they adapt more effectively to the dynamic changes in external environments, thus improving task scheduling efficiency. Consequently, reinforcement learning emerges as a more suitable approach for task scheduling problems when compared to other machine learning techniques.

DeepMind’s team utilized a blend of reinforcement learning and deep learning to dramatically cut energy consumption in Google’s data centers. By monitoring operations and creating a predictive model of energy consumption, which considered around 120 operational variables, they enhanced energy efficiency, achieving a reduction in server energy usage by approximately 40% [23]. Garí et al. employed a Q-learning-based task scheduling method. This approach includes instant reward functions and state aggregation to enhance the management of multiple virtual machines, with a focus on reducing response times in cloud computing settings [24]. Ding et al. crafted a task scheduling architecture for cloud computing, integrating Q-learning with the M/M/n queue theory model, specifically to improve response times in task scheduling [25]. However, despite its robust decision-making capacity, reinforcement learning’s perceptual abilities remain limited, reducing its effectiveness in dynamic cloud environments. Challenges such as slower convergence rates and the limited capacity of discrete reward functions to reflect the effectiveness of actions become prominent as the number of environmental states increases.

To overcome these limitations, the amalgamation of deep learning with reinforcement learning into DRL can augment the perceptual and decision-making capabilities of agents, thereby improving their proficiency in solving complex problems. Li et al. suggested a DRL-based approach for task scheduling, applying it to cloud data centers to optimize makespan [26]. Li et al. introduced a scheduling algorithm based on generative adversarial reinforcement learning. This method, augmented with a discriminator network that incorporates task embedding, has significantly improved and stabilized the learning process [27]. Zhou et al. developed a scheduling framework incorporating a deep learning algorithm selector (DLS), trained on labeled data, and a DRL algorithm selector (DRLS), trained on dynamic scenario feedback, for selecting appropriate scheduling algorithms in various scenarios [28]. Tran et al. introduced a DRL-based task scheduler primarily focused on maintaining service quality in cloud data center task scheduling processes [29]. Tong et al. merged Q-learning with a deep neural network to introduce deep Q-learning for task scheduling, aimed at optimizing makespan in cloud computing workflow scheduling [30]. Swarup et al. addressed task scheduling in IoT within fog environments, proposing a DRL method utilizing target networks and experience replay techniques to improve task response speed [31]. Tang et al. presented a DRL-based representation model capable of adapting to variations in the number of nodes and tasks [32]. Yan et al. devised a DRL method for handling real-time jobs, concentrating on allocating incoming jobs to suitable virtual machines. This strategy is aimed at optimizing energy consumption while maintaining high service quality [33]. Cheng et al. developed a DRL-based scheduling method (DRL-Cloud) for managing workflow tasks with dependency constraints in cloud data centers, with a focus on reducing energy consumption [34]. Dong et al. introduced a DRL-based task scheduling algorithm (RLTS), which dynamically assigns tasks with priority relations to appropriate cloud servers to minimize task execution time [35]. Bi et al. established an Improved Deep Q-learning Network (IDQN) for green data center cloud service providers, aiming to allocate computing resources and schedule user tasks efficiently and effectively [36].

Methods of task scheduling in reinforcement learning signify a novel application of artificial intelligence within distributed graph databases. These reinforcement learning agents acquire knowledge about the patterns of distributed graph databases through interaction with the cloud environment, thereby enhancing the task scheduling process and surpassing traditional fixed scheduling approaches. Despite its advantages, reinforcement learning’s task scheduling optimization for distributed graph databases is not yet complete. Deep learning compensates for the perceptual problems of reinforcement learning, but the introduction of deep learning also brings new issues that need to be addressed. Task scheduling for distributed graph databases remains a multifaceted challenge, especially as cloud environments and task models become increasingly complex, making efficient task scheduling more challenging. DRL methods face several new issues in task scheduling:

(1) Deep learning hinges on a large corpus of labeled data, whereas DRL acquires knowledge through environmental interactions. During the initial phases, the scarcity of data results in both limited environmental understanding by the neural network and rudimentary decision-making by the reinforcement learning agent.

(2) Reinforcement learning operates on scalar rewards, which are characteristically sparse, noisy, and subject to delays. The efficacy of experience data utilization in DRL is suboptimal, leading to an underutilization of the inherent value of this data.

The Q-DRL method distinguishes itself from existing methodologies in several key aspects:

•   Application of the DRL Framework: The Q-DRL approach employs Double Deep Q-Network (Double DQN), a DRL algorithm that autonomously learns and optimizes scheduling decisions. Unlike traditional heuristic and metaheuristic algorithms (such as PSO, FCFS, LCFS, etc.), Q-DRL not only relies on historical data but is also capable of learning and adapting through real-time interaction with the environment.

•   Parallelization of Task Phases: In scheduling workflows, Q-DRL specifically accounts for the dependencies between tasks and conducts a parallelization of the workflow tasks prior to scheduling. This division helps to fully utilize computational resources, increasing the level of task parallelism and system throughput.

•   Adaptive Scheduling Strategy: Q-DRL is designed with a dynamically adaptive scheduling strategy. It optimizes scheduling decisions by continually learning from changes in the environment, allowing the algorithm to better adapt to the evolving workflow loads and system statuses.

•   Reward Function Design: The reward function in Q-DRL considers not only the minimization of the makespan but also aims to minimize response times. This dual consideration enables the algorithm to reduce task completion times while simultaneously enhancing user experience.

•   Load Balancing: The Q-DRL algorithm is specifically tailored for distributed graph databases, optimizing load balancing to ensure efficient utilization of system resources and stability of the system.

3  Methodology

3.1 Distributed Graph Database Workflow Task Scheduling Model

Distributed graph database tasks typically encompass data management, graph querying, and graph analysis. Central servers in distributed graph databases must consider the dependencies between tasks to effectively schedule and distribute tasks across the server network, ensuring the system’s operational requirements are met and stability is maintained. The distributed graph database workflow task model combines various sub-tasks into a complete workflow, which is then dispatched to different servers for execution, thereby enhancing the processing efficiency of the distributed graph database.

The scheduling of distributed graph database workflow tasks refers to the process by which the central server of the distributed graph database automates the scheduling, allocation, and execution of tasks. This process can be divided into several steps: First, constructing a Directed Acyclic Graph (DAG) relationship model for the sub-tasks of the database workflow; then, parallelizing the execution stages and scheduling sequences of the workflow sub-tasks; and finally, using a depth reinforcement learning scheduling algorithm with time optimization and load balancing constraints to dispatch the sub-tasks to the servers for execution.

The structure and attributes of the DAG model assist in task scheduling within distributed graph databases in the following ways:

•   Task Dependencies: The edges in a DAG represent the dependencies between tasks, ensuring that tasks are executed in the correct order and thereby avoiding circular dependencies and potential deadlocks.

•   Parallelism: DAGs facilitate the clear identification of tasks without dependencies, which can be executed in parallel. This promotes the parallel utilization of resources in distributed systems, enhancing execution efficiency.

•   Optimization Paths: Utilizing DAGs, various optimization algorithms can be applied to find the shortest execution path or the most optimal resource utilization path, thus reducing the overall execution time of the workflow.

•   Predictability: Analyzing a DAG can predict the completion time of the entire workflow, identify potential bottlenecks in advance, and allow for the rational allocation and reservation of resources.

In distributed graph databases, DAGs effectively model, schedule, and execute sub-tasks such as graph queries and analyses. By identifying sub-tasks that can be parallelized, the processing efficiency of the database is improved.

Given that the tasks within the distributed graph database workflow are interconnected with dependencies, meaning some tasks must be executed after others, a DAG is utilized to construct the associated model of the distributed graph database workflow tasks. The workflow under consideration is represented by a specific structure DAG W(T,D), where vertices represent sub-tasks, T={t1,t2,…,tn} includes a set of sub-tasks within the workflow and directed edges represent dependencies between tasks, D={Dik|i,k≤n} is the set of these directed edges, indicating dependencies where Dik implies that there is a directed edge from ti to tk, with tk being a sub-task of ti. Each sub-task ti=(jobid,taskid,datai,mi,ci,stime) includes the workflow task number jobid, the sub-task number taskid, the data volume datai of the sub-task, and the demand for memory mi and CPU resources ci, with stime representing the time when the user or application submits the distributed graph database workflow task to the central server, also known as submission time.

An example of a distributed graph database workflow task model with six sub-tasks is shown as Fig. 1. Except for the initial task (Task1, denoted as tstart), the other five tasks need to wait for all parent tasks to finish before they can begin execution, with the parent task set of task ti denoted as PT(ti), and the final task as Task6, denoted as tend.

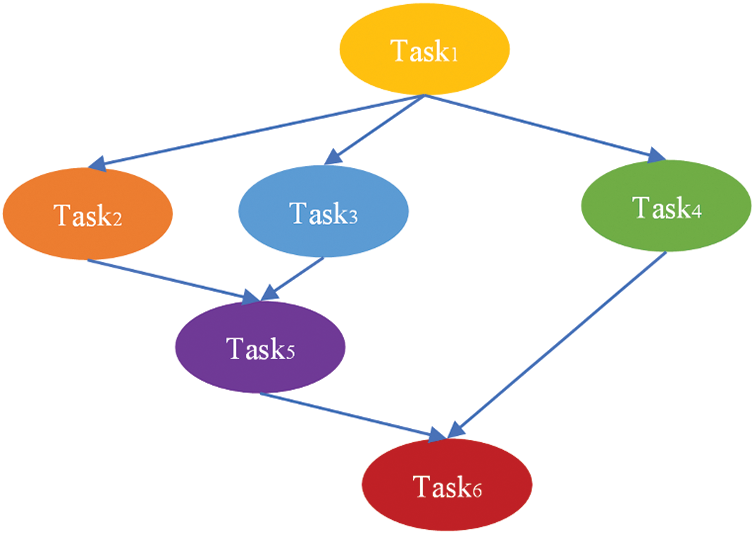
Figure 1: An example of a distributed graph database workflow task model containing 6 subtasks

The inherent total resources of a distributed graph database server can be modeled as V={v1,v2,…,vm}, where m represents the number of servers in the distributed graph database. The resource configuration of any given server is represented as vi=(mipsi,cpui,memi,diski), where mipsi indicates the processing speed of the CPU, cpui denotes the number of CPU cores, memi the size of the memory, and diski the disk capacity. If task ti is scheduled to execute on server vk, the execution time for each task, denoted as ti, is outlined in Eq. (1).

ET(ti)=dataimipsk(1)

The total scheduling time for a workflow task comprises both its execution time and transmission time hi, the latter referring to the bidirectional communication time between the central and local servers. The completion time ECT(ti) of task ti can be represented by Eq. (2). If tstart has no parent tasks, its completion time is simply the combined amount of the execution time and the transmission time. If the task has dependencies, its completion time is the highest value of the completion times in the parent task set PT(ti) plus its own execution time and transmission time.

ECT(ti)={ET(ti)+hi,PT(ti)=∅maxtk∈PT(ti){ET(tk)+hk}+ET(ti)+hi,PT(ti)≠∅(2)

Eq. (3) defines the makespan of the workflow, specifically marking the completion time of the final task, tend. The max function is employed here to account for the possibility that tend may have multiple parallel sub-tasks.

MSjobid=max(ECT(tend))(3)

Since the completion of the workflow hinges on the conclusion of all its sub-tasks due to their interdependencies, the response time of the entire workflow is used as the standard for measurement. The central server schedules the sub-tasks of the workflow task to other servers, and the response time of the workflow is the total time from the central server starting to schedule the sub-tasks to the point when all tasks have signaled completion. If a workflow task cannot be completed due to issues with some sub-tasks, then using the time it began execution as the response time is not practically significant. Therefore, the scheduling start time stime of the first task tstart is taken as the workflow task’s scheduling start time, and the response time of the workflow task is represented by Eq. (4). In scenarios where multiple workflow tasks coexist, the average response time is represented by Eq. (5).

RTjobid=MSjobid−stime(4)

RTave=∑id=1nRTjobidn(5)

In the context of scheduling tasks in a distributed graph database workflow, to accommodate the simultaneous presence of multiple workflow tasks, the concept of makespan MS for the central server of the distributed graph database is also defined, as shown in Eq. (6). Here, STk=uk−start(vk) denotes the completion time of server vk, with uk representing the time when all tasks of multiple workflows scheduled to the k-th server are completed, and start(vk) being the time when the k-th server begins executing tasks, across m servers.

MS=max({ST0,ST1,…,STm})(6)

After the scheduler dispatches tasks to a server, it will immediately occupy the CPU and other relevant resources according to the tasks’ resource requirements. The resources that remain idle on the server are then denoted as remaink=(mipskremain,cpukremain,memkremain,diskkremain), with the server’s resource idleness rate represented as shown in Eq. (7).

RIk=remainkvk(7)

3.2 Workflow Task Scheduling Optimization Design Based on Deep Reinforcement Learning

In the task scheduling of distributed graph database workflows, the key objective is to employ a rational scheduling strategy to minimize the completion time of distributed graph database tasks and maximize scheduling efficiency. Fig. 2 illustrates the workflow task scheduling algorithm framework proposed in this study, which is based on DRL. Upon the arrival of a new workflow, the tasks are first subjected to parallelization division, determining both the execution stages and scheduling sequences of the subtasks. Subsequently, the DRL workflow task scheduling algorithm, which incorporates time optimization and load balancing constraints, is employed to schedule the subtasks to servers to optimize execution time and achieve load balancing.

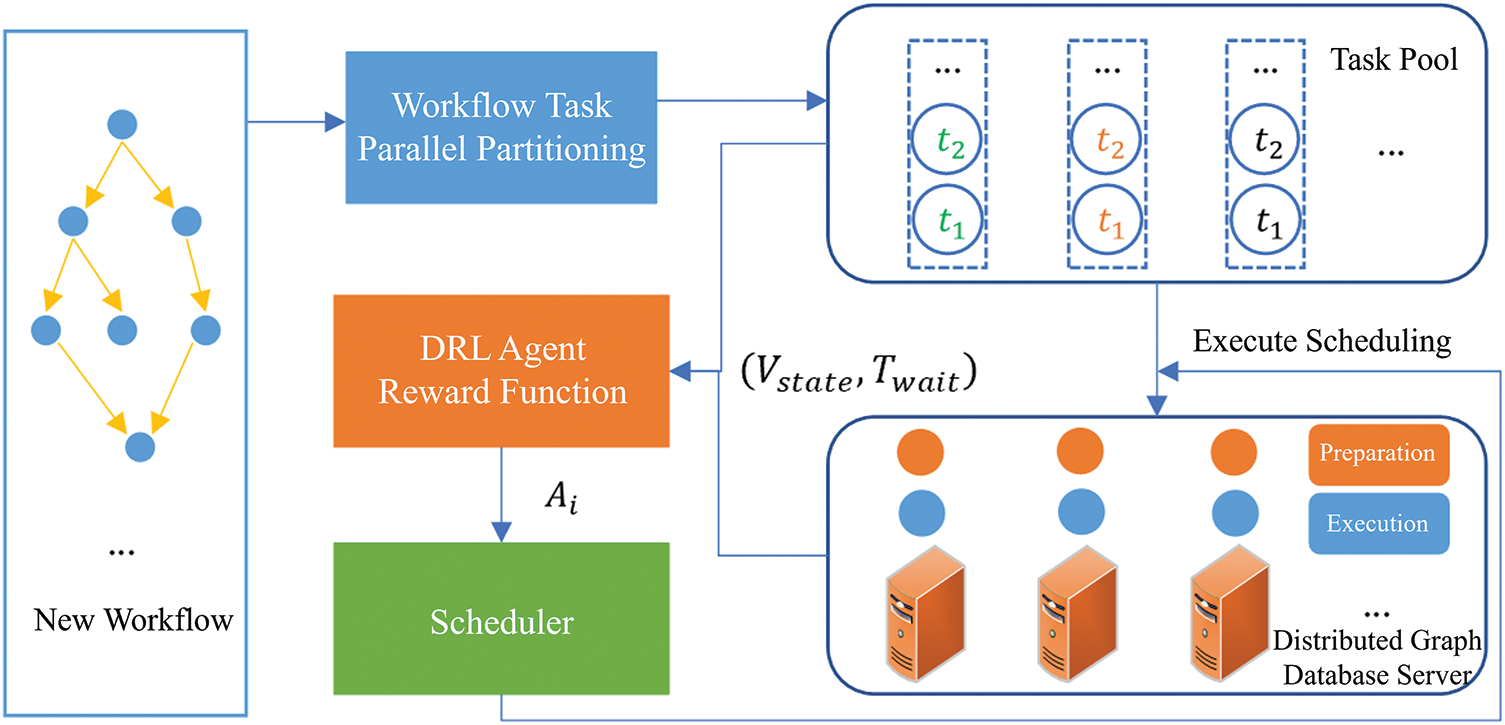
Figure 2: A framework for scheduling algorithms in distributed graph database workflows, utilizing DRL techniques

3.2.1 Parallelized Multi-Workflow Task Stage Division

A parallelization division strategy is used in the scheduling of distributed graph database workflow tasks to enhance the scheduling process by dividing it into parallel execution stages and scheduling sequences. Outlined below are the sequential steps constituting the complete scheduling process:

1. Task Submission: Users or applications submit workflow tasks W(T,D) to the central server of the distributed graph database. Each workflow W(T,D) comprises multiple subtasks interlinked by dependency relations D.

2. Workflow Prioritization: The central server of the distributed graph database sorts the workflows based on their submission time, forming a queue of workflows awaiting scheduling, Ltbs={W1,W2,…,Wn}, where Wn denotes the nth workflow. Workflows submitted earlier are prioritized in the queue for scheduling.

3. Parallelization Division:

a)   Parallelization of execution stages:

For each workflow Wi(T,D) in the queue Ltbs, the central server parallelizes the execution stages based on the dependency relations D, dividing workflow Wi into multiple executable stages. Each stage Mij={tik|PT(tik)⊆∪l=1j−1Mil},∀k contains a set of tasks that can be executed in parallel. Here, tik refers to the k-th task in workflow Wi, PT(tik) represents the parent task set of the kth task in workflow Wi, and the tasks in Mij are those whose all parent tasks are in the previous j−1 stages, indicating that there are no dependencies between them. Thus, Mij is the j-th parallel executable task stage in the i-th workflow.

b)   Parallelization of scheduling sequences

The central server collects feature information of each task and its parent tasks PT(tik), establishing a parallelized scheduling sequence Pij={Mi1,Mi2,…,Mik}, where i represents the workflow index, and j represents the index of parallel executable task stages within the workflow. Hence, Pij is the scheduling sequence for the j-th parallel executable task stage in the i-th workflow.

4. Multi-Workflow Scheduling: The central server retrieves the parallelized scheduling sequence Pij for each workflow Wi, comprising multiple stages Mij that can be executed in parallel. The server then schedules tasks within these stages, distributing them across different servers for parallel execution. This study introduces a novel task scheduling algorithm utilizing DRL, primarily aimed at optimizing execution time and facilitating load balancing within distributed systems.

5. Task Execution and Monitoring: Servers commence the execution of the allocated tasks. The central server of the distributed graph database actively monitors the execution status of all tasks. As soon as a task is completed, the central server immediately checks its child tasks. The algorithm activates a dependent task once all its prerequisite parent tasks have been completed, thus advancing it into the scheduling phase for subsequent processing.

6. Workflow Completion and Removal: Once all subtasks of a workflow are completed, the workflow Wi is considered complete. The central server removes it from the queue of workflows awaiting scheduling, Ltbs={W∈Ltbs|W≠Wi}, and begins scheduling the next workflow.

This process repeats continuously until the queue Ltbs is empty, meaning all workflows have been processed. Throughout this procedure, the central server not only realizes parallel processing of tasks within workflows but also facilitates parallel processing across different workflows, thereby significantly enhancing the parallel processing capabilities and overall execution efficiency of the distributed graph database.

3.2.2 Deep Reinforcement Learning Workflow Task Scheduling Algorithm with Time Optimization and Load Balancing Constraints

The study addressed the optimization of the makespan of distributed graph database workflow tasks, while also considering the response time of the workflow tasks. Given the strong dependency relationships between subtasks within a workflow task, response time is a crucial metric for successful task completion. The DRL model employed in this research is the Double DQN. The paper first outlines the design and definition of the state and action spaces for distributed graph database workflow task scheduling. Subsequently, it introduces an intelligent agent reward function with constraints for time optimization and load balancing, enhancing the perception of workflow completion response time.

During the scheduling process, the concept of online learning is utilized, meaning that the algorithm is always running. As new workflow tasks arrive, they are processed immediately, and the scheduling strategy is updated. The agent refines the action selection policy continuously, aiming to optimize the makespan value MS of the distributed graph database workflow tasks and reduce the average response time RTave, thus achieving load balancing across distributed graph database servers and enhancing processing efficiency.

The specific steps of the proposed DRL workflow task scheduling algorithm, constrained by time optimization and load balancing, are as follows:

1.   Definition and initialization:

a)   Define the state space S

The state of the distributed graph database servers is defined as Vstate=(V1,V2,V3,…,Vk), where Vstate=(V1,V2,V3,…,Vk) includes the server’s resource configuration vk, the completion time of tasks already allocated on the server ECTalloc={ECT(t1),ECT(t2),…,ECT(tn)}, and the server’s idle resource rate RIk.

The state of subtasks within the workflow is defined as Twait=(T1,T2,T3,…), where Ti=(ti,PT(ti)) includes the remaining subtasks ti pending in the current workflow, along with the execution information of each subtask’s parent task PT(ti), to determine if the subtask can be scheduled.

The server state information and pending task information are combined into a set of state space collections S=(S1,S2,S3,…), where each state space Si=(Vstate,Twait).

b)   Define action space A

The action space is a set of scheduling operations that the scheduler can perform, defined by the number of available distributed graph database servers, i.e., A=(1,2,3,…,k).

c)   Initialize the evaluation network Q(s,a,θ) and the target network Q(s,a,θ−)

In Double DQN, the Q value is calculated by a neural network, commonly referred to as the Q network. Its input is the state of the environment, and its output is the expected return of each action, i.e., the Q value. The Double DQN method incorporates two distinct Q networks: the evaluation network, which is responsible for guiding the agent, choosing actions, and calculating loss, and the target network, which is tasked with determining the Temporal Difference (TD) target value TDtarget.

A target network Q(s,a,θ−) is constructed with the same structure as the evaluation network Q(s,a,θ) but different parameters, where θ≠θ−, s is the current state, a is the action taken in state s, θ is the parameters of the evaluation network, and θ− is the parameters of the target network.

2.   Online learning process:

(1) Waiting stage: If no new workflow task is present, the algorithm remains in a waiting state until a new workflow task arrives.

(2) Upon the arrival of a new task: When a new workflow task arrives, the following steps are executed.

For each iteration of the scheduling algorithm:

a) The agent observes the current state s and selects an action a(a∈A), executes action a, transitions to the next state s′, and receives a reward r. The reward r is derived from a reward function with constraints for time optimization and load balancing, considering both the optimization of the distributed graph database workflow task scheduling’s makespan MS and the average response time RTave, as shown in Eq. (8):

R=φ1∗1MS+φ2∗1RTave(8)

where φ1 and φ2 are weights, and φ1+φ2=1.

b) Store the tuple (s,a,r,s′), representing the learned experience of the agent, in the experience replay unit.

c) Randomly sample a minibatch of transitions (s,a,r,s′)label from the experience replay unit.

d) For each sampled transition (s,a,r,s′)label:

① If s′ is a terminal state, set TDtarget=r.

② Otherwise, the evaluation network Q(s,a,θ) is used to find the action a′ that produces the maximum Q value as shown in Eq. (9):

a′=argmaxa∈AQ(s′,a,θ)(9)

Then, the target network Q(s,a,θ−) is used to calculate the target Q value TDtarget as shown in Eq. (10):

TDtarget=r+γ∗Q(s′,a′,θ−)(10)

where γ is the discount factor, used to balance the weight of immediate rewards and future rewards.

e) The loss L(θ) is calculated to measure the discrepancy between the predicted Q value Q(s,a,θ) by the evaluation network and the target Q value TDtarget. The calculation formula for L(θ) is shown in Eq. (11):

L(θ)=E[(TDtarget−Q(s,a,θ))2](11)

After calculating L(θ), gradient descent is used to compute the gradient of the loss function with respect to the parameters θ, as shown in Eq. (12):

∇θ=∂L(θ)∂θ=E[(y−Q(s,a,θ)Q(s,a,θ)∂θ)](12)

The gradient of the loss function with respect to θ, ∇θ, is then used to update the parameters θ, as shown in Eq. (13):

θ=θ+∇θ(13)

f) The initial value for the target network update interval C is defined, setting a threshold for the gradient, and the maximum Cmax and minimum Cmin values for the update interval are established, along with the adjustment step size ∇C. The model achieves a dynamic adjustment in the target network’s update frequency through the update interval parameter C and the gradient, thereby enhancing the network’s learning efficiency. The specific update strategy is as follows:

① If the value of the gradient is less than the threshold, indicating that the network is converging, the number of update intervals can be reduced. That is, when the second norm of the gradient , and C>Cmin, then C=C−∇C.

② In cases where the gradient remains significant despite reaching the update interval C, it is feasible to incrementally increase the value of C for better results. That is, when ‖∇θ‖≥threshold, and C < Cmax, then C=C+∇C.

③ If the current iteration step is an exact multiple of C, then θ−=θ, allowing the parameters of the evaluation network to be copied to the target network so that the target network’s Q value can be used to calculate a more accurate.

The study addressed the optimization of the makespan of distributed graph database workflow tasks, while also considering the response time of the workflow tasks. Given the strong dependency relationships between subtasks within a workflow task, response time is a crucial metric for successful task completion. The DRL model employed in this research is the Double DQN. The paper first outlines the design and definition of the state and action spaces for distributed graph database workflow task scheduling. Subsequently, it introduces an intelligent agent reward function with constraints for time optimization and load balancing, enhancing the perception of workflow completion response time.

The core idea of the Q-DRL scheduling algorithm is to optimize the scheduling strategy through autonomous learning by an agent. This algorithm involves the following key aspects:

•   Architecture: The architecture used is Double Deep Q-Network (Double DQN), which includes two neural networks: An evaluation network and a target network. The evaluation network selects actions according to the current policy and computes loss, while the target network is used to stabilize learning objectives.

•   Training Process: The training process involves defining the state space and action space, as well as designing the agent’s reward function, which includes constraints for time optimization and load balancing. The agent learns by interacting with the environment, collecting experiences, and using experience replay to update the networks, continuously optimizing its action selection strategy.

•   Adaptability: The Q-DRL algorithm can adapt to dynamic changes within the distributed graph database, such as variations in task load or server performance fluctuations. The agent processes new workflow tasks in real time through online learning and updates the scheduling strategy to optimize the completion time of distributed graph database workflow tasks, while also reducing response times and achieving server load balancing.

In this manner, the Q-DRL scheduling algorithm is capable of learning and adjusting strategies in a dynamically changing environment, optimizing task scheduling performance, and enhancing the overall efficiency of distributed graph databases.

The specific implementation of Q-DRL is illustrated in Algorithm 1. Throughout the execution of the algorithm, scheduling decisions for each workflow task are obtained, which determine on which server each sub-task should be executed.

4  Experiment

4.1 Experimental Setup

In this subsection, the proposed algorithm was experimentally validated in a simulated distributed graph database environment. The hardware platform configuration for the experiment consisted of an i9-10980XE CPU, 64 GB of RAM, 8 TB of hard disk space, and an RTX 2080. The software platform was established on a Windows 10 operating system using Python and TensorFlow for algorithm simulation experiments. The dataset used in the experiments was derived from the cluster-trace-v2018 workflow dataset publicly available from the Alibaba Data Center, which includes task information containing DAG dependencies. To assess the performance of the proposed method, it was compared with four other scheduling methods: Random Scheduling, First-fit Scheduling, DRL-Cloud, and IDQN Scheduling. This subsection conducted multiple group experiments to compare and validate the performance of the proposed algorithm under different workflow load quantities and machine elasticity change counts. The proposed algorithm is referred to as Q-DRL for convenience in legend plotting.

4.2 Analysis of Experimental Results

Initially, the algorithm’s scheduling efficacy was evaluated across varying quantities of workflow task loads. Each workflow contained several sub-tasks with interdependencies, with each task having varying resource requirements and instance counts. A virtual machine environment consisting of four units with 1000 MIPS, 1 CPU, and 1 GB each of memory and disk was constructed. Subsequently, the workflow load quantity was dynamically increased for multiple group experiments.

The experimental results for the makespan are illustrated in Fig. 3. Initially, when the number of workflow tasks in the system is small, the difference in the scheduling outcomes of various algorithms is negligible due to the relative abundance of machine resources. However, as the number of workflows in the scheduling process gradually increases, so does the number of subtasks within each workflow, leading to more complex dependencies and parallelisms. The experimental findings indicate that with an increase in the number of workflows, the makespan of both the First-fit and Random scheduling methods rapidly escalates, with the Random method exhibiting instability in its scheduling outcomes due to its inherent randomness. Q-DRL, through its parallel stage division of workflows and the design of a novel reward function, achieves better results. When compared to First-fit and Random methods, Q-DRL achieves an average improvement of 12.4% and 11.9% in makespan, respectively. Compared to other reinforcement learning methods, under the constraints of limited machine resources, Q-DRL enhances the parallel partitioning and execution of workflow tasks. Motivated by the newly designed reward function with time optimization and load balancing constraints, Q-DRL attains lower makespan results than DRL-Cloud and IDQN, with an average performance improvement of 4.4% and 2.6%, respectively. The findings indicate that the suggested approach is capable of delivering efficient scheduling in response to a surge in the number of tasks in distributed graph database workflows, thereby maintaining consistent service functionality.

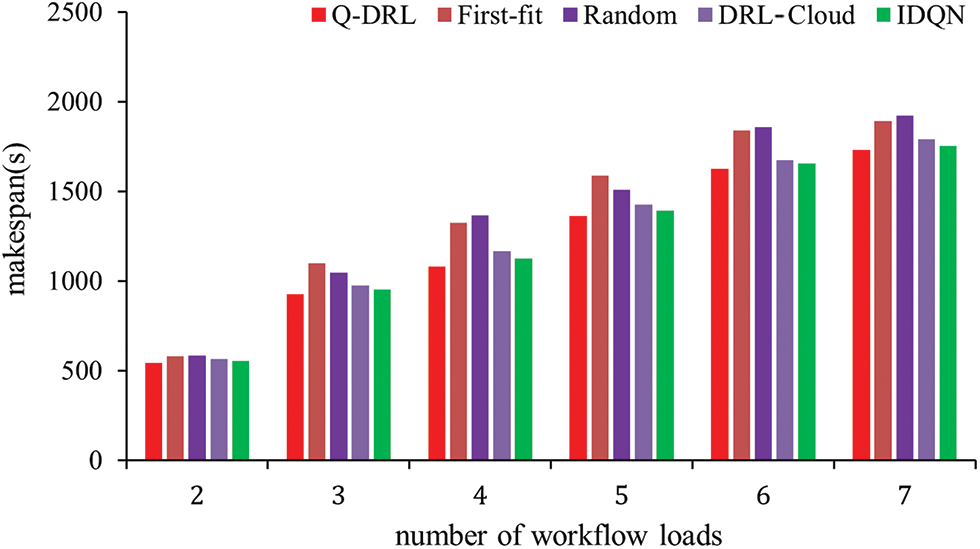
Figure 3: The value of makespan when the number of workflow loads changes

The average response times for workflow tasks, as depicted in Fig. 4, reveal that Q-DRL consistently outperforms both IDQN and DRL-Cloud methods across various workflow loads. As the number of workflow loads increases, so does the count of interdependent subtasks within each workflow, leading to an overall rise in the number of tasks. The response time curves, as a function of workflow load, indicate that the Random scheduling method, due to its stochastic nature, yields unpredictable results and generally results in the longest average response times. The First-fit scheduling method fares slightly better, yet still lags behind other strategies.

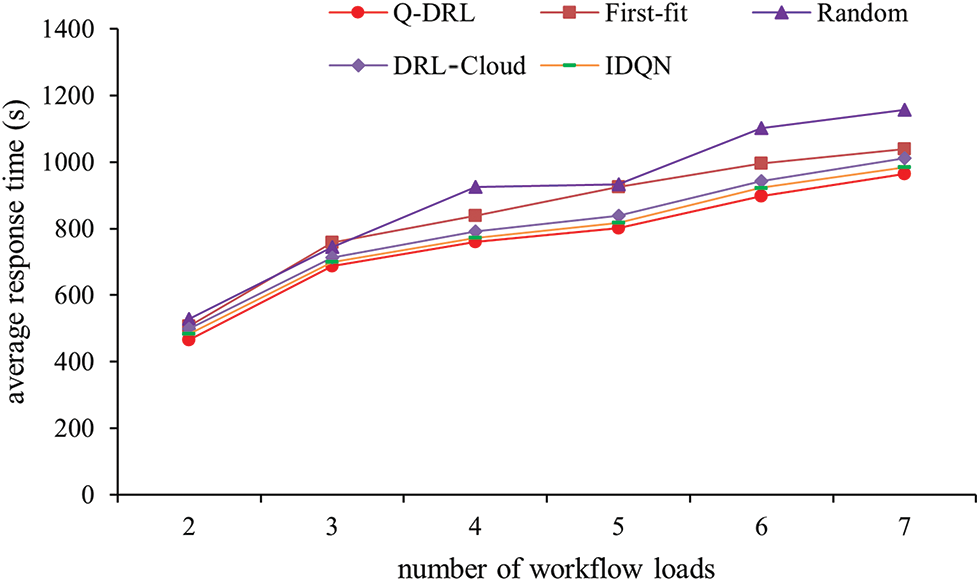
Figure 4: The value of the average response time when the number of workflow loads changes

More specifically, at a workflow count of seven, Q-DRL’s average response time is approximately 2.03% and 4.74% lower than that of IDQN and DRL-Cloud, respectively. As the workflow count decreases to six, the gap widens, with Q-DRL outperforming IDQN and DRL-Cloud by around 2.71% and 4.88%, respectively. With five workflows, the improvement in average response time offered by Q-DRL is approximately 1.96% and 4.53% over IDQN and DRL-Cloud. This trend continues as the number of workflows reduces to four, with Q-DRL maintaining a lead of approximately 1.56% and 4.17% over IDQN and DRL-Cloud, respectively. At a workflow count of three, the difference is 1.86% and 3.51%, and at two workflows, Q-DRL’s advantage over IDQN and DRL-Cloud peaks at 3.52% and 6.43%.

Q-DRL exhibits a substantial advantage in handling both smaller and larger workflow loads. The method’s ability to efficiently parallelize the scheduling of workflow tasks, coupled with a reward function that constrains the optimization process, results in lower average response times for workflows compared to First-fit, Random, DRL-Cloud, and IDQN. Consequently, the proposed Q-DRL approach is adept at optimizing workflow response times while upholding completion deadlines, thus ensuring stable service quality in distributed graph databases, even as system workflow loads increase.

During the experiments, the idle rate of machine resources at each time point was also recorded, and the average idle rate of cluster machine resources throughout the entire scheduling process was calculated, as illustrated in Fig. 5, there is a notable change in performance with increasing workflow volume, the degree of task parallelism also begins to increase, and the resource idle rate starts to decrease but does not continue to drop to zero. This is because the dependency constraints within the workflows mean that resources cannot be fully utilized at all times. When the number of workflows is low, some tasks can only wait to be scheduled due to dependency relationships, leading to gaps in resource utilization. Concurrently, a rise in workflow loads correlates with an increase in the number of parallelizable subtasks, and machine resources are progressively more utilized, leading to a decrease in idle rates.

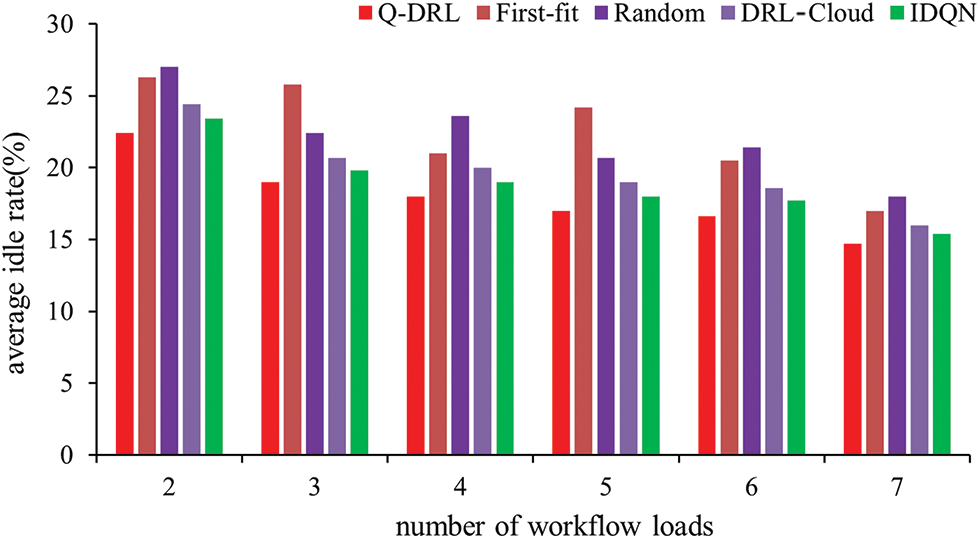
Figure 5: Average idle rate of the cluster under different workload loads

The experimental outcomes demonstrate a superior performance of the Q-DRL algorithm in maintaining lower average idle rates when compared to IDQN and DRL-Cloud across all evaluated workflow scenarios. With two workflows, Q-DRL’s idle rate is 22.4%, presenting reductions of 4.3% and 8.2% relative to IDQN and DRL-Cloud, respectively. For three workflows, the idle rate for Q-DRL is at 19%, yielding a 4.2% improvement over IDQN and 8.2% over DRL-Cloud. At four workflows, Q-DRL registers an 18% idle rate, outperforming IDQN and DRL-Cloud by margins of 5.3% and 10%, respectively. With five workflows, Q-DRL achieves a 17% idle rate, surpassing IDQN by 5.6% and DRL-Cloud by 10.5%. For six workflows, Q-DRL exhibits a 16.6% idle rate, which is 6.2% more efficient than IDQN and 10.8% more than DRL-Cloud. At seven workflows, Q-DRL continues to outperform with a 14.7% idle rate, 4.5% better than IDQN and 8.1% better than DRL-Cloud. Under varying workflow loads, the idle rate for Q-DRL remains consistently lower than that for First-fit, Random, DRL-Cloud, and IDQN scheduling methods, demonstrating that its task scheduling is more parallel than other methods and can utilize system resources more fully and efficiently. Although the method proposed in this paper exhibits excellent performance in the experimental environment, its efficacy in real-world applications will require validation through more extensive testing. Furthermore, future research may revolve around the aforementioned potential domains to further enhance the practicality and robustness of the scheduling approach.

5  Conclusion

This article departs from the scheduling of workflow tasks in distributed graph databases with dependencies and targets the prolonged completion and response times of workflow tasks caused by task dependencies and insufficient parallel partitioning. A method for workflow task scheduling in distributed graph databases, predicated on the principles of DRL, is hereby proposed. Initially, the method employs DAG to build a workflow task model for distributed graph databases to capture the inter-task dependencies. Following this, it partitions the workflow tasks in parallel, extracting feature information of each task and its parent from the workflow task model to establish a sequence for parallel task scheduling. The study then formulates a time-optimized and load-balanced constrained DRL workflow task scheduling model, modeling both the state and action spaces, and introducing a novel reward function. Comprehensive experimental tests were conducted in environments with varying workflow task loads and differing numbers of cluster machines. The efficacy of the proposed algorithm is compared with that of established methods, providing a comprehensive analysis of its performance. The empirical results unequivocally demonstrate that our proposed method not only ensures minimal makespan for workflow scheduling but also significantly diminishes the average response time for workflows. This denotes a marked superiority in performance relative to comparative methodologies.

Acknowledgement: The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.

Funding Statement: This research was funded by the Science and Technology Foundation of State Grid Corporation of China (Grant No. 5108-202218280A-2-397-XG).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Shuming Sha, Wang Luo; dataset preparation and data preprocessing: Naiwang Guo; analysis and interpretation of results: Shuming Sha, Naiwang Guo, Wang Luo, Yong Zhang; draft manuscript preparation: Shuming Sha, Wang Luo, Yong Zhang; manuscript review and finalisation: Shuming Sha, Wang Luo, Yong Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The training data used in this paper were obtained from cluster-trace-v2018. Available online via the following link: https://github.com/alibaba/clusterdata/tree/master/cluster-trace-v2018.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Besta et al., “The graph database interface: Scaling online transactional and analytical graph workloads to hundreds of thousands of cores,” in Proc. SC, 2023, pp. 1–18. [Google Scholar]

2. C. Feng, X. Xu, L. Chen, M. Yu, and X. Guo, “The core technique and application of knowledge graph in power grid company administrative duty,” in Proc. ISAEECE, 2023, vol. 12704, pp. 249–254. doi: 10.1117/12.2680494. [Google Scholar] [CrossRef]

3. R. Sun and J. Chen, “Design of highly scalable graph database systems without exponential performance degradation,” in Proc. BiDEDE, 2023. [Google Scholar]

4. M. Kamm, M. Rigger, C. Zhang, and Z. Su, “Testing graph database engines via query partitioning,” in Proc. ISSTA, 2023, pp. 140–149. [Google Scholar]

5. M. V. D. Boor, S. C. Borst, J. S. H. V. Leeuwaarden, and D. Mukherjee, “Scalable load balancing in networked systems: A survey of recent advances,” SIAM Rev., vol. 64, no. 3, pp. 554–622, 2022. doi: 10.1137/20M1323746. [Google Scholar] [CrossRef]

6. E. Hyytiä and S. Aalto, “On round-robin routing with FCFS and LCFS scheduling,” Perform. Eval., vol. 97, pp. 83–103, 2016. doi: 10.1016/j.peva.2016.01.002. [Google Scholar] [CrossRef]

7. S. Seth and N. Singh, “Dynamic heterogeneous shortest job first (DHSJFA task scheduling approach for heterogeneous cloud computing systems,” Int. J. Inform. Technol., vol. 11, no. 4, pp. 653–657, 2019. doi: 10.1007/s41870-018-0156-6. [Google Scholar] [CrossRef]

8. J. Békési, G. Dósa, and G. Galambos, “A first fit type algorithm for the coupled task scheduling problem with unit execution time and two exact delays,” Eur. J. Oper. Res., vol. 297, no. 3, pp. 844–852, 2022. doi: 10.1016/j.ejor.2021.06.002. [Google Scholar] [CrossRef]

9. C. Gao, V. C. S. Lee, and K. Li, “D-SRTF: Distributed shortest remaining time first scheduling for data center networks,” IEEE Trans. Cloud Comput., vol. 9, no. 2, pp. 562–575, 2018. doi: 10.1109/TCC.2018.2879313. [Google Scholar] [CrossRef]

10. O. Ajayi, F. Oladeji, C. Uwadia, and A. Omosowun, “Scheduling cloud workloads using carry-on weighted round robin,” in Proc. AFRICOMM, Lagos, Nigeria, 2018, pp. 60–71. [Google Scholar]

11. M. H. Shirvani and R. N. Talouki, “A novel hybrid heuristic-based list scheduling algorithm in heterogeneous cloud computing environment for makespan optimization,” Parallel Comput., vol. 108, pp. 102828, 2021. doi: 10.1016/j.parco.2021.102828. [Google Scholar] [CrossRef]

12. G. Zhao, “Cost-aware scheduling algorithm based on PSO in cloud computing environment,” Int. J. Grid Distrib. Comput., vol. 7, no. 1, pp. 33–42, 2014. doi: 10.14257/ijgdc.2014.7.1.04. [Google Scholar] [CrossRef]

13. N. Mansouri, B. M. H. Zade, and M. M. Javidi, “Hybrid task scheduling strategy for cloud computing by modified particle swarm optimization and fuzzy theory,” Comput. Ind. Eng., vol. 130, pp. 597–633, 2019. doi: 10.1016/j.cie.2019.03.006. [Google Scholar] [CrossRef]

14. D. Wu, “Cloud computing task scheduling policy based on improved particle swarm optimization,” in Proc. ICVRIS, 2018, pp. 99–101. [Google Scholar]

15. M. Kumar and S. C. Sharma, “PSO-COGENT: Cost and energy efficient scheduling in cloud environment with deadline constraint,” Sustain. Comput.: Inform. Syst., vol. 19, pp. 147–164, 2018. [Google Scholar]

16. K. Dubey and S. C. Sharma, “A novel multi-objective CR-PSO task scheduling algorithm with deadline constraint in cloud computing,” Sustain. Comput.: Inform. Syst., vol. 32, pp. 100605, 2021. [Google Scholar]

17. N. Meziani, M. Boudhar, and A. Oulamara, “PSO and simulated annealing for the two-machine flowshop scheduling problem with coupled-operations,” Eur. J. Ind. Eng., vol. 12, no. 1, pp. 43–66, 2018. doi: 10.1504/EJIE.2018.089877 [Google Scholar] [CrossRef]

18. S. Mangalampalli, G. R. Karri, and G. N. Satish, “Efficient workflow scheduling algorithm in cloud computing using whale optimization,” Procedia Comput. Sci., vol. 218, pp. 1936–1945, 2023. doi: 10.1016/j.procs.2023.01.170. [Google Scholar] [CrossRef]

19. S. A. Alsaidy, A. D. Abbood, and M. A. Sahib, “Heuristic initialization of PSO task scheduling algorithm in cloud computing,” J. King Saud Univ.-Comput. Inf. Sci., vol. 34, no. 6, pp. 2370–2382, 2022. doi: 10.1016/j.jksuci.2020.11.002. [Google Scholar] [CrossRef]

20. W. Qi, “Optimization of cloud computing task execution time and user QoS utility by improved particle swarm optimization,” Microprocess. Microsyst., vol. 80, pp. 103529, 2021. doi: 10.1016/j.micpro.2020.103529. [Google Scholar] [CrossRef]

21. M. Shokouhifar, “FH-ACO: Fuzzy heuristic-based ant colony optimization for joint virtual network function placement and routing,” Appl. Soft Comput., vol. 107, pp. 107401, 2021. doi: 10.1016/j.asoc.2021.107401. [Google Scholar] [CrossRef]

22. T. Khan, W. Tian, G. Zhou, S. Ilager, M. Gong and R. Buyya, “Machine learning (ML)-centric resource management in cloud computing: A review and future directions,” J. Netw. Comput. Appl., vol. 204, pp. 103405, 2022. doi: 10.1016/j.jnca.2022.103405. [Google Scholar] [CrossRef]

23. J. Gao, “Machine learning applications for data center optimization,” Google White Paper, vol. 21, pp. 1–13, 2014. [Google Scholar]

24. Y. Gari, D. A. Monge, and C. Mateos, “A Q-learning approach for the autoscaling of scientific workflows in the cloud,” Future Gener. Comput. Syst., vol. 127, pp. 168–180, 2022. doi: 10.1016/j.future.2021.09.007. [Google Scholar] [CrossRef]

25. D. Ding, X. Fan, Y. Zhao, K. Kang, Q. Yin and J. Zeng, “Q-learning based dynamic task scheduling for energy-efficient cloud computing,” Future Gener. Comput. Syst., vol. 108, pp. 361–371, 2020. doi: 10.1016/j.future.2020.02.018. [Google Scholar] [CrossRef]

26. F. Li and B. Hu, “DeepJS: Job scheduling based on deep reinforcement learning in cloud data center,” in Proc. ICBDC, 2019, pp. 48–53. [Google Scholar]

27. J. Li, X. Zhang, J. Wei, Z. Ji, and Z. Wei, “GARLSched: Generative adversarial deep reinforcement learning task scheduling optimization for large-scale high performance computing systems,” Future Gener. Comput. Syst., vol. 135, pp. 259–269, 2022. doi: 10.1016/j.future.2022.04.032. [Google Scholar] [CrossRef]

28. G. Zhou, R. Wen, W. Tian, and R. Buyya, “Deep reinforcement learning-based algorithms selectors for the resource scheduling in hierarchical cloud computing,” J. Netw. Comput. Appl., vol. 208, pp. 103520, 2022. doi: 10.1016/j.jnca.2022.103520. [Google Scholar] [CrossRef]

29. M. N. Tran and Y. Kim, “A cloud QoS-driven scheduler based on deep reinforcement learning,” in Proc. ICTC, 2021, pp. 1823–1825. [Google Scholar]

30. Z. Tong, H. Chen, X. Deng, K. Li, and K. Li, “A scheduling scheme in the cloud computing environment using deep Q-learning,” Inf. Sci., vol. 512, pp. 1170–1191, 2020. doi: 10.1016/j.ins.2019.10.035. [Google Scholar] [CrossRef]

31. S. Swarup, E. M. Shakshuki, and A. Yasar, “Energy efficient task scheduling in fog environment using deep reinforcement learning approach,” Procedia Comput. Sci., vol. 191, pp. 65–75, 2021. doi: 10.1016/j.procs.2021.07.012. [Google Scholar] [CrossRef]

32. Z. Tang, W. Jia, X. Zhou, W. Yang, and Y. You, “Representation and reinforcement learning for task scheduling in edge computing,” IEEE Trans. Big Data, vol. 8, no. 3, pp. 795–808, 2020. doi: 10.1109/TBDATA.2020.2990558. [Google Scholar] [CrossRef]

33. J. Yan et al., “Energy-aware systems for real-time job scheduling in cloud data centers: A deep reinforcement learning approach,” Comput. Electric. Eng., vol. 99, pp. 107688, 2022. doi: 10.1016/j.compeleceng.2022.107688. [Google Scholar] [CrossRef]

34. M. Cheng, J. Li, and S. Nazarian, “DRL-cloud: Deep reinforcement learning-based resource provisioning and task scheduling for cloud service providers,” in Proc. ASP-DAC, 2018, pp. 129–134. [Google Scholar]

35. T. Dong, F. Xue, C. Xiao, and J. Li, “Task scheduling based on deep reinforcement learning in a cloud manufacturing environment,” Concurr. Comput., vol. 32, no. 11, pp. e5654, 2020. doi: 10.1002/cpe.5654. [Google Scholar] [CrossRef]

36. J. Bi, Z. Yu, and H. Yuan, “Cost-optimized task scheduling with improved deep q-learning in green data centers,” in Proc. SMC, 2022, pp. 556–561. [Google Scholar]