 Open Access
Open Access
ARTICLE
SGT-Net: A Transformer-Based Stratified Graph Convolutional Network for 3D Point Cloud Semantic Segmentation
1 Faculty of Robot Science and Engineering, Northeastern University, Shenyang, 110167, China
2 State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang, 110016, China
3 Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang, 110169, China
4 SIASUN Robot & Automation Co., Ltd., Shenyang, 110169, China
* Corresponding Author: Suyi Liu. Email:
(This article belongs to the Special Issue: Advanced Artificial Intelligence and Machine Learning Frameworks for Signal and Image Processing Applications)
Computers, Materials & Continua 2024, 79(3), 4471-4489. https://doi.org/10.32604/cmc.2024.049450
Received 08 January 2024; Accepted 15 April 2024; Issue published 20 June 2024
Abstract
In recent years, semantic segmentation on 3D point cloud data has attracted much attention. Unlike 2D images where pixels distribute regularly in the image domain, 3D point clouds in non-Euclidean space are irregular and inherently sparse. Therefore, it is very difficult to extract long-range contexts and effectively aggregate local features for semantic segmentation in 3D point cloud space. Most current methods either focus on local feature aggregation or long-range context dependency, but fail to directly establish a global-local feature extractor to complete the point cloud semantic segmentation tasks. In this paper, we propose a Transformer-based stratified graph convolutional network (SGT-Net), which enlarges the effective receptive field and builds direct long-range dependency. Specifically, we first propose a novel dense-sparse sampling strategy that provides dense local vertices and sparse long-distance vertices for subsequent graph convolutional network (GCN). Secondly, we propose a multi-key self-attention mechanism based on the Transformer to further weight augmentation for crucial neighboring relationships and enlarge the effective receptive field. In addition, to further improve the efficiency of the network, we propose a similarity measurement module to determine whether the neighborhood near the center point is effective. We demonstrate the validity and superiority of our method on the S3DIS and ShapeNet datasets. Through ablation experiments and segmentation visualization, we verify that the SGT model can improve the performance of the point cloud semantic segmentation.Keywords
Semantic segmentation on point cloud becomes a research hotspot in 3D vision, which is applied to various applications such as virtual reality [1], robot visual grabbing [2], and automatic driving [3]. Point cloud data with the advantages of depth information, able to accurately capture the spatial features. However, unlike 2D images, 3D point cloud data have congenital disadvantages such as irregular arrangement, uneven density, and sparsity in continuous space. They are usually represented by voxel, mesh, or point-based features. But voxel, mesh representations commonly have insufficient resolution, high memory cost, and are not directly related to 3D sensor output. Therefore, it is necessary to explore an advanced method to directly process point cloud data.
Previously, 3D semantic segmentation [4–8] based on deep learning makes abundant achievements, which can be classified into voxel based methods [9,10] and point based methods [4,5]. The voxel based methods project point clouds onto regular grids and convert them into voxels. Subsequently, the data is processed using variants of convolutional neural networks (CNN). However, the large amount of data preprocessing and high memory footprint limit the development of voxel-based methods. To process irregular, sparse, and unstructured data, like 3D point clouds, most studies shift the focus of point cloud processing to point-based methods. PointNet [4] is a pioneering deep learning framework for point cloud processing. Due to its global max pooling operation, local features are ignored. To better consider local information, some researchers have achieved promising results in many tasks such as image recognition [11–13] and semantic segmentation by aggregating local features. However, most of them utilize convolution operations to aggregate local features of point clouds, but ignore the establishment of long-range dependencies.
Along other lines of research, GCN utilizes points as vertices and the relationship between points as edges to construct graphs representing non-Euclidean data. Furthermore, GCN can be applied to enhance connections between nodes within features. However, only limited attempts [14–18] apply GCN to 3D point clouds. Motivated by the above works, we develop an efficient feature extractor based on GCN and K Nearest Neighbors (KNN) to capture long-range contexts and neighborhood information. Firstly, the 3D space is parted into non-overlapping cubic windows. Then a dense-sparse sampling strategy is proposed, instead, each vertex only selects the points in the neighborhood after the KNN search, we also sample the distant points as vertices. In this way, each vertex has both neighborhood points and long-range points, which effectively establish long-range context dependency and achieve a significantly enlarged receptive field. In addition, to select whether the neighborhood points searched by KNN around the current center vertex are valid, we propose a similarity measurement module to filter out noise points that may belong to different classes. This can not only improve the precision of network segmentation but also greatly improve the efficiency of the network.
On the other hand, the application of Transformer [19] in point cloud [8,20–22] has received more and more attention in recent years, which can harvest long-range context information by self-attention mechanism. “Vector self-attention” and “subtraction relation” are proposed by Point Transformer [20] for classification and dense prediction of point clouds. Offset-attention with normalization refinement and implicit Laplace operator is proposed by Point Cloud Transformer [8] to aggregate local features. SGT-GCN [23] utilizes a GCN and self-attention to enhance semantic representations by aggregating neighborhood information and focusing on vital relationships. Inspired by the above works, further to emphasize meaningful relationships among the center points, neighborhood points, and distant points, we propose a stratified self-attention mechanism based on Transformer. We utilize the dense-sparse sampling strategy mentioned above to make each “query” have both a dense “Key” at a close distance and a sparse “Key” at a long distance. In this way, the proposed self-attention mechanism redistributes the weight of the relationship between features to further enhance the most vital connections.
The advantages of our proposed SGT module are verified by extensive experiments. However, it is notable that the irregular point distribution and density diversity in the point cloud bring great challenges to the design of 3D GCN. Inspired by 2D CNN Maxpooling operation, graph maximum pool operation is utilized in the SGT module to deal with point cloud features at different scales. As a result, our method can efficiently extract the structure information of irregular 3D point clouds with any shape and size. Moreover, we aim to deem each vertex as a 3D kernel whose shape and weight can be learned during the training phase, which is conducive to faster convergence and stronger performance. The main contributions of our works can be summarized as follows:
1. We propose a novel Transformer-based stratified graph convolutional network for semantic segmentation on the point cloud, enlarging the effective receptive field and building direct long-range dependency.
2. The dense-sparse sampling strategy with similarity measurement is proposed to ensure that the neighbor points searched by KNN are similar to the central points and improve the network efficiency.
3. To further identify the most important connections, we develop a multi-key self-attention mechanism to redistribute the weight of the relationship among the center point, neighborhood points, and distant points.
2.1 Point Based Semantic Segmentation Methods
Due to the irregularity of the point cloud, it was difficult to describe its spatial shape. Therefore, it was impossible to perform the convolution operation on the point cloud like 2D CNN to extract its features. Some previous works proposed various point-based methods to learn high- dimensional semantic features. PointNet [4] and its variant PointNet++ [5] solved the disorder and permutation invariance of point clouds by symmetric function (Maxpooling) and multi-layer perceptron (MLP), which became the first point-based deep learning method for point cloud analysis. Although many methods [6,17] outperformed PointNet and pointNet++ in terms of performance, most networks were based on this architecture. A positional adaptive convolution (PAConv) [24] was proposed with dynamic kernel assembly, whose convolution kernel was assembled from multiple elementary weight matrices, and the weight matrix coefficients were obtained by adaptive learning to better handle irregular and disordered point clouds. Thomas et al. [16] tried to use discrete kernel points to mimic a continuous convolution kernel. Both of the above studies used 3D convolutional kernels to extract features from point clouds, different from both, SGT took the hierarchical graph convolutional network as the main model. References [25–27] decoded the encoded point cloud into two parallel semantic and instance segmentation channels, which jointed semantic and instance features to improve the segmentation performance of the two tasks. RandLA-Net [28] was proposed using a random sampling strategy, which was suitable for large-scale outdoor point cloud processing. But this will lose key point information, resulting in low accuracy of boundary segmentation. In this paper, we proposed a dense-sparse sampling strategy with similarity measurement to reduce the negative impact of random sampling at a low computational cost. DCNet [29] built a novel feature aggregation method to relieve the key feature loss issue. However, most methods focused on aggregating local features or developing global features, failed to directly capture long-range context information and enlarge the effective receptive field. It has been demonstrated to be effective in capturing contexts from a long distance. In addition, some methods required more complex 3D convolution operations, resulting in a large amount of memory and computation, which was not available on mobile devices.
2.2 Graph Convolutional Networks
Graph convolution network (GCN) was a deep learning model based on graph structure, which was mainly applicable to unstructured non-Euclidean data [30]. GCN could learn and aggregate node characteristics, and weighted aggregation was used to complete the prediction task. Point cloud, as a representative of non-Euclidean data, its structure was very suitable for the GCN model. Recently, GCN became more and more popular in 2D image understanding [31], which utilized convolution neural network commonly used in images to solve the problem of non-Euclidean data. Due to the continuous growth of the computing power of graphics processing unit (GPU), GCN was applied to the field of 3D vision. DGCNN [17] utilized a new neural network module EdgeConv to deal with the classification and segmentation of 3D point clouds, which became the first method to apply GCN to point clouds. Because DGCNN is large, a linked dynamic graph CNN (LDGCNN) [32] was proposed to remove the transformation network. LDGCNN applied KNN and shared MLP to extract local features in the central point and its neighbors. Shortcuts were added between the different layers to link the hierarchical features to calculate useful edge vectors. VA-DGCNN [33] proposed a novel, feature-preserving vicinity abstraction (VA) layer for the EdgeConv module. Unlike the original DGCNN, local information is aggregated before further processing, rather than processed one point at a time with neighbors. These methods are improvements on the original DGCNN to achieve better results. But unlike us, we utilize GCN and multi-key self-attention to enhance semantic representation by aggregating neighborhood information and focusing on important relationships. GAPointNet [34] proposed a novel neural network for point cloud analysis, which was able to learn local geometric representations by embedding graph attention mechanism within stacked MLP layers. Lin et al. [18] proposed a 3D graph convolution network, which learned 3D kernels with graph max-pooling mechanisms for extracting geometric features from point cloud data across different scales. Kim et al. [35] developed a low-power graph convolutional network for mobile devices, which greatly reduced memory and computation. Our model and the above methods [18,35] are both lightweight segmentation networks based on GCN. However, we did not use random sampling to reduce the size of the model. The above attempts only used the traditional KNN search algorithm to form local neighborhoods to aggregate local features, which was still difficult to build long-range dependency. To address this, Song et al. [36] proposed a global affinity adaptation module to adapt global priors to the sample via a graph convolutional network built over different categories. Different from the above works, we developed an efficient feature extractor based on GCN and KNN to enlarge the effective receptive field and building direct long-range dependency.
The Transformer network was applied to the field of computer vision originally by Vision in Transformer (VIT) [37], which used patch embedding and Transformer to extract encoder features for image classification. However, the features extracted by VIT were relatively rough and could not complete the detailed tasks. Subsequently, there were several other methods based on Transformer, such as object detection [38], image recognition [13], and image super resolution [39] for 2D image analysis. Most of them applied local and global attention, through convolution, MLP, or linear layer to establish long-range dependencies.
Due to the brilliant success of Transformer in the field of 2D images, which were attracted more attention in 3D point cloud. Point Transformer [20] successfully introduced Transformer into the field of point cloud processing. Guo et al. [8] developed a neighbor embedding mechanism achieved by EdgeConv. A BERT-style pre-training strategy for 3D global Transformer [21] was proposed, which generalized the concept of BERT to 3D point cloud processing. Unlike the above methods, we proposed a multi-key self-attention mechanism to obtain two different scales of attention maps, which achieved a significantly enlarged effective receptive field.
In this section, we introduce the framework of SGT shown in Fig. 1, which contains stratified sample module, graph convolutional module, and Transformer block. The SGT captures long-range context information and enlarges the effective receptive field. In addition, the weight of the relationship among the center point, neighborhood points, and distant points is redistributed by self-attention mechanism. It aims to solve the semantic segmentation problem of complex point cloud environment and reduce the memory occupation of the network.
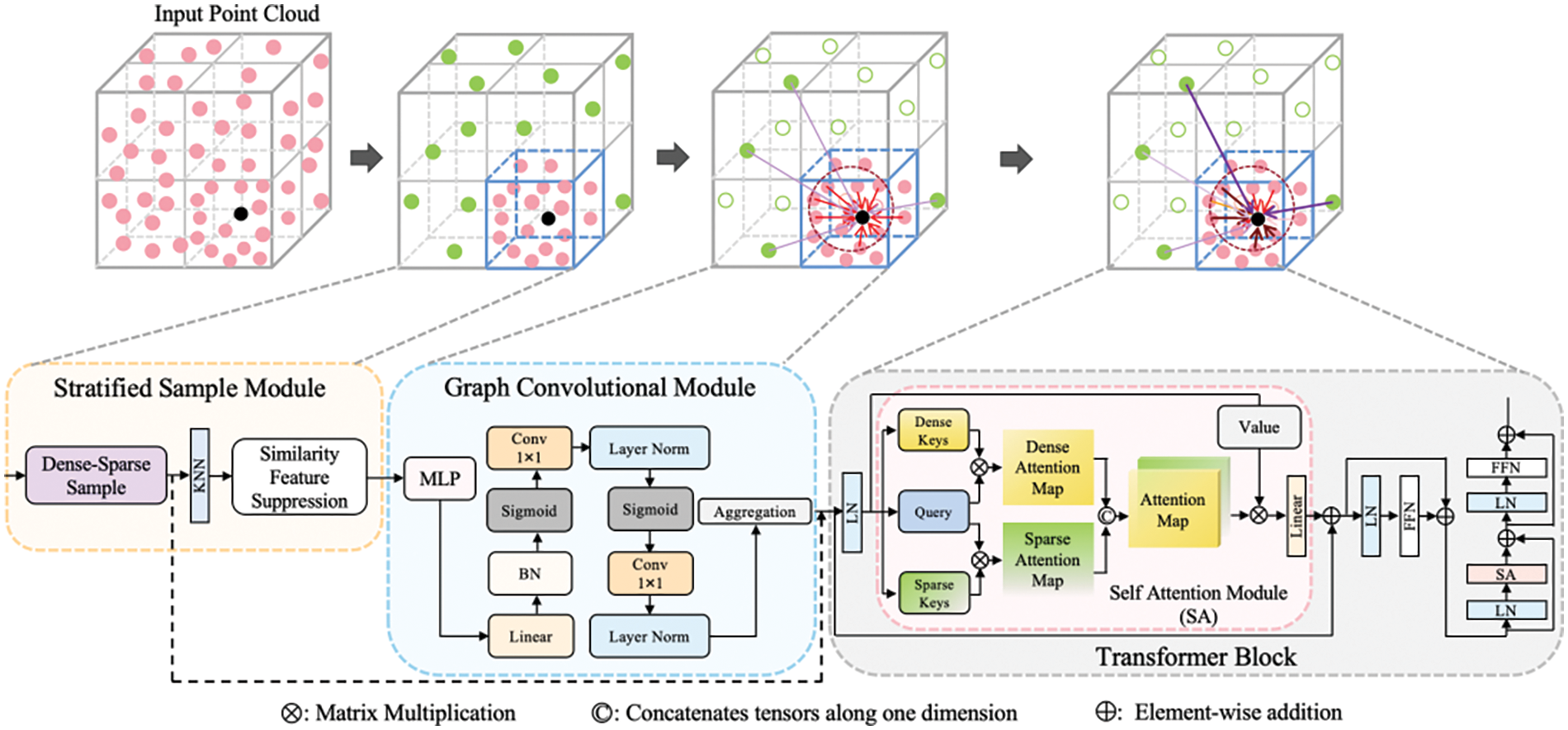
Figure 1: The framework of the proposed 3D semantic segmentation method. The center point (black), dense points in close range (pink), and sparse points in long range (green). The solid points in the third cube are sampling points, while the hollow points are not. The distant edges are established by the GCN module (pink lines), and the near edges (red lines). After the self-attention module, dark connections indicate a large weight, and light connections indicate a small weight
For the convenience of the following description, we define the several notations as follows. The raw point cloud sampled by the farthest point can be regarded as a sequence, which contains a total of
Current semantic segmentation methods mostly only use the traditional KNN search algorithm to generate local neighborhoods to aggregate local features. It is still difficult to interact the information with long-range context. Therefore, to solve the above problems by only adding negligible additional computation, we propose a dense sparse sampling strategy that aggregates local features and extends connectivity. The input point clouds are divided into overlapping cube windows with different scales, as shown in Fig. 2.

Figure 2: Illustration of the dense-sparse strategy for keys sampling
The lower right side of Fig. 2 shows small windows with dense points, and large windows with sparse points in other parts. The farthest point sampling (FPS) is used on the scale of s to reduce the input dense point cloud to sparse point cloud. Following this process, we utilize KNN to search the center points as the vertices. As shown in Fig. 3, a center vertex not only has neighbor points searched by KNN, we randomly select

Figure 3: Illustration of receptive field of vertex
In order to ensure that the neighbor points searched by KNN are similar to the central vertex and improve the network efficiency, we add similarity measurement in the stratified sample module. When instances of different semantic categories are close to each other, the accuracy of instance edge segmentation will be reduced.
The main reason is that GCN uses KNN to search for neighbor points, that is, points with a relatively close distance, which results to classify them into one class. Therefore, we use cosine similarity instead of distance similarity to filter neighborhood points. Two instances that come together more closely are not necessarily of the same semantic class. It could be two completely different semantic categories, or it could be a noise point around a central point. Therefore, distance alone cannot accurately judge the similarity between points, but we can utilize the color information of the point cloud to judge the similarity between the search point and the center by cosine similarity. On the contrary, if two points are relatively far apart in space, using only distance as a measure of similarity is likely to be judged as uncorrelated. However, in indoor scenes, there may be instances with larger volumes, and even if two points are far apart, they may still belong to the same semantic category. Therefore, we use the cosine similarity measure to help our network improve segmentation accuracy and reduce the memory and computation of the network. Cosine similarity is defined as Eq. (1):
where
3.2 Graph Convolutional Module
The point cloud is non-Euclidean data, so it is difficult to process it with traditional convolution neural network. In addition, for point cloud analysis, we need to consider both the feature information and structure information of the points. If feature extraction is done manually, many hidden and complex patterns will be lost and complicated calculations will be brought out. Therefore, the graph convolution neural network is utilized to analyze the point cloud structure. Because GCN needs to transfer the point cloud structure as a graph structure, but the input point cloud after down-sampling is still large, we need to use the KNN search method described in the previous section to perform the graph convolution operation on the local part of the point cloud. In this process, a graph
An asymmetric function combining neighboring information and shape structure is introduced by DGCNN to establish topological relationships between vertices. This asymmetric function is adopted in our study and defined as Eq. (2):
GCN is used to extract geometric relationships, but the extracted geometric relationships are not necessarily key relationships. Therefore, we need to introduce a Transformer block to redistribute the weight of the relationship among the center point, neighborhood points, and distant points. The Transformer block is composed of a multi-key self-attention module and a feed-forward network (FFN). The encoder and decoder in Transformer block both use the multi-key self-attention module. Since every query point only attends to the local points in its own window, the vanilla version Transformer block suffers from limited effective receptive field even with a shifted window. Therefore, it fails to capture long-range contextual dependencies over distant objects, causing false predictions. To adequately reflect long distance and neighborhood points dependencies, in this section, we use the dense-sparse Keys strategy shown in Fig. 2. For each query point
where
3.4 Semantic Segmentation Network
In the 2D world, semantic segmentation tasks have received increasing attention and have achieved great achievements. Previous works [40–42] have proposed various feature aggregation methods and cross layer connections. Motivated by them, we propose a U-shaped model structure, illustrated in Fig. 4. The backbone of this architecture is consisted of several SGT modules mentioned above, point feature embedding module, down sampling modules, and up sampling modules. Where

Figure 4: Architecture of the semantic segmentation network
Because down sampling is necessary to improve network processing speed and reduce memory consumption, we adopt the farthest point sampling in [20] to identify a subset with the requisite cardinality. Then, each input feature goes through a linear layer, a batch normalization layer (BN), an activation function, and Maxpooling to complete the down sampling operation.
For up sampling, we also use the method in [20]. Each input point feature is processed by a linear layer, followed by a BN layer and an activation function, then the subset of the input point set is mapped onto the higher-resolution point set by trilinear interpolation.
To increase the local dependency of point cloud learning, the first layer of our network uses point embedding to establish local geometric context information. Most current methods use linear layers or MLP to map XYZ position information and RGB color information to a high-dimensional feature space. However, the simple use of a linear layer network has a slow convergence rate and also increases the network parameters, which affects the network performance. The point feature from MLP only contains its own xyz and RGB information and lacks local relevance. Therefore, we use the strategy of KPConv [16] for local aggregation and only generate negligible additional computation.
To verify the performance of the proposed point cloud segmentation algorithm, we utilize two public available datasets for experimental validation, namely S3DIS [43] dataset and ShapeNet [44]. The S3DIS dataset is a large-scale real scene 3D segmentation dataset that consists of six areas scanned by a scanner called Matterport, including 272 rooms and approximately 215 million points. Each point in the scene point cloud contains an instance label and a semantic label; In addition to the large-scale real-world scene benchmark S3DIS, we also evaluated our approach on the ShapeNet part dataset. ShapeNet is a constructed synthetic virtual segmentation dataset containing 16 classes with 16881 3D objects. Each point sampled from the shapes is assigned with one of the 50 different parts. The instance annotations from [42] are used as the instance ground-truth labels.
The model architecture is shown in Fig. 4. The feature extracting part is composed of point feature embedding module, down sample module, and SGT module. In the SGT module, we set neighbor number
For the S3DIS dataset, each point has 9 dimensions of features, which are the location information of the point (X, Y, Z), the color features (R, G, B), and the normalized coordinates of the indoor scene. We set the feature dimensions after point embedding layer to 64, and the number of self-attentive heads in trans is set to 3. Each down sampling is 1/4 of the number of points in the previous layer, but the number of the point features and self-attention heads is doubled. Following common practice, we adopt the strategy proposed by [4] to slice the input point cloud into small cubes, each cube containing 4096 points. We use 4 Titan GPUs to train our network for 600 epochs with an Adam optimizer. The batch size is set to 8, the initial learning rate is set to 0.001, and the learning rate is halved for every 20,000 iterations. For the ShapeNet dataset, each object consists of 2048 points, and each point has only 3 dimensional position information (X, Y, Z). We calculate the overall accuracy (oAcc), mean accuracy (mAcc), intersection over union (IOU) for each category, and mean intersection over union (mIOU) with a threshold of 0.5 as evaluation metrics for the semantic segmentation task.
For the S3DIS dataset, we explicitly evaluated the performance of our method on area 5 and the results of the 6-fold cross validation. Note that it is a common practice to analyze the performance of 6-fold cross validation separately, but area 5 on the S3DIS dataset is not in the training set. Therefore, evaluating area 5 can well test the generalization performance of the network. We compare the classical semantic segmentation methods [5,8,16,28,45], the semantic and instance joint segmentation methods [25,26], the GCN based semantic segmentation methods [17,18,29,33], and the results are shown in Table 1.
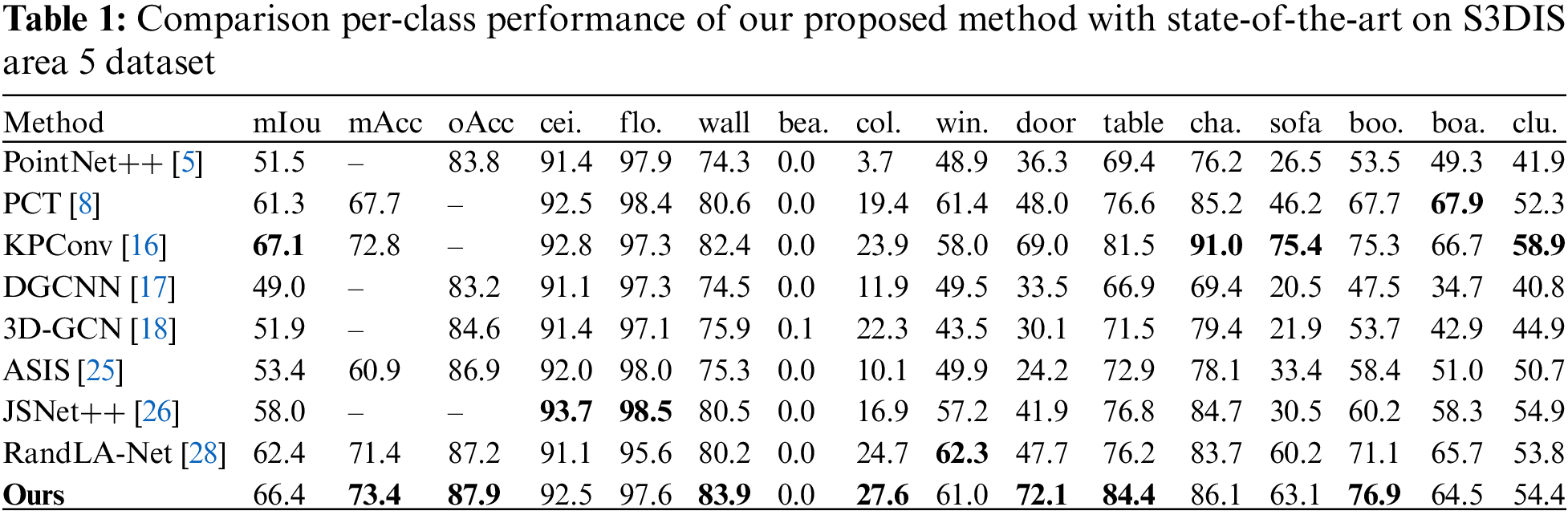
We notice that all methods perform similarly in the ceiling, floor, and beam categories, as they can be easily classified based on the location in the room. However, our method achieved better results in the other categories indicating that the SGT module can capture long-range context information and enlarge the effective receptive field. This is important for background segmentation in indoor scenes. In addition, the segmentation accuracy of our method for foreground categories such as door, table, chair, and clutter is better than the comparison methods. It indicates that our method not only captures long-distance information but also has a stronger ability to recognize local geometric shapes. With the benefit of the complementarity between GCN and Transformer, the SAT-Net finally achieves a leading performance of 73.4 in mAcc and 87.9 in oAcc, respectively.
To avoid overfitting on S3DIS area 5, we further verify the generalization performance of our method by using the 6-fold cross validation, nd the results are shown in Table 2. The performance of SGT-Net is relatively balanced across various categories, achieving the best performance in six of them. Specifically, the proposed SGT-Net can not only achieve leading performance in long-range background category segmentation tasks, such as wall, beam and column, but also achieve optimal performance in short-range foreground category segmentation tasks, such as table, bookcase and clutter.
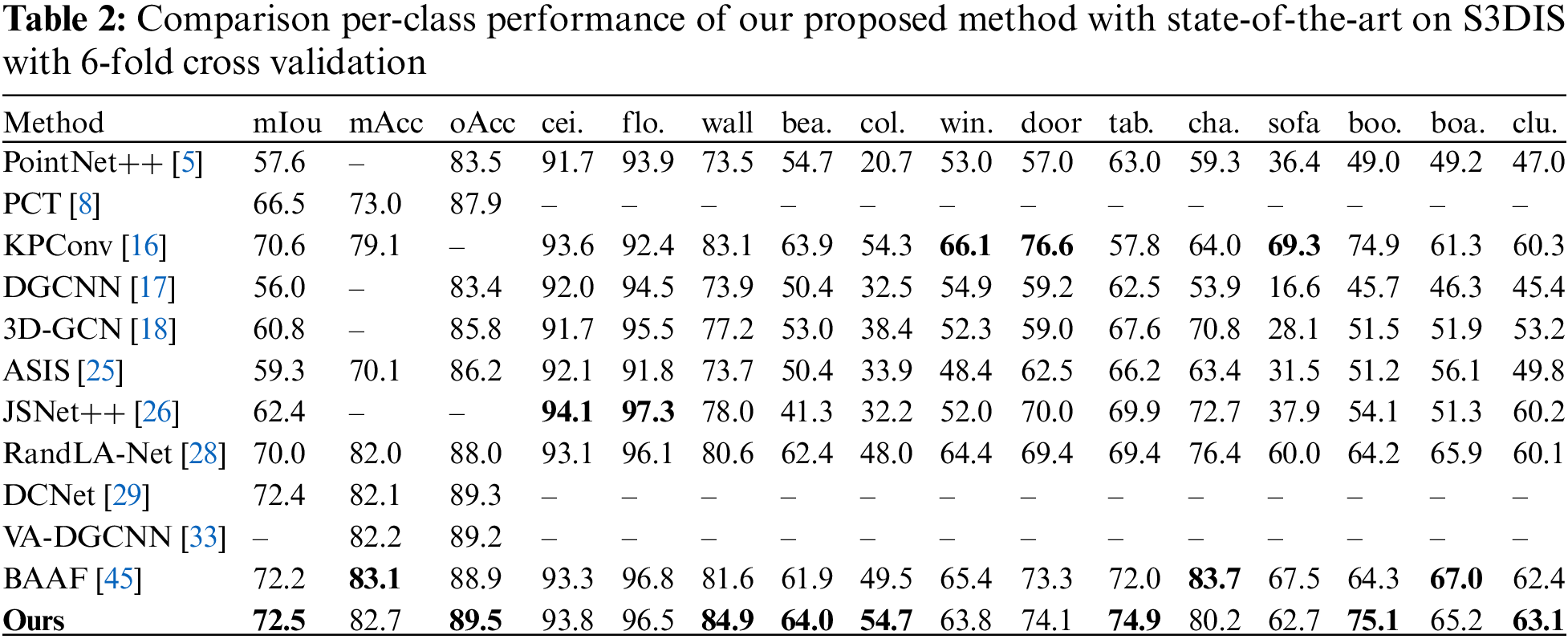
Although our method is inferior to JSNet++ in some background categories (such as ceiling and floor) and inferior to KPConv and BAAF in some foreground categories (such as window, door, chair and sofa), the main contribution and strength of our work is different from those contrasting approaches. JSNet++ designed a mutual promotion strategy for semantic segmentation and instance segmentation and proposed a pointwise correlation module to further improve the accuracy of semantic segmentation. KPConv proposed a convolution directly applied to point clouds to better aggregate local spatial features. However, it did not consider the context of global features, and the calculation cost is large. BAAF introduced a bilateral block to augment the local context of the points and also ignored to extract long-range contexts. This will lose the accuracy of long-range background segmentation in the scene. Our proposed SGT-Net complements the local feature capture capability of GCN with the global feature extraction capability of the attention mechanism, and improves the interaction between global and local features by aggregating long-range and neighborhood information. Besides, we also propose a dense-sparse sampling strategy to enlarge the effective receptive field and develop a self-attention mechanism based on Transformer to redistribute the weight of the relationship among center point, neighborhood points, and distant points. It is worth noting that SGT-Net does not perform much worse in categories that are not as well as the above methods, but the above methods perform much worse in categories that are not as well as ours. For example, it is 22.7%, 22.5%, 24.8% and 20% higher than JSNet++ respectively in beam, column, sofa and bookcase. KPConv does not perform as well as SGT-Net in the segmentation of long-range background categories. BAAF is slightly better than SGT-Net in mAcc (+0.4), but its performance is not as good as ours in the long range of large object segmentation. It can be seen that our method trades off all categories and achieves leading performance of 72.5 in mIoU and 89.5 in oAcc.
Fig. 5 visualizes the segmentation results on area 5 of the S3DIS dataset. When the edges of different instances overlap or closely connected, our method can still accurately segment each instance, while the comparison methods may misclassify semantic categories. For the segmentation of complex edges, the precision of the proposed method is better than that of the comparison methods, and it is closer to the ground truth.

Figure 5: Comparison of our method with the state-of-the-art methods in semantic segmentation task on area 5 of S3DIS dataset. Objects of different colors represent different categories of targets. The red rectangular boxes circle the segmentation details
Besides evaluation on the large-scale indoor dataset S3DIS, we also conduct experiments on ShapeNet [16] to evaluate the performance of our method at part level segmentation. Table 3 presents the class-wise segmentation results. We can observe that our model achieves competitive results on the ShapeNet dataset. In fact, our method and PCT (Point cloud transformer) achieved the best results in most categories. Due to the advantage of the Transformer based feature extraction method, the average accuracy of PCT is slightly better than our method. But its model parameters have also multiplied. We will discuss it in the next section. In addition, we notice that SGPN achieves the best results in certain categories as it takes the advantage of the instance segmentation tasks, which employs additional losses such as similarity matrix and confidence loss to accurately distinguish different instances with the same category. Therefore, the addition of instance information helps with its feature semantic segmentation performance. Fig. 6 visualizes the results of our method on part level segmentation tasks. Our method benefits from the similarity measurement strategy, which is more precise in segmenting part edges and closer to the ground truth.

Figure 6: Part level semantic segmentation results on ShapeNet dataset. Semantic annotation using different colors for different parts
4.5.1 Neighbor Number
We conduct experiments on the receptive field in the stratified sampling module by varying the number of neighbor points and long-range points. We perform ablation experiments on the S3DIS dataset Area 5. The results are shown in Table 4. We can see that the insufficient or excessive number of neighbor points and long-range points can affect the performance of the network in extracting local information and establishing long distance context dependence.

When the number of neighborhood points and long-range points is small (j = 10, k = 10), the performance of segmentation is relatively poor because the network cannot extract effective features. When the number of long-range points increases, the number of noise in the sampling points will increase, which interferes with the establishment of context dependence on the network. Thus resulting in a decline in the segmentation accuracy of the network. When the number of neighborhood points and long-range points is large, the segmentation performance is close to the optimal result, but the computational cost increases. It is not difficult to find from Fig. 7 that when there are enough neighborhood points and long-range points, the robustness of the network becomes better. Therefore, we sample an appropriate number of neighboring points and long-distance points to achieve better performance.

Figure 7: The influence of different number of neighbor points and long-range points on the network performance
4.5.2 Effect of Similarity Measurement Strategy and Self Attention Module
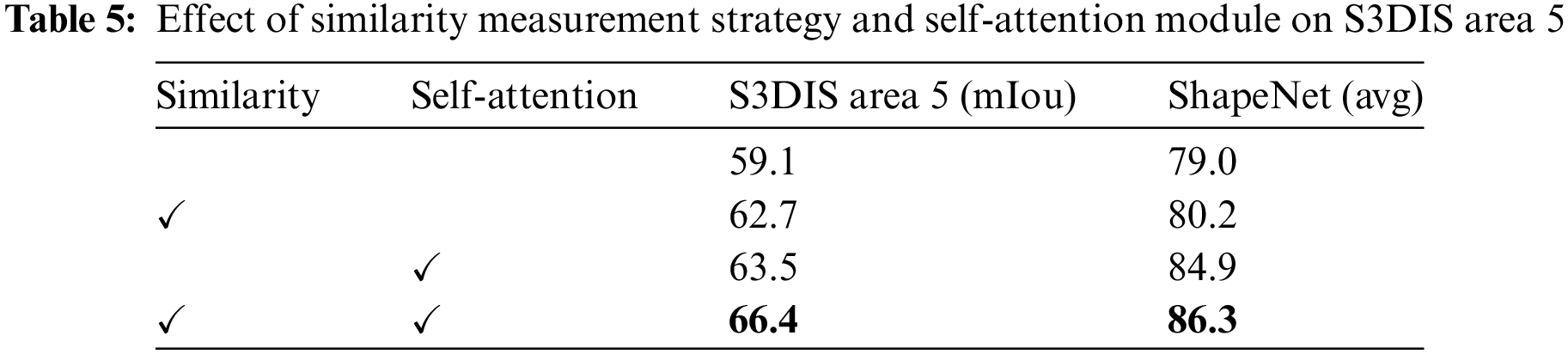
Our network includes two important modules to help the SGT module improve segmentation performance. Therefore, we conduct a series of ablation experiments to verify their effectiveness. Table 5 demonstrates the impact of each module on the backbone network. It can be seen that the best effect is achieved when two modules are working simultaneously. When the self-attention mechanism is not added to the network, but only the similarity measurement mechanism is added. We find that the segmentation accuracy is slightly better than that when neither module is working. From this, we can infer that the proposed similarity measurement mechanism can ensure that the neighbor points searched by KNN are similar to the central vertex and improve the network efficiency. On the contrary, when there is only self-attention module, the segmentation accuracy of the network is improved significantly. It proves that the self-attention module can redistribute the weight of the relationship among the center point, neighborhood points, and distant points to improve the segmentation performance. In addition, as shown in Fig. 3, the self-attention module plays an important role in long-distance background segmentation. Because Transformer is suitable for capturing global features, and our SGT module is good at local feature extraction, the two performances are just complementary.
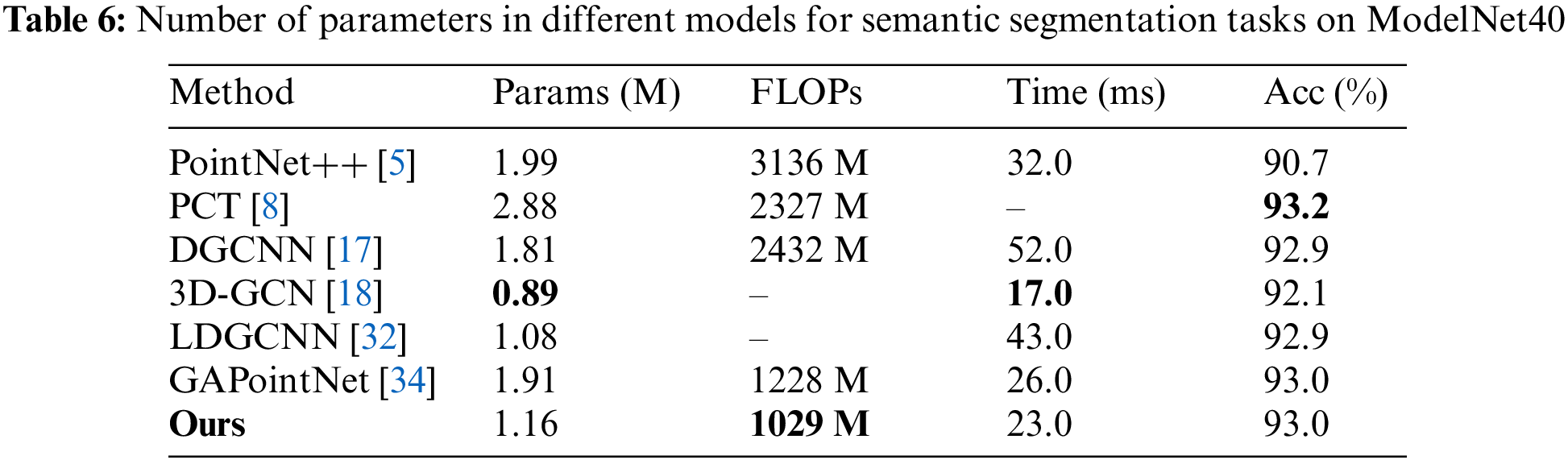
We compare the number of parameters, time, and floating point operations (FLOP) between our method and the comparison methods on the ModelNet40 dataset. The overall accuracy is used to evaluate the segmentation performance. From Table 6, our model achieves segmentation performance comparable to state-of-the-art models. Although the segmentation performance is slightly lower than PCT, the number of parameters, FLOP in our model is only half of that in PCT. The number of parameters in our model is slightly higher than 3D-GCN, and the reason is that 3D-GCN uses a random sampling technique, where the subset points are sampled randomly. In addition, when the support number of the learnable kernels proposed by 3D-GCN increases, its model complexity will increase significantly, resulting in a large memory and computational load.
In this paper, we propose a novel stratified graph convolutional network, named SGT-Net, which can extract long-range contexts and effectively aggregate local features for semantic segmentation in 3D point cloud space. The technical contributions of our network lie in the design of the stratified graph convolution strategy and the weight allocation of attention mechanism based on the Transformer. We propose a novel Transformer-based stratified graph convolutional network for semantic segmentation on the point cloud, enlarging the effective receptive field and building direct long-range dependency. The dense-sparse sampling strategy with similarity measurement is proposed to ensure that the neighbor points searched by KNN are similar to the central points and improve the network efficiency. Experiments show that our method achieves the same or better segmentation performance than the state-of-the-art methods. Although not superior to the latest methods in some respects, we demonstrate that our model can effectively enlarge the receptive field and is computationally more efficient. In particular, SGT-Net shows a remarkable accuracy with only half the number of parameters compared to other methods, which shows great potential for real-time applications, such as robot visual grabbing. The success of this model also verifies the efficiency of graph attention networks not only in calculating the similarity of graph vertexes, but also in understanding geometric relationships.
Acknowledgement: The authors would like to thank the editors and reviewers for their valuable work, as well as the supervisor and family for their valuable support during the research process.
Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant Nos. U20A20197, 62306187 and the Foundation of Ministry of Industry and Information Technology TC220H05X-04.
Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Suyi Liu and Jianning Chi; data collection: Suyi Liu and Chengdong Wu; analysis and interpretation of results: Suyi Liu, Jianning Chi and Xiaosheng Yu; draft manuscript preparation: Suyi Liu and Fang Xu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The training data used in this paper were obtained from S3DIS, ShapeNet, and ModelNet40. Available online via the following link: http://buildingparser.stanford.edu/dataset.html, https://www.shapenet.org/, and http://modelnet.cs.princeton.edu/.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. L. Wang, Y. Liu, X. Liu, and J. Wu, “Automatic virtual portals placement for efficient VR navigation,” presented at the 2022 IEEE Conf. Virtual Reality 3D User Interf. Abstracts Workshops (VRWChristchurch, New Zealand, Mar. 2022, pp. 628–629. [Google Scholar]
2. H. Tian, W. Wu, H. Liu, Y. D. Liu, J. Zou and Y. Zhao, “Robotic grasping of pillow spring based on M-G-YOLOv5s object detection algorithm and image-based visual serving,” J. Intell. Robot. Syst. Theory Appl., vol. 109, no. 3, pp. 67, Nov. 2023. doi: 10.1007/s10846-023-01989-x. [Google Scholar] [CrossRef]
3. F. Ma, Y. Liu, S. Wang, J. Wu, W. Qi and M. Liu, “Self-supervised drivable area segmentation using LiDAR’s depth information for autonomous driving,” presented at the 2023 IEEE/RSJ Int. Conf. Intelligent Robots Syst. (IROSDetroit, MI, USA, Oct. 2023, pp. 41–48. [Google Scholar]
4. C. R. Qi, H. Su, K. Mo, and L. J. Guibas, “PointNet: Deep learning on point sets for 3D classification and segmentation,” presented at the 30th IEEE Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, Jul. 2017, pp. 77–85. [Google Scholar]
5. C. R. Qi, L. Yi, H. Su, and L. J. Guibas, “PointNet++: Deep hierarchical feature learning on point sets in a metric space,” presented at the 31st Int. Conf. Neural Inf. Process. Syst., Red Hook, NY, USA, 2017, pp. 5105–5114. [Google Scholar]
6. W. Wu, Z. Qi, and F. X. Li, “PointConv: Deep convolutional networks on 3D point clouds,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, Jun. 2019, pp. 9613–9622. [Google Scholar]
7. H. Zhao, L. Jiang, C. Fu, and J. Jia, “PointWeb: Enhancing local neighborhood features for point cloud processing,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, Jun. 2019, pp. 5560–5568. [Google Scholar]
8. M. Guo, J. Cai, Z. Liu, T. Mu, and R. R. Martin, “PCT: Point cloud transformer,” Comput. Vis. Media, vol. 7, no. 2, pp. 187–199, Dec. 2020. doi: 10.1007/s41095-021-0229-5. [Google Scholar] [CrossRef]
9. Y. Zhou and O. Tuzel, “VoxelNet: End-to-end learning for point cloud based 3D object detection,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, Jun. 2018, pp. 4490–4499. [Google Scholar]
10. Z. Wu et al., “3D ShapeNets: A deep representation for volumetric shapes,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Boston, MA, USA, Jun. 2015, pp. 1912–1920. [Google Scholar]
11. J. Chen, H. Ren, F. S. Chen, S. Velipasalar, and V. V. Phoha, “Gaitpoint: A gait recognition network based on point cloud analysis,” presented at the IEEE Int. Conf. Image Proc. (ICIPBordeaux, France, Oct. 2022, pp. 1916–1920. [Google Scholar]
12. L. Hui, M. Cheng, J. Xie, J. Yang, and M. M. Cheng, “Efficient 3D point cloud feature learning for large-scale place recognition,” IEEE Trans. Image Proc., vol. 31, pp. 1258–1270, Jan. 2022. doi: 10.1109/TIP.2021.3136714. [Google Scholar] [PubMed] [CrossRef]
13. H. Zhao, J. Jia, and V. Koltun, “Exploring self-attention for image recognition,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, Jun. 2020, pp. 10073–10082. [Google Scholar]
14. J. Chen, Y. Chen, and C. Wang, “Feature graph convolution network with attentive fusion for large-scale point clouds semantic segmentation,” IEEE Geosci. Remote Sens. Lett., vol. 20, no. 7, pp. 1–5, Aug. 2023. doi: 10.1109/LGRS.2023.3330882. [Google Scholar] [CrossRef]
15. F. Hao, J. Li, R. Song, Y. Li, and K. Cao, “Structure-aware graph convolution network for point cloud parsing,” IEEE Trans. Multimed., vol. 25, pp. 7025–7036, Oct. 2023. doi: 10.1109/TMM.2022.3216951. [Google Scholar] [CrossRef]
16. H. Thomas, C. R. Qi, J. E. Deschaud, B. Marcotegui, F. Goulette and L. Guibas, “KPConv: Flexible and deformable convolution for point clouds,” presented at the IEEE Int. Conf. Comput. Vis., Seoul, Korea (SouthOct. 2019, pp. 6410–6419. [Google Scholar]
17. Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein and J. M. Solomon, “Dynamic graph CNN for learning on point clouds,” ACM Trans. Graph., vol. 38, no. 5, pp. 1–12, Oct. 2019. doi: 10.1145/3326362. [Google Scholar] [CrossRef]
18. Z. H. Lin, S. Y. Huang, and Y. C. F. Wang, “Learning of 3D graph convolution networks for point cloud analysis,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 8, pp. 4212–4224, Feb. 2022. doi: 10.1109/TPAMI.2021.3059758. [Google Scholar] [PubMed] [CrossRef]
19. A. Vaswani et al., “Attention is all you need,” arXiv preprint arXiv:1706.03762, Dec. 2017. doi: 10.48550/arXiv.1706.03762. [Google Scholar] [CrossRef]
20. H. Zhao, L. Jiang, J. Jia, P. Torr, V. Koltun and I. Labs, “Point transformer,” presented at the IEEE Int. Conf. Comput. Vis., Montreal, QC, Canada, Oct. 2021, pp. 16239–16248. [Google Scholar]
21. X. Yu, L. Tang, Y. Rao, T. Huang, J. Zhou and J. Lu, “Point-BERT: Pre-training 3D point cloud transformers with masked point modeling,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, Jun. 2022, pp. 19291–19300. [Google Scholar]
22. X. Lai, L. Jiang, L. Wang, H. Zhao, and X. Qi, “Stratified transformer for 3D point cloud segmentation,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., New Orleans, LA, USA, Jun. 2022, pp. 8490–8499. [Google Scholar]
23. L. Wang et al., “SAT-GCN: Self-attention graph convolutional network-based 3D object detection for autonomous driving,” Knowledge-Based Syst., vol. 259, pp. 110080, Jan. 2023. doi: 10.1016/j.knosys.2022.110080. [Google Scholar] [CrossRef]
24. M. Xu, R. Ding, H. Zhao, and X. Qi, “PAConv: Position adaptive convolution with dynamic kernel assembling on point clouds,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit, Nashville, TN, USA, Dec. 2021, pp. 3172–3181. [Google Scholar]
25. X. Wang, S. Liu, X. Shen, C. Shen, and J. Jia, “Associatively segmenting instances and semantics in point clouds,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, Jun. 2019, pp. 4091–4100. [Google Scholar]
26. L. Zhao and W. Tao, “JSNet++: Dynamic filters and pointwise correlation for 3D point cloud instance and semantic segmentation,” IEEE Trans. Circ. Syst. Video Technol., vol. 14, no. 8, pp. 1854–1867, Apr. 2023. doi: 10.1109/TCSVT.2022.3218076. [Google Scholar] [CrossRef]
27. F. Chen et al., “JSPNet: Learning joint semantic & instance segmentation of point clouds via feature self-similarity and cross-task probability,” Pattern Recognit., vol. 122, no. 1, pp. 108250, Feb. 2022. doi: 10.1016/j.patcog.2021.108250. [Google Scholar] [CrossRef]
28. Q. Hu et al., “RandLA-Net: Efficient semantic segmentation of large-scale point clouds,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, Jun. 2020, pp. 11105–11114. [Google Scholar]
29. F. Yin, Z. Huang, T. Chen, G. Luo, G. Yu and B. Fu, “DCNet: Large-scale point cloud semantic segmentation with discriminative and efficient feature aggregation,” IEEE Trans. Circuits Syst. Video Technol., vol. 33, no. 8, pp. 4083–4095, Aug. 2023. doi: 10.1109/TCSVT.2023.3239541. [Google Scholar] [CrossRef]
30. L. Wang, Y. Huang, Y. Hou, S. Zhang, and J. Shan, “Graph attention convolution for point cloud semantic segmentation,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, Jun. 2019, pp. 10288–10297. [Google Scholar]
31. T. Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” arXiv preprint arXiv:1609.02907, Sep. 2017. doi: 10.48550/arXiv.1609.02907. [Google Scholar] [CrossRef]
32. K. Zhang, M. Hao, J. Wang, C. W. de Silva, and C. Fu, “Linked dynamic graph CNN: Learning through point cloud by linking hierarchical features,” presented at the 27th Int. Conf. Mechatron. Machine Vis. Pra. (M2VIPShanghai, China, Nov. 2021, pp. 7–12. [Google Scholar]
33. J. Walcza, A. Wojciechowski, P. Najgebauer, and R. Scherer, “Vicinity-based abstraction: VA-DGCNN architecture for noisy 3D indoor object classification,” presented at the Int. Conf. Comput. Sci., Krakow, Poland, 2021, pp. 229–241. [Google Scholar]
34. C. Chen, L. Z. Fragonara, and A. Tsourdos, “GAPointNet: Graph attention based point neural network for exploiting local feature of point cloud,” Neurocomputing, vol. 438, no. 7553, pp. 122–132, May 2021. doi: 10.1016/j.neucom.2021.01.095. [Google Scholar] [CrossRef]
35. S. Kim, S. Kim, J. Lee, and H. Yoo, “A low-power graph convolutional network processor with sparse grouping for 3D point cloud semantic segmentation in mobile devices,” IEEE Trans. Circ. Syst. I: Regular Paper, vol. 69, no. 4, pp. 1507–1518, Aug. 2022. doi: 10.1109/TCSI.2021.3137259. [Google Scholar] [CrossRef]
36. Z. Song, L. Zhao, and J. Zhou, “Learning hybrid semantic affinity for point cloud segmentation,” IEEE Trans. Circuits Syst. Video Technol., vol. 32, no. 7, pp. 4599–4612, Dec. 2022. doi: 10.1109/TCSVT.2021.3132047. [Google Scholar] [CrossRef]
37. A. Dosovitskiy et al., “An image is worth 16 × 16 words: Transformers for image recognition at scale,” presented at the Int. Conf. Learn. Represent., New Orleans, USA, Oct. 2019, pp. 548–558. [Google Scholar]
38. H. Vaidwan, N. Seth, A. S. Parihar, and K. Singh, “A study on transformer-based object detection,” presented at the IEEE Int. Conf. Intell. Technol., Hubli, India, Jun. 2021, pp. 1–6. [Google Scholar]
39. H. Chen et al., “Pre-trained image processing transformer,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Nashville, TN, USA, Dec. 2021, pp. 12294–12305. [Google Scholar]
40. E. Shelhamer, J. Long, and T. Darrell, “Fully convolutional networks for semantic segmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 4, pp. 640–651, 2017. doi: 10.1109/TPAMI.2016.2572683. [Google Scholar] [PubMed] [CrossRef]
41. O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional networks for biomedical image segmentation,” presented at the Int. Conf. Med. Image Comput. Assist. Intervent., Munich, Germany, Oct. 2015, pp. 234–241. [Google Scholar]
42. V. Badrinarayanan, A. Kendall, R. Cipolla, and S. Member, “SegNet: A deep convolutional encoder-decoder architecture for image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 12, pp. 2481–2495, Jan. 2017. doi: 10.1109/TPAMI.2016.2644615 [Google Scholar] [CrossRef]
43. I. Armeni et al., “3D semantic parsing of large-scale indoor spaces,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, Jun. 2016, pp. 1534–1543. [Google Scholar]
44. L. Yi et al., “A scalable active framework for region annotation in 3D shape collections,” ACM Trans. Graph., vol. 35, no. 6, pp. 6–12, Nov. 2016. doi: 10.1145/2980179.2980238. [Google Scholar] [CrossRef]
45. S. Qiu, S. Anwar, and N. Barnes, “Semantic segmentation for real point cloud scenes via bilateral augmentation and adaptive fusion,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Nashville, TN, USA, Jun. 2021, pp. 1757–1767. [Google Scholar]
46. W. Wang and R. Yu, “SGPN: Similarity group proposal network for 3D point cloud instance segmentation,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, Jun. 2018, pp. 2569–2578. [Google Scholar]
47. X. Yan, C. Zheng, Z. Li, S. Wang, and S. Cui, “PointASNL: Robust point clouds processing using nonlocal neural networks with adaptive sampling,” presented at the IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., Seattle, WA, USA, Jun. 2020, pp. 5588–5597. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF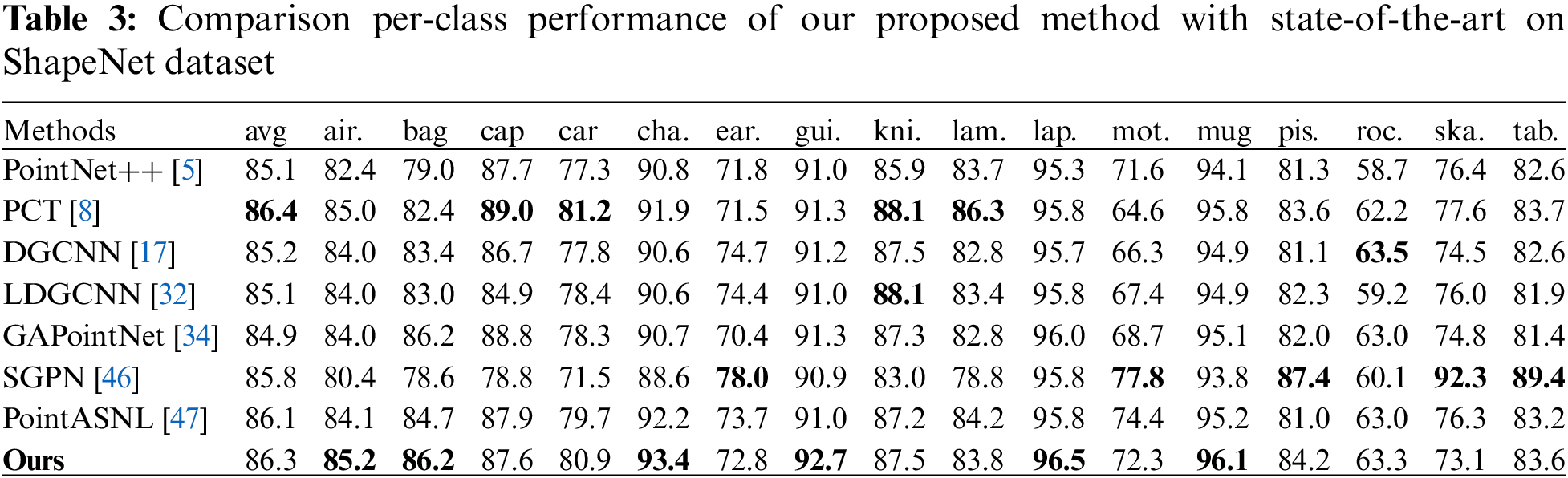
 Downloads
Downloads
 Citation Tools
Citation Tools