MD Simulation of Diffusion Behaviors in Collision Welding Processes of Al-Cu, Al-Al, Cu-Cu

1  Introduction

The last two decades have seen a significant interest in low-density, high-specific-strength metal alloys in the automotive industry, as they offer the potential to reduce weight and improve fuel economy. However, conventional welding methods face challenges in achieving direct welding between such alloys due to differences in thermal properties and solid solubility. To address this issue, various impact-based methods have been proposed, including explosive welding [1], vaporizing foil actuator welding (VFAW) [2], and laser collision welding [3]. Collision welding has been used to join dissimilar and similar combinations, such as Mg/Steel [4], Cu/Al [5], and Al/Al [6]. Despite its successful application in several instances, obtaining detailed dynamic microscopic information during collision welding experiments remains difficult. The extremely fast welding process and micro-sized interfacial morphologies contribute to the complexity of this challenge. As a result, numerical simulations have emerged as a valuable tool for studying collision welding phenomena. Aizawa et al. [7] utilized a Lagrange-Euler coupling model coupling model to investigate optimum processing parameters and successfully validated these parameters through experiments. Li et al. [8] employed the smoothed particle hydrodynamics (SPH) simulation to model the collision welding process. However, these simulations typically focus on spatial scales ranging from a few millimeters to hundreds of millimeters, making it difficult to study atomistic behaviors near the collision interface with these methods. Atomic diffusion phenomena near the welding interface are generally regarded as a crucial joining mechanism for collision welding [9]. Molecular dynamics (MD) simulations can investigate the evolution of atomic-scale structures [10] and help interpret experimental data at the microscopic level. So far, numerous researchers have utilized MD simulations to simulate diffusion processes during collision welding processes. For example, Chen et al. [11] simulated atomic diffusion behaviors at Cu/Al interface and proposed a hybrid method for calculating the thickness of the diffusion layer. Feng et al. [12] investigated the formation processes of the collision interface in explosive welding using MD. MD was also applied to investigate diffusion behaviors of Mo/Au [13] and Hastelloy/stainless steel [14]. Furthermore, MD simulations were employed to simulated the joining mechanism of the Cu/Al joint manufactured by electromagnetic pulse welding [15]. However, there is a lack of comprehensive research on the influence of collision velocity conditions and material combinations on the diffusion behavior near the collision interface. To bridge this gap, this paper employs MD simulations to study atomic diffusion behaviors of Cu-Al, Cu-Cu, and Al-Al during the collision welding process. Aluminum is chosen for its low density and corrosion resistance, while copper is selected for its malleability and thermal conductivity. Both materials find various applications in industrial fields [16]. This study aims to analyze the effects of collision velocity and material combinations, offering valuable insights for determining optimal collision welding parameters.

2  Simulation Details

The MD simulation is based on classical Newtonian mechanics theory, which utilizes computers to calculate the motion equations and trajectories of atoms in the system. The molecular dynamics simulations in this paper were all performed using the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) program developed at Sandia National Laboratories [17]. This study employs the interatomic potential by Cai et al. [18] and the model is selected based on the previous work [11,19–22]. The initial configuration for the simulations is shown in Fig. 1. Based on the reference [11], the dimensions of the simulation box in this study are about 3.6 nm(x) × 3.6 nm(y) × 39.6 nm(z) and size effect do not affect welding behavior. To mitigate the effect of shock waves, two transition regions with three layers of atoms are implemented at the non-contact end of the simulation box along the z-direction. To isolate interactions between the atoms of different samples during the relaxation stage, a vacuum (20 Å) is created between the contact surfaces of the sample. The (0 0 1) planes are set as the contact surfaces of the samples. The Velocity-Verlet algorithm is used to simulate the Newton’s equation of motion. Periodic boundary conditions are applied in the x and y directions. The initial system is relaxed for 30 ps under NPT ensemble at 300 K and zero external pressure to complete initialization. After initialization, we fixed the transition region of the target bulk and then gave the shocked bulk an initial speed to simulate the collision process. In brief, the simulation of the collision welding process can be divided into two stages: The loading stage and the unloading stage. During the simulation, the shocked bulk moves towards the target bulk. When the thickness of the system reaches its minimum length, the transition region of the shocked bulk is fixed. After that, the system relaxes for 1000 ps under the micro-canonical ensemble (NVE). To simulate the unloading stage, the final equilibrium temperature of the NVE simulation is maintained at the end of the loading stage. Subsequently, the system relaxes for another 1000 ps at zero external pressure and under the NPT ensemble. The simulation procedure is shown in Fig. 2. The welding parameters for three combinations (Al-Cu, Al-Al, Cu-Cu) are presented in Table 1. The effect of transverse velocity Vx is studied by fixing the longitudinal velocity at 1.5 km/s and increase Vz from 0.1 to 0.7 km/s with an increment of 0.2 km/s. The effect of longitudinal velocity Vz is studied by fixing the transverse velocity at 0 km/s and increase Vz from 1.5 to 2.5 km/s with an increment of 0.25 km/s. The melting point of copper is 1358 K, while for aluminum it is 933 K [11].

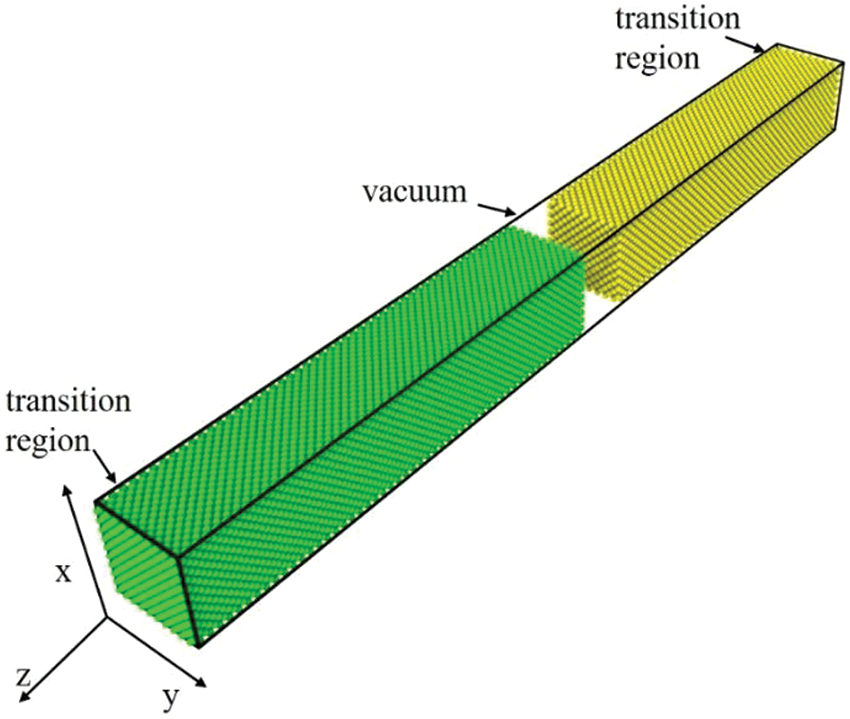
Figure 1: The initial model configuration for MD simulation

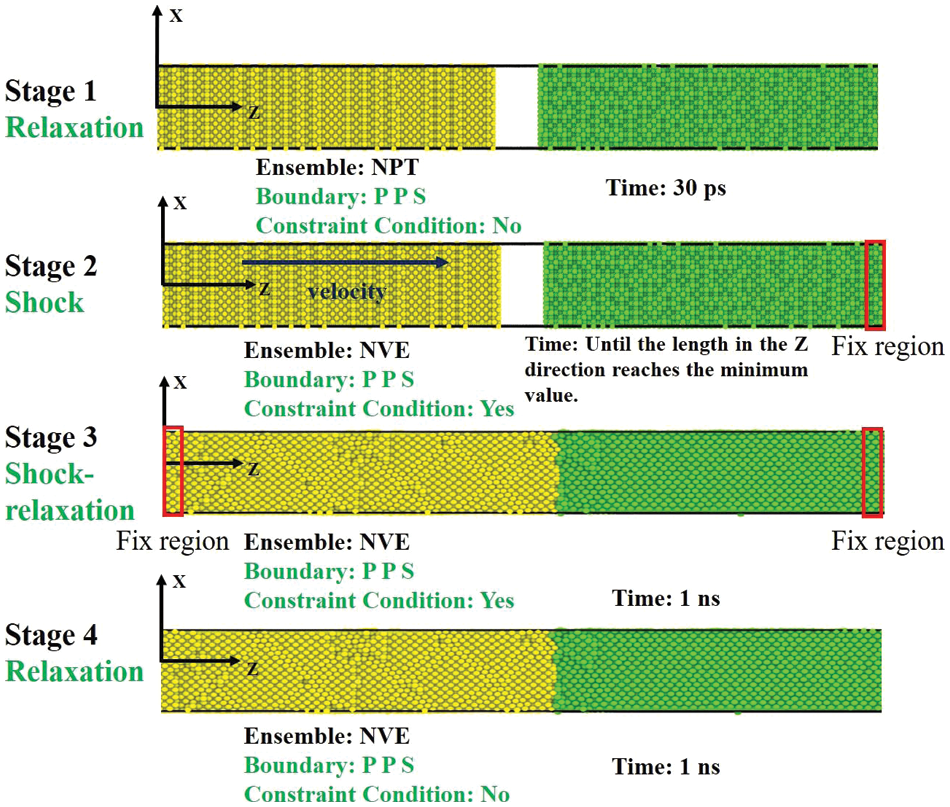
Figure 2: The illustration of the simulation processes

3  Results and Discussions

In this study, the atomistic diffusion behaviors of Al/Cu, Al/Al, and Cu/Cu during collision welding are simulated using MD. The system configuration and atomic potential energy information for Al/Cu, Al/Al, and Cu/Cu after the unloading stage with different velocity conditions are depicted in Figs. 3a–3cand 4a–4c, respectively. The time profiles of the temperature and pressure of three material combinations during the loading stage for Vx=0.7km/s, Vx=0.5km/s, Vx=0.3km/s, Vx=0.1km/s, Vx=0.0km/s are shown in Figs. 5a–5c. The simulated data is obtained and analyzed. The mean square displacement (MSD) can describe the atomic diffusion behavior effectively and diffusion coefficient [23]. According to the Einstein diffusion equation, MSD can be expressed as [19]

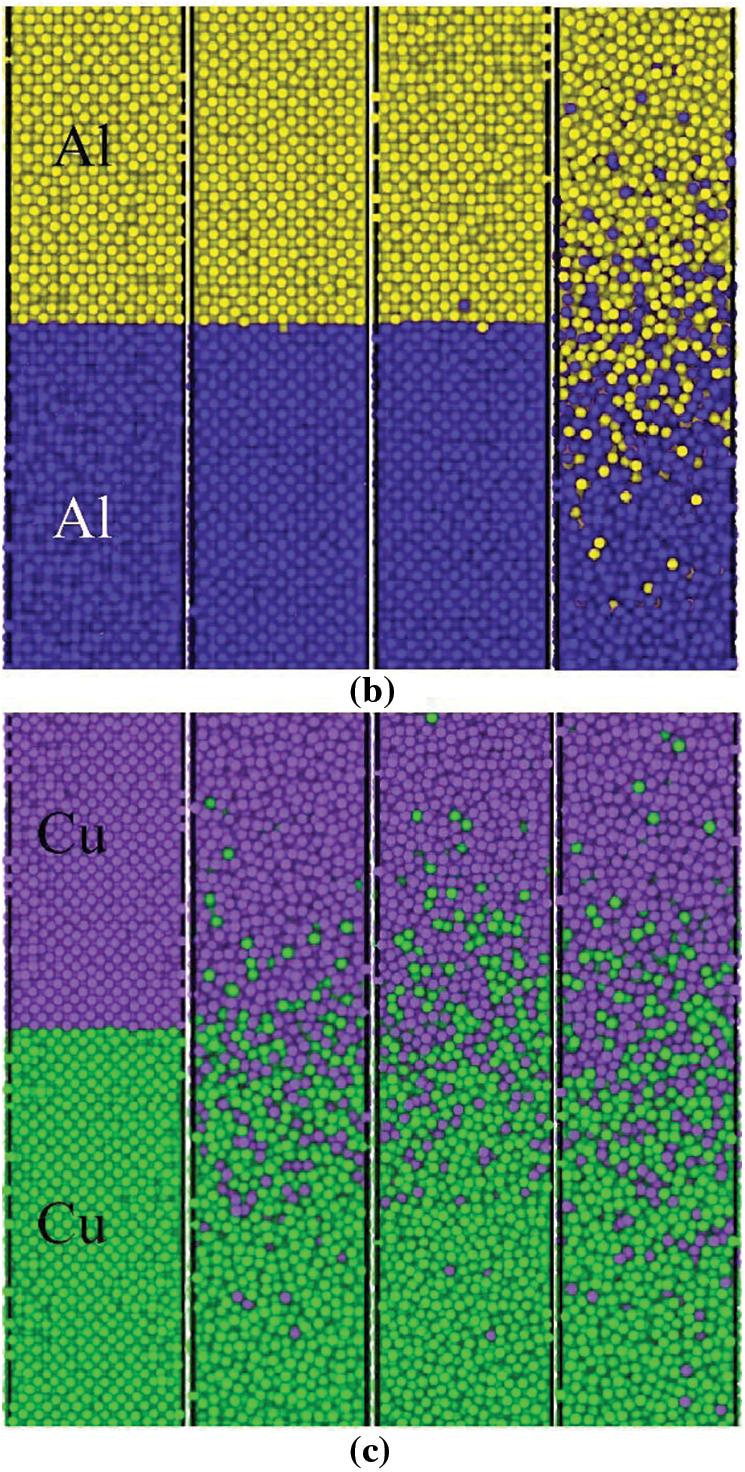
Figure 3: The final configurations of the interface for the (a) Al-Cu system, (b) Al-Al system, and (c) Cu-Cu system after the unloading stage when Vx= 0.1, 0.3, 0.5, 0.7 km/s (from left to right, sequentially)

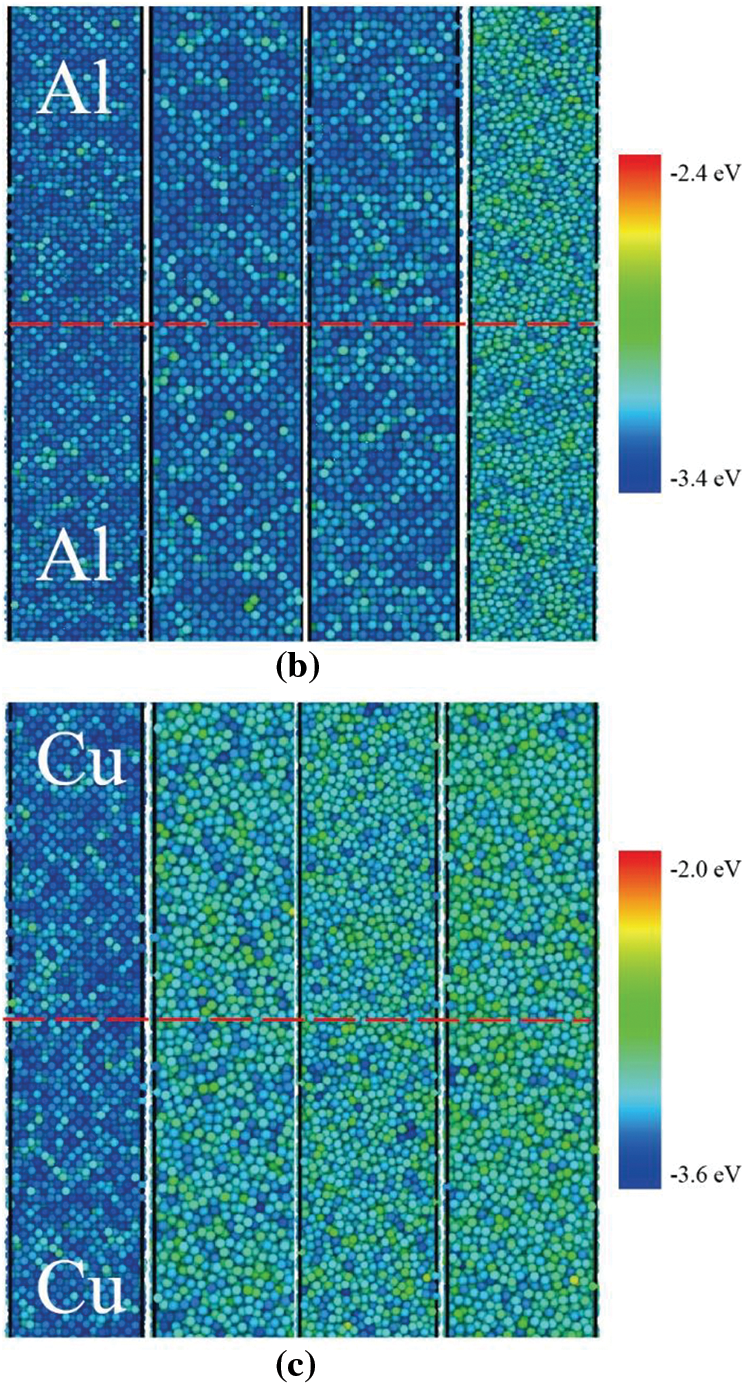
Figure 4: The potential energy distribution for the (a) Al-Cu system, (b) Al-Al system, (c) Cu-Cu system after the unloading stage. The dashed line represents the interface

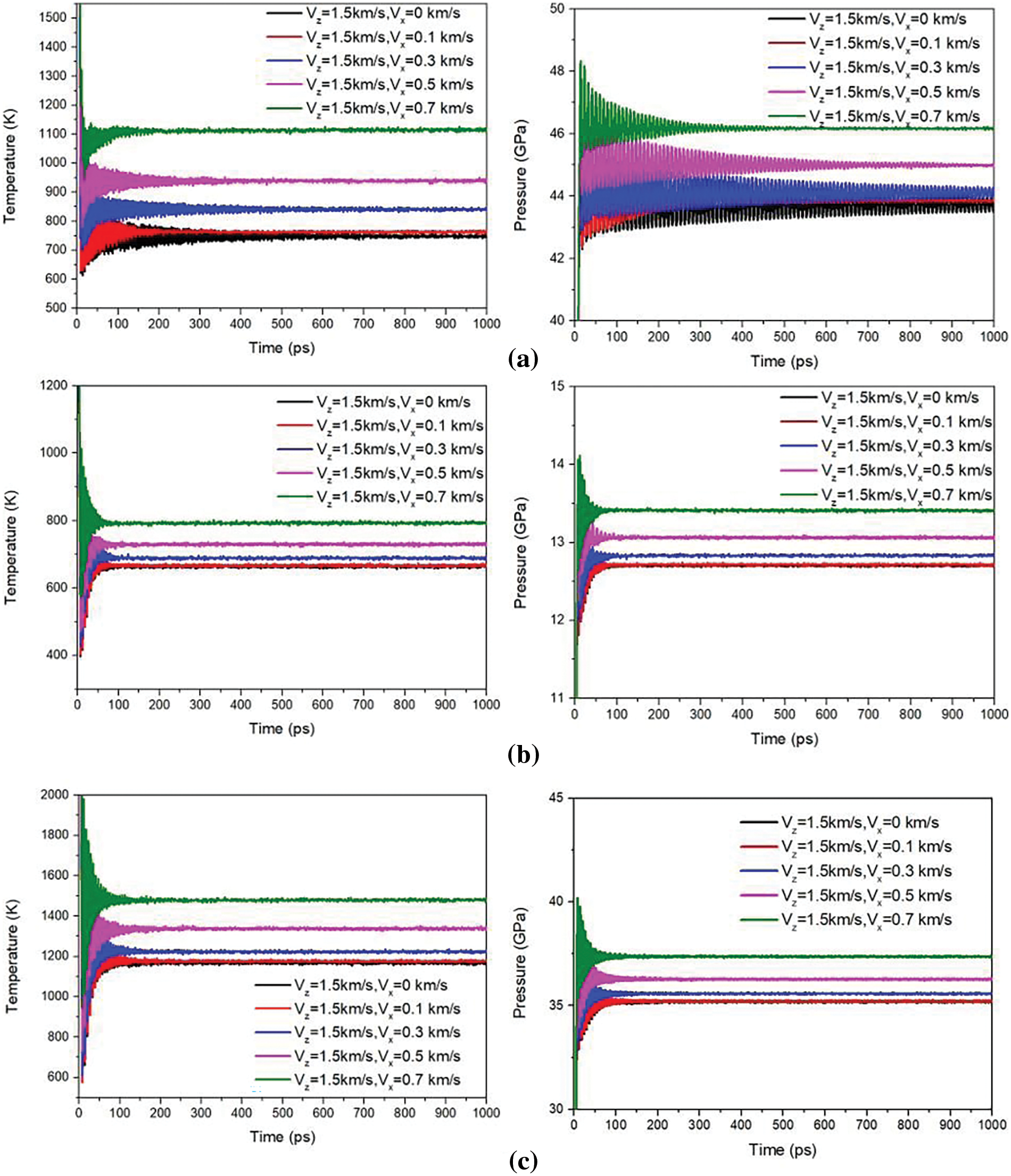
Figure 5: The temperature and pressure profiles of the: (a) Al-Cu system, (b) Al-Al system, and (c) Cu-Cu system during the loading stage

MSD=1N∑i=1N<|ri(t)−ri(0)|2>,(1)

where N stands for the number of atoms; ri(t) and ri(0) represent displacement vectors of the ith atom at time 0 and t, respectively; the computation symbol 〈〉 represents temporal correlation [23]. The correlation between MSD and diffusion coefficient is given as

limt→∞MSD=c+2dDt,(2)

where d stands for dimension (d is 3 in this study); c and D represent constant and diffusion coefficient, respectively. 2dD represent the slope of MSD curves, so D can be calculated by the following formula:

D=16limt→∞[ddt<|ri(t)−ri(0)|2>].(3)

3.1 Diffusion between Al Bulk and Cu Bulk

For the Al/Cu combination, the Al sample is given an initial velocity to model the collision. The system configuration after the unloading stage with different velocity conditions is shown in Fig. 3a. When Vx=0.1km/s, there is no obvious diffusion behavior on the Cu sides. Only a small fraction of the Cu atoms diffuses into the opposite sides. When Vx=0.3km/s, there is still no obvious diffusion on the Cu sides, even though only a few copper atoms and aluminum atoms have diffused into each other. When Vx=0.5km/s, Cu atoms and Al atoms diffuse, and the diffusion layer becomes apparent. When Vx=0.7km/s, both Cu atoms and Al atoms exhibit significant diffusion behaviors, there is little difference in diffusion depth between copper and aluminum atoms. As the transverse velocity increases, the atomic potential energy across the interface also increases (Fig. 4a), while the potential energy of Al atoms that diffuse into the Cu bulk decreases.

The time profiles of the temperature and pressure of the whole system during the loading stage for Vx=0.7km/s, Vx=0.5km/s, Vx=0.3km/s, Vx=0.1km/s, Vx=0.0km/s are shown in Fig. 5a. During the loading process, the initial kinetic energy of the aluminum bulk converts into the internal energy of the entire system, causing a significant increase in system temperature and pressure. The system temperature increases dramatically to approximately 1500, 1200, 900, 850, 800 K, sequentially in a short time, close to 15 ps. The system temperature increases as Vx increases. Although the temperature has exceeded the melting point of aluminum, it is still lower than the melting point of copper (Fig. 5a). At the same time, the system pressure fluctuates significantly. After about 100 ps, the temperature and pressure of the simulation system reach a dynamic equilibrium state. The equilibrium temperatures from MD simulations are 1100, 950, 850, 750, 740 K, sequentially. The equilibrium pressures from MD simulations are about 46, 45, 44, 43, 43 GPa, sequentially. With the increase of Vx, the crystal structure of Al no longer remains intact and becomes amorphous. As a result, numerous vacancies form, while the lattice structure of Cu remains unchanged. As a result, Cu atoms can easily diffuse into the Al sample, while only a few Al atoms can diffuse into the Cu side. So, obvious diffusion behaviors only occur once the system temperature reaches a specific value during the unloading stage. This is perhaps because the melting point of metals increases significantly with an increase in pressure during loading stage [11]. These phenomena can be demonstrated by the increase in potential energy of atoms, as shown in Fig. 4a. This indicates that the energy barrier can be overcome by high-speed collisions, allowing atoms to approach each other at a sufficiently short distance.

Given the results above, the diffusion coefficient (Eq. (3)) shows a correlation with collision velocity. The relationship between the transverse velocities and the diffusion coefficients of Cu and Al is dipicted in Fig. 6a. When the longitudinal velocity is fixed at 1.5 km/s, the tansverse velocity increases by 0.1 km/s from 0.1 to 0.8 km/s. As shown in Fig. 6a, the diffusion coefficient of aluminum atom is always greater than that of copper atom. This indicates that Al atoms diffuse more noticeably with increasing transverse velocities, while Cu atoms diffuse significantly when Vx≥0.6km/s. The data in Fig. 6a shows that the diffusion coefficient is positively correlated with the transverse velocity. The correlation between the longitudinal velocity and the diffusion coefficients of Cu and Al is presented in Fig. 6b. The calculated diffusion coefficient of aluminum atom is larger than that of copper atom. This indicates that Al atoms diffuse more noticeably without transverse velocity during collision processes, and the calculated diffusion coefficient of Cu atoms is almost zero when Vz < 1.75 km/s, it means that there are no diffusion behaviors for Cu atoms. When Vz ≥ 1.75 km/s, the diffusion coefficient of Cu atoms begins to increase and it indicates that Cu atoms diffuse into the opposite side. The data in Fig. 6b shows that the diffusion coefficient is positively correlated with the longitudinal velocity. During collision processes, the diffusion coefficient of aluminum atom is always greater than that of Cu atom, regardless of transvers velocity. The role of transverse velocity in collision welding is important. It can increase the potential energy of atoms near the interface, thereby accelerating the welding processes, as shown in a previous study [11]. Additionally, transverse velocity can help break up the crystal lattice and this causes the diffusion activation energy to decrease to a very small value [24].

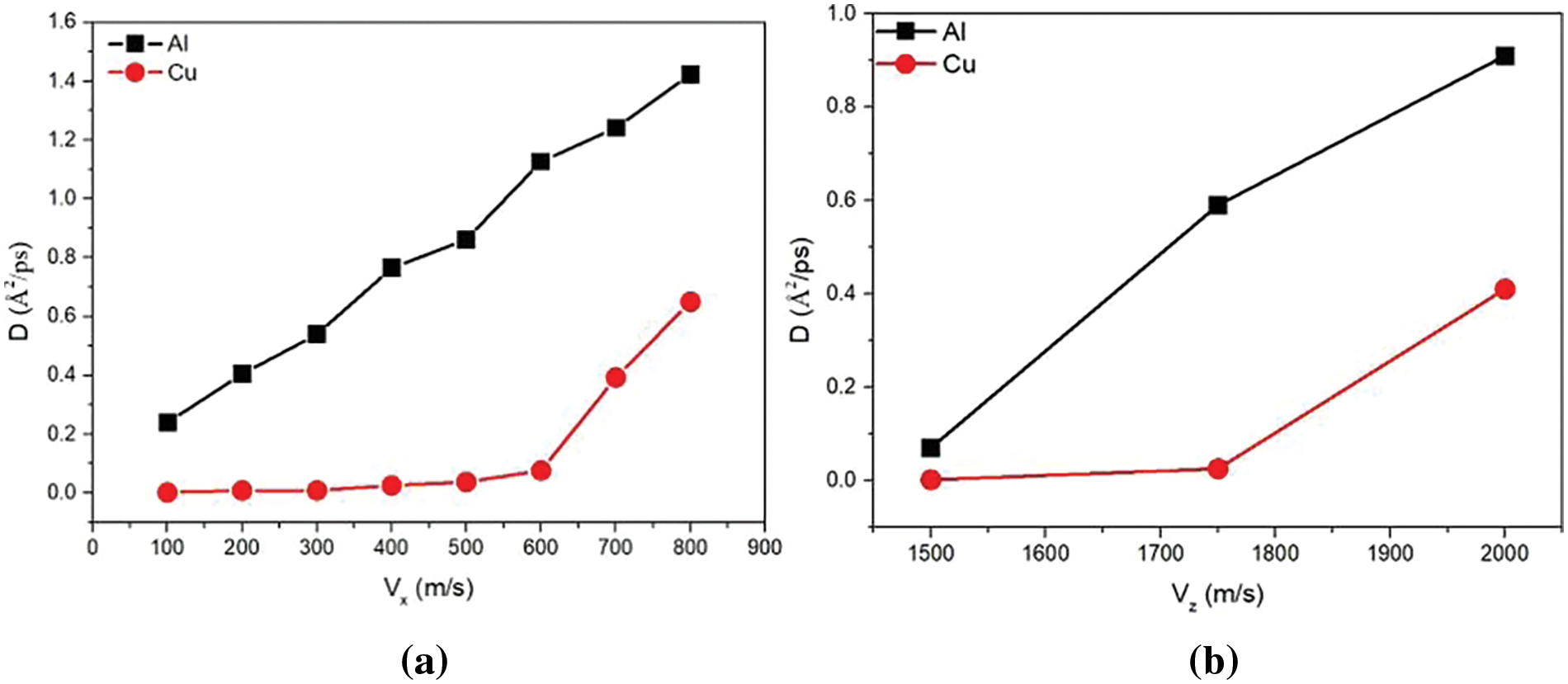
Figure 6: Diffusion coefficients of Cu and Al at different: (a) transverse and (b) longitudinal velocities after unloading stage

3.2 Diffusion between Al Bulk and Al Bulk

For the Al/Al combination, the Al sample is given an initial velocity to model the collision. In this paper, the Al sample used as the shock sample is represented by Al-shock. The system configuration after the unloading stage under different velocity conditions is shown in Fig. 3b. With the increases of Vx, the diffusion behaviors become more obvious and the potential energy of atoms near the interface also increases (Fig. 4b). The time profiles of the system temperature and pressure during the loading stage for Vx=0.7km/s, Vx=0.5km/s, Vx=0.3km/s, Vx=0.1km/s, Vx=0.0km/s are shown in Fig. 5b. During the loading stage, the initial kinetic energy of the Al-shock sample is transformed into the internal energy of the entire system. As a result, the system temperature and pressure increase significantly. The system temperature rises sharply to approximately 1200, 900, 800, 780, 700 K in a period of around 20 ps. At the same time, the system pressure fluctuates intensely. After about 100 ps, the system temperature and pressure reach a dynamic equilibrium state. The equilibrium temperatures from MD simulations are approximately 800, 750, 700, 680, and 660 K, respectively. The equilibrium pressures from MD simulations are approximately 13.5, 13, 12.7, 12.6 and 12.4 GPa, respectively.

According to the data in Fig. 3b, when Vx≤0.3km/s, there is no obvious diffusion behavior. When Vx=0.5km/s, there is still no obvious diffusion behavior on Al sides. But a few Al-shock atoms and Al atoms have diffused into each other. When Vx=0.7km/s, the Al-shock atoms and Al atoms diffuse, the diffusion layer becomes apparent and forms. The thickness of diffusion layer of Al-shock and Al are almost equal. As Vx increases, the crystal structures of both Al-shock and Al are disrupted, resulting in the formation of numerous vacancies on both sides. Because Al-shock and Al have the same material properties, the diffusion depths are equal on both sides and exhibit symmetrical diffusion behavior.

The system temperatures of the samples at Vx= 0.7 km/s are significantly higher than those at other velocities in Fig. 5b. Therefore, noticeable diffusion behaviors only occur when the system temperature reaches a specific value during the unloading stage. This is also shown in Fig. 4b. The potential energy of atoms near the contact surfaces increases as the Vx increases. This indicates that the energy barrier can be overcome by high-speed collisions, allowing atoms to approach each other at a sufficiently short distance.

The diffusion coefficient (Eq. (3)) has a correlation with collision velocity. The relationship between the transverse velocities and the diffusion coefficients of Al-shock and Al is dipicted in Fig. 7a. When the longitudinal velocity is fixed at 1.5 km/s, the tansverse velocity is increased by 0.1 km/s from 0.5 to 0.8 km/s. As shown in Fig. 7a, when Vx<0.6km/s, the diffusion coefficients of Al and Al-shock are zero, there are no diffusion behaviors observed for both Al atoms and Al-shock atoms. When Vx≥600m/s, both Al atoms and Al-shock atoms diffuse noticeably. The data in Fig. 7a shows that the diffusion coefficient is positively correlated with the transverse velocity. The correlation between the longitudinal velocity and the diffusion coefficients of Al-shock and Al is presented in Fig. 7b. The calculated data shows that Al-shock and Al atoms diffuse obviously without transverse velocity during the collision processes when Vz≥1750m/s. The data in Fig. 7b indicates that the diffusion coefficient is positively correlated with the longitudinal velocity. In Al-Al combinations, increasing the longitudinal velocity can result in a greater increase in the diffusion coefficient compared to transverse velocity. This is perhaps because the intense shock with a higher longitudinal velocity can increase the kinetic energy of Al atoms, causing the crystal structures of Al to be more easily disrupted [11].

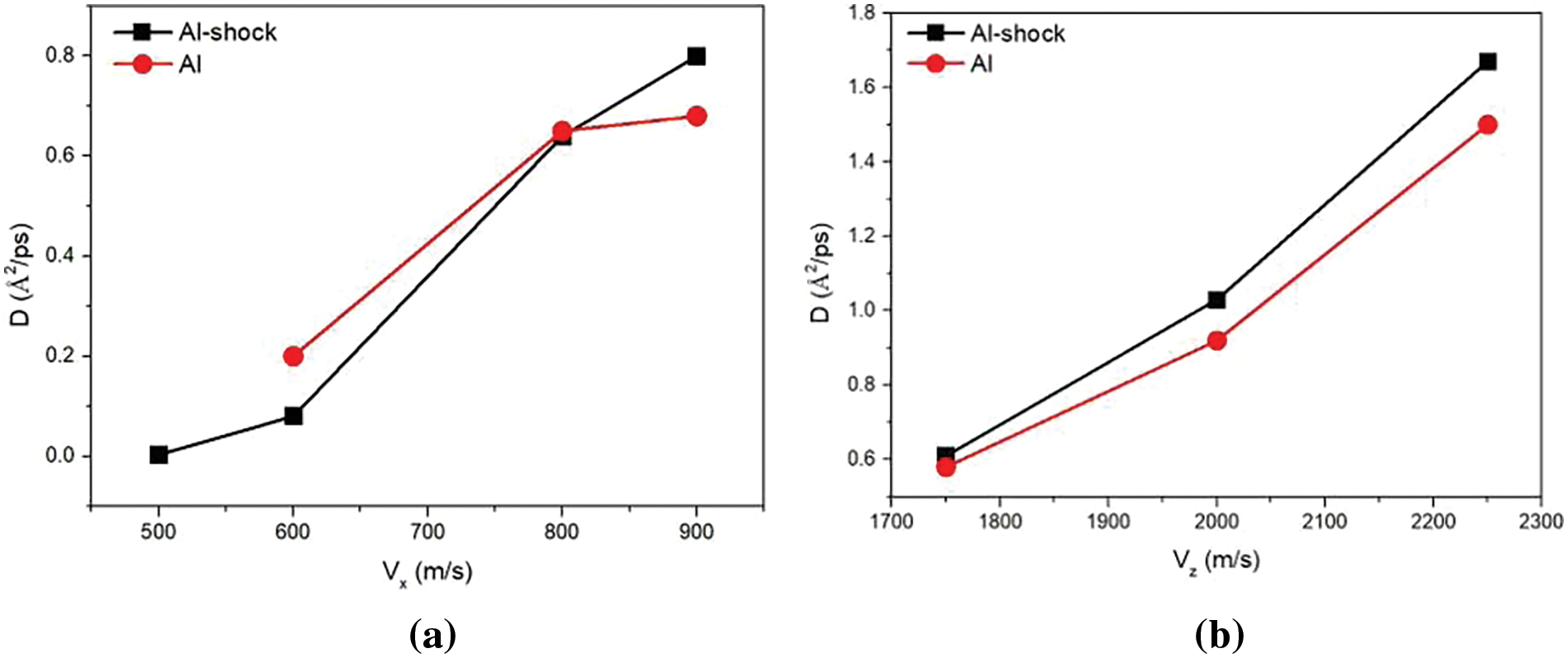
Figure 7: Diffusion coefficients of Al-shocks and Al at different: (a) transverse velocities, (b) longitudinal velocities

3.3 Diffusion between Cu Bulk and Cu Bulk

For the Cu/Cu combination, the Cu sample is given a velocity to model the collision. In this paper, the Cu sample used for shock testing is referred to as Cu-shock. The system configuration after the unloading stage with different velocity conditions is shown in Fig. 3c. As Vx increases, the diffusion behaviors become more apparent and the potential energy of atoms near the interface also increases (Fig. 4c).The time profiles of the temperature and pressure of the whole system during the loading stage for Vx=0.7km/s, Vx=0.5km/s, Vx=0.3km/s, Vx=0.1km/s, Vx=0.0km/s are shown in Fig. 5c. During the loading stage, the initial kinetic energy of the Cu sample converts into the internal energy of the entire system, resulting in a dramatic rise in temperature and pressure in the simulation system. The system temperature quickly rise to about 2000, 1600, 1400, 1300, 1200 K in 20 ps. At the same time, the system pressure fluctuates intensely. After about 100 ps, the system temperature and pressure reach a dynamic equilibrium state. The equilibrium temperatures from MD simulations are about 1500, 1300, 1200, 1180, 1150 K, respectively. The equilibrium pressures from MD simulations are approximately 42.5, 40, 37, 36, and 35 GPa, respectively.

The system configuration after the unloading stage with different velocity conditions is shown in Fig. 3c. When Vx=0.1km/s, there is no obvious diffusion behavior. When Vx≥0.3km/s, the Cu-shock atoms diffuse into the opposite side apparently, but only a few Cu atoms diffuse into the opposite side. The diffusion depths of Cu-shock and Cu are almost equal. The system temperature increases with the increase of Vx and when Vx≥0.3km/s, the system temperature is approaching the melting point of copper and gradually exceeds the melting point until Vx=0.7km/s. This induces the breakup of crystal structures in both Cu-shock and Cu, resulting in the generation of numerous vacancies on both sides. Because Cu-shock and Cu have the same material properties, the diffusion depths are equal on both sides. These phenomena can also be explained in the same way as combinations of Al/Cu and Al/Al.

Based on the results above, there is a correlation between diffusion coefficient (Eq. (3)) and collision velocity. The relationship between the transverse velocities and the diffusion coefficients of Cu-shock and Cu is depicted in Fig. 8. In this case, the longitudinal velocity is fixed at 1.5 km/s and the tansverse velocity is increased in increments of 0.1 km/s from 0.2 to 0.6 km/s. As shown in Fig. 8, when Vx<0.4km/s, the diffusion coefficient of Cu atoms is almost zero, it indicates that only a few Cu atoms diffuse into Cu-shock. With the increasing transverse velocitiy, both Cu and Cu-shock atoms diffuse noticeably. When the longitudinal velocity exceeds 2000 m/s, the Cu-Cu system collapses, making it difficult to calculate the diffusion coefficient without considering the transverse velocity. The data in Fig. 8 shows that the diffusion coefficient is positively correlated with the transverse velocity. It shows the same trend with Al-Cu combinations. For dissimilar material combinations, the diffusion coefficient of the shocked sample increase linearly with increasing velocity, while that of the target sample is not. For similar material combinations, the diffusion coefficients of the shocked sample and the target sample all increase with increasing velocity.

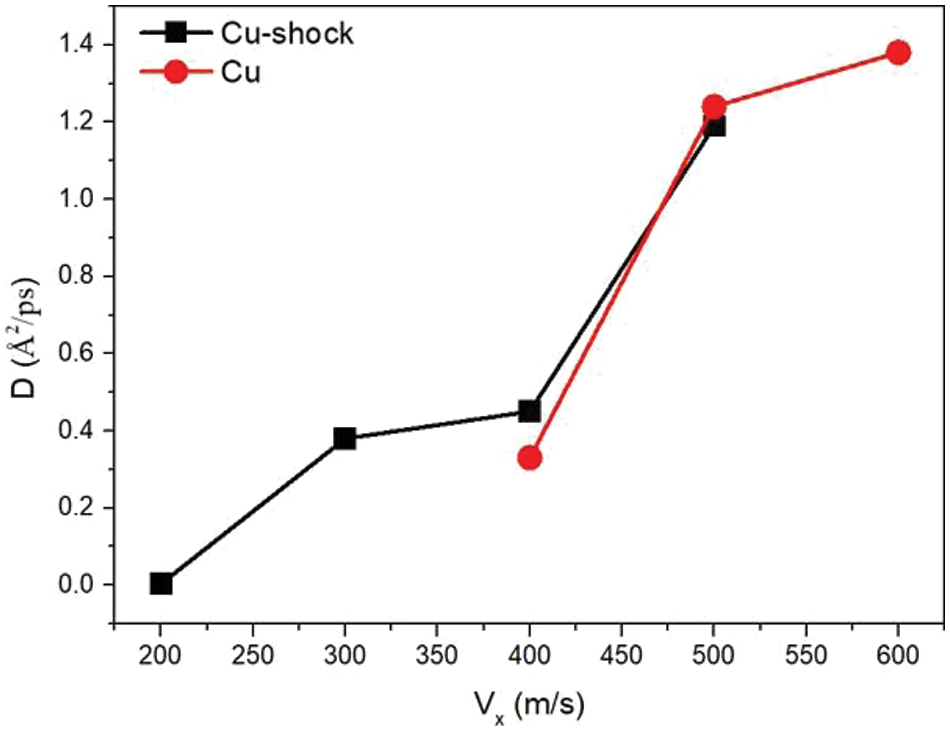
Figure 8: Diffusion coefficients of Cu-shocks and Cu at different transverse velocities

As discussed above, different material combinations exhibit various diffusion phenomena under the same impact velocity condition. For dissimilar material combinations, the transvers velocity can play a dominant role in a diffusion process. This trend is consistent with previous studies [3,4,11]. And for similar material combinations, the diffusion behaviors become more apparent as the impact velocity increases, as verified by the data for Al/Al in [12]. Therefore, the longitudinal velocity also plays a significant role in the diffusion process for similar material combinations. The comprehensive study on similar and dissimilar materials shows that skew collision welding forms a strong welding joint. It is important to choose a collision velocity that is sufficiently high to raise the system temperature close to the fusion point of the metal. For both similar and dissimilar combinations, diffusion behaviors occur during the unloading stage. This is because the kinetic energy caused by the collision at the loading stage transforms into internal energy, resulting in an increase in the temperature of the system. On the other hand, during the unloading stage, the internal energy transforms into kinetic energy, causing a dramatic increase in the diffusivity of atoms. As the vacancy mechanism is a predominated mechanism in diffusion behaviors [25], with the collision velocity increasing, the metal bonds break, and a large number of vacancies are generated, it causes the crystal structures of metal sample to be more easily disrupted. As a result of this, it will be good for metal atoms to diffuse into the opposite side. As a result, the contacted materials form an adhesion joint. But for dissimilar combinations, because the fusion point of copper is higher than that of aluminum, which indicates that bonds between Al and Al atoms are more likely to break than that of Cu atoms. Lattice vacancies or other defects are more likely to occur in aluminum samples, this will facilitate the diffusion of copper atoms into the aluminum sample, by contrast, it requires more energy for the Al atom to diffuse into Cu side, and then consumes the potential energy of aluminum atoms. So, the potential energy of Al atoms diffusing into the Cu bulk decreases during collision process. This is different from the potential energy of similar combinations. This can be a reason why the diffusion behaviors of different combinations are more noticeable than similar combinations.

4  Conclusions

In this study, the atomistic diffusion behaviors at the collision interface during impact welding was simulated using the molecular dynamics method with various metal combinations and velocities. The simulations were conducted under zero pressure for the fixed condition was released along the z direction (Fig. 2). We calculated the diffusion coefficients and discussed the effects of collision velocity conditions and material combinations. The results suggest that process parameters should be selected differently for similar and dissimilar material combinations. In the case of dissimilar material combinations, the transverse velocity should be large enough to achieve significant diffusion behavior. On the other hand, for similar material combinations, the longitudinal velocity seems to have a greater impact on achieving significant diffusion behavior compared to the transverse velocity. However, the longitudinal velocity should be selected carefully for the Cu-Cu system, as exceeding 2000 m/s leads to the collapse of the simulation system. These findings provide valuable insights for optimizing welding parameters.

Acknowledgement: The authors gratefully acknowledge financial support from the Scientific Research Project of Hunan Provincial Department of Education through Grant No. 22C0642.

Funding Statement: This work was supported by the Scientific Research Project of Hunan Provincial Department of Education (22C0642).

Author Contributions: Original draft, software, methodology: Dingyi Jin; data collection, conceptualization: Guo Wei.

Availability of Data and Materials: Data will be made available on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. N. Kahraman, B. Gulenc, and F. Findik, “Corrosion and mechanical-microstructural aspects of dissimilar joints of Ti-6Al–4V and Al plates,” Int. J. Impact Eng., vol. 34, no. 8, pp. 1423–1432, 2007. doi: 10.1016/j.ijimpeng.2006.08.003. [Google Scholar] [CrossRef]

2. J. Cheng, X. Hu, X. Sun, A. Vivek, and G. D. Daehn, “Cullenmulti-scale characterization and simulation of impact welding between immiscible Mg/steel alloys,” J. Mat. Sci. Technol., vol. 59, pp. 149–163, 2020. doi: 10.1016/j.jmst.2020.04.049. [Google Scholar] [CrossRef]

3. Y. Zhang et al., “Application of high velocity impact welding at varied different length scales,” J. Mater. Process. Technol., vol. 211, no. 5, pp. 944–952, 2011. doi: 10.1016/j.jmatprotec.2010.01.001. [Google Scholar] [CrossRef]

4. J. Cheng, X. Hu, and X. Sun, “Molecular dynamics study on interface formation and bond strength of impact-welded Mg-steel joints,” Comput. Mater. Sci., vol. 185, pp. 109988, 2020. doi: 10.1016/j.commatsci.2020.109988. [Google Scholar] [CrossRef]

5. Y. Zhou, C. Li, X. Wang, Z. Liao, X. Shi and C. Yao, “Investigation of flyer plate dynamic behavior in electromagnetic pulse welding,” J. Manuf. Process., vol. 68, pp. 189–197, 2021. doi: 10.1016/j.jmapro.2020.07.047. [Google Scholar] [CrossRef]

6. R. N. Raoelison, T. Sapanathan, E. Padayodi, N. Buiron, and M. Rachik, “Interfacial kinematics and governing mechanisms under the influence of high strain rate impact conditions: Numerical computations of experimental observations,” J. Mech. Phys. Solids, vol. 96, pp. 147–161, 2016. doi: 10.1016/j.jmps.2016.07.014. [Google Scholar] [CrossRef]

7. Y. Aizawa, J. Nishiwaki, Y. Harada, S. Muraishi, and S. kumai, “Experimental and numerical analysis of the formation behavior of intermediate layers at explosive welded Al/Fe joint interfaces,” J. Manuf. Process., vol. 24, pp. 100–106, 2016. doi: 10.1016/j.jmapro.2016.08.002. [Google Scholar] [CrossRef]

8. X. J. Li, F. Mo, X. H. Wang, B. Wang, and K. X. Liu, “Numerical study on mechanism of explosive welding,” Sci. Technol. Weld. Joining, vol. 17, no. 1, pp. 36–41, 2012. doi: 10.1179/1362171811Y.0000000071. [Google Scholar] [CrossRef]

9. Y. Zhu, G. Liao, T. Shi, Z. Tang, and M. Li, “Interdiffusion cross crystal-amorphous interface: An atomistic simulation,” Acta Mater., vol. 112, pp. 378–389, 2016. doi: 10.1016/j.actamat.2016.04.032. [Google Scholar] [CrossRef]

10. R. Y. Dong and B. Y. Cao, “Application of the uniform source-and-sink scheme to molecular dynamics calculation of the self-diffusion coefficient of fluids,” Int. J. Numer. Methods Eng., vol. 92, no. 3, pp. 229–237, 2012. doi: 10.1002/nme.4332. [Google Scholar] [CrossRef]

11. S. Y. Chen, Z. W. Wu, K. X. Liu, X. J. Li, N. Luo and G. X. Lu, “Atomic diffusion behavior in Cu-Al explosive welding process,” J. Appl. Phys., vol. 113, no. 4, pp. 44901, 2013. doi: 10.1063/1.4775788. [Google Scholar] [CrossRef]

12. J. Feng, R. Liu, K. Liu, Q. Zhou, R. Yang and P. Chen, “Atomistic simulation on the formation mechanism of bonding interface in explosive welding,” J. Appl. Phys., vol. 131, no. 2, pp. 25903, 2022. doi: 10.1063/5.0069720. [Google Scholar] [CrossRef]

13. K. Wang, H. Bai, W. Hu, S. Wu, H. Wang and H. Fan, “Investigation of atomic diffusion behavior of Mo/Au interface,” Mater. Chem. Phys., vol. 257, pp. 123839, 2021. doi: 10.1016/j.matchemphys.2020.123839. [Google Scholar] [CrossRef]

14. Y. Ma et al., “Atomic diffusion behavior near the bond interface during the explosive welding process based on molecular dynamics simulations,” Mater. Today Commun., vol. 31, pp. 103552, 2022. doi: 10.1016/j.mtcomm.2022.103552. [Google Scholar] [CrossRef]

15. C. Li, C. Xu, Y. Zhou, D. Chen, X. Wang, and Y. Mi, “Atomic diffusion behavior in electromagnetic pulse welding,” Mater. Lett., vol. 330, pp. 133242, 2023. doi: 10.1016/j.matlet.2022.133242. [Google Scholar] [CrossRef]

16. J. H. Jang, D. G. Nam, Y. H. Parkand, and I. M. Park, “Effect of solution treatment and artificial aging on microstructure and mechanical properties of Al-Cu alloy,” Trans. Nonferrous Met. Soc. China, vol. 23, no. 3, pp. 631–635, 2013. doi: 10.1016/S1003-6326(13)62509-1. [Google Scholar] [CrossRef]

17. S. Plimpton, “Fast parallel algorithms for short-range molecular dynamics,” J. Comput. Phys., vol. 117, no. 1, pp. 1–19, 1995. doi: 10.1006/jcph.1995.1039. [Google Scholar] [CrossRef]

18. J. Cai and Y. Y. Ye, “Simple analytical embedded-atom-potential model including a long-range force for fcc metals and their alloys,” Phys. Rev. B, vol. 54, no. 12, pp. 8398, 1996. doi: 10.1103/PhysRevB.54.8398. [Google Scholar] [PubMed] [CrossRef]

19. L. Xiu and J. F. Wu, “Atomic diffusion behavior in W/Cu diffusion bonding process,” J. Fusion Energy, vol. 34, pp. 769–773, 2015. doi: 10.1007/s10894-015-9884-9. [Google Scholar] [CrossRef]

20. A. Mao et al., “The diffusion behaviors at the Cu-Al solid-liquid interface: A molecular dynamics study,” Results Phys., vol. 16, pp. 102998, 2020. doi: 10.1016/j.rinp.2020.102998. [Google Scholar] [CrossRef]

21. C. Li, D. Li, X. Tao, H. Chen, and Y. Ouyang, “Molecular dynamics simulation of diffusion bonding of Al-Cu interface,” Model. Simul. Mater. Sci. Eng., vol. 22, no. 6, pp. 65013, 2014. doi: 10.1088/0965-0393/22/6/065013. [Google Scholar] [CrossRef]

22. P. V. Polyakova and J. A. Baimova, “The effect of atomic interdiffusion at the Al/Сu interface in an Al/Сu composite on its mechanical properties: Molecular dynamics,” Phys. Met. Metallogr., vol. 124, pp. 394–401, 2023. doi: 10.1134/S0031918X22602116. [Google Scholar] [CrossRef]

23. P. He, D. Xu, T. Lin, and Z. Jiao, “Joint properties between carbon nanotube and gold at different energy levels from molecular dynamics,” Comput. Mater. Sci., vol. 72, pp. 38–41, 2013. doi: 10.1016/j.commatsci.2013.01.037. [Google Scholar] [CrossRef]

24. L. S. Vasil’ev, “To the theory of the anomalously high diffusion rate in metals under shock action: II. Effect of shear stresses and structural and phase state of the diffusion zone on the rate of mass transfer,” Phys. Met. Metallography, vol. 107, pp. 427–434, 2009. doi: 10.1134/S0031918X09050020. [Google Scholar] [CrossRef]

25. C. A. C. Sequeira and L. Amaral, “Role of Kirkendall effect in diffusion processes in solids,” Trans. Nonferrous Met. Soc. China, vol. 24, no. 1, pp. 1–11, 2014. doi: 10.1016/S1003-6326(14)63021-1. [Google Scholar] [CrossRef]