A Multi-Objective Optimization for Locating Maintenance Stations and Operator Dispatching of Corrective Maintenance

1  Introduction

Modern manufacturing is continually challenged by unpredictable variables that disrupt the smooth operation of production lines, leading to significant operational costs despite the incorporation of cutting-edge technology and advanced equipment [1–3]. In this context, machine maintenance, encompassing predictive and corrective approaches, emerges as a critical element. Predictive maintenance, a proactive strategy, employs extensive data analytics to anticipate and prevent machine malfunctions but often faces challenges due to incomplete data collection. On the other hand, corrective maintenance, a reactive approach, is activated after detecting machine faults, aiming to swiftly restore functionality. The advancement of monitoring systems and sensor technologies has bolstered this approach, enhancing real-time anomaly detection and enabling rapid deployment of maintenance teams to mitigate disruptions.

This research focuses on the efficiency of maintenance stations within factories, crucial for operational responsiveness. These hubs, where operators receive alerts and mobilize to address machine malfunctions, play a vital role in enhancing efficiency and reducing downtime, thereby optimizing productivity in manufacturing settings. The corrective maintenance process on production lines entails several steps: Detection of machine issues, notification and mobilization of technicians, diagnosis, repair, verification of functionality, and return of technicians to their stations. Both the fault response time—from detection to repair commencement—and the maintenance duration are critical for maintaining operational efficiency.

The response time in corrective maintenance mirrors that in Emergency Medical Services (EMS), where it is defined as the duration from an emergency report to the start of medical treatment. Just as in EMS, where the strategic location of service points and efficient resource allocation are essential for not only rapid but also quality care [4–8], in manufacturing, response time is influenced by the proximity of maintenance stations and the distribution of technical personnel. The closer the maintenance stations are to the site of the malfunction, the quicker the response for repairs. Thus, the strategic establishment of maintenance stations and the assignment of operators to these stations are crucial in enhancing the efficiency of corrective maintenance and overall production line operations.

The optimization of maintenance personnel dispatch and strategic station selection, a crucial topic for improving efficiency and reducing downtime, has garnered considerable attention across various disciplines. This growing interest is reflected in an increasing body of literature that explores diverse decision-making challenges in this area. Researchers have employed a range of methods, from heuristic to classical techniques, for modeling workforce deployment and station selection. For instance, Qiu et al. [9] proposed a hybrid heuristic model, integrating genetic algorithms and variable neighborhood search strategies, to enhance the dispatch and routing of multi-skilled technicians in equipment maintenance. Similarly, Li et al. [10] developed a multi-objective optimization method that incorporates improved genetic and NSGA-II algorithms for optimizing maintenance, repair, and operations service resources for complex products. Chen et al. [11] introduced an enhanced Non-Dominated Sorting Genetic Algorithm II (NSGA-II) for maintenance personnel dispatch in smart grids. Xu et al. [12] combined a multi-objective selective maintenance optimization method with a personnel allocation model for series-parallel systems, utilizing NSGA-II algorithms to optimize maintenance efficiency in complex systems. Ansari et al. [13] developed a methodology that integrates a knowledge graph, linear programming, and genetic algorithms for efficient human resource allocation in industrial maintenance. Adding to these advancements, Rillo et al. [14] devised a multi-objective mixed-integer linear programming model focused on resource allocation in aircraft line maintenance, while Kim et al. [15] utilized queuing models and optimization strategies for improving maintenance personnel allocation in the naval ship maintenance system. Gkonou et al. [16] introduced a mixed-integer programming optimization model for railway maintenance scheduling and crew allocation, aiming to enhance network reliability and reduce operational costs.

In the agricultural sector, Han et al. [17] created a model for optimizing the placement of temporary agricultural machinery maintenance stations to improve harvest maintenance efficiency. The use of big data was exemplified by Zhang et al. [18], who leveraged vehicle trajectory data to optimize the placement of automobile maintenance stations, blending zoning and advanced algorithms for maximum efficiency. Al Ali et al. [19] introduced a model for optimizing bus depot locations, focusing on maintenance center accessibility to reduce operational costs and improve public transport efficiency. In the industrial domain, David et al. [20] introduced a method for optimizing maintenance locations, enhancing the CRAFT technique to reduce material handling costs. Their approach streamlined maintenance center placement decisions, addressing logistic delays in various sectors. Tönissen et al. [21] developed a model for optimally locating and routing railway rolling stock maintenance facilities, targeting operational efficiency and service cost reduction. In the field of agriculture, Li et al. [22] crafted a mixed-integer linear programming model for optimally locating service stations and spare part centers, with a focus on service cost reduction. In maritime operations, Xin et al. [23] designed an algorithm for strategically locating maintenance bases for marine drones, enhancing operational efficiency and response. Lastly, Malec et al. [24] introduced a mixed-integer linear programming model for optimizing the location of gas network maintenance centers, aiming to enhance service response times and reduce operational costs.

The collective body of work in the field of maintenance resource allocation and station selection, highlighted by these studies, underscores the significant progress and innovative approaches being made. This research domain, characterized by its multidisciplinary involvement, demonstrates a strong practical relevance, addressing a range of complex issues from optimizing technician dispatch in various sectors to strategizing station placements. These advancements not only enhance operational efficiency but also reflect the dynamic nature of the field, where diverse methodologies and sector-specific adaptations contribute to the broader understanding and improvement of maintenance systems.

However, despite extensive research in maintenance personnel dispatching and station selection, a critical gap exists in integrating these aspects, particularly for quick response in corrective maintenance. This deficiency presents a significant opportunity for developing integrated models that can simultaneously optimize personnel deployment and station selection, potentially enhancing operational efficiency and effectiveness in urgent maintenance scenarios. Addressing this gap is crucial for formulating more effective maintenance strategies, particularly in situations demanding timely corrective actions. This paper introduces a novel multi-objective optimization model. This model aims to concurrently optimize maintenance personnel deployment and station selection, taking into account both operator expertise and the spatial layout of factory machinery, with the goal of minimizing response times and labor costs. The expanded focus on integrating these two critical aspects represents a significant advancement in the field, offering the potential to significantly impact maintenance operations in a variety of industries.

In light of the problem’s NP-hard nature, the study innovatively adapted the Non-Dominated Sorting Genetic Algorithm III (NSGA III), integrating the spatial distribution of factory machinery with operator expertise. This approach ensures the prompt assignment of operators to malfunctions, accelerating adjustments, and optimizing resource utilization. To effectively apply this approach to our multi-objective optimization model, which focuses on locating maintenance stations and operator dispatching, we have meticulously designed the coding, crossover, and mutation operators of the algorithm. The research thoroughly examines the algorithm’s performance across varied problem instances. Its effectiveness is validated through extensive experiments covering different machine failure frequencies and diverse operator scenarios, complemented by detailed data analysis from a Taiwanese electronic equipment manufacturer. These experiments provide valuable insights into the algorithm’s real-world applicability and effectiveness in improving maintenance strategies in manufacturing settings. The paper’s expanded focus on integrating these two critical aspects of maintenance represents a significant advancement in the field, offering the potential to significantly impact maintenance operations in various industries.

The paper’s contributions include:

•   The development of a novel multi-objective optimization model for maintenance personnel dispatching and station selection, incorporating the spatial distribution of machinery and operator expertise.

•   The development of the NSGA III + Dispatch method, an adaptation of NSGA III specifically designed for complex multi-objective optimization in locating maintenance stations and operator dispatching.

•   Conducting empirical experiments to validate the model’s effectiveness in real-world maintenance operations.

The rest of this paper is structured as follows: The subsequent section provides a comprehensive literature review related to the topic. Section 3 is dedicated to introducing key definitions, notations, and explaining the proposed mathematical model as well as the optimization framework. Section 4 examines the outcomes of various experiments conducted with the proposed algorithm across multiple scenarios. The article concludes by summarizing the key findings and suggesting future research directions.

2  Related Literature

The determination of site selection also called location determination involves a strategic analysis to identify the most suitable locations for various facilities within a specific area [25]. This analytical process takes into account a range of factors to ascertain the optimal site that aligns with defined objectives [26]. This decision-making process is pivotal in sectors such as manufacturing, retail, and healthcare, affecting their operational success [27–29]. A variety of tools and methods have been developed to address the challenges of site selection. For example, Zhang et al. [30] demonstrated the use of CPLEX optimization software to determine the best locations for emergency medical service stations. Similarly, Wu et al. utilized LINGO software for selecting a location for an automotive service firm [31]. Despite their capabilities, traditional software packages may fall short when dealing with complex, large-scale, or non-linear challenges [6]. In these instances, meta-heuristic approaches, such as Genetic Algorithms (GA) and Particle Swarm Optimization (PSO), have been shown to offer robust solutions [32]. Zambrano-Rey et al.’s use of PSO for optimal retail store site selection is a case in point, illustrating the effectiveness of these advanced methods [33].

The Human Resource Allocation Problem (HRAP) is the challenge of distributing limited human resources across multiple tasks in the most effective manner [34]. Traditional exact methods strive to find the best possible solution, but they can be computationally intensive. In contrast, metaheuristic algorithms are known for delivering efficient, though sometimes less than optimal, solutions [35,36]. In exploring exact methods, Vila et al. [37] harnessed the Branch, Bound, and Remember Algorithm (BBRA) for optimal worker distribution along assembly lines, a strategy similarly employed by Su et al. [38]. For tasks of higher complexity, metaheuristic approaches such as the Non-Dominated Sorting genetic Algorithm II (NSGA II) and PSO have proven effective [35,39]. For instance, Feng et al. implemented NSGA II to improve staffing in emergency departments [40], while Wei et al. combined Ant Colony Optimization (ACO) with PSO to address human resource allocation challenges [41]. Additionally, well-established metaheuristic strategies like Tabu Search (TS) [42,43] and Simulated Annealing (SA) [44,45] have been effectively applied to the HRAP. These techniques have proven instrumental in optimizing the allocation process, ensuring efficiency and effectiveness in human resource management.

In the field of manufacturing, it is common to encounter complex Combinatorial Optimization Problems (COPs). These multifaceted issues require dealing with several goals at once and are known to be NP-hard, a category of problems that are particularly challenging to solve. Traditional methods often fall short when tackling the intricacies of these problems [46,47]. The NSGA-III algorithm stands out as a popular metaheuristic tool, recognized for its ability to handle non-linear problems and multiple objectives with efficiency [48]. Its practical application extends beyond theoretical use, as evidenced by Zhang et al.’s successful implementation in scheduling tasks. They utilized NSGA-III to achieve a balance between carbon emissions, cost, and completion time, demonstrating the algorithm’s applicability in real-world situations [49]. He et al. [50] developed a mathematical model to address the Rush Order Insertion Rescheduling Problem within a Hybrid Flow Shop setting. By applying the NSGA-III algorithm, they effectively orchestrated job sequences and allocated machines. Their goal was to cut down on both processing and transportation times and to align initial scheduling with adaptive rescheduling, accounting for unexpected disruptions. This approach is indicative of their comprehensive effort to optimize workflow efficiency and flexibility in a dynamic manufacturing environment.

In summary, while traditional optimization tools and methods remain pivotal in site selection and resource allocation, the emergence of meta-heuristic algorithms has added a layer of flexibility and efficiency, especially for more complex, large-scale problems. These modern approaches continue to gain traction for their ability to deliver satisfactory outcomes efficiently, balancing multiple objectives in diverse real-world scenarios.

3  Methodology

3.1 Problem Formulation

As outlined in the introduction, this study conducts a comprehensive analysis of a specialized dispatching system used for corrective maintenance in a working factory. Within this system, parameters such as the number and layout of machines, the number of operators, their expertise levels, and the count of maintenance stations are predetermined and clearly defined. The system springs into action upon machine failure, promptly assigning a suitable operator—who is ready, skilled in specific machine maintenance, and available—to the repair task. In cases where all eligible operators are already engaged in other tasks, the system selects the operator capable of completing the current maintenance job in the shortest time. After completing the repair, this operator will return to the maintenance station and then be assigned to the new task at hand. The path taken by the operator from their maintenance station to the faulty machine is a key factor in determining the system’s response time, which is a crucial performance indicator being assessed. Fundamental to our study are the assumptions of an immediate alert mechanism for machine malfunctions and a swift operator response following a first-come, first-served protocol. Additionally, we assume uniform walking speeds for all operators, underscoring the importance of strategically minimizing the distance between machines and maintenance stations to enhance response efficiency.

The complexity of the dispatching landscape is underscored by the intricate balance between human resources and response time. Increasing the workforce can lead to faster repair times but also results in higher operational labor expenses. Conversely, a leaner team, while cost-effective, may inadvertently prolong machine downtime, negatively impacting overall productivity. This study dives into these operational intricacies, aiming to unveil a balanced relationship between workforce size, response times, and labor costs. The system’s design ensures minimal operational interruptions, reallocating the nearest-to-completion operator to a new task when all suitable operators are occupied. We aim to define a balanced operational model that combines these dynamic elements to create a cost-effective, efficient system. By examining the allocation of operators, machine locations, and maintenance station placements in detail, we strive to create a machine maintenance model that offers quick response times without excessive labor costs.

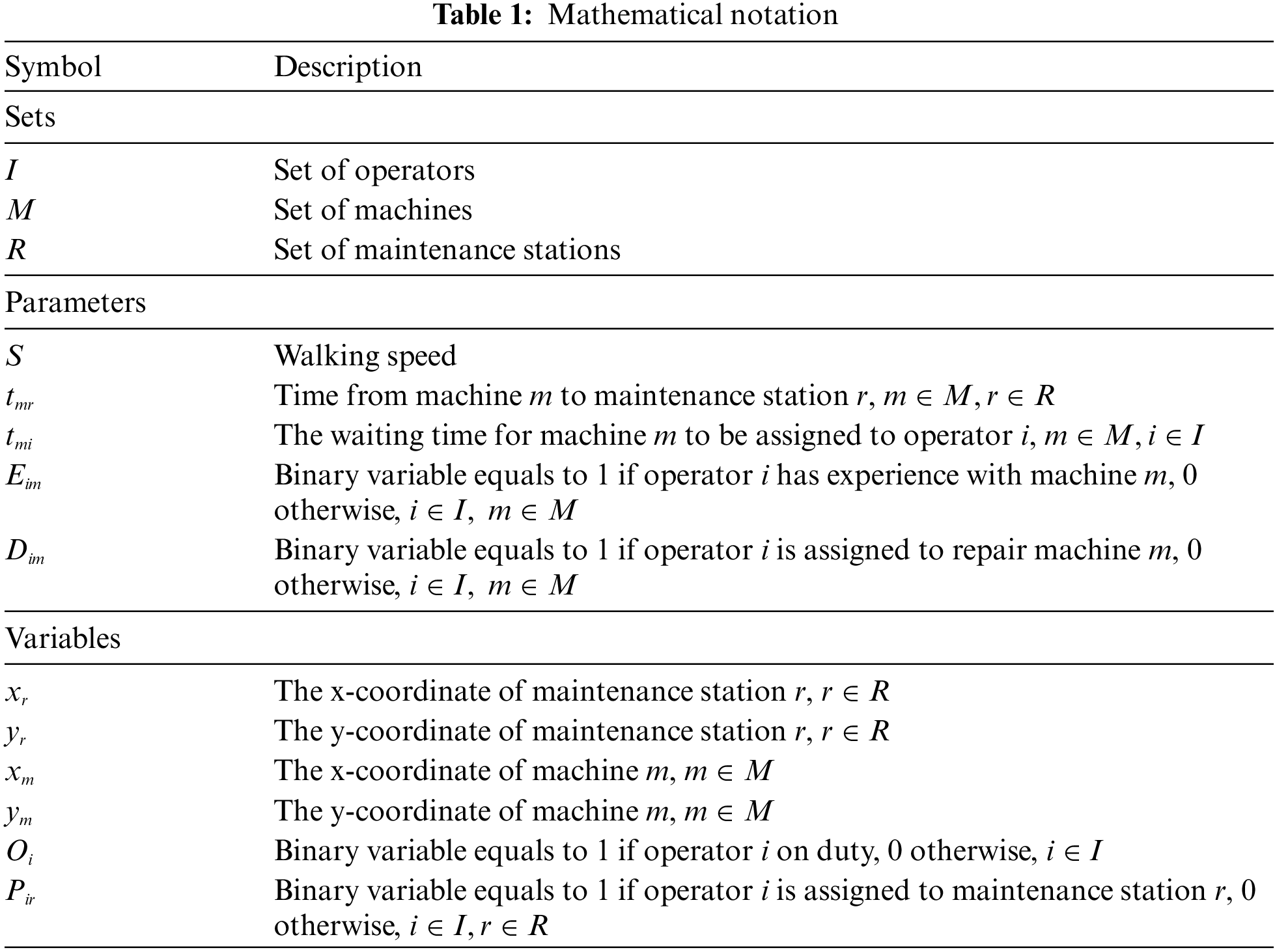
3.1.1 Definition of Variables and Parameters

This section outlines the essential variables and parameters that underpin our examination of the machine maintenance dispatching system.

Variables Description:

•   Round-Trip Time (tmr): This metric measures the complete duration needed for an operator to travel from maintenance station r to machine m and return. The calculation uses the Manhattan Distance and a fixed walking speed (s), as expressed in Eq. (1).

tmr=Manhattandistance(m,r)speed(s)(1)

•   Maintenance Station Location: The placement of a maintenance station should be optimized for accessibility to each machine. The location of a maintenance station should be constrained horizontally between the minimum and maximum x-coordinates as outlined in Eq. (2). and vertically between the minimum and maximum y-coordinates of the machines as defined in Eq. (3).

xm,min≤xr≤xm,max(2)

ym,min≤yr≤ym,max(3)

•   Waiting Time (tmi): This denotes the time machine m awaits the availability of operator i. It is set to zero if the operator is immediately available or extends according to the current repair and travel time if the operator is already engaged.

•   Operator’s Duty Status (Oi): A binary variable where 1 indicates that operator iis actively on duty, while 0 means the operator is off duty.

•   Station Assignment (Pir): A binary variable determining whether operator i is assigned to be waiting for corrective job in maintenance station r.

•   Expertise Level (Eim): Reflects operator i’s skill level regarding machine m, with 1 indicating experienced and 0 indicating less experienced.

•   Maintenance Assignment (Dim): A binary variable indicating whether operator i is tasked with maintaining machine m, with a value of 1 signifying an assignment and 0 indicating no assignment.

Table 1 presents the symbolic definitions of sets, parameters, and variables employed in the formulation.

3.1.2 Mathematical Formulation

This section presents a comprehensive mathematical model formulated to optimize the balance between immediate maintenance requirements and cost-effectiveness. The model integrates a range of sets, parameters, and variables. This is mathematically expressed as:

minimize∑r∈R⁡∑m∈M⁡∑i∈I⁡(tmr×Pir×Dim+tmi×Dim)(4)

minimize∑i∈I⁡Oi(5)

∑i∈I⁡Pir×Oi>0∀r(6)

|I|−|R|>∑i∈I⁡Pir×Oi∀r(7)

∑i∈I⁡Eim×Oi>0∀m(8)

∑m∈M⁡Dim≤Oi∀i(9)

Dim×Oi≤Eim∀i,m(10)

Dim×Oi×tmi≤tmimin∀i,m(11)

Oi,Dim,Eim,Pir∈{0,1}(12)

Eq. (4) delineates the objective function designed to minimize the total response time, encompassing both the walking time of operators and the waiting time of machines for maintenance. The objective function’s first term is dedicated to the travel time component of the response time, applicable only when both Pir and Dim are set to 1. This situation signifies that the operator is allocated to a particular station and is also assigned to a specific machine, thus measuring the time required for the operator to travel to the machine in need of maintenance. The second term of the function captures the waiting time component, calculating the duration a machine waits for maintenance to commence, which is considered only when an operator is specifically assigned to that machine.

Eq. (5) in the model is a key objective function aimed at minimizing the number of operators involved in maintenance tasks. It complements Eq. (4), which focuses on reducing response times and increasing service efficiency by minimizing machine downtime. Together, these equations create a harmonious strategy: Eq. (4) enhances operational efficiency, while Eq. (5) optimizes labor allocation to improve cost-effectiveness. By reducing the active maintenance workforce, Eq. (5) is instrumental in controlling and potentially lowering operational labor costs, ensuring an economically balanced maintenance dispatch system.

To ensure effective system assignment and operational efficiency, several constraints are meticulously applied. Constraints (6) and (7) are established to guarantee that each maintenance station is equipped with at least one operator on standby, ready to respond to maintenance needs. Constraint (8) is imposed to ensure that for every machine requiring maintenance, there is at least one experienced operator available for the task. Further, Constraint (9) ensures that any operator assigned to a maintenance job is currently on duty. Constraint (10) mandates that the assigned operator possesses the requisite experience for the specific maintenance task. Constraint (11) is focused on ensuring that the operator assigned is the one who can become available in the shortest amount of time among all operators, thus optimizing the response time. Finally, Constraint (12) introduces a binary variable into the mathematical framework of the model, enhancing its precision and adaptability in various operational scenarios.

3.1.3 Framework for Optimization

The presented model focuses on enhancing machine maintenance by considering various objectives. First and foremost, it evaluates the competency of operators and the strategic placement of machines, emphasizing the value of both human skills and equipment location in the optimization journey, as depicted in Fig. 1. Subsequently, the system pinpoints optimal locations for maintenance and assesses the positioning of operators and their current tasks. To map out potential solutions, the system uses techniques like generating chromosomes and applying crossover and mutation processes. It then calculates the walking time for each solution to assess its practicality. With this data, the model evaluates the viability of each strategy, estimating the necessary operator count. The Non-Dominated Sorting Genetic Algorithm III (NSGA III) method is employed to refine and select the most effective solutions. In conclusion, the system checks against a “Stop” point to determine if certain benchmarks are achieved. If these criteria are met, the optimal solution is selected. Otherwise, the optimization process persists, leveraging chromosomes, crossover, and mutation techniques until the best possible strategy emerges.

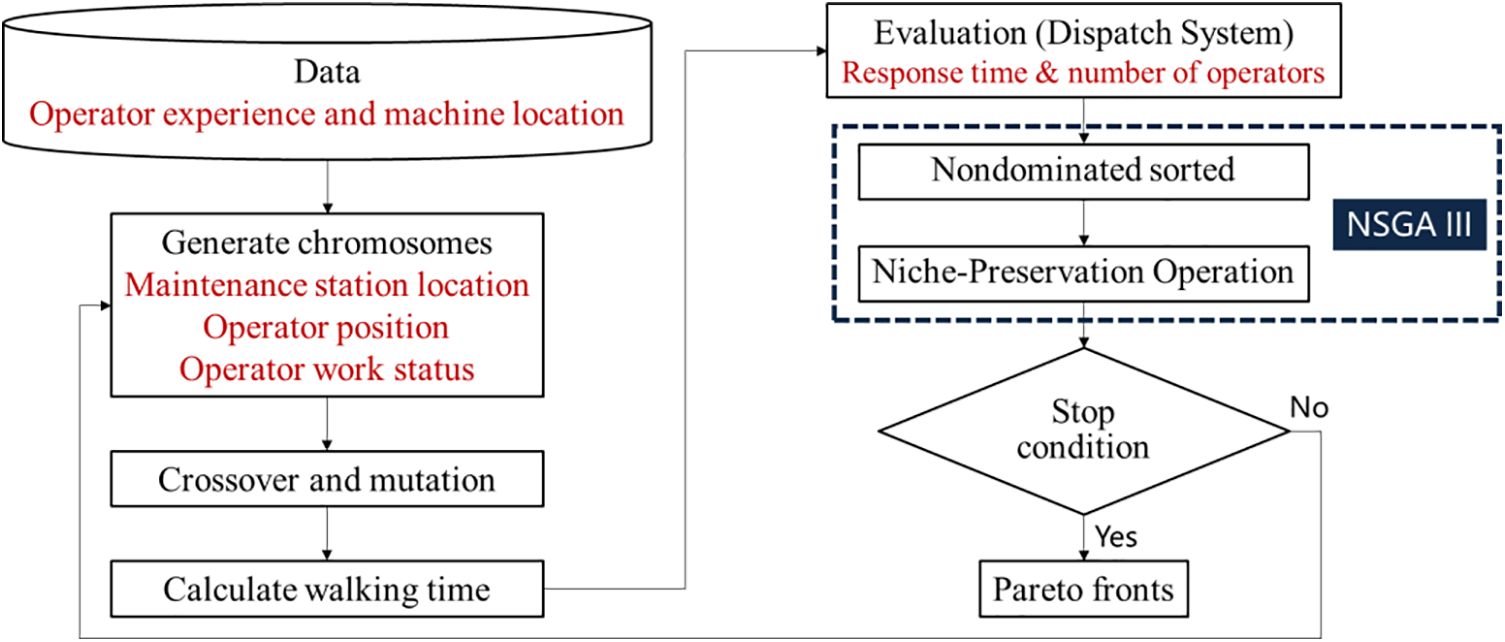
Figure 1: Optimization framework of applying NSGA III on minimizing response time and labor cost

3.2 Designing Multi Objective Genetic Algorithm

In this research, we have innovatively adapted the Non-Dominated Sorting Genetic Algorithm III (NSGA-III), introduced by Deb et al. [51], to create a method we call NSGA III + Dispatch. This adaptation is specifically designed to tackle the unique challenges of multi-faceted maintenance optimization problems, such as the simultaneous optimization of Locating Maintenance Stations and Operator Dispatching. Traditional genetic algorithms, while adept at single-objective optimization, often struggle with the complexities of such multi-objective scenarios.

NSGA-III stands out in its ability to handle multiple objectives effectively through a novel sorting mechanism known as non-dominated sorting. This technique ranks solutions based on their performance across all objectives, categorizing them into different levels of dominance. As a result, NSGA-III identifies a diverse set of optimal solutions, representing various trade-offs among the objectives. This feature is further enhanced by the algorithm’s reference point-based approach for maintaining diversity in the solution set, particularly beneficial in problems with several objectives. It ensures that solutions are distributed across the entire spectrum of potential outcomes, providing decision-makers with a comprehensive understanding of the trade-offs involved, such as the balance between maintenance station location and operator dispatch efficiency.

NSGA-III, renowned for its adaptability to the multifaceted nature of multi-objective problems, stands out for its ability to not only identify optimal solutions but also to present a spectrum of alternatives, highlighting the potential trade-offs. This feature is vital for making well-informed decisions, particularly in situations where optimizing one objective could require concessions in another. As a result, NSGA-III, and by extension, our customized version, NSGA III + Dispatch, are exceptionally suited for tackling the complex optimization challenges found in maintenance operations and related fields.

To effectively apply this approach to our multi-objective optimization model, which focuses on locating maintenance stations and operator dispatching, we have meticulously designed the coding, crossover, and mutation operators of the NSGA III + Dispatch algorithm. The upcoming section details this development. These components are specifically crafted to meet the unique demands and complexities inherent in this particular optimization task.

3.2.1 Chromosome Generation and Initialization

Chromosomes, each embedded with multiple genes, form the population, acting as individual candidate solutions in this study. The chromosome design in this study is illustrated in Fig. 2. Each chromosome is structured with four integral components: The x-coordinate, y-coordinate of the maintenance station on a given graph, the on-duty status of the operator, and the operator’s assigned position.

Figure 2: Chromosome composition

The chromosome’s first and second segments, equal in length, represent the x and y coordinates of maintenance stations, respectively in Fig. 3. Their length corresponds to the total number of stations, aiding in station position optimization and walking time conversion. This is exemplified by explicit coordinate details: Maintenance station 1 at (142, 193), station 2 at (290, 721), and so on, up to station 6 at (367, 467), providing a clear visual representation of station locations. The chromosome’s third segment represents operators’ working status, encoded as 0 for off-duty and 1 for on-duty. Correspondingly, the fourth segment assigns each on-duty operator to a maintenance station, denoting –1 for those off-duty depicted in Fig. 4. This system ensures that each maintenance station’s positional assignment aligns with the operators’ availability and status.

Figure 3: Examples of chromosome representation of maintenance station location

Figure 4: Examples of chromosome structure of operator duty status and position

Fig. 5 exemplifies a complete chromosome configuration, emphasizing mandatory conditions: Each machine should have at least one skilled operator on duty, and operators must be present at every maintenance station. In cases of absence, random assignment or reallocation from well-staffed stations ensures no station is left unmanned. This systematic chromosome generation and initialization provide a robust foundation for intricate computations, aiming for optimal operator allocation and maintenance station positioning while adhering to the constraints of operators’ availability and expertise.

Figure 5: One example of a complete chromosome

3.2.2 Crossover and Mutation

The algorithm begins with creating an initial set of randomly generated chromosomes, establishing a parental population. Each chromosome is then assessed for suitability in crossover and mutation to generate offspring. These chromosomes are comprised of four distinct segments, each with unique characteristics that influence the sites for crossover and mutation.

Crossover: To initiate crossover, first establish the crossover rate Pcross. Then, generate a random probability value; if it is below the crossover rate, proceed with crossover; if not, crossover is bypassed. This process entails swapping gene segments between chromosomes to create a new generation of solutions. The methodology includes several structured steps:

1.    The process begins by assigning a random probability value to the initial chromosome. If this value falls below the crossover rate, the procedure advances to the next step; otherwise, the algorithm proceeds to evaluate the next chromosome and repeat step 1.

2.    A distinct parent chromosome is selected for crossover, distinct from the current chromosome and not previously chosen. For example, as depicted in Fig. 6, the first chromosome is paired with the seventh for crossover.

3.    Within each chromosome segment, two random points are chosen: One in the first half and another beyond the first point. This selection creates a specific segment for crossover. In cases where chromosome parts are interrelated, such as the third and fourth parts, the same segment is used for both. Fig. 6 illustrates the genes within the orange lines as those involved in the crossover.

4.    The crossover is then performed on the chromosomes identified in step 2, with the resulting chromosomes displayed in Fig. 7.

5.    After-crossover, any chromosome not meeting certain criteria undergoes modification. For instance, if a maintenance station lacks assigned operators, as shown in Fig. 8, an operator not currently on duty is randomly chosen, with their duty status altered and assigned accordingly.

6.    Continue repeating steps one through five until every chromosome has been evaluated.

Mutation: The mutation process, integral to the genetic algorithm, commences with establishing a mutation rate (pmtate). Each chromosome is then assessed individually; if a randomly generated probability value is less than Pmtate, mutation occurs. The method involves the following streamlined steps:

1.    Beginning with the first chromosome, mutation is triggered if the probability value is less than the mutation rate. If not, the evaluation moves to the next chromosome.

2.    Each chromosome part undergoes a segment selection process, with a focus on two distinct points before and after the midpoint. The synergy between the third and fourth parts necessitates a shared mutation segment, illustrated in Fig. 9.

3.    The identified segment undergoes mutation. Specific alteration protocols are assigned to different parts of the chromosome, ensuring constraint adherence and variability introduction. The mutation’s outcome is displayed in Fig. 10.

4.    Following mutation, any chromosomes not meeting the constraints are adjusted to ensure compliance.

5.    Continue repeating steps one through four until all chromosomes are thoroughly examined.

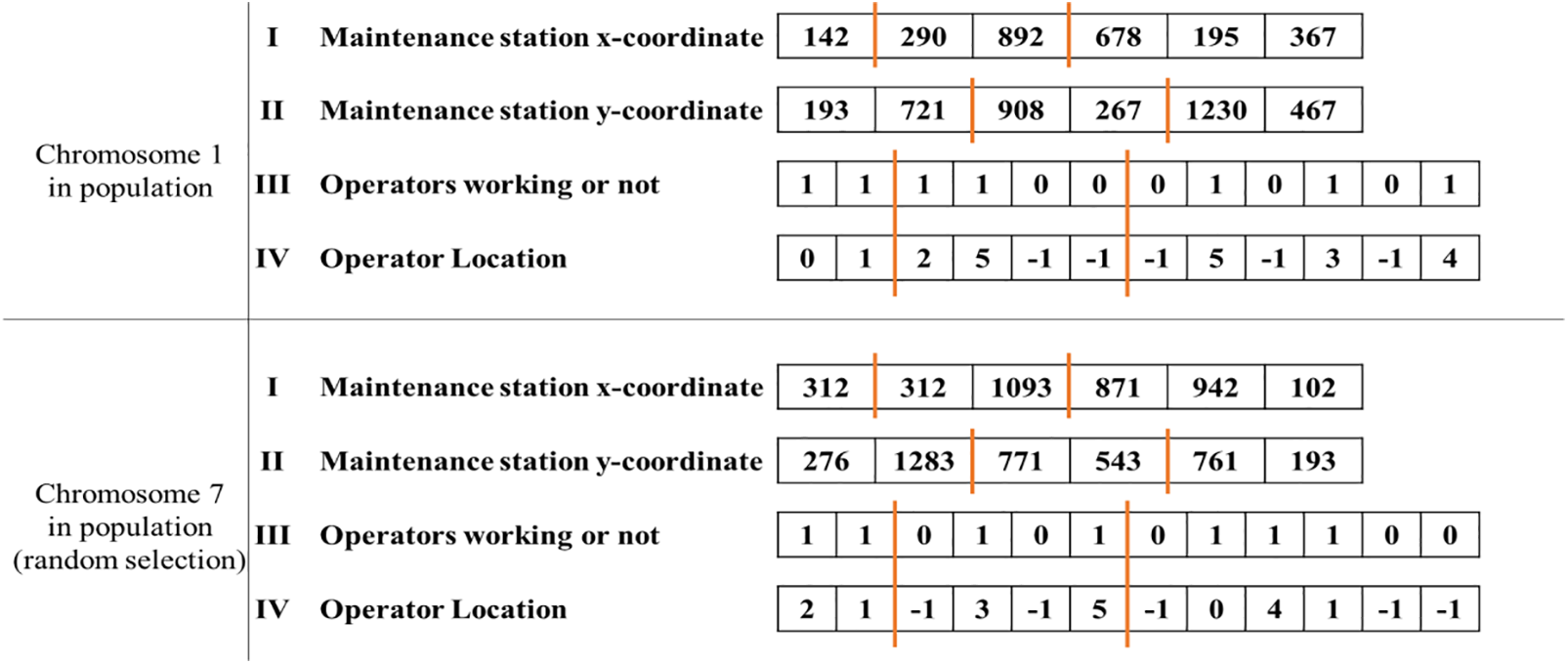
Figure 6: Example of chromosome crossover processes

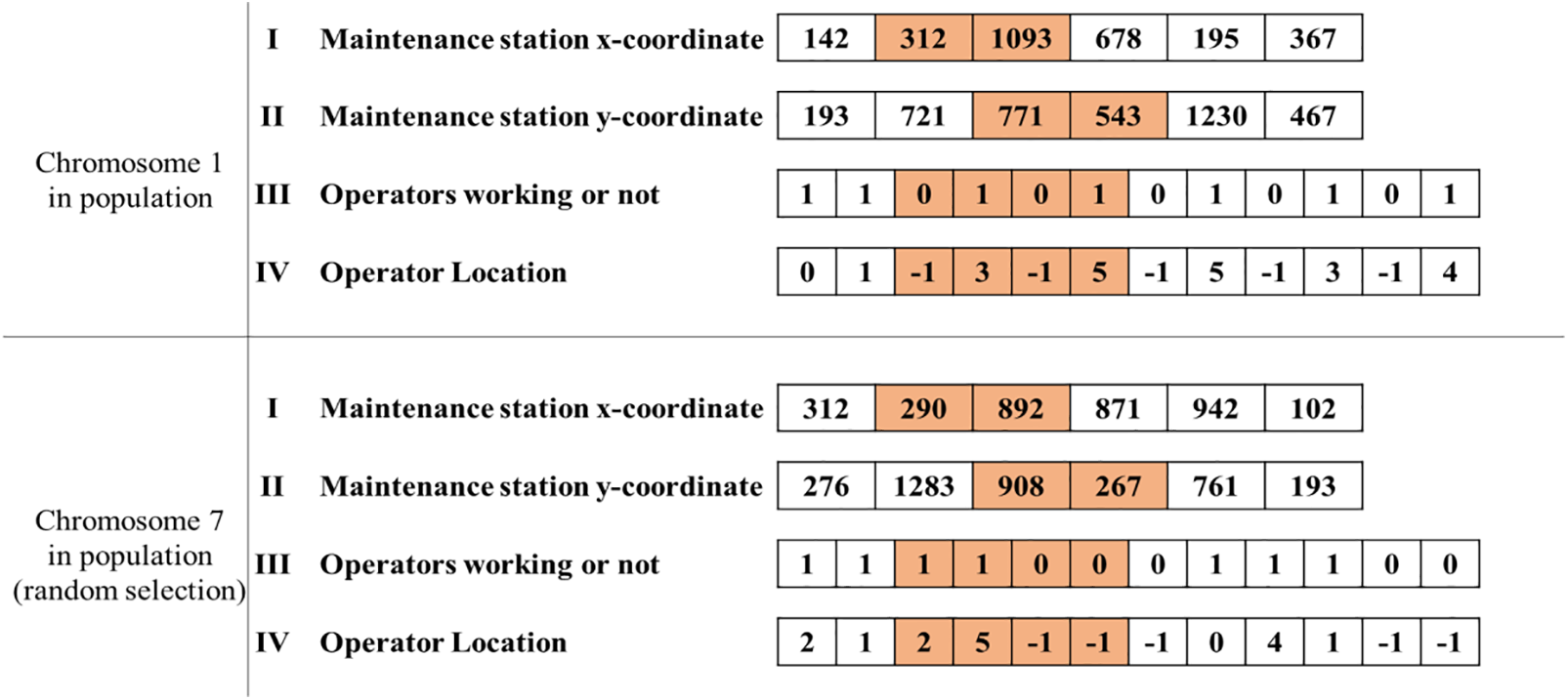
Figure 7: Example of the chromosome after crossover

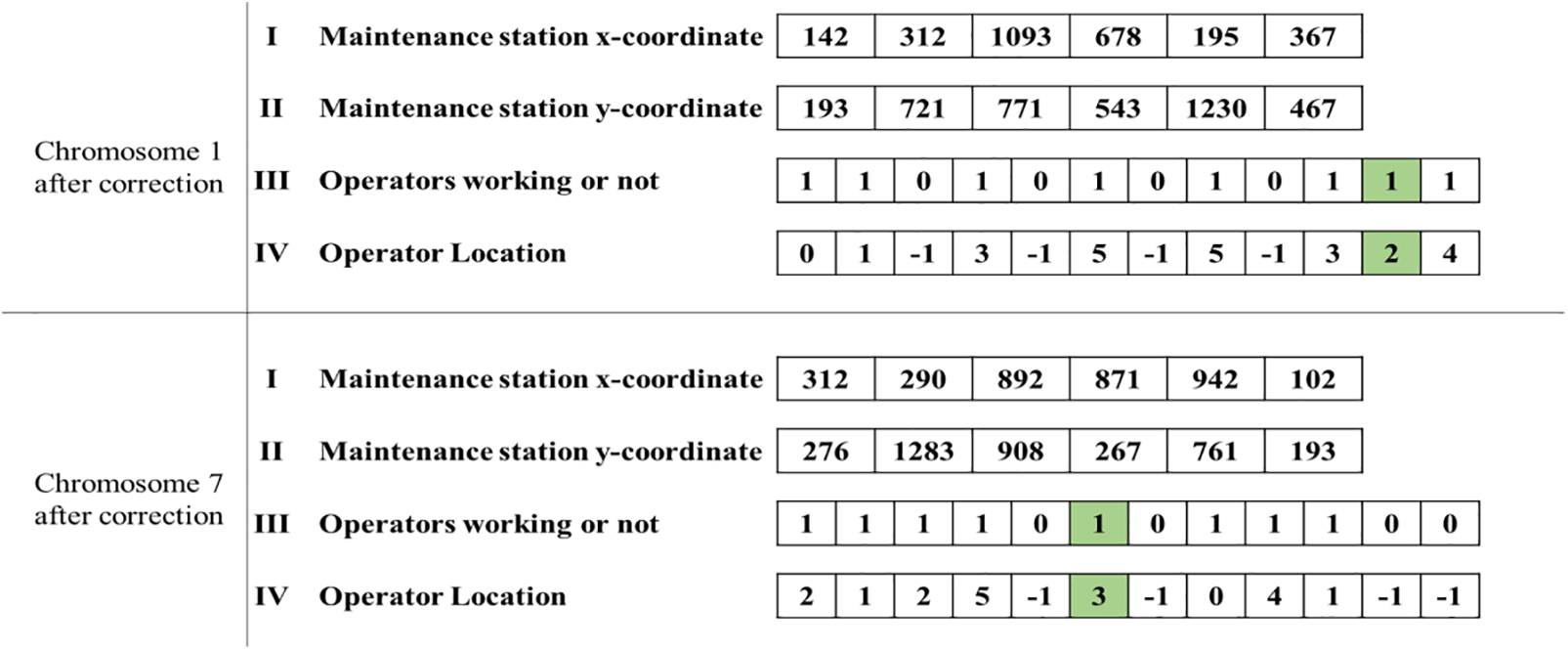
Figure 8: Example of chromosome correction

Figure 9: Chromosome mutation processes

Figure 10: Example of post-mutation chromosome

This concise approach ensures an efficient and effective mutation process, vital for generating diverse and optimized solutions in the genetic algorithm framework.

4  Experiments and Results

This section provides the details conducted to validate the proposed method, utilizing various failure frequencies of production line equipment and differing numbers of operators. Section 4.1 delineates the data required for the simulations and the preprocessing steps undertaken. In Section 4.2, the design of each simulation scenario is elucidated, along with a discussion on the prevailing methodology in the factory. Section 4.3 engages in a comparative analysis between the proposed method and existing factory methods, aiming for validation. The findings from the simulations are concisely summarized in Section 4.4.

4.1 Data Description and Preprocessing

This section outlines the data preparation and analysis utilized in the optimization of machine maintenance dispatch systems. Data was gathered from one of electronic equipment manufacturers in Taiwan, as illustrated in Fig. 11, which included machine coordinates, worker skills, and device malfunction records.

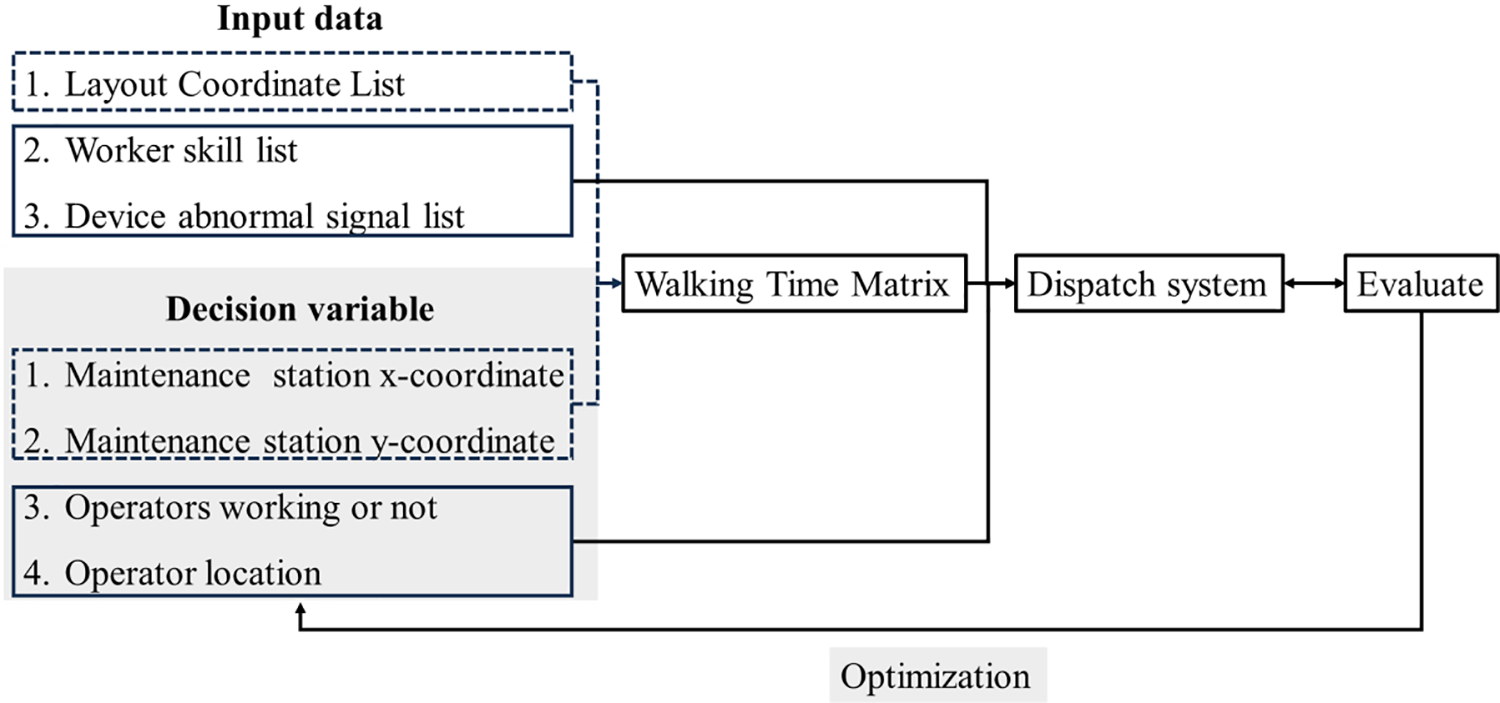
Figure 11: The process of optimizing configurations

The key task was to merge these data sets to create a matrix that captures the walking time between various machines and maintenance stations, a critical factor in optimizing the dispatch system’s efficiency using the NSGA III + Dispatch. The data consolidation involved linking the machine’s spatial coordinates with worker competencies to form a database that facilitates the assignment of maintenance tasks. Through preprocessing steps, including the translation of project and device information into a standard “Device ID” format, the system aligns worker skills with the equipment needs, simplifying the complexity of data into manageable and actionable insights.

The collected data encompasses a detailed account of each machine’s placement and the skill levels of individual workers. This data is meticulously organized and analyzed to assign maintenance tasks most effectively. The system prioritizes tasks based on the critical nature of equipment malfunctions and the availability of appropriately skilled workers. By optimizing task allocation in this manner, the approach facilitates quick and competent responses to equipment issues, thereby reducing idle time and enhancing overall productivity.

4.2 Simulation Rule and Comparison Method

4.2.1 Simulation Rule

This subsection presents four simulation scenarios designed to validate the methodology proposed in this research. A preliminary task involved the definition of machine malfunction frequencies and durations, which were categorized as either high or low based on historical data analyses.

The collected data was evaluated to quantify the daily frequency and standard deviation of machine abnormalities. A statistical threshold, determined by the mean value adjusted by three standard deviations, distinguished high and low-frequency abnormalities. Specifically, high-frequency was defined as the mean plus three standard deviations, and low-frequency as the mean minus three standard deviations, with a minimum set at one to avoid negative values. Machine malfunction timing is then ascertained from the daily malfunction count, segmenting the workday into equal intervals correlating with the number of malfunctions. A malfunction is randomly assigned within each interval, ensuring a distributed occurrence of malfunctions throughout the day while preserving their stochastic nature.

Following the establishment of criteria for identifying high and low-frequency failures and their respective timestamps, we delineated four distinct simulation scenarios. These scenarios are crafted to rigorously evaluate the robustness and adaptability of our proposed methodological framework across varied operational contexts.

1.    Low-Frequency Failures across All Machines: This scenario encapsulates a condition where all operational machines register low-frequency failures. Utilizing the foundational Worker Skill List, we engaged in a comparative analysis, juxtaposing the outcomes derived from traditional factory protocols against those emerging from our novel research-based approach.

2.    High-Frequency Failures across All Machines: Under this scenario, all machines are characterized by high-frequency failure occurrences. The analysis was augmented by an extended Worker Skill List, enhancing the pool of available operators. This expanded dataset facilitated a nuanced comparison between traditional and proposed methodologies, enabling a comprehensive evaluation of their respective efficacies.

3.    Selective High-Frequency Failures (A): In this scenario a subset of machines, specifically device1 and device2, exhibit high-frequency failures while others maintain a low frequency. This selective occurrence facilitates a targeted comparative analysis, illuminating the specific advantages conferred by our proposed method from this research in this specific situation.

4.    Selective High-Frequency Failures (B): Mirroring the third scenario, this context again features selective high-frequency failures, albeit among a different set of machines (device5 to device13). This variation enabled an additional level of detailed examination, assessing the subtle advantages of the suggested approach within this unique operational setting. Table 2 provides a detailed overview of these four simulation scenarios, offering insights into the respective failure frequencies and operator allocations. To mitigate biases and ensure a comprehensive evaluation, three distinct datasets are generated for each scenario, accounting for the inherent randomness associated with machine failures.

4.2.2 Comparison Method

The evaluation of the proposed solution’s validity was conducted through a comparative analysis with the factory’s current methodology for allocating maintenance stations and operators, illustrated in Fig. 12. The prevailing technique relies on pre-existing data, devoid of the capacity for real-time adaptability.

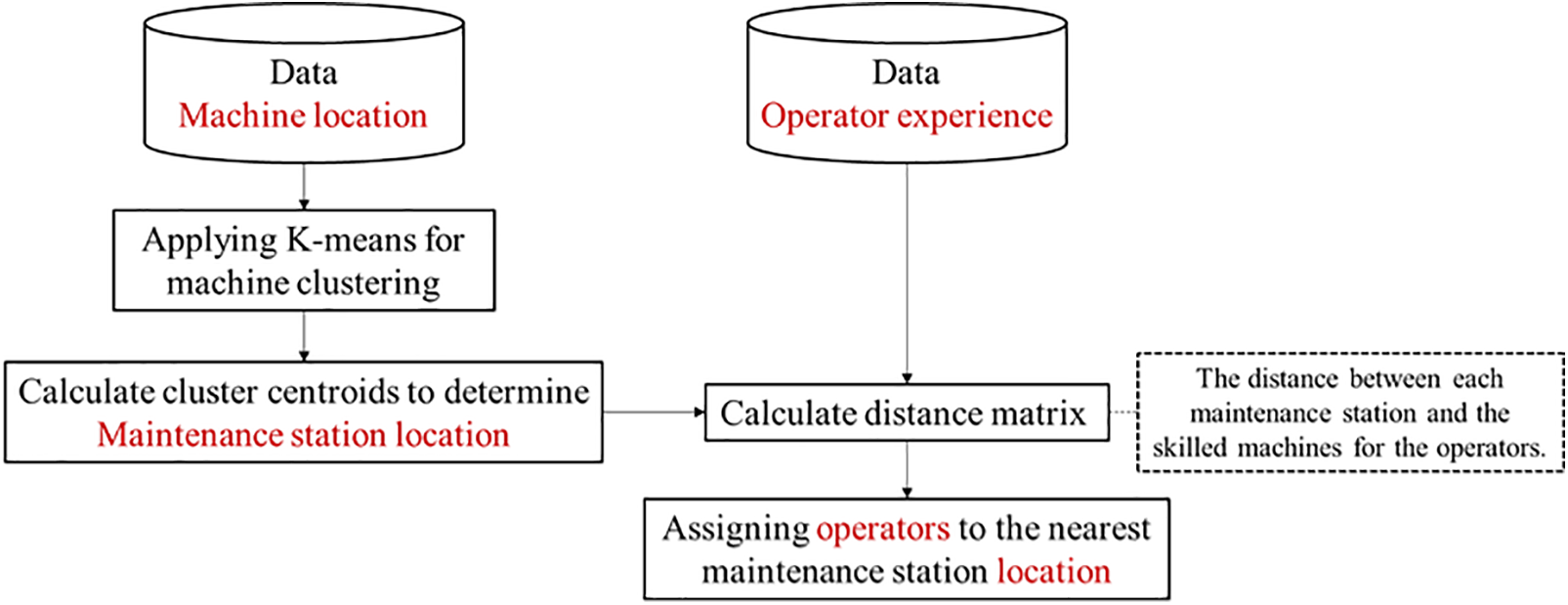
Figure 12: Two-stage process in the existing factory as a benchmark

In the case study of the real-world factory, a two-stage process as a benchmark of this comparison is utilized to ascertain the placements of maintenance stations and operators. A constraint of this approach is the pre-fixed number of maintenance stations, limiting its flexibility. The K-means clustering algorithm is employed to categorize machines of similar types into distinct groups. The central points of these groups, or centroids, are then designated as the locations of the maintenance stations, ensuring an organized distribution aligned with machine types.

Concurrently, an assessment of the operators’ travel time from the maintenance stations to the machines they are skilled at repairing is undertaken. The optimal positions for operators are identified by pinpointing the locations that yield the minimum travel time, facilitating prompt maintenance responses. The proposal in this study is contextualized and assessed against this existing method, spotlighting its potential enhancements in operational adaptability and efficiency.

4.3 Experimental Results

In this section, we present and analyze the results obtained from experiments conducted utilizing the NSGA III + Dispatch algorithm under various scenarios. The NSGA III + Dispatch was employed to optimize both the response time and worker assignment. Each experiment was characterized by a distinct set of parameter configurations specific to NSGA III + Dispatch, with the objective of evaluating the algorithm’s effectiveness under these conditions. The detailed information on the parameter configurations employed in each experiment is provided in Table 3. The chosen parameters for the algorithm in the experiments were thoughtfully selected to effectively evaluate the algorithm’s performance. A population size of 100 ensures a diverse range of potential solutions, enhancing the algorithm’s ability to explore various optimization paths. The setting of 30 iterations for stopping, along with a minimum generation of 100 and a maximum of 1000, strikes a balance between computational efficiency and thorough exploration of the solution space. The crossover rate of 1 maximizes the potential for combining solution traits, while the mutation rate of 0.3 introduces variability, preventing premature convergence and encouraging exploration of new areas in the solution space. These settings collectively aim to provide a comprehensive assessment of the algorithm’s capabilities in optimizing response time and worker assignment under different scenarios.

4.3.1 Low-Frequency Failures across All Machines

In this subsection, the results of an experiment where every machine in the facility experiences infrequent anomalies was presented. Using a setup of 62 machines and 12 operators, the framework proposed in our study was applied.

Fig. 13 illustrates that the NSGA III + Dispatch method surpasses the current factory approach in both response time and resource efficiency. The NSGA III + Dispatch yielded two solutions denoted by orange dots (NSGA III + Dispatch) that outperformed the factory’s current method indicated by blue dot (Factory) by delivering shorter response times and better resource utilization. Table 4 presents these results where the optimal NSGA III + Dispatch solution reduces the response time by 23%, from 238 to 183 s. The secondary solution also showed a 16% improvement, with a response time of 200 s. Statistical analysis at a 95% confidence level indicates the proposed method’s response time is significantly shorter than the factory method. While the factory currently assigns 12 operators with only 7 active, the NSGA III + Dispatch suggests using either 6 or 7 fully active operators. Please note that for both methods, none of 62 assigned tasks were delayed. This demonstrates better human resource optimization and potential savings. Notably, the NSGA III + Dispatch configurations had no delays due to staff shortages, highlighting the model’s ability to maintain operational stability and increase efficiency.

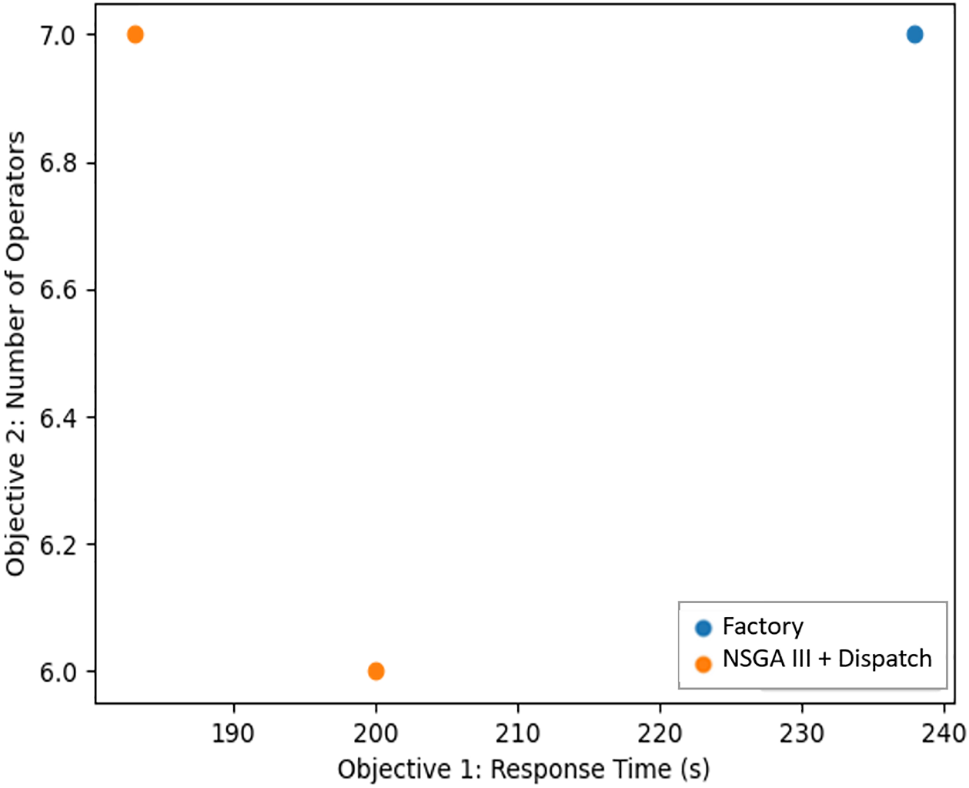
Figure 13: Comparison of low-frequency failures: NSGA III + Dispatch vs. Factory method

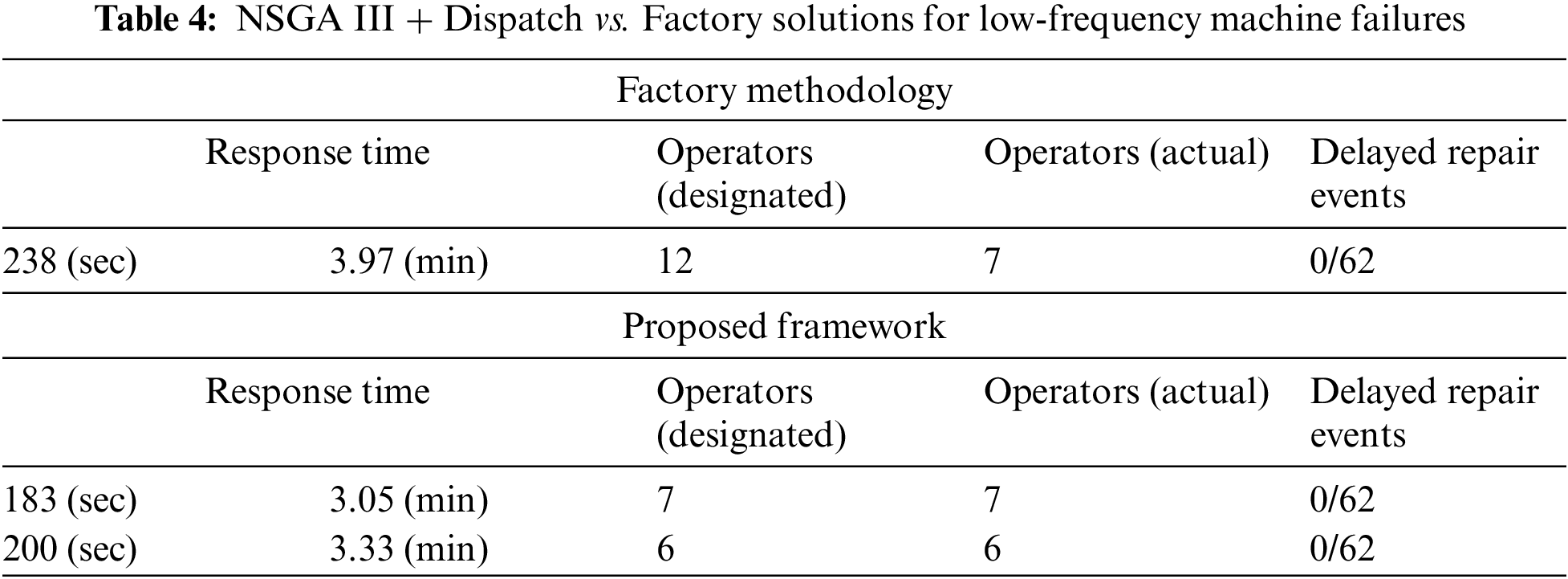
In essence, the NSGA III + Dispatch’s adeptness at managing low-frequency anomalies is manifest. It not only accelerates response times but also refines workforce allocation. This proficiency equips decision-makers with a set of refined options, optimized for both performance and resource allocation, underscoring the proposed method’s practical utility in real-world operational contexts.

4.3.2 High-Frequency Failures across All Machines

In this subsection, an experiment that models a high-frequency failure scenario involving all machines in a factory was presented. The NSGA III + Dispatch algorithm, applied to a setup of 62 machines and 12 operators, demonstrated superior performance compared to the current factory approach, as illustrated in Fig. 14. It delivered enhanced efficiency in response time and workforce utilization, though further filtration and analysis are needed to fully understand the potential implications of the solutions presented.

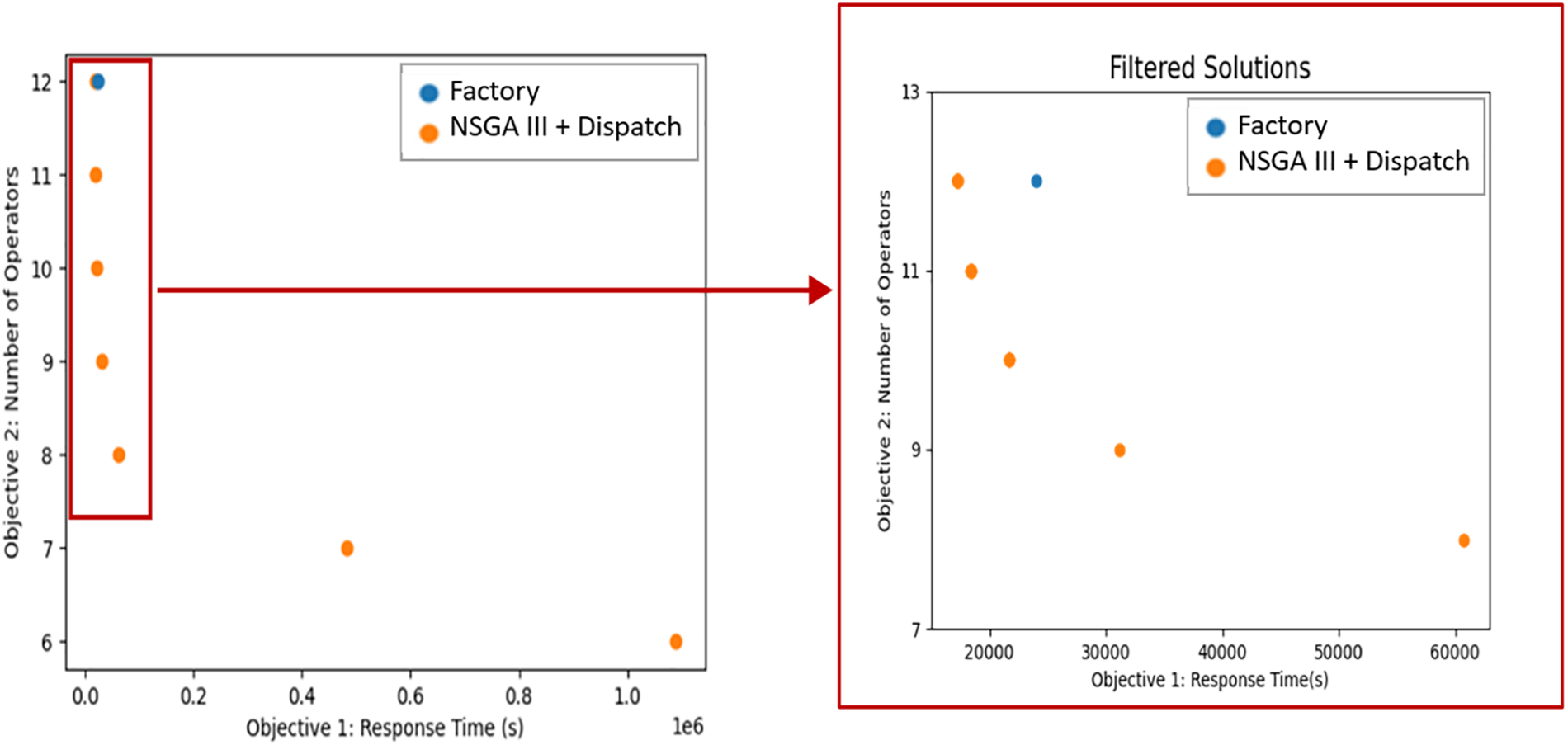
Figure 14: High-frequency failures: NSGA III + Dispatch vs. Factory solutions comparison

Table 5 reveals that with the same 12-operator configuration, the proposed NSGA-III model notably improved response time, indicating a 28.23% efficiency enhancement. Statistical analysis at a 95% confidence level indicates the proposed method’s response time is significantly shorter than the factory method. Additionally, a comparable efficiency was achieved with only 10 operators, showcasing the model’s capability to optimize workforce allocation while maintaining operational effectiveness.

However, in configurations with fewer number of operators, response times were excessively prolonged, making them impractical for managing high-frequency failures as shown in the Fig. 15. A marked reduction in response time was noted with an increase to 8 operators, with further reductions as the operator count increased to 12. Also, the delayed tasks increase along with fewer number of operators. These findings underline the necessity for enough operators to efficiently manage high-frequency failure scenarios.

Figure 15: Changes in response time and delayed maintenance count

In efforts to explore enhanced efficiency and workforce optimization, an expanded simulation was conducted, doubling the operator count and skills to model heightened workforce availability during peak periods. Fig. 16 and Table 6 present the outcomes of this expansion. Remarkably, the NSGA III + Dispatch model required only 18 operators to achieve a 66.44% efficiency improvement, saving the cost of 6 operators against the current method which needs 24 operators while maintaining operational effectiveness.

Figure 16: NSGA III+ Dispatch vs. Factory-operator number expansion comparison

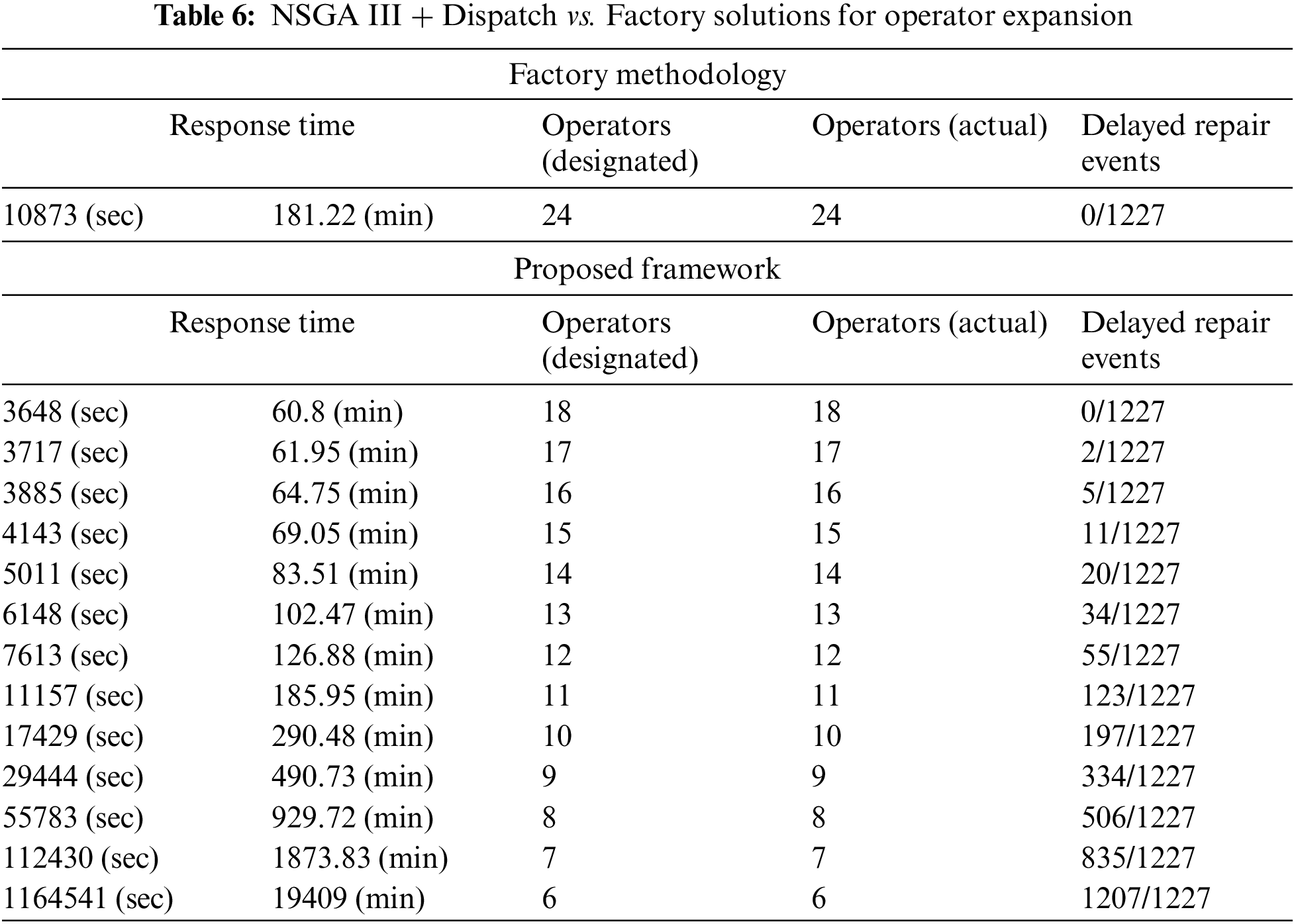
In conclusion, the NSGA III + Dispatch model exhibited marked adaptability and effectiveness in high-frequency failure scenarios. In situations of frequent failures and workforce shortages, the model enhanced response efficiency. Moreover, in scenarios of frequent failures with adequate manpower, it not only bolstered response time efficiency but also offered solutions for significant manpower cost savings, underscoring its comprehensive applicability in varied operational contexts.

4.3.3 Selective High-Frequency Failures (A)

This section outlines an experiment that simulated a specific scenario where two machines, device1 and device2, encountered high-frequency anomalies while the remaining equipment in the factory experienced low-frequency anomalies. The test employed the NSGA III + Dispatch algorithm on a setup of 62 machines and 12 operators, as illustrated in Fig. 17. The results indicate a more efficient response time compared to the factory’s existing methods.

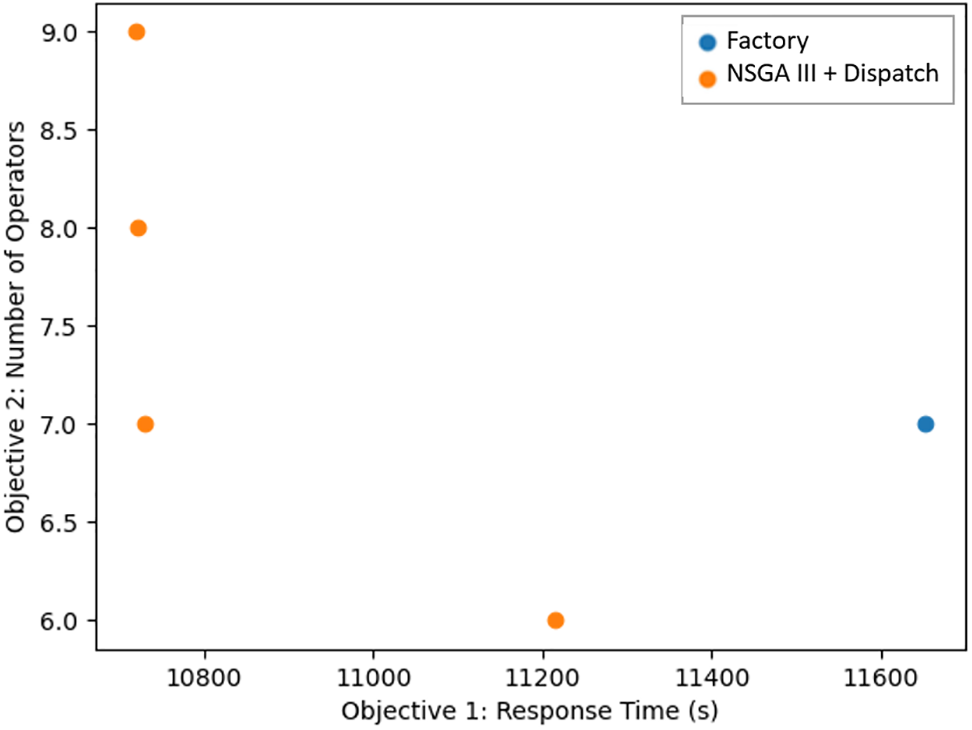
Figure 17: NSGA III + Dispatch vs. Factory—selective high-frequency failures (A)

Table 7 offers a comprehensive comparison between the factory’s current method and the NSGA III + Dispatch framework. Employing the factory’s strategy yields a response time of 11653 s with only 7 active operators. In contrast, the NSGA III + Dispatch model enhances operational efficiency, reducing the response time to 10731 s, a 7.9% improvement, with the same number of operators, here is 7. Statistical analysis at a 95% confidence level indicates the proposed method’s response time is significantly shorter than the factory method. Additionally, the number of delayed repair events is slightly reduced, underscoring the proposed framework’s superior resource utilization.

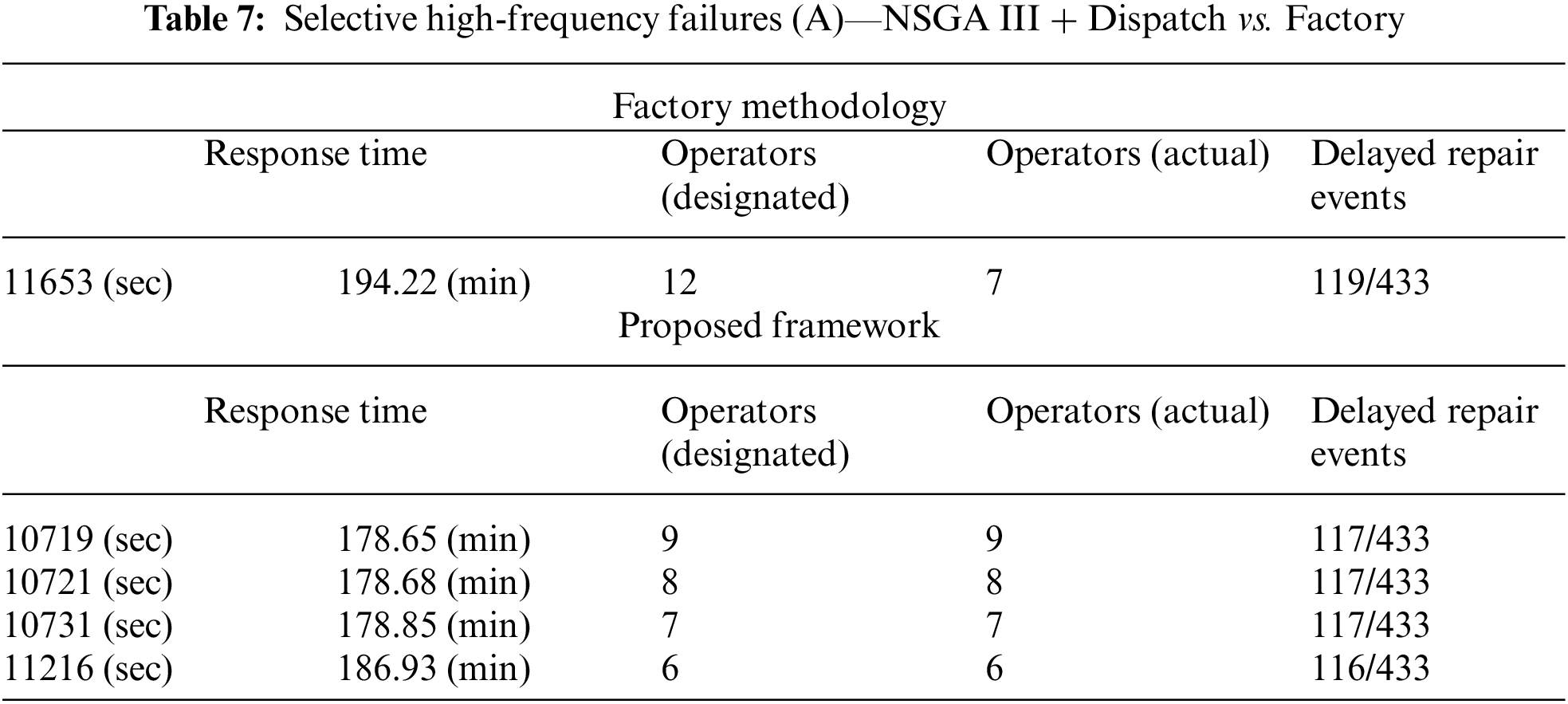
Though the NSGA III + Dispatch model demonstrates enhanced efficiency, practical implementation typically avoids comparing solutions from both the factory and NSGA III + Dispatch methods directly. A more pragmatic approach involves adopting a suitable factory solution informed by the NSGA III + Dispatch-generated solution, warranting further analysis of the latter. In the examined scenario, a total of 443 anomalies were noted, with device1 and device2 accounting for 383, while the remaining devices had only 50 abnormal events. Despite an increased workforce, no additional operators were assigned to these two devices, as all qualified personnel were already deployed. This condition led to diminished marginal utility for each added operator, as illustrated in Table 8.

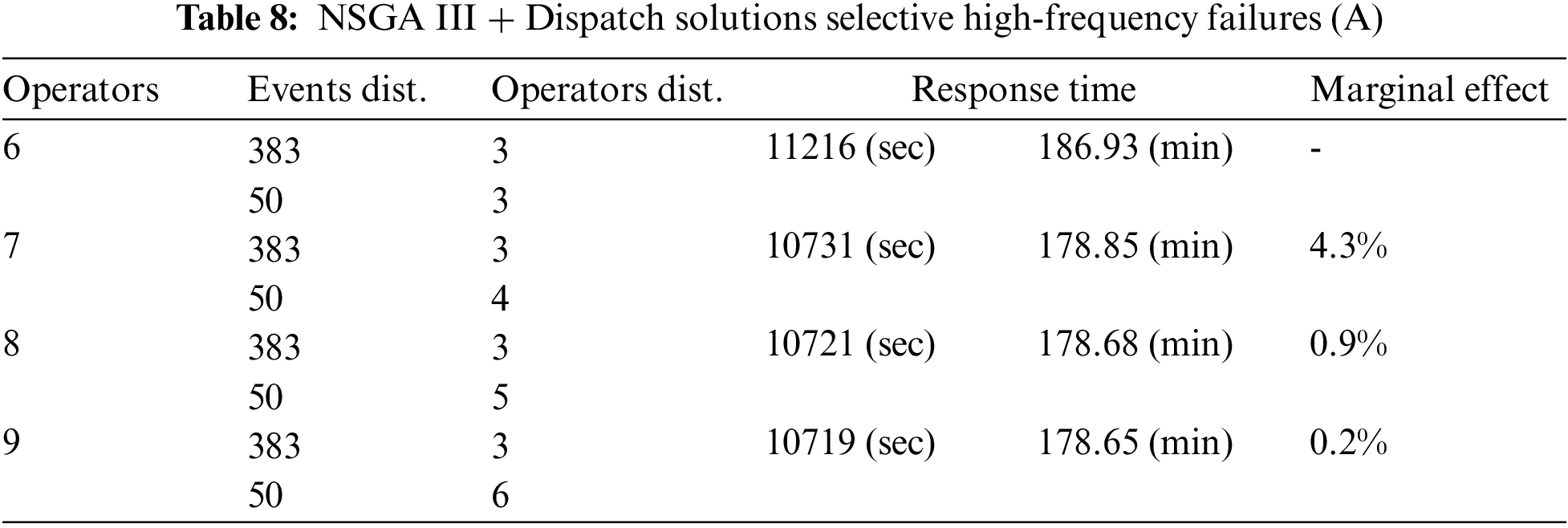
Given the circumstances, a strategic increment in operators skilled in repairing device1 and device2 is advised. This approach is projected to elevate efficiency metrics and enhance the factory’s capacity to address high-frequency anomalies effectively, optimizing both response times and resource allocation.

4.3.4 Selective High-Frequency Failures (B)

This section discusses an experiment where machines labelled device5 to device13 frequently malfunctioned, while the rest experienced fewer maintenance issues. The proposed framework was applied to a setup of 62 machines and 12 operators, generating five different solutions depicted in Fig. 18. The results highlighted varied efficiency levels, dependent on the number of operators deployed.

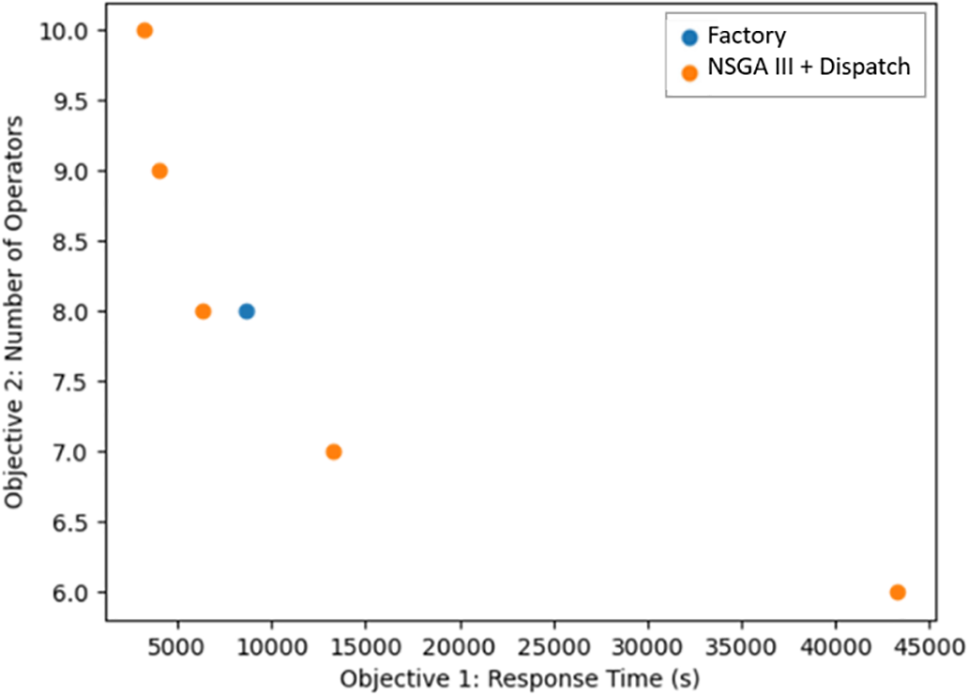
Figure 18: NSGA III + Dispatch vs. Factory—selective high-frequency failures (B)

Fig. 18 illustrates that with 8 operators, our proposed method outperformed the current factory method in response time. For solutions utilizing fewer than 8 operators, the response time was a bit longer, but they offered the benefit of lower manpower costs. Solutions deploying more than 8 operators exhibited reduced response times at increased manpower costs.

Table 9 amplifies these findings. The traditional factory method, utilizing 8 operators, recorded a response time of 8604 s. Our proposed model, with the same number of operators, reduced this time to 6311 s, a saving of over 38 min, and marking a 26.7% improvement in efficiency. This performance elevation also witnessed more delayed repair events, underscoring the enhanced efficiency of our model.

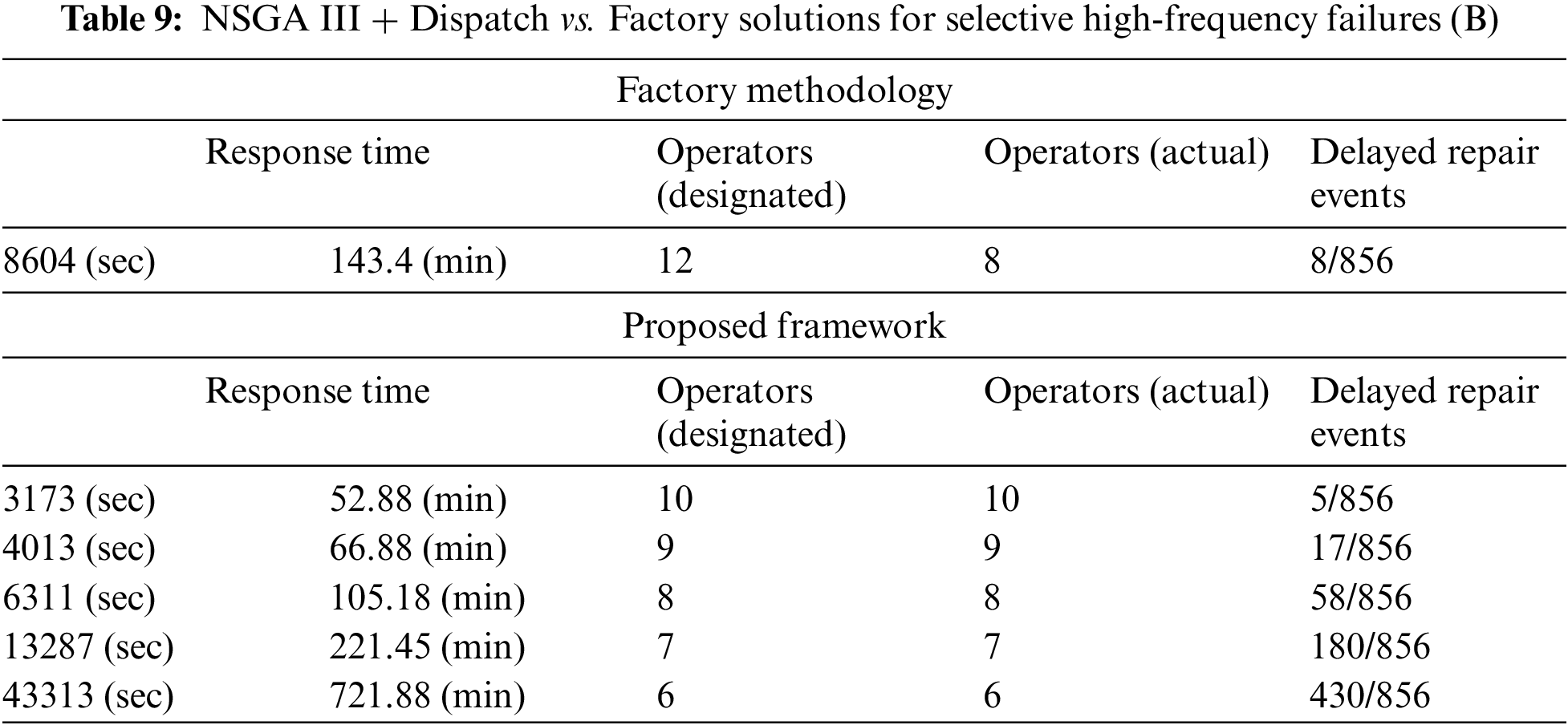
In this scenario, out of 856 recorded abnormal events, a majority (844 incidents) were associated with device5 to device13 while the remaining devices had only 12 incidents. A noteworthy observation was the increased allocation of operators to these devices as the total number of operators increased, an indication of the NSGA III + Dispatch ‘s capability to effectively allocate resources. However, the model maximized the utilization at ten operators, as the remaining two lacked the specific skills to repair these particular devices, as detailed in Table 10.

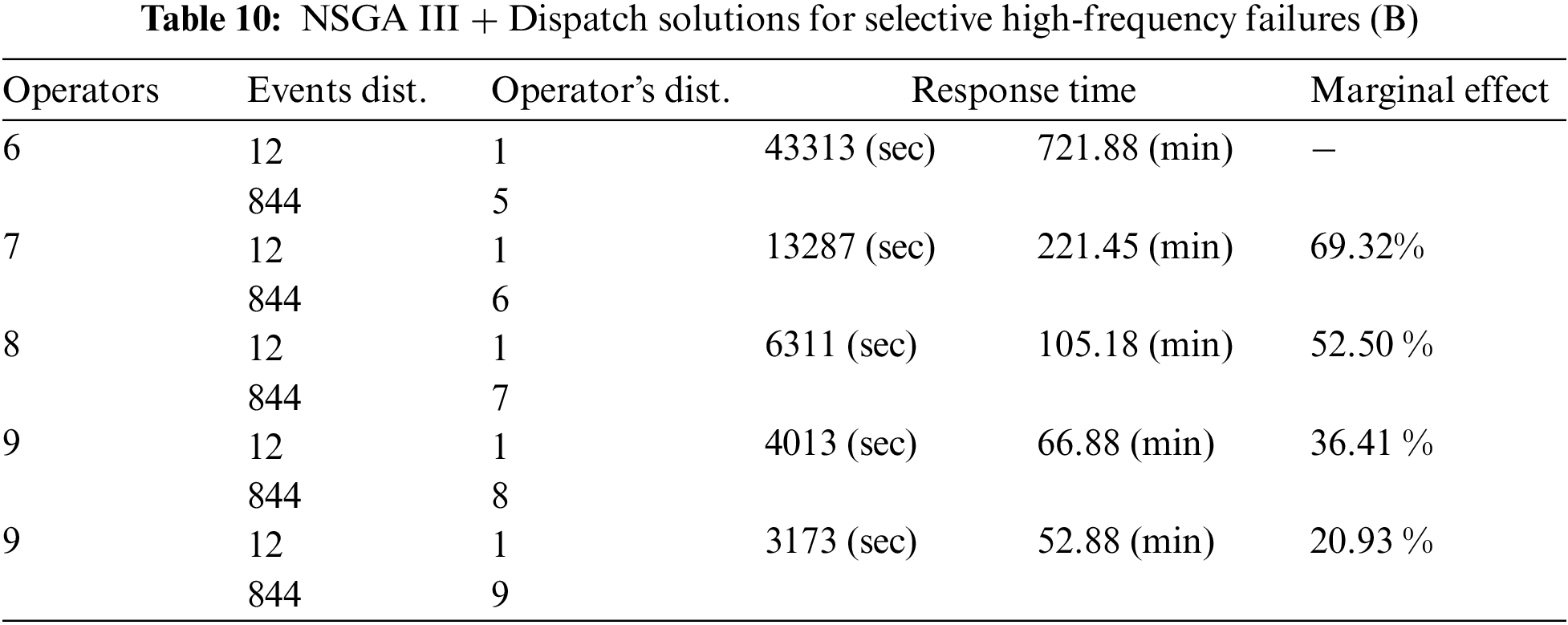
Based on the data, the factory should prioritize training and assigning personnel proficient in repairing devices 5 to 13. Leveraging skilled operators in these contexts can boost maintenance efficiency and address recurring malfunctions effectively. Such a strategy, informed by our model, has the potential to greatly enhance the factory’s responsiveness to machine breakdowns and overall operational efficiency.

4.4 Discussion

The evaluation of the proposed method across four diverse experiments underscores its superior performance over current approaches used in electronic manufacturing industries in handling machine faults under varied conditions. This method consistently outperformed the current strategies, marking notable advancements in response times and manpower efficiency, and presenting a compelling case for its wider adoption in industrial settings. NSGA III + Dispatch’s prominence is particularly notable in scenarios marked by frequent machine faults and constrained resources. Its capability to deliver enhanced operational efficiency while curtailing labor requirements offers a tangible solution to some of the prevalent challenges in manufacturing. The decreased response times and reduced delayed repairs further accentuate its utility, offering a pragmatic approach to machine and manpower allocation.

A deep dive into the outcomes generated by NSGA III + Dispatch reveals an existent gap in the current practice, especially in assigning maintenance personnel to high-frequency fault machines. This inadequacy not only impacts operational efficiency but also escalates operational costs. NSGA III + Dispatch, with its nuanced resource allocation, mitigates these challenges, prompting a reevaluation of the prevailing practices in the factory.

The empirical evidence supports the integration of NSGA III + Dispatch in the manufacturing setup, especially in scenarios marked by resource constraints and frequent machine faults. The insights gleaned from the method’s solutions not only offer immediate remedial strategies but also pave the way for future skill development initiatives for operators. In a nutshell, the adoption of NSGA III + Dispatch transcends immediate operational enhancements, offering a strategic pathway for future skill and resource optimization. Its implementation promises not just elevated operational efficiency and reduced costs, but also a competitive edge in a market where efficiency and cost-effectiveness are integral to sustained success.

This model’s practical implications for manufacturing practitioners include customizable maintenance planning, optimized operator allocation, cost savings, and adaptability in diverse operational conditions. Pilot testing, staff training, accurate data collection, and iterative optimization are essential for effective implementation. These findings offer a comprehensive, applicable framework for maintenance optimization, potentially extending beyond manufacturing to sectors like healthcare, transportation and energy.

While the proposed model shows promise for broad applicability across various manufacturing sectors, its effectiveness in different contexts would benefit from further empirical validation. Adaptations to the model may be necessary to accommodate the unique characteristics and constraints of different manufacturing environments or industries. We recommend that users of the model consider these limitations and assumptions, and where possible, conduct pilot studies to gauge its effectiveness in their specific context before full-scale implementation.

5  Conclusions

In this study, we addressed the critical challenge of optimizing maintenance dispatch systems within manufacturing environments. Our focus was on striking a balance between the urgent needs of corrective maintenance and the overarching goal of cost-effectiveness. We introduced a novel multi-objective optimization model that revolutionizes the way maintenance personnel dispatching and station selection are approached. The essence of our model lies in its integration of the spatial distribution of machinery with the diverse expertise of maintenance operators. This integration allows for a highly precise and effective approach to planning maintenance tasks, aiming to minimize total response times and optimize the number of operators involved. To effectively solve this complex model, we developed the NSGA III + Dispatch method, an innovative adaptation of the Non-Dominated Sorting Genetic Algorithm III (NSGA-III). This method is specifically tailored for the intricate challenges of multi-objective optimization in locating maintenance stations and efficient operator dispatching. It excels in handling multiple objectives, a crucial aspect in the dynamic field of maintenance scheduling and resource allocation. The key elements of the NSGA III + Dispatch, including the coding method, crossover operator, and mutation operator, were carefully designed to enhance its performance in managing multiple objectives. We empirically validated this model through a series of experiments that simulated diverse scenarios, such as varying machine failure frequencies and different operator availability. These experiments utilized real-world data from Taiwanese electronic equipment manufacturers, ensuring the practical applicability of our findings.

Our experimental results demonstrate the NSGA III + Dispatch algorithm’s effectiveness and versatility. Key findings include:

1.    Low-Frequency Failures: The NSGA III + Dispatch method significantly improved response times by up to 23% and enhanced human resource utilization compared to existing practices in low-frequency failure scenarios.

2.    High-Frequency Failures: The algorithm effectively reduced response times by up to 28.23% in high-frequency failure scenarios, even with fewer operators, highlighting its ability to manage intensive maintenance demands efficiently.

3.    Selective High-Frequency Failures (A and B): In selective failure scenarios, the algorithm customized solutions based on specific machine breakdown patterns, improving response times and enabling strategic, cost-effective operator allocation.

4.    Workforce Optimization: In scenarios with an increased operator pool, the NSGA III + Dispatch method achieved similar or better response efficiency with fewer operators than the current practices, showcasing its potential in workforce optimization.

These results affirm the NSGA III + Dispatch model as a powerful tool in manufacturing maintenance management, adeptly addressing dual objectives of minimizing maintenance response times and optimizing human resource usage across various operational contexts. This study presents a theoretical and practical contribution to maintenance optimization, offering an effective framework for enhancing operational efficiency. Future research should focus on refining the algorithm to better handle uncertainties in real-world maintenance scenarios, such as fluctuating machine conditions and unpredictable maintenance durations. Additionally, the development of dynamic scheduling strategies to effectively respond to unforeseen operational changes, like simultaneous machine failures or unexpected maintenance extensions, is vital. These improvements could substantially reduce production downtime and significantly enhance overall maintenance management efficiency.

Acknowledgement: Not applicable.

Funding Statement: We appreciate the financial support from the National Science and Technology Council of Taiwan (Contract Nos. 112-2221-E-011-115 and 111-2622-E-011019) and the support from Intelligent Manufacturing Innovation Center (IMIC), National Taiwan University of Science and Technology (NTUST), Taipei 10607, Taiwan, which is a Featured Areas Research Center in Higher Education Sprout Project of Ministry of Education (MOE), Taiwan (since 2023) was appreciated.

Author Contributions: Study conception and design: C.-L. Yang, M.M. Teshome, Y.Z. Yeh; data collection: C.-L. Yang, Y.Z. Yeh; analysis and interpretation of results: C.-L. Yang, M.M. Teshome, T.Y. Meles, Y.Z. Yeh; investigation: C.-L. Yang, M.M. Teshome, T.Y. Meles, Y.Z. Yeh; manuscript preparation: C.-L. Yang, M.M. Teshome, T.Y. Meles, Y.Z. Yeh. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article (and/or) its supplementary materials.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. Emami-Mehrgani, W. P. Neumann, S. Nadeau, and M. Bazrafshan, “Considering human error in optimizing production and corrective and preventive maintenance policies for manufacturing systems,” Appl. Math Model., vol. 40, no. 3, pp. 2056–2074, 2016. doi: 10.1016/j.apm.2015.08.013. [Google Scholar] [CrossRef]

2. M. Ghaleb, H. Zolfagharinia, and S. Taghipour, “Real-time production scheduling in the Industry-4.0 context: Addressing uncertainties in job arrivals and machine breakdowns,” Comput. Oper. Res., vol. 123, pp. 105031, 2020. doi: 10.1016/j.cor.2020.105031. [Google Scholar] [CrossRef]

3. Z. Wang, J. Zhang, and J. Si, “Dynamic job shop scheduling problem with new job arrivals: A survey,” in Proc. 2019 Chin. Intell. Autom. Conf., Jiangsu, China, 20–22 Sep. 2020, pp. 664–671. [Google Scholar]

4. E. L. D. S. Cabral et al., “Response time in the emergency services,” Syst. Rev. Acta Cir. Bras., vol. 33, pp. 1110–1121, 2018. doi: 10.1590/s0102-865020180120000009. [Google Scholar] [PubMed] [CrossRef]

5. A. Hatami-Marbini, N. Varzgani, S. M. Sajadi, and A. Kamali, “An emergency medical services system design using mathematical modeling and simulation-based optimization approaches,” Decision Anal. J., vol. 3, pp. 100059, 2022. doi: 10.1016/j.dajour.2022.100059. [Google Scholar] [CrossRef]

6. H. Hu, J. He, X. He, W. Yang, J. Nie and B. Ran, “Emergency material scheduling optimization model and algorithms: A review,” J. Traffic Transp. Eng. (Engl. Ed.), vol. 6, no. 5, pp. 441–454, 2019. doi: 10.1016/j.jtte.2019.07.001. [Google Scholar] [CrossRef]

7. H. Toro-Díaz, M. E. Mayorga, S. Chanta, and L. A. McLay, “Joint location and dispatching decisions for emergency medical services,” Comput. Ind. Eng., vol. 64, no. 4, pp. 917–928, 2013. doi: 10.1016/j.cie.2013.01.002. [Google Scholar] [CrossRef]

8. J. Y. Yu, K. L. Huang, W. Z. Sun, and M. H. M. Ma, “The study of guarding and cruising modes of ambulances for emergency medical service,” J. Ind. Prod. Eng., vol. 37, no. 8, pp. 440–450, 2020. doi: 10.1080/21681015.2020.1840449. [Google Scholar] [CrossRef]

9. H. Qiu, J. Wang, D. Wang, and Y. Yin, “Service-oriented multi-skilled technician routing and scheduling problem for medical equipment maintenance with sudden breakdown,” Adv. Eng. Inform., vol. 57, pp. 102090, 2023. doi: 10.1016/j.aei.2023.102090. [Google Scholar] [CrossRef]

10. H. Li, S. Mi, Q. Li, X. Wen, D. Qiao and G. Luo, “A scheduling optimization method for maintenance, repair and operations service resources of complex products,” J. Intell. Manuf., vol. 31, pp. 1673–1691, 2020. doi: 10.1007/s10845-018-1400-4. [Google Scholar] [CrossRef]

11. Y. Chen, N. Zhang, J. Yan, G. Zhu, and G. Min, “Optimization of maintenance personnel dispatching strategy in smart grid,” World Wide Web, vol. 26, no. 1, pp. 139–162, 2023. doi: 10.1007/s11280-022-01019-0. [Google Scholar] [CrossRef]

12. E. Xu, M. Yang, Y. Li, X. Gao, Z. Wang and L. Ren, “A multi-objective selective maintenance optimization method for series-parallel systems using NSGA-III and NSGA-II evolutionary algorithms,” Adv. Prod. Eng. Manage., vol. 16, no. 3, 2021. doi: 10.14743/apem2021.3.407. [Google Scholar] [CrossRef]

13. F. Ansari, L. Kohl, and W. Sihn, “A competence-based planning methodology for optimizing human resource allocation in industrial maintenance,” CIRP Ann., vol. 72, no. 1, pp. 389–392, 2023. doi: 10.1016/j.cirp.2023.04.050. [Google Scholar] [CrossRef]

14. R. S. Wahyudin, W. Sutopo, M. Hisjam, and R. S. Hardiono, “Resource allocation model to find optimal allocation of workforce, material, and tools in an aircraft line maintenance,” in Proc. Int. Multi Conf. Eng. Comput. Sci., Hong Kong, 2016, pp. 2078–0966. [Google Scholar]

15. S. W. Kim and B. K. Yoon, “A study on the optimal allocation of maintenance personnel in the naval ship maintenance system,” J. Korea Acad. Ind. Coop. Soc., vol. 16, no. 3, pp. 1853–1862, 2015. doi: 10.5762/KAIS.2015.16.3.1853. [Google Scholar] [CrossRef]

16. N. Gkonou, E. Nisyrios, and K. Gkiotsalitis, “Combined optimization of maintenance works and crews in railway networks,” Appl. Sci., vol. 13, no. 18, pp. 10503, 2023. doi: 10.3390/app131810503. [Google Scholar] [CrossRef]

17. J. Han, J. Zhang, B. Zeng, and M. Mao, “Optimizing dynamic facility location-allocation for agricultural machinery maintenance using Benders decomposition,” Omega, vol. 105, pp. 102498, 2021. doi: 10.1016/j.omega.2021.102498. [Google Scholar] [CrossRef]

18. S. Zhang, F. Tong, M. Li, S. Jin, and Z. Li, “Research on multi-dimensional optimal location selection of maintenance station based on big data of vehicle trajectory,” Entropy, vol. 23, no. 5, pp. 495, 2021. doi: 10.3390/e23050495. [Google Scholar] [PubMed] [CrossRef]

19. F. Al Ali and N. M. Hassan, “Optimization of bus depot location with consideration of maintenance center availability,” J. Transp. Eng. Part A Syst., vol. 144, no. 2, pp. 05017011, 2018. doi: 10.1061/JTEPBS.0000114. [Google Scholar] [CrossRef]

20. J. David, T. Tuhý, and Z. K. Jančíková, “Method for optimizing maintenance location within the industrial plant,” Acta Logist., vol. 6, no. 2, pp. 55–62, 2019. doi: 10.22306/al.v6i2.122. [Google Scholar] [CrossRef]

21. D. Tönissen and J. Arts, “The stochastic maintenance location routing allocation problem for rolling stock,” Int. J. Prod. Econ., vol. 230, pp. 107826, 2020. doi: 10.1016/j.ijpe.2020.107826. [Google Scholar] [CrossRef]

22. J. Li, W. Ren, and X. Wang, “Joint location-allocation model for multi-level maintenance service network in agriculture,” Appl. Sci., vol. 13, no. 18, pp. 10167, 2023. doi: 10.3390/app131810167. [Google Scholar] [CrossRef]

23. G. Xin, Z. Cheng, and J. Liu, “Design of location algorithm for marine drone aircraft maintenance base station,” in IOP Conf. Ser. Mater. Sci. Eng., 2019, pp. 052030. [Google Scholar]

24. M. Malec, P. Benalcazar, and P. Kaszyński, “Optimal location of gas network maintenance centres: A case study from Poland,” J. Nat. Gas Sci. Eng., vol. 83, pp. 103569, 2020. doi: 10.1016/j.jngse.2020.103569. [Google Scholar] [CrossRef]

25. A. Ahmadi-Javid, P. Seyedi, and S. S. Syam, “A survey of healthcare facility location,” Comput. Oper. Res., vol. 79, pp. 223–263, 2017. doi: 10.1016/j.cor.2016.05.018. [Google Scholar] [CrossRef]

26. T. S. Hale and C. R. Moberg, “Location science research: A review,” Ann. Oper. Res., vol. 123, pp. 21–35, 2003. doi: 10.1023/A:1026110926707. [Google Scholar] [CrossRef]

27. D. Celik Turkoglu, and M. Erol Genevois, “A comparative survey of service facility location problems,” Ann. Oper. Res., vol. 292, pp. 399–468, 2020. doi: 10.1007/s10479-019-03385-x. [Google Scholar] [CrossRef]

28. G. Laporte, S. Nickel, and F. Saldanha-da-Gama, Introduction to Location Science. Cham, Switzerland: Springer, 2019. [Google Scholar]

29. S. H. Owen and M. S. Daskin, “Strategic facility location: A review,” Eur. J. Oper. Res., vol. 111, no. 3, pp. 423–447, 1998. doi: 10.1016/S0377-2217(98)00186-6. [Google Scholar] [CrossRef]

30. Z. H. Zhang and K. Li, “A novel probabilistic formulation for locating and sizing emergency medical service stations,” Ann. Oper. Res., vol. 229, pp. 813–835, 2015. doi: 10.1007/s10479-014-1758-4. [Google Scholar] [CrossRef]

31. P. Wu, C. H. Yang, F. Chu, M. C. Zhou, S. Khaled and S.A. S. Fahad, “Cost-profit trade-off for optimally locating automotive service firms under uncertainty,” IEEE Trans. Intell. Transp., vol. 22, no. 2, pp. 1014–1025, 2020. [Google Scholar]

32. W. Zhang, K. Cao, S. Liu, and B. Huang, “A multi-objective optimization approach for health-care facility location-allocation problems in highly developed cities such as Hong Kong,” Comput. Environ. Urban Syst., vol. 59, pp. 220–230, 2016. doi: 10.1016/j.compenvurbsys.2016.07.001. [Google Scholar] [CrossRef]

33. G. Zambrano-Rey, H. López-Ospina, and J. Pérez, “Retail store location and pricing within a competitive environment using constrained multinomial logit,” Appl. Math. Model., vol. 75, pp. 521–534, 2019. doi: 10.1016/j.apm.2019.05.040. [Google Scholar] [CrossRef]

34. H. W. Kuhn, “The Hungarian method for the assignment problem,” Nav. Res. Logist. Q., vol. 2, no. 1–2, pp. 83–97, 1955. doi: 10.1002/nav.3800020109. [Google Scholar] [CrossRef]

35. S. Bouajaja and N. Dridi, “A survey on human resource allocation problem and its applications,” Operat. Res., vol. 17, pp. 339–369, 2017. doi: 10.1007/s12351-016-0247-8. [Google Scholar] [CrossRef]

36. H. Grillo, M. Alemany, and E. Caldwell, “Human resource allocation problem in the Industry 4.0: A reference framework,” Comput. Ind. Eng., vol. 169, pp. 108110, 2022. doi: 10.1016/j.cie.2022.108110. [Google Scholar] [CrossRef]

37. M. Vila and J. Pereira, “A branch-and-bound algorithm for assembly line worker assignment and balancing problems,” Comput. Oper. Res., vol. 44, pp. 105–114, 2014. doi: 10.1016/j.cor.2013.10.016. [Google Scholar] [CrossRef]

38. C. H. Su and J. Y. Wang, “A branch-and-bound algorithm for minimizing the total tardiness of multiple developers,” Mathematics, vol. 10, no. 7, pp. 1200, 2022. doi: 10.3390/math10071200. [Google Scholar] [CrossRef]

39. S. M. Almufti, “U-turning ant colony algorithm powered by great deluge algorithm for the solution of TSP problem,” M.S. thesis, Dept. of Comp. Eng., Eastern Mediterranean Univ., Gazimağusa, North Cyprus, 2015. [Google Scholar]

40. Y. Y. Feng, I. C. Wu, and T. L. Chen, “Stochastic resource allocation in emergency departments with a multi-objective simulation optimization algorithm,” Health Care Manage. Sci., vol. 20, pp. 55–75, 2017. doi: 10.1007/s10729-015-9335-1. [Google Scholar] [PubMed] [CrossRef]

41. J. Wei, “Optimal allocation of human resources recommendation based on improved particle swarm optimization algorithm,” Math. Probl. Eng., vol. 2022, pp. 13, 2022. [Google Scholar]

42. R. Alvarez-Valdes, E. Crespo, and J. M. Tamarit, “Design and implementation of a course scheduling system using Tabu search,” Eur. J. Oper. Res., vol. 137, no. 3, pp. 512–523, 2002. doi: 10.1016/S0377-2217(01)00091-1. [Google Scholar] [CrossRef]

43. S. A. Shayannia, “Designing a multiobjective human resource scheduling model using the Tabu search algorithm,” Discrete Dyn. Nat. Soc., vol. 2022, pp. 16, 2022. [Google Scholar]

44. N. Manavizadeh, N. S. Hosseini, M. Rabbani, and F. Jolai, “A simulated annealing algorithm for a mixed model assembly U-line balancing type-I problem considering human efficiency and just-in-time approach,” Comput. Ind. Eng., vol. 64, no. 2, pp. 669–685, 2013. doi: 10.1016/j.cie.2012.11.010. [Google Scholar] [CrossRef]

45. M. Xu and C. Li, “Data mining method of enterprise human resource management based on simulated annealing algorithm,” Secur. Commun. Netw., vol. 2021, pp. 1–9, 2021. [Google Scholar]

46. M. Gen, W. Q. Zhang, L. Lin, and Y. S. Yun, “Recent advances in hybrid evolutionary algorithms for multiobjective manufacturing scheduling,” Comput. Ind. Eng., vol. 112, pp. 616–633, 2017. doi: 10.1016/j.cie.2016.12.045. [Google Scholar] [CrossRef]

47. S. Sharma and V. Kumar, “A comprehensive review on multi-objective optimization techniques: Past, present and future,” Arch. Comput. Method Eng., vol. 29, no. 7, pp. 5605–5633, 2022. doi: 10.1007/s11831-022-09778-9. [Google Scholar] [CrossRef]

48. R. H. Bhesdadiya, I. N. Trivedi, P. Jangir, N. Jangir, and A. Kumar, “An NSGA-III algorithm for solving multi-objective economic/environmental dispatch problem,” Cogent Eng., vol. 3, no. 1, pp. 1269383, 2016. doi: 10.1080/23311916.2016.1269383. [Google Scholar] [CrossRef]

49. X. Zhang and Y. X. Wang, “Research on multi-objective flow shop scheduling problem based on improved NSGA-III algorithm,” in Proc. 2021 5th Int. Conf. Electron. Inf. Technol. Comput. Eng., Xiamen, China, Oct. 22–24 2021, pp. 1183–1188. [Google Scholar]

50. X. M. He, S. H. Dong, and N. Zhao, “Research on rush order insertion rescheduling problem under hybrid flow shop based on NSGA-III,” Int. J. Prod. Res., vol. 58, no. 4, pp. 1161–1177, 2020. doi: 10.1080/00207543.2019.1613581. [Google Scholar] [CrossRef]

51. K. Deb and H. Jain, “An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: Solving problems with box constraints,” IEEE Trans. Evol. Comput., vol. 18, no. 4, pp. 577–601, 2013. doi: 10.1109/TEVC.2013.2281535. [Google Scholar] [CrossRef]