 Open Access
Open Access
ARTICLE
Improving the Transmission Security of Vein Images Using a Bezier Curve and Long Short-Term Memory
1 Computer Science and School of Electronics and Telecommunications, University of Sfax, Sfax, 3029, Tunisia
2 LETI Laboratory, University of Sfax, Sfax, 3029, Tunisia
3 Digital Research Center of Sfax, Technopark of Sfax, Sfax, 3029, Tunisia
4 Department of Information Technology, Institute of Graduate Studies and Research, Alexandria University, Alexandria, Egypt
* Corresponding Author: Ahmed H. Alhadethi. Email:
(This article belongs to the Special Issue: Advances and Applications in Signal, Image and Video Processing)
Computers, Materials & Continua 2024, 79(3), 4825-4844. https://doi.org/10.32604/cmc.2024.047852
Received 20 November 2023; Accepted 22 April 2024; Issue published 20 June 2024
Abstract
The act of transmitting photos via the Internet has become a routine and significant activity. Enhancing the security measures to safeguard these images from counterfeiting and modifications is a critical domain that can still be further enhanced. This study presents a system that employs a range of approaches and algorithms to ensure the security of transmitted venous images. The main goal of this work is to create a very effective system for compressing individual biometrics in order to improve the overall accuracy and security of digital photographs by means of image compression. This paper introduces a content-based image authentication mechanism that is suitable for usage across an untrusted network and resistant to data loss during transmission. By employing scale attributes and a key-dependent parametric Long Short-Term Memory (LSTM), it is feasible to improve the resilience of digital signatures against image deterioration and strengthen their security against malicious actions. Furthermore, the successful implementation of transmitting biometric data in a compressed format over a wireless network has been accomplished. For applications involving the transmission and sharing of images across a network. The suggested technique utilizes the scalability of a structural digital signature to attain a satisfactory equilibrium between security and picture transfer. An effective adaptive compression strategy was created to lengthen the overall lifetime of the network by sharing the processing of responsibilities. This scheme ensures a large reduction in computational and energy requirements while minimizing image quality loss. This approach employs multi-scale characteristics to improve the resistance of signatures against image deterioration. The proposed system attained a Gaussian noise value of 98% and a rotation accuracy surpassing 99%.Keywords
Communication and digital technologies have changed society’s daily activities and had major economic and social impacts on information used in all relevant domains [1]. Due to the rapid growth of the Internet, Mobile Networks, and social media, the development of more secure authentication systems with higher performance on mobile devices has increased dramatically [2]. Newly developed technologies make accessing, processing, storing, and transmitting information simpler and more affordable [3]. In this ever-changing and evolving environment, secure communications must be established using an authentication system. It is currently an important target for researchers to develop secure authentication systems using certain authentication techniques [4]. At present, sharing images via the Internet is commonplace, requiring strong authentication techniques to ensure secure transmission. Authentication refers to a service that ensures whether a given block of data has integrity (i.e., that the associated content has not been modified) and was provided by a legitimate sender [5]. Authentication is traditionally ensured through mechanisms that involve message authentication codes (MACs) and digital signatures [6], known as “hard authenticators”. In hard authentication, a MAC (also known as a message digest) or a digital signature of the data to protect called an authenticator is created at the source and transmitted with the data. At the receiver, the authenticator is verified using the received data to deduce whether the received information is, in fact, unmodified and from the alleged sender.
When the data represent an image that can travel through a set of diverse distribution chains, they are susceptible to content-preserving operations such as compression, transcoding, and other standard-format conversions that severely impede the usefulness of hard authentication mechanisms. Any processing of an image that changes its bit representation yet still maintains the validity of the perceptual content may be inaccurately categorized as “inauthentic.” Thus, more recently, there has been a movement toward developing schemes that provide “soft authentication,” in which content-preserving processing is distinguished from unlawful content-changing manipulations. One toolset that was recently applied to soft-authentication, and which is a partial focus of this work, is called semi-fragile digital watermarking. In this method, an authenticator which may consist of a MAC or digital signature for salient parts of an image is used to form a watermark. This watermark is imperceptibly embedded within the original image (commonly called the host). The integration of the authenticator within the image to be secured simplifies the logistical problems associated with the MAC and digital signature data handling during image transmission. Moreover, semi-fragile watermarking can provide information on the degree and location of tampering within an image, allowing for more application-relevant decisions based on credibility [7]. The methodology begins with the utilization of the k-means technique to compress the sending image efficiently. Subsequently, the paper extracts distinctive features from the compressed image using the Histogram of Oriented Gradients (HOG) method. To further enhance the intricacy of the model, the extracted features are incorporated into the LSTM deep learning algorithm. The results obtained from the LSTM are then utilized to generate a sequence of Bezier curves. These curves collectively form the proposed signature, providing a unique and robust representation. In the final step of the process, the outcomes of the LSTM are employed as spatial indicators within the original image, facilitating the concealment of the generated signature.
This article proposes an effective adaptive compression algorithm that achieves notable reductions in computational and energy requirements while maintaining minimal deterioration in image quality throughout the communication. This approach employs multi-scale characteristics to enhance the resilience of signatures against image degradation. This innovative approach not only showcases the effectiveness of combining compression, feature extraction, deep learning, and curve generation but also underscores the practical application of LSTM results in the context of image-based signature hiding. This paper makes a significant contribution by employing a series of sophisticated algorithms and techniques in the domain of image processing. Furthermore, this article is organized as follows. A comprehensive introduction is presented in Section 1. Section 2 presents and discusses the related works. Moreover, the methodology and proposed method are presented in detail in Sections 3 and 4. Section 5 presents and discusses the results of the proposed system. Finally, the conclusion of the research is presented in Section 6.
Paper data transmission requires compression and decompression, especially in scenarios with restricted bandwidth or storage. For example, compression using an upgraded AI-powered model can reduce the fingerprint image size for biometric data encryption, thus increasing the speed of wireless transmission. Data are compressed by deleting extraneous information while maintaining their key qualities. Fingerprints are self-similar, with repeated patterns and structures, enabling compression algorithms to simplify them, thus reducing the fingerprint image size without sacrificing crucial information by quickly recognizing and encoding these patterns. Zhan et al. [8] have employed a deep-learning self-encoder framework to improve image reconstruction and reduce RoI distortion. Many compression strategies, however, have positives and negatives. Mital et al. [9] have proposed compressing an information source utilizing only decoder-side correlated information on stereo image pairs from synchronized and calibrated cameras. While previous methods based on deep neural networks convert the input image into a latent representation, compressing the image with less loss of features through entropy coding, these authors used a cross-attention module in the decoder to align the feature mappings from the input image’s latent representation and the decoder-side information’s latent representation, thus improving the use of correlated patches. Li et al. [10] have proposed a compression domain processing-based method for efficient analysis of Whole-Slide Images (WSIs), which are increasingly significant for modern pathologists. Due to the vast size of WSIs, current methods for analyzing such images involve picture decompression and are computationally costly. Pyramidal magnification structures and compression domain characteristics can be used to assign different decompression depths to WSI patches depending on features directly retained from compressed or partially decompressed patches. Attention-based clustering screens for low-magnification patches, resulting in variable decompression depths for high-magnification patches at different locations. When dealing with sensitive information, such as biometrics, authentication plays a key role in any safe communication system. For example, authentication ensures that only authorized individuals can access and modify encrypted biometric data within the context of the use of enhanced AI-powered models.
Several methods exist for authenticating data, such as the method proposed by Li et al. [11], which makes use of K-Means clustering and the side match methodology to recover and restore mosaiced images. To implement Image Secret Sharing (ISS) without pixel enlargement, Yan et al. [12] presented a new public-key-based bi-directional shadow image authentication mechanism, in which the shadow picture is authenticated only during the decoding phase using conventional dealer-participatory methods, which suffer from substantial pixel expansion and require the storage of supplementary information; however, the approach suggested by the authors permits shadow image authentication in both the encoding and decoding stages, unlike previous methods. Watson’s Visual Model and LLE form the basis of the image-hashing technique reported by Yan et al. [13]. To build hashing sequences that accurately reflect how humans perceive images, the suggested system for such images must be able to reliably differentiate between copies and similar images. First, Watson’s Visual Model is used to modify the weights of the DCT coefficients for non-overlapping image blocks; then, the Hu-invariant moments of each block are combined to build an intermediate feature matrix that is subsequently encrypted using chaotic hashing.
Guarino et al. [14] introduced a TGSB approach for recognizing gender and age groups. This approach employs a transfer learning strategy that is applied to Convolutional Neural Networks (CNNs). These CNNs are trained using image-based representations of touch gestures executed by users on mobile devices. In their study, Guarino et al. [15] investigated the influence of noise on the efficacy of a biometric system by employing pattern recognition techniques for the identification of individuals based on diverse characteristics such as facial features and fingerprints. Abuturb et al. [16] introduced an innovative optical single-channel security system designed for the protection of multiple color images. This system utilizes 3D logistic map biometric keys as a means of authentication, employing a chaotic random phase mask to modulate the biometric key and subsequently encrypting each channel of the original color images individually. Grizheboskya et al. [17] focused on correcting geometric distortions and incorrect scales in fingerprint images. These corrections play a vital role in ensuring precise recognition and identification in biometric systems. The authors of [18] investigated the application of deep learning algorithms for text feature extraction and classification. Researchers have explored the use of Recurrent Neural Networks (RNNs) and LSTM networks to capture sequential information and learn meaningful representations from textual data, leading to improved performance in tasks such as sentiment analysis and text categorization. While reference [19] focused on deep learning-based feature extraction for speech emotion recognition. and propose a model that combines CNNs and LSTM networks to extract discriminative features from speech signals. These learned features are then used for accurately classifying emotional states in speech data.
In the consideration of this paper, the fingerprint data might be signed before compression to guarantee its legitimacy. The fingerprint data itself or some other mechanism (e.g., hash function or a digital signature) may be used to construct the signature, which is a unique identifier. Before employing the Least Significant Bit (LSB) method to embed data in an image, the signature must be generated. After the signature is constructed, it can be included in the compressed fingerprint data by employing the same LSB method. This feature makes it extremely difficult to detect or tamper with the signature during transmission, as it is embedded in the image. The LSB method allows the signature to be recovered from the received picture and compared to the original signature at the receiving end. If the two signatures are consistent, the recipient knows that the data is genuine and that the image was not altered during transmission. It is also crucial to safeguard images against any transmission errors or noise that may be introduced. The use of error-correcting codes allows for the detection and correction of any transmission faults. These codes, along with the compressed fingerprint data and signature, can be embedded in the image using the same LSB method. Transmission faults can be detected and remedied at the receiving end using error-correcting codes. These measures ensure that the data has not been tampered with in transit and can be relied upon when analyzed.
Clustering is a process that involves dividing data into groups that share certain characteristics, according to patterns in the data. K-Means clustering is a clustering technique used to identify clusters of data objects, as illustrated in Fig. 1. Due to the nature of clustering, it is considered an unsupervised learning approach, as we do not need to label the data given that this method recognizes similar patterns between the data [20]. K-Means clustering is a centroid-based algorithm, whereby central points are chosen and data points close to each central point are grouped according to certain properties in the data. Minimizing the sum of distances between the points and their respective cluster centroids is the main process of K-Means clustering [21]. Various distance metrics can be used in the K-Means clustering algorithm to calculate the distance between the data points and centroids [22,23].
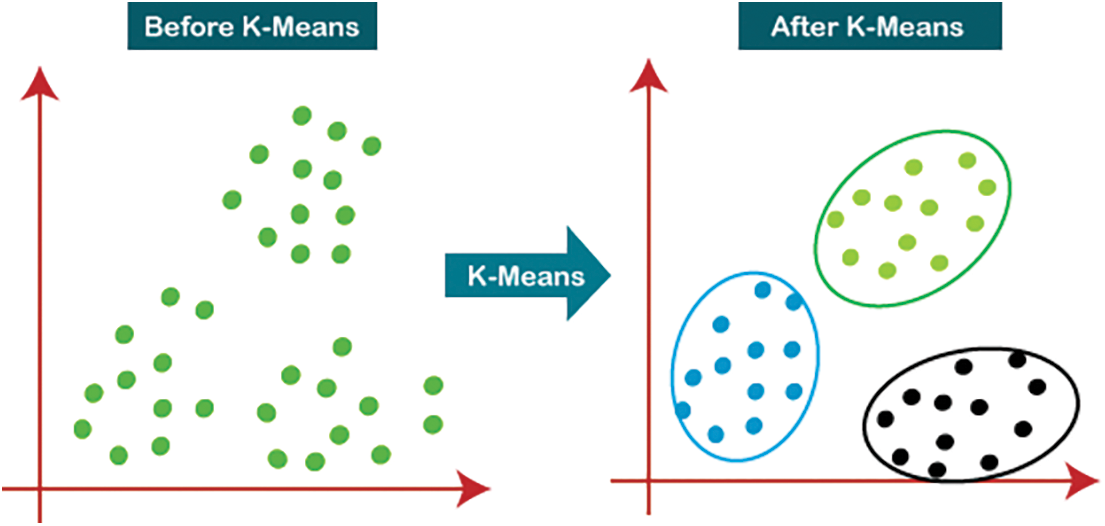
Figure 1: K-Means clustering technique
3.2 Histogram of Oriented Gradients (HOG)
HOG is a feature descriptor of a grayscale image that is formed of a group of normalized gradient histograms, which is obtained as follows: The scan window’s pixels are organized into r × r rectangular cells. The magnitude of the gradient in each cell determines the orientation of the gradient. A histogram is then used to represent all the orientations as votes. For optimal results, fine quantization is used for the gradient orientations. For testing, the range (0, π) is divided into 8 histogram bins and, as the contrast between an object and its backdrop is typically uncertain, (π, 2π) is mirrored [24–26]. The values of the 8c2 histogram bins for each cell are concatenated into a vector B, which is then normalized. This process builds a HOG feature vector with high dimensionality. HOG can be thought of as taking a non-linear function of an image’s edge orientations, concentrating on small spatial areas to eliminate the sensitivity to exact edge localization [27]. HOG is resistant to changes in illumination and can achieve a high degree of computational precision when detecting objects with a variety of textures. Recent high-performance general-purpose processors have the computational capability to perform real-time object detection. However, as such processors consume large amounts of power, they are inappropriate for use in mobile devices with limited battery life. Therefore, low-power, high-performance HOG feature extraction processors are needed, such that the associated range of applications can be expanded. A detection window scans the input images, and each cell’s gradient orientations are combined into a histogram. For increased illumination invariance, histogram normalization can be achieved by combining the local histogram energy over blocks and applying the results, allowing for excellent computational precision in the detection of various textured objects [28]. Each cell in a block is massive, and the histograms (HOG features) are normalized and collected over the detection window [27]. The HOG feature extraction is presented in Fig. 2.
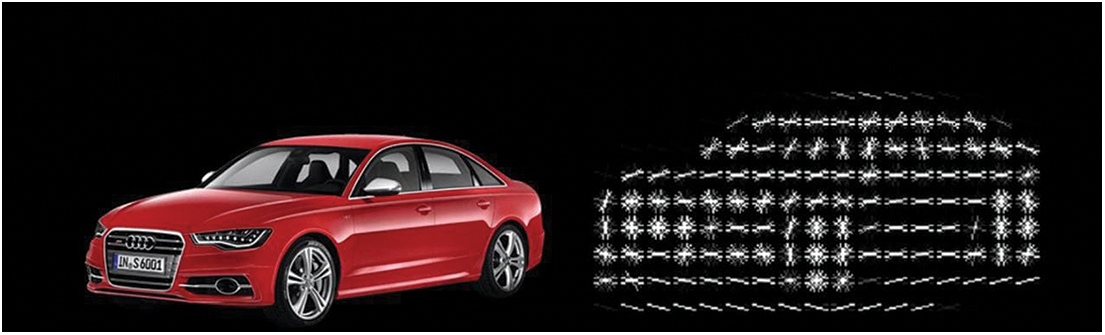
Figure 2: HOG feature extraction
3.3 Long Short-Term Memory (LSTM)
As a subset of the neural network family, RNNs are designed to handle serial data. There are two types of RNNs: Discrete-time RNNs and continuous-time RNNs [29]. These networks are designed with a periodic connection structure, allowing them to update their current state based on both previous and current input data. RNNs are generally artificial neural networks consisting of standard repetitive cells. These types of neural networks are known to be able to identify potential conditions very accurately. RNNs specialize in processing a series of values (e.g., time-series data). Fig. 3 illustrates the general structure of an RNN algorithm [30].
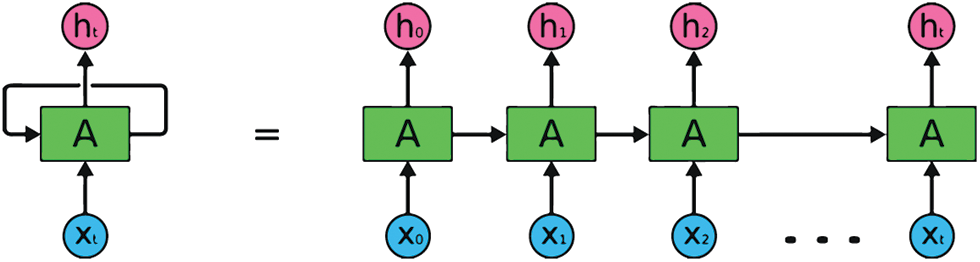
Figure 3: General structure of an RNN algorithm
Most RNNs can process variable-length sequences. However, they cannot typically learn long-term dependencies. To resolve this issue, in 1997, Hochreiter and Schmidhuber proposed a solution called LSTM [31]. LSTM is a type of RNN that is capable of learning and preserving long-term dependencies and is distinguished by the presence of a memory cell. In an LSTM, gates control the insertion or deletion of information within a cell. Three types of gates are used to regulate information flow within the cell: Forget gates, input gates, and output gates. The forget gate determines how much information from the prior cell state is removed. The input gate controls the information that enters the cell state. Then, a vector for a filter layer is generated and attached to the cell state. According to the previous two lines, the old cell state is subsequently updated to a new state. The output layer then selects the cell state information for use as the output [32]. The final LSTM layer at the final time step (n) transmits the output (hn) to a dense layer with a single-output neuron, which calculates the final flow (y). Fig. 4 illustrates the overall structure of the LSTM algorithm [33].
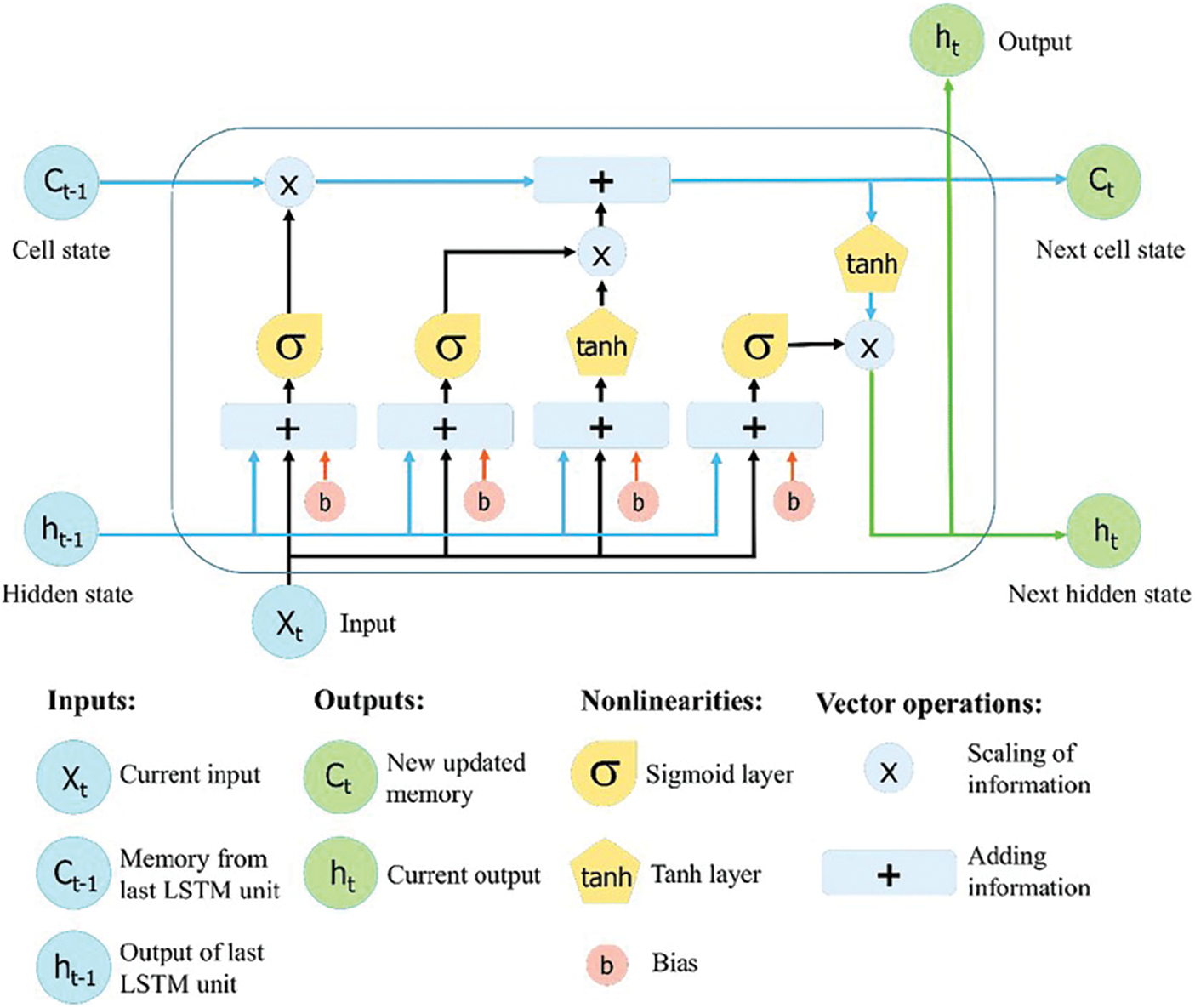
Figure 4: Long short-term memory node structure
The Bezier curve can be described as a parametric curve denoted by P(t), which is a polynomial function of the parameter t. The number of points employed to identify this curve affects the degree of the polynomial. This mechanism generates an approximate curve utilizing certain control points. The curve does not necessarily pass through any of these points; rather, it is attracted toward them [33–36]. This phenomenon can be understood as the points “pulling” on the curve. Each point influences the curve’s orientation by pulling it closer, and this pull is stronger when the curve is closer to the point. An illustration of a cubic Bezier curve is provided in Fig. 5. This curve is defined by four points and a cubic polynomial, making it simple to edit, modify, and/or re-shape. Consequently, this type of curve is popular among researchers. In addition to adding or removing points, the curve may also be edited [35].
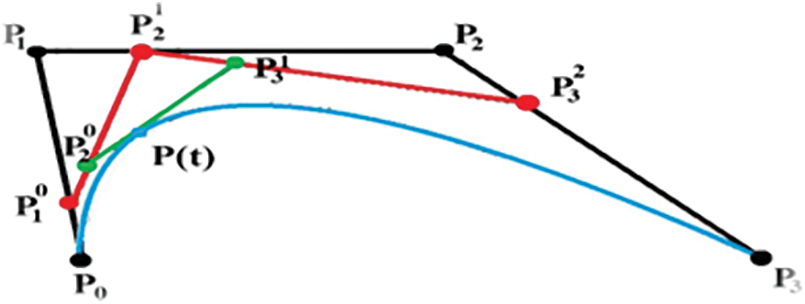
Figure 5: Bezier curve
The parametric formula for a cubic Bezier curve when considering four control points is as follows:
Eq. (1) for a Bezier curve can be transformed into matrix form as follows [35]:
For example, the cubic Bezier curve is defined by its four control points, P0, P1, P2, and P3. The following explains the impact of the control points on the Bezier curve: P0 and P3 are the starting and ending points of the curve, while P1 and P2 determine the direction of the initial curve [36].
Case 1: When t = 0:
Case 2: When t = 1:
Bezier curves are fitted at the first and last points. Fig. 6 shows several examples of Bezier curves and shows how the curves fit the first and last points, but not the control points [33].

Figure 6: Examples of Bezier curves
The finger vein database was used as an example for implementing the proposed system, and different types of medical images can be used. The proposed system was implemented using the 64-bit Python 3.9 language, relying on many libraries, the most important of which are image processing libraries, deep learning libraries, and 2D drawing libraries.
The proposed system consists of two steps: Signature generation and signature matching.
In this step, the sender generates a signature for the vein image to be sent. Fig. 7 presents a block diagram of the proposed system for signature generation. The system first compresses the image using K-Means clustering. The image is composed of pixels, each of which has a three-dimensional representation indicating the intensity values for the red, green, and blue (RGB) colors, which can vary from 0 to 255. The following formula can be used to determine the amount of storage space required for an image with dimensions of 320 × 240 pixels: 320 × 240 × 3 × 8 = 1,843,200 bits. When compressing RGB images via the K-Means clustering approach, k colors associated with the centroids are selected.
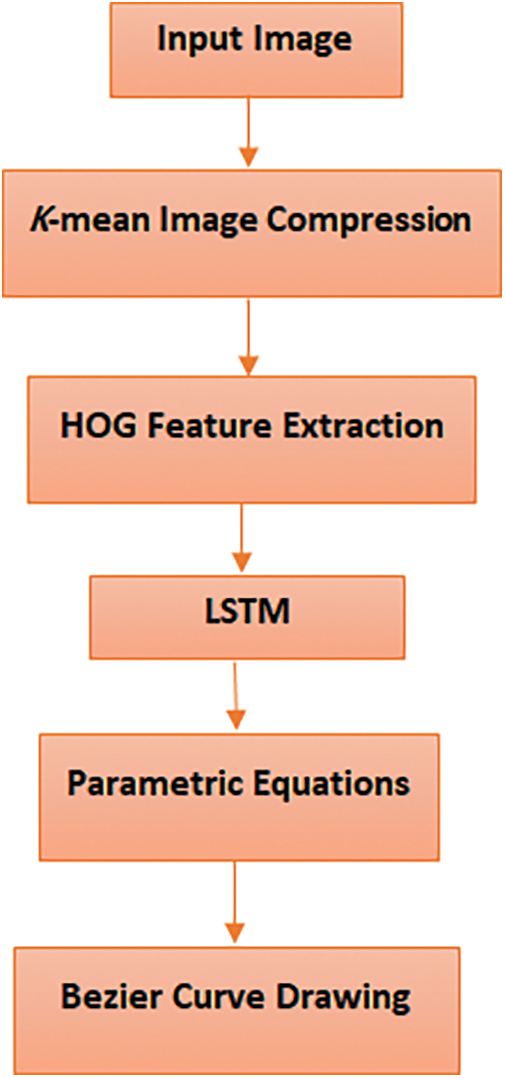
Figure 7: Signature generation block diagram
The remaining colors are then associated with these centroid points, according to the degree of resemblance between them. Each pixel’s value is replaced with the value of the associated centroid point. The image compression size can be determined as follows: If K (centroid points) = 64 is specified, the image size will be 320 × 240 × 6 + 64 × 3 × 8, where the third operand (number 6) indicates the number of bits that can express K values between 0 and 63. If the value of K is increased, the image’s overall quality and size will also increase. The utilized K-Means clustering algorithm is outlined in Algorithm 1.

Feature extraction is the second step. The HOG method describes features by calculating the number of times a vein image has a gradient orientation within a cell. The key steps followed to calculate HOG features are summarized in Algorithm 2.

In the next step, the feature matrix is used as input to a further algorithm to increase the randomness of the numbers, as outlined in Algorithm 3.

These outputs are then used as inputs for the parametric equations to generate Bezier curves, as outlined in Algorithm 4.

In this step, the generated signature is hidden within the compressed image. The locations for this process are selected based on the numbers generated by the LSTM algorithm. Algorithm 5 describes the steps followed to hide the signature. LSB is a technique used in steganography to hide data within an image. This technique involves replacing the least significant bit of each pixel value in the image with the bits of the data to be hidden. As the least significant bit represents the smallest amount of information in a pixel value, modifying it does not significantly affect the quality of the image. When the image is transmitted, the receiver can extract the hidden signature data by extracting the least significant bit of each pixel value to reconstruct the original signature.

In this step, the image including the signature is received by the recipient, which then performs the same processes used in the previous step to generate a signature from the received image. This signature is then matched with the sent signature. Fig. 8 presents the signature matching process.

Figure 8: Signature matching block diagram
Several experiments were conducted on the proposed system. In this paper, the FV-USM was used as a database. The images in the database were collected from 123 classes of 83 males and 40 females, every subject provided four fingers: Left index, left middle, right index, and right middle fingers, resulting in a total of 492 finger classes obtained. Each finger was captured six times in one session individual participated in two sessions. In the first session, a total of 2952 (123 × 4 × 6) images were collected, Fig. 9 illustrates a sample of vein image [37].

Figure 9: Sample vein images from the used data set. Reprinted with permission from [37]. © 2024 Dr. Bakhtiar Affendi Rosdi
To generate a signature, the vein image was chosen, and applied the following steps:
Step 1: The most important practical results of the proposed system in image compression will be explained. The results of image compression were excellent using the K-Mean algorithm. The experiment was carried out using several cases to test the compression algorithm by changing the K value through which the number of colors that should remain in the image is determined. It can also be seen that the values of affect the size of the image after compression. Compress the image using Algorithm 1. Fig. 10 shows the image compression results using different K values.
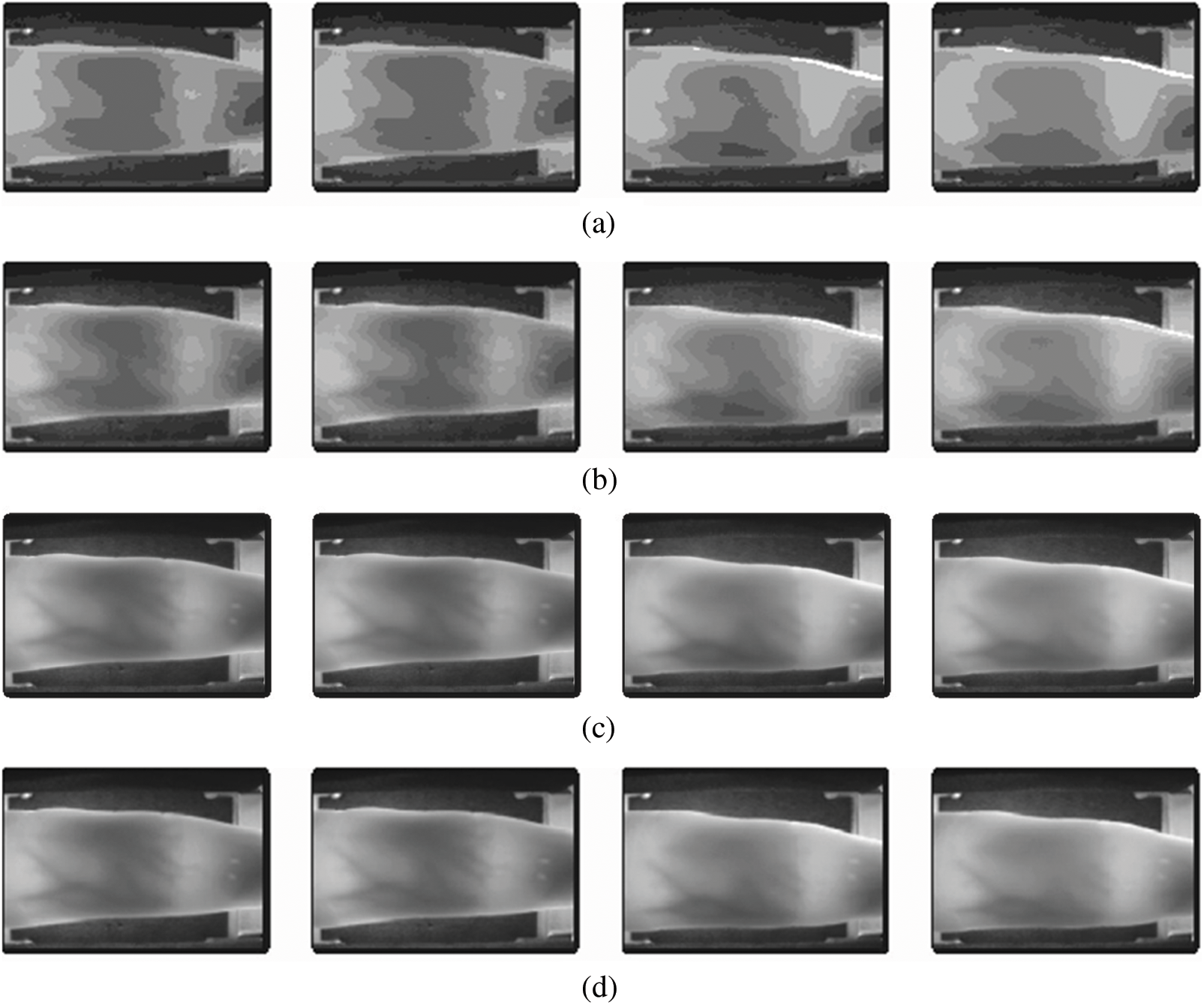
Figure 10: Image compression results (a) K value 16 (b) K value 32 (c) K value 64 (d) K value 128
Note that the clarity of the image and the important parts and the value of their compression were good when using the value of K is 64. Table 1 illustrates compressed results with K = 64 for different images.

Step 2: Extract image features using Algorithm 2. Fig. 11 shows the HOG feature extraction results.

Figure 11: HOG feature extraction results
Step 3: Calculate the LSTM output from the HOG features using Algorithm 3. Table 2 shows sample output values from the LSTM network after processing the HOG features extracted from the vein images. These numerical output values from the LSTM network after processing the HOG features extracted from the vein images. The values in the range of 0 to 1, which is the outputs of LSTM networks when using functions. These values represent the learned representations or encodings of the input data (HOG features) by the LSTM network.

Step 4: Generate a signature using Algorithm 4. Table 3 shows the signatures generated for each vein image. The coordinates

Where xt is the LSTM output value and t is the index of that value.
Step 5: There are many factors of an image to be considered when determining the strength of a system in extracting hidden data from the image, including the addition of noise or rotation to the image. Table 4 illustrates the results of the hiding step.
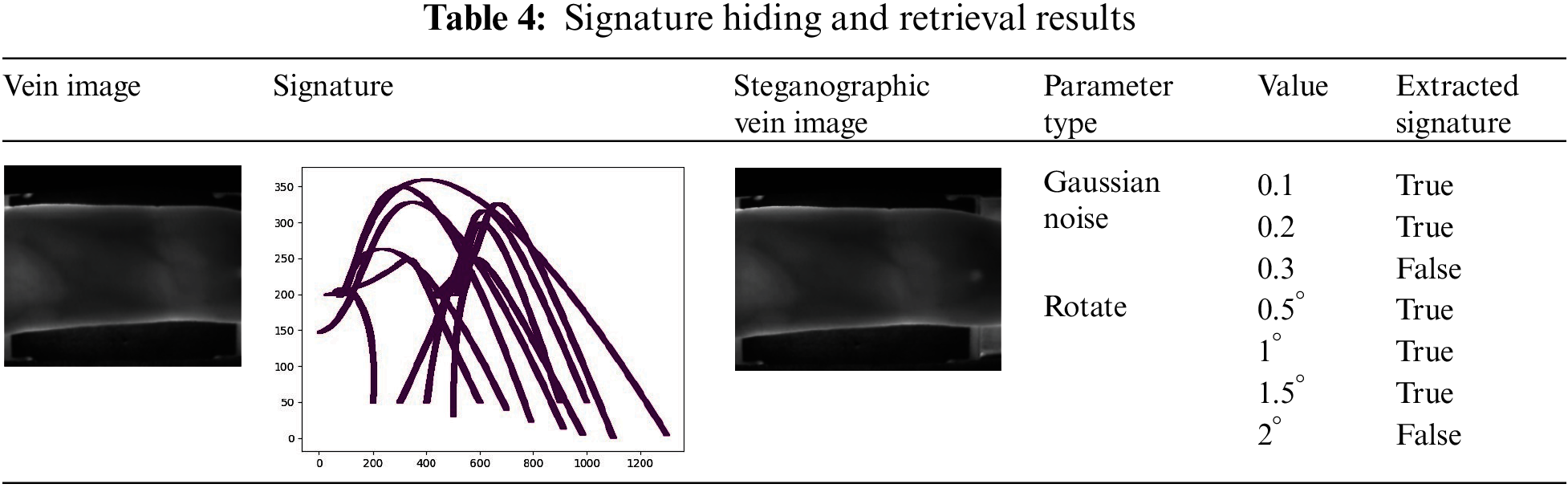
The proposed system was able to retrieve the hidden signature when adding two types of attacks: Gaussian noise and rotation. The intensity of Gaussian noise ranged up to 0.3, while the image was rotated up to 2°. This result indicated a higher percentage than that reported in previous work. The results are detailed in Table 5 which compares the robustness evaluations by scrutinizing the normalized cross-correlation coefficient (NCC).
The proposed system effectively combines adaptive image compression using K-Means clustering, discriminative feature extraction via HOG, increased feature randomness through LSTM networks, unique signature generation using parametric Bezier curves, and robust signature hiding by replacing the least significant bits in the compressed image at LSTM-selected locations. The deep learning-based approach shows high resilience against common image distortions like Gaussian noise up to 0.29 intensity and rotation up to 2 degrees, outperforming some previous methods. Using HOG for extracting distinctive features and LSTM for sequential modeling helps generate highly complex yet content-dependent signatures that are resistant to content-preserving modifications.
Correspondence systems are one of the most important types of systems at present, considering the rapid development of the Internet and electronic correspondence. In this paper, a new system to secure images sent through the Internet was assessed, which was constructed using a series of algorithms and techniques. Image processing algorithms, deep learning, and curve drawing approaches were combined to build a security system. Ultimately, the archived results demonstrated that the use of the HOG technique for feature extraction was effective and that the use of a deep learning technique increased the model’s randomness. However, the proposed system secures a limited type of images, including biometric images and medical images. This requires the use of other algorithms specifically for more feature-extracting image characteristics and algorithms that achieve the best features. An image can also remain safe if it is exposed to Gaussian-type noise in the range of 0–0.29 or rotation 0 to 2 degrees. If the image is exposed to noise greater than this range, the hidden signature will be lost. Moreover, the power to generate a signature was further enhanced using a Bezier curve, which is already considered to be highly random. The system was applied to 2952 vein images, achieving an error rate of 0.001 and yielding an error in only four pictures.
Acknowledgement: The authors would like to extend their appreciation to the University of Sfax for supporting this research.
Funding Statement: The authors confirm that this study did not receive any funding.
Author Contributions: Draft manuscript preparation, design, data collection, analysis, and interpretation of results: Ahmed H. Alhadethi; Ikram Smaoui and Saad M. Darwish reviewed the results and Ahmed Fakhfakh approved the final version of the manuscript.
Availability of Data and Materials: The dataset used in this article is available at http://drfendi.com/fv_usm_database/ (Last Visit 20/7/2018). Additional materials can be requested from the first author.
Conflicts of Interest: The authors declare that they have no conflicts of interest in this manuscript.
References
1. S. N. Atluri and S. Shen, “Global weak forms, weighted residuals, finite elements, boundary elements & local weak forms,” The Meshless Local Petrov-Galerkin (MLPG) Method, vol. 1, pp. 15–64, 2004. [Google Scholar]
2. S. Ilan, “Telecommunications and travel relationships: A review,” Transp. Res. Part A: General, vol. 20, no. 3, pp. 223–238, 1986. doi: 10.1016/0191-2607(86)90096-8. [Google Scholar] [CrossRef]
3. S. Thakur, “Fifth generation (5G) wireless technology,” Int. J. Res. Appl. Sci. Eng. Technol., vol. 9, no. 4, pp. 909–912, 2021. doi: 10.22214/ijraset.2021.33792. [Google Scholar] [CrossRef]
4. B. H. Taher, H. Liu, F. Abedi, H. Lu, A. A. Yassin and A. J. Mohammed, “A secure and lightweight three-factor remote user authentication protocol for future IoT applications,” J. Sens., vol. 2021, no. 7, pp. 1–18, 2021. doi: 10.1155/2021/8871204. [Google Scholar] [CrossRef]
5. N. F. Abdulsattar et al., “Botnet detection employing a dilated convolutional autoencoder classifier with the aid of hybrid shark and bear smell optimization algorithm-based feature selection in FANETs,” Big Data Cogn. Comput., vol. 6, no. 4, pp. 112, 2022. doi: 10.3390/bdcc6040112. [Google Scholar] [CrossRef]
6. Z. A. Zukarnain, A. Muneer, and M. K. Ab Aziz, “Authentication securing methods for mobile identity: Issues, solutions and challenges,” Symmetry, vol. 14, no. 4, pp. 821, Apr. 2022. doi: 10.3390/sym14040821. [Google Scholar] [CrossRef]
7. A. Mahmood, T. Hamed, C. Obimbo, and R. Dony, “Improving the security of the medical images,” Int. J. Adv. Comput. Sci. Appl., vol. 4, no. 9, 2013. doi: 10.14569/issn.2156-5570. [Google Scholar] [CrossRef]
8. G. Alvarez, S. Li, and L. Hernandez, “Analysis of security problems in a medical image encryption system,” Comput. Biol. Med., vol. 37, no. 3, pp. 424–427, 2007. doi: 10.1016/j.compbiomed.2006.04.002. [Google Scholar] [PubMed] [CrossRef]
9. J. Zhang, S. Zhang, H. Wang, Y. Li, and R. Lu, “Image compression network structure based on multiscale region of interest attention network,” Remote Sens., vol. 15, no. 2, pp. 522, 2023. doi: 10.3390/rs15020522. [Google Scholar] [CrossRef]
10. N. Mital, E. Ozyilkan, A. Garjani, and D. Gunduz, “Neural distributed image compression with cross-attention feature alignment,” in Proc. 2023 IEEE Winter Conf. Appl. Comput. Vis., Waikoloa, HI, USA, 2023, pp. 2497–2506. doi: 10.1109/WACV56688.2023.00253. [Google Scholar] [CrossRef]
11. Z. Li, B. Li, K. W. Eliceiri, and V. Narayanan, “Computationally efficient adaptive decompression for whole slide image processing,” Biomed. Opt. Express, vol. 14, no. 2, pp. 667, 2023. doi: 10.1364/BOE.477515. [Google Scholar] [PubMed] [CrossRef]
12. X. Zhou, W. Hong, T. S. Chen, and G. Yang, “Reversible demosaiced image authentication scheme with recoverability using clustering and matching techniques,” J. Inf. Secur. Appl., vol. 73, no. 8–9, pp. 103425, 2023. doi: 10.1016/j.jisa.2023.103425. [Google Scholar] [CrossRef]
13. X. Yan, L. Li, J. Chen, and L. Sun, “Public key based bidirectional shadow image authentication without pixel expansion in image secret sharing,” Front. Inform. Technol. Electron. Eng., vol. 24, no. 1, pp. 88–103, 2023. doi: 10.1631/FITEE.2200118. [Google Scholar] [CrossRef]
14. H. Xing, H. Che, Q. Wu, and H. Wang, “Image perceptual hashing for content authentication based on Watson’s visual model and LLE,” J. Real Time Image Process., vol. 20, no. 1, pp. 507, 2023. doi: 10.1007/s11554-023-01269-9. [Google Scholar] [CrossRef]
15. A. Guarino, D. Malandrino, R. Zaccagnino, C. Capo, and N. Lettieri, “Touchscreen gestures as images. A transfer learning approach for soft biometric traits recognition,” Expert. Syst. Appl., vol. 219, no. 9, pp. 119614, 2023. doi: 10.1016/j.eswa.2023.119614. [Google Scholar] [CrossRef]
16. S. Arora, R. Mittal, H. Kukreja, and M. P. S. Bhatia, “An evaluation of denoising techniques and classification of biometric images based on deep learning,” Multimed. Tools Appl., vol. 82, no. 6, pp. 8287–8302, 2023. doi: 10.1007/s11042-021-11573-w. [Google Scholar] [CrossRef]
17. M. R. Abuturab, “Optical single-channel security system using 3D-logistic map biometric keys for multiple color images,” Opt. Quantum Electron., vol. 55, no. 3, pp. 152, 2023. doi: 10.1007/s11082-022-04493-y. [Google Scholar] [CrossRef]
18. M. B. Er, E. Isik, and I. Isik, “Parkinson’s detection based on combined CNN and LSTM using enhanced speech signals with variational mode decomposition,” Biomed. Signal Process. Control, vol. 70, no. 1, pp. 103006, 2021. doi: 10.1016/j.bspc.2021.103006. [Google Scholar] [CrossRef]
19. M. Rayhan Ahmed, S. Islam, A. K. M. Muzahidul Islam, and S. Shatabda, “An ensemble 1D-CNN-LSTM-GRU model with data augmentation for speech emotion recognition,” Expert. Syst. Appl., vol. 218, no. 4, pp. 119633, May 2023. doi: 10.1016/j.eswa.2023.119633. [Google Scholar] [CrossRef]
20. A. G. Grizhebovskaya, A. V. Mikhalev, and L. P. Dmitrieva, “Geometric distortion correction of images received from biometric fingerprint devices,” J. Math. Sci., vol. 269, no. 3, pp. 317–321, 2023. doi: 10.1007/s10958-023-06283-7. [Google Scholar] [CrossRef]
21. X. Wan, “Application of K-means algorithm in image compression,” IOP Conf. Ser.: Mater. Sci. Eng., vol. 563, no. 5, pp. 052042, 2019. doi: 10.1088/1757-899X/563/5/052042. [Google Scholar] [CrossRef]
22. M. K. Islam, M. S. Ali, M. S. Miah, M. M. Rahman, M. S. Alam and M. A. Hossain, “Brain tumor detection in MR image using superpixels, principal component analysis and template based K-means clustering algorithm,” Mach. Learn. Appl., vol. 5, no. 11, pp. 100044, 2021. doi: 10.1016/j.mlwa.2021.100044. [Google Scholar] [CrossRef]
23. G. Verma and A. Kumar, “Image compression using deep learning based multi-structure feature map and K-means clustering,” Machine Learning, Image Processing, Network Security and Data Sciences, 2020, vol. 1240, pp. 365–374. doi: 10.1007/978-981-15-6315-7_30. [Google Scholar] [CrossRef]
24. T. Kobayashi and N. Otsu, “Image feature extraction using gradient local auto-correlations,” Computer Vision–ECCV 2008, 2008, vol. 5302, pp. 346–358. doi: 10.1007/978-3-540-88682-2_27. [Google Scholar] [CrossRef]
25. T. Kobayashi, “BFO meets HOG: Feature extraction based on histograms of oriented p.d.f. gradients for image classification,” in 2013 IEEE Conf. Comput. Vis. Pattern Recognit., Portland, OR, USA, IEEE, Jun. 2013, pp. 747–754. doi: 10.1109/CVPR.2013.102. [Google Scholar] [CrossRef]
26. S. Routray, A. K. Ray, and C. Mishra, “Analysis of various image feature extraction methods against noisy image: SIFT, SURF and HOG,” in Proc. 2017 2nd IEEE Int. Conf. Electr., Comput. Commun. Technol (ICECCT), Coimbatore, India, 2017. doi: 10.1109/ICECCT.2017.8117846. [Google Scholar] [CrossRef]
27. A. Choudhury, H. S. Rana, and T. Bhowmik, “Handwritten Bengali numeral recognition using hog based feature extraction algorithm,” in 2018 5th Int. Conf. Signal Process. Integr. Netw. (SPIN), Noida, India, 2018, pp. 687–690. doi: 10.1109/SPIN.2018.8474215. [Google Scholar] [CrossRef]
28. K. Cho et al., “Learning phrase representations using RNN encoder-decoder for statistical machine translation,” in Proc. 2014 Conf. Empir. Methods Nat. Lang. Process. (EMNLP), Stroudsburg, PA, USA, Association for Computational Linguistics, 2014, pp. 1724–1734. doi: 10.3115/v1/D14-1179. [Google Scholar] [CrossRef]
29. M. Sundermeyer, R. Schlüter, and H. Ney, “LSTM neural networks for language modeling,” in 13th Annu. Conf. Int. Speech Commun. Assoc. 2012, (INTERSPEECH 2012), Portland, OR, USA, 2012, vol. 1, pp. 194–197. doi: 10.21437/interspeech.2012-65. [Google Scholar] [CrossRef]
30. Y. Yu, X. Si, C. Hu, and J. Zhang, “A review of recurrent neural networks: LSTM cells and network architectures,” Neural Comput., vol. 31, no. 7, pp. 1235–1270, 2019. doi: 10.1162/neco_a_01199. [Google Scholar] [PubMed] [CrossRef]
31. R. C. Staudemeyer and E. R. Morris, “Understanding LSTM—A tutorial into long short-term memory recurrent neural networks,” arXiv:1909.09586, 2019. [Google Scholar]
32. M. Sundermeyer, H. Ney, and R. Schluter, “From feedforward to recurrent LSTM neural networks for language modeling,” IEEE Trans. Audio, Speech and Lang. Process., vol. 23, no. 3, pp. 517–529, 2015. doi: 10.1109/TASLP.2015.2400218. [Google Scholar] [CrossRef]
33. S. Maqsood, M. Abbas, K. T. Miura, A. Majeed, and A. Iqbal, “Geometric modeling and applications of generalized blended trigonometric Bézier curves with shape parameters,” Adv. Differ. Equ., vol. 2020, pp. 550, 2020. doi: 10.1186/s13662-020-03001-4. [Google Scholar] [CrossRef]
34. X. A. Han, Y. Ma, and X. Huang, “A novel generalization of Bézier curve and surface,” J. Comput. Appl. Math., vol. 217, no. 1, pp. 180–193, Jul. 2008. doi: 10.1016/j.cam.2007.06.027. [Google Scholar] [CrossRef]
35. R. Lattarulo, L. González, E. Martí, J. Matute, M. Marcano and J. Pérez, “Urban motion planning framework based on N-Bézier curves considering comfort and safety,” J. Adv. Transport., vol. 2018, no. 3, pp. 1–13, 2018. doi: 10.1155/2018/6060924. [Google Scholar] [CrossRef]
36. Ü. Dinçer and M. Çevik, “Improved trajectory planning of an industrial parallel mechanism by a composite polynomial consisting of Bézier curves and cubic polynomials,” Mech. Mach. Theory, vol. 132, no. 5, pp. 248–263, 2019. doi: 10.1016/j.mechmachtheory.2018.11.009. [Google Scholar] [CrossRef]
37. M. S. Mohd Asaari, S. A. Suandi, and B. A. Rosdi, “Fusion of band limited phase only correlation and width centroid contour distance for finger-based biometrics,” Expert. Syst. Appl., vol. 41, no. 7, pp. 3367–3382, Jun. 2014. doi: 10.1016/j.eswa.2013.11.033. [Google Scholar] [CrossRef]
38. S. P. Vaidya, “Fingerprint-based robust medical image watermarking in hybrid transform,” Vis. Comput., vol. 39, no. 6, pp. 2245–2260, 2023. doi: 10.1007/s00371-022-02406-4. [Google Scholar] [PubMed] [CrossRef]
39. B. Huang, Y. Dai, R. Li, D. Tang, and W. Li, “Finger-vein authentication based on wide line detector and pattern normalization,” in Proc. Int. Conf. Pattern Recognit., Istanbul, Turkey, 2010, pp. 1269–1272. doi: 10.1109/ICPR.2010.316. [Google Scholar] [CrossRef]
40. N. Miura, A. Nagasaka, and T. Miyatake, “Extraction of finger-vein patterns using maximum curvature points in image profiles,” in Proc. 9th IAPR Conf. Mach. Vis. Appl., Tsukuba Science City, Japan, 2005, pp. 347–350. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF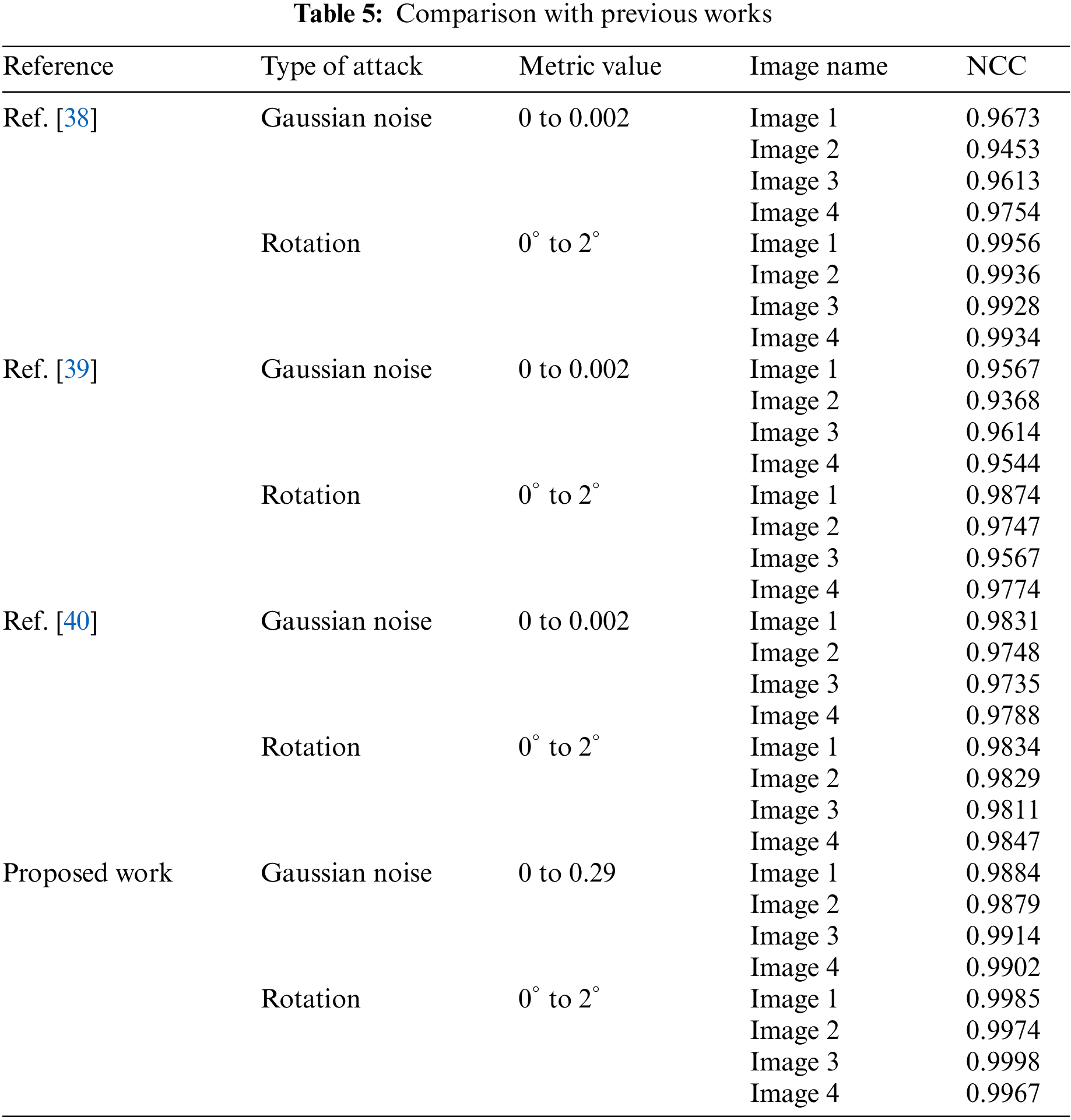
 Downloads
Downloads
 Citation Tools
Citation Tools