 Open Access
Open Access
ARTICLE
Chaotic CS Encryption: An Efficient Image Encryption Algorithm Based on Chebyshev Chaotic System and Compressive Sensing
Key Laboratory of Trustworthy Distributed Computing and Service (BUPT), Ministry of Education, Beijing University of Posts and Telecommunications, Beijing, 100876, China
* Corresponding Author: Jie Yuan. Email:
Computers, Materials & Continua 2024, 79(2), 2625-2646. https://doi.org/10.32604/cmc.2024.050337
Received 03 February 2024; Accepted 03 April 2024; Issue published 15 May 2024
Abstract
Images are the most important carrier of human information. Moreover, how to safely transmit digital images through public channels has become an urgent problem. In this paper, we propose a novel image encryption algorithm, called chaotic compressive sensing (CS) encryption (CCSE), which can not only improve the efficiency of image transmission but also introduce the high security of the chaotic system. Specifically, the proposed CCSE can fully leverage the advantages of the Chebyshev chaotic system and CS, enabling it to withstand various attacks, such as differential attacks, and exhibit robustness. First, we use a sparse trans-form to sparse the plaintext image and then use the Arnold transform to perturb the image pixels. After that, we elaborate a Chebyshev Toeplitz chaotic sensing matrix for CCSE. By using this Toeplitz matrix, the perturbed image is compressed and sampled to reduce the transmission bandwidth and the amount of data. Finally, a bilateral diffusion operator and a chaotic encryption operator are used to perturb and expand the image pixels to change the pixel position and value of the compressed image, and ultimately obtain an encrypted image. Experimental results show that our method can be resistant to various attacks, such as the statistical attack and noise attack, and can outperform its current competitors.Keywords
With the advancement of technology and the continuous development of society, modern individuals are increasingly concerned about the security of information and data. As the primary medium for conveying information, the security of digital images is of paramount importance, encompassing not only personal data but also sensitive areas such as military, political, medical, and commercial domains. Consequently, the encrypted transmission of image information has emerged as a rapidly growing and intriguing field, garnering significant attention within the realms of image processing, data transmission, and computer science [1–4].
Unlike text encryption technology, image encryption techniques often possess unique characteristics, such as high pixel correlation and substantial data storage requirements. Traditional encryption methods typically encompass the advanced encryption standard (AES) [5], international data encryption algorithm (IDEA) [6], and data encryption standard (DES) [7]. However, due to the distinctive features of images, these methods are generally unsuitable for image encryption. Consequently, numerous researchers have proposed various methods to mitigate redundancy in image content during encryption, such as chaos-based encryption methods.
Chaos theory is a method that involves both qualitative discussion and quantitative analysis to examine the characteristics of dynamic systems, such as chemical reactions, weather changes, and social behaviors. It was initially proposed by the meteorologist Lorenz and later rigorously defined mathematically by Li et al. in 1975 [8]. Subsequently, Feigenbaum summarized the universality of common characteristics of chaotic mapping systems, such as the ergodic theorem [9]. Following these developments, chaos theory began to be applied in various fields, including weather forecasting and the study of social behavior. Since then, researchers in diverse disciplines have sought to uncover correlations among internal elements from various irregular phenomena [10,11]. Consequently, chaos has become a prominent research topic.
It is well-known that chaotic systems exhibit several characteristic properties, including pseudo-randomness, ergodicity, unpredictability, and sensitivity to initial conditions and system parameters. These attributes make chaotic systems a promising alternative to traditional image encryption algorithms [12]. Additionally, chaotic systems offer a large key space and can be efficiently implemented in parallel using hardware. Motivated by these advantages, researchers have introduced several chaos-based approaches for image encryption [13–17]. For instance, Talhaoui et al. proposed a real-time image encryption framework utilizing their fractional one-dimensional chaotic map, which significantly enhances both the security and speed of encryption [13]. Tamang et al. utilized chaotic ion-acoustic waves in space plasma to develop a robust image encryption method. By incorporating SHA-512 hash computation and DNA coding, the proposed encryption method demonstrates high resistance against various decryption techniques [18].
While chaotic-based encryption algorithms often exhibit strong encryption performance, it is important to acknowledge that the image encryption process typically involves compression operations for image transmission or storage [19]. Additionally, the order of encryption and compression directly impacts the overall efficiency of digital image performance. For example, encrypted image data may not be compressible [20], posing a challenge in balancing security and compression performance. Common image compression techniques, such as discrete wavelet transform, Fourier transform, and the joint photographic experts group (JPEG) standard, may affect encryption effectiveness. For instance, the size of encrypted bitstreams may vary in JPEG-based compression-encryption approaches due to the removal of JPEG marker codes [21]. To address this challenge, many researchers have proposed encryption-then-compression (ETC) frameworks that aim to satisfy both requirements. However, compared to state-of-the-art image coders without encryption, existing ETC methods often exhibit lower performance [22]. Furthermore, the security of these approaches is susceptible to attacks from jigsaw puzzle solvers when dealing with large images. This issue may arise from the perception of compression and encryption as distinct operations.
As a result, integrating compression into image encryption has become an intriguing topic. Building upon this foundation, several methods based on number theory and chaotic theory have been proposed for image encryption [23,24]. However, these encryption algorithms may be susceptible to plaintext and differential attacks, and the achievable compression may be marginal or even negative [25]. Recently, Candes et al. introduced a sampling and compression framework known as compressive sensing (CS), which overcomes the limitations of the Nyquist sampling theorem [26]. Given the high correlation among adjacent pixels and the strong redundancy in images, several CS-based image encryption methods have emerged [27,28], enabling encryption and compression during the image sampling process. Moreover, the choice of sensing matrix plays a crucial role in these encryption schemes. For instance, Chai et al. proposed an efficient image encryption method based on CS using chaotic principles [27]. Although this encryption algorithm demonstrates effective encryption, it may increase transmission costs due to the utilization of Gaussian random sampling matrices. More recently, some researchers have demonstrated that chaotic sensing matrices can not only ensure the sampling efficiency of CS but also reduce memory complexity, making them easily implementable in software and hardware [29–31]. Consequently, a natural question arises: Can we develop an efficient image encryption algorithm directly based on chaotic systems and CS?
To address this query, we propose a novel image encryption algorithm named chaotic CS encryption (CCSE) in this paper, which combines the strengths of the Chebyshev chaotic system and CS. Our proposed CCSE exhibits resilience against various attacks, including statistical and noise attacks, and outperforms current competitors in terms of performance. Additionally, CCSE can be readily implemented in both software and hardware. The proposed CCSE algorithm first employs a sparse transform to sparsify the plaintext image, followed by applying the Arnold transform to perturb the image pixels. Subsequently, we design a Chebyshev Toeplitz chaotic sensing matrix, which significantly reduces memory and computational complexity and can be easily implemented in hardware. Utilizing the customized Chebyshev Toeplitz sensing matrix, we sample and compress the perturbed image to reduce transmission bandwidth and data volume. Finally, a bilateral diffusion operator and a chaotic encryption operator are utilized to perturb and expand the image pixels, altering both the pixel position and value of the compressed image, thereby producing the encrypted image. The main contributions of this paper are summarized as follows:
(1) We propose a novel image encryption algorithm based on Chebyshev chaotic system and CS, which can not only improve the efficiency of image transmission, but also introduce the high security.
(2) We introduce a Chebyshev Toeplitz chaotic sensing matrix to sample and compress the perturbed image for image encryption, which can obtain considerable encryption and compression performance in the proposed CCSE framework.
(3) We verify that the proposed CCSE algorithm is highly secure and effective through abundant numerical tests, including histogram, robustness, correlation analysis, and statistical attack.
The rest of this paper is organized as follows. Section 2 introduces the related work. Section 3 designs the proposed CCSE framework. Section 4 shows the experimental evaluation. Section 5 concludes the work.
Chebyshev chaotic system of degree μ is defined as:
where
By iterating Eq. (1), we can obtain a set of Chebyshev chaotic sequence
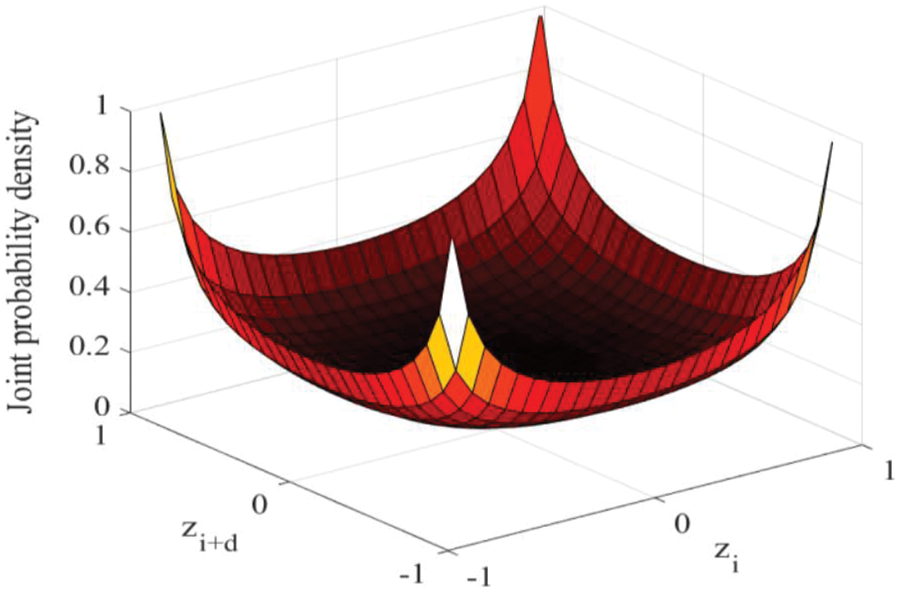
Figure 1: Joint probability function for Chebyshev chaotic sequence
Moreover, Gan et al. have verified that the Chebyshev map’s transient time is zero, which indicates that the Chebyshev’s sequence
2.2 Chaotic-Based Image Encryption Methods
As mentioned in the introduction, strengthening security and enforcing authorized access to sensitive data is the major challenge for digital image services. A straightforward solution to this problem is to make the image less intuitive. To this end, different chaotic-based image encryption methods have been introduced for image security in recent years [13–17,32–34].
For example, Enayatifar et al. designed a chaos-based image encryption by using a hybrid model based on a Logistic chaotic system and deoxyribonucleic acid (DNA) masking [17]. Similar to this work, Zhen et al. proposed a secure image encryption method based on Logistic and spatiotemporal chaotic systems [33]. Due to the extreme sensitivity of chaotic system, the proposed approach can greatly increase the complexity of the cracking algorithm. Motivated by this work, Wang et al. then introduced an image encryption algorithm using cycle shift and chaotic system. The proposed method is proven to be capable of defending against attacks [16]. Following this work, Talhaoui and Wang introduced a real-time image encryption scheme by using their fractional one-dimensional chaotic map, which can significantly improve the security and speed of encryption [13]. To increase the security performance, Alawida et al. designed a hybrid chaotic system, and then applied this chaotic system to image encryption, which is verified to be highly resistant to different attacks [15]. In addition, different researchers have also proposed various image encryption schemes based on one or multiple chaotic systems [32,34].
Although the above chaotic-based encryption methods often have good encryption performance, modern communication systems typically own dual requirements of encryption and compression [26–28]. As a result, it is necessary to embed compression into image encryption in order to satisfy the double requirements. In this work, our proposed CCSE method is such a scheme, which can not only retain the high security of chaotic-based image encryption, but also introduce the advantages of compressive sensing.
Mathematically, let
where
Because of
To solve the problem of Eq. (3), there exist many CS optimization algorithms, such as basis pursuit [35], deep optimization-inspired network [36,37]. The RIP offers a distinct geometrical explanation and gives an exactly united architecture to deal with signal recovery. For images, it is a typical compressed signal and can be directly applied to CS theory.
In this section, we first design the Chebyshev Toeplitz chaotic sensing matrix that meets the RIP, and then introduce the proposed CCSE framework.
3.1 Chebyshev Toeplitz Chaotic Sensing Matrix
We first use Eq. (1) to generate a Chebyshev chaotic sequence
where
Theorem 1. The CTsM,
According to Theorem 1, we can easily obtain that CTsM meets the RIP, which can grantee the sampling efficiency of CS. Moreover, due to the Toeplitz structure of CTsM, this Toeplitz-based matrix
Fig. 2 presents the framework of the proposed CCSE method. CCSE is composed of an encryption process and a decryption process, and they present an inverse relationship. To be more specific, the encryption process includes image sparse representation, an Arnold scrambling operator, a compressive sensing operator, a bilateral diffusion operator, a chaotic scrambling operator. Correspondingly, the decryption process consists of the reverse operation of the above steps.
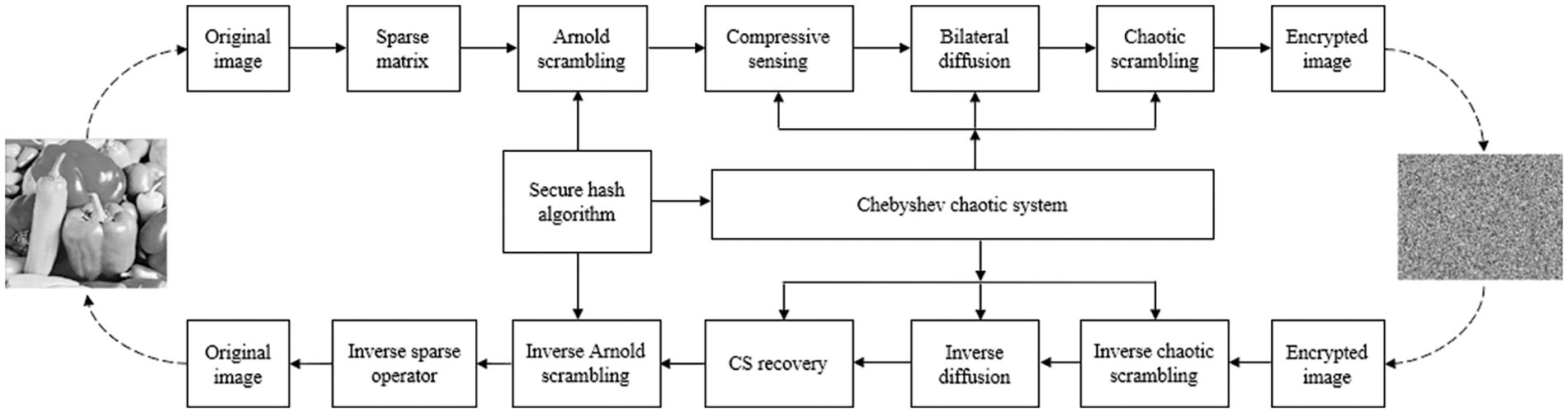
Figure 2: The CCSE framework, which consists of an encryption process and a decryption process, where the decryption process is the reverse of the encryption process
Moreover, the CS operator, bilateral diffusion operator, chaotic scrambling operator are based on Chebyshev chaotic sequence generated by Eq. (1), as shown in Fig. 2. Let
The secure hash algorithm is designed by National institute of standards and technology, and has very high security. Therefore, this operation can increase the correlation between the key and the plaintext image, which can better prevent plaintext attack.
Moreover, the encryption process of the proposed CCSE can be summarized as the following steps:
Step 1 Sparse representation: We use a sparse basis
Note that B can be many sparse transforms, such as Fourier transform and discrete cosine domain.
The sparse coefficients of the image are predominantly comprised of numerous zeros, accompanied by a limited number of larger coefficients. This characteristic results in a sparse representation that effectively reduces the overall complexity associated with processing images. Note that the sparsification defined by Eq. (5) is reversible.
Step 2 Arnold scrambling operator: We utilize the Arnold scrambling operator
where
where (
The Arnold scrambling operator plays a crucial role in evenly distributing the high-frequency information of matrix C across the D space. This redistribution effectively mitigates the block effect, leading to improved outcomes in image CS. Consequently, this operator contributes to a more uniform distribution of information, thereby enhancing the effectiveness of the image compression and reconstruction processes.
Step 3 Compressive sensing: Using (
where
Step 4 Bilateral diffusion operator: This operator consists of a forward diffusion function
Specifically, for an element of
where
After the bilateral diffusion operator, the extraction of information related to the original image from the ciphertext image q becomes a challenging task, consequently enhancing the overall security of the encryption process. The inherent difficulty introduced by this operation serves as a robust protective measure, making it arduous for unauthorized entities to retrieve meaningful details from the encrypted data.
Step 5 Chaotic scrambling operator: We use the Chaotic scrambling operator
where
As descripted in Fig. 2, the decryption process of the proposed CCSE is the reverse of the encryption process. Specially, the decryption process consists of an inverse sparse operator, an inverse Arnold scrambling operator, a CS recovery, an inverse bilateral diffusion operator, and an inverse chaotic scrambling operator. Note that the inverse sparse operator, the inverse Arnold scrambling operator, the inverse bilateral diffusion operator, and the inverse chaotic scrambling operator is the corresponding reverse operations of step 1, step 2, step 4, and step 5 in the encryption process.
For example, the inverse sparse operator can be formed as:
which is the inverse of Eq. (5). By using this inverse sparse operator, we can obtain the reconstructed and decrypted image
Specially, the CS recovery can be converted to some optimization problems, most famously,
In this section, the encryption performance of the proposed CCSE is investigated via numerical experiments. For a fair comparison, we also use several image chaotic encryption methods as the comparison algorithms of CCSE. The results of the compared algorithms are obtained using the author’s publicly available code or by reproducing the methods (in cases where the codes are not available).
4.1 Experimental Setup and Environment
We use the standard test images to test the performance of CCSE. The standard test images include “Lena”, “Pepper”, “Cameraman”. In addition, these numerical experiments are implemented on the MATLAB 2018(R2018b) platform on a computer PC with Intel(R) Xeon(R) Silver 4110 CPU @ 2.10 GHz, 64 G memory, Windows 10 system. In particular, we adopt basis pursuit method [35] as the CS recovery algorithm for CCSE. The quality metric for image recovery is the commonly used peak signal-to-noise ratio (PSNR) defined as:
where
where x
4.2 Encrypted Data and CS Recovery
We take images (“Lena”, “Pepper”, “Cameraman”) of size

Figure 3: Original image, encrypted image, and decrypted image. (a) Original “Lena”, (b) encrypted “Lena”, (c) decrypted “Lena”; (d) Original “Pepper”, (e) encrypted “Pepper”, (f) decrypted “Pepper”; (g) Original “Cameraman”, (h) encrypted “Cameraman”, (i) decrypted “Cameraman”
In addition, to observe in more detail, we adopt various CTsMs with different sizes for CCSE, i.e.,

Figure 4: Encrypted images and decrypted images at different measurement rates. (a) Encrypted “Lena” at τ = 0.4, (b) decrypted “Lena” at τ = 0.4; (c) encrypted “Lena” at τ = 0.6, (d) decrypted “Lena” at τ = 0.6; (e) encrypted “Lena” at τ = 0.8; (f) decrypted “Lena” at τ = 0.8
The proposed CCSE adopts the secure hash algorithm SHA-256 to generate the keys, therefore, the key space for CCSE is
Histogram is a statistical method of data distribution, which is also an efficiency tool to measure the encryption performance of a method. We illustrate the histograms for our proposed CCSE on images “Lena”, “Pepper”, and “Cameraman” in Fig. 5. The second column and fourth column are the histograms of original images and the encrypted images, respectively. According to Fig. 5, we can see that the histogram of the original image exhibits a Gaussian phenomenon, which is unevenly distributed. However, the histogram of encrypted image has no high and low features, which is flat. Moreover, the distribution characteristics of a histogram can be quantitatively verified by calculating the variance of the histogram [43,44]. It can be expressed as:
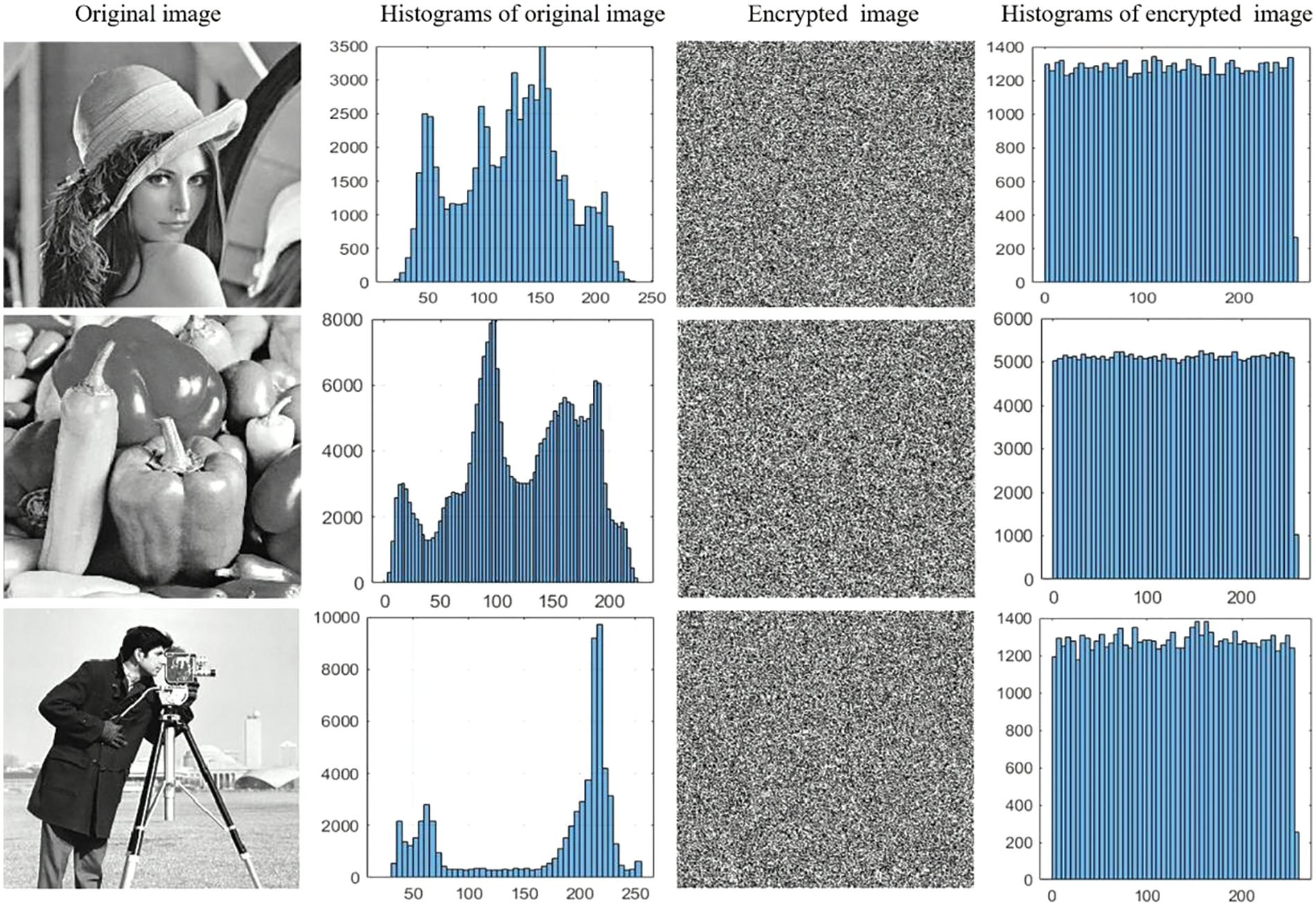
Figure 5: Histograms of original images and the encrypted images. First column: Original images; Second column: Histograms of original images; Third column: The encrypted images; Fourth column: Histograms of encrypted images
where
We calculated the histogram variances for the proposed scheme concerning plain images with a size of

Because the histogram of encrypted image for CCSE is flat, the attackers cannot collect effective information through pixel statistical analysis. As a result, the proposed CCSE can resist statistical analysis.
4.5 Differential Attack Analysis
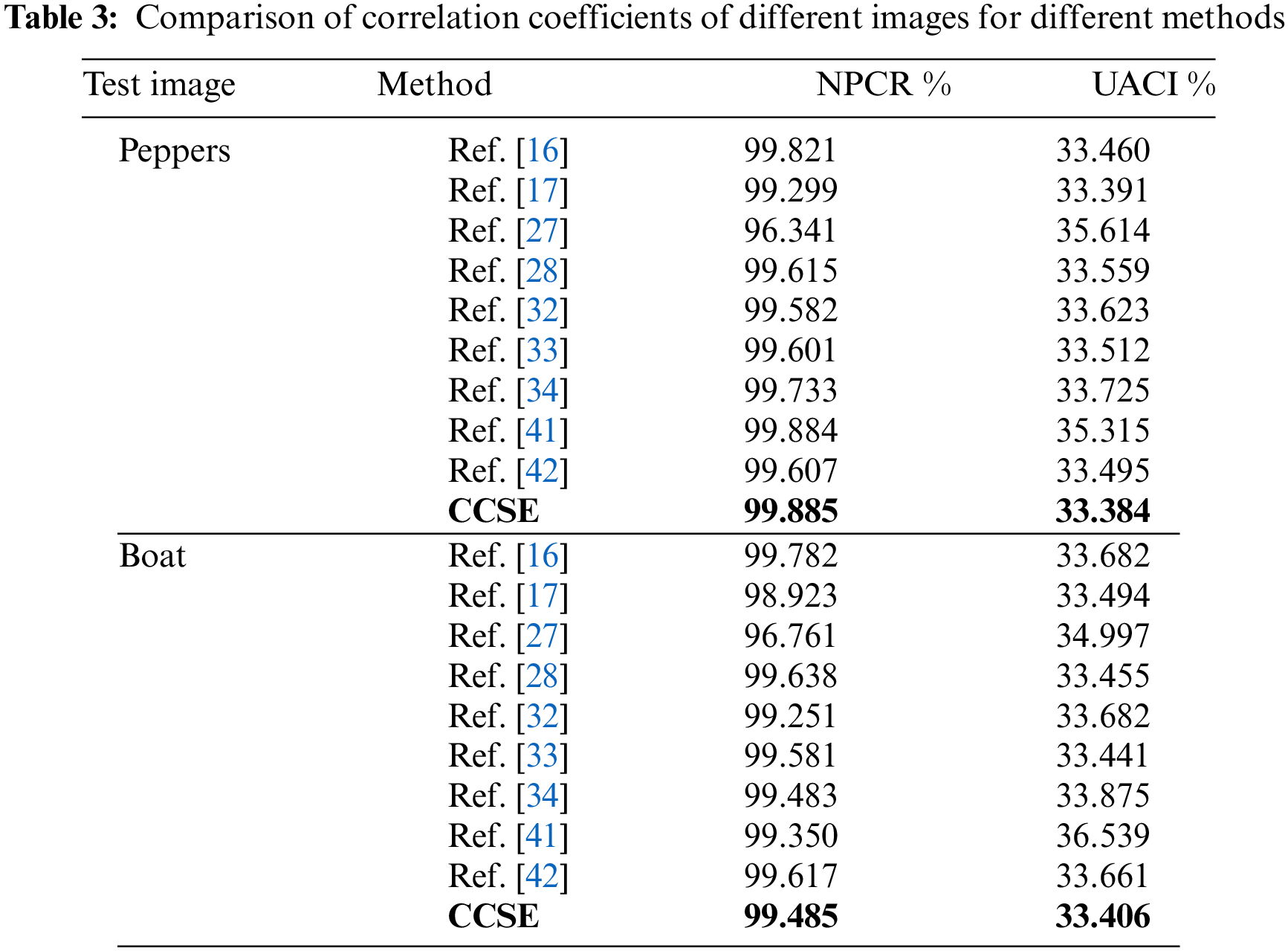
Typically, an attacker may make slight modifications to the original image (e.g., changing only one pixel) and observe the corresponding changes in the encrypted results. Through this approach, the attacker may discover meaningful relationships between two ciphered images and the original image. To assess the impact of this attack on the encryption algorithm, we use two evaluation metrics [16,17], i.e., Number of pixels change rate (NPCR) and Unified average changing intensity (UACI), which are described as following:
and
Note that if
4.6 Information Entropy Analysis
Information entropy is commonly used to evaluate the randomness of an image, and its definition is
where
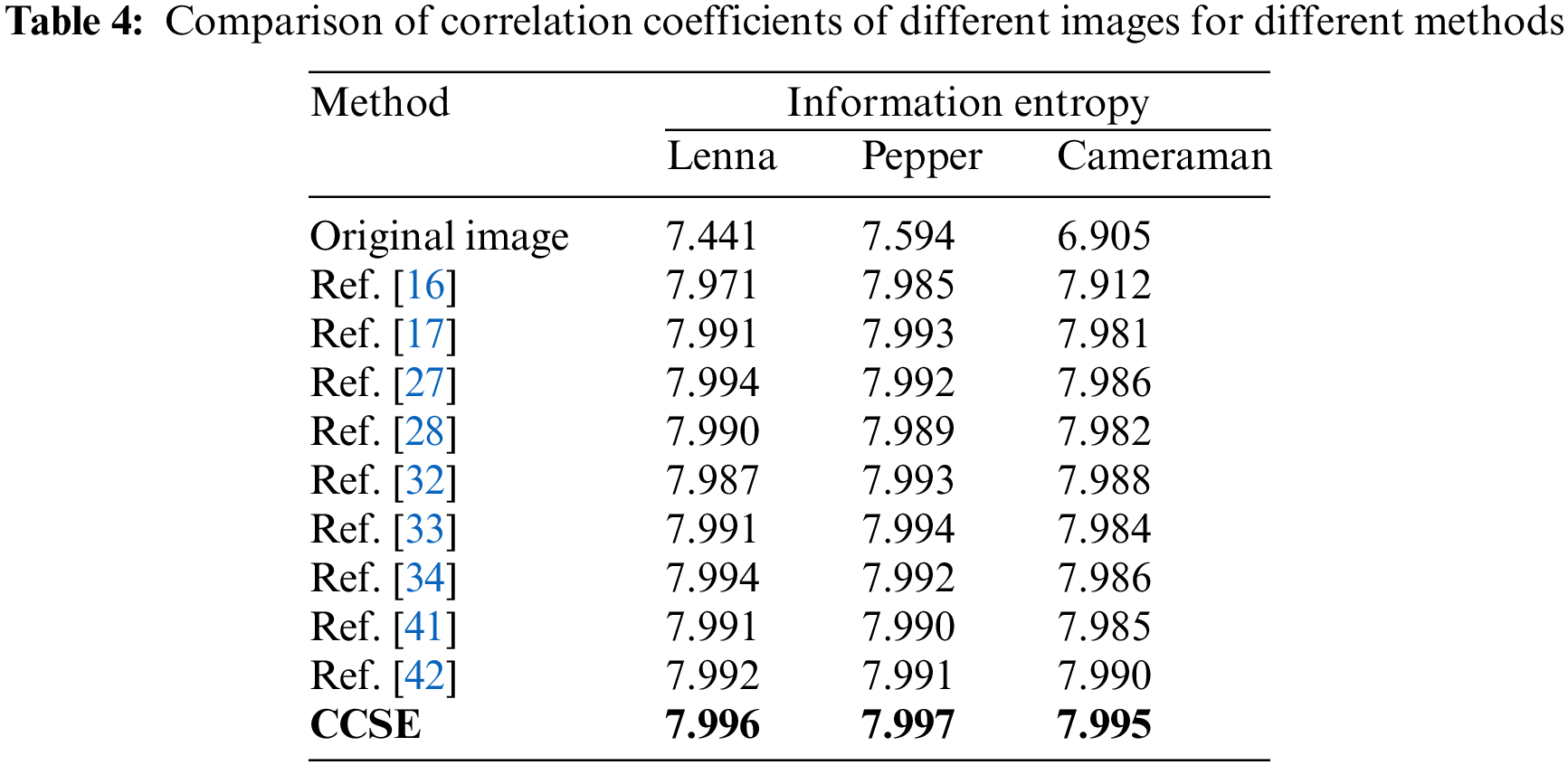
The correlation coefficients of vertical, horizontal and diagonal adjacent pixels are important metrics to measure the encryption performance of a method. Specially, correlation coefficient of adjacent pixels of an encrypted image obtained by an excellent encryption algorithm should be small, close to zero. In this experiment, we randomly choose 10000 pairs of adjacent pixels of an original image and its corresponding encrypted image, and compute the correlation coefficient via
where
Fig. 6 illustrates the correlation distribution of “Lena” and its ciphertext image in three directions for our proposed CCSE. According to Fig. 6, we can see that the correlation distributions of vertical, horizontal and diagonal adjacent pixels for the original “Lena” are linear, however, they have become disorganized, and evenly distributed after encryption. In other words, the correlation coefficients of the encrypted image are weak, and thus the proposed CCSE can resist correlation analysis.
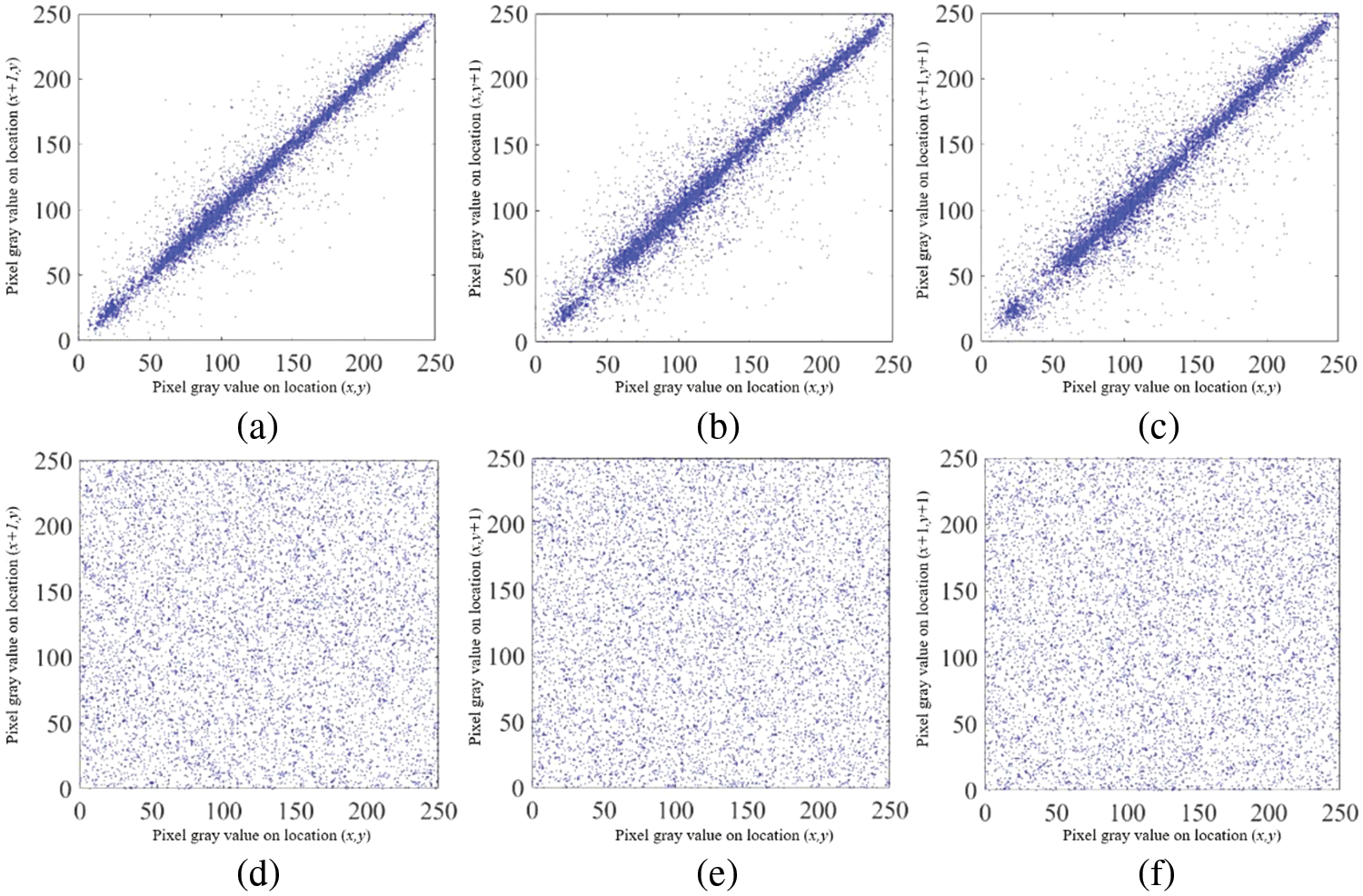
Figure 6: The correlation distribution of “Lena” and its ciphertext image in three directions. (a)–(c) denote the horizontal, vertical, and diagonal correlation distributions of the original “Lena”, respectively; (d)–(f) are the horizontal, vertical, and diagonal correlation distributions of the encrypted “Lena”, respectively
Moreover, Table 5 presents the correlation coefficients of different plaintext images and their encrypted images in three directions. From Table 5, we can see that the original image’s the correlation coefficients generally exceed 0.9. Moreover, compared to other encryption methods, our proposed CCSE owns smaller correlation coefficients in three directions, indicating that CCSE has better encryption characteristics.
4.8 Analysis of Visual Strength
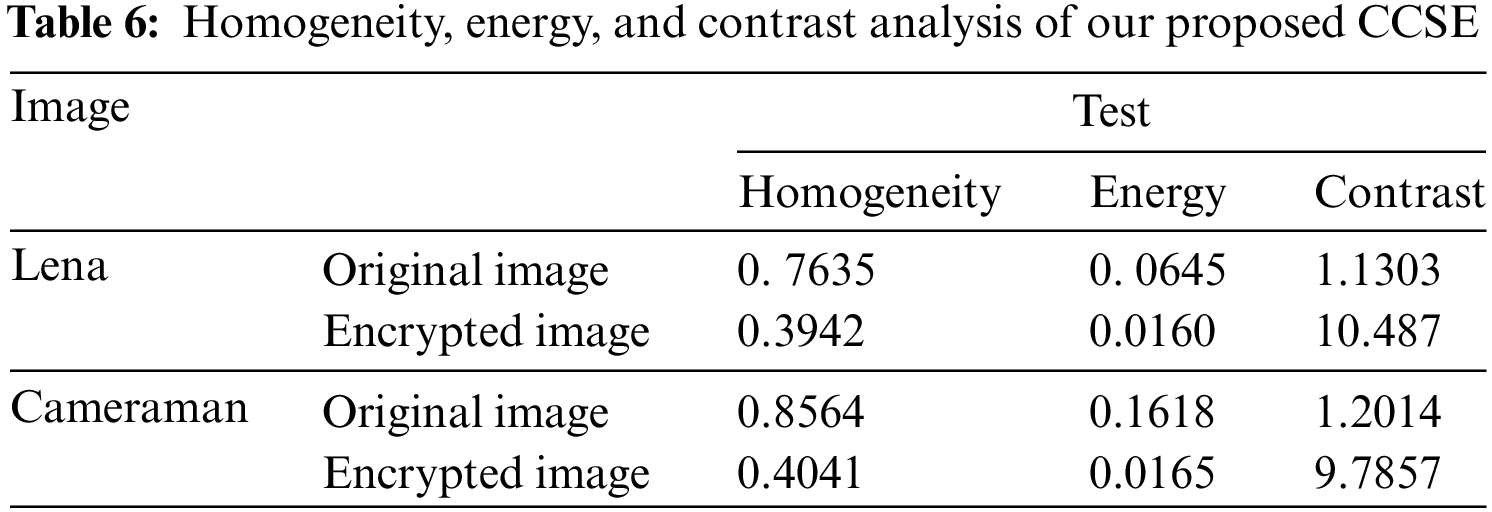
In this part, we conduct tests on Homogeneity, Energy, and Contrast analysis to assess the strength of the proposed CCSE, as shown in Table 6. Homogeneity analysis is used to assess the closeness of distribution from the diagonal of GLCM (Grey Level Co-occurrence Matrix) [45]. Energy analysis is employed to quantify the disorderliness within the texture of the cipher image by is employed to quantify the disorderliness within the texture of the cipher image by summing the squared values of GLCM [46]. Contrast analysis can capture the variations among the pixels in the image [47]. According to Table 6, we can see that our proposed CCSE exhibits excellent encryption performance, effectively ensuring high-quality encryption of images.
4.9 Noise Attack and Robustness
As we all know, images are easily affected by noise during transmission, and may even be maliciously attacked, thus we need to explore the robustness analysis for the encryption method. Based on this observation, we will use Gaussian noise and salt and pepper noise to perform noise attack on the ciphertext images to test the robustness of the algorithm. The Gaussian noise level has mean zero and is controlled by its variance

Figure 7: Different noises and their decrypted images. First row, (a)–(d) are the Gaussian noise with variance
According to Fig. 7, it clearly shows that we can still decrypt the original image from the ciphertext image with different noises, which indicates that the proposed CCSE encryption scheme has good robustness.
4.10 Analysis of Chosen-Plaintext Attacks and Known-Plaintext
As described in before, CCSE use the plaintext image
4.11 Analysis of Computational Time Complexity
We selected Lena as the test image to assess the time required for the proposed encryption and decryption methods. The encryption time represents the duration from the original image to the ciphertext image, while the decryption time signifies the time to restore the original image from the ciphertext image. For the Lena image, the proposed CCSE exhibits an encryption time of 0.4323 s and a decryption time of 0.5745 s. While the encryption time of [32,34] and [45] are 0.6892 s, 0.7521, and 4.4282 s, and the corresponding decryption time are 0.8754 s, 0.7965, and 3.4532 s, respectively. Compared to the method in [32], our proposed CCSE is 37.28% faster in encryption time and 52.38% faster in decryption time. It is evident that this proposed CCSE allows for rapid encryption and decryption of images.
In conclusion, this paper introduces a novel image encryption algorithm, termed chaotic compressive sensing (CS) encryption (CCSE), which addresses the increasing concerns regarding information security in the digital age. The significance of secure image transmission spans across personal privacy, political communications, medical data, and commercial interests. Recognizing these implications, CCSE emerges as a promising solution by combining the efficiency of CS with the robust security provided by chaotic systems. As a result, CCSE can withstand various attacks, such as differential attack, and exhibit robustness. The proposed CCSE employs a sequence of transformations, including sparse transformation, Arnold transformation, and the integration of a Chebyshev Toeplitz chaotic sensing matrix. These transformations collectively facilitate image perturbation, sampling, and compression, thereby reducing transmission bandwidth and data volume without compromising security. Moreover, the incorporation of bilateral diffusion and chaotic encryption operators further enhances the security of CCSE by perturbing and expanding pixel values and positions within the encrypted image. Through extensive experimental validation, CCSE exhibits robustness against statistical and noise attacks, surpassing existing competitors in terms of security and performance. CCSE represents a significant advancement in the field of image encryption, offering a viable solution to the pressing challenges of information security in an increasingly digitized world. Its effectiveness in safeguarding sensitive data across diverse domains underscores its potential for practical implementation and further research exploration.
Our proposed CCSE is more suitable for regular images. However, once the image size becomes too large, it leads to excessive complexity in our approach. In future work, we will develop a more lightweight image chaotic compression encryption scheme based on CCSE. Additionally, CCSE requires collaboration with traditional CS reconstruction algorithms to recover images. However, the slow recovery speed of traditional CS reconstruction algorithms imposes a time constraint on our proposed CCSE. By integrating deep learning techniques with CCSE, we will explore novel image chaos encryption methods aimed at enhancing security and adaptability. Through real-world application validation, especially in areas such as communication and cloud storage, we will assess the performance of these algorithms, ensuring their effectiveness and feasibility in practical scenarios.
Acknowledgement: The authors appreciate the reviewers and editors for their valuable feedback on this work.
Funding Statement: This work was supported by the National Natural Science Foundation of China (Nos. 62002028, 62102040 and 62202066).
Author Contributions: Mingliang Sun: Conceptualization, Methodology, Writing-original and Editing; Jie Yuan: Software, Investigation; Xiaoyong Li: Investigation, Supervision and Writing-original draft; Dongxiao Liu: Funding acquisition and Experimental verification. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available on request from the authors.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. J. Al-Azawi, N. Al-Saidi, H. A. Jalab, R. Ibrahim, and D. Baleanu, “Image splicing detection based on texture features with fractal entropy,” Comput. Mater. Contin., vol. 69, no. 3, pp. 3903–3915, 2021. doi: 10.32604/cmc.2021.020368. [Google Scholar] [CrossRef]
2. S. Boopathi, B. K. Pandey, and D. Pandey, “Advances in artificial intelligence for image processing: Techniques, applications, and optimization,” in Handbook of Research on Thrust Technologies’ Effect on Image Processing. Hershey, USA: IGI Global, 2023, pp. 73–95. [Google Scholar]
3. Y. Hu and L. Nan, “A novel 2D hyperchaotic with a complex dynamic behavior for color image encryption,” Comput. Mater. Contin., vol. 74, no. 3, pp. 6555–6571, 2023. doi: 10.32604/cmc.2023.036090. [Google Scholar] [CrossRef]
4. C. L. Chowdhary, P. V. Patel, K. J. Kathrotia, and M. F. Ijaz, “Analytical study of hybrid techniques for image encryption and decryption,” Sensors, vol. 20, no. 18, pp. 5162, 2020. doi: 10.3390/s20185162. [Google Scholar] [PubMed] [CrossRef]
5. V. Rijmen and J. Daemen, “The advanced encryption standard,” in Proc. Federal Inform. Process. Standards Pub., Nat. Institute Standards Technol., 2001, vol. 26, pp. 137–139. [Google Scholar]
6. S. Basu, “International data encryption algorithm (IDEA)–a typical illustration,” J. Global Res. Comput. Sci., vol. 2, pp. 116–118, 2011. [Google Scholar]
7. D. Coppersmith, “The Data Encryption Standard (DES) and its strength against attacks,” IBM J. Res. Dev., vol. 38, no. 3, pp. 243–250, 1994. doi: 10.1147/rd.383.0243. [Google Scholar] [CrossRef]
8. T. Li and J. Yorke, “Period three implies chaos,” Am. Math. Month., vol. 82, no. 10, pp. 985–992, 1975. [Google Scholar]
9. M. Ayedi, W. H. ElAshmawi, and E. Eldesouky, “Hybrid chaotic salp swarm with crossover algorithm for underground wireless sensor networks,” Comput. Mater. Contin., vol. 72, no. 2, pp. 2963–2980, 2022. doi: 10.32604/cmc.2022.025741. [Google Scholar] [CrossRef]
10. B. Sivakumar, “Chaos theory in geophysics: Past, present and future,” Chaos Solitons & Fractals, vol. 19, no. 2, pp. 441–462, 2004. doi: 10.1016/S0960-0779(03)00055-9. [Google Scholar] [CrossRef]
11. R. Zhao, Y. Zhang, S. Li, W. Wen, S. Yi and R. Lan, “3D mesh encryption with differentiated visual effect and high efficiency based on chaotic system,” Expert. Syst. Appl., vol. 238, no. 2, pp. 122140, 2024. doi: 10.1016/j.eswa.2023.122140. [Google Scholar] [CrossRef]
12. R. Zhao, Y. Zhang, Y. Nan, W. Wen, X. Chai and R. Lan, “Primitively visually meaningful image encryption: A new paradigm,” Inf. Sci., vol. 613, pp. 628–648, 2022. doi: 10.1016/j.ins.2022.08.027. [Google Scholar] [CrossRef]
13. M. Z. Talhaoui and X. Wang, “A new fractional one dimensional chaotic map and its application in high-speed image encryption,” Inf. Sci., vol. 550, no. 2, pp. 13–26, 2021. doi: 10.1016/j.ins.2020.10.048. [Google Scholar] [CrossRef]
14. Y. Hong et al., “A novel approach for image encryption with chaos-RNA,” Comput. Mater. Contin., vol. 77, no. 1, pp. 139–160, 2023. doi: 10.32604/cmc.2023.043424. [Google Scholar] [CrossRef]
15. R. Zhao, Y. Zhang, R. Lan, Z. Hua, and Y. Xiang, “Heterogeneous and customized cost-efficient reversible image degradation for green IoT,” IEEE Internet Things J., vol. 10, no. 3, pp. 2630–2645, 2022. doi: 10.1109/JIOT.2022.3213875. [Google Scholar] [CrossRef]
16. X. Wang, S. Gu, and Y. Zhang, “Novel image encryption algorithm based on cycle shift and chaotic system,” Opt. Lasers Eng., vol. 68, no. 6, pp. 126–134, 2015. doi: 10.1016/j.optlaseng.2014.12.025. [Google Scholar] [CrossRef]
17. R. Enayatifar, A. H. Abdullah, and I. F. Isnin, “Chaos-based image encryption using a hybrid genetic algorithm and a DNA sequence,” Opt. Lasers Eng., vol. 56, pp. 83–93, 2014. doi: 10.1016/j.optlaseng.2013.12.003. [Google Scholar] [CrossRef]
18. J. Tamang et al., “Dynamical properties of ion-acoustic waves in space plasma and its application to image encryption,” IEEE Access, vol. 9, pp. 18762–18782, 2021. doi: 10.1109/ACCESS.2021.3054250. [Google Scholar] [CrossRef]
19. H. L. Gururaj, M. Almeshari, Y. Alzamil, V. Ravi, and K. V. Sudeesh, “Efficient SCAN and chaotic map encryption system for securing E-Healthcare images,” Information, vol. 14, no. 1, pp. 47, 2023. doi: 10.3390/info14010047. [Google Scholar] [CrossRef]
20. J. Jain and A. Jain, “Securing e-healthcare images using an efficient image encryption model,” Scientific Programming, vol. 2022, no. 6489331, pp. 1–11, 2022. doi: 10.1155/2022/6438331. [Google Scholar] [CrossRef]
21. N. Mao, H. He, F. Chen, P. Bellavista, and Y. Yang, “Reversible data hiding of JPEG images based on block sorting and segmented embedding,” Biomed. Signal Process. Control, vol. 87, no. 2, pp. 105555, 2024. doi: 10.1016/j.bspc.2023.105555. [Google Scholar] [CrossRef]
22. T. Chuman, W. Sirichotedumrong, and H. Kiya, “Encryption-then-compression systems using grayscale-based image encryption for JPEG images,” IEEE Trans. Inf. Forensics Secur., vol. 14, no. 6, pp. 1515–1525, 2018. doi: 10.1109/TIFS.2018.2881677. [Google Scholar] [CrossRef]
23. S. Pankaj and M. Dua, “Chaos based medical image encryption techniques: A comprehensive review and analysis,” Inform. Secur. J.: A Global Perspect., vol. 33, no. 3, pp. 1–27, 2024. doi: 10.1080/19393555.2024.2312975. [Google Scholar] [CrossRef]
24. M. Preishuber, T. Hütter, S. Katzenbeisser, and A. Uhl, “Depreciating motivation and empirical security analysis of chaos-based image and video encryption,” IEEE Trans. Inf. Forensics Secur., vol. 13, no. 9, pp. 2137–2150, 2018. doi: 10.1109/TIFS.2018.2812080. [Google Scholar] [CrossRef]
25. S. Bai, G. Zhu, and X. Ji, “Comments on a novel image encryption-compression scheme using hyper-chaos and chinese remainder theorem,” Appl. Mech. Mater., vol. 743, pp. 333–337, 2015. doi: 10.4028/www.scientific.net/AMM.743.333. [Google Scholar] [CrossRef]
26. R. Vershynin, Y. Eldar, and G. Kutyniok, “Compressed sensing, theory and applications,” in Introduction to the Non-Asymptotic Analysis of Random Matrices, Cambridge, UK: Cambridge University Press, 2012, pp. 210–268. [Google Scholar]
27. X. Chai, X. Zheng, Z. Gan, D. Han, and Y. Chen, “An image encryption algorithm based on chaotic system and compressive sensing,” Signal Process., vol. 148, no. 9, pp. 124–144, 2018. doi: 10.1016/j.sigpro.2018.02.007. [Google Scholar] [CrossRef]
28. L. Gong, K. Qiu, C. Deng, and N. Zhou, “An image compression and encryption algorithm based on chaotic system and compressive sensing,” Opt. Laser Technol., vol. 115, no. 1, pp. 257–267, 2019. doi: 10.1016/j.optlastec.2019.01.039. [Google Scholar] [CrossRef]
29. H. Gan, S. Xiao, Y. Zhao, and X. Xue, “Construction of efficient and structural chaotic sensing matrix for compressive sensing,” Signal Process.: Image Commun., vol. 68, pp. 129–137, 2018. [Google Scholar]
30. H. Gan, S. Xiao, and F. Liu, “Chaotic binary sensing matrices,” Int. J. Bifurcat. Chaos, vol. 29, no. 9, pp. 1950121, 2019. doi: 10.1142/S0218127419501219. [Google Scholar] [CrossRef]
31. H. Gan, S. Xiao, Z. Zhang, S. Shan, and Y. Gao, “Chaotic compressive sampling matrix: Where sensing architecture meets sinusoidal iterator,” Circuits Syst. Signal Process., vol. 39, no. 3, pp. 1581–1602, 2020. doi: 10.1007/s00034-019-01223-w. [Google Scholar] [CrossRef]
32. S. Wang, “Research on digital image encryption technology based on chaotic system,” Master thesis, Hangzhou Dianzi University, Hangzhou, China, 2020. [Google Scholar]
33. P. Zhen, G. Zhao, L. Min, and X. Jin, “Chaos-based image encryption scheme combining DNA coding and entropy,” Multimed. Tools Appl., vol. 75, no. 11, pp. 6303–6319, 2016. doi: 10.1007/s11042-015-2573-x. [Google Scholar] [CrossRef]
34. X. Wang, “Digital image compression algorithm based on multi-chaotic system,” Master thesis, Taiyuan University of Technology, Taiyuan, China, 2021. [Google Scholar]
35. P. Wu and J. Cheng, “Deep unfolding basis pursuit: Improving sparse channel reconstruction via data-driven measurement matrices,” IEEE Trans. Wirel. Commun., vol. 21, no. 10, pp. 8090–8105, 2022. doi: 10.1109/TWC.2022.3164091. [Google Scholar] [CrossRef]
36. H. Gan, Y. Gao, C. Liu, H. Chen, T. Zhang and F. Liu, “AutoBCS: Block-based image compressive sensing with data-driven acquisition and noniterative reconstruction,” IEEE Trans. Cybern., vol. 53, no. 4, pp. 2558–2571, 2023. doi: 10.1109/TCYB.2021.3127657. [Google Scholar] [PubMed] [CrossRef]
37. M. Shen, H. Gan, C. Ning, Y. Hua, and T. Zhang, “TransCS: A Transformer-based hybrid architecture for image compressed sensing,” IEEE Trans. Image Process., vol. 31, pp. 6991–7005, 2022. doi: 10.1109/TIP.2022.3217365. [Google Scholar] [PubMed] [CrossRef]
38. J. Haupt, W. U. Bajwa, G. Raz, and R. Nowak, “Toeplitz compressed sensing matrices with applications to sparse channel estimation,” IEEE Trans. Inf. Theory, vol. 56, no. 11, pp. 5862–5875, 2010. doi: 10.1109/TIT.2010.2070191. [Google Scholar] [CrossRef]
39. R. Baraniuk, M. Davenport, R. DeVore, and M. Wakin, “A simple proof of the restricted isometry property for random matrices,” Constr. Approx., vol. 28, no. 3, pp. 253–263, 2008. doi: 10.1007/s00365-007-9003-x. [Google Scholar] [CrossRef]
40. R. Fotohi and F. S. Aliee, “Securing communication between things using blockchain technology based on authentication and SHA-256 to improving scalability in large-scale IoT,” Comput. Netw., vol. 197, no. 3, pp. 108331, 2021. doi: 10.1016/j.comnet.2021.108331. [Google Scholar] [CrossRef]
41. R. Ponuma and R. Amutha, “Compressive sensing based image compression-encryption using novel 1D-chaotic map,” Multimed. Tools Appl., vol. 77, no. 15, pp. 19209–19234, 2018. doi: 10.1007/s11042-017-5378-2. [Google Scholar] [CrossRef]
42. J. Wu, X. Liao, and B. Yang, “Image encryption using 2D Hénon-Sine map and DNA approach,” Signal Process., vol. 153, no. 7, pp. 11–23, 2018. doi: 10.1016/j.sigpro.2018.06.008. [Google Scholar] [CrossRef]
43. Q. Lu, C. Zhu, and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single S-box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. doi: 10.1109/ACCESS.2020.2970806. [Google Scholar] [CrossRef]
44. J. S. Khan and S. K. Kayhan, “Chaos and compressive sensing based novel image encryption scheme,” J. Inf. Secur. Appl., vol. 58, no. 4, pp. 102711, 2021. doi: 10.1016/j.jisa.2020.102711. [Google Scholar] [CrossRef]
45. J. S. Khan et al., “DNA and plaintext dependent chaotic visual selective image encryption,” IEEE Access, vol. 8, pp. 159732–159744, 2020. doi: 10.1109/ACCESS.2020.3020917. [Google Scholar] [CrossRef]
46. P. Kiran and B. D. Parameshachari, “Resource optimized selective image encryption of medical images using multiple chaotic systems,” Microprocess. Microsyst., vol. 91, no. 10, pp. 104546, 2022. doi: 10.1016/j.micpro.2022.104546. [Google Scholar] [CrossRef]
47. F. Masood et al., “A novel image encryption scheme based on Arnold cat map, Newton-Leipnik system and Logistic Gaussian map,” Multimed. Tools Appl., vol. 81, no. 21, pp. 30931–30959, 2022. doi: 10.1007/s11042-022-12844-w. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF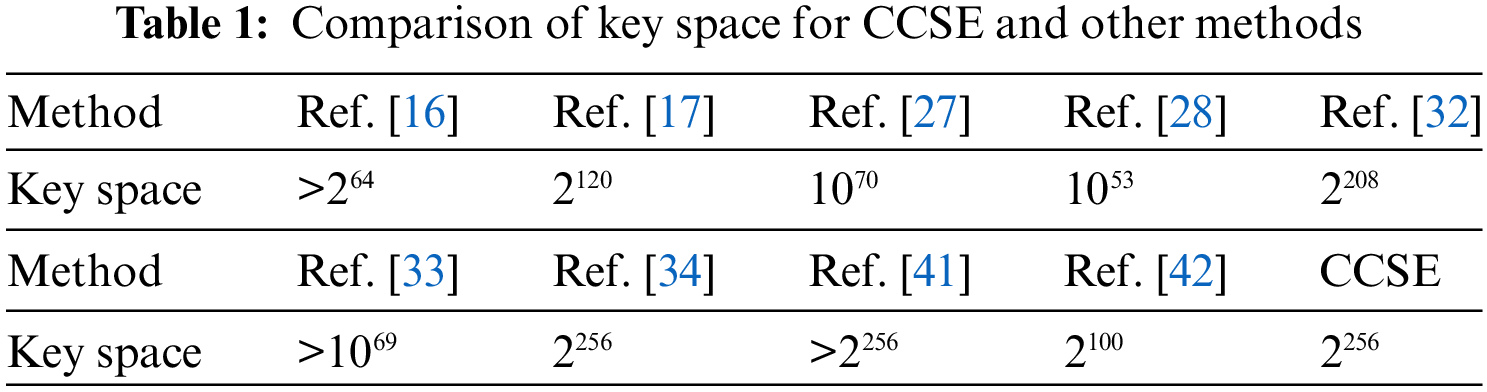
 Downloads
Downloads
 Citation Tools
Citation Tools