A Cooperated Imperialist Competitive Algorithm for Unrelated Parallel Batch Machine Scheduling Problem

1  Introduction

Unlike traditional scheduling, batch processing machines (BPM) scheduling consists of at least one BPM, and on BPM all jobs in a batch are processed simultaneously after the batch is formed. BPM scheduling problems widely exist in many real-life industries such as casting, chemical engineering, semiconductors, transportation, etc. BPM can be divided into parallel BPM and serial BPM, the processing time of a batch on the former is defined as the maximum processing time of all jobs in the batch, and the processing time of a batch on the latter is defined as the sum of processing time of all jobs in the batch. BPM scheduling problems can be divided into single BPM scheduling, parallel machine scheduling, and hybrid flow shop scheduling with BPM, etc., which have received extensive attention.

There are some works about single BPM scheduling problem, in which all batches are processed by a BPM. Uzsoy [1] first studied the problem with job size, proved that it is NP-hard, and proposed a heuristic algorithm to minimize makespan and total completion time. Lee [2] presented a polynomial algorithm and pseudo-polynomial-time algorithm to solve the problem with dynamic job arrivals. Melouk et al. [3] solved the problem with job sizes by a simulated annealing algorithm. Zhou et al. [4] considered the problem with unequal release times and job sizes and proposed a self-adaptive differential evolution algorithm with adaptively chosen mutation operators based on their historical performances to minimize makespan. Yu et al. [5] proposed a branch-and-price algorithm to solve additive manufacturing problems with the minimization of makespan. Zhang et al. [6] presented two heuristics to minimize total weighted earliness and tardiness penalties of jobs.

The parallel BPM scheduling problem has attracted much attention. Regarding the uniform parallel BPM scheduling problem, some results are obtained. Xu et al. [7] presented a Pareto-based ant colony system to simultaneously minimize makespan and maximum tardiness. Jiang et al. [8] presented a hybrid algorithm with discrete particle swarm optimization and genetic algorithm (GA), in which a heuristic and a local-search strategy are introduced. Zhang et al. [9] proposed a multi-objective artificial bee colony (ABC) to solve the problem of machine eligibility in fabric dyeing process. Jia et al. [10] proposed a fuzzy ant colony optimization (ACO) for the problem with fuzzy processing time. Liu et al. [11] designed a GA and a fast heuristic for the problem in coke production. Jia et al. [12] applied two heuristics and an ACO for the problem with arbitrary capacities. Li et al. [13] developed a discrete bi-objective evolutionary algorithm to minimize maximum lateness and total pollution emission cost. Xin et al. [14] developed an efficient 2-approximation algorithm for the problem with different BPM capacities and arbitrary job sizes.

A number of works have been obtained on unrelated parallel BPM scheduling problems. Arroyo et al. [15] proposed an effective iterated greedy for the problem with non-identical capacities and unequal ready times. Lu et al. [16] presented a hybrid ABC with tabu search to minimize the makespan of the problem with maintenance and deteriorating jobs. Zhou et al. [17] provided a random key GA for the problem with different capacities and arbitrary job sizes. Zhang et al. [18] proposed an improved evolutionary algorithm by combining a GA with a heuristic placement strategy for the problem in additive manufacturing. Kong et al. [19] applied a shuffled frog-leaping algorithm with variable neighborhood search for the problem with nonlinear processing time. Song et al. [20] developed a self-adaptive multi-objective differential evolution algorithm to minimize total energy consumption and makespan. Zhang et al. [21] formulated a mixed-integer programming (MIP) model and presented an improved particle swarm optimization algorithm for the problem with production and delivery in cloud manufacturing. Fallahi et al. [22] studied the problem in production systems under carbon reduction policies and used non-dominated sorting genetic algorithm-II and multi-objective gray wolf optimizer to simultaneously minimize makespan and total cost. Xiao et al. [23] proposed a tabu-based adaptive large neighborhood search algorithm for the problem with job sizes, ready times, and the minimization of makespan. Zhang et al. [24] provided a MIP model and a modified elite ant system with local search (MEASL) to minimize the total completion time of the problem with release times, and job sizes. Jiang et al. [25] applied an iterated greedy (IG) algorithm for the problem of release times, job sizes, and incompatible job families. Ji et al. [26] developed a hybrid large neighborhood search (HLNS) with a tabu strategy and local search to solve the problem with job sizes, ready times, and incompatible family. Ou et al. [27] presented an efficient polynomial time approximation scheme with near-linear-time complexity to solve the problem with dynamic arrivals job and rejection.

As stated above, the existing works on single BPM scheduling and parallel BPM scheduling are mainly about job sizes, incompatible family, and BPM capacity constraints, that is, the sum of the weight of all jobs in a batch cannot exceed the prefixed capacity, parallel BPM scheduling problems are handled in actual production processes like coke production, fabric dyeing, and additive manufacturing, which are close to the real situation of manufacturing process and their optimization results have high application values; however, parallel BPM scheduling problems with more constraints are not studied fully. For example, in the moulding process of a foundry [28,29], a batch is first allocated into a sandbox and then the sandbox is added to the assignment machine of the batch, for each batch, has to meet sandbox volume constraint and machine capacity constraint, and complexity of the problem increases. This is a challenge in moulding process in a foundry. On the other hand, release times of all jobs are mostly different in unrelated parallel BPM scheduling problems [24,25], release times have a positive impact on the performance of the schedule and are a frequently considered real-life condition, which also exist in moulding process, so it is necessary to deal with parallel BPM scheduling problem with sandbox volume constraint and release times.

The imperialist competitive algorithm (ICA) is an intelligent optimization algorithm inspired by social and political behavior [30]. Each intelligent optimization algorithm has its own advantages [31–34]. ICA has many notable features such as good neighborhood search ability, effective global search property, good convergence rate, and flexible structure [35]. As the main method of production scheduling [36–40], ICA has been successfully applied to solve parallel machine scheduling problem (PMSP) [41–45]. Lei et al. [37] proposed an ICA with a novel assimilation strategy to deal with low-carbon PMSP. Yadani et al. [46] developed a hybrid ICA for PMSP with two-agent and tool change activities. The good searchability and advantages of ICA in solving PMSP are tested and proven. The parallel BPM scheduling problem is the extended PMSP and the same coding can be used in these two problems. The successful applications of ICA to PMSP reveal that ICA has potential advantages in solving parallel BPM scheduling, so ICA is used.

In this study, an unrelated parallel BPM scheduling problem with release times is considered, which is refined from moulding process of a foundry, and a cooperated imperialist competitive algorithm (CICA) is presented to minimize makespan. To produce high-quality solutions, the number of empires is not used as a parameter and four empires always exist throughout the search process, cooperation between the strongest empire and the weakest empire is applied in the assimilation of these two empires, and a combination of the two remaining empires is used in the assimilation of these two empires. A new imperialist competition is given. Extensive experiments are conducted and the computational results demonstrate that new strategies of CICA are effective and that CICA has promising advantages on considered problems.

The remainder of the paper is organized as follows. The problem description is described in Section 2. Section 3 shows the proposed CICA for unrelated parallel BPM scheduling problems with the release times stage. Numerical test experiments on CICA are reported in Section 4. Conclusions and some topics of future research are given in the final section.

2  Problem Description

Unrelated parallel BPM scheduling problem in moulding process of a foundry is described as follows. n jobs J1,J2,…,Jn are processed by m parallel BPM M1,M2,…,Mm, ri indicates release times of Ji, pik denotes processing time of Ji on machine Mk. All jobs are divided into l families according to materials. Each mater-ial corresponds to a job family and jobs of different families cannot be grouped into a batch. fi∈{1,2,…,l} indicates the family of job Ji, Ji has weight wi and volume vi. There are sufficient sandbox and all sandboxes have the same volume V, all machines are given the same capacity W. Each batch is placed in a sandbox and then sandbox is placed in BPM for moulding, so two constraints are required to be satisfied for each batch: Total volume of all jobs in the batch cannot exceed V and total weight of all jobs in the batch cannot exceed W. Processing time of a batch is maximum processing time of all jobs in the batch. Release time of a batch is maximum release time of job in the batch.

There are some constraints on jobs and machines:

Each BPM can only handle one batch at a time.

No job can be processed in different batches on more than one BPM.

Operations cannot be interrupted.

The problem has three sub-problems: (1) batch formation for deciding which jobs used to form each batch, (2) BPM assignment for choosing a BPM for each batch, (3) batch scheduling for determining processing sequence of all batches on each machine. There are strong coupled relations among them. Batch formation decides directly the optimization content of other two sub-problems and optima solution of the problem can be obtained by comprehensive coordination of three sub-problems.

The goal of problem is to minimize makespan under the condition that all constraints are met.

Cmax=maxi=1,2,…,nCi(1)

where Ci is completion time of Ji, Cmax indicates maximum completion time of all jobs.

Table 1 shows an example with 12 jobs, 3 families and 3 parallel BPMs, W=10, V=10. A schedule of the example is shown in Fig. 1.

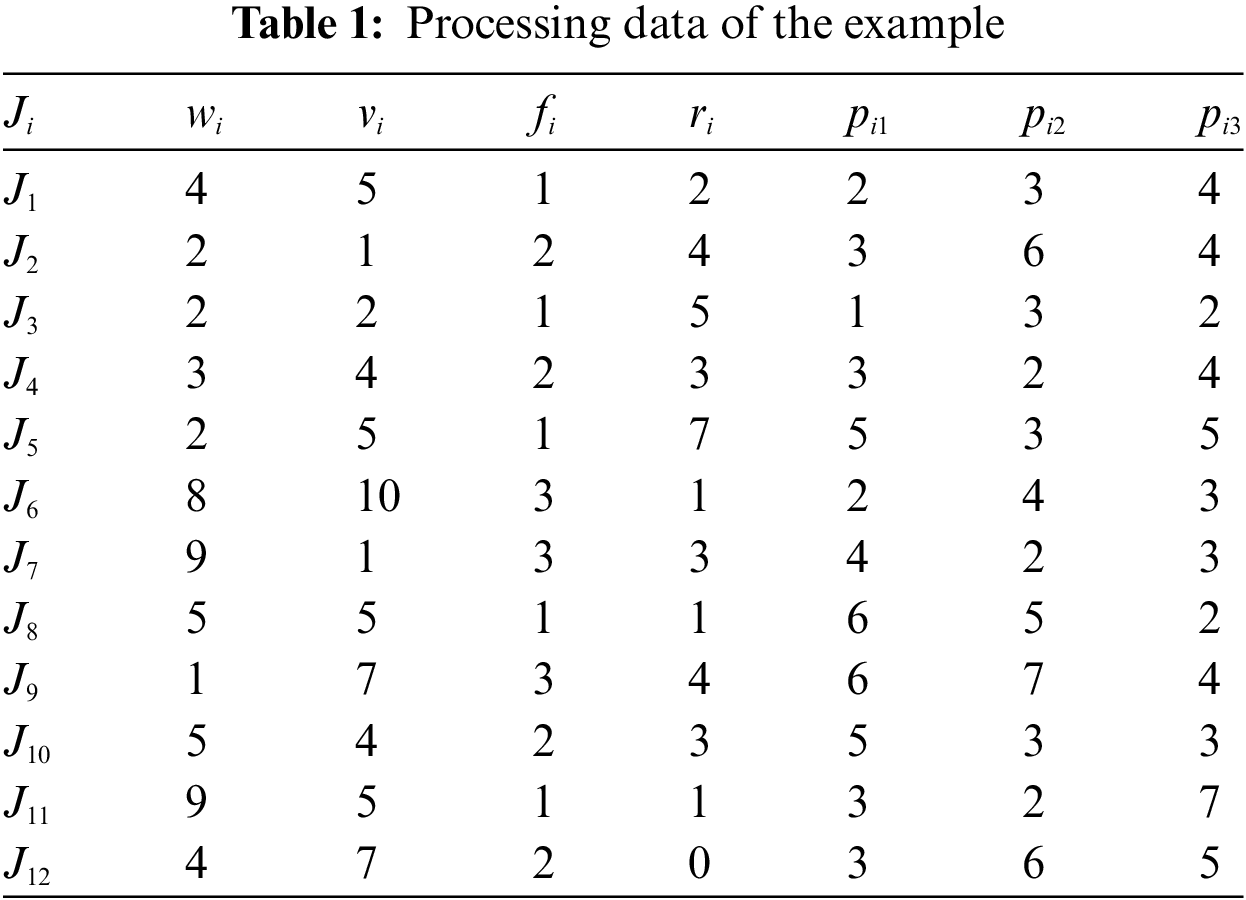
Figure 1: A schedule of the example

3  CICA for Parallel BPM Scheduling

In the existing ICAs [30,35], there are Nim initial empires and Nim is used as parameter. In this study, CICA is proposed, in which Nim is not a parameter and set to be 4 in the whole search process, then assimila-tion based on cooperation between two empires and assimilation with empire combination are implemented respectively and a new imperialist competition is given. The detailed steps of CICA are shown below.

3.1 Initialization and Formation of Four Empires

Lei et al. [47] presented a two-string representation to describe solution of unrelated PMSP, which can be directly used to describe solution of unrelated parallel BPM scheduling problem. For the problem with n jobs and m BPM, its solution is represented as a scheduling string [π1,π2,…,πn], and a machine assignment string [θ1,θ2,…,θn], where πi∈{1,2,…,n}, θi∈{1,2,…,m}.

There are some differences of the above method from coding method [47]: Scheduling string is a perm-utation of all jobs, machine assignment string is used for all batches, the number η of batches is determined by batch formation. Usually, η<n, so only the first η elements of machine assignment string are used in decoding.

The decoding procedure is described below:

Step 1: Let k=1, b-th=1, WBb-th=0, VBb-th=0, let Bb-th be empty. Each job Ji is assigned a marki, if job is not in a batch, marki=0, otherwise marki=1.

Step 2: Repeat the following steps until each job is assigned into a batch.

1) choose first job πb with markπb=0 and the first machine Mθk from machine assignment string, then Bb-th=Bb-th∪{Jπb}, markπb=1, WBb-th=wπb+WBb-th, VBb-th=vπb+VBb-th.

2) repeat the following steps until no job πc can be chosen or WBb-th+wπc>W or VBb-th+vπc>V: Choose a job πc with markπc=0 and fπc=fπb from scheduling string, if WBb-th+wπc<W, VBb-th+vπc<V, then Bb-th=Bb-th∪ {Jπc}, markπc=1, WBb-th=wπc+WBb-th, VBb-th=vπc+VBb-th.

3) Obtain batch Bb-th, b-th=b-th+1, let Bb-th be empty, WBb-th=0, VBb-th=0, k=k+1.

Step 3:η batches are finally formed and processed sequentially in terms of B1,B2,…,Bη.

Where WBb-th and VBb-th are total weight of all jobs and total volume of all jobs in batch Bb-th.

For the example in Table 1, a solution is scheduling string [8, 2, 6, 4, 11, 1, 10, 9, 5, 12, 7, 3] and machine as-signment string [3, 1, 1, 2, 2, 3, 2, 3, 1, 2, 1, 3]. The corresponding schedule is shown in Fig. 1. Job J8 is chosen first, B1={J8}, WB1=5, VB1=5, then find a job J1 with the same family with J8, WB1+w1=9, VB1+ v1=10, B1={J8,J1}. When job J3 is considered, sandbox volume constraint is violated, so B1={J8,J1}. Other batches are obtained in the same way. B2={J2,J4,J10}, B3={J6}, B4={J11}, B5={J9,J7}, B6={J5,J3}. On M1, processing sequence of B1, B6. The processing sequence on M2 and M3 are B4, B5, B7 and B2,B3, respectively. Cmax is 17.

An initial population P with N solutions are randomly generated, then four initial empires are construc-ted based on initial population P.

Four initial empires are constructed in the following way:

Step 1: Calculate cost ci=Cmaxxi of each solution xi∈P, sort all solutions in P in ascending order of cost.

Step 2: Choose four solutions with lowest cost as imperialists, which are IM1, IM2, IM3, IM4, and calc-ulate normalized cost c¯k of IMk, powk andNCk=round(Ncol×powk).

Step 3: Randomly allocate NCk colonies for each imperialist k.

Where round(x) is a function that gives the nearest integer of x, Ncol=N−4 denotes total number of co-lonies. powk=c¯k/∑i=14ci is power of imperialist k, NCk indicates the number of colonies in empire k.

Normalized cost c¯k of IMk is usually defined as c¯k=maxl{cl}−ck, so at least one imperialist has c¯k=0, powk=0 and no allocated colonies and the corresponding empire will have no colony, as a result, assimilation and revolution cannot be done in the empire, c¯k is defined to avoid the above case:

c¯k=2×maxl{cl}−ck(2)

TC¯k of empire k is defined and four empires are sorted in the descending order of TC¯k, suppose TC¯1≥ TC¯2≥TC¯3≥TC¯4, the strongest empire is empire 1, empire 4 is the weakest empire, empires 2,3 have close normalization total cost.

TC¯k=c¯k+ξ∑λ∈Tkc¯λNCk,k=1,2,3,4.(3)

where Tk is set of colonies possessed by imperialist k and ξ is real number, ξ=0.1.

3.2 Assimilation and Revolution

Unlike the previous ICAs [30,35], CICA has new implementation way for assimilation. In CICA, assimilations of empires 1,4 are executed together based on their cooperation because there has greater difference on their normalization total cost, empires 2,3 have close normalization total cost, when their assimilations are done, they are first merged and assimilation is conducted for the merged empire. Nim is fixed to be 4 to achieve the above two kinds of assimilations; moreover, imperialist competition will be simplified.

Cooperation-based assimilation of empires 1,4 is shown as follows:

Step 1: Sort all colonies in empire 1 in the ascending order of ci, decide the first α colonies including the best colony λ∗∈T1, determine the best α colonies of empire 4 using the same approach and include them into a set Λ, τ=1.

Step 2: Repeat the following steps until τ>α: Choose the τ-th colony λ∈T1 and the τ-th colony λ¯∈T4 execute global search between λ,λ¯, a new solution z is obtained, if Cmaxz less than one of Cmaxλ,Cmaxλ¯, suppose Cmaxz<Cmaxλ, then update the set θ with λ and let z substitute for λ; if Cmaxz<Cmaxλ andCmaxz<Cmaxλ¯, then update the set θ with the worse one of λ,λ¯ and let z substitute for the worse one of λ,λ¯.

Step 3: For each colony λ∈Λ, execute global search between λ and λ∗∈T1, a new solution z is obtained, if Cmaxz<Cmaxλ, then update the set θ with λ and let z substitute for λ. If Cmaxz≥Cmaxλ, then conduct global search between λ and IM1, a new solution z is obtained, if Cmaxz<Cmaxλ, then update the set θ with λ and replace λ with z.

Step 4: Choose the best colony in Λ, if it better than IM4, then exchange it with IM4.

Step 5: For each colony λ∈T1∖{λ∗}, conduct global search between λ and λ∗, a new solution z is obtained, if Cmaxz<Cmaxλ, then update θ with λ and replace λ with z; else, execute global search between λ and IM1, a new solution z is obtained, if Cmaxz<Cmaxλ, then update the set θ with λ and replace λ with z.

Step 6: For each colony λ∈T4∖Λ, choose a λ¯∈Λ∪{IM4}, by using roulette selection, execute global search between λ and λ¯, a new solution z is obtained, if Cmaxz<Cmaxλ, then update the set θ with λ and let z su-bstitute for λ.

Where selection probability of each solution xi is (∑y∈Λ∪{IM4}Cmaxy−Cmaxxi)/∑y∈Λ∪{IM4}Cmaxy for roulette selection.

After the best α colonies of empires 1, 4 are decided respectively, then cooperation is conducted by global search on α pairs of the decided best coloniesλ∈T1, λ¯∈T4 in step 2, and the usage of the best colony λ∗∈T1 or IM1 for improving solution quality of the best α colonies of empire 4 in step 3.

Empires 2,3 have close TC¯2,TC¯3 and there are high similarity between them, to avoid the waste of com-puting resource on the worst solutions, empires 2,3 are first combined into a new empire D, assimilation is done on all colonies of D except Q the chosen worst solutions in D.

Combination-based assimilation in empires 2,3 is described below:

Step 1: Obtain temporary empire D by combining empires 2,3 together, imperialists of empire D are defined as IM2 and IM3, choose Q colonies with the biggest cost, let Θ be a set of these colonies.

Step 2: For each colony λ∈D∖Θ, select one imperialist from IM2 and IM3 by roulette selection, suppose IM2 is selected, execute global search between λ and IM2, a new solution z is obtained, if Cmaxz<Cmaxλ, then if λ is one of Q colonies of D with the lowest cost, then random select colony λ¯∈Θ, update θwith λ¯, replace λ with z; if λ is not one of the best Q colonies in D, then conduct multiple neighborhood search on colon λ, random select colony λ¯∈Θ, update θ with λ¯, replace λ with z.

Step 3: Assign all solutions of D into their original empire.

where roulette selection is done, {IM2,IM3} substitutes for Λ∪{IM4}.

The set θ is used to retain historical optimization data in the search process. The process of updating θ with solution x is shown as follows: If the number of solutions in θ is than its maximum size I, then the worst solution is eliminated and x is added to θ if x is better than the worst solution in θ, otherwise, x is added to θ.

Global search is described below: For solutions x and y, if rand≤0.5, order crossover [48] is executed for scheduling strings of x, y, otherwise, two-point crossover [40] is performed between machine assign-ent string of x and y. Where rand is random number following uniform distribution on [0,1].

5 neighborhood structures are applied, 𝒩1 is used to swap two randomly selected πk1 and πk2. 𝒩2 is swap operator on machine assignment string and applied to swap two randomly selected θk1 and θk2, k1,k2< η. 𝒩3 is shown as follows: Decide machine Mk1 with smallest completion time and Mk2 with the biggest comp-letion time, randomly choose θi1=k1 and θi2=k2,i1,i2≤η and swap θi1,θi2. 𝒩4 is executed in the following way: Choose machine Mk1 with biggest completion time, randomly select θi=k1,i≤η, randomly choose Mk2, let θi=k2. 𝒩5 is described as follows: Decide all jobs on a machine with biggest completion time in scheduling string, and sort these jobs in ascending order of release times.

Multiple neighborhood search is below: Let ϑ=1, repeat the following steps until ϑ=5: a new solution z∈𝒩ϑ(x) is obtained, if Cmaxz<Cmaxx, then update θwith x, replace x with z, ϑ=ϑ+1. Where 𝒩ϑ(x) is denotes neighborhood solution set of solution x by using 𝒩ϑ.

When Nim is fixed to be 4, empires 1, 4 with bigger differences on TC¯k can be easily obtained, coope- ration between them can be done and global search ability can be enhanced; meanwhile, empires 2,3 will have close normalized total cost and the search in empire 2 is similar with the search in empire 3 and the waste of computing resource will occur on some worst solutions twice. When the above assimilation is done on empires 2,3, the waste of computing resource will diminish greatly, thus, it can be found that the usage of four empires is appropriate, so Nim is not parameter in CICA and always equal to 4.

Revolution of empire k is conducted in the following way:

Step 1: Determine the number δ of colonies in empire k according to revolution probability R.

Step 2: Sort all colonies of empire k in ascending order of cost and decide δ colonies with the smallest cost, then for each decided colony λ, perform multiple neighborhood on colony λ, a new solution z is obtained, if Cmaxz<Cmaxλ, then replace the worst colony in Tk with λ, replace λ with z; otherwise, if solution z is better than the worst colony of Tk, replace the worst colony of Tk with z.

3.3 Algorithm Description

As stated above, CICA is made up of initialization, formation of four empires, assimilation, revolution and imperialist competition.

Its detailed steps of CICA are shown below:

Step 1: Randomly produce initial population P and construct four initial empires.

Step 2: While the stopping condition is not met, do

        Sort four empires in the descending order of TC¯k.

        Execute assimilation in empires 1,4.

        Perform assimilation in empires 2,3.

        Execute revolution.

        Apply imperialist competition.

       End While

Only four empires are used and exist in the whole search process, so a new imperialist competition is given to adapt this new situation.

The new imperialist competition is described as follows:

1) Calculate TC¯k and EPk,k=1,2,3,4, construct vector [EP1−rand, EP2−rand, EP3−rand, EP4−rand], choose empire g with the biggest EPg−rand as winning empire. Suppose g=1.

2) Choose I colonies with the lowest cost in empire g, for each chosen colony λ, execute global search between λ and IMg, a new solution z is obtained, ifCmaxz<Cmaxλ, then update θ with λ and replace λ with z, then execute multiple neighborhood search on colony λ.

3) Construct vector [EP2−rand,EP3−rand,EP4−rand], empire g with the biggest EPg−rand as winning empire, suppose g=2, then choose I colonies with the lowest cost of empire 2 and execute global search between each chosen colony and IMg as done in step 2).

4) Choose empire g with the biggest EPg−rand from vector [EP3−rand,EP4−rand], suppose g=3, then choose I colonies with the lowest cost of empire 3 and execute global search between each chosen colony and IMg as done in step 2).

5) In empire 4, execute multiple neighborhood search for each solution x∈θ, delete I worst colony from empire 4, add all solutions of θ into empire 4.

Where EPk denotes power of empire k,

EPk=|TC¯k∑i=14TC¯i|(4)

Unlike the existing ICAs [30,35], CICA has four empires and no elimination of empire. In CICA, assimilations of empires 1,4 are handled together and cooperation is used, assimilations of empires 2,3 are conducted on the temporary empire formed by these two empires, a new imperialist competition is also given. These new features can lead to the enhanced global search ability and the avoidance of the waste of computing resource.

4  Computational Experiments

Extensive experiments are conducted to test the performance of CICA for considered parallel BPM scheduling problem. All experiments are implemented by using Microsoft Visual Studio C++2022 and run on 8.0 G RAM 2.4 Hz CPU PC.

4.1 Instances, Comparative Algorithms and Metrics

96 instances are used, each of which depicted by n×l×m, where n∈{10,20,40,60,100,140,180,220,260,300}, l∈{3,4}, m∈{3,4,5}, pik∈[10,50], vi∈[1,10], wi∈[1,10], V=10, W=10, ri∈ [0,25]. pik, vi, wi and ri are integer following uniform distribution in the above intervals. These instances consist of small-scale ones, medium-scale ones and large-scale ones and can be show the optimization ability differences of different algorithms.

Zhang et al. [24] proposed a MEASL to minimize makespan for parallel BPM scheduling problem with release time, job size and processing time. Jiang et al. [25] presented IG algorithm for parallel BPM scheduling problem with release time, job sizes, incompatible job families. Ji et al. [26] provided HLNS to solve parallel BPM scheduling problem with release time, job sizes, incompatible job families and makespan minimization.

MEASL, IG and HLNS can be directly applied to solve the considered parallel BPM scheduling probl-em and the computational results show that these three algorithms have promising advantages on solving parallel BPM scheduling, so they are chosen as comparative algorithms.

To show the effect of new strategies of CICA, CICA is compared with ICA [30,35], in ICA, assimilatio-n of empire k, is done below: For each colony λ∈Tk, execute global search between λ, IMk, a new solution z is obtained, if Cmaxz<Cmaxλ, then replace λ with z. When revolution is done, multiple neighborhood search acts on the chosen colony.

Three metrics are used. For each instance, each algorithm randomly runs 10 times and an elite solution with the smallest makespan is obtained in a run, MIN is the best solution found in 10 runs, MAX denotes the worst elite solutions in 10 runs and AVG indicates the average makespan of 10 elite solutions. MIN, AVG, MAX are used to measure convergence, average performance and stability of algorithms. These metrics are often used to evaluate results of single objective problem.

4.2 Parameter Settings

It can be found that CICA can converges well when 0.6×n s CPU time reaches; moreover, when 0.6×n s CPU time is applied, MEASL, IG, HLNS and ICA also converge fully within this CPU time, so this time is chosen as stopping condition.

Other parameters of CICA, namely N, α, Q, R and I, are tasted by using Taguchi method [49] on instance 140×3×3. The levels of each parameter are shown in Table 2. CICA with each combination runs 10 times independently for the chosen instance.

Fig. 2 shows the result of MIN and S/N ratio, which is defined as −10×log10⁡(MIN2). It can be found in Fig. 2 that CICA with following combination N=60, α=5, Q=6, R=0.5, I=6 can be obtain better results than CICA with other combinations, so above combination is adopted.

Figure 2: Main effect plot for mean MIN and S/N ratio

Parameters of ICA are shown below. N=60, R=0.5, Nim=4 and stopping condition is 0.6×ns CPU time. These settings are obtained by experiments. All parameters of MEASL, IG and HLNS except stopping condition are obtained directly from [24–26]. The experimental results show that those setting of each comparative algorithm are still effective and comparative algorithms with those setting can produce better results than MEASL, IG and HLNS with other settings.

4.3 Results and Discussions

CICA is compared with MEASL, IG, HLNS and ICA. Each algorithm randomly runs 10 times on each instance. Tables 3–5 describe corresponding results of five algorithms. Figs. 3 and 4 show box plots of all algorithms and convergence curves of instances 100×3×3 and 220×3×3. The relative percentage deviation (RPD) between the best performs algorithm and other four algorithms is used in Fig. 3. RPDMIN, RPDAVG, RPDMAX are defined:

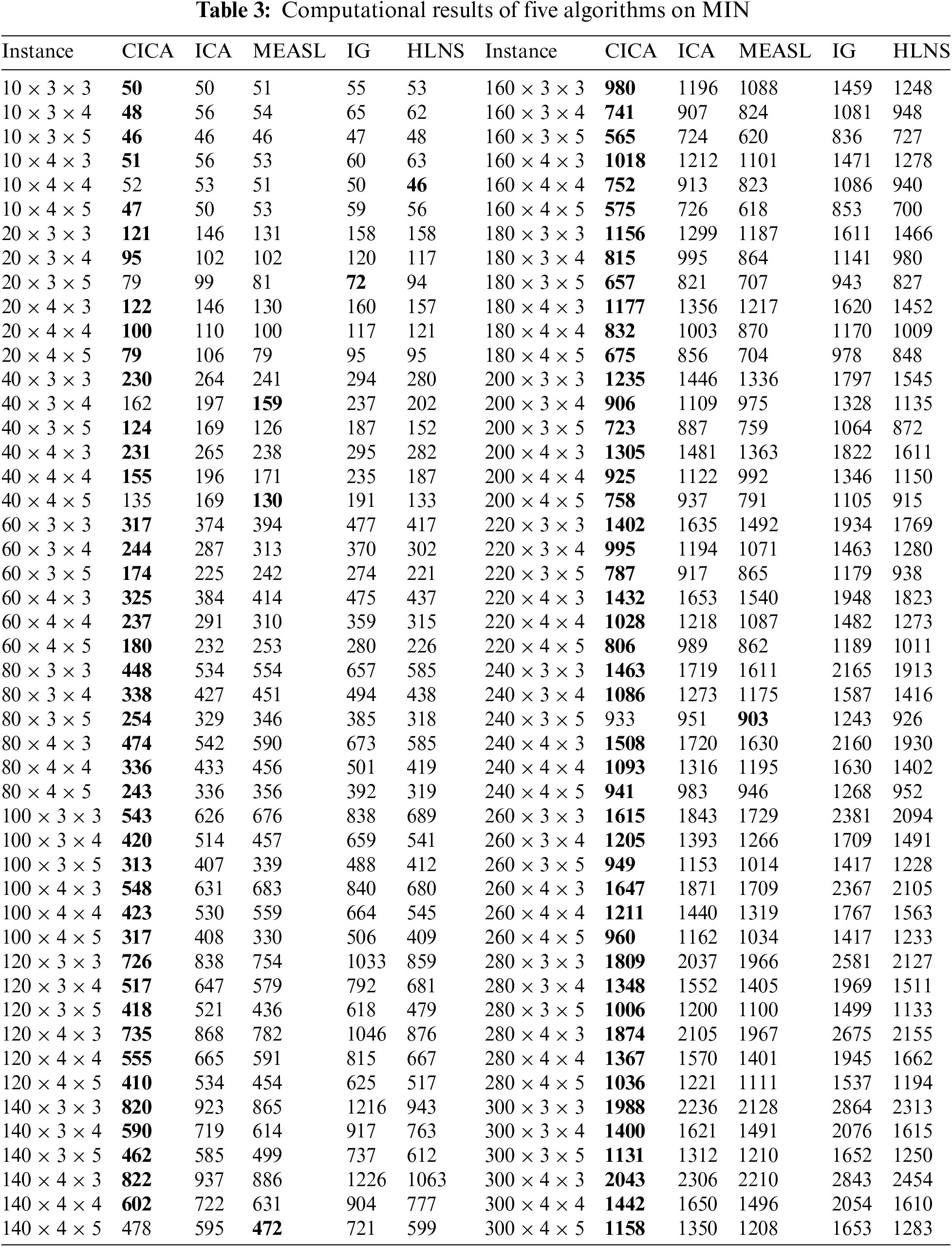
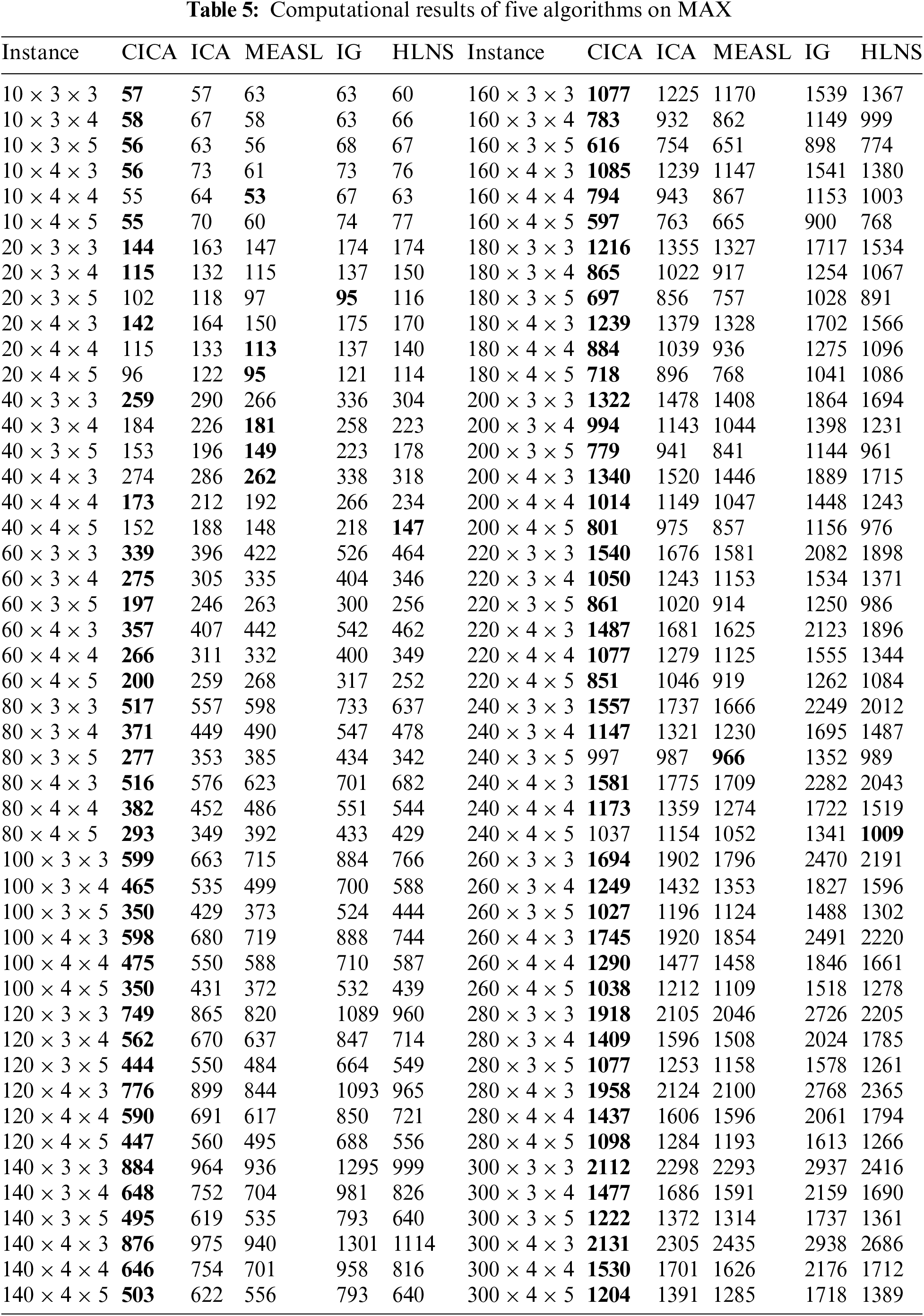
Figure 3: Box plots of five algorithms

Figure 4: convergence curves of instances 100×3×3 and 220×3×3

RPDMIN=MIN−MIN∗MIN∗×100%(5)

where MIN* (MAX*, AVG*) is the smallest MIN (MAX, AVG) obtained by all algorithms, when MIN and MIN* are replaced with MAX(AVG) and MAX*(AVG*), respectively, RPDMAX(RPDAVG) is obtained in the same way.

As shown in Table 3, CICA obtains smaller MIN than ICA on all instances and MIN of CICA is lower than that of ICA by at least 20 on 87 instances. CICA converges better than ICA. This conclusion also can be obtained from Figs. 3 and 4. It can be also found from Tables 4, 5 and Figs. 3, 4 that CICA performs significantly than ICA on AVG and MAX. CICA obtain smaller AVG and MAX than ICA on all instances. It can be concluded that cooperation-based assimilations, combination-based assimilations and new imperial competition process have a positive impact on the performance of CICA.

It can be found from Table 3 that CICA performs better than its comparative algorithms on MIN. CICA produces smaller MIN than three comparative algorithms on 90 of 96 instances; moreover, MIN of CICA is less than that of MEASL by at least 20 on 73 instances, that of IG by at least 20 on 87 instances and that of HLNS by at least 20 on 85 instances. When l and m are the same, with increasing of n, the gap between MIN of CICA and three comparative algorithms is also increasing. CICA has better convergence than MEASL, IG and HLNS. This conclusion can also be drawn from Figs. 3 and 4.

Table 4 describes that CICA obtains smaller AVG than MEASL, IG and HLNS on 88 instances; moreover, AVG of CICA is better than that of its all comparative algorithms by at least 20 on 75 instances. CICA possesses better average performance than its three comparative algorithms. Fig. 3 also illustrates notable average performance differences between CICA and each comparative algorithm.

It also can be seen from Table 5 that MAX of CICA only exceeds that of three comparative algorithms only 10 instances. CICA has smaller MAX than comparative algorithms by at least 20 on 76 instances. Fig. 3 also demonstrates that CICA possesses better stability than its comparative algorithms.

As analyzed above, CICA performs better convergence, average performance and stability than its co-mparative algorithms. The good performances of CICA mainly result from its new strategies. Cooperation-based assimilations of empires 1,4, and combination-based assimilations of empires can effectively improve quality of empires and avoid the waste of computing resources. High diversity can be kept by new imperial competition process. These strategies can make good balance between exploration and exploitation, thus, CICA is a very promising method for solving parallel BPM scheduling problem with release times.

5  Conclusions and Future Topics

This study examines a scheduling problem involving unrelated parallel batch processing machines (BPM) with release times, a scenario that is derived from the moulding process in a foundry. The Cooperated Imperialist Competitive Algorithm (CICA), which does not use the number of empires as a parameter and maintains four empires throughout the search process, is introduced. The algorithm provides two new methods for assimilation through cooperation and combination between empires, and presents a new form of imperialist competition. Extensive experiments are conducted to compare CICA with existing methods and test its performance. The computational results demonstrate that CICA is highly competitive in solving the considered parallel BPM scheduling problems. BPM is prevalent in many real-life manufacturing processes, such as foundries, and scheduling problems involving BPM are more complex than those without BPM. Future research will focus on scheduling problems with BPM, such as the hybrid flow shop scheduling problem with the BPM stage. We aim to use the knowledge of the problem and new optimization mechanisms in CICA to solve these problems. To obtain high-quality solutions, new optimization mechanisms, such as machine learning, are incorporated into meta-heuristics like the imperialist competitive algorithms. We also plan to apply new meta-heuristics, such as teaching-learning-based optimization, to solve the problem. Energy-efficient scheduling with BPM is another future topic. Furthermore, the application of CICA to other problems is also worth further investigation.

Acknowledgement: The authors would like to thank the editors and reviewers for their valuable work, as well as the supervisor and family for their valuable support during the research process.

Funding Statement: This research was funded by the National Natural Science Foundation of China (Grant Number 61573264).

Author Contributions: Conceptualization, Deming Lei; methodology, Heen Li; software, Heen Li; validation, Deming Lei; formal analysis, Deming Lei; investigation, Deming Lei; resources, Heen Li; data curation, Heen Li; writing—original draft preparation, Deming Lei, Heen Li; writing—review and editing, Deming Lei; visualization, Heen Li; supervision, Deming Lei; project administration, Deming Lei. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: All the study data are included in the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Uzsoy, “Scheduling a single batch processing machine with non-identical job sizes,” Int. J. Prod. Res., vol. 32, no. 7, pp. 1615–1635, Jul. 1993. doi: 10.1080/00207549408957026. [Google Scholar] [CrossRef]

2. C. Y. Lee, “Minimizing makespan on a single batch processing machine with dynamic job arrivals Int,” J. Prod. Res., vol. 37, no. 1, pp. 219–236, 1999. doi: 10.1080/002075499192020. [Google Scholar] [CrossRef]

3. S. Melouk, P. Damodaran, and P. Y. Chang, “Minimizing makespan for single machine batch processing with non-identical job sizes using simulated annealing,” Int. J. Prod. Res., vol. 87, no. 2, pp. 141–147, Jan. 2004. [Google Scholar]

4. S. C. Zhou, L. N. Xing, X. Zheng, N. Du, L. Wang and Q. F. Zhang, “A self-adaptive differential evolution algorithm for scheduling a single batch-processing machine with arbitrary job sizes and release times,” IEEE Trans. Cybern., vol. 51, no. 3, pp. 1430–1442, Mar. 2019. doi: 10.1109/TCYB.2019.2939219. [Google Scholar] [PubMed] [CrossRef]

5. Y. G. Yu, L. D. Liu, and Z. Y. Wu, “A branch-and-price algorithm to perform single-machine scheduling for additive manufacturing,” J Manag. Sci. Eng., vol. 8, no. 2, pp. 273–286, Jun. 2023. doi: 10.1016/j.jmse.2022.10.001. [Google Scholar] [CrossRef]

6. H. B. Zhang, Y. Yang, and F. Wu, “Just-in-time single-batch-processing machine scheduling,” Comput. Oper. Res., vol. 140, no. C, pp. 105675, 2022. doi: 10.1016/j.cor.2021.105675. [Google Scholar] [CrossRef]

7. R. Xu, H. P. Chen, and X. P. Li, “A bi-objective scheduling problem on batch machines via a Pareto-based ant colony system,” Int. J. Prod. Econ., vol. 145, no. 1, pp. 371–386, Sep. 2013. doi: 10.1016/j.ijpe.2013.04.053. [Google Scholar] [CrossRef]

8. L. Jiang, J. Pei, X. B. Liu, P. M. Pardalos, Y. J. Yang and X. F. Qian, “Uniform parallel batch machines scheduling considering transportation using a hybrid DPSO-GA algorithm,” Int. J. Adv. Manuf. Technol., vol. 89, no. 5–8, pp. 1887–1900, Aug. 2016. doi: 10.1007/s00170-016-9156-5. [Google Scholar] [CrossRef]

9. R. Zhang, P. Chang, S. J. Song, and C. Wu, “A multi-objective artificial bee colony algorithm for parallel batch-processing machine scheduling in fabric dyeing processes,” Knowl. Based Syst., vol. 116, no. C, pp. 114–129, Jan. 2017. doi: 10.1016/j.knosys.2016.10.026. [Google Scholar] [CrossRef]

10. Z. H. Jia, J. H. Yan, J. Y. T. Leung, K. Li, and H. P. Chen, “Ant colony optimization algorithm for scheduling jobs with fuzzy processing time on parallel batch machines with different capacities,” Appl. Soft Comput, vol. 75, no. 1, pp. 548–561, Feb. 2019. doi: 10.1016/j.asoc.2018.11.027. [Google Scholar] [CrossRef]

11. M. Liu, F. Chu, J. K. He, D. P. Yang, and C. B. Chu, “Coke production scheduling problem: A parallel machine scheduling with batch preprocessings and location-dependent processing times,” Comput. Oper. Res., vol. 104, no. 7, pp. 37–48, Apr. 2019. doi: 10.1016/j.cor.2018.12.002. [Google Scholar] [CrossRef]

12. Z. H. Jia, S. Y. Huo, K. Li, and H. P. Chen, “Integrated scheduling on parallel batch processing machines with non-identical capacities,” Eng. Optim., vol. 52, no. 4, pp. 715–730, May 2019. doi: 10.1080/0305215X.2019.1613388. [Google Scholar] [CrossRef]

13. K. Li, H. Zhang, C. B. Chu, Z. H. Jia, and J. F. Chen, “A bi-objective evolutionary algorithm scheduled on uniform parallel batch processing machines,” Expert. Syst. Appl., vol. 204, no. 6, pp. 117487, Oct. 2022. doi: 10.1016/j.eswa.2022.117487. [Google Scholar] [CrossRef]

14. X. Xin, M. I. Khan, and S. G. Li, “Scheduling equal-length jobs with arbitrary sizes on uniform parallel batch machines,” Open Math., vol. 21, no. 1, pp. 228–249, Jan. 2023. doi: 10.1515/math-2022-0562. [Google Scholar] [CrossRef]

15. J. E. C. Arroyo and J. Y. T. Leung, “An effective iterated greedy algorithm for scheduling unrelated parallel batch machines with non-identical capacities and unequal ready times,” Comput. Ind. Eng., vol. 105, no. C, pp. 84–100, Mar. 2017. doi: 10.1016/j.cie.2016.12.038. [Google Scholar] [CrossRef]

16. S. J. Lu, X. B. Liu, J. Pei, M. T. Thai, and P. M. Pardalos, “A hybrid ABC-TS algorithm for the unrelated parallel-batching machines scheduling problem with deteriorating jobs and maintenance activity,” Appl. Soft Comput, vol. 66, no. 1, pp. 168–182, May 2018. doi: 10.1016/j.asoc.2018.02.018. [Google Scholar] [CrossRef]

17. S. C. Zhou, J. H. Xie, N. Du, and Y. Pang, “A random-keys genetic algorithm for scheduling unrelated parallel batch processing machines with different capacities and arbitrary job sizes,” Appl. Math. Comput., vol. 334, pp. 254–268, Oct. 2018. [Google Scholar]

18. J. M. Zhang, X. F. Yao, and Y. Li, “Improved evolutionary algorithm for parallel batch processing machine scheduling in additive manufacturing,” Int. J. Prod. Res., vol. 58, no. 8, pp. 2263–2282, May 2019. doi: 10.1080/00207543.2019.1617447. [Google Scholar] [CrossRef]

19. M. Kong, X. B. Liu, J. Pei, P. M. Pardalos, and N. Mladenovic, “Parallel-batching scheduling with nonlinear processing times on a single and unrelated parallel machines,” J. Glob. Optim., vol. 78, no. 4, pp. 693–715, Sep. 2018. doi: 10.1007/s10898-018-0705-3. [Google Scholar] [CrossRef]

20. C. Song, “A self-adaptive multiobjective differential evolution algorithm for the inrelated parallel batch processing machine scheduling problem,” Math. Probl. Eng., vol. 2022, pp. 5056356, Sep. 2022. [Google Scholar]

21. H. Zhang, K. Li, C. B. Chu, and Z. H. Jia, “Parallel batch processing machines scheduling in cloud manufacturing for minimizing total service completion time,” Comput. Oper. Res., vol. 146, pp. 1–20, Oct. 2022. [Google Scholar]

22. A. Fallahi, B. Shahidi-Zadeh, and S. T. A. Niaki, “Unrelated parallel batch processing machine scheduling for production systems under carbon reduction policies: NSGA-II and MOGWO metaheuristics,” Soft Comput., vol. 27, no. 22, pp. 17063–17091, Jul. 2023. doi: 10.1007/s00500-023-08754-0. [Google Scholar] [CrossRef]

23. X. Xiao, B. Ji, S. S. Yu, and G. H. Wu, “A tabu-based adaptive large neighborhood search for scheduling unrelated parallel batch processing machines with non-identical job sizes and dynamic job arrivals,” Flex. Serv. Manuf. J., vol. 62, no. 12, pp. 2083, Mar. 2023. doi: 10.1007/s10696-023-09488-9. [Google Scholar] [CrossRef]

24. H. Zhang, K. Li, Z. H. Jia, and C. B. Chu, “Minimizing total completion time on non-identical parallel batch machines with arbitrary release times using ant colony optimization,” Eur. J. Oper. Res., vol. 309, no. 3, pp. 1024–1046, Sep. 2023. doi: 10.1016/j.ejor.2023.02.015. [Google Scholar] [CrossRef]

25. W. Jiang, Y. L. Shen, L. X. Liu, X. C. Zhao, and L. Y. Shi, “A new method for a class of parallel batch machine scheduling problem,” Flex Serv. Manuf. J., vol. 34, no. 2, pp. 518–550, Apr. 2022. doi: 10.1007/s10696-021-09415-w. [Google Scholar] [CrossRef]

26. B. Ji, X. Xiao, S. S. Yu, and G. H. Wu, “A hybrid large neighborhood search method for minimizing makespan on unrelated parallel batch processing machines with incompatible job families,” Sustain., vol. 15, no. 5, pp. 3934, Feb. 2023. doi: 10.3390/su15053934. [Google Scholar] [CrossRef]

27. J. W. Ou, L. F. Lu, and X. L. Zhong, “Parallel-batch scheduling with rejection: Structural properties and approximation algorithms,” Eur. J. Oper. Res., vol. 310, no. 3, pp. 1017–1032, Nov. 2023. doi: 10.1016/j.ejor.2023.04.019. [Google Scholar] [CrossRef]

28. E. Santos-Meza, M. O. Santos, and M. N. Arenales, “A lot-sizing problem in an automated foundry,” Eur. J. Oper. Res., vol. 139, no. 3, pp. 490–500, Jun. 2002. doi: 10.1016/S0377-2217(01)00196-5. [Google Scholar] [CrossRef]

29. S. K. Gauri, “Modeling product-mix planning for batches of melt under multiple objectives in a small scale iron foundry,” Producti. Manag., vol. 3, pp. 189–196, Feb. 2009. doi: 10.1007/s11740-009-0152-6. [Google Scholar] [CrossRef]

30. E. Atashpaz-Gargari and C. Lucas, “Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition,” presented at the 2007 IEEE Cong. on Evoluti. Computati., Singapore, Sep. 25–28, 2007. [Google Scholar]

31. M. Zare et al., “A global best-guided firefy algorithm for engineering problems,” J. Bionic Eng., vol. 20, no. 5, pp. 2359–2388, May 2023. doi: 10.1007/s42235-023-00386-2. [Google Scholar] [CrossRef]

32. G. Hu, Y. X. Zheng, L. Abualigah, and A. G. Hussien, “DETDO: An adaptive hybrid dandelion optimizer for engineering optimization,” Adv Eng. Inform., vol. 57, pp. 102004, Aug. 2023. doi: 10.1016/j.aei.2023.102004. [Google Scholar] [CrossRef]

33. G. Hu, Y. Guo, G. Wei, and L. Abualigah, “Genghis Khan shark optimizer: A novel nature-inspired algorithm for engineering optimization,” Adv. Eng. Inform., vol. 58, pp. 102210, Oct. 2023. doi: 10.1016/j.aei.2023.102210. [Google Scholar] [CrossRef]

34. M. Ghasemi, M. Zaew, A. Zahedi, P. Trojovsky, L. Abualigah and E. Trojovska, “Optimization based on performance of lungs in body: Lungs performance-based optimization (LPO),” Comput. Methods Appl. Mech. Eng., vol. 419, pp. 116582, Feb. 2024. doi: 10.1016/j.cma.2023.116582. [Google Scholar] [CrossRef]

35. S. Hosseini and A. A. Khaled, “A survey on the imperialist competitive algorithm metaheuristic: Implementation in engineering domain and directions for future research,” Appl. Soft Comput., vol. 24, no. 1, pp. 1078–1094, Nov. 2014. doi: 10.1016/j.asoc.2014.08.024. [Google Scholar] [CrossRef]

36. C. Z. Guo, M. Li, and D. M. Lei, “Multi-objective flexible job shop scheduling problem with key objectives,” presented at the 2019 34rd YAC, Jinzhou, China, Jun. 06–08, 2019. [Google Scholar]

37. D. M. Lei, Z. X. Pan, and Q. Y. Zhang, “Researches on multi-objective low carbon parallel machines scheduling,” J. Huazhong Univ. Sci. Technol. Med. Sci., vol. 46, no. 8, pp. 104–109, Aug. 2018. [Google Scholar]

38. M. Li, B. Su, and D. M. Lei, “A novel imperialist competitive algorithm for fuzzy distributed assembly flow shop scheduling,” J. Intell., vol. 40, no. 3, pp. 4545–4561, Mar. 2021. doi: 10.3233/JIFS-201391. [Google Scholar] [CrossRef]

39. J. F. Luo, J. S. Zhou, and X. Jiang, “A modification of the imperialist competitive algorithm with hybrid methods for constrained optimization problems,” IEEE Access, vol. 9, pp. 1, Dec. 2021. doi: 10.1109/ACCESS.2021.3133579. [Google Scholar] [CrossRef]

40. D. M. Lei and J. L. Li, “Distributed energy-efficient assembly scheduling problem with transportation capacity,” Symmetry, vol. 14, no. 11, pp. 2225, Oct. 2022. doi: 10.3390/sym14112225. [Google Scholar] [CrossRef]

41. B. Yan, Y. P. Liu, and Y. H. Huang, “Improved discrete imperialist competition algorithm for order scheduling of automated warehouses,” Comput. Ind. Eng., vol. 168, pp. 108075, Jun. 2019. doi: 10.1016/j.cie.2022.108075. [Google Scholar] [CrossRef]

42. T. You, Y. L. Hu, P. J. Li, and Y. G. Tang, “An improved imperialist competitive algorithm for global optimization,” Turk. J. Elec. Eng. Comp. Sci., vol. 27, no. 5, pp. 3567–3581, Sep. 2019. doi: 10.3906/elk-1811-59. [Google Scholar] [CrossRef]

43. H. Yu, J. Q. Li, X. L. Chen, and W. M. Zhang, “A hybrid imperialist competitive algorithm for the outpatient scheduling problem with switching and preparation times,” J. Intell., vol. 42, no. 6, pp. 5523–5536, Apr. 2022. [Google Scholar]

44. Y. B. Li, Z. P. Yang, L. Wang, H. T. Tang, L. B. Sun and S. S. Guo, “A hybrid imperialist competitive algorithm for energy-efficient flexible job shop scheduling problem with variable-size sublots,” Comput. Ind. Eng., vol. 172, no. B, pp. 108641, Oct. 2022. [Google Scholar]

45. D. M. Lei, H. Y. Du, and H. T. Tang, “An imperialist competitive algorithm for distributed assembly flowshop scheduling with Pm → 1 layout and transportation,” J. Intell., vol. 45, no. 1, pp. 269–284, Jan. 2023. [Google Scholar]

46. M. Yazdani, S. M. Khalili, and F. Jolai, “A parallel machine scheduling problem with two-agent and tool change activities: An efficient hybrid metaheuristic algorithm,” Int. J. Comput. Integr. Manuf., vol. 29, no. 10, pp. 1075–1088, Jul. 2016. [Google Scholar]

47. D. M. Lei and S. S. He, “An adaptive artificial bee colony for unrelated parallel machine scheduling with additional resource and maintenance,” Expert. Syst. Appl., vol. 205, pp. 117577, Nov. 2022. [Google Scholar]

48. J. Deng, L. Wang, S. Y. Wang, and X. L. Zheng, “A competitive memetic algorithm for the distributed two-stage assembly flow-shop scheduling problem,” Int. J. Prod. Res., vol. 54, no. 12, pp. 3561–3577, Aug. 2015. doi: 10.1080/00207543.2015.1084063. [Google Scholar] [CrossRef]

49. J. Deng and L. Wang, “A competitive memetic algorithm for multi-objective distributed permutation flow shop scheduling problem,” Swarm Evol. Comput., vol. 33, pp. 121–131, Feb. 2017. [Google Scholar]