FL-EASGD: Federated Learning Privacy Security Method Based on Homomorphic Encryption

1  Introduction

In the information age, the rapid evolution of machine learning and artificial intelligence has made it more convenient and effective for people to use massive data for various reliable predictions and data analysis, thereby bringing enormous economic benefits to people. However, at the same time, whether domestic or foreign, personal information and corporate data have been leaked, stolen and misused [1]. In the beginning, the main method of data protection was database firewalls, but attackers could bypass the defenses through loopholes to steal data and could not fundamentally solve the problem of privacy leakage during data processing. Subsequently, some scholars have suggested that a possible solution to these problems is cryptographic techniques. The core idea is to collect complete data used for machine learning together and then encrypt the data, which is processed as ciphertext throughout the training process, thus protecting the plaintext of the data [2]. This approach is theoretically sound, but there are security and efficiency issues with centralizing enormous amounts of data in real-world scenarios, and it cannot be implemented well on existing equipment. With the birth and development of distributed machine learning [3], Google Inc. used this idea to first propose federated learning privacy-preserving techniques in 2016 [4]. Federated learning is a distributed data protection technology technique that enables participants to keep data only locally without sharing it, and the training process is completed collaboratively through the shared model of all parties, which is an effective protection for the original data of the participants [5].

During federated learning, data do not leave local storage, which can address privacy and data silos. However, with the advent of attack techniques such as model inference attacks [6], attackers can reverse the inference of the original data through the model parameters, so both the data and the model need to be protected. In the actual federated learning process, the sharing of model parameters could indirectly result in privacy leakage, participants may also passively or actively participate in malicious attacks. An excellent solution to the above problem is to apply homomorphic encryption, which allows the ciphertext to perform the needed operations directly without being decrypted, and the result obtained is identical to that achieved by decrypting the ciphertext and subsequently carrying out the operations. Homomorphic encryption can be applied in the model aggregation phase by implementing the cipher state computation of the model parameters so that the aggregation server aggregates the model in the form of ciphertext, thus improving the privacy of the parameters in the machine learning training process. This can both protect the attacker from obtaining valid information through the aggregation server and reduce encryption and decryption costs.

The synchronized federated learning algorithm necessitates the global synchronization of all working nodes at a specific frequency. However, in practical scenarios, performance variations among parties exist, leading to varying completion times for each training round. Consequently, global training is often delayed until all nodes have uploaded their local models, resulting in reduced efficiency. And more seriously, if there is an exception in one of the parties during the training process, it will directly lead to the federated learning can not complete the training task. Feng et al. [7] introduce a time variable, which does not require all users to participate in this aggregation, but controls the number of models uploaded to the server in this round, thus solving the problem of node performance difference, but it does not consider the local exploration of the local model ground.

The following are the main contributions of this paper:

We propose a homomorphic encryption-based privacy-preserving scheme for federated learning, which applies the machine-learning-friendly Cheon-Kim-Kim-Song (CKKS) fully homomorphic encryption technique to the process of federated learning and substantially enhances the security of data and model parameters, while the model correctness is almost unaffected.

Due to the heterogeneity of the working nodes and the possibility of anomalous conditions, a secure and efficient model aggregation FL-EASGD approach is proposed. Even if there is an individual participant with anomalies, the system is more robust, in addition to preserving the local exploration of the models of the parties.

Through several experiments, we have proven the validity of the above method, and show excellent security advantages with decent performance on the MINIST dataset.

2  Related Work

There are several existing privacy protection methods for federated learning model parameters: Differential privacy [8], homomorphic encryption [9], and secure multi-party computation [10]. These methods can all protect federated learning privacy to varying degrees.

Geyer et al. [11] proposed a joint optimization algorithm for client-side differential privacy protection, which reduces the difference of perturbed gradients and improves aggregation efficiency by normalizing the shared gradient but does not provide strict privacy restrictions for the participating client gradient parameter perturbations. Aledhari et al. [12] proposed an improved Stochastic Gradient Descent (SGD) algorithm based on differential privacy, which adds a certain amount of noise when the participants share the gradient. Although this will have an impact on the training results, the overall accuracy is still relatively good and meets the expected privacy requirements. Bonawitz et al. [13] combine secure multi-party computation into federated learning scenarios and securely aggregate the gradients of each client from multiple client scenarios. However, the sharing of parameters such as key negotiation is very complicated, resulting in great communication pressure. Angulo et al. [14] proposed a classification model training method based on homomorphic encryption and federated learning, analyzed the attack on federated learning under given conditions, proposed an MLP neural network training protocol to achieve privacy protection in multi-classification problems, and improved the accuracy of model training compared with differential privacy added noise. However, the computing scenario is limited because this method is based on Pailler additive homomorphic encryption. Febrianti et al. [15] proposed a privacy-preserving federated learning algorithm, utilizing the BFV fully homomorphic encryption algorithm to safeguard the deep learning model based on a convolutional neural network (CNN) against malicious attackers. However, it does not consider the difference in the performance of worker nodes or even abnormal conditions, and the performance between devices will affect the efficiency of overall training. Qiu et al. [16] proposed a privacy-enhanced federated averaging (Per-FedAvg) method to protect model parameters, using CKKS encryption to have a wider range of computational scenarios and higher efficiency than the Paillier encryption method. To reduce the impact of device performance on training, Nishio et al. [17] proposed the FedCS method, which collects device information from randomly selected participants on the aggregate server side to balance the performance differences between participants and with little or no reduction in model accuracy and efficiency of training. Feng et al. [7] leveraged the smart contract technology of blockchain in the model aggregation process of federated learning, thereby addressing the security concerns associated with centralized servers. In this paper, the optimization of the [7] solution to the performance difference problem scheme makes the utilization of the global model more flexible and is reflected in the method FL-EASGD proposed in this paper.

In summary, the schemes that both protect data privacy and consider the performance difference of the working nodes and the emergence of anomalous problems in the process of federated learning are relatively immature, so this paper mainly integrates the above problems to study schemes that are secure, efficient, and robust.

3  Preliminaries

3.1 Homomorphic Encryption

Homomorphic encryption is a secure encryption method proposed by Rivest et al. [18] in 1978. Homomorphic encryption encrypts the initial plaintext data into ciphertext data by means of a cryptographic function and then performs computation on the ciphertext data directly without decryption. The result obtained is essentially consistent with performing the same calculation on the decrypted plaintext. Because of this powerful feature of homomorphic encryption, we do not need to perform frequent encryption and decryption operations between the server and the client, which can largely reduce the overhead of communication and computational resources. In addition, the data are transmitted in the form of ciphertext so that no one else, including the server, knows the exact content of the data, which makes it possible to perform many operations on the private ciphertext data even in an untrusted environment. As a result, data can be effectively prevented from being illegally stolen or tampered with. In summary, the use of homomorphic encryption improves data availability and security, and user privacy information is well protected. Until now, there has been no fully uniform classification standard for homomorphic encryption. According to the different types and times of ciphertext operations, this paper can divide homomorphic encryption into three categories.

(1)   Partial homomorphic encryption: Only a single type of addition or multiplication operation is supported, and there is no limit on the number of times.

(2)   Somewhat homomorphic encryption: Supports addition and multiplication, but the number of operations is limited.

(3)   Fully homomorphic encryption: Supports any number of addition or multiplication operations.

The most famous homomorphic encryption algorithm is the additive homomorphic-only cryptographic algorithm proposed by Paillier [19] at EUROCRYPT in 1999. Due to its high efficiency and complete proof of security, Paillier encryption has been used in a wide range of practical applications in academia and industry. which is an extremely common scheme used for partial homomorphic encryption in privacy computing scenarios. However, as computing scenarios become increasingly complex, the Paillier solution cannot meet the needs of complex computing.

Cheon et al. [20], four Korean researchers in 2017, proposed the CKKS algorithm which is an approximate computationally fully homomorphic encryption algorithm. It supports addition, subtraction, and multiplication of floating-point vectors in ciphertext space and maintains homomorphism, but only supports finite multiplication. Although floating-point arithmetic produces very small inaccuracies, this is consistent with the core idea of the CKKS algorithm which is approximate calculation. The main application scenario of this paper is machine learning, and CKKS supports real number computation and vector operations friendly to machine learning. In addition, because of the allowable error and relaxed accuracy constraints, some implementation details have been simplified, which leads to a significant improvement in the computational efficiency of CKKS.

The specific structure of CKKS is as follows:

CKKS.KenGen(1λ): Let ql=pl for l=1,…,L. Sampled polynomial s←HWT(h),a←U(RqL),e←DG(σ2). Output the private key sk←(1,S) and output the public key pk←(b,a)∈R2qL, where b=−as+emod qL. s←HWT(h) denotes N coefficients uniformly sampled from {1,−1,0} and ensures that the number of nonzero coefficients is exact h. These coefficients form the polynomial Rq. e←DG(σ2) denotes the sampling of N coefficients from a discrete Gaussian distribution thus obtaining the polynomial e∈Rq.

CKKS.Enc(m): Sampled polynomial v←ZO(0.5),e0,e1←DG(σ2), output redaction ct←v⋅pk+(m+e0,e1)(modqL). v←ZO(0.5) denotes sampling N coefficients uniformly from {1,−1,0} and ensuring that 1 occurs with probability ρ/2. −1 occurs with probability ρ/2 and 0 occurs with probability 1−ρ.

CKKS.Decsk(ct): Let the ciphertext ct=(c0,c1)∈R2qL, and output the plaintext polynomial m←c0+c1⋅s(mod qL).

3.2 Federated Learning

Federated learning is a distributed machine learning technology that can practically assist various industries in model training and model prediction while satisfying the protection of user privacy and data security. When performing model training, only to exchange the parameter information of the model without exchanging data. Specifically, the federated learning algorithm has the following characteristics: (1) at least two participants are involved in federated learning, conducting local machine learning training and model sharing, and each participant must have the original data used to train the shared model. (2) At any point in the conduct of federal learning, the data of each user is retained locally, only transfer and exchange information such as model parameters; that is, the data do not move the model moves. (3) The difference in performance between federated learning models and centralized models should be within acceptable limits. That is, let Mfl be the performance of the federated learning model and Mcent be the centralized model, δ be non-negative real numbers, satisfying |Mfl−Mcent|<δ.

A typical application scenario of federated learning is as follows: Different hospitals have electronic health records of different patient groups, and data sharing is not possible among hospitals due to the sensitive privacy of patients [21]. In such a case, hospitals in other parties can use their respective data to build local machine models, and model sharing makes a more effective use of the healthcare data.

3.3 Stochastic Gradient Descent

Stochastic Gradient Descent (SGD) is an iterative optimization method commonly used to determine the optimal parameters of a model. This technique involves randomly sampling from the training dataset, computing the gradient, and subsequently updating the model’s parameters. The process unfolds as follows:

(1)   In each iteration, SGD randomly selects a sample from the training set.

(2)   Calculate the gradient of that sample.

(3)   Update the model parameters based on the calculated gradient.

(4)   Repeat the above steps until the stopping condition is met.

As SGD utilizes random samples in each iteration, it possesses the potential to escape local optimal solutions and explore a superior global optimal solution.

4  System Model

The architecture of the system model is shown in Fig. 1, and the model includes two roles: Cloud server and local client.

Figure 1: Model architecture

4.1 Algorithmic Process

The specific process is that the client performs model training locally (as shown in Algorithm 1) and then applies the CKKS to encrypt the model parameters and upload the ciphertexts of the model parameters. Table 1 lists the main symbols used in this paper and their interpretations.

After the global update is complete, the global model parameters from the server side are sent to each participant, and then each participant decrypts them, using the global model to update its model. The server side receives the encrypted model parameters, aggregates the ciphertexts of the model parameters and updates the global model parameters through secure aggregation (as shown in Algorithm 2), sends them down to the clients participating in training, continuously repeats the update steps, and iterates repeatedly until it meets the preset conditions or converges to stop training.

The Federated Averaging Algorithm (FedAvg) [22] is widely used in many federal learning programs, based on the following idea: The server simply calculates the average of all the model parameters as the global model parameter for the current round, sends this global model parameter to the local device, and continues iterating until convergence. In this paper, for model aggregation, we propose an improved elastic average gradient descent algorithm (EASGD) [23], which is called FL-EASGD.

EASGD has been optimized based on SGD, the purpose of which is to retain the useful information explored by each worker node itself. The fully consistent aggregation algorithms represented by SGD, on the other hand, will definitely aggregate a global model at some point, such as the most widely used FedAvg algorithm, which is that the local nodes will replace the obtained global model completely with the local model, which is not always the most suitable choice for optimization problems with many local optimal points, such as deep learning.

EASGD balances global consistency with local model independence. In other words, it can not only constrain the local model from too much of a deviation of the global model through the aggregation of the global model but also partially retain the parameter information of the global model in history. Studies have shown that EASGD performs well in terms of accuracy and stability.

However, EASGD does not well meet our need for the robustness of the system model when there are individual nodes with problems. Therefore, we propose a safety and efficient aggregation algorithm called FL-EASGD that considers node fault tolerance in this paper.

EASGD is based on the selection of a preset time T. The selected T ensures as much as possible that the participants are able to complete the local training task under normal circumstances. Since the commonality of the synchronization, algorithm is that all worker nodes meet at a certain frequency for global synchronization, to overcome the problems of low overall operation and even inability to complete training tasks when some worker nodes have problems, we do not require all users to participate in this aggregation but instead guarantee minimum number of participants upload their models to the server.

The specific ideas are as follows: If the number of upload parameter nodes is less than N at the preset time T, it means that some worker nodes have abnormal conditions, the factor of the previous round of global parameters is increased, and aggregation is performed. If the number of uploaded parameter nodes is equal to N at the preset time T, the parameters of all uploaded nodes are aggregated.

Through the above algorithm, the normal training of the global model when the worker node is abnormal is not only guaranteed but the utilization rate of the worker node dataset is also guaranteed.

4.2 Security Analysis

(1) For honest but curious servers

The greatest advantage of federated learning is that it can ensure joint training when the data are local to ensure the privacy and security of all participants. However, assuming the aggregation server is honest but curious, the server can spy on the plaintext of model parameters from the traditional federated learning process and then use attacks such as gradient inference to push out the local data of the participants. The security model proposed in this paper first allows participants to train locally in plaintext form, then encrypts the model parameters using the CKKS, and the model parameter ciphertext is then sent to the aggregation server.

Therefore, the ciphertexts received by the server from each participant can only perform the ciphertext aggregation computation task according to the aggregation algorithm. Throughout the process, it would be impossible for an honest but curious server to deduce valid information from the ciphertext. It is not feasible even if the server changes from curiosity to malicious cracking of the ciphertext. The CKKS algorithm based on the LWE problem on the lattice has indistinguishable security under selective plaintext attacks with quantum-resistant properties [24]. Therefore, the model is safe for honest but curious servers.

(2) For collusion between multiple parties

Suppose a client participant on one side wants to obtain the model parameters of the other participant and thus uses methods such as inference attacks to obtain the other participant’s local data. Again, this is unrealistic because in both the training phase and the aggregation phase, each participant can obtain the global ciphertext of the model parameters at most, and even if there is a private key, it can only decrypt the global model parameters and cannot obtain the model parameters of any participant. Assume that in the extreme case, all participants except the participant p collude with each other, including the server, the gradient information of the participants is safe, that is, the colluding party cannot obtain the gradient information of p. Assume that the collusion party obtains the weight Wpn of the nth round and the weight Wpn+1 of the n+1th round of participant p, that is, Wpn+1−Wpn=−α(Wpn−Wgn). Since only p itself knows the value of α, the collusion party cannot obtain the gradient information of p. Therefore, the model is safe for curious clients.

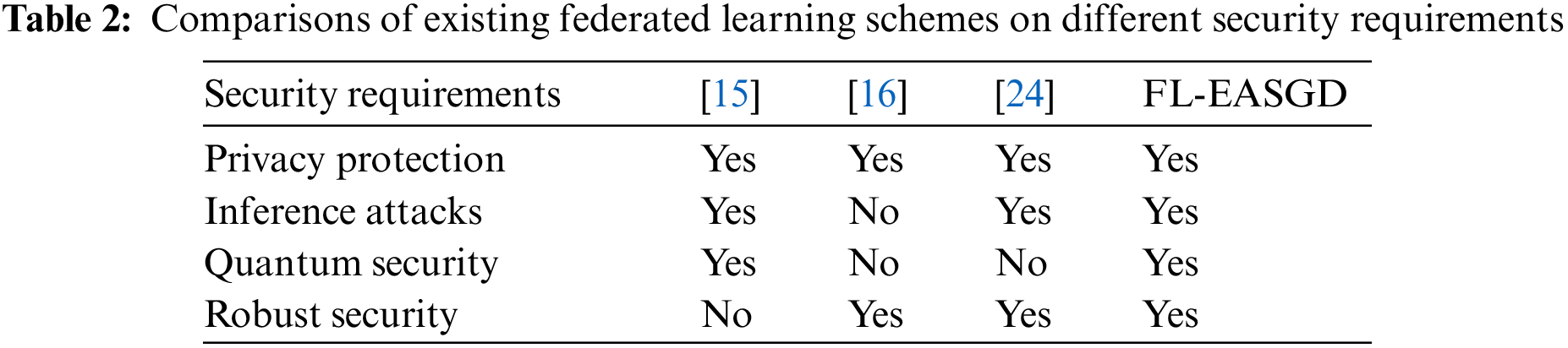
In addition, we compared existing federated learning schemes on different security requirements, and the results are shown in Table 2.

5  Experiment Evaluation

To demonstrate the feasibility of the above federated learning privacy security model, simulation experiments are designed to evaluate the performance metrics such as accuracy and computational overhead of the scheme. The lab environment CPU is configured as I7-12700H, the GPU is an NVIDIA GeForce RTX 3060, and the memory is 16 GB. The development environment uses the PyTorch neural network framework based on the Python language to build deep learning models. We use the MNIST dataset, which is a standard dataset for deep learning models. The dataset contains 10 classes of grayscale handwritten digital images with a size of 28 × 28 and labels from digit 0 to digit 9, for a total of 60,000 training samples and 10,000 test samples, which is well suited to validate our proposed privacy model. The model uses a fully connected deep neural network (DNN). DNN hyperparameter settings: The neural network consists of a total of three linear layers: The first layer has inputs and outputs of 784 and 20, the second layer has inputs and outputs of 20 and 20, and the third layer has inputs and outputs of 20 and 10. The activation functions all use the ReLU activation function. Set 5 participants, the learning rate is 0.015, the local iteration round is 5, and the global iteration round is 3. In the FL-EASGD algorithm, both the smoothing coefficient and the constraint coefficient are set to 0.8.

5.1 Accuracy Analysis

To prove that our proposed model is effective, the training accuracy of the global model will be verified from three schemas. (1) Federal average (FedAvg) under normal operation: At present, the most popular federated learning algorithm is that the server simply aggregates the uploaded model plaintext of all users to obtain the global model. (2) FL-EASGD under normal operation: All local nodes operate normally, the local model is encrypted and uploaded to the server, and the server uses the FL-EASGD algorithm for ciphertext aggregation. (3) Simulate the FL-EASGD anomaly under the condition of 0 to 1 random abnormal nodes: Only the normal node encrypts the local model and uploads it to the server, and the server uses the FL-EASGD algorithm for ciphertext aggregation.

Since the FedAvg algorithm cannot consider the aggregation situation under the abnormal node, the experiment is not carried out here. Then, according to the experimental results in the figure below, the above verification is further analyzed and summarized.

As seen in Fig. 2, as the number of global rounds increases, the accuracy of all three cases tends to increase when all other experimental conditions are the same. One of the highest accuracy rates after completing 3 rounds of global iterations was FedAvg, with an accuracy of 0.95. The accuracy of FL-EASGD when all the nodes are functioning normally and the accuracy of FL-EASGD when there are 0 to 1 abnormal nodes are both 0.93%. The accuracy of FedAvg is approximately two percentage points higher than our algorithm’s accuracy, a loss that is perfectly acceptable for trading confidentiality for accuracy. Moreover, the FedAvg algorithm does not consider the aggregation under abnormal nodes and may not be able to complete the whole training when the nodes are abnormal, whereas FL-EASGD’s accuracy is almost unaffected under the condition of 0 to 1 node, so we can consider FL-EASGD as a feasible and safe aggregation scheme that hardly affects the accuracy of the model.

Figure 2: Accuracy assessment for each global epoch

5.2 Local Run and Server Aggregation Time Analysis

In the process of federated learning, time cost is also one of the evaluation indicators. Since our proposed algorithm requires the use of homomorphic encryption algorithms, the encryption and decryption of the algorithm will inevitably increase a portion of the computational cost. Through experiments, we analyze the average time of the local node and server operation under the FL-EASGD scheme, which mainly includes the time of encryption and decryption of the local node and the time of the server’s ciphertext computation.

Fig. 3 shows the average time of local node running. The local running time of each round is basically stable within the difference of two seconds. The time of FL-EASGD is higher than the FedAvg time but lower than the time of the Paillier encryption scheme, which indicates that the local running time of the scheme we used is more efficient than the parametric scheme of the Paillier encryption model in terms of local running time under the same experimental conditions. The increase in time of the encryption scheme over FedAvg is mainly the decryption time of the local node to the global node vs. the encryption time to the local model, which is acceptable for privacy preservation purposes by trading the increase in time cost for privacy enhancement. Table 3 shows the aggregation time of the FL-EASGD server, as seen in Table 3, with the increase of global rounds, the aggregation time also increases, this is because with the increase in the number of operations, the seed value in the encryption and decryption algorithms increases, the ciphertext noise increases, the size of the ciphertext increases, the cost of the computation increases, and the computational time increases along with it. Overall, the aggregation time of the server is longer than that of the local operation but still within the acceptable range, which is in line with the resource constraints of the local participants.

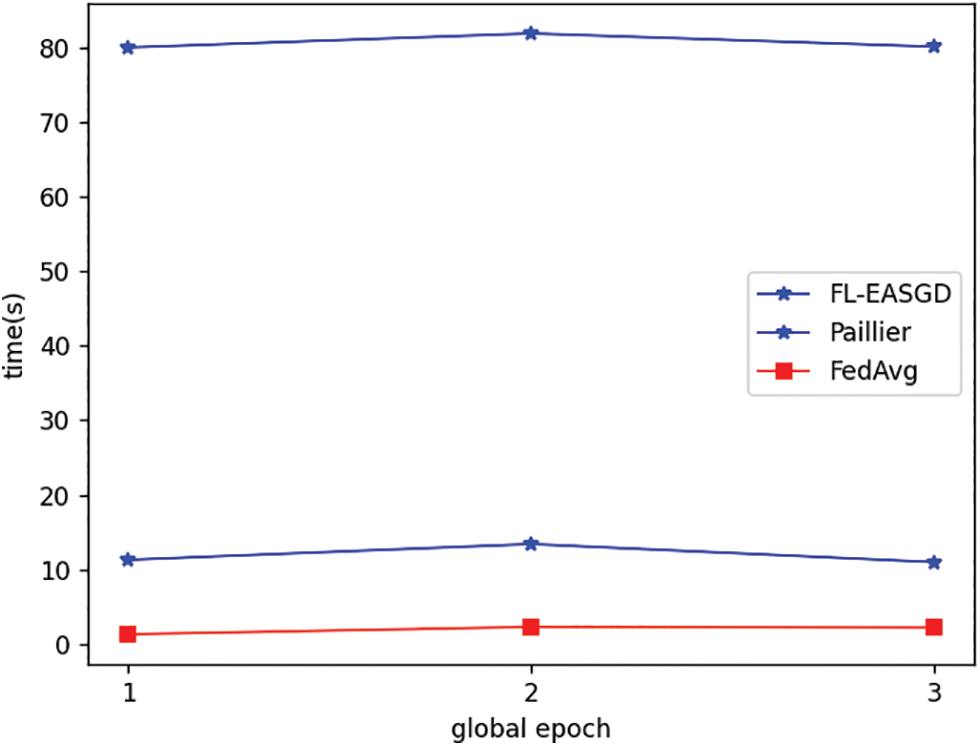
Figure 3: Average local participants running time per epoch

5.3 Communication Cost Analysis

In the process of federated learning, the transmission of model parameters between participants and the server incurs a portion of the communication cost. Additionally, the communication overhead is also a metric used to evaluate the effectiveness of an aggregation scheme. Suppose that there are n parties, each party has m model parameters, each model parameter plaintext size is x, and each model parameter ciphertext size is y.

The cost of the party communication during the FL-EASGD federated learning process is the cost when the encrypted model parameters are uploaded to the server, and the size is n∗m∗y. The server-side communication time consists of two parts: One is the server-side, and the initialized model is first sent to each participant in plaintext, with a size of n∗m∗x. The second is the time when the updated global ciphertext parameters are sent to the participants, and the size is n∗m∗y.

Table 4 compares the communication cost between FL-EASGD and FedAvg, from which we can see the communication cost is mainly different from the time when the server sends the global ciphertext parameter to the participants, and the difference is O(n∗m∗y−n∗m∗x), without incurring additional time overhead, so this is an increase in the cost of communication necessary to increase privacy.

6  Conclusion

In this paper, a privacy protection scheme we have proposed is that we combine fully homomorphic encryption algorithms and federated learning techniques to address issues such as data privacy leakage in the machine learning process. Specifically, it involves the design of efficient and secure model aggregation algorithms based on resilient mean stochastic gradient descent algorithms, taking into account the presence of anomalies in local working nodes and uneven data quality. However, this article still has many shortcomings. The aggregation server is still centralized, and it may still be susceptible to distributed denial-of-service attacks. In the future, we may be possible to combine decentralized blockchain technology with the elimination of central servers. In addition, the article did not consider the incentive mechanism, and there may be lazy nodes that do not provide data. In the future, by combining blockchain and incentive mechanisms, a more efficient model will be designed and compared with the efficiency of existing leading solutions.

Acknowledgement: All authors would like to thank the anonymous reviewers for their constructive suggestions, which improved the quality of this work.

Funding Statement: This work was supported by the NSFC (Grant Nos. 72293583, 72293580).

Author Contributions: The authors confirm their contribution to the paper as follows: Study conception and design: Hao Sun, Xiubo Chen, Kaiguo Yuan; security proofs: Hao Sun, Xiubo Chen; analysis and interpretation of results: Hao Sun, Kaiguo Yuan; draft manuscript preparation: Hao Sun, Xiubo Chen, Kaiguo Yuan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. M. Gaff, H. E. Sussman, and J. Geetter, “Privacy and big data,” Computer, vol. 47, no. 6, pp. 7–9, 2014. doi: 10.1109/MC.2014.161. [Google Scholar] [CrossRef]

2. N. Dowlin, R. Gilad-Bachrach, K. Laine, K. Lauter, M. Naehrig and J. Wernsing, “CryptoNets: Applying neural networks to encrypted data with high throughput and accuracy,” in Proc. ICML, New York, NY, USA, 2016, pp. 201–210. [Google Scholar]

3. J. Verbraeken et al., “A survey on distributed machine learning,” ACM Comput. Surv., vol. 53, no. 2, pp. 1–33, Mar. 2020. [Google Scholar]

4. J. Konen, H. B. Mcmahan, F. X. Yu, P. Richtarik, and D. Bacon, “Federated learning: Strategies for improving communication efficiency,” arXiv:1610.05492, 2016. [Google Scholar]

5. S. Sharma and S. Kumar, “Federated learning approaches to diverse machine learning model: A review,” in IOT Smart Syst. Singapore: Springer, 2023, pp. 259–269. [Google Scholar]

6. R. Shokri, M. Stronati, C. Song, and V. Shmatikov, “Membership inference attacks against machine learning models,” in Proc. IEEE Symp. Secur. Priv., 2017, pp. 3–18. [Google Scholar]

7. C. Feng, B. Liu, K. Yu, S. K. Goudos, and S. Wan, “Blockchain-empowered decentralized horizontal federated learning for 5G-enabled UAVs,” IEEE Trans. Ind. Inform., vol. 18, no. 5, pp. 3582–3592, May 2022. doi: 10.1109/TII.2021.3116132. [Google Scholar] [CrossRef]

8. M. Abadi et al., “Deep learning with differential privacy,” in Proc. ACM SIGSAC Conf. Comput. Communi. Security, 2016, pp. 308–318. [Google Scholar]

9. L. T. Phong, Y. Aono, T. Hayashi, L. Wang, and S. Moriai, “Privacy-preserving deep learning via additively homomorphic encryption,” IEEE Trans. Inf. Forensics Secur., vol. 13, no. 5, pp. 1333–1345, May 2018. doi: 10.1109/TIFS.2017.2787987. [Google Scholar] [CrossRef]

10. V. Mothukuri, R. M. Parizi, S. Pouriyeh, Y. Huang, A. Dehghantanha and G. Srivastava, “A survey on security and privacy of federated learning,” Future Gener. Comput. Syst., vol. 115, no. 4, pp. 619–640, Feb. 2021. doi: 10.1016/j.future.2020.10.007. [Google Scholar] [CrossRef]

11. R. C. Geyer, T. Klein, and M. Nabi, “Differentially private federated Learning: A client level perspective,” arXiv:1712.07557, 2017. [Google Scholar]

12. M. Aledhari, R. Razzak, R. M. Parizi, and F. Saeed, “Federated Learning: A survey on enabling technologies, protocols, and applications,” IEEE Access, vol. 8, pp. 140699–140725, Jul. 2020. doi: 10.1109/ACCESS.2020.3013541. [Google Scholar] [PubMed] [CrossRef]

13. K. Bonawitz et al., “Practical secure aggregation for privacy-preserving machine learning,” in Proc. ACM SIGSAC Conf. Comput. Communi. Security, New York, NY, USA, 2017, pp. 1175–1191. [Google Scholar]

14. E. Angulo, J. Márquez, and R. Villanueva-Polanco, “Training of classification models via federated learning and homomorphic encryption,” Sensors, vol. 23, no. 4, pp. 1966–1984, Feb. 2023. doi: 10.3390/s23041966. [Google Scholar] [PubMed] [CrossRef]

15. W. Febrianti, O. C. Ferhat, S. Salih, K. Murat, and C. Umit, “Homomorphic encryption and federated learning based privacy-preserving CNN training: COVID-19 detection use-case,” in Proc. Eur. Interdiscip. Cybersecur. Conf., New York, NY, USA, 2022. [Google Scholar]

16. F. Qiu, H. Yang, L. Zhou, C. Ma, and L. M. Fang, “Privacy preserving federated learning using CKKS homomorphic encryption,” in Proc. Wirel. Algor. Syst. Appl., 2022, pp. 427–470. [Google Scholar]

17. T. Nishio and R. Yonetani, “Client selection for federated learning with heterogeneous resources in mobile edge,” arXiv:1804.08333, 2018. [Google Scholar]

18. R. Rivest, L. Adleman, and M. L. Detrouzos, “On data banks and privacy homomorphism,” in Proc. Found. Secure Comput., New York, NY, USA, 1978, pp. 169–179. [Google Scholar]

19. P. Paillier, “Public-key cryptosystems based on composite degree residuosity classes,” in Proc. Int. Conf. Theory Appl. Cryptograp. Tech., 1999, pp. 223–238. [Google Scholar]

20. J. H. Cheon, A. Kim, M. Kim, and Y. Song, “Homomorphic encryption for arithmetic of approximate numbers,” in Proc. Adv. Cryptol.–ASIACRYPT 2017, Nov. 2017, pp. 409–437. [Google Scholar]

21. J. Xu et al., “Federated learning for healthcare informatics,” J. Healthc. Inform. Res., vol. 5, no. 1, pp. 1–19, Oct. 2020. doi: 10.1007/s41666-020-00082-4. [Google Scholar] [PubMed] [CrossRef]

22. H. B. McMahan et al., “Communication-efficient learning of deep networks from decentralized data,” arXiv:1602.05629, 2016. [Google Scholar]

23. S. Zhang, A. E. Choromanska, and Y. LeCun, “Deep learning with elastic averaging SGD,” in Proc. Adv. Neural Inf. Process. Syst., Montreal, Canada, Dec. 2015, pp. 685–693. [Google Scholar]

24. O. Regev, “The learning with errors problem,” in Proc. IEEE 25th Annual Conf. Comput. Complex., MA, USA, 2010, pp. 191–204. [Google Scholar]