 Open Access
Open Access
ARTICLE
Attribute Reduction of Hybrid Decision Information Systems Based on Fuzzy Conditional Information Entropy
1 School of Big Data and Artificial Intelligence, Chizhou University, Chizhou, 247000, China
2 Anhui Education Big Data Intelligent Perception and Application Engineering Research Center, Chizhou, 247000, China
* Corresponding Author: Qinli Zhang. Email:
Computers, Materials & Continua 2024, 79(2), 2063-2083. https://doi.org/10.32604/cmc.2024.049147
Received 28 December 2023; Accepted 13 March 2024; Issue published 15 May 2024
Abstract
The presence of numerous uncertainties in hybrid decision information systems (HDISs) renders attribute reduction a formidable task. Currently available attribute reduction algorithms, including those based on Pawlak attribute importance, Skowron discernibility matrix, and information entropy, struggle to effectively manages multiple uncertainties simultaneously in HDISs like the precise measurement of disparities between nominal attribute values, and attributes with fuzzy boundaries and abnormal values. In order to address the aforementioned issues, this paper delves into the study of attribute reduction within HDISs. First of all, a novel metric based on the decision attribute is introduced to solve the problem of accurately measuring the differences between nominal attribute values. The newly introduced distance metric has been christened the supervised distance that can effectively quantify the differences between the nominal attribute values. Then, based on the newly developed metric, a novel fuzzy relationship is defined from the perspective of “feedback on parity of attribute values to attribute sets”. This new fuzzy relationship serves as a valuable tool in addressing the challenges posed by abnormal attribute values. Furthermore, leveraging the newly introduced fuzzy relationship, the fuzzy conditional information entropy is defined as a solution to the challenges posed by fuzzy attributes. It effectively quantifies the uncertainty associated with fuzzy attribute values, thereby providing a robust framework for handling fuzzy information in hybrid information systems. Finally, an algorithm for attribute reduction utilizing the fuzzy conditional information entropy is presented. The experimental results on 12 datasets show that the average reduction rate of our algorithm reaches 84.04%, and the classification accuracy is improved by 3.91% compared to the original dataset, and by an average of 11.25% compared to the other 9 state-of-the-art reduction algorithms. The comprehensive analysis of these research results clearly indicates that our algorithm is highly effective in managing the intricate uncertainties inherent in hybrid data.Keywords
Symbols and Notations Used in the Paper
| Symbols and notations | Meaning |
| A set of objects | |
| A set of attributes | |
| BA | Set of conditional attributes |
| D | The decision attribute |
| The power set of X | |
| |Y| | The cardinality of Y |
| I | [0,1] |
| A set of all fuzzy sets on X | |
| A set of all fuzzy relationship on X | |
| R | A fuzzy relationship |
| Rx | The fuzzy information granule of x |
| θ | The threshold value of tolerance relationship |
| P | A subset of conditional attributes |
| A tolerance relationship determined by θ and P |
In information systems, the attributes of data are not of equal importance. Some of them may not have a direct or significant impact on decision-making. These attributes are considered as redundant. The objective of attribute reduction is to eliminate these redundant attributes, while maintaining the same classification accuracy, to facilitate more concise and efficient decision-making. Attribute reduction is also called feature selection.
With the emergence of the era of big data, the intricacies and diversities of data have been constantly on the rise. Many datasets encompass both nominal and real-valued attributes, which are referred to as hybrid data. Such hybrid data can be found in various domains, including finance, healthcare, and e-commerce. The hybrid data encompass diverse attributes, necessitating distinct methodologies and strategies for their manipulation. The complexity intensifies the challenges of attribute reduction. Primarily, the disparities among nominal attribute values prove challenging to assess accurately using Euclidean distance. Furthermore, data may encompass uncertainties such as fuzzy attributes and anomalous attribute values. The reduction of attributes in hybrid data is a pivotal research topic in the field of data mining and lies at the heart of rough set theory. This line of research not only enhances the efficiency and precision of data processing but also fosters the advancement of data mining and machine learning. Consequently, exploring the attribute reduction problem in mixed information systems holds profound theoretical significance and practical relevance [1].
The classical rough set theory is limited in its ability to handle continuous data, hence it has been enhanced to include neighborhood rough sets and fuzzy rough sets as extensions. Currently, numerous scholars have delved into the intricacies of attribute reduction by using neighborhood rough sets and fuzzy rough sets, ultimately yielding impressive outcomes.
Neighborhood rough sets can effectively handle continuous values and have been widely applied in attribute reduction. Fan et al. [2] established a max-decision neighborhood rough set model and successfully applied it to achieve attribute reduction for information systems, leading to more accurate and concise decision-making. Shu et al. [3] proposed a neighborhood entropy-based incremental feature selection framework for hybrid data based on the neighborhood rough set model. In their study, Zhang et al. [4] conducted the entropy measurement on the gene space, utilizing the neighborhood rough sets, for effective gene selection. Zhou et al. [5] put forward an online stream-based attribute reduction method based on the new neighborhood rough set theory, eliminating the need for domain knowledge or pre-parameters. Xia et al. [6] built a granular ball neighborhood rough set method for fast adaptive attribute reduction. Liao et al. [7] developed an effective attribute reduction method for handling hybrid data under test cost constraints based on the generalized confidence level and vector neighborhood rough set models. None of the above methods provides a specific strategy for handling the differences between nominal attribute values. Instead, they use Euclidean distance to measure the differences between nominal attribute values, or use category information to simply define the differences between nominal attribute values as 1 or 0.
Fuzzy rough sets are capable of effectively dealing with the ambiguity in real-world scenarios, and have also been successfully applied in attribute reduction. Yuan et al. [8] established a unsupervised attribute reduction model for hybrid data based on fuzzy rough sets. Zeng et al. [9] examined the incremental updating mechanism of fuzzy rough approximations in response to attribute value changes in a hybrid information system. Yang et al. [10] considered the uncertainty measurement and attribute reduction for multi-source fuzzy information systems based on a new multi-granulation rough sets model. Wang et al. [11] utilized variable distance parameters and, drawing from fuzzy rough set theory, developed an iterative attribute reduction model. Singh et al. [12] came up with a fuzzy similarity-based rough set approach for attribute reduction in set-valued information systems; Jain et al. [13] created an attribute reduction model by using the intuitionistic fuzzy rough set. The above methods are either not suitable for handling mixed data or do not have special techniques for handling nominal attribute values and abnormal attribute values.
Information entropy quantifies the uncertainty of knowledge and can be used for the attribute reduction. Li et al. [14] used conditional information entropy to measure the uncertainty and reduce the attributes of multi-source incomplete information systems. Vergara et al. [15] summarized the feature selection methods based on the mutual information. Li et al. [16] measured the uncertainty of gene spaces and designed a gene seleciton algorithm using information entropy. Zhang et al. [17] defined a fuzzy information entropy of classification data based on the constructed fuzzy information structure and used it for attribute reduction. Zhang et al. [18] constructed a hybrid data attribute reduction model utilizing the λ-conditional entropy derived from fuzzy rough set theory. Sang et al. [19] proposed an incremental attribute reduction method using the fuzzy dominance neighborhood conditional entropy derived from fuzzy dominant neighborhood rough sets. Huang et al. [20] defined a new fuzzy conditional information entropy for fuzzy
Akram et al. [21,22] presented the concept of attribute reduction and designed the associated attribute reduction algorithms based on the discernibility matrix and discernibility function. These methods are intuitive and easy to comprehend, enabling the calculation of all reducts. However, they exhibit a high computational complexity, rendering them unsuitable for large datasets.
The comprehensive overview of the strengths and weaknesses of diverse attribute reduction algorithms can be found in Table 1.

1.3 Motivation and Contribution
Hybrid data is a common occurrence in data mining. They have been observed that nominal attributes significantly impact the measurement of data similarity, and Euclidean distance do not work well when dealing with nominal attribute values, yet the majority of current reduction algorithms rely heavily on Euclidean distance. Therefore, the supervised distance, a novel metric specifically for measuring the difference between nominal attribute values, has been meticulously crafted. Existing attribute reduction algorithms often exhibit sensitivity to abnormal attribute values and lack an efficient mechanism to address them. Consequently, this article introduces a novel fuzzy relationship that replaces similarity measurements based on attribute values with the count of similar attributes. This innovative approach effectively filters out abnormal attribute values, enhancing the overall accuracy and robustness of the algorithm. Due to the fact that the fuzzy conditional information entropy not only considers the fuzziness of data but also has a certain anti-noise ability, this paper uses fuzzy conditional information entropy to reduce the attributes of mixed data. The article’s novelty and contribution are outlined below:
1. A new distance metric called the supervised distance is introduced. The supervised distance metric, which considers the decision attribute that affect attribute similarity, leads to more precise attribute reduction.
2. Based on the new distance measurement, a new fuzzy relationship determined by the quantity of attributes with similar values is established. This approach views the relationship from the perspective of “feedback on parity of attribute values to attribute sets”, resulting in a fuzzy relation that is robust to a few abnormal attributes.
3. The fuzzy conditional information entropy is defined based on the new fuzzy relationship and an advanced attribute reduction algorithm is developed based on the fuzzy conditional information entropy. This algorithm incorporates an innovative distance function, an innovative fuzzy relationship, and fuzzy conditional information entropy.
4. Through meticulous experimental validation, this study clearly demonstrates that the fuzzy relation offers superior performance to the equivalence relation when dealing with hybrid data, effectively handling its complexity and uncertainties.
The structure of this paper is outlined as follows. Section 2 provides a brief overview of fuzzy relationships and HDISs, laying the foundation for the subsequent sections. Section 3 describes the method in detail. Section 4 presents the experimental results and discusses them. Section 5 summarizes the paper.
In this section, we will review some fundamental concepts of fuzzy relations and HDISs.
Let
Let
Let
Then
If R is a fuzzy set on
Let
Definition 2.1. Reference [24] Let R be a fuzzy relation on X. Then R is
1) Reflexive, if R(x,x) = 1 (
2) Symmetric, if R(x,y) = R(y, x) (
3) Transitive, if
If R is reflexive, symmetric, and transitive, then R is called a fuzzy equivalence relation on X. If R is reflexive and symmetric, then R is called a fuzzy tolerance relation on X.
Let
Then
According to (1),
Then
2.2 Hybrid Decision Information Systems
Definition 2.2. Reference [25] (X,C) is called an information system (IS), if
If
Definition 2.3. Let (X,B,d) is a decision information system. Then (X,B,d) is known as a hybrid decision information system (HDIS), if
Example 2.4. Table 2 shows an HDIS, where

To accurately measure the difference between two attributes in HDISs, we have developed a novel distance function that accounts for various types of attributes and missing data. This innovative approach allows for a more comprehensive assessment of the similarity or dissimilarity between different attributes in the system.
We first assign a definition for the distance between categorical attribute values to enable further distance definition of hybrid data.
Definition 3.1. For an HDIS (X,B,d), let
Then
Example 3.2. (Continue with Example 2.4)
Definition 3.3. For an HDIS (X,B,d), let
The distribution of attribute values defines a distance that is well-suited for the characteristics of classification data.
Proposition 3.4. Let (X,B,d) be an HDIS. Then the following conclusions are valid:
1)
2)
Proof. 1) The conclusion is self-evidently valid.
2)
Since
we have
Definition 3.5. For an HDIS (X,B,d), let
Definition 3.6. For an HDIS (X,B,d), let
Example 3.7. (Continuation of Example 2.4) According to Definitions 3.1–3.6, we have
1)
2)
3)
4)
5)
Definition 3.8. For an HDIS (X,B,d),
Example 3.9. (Continuation of Example 2.4) Here are the distance matrices of
Definition 3.10. For an HDIS (X,B,d),
Let
Definition 3.11. Let (X,B,d) be an HDIS.
Then
The matrix representation of
Let
According to (1),
Let
Let
Proposition 3.12. Let (X,B,d) be an HDIS. If
Proof. According to Definition 3.11,
Since
Thus,
Since
3.3 Fuzzy Conditional Information Entropy in HDISs
This section explores the concept of fuzzy entropy measures in HDISs to measure the uncertainty of HDISs.
Definition 3.13. (X,B,d) is an HDIS. Let
Proposition 3.14. (X,B,d) is an HDIS. Let
Proof. Since
Thus,
The following conclusion follows directly from Definition 3.13:
Definition 3.15. (X,B,d) is an HDIS. Let
Lemma 3.16. (X,B,d) is an HDIS. Let
Proof.
Thus,
Proposition 3.17. (X,B,d) is an HDIS. Let
Proof. According to Lemma 3.16,
Proposition 3. 18. (X,B,d) is an HDIS.
1) If
2) If
Proof. 1) Let
Hence,
According to Proposition 3.17, we have
Let
Then
Since the function f(x, y) exhibits monotonic increases in both x and y,
Hence,
2) Let
According to Proposition 3.17, we have
It follows from the monotonicity of f(x,y) that
Hence
Definition 3.19. (X,B,d) is an HDIS. Let
Lemma 3.20. (X,B,d) is an HDIS. Let
The equality holds as
Proof. The conclusion is self-evident.
Proposition 3.21. (X,B,d) is an HDIS. Let
Proof. Since
Proposition 3.22. (X,B,d) is an HDIS. Let
Proof.
Theorem 3.23. (X,B,d) is an HDIS. Let
Proof.
Thus,
Since
Hence,
3.4 An Attribute Reduction Algorithm Utilizing Fuzzy Conditional Information Entropy

Definition 3.24. (X,B,d) is an HDIS. Let
Let coo (B) denote the collection of all coordination subsets of B.
Definition 3.25. (X,B,d) is an HDIS. Let
Let red(B) denote the collection of all reducts of B.
In accordance with the aforementioned definitions and Proposition 3.18, Algorithm 1 for attribute reduction is hereby presented.
The time complexity of Algorithm 1 is shown in Table 3.

4 Experimental Results and Discussions
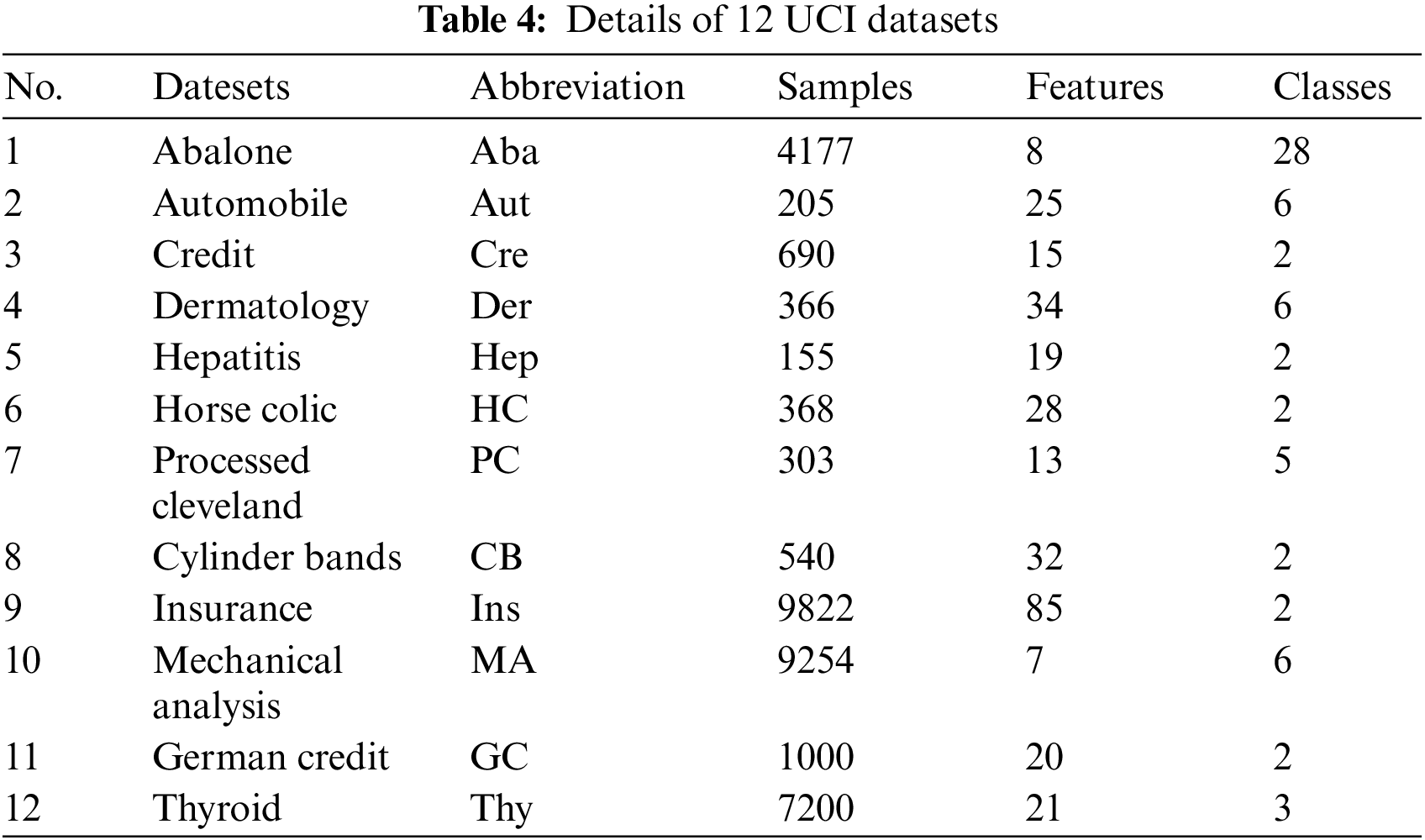
Across all experiments, we utilized twelve University of California Irvine (UCI) datasets with hybrid attributes to evaluate our approach. Table 4 offers comprehensive details on each dataset.
4.2 The Property of Monotonicity in Fuzzy Conditional Information Entropy
To verify the monotonicity of fuzzy conditional information entropy (FCIE), we calculate the fuzzy conditional information entropy of each dataset as the number of attributes increases.
Fig. 1 demonstrates that the fuzzy conditional information entropy consistently rises as the number of attributes increases, highlighting its monotonic behavior. The monotonicity displayed in Fig. 1 is a result of the parameter

Figure 1: Monotonicity of fuzzy conditional information entropy
4.3 The Influence of
The parameter
In the experiment, a decision tree classifier was employed, and the obtained results were the mean of six iterations of 10-fold cross-validation. The complete dataset is evenly divided into 10 distinct subsets. Of these, 9 subsets are designated as training datasets, while the remaining subset serves as the test dataset. This rotation is repeated until the test dataset has undergone all 10 subsets, ensuring comprehensive evaluation. The number of epochs is 60.
Fig. 2 shows the classification accuracy of the reduction results obtained by algorithm IARFCIE with different values of parameter


Figure 2: Accuracy of classification for 12 datasets under different parameter settings

4.4 Performance Comparison Results of IARFCIE and Other State-of-the-Art Attribute Reduction Algorithms
In this section, we present a comprehensive comparison of the proposed algorithm IARFCIE with nine state-of-the-art attribute reduction algorithms: The positive region backward deletion algorithm (PRBDA), the belief-based attribute reduction algorithm (BARA) [1], the cost-sensitive attribute-scale selection algorithm (CSASSA) [7], the entropy-approximate reduction algorithm (EARA) [11], the information-preserving reduction algorithm (IPRA) [26], the random forest algorithm (RFA) [27], the relief algorithm (RA) [28], the mutual information algorithm (MIA) [18], and the neighborhood rough set algorithm (NRSA) [2]. Tables 6 and 7 show the reduction results of 10 reduction algorithms on 12 datasets. Table 8 presents the classification accuracy achieved by 10 attribute reduction algorithms, as well as the original datasets, when utilizing decision tree (DT) classifier. The experimental results are obtained by averaging 10 runs of ten-fold cross-validation.



Tables 6–8 demonstrate that IARFCIE outperforms all other algorithms and raw datasets across the 12 datasets when utilizing the DT classifier. Despite selecting more features than EARA, CSASSA, RFA, and RA, there is minimal difference in the number of selected features and IARFCIE significantly surpasses their accuracy.
CSASSA and RA selected very few features, but their accuracy was also very low, indicating that they suffered from underfitting. PRBDA selected a very large number of features, but its accuracy was not very high, indicating that it suffered from overfitting.
The superior performance of IARFCIE can be attributed to two factors: Firstly, it does not rely on Euclidean distance, instead utilizing a novel distance metric. As is widely recognized, Euclidean distance is unsuitable for assessing the differences between nominal attribute values. The novel distance metric, which employs probability distributions to measure differences between nominal attribute values, aligns more closely with their inherent characteristics. Secondly, the algorithm introduces a new fuzzy relation that replaces similarity calculations based on distance with those derived from the number of attributes. This updated similarity measure effectively filters out a small number of outliers, thereby enhancing the robustness of the reduction algorithm.
5 Conclusions and Future Works
In this article, we introduce a novel difference metric that incorporates decision attributes. This metric offers a more accurate measurement of disparities between nominal attribute values. Subsequently, based on this new metric, we define a novel fuzzy relationship. This fuzzy relationship effectively filters out abnormal attribute values by utilizing the number of similar attributes to determine sample similarity. Furthermore, utilizing this new fuzzy relationship, we define a fuzzy conditional information entropy. An attribute reduction algorithm, formulated on the basis of fuzzy conditional information entropy, is then developed. Experimental results demonstrate that this attribute reduction algorithm not only exhibits a significant attribute reduction rate but also surpasses the original dataset as well as other attribute reduction algorithms in terms of average classification accuracy. Consequently, the novel metric and fuzzy relationship introduced in this article are effective in addressing the challenges associated with accurately measuring disparities between nominal attribute values and the sensitivity of attribute reduction algorithms towards abnormal attribute values. This study introduces a fresh perspective on reducing attributes in hybrid data by enhancing distance and fuzzy relationships. However, optimizing the parameters of the algorithm through grid search can significantly impact its efficiency. To address this issue, we aim to explore automatic parameter optimization methods as a future research direction.
Acknowledgement: The authors would like to thank the anonymous reviewers for their valuable comments.
Funding Statement: This work was supported by Anhui Province Natural Science Research Project of Colleges and Universities (2023AH040321) and Excellent Scientific Research and Innovation Team of Anhui Colleges (2022AH010098).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xiaoqin Ma; analysis and interpretation of results: Jun Wang, Wenchang Yu; draft manuscript preparation: Qinli Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. X. Chu et al., “Multi-granularity dominance rough concept attribute reduction over hybrid information systems and its application in clinical decision-making,” Inform. Sci., vol. 597, pp. 274–299, 2022. doi: 10.1016/j.ins.2022.03.048. [Google Scholar] [CrossRef]
2. X. D. Fan, W. D. Zhao, C. Z. Wang, and Y. Huang, “Attribute reduction based on max-decision neighborhood rough set model,” Knowl-Based Syst., vol. 151, no. 1, pp. 16–23, 2018. doi: 10.1016/j.knosys.2018.03.015. [Google Scholar] [CrossRef]
3. W. H. Shu, W. B. Qin, and Y. H. Xie, “Incremental feature selection for dynamic hybrid data using neighborhood rough set,” Knowl-Based Syst., vol. 194, no. 22, pp. 28–39, 2020. doi: 10.1016/j.knosys.2020.105516. [Google Scholar] [CrossRef]
4. J. Zhang, G. Q. Zhang, Z. W. Li, L. Qu, and C. Wen, “Feature selection in a neighborhood decision information system with application to single cell RNA data classification,” Appl. Soft Comput., vol. 113, no. 1, pp. 107876, 2021. doi: 10.1016/j.asoc.2021.107876. [Google Scholar] [CrossRef]
5. P. Zhou, X. G. Hu, P. P. Li, and X. D. Wu, “Online streaming feature selection using adapted neighborhood rough set,” Inform. Sci., vol. 481, no. 5, pp. 258–279, 2019. doi: 10.1016/j.ins.2018.12.074. [Google Scholar] [CrossRef]
6. S. Y. Xia, H. Zhang, W. H. Li, G. Y. Wang, E. Giem and Z. Z. Chen, “GBNRS: A novel rough set algorithm for fast adaptive attribute reduction in classification,” IEEE Trans. Knowl. Data Eng., vol. 34, no. 3, pp. 1231–1242, 2022. doi: 10.1109/TKDE.2020.2997039. [Google Scholar] [CrossRef]
7. S. J. Liao, Y. D. Lin, J. J. Li, H. L. Li, and Y. H. Qian, “Attribute-scale selection for hybrid data with test cost constraint: The approach and uncertainty measures,” Int. J. Intell Syst., vol. 37, no. 6, pp. 3297–3333, 2022. doi: 10.1002/int.22678. [Google Scholar] [CrossRef]
8. Z. Yuan, H. Chen, T. Li, Z. Yu, B. Sang and C. Luo, “Unsupervised attribute reduction for mixed data based on fuzzy rough set,” Inform. Sci., vol. 572, no. 1, pp. 67–87, 2021. doi: 10.1016/j.ins.2021.04.083. [Google Scholar] [CrossRef]
9. A. P. Zeng, T. R. Li, J. Hu, H. M. Chen, and C. Luo, “Dynamical updating fuzzy rough approximations for hybrid data under the variation of attribute values,” Inform. Sci., vol. 378, no. 6, pp. 363–388, 2017. doi: 10.1016/j.ins.2016.07.056. [Google Scholar] [CrossRef]
10. L. Yang, X. Y. Zhang, X. H. Xu, and B. B. Sang, “Multi-granulation rough sets and uncertainty measurement for multi-source fuzzy information system,” Int. J. Fuzzy Syst., vol. 21, no. 6, pp. 1919–1937, 2019. doi: 10.1007/s40815-019-00667-1. [Google Scholar] [CrossRef]
11. C. Z. Wang, Y. Wang, M. W. Shao, Y. H. Qian, and D. G. Chen, “Fuzzy rough attribute reduction for categorical data,” IEEE Trans. Fuzzy Syst., vol. 28, no. 5, pp. 818–830, 2020. doi: 10.1109/TFUZZ.2019.2949765. [Google Scholar] [CrossRef]
12. S. Singh, S. Shreevastava, T. Som, and G. Somani, “A fuzzy similarity-based rough set approach for attribute selection in set-valued information systems,” Soft Comput., vol. 24, no. 6, pp. 4675–4691, 2020. doi: 10.1007/s00500-019-04228-4. [Google Scholar] [CrossRef]
13. P. Jain, A. K. Tiwari, and T. Som, “A fitting model based intuitionistic fuzzy rough feature selection,” Eng. Appl. Artif. Intell., vol. 89, pp. 1–13, 2020. doi: 10.1016/j.engappai.2019.103421. [Google Scholar] [CrossRef]
14. Z. W. Li, Q. L. Zhang, S. P. Liu, Y. C. Peng, and L. L. Li, “Information fusion and attribute reduction for multi-source incomplete mixed data via conditional information entropy and D-S evidence theory,” Appl. Soft Comput., vol. 151, no. 11, pp. 111149, 2023. doi: 10.1016/j.asoc.2023.111149. [Google Scholar] [CrossRef]
15. J. Vergara and P. Estevez, “A review of feature selection methods based on mutual information,” Neur. Comput. App., vol. 24, no. 1, pp. 175–186, 2014. doi: 10.1007/s00521-013-1368-0. [Google Scholar] [CrossRef]
16. Z. W. Li, Q. L. Zhang, P. Wang, Y. Song, and C. F. Wen, “Uncertainty measurement for a gene space based on class-consistent technology: An application in gene selection,” Appl. Intell., vol. 53, no. 2, pp. 5416–5436, 2022. doi: 10.1007/s10489-022-03657-3. [Google Scholar] [CrossRef]
17. Q. L. Zhang, Y. Y. Chen, G. Q. Zhang, Z. W. Li, L. J. Chen and C. F. Wen, “New uncertainty measurement for categorical data based on fuzzy information structures: An application in attribute reduction,” Inform. Sci., vol. 580, no. 5, pp. 541–577, 2021. doi: 10.1016/j.ins.2021.08.089. [Google Scholar] [CrossRef]
18. X. Zhang, C. L. Mei, D. G. Chen, and J. H. Li, “Feature selection in mixed data: A method using a novel fuzzy rough set-based information entropy,” Pattern Recogn., vol. 56, pp. 1–15, 2016. doi: 10.1016/j.patcog.2016.02.013. [Google Scholar] [CrossRef]
19. B. B. Sang, H. M. Chen, L. Yang, T. R. Li, and W. H. Xu, “Incremental feature selection using a conditional entropy based on fuzzy dominance neighborhood rough sets,” IEEE Trans. Fuzzy Syst., vol. 30, no. 6, pp. 1683–1697, 2021. doi: 10.1109/TFUZZ.2021.3064686. [Google Scholar] [CrossRef]
20. Z. H. Huang and J. J. Li, “Discernibility measures for fuzzy β covering and their application,” IEEE Tansa. Cybernet., vol. 52, no. 9, pp. 9722–9735, 2022. doi: 10.1109/TCYB.2021.3054742. [Google Scholar] [PubMed] [CrossRef]
21. M. Akram, H. S. Nawaz, and M. Deveci, “Attribute reduction and information granulation in Pythagorean fuzzy formal contexts,” Expert. Syst. Appl., vol. 222, no. 1167, pp. 119794, 2023. doi: 10.1016/j.eswa.2023.119794. [Google Scholar] [CrossRef]
22. M. Akram, G. Ali, and J. C. R. Alcantud, “Attributes reduction algorithms for m-polar fuzzy relation decision systems,” Int. J. Approx. Reason., vol. 140, no. 3, pp. 232–254, 2022. doi: 10.1016/j.ijar.2021.10.005. [Google Scholar] [CrossRef]
23. L. A. Zadeh, “Fuzzy sets,” Inform. Control, vol. 8, no. 3, pp. 338–353, 1965. doi: 10.1016/S0019-9958(65)90241-X. [Google Scholar] [CrossRef]
24. D. Dubois and H. Prade, “Rough fuzzy sets and fuzzy rough sets,” Int. J. Gen. Syst., vol. 17, no. 2–3, pp. 191–209, 2007. doi: 10.1080/03081079008935107. [Google Scholar] [CrossRef]
25. Z. Pawlak, “Rough sets,” Int. J. Inf. Comput. Sci., vol. 11, no. 5, pp. 341–356, 1982. doi: 10.1007/BF01001956. [Google Scholar] [CrossRef]
26. Q. H. Hu, D. Yu, and Z. Xie, “Information-preserving hybrid data reduction based on fuzzy-rough techniques,” Pattern Recogn. Lett., vol. 27, no. 5, pp. 414–423, 2006. doi: 10.1016/j.patrec.2005.09.004. [Google Scholar] [CrossRef]
27. E. Sylvester et al., “Applications of random forest feature selection for fine-scale genetic population assignment,” Evol. Appl., vol. 11, no. 2, pp. 153–165, 2018. doi: 10.1111/eva.12524. [Google Scholar] [PubMed] [CrossRef]
28. R. J. Urbanowicz, M. Meeker, W. Lacava, R. S. Olson, and J. H. Moore, “Relief-based feature selection: Introduction and review,” J. Biomed. Inform., vol. 85, no. 4, pp. 189–203, 2018. doi: 10.1016/j.jbi.2018.07.014. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools