A Novel Scheduling Framework for Multi-Programming Quantum Computing in Cloud Environment

Decision Variables

1  Introduction

Quantum computers have gained widespread attention in recent years due to their extraordinary capabilities in solving problems that are difficult for classical computing, such as physical and chemical simulations [1,2], database searches [3], and machine learning [4].

Recently, Google, IBM, Intel, and Honeywell have announced their respective quantum computers with 72, 65, 49, and 10 quantum bits, respectively [5–8]. Despite the rapid development of quantum computers, the current stage of development of quantum devices is still the noise intermediate-scale quantum (NISQ) era [9], in which quantum devices are highly susceptible to interference from environmental noise and, therefore, error-prone. To reduce this noise, quantum computers require complex control circuits, advanced microwave equipment, cryogenic refrigeration systems capable of maintaining temperatures in the milli-kelvin range, a shielded environment to protect against external disturbances and efficient control systems [10]. These demanding environmental conditions and the high cost of equipment make it difficult for the average user to have access to local quantum computing resources (personal quantum computers). As an extremely scarce and expensive resource, cloud providers of quantum services offer cloud quantum computing services for the average user. Cloud provider giants such as IBM, Google, Microsoft, and Honeywell, as well as startups such as Xanadu, Rigetti, IonQ, and D-Wave, currently provide quantum hardware. Quantum computing cloud services are advantageous due to their accessibility, ease of use, and scalability. Users can access quantum resources easily through cloud services [7,11,12].

As quantum computing technology develops, the number of users of quantum computing as a cloud service is expected to grow exponentially over the next decade. However, the quantum cloud provider uses time-based resource sharing to manage access to its backends. The limited quantum resources [9,11,12] lead to a large number of pending tasks on each quantum device in general, causing users to wait a long time in the queue. This is one of the limitations of current cloud quantum computing systems. To address this issue, some researchers have proposed implementing multi-programming on NISQ computers [13–17] to enhance the utilization of robust qubits on individual quantum machines. However, it is important to note that while this technique effectively improves the throughput of a single quantum backend, it does not optimize the overall throughput of the quantum cloud service. This stems from the multi-programming approach’s ongoing necessity for users to specify the backend for execution, with users remaining uninformed about the queueing status on the backend quantum computers. This leads to notable variations in the number of queued tasks across various backends, with a considerable range of 10 to 1000 quantum tasks queued on different quantum machines at any given moment, exhibiting substantial randomness [18]. This leads to a subpar user experience and, to some extent, hinders the development of quantum algorithms and applications. In response to this challenge, the paper introduces a quantum task scheduling and resource management framework called MTMB, tailored to handle multiple quantum tasks across multiple quantum backends. Unlike previous approaches that utilize multi-programming techniques with single-backend scheduling algorithms, our framework considers all tasks and quantum computing resources available at the current cloud service. It efficiently allocates tasks to the optimal quantum backend while ensuring fairness between users. It also utilizes various multi-programming techniques in different quantum backends to improve the overall throughput of the quantum cloud. Furthermore, our framework removes the need for users to specify the quantum backend, significantly reducing their workload.

The rest of the paper is organized as follows. First, we present the background and motivation of the circuit scheduling in Section 2 and Section 3. Then, we introduce the architecture of MTMB in Section 4. Afterward, Section 5 mainly includes the experiment and evaluation of our method. Finally, we summarize our findings in Section 6.

2  Background

This section presents knowledge about quantum computing fundamentals [19–22] and multi-programming techniques [13–17]. Related work is discussed to ensure that quantum task scheduling and resource management problems can be formulated and understood.

2.1 Quantum Computing Basics

Quantum computing exploits the properties of quantum states (such as the superposition principle and quantum entanglement) to perform computations. It is considered the next generation of information processing technology and is theoretically effective in solving many classical intractable problems. Quantum computing is accomplished by manipulating several quantum bits through a series of quantum gates. Quantum bits are somehow similar to the “bits” in classical computing. A quantum bit can exist in quantum state of either 1 or 0 or in a superposition of both. This property of state superposition makes quantum computing far superior to classical computing for certain problems.

Quantum gates are used to alter the state of quantum bits, and quantum computing is achieved by manipulating quantum bits through quantum gates, which is similar to classical logic gates. The four commonly used quantum gates are Pauli-X Gate (X), Hadamard Gate (H), Pauli-Y Gate (Y), and Controlled NOT Gate (CNOT), where X, H, and Y are single-qubit gates that operate on only a single quantum bit, and the CNOT gate is a two-qubit gate that works on two quantum bits. It is possible to decompose any quantum gate involving three or more quantum bits can be decomposed into single-qubit and two-qubit gates [21,22].

2.2 Multi-Programming Mechanism

The multi-programming mechanism is a recent proposal to improve the single-computer throughput of quantum computers. It compiles multiple quantum circuits together at compilation time based on the characteristics of quantum backends. Fig. 1 shows two five-qubit circuits are assembled onto the IBMQ Toronto simultaneously. The throughput of the quantum computer increases from 18.5% to 27% with parallel execution compared to running separately, resulting in a general decrease in total running time.

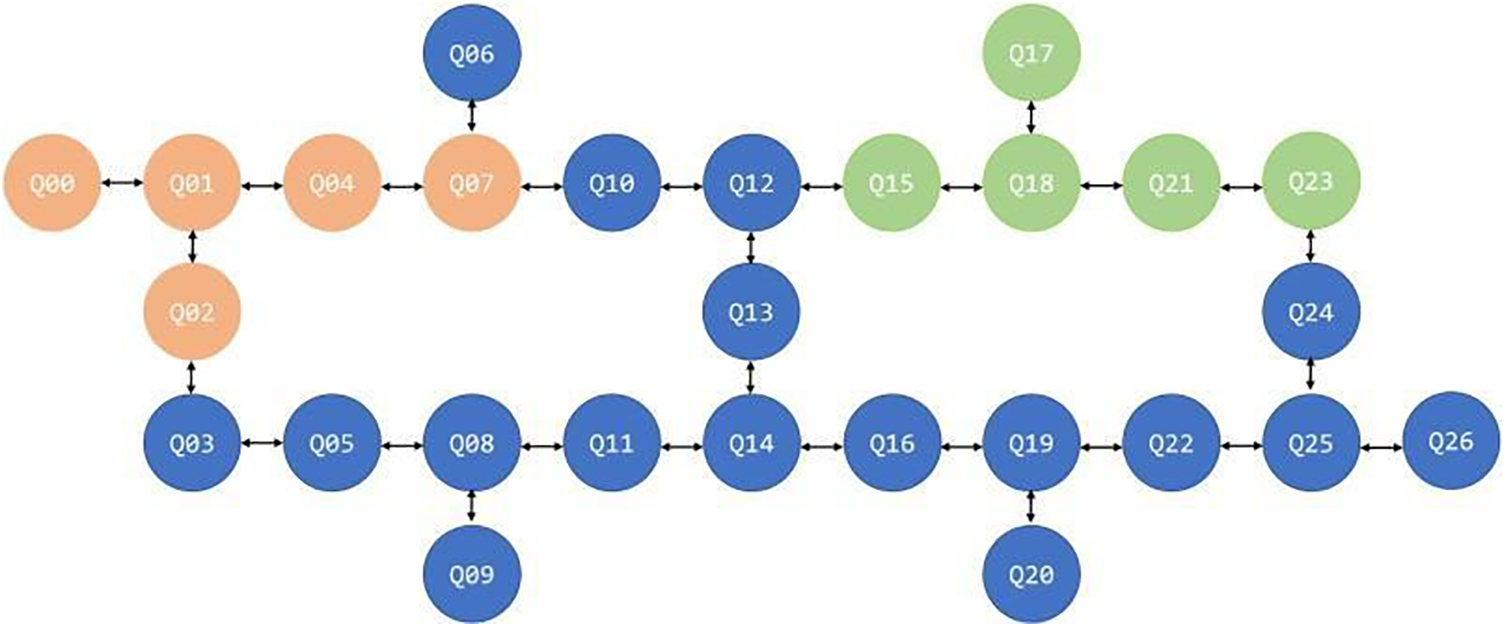
Figure 1: Two circuits for multi-programming

It is important to note that implementing a multi-programming mechanism can be challenging. As the throughput increases, the circuit fidelity of parallel operations decreases due to the additional crosstalk introduced when executing multiple programs. In addition, the number of highly reliable single and double quantum bit pairs on quantum computers limits the implementation of multi-programming. Previous studies [13–15,17] have enhanced the accuracy of parallel operations on circuits by taking into account the characteristics of single-bit, double-bit, cross-talk, and measurement errors and selecting the appropriate physical bits for mapping. Our work focuses on improving the fidelity of circuit parallel operation while guaranteeing user fairness and maximizing the mapping efficiency as much as possible. The detailed algorithm will be presented in Chapter 4.

2.3 Related Work

To our knowledge, no research has integrated back-end auto-allocation, multi-programming technology, and adaptive scheduling tuning into a quantum task scheduling framework. However, some existing studies have addressed these challenges. This section describes the related research for each challenge.

The first challenge addressed is the automated allocation of the backend, which involves mapping quantum circuit calculations to physical resources and executing them. Several attempts have been made to automate the hardware selection process. Ravi et al. [18] proposed an improved adaptive task scheduling method for the quantum cloud. The Quantum Resource Estimator, presented by Suchara et al. [23], achieves QPU selection by estimating factors such as the number of physical qubits, execution time, and the success probability of operating a quantum algorithm on the QPU. Additionally, Salm et al. [24] have developed an automatic framework that precisely transforms quantum circuits into various programming languages. The resulting circuits are compiled with multiple compilers on different quantum backends, with the resulting compilation prioritized according to user requirements. Finally, specific circuits are executed on the most suitable available quantum computers. The authors later expanded their framework to enable automated selection of quantum compilers and backends based on past executions, prior to translating and compiling input circuits. This guarantees the precision of future execution results. Although these studies represent significant progress in automating hardware selection, none of them systematically integrate circuit aggregation.

Multi-programming technology can effectively solve the quantum backend utilization problem. The multi-programming technology was first proposed by Das et al. [13] through the development of a Fair and Reliable Partitioning (FRP) method. Liu et al. [17] subsequently enhanced this mechanism by introducing QuCloud, a cloud-based technology that encompasses a novel qubit mapping approach and compilation task scheduler for multiprogramming quantum computers. Niu et al. [14] addressed the issue of the QPU partitioning issue with a hardware-aware multiprogramming compiler that takes into account the hardware topology, calibration data, and crosstalk effects to confidently assign partitions to distinct quantum circuits. Additionally, there are circuit parallel operation schemes that are optimized for specific domains, as demonstrated by Mineh et al. [25]. Their study examined the impact of multi-programming technology on the variational quantum eigensolver. Meanwhile, Park et al. [26] proposed a quantum multi-programming algorithm for Grover’s search. These studies have approached the issue from the perspective of backend partitioning or domain specificity. However, our research focuses on selecting multiple quantum circuits to execute aggregation on distinct backends.

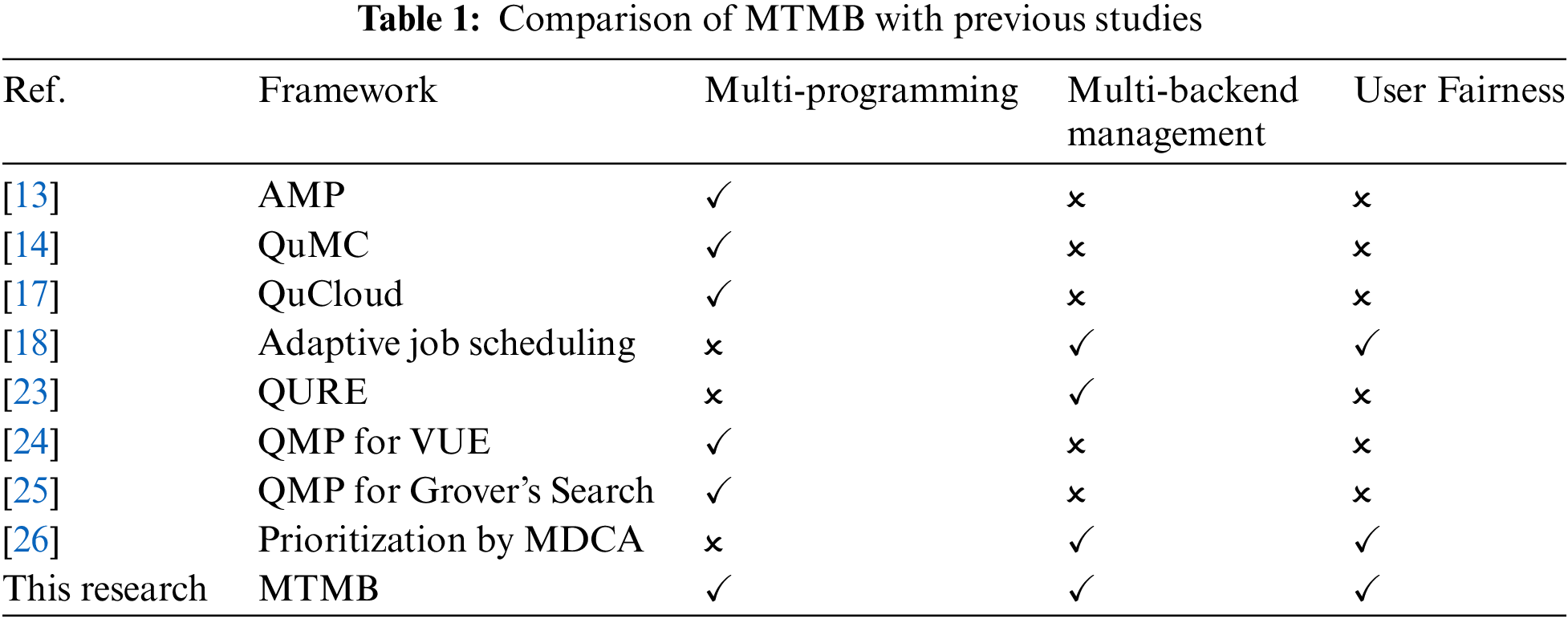
This work combines the advantages of the above two aspects and proposes a quantum task scheduling and resource management framework for multiple quantum tasks and multiple backends (MTMB). The framework schedules different quantum circuits to backends for parallel execution based on the queueing circuit characteristics and backend characteristics. The aim is to increase the throughput of the quantum cloud and reduce the waiting time of users while ensuring fairness among them. In addition, heuristic algorithms are used to dynamically adjust the granularity of the parallel circuit search, maintaining a dynamic balance between parallel search efficiency and execution fidelity. Table 1 illustrates the difference between MTMB and previous methods.

3  Motivation

Cloud quantum providers currently offer quantum computing accessible to anyone. As a result, there is a wide range of expertise among users, leading to variation in the design of quantum circuits and the required quantum backends for circuit execution. Users must select the backend where the task will run before submission, making it necessary for users to consider the various constraints of different quantum computing devices. This is crucial for achieving the task. This imposes an unnecessary burden on users.

Additionally, customers may not be aware of the queueing situation on each quantum backend, resulting in significant differences in waiting time for users who submit tasks to different quantum backends simultaneously. We propose delegating the choice to our framework, which includes a quantum hardware selector and a mapping optimizer. This framework will map the user-submitted circuits based on the existing queues and fidelity of each quantum backend on a merit basis. This will reduce the confusion among researchers about the selection of quantum backends and allow users to focus on their algorithms and applications. It will also ensure fairness among users.

The demand for cloud quantum computing has increased in recent years, resulting in longer queues after users submit their tasks [15]. Providers must consider how to improve the throughput of the quantum cloud. The proposed architecture in this paper includes load balancing among multiple quantum backends and executing multiple quantum circuits in parallel on a single backend to increase the load of the quantum cloud while ensuring user fairness and computational quality. Additionally, the framework can dynamically adjust the parallelism depending on the current moment of multi-user task submission to balance fidelity and queuing time more effectively.

4  Proposed Solution

The paper depicts the structure in Fig. 2. Users submit their running circuits on the user side, which then enter the user submission queue in the order they were submitted. The circuit with the longest current waiting time is fed to the Parallel Selector as the main circuit. The Parallel Selector selects K parallel circuits that are appropriate for multi-programming execution, based on the circuit’s properties. The selected circuits should be located as close as possible to the depth of the main circuit, while minimizing the number of CNOT gates and bits used. Next, the main and parallel circuits are inputted into the Hardware Selector, which assigns appropriate quantum backends based on their load and the number of main circuit bits. Finally, the Mapping Optimizer is used to map multiple circuits onto the selected quantum backend and output them to the queue of each waiting backend for execution. During the mapping process, it is essential to prioritize the main circuits before the parallel circuits. As multiple circuits run simultaneously, it is necessary to separate the outcomes and deliver them to the user through a Result Distributor. A detailed description of each module’s functions and implementation is elaborated below.

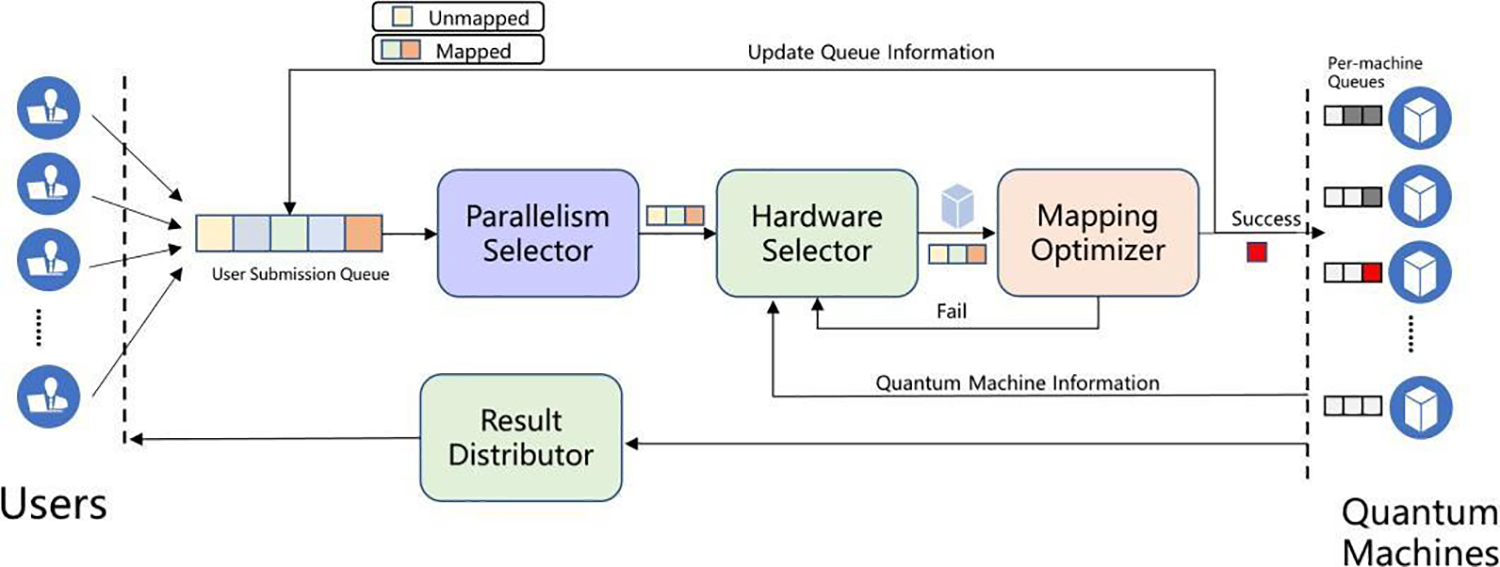
Figure 2: Scheduling framework structure

4.1 Parallelism Selector

To enhance the quantum cloud throughput, we implement parallel execution of multiple circuits on each quantum backend whenever possible. As the number of user-submitted circuits increases, selecting the appropriate parallel circuits from the user-submitted queue can cause significant overhead. Therefore, the following strategy is designed.

First, to ensure fairness among users, we select the circuit with the longest dwell time as the main circuit from the queue based on the first-in-first-out principle. The remaining circuits are then sorted according to their circuit characteristics. The sorting principles are as follows: 1. The depth of the circuit should differ from the depth of the main circuit by the smallest possible amount. 2. The circuit should occupy as few quantum bits as possible. 3. The circuit should contain the minimum number of multi-bit gates, with a focus on CNOT gates in this experiment. When considering circuit depth, if there is a large difference in depth between parallel circuits, such as a main circuit C1 depth of 30 and a parallel circuit C2 depth of 210, the execution time of the main circuit C1 is extended during parallel operation. If circuit C1 is measured beforehand, it will interfere with the state of other quantum bits leading to a loss of fidelity [13,27]. As a result, all the gates in parallel circuit C2 need to be executed before the quantum bits’ measurement operations in the main circuit C1 can be performed. This can result in significant coherence errors and a reduction in fidelity in main circuit C1 over an extended period [13,28]. To tackle this issue, we aim to choose circuits with minimal differences in depth.

Using fewer quantum bits can improve the success rate of parallel operations and make it easier to achieve physical isolation in hardware during mapping optimization, reducing runtime crosstalk. The mapping optimization section provides detailed information on this.

Crosstalk, which refers to the undesired interactions between quantum bits in a chip [29–31], is a significant source of noise in quantum chips. One type of crosstalk is more intense and caused by simultaneous operations between particular quantum bit pairs [31,32]. The crosstalk is primarily caused by CNOT gates. When fewer CNOT gates are present, there is less crosstalk with the main circuit, resulting in improved circuit accuracy. As a result, the number of CNOT gates is a critical factor to consider.

After sorting the remaining queues, the K circuits with the highest rank are selected and fed into the hardware selector along with the main circuit. To adapt the framework to different load cases, the value of K will be dynamically modified based on the machine queues and user submission queues in the background. K will be reduced when the ratio of the sum of the number of tasks waiting in each machine queue to the number of tasks waiting in the user submission queue is very small in a low load case. This speeds up the scheduling execution, but at the same time reduces the amount and possibility of parallelism. Consequently, the fidelity is enhanced to some extent. K increases when the ratio of the total number of tasks waiting in each machine’s queue to the number of tasks waiting in the user submission queue is high under heavy load. This is because the backend load is already significant enough that the scheduler’s execution time no longer needs to be considered. Increasing K at this point enhances the likelihood of parallelism and boosts the throughput of the Quantum Cloud.

4.2 Hardware Selector

After selecting the K optimal parallel circuits, the parallel selector inputs them to the hardware selector, which determines the appropriate quantum backend. The quantum backend is subject to bit mapping in the specific order of the main circuit being handled first, followed by the parallel circuit. If the mapping is successful, the result is entered into the single backend queue. If not, the process returns to select the new quantum backend.

When selecting quantum backends, it is crucial to have sufficient quantum bits to complete the user-submitted circuit. This paper uses the number of quantum bits in the main circuit as the benchmark. This approach has two benefits: Firstly, completing the primary circuit in one mapping avoids unnecessary scheduling delays, and secondly, it provides an equal opportunity for the selection of quantum backends. If K parallel circuit bits are used as a benchmark, the probability of selection for a quantum backend with a low number of quantum bits decreases significantly, thereby impacting the overall throughput of the quantum cloud.

Besides the number of quantum bits, another important factor is the queuing time of each quantum backend. In this paper, we estimate the queuing time of each quantum backend based on two features: The queue length and the number of quantum circuits running in the queue. We then prioritize mapping the circuits to backends with shorter queuing time to improve the quantum cloud’s throughput and achieve load balancing.

4.3 Mapping Optimizer

After obtaining the set of candidate parallel circuits and quantum backends, they need to be bit-mapped to fulfill the circuit parallelism requirements and guarantee operation fidelity. Various multi-programming quantum bit-mapping schemes exist, such as QuCloud proposed by Liu et al. [17,33], which primarily focus on the robust quantum bit allocation in the quantum backend and reduction of swap gates at compile-time. It should be noted that the proposed schemes do not take into account the perspectives of quantum cloud and do not ensure fairness and scheduling efficiency among users. In contrast, our suggested mapping approach concentrates on the aforementioned factors, prioritizes user impartiality while ensuring accuracy, and maximizes mapping efficiency via heuristics, outlined below.

Firstly, the principal circuit of the given parallel circuits is bit-mapped. If the initial mapping attempt is successful, the remaining parallel circuits are subsequently mapped. If the attempt is unsuccessful, it will be returned directly to the hardware selector, which can choose another suitable quantum backend to map the main circuit until the attempt is successful. If there is no quantum backend available, the user will be informed directly. This process aims to adhere to the principle of first-come, first-served users, equalize the user waiting time, and ensure the user experience. We utilize an overall greedy strategy for the specific mapping scheme. A partitioned fidelity fraction metric has been developed, which uses single-bit gate fidelity, double-bit gate fidelity, and measurement fidelity as bit characteristics within a quantum backend. The Eq. (1) demonstrates this metric.

SCORE=W1D+W2S+W3M(1)

D represents the two-bit gate fidelity, S represents the single-bit gate fidelity, M represents the measurement fidelity, and W represents the weight factor whose sum is 1. When evaluating candidate circuits, we designate the number of two-qubit gates as a feature and give priority to mapping circuits with a greater number of such gates to physical qubit pairs with better fidelity. The fidelity and other values of each quantum backend are predetermined during calibration, and the number of two-qubit gates in the circuit can be obtained from the circuit’s properties. Consequently, our proposed heuristic mapping algorithm satisfies user fairness while ensuring high scheduling efficiency.

To enhance the accuracy of multi-programming, physical buffers are utilized. The crosstalk between adjacent quantum bits is substantially higher than that between quantum bits separated by one hop. Once a circuit is mapped to a quantum backend, the n-hop bits around the mapped quantum bit become inactivated. Although this reduces the throughput somewhat, it concurrently increases the fidelity.

4.4 Result Distributor

As quantum circuits are executed in parallel on multiple quantum backends, the results must be separated and returned to the user. The scheduler groups the user’s identification, the parallel circuit, and the chosen quantum backend by the scheduler in a set, which is stored in the database before being sent to every quantum backend queue. After executing the quantum backends, the resulting information is divided and stored in the database based on the user and circuit information. The client call retrieves this information.

5  Evaluation

5.1 Methodology

5.1.1 Metrics

We use three evaluation metrics in the evaluation of this framework:

Trial Reduction Factor (TRF) [28]: TRF is defined as the ratio of the trials needed when quantum circuits are performs independently to the trials required when they are executed simultaneously. It is used to evaluate a quantum backend throughput, and the average TRF of all backends can be used to evaluate the quantum cloud throughput.

Probability of a Successful Trial (PST) [34]: PST is defined as the number of trials with expected results divided by the total number of trials, as shown in the following equation. It is used to evaluate the fidelity of the quantum backend on the quantum cloud.

Scheduling Time Ratio (STR): STR is defined as the ratio of the time spent by a circuit from commit until it is assigned to the waiting queue of each backend for different values of K vs. when K=1. It is used to evaluate scheduling time consumption.

User Waiting Time (WT): WT refers to the period of time between the submission of a task and the receipt of the result. In our experiments, we divide it into two parts: Task queuing time and task execution time.

5.1.2 Dataset

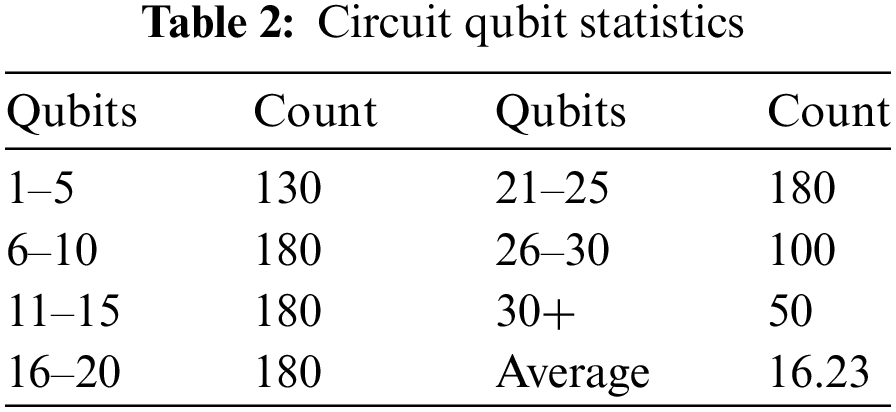
The dataset used in this study was collected from several previous works, namely RevLib [35], QASM-Bench [36], Quiper [37], and Scaffold [38]. These test suites include quantum algorithms with varying quantum bit counts and gate operation depths from multiple domains, such as optimization, simulation, quantum algorithms. We selected one thousand circuits with diverse characteristics from this set to model user inputs for assessing the throughput of our suggested scheduling framework. Sixty circuits were selected for evaluation of their fidelity. These benchmarks are commonly employed in experiments related to quantum technologies and incorporate circuits with a range of quantum bit quantities, which are further detailed in Table 2, where Qubits represents the range of quantum bit numbers within a circuit, and Count represents the quantity of circuits with the same number of quantum bits.

5.1.3 Evaluation Comparisons

To evaluate the performance of MTMB, we compared it with two baselines. The first baseline is a scheduling framework that only considers fidelity, called Fidelity Only. Its objective is to maximize the fidelity of user-submitted quantum circuits. However, it does not take into account the backend queuing situation, throughput, or require multi-programming technology when selecting the backend and mapping. To obtain the optimal fidelity result, the quantum cloud backend must only select the optimal quantum bit. Another framework, known as Waiting Time-Only, aims to minimize the user’s waiting time without considering other factors such as circuit fidelity. This is accomplished by maximizing the number of parallel runs of circuits and performing load balancing directly on the quantum cloud backend.

5.1.4 Quantum Cloud Simulation Infrastructure

This paper presents the results of our experiments in simulating a quantum cloud environment using the IBM Qiskit [39] simulator and the IBM Quantum Backend Device Model to conduct our experiments. Ten simulated backends were selected, namely “Vigo”, “Guadalupe”, “Tokyo”, “Boeblingen”, “Toronto”, “Montreal”, “Cambridge”, “Rochester”, “Manhattan”, and “Washington”. Table 3 presents their respective qubit numbers, and additional information can be found on the IBM Quantum Systems website [39]. These ten simulated backends create a quantum cloud environment that offers quantum computing services to external users. It is important to note that while the simulated quantum circuit on the fake backend maintains fidelity to the real environment, there is a significant difference in runtime. In the actual backend, the running time of the circuit is primarily determined by the number of shots due to the coherence of quantum bits. To accurately reproduce this scenario, we fixed the running time of the circuit during the scheduling experiment. This was necessary to complete the waiting time experiment.

5.1.5 Experimental Hyperparameter Setting

This section outlines the process of setting hyperparameters for the experiment. The initial step is to determine the number of candidate circuits, which is denoted as K. A dynamic adjustment approach is adopted, where K is adjusted to 6 when the total size of all backend queues exceeds twice the size of the current user submission queue. When the total number of backend queues does not exceed the current submission queue, K is set to 2. During the equilibrium period, K is set to 4. In the mapping optimization algorithm, we heuristically set the values of parameter W to 0.4, 0.3, and 0.3 for W1, W2, and W3 respectively to ensure a reasonable mapping of physical qubits. The physical isolation hop count n is set to 1, and the number of quantum circuit shots is fixed at 1024. The circuit’s running time is set to 10 s under high load conditions and 5 s under low load conditions.

5.2 Experimental Results

5.2.1 Throughput Evaluation

We entered 1000 circuits randomly into the proposed framework and conducted 50 experiments. The average scheduling of each backend is illustrated in Fig. 3.

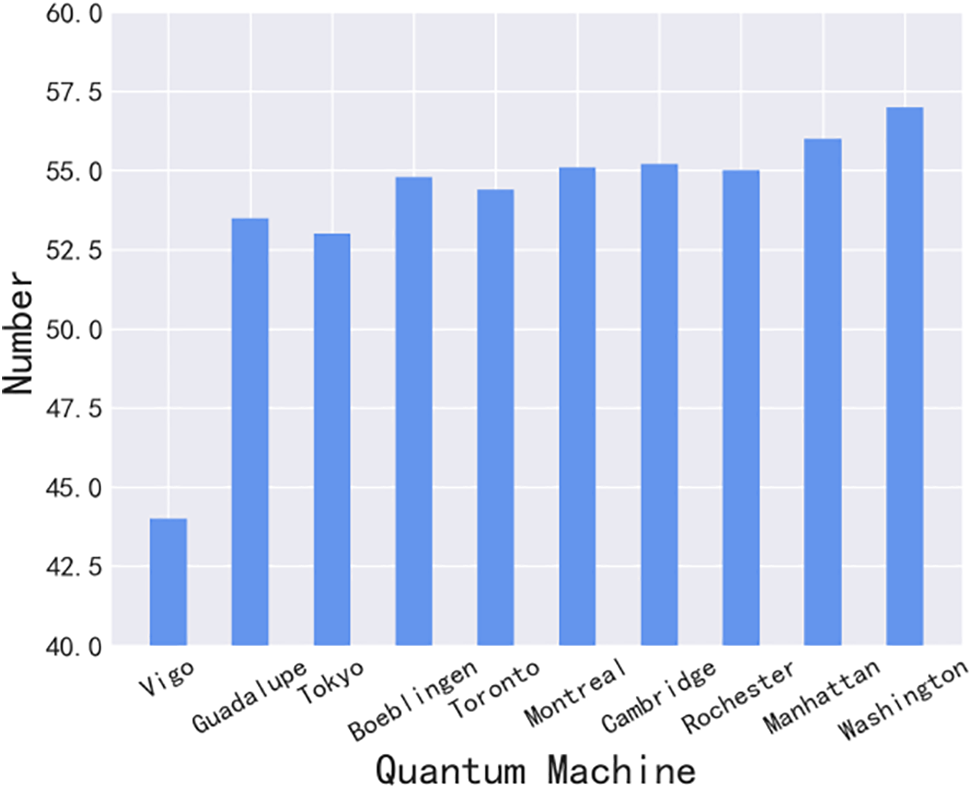
Figure 3: Distribution of quantum circuits in each backend

Overall, it is evident that the ten quantum backends achieve load balancing, and our framework distributes circuits on the quantum cloud as tasks to different backends efficiently after parallel selection. This provides evidence of the efficacy of our proposed framework. The number of tasks running on “Vigo” is slightly less than those on the other four quantum backends. This can be explained by the fact that it only has five quantum bits, while the average number of bits in the dataset is 16.23. Thus, “Vigo” is unable to execute most quantum circuits. The remaining four backends are assigned approximately the same number of tasks, and they have enough bits to support the majority of circuits in the dataset.

Fig. 4 depicts the average TRF of the ten quantum backends after framework scheduling, following to 50 trials. Our proposed framework increases the throughput of the quantum cloud by more than two times.

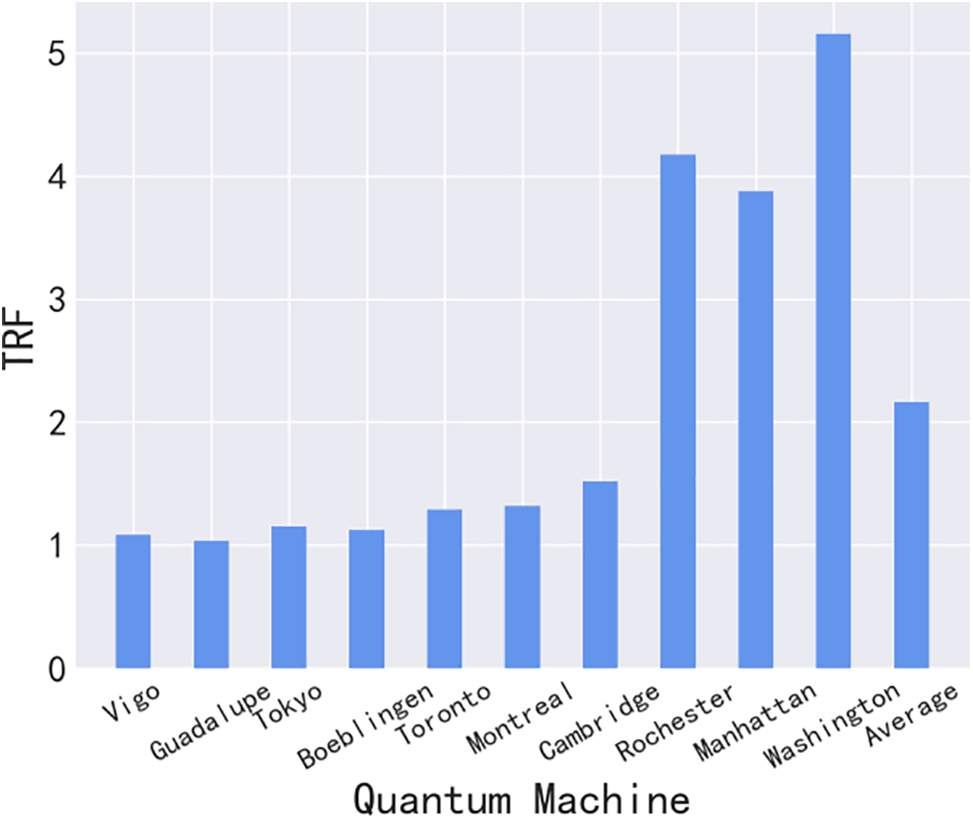
Figure 4: Throughput of each quantum backend and quantum cloud

Overall, the TRF rises as the count of backend bits increases. It is essential to note that the experimental dataset’s “Vigo” and “Guadalupe” backends exhibit a below-average number of qubits, restricting their concurrent circuit execution capabilities. As a result, their TRF remains near 1. Conversely, backends with more bits (such as “Washington”) can deliver up to a 5x increase in TRF. The greater the quantity of qubits in the backend, the more quantum circuits can run in parallel resulting in improved throughput. Additionally, the TRF varies slightly among backends with the same bit count, such as “Toronto” and “Montreal”. Because the TRF is not only affected by the queue sequence but also by the qubit connection structure of the two backends.

5.2.2 Fidelity Evaluation

To improve the simulation’s efficiency, we again selected 100 circuits from the above 1000 circuits for fidelity evaluation experiments. The fidelity experiments were conducted using our proposed framework after multi-programming. Subsequently, the parallel circuits were separated into distinct runs on selected backends to compare the fidelity of separate runs with that of parallel runs. The results are shown in the Fig. 5. It is apparent that the fidelity of the individual runs is marginally higher compared to that of the multiprogramming mode on all backends apart from “Vigo”. Still, there is no significant difference between the two, which proves the effectiveness of our mapping scheme. Despite the difference in fidelity is not significant enough to impact the user, the enhanced throughput greatly enhances the user experience.

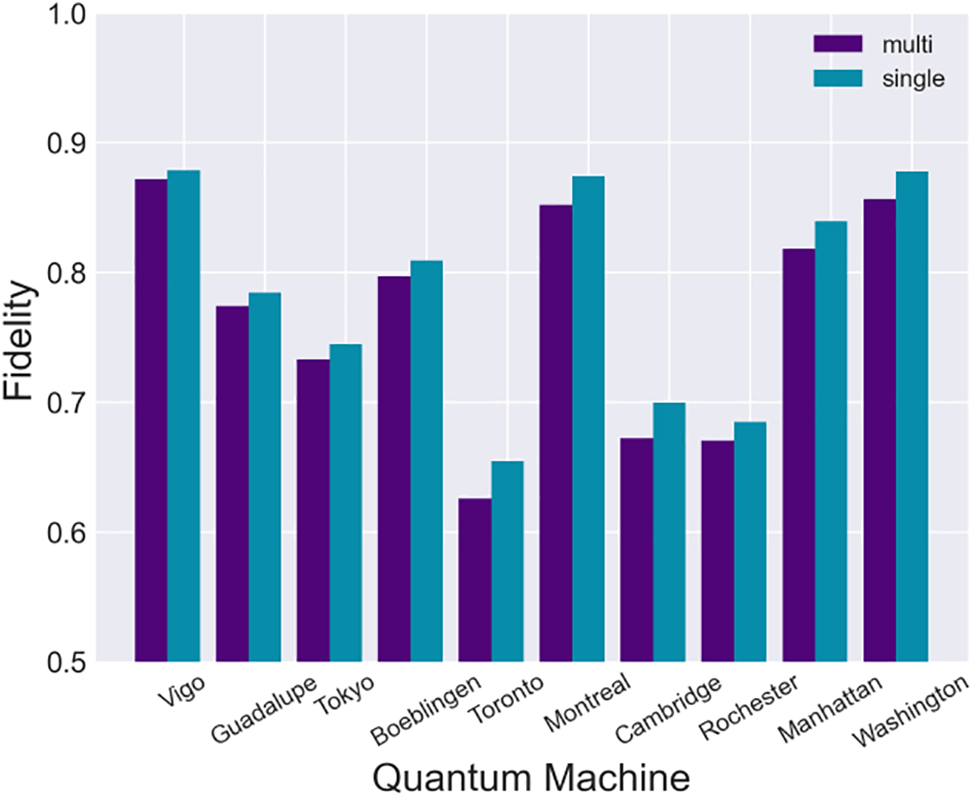
Figure 5: Fidelity across (simulated) quantum backends

5.2.3 Comparison with Baselines

To demonstrate the effectiveness of the proposed framework, we will compare it with two different baseline scheduling schemes under varying loads. Fig. 6 illustrates the comparison under high load. Fig. 6a displays the average fidelity after performing a series of circuits on a simulated quantum cloud system under high load. In high load situations, it is ideal to accept some loss of fidelity to improve user experience. However, it is still necessary to maintain sufficient fidelity to achieve practical benefits. Even under high loads, the average fidelity of MTMB is not significantly different from the Fidelity-Only scheme, within 5%. However, it is approximately 10% better than the Waiting Time-Only scheme. Fig. 6b illustrates the difference in user waiting time among the three schemes under high load, with MTMB being very close to the waiting time of Waiting Time-Only, which is ideal under high load. Furthermore, MTMB’s waiting time is on average approximately 60% lower than that of the Fidelity-Only scheme. MTMB achieved a relatively high level of fidelity without sacrificing too much waiting time. Therefore, it is the optimal choice for the system under high loads.

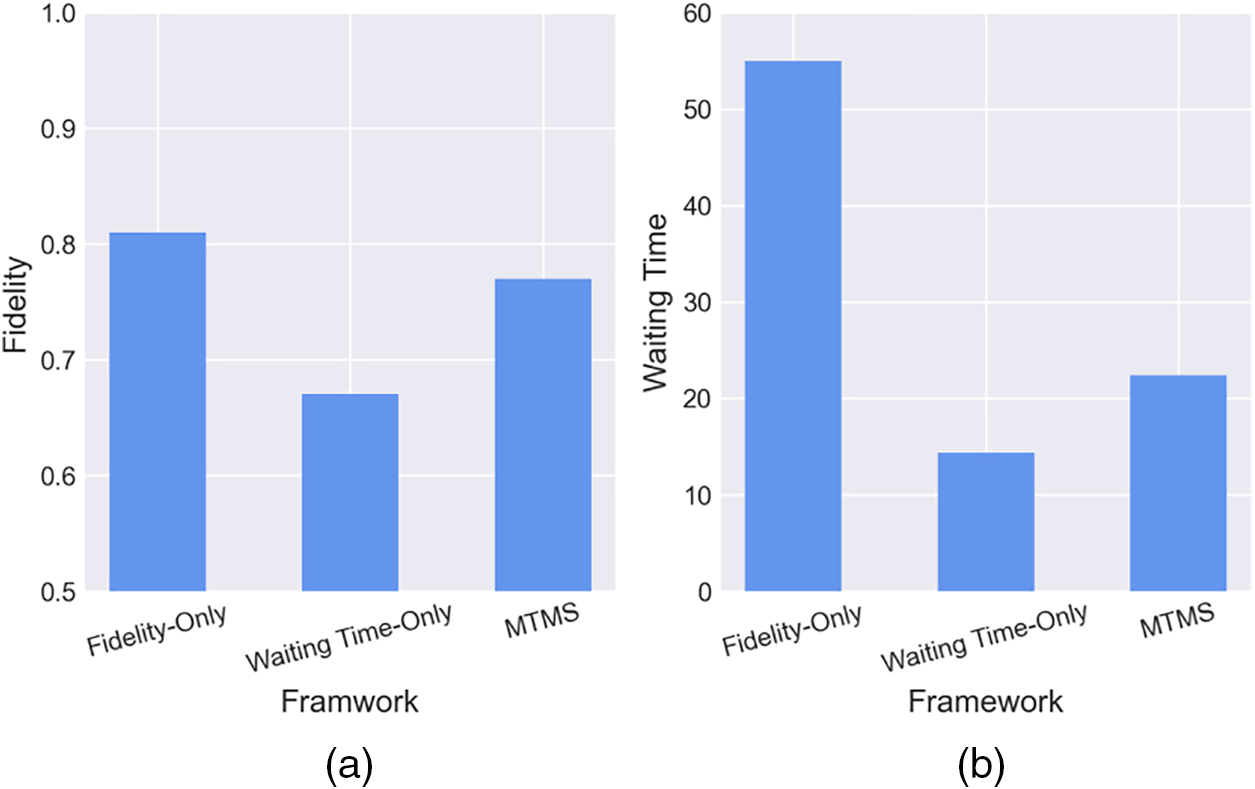
Figure 6: High load comparison between MTMB and baselines

Fig. 7 illustrates the comparison under low load conditions. The objective in these conditions is to improve the fidelity of the circuit as much as possible, as queuing time becomes less important. From Fig. 7a, it is evident that the Fidelity-Only scheme achieves the highest fidelity as it solely aims to improve fidelity. The fidelity of the MTMS scheme is very close to that of the Fidelity-Only scheme, while the Waiting Time-Only scheme has much lower fidelity. Fig. 7b displays the waiting time of the user during low load conditions. As anticipated, the Waiting Time-Only scheme has the shortest waiting time and maximizes the throughput of the quantum cloud. The Fidelity-Only scheme still has a high waiting time under low loads due to its lack of multiprogramming. MTMB shows a longer waiting time than the Waiting Time-Only scheme, but still much lower than Fidelity-Only scheme. Under low load conditions, MTMB achieves better queuing time without sacrificing fidelity. This is the optimal choice under such conditions.

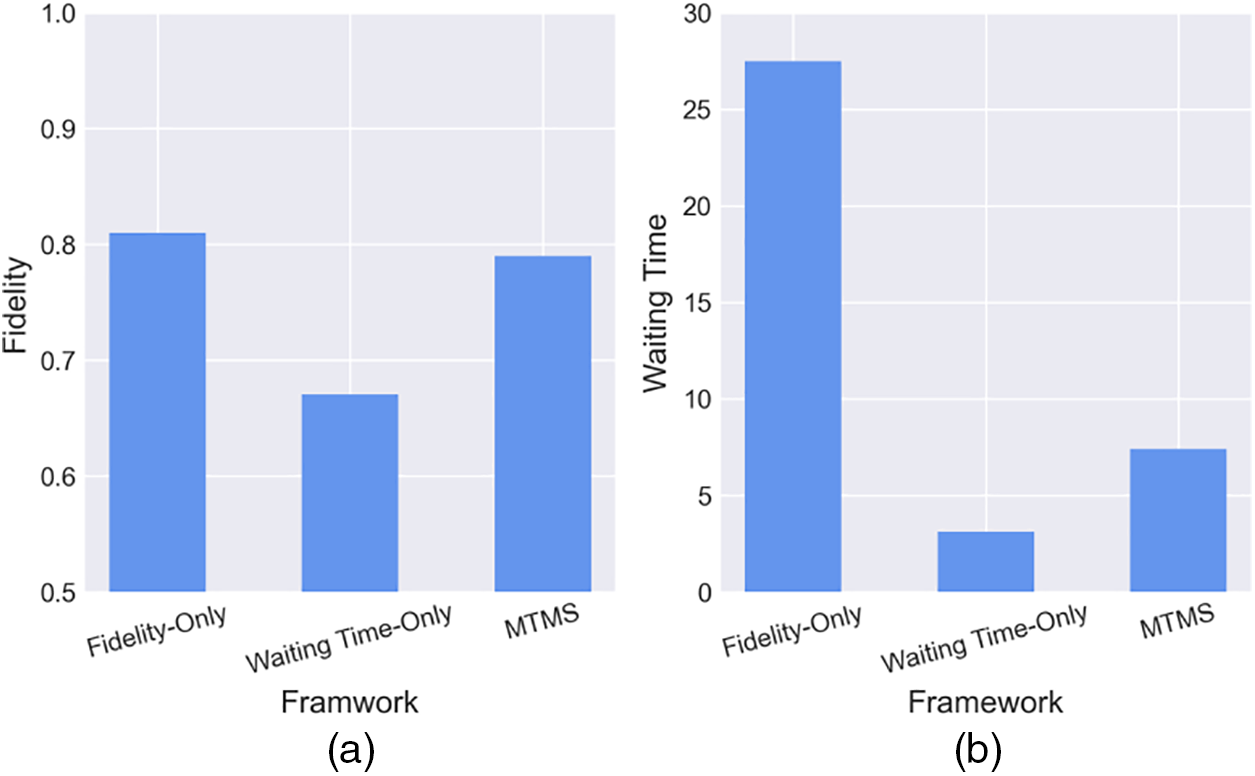
Figure 7: Low load comparison between MTMB and baselines

5.2.4 Hyperparameter Influence

To assess the impact of the parameter K in Section 4.2 on the throughput of the quantum cloud and each backend in the cloud, we fixed K to different values, and then calculated the TRF of each backend and the entire quantum cloud with varying K. Fig. 8 illustrates the changes in TRF of four representative backends and the quantum cloud with varying K. In general, the quantum cloud throughput increases as K increases. Larger values of K enable additional circuits to be provided to the mapping optimizer, thereby affording the optimizer greater acuity with regards to parallel mapping and making parallel execution of multi-programming easier. The throughput of “Vigo” hardly changes with rising K, which is still caused by its small number of quantum bits. However, the throughput increases for the rest of the backend with larger quantum bits. It is noteworthy that the throughput ceases to increase after a certain value of K due to the constraints of quantum bits quantities. Although increasing K can enhance the throughput of the quantum cloud to some extent, it also increases its scheduling time, as described in Section 5.2.3.

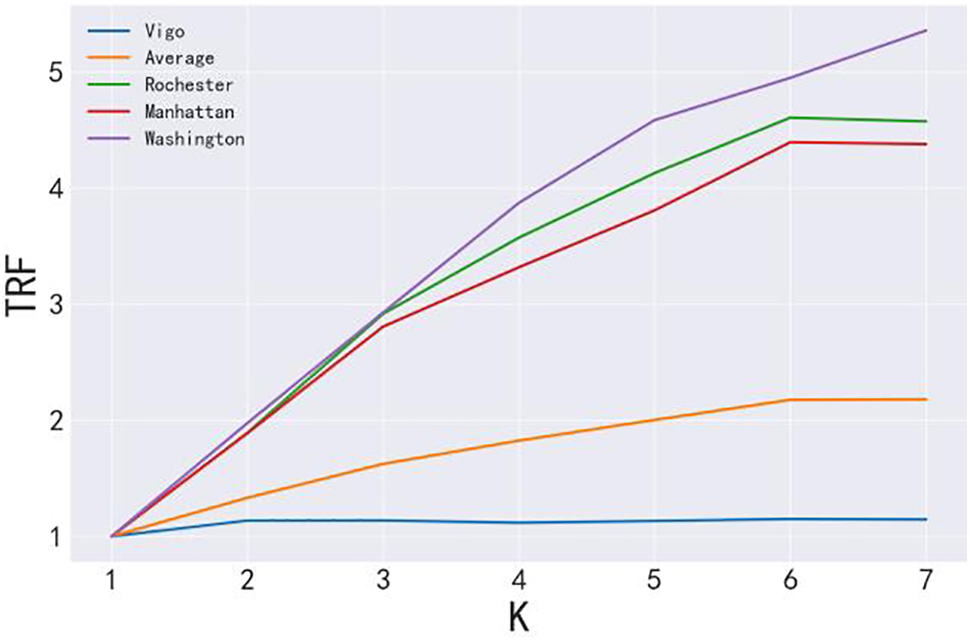
Figure 8: Relationship between the size of K and the throughput of quantum backends

Scheduling time is strongly related with the framework running platform and device performance, so the scheduling time ratio is used here as a metric. We mainly focus on the effect of different K values on scheduling time. We set the K values from 1 to 7, perform many experiments, and calculate the time ratio. When K=1, no multi-programming technique is used, and only the current main circuit is assigned to the appropriate quantum backend queue. As shown in Fig. 9, the scheduling time ratio increases linearly as K increases. This is as expected. When the value of K increases, the mapping optimizer spends more time retrieving the possibility of multi-programming and its scheduling time then grows. Therefore, it is critical to choose the appropriate K size to achieve balance in scheduling.

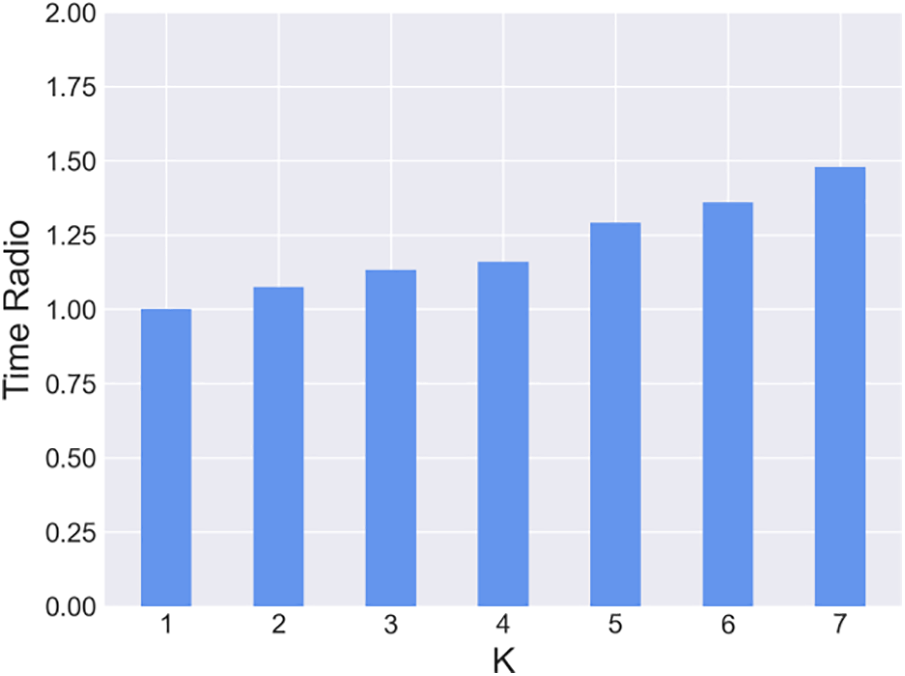
Figure 9: Scheduling time ratio

To investigate the effect of physical buffers on fidelity, we conducted fidelity experiments on circuits implemented in parallel with different numbers of physically isolated hops (n=0, 1, and 2) and compared the results with those of circuits executed individually. The experimental results, as shown in Fig. 10, indicate that fidelity is at its lowest when there is no physical buffer (i.e., n = 0). When n equals 1, there is a significant improvement in fidelity. However, when n exceeds 1, the increase in fidelity is limited. Therefore, it is typically set to 1 during scheduling to maximize system throughput without compromising fidelity.

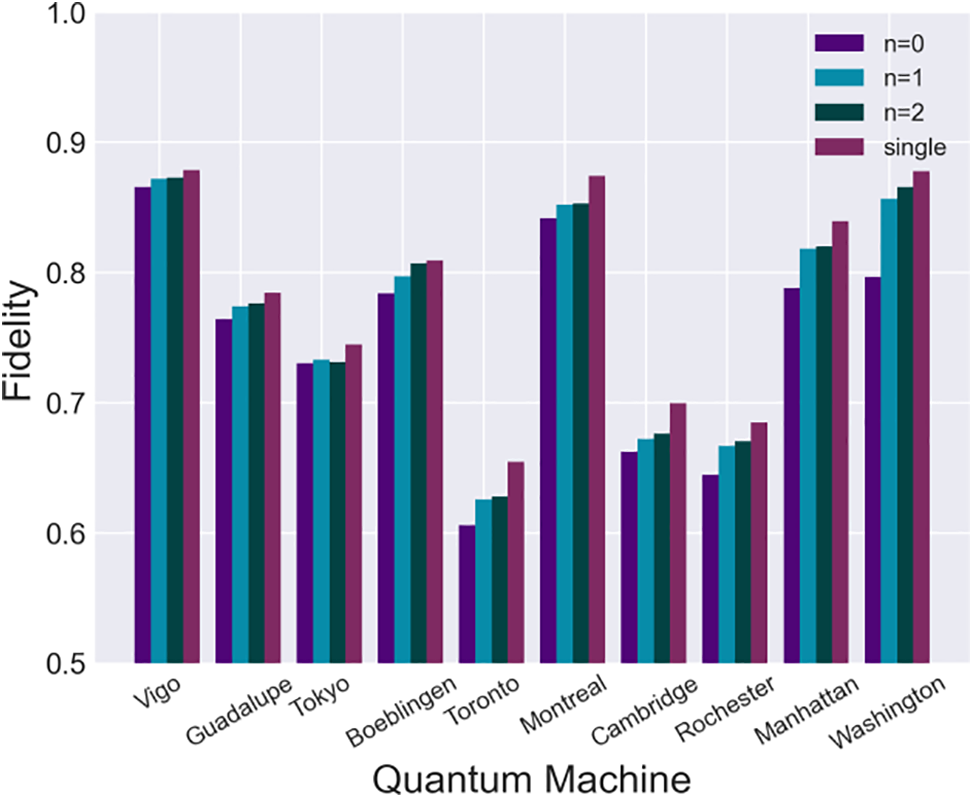
Figure 10: Physical buffer size n and fidelity

6  Conclusion

This paper proposes a novel task scheduling framework, MTMB, for quantum cloud environments to achieve effective management of quantum resources and improve user experience. MTMB automates the entire process, allowing users to submit quantum tasks without considering the availability and load of the back-end hardware. Upon user input, MTMB selects the appropriate quantum backend for task submission based on its state. It then dynamically selects circuits for aggregation and completes quantum bit mapping, taking into account the current load condition of the quantum cloud. Finally, the results are obtained, split, and returned to the user. The MTMB manages the unified back-end, reducing user burden and improving quantum cloud performance. Internal aggregation of quantum circuits can improve quantum bit utilization and backend throughput. Additionally, dynamically changing the scheduling scheme according to different loads enables MTMB to balance circuit fidelity and user queuing time. Our experiments have confirmed the efficacy of MTMB in managing quantum tasks and backend resources, laying the groundwork for more complex quantum cloud scheduling endeavours.

Notation List

Acknowledgement: We are grateful to the participants of the CQCC conference for their valuable feedback and discussions.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Danyang Zheng, Zheng Shan, Jinchen Xv, Feng Yue; data collection: Danyang Zheng; analysis and interpretation of results: Zhiheng Wang, Danyang Zheng, Qiming Du; draft manuscript preparation: Danyang Zheng. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author, Zheng Shan, upon reasonable request.

Conflicts of Interest: The authors declare that there is no conflict of interest regarding the publication of the paper.

References

1. R. P. Feynman, “Simulating physics with computers,” Int. J. Theor. Phys., vol. 21, no. 6/7, pp. 567-488, 1981. [Google Scholar]

2. H. Chan, R. Meister, T. Jones, D. P. Tew, and S. C. Benjamin, “Grid-based methods for chemistry simulations on a quantum computer,” Sci. Adv., vol. 9, no. 9, pp. 7484, 2023. doi: 10.1126/sciadv.abo7484. [Google Scholar] [PubMed] [CrossRef]

3. Y. Zeng, Z. M. Dong, H. Wang, J. He, Q. J. Huang and S. Chang, “A general quantum minimum searching algorithm with high success rate and its implementation,” Sci. China Phys., Mech. & Astron., vol. 66, no. 4, pp. 240315, 2023. doi: 10.1007/s11433-022-2060-3. [Google Scholar] [CrossRef]

4. A. Zeguendry, Z. Jarir, and M. Quafafou, “Quantum machine learning: A review and case studies,” Entropy, vol. 25, no. 2, pp. 287, 2023. doi: 10.3390/e25020287. [Google Scholar] [PubMed] [CrossRef]

5. Honeywell, Get to Know Honeywell’s Latest Quantum Computer System Model H1. 2020. Accessed: Aug. 10, 2023. [Online]. Available: https://www.honeywell.com/us/en/news/2020/10/get-to-know-honeywell-s-latest-quantum-computer-system-model-h1 [Google Scholar]

6. J. Gambetta, IBM’s Roadmap for Scaling Quantum Technology. IBM Research Blog, 2020. Accessed: Aug. 10, 2023. [Online]. Available: https://research.ibm.com/blog/ibm-quantum-roadmap [Google Scholar]

7. J. Hsu, “Intels 49-qubit chip shoots for quantum supremacy,” in Ces 2018, Los Angeles, CA, USA, Jan. 9–12, 2018. [Google Scholar]

8. J. Kelly, Preview of Bristlecone, Google’s New Guan-Tumprocessor. 2018. Accessed: Aug. 10, 2023. [Online]. Available: https://blog.research.google/2018/03/a-preview-of-bristlecone-googles-new.html [Google Scholar]

9. J. Preskill, “Quantum computing in the NISQ era and beyond,” Quantum, vol. 2, pp. 79, 2018. [Google Scholar]

10. H. E. Euch, M. Zidan, A. Abdelaty, M. Abdel-Aty, and A. Khjalil, “Quantum random access memory system,” US Patent 11093850 B2, Aug. 17, 2021. [Google Scholar]

11. D. Castelvecchi, “IBM’s quantum cloud computer goes commercial,” Nature, vol. 543, no. 7644, pp. 159, 2017. doi: 10.1038/nature.2017.21585. [Google Scholar] [PubMed] [CrossRef]

12. Google, Quantum Computing Playground. 2014. Accessed: Aug. 10, 2023. [Online]. Available: https://experiments.withgoogle.com/quantum-computing-playground [Google Scholar]

13. P. Das, S. S. Tannu, P. J. Nair, and M. Qureshi, “A case for multi-programming quantum computers,” in Proc. 52nd Annu. IEEE/ACM Int. Symp. Microarchitecture, Columbus, OH, USA, Oct. 12–16, 2019, pp. 291–303. [Google Scholar]

14. S. Niu and A. Todri-Sanial, “Enabling multi-programming mechanism for quantum computing in the NISQ era,” Quantum, vol. 7, pp. 925, 2023. doi: 10.22331/q-2023-02-16-925. [Google Scholar] [CrossRef]

15. X. Dou and L. Liu, “A new qubits mapping mechanism for multi-programming quantum computing,” in Proc. ACM Int. Conf. Parallel Archit. Compil. Tech., New York, NY, USA, Oct. 12–16, 2020, pp. 349–350. [Google Scholar]

16. S. Resch et al., “Accelerating variational quantum algorithms using circuit concurrency,” arXiv preprint arXiv:2109.01714, 2021. [Google Scholar]

17. L. Liu and X. Dou, “Qucloud: A new qubit mapping mechanism for multi-programming quantum computing in cloud environment,” in 2021 IEEE Int. Sym. High-Perform. Comput. Archit., Seoul, South Korea, Feb. 27–Mar. 03, pp. 167–178. [Google Scholar]

18. G. S. Ravi, K. N. Smith, P. Murali, and F. T. Chong, “Adaptive job and resource management for the growing quantum cloud,” in 2021 IEEE Int. Conf. Quantum Comput. Eng., Broomfield, CO, USA, Oct. 18–22, 2021, pp. 301–312. [Google Scholar]

19. R. V. Meter and D. Horsman, “A blueprint for building a quantum computer,” Commun. ACM, vol. 56, no. 10, pp. 84–93, 2013. doi: 10.1145/2494568. [Google Scholar] [CrossRef]

20. F. T. Chong, D. Franklin, and M. Martonosi, “Programming languages and compiler design for realistic quantum hardware,” Nat., vol. 549, no. 7671, pp. 180–187, 2017. doi: 10.1038/nature23459. [Google Scholar] [PubMed] [CrossRef]

21. X. Fu et al., “An experimental microarchitecture for a superconducting quantum processor,” in Proc. 50th Annu. IEEE/ACM Int. Symp. Microarchitecture, Boston, MA, USA, Oct. 14–18, 2017, pp. 813–825. [Google Scholar]

22. A. Barenco et al., “Elementary gates for quantum computation,” Phys. Rev. A, vol. 52, no. 5, pp. 3457–3467, 1995. doi: 10.1103/PhysRevA.52.3457. [Google Scholar] [PubMed] [CrossRef]

23. M. Suchara, J. Kubiatowicz, A. Faruque, F. T. Chong, C. Y. Lai and G. Paz, “QuRE: The quantum resource estimator toolbox,” in 2013 IEEE 31st Int. Conf. Comput. Des., Asheville, NC, USA, Oct. 06–09, 2013, pp. 419–426. [Google Scholar]

24. M. Salm, J. Barzen, F. Leymann, and B. Weder, “Prioritization of compiled quantum circuits for different quantum computers,” in 2021 IEEE Int. Conf. Softw. Anal., Evol. Reengineering, Honolulu, HI, USA, Mar. 09–2, 2021, pp. 1258–1265. [Google Scholar]

25. L. Mineh and A. Montanaro, “Accelerating the variational quantum eigensolver using parallelism,” Quantum Sci. Technol., vol. 8, no. 3, pp. 035012, 2023. doi: 10.1088/2058-9565/acd0d2. [Google Scholar] [CrossRef]

26. G. Park, K. Zhang, K. Yu, and V. Korepin, “Quantum multi-programming for grover’s search,” Quantum Inf. Process., vol. 22, no. 1, pp. 79, 2023. doi: 10.1007/s11128-022-03793-2. [Google Scholar] [CrossRef]

27. J. Clarke and F. K. Wilhelm, “Superconducting quantum bits,” Nature, vol. 453, no. 7198, pp. 1031–1042, Apr. 13–17, 2008. doi: 10.1038/nature07128. [Google Scholar] [PubMed] [CrossRef]

28. S. S. Tannu and M. K. Qureshi, “Not all qubits are created equal: A case for variability-aware policies for NISQ-era quantum computers,” in Proc. Twenty-Fourth Int. Conf. Archit. Support Program. Lang. Oper. Syst., Providence, RI, USA, Apr. 13–17, 2019, pp. 987–999. [Google Scholar]

29. S. Sheldon, E. Magesan, J. M. Chow, and J. M. Gambetta, “Procedure for systematically tuning up cross talk in the cross-resonance gate,” Phys Rev A, vol. 93, no. 6, pp. 060302, 2016. doi: 10.1103/PhysRevA.93.060302. [Google Scholar] [CrossRef]

30. J. M. Gambetta et al., “Characterization of addressability by simultaneous randomized benchmarking,” Phys. Rev. Lett., vol. 109, no. 24, pp. 240504, 2012. doi: 10.1103/PhysRevLett.109.240504. [Google Scholar] [PubMed] [CrossRef]

31. C. Ospelkaus, C. E. Langer, J. M. Amini, K. R. Brown, D. Leibfried and D. J. Wineland, “Trapped-ion quantum logic gates based on oscillating magnetic fields,” Phys. Rev. Lett., vol. 101, no. 9, pp. 259, 2008. doi: 10.1103/PhysRevLett.101.090502. [Google Scholar] [PubMed] [CrossRef]

32. A. Somoroff, Q. Ficheux, R. A. Mencia, H. Xiong, R. Kuzmin and V. E. Manucharyan, “Millisecond coherence in a superconducting qubit,” Phys. Rev. Lett., vol. 130, no. 26, pp. 267001, 2023. doi: 10.1103/PhysRevLett.130.267001. [Google Scholar] [PubMed] [CrossRef]

33. L. Liu and X. Dou, “QuCloud+: A holistic qubit mapping scheme for single/multi-programming on 2D/3D NISQ quantum computers,” arXiv preprint arXiv:2207.14483, 2022. [Google Scholar]

34. T. Last et al., “Quantum inspire: QuTech’s platform for co-development and collaboration in quantum computing,” Nov. Pattern. Technol. Semicond., MEMS/NEMS and MOEMS 2020, vol. 11324, pp. 49–59, 2020. doi: 10.1117/12.2551853. [Google Scholar] [CrossRef]

35. R. Wille, D. Große, L. Teuber, G. W. Dueck, and R. Drechsler, “RevLib: An online resource for reversible functions and reversible circuits,” in 38th Int. Symp. Mult. Valued Log., Dallas, Texas, USA, May 22–24, 2008, pp. 220–225. [Google Scholar]

36. A. W. Cross, L. S. Bishop, J. A. Smolin, and J. M. Gambetta, “Open quantum assembly language,” arXiv preprint arXiv:1707.03429, 2017. [Google Scholar]

37. A. S. Green, P. L. F. Lumsdaine, N. J. Ross, P. Selinger, and B. Valiron, “Quipper: A scalable quantum programming language,” in Proc. 34th ACM SIGPLAN Conf. Program. Lang. Des. Implement., Seattle, WA, USA, Jun. 16–19, 2013, pp. 333–342. [Google Scholar]

38. G. Aleksandrowicz et al., Qiskit: An Open-source Framework for Quantum Computing. 2019. Accessed: Aug. 10,2023. [Online]. Available: https://zenodo.org/records/2562111 [Google Scholar]

39. IBM, IBM Quantum Systems. 2017. Accessed: Aug. 10, 2023. [Online]. Available: https://quantum-computing.ibm.com/services?systems=all [Google Scholar]