Positron Emission Tomography Lung Image Respiratory Motion Correcting with Equivariant Transformer

1  Introduction

With the advancement of medical imaging technology, medical images have become a crucial reference for disease diagnosis. Among various imaging modalities, Positron Emission Tomography (PET) stands out by providing functional information based on the disease state. However, the extended duration of PET scanning often results in image artifacts due to physiological movements, such as respiration. These artifacts can significantly impact physicians’ ability to diagnose lung lesions and formulate effective treatment plans, underscoring the importance of eliminating such artifacts from PET lung images [1].

Traditional methods to address these artifacts predominantly employ gating methods [2]. These methods, while effective, often select only the relevant temporal phase data during the reconstruction process [3], leading to a loss of valuable metabolic information, and the hardware cost of gating methods is quite high. Deformable image registration (DIR) offers a solution to this limitation. Unlike gating methods, DIR generates a comprehensive deformation process based on the input image, aligning it with a fixed image [4]. In recent years, deep learning-based DIR methods, such as VoxelMorph (VM) [5], VTN [6], and CycleMorph [7], have gained traction. These methods leverage CNNs as their backbone, treating fused sequences as the primary subject for feature distribution learning. This approach has shown superior performance in deformable image registration tasks, as depicted in Fig. 1a. The integration of attention mechanisms further augments the characterization of long-sequence spatial relationships [8]. Notably, models like Vit [9], TransMorpher (TM) [10], and Swin-voxelmorph [11] incorporate the Transformer module to bolster feature learning in fused sequences, leading to enhanced registration performance, as illustrated in Fig. 1b. Previously, researchers have delved into understanding the mapping relationship between moving and fixed images. Dual-stream pyramid registration network (DPRN) [12] employs a convolutional feature pyramid, utilizing the Pyramid registration (PR) block to facilitate feature mapping between moving and fixed images, as depicted in Fig. 1c.

Figure 1: Pipelines of the previous medical image registration models

Despite these advancements, a common limitation in these networks is their sole reliance on a single fusion sequence. This approach often overlooks the interplay between input and fused sequences, this makes most existing standard networks cannot be unable to fit the respiratory motion correction task in PET lung images. In response to these challenges, we introduce the Triple Equivariant Motion Decomposition Transformer (TEMT) architecture tailored for PET lung image, as illustrated in Fig. 1d. In this architecture, firstly, triple sequence feature extraction utilizing a pyramid structure, the architecture achieves triple sequence feature extraction and deformation propagation [13]. Secondly, the TEMT module streamlines motion decomposition, transitioning from motion sequences to fusion sequences, and subsequently from fusion sequences to fixed-point sequences. The overarching goal is to minimize the motion distance between these sequences. Lastly, the Adaptive Competitive Weighting Module (ACWM) astutely identifies pivotal manifolds within the Lie groups, subsequently amalgamating high-level motions through a competitively weighted strategy. The salient contributions of this paper can be delineated as:

(1) In this study, we introduce the TEMT network, a novel approach designed to decompose and reconstruct respiratory motion in PET imaging. This strategy effectively addresses the challenge of respiratory-induced artifacts by breaking down the breathing cycle into localized stages, such as pulmonary expansion and contraction. By reconstituting local movements, TEMT can eliminate the artifacts caused by respiratory motion. The implications of this approach are significant as it offers a more refined analysis of respiratory dynamics, which is essential for accurate medical imaging.

(2) Motion Mode Enrichment: Building on existing foundations, our research advances the use of the multi-head attention mechanism within Transformer blocks for medical imaging applications. We have innovatively exploited this mechanism to perform multi-faceted motion decomposition, while simultaneously introducing a non-fixed coordinate axis mechanism derived from Lie algebra.

(3) Attention Mechanism in Competitive Weighting: We have integrated the attention mechanism with a multi-head motion competitive weighting module to create a ACWM block. This innovative combination ensures the effectiveness of the low-dimensional manifold features of respiratory motion as learned by the multi-head attention mechanism and the principles of Lie algebra. Furthermore, this integration significantly mitigates the interference from extraneous motions.

2  Related Work

PET image lung respiratory motion correction is crucial for the staging of lung cancer, as it helps determine the invasiveness of tumors. In recent years, the development of DIR has brought further hope for the improved accuracy of PET image lung respiratory motion correction.

In 2019, Guha et al. [5] developed a deformation field learning network called VM for medical image registration. Their Voxelmorph model achieved DSC scores of 0.786 and 0.772 on the T1-weighted brain MRI datasets OASIS and ABIDE, respectively. In 2020, Boah Kim et al. proposed CycleMorph [7], a topology-preserving network that enhances image registration performance through cycle consistency. The CycleMorph model achieved an ssim index of 0.965 on brain MR and CT data, demonstrating the effectiveness of using cycle consistency for feature extraction and medical image registration.

In 2021, Chen et al. [9] first introduced the transformer mechanism [14] into the registration model and proposed the Vit registration architecture. They further optimized and improved the Vit network in 2022 [10], with diffeomorphic variants ensuring topology-preserving deformations and the Bayesian variant providing a well-calibrated registration uncertainty estimate. In 2023, Wang et al. used five deformation field learning methods (VM, TM [10], DMR [15], Xmorpher [16], and ModeT [17]) on brain MRI datasets. Among these methods, ModeT demonstrated the highest accuracy with a precision of 62.8%, while the second-best method, DMR, had a precision of 60.6%.

It was not until 2022 that Hou et al. [18] proposed combining VM with Resnet and using the DIR method for PET image lung respiratory motion correction instead of the traditional gate-based method, achieving an effectiveness of 75.10% on a simulated dataset. However, several limitations have been identified in existing research, including the lack of dedicated registration models specifically for PET image lung respiratory motion correction, insufficient clinical studies, lower accuracy due to significant lung deformation in clinical data centers, and the need for further validation and sensitivity to image variability. In addition, computational resources, ethical considerations, and regulatory barriers pose significant obstacles to clinical adoption. Successful integration into clinical workflows and long-term monitoring and validation are also crucial to ensure safe and effective use in healthcare.

Our research addresses these limitations by proposing a new TEMT model that explicitly combines simulation and clinical datasets to simulate mild cyclic deformations and clinical respiratory deformations. By evaluating different registration architectures, we seek to enhance our understanding of their applicability to accurate deformations. The proposed model improves the accuracy of PET image pseudo-shadow elimination.

3  Materials and Methods

The proposed network operates in two distinct stages: Feature representation learning [19] and motion representation learning between feature pairs. The initial stage is dedicated to extracting multilevel features from lung PET images,and The CNN feature extraction module we use is consistent with normal registration network like ModeT [17]. In contrast, the subsequent stage zeroes in on discerning the motion deformation relationship between these feature pairs.

For the lung PET image sampling process, the triple sequences are pivotal. Under normal conditions, respiratory motion encompasses two states: Alveolar expansion and contraction. However, artifacts emerge when the patient exhibits a third state, post-contraction expansion, leading to an asymmetric cyclic motion [20]. Contrary to mainstream models that predominantly concentrate on moving and fixed sequences, our approach recognizes and incorporates distinct features within both the respiratory motion and fixed sequences. Instead of dismissing these unique features as noise, our method leverages them, transitioning from the motion sequence to the fusion sequence, and subsequently to the fixation sequence. This methodology substantially curtails cross-noise interference between sequences, as mathematically represented in Eqs. (1) and (2):

TFM(B)=φ1(TM(B+NM))(1)

TF(B+NF)=φ2(TFM(B))(2)

Here, TM, TFM and TF signify the characteristic information of the motion, fusion, and fixed sequences, respectively. B embodies the underlying information shared across all three sequences, such as the physical distribution of organs like the lungs and heart. NM and NF denote the unique features of the motion and fixed sequences, respectively. The functions M-FM and FM-F represent the deformation field TM to TFM and from TFM to TF, respectively. Our approach harnesses batch motion learning across these sequences, mitigating the complexities associated with high-dimensional motion feature learning.

Artifact images encapsulate the respiratory process within a patient’s lung sequence. When considering respiratory motion, it is noteworthy that while different individuals may exhibit similar localized motion, the weight distributions of these motions can vary. This motion process can be visualized as a group of streamers. The group equivariant theory [21] integrates equivariant forms into machine vision learning processes, introducing Lie groups into feature learning. The primary objective of group equivariant convolution is to mitigate stream shape noise during the convolutional learning phase. While numerous researchers have endeavored to incorporate the concept of Lie groups into Transformer models [22–25], such integration often amplifies computational demands. This heightened computational requirement poses challenges, especially in the realm of three-dimensional image processing. In our research, we harness equivariant concepts in the generalization of base motions, aiming for both cost-effectiveness and enhanced motion estimation efficiency.

Fig. 2 showcases our proposed TEMT registration network, which adopts a triple sequence pyramid registration structure to ensure image stability. The network initiates its operation by ingesting two primary inputs: A fixed image If and a moving image Im. Through a series of 5-layer convolutional blocks, the encoder extracts features from these input images, subsequently fusing them to discern feature interactions. This process yields three distinct characteristic sequences:M1−5, FM1−5 and F1−5. The highest resolution feature maps, specifically M5, FM5 and F5, are channeled into the TEMT. Here, an array of base motions is generated. These motions are then directed to the ACWM, where the weights of the φ5 component and φ4 are determined. The culmination of this process is a high-level deformation termed φ4. This deformation field is subsequently applied to deform the feature map M4, resulting in a transformed output feature map, denoted as M4 ′.

Figure 2: TEMT-Net structure diagram; The encoder extracts three sequence features. The kinematic modes between the sequences are obtained by the TEMT module and decomposed, expanded, and fused to obtain the final total deformation field

The described process is iterative in nature. After deformation, the feature map is reintroduced into TEMT alongside other relevant parameters. This cyclical procedure is consistently executed until the generation of φn, where n denotes the specific layer of the feature map under consideration. A more detailed representation of this iterative sequence is provided in Eq. (3):

φ⊃φ1⊃φ2⊃φ3⊃φ4⊃φ5(3)

Within our framework, the element of the subgroup is employed as a representative for any constituent within the main group. It is worth noting that as the diversity of elements within the subgroup expands, it can infinitely approximate the elements of the primary group. This iterative refinement continues until the entire manifold is deformed, culminating in the production of the registration sequence.

3.1 TEMT Block

In registration networks rooted in deep learning, each position within the low-resolution feature map encapsulates motion information corresponding to a substantial region in the original image. This often encompasses multiple low-dimensional motions [26]. To adeptly capture these low-dimensional motions, we leverage a two-channel multi-head neighborhood attention mechanism, as shown in Fig. 3. This mechanism, operating at the low-resolution level, decomposes motions between sequences [27]. The dual benefit of this approach is the preservation of global motion information while simultaneously pinpointing local motions at varied locations, thereby enhancing registration accuracy.

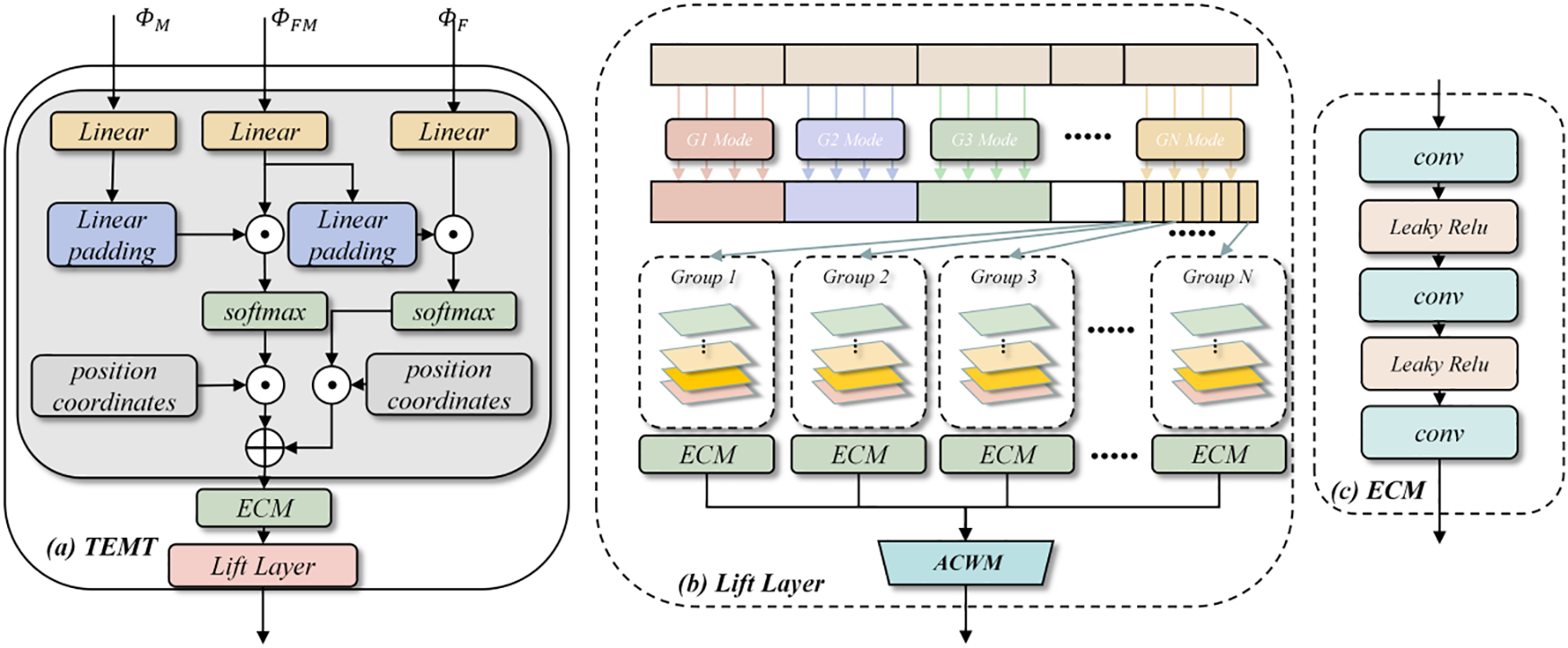
Figure 3: Overview of TEMT module: (a) Integral motion learning Transformer; (b) Lift Layer block for motion mode expansion; (c) Encoder for Lie group key information extraction

Let us consider the entities M, FM and F. These are members of Rc×h×w×l and symbolize the moving, fusion, and fixed feature mappings, respectively, at a specific tier of the hierarchical encoder. To further elucidate:

1.    h,w and l delineate the dimensions of the feature mapping.

2.    c represents the number of channels.

The feature sequence M, FM and F are subjected to linear projection proj and normalization (LN). This transformation process is articulated in Eqs. (4)–(7):

Q=LN(proj(F)),K=LN(proj(M)),Q(K)fm=LN(proj(FM))(4)

Q={Q(1),Q(2),…,Q(s)}(5)

K={K(1),K(2),…,K(s)}(6)

Q(K)fm={Q(K)fm(1),Q(K)fm(2),…,Q(K)fm(s)}(7)

The primary intent behind the mapping operation is weight sharing. These weights are initialized using samples drawn from N(0,1e−5), with the deviation initialized to zero. The sequences Q(K)fm and K subsequently undergo processing via a dual channel for division. Here, Q(K)fm relates to Kfm in the context of Q and Qfm in the context of K.

Drawing from linear algebra principles, the NA (Neighborhood Attention) is derived from this dual channel. The neighborhood surrounding any given point p is denoted by c(p). The computation for neighborhood attention is detailed in Eqs. (8) and (9):

NA1(p,s)=softmax(Q(s)⋅Kfmc(p)(s)+B(s))(8)

NA2(p,s)=softmax(Qfm(s)⋅Kc(p)(s)+B(s))(9)

where B∈Rs×n×n signifies the deviation of the neighborhood’s relative position. This deviation is amenable to optimization through continuous learning. Occasionally, the registration task may require the deformation of voxels beyond the provided sequence. To address this, boundary voxel motion learning is achieved by padding the moving feature mapping with zeros subsequent to the linear mapping of Kfm and K.

Following the prior steps, the neighboring attention matrix for each channel’s position is computed. This step decomposes the motion information of the low-resolution voxels and sequentially computes their similarities. This approach effectively reduces computational demands, making it particularly apt for 3D medical image registration. As a result, decomposition manifolds for the layer feature map s are derived, as detailed in Eq. (10):

φp(s)=Concat(NA1(p,s)V+NA(p),NA2(p,s)+NA(p))(10)

φ(s) is in ∈Rh×w×l×3, while V∈Rn×n×n. V(X) represents the relative positional coordinates of a neighborhood’s center of mass. The rotation vectors, denoted by g∈R3, can be characterized by the rotation axis α and the rotation angle θ, as detailed in Eq. (11):

θ=||g||,α=g||g||(11)

when the rotation vector g is applied to the coordinate system of the s regular manifolds, the resulting preliminary space mappings are Sg∈R6. An ensemble of rotation vectors g constitutes the Lie group LieN(g1,g2,g3,…,gN). LieN represents the N algebraic group within the SO3 3D Lie groups space. The manifolds within this Lie groups space can be expressed as LieN(φp(s)). However, not all the manifolds LieN(φp(s)) are valid. The geometric manifolds in the R6-space must be translated back to the Euclidean space. To achieve this, we extract the pertinent features of the central LieN(φp(s)) entities via the Equivariance Competitive Module (ECM) module. By performing a weighted summation of multiple vectors, we obtain the base manifolds of the voxels. These represent the low-dimensional motions that constitute the high-dimensional motions, as further detailed in the ECM module and Eq. (12):

φp(s)=ECM(φp(s)⋅g1(θ,α),φp(s)⋅g2(θ,α)…φp(s)⋅gN(θ,α))(12)

3.2 ACWM Block

To ensure the precise amalgamation of the low-dimensional motions derived from the TEMT decomposition within high-resolution feature maps, we employ an adaptive learning approach. This approach discerns vital information across each channel and spatial location using the Convolutional Block Attention Module (CBAM) attention module [28]. This method aids in capturing pivotal features within the manifolds more effectively.

As depicted in Fig. 4, we commence by up-sampling the multi-head neighboring manifold field (not utilized in the TEMT module). Subsequently, the CBAM attention module identifies the effective deformations inherent in each sub-deformation field. The culmination of this process is the judicious fusion of these deformation fields. The Weighting Competitive Module (WCM) module then oversees the synthesis of the final kinematic modes for each voxel within the feature map. Within this module, deformation fields extracted from the TEMT module are restructured. This reorganization produces the final motion, learned from the features at that specific level, and correlates the varied deformation information. The motion process between the moving sequence M and the fixation sequence F, is derived using a composite competitive weighting operation, as detailed in Eqs. (13)–(15):

φ(1),φ(2),…,φ(s)=CBAM(φ(1),φ(2),…,φ(s))(13)

w(1),w(2),…,w(s)=WCM(cat(φ(1),φ(2),…,φ(s)))(14)

φ=w(1)φ(1)+w(2)φ(2)+,…+,w(s)φ(s)(15)

where CBAM amplifies the convolutional networks’ selective attention to features by merging both spatial and channel attention mechanisms. WCM represents the distribution of blocks utilized to compute the weights, as illustrated on the right side of Fig. 4.

Figure 4: Adaptive competitive weighting module

4  Experimental

4.1 Datasets and Indicators

Simulation Datasets: Simulations were executed using GEANT4 Application Tomographic Emission (GATE v8.0). Both Geometric phantom Registration Datasets (GPReg) and NURBs (Non-Uniform Rational B-Splines) Cardiac Torso (NCAT) [29] were employed to simulate lung voxels. The NCAT simulation platform, crucial for accurately combining the low-dimensional motions of the TEMT decomposition in the body membrane, was used to construct three-dimensional Lung Voxel phantom Registration datasets (LVPReg) with motion artifacts using the simulated PET device. Additionally, NCAT simulation produced Cardiopulmonary Voxel Phantom Registration datasets (CVPReg). The geometric body membrane was a small cylinder with dimensions: Diameter of 20 mm and height of 42.5 mm. The simulation produced 120 images of size 128 × 128 × 16, with a respiratory cycle set at 5 s and diaphragm movement during respiration ranging between 1 cm and 3 cm. For the data-enhanced body model images, 180 cases of size 128 × 128 × 32 were created. All datasets were divided using an 8:2 ratio for training and testing sets. Detailed simulation parameters are shown in Table 1.

Clinical Registration Datasets (CliReg): Clinical data for the experiments were sourced from the First People’s Hospital of Yunnan Province. The data collection adhered to the Declaration of Helsinki, was approved by the Ethics Committee of the First People’s Hospital of Yunnan Province (No.KHLL2023-KY125), and all participating patients provided informed consent. The dataset comprised 66 patients, with 11 cases for testing and 55 for training. To optimize the data for the model, preprocessing steps were applied, including cropping and zero-mean normalization. The cropped images, with dimensions of 96 × 96 × 64, were then fed into the network. In this experiment, the fixed image is the predicted image generated by the PET/CT scanner using the gating method during the reconstruction process. The preprocessed PET image is shown in Fig. 5.

Figure 5: Original PET image and preprocessed PET Image

Evaluation indicators:

To thoroughly assess the registration methods, we employed three objective metrics:

1. Dice Similarity Coefficient (DSC): This metric gauges the ensemble similarity between the generated image and the target image. It is particularly sensitive to local feature similarity, highlighting the congruence of regional contours.

2. Pearson Correlation Coefficient (CC): The CC quantifies the linear correlation between the predicted de-artifact image and the target image. It evaluates the overlap between corresponding regions, providing insights into the accuracy of the registration.

3. Hausdorff Distance (HD): This metric evaluates the shape difference and registration accuracy between the predicted and target images. It measures the extent of overlap between the two images.

All metrics were computed using a 3D approach. Ideally, a superior registration should produce a larger DSC and CC, but a smaller HD. To bolster confidence in these results and enable more robust comparisons, a 95% confidence interval has been incorporated into the statistical review [30].

4.2 Experimental Setup

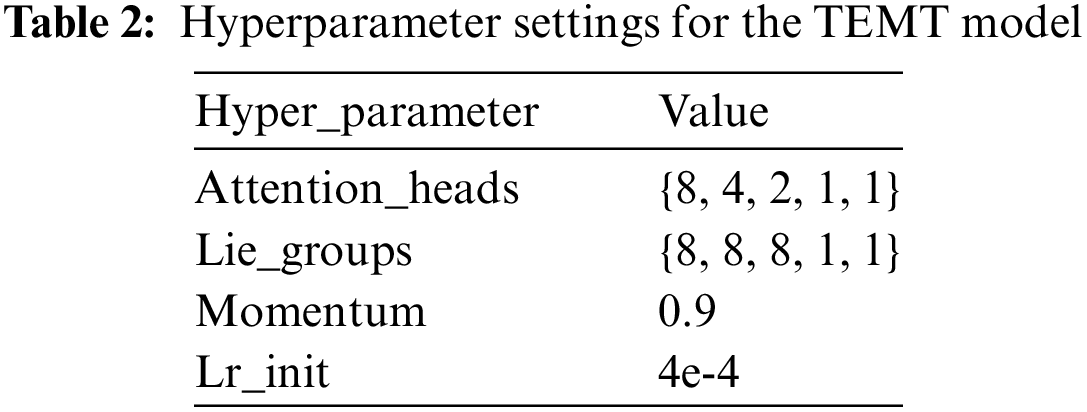
For the CNN encoder, we used the same characteristics extraction structure [31]. In the motion learning process, we utilized the loss function with MSE (mean square error). This paper uses Pycharm as the compiler. The programming language is Python3.7, the experimental framework is Pytorch 1.13, and the computer hardware configuration is Intel(R) Core(TM) i11-10700F CPU@2.90 GHz, 64 GB RAM, NVIDIA GeForce RTX 3060 12G graphic memory, 64 Bit Windows10 operating system. All experiments network configuration is the same. Table 2 provides a detailed overview of the hyperparameter settings for the TEMT model. Key parameters include Attention_heads, which specifies the count of multi-head attention heads; Lie_groups denoting the number of groups in the modal enhancement process; momentum indicating the speed of learning rate decay; and Lr_init representing the initial learning rate. We employed the Adam optimizer, as outlined in Eq. (16), with a strategy for decaying the learning rate.

lrm=lrinit⋅(1−m−1M)0.9,m=1,2,…,M(16)

4.3 Experimental Results of Simulation Datasets

This section compares our approach with several state-of-the-art deep learning registration methods. Fig. 6 shows the visual comparison of each model and the RGB visualization of the deformation field. Tables 3 and 4 are the numerical results of Different registration methods on GPReg and LVPReg, and the column Detail Operation (DOP) of Tables 3 and 4 represents the number of sequences and the main methodology used in the model,Trans means Transformer, and the best results are marked in boldface.

Figure 6: PET image comparison before and after preprocessing

From Tables 3 and 4, it can be observed that as image detail complexity increases, the expressive power of each model decreases. Our method consistently achieves the best registration accuracy and stability, particularly in terms of CC and HD metrics. The only exception is with the DSC metric, where TM outperforms our registration network. Though the change in the deformation gradient is minimal across the GPReg, LVPReg, and CVPReg, it is evident that the TEMT is more effective in quantifying the metrics than both the dominant single-sequence and the pyramidal double-sequence methods.The deformability of the clinical data is much greater than that of the simulation data, but as can be seen from Table 5, our model is very stable while the effectiveness of other models declines.

4.4 CliReg’s Experimental Results

Fig. 7 visualizes the registration images from the different methods on the CliReg dataset and the corresponding deformation fields in RGB channels presenting motion in all directions within the manifold space. In Table 3, it can be seen that the performance of each model decreases under the CliReg dataset and that our network is still able to show superior results for overall and detailed feature learning in the presence of complex pathology features.

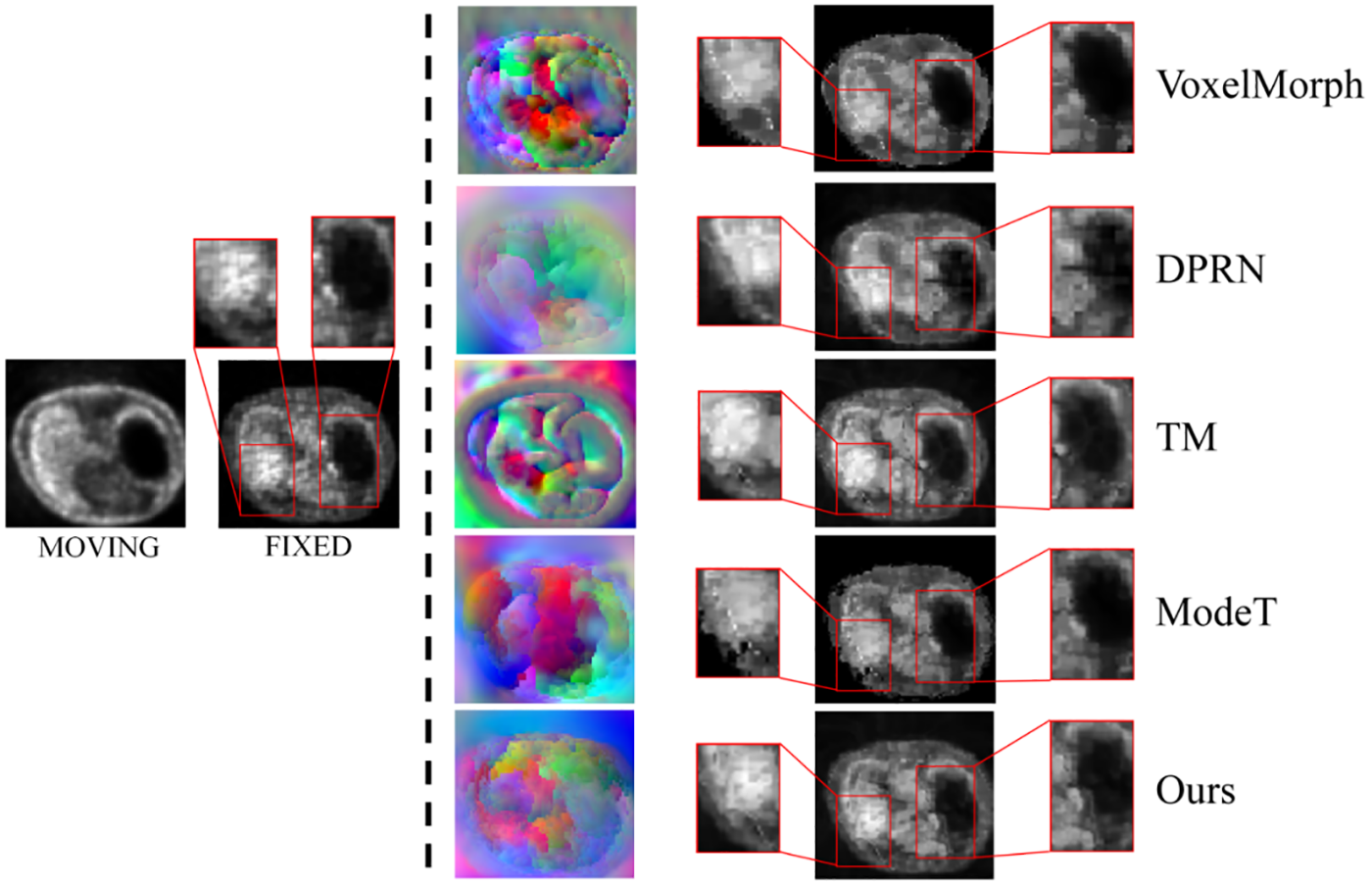
Figure 7: Visualization of the RGB form of the deformation field on the CliReg dataset using different depth methods and lung image registration results from top to bottom

4.5 Ablation Experiment

In this section, we conduct ablation experiments from three perspectives: 1) Comparing the effects of triple vs. double sequences, 2) Evaluating the importance of each module within the network, 3) Analyzing the effects of different equivariant motion decomposition layers and find the definition of the dividing line of the low-dimensional and high-dimensional movements. All experiments were performed on the CliReg dataset.

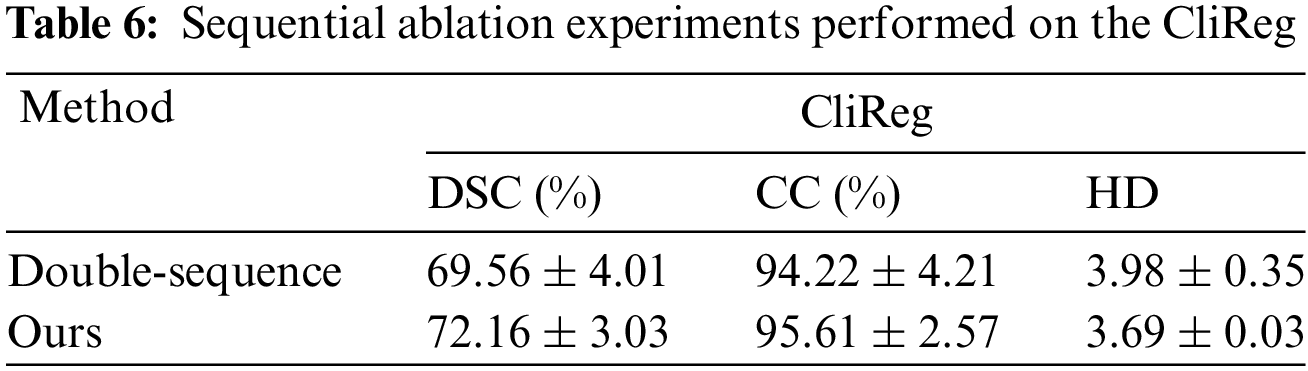
Sequence Ablation: The triple sequence method enhances the feature information acquired in image pairs compared to both single and double sequences. It derives intermediate sequences between motion and fixation, reducing the gradient change when transitioning directly from motion to fixation. In this experiment, we aim to compare the effects of the triple sequence vs. the double sequence. The quantization results for these four models are presented in Table 6.

Module Ablation: In this paper, the role of TEMT in the network is to enrich base motion modalities. It extracts the desired base motion using the attention competition weighting module, integrating it into the advanced motion.

In this section, we analyze the impact of individual modules on the registration network. To evaluate the performance of each module, we designed four sets of experiments: “NO-DT”, “NO-EQ”, “NO-AW” and “Ours”. “NO-DT” denotes the equivariant motion decomposition module without the two-branch multi-head Transformer. Instead, it directly participates in the learning of fixed-point sequential deformation using a fusion sequence. “NO-EQ” refers to the non-equivariant registration network, which excludes Lie groups from the motion decomposition process. “NO-AW” signifies the competitive weighting module, but without the attention module to emphasize significant motion learning. “Ours” represents our proposed registration model, which incorporates the full triple sequence equivariant motion decomposition. The quantization results for these four models are presented in Table 7.

Table 8 demonstrates the effectiveness of the modules within the TEMT architecture for the registration task. Among them, equivariant significantly boosts the network’s performance.

5  Discussion

In this section, we discuss the role of triple sequences for higher dimensional motions, the fitness of Lie groups in lower dimensions during motion decomposition, as well as lightweight architecture CNN.

5.1 The Role of Triple Sequences for Higher Dimensional Motions

From Figs. 6 and 7, which detail the results of five comparison experiments across four datasets, it is evident that the three-sequence model outperforms existing fusion sequences and dual sequences. This superiority is observed in both CNN and Transformer models, especially in terms of overall feature learning and detailed feature reproduction. Fusion sequences are derived by learning the common features between motion sequences and fixation sequences. These sequences are then progressively aligned to the fixation sequences. However, this approach often results in the neglect of inherent features of the fixation sequence.

Recent comparisons between DPRN and ModeT have highlighted structural similarities in their approaches to learning motion information from images. Both models are designed to learn a singular mapping of motion information between images by exploiting multi-resolution features. However, their primary focus has been to treat motion information as a feature to be learned, rather than as a distinct entity requiring specialized treatment. DPRN utilizes CNNs for the learning of motion features. While this can capture motion characteristics to a certain extent, it does not efficiently optimize for motion smoothness, particularly in the critical regions between high and low metabolic areas in PET images. ModeT, on the other hand, shows proficiency in aligning internal organs of patients. Although ModeT’s learning from low-resolution information is robust, it tends to leave residuals at the edges of lung images, indicating a potential suboptimal integration of motion.

These findings suggest that while DPRN and ModeT share a conceptual framework, there is a clear need for improved mechanisms that can handle the subtleties of motion within PET imaging, especially across metabolically diverse regions.

In contrast, the triple sequence approach of TEMT refines motion learning, leading to smoother deformation gradients and more logically coherent final motion outcomes.

5.2 The Role of Lie Groups for Low-Dimensional Motions

Fig. 8 illustrates the multi-level deformation field learning of our method, using the registration of an image pair as an example. Deep semantics correspond to the underlying motion, and the Lie group is constructed around this motion’s coordinate system. This Lie group serves as a foundation for deformations between high-level feature maps. As the resolution of the feature map increases, the texture of the lung becomes more pronounced, leading to a gradual enhancement in the details of lung motion information.

Figure 8: The qualitative comparison on the CliReg

However, not all Lie groups prove to be effective. Experiments presented in Table 6 indicate that the model’s efficiency diminishes rapidly when Lie groups map high-dimensional motion. This decline in efficiency can be attributed to high-dimensional Lie groups introducing a significant amount of redundant information into the final deformation field. This excess information places a substantial strain on the ACWM module. Consequently, we have opted to exclude Lie groups from high-dimensional motion learning.

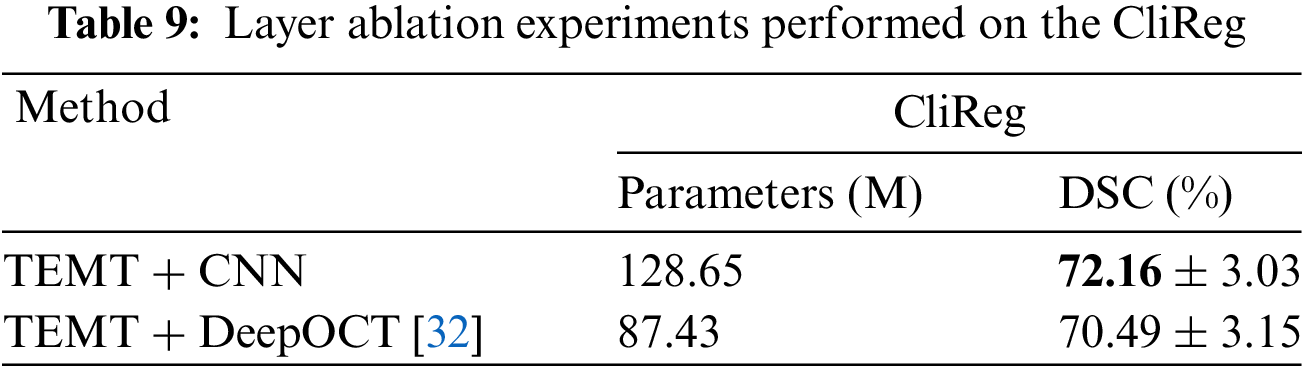
5.3 The Role of a Lightweight Architecture CNN

The traditional standard model focuses on the study of the flow field, and ignores the feature extraction and lightweight of the CNN module. Especially for our TEMT network, the number of parameters increases greatly when multi-head attention and Lie group modules are added. For this reason, we replace the CNN feature extraction module and use a lightweight CNN module DeepOCT [32] to conduct comparative experiments. It is found in the Table 9 that while the number of parameters is greatly reduced to facilitate the deployment of reasoning, the accuracy is not reduced much. This is very helpful for future clinical deployment and promotion.

6  Conclusion

In this study, we introduced the TEMT architecture, a novel deep learning-based registration framework for addressing respiratory motion artifacts in PET imaging. TEMT is compared with various deep learning models, including VM, VTN, DPRN, VIT, TM, MODET, DMR, and our TEMT model, which is based on multi-head attention and manifold learning. Following the evaluation using preferred quality metrics, our model demonstrated significant performance improvements. Specifically, the CC metrics on three different Gate simulated datasets achieved 98.68%, 97.50%, and 99.28%, respectively. In a clinical dataset, the similarity generated was 95.61%, particularly noteworthy in the DSC score, surpassing the comparison models by more than 5.7%. These results underscore the effectiveness of our model in correcting respiratory artifacts in PET images.

To validate the model’s generalization capabilities, we conducted an extensive comparative analysis, progressively complicating motion deformations through simulated and clinical experiments. The study experimented with four single-modality PET image datasets. To strengthen the model’s generalization ability and facilitate its deployment, inspired by [32,33], it is necessary to use datasets with a richer variety of modalities for cross-modality dataset experiments. Additionally, considering the inference capability during the model’s deployment process, the lightweight design of the CNN module is crucial.

In our future work, our primary focus will be on enhancing the accuracy of respiratory artifact correction and the lightweight design of the model. We intend to incorporate CT images as a reference in the process of correcting PET image artifacts. Additionally, we plan to reduce the number of trainable parameters [32] to provide standardized analysis and a lightweight architecture suitable for clinical application.

Acknowledgement: The authors would like to thank the Yunnan Key Laboratory of Smart City in Cyberspace Security for providing the computing resources for the development of this study.

Funding Statement: This work was supported by the National Natural Science Foundation of China (No. 82160347); Yunnan Provincial Science and Technology Department (No. 202102AE090031); Yunnan Key Laboratory of Smart City in Cyberspace Security (No. 202105AG070010).

Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: Haowei Ye, Jie Ning; numerical implementation: Hui Zhou; data collection: Jianfeng He, Bo She; analysis and interpretation of results: Haowei Ye, Jianfeng He, Bo She; draft manuscript preparation: Jie Ning, Hui Zhou. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets generated during this study are not publicly available due to privacy and ethical considerations; however, anonymized data can be provided by the corresponding author upon reasonable request and with the approval of the ethics committee. Researchers interested in accessing the data should contact the corresponding author (Prof. She, khyyyb@163.com) for further information.

Ethics Approval: The study was conducted in accordance with the Declaration of Helsinki, and the protocol was approved by the Ethics Committee of the First People’s Hospital of Yunnan Province (No. KHLL2023-KY125), and all participating patients provided informed consent.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. F. Zeng et al., “Diagnostic performance of zero-TE lung MR imaging in FDG PET/MRI for pulmonary malignancies,” Eur. Radiol., vol. 30, no. 9, pp. 4995–5003, 2020. doi: 10.1007/s00330-020-06848-z. [Google Scholar] [PubMed] [CrossRef]

2. S. Y. Kang, B. S. Moon, H. O. Kim, H. J. Yoon, and B. S. Kim, “The impact of data-driven respiratory gating in clinical F-18 FDG PET/CT: Comparison of free breathing and deep-expiration breath-hold CT protocol,” Ann. Nucl. Med., vol. 35, no. 3, pp. 328–337, 2021. doi: 10.1007/s12149-020-01574-4. [Google Scholar] [PubMed] [CrossRef]

3. N. J. P. C. Efthimiou, “New challenges for PET image reconstruction for total-body imaging,” PET Clin., vol. 15, no. 4, pp. 453–461, 2020. [Google Scholar] [PubMed]

4. G. Balakrishnan, A. Zhao, M. R. Sabuncu, J. Guttag, and A. V. Dalca, “An unsupervised learning model for deformable medical image registration,” in 32nd IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Salt Lake City, UT, USA, 2018, pp. 9252–9260. [Google Scholar]

5. G. Balakrishnan, A. Zhao, M. R. Sabuncu, J. Guttag, A. V. Dalca, “VoxelMorph: A learning framework for deformable medical image registration,” IEEE Trans. Med. Imaging., vol. 38, no. 8, pp. 1788–1800, 2019. doi: 10.1109/TMI.2019.2897538. [Google Scholar] [PubMed] [CrossRef]

6. S. Zhao, T. Lau, J. Luo, I. Eric, C. Chang and Y. Xu, “Unsupervised 3D end-to-end medical image registration with volume tweening network,” IEEE J. Biomed. Health Inform., vol. 24, no. 5, pp. 1394–1404, 2019. [Google Scholar] [PubMed]

7. B. Kim, D. H. Kim, S. H. Park, J. Kim, J. G. Lee and J. C. Ye, “CycleMorph: Cycle consistent unsupervised deformable image registration,” Med. Image Anal., vol. 71, pp. 102036, 2021. [Google Scholar] [PubMed]

8. M. H. Guo et al., “Attention mechanisms in computer vision: A survey,” Comput. Vis. Media., vol. 8, no. 3, pp. 331–368, 2022. [Google Scholar]

9. J. Chen, Y. He, E. C. Frey, Y. Li, and Y. Du, “ViT-V-Net: Vision transformer for unsupervised volumetric medical image registration,” 2021. Accessed: Apr. 13, 2021. [Online]. Available: https://arxiv.org/abs/2104.06468 [Google Scholar]

10. J. Chen, E. C. Frey, Y. He, W. P. Segars, Y. Li and Y. Du, “TransMorph: Transformer for unsupervised medical image registration,” Med. Image Anal., vol. 82, pp. 102615, 2022. [Google Scholar] [PubMed]

11. Y. Zhu and S. Lu, “Swin-VoxelMorph: A symmetric unsupervised learning model for deformable medical image registration using swin transformer,” in 25th. Int. Conf. Medical Image Comput. Comput.-Assist. Interven. (MICCAI), Singapore, 2022, pp. 78–87. [Google Scholar]

12. M. Kang, X. Hu, W. Huang, M. R. Scott and M. Reyes, “Dual-stream pyramid registration network,Medical image analysis,” Med. Image Anal., vol. 78, pp. 102379, 2022. [Google Scholar] [PubMed]

13. D. Zhang, H. Zhang, J. Tang, M. Wang, X. Hua and Q. Sun, “Feature pyramid transformer,” in 16th. Proc. Euro. Conf. Comput. Vis. (ECCV), Glasgow, UK, 2020, pp. 323–339. [Google Scholar]

14. K. Han et al., “A survey on vision transformer,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 45, no. 1, pp. 87–110, 2022. doi: 10.1109/TPAMI.2022.3152247. [Google Scholar] [PubMed] [CrossRef]

15. J. Chen et al., “Deformer: Towards displacement field learning for unsupervised medical image registration,” in 25th. Int. Conf. Med. Image. Comput. Comput .Assist. Interv. (MICCAI), Singapore, 2022, pp. 141–151. [Google Scholar]

16. J. Shi et al., “XMorpher: Full transformer for deformable medical image registration via cross attention,” in 25th. Int. Conf. Med. Image. Comput. Comput .Assist. Interv. (MICCAI), Singapore, 2022, pp. 217–226. [Google Scholar]

17. H. Wang, D. Ni, and Y. Wang, “ModeT: Learning deformable image registration via motion decomposition transformer,” 2023. Accessed: Jun. 09, 2023. [Online]. Available: https://arxiv.org/abs/2306.05688 [Google Scholar]

18. Y. Hou, J. He and B. She, “Respiratory motion correction on PET images based on 3D convolutional neural network,” KSII Trans. Internet Inf. Syst., vol. 16, no. 7, pp. 2191–2208, 2022. [Google Scholar]

19. J. Q. Zheng, Z. Wang, B. Huang, N. H. Lim, and B. W. Papiez, “Residual aligner network,” 2022. Accessed: Mar. 07, 2022. [Online]. Available: https://arxiv.org/abs/2203.04290 [Google Scholar]

20. S. Sharif, R. A. Naqvi, Z. Mehmood, J. Hussain, A. Ali and S. W. Lee, “MedDeblur: Medical image deblurring with residual dense spatial-asymmetric attention,” Math., vol. 11, no. 1, pp. 115, 2022. doi: 10.3390/math11010115. [Google Scholar] [CrossRef]

21. T. Cohen and M. Welling, “Group equivariant convolutional networks,” in 33rd Int. Conf. Proc. Mach. Learn. Res. (PMLR), New York, USA, 2016, pp. 2990–2999. [Google Scholar]

22. L. He, Y. Dong, Y. Wang, D. Tao, and Z. Lin, “Gauge equivariant transformer,” in 35th. Int. Conf. Neural Inf. Process. Syst. (NeurIPS), 2021, vol. 34, pp. 27331–27343. [Google Scholar]

23. M. J. Hutchinson, C. Le Lan, S. Zaidi, E. Dupont, Y. W. Teh and H. Kim, “LieTransformer: Equivariant self-attention for Lie groups,” in Proc. 38th Int. Conf. on Mach. Learn., 2021, vol. 139, pp. 4533–4543. [Google Scholar]

24. P. Ding, D. Soselia, T. Armstrong, J. Su, and F. Huang, “Reviving shift equivariance in vision transformers,” 2023. Accessed: Jun. 13, 2023. [Online]. Available: https://arxiv.org/abs/2306.07470 [Google Scholar]

25. R. Xu, K. Yang, K. Liu, and F. He, “E(2)-equivariant vision transformer,” 2023. Accessed: Jun. 11, 2023. [Online]. Available: https://arxiv.org/abs/2306.06722 [Google Scholar]

26. Z. Teed and J. Deng, “RAFT-3D: Scene flow using rigid-motion embeddings,” in 34th IEEE/CVF Conf. Comput. Vis. Pattern Recognit. (CVPR), 2021, pp. 8375–8384. [Google Scholar]

27. J. Abderezaei, A. Pionteck, A. Chopra, and M. Kurt, “3D Inception-based TransMorph: Pre- and post-operative multi-contrast MRI registration in brain tumors,” 2022. Accessed: Dec. 08, 2022. [Online]. Available: https://arxiv.org/abs/2212.04579 [Google Scholar]

28. S. Woo, J. Park, J. Y. Lee, and I. S. Kweon, “CBAM: Convolutional block attention module,” in 15th. Proc. Euro. Conf. Comput. Vis. (ECCV), Munich, Germany, 2018, pp. 3–19. [Google Scholar]

29. W. P. Segars, Development and Application of the New Dynamic Nurbs-Based Cardiac-Torso (NCAT) Phantom. USA: The University of North Carolina at Chapel Hill, 2001. [Google Scholar]

30. G. Altan, Y. Kutlu and N. Allahverdi, “Deep learning on computerized analysis of chronic obstructive pulmonary disease,” IEEE J. Biomed. Health Inform., vol. 24, no. 5, pp. 1344–1350, 2019. [Google Scholar]

31. X. Li, J. Lv, Y. Huo, B. Dong, R. M. Leahy and Q. Li, “Multiscale multimodal medical imaging: Third international workshop,” in Conj. with MICCAI 2022, Singapore, Springer Nature, vol. 13594, 2022, pp. 98–109. [Google Scholar]

32. G. J. E. S. Altan and A. I. J. Technology, “DeepOCT: An explainable deep learning architecture to analyze macular edema on OCT images,” Eng. Sci. Technol. Int J., vol. 34, pp. 101091, 2022. [Google Scholar]

33. S. Sharma and P. K. Mandal, “A comprehensive report on machine learning-based early detection of Alzheimer’s disease using multi-modal neuroimaging data,” ACM Comput. Surv., vol. 55, no. 2, pp. 1–44, 2022. doi: 10.1145/3492865. [Google Scholar] [CrossRef]