Nonlinear Registration of Brain Magnetic Resonance Images with Cross Constraints of Intensity and Structure

1  Introduction

Deformable image registration establishes the spatial transformation between voxels in fixed and moving images. This technique finds extensive applications in diverse domains, including medical image analysis [1–3], surgical navigation [4,5], and aided diagnosis [6,7]. Through registering brain Magnetic Resonance (MR) images for different individuals into a common spatial coordinate system, it becomes possible to calculate developmental differences between the different individuals, and explore the patterns of brain growth and development [8–10]. The application of algorithms in the registration field has yielded improved results and can facilitate efficient comparisons of patients, aiding doctors in diagnosis and lowering the costs of treatment. However, the registration problem persists as a difficult task due to the absence of appropriate constraint methods for extracting correspondences between images. As a result, maintaining semantic consistency in the deformation field generated is challenging.

Traditional registration methods gradually refine deformation estimation through iterative optimization, which typically demands substantial computational resources. Examples of such methods include Demons [11], Large Diffeomorphic Distance Metric Mapping (LDDMM) [12], and symmetric normalization (SyN) [13]. With the wide application of deep learning in computer vision tasks, deep learning-based methods exhibit excellent performance and hold significant potential in solving the shortcomings of the low efficiency of traditional registration methods. Various models have been developed based on deep learning architectures. For instance, models based on Convolutional Neural Networks (CNNs) are widely employed in registration tasks [14–17], with VoxelMorph [14] being a seminal example. VoxelMorph, a pioneer in introducing the unet architecture to registration models, successfully bridges the transition from conventional to deep learning-based registration methods. SYMNet [15] utilizes the Fully Convolutional Network (FCN) for feature extraction and incorporates a diffeomorphic structure to maintain the smooth invertibility of deformation fields. While this approach achieves lower Jacobian values, its impact on improving registration outcomes is not pronounced. Inverse-Consistent deep Network (ICNet) [16], by computing both forward and backward deformation fields, ensures the invertibility of deformation fields. Building upon ICNet, CycleMorph [17] introduces refinements by calculating the reverse deformation field of the backward deformation field, thus establishing a cyclically constrained network. Although these methods produce smoother and more invertible deformation fields, they fall short of achieving high-precision registration results.

Given the widespread success of the Transformer architecture in visual tasks, many researchers have integrated it into registration tasks [18–21], yielding significant improvements. Transmorph [18] proposes a hybrid model combining Transformer and CNN, followed by C2FViT [19], which entirely replaces CNN for feature extraction. Swin-VoxelMorph [20] further enhances model performance by introducing the Swin-Transformer structure. Subsequently, XMorpher [21] builds upon Swin-Transformer and incorporates cross-attention mechanisms in the encoder and decoder sections, achieving superior registration outcomes. Experimental results demonstrate that the Transformer structure, particularly the Swin-Transformer, significantly elevates registration accuracy. However, these models demand substantial computational resources and prolonged processing times, posing stringent requirements on hardware infrastructure.

Several scholars have explored the use of Generative Adversarial Network (GAN) networks to address registration challenges [22–24], exemplified by models such as ASNet [22] and Deform-GAN [23], employing a set of GAN networks for registration. These models require at least two modalities of information, generating one modality from another. Nevertheless, clinical data often lacks multiple modalities, constraining their applicability. SymReg-GAN [24] adeptly tackles this limitation by proposing a bidirectional GAN registration network, enforcing bidirectional constraints on deformation fields. Despite the potential of GAN networks in registration, their intrinsic limitations, particularly the issue of ‘creating information from nothing,’ may introduce information in generated images that does not exist in the original images, a phenomenon deemed unacceptable in the context of medical imaging.

The models described [11–24] typically use a single-stream encoder-decoder network, focusing solely on intensity images as input. This might limit their applicability in real-world clinical settings due to insufficient constraint information for model training. Although some methods introduce semi-supervised registration models, the segmentation image often only validates the model’s registration effect, overlooking semantic consistency between the label and the image. It is crucial to highlight that intensity images and segmentation images carry identical semantic information, encompassing features like edges, contours, and distortion levels. However, they employ different voxel classification methods. To fully exploit this information, we aim for a registration method that optimally utilizes both types. Voxelmorph introduces the incorporation of an auxiliary loss to constrain the registration impact of the segmentation mask. Inspired by this approach, we have designed a dual-channel registration model in which both intensity images and segmentation images serve as input data. This design enables the model to learn not only intensity information but also anatomical information. To enhance the extraction of crucial features from our dual input channels, we have introduced a cross constraint module. In this module, using intensity images as an example, the moving intensity image experiences deformation through the deformation field associated with intensity images, generating a ‘moved’ image. Simultaneously, the same moving intensity image undergoes deformation using the deformation field linked to segmentation images, resulting in another ‘moved’ image. A similar process is applied to the second input channel, extending the concept of cross constraints to foster mutual influence between the two input channels and their respective deformation fields. To encourage alignment between these deformation fields, a similarity loss is calculated by comparing the two generated ‘moved’ images. The objective is to enforce a high degree of consistency between the two deformation fields. This strategy guarantees that information from both intensity and segmentation channels plays a crucial role in the registration process, leading to enhanced accuracy. In contrast to many network models relying on labeled images for supervision, our approach focuses on ensuring semantic-level consistency between intensity and segmentation images, concurrently exploring the potential relationship between the two learned deformation fields.

In the context of deformable image registration, maintaining semantic consistency in the deformation field with minimal singularities presents a significant challenge. Semantic consistency here means that the deformation fields obtained by the two channels are the identical. Some researchers have employed methods like Mean Square Error (MSE) [15] or length constraint [16] to measure similarity between the two deformation fields. Although these methods can constrain the obtained deformation field to a certain extent, the expansion of the three-dimensional deformation field into one-dimensional numerical calculation ignores the essential property of the deformation field as a vector field that results in inaccurate registration results. Therefore, we utilize a cosine similarity loss function to constrain the directional consistency between the learned two deformation fields and try to suppress the semantic inconsistency caused by large deformation. The designed framework is utilized based on the consistency of semantic information between intensity images and segmentation images, and to maintain the semantic consistency of the deformation field. To address the challenges mentioned above, we have introduced a novel dual-channel cross constraint network for medical image registration. It is worth noting that some existing deep neural network models also employ a dual-channel input architecture, such as Dual-PRNet [25], PIViT [26], NICE-Net [27], NICE-Trans [28]. However, unlike our approach, they separate the moving and fixed images into two parameter-sharing channels for input. Their objective is to reduce the parameter count in the encoder section. In contrast, our dual-channel approach aims to incorporate information from both grayscale and segmented modalities.

To summarize, this paper makes the following contributions: (1) We propose a dual-channel cross constrained network that leverages both intensity and anatomical information to constrain the deformation field. (2) We propose a directional consistency constraint to effectively constrain the obtained two deformation fields by the dual-channel cross constrained network.

The structure of this article is outlined as follows: The first section, Introduction, delves into traditional registration methods and deep learning registration approaches. It analyzes some prevailing issues within the current mainstream single-stream registration networks, leading to the introduction of our innovative dual-channel cross-constrained registration network. In the second section, Method, we expound on two key innovations of our approach: The cross-constraint module and the direction consistency module. Additionally, we provide an in-depth explanation of the loss functions utilized during the training process for these two modules. Moving on to the third part, Experiment, we elaborate on the datasets and preprocessing, experimental settings, as well as the results and their analysis. The fourth section, Discussion, scrutinizes the results of ablation experiments, substantiating the efficacy of both the cross-constraint module and the direction consistency module. Finally, the concluding section, Conclusion, offers a comprehensive summary of the entire article.

2  Methods

The current supervised registration methods typically involve training a model to learn a deformation field from a pair of intensity images. Subsequently, the corresponding segmentation image is input into this deformation field for spatial transformation to evaluate the registration results. However, considering that segmentation images are only used for validation, their information is not fully utilized. In order to better exploit the information contained in segmentation images, we propose a dual-channel cross-constraint network. Specifically, unlike conventional supervised models, our model treats segmentation images as inputs of equal importance alongside intensity images. The inputs of the two channels learn their respective deformation fields, and the moving image is cross-input into the deformation field of the other channel for spatial transformation. It is noteworthy that intensity images use Normalized Cross Correlation (NCC) loss, while segmented images use Dice loss. This approach ensures that each branch of the model calculates both Dice and NCC losses, incorporating information from both their own branch and the other channel, leading to improved registration outcomes.

The primary components of our proposed dual-channel cross constraint network are two modules. Firstly, there is the dual-channel cross constraint module, responsible for producing two deformation fields and facilitating the fusion of information across channels. Additionally, we have the directional consistency network module, which imposes further constraints on the two deformation fields. Subsequent sections offer detailed elucidations for each module.

2.1 Dual-Channel Cross Constraint Networks

The dual-channel cross constraint network is constructed upon VoxelMorph architecture as backbone, introducing a novel dual-stream framework. In the single-stream encoder-decoder structure, the moving intensity image is mapped through the spatial transform of the obtained deformation field for the moved image, and then the NCC loss between the moved image and fixed image is calculated. To achieve cross constraints, the input intensity image and segmentation image are both mapped by the deformation field generated with itself stream and the deformation field generated with another stream. Therefore, the moving images are mapped by two deformation fields to generate two moved images, both of which are calculated with the fixed image for NCC loss or Dice loss, respectively (depending on whether the input image is an intensity image or a segmentation image). The network framework diagram is shown in Fig. 1.

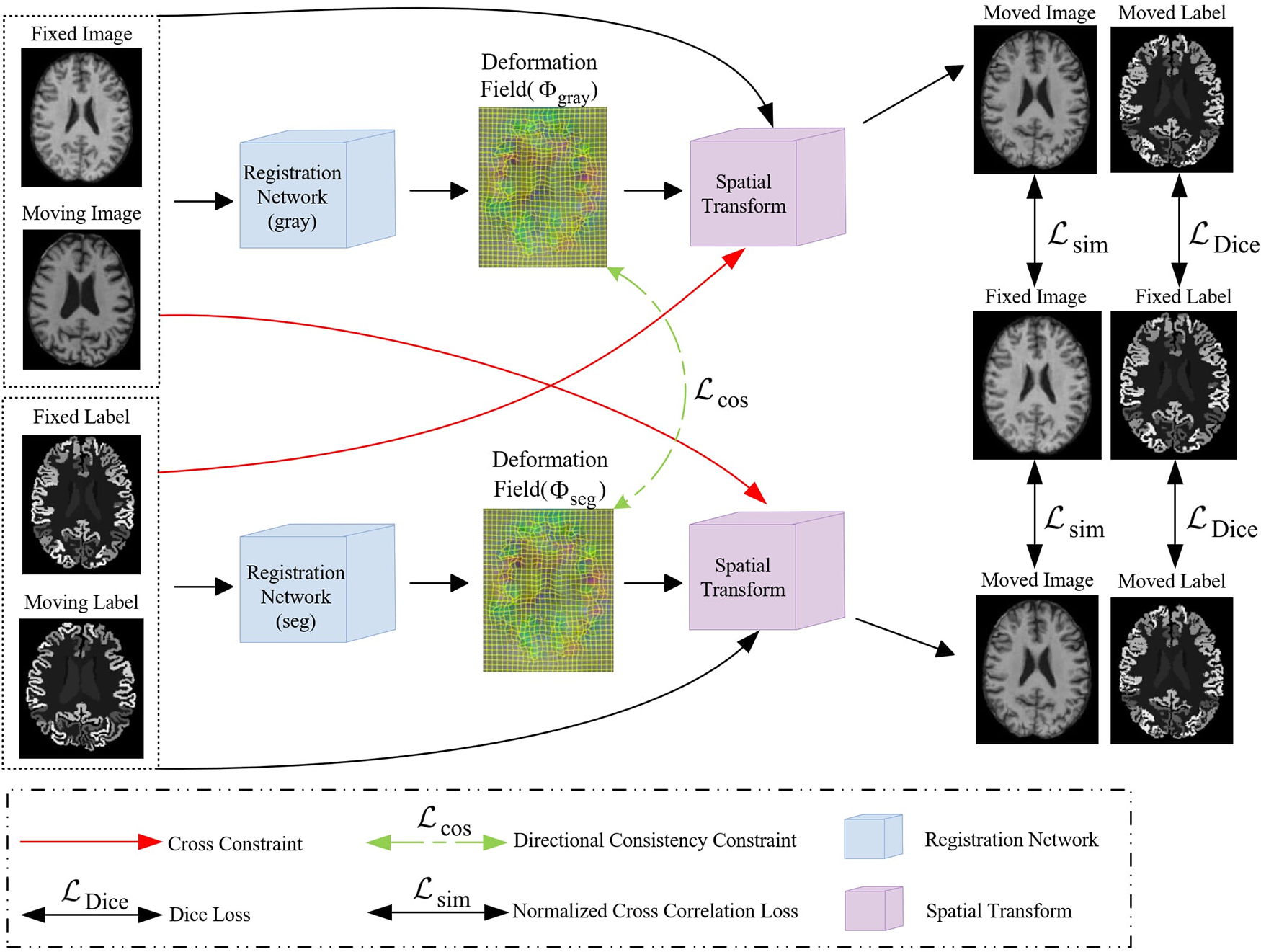
Figure 1: An illustration of our proposed Dual-channel cross constraint network networks

Two UNet networks are used to learn the deformation fields corresponding to the intensity and segmentation images, both intensity and segmentation images are concurrently fed into their designated deformation field computations while also entering the computation of the other, and directional consistency (ℒcos) is used to constrain the two deformation fields. ℒ Dice is used to compute the similarity between segmentation images, and ℒ sim is used to compute the similarity between intensity images. And the registration network employs a 3D UNet architecture.

Specifically, the backbone comprises a dual-stream encoder-decoder, adopting the same architecture as UNet [29] that contains five convolutional. And each layer contained a convolutional layer followed by a Relu layer, using a 3 × 3 × 3 convolutional kernel with a stride of 1, the feature map obtained after the entire encoding operation is 1/16 of the input image’s resolution. In the decoder, the feature map obtained by the encoder is input to the corresponding part of the decoder by a skip connection. The lower-resolution convolutional maps are up-sampled and combined with the higher-resolution ones from encoding layers. This process is followed by a 3 × 3 × 3 convolutional layer and ReLU activation. Consequently, we obtain two deformation fields, one derived from the intensity image and the other from the segmentation image, respectively. The UNet structure employed in our framework is shown in Fig. 2.

Figure 2: Framework of the UNet that utilized to estimate the deformation field. The 3D feature maps generated by the encoder and decoder are represented by blue and purple rectangular blocks, respectively, with blue lines indicating skip connections

Cross constraints in the implementation rely on two loss functions: Normalized Cross Correlation (NCC) loss and Dice loss. The utilization of these two loss functions effectively constrains the two channels, enabling the model to learn more semantic-level consistency features and thereby enhancing the registration effectiveness. Below are detailed introductions to each of these loss functions.

2.1.1 NCC Loss

We assess image alignment between two input images using the Normalized Cross Correlation (NCC) as a similarity measure. The formula for computing the correlation coefficient, as indicated in Eq. (1).

NCC(I,J)=∑x∈Ω∑xi(I(xi)−I¯(x))(J(xi)−J¯(x))∑xi(I(xi)−I¯(x))2∑xi(J(xi)−J¯(x))2(1)

I¯(x), J¯(x) represent the average value of two local windows Ω with a size of 9 centered on x, respectively. Specifically, our proposed similarity loss function, denoted as ℒ sim comprises two terms: Calculating the similarity of the intensity images into the deformation field formed by the intensity images ℒgray_sim and calculating the similarity of the intensity images into the deformation field formed by the segmentation images ℒseg_sim, as shown in Eqs. (2)–(4). Further, Φgray and Φseg represent the deformation field formed by intensity images and segmentation images, respectively. X(Φgray) represents the moved intensity image after deformation under the action of deformation field Φgray. X(Φseg) represents the moved intensity image after deformation under the action of deformation field Φseg, and Y represents the fixed intensity image.

ℒsim=ℒgray_sim+ℒseg_sim(2)

With,

ℒgray_sim=−NCC(X(Φgray),Y)(3)

And,

ℒseg_sim=−NCC(X(Φseg),Y)(4)

2.1.2 Dice Loss

We calculate Dice score using the segmentation images as the constraint. Ik, Jk represent the Φ voxel belonging to structure k in image I, image J, respectively, as indicated in Eq. (5), if the image I and the image J corresponding structure overlaps well, then the Dice value is 1, otherwise it is 0.

Dice(Ik,Jk)=1−2|Ik∩Jk||Ik|+|Jk|(5)

We calculate the Dice loss ℒ Dice overall structure k∈[1,K] as shown in Eqs. (6) and (7):

ℒ seg_Dice=−1K∑k=1KDice(Xsegk(Φseg),Ysegk)(6)

Xsegk(Φgray) represents the moved segmentation image after deformation under the action of deformation field Φgray, Xsegk(Φseg) represents the moved segmentation image after deformation under the action of deformation field Φseg, and Y segk represents the fixed segmentation image, so the Dice loss after cross constraints is calculated as shown in Eq. (8):

ℒ gray_Dice=−1K∑k=1KDice(Xsegk(Φgray),Ysegk)(7)

ℒ Dice=ℒ gray_Dice+ℒ seg_Dice(8)

2.2 Direction Consistent Networks

In our proposed channel cross constraint network, we generate two deformation fields from two pairs input images. We choose the cosine similarity function to calculate the similarity of two deformation fields in the x, y and z directions.

2.2.1 Cosine Similarity Function

To achieve a better constraint, we calculate the cosine similarity of the three-channel from deformation field obtained by the decoder according to the direction. The calculation formula for the similarity loss function in a single direction is as shown in Eq. (9):

Cosine(A,B)=A⋅B∥A∥×∥B∥=∑i=1n⁡(Ai×Bi)∑i=1n⁡Ai2×∑i=1n⁡Bi2(9)

A, B represent the vectors corresponding to the two deformation fields in the same directions, and n represents the number of voxels in the deformation field in this direction, then add up the calculation results in the three directions. When the cosine value is negative, implying an angle greater than 90 degrees, which is not in line with the actual situation. Therefore, we improve based on the original formula, increase the penalty for negative results, and better realize the direction consistency and topology preservation of the deformation field. The improved formula is as shown in Eqs. (10) and (11):

Similarity =2∗Cosine (Φgray , Φseg)−|Cosine (Φgray , Φseg)|(10)

ℒcos=1−Similarity(Φgray,Φseg)(11)

2.3 Smooth Loss

We apply diffusion regularization to the deformation field gradient for constraining the global smoothness, as shown in Eq. (12), Ω presents whole deformation space.

ℒ smooth(Φ)=∑p∈Ω||∇(Φ(p))||2(12)

In summary, our loss function is as shown in Eq. (13):

ℒ=ℒ sim+ℒ Dice+ℒcos+λℒ smooth(13)

where λ is a regularization parameter, we set it to 4 during the experimental process.

3  Experiment

3.1 Experimental Data and Preprocessing

We have evaluated our experimental method for the brain atlas registration task on four public datasets LPBA40 [30], OASIS-1 [31,32], OASIS-3 [33], and ADNI [34]. And the dataset was divided into training and testing sets as follows: 30 in the LPBA40 dataset are used as training and 9 as testing, 331 in the OASIS-1 dataset are used for training and 82 for testing, and both OASIS-3 and ADNI datasets select 405 as training data and 103 as testing data.

For the LPBA40 and OASIS-1 datasets, we directly use the preprocessed public version. In the LPBA40 dataset, all MRI scans were annotated with 56 regions of interest (ROIs) and center-cropped to 160 × 192 × 160. In the OASIS-1 dataset, all MRI scans were accompanied by annotations for 35 ROIs and center-cropped to 160 × 192 × 224. For the OASIS-3 and ADNI datasets, we perform standard preprocessing procedures for each MR scan by IBEAT V2.0 Cloud [35–38]. Each MRI scan encompassed 133 ROIs. We then perform isotropic voxel resampling on all MR scans, setting the voxel sizes to 13 mm, and then interpolate the preprocessed MRI scans to achieve dimensions of 255 × 255 × 255. Subsequently, we conducted center-cropping on the images, resulting in final dimensions of 160 × 192 × 224.

3.2 Experiment Settings

Our proposed method was conducted using PyCharm as the software, running on hardware equipped with an NVIDIA GeForce RTX 3090 graphics card and a 12th Gen Intel(R) Core(TM) i9-12900KF CPU clocked at 3.20 GHz. The experiment utilized PyTorch version 1.9, with CUDA version 11.1, as the underlying framework. For optimization, we employed the Adam solver, and set the learning rate to 1e-4. The training process was conducted for 15000 iterations, and we utilized a batch size of 1.

3.3 Experimental Results and Analysis

We adopted the mean and variance of the Dice score and Jacobian determinant value from a pair of registered images (test phase) as our evaluation metrics.

To compare our proposed dual-stream architecture with the single-stream network structure commonly used by networks like VoxelMorph, we only activate the encoder-decoder channel corresponding to intensity images during testing, without requiring label information. As shown in Table 1, both the deep learning-based registration methods VoxelMorph and SYMNet show improvements in registration performance compared to the traditional registration method SYN, our method achieved a mean Dice score of 0.699 on LPBA40, 0.799 on OASIS-1, 0.645 on OASIS-3, and 0.635 on ADNI. The proposed dual-stream architecture exhibits enhancements over the single-stream counterpart, with performance improvements of +2.0%, +1.9%, +11.0%, and +5.7%, respectively. Our method demonstrates the best performance across four public datasets in terms of the average Dice score, particularly in the OASIS-3 and ADNI datasets.

Results of the Jacobian determinant indicate that our method is inferior to SYMNet in terms of the smooth deformation field. This distinction arises from SYMNet’s integration of the diffeomorphism concept. SYMNet incorporates velocity field at different times to perform positive and negative bidirectional registration to obtain the final deformation. During this process, the deformation remains entirely reversible, resulting in a smooth deformation field. Although we also employ the direction consistency module to constrain the topological invariance for the deformation field, its impact is more prominently for the improvement of Dice score.

As we did not uniformly preprocess all datasets, we present the results for thirteen different anatomical structures on each of the four datasets. Dice scores for each anatomical structure on the four datasets are depicted in Figs. 3–6. These results reveal that our method outperforms other methods on the majority of anatomical structures, especially in the TMP, SFG, SMG, and SMC regions of OASIS-3 and ADNI datasets.

Figure 3: The Dice scores for each anatomical structure achieved by Affine, SyN, SYMNet, VoxelMorph, and our method (Dual-VoxelMorph) on the LPBA40 dataset. For visualization purposes, the left-right symmetrical structure of the brain takes its mean value

Figure 4: The Dice scores for each anatomical structure achieved by Affine, SyN, SYMNet, VoxelMorph, and our method (Dual-VoxelMorph) on the OASIS-1 dataset. For visualization purposes, the left-right symmetrical structure of the brain takes its mean value

Figure 5: The Dice scores for each anatomical structure achieved by Affine, SyN, SYMNet, VoxelMorph, and our method (Dual-VoxelMorph) on the OASIS-3 dataset. For visualization purposes, the left-right symmetrical structure of the brain takes its mean value. SPL refers to the superior parietal lobule, SOG refers to superior occipital gyrus, TMP refers to the temporal pole, SFG refers to the superior frontal gyrus, SMG refers to the supramarginal gyrus and SMC refers to the supplementary motor cortex

Figure 6: The Dice scores for each anatomical structure achieved by Affine, SyN, SYMNet, VoxelMorph, and our method (Dual-VoxelMorph) on the ADNI dataset. For visualization purposes, the left-right symmetrical structure of the brain takes its mean value. SPL refers to the superior parietal lobule, SOG refers to the superior occipital gyrus, TMP refers to the temporal pole, SFG refers to the superior frontal gyrus, SMG refers to the supramarginal gyrus and SMC refers to the supplementary motor cortex

3.4 Visualized Results and Analysis

We randomly select four subjects result in the test set for visual display, as shown in Fig. 7. Notably, we have outlined the cingulate gyrus with a distinctive red circle for emphasis. It is evident from the figures that, in comparison to other methods, our registration demonstrates superior alignment with the fixed image, particularly in the case of the left cingulate gyrus. In subject 3, the registration result is similar to the VoxclMorph method, but the boundary obtained by our method is smoother. In Fig. 3, the effect of cingulate gyrus (fifth column) is that the Dice score obtained by our method is better than other methods.

Figure 7: Results of registration for four subjects in the LPBA40 dataset. Each column from left to right is arranged as follows: The moving image, results of SyN, SYMNet, VoxelMorph, our method, and the fixed image. The caudate, cingulate gyrus, cuneus, and insular cortex are colored in rose red (left), milky yellow (right), blue-green (left), dark green (right), turmeric (left), light green (right), milky white (left) and reddish brown (right), respectively

In Fig. 8, we have highlighted the left side of the cerebellum cortex with a distinctive red circle, serving as a visual representation. In the four individuals shown above, the highlighted area within the red circle demonstrates that our method can achieve a more complete edge line, closely resembling the shape of the fixed image. The visualized results correspond to the quantitative results in column 10 of the boxplot Fig. 4.

Figure 8: Results of registration for four subjects in the OASIS-1 dataset. Each column from left to right is arranged as follows: The moving image, results of SyN, SYMNet, VoxelMorph, our method, and the fixed image. The Cerebellum-Cortex is colored green (left) and rose red (right)

As illustrated in Fig. 9, we have outlined in red the first row of results, focusing on subject 1. Notably, our method yields moved images with more favorable outcomes in terms of gullies, displaying smoother and more continuous curves. In subjects 2 and 3, our method can obtain the results of the deepest part of the ravine. For subject 4, the moved images obtained by SYMNet and VoxelMorph are scattered. In contrast, our method’s results present tissue boundaries with greater continuity and coherence, aligning with the outcomes depicted in Fig. 5.

Figure 9: Results of registration for four subjects in the OASIS-3 dataset. Each column of images from left to right is arranged as follows: The moving image, results of SyN, SYMNet, VoxelMorph, our method, and the fixed image. The SMG is colored in turquoise (left) and white (right)

In the display of results for subjects 1 and 2 in Fig. 10, we have outlined the right superior marginal gyrus (SMG) using a distinctive red circle. Comparing the results, it becomes evident that our registration method yields moved images with clear and well-defined edges. For subjects 3 and 4, we circled the left SMG with a red circle. The comparison results show that our registration method works better for deep ravines. From the visual results, we found that SYMNet’s performance is not bad. In Fig. 6, although SYMNet’s quantitative results are much lower than VoxelMorph and our method. That is due to the use of diffeomorphism, forward and reverse bidirectional registration strategy for SYMNet.

Figure 10: Results of registration for four subjects in the ADNI dataset. Each column of images from left to right is arranged as follows: The moving image, results of SyN, SYMNet, VoxelMorph, our method, and the fixed image. The SMG is colored in turquoise (left) and white (right)

4  Discussion

4.1 Ablation Experiment

We provide ablation experiments for further validation of individual components developed in our model. We separately evaluate the cross constraints implemented by dual-stream structure, direction consistency constraint module, and Jacobi loss to the model. Jdet represents the Jacobian constraint, Cross represents the cross constraint, and Cos and MSE respectively represent whether to use the cosine loss function or the MSE loss function in the direction consistency constraint. The results of the six groups of experiments conducted on the OASIS-3, ADNI, and OASIS-1 datasets are presented in Tables 2–4, respectively, the first group of experiments represents the VoxelMorph experiment, serving as the control group for our ablation experiments.

Additionally, due to the small amount of LPBA40 dataset, there are only 9 tests, the ablation experiment is no longer performed on it.

4.1.1 Ablation Experiments on the OASIS-3 Dataset

Table 2 compares the results of six groups ablation experiments. Based on the Jacobian results obtained from the deformation field in the previous experiment, we implemented the Jacobian function to smooth the deformation field (comparative experiments 1, 4, and 6). The results indicate that the change of the deformation field is negligible but the dice value will decrease after introducing the constraint of the Jacobian function. Comparing the results of experiments 1, 2, and 4, the experimental results have been significantly improved by dual-channel cross constraints, from 0.604 to 0.641, it demonstrates that our dual-channel structure is effective. The results of experiments 3 and 4 confirmed the effectiveness of the direction consistency constraint module, and the results were slightly improved. Further comparing the results of experiments 4 and 5, if we replace the metric function between the two deformation fields from cosine similarity to MSE, the Dice value will drop significantly, which indicates that an inappropriate loss function will be important for the registration task.

4.1.2 Ablation Experiments on the ADNI Dataset

Table 3 compares the results of six groups of ablation experiments. Comparing the results of experiments 1, 4, and 6, after introducing the Jacobian constraint, the best experimental results were achieved. Although the value of the Jacobian was not reduced, considering that the results of the Jacobian ratio were all less than 0.005, the impact was not significant. Comparing the results of experiments 1, 2, and 4, the dual-channel cross constraints boost Dice sore from 0.599 to 0.643, demonstrating the effectiveness of the module. Furthermore, in the comparison of results from experiments 3, 4, and 5, it is clear that the cosine similarity loss function performs much better than the MSE.

4.1.3 Ablation Experiments on the OASIS-1 Dataset

Table 4 compares the results of six groups of ablation experiments. Comparing the results of experiments 1, 4, and 6, it is consistent with the performance of the ADNI data set, and the OASIS-1 data set also achieved the best results under the constraint of Jacobian loss. Comparing the results of experiments 1, 2, and 4, the dual-channel cross constraint contributes the most to the improvement of the result, and the Dice value increases from 0.785 to 0.800. Additionally, comparing the results of experiments 3, 4, and 5, The direction consistency constraint also played an important role in promoting the model.

In summary, while the ablation experiment results exhibit slightly different across the three datasets, they consistently highlight the significant contributions of two key innovations: The dual-channel cross constrained network structure and the directional consistency constraint. These components have played a crucial role in enhancing the accuracy of the registration in our method. In addition, our method can work on different data sets, which also verifies that our model has strong generalization.

5  Conclusion

This paper introduces an innovative registration network, leveraging a dual-channel cross-constrained approach. Our method effectively utilizes semantic-level consistency information between intensity and segmentation images to improve registration accuracy. Additionally, to ensure topological preservation of the deformation field, we introduce a consistency similarity function, strengthening penalties for included angles exceeding 90 degrees. A comprehensive set of experiments demonstrates the consistent outperformance of our method compared to the baseline across all four publicly available datasets.

Acknowledgement: Not applicable.

Funding Statement: This work was supported in part by National Natural Science Foundation of China (Grant Nos. 62171130, 62172197, 61972093), the Natural Science Foundation of Fujian Province (Grant Nos. 2020J01573, 2022J01131257, 2022J01607), Fujian University Industry University Research Joint Innovation Project (No. 2022H6006) and in part by the Fund of Cloud Computing and Big Data for Smart Agriculture (Grant No. 117-612014063), National Natural Science Foundation of China (Grant No. 62301160), Nature Science Foundation of Fujian Province (Grant No. 2022J01607).

Author Contributions: The authors confirm contribution to the paper as follows: Model framework design and code implementation: Han Zhou, Hongtao Xu; data preprocessing: Han Zhou, Xinyue Chang; analysis and interpretation of results: Han Zhou, Wei Zhang; draft manuscript preparation: Han Zhou, Heng Dong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: In our paper, we utilized four datasets. You can access the preprocessed datasets for LPBA40 and OASIS-1, while the datasets for OASIS-3 and ADNI remain unprocessed. Please note that the preprocessing for OASIS-3 and ADNI was done using the iBeat software, and unfortunately, we are unable to share the processed data at the moment. You can use FreeSurfer to perform preprocessing on these datasets on your own. LPBA40: https://www.loni.usc.edu/research/atlas_downloads; OASIS-1: https://github.com/adalca/medical-datasets/blob/master/neurite-oasis.md; OASIS-3: https://www.oasis-brains.org/#access; ADNI: https://adni.loni.usc.edu/data-samples/access-data/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. V. Dalca, G. Balakrishnan, J. Guttag, and M. R. Sabuncu, “Unsupervised learning for fast probabilistic diffeomorphic registration,” in Medical Image Computing and Computer Assisted Intervention–MICCAI 2018, vol. 11070, pp. 729–738, 2018. doi: 10.1007/978-3-030-00928-1. [Google Scholar] [CrossRef]

2. Y. Fu, Y. Lei, T. Wang, W. J. Curran, T. Liu and X. Yang, “Deep learning in medical image registration: A review,” Phys. Med. Biol., vol. 65, no. 20, pp. 20TR01, Oct. 2020. doi: 10.1088/1361-6560/ab843e. [Google Scholar] [PubMed] [CrossRef]

3. S. P. Singh, L. Wang, S. Gupta, H. Goli, P. Padmanabhan and B. Gulyás, “3D deep learning on medical images: A review,” Sensors, vol. 20, no. 18, pp. 5097, Jan. 2020. doi: 10.3390/s20185097. [Google Scholar] [PubMed] [CrossRef]

4. A. F. de Geer et al., “Registration methods for surgical navigation of the mandible: A systematic review,” Int. J. Oral Maxillofac. Surg., vol. 51, no. 10, pp. 1318–1329, Oct. 2022. doi: 10.1016/j.ijom.2022.01.017. [Google Scholar] [PubMed] [CrossRef]

5. H. Yoo and T. Sim, “Automated machine learning (AutoML)-based surface registration methodology for image-guided surgical navigation system,” Med. Phys., vol. 49, no. 7, pp. 4845–4860, Jul. 2022. doi: 10.1002/mp.15696. [Google Scholar] [PubMed] [CrossRef]

6. T. C. W. Mok and A. C. S. Chung, “Unsupervised deformable image registration with absent correspondences in pre-operative and post-recurrence brain tumor MRI scans,” 2022. doi: 10.48550/arXiv.2206.03900. [Google Scholar] [CrossRef]

7. A. Nayak et al., “Computer-aided diagnosis of cirrhosis and hepatocellular carcinoma using multi-phase abdomen CT,” Int. J. CARS, vol. 14, no. 8, pp. 1341–1352, Aug. 2019. doi: 10.1007/s11548-019-01991-5. [Google Scholar] [PubMed] [CrossRef]

8. D. Wei et al., “An auto-context deformable registration network for infant brain MRI,” 2020. doi: 10.48550/arXiv.2005.09230. [Google Scholar] [CrossRef]

9. L. Wei, S. Hu, Y. Gao, X. Cao, G. Wu and D. Shen, “Learning appearance and shape evolution for infant image registration in the first year of life,” in Machine Learning in Medical Imaging, Cham: Springer International Publishing, 2016, pp. 36–44, doi: 10.1007/978-3-319-47157-0_5 [Google Scholar] [CrossRef]

10. L. Wei et al., “Learning-based deformable registration for infant MRI by integrating random forest with auto-context model,” Med Phys., vol. 44, no. 12, pp. 6289–6303, Dec. 2017. doi: 10.1002/mp.12578. [Google Scholar] [PubMed] [CrossRef]

11. T. Vercauteren, X. Pennec, A. Perchant, and N. Ayache, “Diffeomorphic demons: Efficient non-parametric image registration,” NeuroImage, vol. 45, no. 1, pp. S61–S72, Mar. 2009. doi: 10.1016/j.neuroimage.2008.10.040. [Google Scholar] [PubMed] [CrossRef]

12. J. Glaunès, A. Qiu, M. I. Miller, and L. Younes, “Large deformation diffeomorphic metric curve mapping,” Int. J. Comput Vis, vol. 80, no. 3, pp. 317–336, Dec. 2008. doi: 10.1007/s11263-008-0141-9. [Google Scholar] [PubMed] [CrossRef]

13. B. B. Avants, C. L. Epstein, M. Grossman, and J. C. Gee, “Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain,” Med. Image Anal., vol. 12, no. 1, pp. 26–41, Feb. 2008. doi: 10.1016/j.media.2007.06.004. [Google Scholar] [PubMed] [CrossRef]

14. G. Balakrishnan, A. Zhao, M. R. Sabuncu, J. Guttag, and A. V. Dalca, “VoxelMorph: A learning framework for deformable medical image registration,” IEEE Trans. Med. Imaging., vol. 38, no. 8, pp. 1788–1800, Aug. 2019. doi: 10.1109/TMI.2019.2897538. [Google Scholar] [PubMed] [CrossRef]

15. J. Zhang, “Inverse-consistent deep networks for unsupervised deformable image registration,” 2018. doi: 10.48550/arXiv.1809.03443. [Google Scholar] [CrossRef]

16. T. C. W. Mok and A. C. S. Chung, “Fast symmetric diffeomorphic image registration with convolutional neural networks,” in 2020 IEEE/CVF Conf. Comput. Vis. Pattern Recogn. (CVPR), Seattle, WA, USA, IEEE, Jun. 2020, pp. 4643–4652. doi: 10.1109/CVPR42600.2020.00470. [Google Scholar] [CrossRef]

17. B. Kim, D. H. Kim, S. H. Park, J. Kim, J. G. Lee and J. C. Ye, “CycleMorph: Cycle consistent unsupervised deformable image registration,” 2020. doi: 10.48550/arXiv.2008.05772. [Google Scholar] [CrossRef]

18. J. Chen, E. C. Frey, Y. He, W. P. Segars, Y. Li and Y. Du, “TransMorph: Transformer for unsupervised medical image registration,” Med. Image Anal., vol. 82, pp. 102615, Nov. 2022. doi: 10.1016/j.media.2022.102615. [Google Scholar] [PubMed] [CrossRef]

19. T. C. W. Mok and A. C. S. Chung, “Affine medical image registration with coarse-to-fine vision transformer,” 2022. doi: 10.48550/arXiv.2203.15216. [Google Scholar] [CrossRef]

20. Y. Zhu and S. Lu, “Swin-VoxelMorph: A symmetric unsupervised learning model for deformable medical image registration using swin transformer,” in Medical Image Computing and Computer Assisted Intervention—MICCAI 2022, Cham: Springer Nature Switzerland, 2022, pp. 78–87. doi: 10.1007/978-3-031-16446-0_8 [Google Scholar] [CrossRef]

21. J. Shi et al., “XMorpher: Full transformer for deformable medical image registration via cross attention,” 2022. doi: 10.48550/arXiv.2206.07349. [Google Scholar] [CrossRef]

22. Y. Hu et al., “Adversarial deformation regularization for training image registration neural networks,” in Med. Image Comput. Comput. Assist. Interv.–MICCAI 2018, vol. 11070, pp. 774–782, 2018. doi: 10.1007/978-3-030-00928-1. [Google Scholar] [CrossRef]

23. X. Zhang, W. Jian, Y. Chen, and S. Yang, “Deform-GAN: An unsupervised learning model for deformable registration,” 2020. doi: 10.48550/arXiv.2002.11430. [Google Scholar] [CrossRef]

24. Y. Zheng et al., “SymReg-GAN: Symmetric image registration with generative adversarial networks,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 44, no. 9, pp. 5631–5646, Sep. 2022. doi: 10.1109/TPAMI.2021.3083543. [Google Scholar] [PubMed] [CrossRef]

25. M. Kang, X. Hu, W. Huang, M. R. Scott, and M. Reyes, “Dual-stream pyramid registration network,” 2023. doi: 10.48550/arXiv.1909.11966. [Google Scholar] [CrossRef]

26. T. Ma et al., “PIViT: Large deformation image registration with pyramid-iterative vision transformer, syeda-mahmood,” in Medical Image Computing and Computer Assisted Intervention—MICCAI 2023,Cham: Springer Nature Switzerland, 2023, pp. 602–612. doi: 10.1007/978-3-031-43999-5_57 [Google Scholar] [CrossRef]

27. M. Meng, L. Bi, D. Feng, and J. Kim, “Non-iterative coarse-to-fine registration based on single-pass deep cumulative learning,” in Medical Image Computing and Computer Assisted Intervention—MICCAI 2022, Cham: Springer Nature Switzerland, 2022, vol. 13436, pp. 88–97. doi: 10.1007/978-3-031-16446-0_9 [Google Scholar] [CrossRef]

28. M. Meng et al., “Non-iterative coarse-to-fine transformer networks for joint affine and deformable image registration,” in Medical Image Computing and Computer Assisted Intervention—MICCAI 2023,Cham: Springer Nature Switzerland, 2023, vol. 14229, pp. 750–760. doi: 10.1007/978-3-031-43999-5_71 [Google Scholar] [CrossRef]

29. O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional networks for biomedical image segmentation,” 2015. doi: 10.48550/arXiv.1505.04597. [Google Scholar] [CrossRef]

30. D. W. Shattuck et al., “Construction of a 3D probabilistic atlas of human cortical structures,” NeuroImage, vol. 39, no. 3, pp. 1064–1080, Feb. 2008. doi: 10.1016/j.neuroimage.2007.09.031. [Google Scholar] [PubMed] [CrossRef]

31. A. Hoopes, M. Hoffmann, D. N. Greve, B. Fischl, J. Guttag and A. V. Dalca, “Learning the effect of registration hyperparameters with HyperMorph,” 2022. doi: 10.59275/j.melba.2022-74f1. [Google Scholar] [CrossRef]

32. D. S. Marcus, T. H. Wang, J. Parker, J. G. Csernansky, J. C. Morris and R. L. Buckner, “Open Access Series of Imaging Studies (OASISCross-sectional MRI data in young, middle aged, nondemented, and demented older adults,” J. Cogn. Neurosci., vol. 19, no. 9, pp. 1498–1507, 2007. doi: 10.1162/jocn.2007.19.9.1498. [Google Scholar] [PubMed] [CrossRef]

33. P. J. LaMontagne et al., “OASIS-3: Longitudinal neuroimaging, clinical, and cognitive dataset for normal aging and Alzheimer disease,” medRxiv, Dec. 2019. doi: 10.1101/2019.12.13.19014902. [Google Scholar] [CrossRef]

34. M. W. Weiner et al., “The Alzheimer’s disease neuroimaging initiative 3: Continued innovation for clinical trial improvement,” Alzheimers Dement, vol. 13, no. 5, pp. 561–571, May 2017. doi: 10.1016/j.jalz.2016.10.006. [Google Scholar] [PubMed] [CrossRef]

35. L. Wang et al., “Volume-based analysis of 6-month-old infant brain MRI for autism biomarker identification and early diagnosis,” in Medical Image Computing and Computer Assisted Intervention–MICCAI 2018, Granada, Spain, Springer, 2018, pp. 411–419. [Google Scholar]

36. G. Li et al., “Measuring the dynamic longitudinal cortex development in infants by reconstruction of temporally consistent cortical surfaces,” NeuroImage, vol. 90, pp. 266–279, Apr. 2014. doi: 10.1016/j.neuroimage.2013.12.038. [Google Scholar] [PubMed] [CrossRef]

37. G. Li et al., “Computational neuroanatomy of baby brains: A review,” NeuroImage, vol. 185, pp. 906–925, Jan. 2019. doi: 10.1016/j.neuroimage.2018.03.042. [Google Scholar] [PubMed] [CrossRef]

38. G. Li, L. Wang, F. Shi, J. H. Gilmore, W. Lin and D. Shen, “Construction of 4D high-definition cortical surface atlases of infants: Methods and applications,” Med. Image Anal., vol. 25, no. 1, pp. 22–36, Oct. 2015. doi: 10.1016/j.media.2015.04.005. [Google Scholar] [PubMed] [CrossRef]