LDAS&ET-AD: Learnable Distillation Attack Strategies and Evolvable Teachers Adversarial Distillation

1  Introduction

In recent years, deep neural networks (DNNs) have become increasingly popular for solving complex real-world problems, including computer vision [1], natural language processing [2], and other fields [3]. However, Szegedy et al. [4] have revealed that DNNs are susceptible to adversarial examples (AEs), which involve imperceptible perturbations on input. These perturbations can easily mislead the prediction model, posing a challenge to the development of DNNs in trust-sensitive fields like autonomous driving [5], facial authentication [6], and healthcare [1].

To combat adversarial attacks, various defense strategies have emerged, including input preprocessing [7–9], adversarial training (AT) [10–13], and certified defense [14–17]. Among them, AT is considered one of the most effective methods for improving the robustness of DNNs. It achieves this by incorporating AEs into the training procedure through a minimax formulation [13]. However, learning directly from AEs is challenging due to the difficult optimization of loss with hard labels [18], hindering improvements in both clean accuracy and adversarial robustness.

Recent studies have shown that knowledge distillation (KD) can enhance AT by providing data-driven soft labels to smooth the hard labels. Adversarial distillation (AD) methods aim to have target models to mimic the outputs or features of either a single adversarially pre-trained teacher [19–21] or both an adversarially pre-trained teacher and a standard pre-trained teacher [22–24]. By utilizing the guidance of these teachers, the target model can learn the ability to identify AEs and clean samples simultaneously. In the aforementioned methods, the target models fully trust teacher models. Zhu et al. [25] noted that the knowledge from static teacher models becomes less reliable over time, as they become progressively less accurate in predicting stronger AEs. To enhance the reliability of guidance received by the target model, Introspective Adversarial Distillation (IAD) was introduced to encourage the target model to partially trust the teacher model and gradually trust itself more. However, the parameters of the teacher models remain constant, hindering the target model from acquiring increasingly reliable knowledge from the teachers.

Additionally, the fixed sample-agnostic and student-egocentric attack strategies used to generate AEs may not be suitable for distillation, limiting the target model’s generalization performance improvement.

To address the reliability reduction of teacher knowledge in KD, the emerging field of learning to teach (L2T) distillation algorithms [26] has made significant progress. Existing L2T distillation techniques involve fine-tuning teachers to enforce similarity between the outputs of teacher and student models on the training set [27–30], maximizing the student model’s generalization ability on a held-out dataset [31–34], and incorporating distillation influence to estimate the impacts of each training sample on the student’s validation performance [35]. By incorporating distillation influence and self-evolution into the teacher’s learning process, Reference [35] prioritized samples likely to enhance the student’s generalization ability, resulting in superior performance when updating the teacher model. However, existing L2T distillation techniques only utilize the clean accuracy of the student model to update the standard teacher, without considering updating the robust teacher to enhance the target model’s robustness.

To solve the issue of limited generalization performance caused by fixed attack strategies, some works [12,36–38] have improved AT by exploiting different attack strategies at different training stages. Reference [12] proposed a novel AT framework by introducing a learnable attack strategy (LAS-AT), which consists of a target network trained with AEs to improve robustness and a strategy network that automatically produces attack strategies based on the target model’s robustness and the given sample. This framework requires less domain expertise. However, directly extending it into the AD framework makes the generated AEs independent of the teacher model and unsuitable for distillation, hindering the closer matching between teacher and target models.

In this paper, an adversarial defense method called Learnable Distillation Attack Strategies and Evolvable Teachers Adversarial Distillation (LDAS&ET-AD) is proposed, which aims to improve the performance of AD by enhancing the quality of AEs and the reliability of teacher knowledge. Our contributions are summarized as follows:

1.    A learnable distillation attack strategies generating mechanism is proposed to automatically generate sample-dependent attack strategies tailored for distillation. A strategy model is introduced to generate attack strategies capable of misleading the target model and creating maximum divergence between the target and teacher models by competing with the target model in minimizing or maximizing the AD loss. AEs are produced by perturbing clean samples in the direction of the gradient of the difference between the target and teacher models, causing a closer match between them.

2.    A teacher evolution strategy is devised to enhance the reliability and effectiveness of knowledge in improving the target mode’s generalization performance on both clean samples and AEs. The adversarial distillation influence, which estimates the impact of distillation from each training sample and AE on the target model’s performance on the validation set and AEs, is introduced to assign loss weights of the training samples and AEs. The standard and robust teachers are fine-tuned on prioritized samples that are likely to enhance the target model’s clean and robust generalization abilities, respectively.

To evaluate the effectiveness of the LDAS&ET-AD method, we construct two typical DNNs, namely ResNet-18 and MobileNet-V2, and test them against various adversarial attacks on the CIFAR-10 and CIFAR-100 datasets. In comparison to state-of-the-art adversarial defense techniques, our method demonstrates robustness enhancements ranging from 0.80% to 1.47% for the CIFAR-10 dataset and 1.43% to 2.11% for the CIFAR-100 dataset when applied to ResNet-18. When implemented on MobileNet-V2, our method showcases improvements ranging from 1.20% to 2.55% for the CIFAR-10 dataset and 1.23% to 2.30% for the CIFAR-100 dataset.

The remainder of the paper is organized as follows: Section 2 reviews related background and recent research. Section 3 describes the proposed LDAS&ET-AD method in detail. Section 4 presents experimental results and comparisons. Section 5 gives discussions. Section 6 concludes the paper and Section 7 provides limitations.

2  Related Work

2.1 Adversarial Attacks and Adversarial Training

Since the identification of DNNs’ vulnerability to adversarial attacks, several effective attack algorithms have been proposed [13,39–41]. These methods can be categorized as white-box attacks and black-box attacks based on the adversary’s knowledge. White-box attacks such as the fast gradient sign method (FGSM) [39], projection gradient descent method (PGD) [13], and Carlini Wagner Attack (CW) [40], have full access to all the parameter information of the attacked model. To comprehensively evaluate the effectiveness of the proposed defense method, we employ PGD [13], FGSM [39], CW [40], and AutoAttack (AA) [41].

To mitigate the threat of adversarial attacks, various defense methods have been proposed [5,10,14]. AT [10–13], which adds adversarial perturbations to the inputs during training, has proven to be one of the most effective approaches for enhancing the DNNs’ adversarial robustness. Madry et al. [13] formulated standard AT (SAT) as a minimax optimization problem, where the inner maximization represents the attack strategy guiding AE generation. Solving the inner maximization problem in SAT is achieved using the PGD attack.

Several studies have proposed methods to improve the performance of SAT. Zhang et al. [10] introduced TRadeoff-inspired Adversarial DEfense via Surrogate-loss minimization (TRADES) to balance adversarial robustness and clean accuracy. Wang et al. [42] further improved performance by Misclassification-Aware Adversarial Training (MART). While these methods employed fixed attack strategies, other studies [12,36–38] demonstrated that employing different attack strategies at different training phases can further improve AT. Cai et al. [36] introduced curriculum adversarial training (CAT), which employs AEs generated by attacks with varying strengths in a curriculum manner. Zhang et al. [37] proposed friendly adversarial training (FAT) that trains a DNN using both wrongly-predicted and correctly-predicted AEs. Wang et al. [38] introduced First-Order Stationary Condition for constrained optimization (FOSC) as a quantitative indicator for assessing AE convergence quality. However, these methods rely on manually designed metrics to evaluate the AE difficulty and still use a single strategy at each stage, thus limiting the robustness improvement and requiring domain expertise. Jia et al. [12] proposed a learnable attack strategy that allows the strategy model to automatically produce sample-dependent attack strategies using a gaming mechanism. However, when directly applied to AD, this method generated the AEs that are independent of the teacher model and not applicable for distillation, thus limiting the closer match between teacher and student models.

To address this limitation and generate sample-dependent attack strategies advantageous to distillation, reference [12] is improved and introduced into the AD framework. This improvement considers the differences in output between the target and teacher models, resulting in a closer match between them.

2.2 Adversarial Distillation

Recently, there has been a growing body of research highlighting the potential for improving AT through the integration of KD. KD offers data-driven soft labels to smooth the hard labels. In Adversarially Robust Distillation (ARD) [19], the target model was encouraged to mimic the softmax output of an adversarially pre-trained teacher model on clean input when facing an adversary. In Robust Soft Label Adversarial Distillation (RSLAD) [21], the generation of AEs and the training of target models were guided by the Robust Soft Labels (RSLs) derived from adversarially pre-trained teachers. Adversarial Knowledge Distillation (AKD) [20] leveraged a linear combination of the AEs’ predictions from the teacher model and the original labels, effectively guiding the student model’s predictions on AE.

However, these methods only utilize the knowledge of adversarially pre-trained teachers to enhance the adversarial robustness of the target model, overlooking considerations related to clean accuracy. Chen et al. [23] imposed the adversarial predictions of the target model to mimic those of standard teachers and robust teachers, hereinafter referred to as self-teacher training (STS). This method notably improves accuracy on both clean samples and AEs, yet it heavily relies on trust in teacher models. IAD [25] highlighted the diminishing reliability of teacher guidance, advocating for a gradual development of confidence in the student model’s adversarial robustness while partially trusting the teacher model. The methods mentioned earlier predominantly focus on distilling logit knowledge from the teacher model. Vanilla Feature Distillation Adversarial Training (VFD-Adv) [22] distilled feature knowledge from the teacher’s intermediate layer, aligning features of clean examples from the teacher model with those from the student model in the feature space. We utilize logit distillation since it requires less computational and storage costs and logits are at a higher semantic level than deep features.

The baseline in our paper is STS presented in [23], and we use the same AD framework. The adversarial robustness and clean accuracy of the target model are simultaneously improved by leveraging the standard and robust teachers to provide clean and robust knowledge, respectively. Recognizing the decreasing reliability of teacher knowledge during training [24], we update the parameters of teacher models by incorporating supervision from the training set and AEs, as well as feedback from the target model’s performances on the validation set and AEs.

2.3 Learning to Teach Distillation

Current AD techniques employ the conventional two-stage offline KD technique, where the teacher model’s parameters remain unchanged during the distillation process. However, this technique cannot guarantee a match between the teacher and student models, especially when there is a significant difference in predictive performance between them. Additionally, two-stage offline KD cannot adjust the knowledge transfer process in real time based on the learning status of the student model. To address these issues, L2T distillation has been proposed [26], which involves training the student model and fine-tuning the teacher model simultaneously, allowing the teacher model to adjust its behavior based on the feedback from the student model.

Online distillation [27–30] is a commonly used L2T algorithm, which involves simultaneously training the student and teacher models and ensuring similarity between their outputs on the training set by minimizing the Kullback-Leibler (KL) divergence between them. However, this only considers the knowledge transfer on the training set without considering the validation performance of the student model. Meta distillation [31–34] addresses this issue by fine-tuning the teacher model to minimize the loss of the updated student on the validation set. However, the teacher model only receives supervision from the student model, which can result in performance degradation.

Recently, Ren et al. [35] proposed a novel L2T distillation framework called Learning Good Teacher Matters (LGTM), which introduced the distillation influence to assign a loss weight to each training sample based on the student model’s performance on the validation set. However, this method does not consider the accuracy of the target model on AEs as feedback to fine-tune the robust teacher.

To improve the reliability and effectiveness of the standard and robust teachers’ knowledge in the generalization ability of the target model on both clean samples and AEs, LGTM [35] is extended and incorporated into the AD framework. We use feedback from the target model on the validation data and AEs to update both standard and robust teachers. Fine-tuning the teachers narrows the capacity gap between the teacher and target models and makes teacher models more adaptable to the stronger AEs, increasing their reliability. Additionally, due to the involvement of teacher knowledge in the AE generation in our method, more reliable teachers can also improve the quality of AEs.

3  Method

3.1 Method Overview

Existing AD techniques employ fixed and sample-agnostic attack strategies that are centered around the target model, which leads to AEs being irrelevant to the teacher models and unsuitable for AD. Besides, static teachers face challenges in accurately predicting stronger AEs generated by the increased robustness of the target model. Distilling unreliable knowledge can hurt the performance of the target model. To enhance the suitability of AEs for distillation and improve the reliability and effectiveness of teachers’ knowledge in promoting the generalization performance of the target model, LDAS&ET-AD is proposed to generate AEs by leveraging a learnable distillation attack strategies generating mechanism that considers prediction differences between the teacher and target models, as well as update teachers by using a teacher evolution strategy that takes into account the performance of the target model on validation set and AEs. The proposed AD framework, depicted in Fig. 1, comprises a target model, a strategy model, and standard and adversarially pre-trained teacher models.

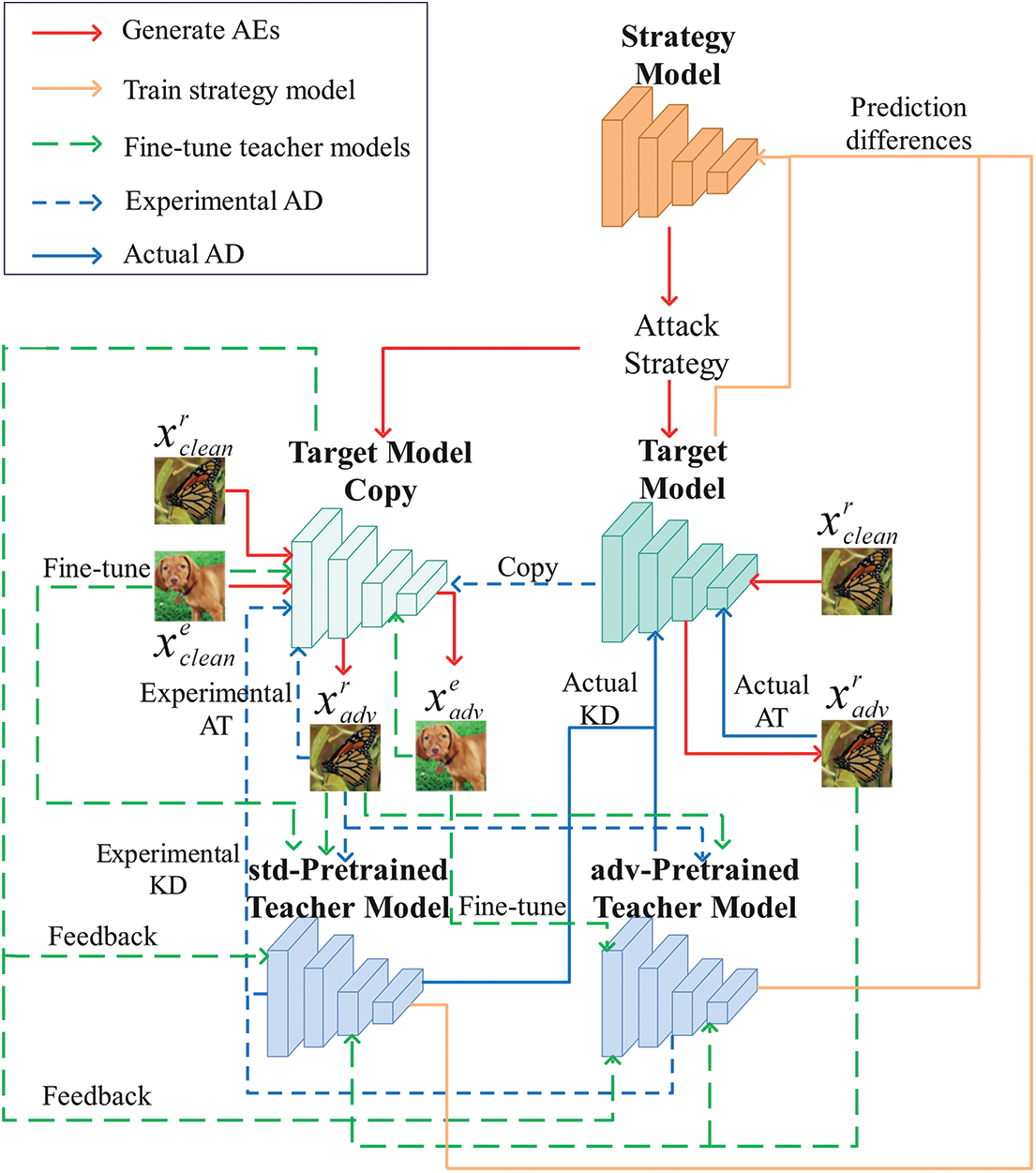
Figure 1: The framework of proposed LDAS&ET-AD. Given a clean training image xcleanri, the strategy model generates an attack strategy a. The target model utilizes a to generate an AE xadvri. The update of the target model consists of experimental updates and actual updates. In each training step, we first obtain a copy of the target model and experimentally update it using the AD loss. Then, we sample xcleane from the validation set and generate AEs xadve, and calculate the losses of the copied model on these samples. The losses provide feedback signals to fine-tune the teachers by calculating adversarial distillation influence. The losses of the teachers on the training set and AEs are also utilized to update teachers. Finally, we discard the copied target model and employ the updated teachers to guide the training of the target model on the same training batches and AEs

The training process consists of two stages: Generating AEs and fine-tuning teachers.

1.    In the stage of generating AEs, the target model and the strategy model compete with each other in minimizing or maximizing the same objective function. The strategy model is trained to automatically generate attack strategies that produce AEs capable of misleading the target model and inducing maximum divergence between the target and teacher models. The target model is trained to defend against AEs generated by the attack strategies while receiving guidance from both standard and adversarially pre-trained teachers to minimize the prediction distance with them.

2.    In the stage of fine-tuning teachers, a temporary copy of the target model first performs experimental AD and provides feedback for fine-tuning teachers based on its accuracy on the validation set and AEs. The standard and adversarially pre-trained teachers are then fine-tuned based on their performances on the training set and AEs, respectively, as well as the feedback provided by the temporary copy of the target model. Finally, the parameters of the target model are actually updated under the guidance of fine-tuned teachers’ knowledge.

In the subsequent section, we provide a detailed description of the learnable distillation attack strategies generating mechanism that considers prediction differences, as well as the teacher evolution strategy that takes into account the validation performance of the target model. The equation symbols and abbreviations used throughout this paper are summarized in Tables 1 and 2, respectively.

3.2 Learnable Distillation Attack Strategies Generating Mechanism Considering Prediction Differen- ces between Teacher and Target Models

An attack strategy is determined by the values chosen for attack parameters, such as the maximal perturbation strength ε, attack step size α, and attack iteration I. These parameters play a crucial role in the inner optimization problem of AT, significantly impacting performance. Given a clean image xcleani and its ground truth (GT) label ycleani, the generation of AE xadvi using an attack strategy a at the mth training step can be defined as follows:

xadvi=xcleani+δ=g(xcleani,a,θtarm)(1)

where δ represents the adversarial perturbation, θtarm is the parameters of the target model at the mth training step, g(⋅) denotes the PGD attack employed in our method following [13]. Concretely, PGD recursively searches:

xadvi(n+1)=∏ℬε[xadvi(0)]xadvi(n+1)+α⋅sign(∇xadvi(n)L(fθtarm(xadvi(n)),ycleani))(2)

until a stopping criterion is met. xadvi(n) are the AEs at step n, and ∏ℬε[xadvi(0)](⋅) is the projection function that projects the AEs back into the ε-ball centered at xadvi(0), L(fθtarm(xadvi(n)),ycleani) is the cross-entropy (CE) loss between fθtarm(xadvi(n)) and ycleani. For simplicity, we annotate ∂f/∂v as ∇v.

Current AD techniques still rely on fixed sample-agnostic and student-egocentric attack strategies, where the attack parameters are artificially set and remain unchanged during training. The loss function for current AD at the mth training step can be expressed as:

minθtarm⁡E(xcleanr,ycleanr)∼Dtrain[maxδ=(xadvr−xcleanr)∈Ω𝒫⁡(1−λstd−λadv)⋅L(fθtarm(xadvr),ycleanr)+λstd⋅KL(fθtarm(xadvr),fθstd−T(xadvr))+λadv⋅KL(fθtarm(xadvr),fθadv−T(xadvr))](3)

where fθtarm(⋅) denotes the target model at the mth training step, fθstd−T(⋅) and fθadv−T(⋅) represent the static standard and adversarially pre-trained teachers, respectively. Dtrain denotes the distribution of the clean training examples xcleanr and their GT labels ycleanr. Ω𝒫 represents a bound defined as Ω𝒫={δ:||δ||𝒫≤ε}. xadvr are the AEs of xcleanr. L(fθtarm(xadvr),ycleanr) represents the CE loss of the target model between fθtarm(xadvr) and ycleanr. KL(fθtarm(xadvr),fθstd−T(xadvr)) and KL(fθtarm(xadvr),fθadv−T(xadvr)) are the KL divergence between fθtarm(xadvr) and fθstd−T(xadvr) and between fθtarm(xadvr) and fθadv−T(xadvr). λstd and λadv are hyperparameters that control the guidance ratio of the standard and robust teachers, respectively. The target model is trained to minimize both the AT loss and the prediction distance with standard and adversarial pre-trained teachers on AEs. The process of AE generation in existing AD methods is illustrated in Fig. 2a, which results in AEs unsuitable for distillation, limiting the closeness between the teacher and target models.

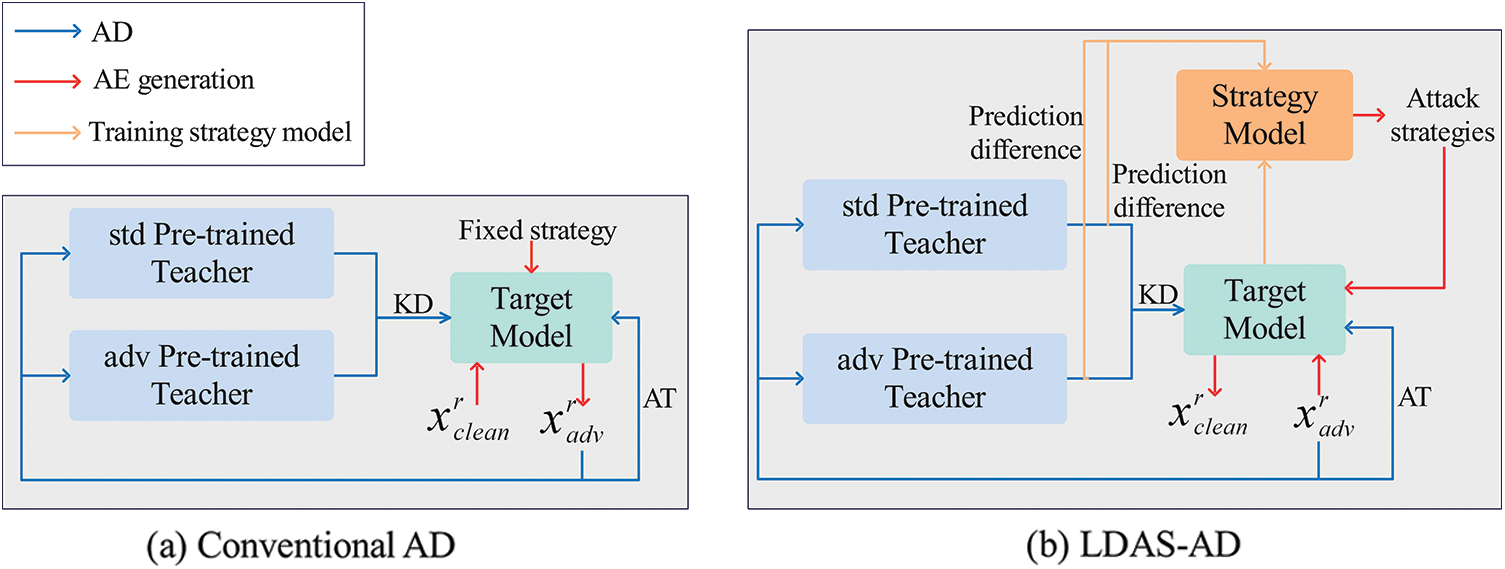
Figure 2: Comparison of the attack strategies of vanilla AD and our LDAS&ET-AD

3.2.1 The AD Loss of Target Model

To enhance the suitability of AEs for distillation, a learnable distillation attack strategies generating mechanism that takes into account the prediction disparities between the teacher and target models is introduced into the AD framework. A strategy model is utilized to automatically produce sample-dependent attack strategies by competing with the target model in minimizing or maximizing the AD loss. Consequently, the generated AEs not only mislead the target model but also maximize the difference in predictions between the target and teacher models. In this worst-case scenario of AD, updating the parameters of the target model towards correctly classifying and minimizing the difference makes the AEs more suitable for distillation and brings the target and teacher models closer together. The attack strategies are based on the given samples xcleani, where the attack parameters are related to the strategy model’s parameters θstra and the samples a∼p(a|xcleani;θstra). The loss function of AD with a learnable distillation attack strategies generating mechanism can be written as follows:

minθtarm⁡E(xcleanr,ycleanr)∼Dtrain[maxθstra⁡Ea∼p(a|xcleanr;θstra)(1−λstd−λadv)⋅L(fθtarm(xadvr),ycleanr)+λstd⋅KL(fθtarm(xadvr),fθstd−T(xadvr))+λadv⋅KL(fθtarm(xadvr),fθadv−T(xadvr))](4)

3.2.2 The Evaluating Loss of Strategy Model

The evaluation metric proposed in [12] serves as a guiding principle for the training of the strategy model in our approach. First, an attack strategy a is employed to create AEs and then the target model is updated based on these samples using first-order gradient descent for one step, as described in Eq. (4). If the updated target model can effectively defend against the AEs generated by another attack strategy a^, a can be considered effective. The evaluation metric of robustness can be defined as follows:

L2(θstra)=−L(fθtarm+1(x^advr),ycleanr)(5)

where x^advr=g(xcleanr,a^,θtarm+1) presents the AEs generated by another attack strategy a^, which is used to evaluate the robustness of the one-step updated target model fθtarm+1.

Furthermore, an effective attack strategy should ensure good performance in predicting clean samples. Thus, we also consider the performance of the one-step updated target model in predicting clean samples for training the strategy model. The evaluation metric of clean accuracy can be defined as follows:

L3(θstra)=−L(fθtarm+1(xcleanr),ycleanr)(6)

3.2.3 The AD Process with Learnable Distillation Attack Strategies

During the initial training stage, the target model is susceptible to attacks and there are significant differences in predictions between the target and pre-trained teacher models. Therefore, effective attack strategies can be easily generated by the strategy model. As the training process progresses, the target model becomes more robust, and the prediction differences decrease. Consequently, the strategy model needs to learn how to generate attack strategies that can produce stronger AEs.

The game formulation between the target and teacher models can be defined as follows:

minθtarmE(xcleanr,ycleanr)∼Dtrain[maxθstraEa∼p(a|xcleanr;θstra)L1(θstra,θtarm,θstd−T,θadv−T)+αL2L2(θstra)+αL3L3(θstra)](7)

where L1(θstra,θtarm,θstd−T,θadv−T)=(1−λstd−λadv)⋅L(fθtarm(xadvr),ycleanr)+λstd⋅KL(fθtarm(xadvr),fθstd−T(xadvr))+λadv KL(fθtarm(xadvr),fθadv−T(xadvr)) is a function of the parameters of the target model, strategy model, and two teacher models. L2 and L3 involve the parameters of the strategy model. αL2 and αL3 are the trade-off hyperparameters of the two loss terms. The target model and strategy model are alternatively optimized using the REINFORCE algorithm [12]. The alternative update is controlled by a hyperparameter k, where we update θtar every k times of updating θstra. Fig. 2b illustrates the generation process of AEs in our proposed LDAS&ET-AD.

3.3 Teacher Evolution Strategy Considering the Validation Performance of the Target Model

As the robustness of the target model increases and AEs become stronger, the reliability of static teachers’ knowledge diminishes. This unreliable guidance not only negatively impacts the performance of the target model, but also affects the quality of AEs that rely on the knowledge of teacher models. To enhance the reliability and effectiveness of teachers’ knowledge in promoting the generalization performance of the target model, a teacher evolution strategy is introduced in our AD framework. This strategy takes into consideration the validation performance of the target model. The feedback for fine-tuning teachers is determined by the adversarial distillation influence, which extends the distillation influence proposed in [35].

3.3.1 Adversarial Distillation Influence

To ensure both clean accuracy and adversarial robustness of the target model, it is necessary to update both standard and adversarially pre-trained teachers. Therefore, we expand the distillation influence and difference approximation method [35], which does not consider adversarial robustness. The adversarial distillation influence measures the change in clean accuracy and adversarial robustness of the target model on validation data and AEs when the AE of a training sample is included in the AD process. Specifically, the adversarial distillation influence of the standard teacher is determined by calculating the similarity of gradients between the AE of the training sample zadvri=(xadvri,ycleanri) before updating the target model parameters and the validation batch zcleane=(xcleane,ycleane) after updating (Eq. (8)). The adversarial distillation influence of the robust teacher is obtained by calculating the similarity of gradients between the AE of the training sample zadvri before updating and the AE of the validation batch zadve=(xadve,ycleane) after updating (Eq. (9)).

Istd_adi(zadvri,zcleane)=∇θtarmKL(fθstd−Tm(xadvri),fθtarm(xadvri))T∇θtarmL(ycleane,fθtarm+1(xcleane))(8)

Iadv_adi(zadvri,zadve)=∇θtarmKL(fθadv−Tm(xadvri),fθtarm(xadvri))T∇θtarmL(ye,fθtarm+1(xadve))(9)

where θtarm and θtarm+1 are the parameters of the target model before and after the update, respectively. θstd−Tm and θadv−Tm are the parameters of the standard and robust teachers before fine-tuning.

3.3.2 The Fine-Tuning Loss of Teacher Models

The adversarial distillation influence highlights the importance of each training sample’s AE in improving the target model’s generalization performance. Therefore, we consider it as feedback from the target model’s performance on the verification set and use it to assign a weight to each AE for fine-tuning the teacher models. This fine-tuning process enhances the teachers’ teaching abilities. The weighted fine-tuning losses can be defined as Eq. (10) for the standard teacher and Eq. (11) for the robust teacher:

Lstd−adi=1Br∑i=1Brwstdi⋅KL(fθstd−Tm(xadvri),fθtarm(xadvri))(10)

Ladv−adi=1Br∑i=1BrwadviKL(fθadv−Tm(xadvri),fθtarm(xadvri))(11)

where Br is the batch size of a training batch, wstdi=Istd−adi(zadvri,zcleane) and wadvi=Iadv−adi(zadvri,zadve). And we approximate them by:

Lstd−adi≈L∼std−adi=1Br⋅[∑i=1Br(KL(fθstd−Tm(xadvri),fθtarms+(xadvri))/2γ)−(KL(fθstd−Tm(xadvri),fθtarms−(xadvri))/2γ)](12)

Ladv−adi≈L∼adv−adi=1Br⋅[∑i=1Br(KL(fθstd−Tm(xadvri),fθtarma+(xadvri))/2γ)−(KL(fθstd−Tm(xadvri),fθtarma−(xadvri))/2γ)](13)

where θtarms±=θtarm±γ⋅L(ycleane,fθtarm+1(xcleane)), θtarma±=θtarm±γ⋅L(ycleane,fθtarm+1(xadve)) and γ is a small scalar.

In addition to improving teaching abilities, teacher models should also focus on minimizing CE loss related to GT labels (clean accuracy for the standard teacher and adversarial robustness for the robust teacher). This is crucial for optimizing their reasoning performance. The overall losses for fine-tuning the standard teacher and robust teacher can be defined as Eqs. (14) and (15), respectively.

Lstd−tea=L~std−adi+Lstd−auxLstd−aux=αstd⋅L(ycleanr,fθstd−Tm(xcleanr))+(1−αstd)⋅KL(fθstd−Tm(xadvr),fθtarm(xadvr))(14)

Ladv−tea=L~adv−adi+Ladv−auxLadv−aux=αadv⋅L(ycleanr,fθadv−Tm(xadvr))+(1−αadv)⋅KL(fθadv−Tm(xadvr),fθtarm(xadvr))(15)

where the hyperparameters αstd and αadv control the self-evolution of standard teacher and robust teacher, respectively.

3.3.3 The Fine-Tuning Process

To obtain adversarial distillation influence involving gradients before and after updating the target model parameters, an experimental update mechanism is introduced as shown in Fig. 3a. First, a temporary copy of the current target model fθtarm is created. This copy is then experimentally updated by applying the AD loss on the AEs generated using the learnable distillation attack strategies generating mechanism, as proposed in Section 3.2. The losses of the updated copy fθtarm+1 on the validation set and their AEs are calculated to obtain the adversarial distillation influence.

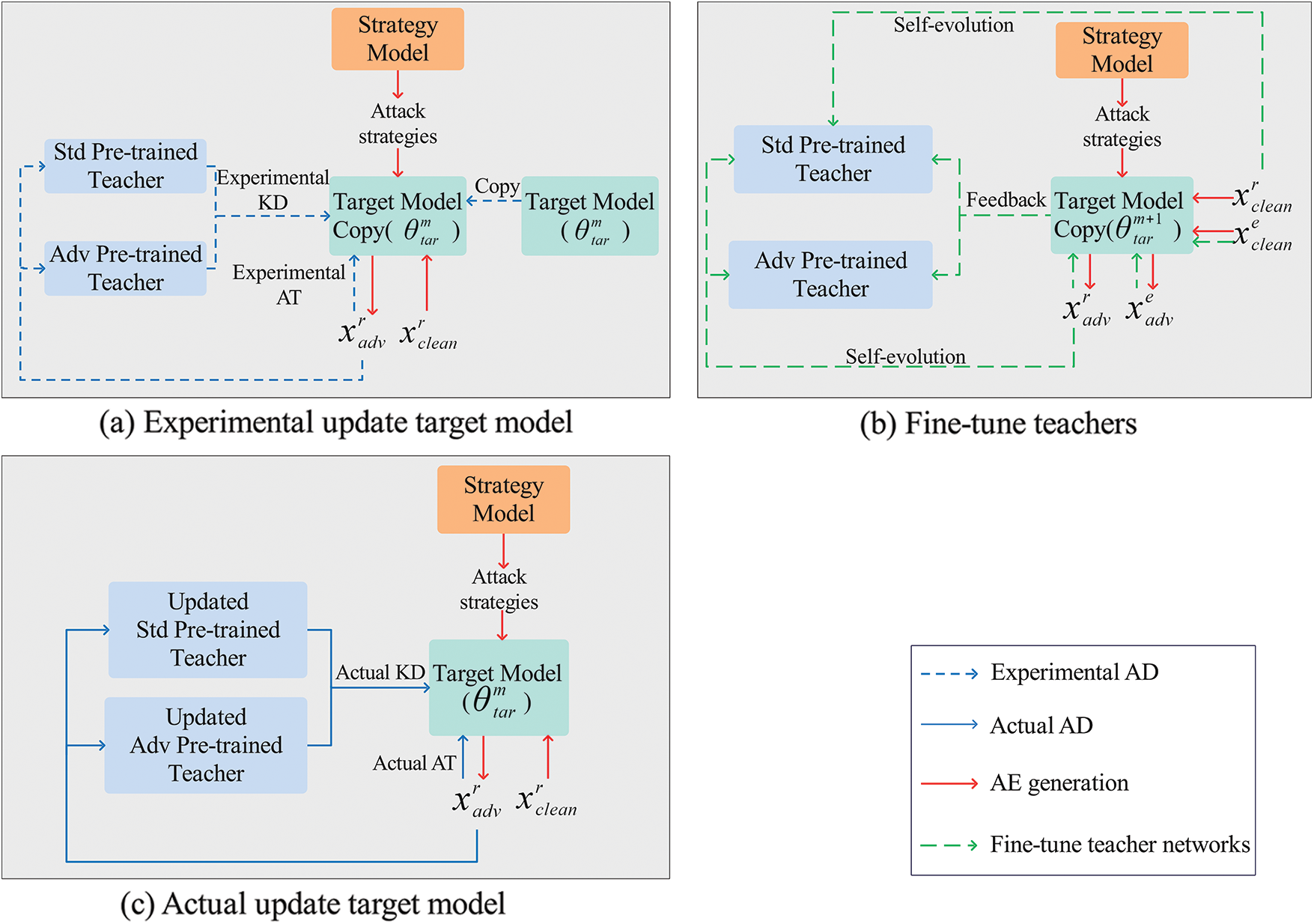
Figure 3: The workflow of teacher evolution strategy in our LDAS&ET-AD

The adversarial distillation influence serves as feedback from the target model on the validation set for fine-tuning the teachers fθstd−Tm and fθadv−Tm to improve their teaching abilities. Their training performance is also taken into account to achieve self-evolution as described in Fig. 3b.

After fine-tuning the teachers, the real target model fθtarm is actually updated through the AD of the fine-tuned teachers fθstd−Tm+1 and fθadv−Tm+1 by Eq. (7), as depicted in Fig. 3c. The entire process of our LDAS&ET-AD is presented in Algorithm 1.

4  Experiments

4.1 Experiment Setup

4.1.1 Datasets and Competitive Methods

We conducted experiments on various benchmark datasets, including CIFAR-10 and CIFAR-100 [43]. All models were implemented in PyTorch and trained on a single RTX 2080 Ti GPU. We compared our LDAS&ET-AD with baseline STS [23]. Besides, standard training (ST) method and four state-of-the-art adversarial defense methods (SAT [13], TRADES [10], LAS-AT [12], and IAD [25]) were considered for comparison.

4.1.2 Student, Teacher, and Strategy Models

We considered ResNet-18 [44] and MobileNet-V2 [45] as the target models. Their structures are described in Table 3. The pre-trained models with the same architectures were utilized as self-teachers, following previous work [23]. One model could be trained using either AT or ST way, resulting in two self-teachers: Adversarial and standard pre-trained self-teachers. The models with the same architectures were chosen as the strategy models.

4.1.3 Training Settings

We trained the target models and the pre-trained teachers using the Stochastic Gradient Descent (SGD) optimizer with a momentum of 0.9 and weight decay 5e-4. The training process consisted of 200 epochs with a batch size of 128. The learning rate started from 0.1 for ResNet-18 and 0.01 for MobileNet-V2 and decayed to one-tenth at epochs 50 and 150, respectively. The strategy model in our method employed an SGD momentum optimizer with a learning rate of 0.001 for ResNet-18 and 0.0001 for MobileNet-V2. The pre-trained teachers were fine-tuned using an SGD momentum optimizer with a learning rate of 0.01. For ST, we trained the models for 100 epochs on clean images with standard data augmentations. The learning rate was divided by 10 at the 75th and 90th epochs. We strictly followed the original settings of SAT [13], TRADES [10], and LAS-AT [12]. For STS [23] and IAD [25], we used the same self-teachers as our LDAS&ET-AD. A 10-step PGD (PGD-10) with a random start size of 0.001, step size 2/255 was employed to solve the inner maximization.

In our method, we actually updated the target model every k= 30 times updating the strategy model. The hyperparameters αstd and αadv related to the balance between self-evolution and knowledge transfer were set to 0.8 and 0.7, respectively. The trade-off hyperparameters αL2 and αL3 were set to 2.0 and 4.0. These selections were based on the results of ablation studies in Section 5. The selection of the hyperparameters of attack strategies was followed by [12]. Specifically, the maximum perturbation strength ranged from 3 to 15, the attack step ranged from 1 to 6, and the attack iteration ranged from 3 to 15. We set λSTS1 to 0.25 and λSTS2 to 0.5, as recommended in [23].

4.1.4 Evaluation Attacks

After training, we evaluated the models against four commonly used adversarial attacks: FGSM [39], PGD [13], CW∞ [40], and AA [41]. The maximum perturbation allowed for evaluation was set to 8/255 for both datasets. The perturbation steps for PGD and CW∞ were both set to 20. We calculated the natural accuracy (‘Natural’ in Tables) on the natural test data and the robust accuracy on the adversarial test data generated by FGSM, PGD, CW∞, and AA attacks, following [24].

4.2 Adversarial Robustness Evaluation

In accordance with previous studies [24], we reported the test accuracy at both the best checkpoint and the last checkpoint. The best checkpoint of ST is chosen based on its performance on clean test examples, while the best checkpoints of SAT [13], TRADES [10], LAS-AT [12], STS [23], IAD [25], and our LDAS&ET-AD are selected based on their robustness against the PGD attack.

4.2.1 Comparison with Baseline

The test accuracy of our LDAS&ET-AD and the baseline STS [23] are presented in Table 4 for CIFAR-10 and Table 5 for CIFAR-100.

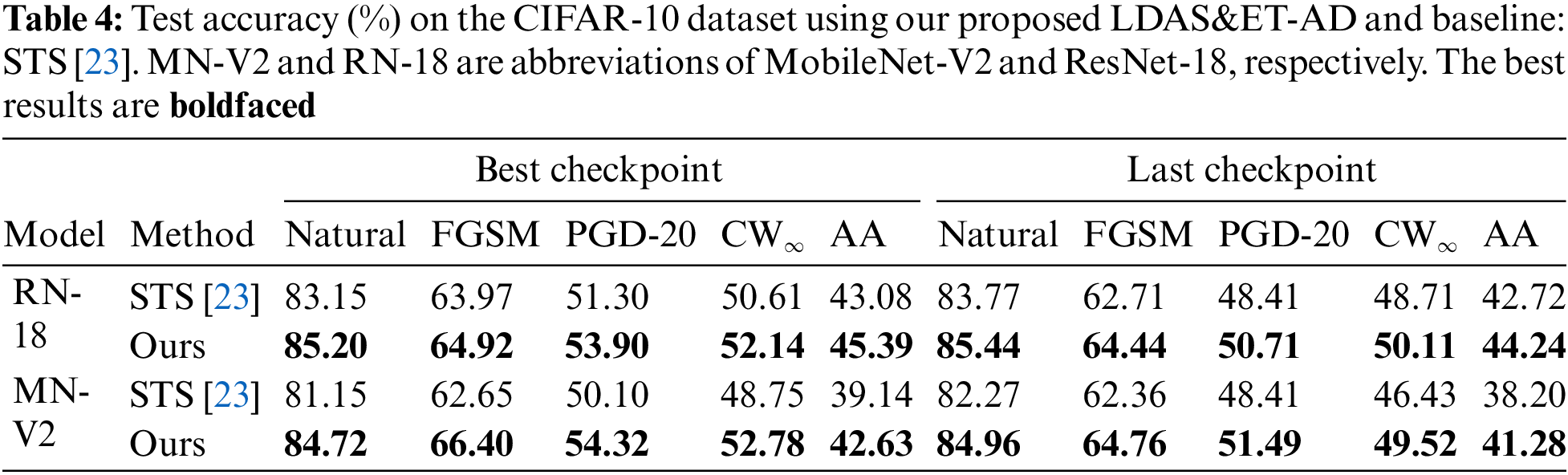
Our LDAS&ET-AD builds upon the AD framework proposed in [23] which applies a robust teacher and a clean teacher to guide robustness and clean accuracy simultaneously. We have made improvements in two aspects: AE generation and teacher knowledge.

Firstly, instead of using hand-crafted strategies, sample-dependent attack strategies are automatically generated by the strategy network, which takes into account the prediction distance between target and teacher models. This results in more suitable AEs for AD and a closer match of target and teacher models. Secondly, the model parameters of the teachers are fine-tuned based on the validation performance of the target model, rather than being static, making teacher knowledge more helpful in improving the generalization performance of the target model and the quality of AEs involving teacher knowledge.

As shown in Tables 4 and 5, our LDAS&ET-AD outperforms the baseline on both CIFAR-10 and CIFAR-100 datasets, at either the best or the last checkpoints. Specifically, for ResNet-18, LDAS&ET-AD improves accuracy by 2.05%, 0.95%, 2.60%, 1.53%, and 2.31% under clean, FGSM, PGD-20, CW∞, and AA attacks on CIFAR-10 dataset, and by 2.39%, 3.42%, 3.69%, 4.27%, and 3.98% on CIFAR-100 dataset compared to benchmark results. For MobileNet-V2, LDAS&ET-AD brings 3.57%, 3.75%, 4.22%, 4.03%, and 3.49% improvements on CIFAR-10 dataset and 2.59%, 3.01%, 2.33%, 3.32%, and 3.33% improvements on CIFAR-100 dataset.

In conclusion, our LDAS&ET-AD consistently improves clean and adversarial accuracy on two commonly used datasets against four attacks when applied to two target models compared to the baseline. This indicates the effectiveness of (I) considering the prediction differences of teacher and target models in the generation of sample-dependent AEs, and (II) fine-tuning the teacher models based on the accuracy of the target model on the validation set and AEs in improving AD.

4.2.2 Comparison with State-of-the-Art Adversarial Defense Methods

We present the test results of our LDAS&ET-AD framework applied to ResNet-18 and MobileNet-V2 target models in comparison to state-of-the-art adversarial defense methods on CIFAR-10 and CIFAR-100 datasets in Tables 6 and 7, respectively.

As shown in the tables, LAS-AT [12], an AT framework incorporating learnable attack strategies, outperforms SAT [13] and TRADES [10] in terms of adversarial robustness due to the automatic generation of sample-dependent attack strategies. IAD [25] solve the problem of reduced reliability of teacher guidance in AD is alleviated by partially instead of fully trusting the teacher model. These observations highlight the effectiveness of KD, learnable attack strategies, and reliable teachers in enhancing AT on both CIFAR-10 and CIFAR-100 datasets. Our LDAS&ET-AD introduces a learnable distillation attack strategies generating mechanism and a teacher evolution strategy into the AD framework to integrate their benefits of them.

Compared to state-of-the-art AT methods (SAT [13], TRADES [10], and LAS-AT [12]), our proposed method introduces the AD of evolvable teachers, which can provide more reliable soft labels to better smooth hard labels in AT. In addition, maximizing the prediction distance between teacher and target models is introduced to automatically generate attack strategies by the strategy model, making AEs more suitable for distillation and leading to a closer match between the teacher and target models. The results in Tables 6 and 7 demonstrate superior clean accuracy and robustness against four different attacks on both CIFAR-10 and CIFAR-100 datasets. Specifically, for ResNet-18, our LDAS&ET-AD outperforms the best AT method with improvements of 1.24%, 0.80%, 1.28%, 1.47%, and 2.61% in clean, PGD-20, CW∞, and AA accuracy on CIFAR-10 dataset, and 3.52%, 2.04%, 1.52%, 2.55%, and 1.20% on CIFAR-100 dataset. For MobileNet-V2, our proposed method improves accuracy by 2.38%, 1.58%, 1.86%, 2.11%, and 2.18% on CIFAR-10 dataset, and 2.20%, 1.98%, 1.46%, 2.30%, and 4.36% on CIFAR-100 dataset.

IAD [25] encourages the target model to partially trust the teacher models and gradually trust itself more as the teacher models become progressively unreliable. The teacher knowledge in our proposed method has a more significant effect on improving the generalization performance of the target model since the teacher models in our method are updated based on the validation performance of the target model. Besides, the generation of sample-dependent attack strategies that consider teacher knowledge enhances the quality of AEs. The results highlight the superior performance of our LDAS&ET-AD on both CIFAR-10 and CIFAR-100 datasets. Specifically, our LDAS&ET-AD improves the accuracy of ResNet-18 by 1.80%, 0.97%, 2.58%, 1.82%, and 1.40% in terms of clean, FGSM, PGD-20, CW∞, and AA accuracy on CIFAR-10 dataset, and 3.95%, 3.54%, 3.50%, 4.10%, and 3.46% on CIFAR-100 dataset. For MobileNet-V2, our LDAS&ET-AD shows improvements of 4.23%, 3.70%, 3.57%, 3.83%, and 1.43% on CIFAR-10 dataset, and 3.31%, 3.02%, 1.91%, 3.23%, and 1.23% on CIFAR-100 dataset.

Overall, our LDAS&ET-AD surpasses state-of-the-art adversarial defense methods against various attacks using different models due to the more reliable teachers and more suitable AEs for distillation by introducing the learnable distillation attack strategies generating mechanism that considers prediction differences between the teacher and target models, as well as the teacher evolution strategy that takes into account the validation performance of target model in the AD framework.

5  Analysis and Discussion

To comprehensively understand our LDAS&ET-AD, we conducted a series of experiments on the CIFAR-10 dataset. These experiments encompassed ablation studies of each component, utilization of diverse dynamic attack strategies generating methods, adoption of distinct teacher fine-tuning methods based on L2T distillation, exploration of different k concerning the optimized frequency of the strategy model, examination of different αstd and αadv associated with the self-evolution of the teachers, and investigation of different αL2 and αL3 related to the trade-off between robustness and clean accuracy. Subsequently, we delve into the training and inference complexity of our LDAS&ET-AD. The ResNet-18 model was selected as the backbone model.

5.1 Ablation of LDAS&ET-AD

We conducted a set of ablation studies to better grasp the impact of each component in our LDAS&ET-AD.

Firstly, the learnable distillation attack strategies generating mechanism in our LDAS&ET-AD was replaced with the fixed distillation attack strategy in STS [23] considering prediction differences between student and teacher, denoted as Fixed Distillation Attack Strategy and Evolvable Teachers Adversarial Distillation (FDAS&ET-AD), to verify the effectiveness of the introduction of learnable attack strategies. Besides, this mechanism was replaced with the learnable attack strategies in LAS-AT [12], denoted as Learnable Attack Strategy and Evolvable Teachers Adversarial Distillation (LAS&ET-AD), to demonstrate the importance of the consideration of the prediction differences.

Secondly, we fine-tuned the model parameters of one, denoted as Learnable Distillation Attack Strategies and Evolvable Robust Teachers Adversarial Distillation (LDAS&ERoT-AD) and Learnable Distillation Attack Strategies and Evolvable Standard Teachers Adversarial Distillation (LDAS&EStT-AD), or none, denoted as Learnable Distillation Attack Strategies Adversarial Distillation (LDAS-AD), of the two pre-trained teachers in our LDAS&ET-AD. The purpose was to illustrate the different effects of each teacher’s update on performance improvement. Subsequently, the test clean and adversarial accuracy of the trained target models were evaluated. The results of the ablation studies are presented in Table 8.

As shown in Table 8, our LDAS&ET-AD outperforms all five variants against all four attacks. Firstly, our LDAS&ET-AD automatically generates sample-dependent and increasingly stronger attack strategies, enabling the creation of AEs that can adapt to more robust target models. Consequently, our LDAS&ET-AD outperforms FDAS&ET-AD, resulting in improvements of 1.81%, 0.67%, 2.27%, 0.96%, and 2.18% in clean, FGSM, PGD-20, CW∞, and AA accuracy, respectively. Furthermore, by incorporating prediction differences into the learnable attack strategies, AEs are not only able to mislead the target model but also maximize the prediction discrepancy between the target and teacher models, achieving a closer match between them. Therefore, our LDAS&ET-AD outperforms LAS&ET-AD in terms of clean, FGSM, PGD-20, CW∞, and AA accuracy by 1.01%, 0.29%, 1.80%, 0.06%, and 1.11%, respectively. These findings highlight the superiority of introducing the learnable attack strategies and prediction differences into the AD framework due to the generation of AEs that are more suitable for AD and a closer match between the teacher and target models.

Secondly, fine-tuning only the adversarially pre-trained teacher in LDAS&ERoT-AD ensures the reliability and effectiveness of adversarial knowledge which aims to guide the target model in accurately classifying AEs. Therefore, LDAS&ERoT-AD outperforms LDAS-AD solely in terms of adversarial robustness. LDAS&EStT-AD, on the other hand, only updates the standard pre-trained teacher to enhance the quality of clean knowledge, which is designed to specifically enhance the clean accuracy of the target model. LDAS&EStT-AD achieves higher accuracy on clean samples compared to LDAS-AD. Our LDAS&ET-AD, which fine-tunes both teacher models, shows improved clean, FGSM, PGD-20, CW∞, and AA accuracy by 0.71%, 0.21%, 0.39%, 0.31%, and 0.86%, respectively, compared to the methods that either do not update or only update one teacher. The experimental results indicate that fine-tuning both robust and standard teachers has positive effects on improving both clean accuracy and adversarial robustness of the target model, highlighting the potential of evolvable standard and robust teachers.

5.2 Comparison of Different Dynamic Attack Strategies Generating Methods

To verify the superiority of the learnable distillation attack strategies generating mechanism in our LDAS&ET-AD over other dynamic hand-crafted attack strategies generating methods, we replaced it with CAT [36], FOCS [38], and FAT [37] and considered prediction differences, denoted as Curriculum Distillation Attack Strategy and Evolvable Teachers Adversarial Distillation (CDAS&ET-AD), First-Order Stationary Condition Distillation Attack Strategy and Evolvable Teachers Adversarial Distillation (FOCSDAS&ET-AD), and Friendly Distillation Attack Strategy and Evolvable Teachers Adversarial Distillation (FriDAS&ET-AD), respectively. The results are shown in Table 9.

The obtained results demonstrate that the learnable distillation attack strategies generating mechanism in our LDAS&ET-AD outperforms all three variants. This improvement can be attributed to the AEs being more suitable for AD of the increasingly robust target model. Specifically, compared to the best variant, our LDAS&ET-AD achieves higher accuracy in clean, FGSM, PGD-20, CW∞, and AA attacks by 0.96%, 0.32%, 1.04%, 0.23%, and 1.14%, respectively. These findings emphasize the advantages of introducing learnable attack strategies in the proposed LDAS&ET-AD method for generating AEs suitable for AD when compared to other dynamic hand-crafted attack strategy methods.

5.3 Comparison of Different Teacher Fine-Tuning Methods Based on L2T Distillation

To assess the superiority of the teacher fine-tuning strategy in our LDAS&ET-AD over other teacher fine-tuning methods based on L2T distillation, we replace it with (1) meta distillation [31], which considers feedback from the target model on the validation set while all training samples equally and solely receiving supervision from the target model, referred to as Learnable Distillation Attack Strategy and Mate Adversarial Distillation (LDAS&meta-AD) and (2) online distillation [27], which enforces similarity between the outputs of the target and teacher models on the training set without considering the target model’s performance on the validation set, denoted as Learnable Distillation Attack Strategy and Online Adversarial Distillation (LDAS&OL-AD). The results are presented in Table 10.

Table 10 demonstrates that our LDAS&ET-AD outperforms all two variants, achieving the highest test accuracy on both clean samples and AEs. Our LDAS&ET-AD uses the target model’s performance on the verification set as feedback to assign the loss weight of each training sample for fine-tuning of teacher models, enhancing the effectiveness of the teachers’ knowledge in the generalization ability of the target model on both clean samples and AEs. This improvement is achieved by introducing adversarial distillation influence. Additionally, the training of teacher models is also supervised by the AEs of the training set, improving the reliability of their knowledge. Our LDAS&ET-AD demonstrates significant improvements compared to the best variant, achieving enhancements of 0.96%, 0.32%, 1.04%, 0.23%, and 1.14% on clean, FGSM, PGD-20, CW∞, and AA accuracy, respectively. These results validate the effectiveness of the teacher fine-tuning teacher strategy in our proposed LDAS&ET-AD, surpassing other teacher fine-tuning methods.

5.4 Comparison of Different k Values

The hyperparameter k controls the alternating update of θtar and θstra. Every k times θtar are updated, θstra are updated once. It affects not only performance but also training efficiency. Firstly, the efficiency of the proposed method decreases with the increase of k. Smaller k results in more frequent updates of θstra, thus requiring more training time. Secondly, selecting an appropriate k is crucial for the adversarial robustness of the target model. If k is too small, the target model’s discrimination ability towards attack strategies generated by the strategy model may be impaired. This, in turn, affects the diversity of attack strategies and the update stability of the teacher models. On the other hand, if k is excessively large, the generation ability of the strategy model may be compromised, resulting in insufficiently effective AEs for updating the teacher and target models. To determine the optimal k, we conducted experiments on hyperparameter selection. The performance results are depicted in Fig. 4, and the efficiency results are listed in Table 11.

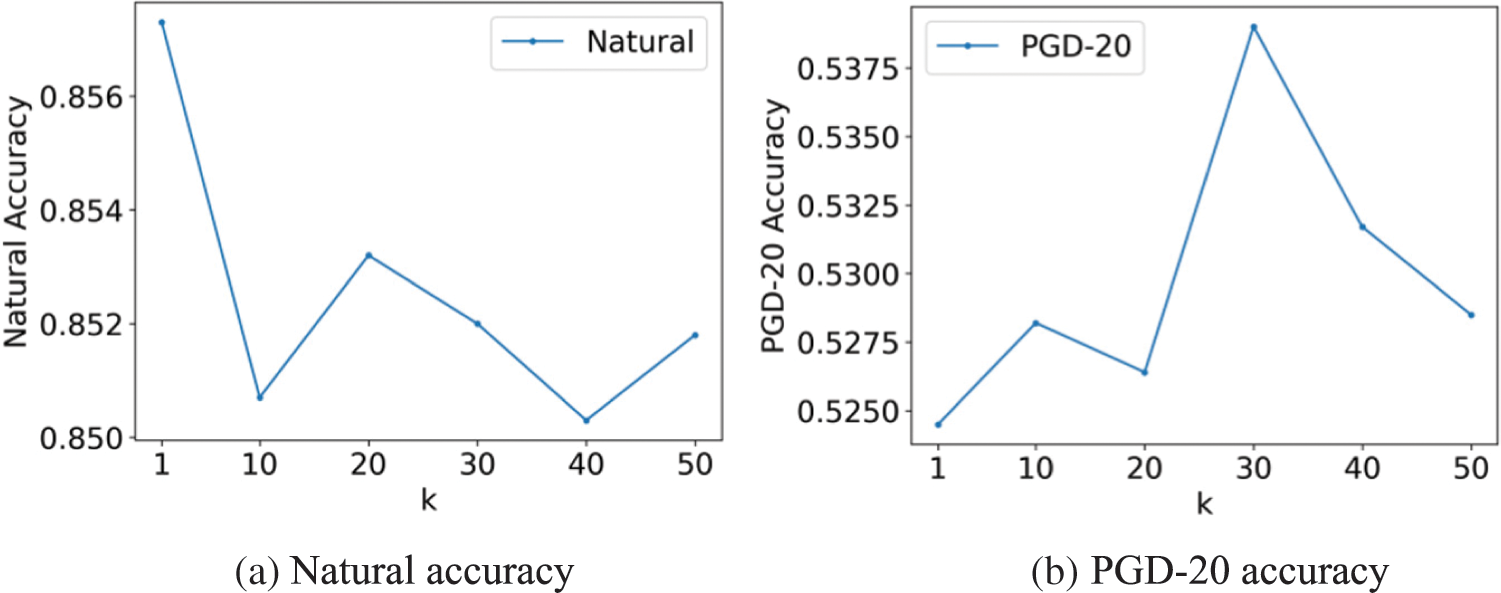
Figure 4: The accuracy on the CIFAR-10 dataset with the ResNet-18 target model trained using our LDAS&ET-AD about different values of k

Fig. 4 shows how the selection of k impacts the clean and PGD-20 accuracy of the target model and there is a trade-off between these two metrics. Specifically, when k is too small, the target model exhibits poor discrimination ability against attack strategies generated by the frequently updated strategy model. Consequently, the diversity of attack strategies diminishes, leading to low-quality AEs, lower adversarial robustness, and higher clean accuracy of the target model. Conversely, when k is too large, the attack strategies generated by the strategy model with low generation ability become approximately fixed, preventing the target model from achieving optimal adversarial robustness. The results in Fig. 4 indicate that the proposed LDAS&ET-AD achieves the best adversarial robustness when k is set to 30.

Table 11 demonstrates that the training time of the proposed LDAS&ET-AD decreases with the increase of k. As k increases, the update frequency of the strategy model decreases, resulting in a decrease in the overall training time.

Considering both efficiency and adversarial robustness, we set k to 30.

5.5 Comparison of Different αstd and αadv Values

The hyperparameters αstd and αadv play vital roles in controlling the self-evolution of standard and robust teachers and impact the guidance quality for classifying clean samples and AEs. Specifically, an excessive focus on self-evolution may lead to neglecting the feedback provided by the target model, resulting in guidance not meeting the target model’s needs. Besides, a lack of focus on self-evolution may hinder teachers from enhancing their abilities, reducing the reliability of teacher knowledge. The controlled experiments were conducted to analyze the impact of self-evolution on the target model’s performance.

We fix αstd at 0.6 and vary αadv from {1.0, 0.9, 0.8, 0.7, 0.6, 0.5} to evaluate the adversarial robustness of ResNet-18 on CIFAR-10 against PGD-20 attack since αadv controls fine-tuning of the robust teacher and mainly affects the robustness of the target model. Fig. 5a demonstrates that when αadv is too large, the feedback from the target model has little influence on the robust teacher’s update. Consequently, the fine-tuned robust teacher does not significantly improve the generalization performance of the target model on AEs. Conversely, when αadv is too small, neglect of self-evolution causes performance degradation. The guidance from low-performance teachers impairs the robustness of the target model. Both situations result in suboptimal adversarial robustness. The results indicate that LDAS&ET-AD achieves the best robustness when αadv is set to 0.7.

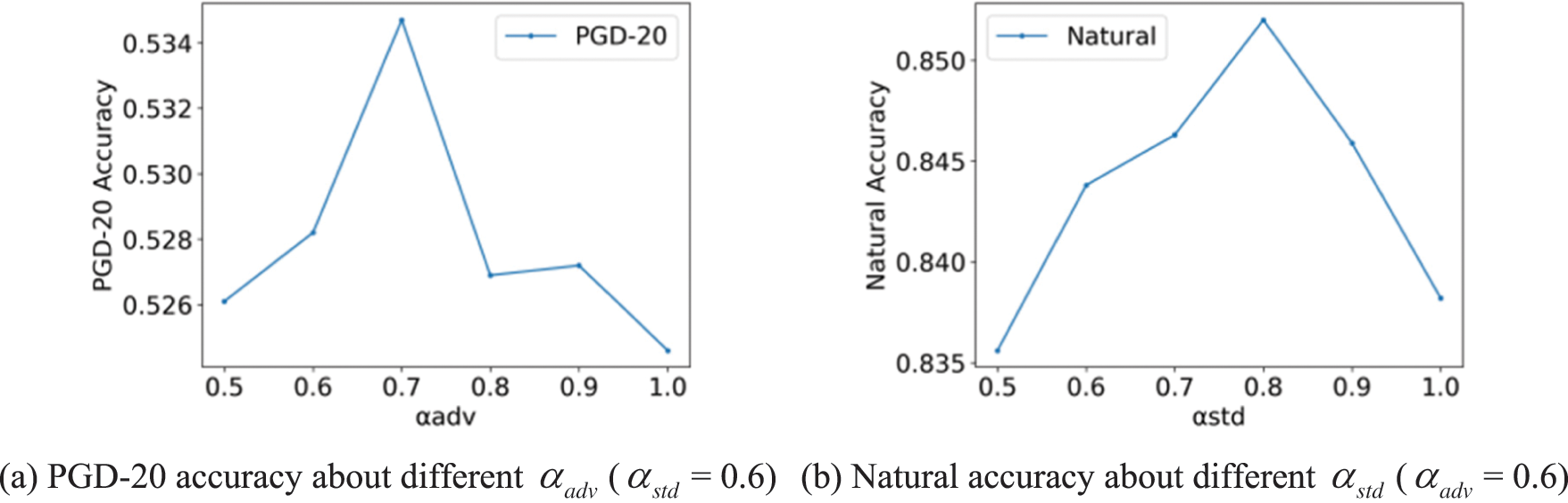
Figure 5: Test accuracy on CIFAR-10 dataset with ResNet-18 target model trained using our LDAS&ET-AD about different values of αstd and αadv

Next, we fix αadv at 0.7 and vary αstd from {1.0, 0.9, 0.8, 0.7, 0.6, 0.5} to evaluate the clean accuracy of ResNet-18 on CIFAR-10 since αstd controls fine-tuning of the standard teacher and mainly affects the clean accuracy of the target model. Consistent with the analysis of αadv, both excessively large and small αadv hamper the fine-tuning of the standard teacher, preventing the target model from achieving optimal generalization on clean samples. Fig. 5b illustrates that LDAS&ET-AD performs well when αstd is set to 0.8.

In conclusion, we set αstd to 0.8 and αadv to 0.7 to strike a balance between self-evolution and target model feedback, ensuring the best performance of LDAS&ET-AD.

5.6 Comparison of Different αL2 and αL3 Values

The hyperparameters αL2 and αL3 balance the trade-off between evaluating robustness loss term and predicting clean samples loss term in attack strategies generating mechanism. When αL2 is relatively large compared to αL3, it may result in lower clean accuracy. Conversely, an excessively large αL3 can lead to insufficient attention to robustness, resulting in low adversarial robustness. We present the performance of our proposed LDAS&ET-AD with various αL2 and αL3 pairs on CIFAR-10 using the ResNet-18 target model in Table 12.

Firstly, we fix αL2 at 2 and vary αL3 from {2, 4, 6} to evaluate performance. As αL3 increases, the total loss function places more emphasis on the robustness evaluation loss term. The results in Table 12 demonstrate that the clean accuracy shows a downward trend. Although the best robustness is achieved when αL3 is 4, there is only a small improvement compared to when αL3 is 2. The robustness continues to increase, and the optimal value is still achieved when αL3 is 4, but the difference is minimal compared to when αL3 is 2.

Secondly, we fix αL3 at 4 and vary αL2 from {2, 4, 6}. As αL2 increases, the total loss function focuses more on the clean accuracy loss term. It can be observed from the results in Table 12 that increasing αL2 leads to robustness decreasing and clean accuracy with little change. This indicates that when αL3 is fixed at 4, the clean accuracy is not sensitive to the change of αL2.

Although the performance of the target model is affected by αL2 and αL3, the changes do not occur within a large range. Therefore, the proposed method is not highly sensitive to these two hyperparameters, which aligns with the observation in [12]. Overall, we set αL2 to 2 and αL3 to 4.

5.7 Training and Inference Complexity

The proposed method entails a higher training complexity than the baseline, primarily due to the training of the strategy model parameters and the fine-tuning of the teacher models. However, our LDAS&ET-AD offers pronounced improvements over state-of-the-art adversarial defense methods. Specifically, the sample-dependent attack strategies generated by the strategy model in the game with the target model are highly effective, as are the more reliable teacher models fine-tuned according to the validation performance of the target model. In contrast, fixed hand-crafted attack strategies and static teacher models are far less effective.

Besides, to ensure a suitable trade-off between efficiency and robustness during the training of the strategy model, we have considered various factors, including the frequency of updating parameters. We have also introduced a finite difference approximation [35] to address the slowness of computing per-sample gradients and improve computational efficiency. Importantly, no additional complexity is introduced in the inference stage. However, we acknowledge that further work is necessary to reduce the training complexity of our approach.

6  Conclusion

To enhance the quality of AEs and the reliability of teacher knowledge in existing AD techniques, an AD method LDAS&ET-AD is proposed. Firstly, a learnable distillation attack strategies generating mechanism is developed to automatically create sample-dependent AEs well-suited for AD. A strategy model is introduced to produce attack strategies by competing with the target model in minimizing or maximizing the AD loss. Secondly, a teacher evolution strategy is devised to enhance the reliability and effectiveness of knowledge in improving the target model’s generalization performance. The model parameters of the standard and robust teachers are dynamically adjusted based on the target model’s performance on the validation set and AEs. We evaluate the method using ResNet-18 and MobileNet-V2 on the CIFAR-10 and CIFAR-100 datasets. Experiments demonstrate the superiority of our proposed LDAS&ET-AD method over state-of-the-art adversarial defense techniques in improving robustness against various adversarial attacks. The results confirm that introducing teacher knowledge to enhance the applicability of AEs and considering the target model’s validation performance to improve the reliability of the teacher knowledge are effective in promoting robustness.

7  Limitations and Prospects

While the proposed LDAS&ET-AD method demonstrates superiority over existing AD methods, it is essential to recognize its limitations. Firstly, the reliance on a separate validation set is crucial for obtaining feedback to fine-tune the teachers. However, this approach results in a reduction of training samples, which may impact performance, particularly in datasets of limited or moderate size. Exploring an alternative approach that leverages all data samples for both training and validation holds the potential for extracting more comprehensive information from the dataset. This avenue warrants further exploration in future research. Secondly, the proposed method involves various hyperparameters that significantly influence performance, necessitating manual configuration based on experimental results. This trial-and-error method demands additional time. To address this challenge, future endeavors will encompass the introduction of automatic hyperparameter optimization methods such as Random Search and Bayesian Optimization to identify the optimal combination of hyperparameters. Lastly, while our experiments have primarily focused on image classification tasks, which are relatively straightforward for current deep learning models, it is imperative for future work to extend the application of LDAS&ET-AD to more complex computer version tasks, and other domains such as natural language processing, and beyond. Such expansion will provide a more comprehensive evaluation of the method’s efficacy across diverse applications.

Acknowledgement: The authors are very grateful to the editors and all anonymous reviewers for their insightful comments.

Funding Statement: This study was funded by the National Key Research and Development Program of China (2021YFB1006200); Major Science and Technology Project of Henan Province in China (221100211200). Grant was received by S. Li.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: S. Li, X. Yang; data collection: G. Cheng; analysis and interpretation of results: S. Li, W. Liu, W. Guo; draft manuscript preparation: S. Li, H. Hu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data underlying this article will be shared on reasonable request to the corresponding author.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. S. Kumar and A. Rajendran, “Deep convolutional neural network for brain tumor segmentation,” J. Electr. Eng. Technol., vol. 18, no. 5, pp. 3925–3932, 2023. doi: 10.1007/s42835-023-01479-y. [Google Scholar] [CrossRef]

2. Z. Ji et al., “Survey of hallucination in natural language generation,” ACM Comput. Surv., vol. 55, pp. 1–38, 2022. [Google Scholar]

3. L. Chai, J. Du, Q. Liu, and C. Lee, “A cross-entropy-guided measure (CEGM) for assessing speech recognition performance and optimizing DNN-based speech enhancement,” IEEE/ACM Trans. Audio Speech Lang. Process., vol. 29, pp. 106–117, 2021. doi: 10.1109/TASLP.2020.3036783. [Google Scholar] [CrossRef]

4. C. Szegedy et al., “Intriguing properties of neural networks,” in 2014 Int. Conf. Learn. Rep., Alberta, USA, 2014. [Google Scholar]

5. Z. Xiong, H. Xu, W. Li, and Z. Cai, “Multi-source adversarial sample attack on autonomous vehicles,” IEEE Trans. Vehicular Technol., vol. 70, no. 3, pp. 2822–2835, 2021. doi: 10.1109/TVT.2021.3061065. [Google Scholar] [CrossRef]

6. M. Shen, H. Yu, L. Zhu, K. Xu, Q. Li and J. Hu, “Effective and robust physical-world attacks on deep learning face recognition systems,” IEEE Trans. Inf. Forensics Secur., vol. 16, pp. 4063–4077, 2021. doi: 10.1109/TIFS.2021.3102492. [Google Scholar] [CrossRef]

7. A. Kherchouche, S. A. Fezza, and W. Hamidouche, “Detect and defense against adversarial examples in deep learning using natural scene statistics and adaptive denoising,” Neural Comput. Appl., vol. 34, no. 24, pp. 21567–21582, 2021. doi: 10.1007/s00521-021-06330-x. [Google Scholar] [CrossRef]

8. A. Singh, L. Kumar Awasthi, Urvashi, M. Shorfuzzaman, A. Alsufyani and M. Uddin, “Chained dual-generative adversarial network: A generalized defense against adversarial attacks,” Comput. Mater. Contin., vol. 74, no. 2, pp. 2541–2555, 2023. doi: 10.32604/cmc.2023.032795 [Google Scholar] [CrossRef]

9. X. Jia, X. Wei, X. Cao, and H. Foroosh, “ComDefend: An efficient image compression model to defend adversarial examples,” in Proc. 2022 IEEE/CVF Conf. Comput. Vis. Pattern Recognit., New Orleans, USA, 2018, pp. 6077–6085. [Google Scholar]

10. H. Zhang, Y. Yu, J. Jiao, E. P. Xing, L. E. Ghaoui and M. I. Jordan, “Theoretically principled trade-off between robustness and accuracy,” in 36th Int. Conf. Mach. Learn., California, USA, 2019, pp. 7472–7482. [Google Scholar]

11. M. Haroon and H. Ali, “Adversarial training against adversarial attacks for machine learning-based intrusion detection systems,” Comput. Mater. Contin., vol. 73, no. 2, pp. 3513–3527, 2022. [Google Scholar]

12. X. Jia, Y. Zhang, B. Wu, K. Ma, J. Wang and X. Cao, “LAS-AT: Adversarial training with learnable attack strategy,” in Proc. 2022 IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Louisiana, USA, 2022, pp. 13388–13398. [Google Scholar]

13. A. Madry, A. Makelov, L. Schmidt, D. Tsipras, and A. Vladu, “Towards deep learning models resistant to adversarial attacks,” in 5th Int. Conf. Learn. Rep., Toulon, France, 2017. [Google Scholar]

14. S. Nandi, S. Addepalli, H. Rangwani, and R. V. Babu, “Certified adversarial robustness within multiple perturbation bounds,” in Proc. 2023 IEEE/CVF Conf. Comput. Vis. Pattern Recognit. Workshops, Vancouver, Canada, 2023, pp. 2298–2305. [Google Scholar]

15. Z. Zhang et al., “Boosting verified training for robust image classifications via abstraction,” in Proc. 2023 IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Vancouver, Canada, 2023, pp. 16251–16260. [Google Scholar]

16. J. Zhang, Z. Chen, H. Zhang, C. Xiao, and B. Li, “DiffSmooth: Certifiably robust learning via diffusion models and local smoothing,” in 32nd USENIX Secur. Symp., California, USA, 2023. [Google Scholar]

17. V. Voráček and M. Hein, “Improving l1-certified robustness via randomized smoothing by leveraging box constraints,” in Int. Conf. Mach. Learn., Hawaii, USA, 2023, pp. 35198–35222. [Google Scholar]

18. C. Liu, M. Salzmann, T. Lin, R. Tomioka, and S. E. Susstrunk, “On the loss landscape of adversarial training: Identifying challenges and how to overcome them,” in Neural Inf. Process. Syst., Vancouver, Canada, 2020. [Google Scholar]

19. M. Goldblum, L. H. Fowl, S. Feizi, and T. Goldstein, “Adversarially robust distillation,” in Assoc. Advan. Artif. Intell., Hawaii, USA, vol. 34, no. 2, pp. 3996–4003, 2019. [Google Scholar]

20. J. Maroto, G. Ortiz-Jiménez, and P. Frossard, “On the benefits of knowledge distillation for adversarial robustness,” arXiv preprint arXiv:2203.07159, 2022. [Google Scholar]

21. B. Zi, S. Zhao, X. Ma, and Y. Jiang, “Revisiting adversarial robustness distillation: Robust soft labels make student better,” in Proc. 2021 IEEE/CVF Int. Conf. Comput. Vis., Montreal, Canada, 2021, pp. 16423–16432. [Google Scholar]

22. G. Cao et al., “Vanilla feature distillation for improving the accuracy-robustness trade-off in adversarial training,” arXiv preprint arXiv:2206.02158, 2022. [Google Scholar]

23. T. Chen, Z. A. Zhang, S. Liu, S. Chang, and Z. Wang, “Robust overfitting may be mitigated by properly learned smoothening,” in 2021 Int. Conf. Learn. Rep., 2021. [Google Scholar]

24. S. Zhao, J. Yu, Z. Sun, B. Zhang, and X. Wei, “Enhanced accuracy and robustness via multi-teacher adversarial distillation,” in Eur. Conf. Comput. Vis., 2022, vol. 13664, pp. 585–602. doi: 10.1007/978-3-031-19772-7. [Google Scholar] [CrossRef]

25. J. Zhu et al., “Reliable adversarial distillation with unreliable teachers,” in Int. Conf. Learn. Rep., Vienna, Austria, 2021. [Google Scholar]

26. Y. Fan, F. Tian, T. Qin, X. Y. Li, and T. Y. Liu, “Learning to teach,” in Int. Conf. Learn. Rep., Vancouver, Canada, 2018. [Google Scholar]

27. Y. Zhang, T. Xiang, T. M. Hospedales, and H. Lu, “Deep mutual learning,” in 2018 IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Utah, USA, 2017, pp. 4320–4328. [Google Scholar]

28. X. Lan, X. Zhu, and S. Gong, “Knowledge distillation by On-the-Fly native ensemble,” in Neural Inf. Process. Syst., Montreal, Canada, 2018. [Google Scholar]

29. C. Li, G. Li, H. Zhang, and D. Ji, “Embedded mutual learning: A novel online distillation method integrating diverse knowledge sources,” Appl. Intell., vol. 53, no. 10, pp. 11524–11537, 2022. doi: 10.1007/s10489-022-03974-7. [Google Scholar] [CrossRef]

30. B. Qian, Y. Wang, H. Yin, R. Hong, and M. Wang, “Switchable online knowledge distillation,” in Eur. Conf. Comput. Vis., Tel Aviv, Israel, 2022, pp. 449–466. [Google Scholar]

31. W. Zhou, C. Xu, and J. Mcauley, “BERT learns to teach: Knowledge distillation with meta learning,” in Annual Meet. Assoc. Comput. Lingist., Bangkok, Thailand, 2021. [Google Scholar]

32. H. Zhu, Z. Chen, and S. Liu, “Learning knowledge representation with meta knowledge distillation for single image super-resolution,” J. Vis. Commun. Image Represent., vol. 95, no. 9, pp. 103874, 2022. doi: 10.1016/j.jvcir.2023.103874. [Google Scholar] [CrossRef]

33. H. Pham, Q. Xie, Z. Dai, and Q. V. Le, “Meta pseudo labels,” in Proc. 2021 IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Nashville, USA, 2020, pp. 11552–11563. [Google Scholar]

34. A. Abu, Y. Abdukarimov, N. A. Tu, and M. Lee, “Meta pseudo labels for chest x-ray image classification,” in Proc. 2022 IEEE Int. Conf. Syst., Man, Cybernet., Prague, Czech Republic, 2022, pp. 2735–2739. [Google Scholar]

35. Y. X. Ren, Z. H. Zhong, X. J. Shi, Y. Zhu, C. Yuan and M. Li, “Tailoring instructions to studentss learning levels boosts knowledge distillation,” in Annual Meet. Assoc. Comput. Linguist., Toronto, Canada, 2023. [Google Scholar]

36. Q. Cai, M. Du, C. Liu, and D. X. Song, “Curriculum adversarial training,” in 27th Int. Joint Conf. Artif. Intell., Stockholm, Sweden, 2018. [Google Scholar]

37. J. Zhang et al., “Attacks which do not kill training make adversarial learning stronger,” in 37th Int. Conf. Mach. Learn., Florida, USA, 2002. [Google Scholar]

38. Y. Wang, X. Ma, J. Bailey, J. Yi, B. Zhou and Q. Gu, “On the convergence and robustness of adversarial training,” in 38th Int. Conf. Mach. Learn., Vienna, Austria, 2021. [Google Scholar]

39. I. J. Goodfellow, J. Shlens, and C. Szegedy, “Explaining and harnessing adversarial examples,” in 3rd Int.Conf. Learn. Represent., San Diego, CA, USA, 2015, pp. 1–11. [Google Scholar]

40. N. Carlini and D. A. Wagner, “Towards evaluating the robustness of neural networks,” in 2017 IEEE Symp. Secur. Priv., California, USA, 2016, pp. 39–57. [Google Scholar]

41. F. Croce and M. Hein, “Reliable evaluation of adversarial robustness with an ensemble of diverse parameter-free attacks,” in Int. Conf. Mach. Learn., Maryland, USA, 2020. [Google Scholar]

42. Y. Wang, D. Zou, J. Yi, J. Bailey, X. Ma and Q. Gu, “Improving adversarial robustness requires revisiting misclassified examples,” in 7th Int. Conf. Learn. Represent., New Orleans, USA, 2019. [Google Scholar]

43. A. Krizhevsky, “Learning multiple layers of features from tiny images,” M.S. dissertation, Univ. of Toronto, Canada, 2009. [Google Scholar]

44. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in 2016 IEEE Conf. Comput. Vis. Pattern Recognit., Massachusetts, USA, 2015, pp. 770–778. [Google Scholar]

45. M. Sandler, A. G. Howard, M. Zhu, A. Zhmoginov, and L. Chen, “MobileNetV2: Inverted residuals and linear bottlenecks,” in 2018 IEEE/CVF Conf. Comput. Vis. Pattern Recognit., Utah, USA, 2018, pp. 4510–4520. [Google Scholar]