Shear Let Transform Residual Learning Approach for Single-Image Super-Resolution

1  Introduction

Super-resolution (SR) refers to the process of generating high-resolution (HR) videos or images from one or more low-resolution (LR) inputs. This is accomplished through advanced algorithms that effectively fill in missing details and enhance overall image quality. SR can improve the resolution of images captured by lower-quality cameras, resulting in sharper and more detailed visuals.

SR is divided into single-image SR (SISR) and multi-image SR. SISR techniques involve utilizing a single LR image as the input. However, numerous LR images are used in multi-image SR algorithms to produce an HR output. This offers an economical and practical solution to updating native hardware, such as camera sensors, across various applications, including satellite imaging [1], aerial imaging [2], security and surveillance imaging [3], and medical imaging [4]. The scientific community has recently concentrated its efforts on studying SR.

Single-image SR (SISR) is a fundamental problem that involves estimating an HR image from a single LR image [5]. Recovering missing high-frequency (HF) details is crucial for SISR [6]. The quest for HR images containing HF information highlights the importance of these specific details.

Today’s main SR techniques are interpolation-based, reconstruction-based, and learning-based. Interpolation-based approaches [5,6], while widening the range of the image, may produce oscillating and zigzagging images that are too smooth. Reconstruction-based approaches’ [7,8] representation and performance rely on the prior information used with the HR image. The reconstruction quality may deteriorate rapidly if the given input image is too small, or the amplification factor is too large.

The learning-based method [9–11] is more effective than earlier methods because it learns the mapping relationship between the HR and LR images. Convolutional Neural Networks (CNNs) [12–17] and Generative Adversarial Networks (GANs) [18–20] are two types of neural networks. They have superior representational and learning capacities and outperform standard learning approaches.

Deep neural networks, particularly deep CNNs, are used today and have proven highly effective in SR tasks. A key advantage of using deep CNNs for SR is their ability to learn complex, non-linear mappings between LR and HR images, capturing subtle details and textures that simpler models may overlook. Furthermore, CNNs can be trained with large datasets, enhancing their generalization performance on new, unseen data–a crucial aspect in SR tasks where the aim is to produce high-quality images absent from the training data. CNNs have significantly advanced the state-of-the-art in SR and facilitated the development of high-performance systems for various applications [21].

An example based SISR approach for remote sensing images was proposed. It calculates the shearlet coefficients for the desired HR image using the provided LR image instead of estimating a residual image between the high and LR images. To achieve exceptional performance, a convolutional neural network called the Enhanced Deep Super-Resolution (EDSR) [22] network is utilized. This study’s contributions lie in developing an innovative SR approach tailored to the needs of remote sensing imagery. By combining deep shearlet residual learning with the EDSR network, it achieves remarkable improvements in image quality, making it a valuable asset for applications such as surveillance, security, and remote area monitoring.

The present paper provides the following contributions:

1.    Combining deep shearlet residual learning with the EDSR network.

2.    The experimental outcomes demonstrate that the proposed ST residual learning approach performs better than conventional methods regarding peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) metrics.

2  Related Work

The first deep CNN for image SR was trained by Dong et al. [21]. The authors utilized an SR convolutional neural network (SRCNN) consisting of three layers, where the CNN was trained to map LR images to HR images in an end-to-end manner. The Super-Resolution Residual Network (SRResNet) [20] is a deep learning architecture to elevate SISR by enhancing image resolution while preserving photo-realism. In contrast to traditional SR methods, which have frequently grappled with the challenge of producing visually coherent and realistic results in addition to sharper images, the authors have introduced an innovative framework. This novel paradigm leverages the capabilities of GANs to usher in a transformative era of achieving photo-realistic SISR.

The residual net has demonstrated an excellent ability to shorten training times and accelerate convergence rates. Considering this notion, a Very Deep Convolutional Network for Super-Resolution (VDSR), a 20-layer CNN architecture that used adaptive gradient clipping and residual learning to lessen the difficulty of training, was proposed by Kim et al. [23]. The goal of estimating an HR image was shifted to estimating a residual image between the HR and LR images. This approach enhanced performance by integrating residual learning into the image SR process.

Zhang et al. [24,25] proposed two powerful SR techniques, namely the Residual Dense Network (RDN) and Residual Channel-Attention Network (RCAN), which employ Residual Dense Blocks (RDBs) and Residual Channel-Attention Blocks (RCABs), respectively. These networks have demonstrated superior performance over other existing state-of-the-art SR techniques for natural images.

Muhammad et al. [26] proposed an Inception ResNet for magnetic resonance imaging (MRI) images, called IRMRIS, which comprises two ResNet and Inception blocks with end-to-end connections, subsequently accompanied by the PReLU non-linear activation function. They utilized a deconvolution layer for learning the upsampling filters. The reconstructed output is then upscaled via a deconvolution layer to produce the final high-resolution MRI image. Experimental results show sharper and cleaner texture details.

The Deep Residual Squeeze and Excitation Network (DRSEN) was proposed by Gu et al. [27] to enhance the representation of deep networks. The authors employed a residual squeeze and excitation block (RSEB), which incorporates a local feature fusion module to utilize the features of both the input and the block. The squeeze and excitation module is leveraged to dynamically modify channel-wise feature responses by modelling the dependencies between channels, thereby enhancing the network’s capabilities. Additionally, it utilizes a global residual path approach, removing repetitive convolutional layers to minimize the parameters and computation needed.

Wang et al. [28] used symmetric local fusion blocks within a convolutional neural network (SR-SLFB). This approach enhances the reconstruction of high-frequency information. By incorporating local fusion within the residual block, it mitigates the issue of inadequate high-frequency feature extraction and enhances the accuracy of reconstructing remote sensing images with deep networks. To optimize global feature utilization and reduce network complexity, a residual method is employed, establishing symmetric jump connections between the local fusion blocks to ensure their mutual symmetry.

Some studies have attempted to enhance performance by combining CNNs and sparse transform-domain representations. According to Guo et al. [14], the first image SR technique utilized the wavelet domain. The authors constructed a deep wavelet super-resolution (DWSR) network to capture HR images by calculating the “missing details” of the wavelet coefficients in the LR image. To produce high-quality HR images with fewer artifacts, they employed a deep CNN in the transform domain and incorporated additional structural information in the wavelet domain throughout the reconstruction process. Huang et al. [16] developed a revolutionary deep-CNN Network and wavelet-integrated Identity Preserving Adversarial (WIPA) to reconstruct facial images. The remarkable aspect of this architecture is the eventual halving of the residual module depth to adjust for the high computational load brought on by feature size duplication after the transposed convolutional layer (ConvTr layers). A novel SR network for medical images was proposed by Sang et al. [29] in the non-subsampled contourlet transform (NSCT) domain and is known as the granular multiscale network (GMSN).

Hsu et al. [30] proposed a novel architecture for Structure Scale Preservation (SSP), which enables the integration and learning of structure preservation subnetworks on every level. They also introduced innovative Low-to-High-Frequency Information Transmission (L2HIT) and Detail Enhancement (DE) mechanisms, using Structure Scale Fusion (SSF) in combination with inverse Wavelet Transform (WT). This approach preserves low-frequency structures while reconstructing high-frequency details, enhancing detail fidelity and preventing structural distortion. Experimental results show that the wavelet pyramid recurrent structure preserving attention network (WRSANet), outperforms other methods, particularly in preserving context structure and texture details.

Dharejo et al. [31] utilized the 1st instance of a multi-attention GAN alongside a WT method for enhancing the resolution of medical images. The WT separates the LR image into multiple frequency bands, while the GAN incorporates multi-attention and upsampling blocks to make predictions about high-frequency components. The authors utilized GANs to develop a perceptual loss function that more effectively super-resolves LR features, resulting in enhanced perceptual quality of the resulting images with increased accuracy and richer texture information. Wang et al. [32] proposed the shearlet transform (ST) to the deep medical super-resolution network (DMSRN), which combines local residual learning with global residual learning. This was designed to increase the depth of the network without raising any parameters. To predict residual images, Geng et al. [33] introduced a deep shearlet residual learning network (DSRLN) based on the ST, which gives the best possible sparse approximation. By adopting a dual-path and data weighting strategy during the training process, a deep 20-layer CNN is employed to learn the target residual image. Evaluations on general natural and remote sensing datasets demonstrated improved quality of the regenerated images. Table 1 summarizes the related work for the SISR with the convolutional neural network.

The previously proposed techniques focused on the image space domain for SR, but those approaches can result in fuzzy images with lost textural features. The advantages of employing the transform domain for SR to improve SR outcomes are investigated, specifically capturing additional structural features in images to eliminate artifacts. While wavelets effectively represent one-dimensional signals, they struggle with high-dimensional signals. Using the Curvelet and contourlet transformations allows for the exploitation of the anisotropy of curved surfaces along edges. However, Curvelet lacks a geometric multi-resolution representation, and Contourlet is computationally expensive. To address these limitations and achieve outstanding performance, ST was applied [34].

3  Background

3.1 Background on the Shearlet Transform

The ST [34] is a framework that offers optimal sparse approximations [35]. By utilizing filter banks, it operates effectively and can represent images across multiple-scale frequency bands. Furthermore, in image SR, where HF details are essential, image representations at different frequencies showcase various features. By enhancing some frequencies and suppressing others, it is simple to design a spatial filter selective for extracting features in frequency domains. Thus, the shearlet-based technique boasts a greater feature extraction ability and offers remarkable performance [36].

One advantage of the ST is its well-localized properties in the frequency and time domains. These properties prove valuable for capturing an image’s structural information. Thus, the edge and structural information within the HR-estimated image can be preserved by employing SR in the ST domain [32,33].

3.1.1 Shearlet Transform

The ST is defined in terms of band-limited generators. The frequency domain of the shearlets is shown as cones and tiling in Fig. 1. The Fourier domain is partitioned into four cones by the ST, which eliminates a square at the center to isolate the low-frequency region.

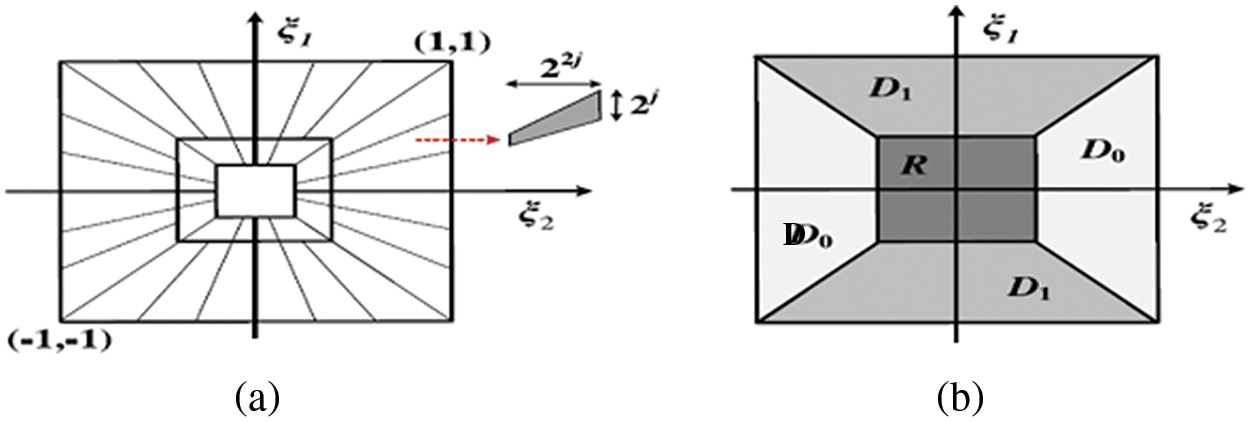
Figure 1: The way the shearlet’s frequency tiling is organized. (a) Support for shearlets φj,k,c in the frequency domain, which is divided into tiles with a trapezoidal form. (b) The centered rectangle R and the cones D0 and D1 in the frequency domain

The two-dimensional ST is defined as

φj,k,c=|detdetL|j2φ(MkLjX−c)(1)

where the scale, direction, and cone parameters, are j,k,andc, respectively. Satisfy j,k∈Z,c∈Z2.φ∈l2(R2). The |detdetL|= 1, L and M are 2 × 2 invertible matrices. L and M are controlling the scale and orientation of the ST, respectively.

Let L and M meet the condition:

L=L0=[4002],M=M0=[1101](2)

Or can be

L=L0=[2004],M=M0=[1011](3)

Then, the ST functions can be written as:

φj,k,c0(X)=232jφ0(M0kL0jx−c)(4)

φj,k,c1(X)=232jφ1(M1kL1jx−c)(5)

where j≥0,−2j≤k≤2j−1,c∈Z2 for any ε=(ε1,ε2)∈R2,ε1≠0, The fundamental function is stated as

φ(0)(ε)=φ^(0)(ε1,ε2)=φ^1(ε1)φ^2(ε2ε1)(6)

φ(1)(ε)=φ^(1)(ε1,ε2)=φ^1(ε2)φ^2(ε1ε2)(7)

where the Fourier transform of φ is indicated by φ^. As shown in Fig. 1b, the ST was revised to incorporate constraints compatible with the regions outlined by the horizontal cone:

D0={(ε1,ε2)∈R2:|ε1|≥1,|ε1ε2|≥1}(8)

the vertical cone as:

D1={(ε1,ε2)∈R2:|ε2|≥1,|ε1ε2|≤1}(9)

and the centered rectangle as

R={(ε1,ε2)∈R2:‖(ε1,ε2)‖∞≤1}(10)

3.2 The Enhanced Deep Super-Resolution (EDSR) Learning Network

The EDSR [22] network is an SISR architecture that has achieved top-of-the-line performance on SR benchmarks. The EDSR architecture comprises a series of convolutional layers with residual connections. Similar to ResNet [37], the network takes the LR image as an input and produces the HR image as an output. The residual connections allow the network to learn the residual mapping between the LR and HR images. Consequently, the training procedure gains stability, and the quality of the produced images is improved. Unlike ResNet, EDSR takes out the network’s batch normalization layers (this technique normalizes the inputs of each network layer to have a zero mean and unit variance). It is recommended to remove batch normalization layers since they normalize features and remove network range flexibility. As batch normalization layers utilize matching memory allocation to the preceding convolutional layers, GPU memory utilization is effectively reduced. The GPU memory usage is correspondingly lowered. Without the batch normalization layer, the EDSR can train using 40% less GPU memory usage [22].

Incorporating more parameters is a straightforward approach to enhancing the efficiency of a neural network model. The efficacy of a convolutional neural network can be amplified by introducing extra filters or layering additional layers. In a general CNN architecture, the number of layers (depth) is represented by B, the number of feature channels (width) by F, and the parameters amount to approximately O(BF2). Consequently, given limited computational resources, increasing F rather than B can optimize the model’s capacity while roughly maintaining O(BF) memory utilization [22].

However, exceeding a specific threshold for the number of feature maps would cause the training process to become numerically unstable. By using residual scaling (this technique scales the residual connections by a learnable parameter before adding them back to the output of each convolutional layer. This helps control the residual signal’s magnitude and prevent it from dominating the network output.) [38] with a factor of 0.1, EDSR was able to overcome this problem. After the final convolution layers, each residual block has constant scaling layers. These modules significantly stabilize the training process when several filters are used.

Using the residual blocks in Fig. 2b to build the EDSR model, the structure of SRResNet [20] as presented in Fig. 2a is simther to the EDSR model. EDSR excludes ReLU activation layers outside the residual blocks. Setting B = 32 and F = 256 with a scaling factor of 0.1 and loss function Mean Absolute Error (MAE) but without the batch normalization layers, the single-scale model EDSR was constructed. The model architecture is depicted in Fig. 3. Using the pre-trained x2 network to initialize the model parameters while training the EDSR for upsampling factors x3 and x4. This pre-training method speeds up training and enhances performance.

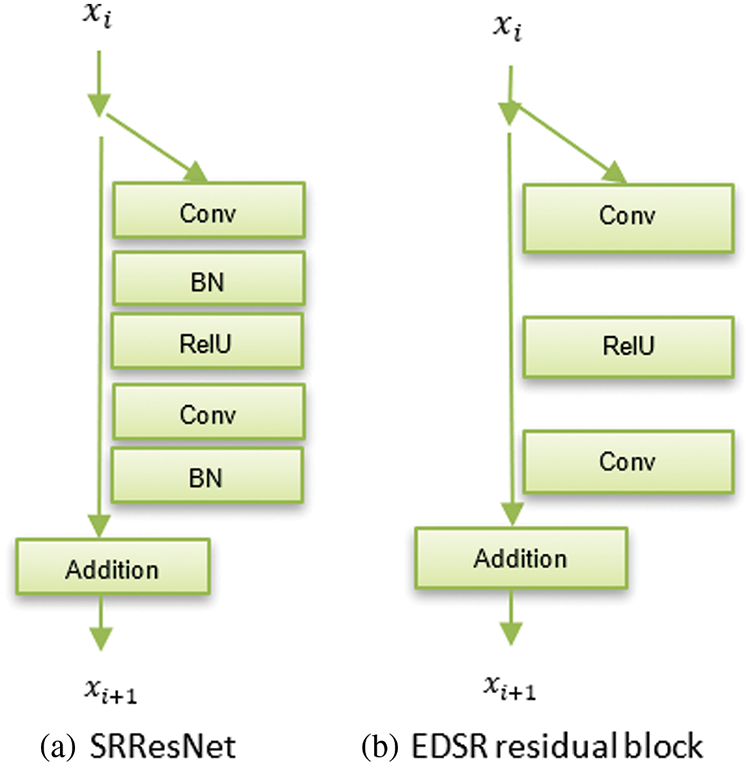
Figure 2: Residual block comparison for (a) SRResNet residual block (b) Enhanced deep super-resolution residual block

Figure 3: The enhanced deep super-resolution network’s architecture

4  The Proposed ST Residual Learning Approach

The SISR task aims to reconstruct an HR image from a single LR one. Let Y be the HR image and X be the LR. The objective of deep learning techniques in image SR is to learn a mapping function that can learn from a training set of LR images and generate their HR counterparts, denoted by {(Xi,Yi)}i=1N where the HR image is Yi and the corresponding LR image is Xi.

Given that Xi = I (D (Yi)), the down-sampling operator is denoted by D (·) and the interpolation operator is denoted by I (·), with the same scale factor. Here, bi-cubic interpolation is used. The objective of deep learning is learning the mapping function F(θ) with parameters θ from {(Xi,Yi)}i=1N. It inputs X = I (D (Y)), the bi-cubic interpolated image and outputs Y^=F(X;θ) as an estimated HR image.

A relative learning approach was introduced to CNN image SR, which improved performance by changing the challenge of estimating the HR image to predicting a residual image R=Y−X among the HR and LR images. The CNN residual learning method [39] was introduced to tackle the degradation performance issue, where training accuracy declines as the network depth increases. In residual learning-based image SR approaches, the loss function is typically the mean squared error (MSE) which is between Ri which is the predicted residual image and Ri^ which is the estimated residual image.

Ls(θ)=1N∑i=1N‖Ri^−(Yi−Xi)‖F2(11)

It can be calculated Ri^=F(Xi;θ) by a neural network predefined parameter θ.

The MSE loss function is not always the optimal choice. When the error exceeds 1, the MSE squares the error, making it more sensitive. The Mean Absolute Error (MAE) serves as the secondary loss function. Due to the constant derivative of the MAE loss function, it oscillates around its stable value during the latter phase of training with a constant learning rate, leading to reduced convergence accuracy. Consequently, the network was trained by using the MAE loss function, which is stated as

LA(θ)=1N∑i=1N‖Ri^−(Yi−Xi)‖1(12)

An SISR approach was proposed based on providing an LR image for estimating the shearlet coefficients of the desired HR image. Combined with a single-scale SR architecture called the EDSR [22]. For improving SISR performance in remote sensing images, a residual neural network based on the ST is proposed. The ST is chosen for its excellent sparse approximation. Initially, images are transformed into the shearlet domain, and their coefficients are fed into the EDSR network. The HR image is subsequently reconstructed using the inverse ST. The experimental results demonstrate outstanding image recovery performance, successfully restoring global topology and local edge detail information. This improvement can be attributed to the ST and EDSR model combination.

The proposed ST residual learning approach is depicted in Fig. 4. The ST residual learning approach comprises an ST unit, an EDSR network, and an inverse ST unit. The ST unit decomposes the bicubic interpolated input LR image to an LF sub-band and four HF sub-bands. The resulting shearlet coefficients are applied to the EDSR network, and then, to reconstruct the final HR image, a 2D inverse ST is used.

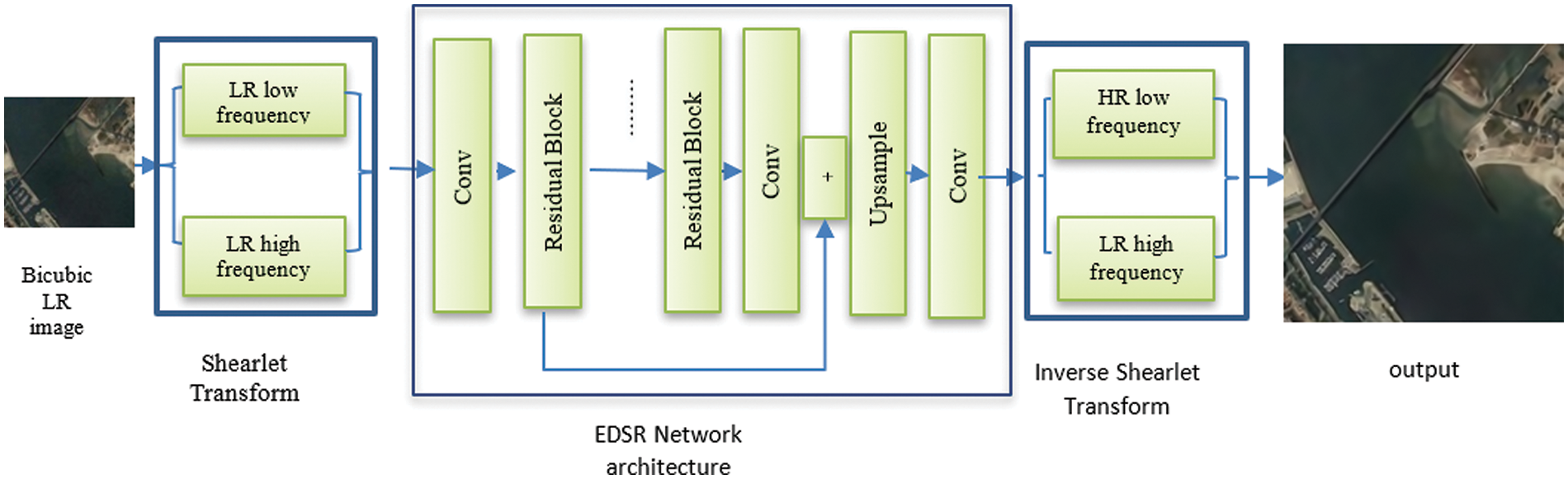
Figure 4: Block diagram for the proposed shearlet residual learning approach

4.1 Implementation of the ST

In the frequency domain, the shearlet filter is denoted by φ^j,k,c, and the overall number of scales for the ST is j (the scale parameter). For each scale j in every cone, the shearing parameter, k, runs from −2dj to 2dj. where dj is the parameter for the shearing level determined by the vector for the shearing level of size J, dj = (d1,d2,..., dj). Concerning the cone parameters c = 0, 1, and 2, while the horizontal shearlet filters are defined with c = 1 and the vertical ones with c = 2, the LF shearlet filter is indexed by c = 0. Keep in mind that the filters φ^j,k,1, and φ^j,k,2, are nearly identical when k = 2dj. Therefore, at each scale j, the shearlet filters’ boundary in the vertical cones are eliminated to enhance both consistency and effectiveness. As a result, rj=2(2.2dj+1)−2=2dj+1 can be used to compute the number of shearlet filters generated at each scale j, and R=1+∑j=1Jrj can be used to calculate the redundancy of the specified ST. For a 2D image X and the generated shearlet filter consisting of R filters with frequency responses φ^j,k,c, the shearlet coefficients SHj,k,c(X) of dimensions a × b related to φ^j,k,c are obtained by convolving the spatial domain representation of the shearlet filter SHj,k,c with the input image X. It is calculated through element-wise multiplication in the frequency domain, using the fast Fourier transform (FFT) and its inverse (IFFT). The result, SH(X), is a 3D tensor with dimensions a × b × R, containing all the shearlet coefficients SHj,k,c(X) corresponding to the shearet filter bank φ^j,k,c for each (j, k, c).

The shearing parameters are set to dj=(0,0), and the scale parameter is set to j=2. With this configuration, the associated shearlets total R=9, the LF path’s channel cL=1, and the HF path’s channel cH=8.

4.2 Implementation of EDSR

In the construction of the single-scale EDSR model, ReLU activation layers are omitted except within the residual blocks. The model was built with specific parameters: depth is set to B = 32, feature channels are F = 256, a scaling factor of 0.1, and the Mean Absolute Error (MAE) as the loss function. Notably, batch normalization layers were not included in this model. The architecture of the EDSR entails a series of meticulously designed components. First, the input is preprocessed by normalizing it, which involves subtracting the RGB mean, ensuring that the model works effectively with the given data. Following this, a Conv2d layer is employed with 64 filters and a kernel size of 3, enhancing the feature extraction process. The heart of the model lies in its ResBlocks, where 8 ResBlocks are utilized in this specific implementation. Each ResBlock consists of a Conv2d layer followed by an addition operation that combines the output of the ResBlock and the original input, enabling the model to learn residual features that enhance image SR. Finally, an upsampling step is carried out, achieved by using a combination of Conv2d and pixel shuffle operations, which helps increase the spatial resolution of the image. This comprehensive architecture ensures that EDSR can effectively upscale LR images to produce high-quality, super-resolved outputs.

During the model training, the ADAM optimizer [13] is utilized, with the parameters β1=0.9,β2=0.999, and ϵ=10−8, while 16 was chosen as the minibatch size. The initial learning rate is established to be 10−4 at the beginning and reduced by half every 2∗105 minibatch updates. The model was trained for 300 K iterations.

The training LR images for both datasets are divided into 48 × 48-pixel patches with the corresponding HR patches without overlapping. Each training image is rotated by 90 degrees, 180 degrees, and 270 degrees and then horizontally inverted to augment the training set. The model by factor x2 is built from the beginning to the end. Then, this x2 model is used as a pre-trained network for different scales (x3 and x4) once it converges.

5  Experimental Results

Remote sensing images are employed in this section to evaluate the proposed ST residual learning approach. The experimental setup is provided first, followed by information on data preparation and parameter adjustments. The enhancement in performance provided by the proposed ST residual learning approach is demonstrated. It is then compared to state-of-the-art SISR approaches. The proposed approach was implemented with the PyTorch framework and trained on an NVIDIA Tesla K80. ShearLab in the MATLAB (R2017b) environment was used to implement the ST and inverse transform.

5.1 Dataset

5.1.1 NWPURESISC45 Dataset

The NWPURESISC45 dataset [40] was invented by Northwestern Polytechnical University (NWPU). The benchmark for classifying remote sensing images is the dataset RESISC. This dataset comprises 31,500 images, with 700 images per class for 45 classes. HR images are 256 × 256 pixels, where the spatial resolution ranges from 30 to 0.2 meters per pixel. Each class received 700 randomly selected images, 550 of which were utilized for training and 150 for testing. Furthermore, each training image undergoes rotations of 90 degrees, 180 degrees, and 270 degrees, respectively. They are horizontally inverted after the rotations to expand the training set further.

5.1.2 The UCMerced Dataset

The UCMerced dataset [41] is widely recognized as one of the most commonly used datasets for processing remotely sensed data. It comprises 2100 images depicting various land surfaces on Earth. The dataset encompasses 21 different categories of low-light land use images involving agricultural areas (AGI), baseball diamonds (BD), beaches (BE), airplanes (APL), chaparral (CP), buildings (BU), forests (FO), golf courses (GC), freeways (FW), dense residential areas (DR), harbors (HA), intersections (IS), mobile-home parks (MHP), medium residential areas (MR), rivers (RI), overpasses (OP), runways (RW), storage tanks, sparse residential areas, parking lots (PL), and tennis courts (TC). Each classification consists of hundreds of 256 × 256 pixel images, and the spatial resolution in the red, green and blue (RGB) color space is 0.3 meters per pixel. These images were initially captured from aerial orthoimagery obtained from the United States Geological Survey (USGS) National Map. For each class, 90 images are used for training and the remaining images are used for testing. Moreover, each training image is subjected to rotations of 90 degrees, 180 degrees, and 270 degrees, respectively. After these rotations, horizontal flipping is applied to augment the training dataset further.

5.2 Evaluation Metric

The commonly used PSNR and SSIM are employed to perform quantitative assessments on the reconstructed images described by the following equations [42]:

PSNR(Y,Y^)=20log10(YMSE(Y,Y^))(13)

SSIM(Y,Y^)=(2μYμY^+c1)(2σYY^+c2)(μY2+μY^2+c1)(σY2+σY^2+c2)(14)

where the HR ground-truth image is denoted by Y and Y^ is the resulting HR image. The image’s maximum pixel value is max (Y), and MSE(Y,Y^)=1ab‖Y−Y^‖F2.

The average of Y is denoted by μY, while the average of Y^ is denoted by μY^, the variance of Y is denoted by σY2, while the variance of Y^ is denoted by σY^2, the covariance of Y and Y^ is denoted by σYY^. Finally, to stabilize the division with a small denominator, two small constants, c1 and c2 are used.

5.3 Remote Sensing Image Experiment Results

The average PSNRs and SSIMs for the NWPU-RESISC45 and UCMerced testing datasets are displayed in Table 2, with up-sampling factors of 2, 3, and 4, respectively. that displays the evaluation measure of the final 256 * 256-pixel HR images. It was observed that the range of PSNR readings lies within a reasonable range. This shows that the rebuilt image’s quality has improved. Furthermore, the SSIM is close to one, indicating that the reconstructed and original images (before downsampling) are structurally identical.

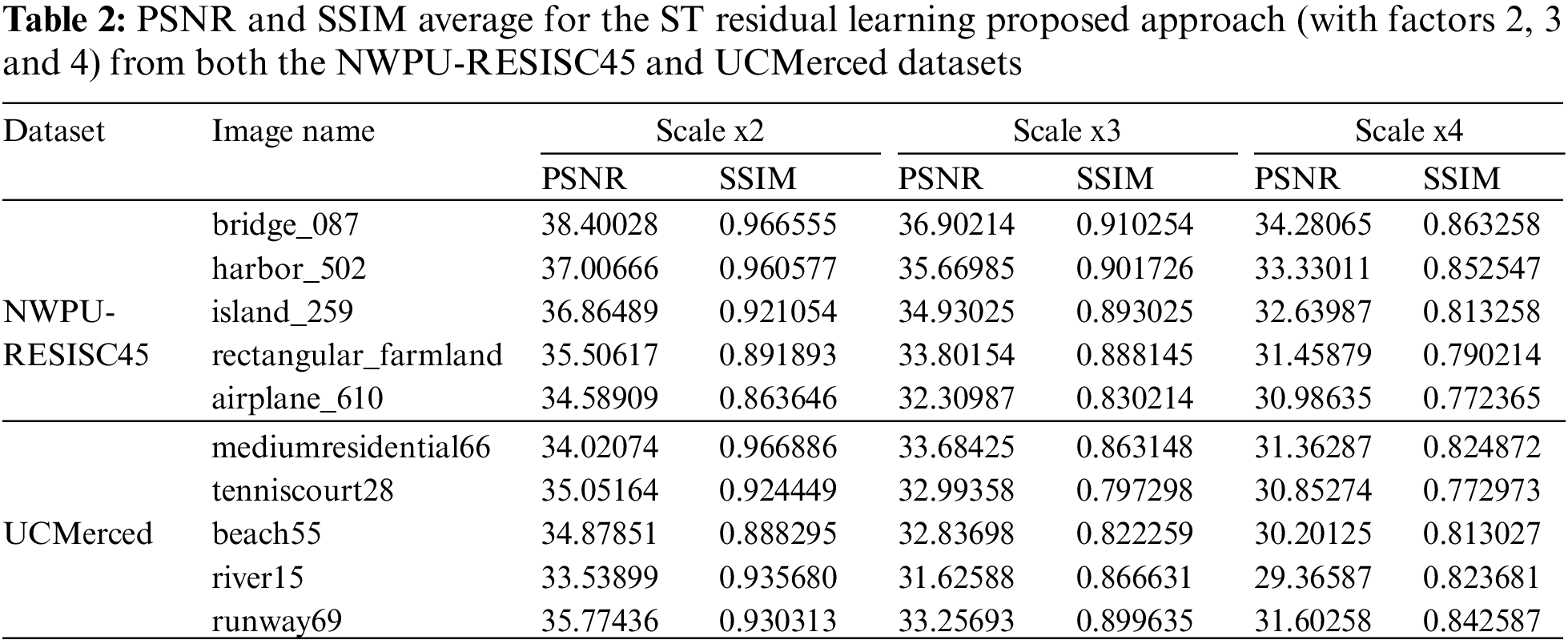
The proposed ST residual learning approach achieves high PSNR and SSIM scores in both datasets, demonstrating its robustness and ability to consistently produce high-quality results across various scales (x2, x3 and x4). In the case of the NWPU-RESISC45 dataset, the resulting HR images exhibited PSNR scores within the range of 38.4 to 32.8, and SSIM scores between 0.966 and 0.702. Similarly, for the UC Merced dataset, the PSNR values ranged from 37.6 to 31.2, and the SSIM scores ranged from 0.959 to 0.697.

Finally, the proposed ST residual learning approach produced a satisfying outcome. This implies that the proposed ST residual learning approach generates an HR image. The enhanced results were achieved by combining the ST and EDSR models. The EDSR model reduces memory usage by approximately 40% during training compared to SRResNet and benefits from utilizing a pre-trained network by scale x2 for the x3 and x4 scale models, which enables faster training convergence than starting from random initialization. Additionally, the ST boasts superior sparse representation capabilities.

5.4 Visualization Results

Fig. 5 depicts four samples chosen for visualization the original images (256 * 256), LR images 128 * 128 (Bicubic down-sampling) and resulting HR images (256 * 256) from the employed datasets regarding PSNR and SSIM. As a result, the proposed ST residual learning approach demonstrates superior performance, showcasing enhanced image recovery with the successful restoration of global topology and local edge detail information. This improvement is attributed to the ST and EDSR model combination.

Figure 5: Example LR and subsequent HR images using the proposed ST residual learning approach in terms of PSNR and SSIM from both datasets NWPU-RESISC45 and UCMerced

6  Ablation Study

The proposed ST residual learning approach integrates the ST with the EDSR network, which delivers superior performance and advanced image restoration, it excels at preserving the global topology and intricate details of local edges. Integrating the ST and EDSR models is responsible for the remarkable improvement achieved.

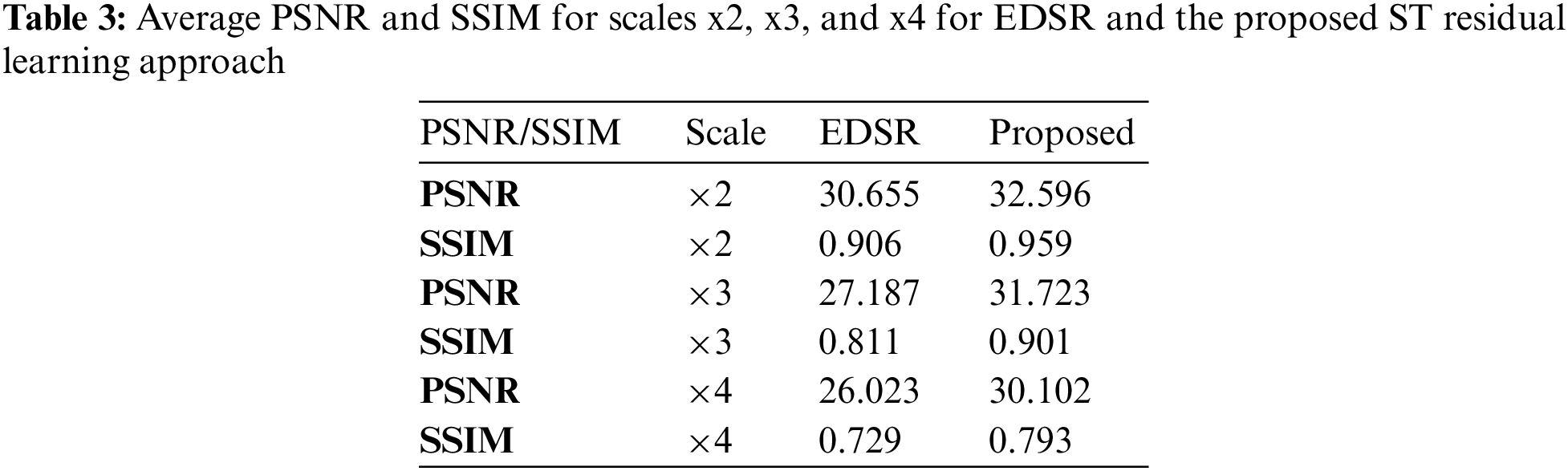
To validate the effectiveness of the proposed approach, a comparison was made between the proposed approach and the EDSR network. EDSR serves as a benchmark for SR tasks. As mentioned in Table 3, the proposed approach shows improved PSNR and SSIM measurements over the EDSR network, and the notable improvement achieved can be credited to integrating the ST and EDSR models.

7  Comparative Analysis Using Cutting-Edge Technology

Table 4 demonstrates the average PSNR and SSIM experimental outcomes for the benchmark networks, Bicubic, SRResNet [20], EDSR [22], DSRLN [33], DRSEN [27] and SR-SLFB [28] for scales of 2, 3, and 4 on the remote sensing images.

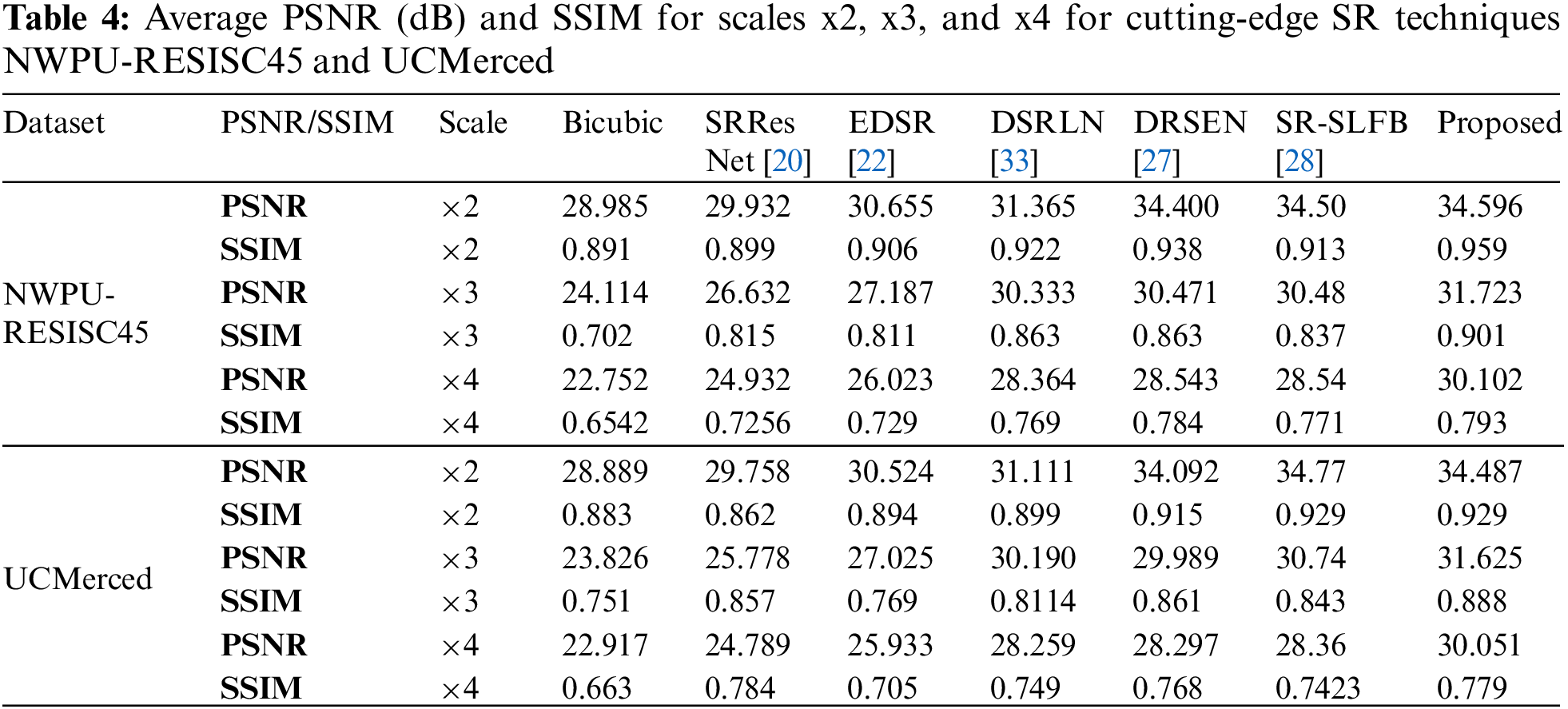
The PSNR and SSIM average objective criteria values from the NWPU-RESISC45 and UCMerced datasets are evaluated. Below are the results obtained for the HR images: PSNR = 32.596 and SSIM = 0.959 for x2, PSNR = 31.723 and SSIM = 0.901 for x3, and PSNR = 30.102 and SSIM = 0.793 for x4. The reported analysis and outcomes reveal that the proposed ST residual learning approach outperformed other networks and improved reasonably. It extended the input LR images from 128 * 128 to 256 * 256 HR images. This demonstrates that the ST residual learning approach can produce an SR image while restoring the global topology and local edge detail information. The improved outcomes were obtained by combining the ST and EDSR models. Compared to SRResNet, the EDSR model uses approximately 40% less memory during training and benefits from utilizing a pre-trained network for x2 scaling for the x3 and x4 scale models, allowing for faster training convergence than beginning from random initialization. The ST also has superior sparse representation capabilities.

8  Conclusion

This research explicitly uses the NWPU-RESISC45 and UCMerced testing datasets to propose a residual neural network based on the ST for boosting SISR performance in remote sensing images. The ST is chosen for its excellent sparse approximation. Initially, images are transformed into the shearlet domain, and their coefficients are fed into the EDSR network. The HR image is subsequently reconstructed using the inverse ST. Experimental results indicate that our proposed ST residual learning approach offers higher performance and superior image recovery, successfully preserving global topology and local edge detail information. The ST and EDSR model combination is responsible for this improvement. Regarding image quality, comparative analyses reveal that our methodology outperforms current state-of-the-art methods, with an average value for PSNR of 35 and an SSIM average of 0.9.

As part of our future plans, utilizing an enhanced multiscale SR network (MDSR) that offers the benefits of reduced model size and faster training time while effectively handling SR at multiple scales.

Acknowledgement: The authors express their gratitude to all the contributors.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Israa Ismail and Ghada Eltaweel; data collection: Israa Ismail; analysis and interpretation of results: Israa Ismail, Ghada Eltaweel and Mohamed Meselhy Eltoukhy; draft manuscript preparation: Israa Ismail and Mohamed Meselhy Eltoukhy. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data are openly available in a public repository that issues datasets with DOIs.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Liebel and M. Körner, “Single-image super resolution for multispectral remote sensing data using convolutional neural networks,” Int. Arch. Photogramm, Remote Sens. Spat. Inf. Sci., vol. 41, pp. 883–890, 2016. [Google Scholar]

2. T. Wang, W. Sun, H. Qi, and P. Ren, “Aerial image super resolution via wavelet multiscale convolutional neural networks,” IEEE Geosci. Remote Sens. Lett., vol. 15, no. 5, pp. 769–773, 2018. doi: 10.1109/LGRS.2018.2810893. [Google Scholar] [CrossRef]

3. Y. Pang, J. Cao, J. Wang, and J. Han, “JCS-Net: Joint classification and super-resolution network for small-scale pedestrian detection in surveillance images,” IEEE Trans. Inform. Forensic. Secur., vol. 14, no. 12, pp. 3322–3331, 2019. doi: 10.1109/TIFS.2019.2916592. [Google Scholar] [CrossRef]

4. Y. Li, B. Sixou, and F. Peyrin, “A review of the deep learning methods for medical images super resolution problems,” IRBM, vol. 42, no. 2, pp. 120–133, 2021. doi: 10.1016/j.irbm.2020.08.004. [Google Scholar] [CrossRef]

5. S. Hyun and J. Heo, “VarSR: Variational super-resolution network for very low resolution image,” in Eur. Conf. Comput. Vis., Cham, Springer International Publishing, 2020, pp. 431–447. [Google Scholar]

6. L. Yue, H. Shen, J. Li, Q. Yuan, H. Zhang and L. Zhang, “Image super-resolution: The techniques, applications, and future,” Signal Process., vol. 128, pp. 389–408, 2016. doi: 10.1016/j.sigpro.2016.05.002. [Google Scholar] [CrossRef]

7. C. Jiang, Q. Zhang, R. Fan, and Z. Hu, “Super-resolution CT image reconstruction based on dictionary learning and sparse representation,” Sci. Rep., vol. 8, no. 1, pp. 8799, 2018. doi: 10.1038/s41598-018-27261-z. [Google Scholar] [PubMed] [CrossRef]

8. J. Zhang, M. Shao, L. Yu, and Y. Li, “Image super-resolution reconstruction based on sparse representation and deep learning,” Signal Process.: Image Commun., vol. 87, pp. 115925, 2020. [Google Scholar]

9. T. Li, X. Dong, and H. Chen, “Single image super-resolution incorporating example-based gradient profile estimation and weighted adaptive p-norm,” Neurocomputing, vol. 355, no. 10, pp. 105–120, 2019. doi: 10.1016/j.neucom.2019.04.051. [Google Scholar] [CrossRef]

10. Q. Yang, Y. Zhang, and T. Zhao, “Example-based image super-resolution via blur kernel estimation and variational reconstruction,” Pattern Recognit. Lett., vol. 117, pp. 83–89, 2019. doi: 10.1016/j.patrec.2018.12.008. [Google Scholar] [CrossRef]

11. Y. Liu, S. Zhang, J. Xu, J. Yang, Y. W. Tai, “An accurate and lightweight method for human body image super-resolution,” IEEE Trans. Image Process., vol. 30, pp. 2888–2897, 2021. doi: 10.1109/TIP.2021.3055737. [Google Scholar] [PubMed] [CrossRef]

12. S. Kaji and S. Kida, “Overview of image-to-image translation by use of deep neural networks: Denoising, super-resolution, modality conversion, and reconstruction in medical imaging,” Radiol. Phys. Technol., vol. 12, no. 3, pp. 235–248, 2019. doi: 10.1007/s12194-019-00520-y. [Google Scholar] [PubMed] [CrossRef]

13. C. Dong, C. C. Loy, and X. Tang, “Accelerating the super-resolution convolutional neural network,” in Comput. Vision-ECCV 2016: 14th Eur. Conf., Amsterdam, The Netherlands, Springer International Publishing, Oct. 11–14, 2016, pp. 391–407. [Google Scholar]

14. T. Guo, H. Seyed Mousavi, T. Huu Vu, and V. Monga, “Deep wavelet prediction for image super-resolution,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. Workshops, Honolulu, HI, USA, 2017, pp. 104–113. [Google Scholar]

15. T. Guo, H. S. Mousavi, and V. Monga, “Adaptive transform domain image super-resolution via orthogonally regularized deep networks,” IEEE Trans. Image Process., vol. 28, no. 9, pp. 4685–4700, 2019. doi: 10.1109/TIP.2019.2913500. [Google Scholar] [PubMed] [CrossRef]

16. H. Huang, R. He, Z. Sun, and T. Tan, “Wavelet-srnet: A wavelet-based CNN for multi-scale face super resolution,” in Proc. IEEE Int. Conf. Comput. Vis., Venice, Italy, 2017, pp. 1689–1697. [Google Scholar]

17. Y. Tai, J. Yang, X. Liu, and C. Xu, “Memnet: A persistent memory network for image restoration,” in Proc. IEEE Int. Conf. Comput. Vis., Venice, Italy, 2017, pp. 4539–4547. [Google Scholar]

18. Y. Gu et al., “MedSRGAN: Medical images super-resolution using generative adversarial networks,” Multimed. Tools Appl., vol. 79, no. 29–30, pp. 21815–21840, 2020. doi: 10.1007/s11042-020-08980-w. [Google Scholar] [CrossRef]

19. J. He, J. Zheng, Y. Shen, Y. Guo, and H. Zhou, “Facial image synthesis and super-resolution with stacked generative adversarial network,” Neurocomputing, vol. 402, no. 8, pp. 359–365, 2020. doi: 10.1016/j.neucom.2020.03.107. [Google Scholar] [CrossRef]

20. C. Ledig et al., “Photo-realistic single image super-resolution using a generative adversarial network,” in Proc. IEEE Int. Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, 2017, pp. 4681–4690. [Google Scholar]

21. C. Dong, C. C. Loy, K. He, and X. Tang, “Image super-resolution using deep convolutional networks,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 38, no. 2, pp. 295–307, 2015. doi: 10.1109/TPAMI.2015.2439281. [Google Scholar] [PubMed] [CrossRef]

22. B. Lim, S. Son, H. Kim, S. Nah, and K. Mu Lee, “Enhanced deep residual networks for single image super-resolution,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. Workshops, Honolulu, HI, USA, 2017, pp. 136–144. [Google Scholar]

23. J. Kim, J. K. Lee, and K. M. Lee, “Accurate image super-resolution using very deep convolutional networks,” in Proc. IEEE Conf. Comp. Vis. Pattern Recognit., Las Vegas, NV, USA, 2016, pp. 1646–1654. [Google Scholar]

24. Y. Zhang, Y. Tian, Y. Kong, B. Zhong, and Y. Fu, “Residual dense network for image super-resolution,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, 2018, pp. 2472–2481. [Google Scholar]

25. Y. Zhang et al., “Image super-resolution using very deep residual channel attention networks,” in Proc. Eur. Conf. Comput. Vis. (ECCV), Germany, 2018, pp. 286–301. [Google Scholar]

26. W. Muhammad, Z. Bhutto, S. Masroor, M. H. Shaikh, J. Shah and A. Hussain, “IRMIRS: Inception-ResNet-based network for MRI image super-resolution,” Comput. Model. Eng. Sci., vol. 136, no. 2, pp. 1121–1142, 2023. doi: 10.32604/cmes.2023.021438. [Google Scholar] [CrossRef]

27. J. Gu, X. Sun, Y. Zhang, K. Fu, and L. Wang, “Deep residual squeeze and excitation network for remote sensing image super-resolution,” Remote Sens., vol. 11, no. 15, pp. 1817, 2019. doi: 10.3390/rs11151817. [Google Scholar] [CrossRef]

28. X. Wang and W. Lu, “Super-resolution reconstruction of remote sensing images based on symmetric local fusion blocks,” Int. J. Inf. Secur. Priv. (IJISP), vol. 17, no. 1, pp. 1–14, 2023. doi: 10.4018/IJISP. [Google Scholar] [CrossRef]

29. Y. Sang, J. Sun, S. Wang, K. Li, and H. Qi, “Medical image super-resolution via granular multi-scale network in NSCT domain,” in 2020 IEEE Int. Conf. on Multimed, Expo (ICME), London, UK, IEEE, 2020, pp. 1–6. [Google Scholar]

30. W. Y. Hsu and P. W. Jian, “Wavelet pyramid recurrent structure-preserving attention network for single image super-resolution,” IEEE Trans. Neur. Netw. Learn. Syst., pp. 1–15, 2023. doi: 10.1109/TNNLS.2023.3289958. [Google Scholar] [PubMed] [CrossRef]

31. F. A. Dharejo et al., “Multimodal-boost: Multimodal medical image super-resolution using multi-attention network with wavelet transform,” IEEE/ACM Trans. Comput. Biol. Bioinform., vol. 1, pp. 1–14, 2022. [Google Scholar]

32. C. Wang et al., “Medical image super-resolution via deep residual neural network in the shearlet domain,” Multimed. Tools Appl., vol. 80, no. 17, pp. 26637–26655, 2021. doi: 10.1007/s11042-021-10894-0. [Google Scholar] [CrossRef]

33. T. Geng, X. -Y. Liu, X. Wang, G. Sun, “Deep shearlet residual learning network for single image super-resolution,” IEEE Trans. Image Process., vol. 30, pp. 4129–4142, 2021. doi: 10.1109/TIP.2021.3069317. [Google Scholar] [PubMed] [CrossRef]

34. S. Vagharshakyan, R. Bregovic, and A. Gotchev, “Light field reconstruction using shearlet transform,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 40, no. 1, pp. 133–147, 2017. doi: 10.1109/TPAMI.2017.2653101. [Google Scholar] [PubMed] [CrossRef]

35. A. Duval-Poo, F. O. Miguel, and E. DeVito, “Edges and corners with shearlets,” IEEE Trans. Image Process., vol. 24, no. 11, pp. 3768–3780, 2015. doi: 10.1109/TIP.2015.2451175. [Google Scholar] [PubMed] [CrossRef]

36. S. Alinsaif and J. Lang, “Shearlet-based techniques for histological image classification,” in IEEE Int. Conf. Bioinform. Biomed. (BIBM), San Diego, CA, USA, IEEE, 2019, pp. 1424–1431. [Google Scholar]

37. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” arXiv preprint arXiv:1512.03385, 2016. [Google Scholar]

38. C. Szegedy, S. Ioffe, V. Vanhoucke, and A. Alemi, “Inception-v4, inception-resnet and the impact of residual connections on learning,” in Proc. AAAI Conf. Artif. Intell., California, USA, 2017, vol. 31. [Google Scholar]

39. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Las Vegas, NV, USA, 2016, pp. 770–778. [Google Scholar]

40. G. Cheng, J. Han, and X. Lu, “Remote sensing image scene classification: Benchmark and state of the art,” Proc. IEEE, vol. 105, no. 10, pp. 1865–1883, 2017. doi: 10.1109/JPROC.2017.2675998. [Google Scholar] [CrossRef]

41. Y. Yang and S. Newsam, “Bag-of-visual-words and spatial extensions for land-use classification,” in ACM SIGSPATIAL Int. Conf. Adv. Geogr. Inf. Syst. (ACM GIS), 2010, pp. 270–279. [Google Scholar]

42. U. Sara, M. Akter, and M. S. Uddin, “Image quality assessment through FSIM, SSIM, MSE and PSNR—A comparative study,” J. Comput. Commun., vol. 7, no. 3, pp. 8–18, 2019. doi: 10.4236/jcc.2019.73002. [Google Scholar] [CrossRef]