Side-Channel Leakage Analysis of Inner Product Masking

1  Introduction

Masking is a commonly considered countermeasure against side-channel attacks. In a masking implementation, the sensitive intermediate values are randomly divided into d+1 shares to eliminate the statistical properties of power consumption, and each share performs the entire computation individually. Initially, Chari et al. suggested using this segmentation technique and demonstrated that the complexity of executing an effective attack in a high-noise environment increases exponentially with the number of shares [1]. The development of higher-order side-channel analysis (HO-SCAs) makes it no longer secure to use a single computation as a form of mask encoding. In recent years, researchers have proposed coding-based masking schemes with higher algebraic complexity, such as IPM [2–4], Direct Sum Masking (DSM) [5] and Leakage Squeezing (LS) [6], to improve the trusted security of devices. A second-order IPM has been proven to provide third-order side-channel security with significantly lower implementation overhead than third-order BMs [4].

In general, the security of the practical application of a masking scheme is determined by two main factors: The adversarial and implementation conditions. The former can be attributed to the leakage (univariate or multivariate attacks) available to the adversary. Obviously, the shares must be generated on the device, which can reveal information in any mask implementation. The latter is reflected in the character of the leakage function, where the deterministic part of the traditional leakage function is linear in bits (e.g., the Hamming weight (HW) function). More complex encodings can improve the security order of bounded moment leakage models in the case of linear leakage functions. However, several researches (e.g., [4,7]) have demonstrated that employing nonlinear leakage functions for the evaluation of masking schemes to evaluate masking schemes can lead to reorganization and decreased security order.

Related Works Some new advances have been made in studying the security of masking schemes under adversarial condition. In [8], researchers demonstrated an approach to speed up higher-order template attacks using the Fast Fourier Transform. This method for analyzing multivariate leakage applies to a wide range of masking schemes. Furthermore, deep learning based side-channel analysis (DL-SCA) deals with the complex dependencies between measurements and sensitive values by extracting important features. During the learning phase, the model output is compared with the given labels and updated with the internal parameters of the network. This technique is particularly effective in executing attacks on higher-order mask implementations in the presence of multivariate leakage. As demonstrated in [9], a novel DL-SCA technique can exploit side-channel collisions in a black-box environment, localize input-dependent leakages in masked implementations. In terms of implementation condition, Wang et al. investigated the nonlinear leakage of coding-based masking schemes that maintain high security despite constraints [10].

Contributions In this paper, we investigate the specific security of IPM under adversarial and implementation conditions. Our contributions are as follows.

Firstly, we conducted a systematic assessment of the information leakage of IPM using a quantitative approach. In the adversarial condition, it is clear that compared to BM, by adjusting the public L2 value of IPM, the slope of the information theory curve of the univariate analysis decreases more, corresponding to a higher level of security. In the bivariate case, we observe that the security of the IPM is compromised (as reflected by the decreasing slope of the curves), but the good properties of the IPM gained by the “security order amplification” are not annihilated, and the mutual information (MI) of the IPM is still much lower than that of the BM. In the implementation condition, we construct two polynomial leakage functions and connect them to the security order amplification, and the results show that the high security of IPM disappears when the leakage function is not linear in bits. The experiments on nonlinear leakage show that the degree and linear component of the nonlinear function affects the quantization results. The evaluation was performed using a leakage function with a lower degree or linear component dominant, demonstrating a more robust security. Finally, we complement the nonlinear leakage study of IPM in three aspects (polynomial coefficients, SNR and the public parameters L, respectively).

Outline The paper is structured as follows: Section 2 provides an overview of the IPM, including probing security and univariate and multivariate attacks. Section 3 presents the construction of the nonlinear leakage function and connects it to the security order amplification. Section 4 presents the leakage analysis of the IPM. Finally, Section 5 concludes the paper.

2  Preliminaries

In the following, Fq is a finite field in characteristic 2. Vector x=(x1,x2,⋯,xn) ([x]2 represented in binary) is denoted using bold letters in the finite field Fq, whereas unbold letters denote an element x (with its representation [x]2 in binary). The field addition is denoted by ⊕. The probability of an occurrence of an event x is denoted as Pr[x], and the information entropy of a random variable c is defined as H[c].

2.1 Inner Product Masking

The masking scheme is a common countermeasure to resist SCA. The principle is to split a single sensitive intermediate value into n shares, and each share performs all operations individually and always independently of the sensitive intermediate value. If an attacker can only get information from n points of the n th-order masking, this does not retrieve the hidden intermediate values. In other words, it allows the attacker to retrieve sensitive information only after obtaining all n shares. BM was the first masking scheme proposed and widely studied by researchers. It uses the addition operation ⊕ over a finite field to concatenate each share, as shown in Eq. (1).

s=s1⊕s2⊕⋯⊕sn(1)

where s represents the sensitive intermediate value, and si represents the ith share. In general, n−1 shares are generated randomly and independent of each other.

Researchers have sought to enhance security requirements by intensifying the algebraic complexity of the masking scheme. A variety of masking schemes have been proposed and unified through a generalization approach [11]. One representative scheme is the IPM. In IPM, the sensitive variable s is split into the inner product of vectors L and R of length n, expressed by the following Eq. (2):

s=⟨L,R⟩=∑i=1nLiRi=L1R1⊕L2R2⊕⋯⊕LnRn,(2)

where L=(L1,L2,⋯,Ln) is public and L1=1. In earlier research by Balasch et al. demonstrated that the IPM leakage is always smaller than BM for the same number of shares. In fact, the security of IPM depends not only on the number of share but also on the encoding of sensitive variables and mask materials in the cryptographic operation. The feature under observation garnered the interest of researchers, prompting Poussier et al. to conduct the initial investigation into the encoding format of IPM [12], represented by Eq. (3).

Z=XG+YH,(3)

where X and Y are sensitive variables, the random mask vector, and G and H are the generating matrices of codes C and D. In the multiplication of the random mask Y by H, some of the bits in these shares are mixed and added to the sensitive values by coordinates, which undoubtedly increases the algebraic complexity of the encoding. As a result, a completely new parameter characterizing the security of the IPM is proposed (i.e., the dual distance of code D). This effect corresponds to the “security order amplification” results presented by Wang et al. [13]. Recently, Cheng et al. demonstrated the selection process for optimal coding to maximize the side-channel resistance of IPM [14]. Ming et al. analyzed the security of IPM against a non-profiled side-channel attack (correlation coefficient attack) and suggested a new approach to measure higher-order correlation analysis efficiency [15].

2.2 Word and Bit-Probing Security

The concept of probing security of a masking scheme comes from the probing model introduced in [16]. In general, a scheme is considered as d-order probing security if the distribution of any d or fewer intermediate variables manipulated during the execution is independent of any secret. Previous research has shown that the detection security of an IPM with n shares is d=n−1. We introduce the more stringent security guarantee of bit probing security d′, where each probing computes only one bit in the encoding. It means any combination of d′ bits is independent of [x]2. If one wants to recover a bit from [x]2, then the minimum number of sub-equations is required for d′+1. In IPM, the bit probing security d′ is usually related to the dual distance of the code D in Eq. (3) (i.e., the minimum number of columns in H that are linearly dependent), as proven in [12]. We recall the two codes C and D in the IPM encoding, in which the dimension of C and D is k and k(n−1). The generator matrices of C and D are as follows:

G=(1⋯10⋯0),H=(l2l3⋮ln|1k0k⋯0k⋮⋮⋯⋮⋮⋮⋯⋮0n0k⋯1k),(4)

where li denotes the k×k binary matrix of Li multiplied by [x]2 in F2k, i.e., [Li⋅x]2=(li×([x]2)T)T. 1k is defined as the k×k identity matrix, 0k is defined as the k×k zero matrix. Therefore, Eq. (3) can expressed as:

Z=[x]2G+YH=([x]20⋯0)+(([L2⋅Y2]2+⋯+[Ln⋅Yn]2)[Y2]2⋯[Yn]2)=([Z1]2[Z2]2⋯[Zn]2).(5)

In order to make the IPM have the best probing security, the dual distance d′ can be maximised by choosing the optimal public parameter L=(L1,L2,⋯,Ln).

2.3 Univariate and Multivariate Attack

Let p∈{1,⋯,P} be the known plaintexts or ciphertexts of the cryptographic device, let key∗ is the secret key (key′ is the guessing key to execute the attack) and let Ni for i∈{1,⋯,n} is the Gaussian noise. Therefore, the sensitive intermediate value state is: state=p+key∗. The leakage generated by each share when performing the attack on IPM is Ai=HW(Zi)+Ni. Hence, we have overall leakages for all shares:

A=(A1,A2,A3,⋯,Ad),=HW(state+L2Y2+⋯+LdYd)+N1,HW(Y2)+N2,HW(Y3)+N3,⋯,HW(Yd)++Nd.(6)

An attack is considered univariate if it utilizes a unidimensional leakage vector A=[A1]. We say an attack is bivariate, utilizing the bidimensional leakage vector A=[A1,A2]. More generally, an attack is d-variate if it utilizes a multidimensional leakage vector A=[A1,A2,⋯,Ad] of multiple samples. Note that in the optimal attack setting, it is often challenging for a multivariate attack to measure each share independently, which may be one reason why some adversaries limit themselves to univariate attacks when possible. Of course, setting aside leakage samples may only result in a loss of information, leading to a suboptimal attack. In the univariate case, the leakage of all shares is superimposed as one, i.e., satisfied:

A=∑i=1dAi=A1+A2+A3+⋯+Ad,=[(HW(state+L2Y2+⋯+LdYd)+N1]+[(HW(Y2)+N2)]+⋯+[(HW(Yd)+Nd)].(7)

The optimal univariate attack measures the sum of leakages for each trace, then the correct key key∗ is guessed as:

key∗=arg⁡maxkey′∑p=1Plog∑Y2exp−14σ2⋅{(Ap−HW(p+key′+L2Y2)−HW(Y2))2}(8)

The bivariate attack measures Ap1 and Ap2, and the attack guesses the correct key key∗ as:

key∗=arg⁡maxkey′∑p=1Plog∑Y2exp−12σ2⋅{(Ap1−HW(p+key′+L2Y2))2+(Ap2−HW(Y2))2}.(9)

3  Connect Nonlinear Function of Security Order Amplification

3.1 Bounded Moment Model and Security Order Amplification

The bounded moment leakage model aims to formally demonstrate the security of parallel implementations of mask applications and relate them to probing security [17]. In this theory, an n-share masking application that manipulates the secret x over N cycles encoded in the form x = (x0, ⋯, xn−1) for all shares. Similarly, we define Zc as the set of manipulated shares corresponding to the cycle c (0≤c≤N−1), with the cardinal of Zc denoted by nc. If the leakage Zc in cycle c follows a linear model, we have:

Lc=ac0Lc0(Zc(0))+⋯+acnc−1Lcnc−1(Zc(nc−1))+rc,(10)

where aci∈R, Lci is the deterministic leakage part coming from the manipulation share Zc(i) and rc is the random noise variable. It is worth noting that the computation of Eq. (10) above must ensure that the leakage corresponding to the different shares is independent. Otherwise, it is not possible to reflect the security order in the bounded moment and noise leakage models.

However, the actual security of the encoding may be higher than d when the leakage function is linearly related to the bits of the variable. In IPM, it interpreted as security order amplification. Since we assume that the leakage function Li is linear in the bits of xi, the leakage can expressed as:

Leakagei=Li(xi)+ri=ai+ai0×[xi]2(0)+⋯+aik−1×[xi]2(k−1)+ri=ai0×([xi]2(0)+aiai0)+⋯+aik−1×[xi]2(k−1)+ri=aij×(Di0[xi]2(0))+⋯+aik−1×(Dik[xk]2(0))+ri,(11)

with Dij, j∈[0,k−1] a deterministic function in the bit j of xi. We can see that Eqs. (10) and (11) have the same form, i.e., the serial implementation has the same bounded security as the parallel implementation has cycle N=n and cardinal nc=k. Thus, the bounded moment security order d′ of the IPM is equivalent to the bit probing security of its corresponding encoding [xi]2. However, this assumption of linearity exists only in an ideal adversarial situation, and deviation from this assumption may make security assessment challenging. Several studies have shown (e.g., [18,19]) that by applying a nonlinear transformation to a linear leakage function, and this tends to change the linear properties of the function, which in turn affects the actual attack efficacy and evaluation results.

3.2 Nonlinear Function of Security Order Amplification

The premise that IPM has security order amplification is the linear function quantifies the leakage in bits. The leakage function that deviates from this case can derive two asymptotic assumptions. The first is that the leakage function is nonlinear but can still perform operations in units of bits. The other is a nonlinear function that operates in units of words. In our construction, the nonlinear function is a polynomial which consisting of a linear component and one or more nonlinear components, each of which is a power function of the linear component. We construct two leakage functions to satisfy each of the two assumptions. The first one is that the compound leakage function is nonlinear in bits. The second is that the like_hamming leakage function is nonlinear in word.

Definition1(Compoundleakagefunction). Given functions f:P→Q and g:Q→O, g∘f is a compound leakage function if g∘f:P→O is satisfied.

Theorem1. Given x∈Fq, bi∈(0,1) and f≡HW(x), exists function set Φ={gi(f)|gi(f)=bi8i−1fi, i∈[1,n]}, such that the sum of any ordered subset Φ′ (|Φ′|≥2) is a compound leakage function, which denoted as g∘f(x)=∑i∈[1,|Φ′|]gi(f).

Proof. Given bi∈(0,1), gi(f) converts the linear leakage values using the nonlinear function gi(x)=bi8i−1fi∈[0,8bi]. Thus, the sum of the nonempty subsets Φ′ for Φ is equivalent to a superposition of multiple compound leakage functions (where g1(x) is considered a mapping of itself), and the result is still a compound leakage function.

We use the leakage function g∘f=b1f+b28f2 of degree equal to 2 (Also, other cases can substitute) as a derivation example of security order amplification. We have the following equation:

Leakagei=g∘f(xi)+ri=b1(Li(xi))+b28(Li(xi))2+ri=b1(ai+ai0×[si]2(0)+⋯+aik−1×[si]2(k−1))+b28(ai+ai0×[si]2(0)+⋯+aik−1×[si]2(k−1))2+ri=b1((ai0×([si]2(0))+aiai0)+⋯+aik−1×[si]2(k−1))+b28((ai0×([si]2(0))+aiai0)+⋯+aik−1×[si]2(k−1))2+ri=b1(aij×(Di0[xi]2(0))+⋯+aik−1×(Dik[xk]2(0)))+b28(aij×(Di0[xi]2(0))+⋯+aik−1×(Dik[xk]2(0)))2+ri=(aij×(Di0[xi]2(0)))×(b1+b28×(aij×(Di0[xi]2(0)))+⋯+b24×(aik−1×(Dik[xk]2(0))))+⋯+(aik−1×(Dik[xk]2(0)))×(b1+b24×(aij×(Di0[xi]2(0)))+⋯+b28×(aik−1×(Dik[xk]2(0))))+ri(12)

Obviously, the leakage function is not linear in bits but is a nonlinear combination of k bits. It is equivalent to the fact that the probing security of a serial implementation of equivalent encoding corresponds to the case where a probe can probe one word, and the n different leakages {Leakagei}i=0n−1 is not to be regarded as a parallel implementation of equivalent encoding with cycle N=n. That is, if the leakage of shares is independent, and the different bits of each element cannot operate independently, it cannot have the d′-order probing security of the bit and does not have the d′-order security of the bounded moment. Thus, the high bit probing security of the IPM in choosing the optimal parameter L under the linear assumption disappears and returns to the same probing security order as the BM.

Definition2(like_hammingleakagefunction). Given X∈Fq, the function h: X→Y∈[0, ρ] is a like_hamming leakage function.

Theorem2. Let cj∈(0,1), s∈Fq. Let ρ be a positive integer belonging to (0,8], there is function set Ω={hj(s)|hj(s)=ρ⋅cj(s255)j,j∈[1,n]}, such that the sum of any ordered subset Ω′ (|Ω′|≥2) is a like_hamming leakage function, which denoted as h(s)=∑j∈[1,|Ω′|]hj(s).

Proof. Given cj∈(0,1) and ρ⋅(s255)j∈[0,ρ], h=∑j∈[1,|Ω′|]hj(s)=ρ⋅c1(s255)+⋯+ρ⋅cj(s255)j. h has maximum value hmax=(ρ⋅c1+⋯+ρ⋅cj) if and only if (s255)j,j∈[1,|Ω′|]=1. Let ∑j∈[1,|Ω′|]cj=1, then we have hmax=ρ. It proved that the sum of any subsets of Ω′ in the set Ω belongs to [0, ρ] (Let ρ=8, then we have the maximum value of the leakage function in concordance with HW.) and h is a like_hamming function.

Similarly, we use the like_hamming function with degree equal to 2 to compute the leakage. The leakage of manipulated share xi can represented as:

Leakagei=h(xi)+ri=ρ×c1⋅(xi255)+ρ×c2⋅(xi255)2+ri.(13)

In this case, the leakage function is not linear to the bits of the variable but nonlinear to the word. Therefore, we cannot represent leakage in Eq. (11), and security order amplification does not hold. In other words, the IPM only implies d-order word probing security and not d′-order bit probing security.

4  Experimental Validation and Analysis

In this section, the leakage of IPM under the adversarial and implementation conditions is analysed experimentally, including correlation analysis, linear leakage analysis and nonlinear leakage analysis. In the correlation and nonlinear leakage analysis, the degree of the leakage function is set to 2, 3, and 4 (from left to right), and the results are additionally plotted when the coefficients are unconstrained by the constraints, respectively. In the study of the public parameters, L2 was set to 5, 7, and 17 to observe the leakage of the first-order IPM.

4.1 Correlation Analysis of the Leakage

In the previous section, we constructed two nonlinear leakage functions and showed the relationship between the leakage functions and the security order amplification. For verification of the actual quantification of leakage, we assume that there are enough samples to correlate the simulated power consumption obtained under the nonlinear function with really collected leakage, and the dataset is a first-order IPM-protected AES-128 implemented on a Xilinx Spardan-6 FPGA mounted on a SAKURA-G FPGA board designed for hardware security research and development. We collected 20 k power traces using a random plaintext and a constant key and used these data to perform correlation experiments with the quantification data. Since the output of the polynomial function is related to the degree and the coefficients, we set the coefficients of the linear component to be larger than the coefficients of the nonlinear component (the linear component of both functions is larger than or equal to the nonlinear component in the absence of coefficients). In addition, to investigate the quantisation ability of the leakage function even further, we additionally considered the case of deviation ∑i=1|Φ′|bi=1 (or ∑j=1|Ω′|cj=1).

We investigate the correlation between the collected power traces and the quantitative results of the two nonlinear functions. We computed correlation coefficients for 700 points of data selected from 20,000 power traces. The first set of experiments was conducted under the constraints, and the results are shown in Figs. 1 and 2. The correlation coefficients of the compound leakage function and the like_hamming leakage function have a marked difference. This distinction is related to the data distribution, which in turn is determined by the nature of the function itself. The compound leakage function is a leakage function that is nonlinear on bits, whereas the like_hamming leakage function is nonlinear on words. The former retains a certain quantisation property of HW on bits, which exhibits correlation coefficients that are closer to it. The increase in degree causes the coefficients to be rescaled, which weakens the function’s ability to quantify leakage, thus presenting a reduced correlation coefficient. On the other hand, we observed the correlation coefficients when the linear component was dominant for comparison. The results show that correlation coefficients are almost similar to those of the HW leakage function. This is essentially consistent with the linear regression experiment in [15], where the linear component is dominated equivalently to the nonlinear component being negligible. Figs. 3 and 4illustrate the results of the correlation analysis with unconstrained coefficients, which is consistent with the conclusions of the constrained analysis.

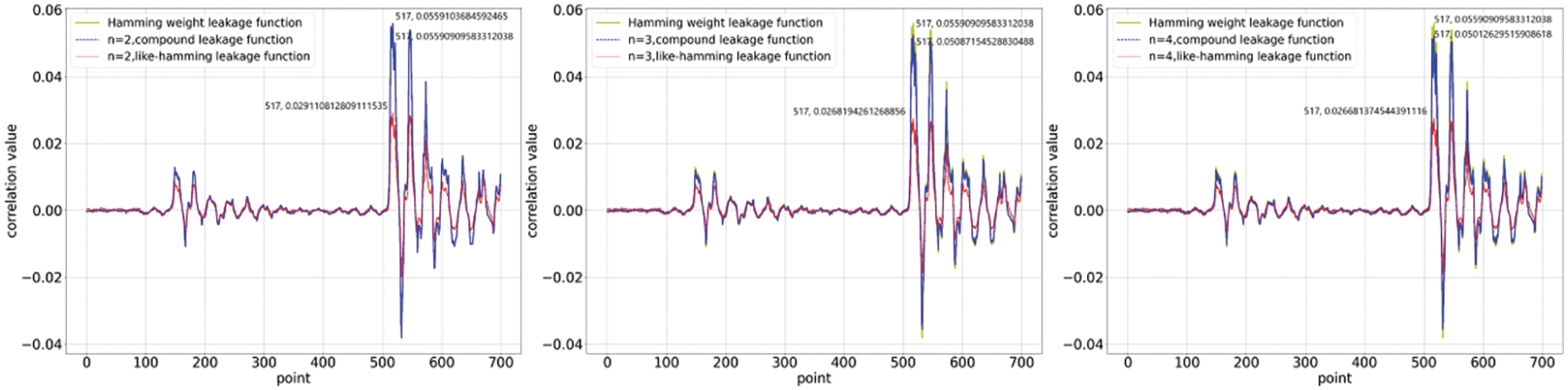
Figure 1: Calculation of correlation coefficients when the function coefficients are constrained and the linear component is dominated

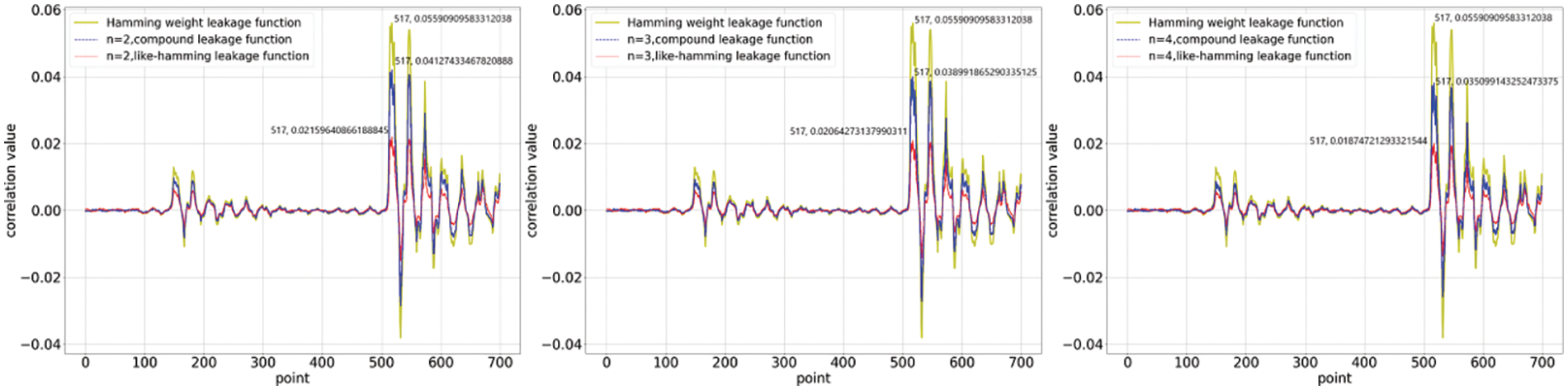
Figure 2: Calculation of correlation coefficients when the function coefficients are constrained

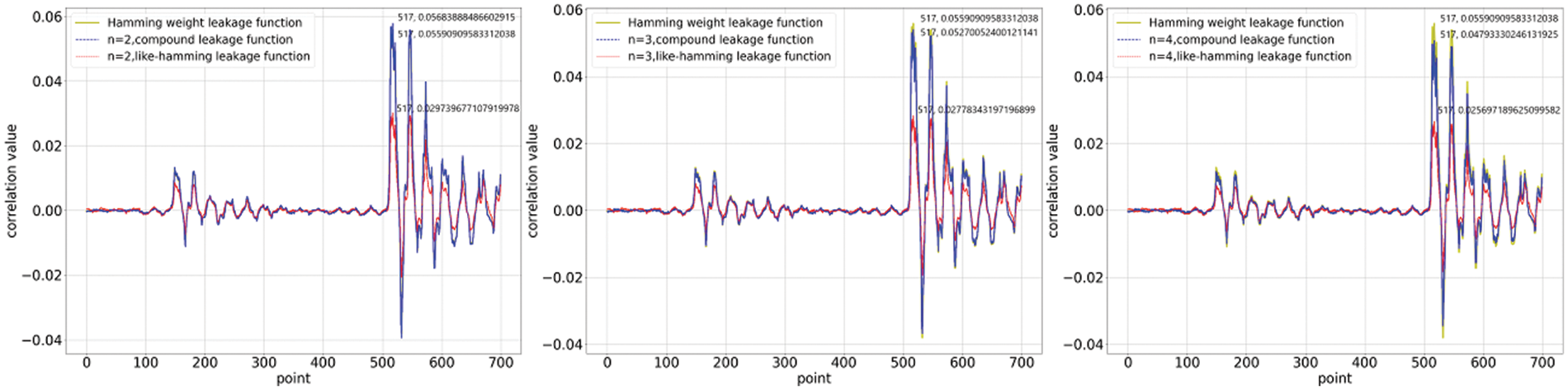
Figure 3: Calculation of correlation coefficients when the function coefficients are unconstrained and the linear component is dominated

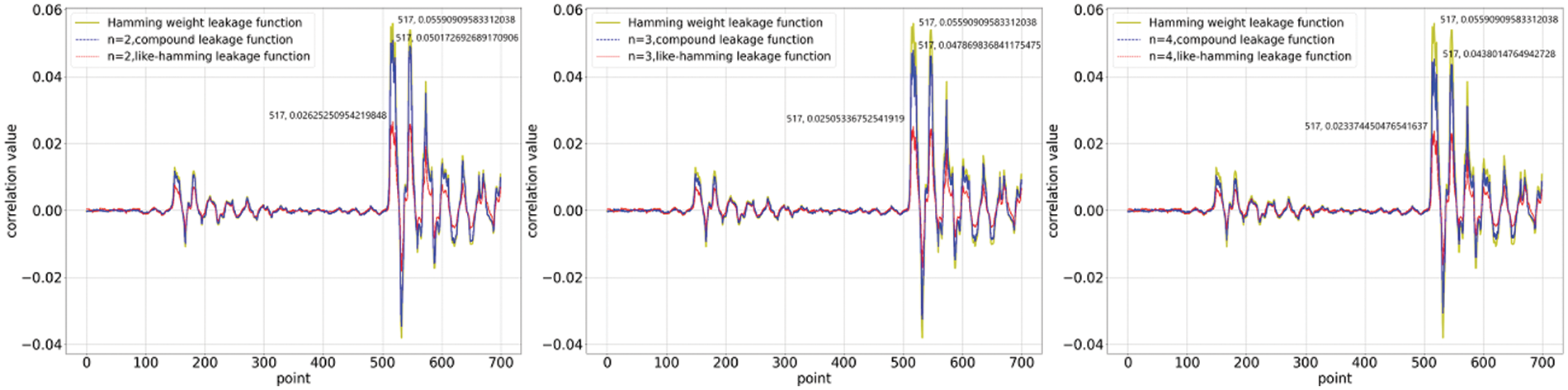
Figure 4: Calculation of correlation coefficients when the function coefficients are unconstrained

4.2 Linear Leakage Analysis of IPM

It is well known that Mutual Information (MI) [20] reflects information leakage between shares and masked variables, independently of their adversaries. This step quantifies the security of the device’s PDF towards the adversary when countermeasures are used. It can also used as an objective metric for assessing the quality of countermeasures when facing an attack by the strongest adversary.

MI(S;A1)=H[S]+∑s∈SPr[s]×∑A1∈APr[A1|s]×log2⁡Pr[s|A1](14)

In Eq. (14), the Pr[A1|s] is the conditional probability of random share s given a leakage A1. The Pr[s|A1]=Pr[A1|s]⋅Pr[s]∑s∗Pr[A1|s∗]⋅Pr[s∗] is the conditional probability of leakage A1 given random share s, where s∗ is the real share. The MI in the bivariate case:

MI(S;A1,A2)=H[S]+∑s∈SPr[s]×∑A1,A2∈APr[A1,A2|s]×log2⁡Pr[s|A1,A2](15)

Our information-theoretic analysis of IPM is shown in Figs. 5 and 6. It also plotted the observation for a BM and an unprotected s (i.e., for which the adversary can observe A=HW(s)⊕N). Fig. 5 shows the results for the univariate case, where we first observe that the level of leakage in response to different values of L is not consistent. At low noise levels, the high algebraic complexity that IPM has significantly reduced leakage compared to BM. It can be explained by the fact that one bit of each share in BM directly changes a secret bit, whereas the introduction of public parameter L in IPM makes this feature change. At the high noise level, the slopes of the unprotected and BM curves are changed from −1 to −2, which reduces the possibility of information leakage. The measurement of IPM indicates that adjusting the public parameter can further reduce information leakage. That is, the slope of the curve can reduced to −3 or even −4. In summary, if the leakage function linearly mixes the bits in the encoding, then the higher dual distance of the matrix H obtained by security order amplification of the chosen public parameters L, the higher security order will be in the bound moment model.

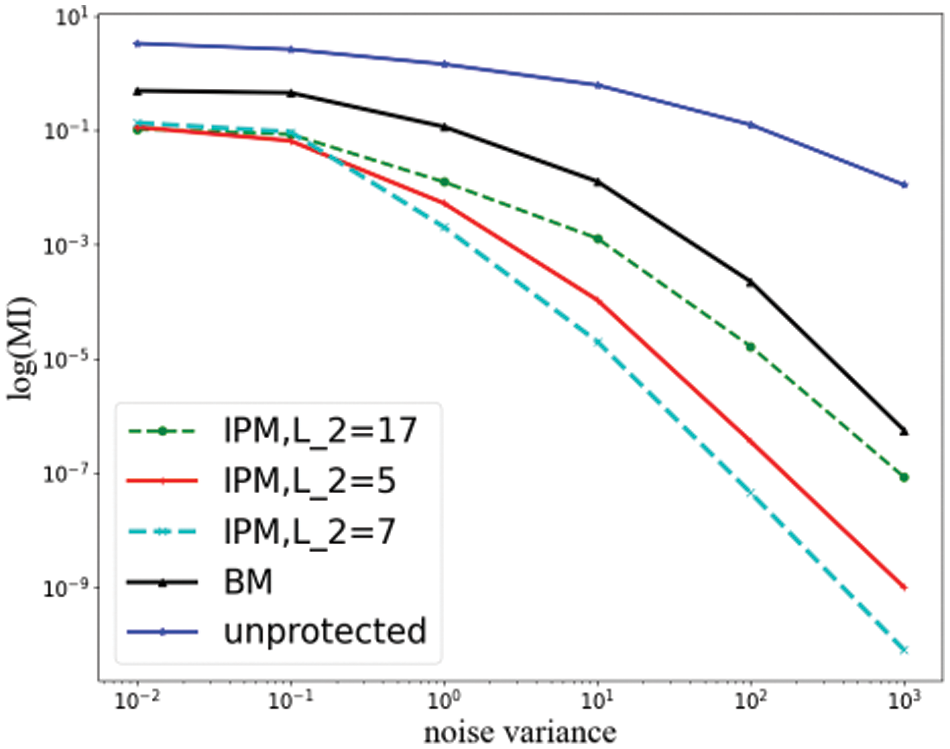
Figure 5: Information-theoretic analysis of IPM under univariate attacks

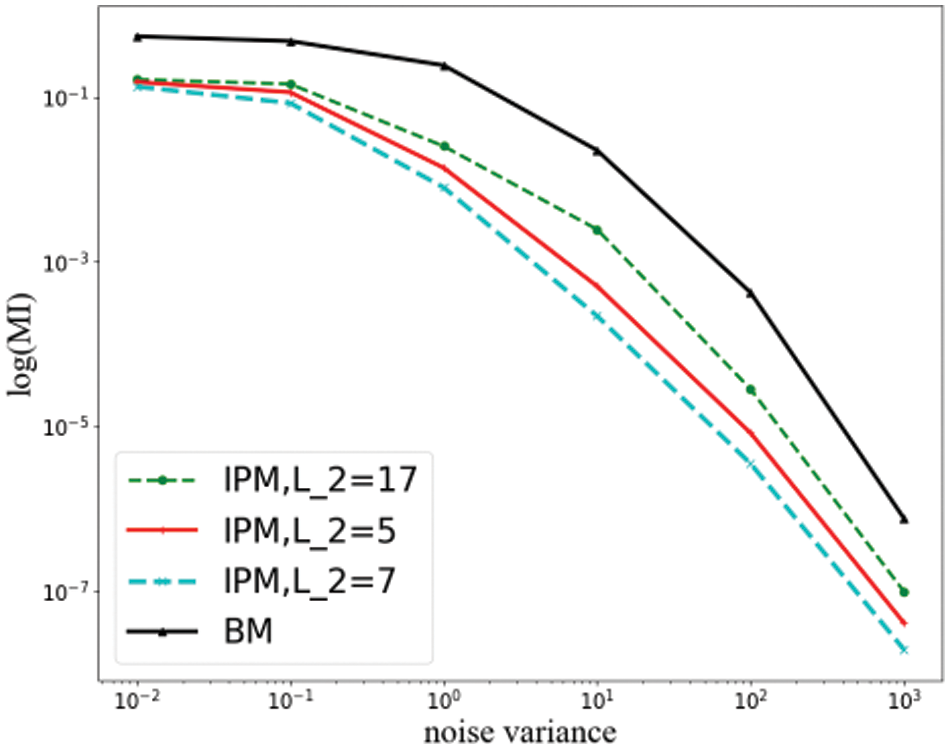
Figure 6: Information-theoretic analysis of IPM under bivariate attacks

In the bivariate case, we first observe a convergence of the security orders obtained by security order amplification, which is shown in the figure as a regression of the slopes of the information curves with different parameters, implying that the differences between the security features are decreasing. Despite the further increase in the leaked information under the bivariate attack, the security features in the bounded moment model are still retained. The difference between the slopes of these curves becomes less prominent but is still steadily larger than the slopes of the BM’s curves, indicating that the IPM still maintains its security order robustness in the face of bivariate attacks.

4.3 Nonlinear Leakage Analysis of IPM

In the section, we use the polynomial leakage function from Section 3.2 to perform an information theoretic analysis of IPM. Figs. 7 and 8show the effect of the degree and the linear component in the polynomial function on the evaluation results, respectively.

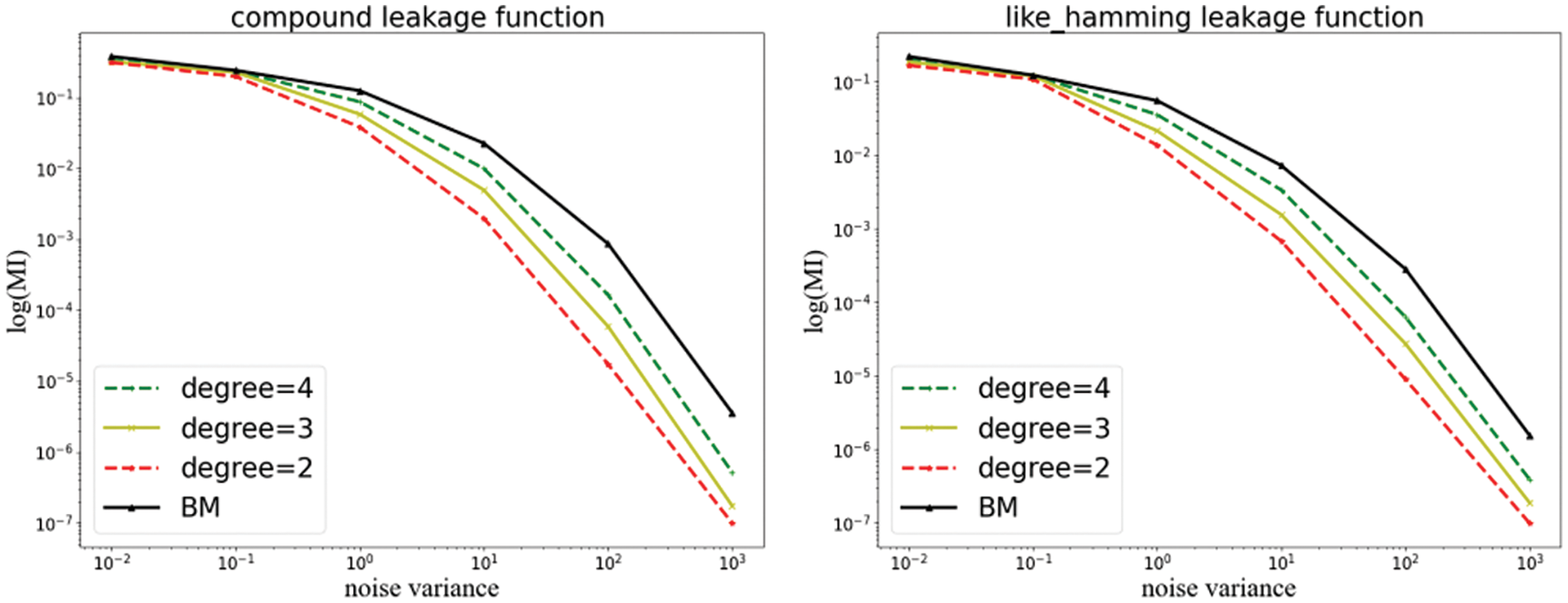
Figure 7: Information-theoretic analysis of IPM with polynomial functions of different degrees

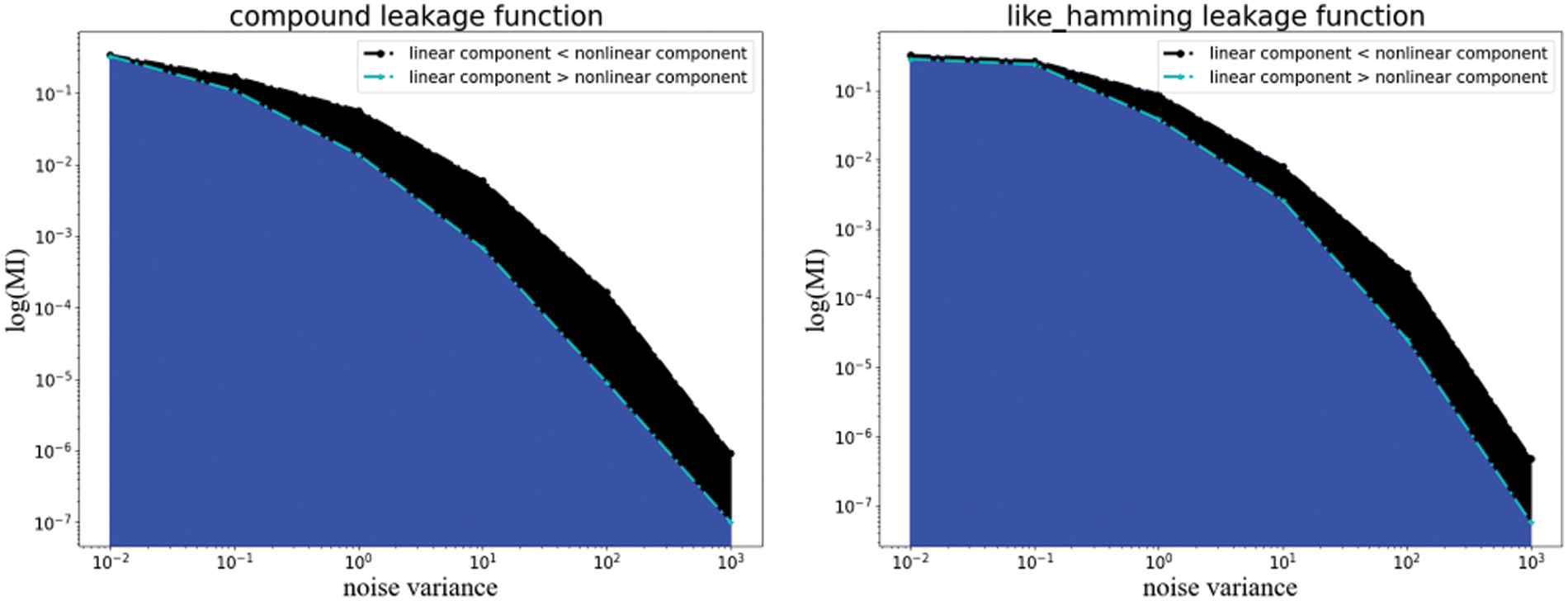
Figure 8: Information-theoretic analysis of IPM with polynomial functions of linear component

In Fig. 7, we calculate the MI for different degrees of the leakage function. We can see that the leakage of IPM is smaller than BM. Furthermore, in terms of finite noise levels, Fig. 7 shows that the smallest noise levels (i.e., smaller degrees) have higher security levels (reflected by the slopes of the curves). This relation can be explained as follows. Assuming that the corresponding linear leakage llinear(x)+N in the IPM only contains information about its third-order moments, and since the distribution of shares is uniform, we can extract the first-order information from the third-power leakage (llinear(x)+N)3 but also raise the noise to the third power. Say now the leakage function is not linear anymore, but nonlinear. Then the same first-order information will be found in samples of the form lnonlinear(x)+N, i.e., without amplifying the noise.

On the other hand, we observe that leakage functions dominated by linear component are usually able to retrieve higher security, and the result is displayed in Fig. 8. The larger the linear component is, and the nonlinear component is almost negligible. Then, the PDF of the quantised leakage is closer to the PDF of the linear leakage, and the security order can retrieve is closer to the security order in the linear case. As part of the supporting evidence, the study in [12] suggests that linear regression estimates a suitable tool for leakage linearity, which allows estimating how the data is leaked at the bit level. Similarly, references [21] and [10] show security studies using nonlinear leakage functions.

4.4 More Experiments for Observation and Comparison

4.4.1 Nonlinear Leakage Analysis with Coefficients

In this section, we add some observations from the function coefficients. The increase in degree requires a rescaling of the coefficients between the components, which can make the leakage of the same xi not consistent. The study of linear components in the previous section shows that linear components are significantly more dominant than higher-order nonlinear components. We set the coefficients of the linear components always to be larger than the nonlinear components, and the coefficients of the original nonlinear terms do not change with increasing degrees, which means that the new higher-order nonlinear components cause the coefficients of the linear components to decrease. The experimental results are displayed in Figs. 9 and 10. Although adjusting the coefficients changes the distribution of the quantitative data, this has a negligible effect on the security order. Once the security order amplification depends assumption is no longer satisfied, the MI curves are nearly identical in slope. That is, the IPM only satisfies the d-order word level probing security order and not the d′-order bit probing security order.

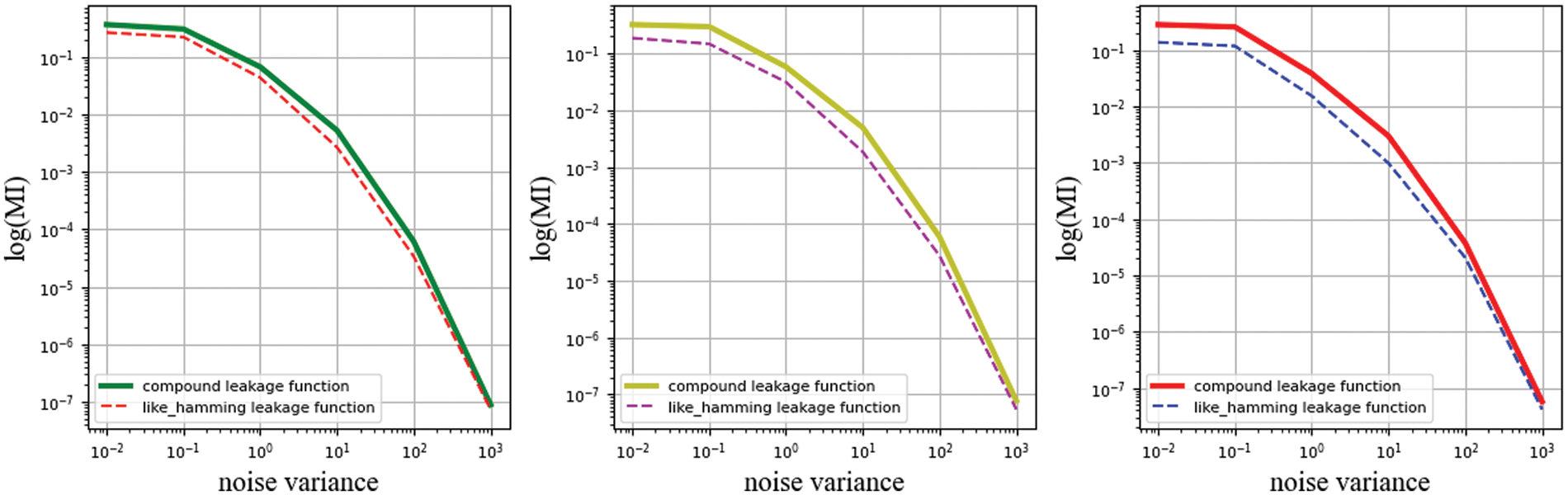
Figure 9: The coefficients are constrained by different function to calculate MI

Figure 10: The coefficients are unconstrained by different function to calculate MI

4.4.2 Nonlinear Leakage Analysis with Different SNR

If a device utilizes higher Gaussian noise levels to reduce leakage, the SNR can considered as a more straightforward metric. This technique restrict leakage evaluation to the so-called “first-order information”, assessing the leakage of each share using the first-order statistical moments of the leakage PDF [22].

SNR=var^si(E^ni(lsi))E^si(var^ni(lsi))(16)

where E^ represents the sample mean operator, var^ is the sample variance.

In previous experimental results, we observed that MI decreases exponentially for sufficiently large noise. An intuitive assumption is that if the IPM has a sufficiently high noise level, this will be sufficient for signal concealment. Therefore, a remarkably straightforward expression is to plot the MI metric at different SNRs, as shown in Figs. 11 and 12. We can clearly observe the calculated MI values for the two functions at different SNRs. At lower SNR, the value of MI is low, which coincides with our conjecture. Another observation unfolds across functions, where the differences between functions make the amount of noise added to achieve the same SNR differently. The amount of quantitative information directly contributes to the difference where the two functions reach the critical point. The assessor may opt to calculate it after reducing dimensionality or express the condition directly in a function of the MI. Furthermore, the observations demonstrate that the effect of the amount of noise on MI is generalised and not restricted to one or a class of functions.

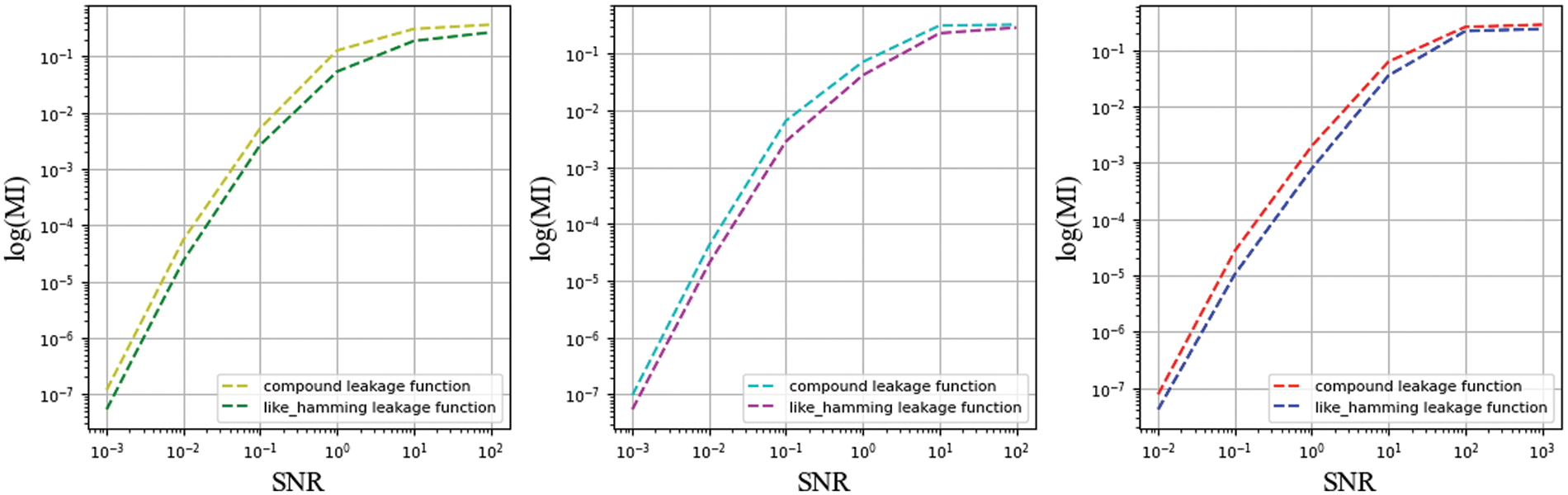
Figure 11: Function coefficients constrained by MI for different SNRs

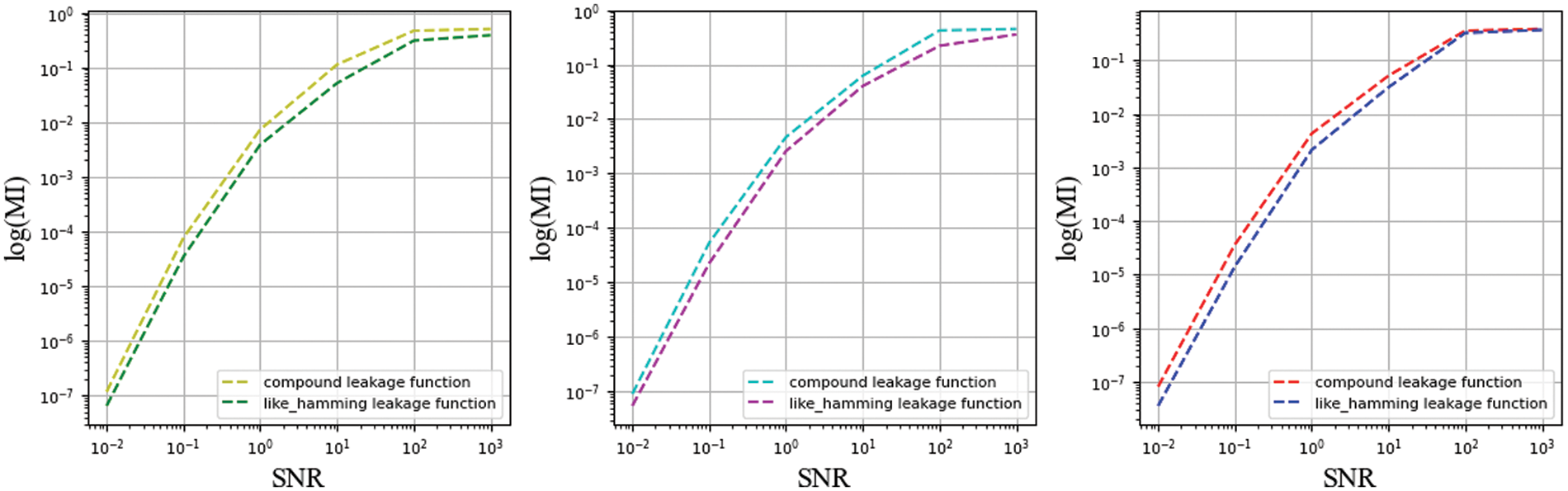
Figure 12: Function coefficients unconstrained by MI for different SNRs

4.4.3 Nonlinear Leakage Analysis with Different L Values

Given the preceding observations of the IPM in the identical L vector, the subsequent logical progression is to explore the effects of a departure from this presumption. The heightened algebraic complexity of IPM facilitates reduced linear leakage compared to BM at low noise levels. The results of the information-theoretic analysis are given in Figs. 13 to 16. Also, we again report on the leakage of an unprotected s and a BM encoding.

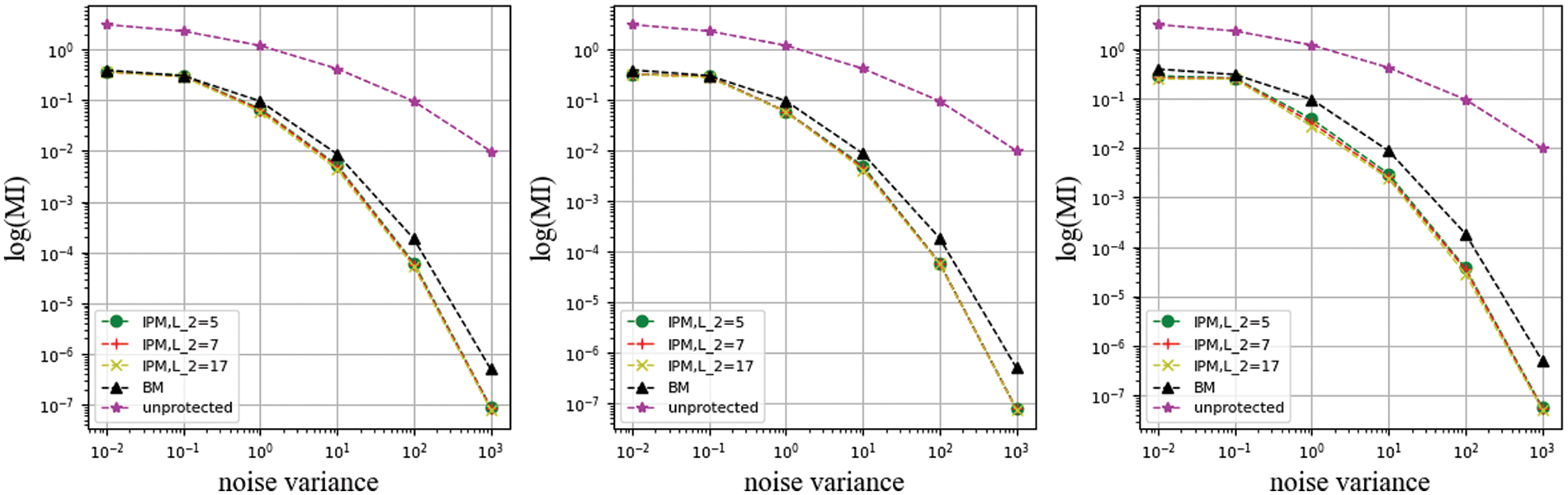
Figure 13: Use compound leakage function with coefficient constrained of different L2 values

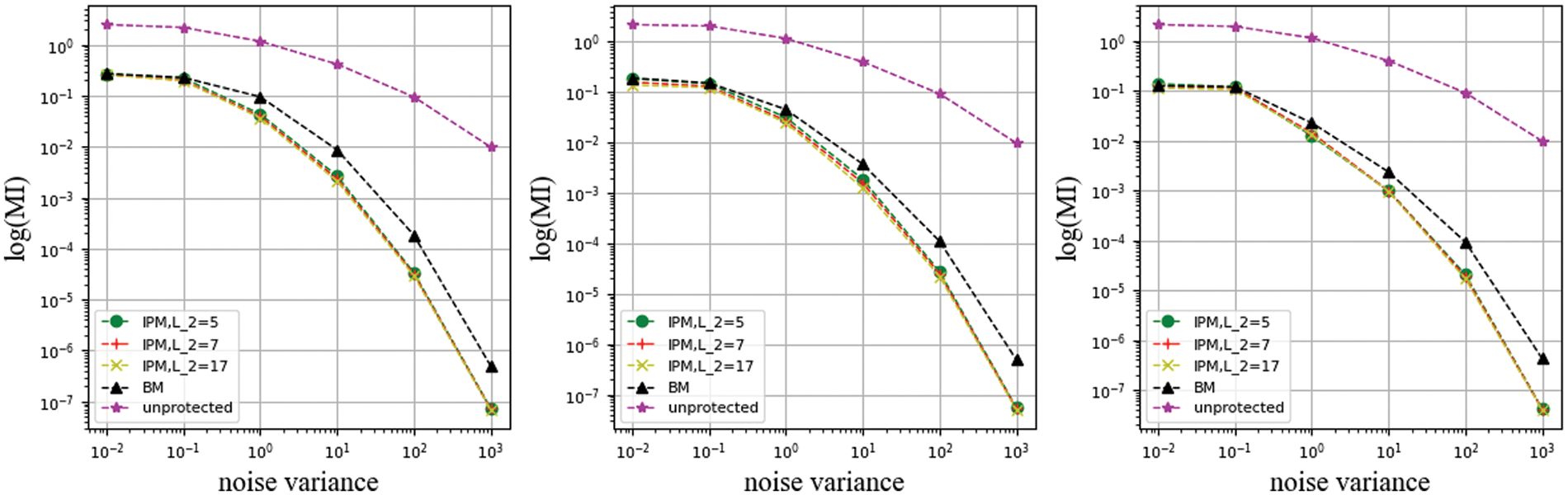
Figure 14: Use like_hamming leakage function with coefficient constrained of different L2 values

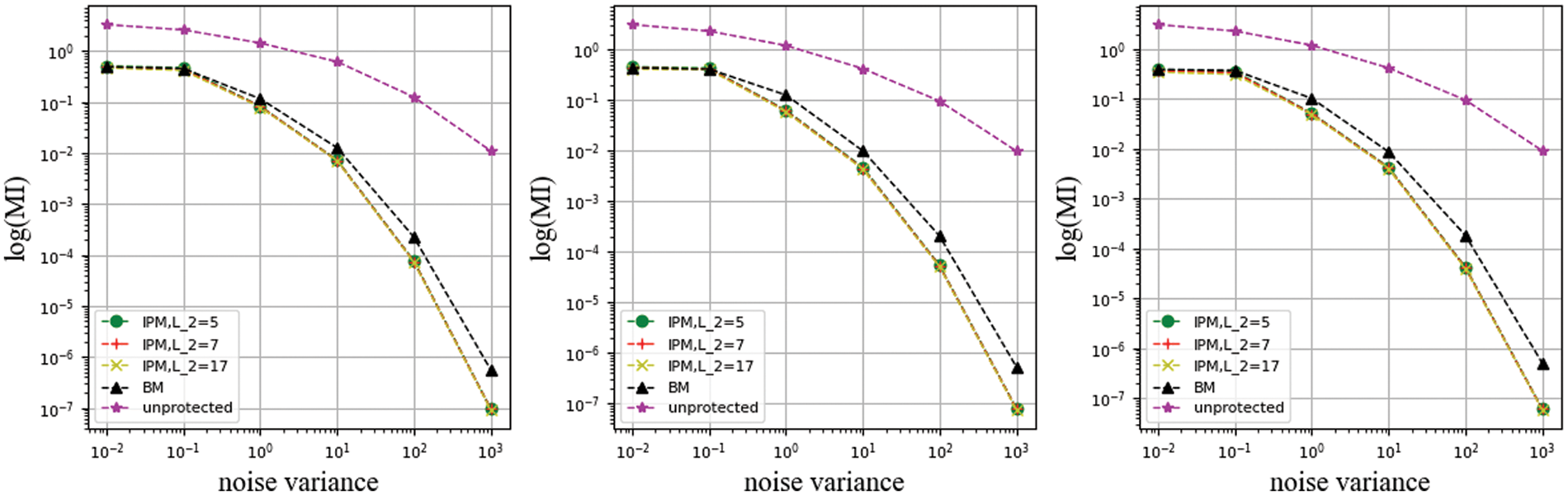
Figure 15: Use compound leakage function with coefficient unconstrained of different L2 values

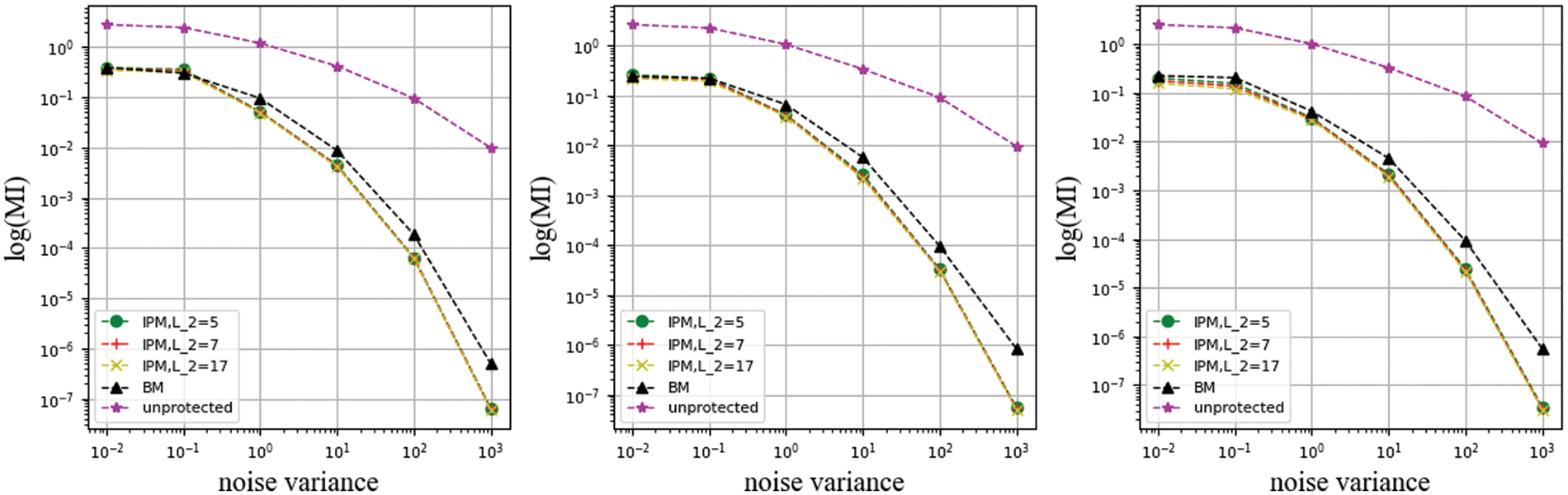
Figure 16: Use like_hamming leakage function with coefficient unconstrained of different L2 values

In this set of experiments, it can be seen that the IPM with different public parameters L expresses nearly the same slope of the curve as the BM in the high noise levels. It confirms the analysis in Section 5 that the nonlinear function makes the security features obtained by the IPM through security order amplification disappear and return to nearly the same security order as the BM. In the low noise level, the nonlinear function compensates for the algebraic complexity of the BM and makes the distance between the BM and the IPM disappear. This means that the security order amplification of IPM depends on the specific implementation.

5  Conclusion

In the paper, we investigated information leakage in IPM under adversarial and implementation conditions. In the adversarial condition, we observe the specific security of IPMs in the face of univariate and multivariate forms of leakage. The security features of IPM converged in the univariate case, but its security features did not disappear. In the implementation condition, we studied the information leakage of IPM under nonlinear functions. We constructed two leakage functions with different quantitative capabilities and analysed the impact of certain characteristic metrics of the functions on the evaluation results. The experimental results show that the high security level of IPM is gradually disappearing under nonlinear conditions, which means that the security order amplification of IPM is strictly dependent on the specific implementation.

Acknowledgement: The authors also gratefully acknowledge the helpful comments and suggestions of the reviewers and editors, which have improved the presentation.

Funding Statement: This research is supported by the Hunan Provincial Natrual Science Foundation of China (2022JJ30103), “the 14th Five-Year” Key Disciplines and Application Oriented Special Disciplines of Hunan Province (Xiangjiaotong [2022] 351) the Science and Technology Innovation Program of Hunan Province (2016TP1020).

Author Contributions: Yuyuan Li: Conceptualization, Writing-Original Draft; Lang Li: Writing-Review and Editing, Supervision; Yu Ou: Term, Project Administration, Formal Analysis. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: There is no availability data and materials.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Chari, C. S. Jutla, J. R. Rao, and P. Rohatgi, “Towards sound approaches to counteract power-analysis attacks,” presented at the CRYPTO 1999, Santa Barbara, California, USA, vol. 1666, Aug. 15–19, 1999, pp. 398–412. doi: 10.1007/3-540-48405-1. [Google Scholar] [CrossRef]

2. J. Balasch, S. Faust, B. Gierlichs, and I. Verbauwhede, “Theory and practice of a leakage resilient masking scheme,” presented at the ASIACRYPT 2012, Beijing, China, vol. 7658, Dec. 2–6, 2012, pp. 758–775. doi: 10.1007/978-3-642-34961-4_45. [Google Scholar] [CrossRef]

3. J. Balasch, S. Faust, and B. Gierlichs, “Inner product masking revisited,” presented at the EUROCRYPT 2015, Sofia, Bulgaria, vol. 9056, Apr. 26–30, 2015, pp. 486–510. doi: 10.1007/978-3-662-46800-5_19. [Google Scholar] [CrossRef]

4. J. Balasch, S. Faust, B. Gierlichs, C. Paglialonga, and F. X. Standaert, “Consolidating inner product masking,” presented at the ASIACRYPT 2017, Hong Kong, China, vol. 10624, Dec. 3–7, 2017, pp. 724–754. doi: 10.1007/978-3-319-70694-8_25. [Google Scholar] [CrossRef]

5. C. Carlet et al., “Polynomial direct sum masking to protect against both SCA and FIA,” J. Cryptogr. Eng., vol. 9, pp. 303–312, 2019. doi: 10.1007/s13389-018-0194-9. [Google Scholar] [CrossRef]

6. H. Maghrebi, S. Guilley, and J. L. Danger, “Leakage squeezing countermeasure against high-order attacks,” presented at the WISTP 2011, Heraklion, Crete, Greece, vol. 6633, Jun. 1–3, 2011, pp. 208–223. doi: 10.1007/978-3-642-21040-2_14. [Google Scholar] [CrossRef]

7. V. Grosso, F. X. Standaert, and E. Prouff, “Low entropy masking schemes, revisited,” presented at the CARDIS 2013, Berlin, Germany, vol. 8419, Nov. 27–29, 2014, pp. 33–43. doi: 10.1007/978-3-319-08302-5_3. [Google Scholar] [CrossRef]

8. M. Ouladj et al., “Spectral approach to process the (multivariate) high-order template attack against any masking scheme,” J. Cryptogr. Eng., vol. 12, pp. 75–93, 2022. doi: 10.1007/s13389-020-00253-4. [Google Scholar] [CrossRef]

9. M. Staib and A. Moradi, “Deep learning side-channel collision attack,” presented at the TCHES 2023, vol. 2023, 2023, pp. 422–444. doi: 10.46586/tches.v2023.i3.422-444. [Google Scholar] [CrossRef]

10. W. Wang, Y. Yu, and F. X. Standaert, “Provable order amplification for code-based masking: How to avoid non-linear leakages due to masked operations,” IEEE Trans. Inf. Forensic. Secur., vol. 14, pp. 3069–3082, 2019. doi: 10.1109/TIFS.2019.2912549. [Google Scholar] [CrossRef]

11. W. Wang, P. Méaux, G. Cassiers, and F. X. Standaert, “Efficient and private computations with code-based masking,” presented at the TCHES 2020, vol. 2020, 2020, pp. 128–171. doi: 10.13154/tches.v2020.i2.128-171. [Google Scholar] [CrossRef]

12. R. Poussier, Q. Guo, F. X. Standaert, C. Carlet, and S. Guilley, “Connecting and improving direct sum masking and inner product masking,” presented at the CARDIS 2017, Lugano, Switzerland, vol. 10728, Nov. 13–15, 2018, pp. 123–141. doi: 10.1007/978-3-319-75208-2_8. [Google Scholar] [CrossRef]

13. W. Wang et al., “Inner product masking for bitslice ciphers and security order amplification for linear leakages,” presented at the CARDIS 2016, Cannes, France, vol. 10146, Nov. 7–9, 2017, pp. 174–191. doi: 10.1007/978-3-319-54669-8_11. [Google Scholar] [CrossRef]

14. W. Cheng, S. Guilley, C. Carlet, S. Mesnager, and J. L. Danger, “Optimizing inner product masking scheme by a coding theory approach,” IEEE Trans. Inf. Forensic. Secur., vol. 16, pp. 220–235, 2021. doi: 10.1109/TIFS.2020.3009609. [Google Scholar] [CrossRef]

15. J. Ming, Y. Zhou, W. Cheng, and H. Li, “Optimizing higher-order correlation analysis against inner product masking scheme,” IEEE Trans. Inf. Forensic. Secur., vol. 17, pp. 3555–3568, 2022. doi: 10.1109/TIFS.2022.3209890. [Google Scholar] [CrossRef]

16. Y. Ishai, A. Sahai, and D. Wagner, “Private circuits: Securing hardware against probing attacks,” presented at the CRYPTO 2003, Santa Barbara, California, USA, vol. 2729, Aug. 17–21, 2003, pp. 463–481. doi: 10.1007/978-3-540-45146-4_27. [Google Scholar] [CrossRef]

17. G. Barthe, F. Dupressoir, S. Faust, B. Grégoire, F. X. Standaert and P. Y. Strub, “Parallel implementations of masking schemes and the bounded moment leakage model,” presented at the EUROCRYPT 2017, Paris, France, vol. 10210, Apr. 30–May 4, 2017, pp. 535–566. doi: 10.1007/978-3-319-56620-7_19. [Google Scholar] [CrossRef]

18. E. Peeters, F. X. Standaert, and J. J. Quisquater, “Power and electromagnetic analysis: Improved model, consequences and comparisons,” Integr., vol. 40, pp. 52–60, 2007. doi: 10.1016/j.vlsi.2005.12.013. [Google Scholar] [CrossRef]

19. Q. Tian, M. O’neill, and N. Hanley, “Can leakage models be more efficient? Non-linear models in side channel attacks,” presented at the WIFS 2014, Atlanta, GA, USA, Dec. 3–5, 2014, pp. 215–220. doi: 10.1109/WIFS.2014.7084330. [Google Scholar] [CrossRef]

20. O. Bronchain, J. M. Hendrickx, C. Massart, A. Olshevsky, and F. X. Standaert, “Leakage certification revisited: Bounding model errors in side-channel security evaluations,” presented at the CRYPTO 2019, Santa Barbara, California, USA, vol. 11692, Aug. 17–21, 2019, pp. 713–737. doi: 10.1007/978-3-030-26948-7_25. [Google Scholar] [CrossRef]

21. C. Whitnall, E. Oswald, and F. X. Standaert, “The myth of generic DPA…and the magic of learning,” presented at the CT-RSA 2014, San Francisco, CA, USA, vol. 8366, Feb. 25–28, 2014, pp. 183–205. doi: 10.1007/978-3-319-04852-9_10. [Google Scholar] [CrossRef]

22. S. Mangard, E. Oswald, and F. X. Standaert, “One for all-all for one: Unifying standard differential power analysis attacks,” IET Inf. Secur., vol. 5, pp. 100–110, 2011. doi: 10.1049/iet-ifs.2010.0096. [Google Scholar] [CrossRef]