An Elite-Class Teaching-Learning-Based Optimization for Reentrant Hybrid Flow Shop Scheduling with Bottleneck Stage

1  Introduction

A hybrid flow shop scheduling problem (HFSP) is a typical scheduling problem that exists widely in many industries such as petrochemicals, chemical engineering, and semiconductor manufacturing [1,2]. The term ‘reentrant’ means a job may be processed multiple times on the same machine or stage [3]. A typical reentrant is a cyclic reentrant [4,5], which means that each job is cycled through the manufacturing process. As an extension of HFSP, RHFSP is extensively used in electronic manufacturing industries, including printed circuit board production [6] and semiconductor wafer manufacturing [7], etc.

RHFSP has been fully investigated and many results have been obtained in the past decade. Xu et al. [8] applied an improved moth-flame optimization algorithm to minimize maximum completion time and reduce the comprehensive impact of resources and environment. Zhou et al. [9] proposed a hybrid differential evolution algorithm with an estimation of distribution algorithm to minimize total weighted completion time. Cho et al. [10] employed a Pareto genetic algorithm with a local search strategy and Minkowski distance-based crossover operator to minimize maximum completion time and total tardiness. Shen et al. [11] designed a modified teaching-learning-based optimization (TLBO) algorithm to minimize maximum completion time and total tardiness, where Pareto-based ranking method and training phase are adopted.

In recent years, RHFSP with real-life constraints has attracted much attention. Lin et al. [12] proposed a hybrid harmony search and genetic algorithm (HHSGA) for RHFSP with limited buffer to minimize weighted values of maximum completion time and mean flowtime. For RHFSP with missing operations, Tang et al. [13] designed an improved dual-population genetic algorithm (IDPGA) to minimize maximum completion time and energy consumption. Zhang et al. [14] considered machine eligibility constraints and applied a discrete differential evolution algorithm (DDE) with a modified crossover operator to minimize total tardiness. Chamnanlor et al. [15] adopted a genetic algorithm hybridized ant colony optimization for the problem with time window constraints. Wu et al. [16] applied an improved multi-objective evolutionary algorithm based on decomposition to solve the problem with bottleneck stage and batch processing machines.

In HFSP with H stages, each job is processed in the following sequence: Stage 1, stage 2, ⋯, stage H. If processing time of each job at a stage is significantly longer than its processing time at other stages, then that stage is the bottleneck stage. The bottleneck stages often occur in real-life manufacturing processes when certain stages of the process are slower than others, limiting the overall efficiency of the process [16–21]. These stages may arise due to resource constraints, process complexity or other factors. Bottleneck stage is a common occurrence in real-life manufacturing processes, such as seamless steel tube cold drawing production [16], engine hot-test production [20] and casting process [21]. More processing resources or times are needed at the bottleneck stage, and the production capacity of the whole shop will be limited because of bottleneck stage. There are some works about HFSP with the bottleneck stage. Costa et al. [17] considered HFSP with bottleneck stage and limited human resource constraint and applied a novel discrete backtracking search algorithm. Shao et al. [18] designed an iterated local search algorithm for HFSP with the bottleneck stage and lot-streaming. Liao et al. [19] developed a new approach hybridizing particle swarm optimization with bottleneck heuristic to fully exploit the bottleneck stage in HFSP. Zhang et al. [20] studied a HFSP with limited buffers and a bottleneck stage on the second process routes and proposed a discrete whale swarm algorithm to minimize maximum completion time. Wang et al. [21] adopted an adaptive artificial bee colony algorithm for HFSP with batch processing machines and bottleneck stage.

As stated above, RHFSP with real-life constraints such as machine eligibility and limited buffer has been investigated; however, RHFSP with bottleneck stage is seldom considered, which exists in real-life manufacturing processes such as seamless steel tube cold drawing production [16]. The modelling and optimization on reentrance and bottleneck stage can lead to optimization results with high application value, so it is necessary to deal with RHFSP with the bottleneck stage.

TLBO [22–26] is a population-based algorithm inspired by passing on knowledge within a classroom environment and consists of the teacher phase and learner phase. TLBO [27–31] has become a main approach to production scheduling [32–35] due to its simple structure and fewer parameters. TLBO has been successfully applied to solve RHFSP [11] and its searchability and advantages on RHFSP are tested; however, it is rarely used to solve RHFSP with the bottleneck stage, which is an extension of RHFSP. The successful applications of TLBO to RHFSP show that TLBO has potential advantages to address RHFSP with bottleneck stage, so TLBO is chosen.

In this study, the reentrance and bottleneck stages are simultaneously investigated in a hybrid flow shop, and an elite-class teaching-learning-based optimization (ETLBO) is developed. The main contributions can be summarized as follows: (1) RHFSP with bottleneck stage is solved and a new algorithm called ETLBO is proposed to minimize maximum completion time. (2) In ETLBO, teachers are divided into formal ones and substitute ones. The teacher phase consists of teacher competition and teacher teaching, the learner phase is replaced by reinforcement research of elite class; adaptive adjustment on teachers and classes is applied based on class quality, and class quality is determined by the number of elite solutions in class. (3) Extensive experiments are conducted to test the performances of ETLBO by comparing it with other existing algorithms from the literature. The computational results demonstrate that new strategies are effective and ETLBO has promising advantages in solving RHFSP with bottleneck stage.

The remainder of the paper is organized as follows. The problem description is described in Section 2. Section 3 shows the proposed ETLBO for RHFSP with the bottleneck stage. Numerical test experiments on ETLBO are reported in Section 4. Conclusions and some topics of future research are given in the final section.

2  Problem Description

RHFSP with bottleneck stage is described as follows. There are n jobs J1,J2,⋯,Jn and a hybrid flow shop with H stages. Stage k has Sk≥1 machines Mk1,Mk2,⋯,MkSk, and at least one stage exists two or more identical parallel machines. Each job is processed L(L>1) times in the following sequence: Stage 1, stage 2, ⋯, stage H, which means each job is reentered L−1 times. Each job must be processed in the last H stages before next processing can begin until its L processings are finished. pik represents the processing time of job Ji at stage k.There is a bottleneck stage b, b∈(1,H). pib is often more than about 10×pik such as casting process [21], k≠b.

There are the following constraints on jobs and machines:

All jobs and machines are available at time 0.

Each machine can process at most one operation at a time.

No jobs may be processed on more than one machine at a time.

Operations cannot be interrupted.

The problem can be divided into two sub-problems: scheduling and machine assignment. Scheduling is applied to determine processing sequence for all jobs on each machine. Machine assignment is used for selecting appropriate machine at each stage for each job. There are strong coupled relationships between these two sub-problems. The optimization contents of scheduling are directly determined by the machine assignment. To obtain an optimal solution, it is necessary to efficiently combine the two sub-problems.

The goal of the problem is to minimize maximum completion time when all constraints are met.

Cmax=maxi=1,2,⋯,n{Ci}(1)

where Ci is the completion time of job Ji, and Cmax denotes maximum completion time.

An example is shown in Table 1, where n=5, H=3, L=2, b=2, S1=2, S2=4, S3=3. A schedule of the example with Cmax=749 is displayed in Fig. 1. Oikl denotes the operation in which job Ji is processed for the l-th time at stage k.

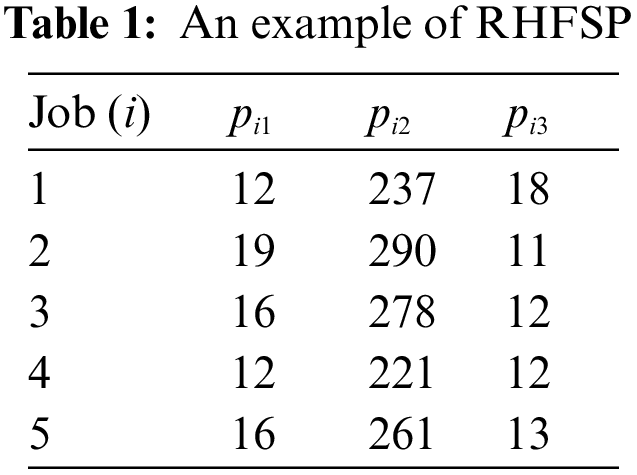
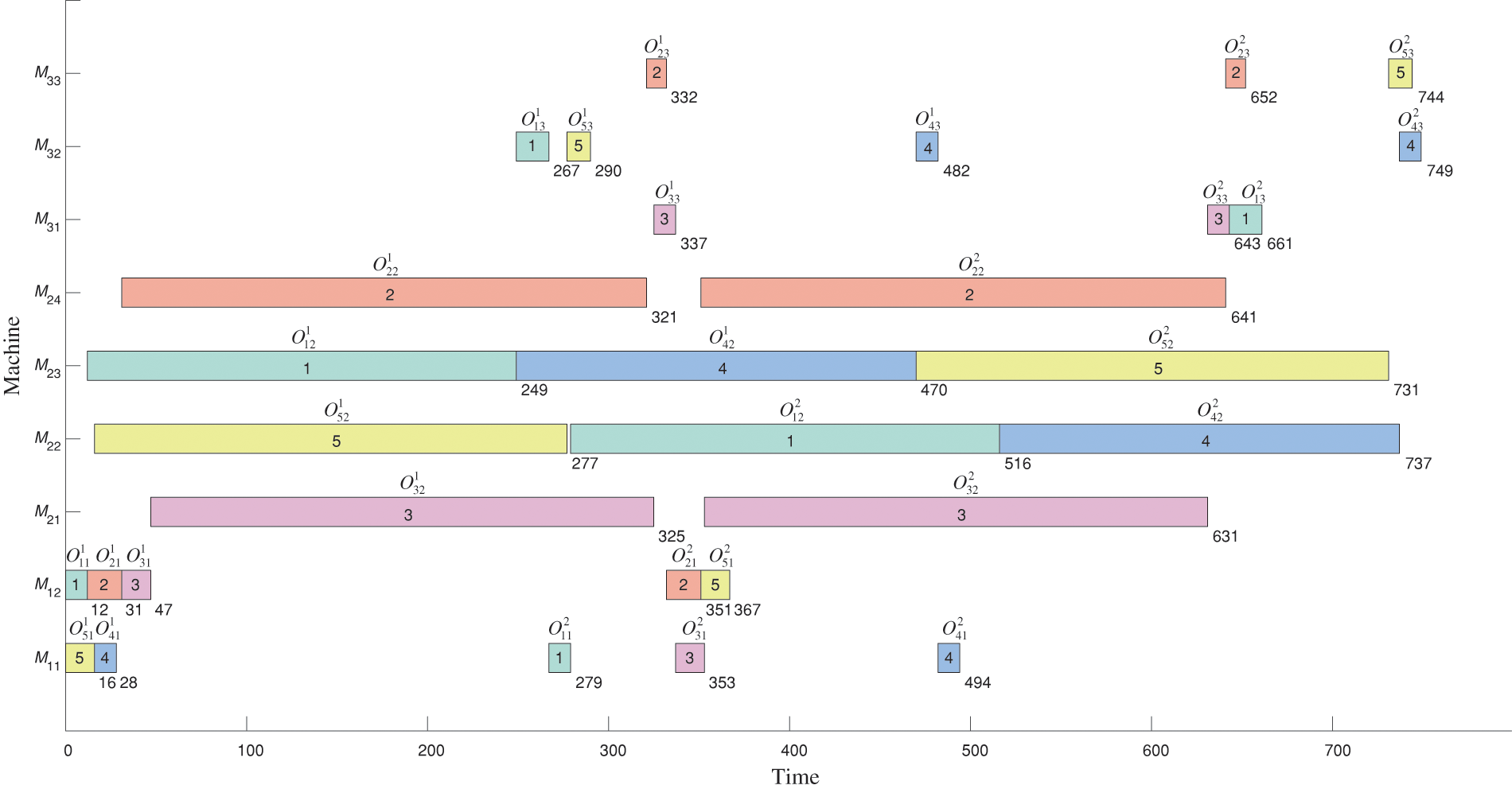
Figure 1: A schedule of the example

3  ETLBO for RHFSP with Bottleneck Stage

Some works are obtained on TLBO with multiple classes; however, in the existing TLBO [36–39], competition among teachers is not used, reinforcement search of some elite solutions and adaptive adjustment on classes and teachers are rarely considered. To effectively solve RHFSP with bottleneck stage, ETLBO is constructed based on reinforcement search of elite class and adaptive adjustment.

3.1 Initialization and Formation of Multiple Classes

To solve the considered RHFSP with reentrant feature, a two-string representation is used [12]. For RHFSP with n jobs, H stages and L processing, its solution is represented by a machine assignment string [q11,q12,⋯,q1H×L|q21,q22,⋯,q2H×L|⋯|qn1,qn2,⋯,qnH×L] and a scheduling string [π1,π2,⋯,πn×H×L], where πi∈ [1,2,⋯,n], qi((l−1)×H+k) is the machine for the l-th processing at stage k for job Ji.

In scheduling string, the frequency of occurrence is H×L for each job Ji. Take job J1 as an example, when g<H, the g-th 1 corresponds to O1g1; when H<g≤2H, the g-th 1 denotes O1g2, and so on. The whole machine assignment string is divided into n segments, each segment corresponds to the assigned machines at all stages in the l-th processing for a job.

The decoding procedure to deal with reentrant feature is shown below. Start with job π1, for each job πi, decide its corresponding operation Oπigl, which is processed on a assigned machine for Oπigl by machine assignment string.

For the example in Section 2, the solution is shown in Fig. 2. For job J4, a segment of [1, 3, 2, 1, 2, 2] is obtained from machine assignment string, in the segment, 1, 3, 2 means that operation O411,O421,O431 are processed on machines M11,M23,M32 respectively in the first processing, completion times of three operations are 28, 470, 482; 1, 2, 2 indicates that O412,O422,O432 are processed on machines M11,M22,M32 in the second processing, their corresponding completion times are 494, 737, 749, respectively. A schedule of the decoding as shown in Fig. 1.

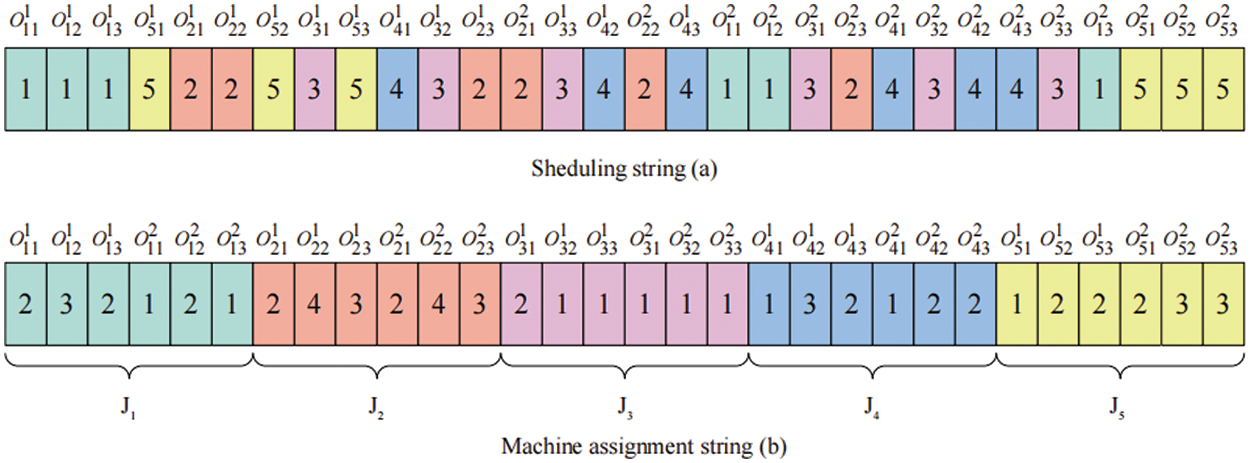
Figure 2: A coding of the example

Initial population P with N solutions are randomly produced.

The formation of multiple classes is described as follows:

1.    Sort all solutions of P in ascending order of Cmax, suppose that Cmax(x1)≤Cmax(x2)≤⋯≤Cmax(xN), first (α+β) solutions are chosen as teachers and formed as a set Ω, and remaining solutions are learners.

2.    Divide all learners into α classes by assigning each learner xi to class Cls(i−1)(mod α)+1.

3.    Each class Clsr is assigned a formal teacher in the following way, r=1, repeat the following steps until r>α: Randomly select a teacher from Ω as the formal teacher xteacherr of Clsr, Ω=Ω∖xteacherr, r=r+1.

where Cmax(x) denotes the maximum completion time of solution x.

The remaining β solutions in Ω are regarded as substitute teachers, Ω={xteacherα+1,⋯,xteacherα+β}. Teachers are not assigned to classes, and each class consists only of learners.

3.2 Search Operators

Global search GS(x,y) is described as follows. If rand≤0.5, then order-based crossover [12] is done on scheduling string of x and y; otherwise, two-point crossover [40] is executed on machine assignment string of x and y, a new solution z is obtained, if Cmax(z)<Cmax(x), then replace x with z, where random number rand follows uniform distribution on [0, 1].

Ten neighborhood structures 𝒩1−𝒩10 are designed, 𝒩1−𝒩5 are about scheduling string and 𝒩6−𝒩10 are related to machine assignment string. 𝒩7, 𝒩9 are the strategies for the bottleneck stage. 𝒩1 is the swapping of two randomly chosen πi and πj. 𝒩2 is used to generate solutions by inserting πi into the position of πj. 𝒩3 is shown below. Stochastically choose Ji, Jj, a,b∈[1,L], c,d∈[1,H], determine Oica, Oidb, Ojca, Ojdb and their corresponding genes πe, πf, πg, πh, respectively, then swap πe, πf and exchange πg, πh on scheduling string. Taking Fig. 2 as an example, randomly select J1, J5, a=1, b=2, c=2, d=3, determine O121, O132, O521, O532 and their corresponding genes π2=1, π27=1, π7=5, π30=5, then swap π2=1 and π7=5, and exchange π27=1 and π30=5.

𝒩4 is show below. Stochastically select two genes πj and πk of Ji, and invert genes between them. 𝒩5 is described below. Randomly choose a job Ji, determine its corresponding H×L genes and delete them from scheduling string, then for each gene of Ji, insert the gene into a new randomly decided position k in scheduling string. For the example in Fig. 2, randomly select job J3 and delete its all genes π8,π11,π14, π20,π23,π26 from scheduling string, which becomes [1, 1, 1, 5, 2, 2, 5, 5, 4, 2, 2, 4, 2, 4, 1, 1, 2, 4, 4, 4, 1, 5, 5, 5], start with π8, for each gene, insert it into a randomly chosen position on scheduling string, scheduling string finally becomes [3, 1, 3, 1, 1, 5, 3, 2, 2, 5, 5, 4, 2, 2, 3, 4, 3, 2, 4, 1, 1, 2, 3, 4, 4, 4, 1, 5, 5, 5].

𝒩6 is shown as follows. Randomly select a machine qig, determine the processing stage k for this machine, qig=h, where h is stochastically chosen from {1,2,⋯,Sk}∖{qig}. 𝒩7 is similar to 𝒩6 expect that qig is the machine at bottleneck stage b. When 𝒩8 is executed, Ji and Jj are randomly selected, then qi1,qi2,⋯,qiH×L of Ji and qj1,qj2,⋯,qjH×L of Jj are swapped, respectively. 𝒩9 has the same steps as 𝒩8 expect that only swap machines at bottleneck stage b of Ji and Jj. 𝒩10 is shown as follows. Stochastically decided a job Ji, w=1, repeat the following steps until w>H×L: Perform 𝒩6 for qiw, w=w+1.

𝒩7, 𝒩9 are proposed for the bottleneck stage due to the following feature of the problem: The new machine of a job Ji at the bottleneck stage b or the swap between machines at bottleneck stage b of Ji and Jj can significantly optimize the corresponding objective values with a high probability.

Multiple neighborhood search is executed in the following way. Let t=1, repeat the following steps until t>10: For solution x, produce a new solution z∈𝒩t(x), if Cmax(z)<Cmax(x), replace x with z, t=11; otherwise t=t+1, where 𝒩t(x) denotes the set of neighborhood solutions generated by 𝒩t on x.

3.3 Class Evolution

Class evolution is composed of teacher competition, teacher’s teaching and reinforcement search of elite class. Let Λ={xteacher1,⋯,xteacherα+β}.

Teacher competition is described as follows:

1.    For each teacher xteacheri∈Λ, stochastically select teacher xteacherj∈Λ, i≠j, perform GS(xteacheri, xteacherj), and execute multiple neighborhood search on xteacheriw times.

2.    For each formal teacher xteacherr, r=1,2,⋯,α, let t=α+1, repeat the following steps until t>α+β: IfCmax(xteachert)<Cmax(xteacherr), then swap xteacherr and xteachert∈Ω, t=t+1.

When xteacherr and xteachert∈Ω are swapped, let xtmp=xteacherr, Ω=Ω∖{xteachert}, xteacherr is replaced with xteachert, then xtmp is added into Ωand xtmp becomes new xteachert.

Teacher teaching is shown below. For each learner xi∈Clsr, perform GS(xi,xteacherr) and execute multiple neighborhood search on xi, determine a learner xworst∈Clsr with the biggest maximum completion time, randomly choose a substitute teacher xteachert∈Ω, and perform GS(xworst,xteachert).

Reinforcement search of elite class is performed in the following way. Sort all solutions in population P in ascending order of Cmaxx, and construct an elite class Cls∗ with the best γ×N solutions; for each elite solution xi∗∈Cls∗, randomly select another elite solution xj∗∈Cls∗, perform GS(xi∗,xj∗) and execute multiple neighborhood search w times on xi∗, where γ×N>(α+β).

Unlike the previous TLBO [40–43], ETLBO has reinforcement search of elite class used to substitute for learner phase. Since elite solutions are mostly composed of teachers and good learners, better solutions are more likely generated by global search and multiple neighborhood search on these elite solutions, and the waste of computational resources can be avoided on interactive learning between those worse learners with bigger Cmaxx.

3.4 Adaptive Adjustment on Teachers and Classes

Class quality is determined by the number of elite solutions in class. The quality Cqur of class Clsr is defined as follows:

Cqur=|{xi∈Clsr|xi∈Cls∗}|(2)

Adaptive adjustment on teachers and classes is shown below:

(1)   Sort all classes in descending order of Cqur, suppose that Cqu1≥Cqu2≥⋯≥Cquα, r=1, repeat the following steps until r>(α−1), swap the best learner in Clsr and the worst learner in Clsr+1.

(2)   For each solution xi∈P, let j=1, repeating the following steps until j>(α+β): If Cmax(xi)< Cmax(xteacherj) and xi∈Clsr, then swap xteacherj and xi∈Clsr; if Cmax(xi)<Cmax(xteacherj) and xi∈Λ, then swap xteacherj and xi∈Λ.

(3)   Let r=1 and Θ be empty, repeat the following steps until r>α: for class Clsr, select a teacher xteacheri∈Λ by roulette selection [13], and swap xteacherr and xteacheri∈Λ, then Λ=Λ∖{xteacherr}, Θ=Θ∪{xteacherr}, r=r+1.

(4)   Ω=Λ, Λ=Λ∪Θ.

When roulette selection is done, selection probability probi=1/Cmaxxteacheri/∑xteacherj∈Λ1/Cmaxxteacherj is used.

In step (1), communication between classes Clsr and Clsr+1 is done to avoid excessive differences among classes in solution quality. In step (2), the best learner can become teacher. In step (3), the formal teacher of each class is adjusted adaptively. Substitute teachers are updated in step (4). The above adaptive adjustment on learners and teachers can maintain high population diversity and make global search ability be effectively enhanced.

3.5 Algorithm Description

The search procedure of ETLBO is shown below:

1.    Randomly produce an initial population P with N solutions and divide population into α classes.

2.    Execute teacher competition.

3.    Perform teacher’s teaching.

4.    Implement reinforcement search of elite class.

5.    Apply adaptive adjustment on teachers and classes.

6.    If the termination condition is not met, go to step (2); otherwise, stop search and output the optimum solution.

Fig. 3 describes flow chart of ETLBO.

Figure 3: Flow chart of ETLBO

ETLBO has the following new features. Teachers are divided into formal ones and substitute ones. Teacher competition is applied between formal and substitute teachers. Teacher’s teaching is performed and reinforcement search of elite class is used to replace learner phase. Adaptive adjustment on teachers and classes is conducted based on class quality assessment. These features promote a balance between exploration and exploitation, then good results can finally be obtained.

4  Computational Experiments

Extensive experiments are conducted to test the performance of ETLBO for RHFSP with bottleneck stage. All experiments are implemented by using Microsoft Visual C++ 2022 and run on i7-8750H CPU (2.20 GHz) and 24 GB RAM.

4.1 Test Instance and Comparative Algorithms

60 instances are randomly produced. For each instance depicted by n×H×L, where L∈{2,3}, n∈[10,100], H∈{3,4,5}. If H=3, then b=2, Sb=4; if H=4, then b=3, Sb=5; if H=5, then b=4, Sb=6; if k≠b, Sk∈[2,4], pik∈[10,20]; otherwise, pik∈[200,300]. Sk and pik are integer and follow uniform distribution within their intervals.

For the considered RHFSP with maximum completion time minimization, there are no existing methods. To demonstrate the advantages of ETLBO for the RHFSP with bottleneck stage, hybrid harmony search and genetic algorithm (HHSGA, [12]), improved dual-population genetic algorithm (IDPGA, [13]) and discrete differential evolution algorithm (DDE, [14]) are selected as comparative algorithms.

Lin et al. [12] proposed an algorithm named HHSGA for RHFSP with limited buffer to minimize weighted values of maximum completion time and mean flowtime. Tang et al. [13] designed IDPGA to solve RHFSP with missing operations to minimize maximum completion time and energy consumption. Zhang et al. [14] applied DDE to address RHFSP with machine eligibility to minimize total tardiness. These algorithms have been successfully applied to deal with RHFSP, so they can be directly used to handle the considered RHFSP by incorporating bottleneck formation into the decoding process; moreover, missing judgment vector and related operators of IDPGA are removed.

A TLBO is constructed, it consists of a class in which the best solution be seen as a teacher and remaining solutions are students, and it includes a teacher phase and a learner phase. Teacher phase is implemented by each learner learning from the teacher and learner phase is done by interactive learning between a learner and another randomly selected learner. These activities are the same as global search in ETLBO. The comparisons between ETLBO and TLBO are applied to show the effect of new strategies of ETLBO.

4.2 Parameter Settings

It can be found that ETLBO can converge well when 0.5×n×H×L seconds CPU time reaches; moreover, when 0.5×n×H×L seconds CPU time is applied, HHSGA, IDPGA, DDE, and TLBO also converge fully within this CPU time, so this time is chosen as stopping condition.

Other parameters of ETLBO, namely N, α, β, γ, and w, are tested by using Taguchi method [44] on instance 50×4×2. Table 2 shows the levels of each parameter. ETLBO with each combination runs 10 times independently for the chosen instance.

Fig. 4 shows the results of MIN and S/N ratio, which is defined as −10×log10⁡(MIN2) and MIN is the best solution in 10 runs. It can be found in Fig. 4 that ETLBO with following combination N=50, α=3, β=2, γ=0.2, w=2 can obtain better results than ETLBO with other combinations, so above combination is adopted.

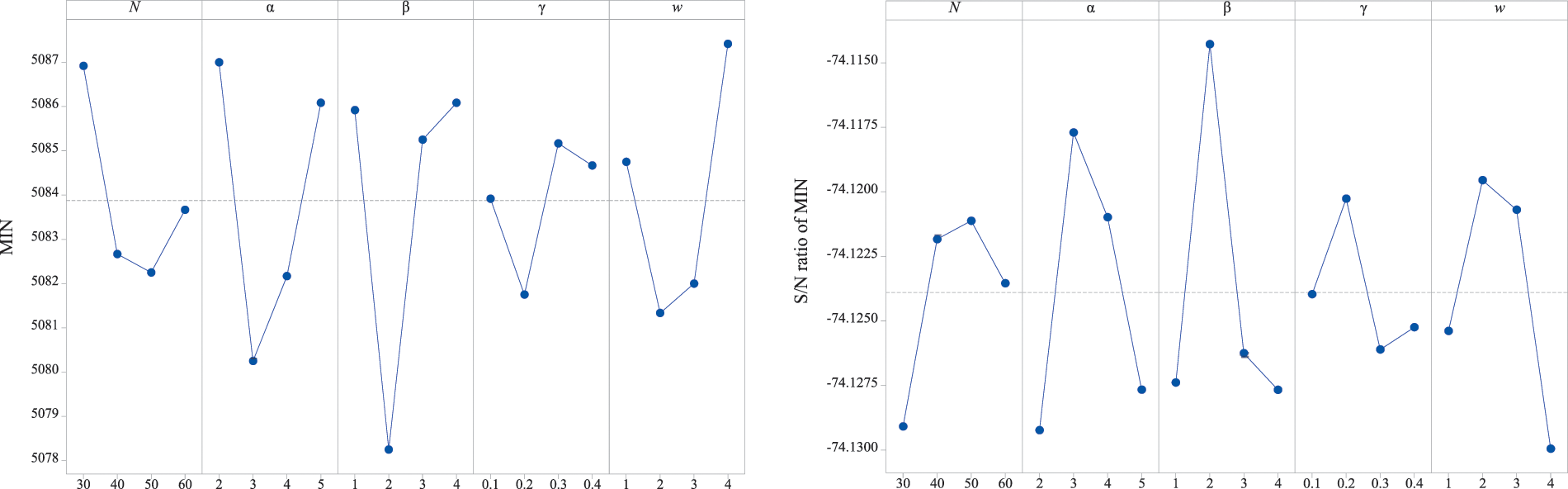
Figure 4: Main effect plot for mean MIN and S/N ratio

TLBO have N and stopping condition are given with the same settings as ETLBO. All parameters of HHSGA, IDPGA and DDE except stopping condition are obtained directly from [12–14]. The experimental results show that those settings of each comparative algorithm are still effective and comparative algorithms with those settings can produce better results than HHSGA, IDPGA and DDE with other settings.

4.3 Result and Discussions

ETLBO is compared with HHSGA, IDPGA, DDE and TLBO. Each algorithm randomly runs 10 times for each instance. AVG, STD denotes the average and standard deviation of solutions in 10 run times. Tables 3–5describe the corresponding results of five algorithms. Figs. 5 and 6 show box plots of all algorithms and convergence curves of instance 50×3×3 and 70×5×2. The relative percentage deviation (RPD) between the best performs algorithm and other four algorithms is used in Fig. 5. RPDMIN, RPDAVG, RPDSTD are defined:

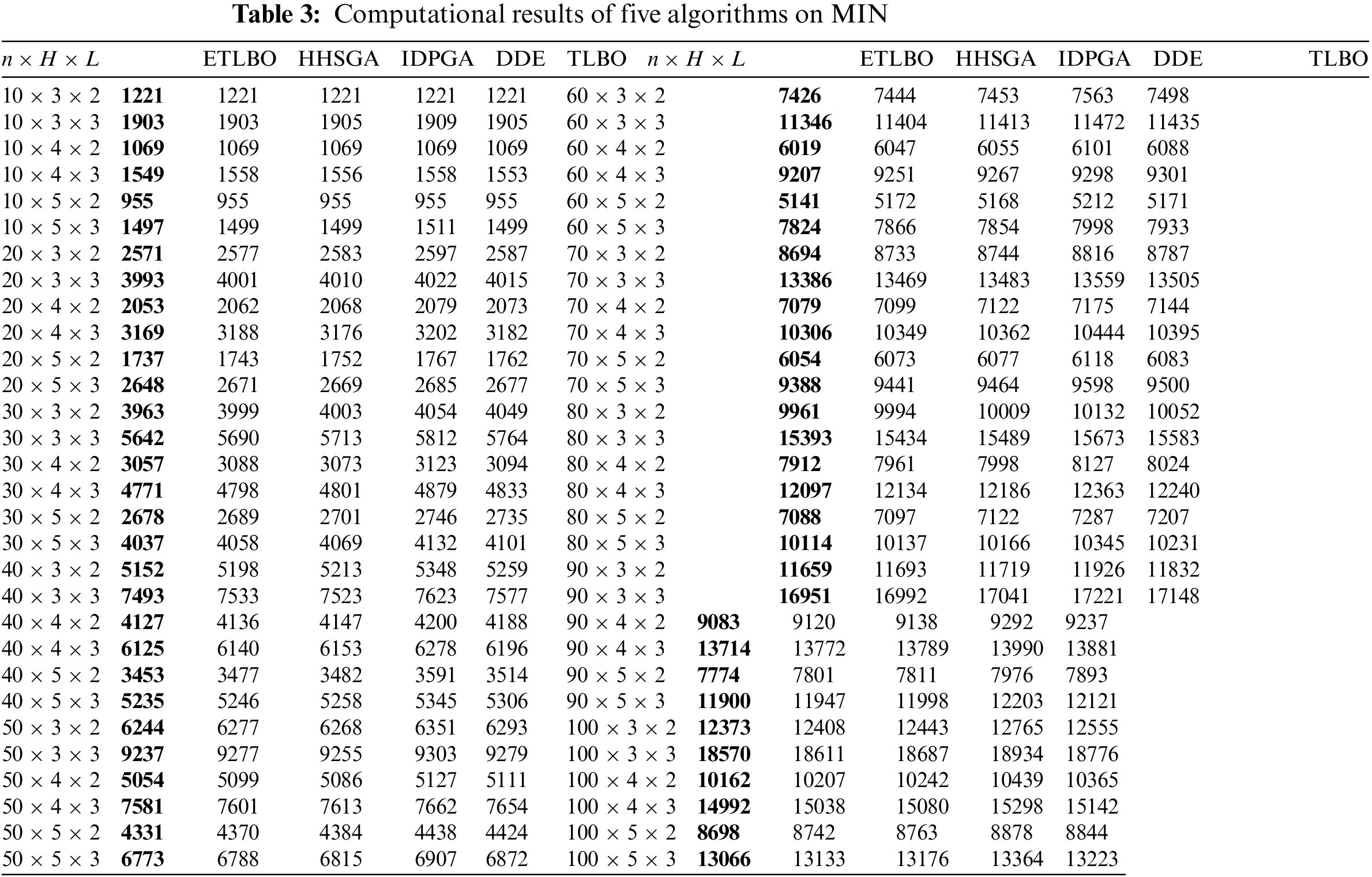
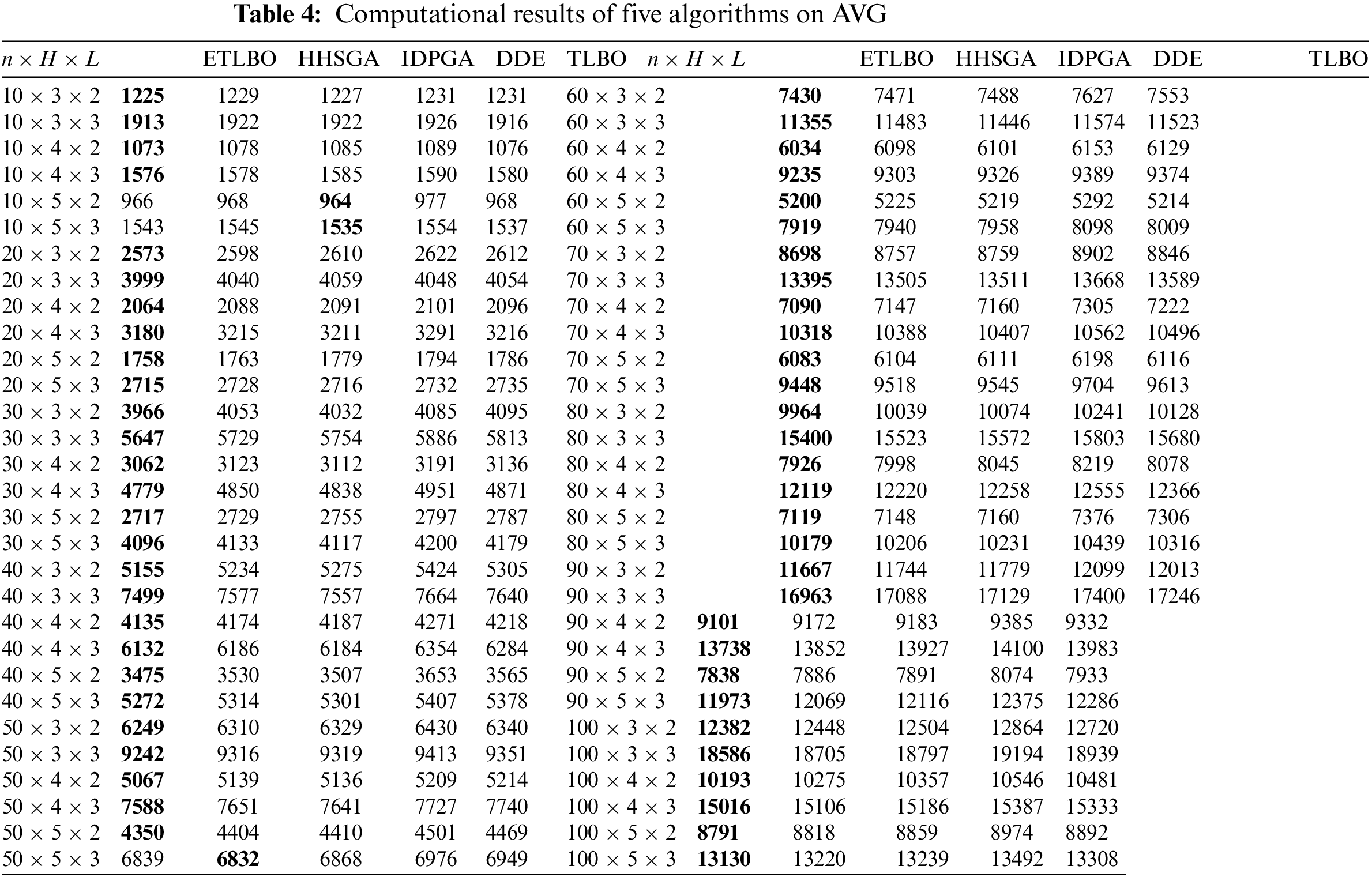
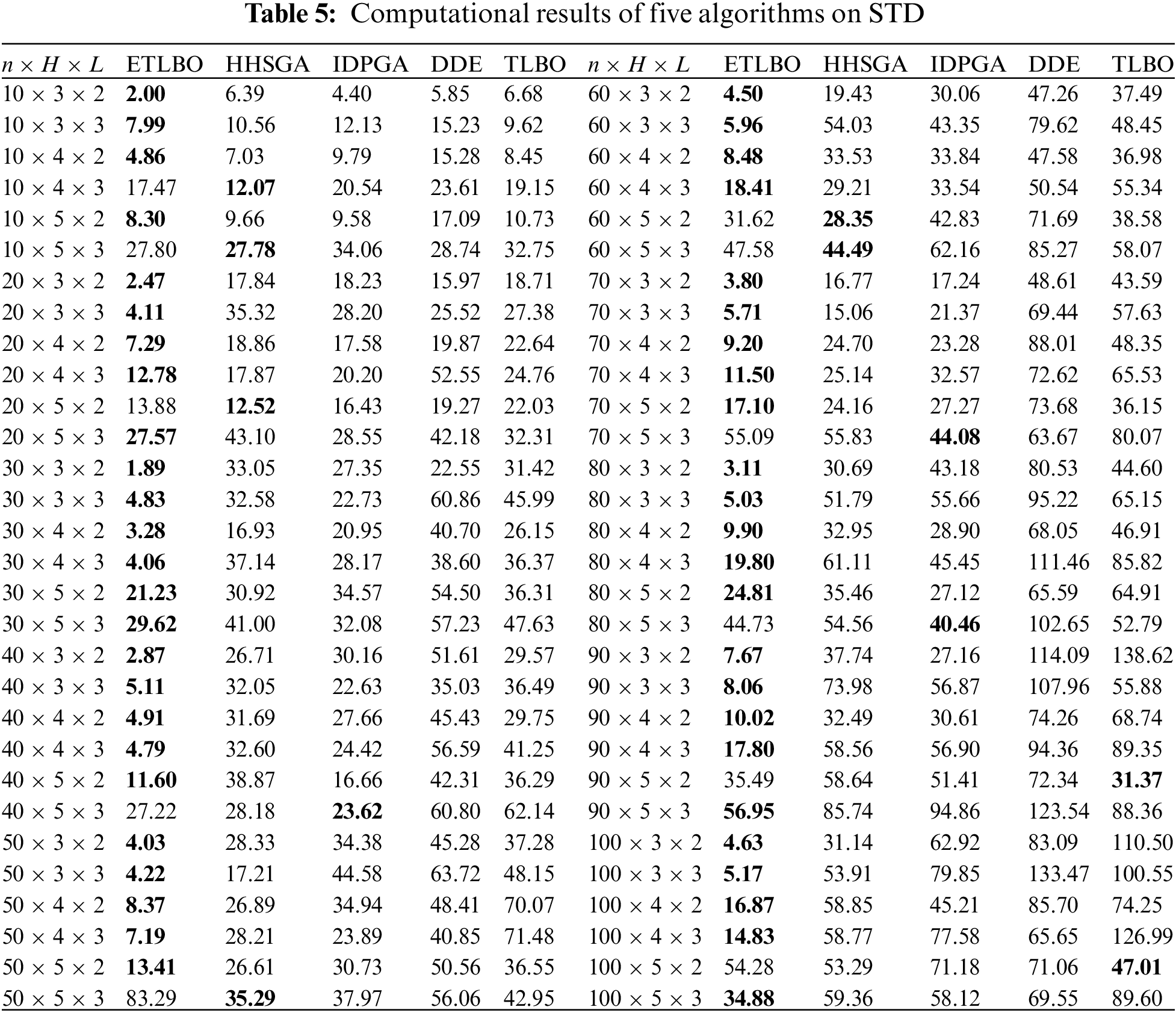
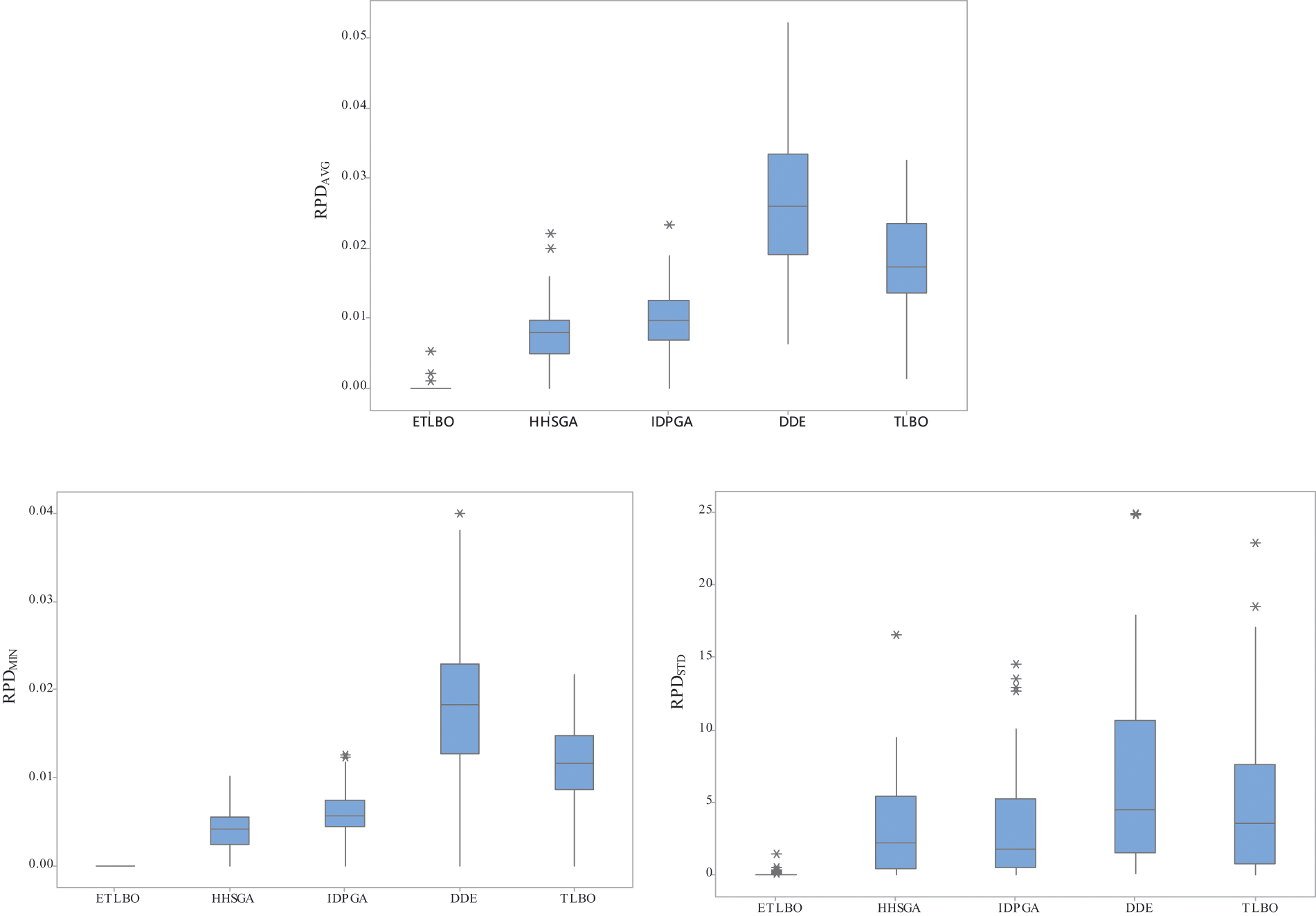
Figure 5: Box plots for all algorithms

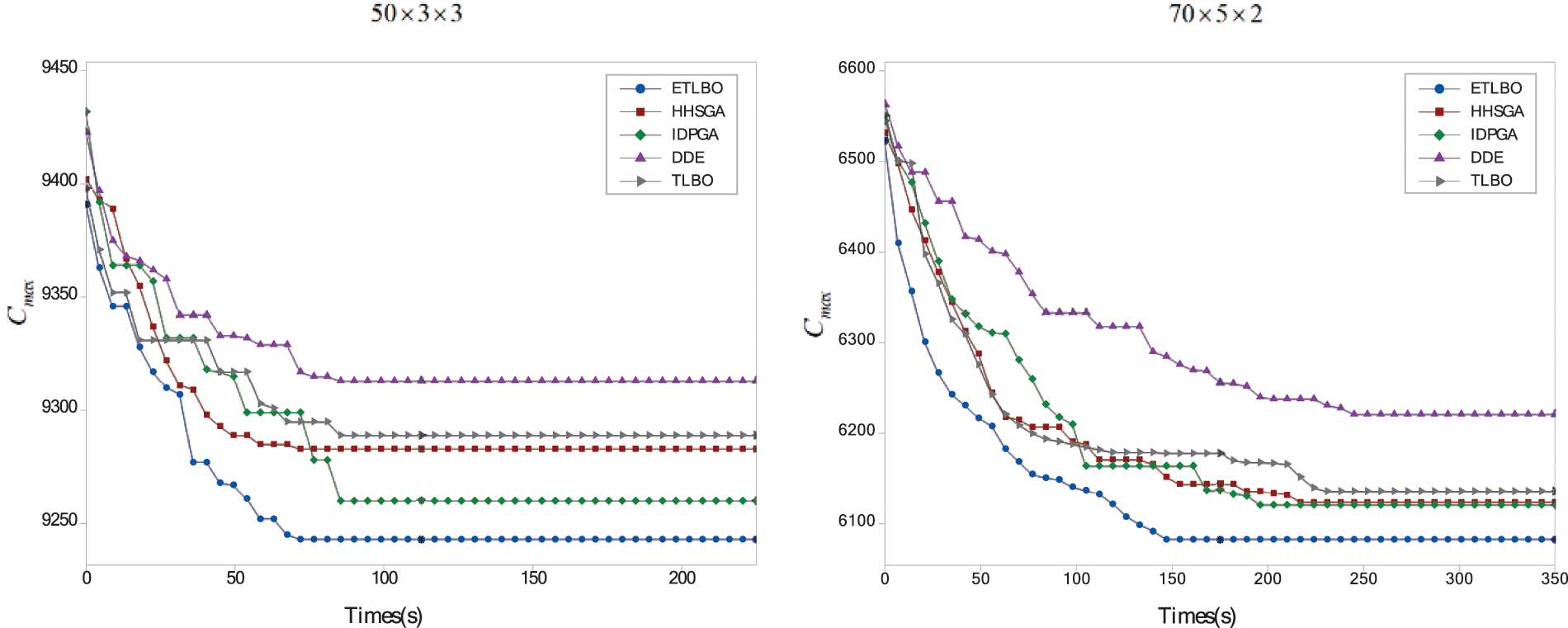
Figure 6: Convergence curves of instance 50×3×3 and 70×5×2

RPDMIN=MIN−MIN∗MIN∗×100%(3)

where MIN* (MAX*, STD*) is the smallest MIN (MAX, STD) obtained by all algorithms, when MIN and MIN* are replaced with STD(AVG) and STD*(AVG*), respectively, RPDSTD(RPDAVG) is obtained in the same way.

Table 6 describes the results of a pair-sample t-test, in which t-test (A1, A2) means that a paired t-test is performed to judge whether algorithm A1 gives a better sample mean than A2. If the significance level is set at 0.05, a statistically significant difference between A1 and A2 is indicated by a p-value less than 0.05.

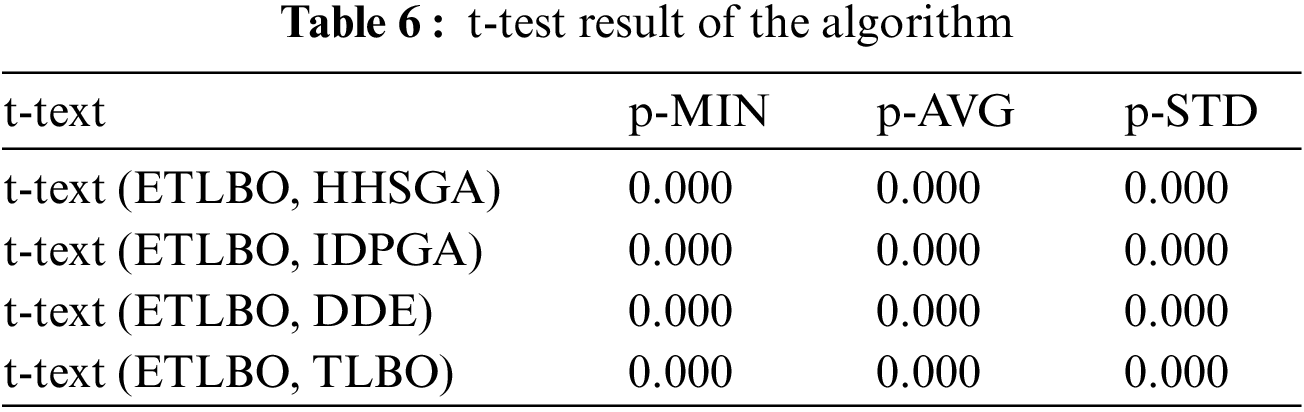
As shown in Tables 3–5, ETLBO obtains smaller MIN than TLBO on all instances and MIN of ETLBO is lower than that of TLBO by at least 50 on 46 instances. It can be found from Table 4 that AVG of ETLBO is better than that of TLBO on 59 of 60 instances and SFLA is worse AVG than ETLBO by at least 50 on 45 instances. Table 5 shows that ETLBO obtains smaller STD than TLBO on 58 instances. Table 6 shows that there are notable performance differences between ETLBO and TLBO in a statistical sense. Fig. 5 depicts the notable differences between STD of the two algorithms, and Fig. 6 reveals that ETLBO significantly converges better than TLBO. It can be concluded that teacher competition, reinforcement search of elite class and adaptive adjustment on teachers and classes have a positive impact on the performance of ETLBO.

Table 3 describes that ETLBO performs better than HHSGA and IDPGA on MIN for all instances. As can be seen from Table 4, ETLBO produces smaller AVG than with the two comparative algorithms on 57 of 60 instances; moreover, AVG of ETLBO is less than that of HHSGA by at least 50 on 26 instances and IDPGA by at least 50 on 48 instances. Table 5 also shows that ETLBO obtains smaller STD than the two comparative algorithms on 49 instances. ETLBO converges better than HHSGA and IDPGA. The results in Table 6, Figs. 5 and 6 also demonstrate the convergence advantage of ETLBO.

It can be concluded from Tables 3–5that ETLBO performs significantly better than DDE. ETLBO produces smaller MIN than DDE in all instances, also generates better AVG than DDE by at least 50 on 45 instances and obtains better STD than or the same STD as DDE on nearly all instances. ETLBO performs notably better than DDE, and the same conclusion can be found in Table 6. Fig. 5 illustrates the significant difference in STD, and Fig. 6 demonstrates the notable convergence advantage of ETLBO.

As analyzed above, ETLBO outperforms its comparative algorithms. The good performance of ETLBO mainly results from its teacher competition, reinforcement search of elite class and adaptive adjustment on teachers and classes. Teacher competition is proposed to make full use of teacher solutions, reinforcement search of elite class performs more searches for better solutions to avoid wasting computational resources, adaptive adjustment on teachers and classes dynamically adjusts class composition according to class quality, as a result, which can effectively prevent the algorithm from falling into local optima. Thus, it can be concluded that ETLBO is a promising method for RHFSP with bottleneck stage.

5  Conclusion and Future Work

This study considers RHFSP with bottleneck stage, and a new algorithm named ETLBO is presented to minimize maximum completion time. In ETLBO, teachers are divided into formal teachers and substitute teachers. A new teacher phase is implemented, which includes two types of teachers’ competition and teaching phases. Reinforcement search of the elite class is used to replace the learner phase. Based on class quality, adaptive adjustment is made for classes and teachers to change the composition of them. The experimental results show that ETLBO is a very competitive algorithm for the considered RHFSP.

In the near future, we will continue to focus on RHFSP and use other meta-heuristics such as artificial bee colony algorithm and imperialist competitive algorithm to solve it. Some new optimization mechanisms, such as cooperation and reinforcement learning, are added into meta-heuristics are our future research topics. Fuzzy RHFSP and distributed RHFSP are another of our directions. Furthermore, the application of ETLBO to deal with other scheduling problems is also worthy of further investigation.

Acknowledgement: The author would like to thank the editors and reviewers for their valuable work, as well as the supervisor and family for their valuable support during the research process.

Funding Statement: This research was funded by the National Natural Science Foundation of China (Grant Number 61573264).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Deming Lei, Surui Duan; data collection: Surui Duan; analysis and interpretation of results: Deming Lei, Surui Duan, Mingbo Li, Jing Wang; draft manuscript preparation: Deming Lei, Surui Duan, Mingbo Li, Jing Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data supporting this study are described in the first paragraph of Section 4.1.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Low, C. J. Hsu and C. T. Su, “A two-stage hybrid flowshop scheduling problem with a function constraint and unrelated alternative machines,” Comput. Oper. Res., vol. 35, no. 3, pp. 845–853, Mar. 2008. doi: 10.1016/j.cor.2006.04.004. [Google Scholar] [CrossRef]

2. R. Ruiz and J. A. Vázquez-Rodríguez, “The hybrid flow shop scheduling problem,” Eur. J. Oper. Res., vol. 205, no. 1, pp. 1–18, Aug. 2010. doi: 10.1016/j.ejor.2009.09.024. [Google Scholar] [CrossRef]

3. J. Dong, and C. Ye, “Green scheduling of distributed two-stage reentrant hybrid flow shop considering distributed energy resources and energy storage system,” Comput. Ind. Eng., vol. 169, pp. 108146, Mar. 2022. doi: 10.1016/j.cie.2022.108146. [Google Scholar] [CrossRef]

4. J. S. Chen, “A branch and bound procedure for the reentrant permutation flow-shop scheduling problem,” Int. J. Adv. Manuf. Technol., vol. 29, pp. 1186–1193, Aug. 2006. doi: 10.1007/s00170-005-0017-x. [Google Scholar] [CrossRef]

5. J. C. H. Pan and J. S. Chen, “Minimizing makespan in re-entrant permutation flow-shops,” J. Oper. Res. Soc., vol. 54, pp. 642–653, Jun. 2003. doi: 10.1057/palgrave.jors.2601556. [Google Scholar] [CrossRef]

6. S. Kumar and M. K. Omar, “Stochastic re-entrant line modeling for an environment stress testing in a semiconductor assembly industry,” Appl. Math. Comput., vol. 173, no. 1, pp. 603–615, Feb. 2006. doi: 10.1016/j.amc.2005.04.050. [Google Scholar] [CrossRef]

7. Y. H. Lee and B. Lee, “Push-pull production planning of the re-entrant process,” Int. J. Adv. Manuf. Technol., vol. 22, pp. 922–931, Aug. 2003. doi: 10.1007/s00170-003-1653-7. [Google Scholar] [CrossRef]

8. F. Xu et al., “Research on green reentrant hybrid flow shop scheduling problem based on improved moth-flame optimization algorithm,” Process., vol. 10, no. 12, pp. 2475, Nov. 2022. doi: 10.3390/pr10122475. [Google Scholar] [CrossRef]

9. B. H. Zhou, L. M. Hu and Z. Y. Zhong, “A hybrid differential evolution algorithm with estimation of distribution algorithm for reentrant hybrid flow shop scheduling problem,” Neural. Comput. Appl., vol. 30, no. 1, pp. 193–209, Jul. 2018. doi: 10.1007/s00521-016-2692-y. [Google Scholar] [CrossRef]

10. H. M. Cho et al., “Bi-objective scheduling for reentrant hybrid flow shop using Pareto genetic algorithm,” Comput. Ind. Eng., vol. 61, no. 3, pp. 529–541, Oct. 2011. doi: 10.1016/j.cie.2011.04.008. [Google Scholar] [CrossRef]

11. J. N. Shen, L. Wang and H. Y. Zheng, “A modified teaching-learning-based optimisation algorithm for bi-objective re-entrant hybrid flowshop scheduling,” Int. J. Prod. Res., vol. 54, no. 12, pp. 3622–3639, Jun. 2016. doi: 10.1080/00207543.2015.1120900. [Google Scholar] [CrossRef]

12. C. C. Lin, W. Y. Liu, and Y. H. Chen, “Considering stockers in reentrant hybrid flow shop scheduling with limited buffer capacity,” Comput. Ind. Eng., vol. 139, pp. 106154, Jan. 2020. doi: 10.1016/j.cie.2019.106154. [Google Scholar] [CrossRef]

13. H. T. Tang et al., “Hybrid flow-shop scheduling problems with missing and re-entrant operations considering process scheduling and production of energy consumption,” Sustainability, vol. 15, no. 10, pp. 7982, May 2023. doi: 10.3390/su15107982. [Google Scholar] [CrossRef]

14. X. Y. Zhang and L. Chen, “A re-entrant hybrid flow shop scheduling problem with machine eligibility constraints,” Int. J. Prod. Res., vol. 56, no. 16, pp. 5293–5305, Dec. 2017. doi: 10.1080/00207543.2017.1408971. [Google Scholar] [CrossRef]

15. C. Chamnanlor et al., “Embedding ant system in genetic algorithm for re-entrant hybrid flow shop scheduling problems with time window constraints,” J. Intell. Manuf., vol. 28, pp. 1915–1931, Dec. 2017. doi: 10.1007/s10845-015-1078-9. [Google Scholar] [CrossRef]

16. X. L. Wu and Z. Cao, “An improved multi-objective evolutionary algorithm based on decomposition for solving re-entrant hybrid flow shop scheduling problem with batch processing machines,” Comput. Ind. Eng., vol. 169, pp. 108236, Jul. 2022. doi: 10.1016/j.cie.2022.108236. [Google Scholar] [CrossRef]

17. A. Costa, V. Fernandez-Viagas, and J. M. Framiñan, “Solving the hybrid flow shop scheduling problem with limited human resource constraint,” Comput. Ind. Eng., vol. 146, pp. 106545, Aug. 2020. doi: 10.1016/j.cie.2020.106545. [Google Scholar] [CrossRef]

18. W. Shao, Z. Shao, and D. Pi, “Modelling and optimization of distributed heterogeneous hybrid flow shop lot-streaming scheduling problem,” Expert. Syst. Appl., vol. 214, pp. 119151, Mar. 2023. doi: 10.1016/j.eswa.2022.119151. [Google Scholar] [CrossRef]

19. C. J. Liao, E. Tjandradjaja, and T. P. Chung, “An approach using particle swarm optimization and bottleneck heuristic to solve hybrid flow shop scheduling problem,” Appl. Soft Comput., vol. 12, no. 6, pp. 1755–1764, Jun. 2012. doi: 10.1016/j.asoc.2012.01.011. [Google Scholar] [CrossRef]

20. C. Zhang et al., “A discrete whale swarm algorithm for hybrid flow-shop scheduling problem with limited buffers,” Robot. CIM-Int. Manuf., vol. 68, pp. 102081, Oct. 2020. doi: 10.1016/j.rcim.2020.102081. [Google Scholar] [CrossRef]

21. J. Wang, D. Lei, and H. Tang, “An adaptive artificial bee colony for hybrid flow shop scheduling with batch processing machines in casting process,” Int. J. Prod. Res., pp. 1–16, Nov. 2023. doi: 10.1080/00207543.2023.2279145. [Google Scholar] [CrossRef]

22. R. V. Rao, V. J. Savsani, and D. P. Vakharia, “Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems,” Comput. Aided. Des., vol. 43, no. 3, pp. 303–315, Mar. 2011. doi: 10.1016/j.cad.2010.12.015. [Google Scholar] [CrossRef]

23. M. K. Sun, Z. Y. Cai, and H. A. Zhang, “A teaching-learning-based optimization with feedback for L-R fuzzy flexible assembly job shop scheduling problem with batch splitting,” Expert. Syst. Appl., vol. 224, pp. 120043, Aug. 2023. doi: 10.1016/j.eswa.2023.120043. [Google Scholar] [CrossRef]

24. A. Baykasoğlu, A. Hamzadayi, and S. Y. Köse, “Testing the performance of teaching-learning based optimization (TLBO) algorithm on combinatorial problems: Flow shop and job shop scheduling cases,” Inf. Sci., vol. 276, pp. 204–218, Aug. 2014. doi: 10.1016/j.ins.2014.02.056. [Google Scholar] [CrossRef]

25. Z. Xie et al., “An effective hybrid teaching-learning-based optimization algorithm for permutation flow shop scheduling problem,” Adv. Eng. Softw., vol. 77, pp. 35–47, Nov. 2014. doi: 10.1016/j.advengsoft.2014.07.006. [Google Scholar] [CrossRef]

26. W. Shao, D. Pi, and Z. Shao, “An extended teaching-learning based optimization algorithm for solving no-wait flow shop scheduling problem,” Appl. Soft Comput., vol. 61, pp. 193–210, Dec. 2017. doi: 10.1016/j.asoc.2017.08.020. [Google Scholar] [CrossRef]

27. C. Song, “A hybrid multi-objective teaching-learning based optimization for scheduling problem of hybrid flow shop with unrelated parallel machine,” IEEE Access, vol. 9, pp. 56822–56835, Apr. 2021. doi: 10.1109/ACCESS.2021.3071729. [Google Scholar] [CrossRef]

28. R. Buddala and S. S. Mahapatra, “Improved teaching-learning-based and JAYA optimization algorithms for solving flexible flow shop scheduling problems,” J. Ind. Eng. Int., vol. 14, pp. 555–570, Sep. 2018. doi: 10.1007/s40092-017-0244-4. [Google Scholar] [CrossRef]

29. B. J. Xi and D. M. Lei, “Q-learning-based teaching-learning optimization for distributed two-stage hybrid flow shop scheduling with fuzzy processing time,” Complex Syst. Model. Simul., vol. 2, no. 2, pp. 113–129, Jun. 2022. doi: 10.23919/CSMS.2022.0002. [Google Scholar] [CrossRef]

30. U. Balande and D. Shrimankar, “A modified teaching learning metaheuristic algorithm with opposite-based learning for permutation flow-shop scheduling problem,” Evol. Intell., vol. 15, no. 1, pp. 57–79, Mar. 2022. doi: 10.1007/s12065-020-00487-5. [Google Scholar] [CrossRef]

31. X. Ji et al., “An improved teaching-learning-based optimization algorithm and its application to a combinatorial optimization problem in foundry industry,” Appl. Soft Comput., vol. 57, pp. 504–516, Aug. 2017. doi: 10.1016/j.asoc.2017.04.029. [Google Scholar] [CrossRef]

32. R. Buddala and S. S. Mahapatra, “An integrated approach for scheduling flexible job-shop using teaching-learning-based optimization method,” J. Ind. Eng. Int., vol. 15, no. 1, pp. 181–192, Mar. 2019. doi: 10.1007/s40092-018-0280-8. [Google Scholar] [CrossRef]

33. M. Rostami and A. Yousefzadeh, “A gamified teaching-learning based optimization algorithm for a three-echelon supply chain scheduling problem in a two-stage assembly flow shop environment,” Appl. Soft Comput., vol. 146, pp. 110598, Oct. 2023. doi: 10.1016/j.asoc.2023.110598. [Google Scholar] [CrossRef]

34. R. Buddala and S. S. Mahapatra, “Two-stage teaching-learning-based optimization method for flexible job-shop scheduling under machine breakdown,” Int. J. Adv. Manuf. Technol., vol. 100, pp. 1419–1432, Feb. 2019. doi: 10.1007/s00170-018-2805-0. [Google Scholar] [CrossRef]

35. J. Jayanthi et al., “Segmentation of brain tumor magnetic resonance images using a teaching-learning optimization algorithm,” Comput. Mater. Contin., vol. 68, no. 3, pp. 4191–4203, Mar. 2021. doi: 10.32604/cmc.2021.012252. [Google Scholar] [CrossRef]

36. D. M. Lei, B. Su, and M. Li, “Cooperated teaching-learning-based optimisation for distributed two-stage assembly flow shop scheduling,” Int. J. Prod. Res., vol. 59, no. 23, pp. 7232–7245, Nov. 2020. doi: 10.1080/00207543.2020.1836422. [Google Scholar] [CrossRef]

37. D. M. Lei and B. Su, “A multi-class teaching-learning-based optimization for multi-objective distributed hybrid flow shop scheduling,” Knowl. Based. Syst., vol. 263, pp. 110252, Jan. 2023. doi: 10.1016/j.knosys.2023.110252. [Google Scholar] [CrossRef]

38. A. Dubey, U. Gupta, and S. Jain, “Medical data clustering and classification using TLBO and machine learning algorithms,” Comput. Mater. Contin., vol. 70, no. 3, pp. 4523–4543, Oct. 2021. doi: 10.32604/cmc.2022.021148. [Google Scholar] [CrossRef]

39. D. M. Lei and B. J. Xi, “Diversified teaching-learning-based optimization for fuzzy two-stage hybrid flow shop scheduling with setup time,” J. Intell. Fuzzy Syst., vol. 41, no. 2, pp. 4159–4173, Sep. 2021. doi: 10.3233/JIFS-210764. [Google Scholar] [CrossRef]

40. D. M. Lei, L. Gao, and Y. L. Zheng, “A novel teaching-learning-based optimization algorithm for energy-efficient scheduling in hybrid flow shop,” IEEE Trans. Eng. Manage., vol. 65, no. 2, pp. 330–340, May. 2018. doi: 10.1109/TEM.2017.2774281. [Google Scholar] [CrossRef]

41. A. Sharma et al., “Identification of photovoltaic module parameters by implementing a novel teaching learning based optimization with unique exemplar generation scheme (TLBO-UEGS),” Energy Rep., vol. 10, pp. 1485–1506, Nov. 2023. doi: 10.1016/j.egyr.2023.08.019. [Google Scholar] [CrossRef]

42. M. Arashpour et al., “Predicting individual learning performance using machine-learning hybridized with the teaching-learning-based optimization,” Comput. Appl. Eng. Educ., vol. 31, no. 1, pp. 83–99, Jan. 2023. doi: 10.1002/cae.22572. [Google Scholar] [CrossRef]

43. A. K. Shukla, S. K. Pippal, and S. S. Chauhan, “An empirical evaluation of teaching-learning-based optimization, genetic algorithm and particle swarm optimization,” Int. J. Comput. Appl., vol. 45, no. 1, pp. 36–50, Jan. 2023. doi: 10.1080/1206212X.2019.1686562. [Google Scholar] [CrossRef]

44. J. Deng and L. Wang, “A competitive memetic algorithm for multi-objective distributed permutation flow shop scheduling problem,” Swarm Evol. Comput., vol. 32, pp. 121–131, Feb. 2017. doi: 10.1016/j.swevo.2016.06.002. [Google Scholar] [CrossRef]