 Open Access
Open Access
ARTICLE
Ghost Module Based Residual Mixture of Self-Attention and Convolution for Online Signature Verification
1 Department of Computer Technology, School of Computer Science and Engineering, Shenyang Jianzhu University, Shenyang, 110168, China
2 Liaoning Province Big Data Management and Analysis Laboratory of Urban Construction, Shenyang Jianzhu University, Shenyang, 110168, China
3 Shenyang Branch of National Special Computer Engineering Technology Research Center, Shenyang Jianzhu University, Shenyang, 110168, China
* Corresponding Author: Shuai Yuan. Email:
Computers, Materials & Continua 2024, 79(1), 695-712. https://doi.org/10.32604/cmc.2024.048502
Received 09 December 2023; Accepted 26 February 2024; Issue published 25 April 2024
Abstract
Online Signature Verification (OSV), as a personal identification technology, is widely used in various industries. However, it faces challenges, such as incomplete feature extraction, low accuracy, and computational heaviness. To address these issues, we propose a novel approach for online signature verification, using a one-dimensional Ghost-ACmix Residual Network (1D-ACGRNet), which is a Ghost-ACmix Residual Network that combines convolution with a self-attention mechanism and performs improvement by using Ghost method. The Ghost-ACmix Residual structure is introduced to leverage both self-attention and convolution mechanisms for capturing global feature information and extracting local information, effectively complementing whole and local signature features and mitigating the problem of insufficient feature extraction. Then, the Ghost-based Convolution and Self-Attention (ACG) block is proposed to simplify the common parts between convolution and self-attention using the Ghost module and employ feature transformation to obtain intermediate features, thus reducing computational costs. Additionally, feature selection is performed using the random forest method, and the data is dimensionally reduced using Principal Component Analysis (PCA). Finally, tests are implemented on the MCYT-100 datasets and the SVC-2004 Task2 datasets, and the equal error rates (EERs) for small-sample training using five genuine and forged signatures are 3.07% and 4.17%, respectively. The EERs for training with ten genuine and forged signatures are 0.91% and 2.12% on the respective datasets. The experimental results illustrate that the proposed approach effectively enhances the accuracy of online signature verification.Keywords
Online Signature Verification (OSV) technology is a biometric authentication technique aimed at establishing a high-accuracy and robust system to determine whether a signature sample is genuine or forged. Unlike offline signatures, online signatures are real-time signals that vary with time and primarily capture dynamic information, such as signature trajectory, pressure, vertical and horizontal deviations, and velocity, which are collected using signature devices like electronic tablets [1–3]. Online signatures are widely accepted in society due to their ease of collection, resistance to imitation, and high security [4,5]. However, the instability of online signatures makes them susceptible to changes of the signer’s physiological state, psychological fluctuations, and surrounding environment. Additionally, the limited number of online signature samples results in significant challenges for achieving high verification accuracy [6–8]. Therefore, achieving effective personal identification through OSV technology is crucial for determining the legal validity of handwritten signatures. In-depth research on online signature verification can address challenges related to stability and accuracy, thereby fostering its application and development in areas such as e-commerce and e-government.
Convolution and self-attention mechanisms, as potent techniques in deep learning, are frequently employed in current methods for handwritten signature verification. Consequently, methods for handwritten signature verification can be categorized into convolution-based and self-attention-based approaches. Each of these approaches has its unique advantages and limitations: Convolution demonstrates excellent performance in data processing, capturing local features and spatial information. However, it is constrained by the design of local receptive fields and parameter sharing, which may impede its ability to handle long-range dependencies and global information. On the other hand, the self-attention mechanism offers advantages in capturing global dependencies and dynamically computing attention weights, making it suitable for processing sequential data and global information. Nevertheless, when dealing with large-scale data, it may encounter significant computational overhead and might excessively focus on global information, potentially lacking the ability to handle local features.
To enhance the performance and accuracy of handwritten signature verification, while minimizing computational overhead and effectively handling local and global features, we propose a novel one-dimensional Ghost-ACmix Residual Network (1D-ACGRNet) that integrates convolution and self-attention mechanisms. The main contributions are as follows:
First of all, we introduce a novel Ghost-ACmix residual structure that combines the strengths of convolution and self-attention mechanisms to extract feature information. This approach allows for a synergistic utilization of global and local signature features, effectively addressing the issue of insufficient feature representation in signatures.
Then, recognizing that the fusion of convolution and self-attention increases model complexity and computational overhead, we propose a Ghost-based Convolution and Self-Attention (ACG) module. In this module, during the underlying convolution operations of both convolution and self-attention, a straightforward feature transformation is employed to replace the conventional convolution process, acquiring more comprehensive feature information. The advantage of this approach lies in reducing feature redundancy and lowering computational costs, thereby, enhancing computational efficiency while maintaining model performance.
Finally, we employ the random forest algorithm for feature selection on global features, filtering out redundant information based on feature importance scores. We also adapt the Principal Component Analysis (PCA) method for feature dimensionality reduction, thereby, further reducing the computational load of the model.
After decades of exploration and research, numerous online handwritten signature verification methods have been proposed. Generally, these methods can be categorized into two types according to the approach of feature extraction: Parameter-based methods and function-based methods. The parameter-based signature verification methods primarily extracted a fixed-length feature vector from the time-series data of the entire or partial sampling points of signatures. Then, they transformed the comparison between two signatures into a comparison between their respective feature vectors. Jain et al. [9] considered the stroke count as a global feature. Lee et al. [10] used average speed, average pressure, and the number of pen lifts during the signature as global features. Ibrahim et al. [11] extracted 35 global features, including maximum signature velocity, pen-down count, signature aspect ratio, etc., for signature verification. This method showed acceptable overall verification performance, but some signers had relatively low verification accuracy. Fierrez-Aguilar et al. [12] introduced 100 global features and ranked them based on their discriminatory power in differentiating genuine and forged signatures. Vorugundi et al. [13] combined a one-dimensional convolutional neural network (1D-CNN) with a Siamese neural network (SNN) and used the extracted global feature set to represent online handwritten signatures. Additionally, some transform methods, such as wavelet transform [14], Fourier transform [15], i-vector [16], have also been applied for extracting global features from online handwritten signatures.
With the continuous development of deep learning and signature devices, many researchers have been devoted to adopting deep learning methods for online signature authentication. Recurrent Neural Networks (RNN) and Long Short Term Memory (LSTM) networks were widely used in this context. Tolosana et al. [17] investigated different types of RNN networks for signature authentication and proposed a multi-RNN Siamese network as well as a Siamese network combining LSTM and Gate Recurrent Unit (GRU). Greff et al. [18] conducted an analysis of eight different LSTM variants across three distinct tasks: Speech recognition, handwriting recognition, and polyphonic music modeling. Furthermore, Li et al. [19] proposed a Stroke-Based RNN model that combined signature stroke information with RNN networks in 2019. Lai et al. [20] proposed a method for synthesizing dynamic signature sequences to address the problem of lacking forged signatures during training. Vorugunti et al. [21] merged manually extracted features with features extracted by Autoencoders (AE) and applied the Depthwise Separable Convolutional Neural Network (DWSCNN) for the first time to online signature verification tasks. Additionally, a language-independent shallow model Shallow Convolutional Neural Network (sCNN) [22] based on a convolutional neural network (CNN) has been introduced. This model had a simple structure, using a custom shallow CNN to automatically learn signature features from the training data for signature authentication.
The function-based online signature verification methods treated the time-series data of all or partial sampling points as feature information and performed signature verification by calculating the distance between the template signature and the test signature. This approach retained information from all sampling points, providing more data and higher security. Kholmatov et al. [23] improved the Dynamic Time Warping (DTW) method by constructing a three-dimensional feature vector for each signature using the distance between the current sample and all reference samples. Song et al. [24] selected five stable local temporal features: x-axis velocity, y-axis velocity, pressure, y-axis acceleration, and centripetal acceleration, and used the DTW-SCC algorithm for signature verification. Lai et al. [25] proposed an online handwritten signature verification method based on RNN and signature Length Normalized Path Signature (LNPS) descriptor to address the problem of inconsistent signature lengths, but this method involved heavy model computation. In addition, the Information Divergence-Based Matching Strategy [26], Gaussian Mixture Model (GMM) [27], and other methods have also been applied to function-based signature verification.
From the above-mentioned research work, it can be concluded that researchers have made significant progress in the field of online signature authentication over the years. However, there are still some challenges that need to be addressed. Firstly, improving the accuracy of online signature verification is still a primary focus and a difficult task in current research. Previous studies mainly used traditional methods or convolutional methods for feature extraction from online signatures. However, online signatures are complex and contain multiple types of information, and susceptible to various external factors. In the process of feature extraction, the global or local information of the features is often overlooked, leading to limited effectiveness in feature extraction. Secondly, reducing the computational cost of signature verification, eliminating redundant information, and lightening the model structure pose significant challenges in online signature authentication methods. Moreover, signatures that have been deliberately forged over time are difficult to distinguish from genuine signatures. Therefore, distinguishing between proficient forgeries and genuine penmanship is a challenging aspect in online signature authentication.
2.3 Residual Network Architecture
ResNet, short for Residual Network, is a widely recognized and significant neural network architecture in deep learning, proposed by He et al. in 2016 [28]. ResNet was designed to address the issues of vanishing and exploding gradients that occur in deep neural networks. In deep neural networks, as the number of layers increases, the information propagation may suffer from the problem of vanishing gradients. This leads to difficulties in network convergence of training very deep neural networks. ResNet addresses this issue by introducing a residual learning approach. It utilizes “residual blocks,” which allow the network to directly learn the residual part of the target function. By using residual blocks, even for a very deep network, the information propagation path becomes more direct with reducing gradient decay and making it easier to train and optimize deeper networks. The core idea of ResNet is to introduce skip connections or “shortcut connections” in the network, enabling the direct transfer of information between different layers. By incorporating skip connections, ResNet enables the flow of information across layers, facilitates the training of very deep neural networks and addresses the vanishing gradient problem, and ultimately leads to improved performance and convergence.
2.4 Integration of Self-Attention and Convolution
Convolution and self-attention are two powerful representation learning techniques that are considered as independent methods. However, they have strong inherent connections because much of their computations actually involve similar operations. Specifically, traditional convolution can be decomposed into smaller convolutions, which are then shifted and summed. Similarly, in the self-attention module, the projections of queries, keys, and values can be seen as multiple convolutions, followed by computation of attention weights and aggregation of values. As a result, the first stage of both modules involves similar operations. Moreover, the first stage is computationally more intensive compared with the second stage. Their operations can be used to perform an elegant fusion of both seemingly distinct methods, known as the hybrid model (ACmix) [29], which simultaneously leverages the advantages of both self-attention and convolution while having the minimum computational overhead compared with pure convolution or self-attention counterparts.
The Ghost block [30] is a lightweight convolutional block that achieves comparable performance to standard convolution with fewer parameters and lower training costs. Traditional convolutions require significant computations and parameters to extract feature maps, often resulting in feature maps containing rich or redundant information, with many feature maps being similar. The Ghost block obtains some “ghost” feature maps through linear transformations, which can be derived from other feature maps. The Ghost block divides the convolution process into two parts: Standard convolution and transformations (identity mapping and depth-wise convolution). During this process, the Ghost block introduces the concept of “Ghost” dividing the input feature maps into main and ghost parts. The main part consists of a small portion of feature maps generated by convolutions, preserving the primary feature information, while the ghost part consists of feature maps generated by identity mapping, assisting computations for providing additional information. This design allows the Ghost block to maintain low computational and memorial overhead while offering high model expressiveness and accuracy.
Another advantage of the Ghost block is its adaptability and pluggability. It can be integrated into various convolutional neural network structures and model architectures. By applying the Ghost block to different parts of a network model, lightweight and efficient goals can be achieved without the need to redesign the entire model.
3.1 Whole Framework of the Proposed Method
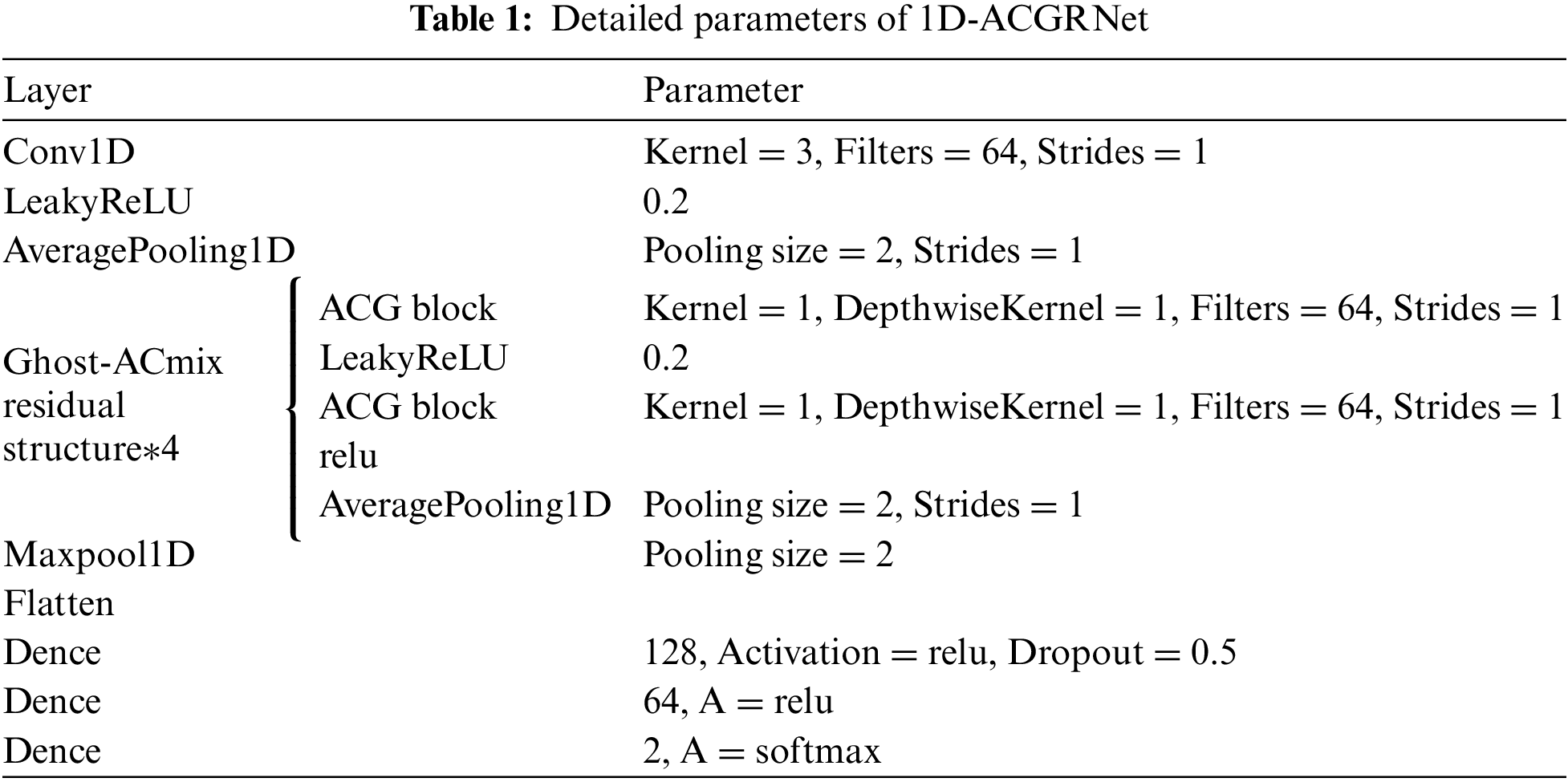
The overall framework of our proposed online signature verification method based on the 1D-ACGRNet model is illustrated in Fig. 1. It primarily consists of two main components: Feature extraction and selection, as well as the Ghost-ACmix residual module for signature verification. In the first part of feature extraction and selection, the original dataset undergoes feature extraction, resulting in a 54-dimensional global feature vector. Subsequently, a random forest algorithm [31] is employed to determine the importance of each feature dimension, leading to the removal of redundant features with importance scores below 0. Additionally, PCA [31] is used to reduce the dimensionality of 54 global features. The resulting four global features are combined with the features extracted to form the feature information. The second part is the 1D-ACGRNet model signature authentication. The stable global features processed in the first stage are input into a convolutional layer, followed by LeakyReLU activation and Average Pooling. The output is then fed into four Ghost-ACmix residual modules for feature modeling, and then output to the classifier composed of the full connection layer and SoftMax function for classification, and finally obtains the signature authenticity. Table 1 provides the specific parameters of the model.

Figure 1: Whole framework of the proposed method
3.2 Ghost-ACmix Residual Structure
In traditional deep neural networks, with the network depth increases, the gradient signal becomes very small, making training difficult or even impossible. This paper employs the Ghost-ACmix residual structure as shown in Fig. 2, which introduces skip connections to allow information to bypass certain layers, effectively overcoming the problem of vanishing gradients.

Figure 2: Ghost-ACmix residual structure
Considering that conventional online signature verification methods often overlook either global or local information, leading to incomplete feature extraction and insufficient accuracy, given that online signature authentication techniques are often deployed on small-capacity embedded devices, requiring a reduction in overall model parameters and computational complexity, we adopt the ACG block combining convolution and self-attention with the Ghost method to replace the standard convolutional part in the residual structure. This approach aims to improve model performance while remaining lightweight. Assuming that the input to the residual structure is denoted as x, the output y(x) can be represented by the following equation:
The convolutional and self-attention modules typically follow different design paradigms. Traditional convolutional operations utilize aggregation functions over local receptive fields, applying weighted summation to the data within each window based on the convolution filter weights. In contrast, self-attention modules apply weighted averaging operations based on the context of input features, where attention weights are dynamically computed as similarity functions between relevant pairs of pixels. This flexibility allows the attention module to adaptively focus on different regions and capture more diverse information features. The specific operation is shown in Fig. 3.

Figure 3: ACG block
For the convolution operation, given a convolution kernel K of size 1 × k, it can be decomposed into k sets of 1 × k convolution kernels, followed by subsequent shifting and summation operations. The specific decomposition process is as follows.
The convolutional kernel K of size 1 × k is decomposed into k individual 1 × 1 convolutional kernels, denoted as Kp, where p ∈ {0, 1,...,k − 1}. The input feature map is F ∈ RCin × W, and the output feature map is G ∈ RCout × W. The tensors fi ∈ RCin and gi ∈ RCout represent the feature tensors of pixels i in F and G respectively. Utilizing these 1 × 1 convolutional kernels, convolution operations are performed with the corresponding positions of fi, resulting in k feature maps denoted as gip. Due to the high computational complexity of tensor displacement, a fixed-kernel depth convolution is used to perform the tensor displacement operation. Shift and sum the k feature maps to obtain the pixel value gi in the final output feature G.
By such decomposition, the standard convolution can be achieved through a series of smaller 1 × 1 convolutional kernels and a two-step process of shifting and summation.
For self-attention operations, the attention module can also be decomposed into two stages. In the first stage, the input features are projected into query q, key k, and value v using a 1 × 1 convolution. Similarly, let the input features be represented as F ∈ RCin × W, and the output features as G ∈ RCout × W. This facilitates the transformation of fi ∈ RCin and gi ∈ RCout representing F and G corresponding pixel i feature tensor. qi, ki, vi respectively denote tensors of query, key, and value for pixel i. Wq, Wk, Wv correspondingly refer to the weights associated with query q, key k, and value v.
The second stage involves computing attention weights and performing a weighted sum. The attention weights A are computed by taking the dot product of the query q and key k, followed by scaling the result using the scaling factor
Therefore, by weighting and summing the value vectors v using attention weights, the pixel gi in the output feature G can be computed.
Decomposing the Self-Attention into two stages makes the computation process more efficient, as a significant portion of computations is concentrated in the first stage, similar to the computation pattern in traditional convolutions. Since both Convolution and Self-Attention apply convolutional operations in the first stage, it is possible to perform the first-stage computation only once and then separately pass the intermediate features to the convolution and self-attention paradigms for computation, finally combining them through weighted summation. This integration fully leverages the advantages of both, while reducing computational costs.
Although this processing approach reduces the parameter count to some extent, there still exists a significant amount of redundancy in the intermediate features. To address this issue, Fig. 4 represents the idea of the Ghost block introduced in this paper. In the first stage of obtaining intermediate features, the first set of intermediate features is generated through a 1 × 1 convolution. Subsequently, the Ghost block is employed to generate the remaining sets of intermediate features. By using the Ghost block, the overall parameter count of the model is reduced, and the problem of feature redundancy is effectively avoided.

Figure 4: Ghost block
As depicted in Fig. 1, the classifier of the 1D-ACGRNet model is composed of several layers including Flatten layer, Dropout layer, Relu activation function layer, and three fully connected layers [128, 64, 2]. In the Flatten layer, the features produced by four Ghost-ACmix residual structures are flattened into a one-dimensional array and fed into the fully connected layers. Considering that the front-end network has already captured significant features relevant to signature authentication through max-pooling layers, we introduce a single Dropout layer (0.5) in the first fully connected layer to eliminate redundant feature information. Ultimately, the SoftMax activation function is employed to predict the authenticity of each signature sample. The design of the entire classifier aims to fully exploit effective features and prevent overfitting, thus, enhancing the performance of signature verification.
4.1 Datasets and Preprocessing
The experimental datasets in this study include the MCYT-100 datasets and the SVC-2004 Task2 datasets, which are described as follows:
The MCYT-100 datasets are a publicly available datasets commonly used for research in online signature verification. The datasets are released by the BiDA Laboratory at the Autonomous University of Madrid. The MCYT-100 Spanish datasets are consist of 100 users, and each user has 25 genuine and forged signature samples. The signature feature information includes five time-series features: Abscissa, ordinate, pen pressure, pen horizontal angle, and pen vertical angle.
The SVC-2004 Task2 Chinese-English datasets are subset datasets provided at the First International Signature Verification Competition held by the Hong Kong University of Science and Technology in 2004. The datasets contain a relatively small number of signatures and consist 40 users, with each user having 20 genuine and forged signature samples. The signature feature information includes seven time-series features: Abscissa, ordinate, pen pressure, time, pen horizontal angle, pen vertical angle, and pen-up/pen-down flag. For the sake of model generalization, the time and pen-up/pen-down flag time-series features in the dataset were not used during the experiment.
To mitigate the impact of input device variations and the influence of the number, size, and location of sampling points on each signature input, we employed smoothing and normalization on the signature feature sequence X and Y coordinates. This is done to eliminate data errors originating from data acquisition equipment and individual user factors. We utilized a five-point cubic smoothing filter to process the feature data. The time sequence of the signature is represented as T, where n denotes the number of sampling points, X and Y represent the abscissa and ordinate trajectory feature sequence, P signifies the pressure sequence feature, and AZ and AL denote the horizontal and vertical angular features, respectively. For the signature feature sequence {T1, T2,...,Tn}, where in Ti ∈ {X, Y}, Ti* corresponds to the smoothed data points, i = (1, 2,...,n), while n represents the count of signature samples. The smoothing process is as follows:
Subsequently, the selected features are normalized to scale the data of the five feature sequences within the range of [0, 1]. The formula for normalization is as follows:
After computation, a total of 54 global signature features are extracted, as detailed in the following Table 2.
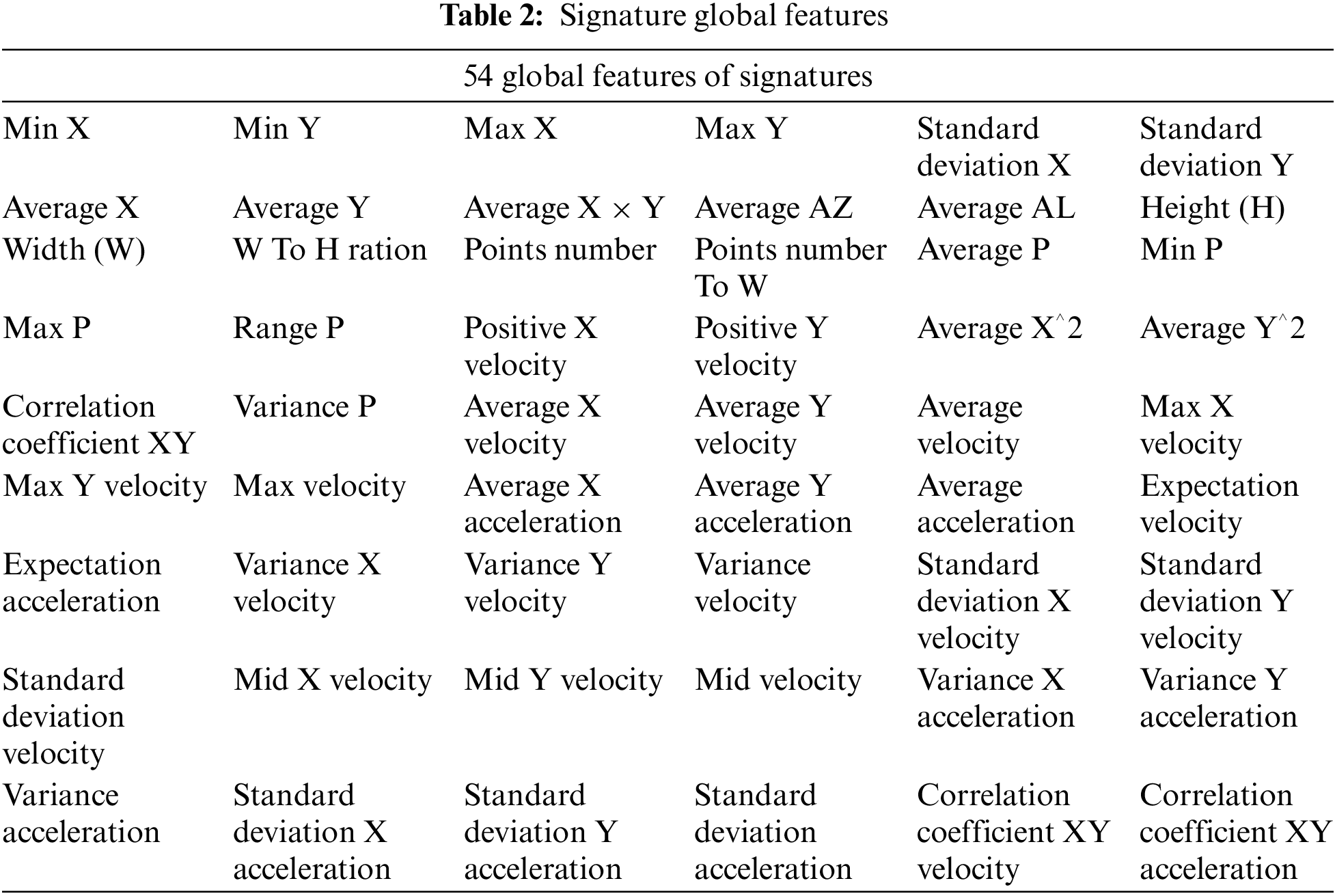
In the process of using multiple global features, the issue of feature redundancy inevitably arises. These redundant features not only increase the complexity of model training but may also negatively impact the model performance in authenticating genuine and forged signatures. To mitigate this drawback, this study employs a random forest feature selection method based on ensemble learning strategies to select features from the 54 extracted global features. This method assigns importance weights to each feature, and features with an importance weight of zero are removed. Simultaneously the PCA method is adopted to reduce 54 global features to four dimensions for filtering out effective features from the numerous global features.
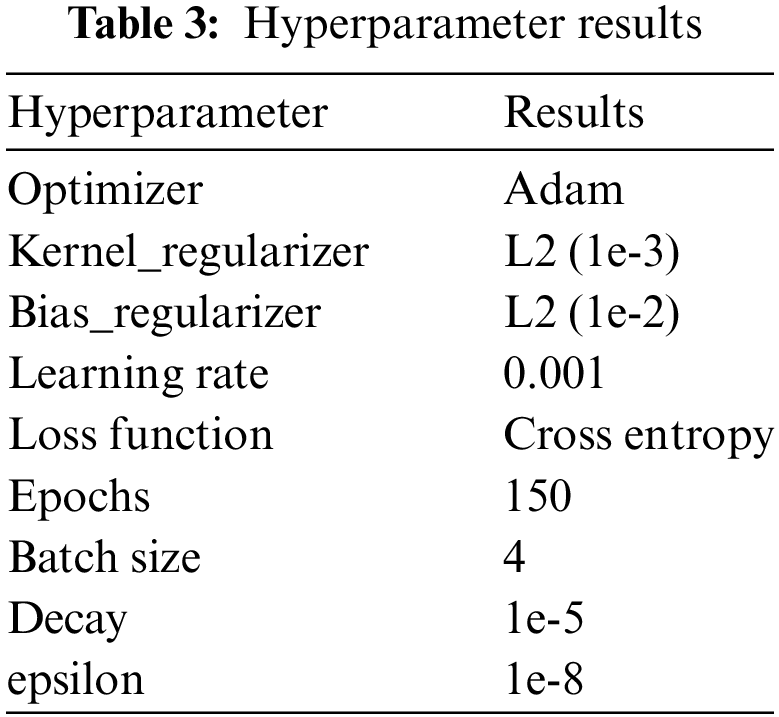
This study primarily conducted network hyperparameter optimization, training, and validation experiments using Python 3.8 and the TensorFlow 2.3 deep learning library. The adaptive moment estimation (Adam) optimizer is employed in this research. To ensure the convergence of the network model and mitigate overfitting, the model weight with the highest validation rate is selected as the final trained model after multiple iterations of training. Table 3 shows the results of hyperparameter optimization during the model learning process.
In this research, a variety of metrics are employed to assess the model. The formulas for these evaluation metrics are as follows:
Accuracy (ACC) is utilized to measure overall correctness. The False Acceptance Rate (FAR) quantifies the rate of incorrectly accepting forged signatures, while the False Rejection Rate (FRR) gauges the rate of incorrectly rejecting genuine signatures. The Equal Error Rate (EER) represents the point where FAR equals FRR, with lower values indicating superior performance. The Receiver Operating Characteristic (ROC) curve illustrates the trade-off between FAR and FRR. The Confusion Matrix (CM) presents detailed classification outcomes, including True Positives, True Negatives, False Positives, and False Negatives.
5.1 Analysis of Model Performance
To assess the overall performance of the model, this section presents a comprehensive analysis of signature authentication performance on the MCYT-100 and SVC-2004 Task2 datasets. This analysis includes the evaluation of authentication performance for all users. During the experimental process, the selected feature set after feature selection is employed as the input to the network. The experiment employed five genuine and forged signatures for training.
To further validate the effectiveness of the proposed method, we conducted experiments on both the 1D-ACGRNet model and the 1D-RNet model, comparing their EER and plotting ROC curves for comparison. From Fig. 5, it can be observed that on the MCYT dataset, the EER for signature verification with the 1D-RNet model is 4.37%, and the one for the 1D-ACGRNet model is 3.07%, and the improved 1D-ACGRNet model shows a significant decrease in EER by 1.30%. On the SVC dataset, the 1D-RNet model EER for signature verification is 4.76%, while the 1D-ACGRNet model EER is 4.17%, which indicates a reduction of 0.59% compared with the former.

Figure 5: The ROC curves of the MCYT dataset and the SVC dataset for two model architectures
In this subsection, we conduct comprehensive performance experiments using both the SVC dataset and the MCYT dataset, and the experimental results are presented in Table 4. It can be observed that with the increase in training data, FAR, FRR, and EER all show a decreasing trend on both datasets, while ACC shows improvement. The detailed data of the confusion matrix corresponding to Table 4 is illustrated in Fig. 6. The experimental results prove that on both the MCYT and SVC datasets, the 1D-ACGRNet model exhibits substantial overall performance enhancement in signature verification, confirming the effectiveness of the 1D-ACGRNet model.
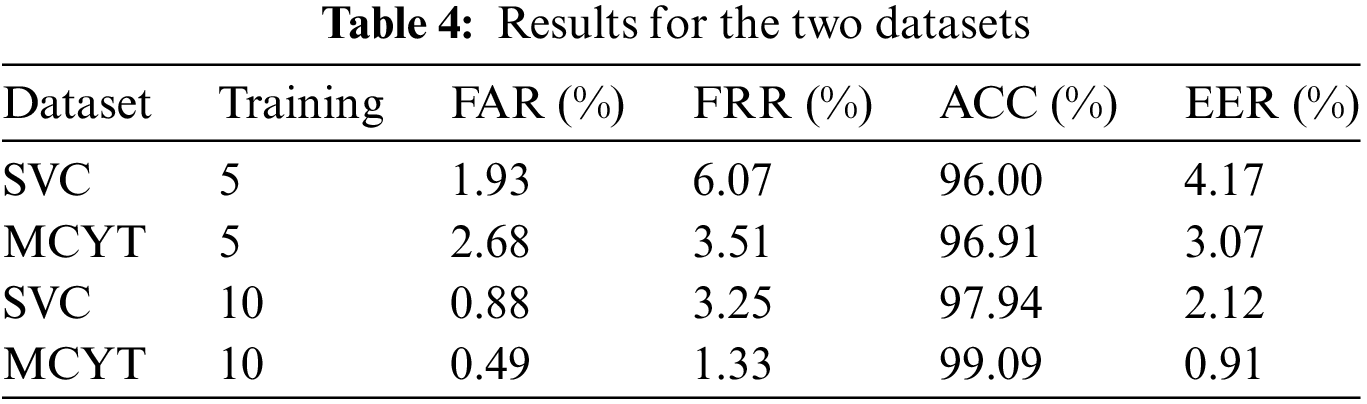

Figure 6: Confusion matrix of SVC and MCYT datasets
5.2 Analysis of Ablation Experiments
We employ “ablation experiments” to qualitatively and quantitatively analyze the impact of various components within the research model. To ensure the robustness of the model, the experiment adopts a stratified k-fold cross-validation method, dividing the signature data of each user into k equal parts, with one part as the training data, conducting k rounds of training and validation to ensure that each data subset participates in the testing phase. In this experiment, we ensure that the training data volume for each round is 5. Table 5 provides the specific results of the experiment. In conclusion, the enhanced model employed in this study has demonstrated significant performance improvements. This model not only enhances accuracy but also reduces computational costs, rendering it more suitable for online signature verification.
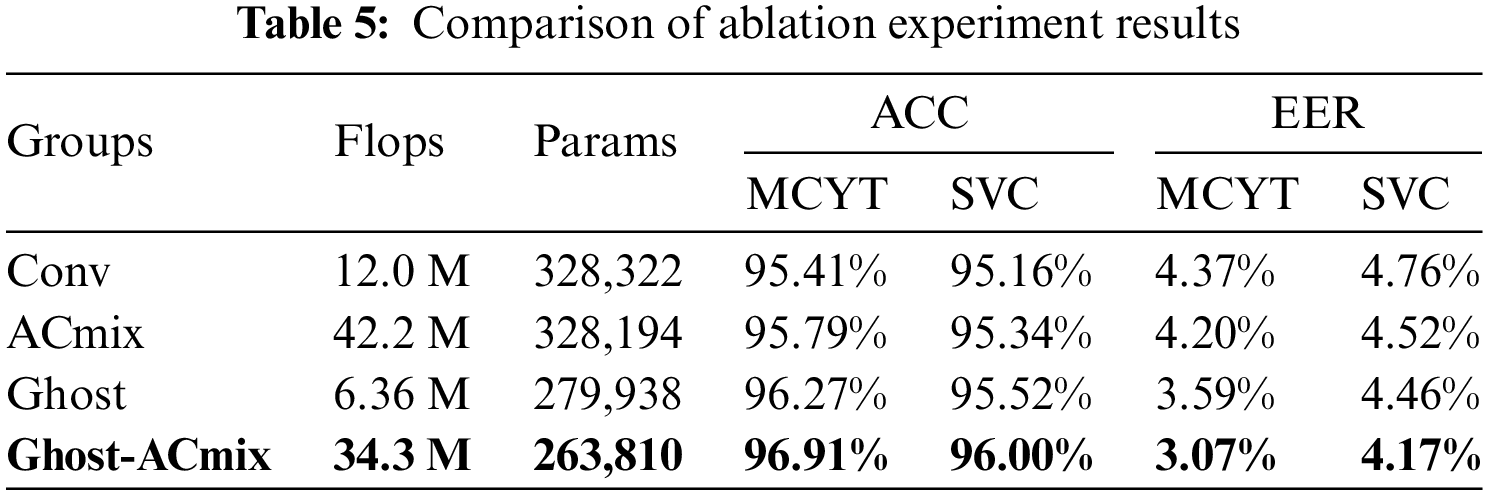
5.3 Comparison with Similar Work
To further validate the effectiveness of the proposed method, this section compares the performance of our approach with other methods. Table 6 presents experimental results obtained by different methods proposed by predecessors on the MCYT dataset and SVC dataset. When training with 5 genuine and forged signatures, as well as with 10 genuine and forged signatures, the equal error rates (EER) are consistently lower than those of other methods. This further validates the effectiveness of the proposed online handwritten signature verification method based on the one-dimensional Ghost-ACmix Residual Neural Network (1D-ACGRNet) introduced in this study.
This paper proposes an online signature verification method using a 1D-ACGRNet, which integrates convolution and self-attention mechanisms into a residual network. It is the first application of a residual network embedded with a mixture of convolution and self-attention mechanisms in this field. Convolution and self-attention are proficient in extracting local and global information from data, respectively. By combining them, the signature information becomes more comprehensive, thereby enhancing the overall accuracy of the model. Simultaneously applying feature selection removes redundant global features, which are combined with feature dimensionality reduction methods to obtain effective feature information. And the ghost method is further introduced to reduce the model’s computational complexity. The experimental results indicate that, when training samples are employed with 5 genuine and forgery signature data on the MCYT-100 and SVC-2004 Task2 datasets, the equal error rates of this study are 3.07% and 4.17%, respectively. When using 10 genuine and forgery signatures, the equal error rates are 0.91% and 2.12%. Compared with previous research, the proposed method in this paper has implemented some improvement in performance.
Acknowledgement: The authors would like to present appreciation to National Natural Science Foundation of China and Liaoning Provincial Science and Technology Department Foundation.
Funding Statement: This work is supported by National Natural Science Foundation of China (Grant No. 62073227) and Liaoning Provincial Science and Technology Department Foundation (Grant No. 2023JH2/101300212).
Author Contributions: The authors confirm contribution to the paper as follows: Study conception and design: F. Luan, X. Mu; data collection: X. Mu; analysis and interpretation of results: F. Luan, X. Mu, S. Yuan; draft manuscript preparation: X. Mu, S. Yuan. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Due to the nature of this research, participants of this study did not agree for their codes to be shared publicly, and supporting datasets are available. The SVC-2004 Task2 database is openly at: https://cse.hkust.edu.hk/svc2004/download.html. The MCYT-100 database is openly at: http://atvs.ii.uam.es/atvs/mcyt100s.html.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. M. M. Hameed, R. Ahmad, L. M. Kiah, G. Murtaza, and N. Mazhar, “OffSig-SinGAN: A deep learning-based image augmentation model for offline signature verification,” Comput. Mater. Contin., vol. 76, no. 1, pp. 1267–1289, Jun. 2023. doi: 10.32604/cmc.2023.035063. [Google Scholar] [CrossRef]
2. P. Wei, H. Li, and P. Hu, “Inverse discriminative networks for handwritten signature verification,” in Proc. CVPR, Long Beach, CA, USA, Jun. 2019, pp. 5757–5765. [Google Scholar]
3. A. Sharma and S. Sundaram, “A novel online signature verification system based on GMM features in a DTW framework,” IEEE Trans. Inf. Forensics Secur., vol. 12, no. 3, pp. 705–718, Mar. 2017. doi: 10.1109/TIFS.2016.2632063. [Google Scholar] [CrossRef]
4. L. Nanni, E. Maiorana, A. Lumini, and P. Campisi, “Combining local, regional and global matchers for a template protected on-line signature verification system,” Expert Syst. Appl., vol. 37, no. 5, pp. 3676–3684, May 2010. doi: 10.1016/j.eswa.2009.10.023. [Google Scholar] [CrossRef]
5. N. Sae-Bae and N. Memon, “Online signature verification on mobile devices,” IEEE Trans. Inf. Forensics Secur., vol. 9, no. 6, pp. 933–947, Jun. 2014. doi: 10.1109/TIFS.2014.2316472. [Google Scholar] [CrossRef]
6. L. Mehwish, M. Shahzad, D. L. Das, J. A. Hussain, and C. A. Ali, “Online signature verification using deep learning based aggregated convolutional feature representation,” J. Intell. Fuzzy Syst., vol. 43, no. 2, pp. 2005–2013, Jun. 2022. doi: 10.3233/JIFS-219300. [Google Scholar] [CrossRef]
7. J. Richiardi and A. Drygajlo, “Gaussian mixture models for on-line signature verification,” in Proc. 2003 ACM SIGMM Workshop on Biometrics Methods and Applicati., Melbourne, VIC, Australia, Nov. 2003, pp. 115–222. [Google Scholar]
8. A. Humm, J. Hennebert, and R. Ingold, “Gaussian mixture models for chasm signature verification,” in Proc. MLMI, Bethesda, MD, USA, May 2006, pp. 102–113. [Google Scholar]
9. A. K. Jain, F. D. Griess, and S. D. Connell, “On-line signature verification,” Pattern Recognit., vol. 35, no. 12, pp. 2963–2972, Dec. 2002. doi: 10.1016/S0031-3203(01)00240-0. [Google Scholar] [CrossRef]
10. L. L. Lee and T. Berger, “Reliable on-line human signature verification system for point-of-sales applications,” in Proc. ICPR, Jerusalem, Israel, Oct. 1994, pp. 19–23. [Google Scholar]
11. M. T. Ibrahim, M. Kyan, and L. Guan, “On-line signature verification using global features,” in Proc. CCECE, St. John’s, NL, Canada, May 2009, pp. 682–685. [Google Scholar]
12. J. Fierrez-Aguilar, L. Nanni, J. Lopez-Peñalba, J. Ortega-Garcia, and D. Maltoni, “An on-line signature verification system based on fusion of local and global information,” in Proc. AVBPA, Hilton Rye Town, NY, USA, Jul. 2005, pp. 523–532. [Google Scholar]
13. C. S. Vorugunti, G. Devanur, S. P. Mukherjee, and V. Pulabaigari, “OSVNet: Convolutional siamese network for writer independent online signature verification,” in Proc. ICDAR, Sydney, NSW, Australia, Sep. 2019, pp. 1470–1475. [Google Scholar]
14. D. Z. Lejtman and S. E. George, “On-line handwritten signature verification using wavelets and back-propagation neural networks,” in Proc. ICDAR, Seattle, WA, USA, Sep. 2001, pp. 992–996. [Google Scholar]
15. O. Alpar and O. Krejcar, “Online signature verification by spectrogram analysis,” Appl. Intell., vol. 48, pp. 1189–1199, May 2018. [Google Scholar]
16. H. Zeinali, B. BabaAli, and H. Hadian, “Online signature verification using i-vector representation,” IET Biom., vol. 7, no. 5, pp. 405–414, Sep. 2018. doi: 10.1049/iet-bmt.2017.0059. [Google Scholar] [CrossRef]
17. R. Tolosana, R. Vera-Rodriguez, J. Fierrez, and J. Ortega-Garcia, “Exploring recurrent neural networks for on-line handwritten signature biometrics,” IEEE Access, vol. 6, pp. 5128–5138, Jan. 2018. [Google Scholar]
18. K. Greff, R. K. Srivastava, J. Koutník, B. R. Steunebrink, and J. Schmidhuber, “LSTM: A search space odyssey,” IEEE Trans. Neural Netw. Learn Syst., vol. 28, no. 10, pp. 2222–2232, Oct. 2012. doi: 10.1109/TNNLS.2016.2582924. [Google Scholar] [PubMed] [CrossRef]
19. C. Li et al., “A stroke-based RNN for writer-independent online signature verification,” in Proc. ICDAR, Sydney, NSW, Australia, Sep. 2019, pp. 526–532. [Google Scholar]
20. S. Lai, L. Jin, L. Lin, Y. Zhu, and H. Mao, “SynSig2Vec: Learning representations from synthetic dynamic signatures for real-world verification,” in Proc. AAAI Conf. Artif. Intell., Apr. 2020, pp. 735–742. [Google Scholar]
21. C. S. Vorugunti, V. Pulabaigari, R. K. S. S. Gorthi, and P. Mukherjee, “OSVFuseNet: Online signature verification by feature fusion and depth-wise separable convolution based deep learning,” Neurocomputing, vol. 409, pp. 157–172, Oct. 2020. doi: 10.1016/j.neucom.2020.05.072. [Google Scholar] [CrossRef]
22. A. Jain, S. K. Singh, and K. P. Singh, “Handwritten signature verification using shallow convolutional neural network,” Multimed. Tools. Appl., vol. 79, pp. 19993–20018, Apr. 2020. doi: 10.1007/s11042-020-08728-6. [Google Scholar] [CrossRef]
23. A. Kholmatov and B. Yanikoglu, “Identity authentication using improved online signature verification method,” Pattern Recognit. Lett., vol. 26, no. 15, pp. 2400–2408, Nov. 2005. doi: 10.1016/j.patrec.2005.04.017. [Google Scholar] [CrossRef]
24. X. Song, X. Xia, and F. Luan, “Online signature verification based on stable features extracted dynamically,” IEEE Trans. Syst. Man Cybern. Syst., vol. 47, no. 10, pp. 2663–2676, Oct. 2017. doi: 10.1109/TSMC.2016.2597240. [Google Scholar] [CrossRef]
25. S. Lai, L. Jin, and W. Yang, “Online signature verification using recurrent neural network and length-normalized path signature descriptor,” in Proc. ICDAR, Kyoto, Japan, Nov. 2017, pp. 400–405. [Google Scholar]
26. L. Tang, W. Kang, and Y. Fang, “Information divergence-based matching strategy for online signature verification,” IEEE Trans. Inf. Forensics Secur., vol. 13, no. 4, pp. 861–873, Apr. 2018. doi: 10.1109/TIFS.2017.2769023. [Google Scholar] [CrossRef]
27. O. Miguel-Hurtado, L. Mengibar-Pozo, M. G. Lorenz, and J. Liu-Jimenez, “On-line signature verification by dynamic time warping and gaussian mixture models,” in Proc. ICCST, Ottawa, ON, Canada, Oct. 2007, pp. 23–29. [Google Scholar]
28. K. He, X. Zhang, S. Ren, and J. Sun, “Deep residual learning for image recognition,” in Proc. CVPR, Las Vegas, NV, USA, Jun. 2016, pp. 770–778. [Google Scholar]
29. X. Pan et al., “On the integration of self-attention and convolution,” in Proc. CVPR, New Orleans, LA, USA, Jun. 2022, pp. 805–815. [Google Scholar]
30. K. Han, Y. Wang, Q. Tian, J. Guo, C. Xu and C. Xu, “GhostNet: More features from cheap operations,” in Proc. CVPR, Seattle, WA, USA, Jun. 2020, pp. 1577–1586. [Google Scholar]
31. Á. Michelena, J. Aveleira-Mata, E. Jove, H. Alaiz-Moretón, H. Quintián and J. L. Calvo-Rolle, “Development of an intelligent classifier model for denial of service attack detection,” Int. J. Interact. Multi., vol. 8, no. 3, pp. 33–42, Aug. 2023. doi: 10.9781/ijimai.2023.08.003. [Google Scholar] [CrossRef]
32. H. Tan, L. He, Z. Huang, and H. Zhan, “Online signature verification based on dynamic features from gene expression programming,” Multimed. Tools. Appl., vol. 83, pp. 15195–15221, May 2021. doi: 10.1007/s11042-021-11063-z. [Google Scholar] [CrossRef]
33. L. Yang, Y. Cheng, X. Wang, and Q. Liu, “Online handwritten signature verification using feature weighting algorithm relief,” Soft Comput., vol. 22, pp. 7811–7823, Aug. 2018. doi: 10.1007/s00500-018-3477-2. [Google Scholar] [CrossRef]
34. W. H. Khoh, T. S. Ong, Y. H. Pang, and A. B. J. Teoh, “Score level fusion approach in dynamic signature verification based on hybrid wavelet-fourier transform,” Secur. Commun. Netw., vol. 7, no. 7, pp. 1067–1078, Jul. 2014. doi: 10.1002/sec.829. [Google Scholar] [CrossRef]
35. H. Bian, F. Luan, and S. Yuan, “Online handwritten signature verification based on feature selection and ghost residual network,” Comput. Sci. Appl., vol. 13, no. 3, pp. 635–646, Mar. 2023 (In Chinese). [Google Scholar]
36. C. S. Vorugunti, R. K. S. Gorthi, and V. Pulabaigari, “Online signature verification by few-shot separable convolution based deep learning,” in Proc. ICDAR, Sydney, NSW, Australia, Sep. 2019, pp. 1125–1130. [Google Scholar]
37. Q. Shen, F. Luan, and S. Yuan, “Multi-scale residual based siamese neural network for writer-independent online signature verification,” Appl. Intell., vol. 52, pp. 14571–14589, Mar. 2022. doi: 10.1007/s10489-022-03318-5. [Google Scholar] [CrossRef]
38. M. Okawa, “Online signature verification using single-template matching with time-series averaging and gradient boosting,” Pattern Recognit., vol. 102, pp. 107227, Jun. 2020. doi: 10.1016/j.patcog.2020.107227. [Google Scholar] [CrossRef]
39. R. Doroz, P. Kudlacik, and P. Porwik, “Online signature verification modeled by stability oriented reference signatures,” Inf. Sci., vol. 460, pp. 151–171, Sep. 2018. doi: 10.1016/j.ins.2018.05.049. [Google Scholar] [CrossRef]
40. M. Diaz, M. A. Ferrer, and J. J. Quintana, “Anthropomorphic features for on-line signatures,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 41, no. 12, pp. 2807–2819, Dec. 2019. doi: 10.1109/TPAMI.2018.2869163. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF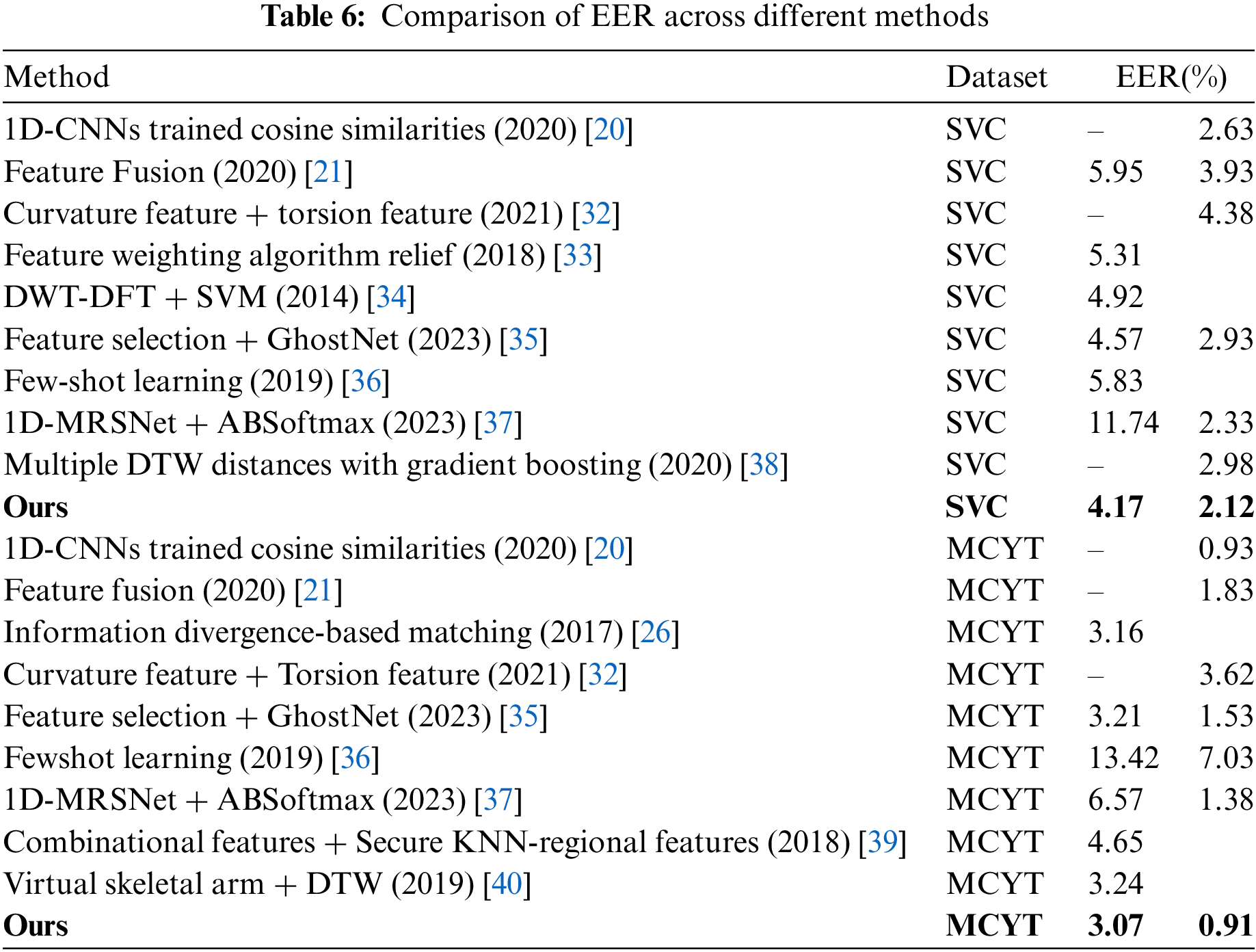
 Downloads
Downloads
 Citation Tools
Citation Tools