A Game-Theoretic Approach to Safe Crowd Evacuation in Emergencies

1  Introduction

In an emergency, whether it is natural like a fire and earthquake, or man-made activity, like a terrorist attack; efficiently evacuating a crowd can be critical to minimize the casualties and damage to properties and the environment. Crowd evacuation is a complex procedure and topic both in city and building designing, robotics, etc., as it involves the behavior of large groups of people experiencing panic, fear, or confusion. There are many models developed for crowd evacuation, like the simulation of pedestrian dynamics force-based model [1,2]. Pedestrian flow is presented by fluid motion [3]. In [4,5], grid cells represent the space set. In [4], the lattice gas model was used to study the pedestrian flow properties to simulate crowd evacuation from a hall. However, like all models, the lattice gas model has some limitations that include evacuees moving discretely and simple rules governing their movements; this assumption may be suitable for some crowds, but it may not accurately reflect the behavior of individuals in large and complex groups.

In [6], two factors namely, conflict and pedestrian direction cost occurred while pedestrians moved to remove the obstacles from the exit. In [7,8], Agent-based Modelling (ABM) is used to simulate the evacuation of the crowd from the arena. In contrast, this model requires detailed data on the behavior and properties of individuals in the crowd, which may not be available in real-world scenarios. It is computationally expensive and requires significant processing power to simulate large groups, which are some of the limitations of this model. In [9], the critical properties of ABM are autonomy, responsiveness, proactivity, and social interaction, which makes it a perfect fit for scenarios requiring autonomous and adaptable participant agents. In [10], these models have advantages and dis-advantages as they can produce self-organized and collective phenomena like the fast-er-is-slower effect, lane formation, etc. In [11], the researcher proposes the ABM approach as an extended social force model that incorporates group structures and dynamics and applies it to simulate pedestrian crowds in various scenarios with limitations like computational complexity, data collection, and simplified group structures. In [12], the researchers utilize a multi-agent system (MAS) approach to propose a model that combines individual pedestrian behavior with the behavior of trained leaders who help the crowd during building evacuation. The MAS approach allows for modelling pedestrians’ and trained leaders’ individual and collective behaviors and their interactions. The limitations of the proposed model include simplified assumptions about human behavior and the lack of validation for its effectiveness in real-world scenarios. In [13], the limitations ad-dressed in the social force model for pedestrian crowd evacuation simulation during emergencies include the assumption that trained leaders consistently positively impact evacuation results, disregarding cognitive processes, which may not hold in real-world scenarios. Reference [14] proposes an agent-based model for simulating crowd behavior during emergencies. The model incorporates psychological models, roles, and communication to capture the behavior of individuals and groups within a crowd. Reference [15] proposes an agent-based model for simulating crowd behavior that incorporates the general adaptation syndrome (GAS) theory to capture the effects of stress and fatigue on individuals. The limitations of the model addressed are that the model focuses on the behavior of individuals within a crowd and does not consider external factors that may impact crowd behavior, such as environmental conditions. Reference [16] proposes a game-theory-based model for simulating pedestrian evacuation behavior in emergencies. The proposed model considers individual preferences for exit routes to optimize evacuation time and minimize congestion, but its practical application in real-world scenarios with large crowds is limited due to significant computational resource requirements. In [17], the authors propose a game-theoretical model that simulates herding behavior in human crowds, accounting for emotional and rational factors in emergency evacuation scenarios. Still, limitations include assumptions of perfect information, static emotions, decision-making, and discussions on evacuation routes affected by obstacles and crowd dynamics with various configurations [18,19]. To improve the overall crowd evacuation efficiency a suitable layout of obstacles is the best choice [20]. During crowd evacuation, the selection of exits is a crucial factor that reflects the behaviors of evacuees, with distance to the chosen exit typically being one of the most significant factors [21]. In [22], cellular automata (CA) model is used by applying game theory (GT) to investigate the choice of exit by pedestrians. One of the limitations is that the model assumes individuals have a static level of choice firmness, which may not accurately capture the decision-making process of real individuals who multiple factors can influence in a dynamic environment. In [23], evacuation models are divided into two types: The macroscopic and the microscopic models. In macroscopic models [24], the pedestrian characters resemble fluid dynamics and are often implemented in crowd simulations without adequately considering their behaviors. Microscopic models, a simulation model, capture the behavior of respective agents within a crowd during evacuations. The model operates at a microscopic level, meaning that it simulates the behavior of individual agents such as pedestrians or vehicles, rather than analyzing the overall movement of the crowd. Microscopic models have been divided into the social force model and the CA model [25].

In this research, a game theoretic model that incorporates removing large obstacles to simulate crowd evacuation has been proposed. Game setup exhibits several levels of cooperation and competition (payoff) between the players (evacuees). The payment of one player is equivalent to the gain of another and so on. This can be segregated into support, oppose, and evade categories. We considered a room with four exits at different locations, where we created different scenarios for obstacles placement which volunteers will remove. We employ the Next Cell Conflict (NCC) game to solve the conflict between the evacuees as they select the same desired cell to move in. We used the volunteer selection game to choose the group of volunteers [26]. Once selected, a task allocation game is employed which will explain how the large obstacles are removed by the volunteers when more large obstacles exist. In this regard, two types of factors exist: 1. Conflict when two or more evacuees want to move to one grid cell 2. Evacuees must decide whether to become a volunteer or not to remove the obstacles from the exit. To determine the movement of evacuees, we have used Floor Fields [27]. Parameters affecting the evacuation process are the placement of obstacles, removing obstacles from the exits, selection of volunteer group, time spent removing the obstacle, and repulsive floor field (RFF) strength to see obstacles from a distance. Eventually, we conducted various experiments that are shown through graphs and simulations. To summarize, following are the main contributions of the study:

1.    A detailed model-based analysis of crowd evacuation during disaster/emergency has been investigated while considering various levels of cooperation and competition among evacuees.

2.    A comprehensive literature review has been performed to figure out details about the type of games used in different occasions/situations.

3.    To address real-life situations, different scenarios for obstacle placement and size of obstacles are investigated in the proposed game theoretic model.

4.    By investigating several games and situations, the overall evacuation time and efficiency of crowd evacuation has been improved.

5.    Three games are introduced for volunteer selection, next cell selection, and task allocation to adequately evacuate the crowd and remove the obstacles of various sizes from the exits.

The rest of the paper is divided into eight sections. Section 2 provides literature review and the related worktable of state-of-the-art in game theoretic evacuation. Section 3 presents the crowd evacuation model and the table of abbreviations. Section 4 provides the game theoretic evacuation. Section 5 presents the game simulation. Section 6 presents the results of the experiments. Section 7 presents the discussion, limitations, and future work, and finally, Section 8 concludes the paper.

2  Literature Review

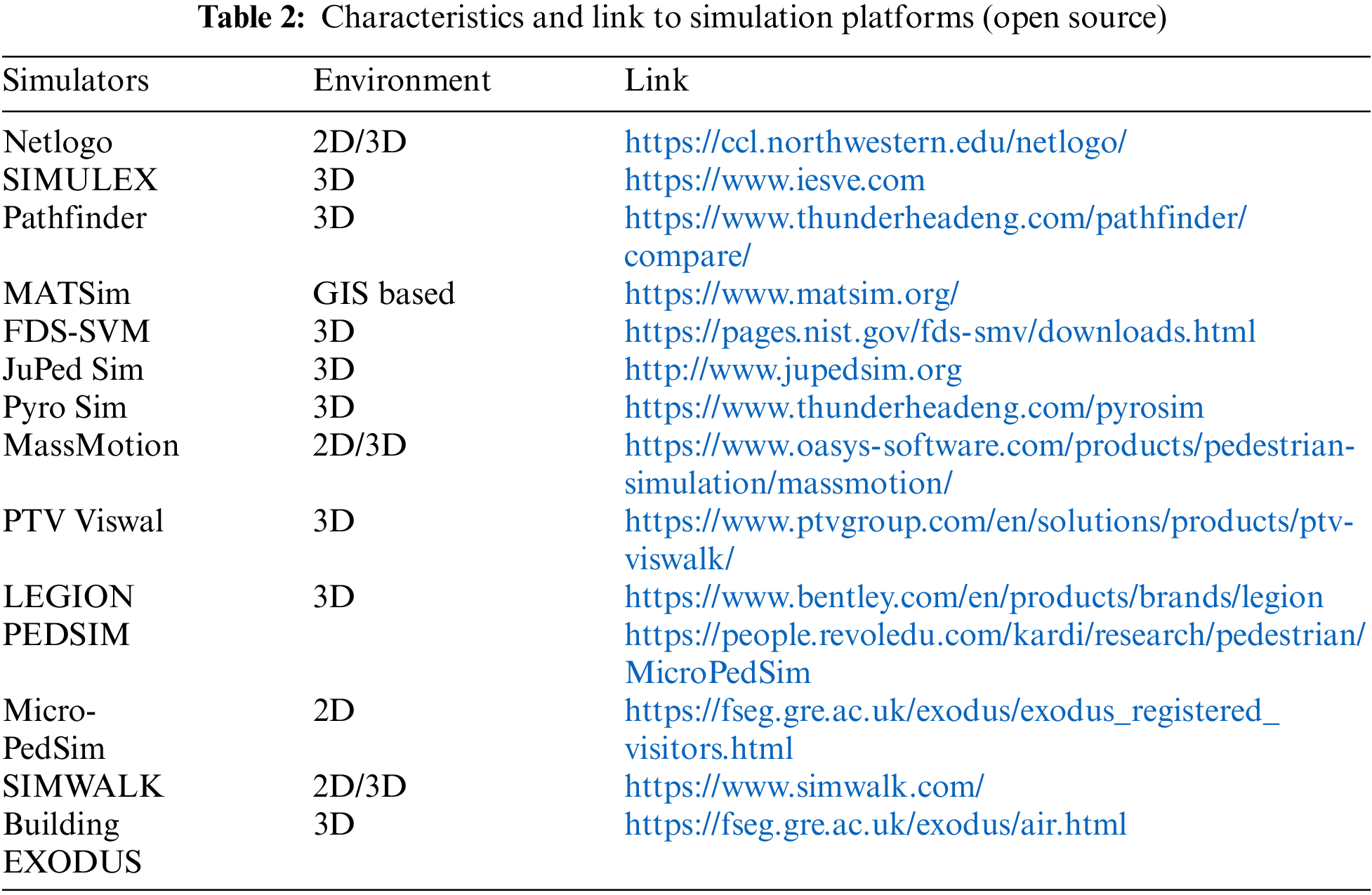
Game theory (GT) is the best tool to resolve conflict and cooperation issues in decision-making, where both exist simultaneously [28]. The authors use a noncooperative multistep game framework to represent the decision-making processes of different stakeholders in a crisis scenario, including authorities, victims, and potential attackers. The model considers the interdependencies between different events and stakeholders and seeks to identify optimal strategies for managing them. Some of the limitations are assumptions about the rationality that the model assumes that all stakeholders behave rationally and make optimal decisions based on their preferences and beliefs. Human behavior is often influenced by emotions, biases, and other factors that may not be captured by a purely rational model. The model is based on a lattice gas approach that represents individuals as particles that move and interact with each other based on simple rules. The model includes factors such as pedestrian density, panic intensity, and obstacles in the environment. The limitations of this model include simple representation of human behavior, limited applicability [1]. A cellular automaton model for simulating the evacuation process in the presence of obstacles. The model represents individuals as cells in a grid-like environment and simulates their movement based on a set of predefined rules. The model also incorporates obstacles in the environment, such as walls and obstacles, which affect the movement of individuals. However, individuals behaving according to a set of predefined rules and do not consider complex decision-making processes or emotional factors is one of the limitations [29]. Reference [30] proposes a cellular automata model that integrates spatial games and memory effects to simulate crowd evacuation behavior in emergency situations. The model represents individuals as agents with spatial memory and simulates their movement based on a set of predefined rules that include strategic decision-making based on spatial games. The model assumes that individuals behave rationally and make strategic decisions based on spatial games. However human behavior during emergency situations may be influenced by a wide range of factors, including emotions, social norms, and cognitive biases, which are not captured by the model is one of the norms. In [26], a GT-based simulation model for evacuation is proposed. The model uses a combination of social force model and game theory to simulate the evacuation process, considering the removal of obstacles. The GT component involves the decision-making of agents to determine the best exit route and avoid congestion, while the social force model is used to calculate the movement of agents based on their interactions with each other and the environment. The study in [31] is a decision-making model based on Bayesian GT where the model considers the decision-making process of individuals during an evacuation, considering their rationality, perception of risk, and social interactions. One of the limitations of this model is that it does not consider the psychological and emotional factors that may affect the decision-making and behavior of agents during an evacuation. Additionally, the model assumes that agents have perfect information about the environment and the location of obstacles, which may not always be the case in real-world evacuation scenarios. Reference [32] is a game-theoretic approach where model aims to investigate how the cry wolf effect affects evacuation decisions in emergency situations. The cry wolf effect refers to situations where people become skeptical of warnings because they have received false alarms in the past. Reference [33] is an evolutionary game-theoretic approach. The approach involves modeling the potential crowd behaviors using evolutionary GT, which considers the interactions and decisions of individuals within a group during an evacuation. The model aims to identify the critical factors affecting evacuation dynamics and predict the possible outcomes of different crowd behaviors. One of the limitations of this approach is that it assumes rational and selfish behavior of the individuals within the crowd, which may not always be the case in real-world emergency situations. Reference [34] is a cellular automaton model that integrates GT to resolve conflicts during the evacuation process. The limitations of this model are the model assumes all individuals are rational decision-makers who always act in their best interest, which may not be the case in real-world emergency situations. The model does not consider differences in physical ability, knowledge, and behavior of individuals during the evacuation process and the impact of social influence on the decision-making process of individuals during the evacuation process. In [35], authors examined pedestrian evacuation in a hall using a cellular automaton model incorporating game strategy updates. The researchers investigated the correlation between the pedestrian flow rate and evacuation time, as well as the effect of noise on the variation of cooperative proportion over time, for various initial cooperative proportions. Reference [36] is a lattice gas model coupled with an evolutionary GT. The model considers the interactions between pedestrians and obstacles, and their decision-making process to reach their destinations. The evolutionary game aspect of the model allows for the emergence of cooperation and competition among pedestrians. The limitations of the model include the assumption of a homogeneous pedestrian population with identical preferences and capabilities. The model also does not consider the impact of individual characteristics such as age, gender, or physical disabilities as well as the effect of panic or other unexpected events that may occur during an evacuation. These are potential considerations for future work. Table 1 provides a summary of game types used in crowd evacuation studies while Table 2 provides characteristics and links to simulation platforms frequently used in the literature.

In contrast to the games utilized in the literature, the proposed study involves multiple games instead of single game especially in the emergency evacuation scenarios which is evident in Table 1. Multiple games help to address the behavior modelling more adequately and precisely considering various aspects and scenarios. Such as volunteer selection, next cell selection, and task allocation to adequately evacuate the crowd and remove the obstacles of various sizes from the exits. This makes strategically sturdier, helps in an improved payoff and better goal achievement in an emergency evacuation situation. Additionally various topologies of players and hazards are considered with different types of exits to comprehend the situation.

3  Proposed Crowd Evacuation Model

In the proposed model, we consider a room in a building which is represented by a grid of square cells of equal size. The room has multiple exits, and at least one of the exits is blocked by obstacles, where the size of obstacles may be small or large. The size of small obstacles is like the size of one grid cell, which can be easily removed by a single agent. However, large obstacles can occupy multiple grid cells and can only be removed by a group of agents. The number of agents required to remove these large obstacles depends on the size of the obstacles. We assume that dozens of pedestrians are inside the room during the evacuation. Moreover, the pedestrians are of two types: (a) evacuees or departer and (b) volunteers or aides. The volunteer voluntarily decides to remove obstacles to open the exits/paths, whereas an evacuee follows the instructions given by the volunteer, i.e., volunteers help evacuees, and evacuees cooperate with volunteers in turn. Furthermore, evacuees may decide to leave the room or not, and they may choose the appropriate exit. The proposed taxonomy is shown in Fig. 1. The game setup is comprised of five parts namely, behavior that represents possible players’ behaviors during the evacuation, targets represent the possible outcomes in the form of adequate evacuation tasks, environment features represent the spatial layout of the evacuation site, scenarios represent possible type of emergency events while techniques represent the solution games and their evaluation criteria.

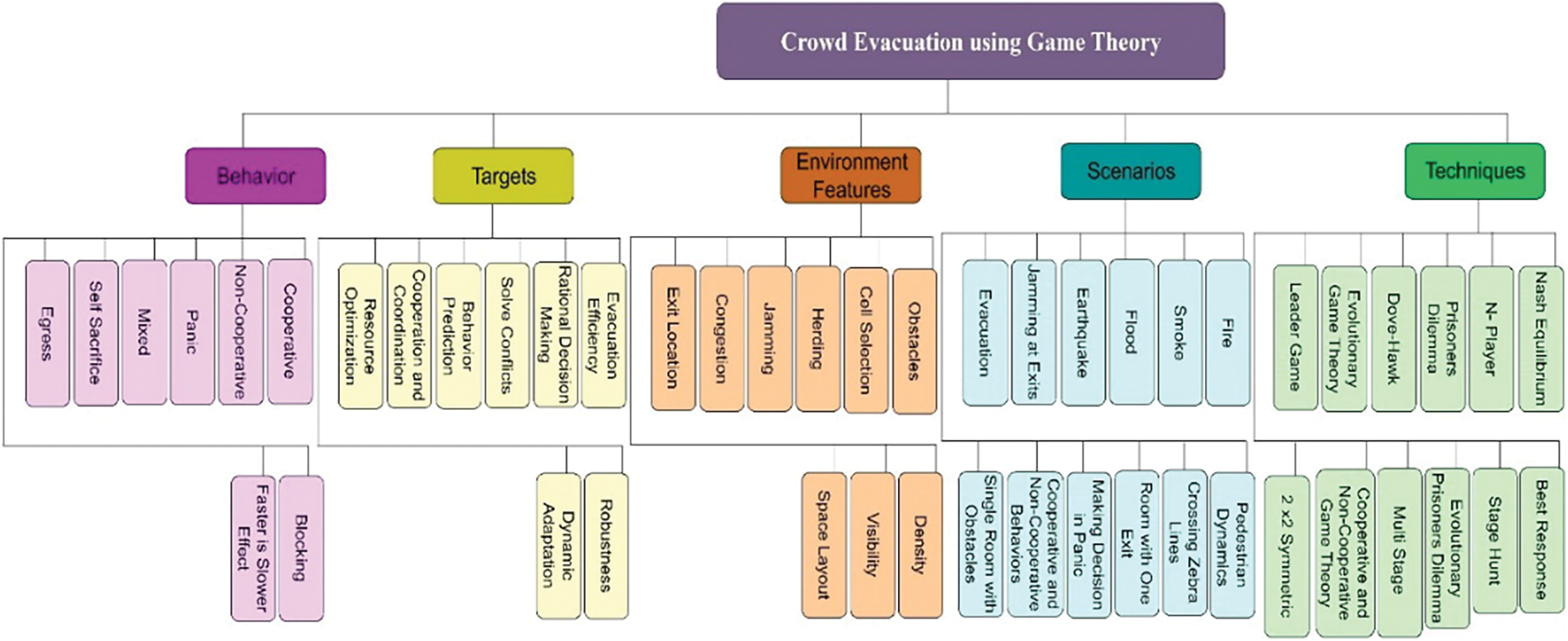
Figure 1: Proposed taxonomy for crowd evacuation using game theory

3.1 Transition Probability

Transition probability refers to the probability of a pedestrian moving from one cell or location to another in the evacuation area. This probability is influenced by various factors, such as the pedestrian’s current location, the density of other pedestrians in the surrounding area, the presence of obstacles or hazards, and the pedestrian’s preferred direction of movement.

We use Moore’s Neighborhood [26], where an evacuee will move in eight directions. The Von Neumann neighborhood is also possible, but it will restrict the evacuee from moving in only four directions. A room is represented by grid cells composed of rows and columns. Rows are represented by vj. The following equation can compute adjacent grid cells transition probability:

P(u_i,v_j)=(1−q)∗P(u_i−1,v_j−1)+q4∗[P(u_i−1,v_j)+P(u_i−1,v_j+1)+P(u_i,v_j−1)+P(u_i,v_j+1)+P(u_i+1,v_j−1)+P(u_i+1,v_j)+P(u_i+1,v_j+1)](1)

whereas in Eq. (1), P(u_i,v_j) represents grid cells transition probabilities of evacuees/pedestrians. q is the evacuee/pedestrian probability when they select to move to one of the eight directions except moving in a straight direction, which is represented in Fig. 2. In Eq. (1), we assume that an evacuee only moves in eight directions, where the current probability of an evacuee can be calculated by using the previous transition probability of adjacent grid cells. The use of an extended Moore’s neighborhood in crowd evacuation allows for a realistic representation of the interactions between individuals in a crowd. In the extended Moore’s neighborhood, everyone’s movement is influenced not only by their immediate neighbors but also by those in the diagonal direction. This allows for a more accurate representation of the potential for individuals to move in a diagonal direction during an evacuation, which can be necessary for avoiding obstacles or congestion. For the calculation of extended Moore’s neighborhood, Eq. (2) is used:

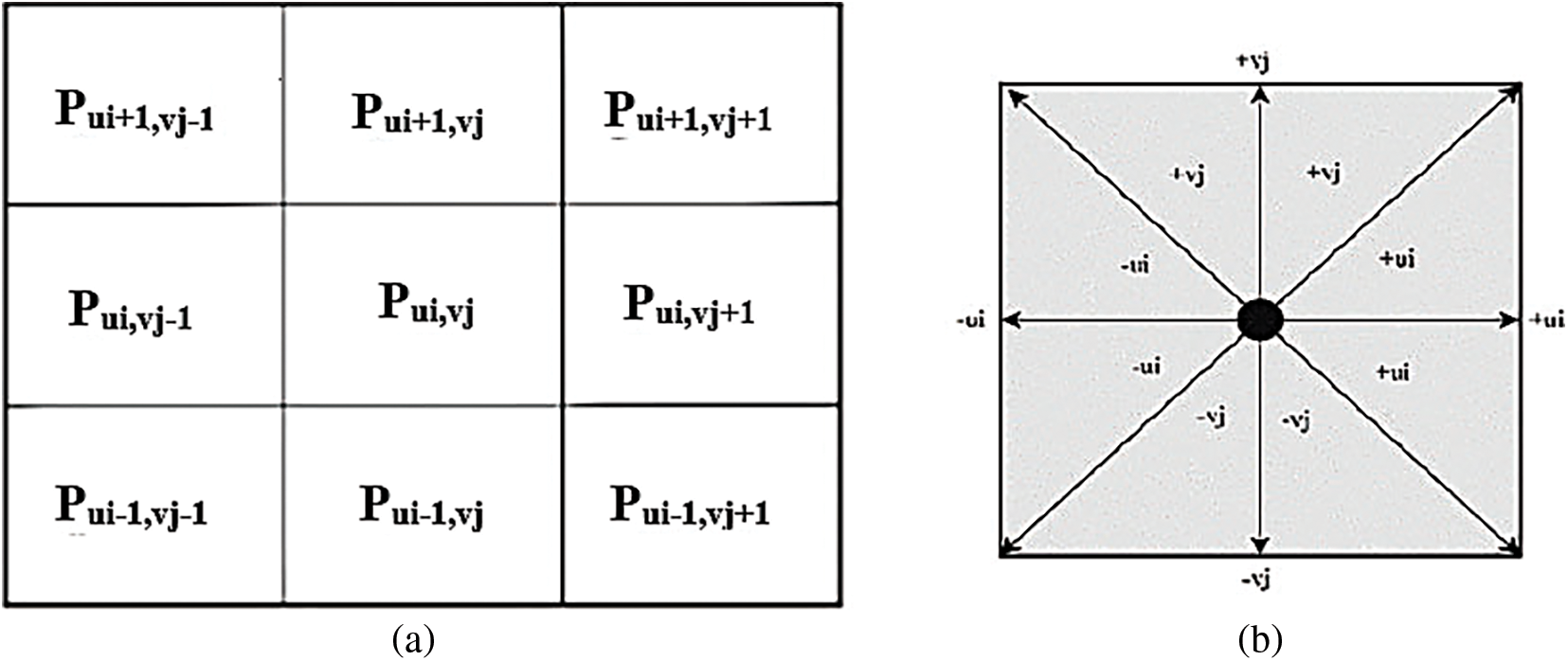
Figure 2: Transition probabilities. (a) Through quadrants; (b) Through Moore’s neighborhood

P(u_i,v_j)=(1−q)∗P(u_i−1,v_j−1)+q8∗[P(u_i−2,v_j−2)+P(u_i−2,v_j−1)+P(u_i−2,v_j)+P(u_i−2,v_j+1)+P(u_i−2,v_j+2)+P(u_i−1,v_j−2)+P(u_i,v_j−2)+P(u_i,v_j+2)+P(u_i+1,v_j−2)+P(u_i+1,v_j+2)+P(u_i+2,v_j−2)+P(u_i+2,v_j−1)+P(u_i+2,v_j)+P(u_i+2,v_j+1)+P(u_i+2,v_j+2)](2)

Eq. (2) recursively computes the probabilities at position (u_i,v_j) based on its neighboring cells. An evacuee can move in eight directions based on Moore’s Neighborhood, as shown in Fig. 2a. However, agents can only move to four adjacent cells in the Von Neumann neighborhood, as shown in Fig. 3. The gray shades show evacuee (maroon color) can move in these directions.

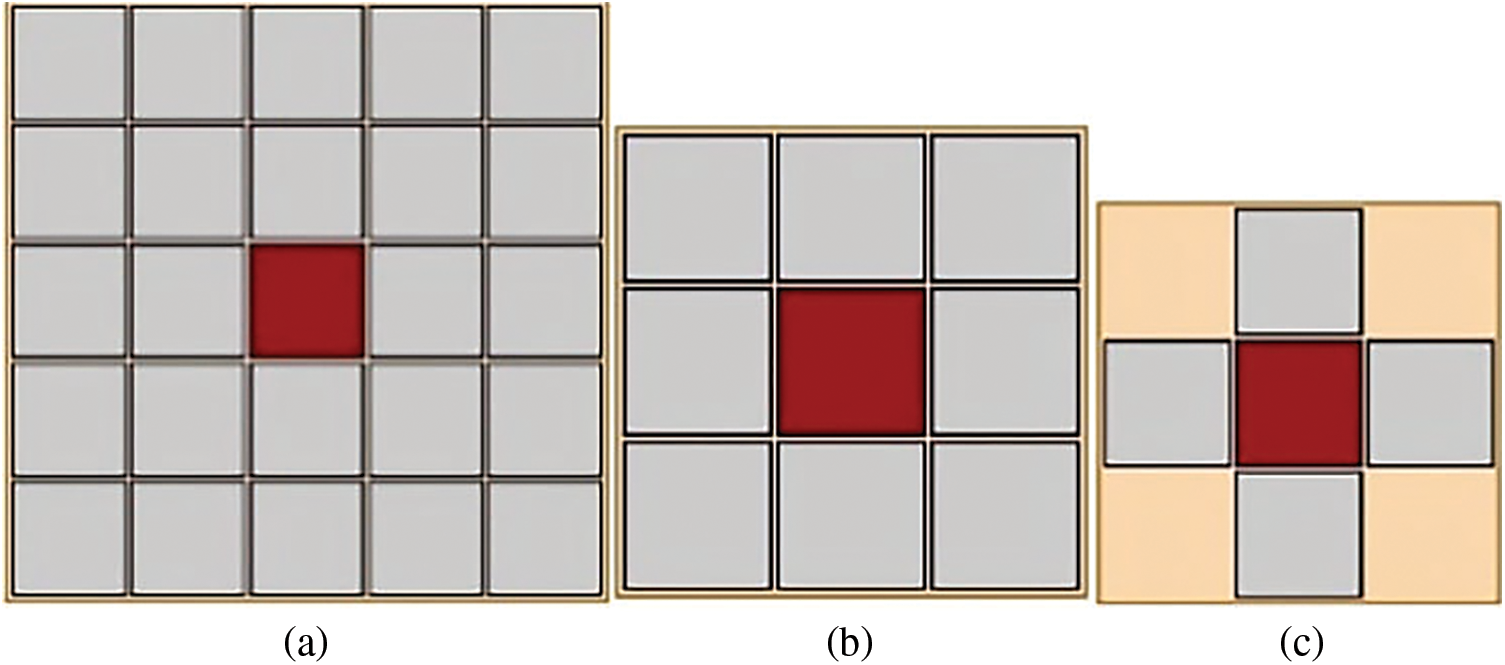
Figure 3: Neighborhood types. (a) Extended Moore’s neighborhood; (b) Moore’s neighborhood; and (c) Von Neumann neighborhood

In the proposed model, the size of the room is 80 × 80 meters, and it has square grid cells. The highest Floor Field (FF) is assigned to grid cells of walls, preventing evacuees from crossing walls. The exits are given the lowest value, so evacuees follow the direction towards the exits. Initially, each cell is unoccupied, but later the cells may be occupied by obstacles and pedestrians. The size of the cell is 0.4 m2 × 0.4 m2. Only one pedestrian can occupy an empty grid cell at a certain time instant. All the evacuees are distributed randomly inside the room with density φ. The changing effects of all pedestrains and exits are captured by (a) static floor field (SFF); (b) dynamic floor field (DFF); (c) repulsive floor field (RFF); and (d) interactions among pedestrians. Table 3 lists the abbreviations and their meanings used in the study.

3.2 Floor Fields

The evacuees move toward the exits using the floor fields mentioned in Section 3.1, as room is composed of grid cells and after determining the location of exits, where boundary of walls and obstacles are given constant value. The boundary of walls and obstacles have the highest value because they will help evacuees/pedestrians to avoid them.

3.2.1 Static Floor Field (SFF)

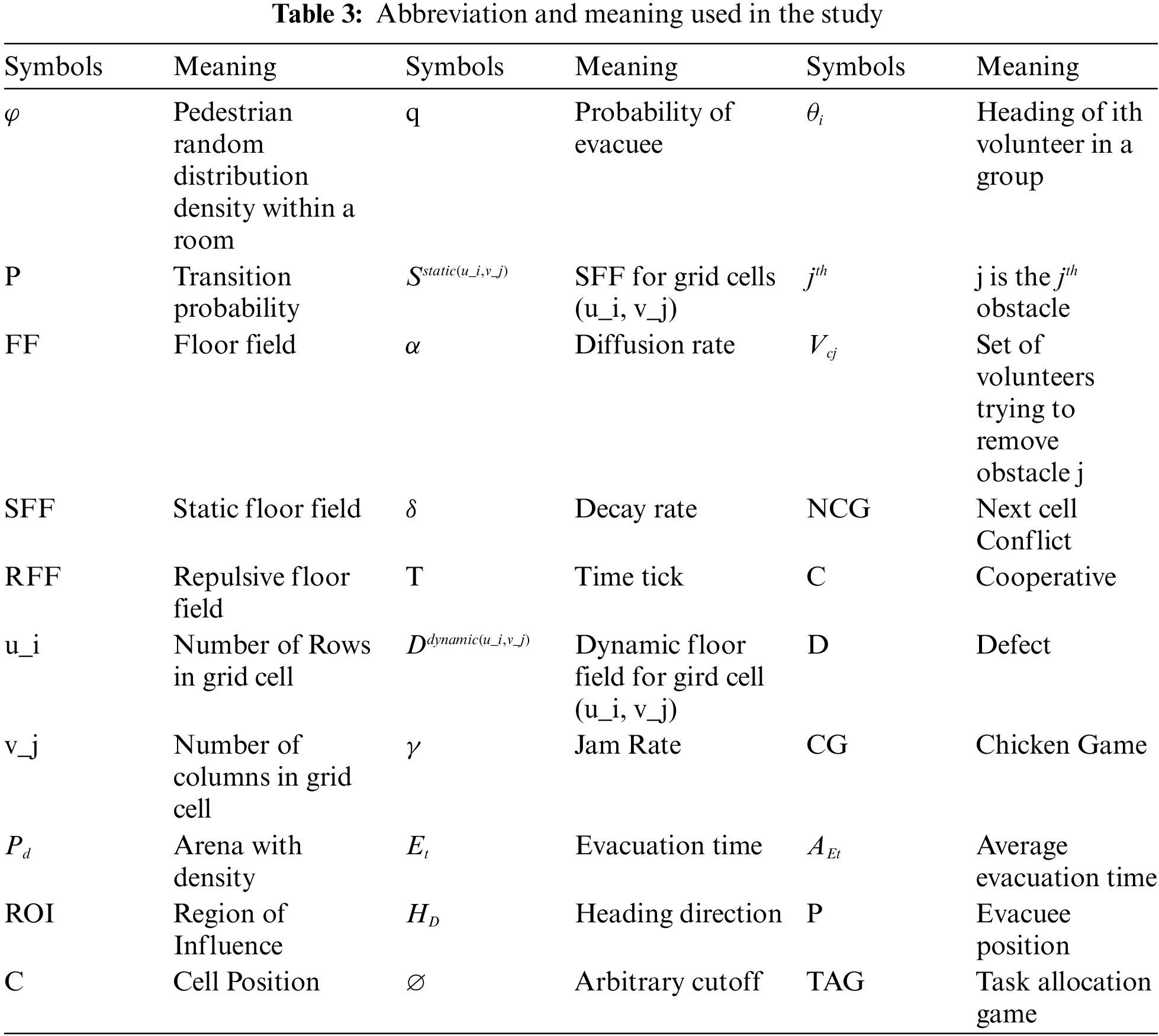
Static floor field means the values of walls and obstacles will not change and is not time dependent, e.g., windows shape, exit location, etc. A SFF helps to find and choose the shortest distance to the specific emergency exit that helps to evacuate the pedestrians from the area [50]. In this research, we assumed a room composed of 16 × 16 grid cells with four exits at different locations and blocked with four different obstacles. Obstacles are placed in front of doors, composed of two grid cells. Doors are also composed of two grid cells, as shown in Fig. 4. The circle in red color indicates the hazard area. SFF for room of cells (u_i,v_j) is represented as Sstatic(u_i,v_j) and its working rules are proposed in [29]. Adjacent cells to walls, values are assigned according to mentioned rules:

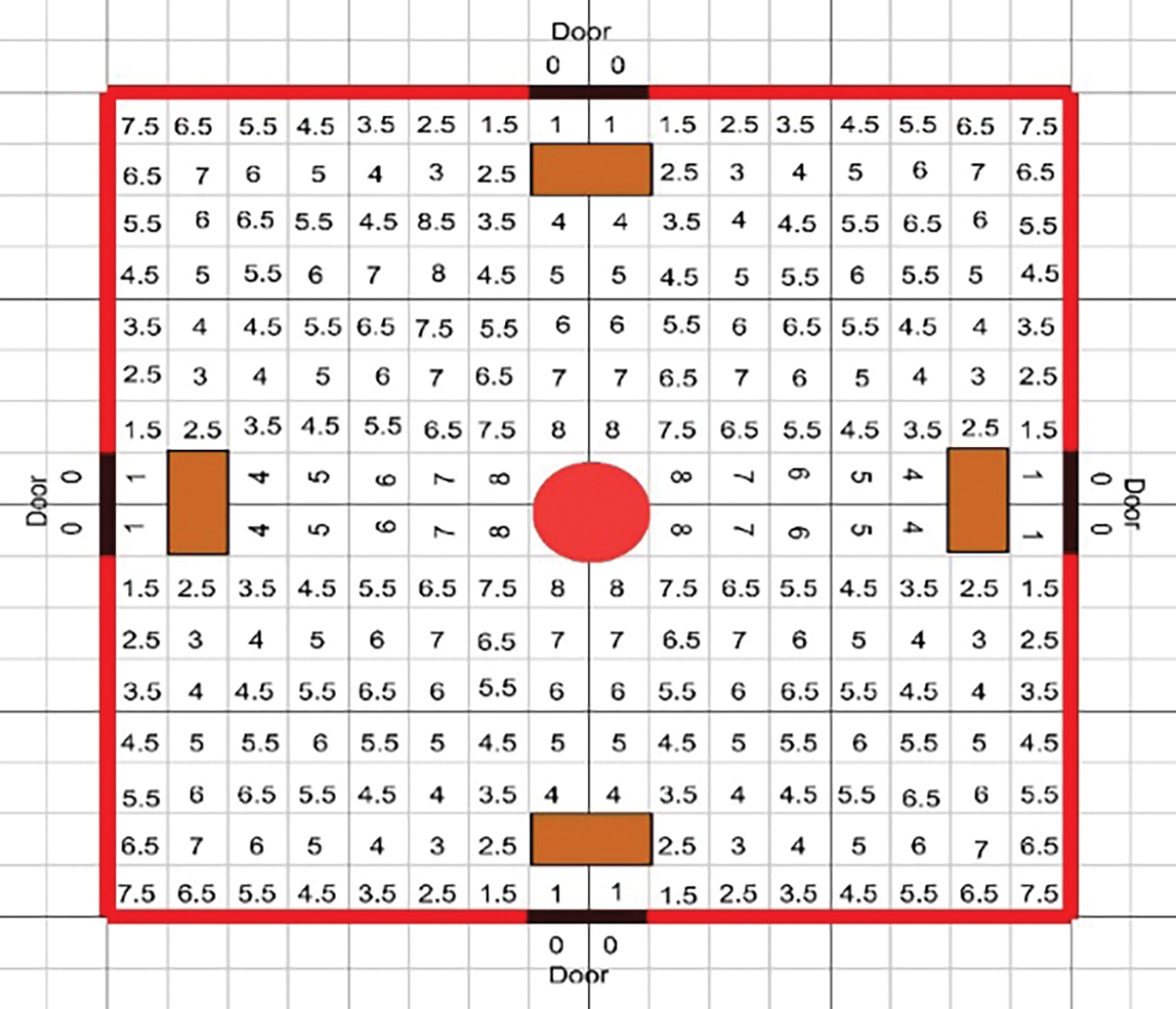
Figure 4: SFF distribution. Doors contain lowest value, “0”, and consist of two grid cells. The room’s walls contain the highest value, “100”, so no evacuee can surpass the walls

For the cells in the vertical and horizontal direction, the value is computed as follows:

a)   The total value of the previous cell +1, whereas the diagonal direction value is computed as the total value of the previous diagonal cell +1.5.

b)   Step a is represented until all cells are computed.

c)   Obstacles are given the highest value.

3.2.2 Dynamic Floor Field

DFF helps the pedestrians in movement, when DFF changes, as it depends on time, the number of pedestrians will also change, i.e., pedestrians shuffle inside the room with a new location and assign new floor fields value. DFF is used in evacuation processes because it helps in pedestrians’ motion as it is used to assign non-negative weight to each cell. Using DFF in evacuation models, pedestrians who move to their desired cells/exits leave a trace in the form of a boson behind called a virtual trace with its properties [51]. Two dynamics of DFF are diffusion and decay, to represent them, two procedures metrics are used, i.e., ∝∈[0,1]. So, the DFF process can be computed as:

Ddynamic(u_i,v_j)=Ddynamic(u_i,v_j)(T,α,δ)(3)

The process of diffusion is computed as follows:

Ddynamic(u_i,v_j)(T+1)=Ddynamic(u_i,v_j)(T+0.5)−αDdynamic(u_i,v_j)(T+0.5)+α8[Ddynamic(u_i−1,v_j+1)(T+0.5)+Ddynamic(u_i,v_j+1)(T+0.5)+Ddynamic(u_i+1,v_j+1)(T+0.5)+Ddynamic(u_i−1,v_j)(T+0.5)+Ddynamic(u_i+1,v_j)(T+0.5)+Ddynamic(u_i−1,v_j−1)(T+0.5)+Ddynamic(u_i,v_j−1)(T+0.5)+Ddynamic(u_i+1,v_j−1)(T+0.5)](4)

whereas in Eq. (4), Ddynamic(u_i,v_j) represents the DFF for grid cells (u_i,v_j), T represents time ticks and 0.5 represents half of the time. Here, (T+0.5) in Eq. (4) represents a half step in the diffusion process. It allows for accurate dynamics modelling because it considers the changes in the field that occur in full-time steps. The parameter ∝ represents the total rate of diffusion, and the value 1/8 is used for the weight to contribute from adjacent cells and helps calculate the updated field at a time (T+1). The process of decay is computed as follows:

Ddynamic(u_i,v_j)(T+0.5)=Ddynamic(u_i,v_j)(T)−δDdynamic(u_i,v_j)(T)(5)

In Eq. (5), Ddynamic(u_i,v_j)(T) represents the DFF at time T. δ represents the decay rate, and (T+1) represents the next time step in the model. Eq. (4) shows the reduction in evacuees’ density each time evacuees exit the room, modelled as a density φ of the current density. In some situations, pedestrians stuck in a jam can exchange their positions with neighbours, as shown in Fig. 3. This way, the equation for jam is as follows:

Ddynamic(u_i,v_j)(T+1)=Ddynamic(u_i,v_j)(T)+γ[Ddynamic(u_i−1,v_j)(T)+Ddynamic(u_i+1,v_j)(T)+Ddynamic(u_i,v_j−1)(T)+Ddynamic(u_i,v_j+1)(T)−4Ddynamic(u_i,v_j)(T)](6)

In Eq. (6), γ represents the jam rate. Eq. (6) shows the increase in crowd density at each time step as evacuees become stuck in a jam and cannot move. The cell exchange mechanism also allows the volunteers to advance toward the obstacles. Fig. 5 explains the next cell selection by exchanging the positions per their direction of movement refers to a method used in some crowd evacuation models where pedestrians select their next move based on the direction, they are currently moving in. Specifically, pedestrians swap their positions with each other in the cell they want to move to as shown in Figs. 5c and 5d if that pedestrian is moving in the same direction as they are.

Figure 5: Next cell selection by exchanging the positions per the direction of movement

This allows for smoother and more efficient movement in the crowd as pedestrians are less likely to collide or obstruct each other. The evacuees move toward the exits using FF mentioned in Section 3. The SFF is a constant value assigned to each grid cell based on its shortest distance from a specific emergency exit and room geometry. The DFF changes over time based on the environment of the other pedestrians. It captures the current situation and changes with time, such as the psychology/behavior based on the density of the pedestrians. The DFF has a decay rate and diffusion, updated at each time step. The diffusion does not change the grid cell value of the obstacles. The volunteers remove the obstacle due to this distinct role. Further, volunteers’ movements are not affected by the DFF. During the obstacle removal, the evacuee should create minimum hindrances for the volunteers, and the space near the obstacles should be clear, especially when there are large obstacles. To handle this issue, we employ RFF [52]. In [26], a floor field has been presented to remove small obstacles, and the evacuee predicts the movement of the volunteer. However, in our model, multiple agents collectively push a large obstacle to clear the path for evacuation. Moreover, if the sum of the forces applied by all the agents in a group is toward the destination which results in the obstacle will move towards the destination. The heading vector (H→) of the group is computed based on a sum of individual direction vectors of each volunteer in a group:

H→=Vcjejθi∥∑i∈Vcjejθi∥(7)

where j is the jth obstacle, Vcj denotes the volunteers trying to remove obstacle j, Vcj denotes the volunteers trying to remove obstacle j. θi is the heading of the ith volunteer in the group and e is direction of volunteers. RFF is updated based on the collective heading of the group. Eq. (7) presents the average direction of crowd evacuation, given a set of evacuees with velocity vectors Vcj and orientation angles θi. The denominator is the magnitude of the sum of all the velocity vectors in the crowd, and the numerator is the sum of all velocity vectors, each multiplied by their respective orientation angles. In the proposed model, Eq. (7) simulates the collective behavior of individuals as they move away from danger or obstacles. The presence of obstacles can alter the average direction of evacuation, and the removal of obstacles by volunteers can impact the overall evacuation process. The dynamics of the RFF are like the DFF; it has a decay rate and diffusion rate. The area in the cone of vision is called the region of interference (ROI) of the obstacle. The size of the ROI depends on the size of the obstacle. The purpose of RFF is to handle a situation where volunteers remove obstacles, and the pedestrians keep enough free space available to move the obstacles. This floor field is like the repulsive behavior in a swarm. Furthermore, RFF cannot be computed based on individual volunteers’ direction in the group. Hence, the sum of the directions of a group has been considered.

4  Game Theoretic Evacuation

The SFF, DFF, and RFF determine the movement of the normal pedestrian. However, once a pedestrian becomes a volunteer, the movement is computed based on the removed obstacles to new position. To simplify the proposed model, the destination of the obstacle is predefined, and the volunteer floor field (VFF) is computed to guide the volunteers to push the obstacle to that destination. It is further assumed that no two obstacle destinations cross each other. This floor field is computed using the shortest path between the obstacle and the destination. The shortest path is computed using the A* algorithm. Game theory can be applied to model the behaviors of agents in conflict-of-interest situations, i.e., cooperative, and non-cooperative. The agents, also called players, are required to predict/know the decisions of each other. Sometimes, there may be conflicts between two players because both have the same interest. We use the volunteer selection game, next-cell conflict game and task allocation game to remove the conflict between players.

4.1 Next-Cell Conflict Game

The evacuees update their movement simultaneously and compute their next cell using floor fields. However, conflict may arise because multiple evacuees may choose the same cell as their next destination. Only one evacuee is allowed to occupy an empty cell, and if multiple evacuees wish to move into the same cell, there should be a mechanism to regulate this movement. We have used the Chicken Game (CG) to resolve such conflicts. The pedestrian decides to cooperate (C) or defect (D). If one of the evacuees does not cooperate, he/she will be allowed to move with payoff (−c), whereas the cooperative evacuee will not move but get payoff (0). If both evacuees do not cooperate, both get a payoff (v − c) and are equally probable to be selected. The payoff to get into the desired cell is v, and the cost of defection is c. If both evacuees decide to cooperate (C), both will remain motionless and be awarded (0) payoff. The utility function is described in Eq. (8).

UF(u_i,v_j)={1/m;ifG(xj)=0[forallcooperative](−c).L(xj);ifG(xj)>1(1−c).L(xj);ifG(xj)=1(8)

where UF is a utility function of cells (u_i, v_j), 1/m is the payoff. If all evacuees in the game are cooperative, they will get their desired location. If anyone evacuee is willing to compete, they will get (1-c), and others will get 0. If at least two evacuees compete, they will get -c, and the other will get 0. L(xj) indicates the function, and when xj competes, the L(xj) = 1; otherwise, 0 and G(xj) represent the total number of competitive evacuees. The NCG payoff matrix is in Fig. 6.

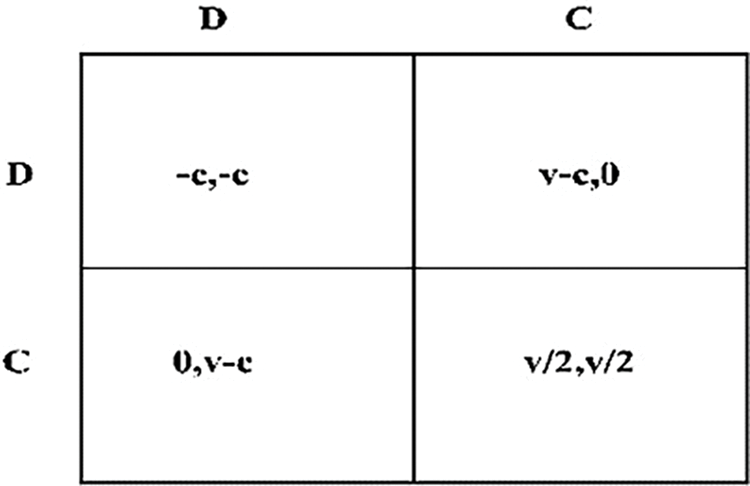
Figure 6: Payoff matrix for selection game

4.2 Volunteer Selection Game

We have used the volunteer dilemma game to analyze volunteer selection. The pedestrian in the ROI of the obstacle decides either to remove the obstacle or not. A pedestrian who decides to remove the obstacle becomes a volunteer. A volunteer dilemma is a social dilemma game in which a person in a group must choose either to make a costly contribution and deliver benefits to all other members of the group or avail themselves of a free ride on the contributions of others. A game in which only one person contributes to deliver benefits to all members of the group is called a volunteer game their [53]. The task of the volunteer is to remove the obstacles and guide the evacuees so that they can evacuate from the area safely. Dikemann first introduced the volunteer’s game in 1985 in social sciences. It is an N-person game in which public goods are produced if only if one player decides to pay the cost. The strategy depends on the willingness of evacuees to remove the obstacle from the exit. Each player in an ROI chooses either Volunteer/Aide (A) or Abstain (I). The benefit received by individuals for participating in volunteering efforts is presented in Eq. (9).

bI={b,ifK<q,0,ifK≥q,(9)

where bI is th benefit received by individual. K is the total number of volunteers in a collective manner. It is determined on comparison between the values of K and q. Where if K < q is true, then the number of volunteers required is then the threshold q, and then the individual receives a benefit of b. If K ≥ q means the number of volunteers required is equal to or greater than the threshold q, then the individual receives no benefit.

bA={b,ifK<q,0,ifK≥q,(10)

UI=∑i=1N⁡f(v−bI)(11)

UA=∑i=1N⁡f(v−bA)−p(12)

Eq. (11) is used in the context of the volunteer selection problem, where the main goal is to remove the obstacles near exits. In a crowd evacuation scenario where obstacles need to be removed, the volunteer’s dilemma game can be used to choose potential volunteers in the following manner:

1.    Evacuees decide whether to become a volunteer or not to remove the obstacles based on their self-interest and pay the cost (p) of volunteering.

2.    If the number of volunteers (Nv) is equal to or greater than a certain threshold (s), then public good (obstacle removal) is produced, each volunteer gets a maximum payoff v.

3.    If the number of volunteers is less than the threshold, then public good is not produced, and each evacuee incurs a cost (s > p) for the failure to remove the obstacles.

4.    The decision of each evacuee depends on their self-interest and the expected payoff from volunteering or not volunteering is represented in Eq. (13).

Ui=[Nv≥s]∗(v−p)+[Nv<s]∗(−s)(13)

In Eq. (13), Ui is evacuee ith payoff, Nv is the number of volunteers, s is the threshold for producing the public good, v is the maximum payoff for producing the public good, p is the cost for each evacuee to volunteer, and s > p is the cost for each evacuee if the public good is not produced. The value of K depends on the number of volunteers required to remove all obstacles near the exit. This is required to be computed in a decentralized fashion, which is possible using crowd wisdom. The problem associated with crowd wisdom to estimate the total number of volunteers required may be difficult.

4.3 Task Allocation Game

Once we have enough volunteers to remove obstacles, the next issue is to explain how the volunteers would remove large obstacles, specifically if there is more than one large obstacle. The volunteers must decide to remove one of the obstacles in a decentralized manner. We have employed the decentralized version of Minority Game (MG), in which players only decide based on their neighborhood. The players get local information and act regardless of the global situation. Each evacuee has a gene that defines the probability (p) of the player’s decision to choose an action that the strategy predicts. A player, who decides based on trends, has more chance to be in the minority. This divides the population of players into two groups. The number of volunteers required to remove the obstacles is a cutoff for the game. We use arbitrary cutoff (ϕ) instead of 50 % (N/2) in crude MG. It has been shown in [54] that even if the cutoff is very small (compared to N/2), it behaves similarly to MG.

5  Game Simulation

In this model, every pedestrian has its state. The state of the pedestrians is composed of factors including evacuee position (P), cell position (C), density (φ), heading direction (HD), and a set of strategies for games. The crowd evacuation process of the proposed model is shown in Fig. 7. It describes the phases of the simulation:

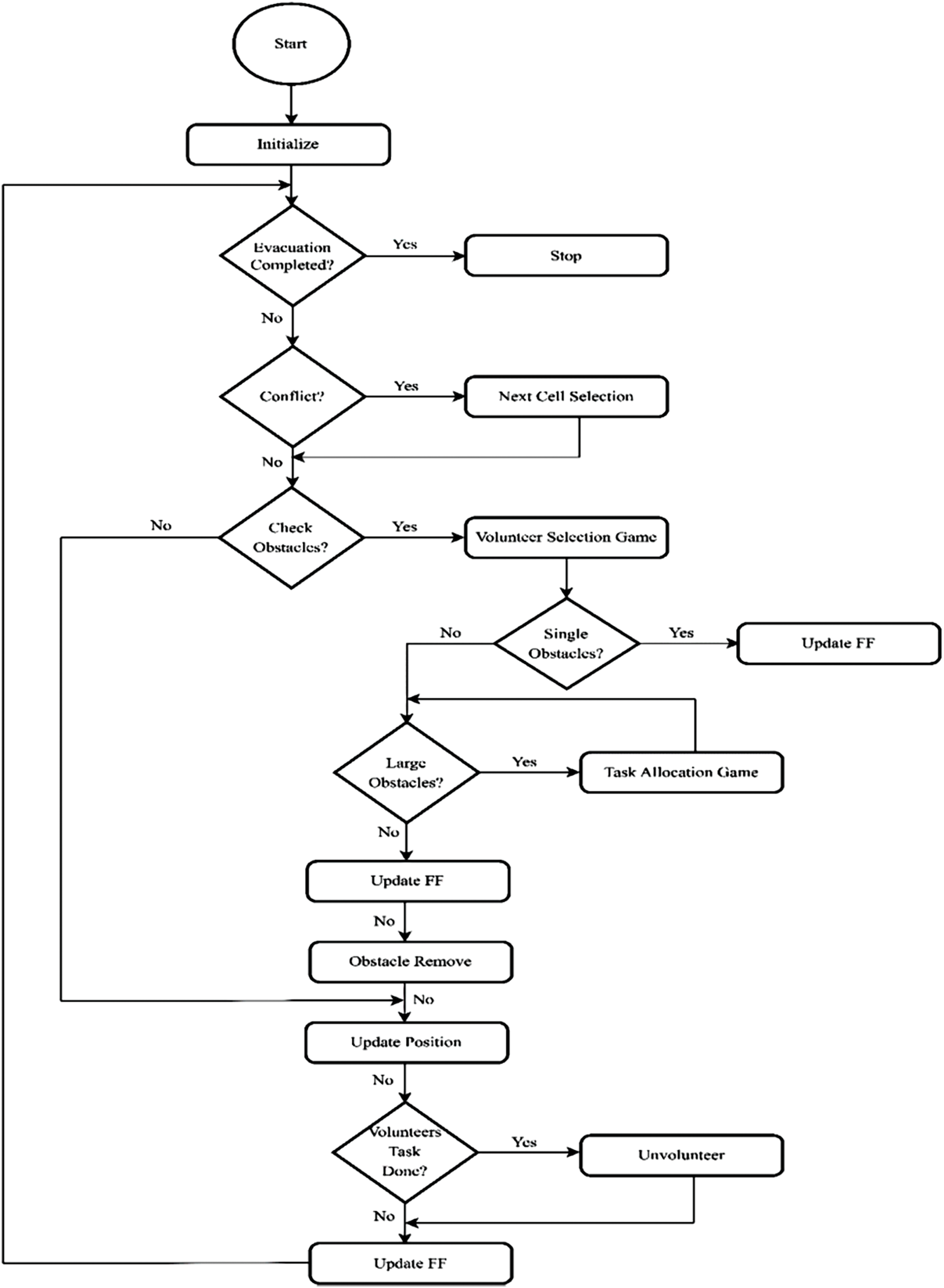
Figure 7: Flow chart of the proposed system

1.    The system is initialized; all evacuees are distributed randomly within a room. The simulation is stopped if the evacuation process is completed.

2.    If players sense the possible jam in their visibility range, they decide to wait until their frustration level is high enough to change their exit; secondly, it depends on the type of jam; if it is due to an obstacle, they may decide to be a volunteer.

3.    If players are in the ROI of obstacles, the pedestrian plays a volunteer selection game (public good game), a social dilemma game.

4.    If an obstacle is small (and it is in a single cell) and it is in the cone of the vision of the volunteer. The floor field between the object and the destination will be updated.

5.    If obstacle(s) is(are) large, then volunteers will play a task allocation game. Those in the minority will be part of a collective (group) to remove that large obstacle. The floor field for that object will be updated.

6.    All the evacuees, including volunteers/aide and other departers/evacuees, select one empty cell, which will be their desired cell, in which they are willing to move in. If one or more than one selects one desired cell, conflict will occur. Next Cell Selection game will be played to solve this conflict. This game will create a sequence of pedestrians who wish to go to the desired cell.

7.    SFF and DFF will be updated when volunteers remove obstacles.

8.    When the positions of evacuees, volunteers and obstacles have been updated, DFF will be updated again. In this phase, if the aide wants to unaided themselves, their positions will be updated, and they will become evacuees.

5.1 Simulation Environment

Netlogo is used to perform simulations of the proposed work. The pedestrians were uniformly distributed in the arena with density Pd; they could interact with each other in Moore’s neighborhood. The Evacuation time Et is the number of ticks (discrete simulation steps) required to evacuate all the pedestrians completely; moreover, AEt is the average evacuation time. Fig. 8a shows a room of size 80 × 80 with four exits of different sizes, Fig. 8b shows the initial population in that room, and Fig. 8c shows the evacuation process, where one of the exits E–I is blocked, jamming happens in front of it.

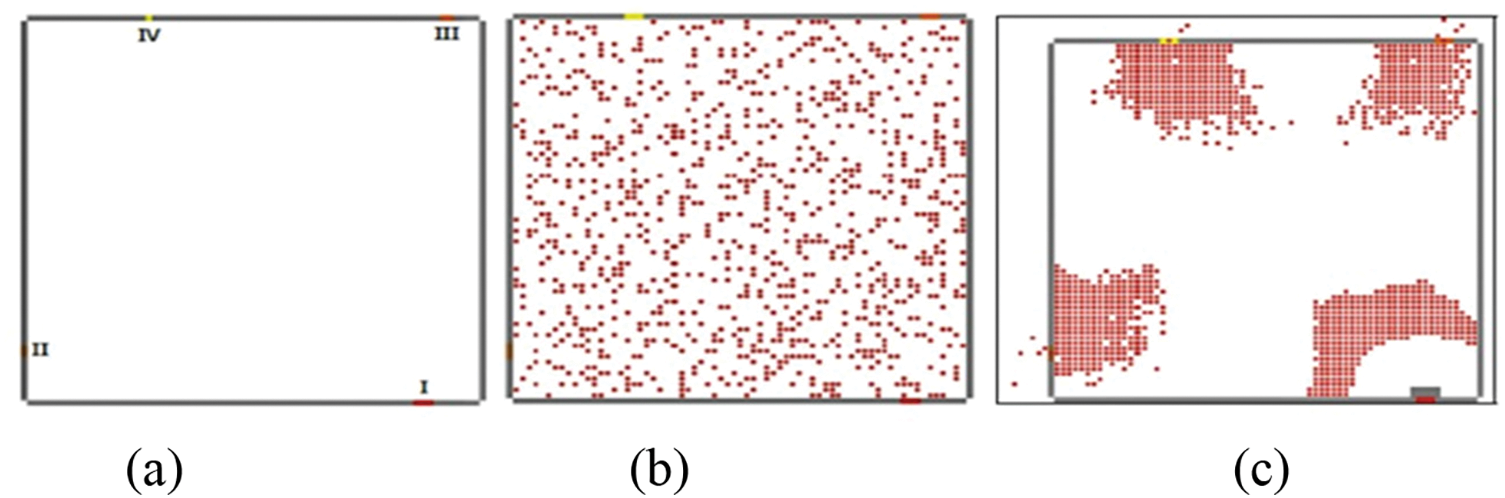
Figure 8: (a) The evacuation arena of size 80 × 80 with four exits of size E–I =3, E–II = 2, E–III = 2, E–IV = 1; (b) Initial population; (c) Exit E–I is blocked by a large obstacle and jamming in front of it, volunteers will collectively remove the obstacle

Fig. 9 shows two experiments for different numbers of exits. In Figs. 10a and 10b, if exit is blocked by an obstacle, there are two possibilities for evacuees to choose either nearest exit or go to random exit. In the case of nearest exit, there is a chance of jamming but when they choose other exits then they travel more. If the obstacle is placed at the front of the exit. Agent decides whether to remove the obstacle or go to other exits. Density of crowd and time of obstacle removal is changing with time. It is proven that re-moving obstacles is good. Parameters are: Time, density of crowd, how much time it will take to remove? And how much time it will take to move to another exit? In few times, nearest exit selection has more time because nearest exit is crowded. In random case, the population is not crowded on one exit. That is why random exit takes less time in obstacle removal as density of people increased. Similar situations observed in the studies [55,56].

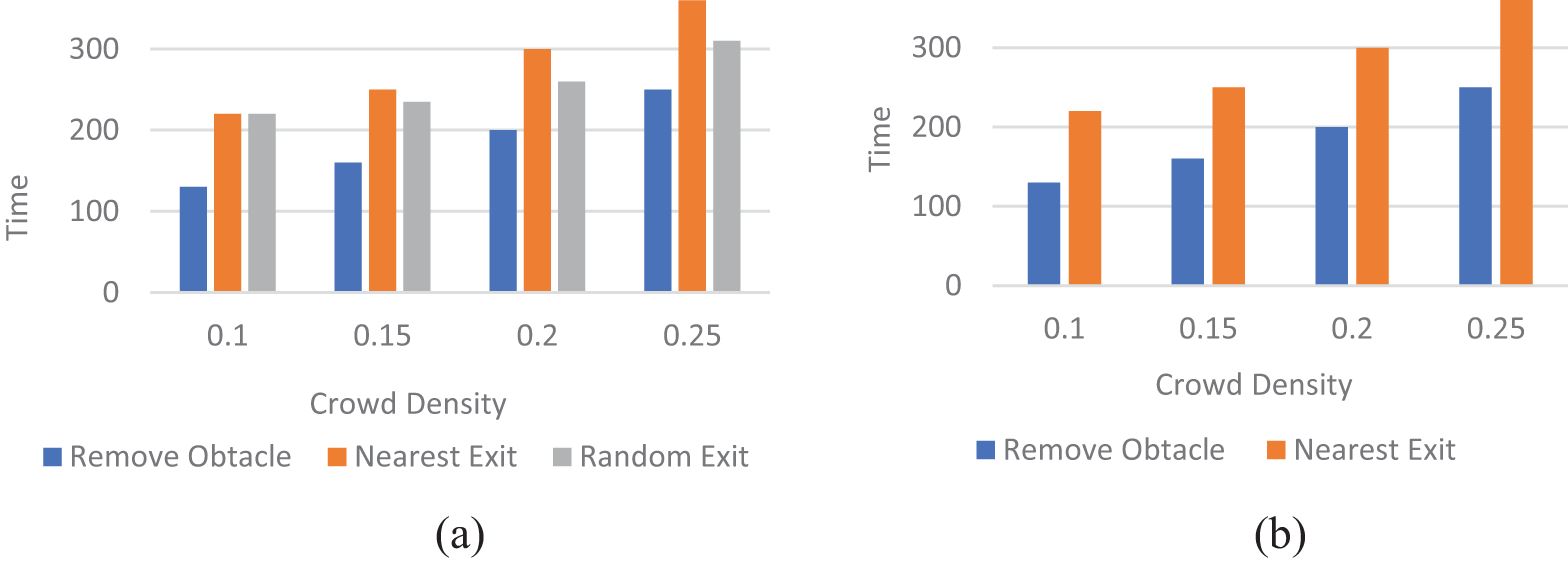
Figure 9: Evacuation time for obstacle removal or moving to another unblocked exit

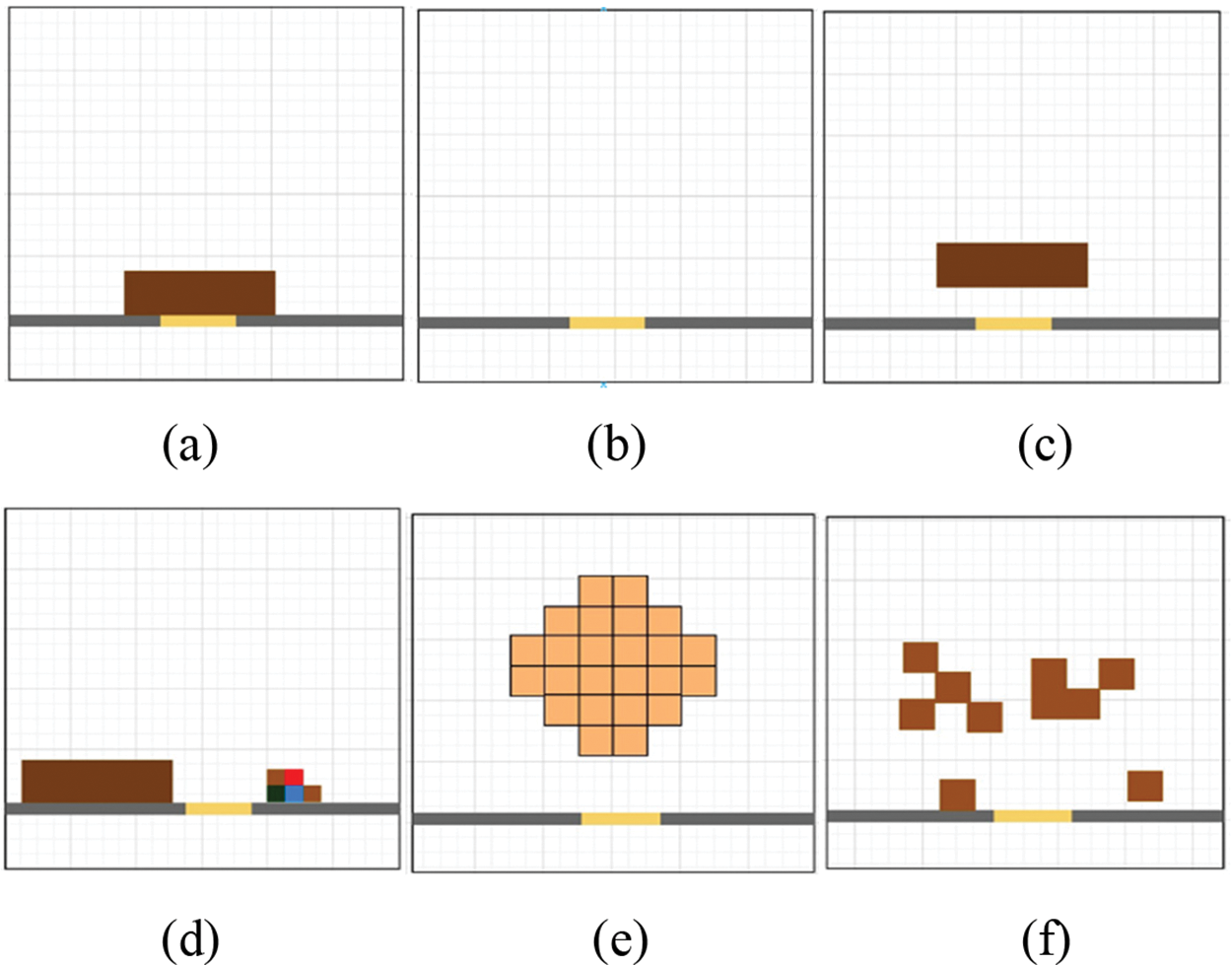
Figure 10: (a) Completely blocked as alpha = 0, if alpha < = 2, then evacuees cannot cross it, (b) obstacle completely removed, (c) move the obstacle to the center (d) obstacle on the sides of the exit (e) other shapes of the obstacles (f) small-size obstacles that the single volunteer can remove

6  Results and Discussion

6.1 Collective Obstacles Removal

Evacuees choose an appropriate exit and move towards that exit using floor fields. They do not know any blockage status of the exit until they come into the region of influence of the obstacles. They may move toward another supposedly unblocked exit if the exit is blocked. The more time they spend in a jam, their frustration level increases, which increases the probability of changing their mind and moving toward another exit. However, the movement of the pedestrians toward the new exit may create a jam/herding situation. There may be an additional risk of travelling toward the other exit, which may be blocked completely. Some evacuees may decide to remove the obstacles [26]. Fig. 10 depicts various types of obstacles and their possible positions.

Moreover, in most cases, the obstacles may be large and heavy, which is impossible for a single evacuee to remove. In this case, some of the evacuees (volunteers) must cooperate to remove those obstacles. Two aspects of cooperative obstacle removal have been analyzed. First, the volunteer dilemma is analyzed, where at least one agent should volunteer, which will benefit the whole population; however, for large obstacles removal, more than one evacuee must volunteer. Secondly, sufficient volunteers should cooperate to remove the large obstacles collectively. There is no leader in this situation and no communication or negotiation mechanism to recruit additional volunteers. The volunteers should cooperate in a decentralized way. If the obstacles were not removed due to volunteer rate or lack of cooperation for collective removal, it would increase the frustration level, and evacuees may move toward the other exits, and they may interfere with the evacuees moving toward this blocked exit, which may create jamming around the blocked exits.

It will also increase the number of evacuees at other exits as well. This jamming effect increases the evacuation time. Fig. 11 shows that the evacuation time increases for the lower densities, e.g., when the value of μ is less than 120 and 150, shown in Figs. 11a and 11b, respectively. The reason for this is the large number of agents near the blocked exit. However, for the higher densities, the evacuation time increases with an increase in μ. The jamming decreases gradually as pedestrians move towards the other exit and exits are opened by the volunteers. This shows that it is desirable to remove obstacles as early as possible; otherwise, after a certain time, obstacle removal will increase the efficiency of the evacuation process. Fig. 11c shows the number of agents at the exits on different values of the μ. It Illustrates that the jamming effect decreases over time; however, it in-creases the number of evacuees at unblocked exits, thus increasing the evacuation time.

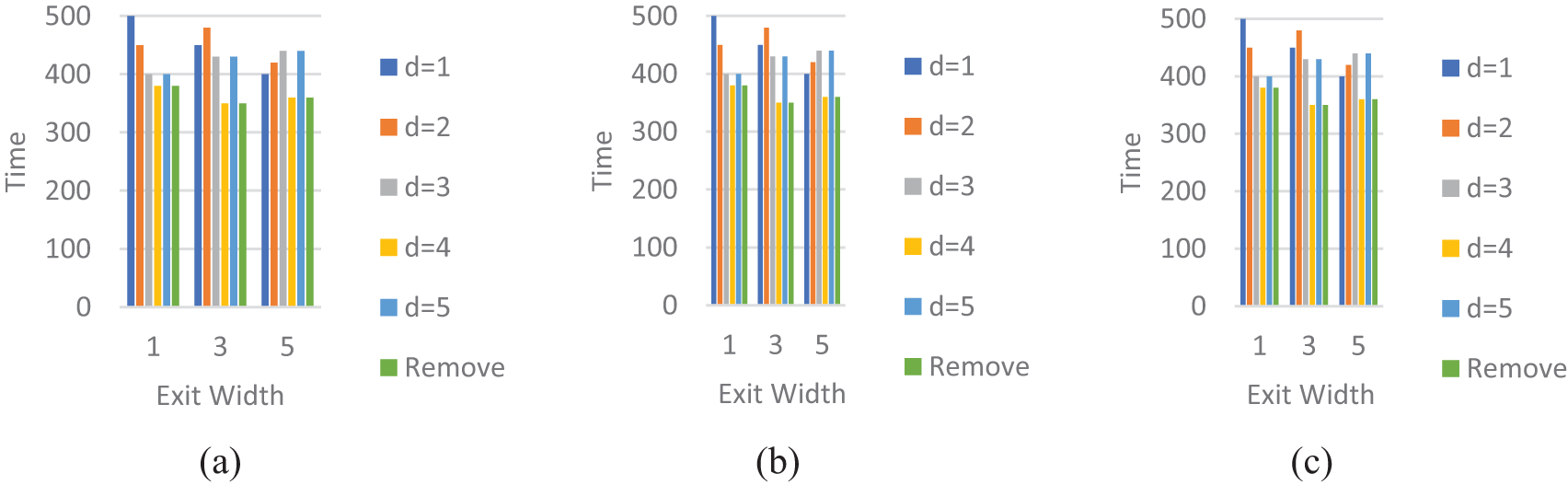
Figure 11: Moving obstacles to the center (case-II) for the population p = 0.2 (a) size of an obstacle is 5 (b) size of an obstacle is 9 (c) size of an obstacle is 13

The evacuation by the selected exit through diffusion is shown by color scheming (Fig. 12). The lighter color shows that these evacuees will evacuate first, and the dark color shows they are far from the exit.

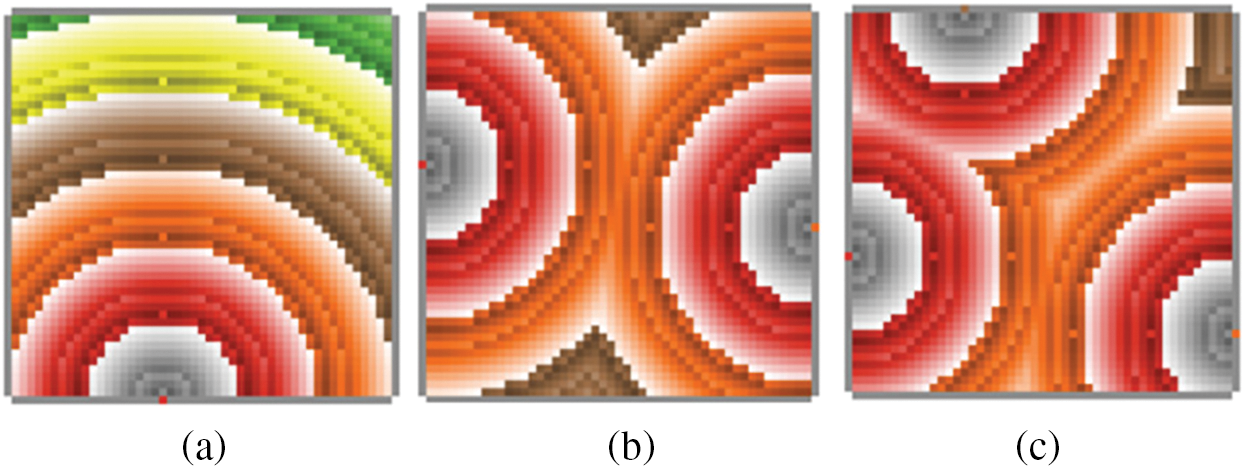
Figure 12: Distance to the exits

6.2 Type and Number of Obstacles Removed

We investigated the effect of several different obstacles on the evacuation process. The volunteers start to remove obstacles and cooperate to remove obstacles after μ timestamps. Removing the obstacle as soon as possible is desirable, as shown in Fig. 13. We have studied the impact of obstacle removal on evacuation concerning with the μ. If obstacles are partially removed, then it decreases the evacuation flow rate. Fig. 13a shows the effect of exit selection. In this experiment, there are multiple unblocked exits. If all the agents select the nearest exit, it has been noted that jamming occurs in that direction, and a huge flow toward that exit increases the evacuation time compared to random exit selection. In Fig. 13b, we have compared evacuation time for the cases of (i) removing obstacles by volunteers and (ii) evacuees moving to the other exit. The results show that it is better to remove the obstacle. It has been stated earlier that evacuation time in case (ii) increases due to jamming, extra distance travelled by the agents and the number of evacuees at remaining unblocked exits.

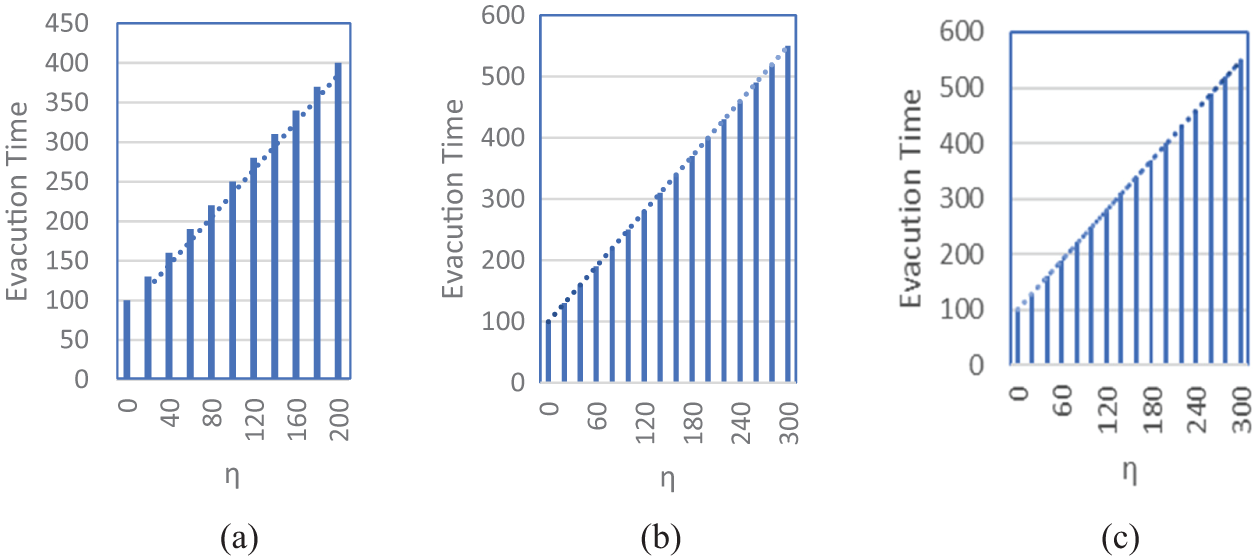
Figure 13: Mu-Value-III volunteer effect with exit size 3 (a) population size p = 0.1 (b) population size p = 0.2 (c) population size p = 0.3

There are three possible options to remove the large/small obstacles:

Case I – Remove Completely: In this case, it is considered that the combination of small and large obstacles has blocked the exit. The obstacle’s width is smaller than the exit, and the volunteer’s matters have taken those obstacles outside the arena or away from the exit (Dobs > 7). Fig. 14b shows that the obstacles have been removed completely.

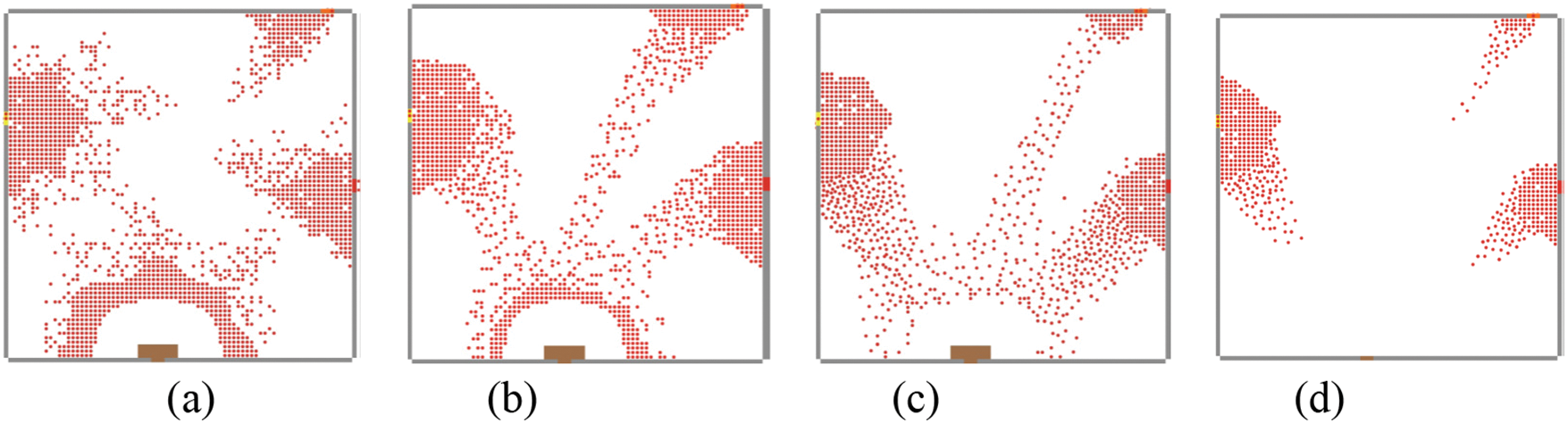
Figure 14: Evacuation process, (a) jamming occurs at exit-III (b) (c) the frustration level of evacuees increases over time, and some of the evacuees decide to change here exit, and (d) a large obstacle has been removed, but most of the evacuees have already changed

Case II – Center: It is extremely challenging to move very large obstacles to Dobs > 7 due to the large number of evacuees, the shape/weight/size of the obstacles, and consensus among the volunteers. In literature, it has been shown that obstacles in front of an exit at certain distances may improve evacuation/increase flow rate. We have investigated the effect of obstacles at different distances for the exit on evacuation efficiency. Fig. 14c shows the obstacle removed to the center in front of the exit.

Case III – Sides: One of the feasible options to remove obstacles is to place the obstacles on the sides of the exits. In this case, the exit can be opened parts as well. We have investigated the effect of the size and distance of obstacles from the exit. Fig. 14d shows the obstacles that have moved to the sides of the exit. This depicts the large obstacle at α = 1.

The results of experiments to move in front of the exit (Case-II) are shown in Fig. 11 for population Pd = 0.2. The experiments were conducted for three obstacle lengths {5, 9, 13}, Three widths of the exit {1, 3, 5} and five distances of obstacle from the exit {1, 2, 3, 4, 5}. The results have also been compared to completely removing the obstacle (Case-I). The results in Fig. 14 show that the obstacles have slightly improved evacuation time in front of the exit. We could not find a relationship between obstacles position and evacuation efficiency. It largely depends on the width of the exit, the size of the obstacles, the distance of the obstacle from the exit and the position of the exit. It is not easy to find an optimized combination of these parameters. Fig. 15 shows different types of obstacles and their possible positions in an arena. We have investigated the effect of different obstacles, their positions and the distance between the obstacle and the exit. The results for Case-III, in which the obstacles are moved to the sides of the exit, are shown in Fig. 15 for population density Pd = 0.2. The experiments were conducted for three obstacle lengths {5, 9, 13}, Three widths of the exit {1, 3, 5} and four distances of obstacle from the exit {partial, 0, 2, 4} were considered. The results show that distance of the obstacle is directly proportional to the evacuation time. If the distance is more than 7, then the obstacle does not affect the evacuation time. We have noticed that it is a reasonable choice to remove the obstacle to the sides; however, the distance should be at least more than 4.

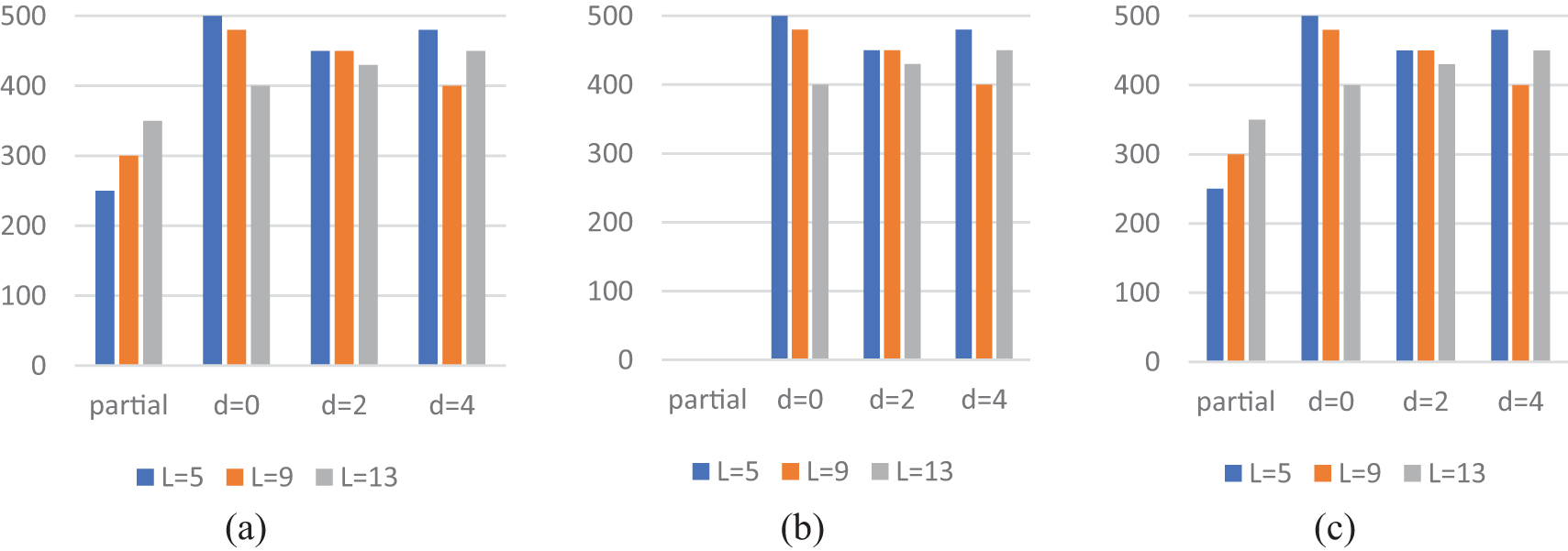
Figure 15: Population p = 0.2 (a) Obstacle size 5 (b) Obstacle size 9 (c) Obstacle size 13

7  Discussion, Limitations and Future Work

The experimental results show that cooperative obstacle removal is a complex task in emergencies due to its aspects in social interaction and social dilemmas, environmental and behavioral complexities [57]. The study presents a detailed analysis of cooperation and competition in emergencies. The proposed method attempts to understand cooperation in removing large obstacles in an emergency evacuation but has limitations. The consensus among the volunteers to move the obstacle towards a certain point is challenging. Besides consensus, the rotation and movement of a large obstacle are very difficult to simulate. The obstacles, especially large ones, may support debris; if volunteers attempt to remove them, it may cause further damage. In the proposed model, we have ignored this aspect. It is very difficult to analyze obstacles’ different shapes, orientation, and weight. Furthermore, this work can be improved in the following directions:

1.    A consensus must be developed to remove the obstacles in a suitable direction.

2.    Sometimes, agents move in a group of clusters (e.g., friends, families, pets, etc.), and such group dynamics are linked to the volunteering rate.

3.    It would be interesting to study further the effect of failure on the volunteering rate to produce enough volunteers to remove obstacles.

8  Conclusions

In this study, a crowd evacuation model integrated with game theory to investigate cooperation and competition for large obstacle removal has been presented. Minority and public-based games have been employed to describe volunteer behavior and their dynamics of choosing specific obstacles in a decentralized way. A good public game helps in selecting potential volunteers depending on their willingness, while the minority games help analyze how they reach collective solutions to remove the large obstacles. During the movement, conflict may arise because more than one agent may wish to move to the same cell; such conflict was handled using Chicken game. This game creates a sequence for that agent and allows it to occupy that cell. The assumed large obstacles vary in size and type, and block the exits, hence hindering the evacuation. In this regard, various case studies (scenarios) have been created to investigate large obstacle removal, such as the placement of obstacles in front of the exit (center), on the sides of the exits, removing obstacles completely, and so on. Removing obstacles to the center improves the evacuation time, depending on the parameters. It was observed that while removing obstacles aside, it is better to put them away from the exits. However, the volunteers pay higher costs. In most cases, evacuees would remove obstacles because it is better than moving toward another exit. Removing obstacles from exits increases the efficiency of the overall system. In the future, the model can be extended to investigate various combinations of games with dynamic payoffs while considering complex and constrained real-life scenarios.

Acknowledgement: The authors acknowledge the study to the collaborative teamwork.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Imran Khan and Jamaluddin Mir; Data curation, Maqsood Mahmud and Asiya Salam; Formal analysis, Jamaluddin Mir, Sardar Biabani, May Aldossary and Mustafa Youldash; Funding acquisition, Ashraf Saadeldeen and Dania AlKhulaifi; Investigation, Sardar Biabani and May Aldossary; Methodology, Maria Gul, Imran Khan and Gohar Zaman; Project administration, Atta Rahman; Resources, May Aldossary, Ashraf Saadeldeen, Maqsood Mahmud and Asiya Salam; Software, Maria Gul and Gohar Zaman; Supervision, Imran Khan; Validation, Atta Rahman, Jamaluddin Mir, Mustafa Youldash, Asiya Salam; Visualization, Sardar Biabani; Writing–original draft, Maria Gul and Gohar Zaman; Writing–review & editing, Atta Rahman, Dania AlKhulaifi, and Abdullah AlTurkey.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors have no conflicts of interest to report regarding the study.

References

1. C. Niu, W. Wang, H. Guo, and K. Li, “Emergency evacuation simulation study based on improved YOLOv5s and anylogic,” Appl. Sci., vol. 13, no. 1, pp. 5812, 2023. doi: 10.3390/app13095812. [Google Scholar] [CrossRef]

2. Y. Tong and N. W. F. Bode, “Simulation investigation on crowd evacuation strategies for helping vulnerable pedestrians at different stages of egress,” Int. J. Disast. Risk Re., vol. 84, no. 6803, pp. 103479, Jan. 2023. doi: 10.1016/j.ijdrr.2022.103479. [Google Scholar] [CrossRef]

3. R. Herzog, J. F. Pietschmann, and M. Winkler, “Optimal control of Hughes’ model for pedestrian flow via local attraction,” Appl. Math. Optim., vol. 88, no. 3, pp. 87, 2023. doi: 10.1007/s00245-023-10064-8. [Google Scholar] [CrossRef]

4. M. Haghani, “The knowledge domain of crowd dynamics: Anatomy of the field, pioneering studies, temporal trends, influential entities and outside-domain impact,” Phys Stat. Mech. Its Appl., vol. 580, no. 1, pp. 1–15, 2021. doi: 10.1016/j.physa.2021.126145. [Google Scholar] [CrossRef]

5. G. Bazior, D. Pałka, and J. Wąs, “Using cellular automata to model high density pedestrian dynamics,” Comput. Sci.–ICCS 2020, vol. 12137, pp. 486–498, May, 2020. doi: 10.1007/978-3-030-50371-0_36. [Google Scholar] [CrossRef]

6. X. Han et al., “The effect of moving obstacle on regulation of pedestrian flow in a single exit room,” J. Stat. Mech., vol. 2022, no. 1, pp. 023407, Feb. 2022. doi: 10.1088/1742-5468/ac4c3f. [Google Scholar] [CrossRef]

7. J. Y. Huang et al., “An overview of agent-based models for transport simulation and analysis,” J. Adv Transport., vol. 2022, no. 1, pp. 17, 2022. doi: 10.1155/2022/1252534. [Google Scholar] [CrossRef]

8. X. Cui, J. Ji, and X. Bai, “Algorithm and examples of an agent-based evacuation model,” Fire, vol. 6, no. 1, pp. 11, 2023. doi: 10.3390/fire6010011. [Google Scholar] [CrossRef]

9. R. Liu, D. Jiang, and L. Shi, “Agent-based simulation of alternative classroom evacuation scenarios,” Front Archit. Res., vol. 5, no. 1, pp. 111–125, Mar. 2016. doi: 10.1016/j.foar.2015.12.002. [Google Scholar] [CrossRef]

10. X. Zheng, T. Zhong, and M. Liu, “Modeling crowd evacuation of a building based on seven methodological approaches,” Build. Environ., vol. 44, no. 3, pp. 437–445, Mar. 2009. doi: 10.1016/j.buildenv.2008.04.002. [Google Scholar] [CrossRef]

11. F. Qiu and X. Hu, “Modeling group structures in pedestrian crowd simulation,” Simul. Model. Pract. Theory., vol. 18, no. 2, pp. 190–205, Feb. 2010. doi: 10.1016/j.simpat.2009.10.005. [Google Scholar] [CrossRef]

12. C. Şahin, J. Rokne, and R. Alhajj, “Human behavior modeling for simulating evacuation of buildings during emergencies,” Phys Stat. Mech. Its Appl., vol. 528, no. 15, pp. 121432, Aug. 2019. doi: 10.1016/j.physa.2019.121432. [Google Scholar] [CrossRef]

13. L. Hou, J. G. Liu, X. Pan, and B. H. Wang, “A social force evacuation model with the leadership effect,” Phys Stat. Mech. Its Appl., vol. 400, pp. 93–99, Apr. 2014. doi: 10.1016/j.physa.2013.12.049. [Google Scholar] [CrossRef]

14. Y. Papelis, R. Kady, L. Bair, and E. Weisel, “Modeling of human behavior in crowds using a cognitive feedback approach,” Simulation, vol. 93, no. 7, pp. 567–578, 2017. doi: 10.1177/0037549716673153. [Google Scholar] [CrossRef]

15. S. Kim, S. J. Guy, D. Manocha, and M. C. Lin, “Interactive simulation of dynamic crowd behaviors using general adaptation syndrome theory,” in Proc. ACM SIGGRAPH Symp. Interact. 3D Graph. Games, Costa Mesa California, ACM, Mar. 2012, pp. 55–62. doi: 10.1145/2159616.2159626. [Google Scholar] [CrossRef]

16. S. M. Lo, H. C. Huang, P. Wang, and K. K. Yuen, “A game theory-based exit selection model for evacuation, Fire Saf,” Fire Saf. J., vol. 41, no. 5, pp. 364–369, Jul. 2006. doi: 10.1016/j.firesaf.2006.02.003. [Google Scholar] [CrossRef]

17. K. Zia, A. Ferscha, A. Din, and U. Farooq, “Quantifying the interplay of emotions and rationality in herding: A game-theoretic simulation study,” Adapt. Behav., vol. 24, no. 2, pp. 119–129, Apr. 2016. doi: 10.1177/1059712316635719. [Google Scholar] [CrossRef]

18. S. K. Wong, Y. S. Wang, P. K. Tang, and T. Y. Tsai, “Optimized evacuation route based on crowd simulation,” Comput. Vis. Media., vol. 3, no. 3, pp. 243–261, Sep. 2017. doi: 10.1007/s41095-017-0081-9. [Google Scholar] [CrossRef]

19. A. E. Ünal, C. Gezer, B. K. Pak, and V. C. Güngör, “Generating emergency evacuation route directions based on crowd simulations with reinforcement learning,” in Proc. ASYU’22, Antalya, Turkey, 2022, pp. 1–6. doi: 10.1109/ASYU56188.2022.9925560. [Google Scholar] [CrossRef]

20. Y. Zhao et al., “Optimal layout design of obstacles for panic evacuation using differential evolution,” Phys Stat. Mech. Its Appl., vol. 465, pp. 175–194, Jan. 2017. doi: 10.1016/j.physa.2016.08.021. [Google Scholar] [CrossRef]

21. L. Jiang, J. Li, C. Shen, S. Yang, Z. Han and Z. K. Gao, “Obstacle optimization for panic flow-reducing the tangential momentum increases the escape speed,” PLoS One, vol. 9, no. 12, pp. e115463, 2014. doi: 10.1371/journal.pone.0115463 [Google Scholar] [PubMed] [CrossRef]

22. W. L. Wang, F. F. Wan, and S. M. Lo, “Game theory model of exit selection in pedestrian evacuation considering visual range and choice firmness,” Chin Phys. B, vol. 29, no. 8, pp. 084502, Jul. 2020. doi: 10.1088/1674-1056/ab973a. [Google Scholar] [CrossRef]

23. N. Bellomo, B. Piccoli, and A. Tosin, “Modeling crowd dynamics from a complex system viewpoint,” Math. Models Methods Appl. Sci., vol. 22, no. supp02, pp. 1230004, 2012. doi: 10.1142/S0218202512300049. [Google Scholar] [CrossRef]

24. A. Corbetta and F. Toschi1, “Physics of human crowds,” Annu. Rev. Condens. Matter Phys., vol. 14, no. 1, pp. 311–333, Mar. 2023. doi: 10.1146/annurev-conmatphys-031620-100450. [Google Scholar] [CrossRef]

25. J. Tanimoto, A. Hagishima, and Y. Tanaka, “Study of bottleneck effect at an emergency evacuation exit using cellular automata model, mean field approximation analysis, and game theory,” Phys Stat. Mech. Its Appl., vol. 389, no. 24, pp. 5611–5618, Dec. 2010. doi: 10.1016/j.physa.2010.08.032. [Google Scholar] [CrossRef]

26. G. W. Lin and S. K. Wong, “Evacuation simulation with consideration of obstacle removal and using game theory,” Phys. Rev. E, vol. 97, no. 6, pp. 062303, 2018. doi: 10.1103/PhysRevE.97.062303 [Google Scholar] [PubMed] [CrossRef]

27. K. Wang, Y. Li, and S. Qian, “Analysis of indoor guided pedestrian evacuation dynamics in single and multiple exit scenarios: Toward a unified scheme for guide assignment,” Transp Res. Rec., vol. 2676, no. 11, pp. 632–647, 2022. doi: 10.1177/03611981221094580. [Google Scholar] [CrossRef]

28. U. Gupta and N. Ranganathan, “Multievent crisis management using noncooperative multistep games,” IEEE Trans. Comput., vol. 56, no. 5, pp. 577–589, May 2007. doi: 10.1109/TC.2007.1023. [Google Scholar] [CrossRef]

29. A. Varas et al., “Cellular automaton model for evacuation process with obstacles,” Phys Stat. Mech. Its Appl., vol. 382, no. 2, pp. 631–642, Aug. 2007. doi: 10.1016/j.physa.2007.04.006. [Google Scholar] [CrossRef]

30. M. Mitsopoulou, N. I. Dourvas, G. C Sirakoulis, and K. Nishinari, “Spatial games and memory effects on crowd evacuation behavior with cellular automata,” J. Comput. Sci., vol. 32, no. 1, pp. 87–98, Mar. 2019. doi: 10.1016/j.jocs.2018.09.003. [Google Scholar] [CrossRef]

31. B. L. Mesmer and C. L. Bloebaum, “Incorporation of decision, game, and Bayesian game theory in an emergency evacuation exit decision model,” Fire Saf. J., vol. 67, no. 1, pp. 121–134, Jul. 2014. [Google Scholar]

32. A. Rigos, E. Mohlin, and E. Ronchi, “The cry wolf effect in evacuation: A game-theoretic approach,” Phys. Stat. Mech. Its Appl., vol. 526, no. 1, pp. 120890, Jul. 2019. doi: 10.1016/j.physa.2019.04.126. [Google Scholar] [CrossRef]

33. A. M. Ibrahim, I. Venkat, and P. de Wilde, “The impact of potential crowd behaviours on emergency evacuation: An evolutionary game theoretic approach,” J. Artif. Soc. Soc. Simul., vol. 22, no. 1, pp. 1–15, 2019. doi: 10.18564/jasss.3837. [Google Scholar] [CrossRef]

34. H. Tian, Y. Wei, L. Dong, Y. Xue, and R. Zheng, “Resolution of conflicts in cellular automaton evacuation model with the game-theory,” Phys Stat. Mech. Its Appl., vol. 503, no. 1, pp. 991–1006, Aug. 2018. doi: 10.1016/j.physa.2018.08.140. [Google Scholar] [CrossRef]

35. H. N. Wang, D. Chen, W. Pan, Y. Xue, and H. D. He, “Evacuation of pedestrians from a hall by game strategy update,” Chin Phys. B, vol. 23, no. 8, pp. 080505, Jun. 2014. doi: 10.1088/1674-1056/23/8/080505. [Google Scholar] [CrossRef]

36. Q. Y. Hao, R. Jiang, M. B. Hu, B. Jia, and Q. S. Wu, “Pedestrian flow dynamics in a lattice gas model coupled with an evolutionary game,” Phys. Rev. E, vol. 84, no. 3, pp. 036107, Sep. 2011. doi: 10.1103/PhysRevE.84.036107 [Google Scholar] [PubMed] [CrossRef]

37. T. Bjørnskau, “The Zebra Crossing Game–using game theory to explain a discrepancy between road user behaviour and traffic rules,” Saf. Sci., vol. 92, no. 1, pp. 298–301, Feb. 2017. doi: 10.1016/j.ssci.2015.10.007. [Google Scholar] [CrossRef]

38. S. Bouzat and M. N. Kuperman, “Game theory in models of pedestrian room evacuation,” Phys. Rev. E, vol. 89, no. 3, pp. 032806, Mar. 2014. doi: 10.1103/PhysRevE.89.032806 [Google Scholar] [PubMed] [CrossRef]

39. M. Braglia, D. Castellano, and R. Gabbrielli, “A novel game theory-based exit selection model in emergency conditions,” Adv. Complex Syst., vol. 16, no. 7, pp. 1350018, Oct. 2013. doi: 10.1142/S0219525913500185. [Google Scholar] [CrossRef]

40. H. Chizari et al., “Agent-based approach for modeling evacuee uncertainty behavior using game theory model,” Life Sci. J., vol. 10, no. 3, pp. 1350–1355, 2013. [Google Scholar]

41. H. Ehtamo, S. Heliövaara, T. Korhonen, and S. Hostikka, “Game theoretic best-response dynamics for evacuees’ exit selection,” Adv. Complex Syst., vol. 13, no. 1, pp. 113–134, Feb. 2010. doi: 10.1142/S021952591000244X. [Google Scholar] [CrossRef]

42. J. Gou, X. Cai, and S. Dou, “Behavior simulation of ‘Chinese style road crossing’ based on evolutionary game theory,” in Proc. LISS, Sydney, NSW, Australia, 2016, pp. 1–6. doi: 10.1109/LISS.2016.7854554. [Google Scholar] [CrossRef]

43. J. Guan, K. Wang, and F. Chen, “A cellular automaton model for evacuation flow using game theory,” Phys Stat. Mech. Its Appl., vol. 461, no. 1, pp. 655–661, Nov. 2016. doi: 10.1016/j.physa.2016.05.062. [Google Scholar] [CrossRef]

44. W. Li, J. Zhu, H. Li, Q. Wu, and L. Zhang, “A game theory based on monte carlo analysis for optimizing evacuation routing in complex scenes,” Math. Probl. Eng., vol. 2015, no. 1, pp. e292093, 2015. doi: 10.1155/2015/292093. [Google Scholar] [CrossRef]

45. M. Chen and C. H. Zhu, “Research on passengers’ evacuation model in ships based on agent theory,” in Proc. ICMA, Tianjin, China, Aug., 2014, pp. 441–446. doi: 10.1109/ICMA.2014.6885738. [Google Scholar] [CrossRef]

46. M. Nakata, A. Yamauchi, J. Tanimoto, and A. Hagishima, “Dilemma game structure hidden in traffic flow at a bottleneck due to a 2 into 1 lane junction,” Phys. Stat. Mech. Its Appl., vol. 389, no. 23, pp. 5353–5361, Dec. 2010. doi: 10.1016/j.physa.2010.08.005. [Google Scholar] [CrossRef]

47. D. Shi, W. Zhang, and B. Wang, “Modeling pedestrian evacuation by means of game theory,” J. Stat. Mech. Theory Exp., vol. 2017, no. 4, pp. 043407, Apr. 2017. doi: 10.1088/1742-5468/aa68b3. [Google Scholar] [CrossRef]

48. A. Talebpour, H. S. Mahmassani, and S. H. Hamdar, “Modeling lane-changing behavior in a connected environment: A game theory approach,” Transp Res. Procedia., vol. 7, no. 1, pp. 420–440, Jan. 2015. doi: 10.1016/j.trpro.2015.06.022. [Google Scholar] [CrossRef]

49. X. Zheng and Y. Cheng, “Modeling cooperative and competitive behaviors in emergency evacuation: A game-theoretical approach,” Comput. Math. Appl., vol. 62, no. 12, pp. 4627–4634, Dec. 2011. doi: 10.1016/j.camwa.2011.10.048. [Google Scholar] [CrossRef]

50. C. Wang and J. Wang, “A modified floor field model combined with risk field for pedestrian simulation,” Math. Probl. Eng., vol. 2016, no. 1, pp. e9653860, Feb. 2016. doi: 10.1155/2016/9653860. [Google Scholar] [CrossRef]

51. X. Yang, B. Wang, and Z. Qin, “Floor field model based on cellular automata for simulating indoor pedestrian evacuation,” Math. Probl. Eng., vol. 2015, no. 1, pp. 820306, 2015. doi: 10.1155/2015/820306. [Google Scholar] [CrossRef]

52. D. Alejo, J. A. Cobano, G. Heredia, and A. Ollero, “A reactive method for collision avoidance in industrial environments,” J. Intell. Robot. Syst., vol. 84, no. 1–4, pp. 745–758, Dec. 2016. doi: 10.1007/s10846-016-0359-7. [Google Scholar] [CrossRef]

53. J. K. Goeree, C. A. Holt, and A. M. Smith, “An experimental examination of the volunteer’s dilemma,” Games Econ. Behav., vol. 102, no. 1, pp. 303–315, Mar. 2017. doi: 10.1016/j.geb.2017.01.002. [Google Scholar] [CrossRef]

54. Y. Wang, G. Yu, and R. Yin, “A distributed user association method for LTE-U by enabling Q-Learning in Minority Game,” in Proc. ICCC, Changchun, China, 2019, pp. 455–460. doi: 10.1109/ICCChina.2019.8855939. [Google Scholar] [CrossRef]

55. S. K. Sood and K. S. Rawat, “A fog assisted intelligent framework based on cyber physical system for safe evacuation in panic situations,” Comput. Commun., vol. 178, no. 1, pp. 297–306, 2021. doi: 10.1016/j.comcom.2021.08.022 [Google Scholar] [PubMed] [CrossRef]

56. S. K. Sood and K. S. Rawat, “Fog-assisted virtual reality-based learning framework to control panic,” Expert. Syst., vol. 2022, no. 39, pp. e12700, 2022. doi: 10.1111/exsy.12700. [Google Scholar] [CrossRef]

57. A. Rahman, S. Dash, A. K. Luhach, N. Chilamkurti, S. Baek and Y. Nam, “A neuro-fuzzy approach for user behaviour classification and prediction,” J. Cloud Comput., vol. 8, no. 17, pp. 1–15, 2019. doi: 10.1186/s13677-019-0144-9. [Google Scholar] [CrossRef]