A Dual Discriminator Method for Generalized Zero-Shot Learning

1  Introduction

Traditional image classification methods need to collect a large number of images with annotations for model training, but for some new things that cannot massively collect training images, traditional image classification methods can not directly classify the new things. The emergence of zero-shot learning can solve this problem. Zero-shot learning learns from existing samples and then infers the categories of new things. Zero-shot learning recognizes new things using linguistic descriptions of the new things, and we refer to the linguistic descriptions as semantic features in this paper.

Two types of features are needed in zero-shot learning: Sample features (visual features) and the semantic features mentioned above. These two types of features belong to different feature spaces, and aligning these two types of features is very important. Aligning semantic and visual features is usually done by mapping them to the same feature space [1–5]. We refer to these methods as embedding methods [6,7]. However, these methods sometimes only consider information from the seen classes, which can cause a decrease in the accuracy when classifying the unseen class samples.

Addressing the problem of misclassification results for unseen classes, some researchers add information about unseen classes to their models, methods commonly used nowadays are generative models [8–11]. Although the generative models can get good classification results, these methods need to train the generative model first and then use the generative model to obtain pseudo-samples about unseen classes. Then, a classifier is trained using pseudo-samples. The generative model methods make the process more complicated than other methods. Incorporating unseen class semantic features into the loss function [12] or adding a calibration term to the classification [13,14] is another technique to increase the classification accuracy of unseen class samples. In addition, some literature has also noted that the similarity between features also leads to a decrease in the zero-shot classification accuracy. Zhang et al. [15] proposed imposing orthogonality constraints between semantic features to differentiate between semantic features of different classes. This approach increased the differences between different categories and alleviated domain shift problems.

We have similarly employed adding information about unseen classes to the model. Unlike the methods mentioned above, a new feature alignment method is proposed in our model. In this paper, except the traditional mapping approach, we further use a dual discriminator approach to align the semantic and visual features. Instead of increasing the distance between different categories’ visual and semantic features, we increased the consistency between the hidden space visual features with all class semantic features. This approach not only aligns features but also provides information about unseen classes. A new feature fusion approach is also used for classifier training to alleviate the bias problem. Our contributions are as follows:

(1)   We propose a new model structure for solving the alignment problem of different modal features and the domain shift problem.

(2)   To make a better alignment of semantic and visual features, this paper proposes a dual discriminator module and this dual discriminator method can provide information about the unseen classes.

(3)   We propose a new feature fusion method by which the seen class features are perturbed to reduce the degree to which the classification results in the model are biased toward the seen classes and provide information on the unseen classes.

(4)   Our method was validated on four different datasets. The experimental results demonstrate that the proposed model obtains promising results, especially in aPY dataset (5.1%).

2  Related Works

2.1 Zero-Shot Learning

Semantic features and visual features belong to different feature spaces with different dimensions, respectively. Usually, it is a choice to map these two features to the same feature space. Figs. 1a and 1b show the two mapping methods: From semantic space to visual space and from visual space to semantic space. Liu et al. [6] proposed a Low-Rank Semantic Autoencoder (LSA) to enhance the zero-shot learning capability. Before classification, they used a mapping matrix to map semantic features to visual space. Tang et al. [4] mapped visual features to the semantic space and realized feature alignment and classification by calculating the mutual information between semantic features and visual features. In addition to the two mapping methods in Figs. 1a and 1b, common feature space can be used in some literature. Hyperbolic spaces can maintain a hierarchy of features. Liu et al. [16] proposed to map the visual features and the semantic features into hyperbolic space. Li et al. [17] used direct sum decomposition for semantic features; the semantic features were decomposed into subspaces. The method in the literature [17] embedded semantic features and visual features into the common space. In addition, another method that maps semantic features to the visual space while projecting visual features to the semantic space. This method reduces the domain shift problem and allows better alignment of both features [5,18,19]. These methods mentioned above only consider the information of the seen class when training the models but ignore the information provided by the unseen class semantic features. The compression of the unseen class information leads to the misclassification of the samples of the unseen class. Especially for generalized zero-shot, neglecting the unseen class information can cause most samples to be biased towards the seen classes.

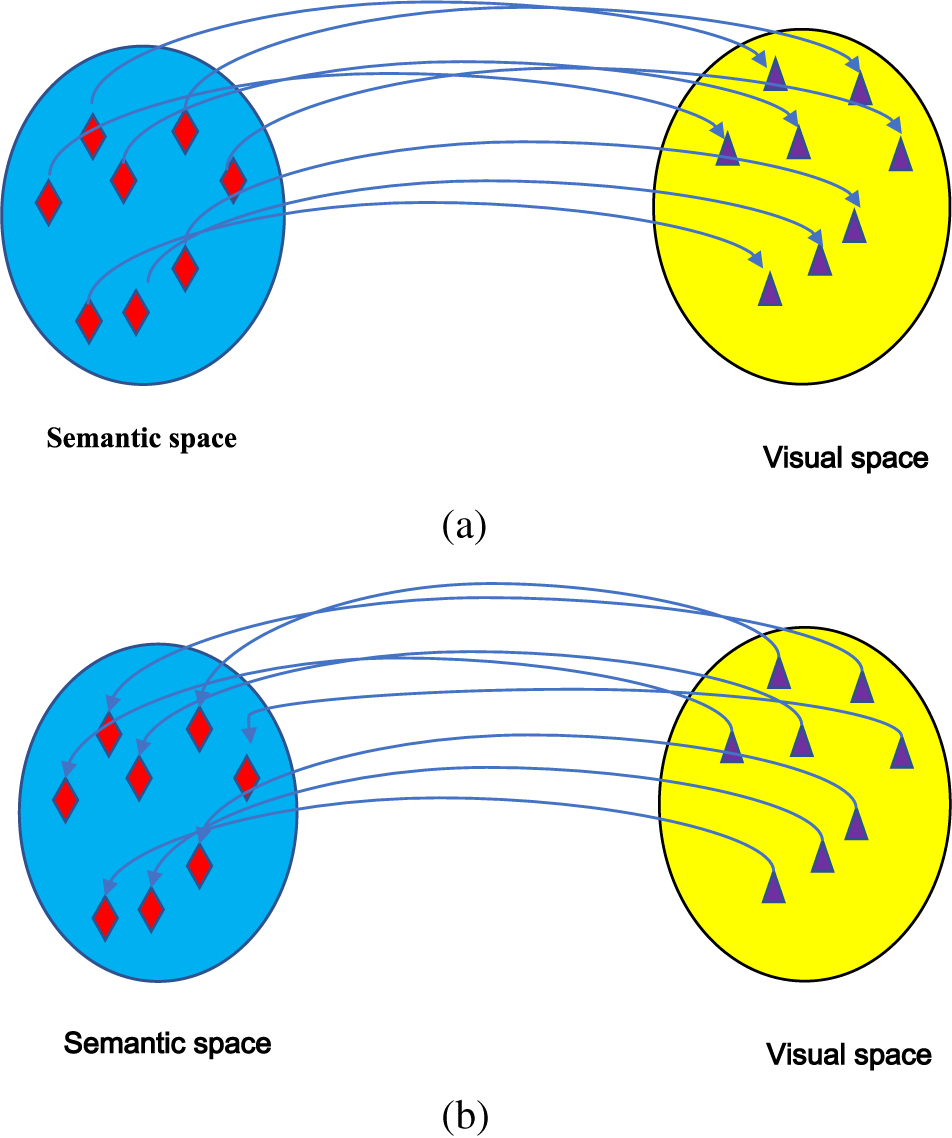
Figure 1: Embedding methods

2.2 Domain Shift Problem

Since the unseen class samples only appear in the test set and the distribution is not the same between the seen class samples and the unseen class samples, this leads to a bias in the model when classifying the unseen class samples, and this phenomenon is domain shift problem. Especially for test sets containing the seen class categories, the unseen class samples are more likely to be misclassified as one of the seen class categories. Adding information about unseen classes to the model is proposed to address the problem mentioned above. Some researchers proposed generative models to generate unseen class samples [8–10,20]. These methods use pseudo-samples instead of real samples for training the classifier. Huynh et al. [12] proposed another method. They proposed to add a term about the unseen class information in the loss function so that the information about the unseen class will not be too compressed. In addition to these two methods mentioned above, Jiang et al. [21] used class similarity as the coefficients in the loss function to improve the classification accuracy. In order to make semantic features more distinguishable, some researchers have imposed constraints on the semantic features of all classes, and such restrictions can distinguish the semantic features of different classes. In this way, all the features can be better categorized when mapped to the same feature space and alleviate the domain shift problem. Wang et al. [22] proposed to add orthogonal constraints to class prototypes in all class prototypes. Zhang et al. [15] proposed bi-orthogonal constraints on the latent semantic features and used the discriminator to reduce the modality differences. Zhang et al. [23] proposed corrected attributes for both seen and unseen class semantic features; the corrected attributes can be discriminative in zero-shot learning and alleviate the domain shift problem. Shen et al. [24] used spherical embedding space to classify the unseen class samples, this method used different radius and spherical alignments on angles to alleviate the prediction bias.

In the literature [15], the authors proposed the use of an adversarial network to distinguish the semantic features and visual features. Our method also uses a discriminator for the semantic features and visual features. Still, there is no orthogonality restriction on the semantic features in our method, and this paper employs a dual discriminator approach to align the features of different modalities. This dual discriminator can provide part of the information about the unseen class. To alleviate the problem that most of the unseen class samples are always classified into seen classes, we propose a feature fusion method that can reduce the seen class’s information and increase the unseen class’s information to some extent.

3  A Dual Discriminator Method for Generalized Zero-Shot Learning

3.1 Definition of Problem

The training set can be denoted by 𝒯={Xt,At,Yt}. We use 𝒰={Xu,Au,Yu} to represent the unseen classes. X represents the visual features, A represents the semantic features and Y represents the labels. We use the subscript t and u to represent seen classes and unseen classes. In conventional zero-shot learning (CZSL), the unseen samples can be classified into the unseen classes. In generalized zero-shot learning (GZSL), test samples are classified into all classes (both seen and unseen classes).

3.2 The Architecture of the Proposed Method

The proposed method is shown in Fig. 2. We only consider GZSL in this paper. The visual features Xt are encoded to get the hidden space features Zt1, Zt2, and Zt1 = Zt2. The hidden space features are aligned with the seen class semantic features At and unseen class semantic features Au through two discriminators. The features in the hidden space are decoded to get new visual features X~t1 and X~t2, and the new visual features are fused with the original visual features as the input features f1 and f2 to the classifier. We use lowercase letters to represent a feature. Each part of the model is described in detail below.

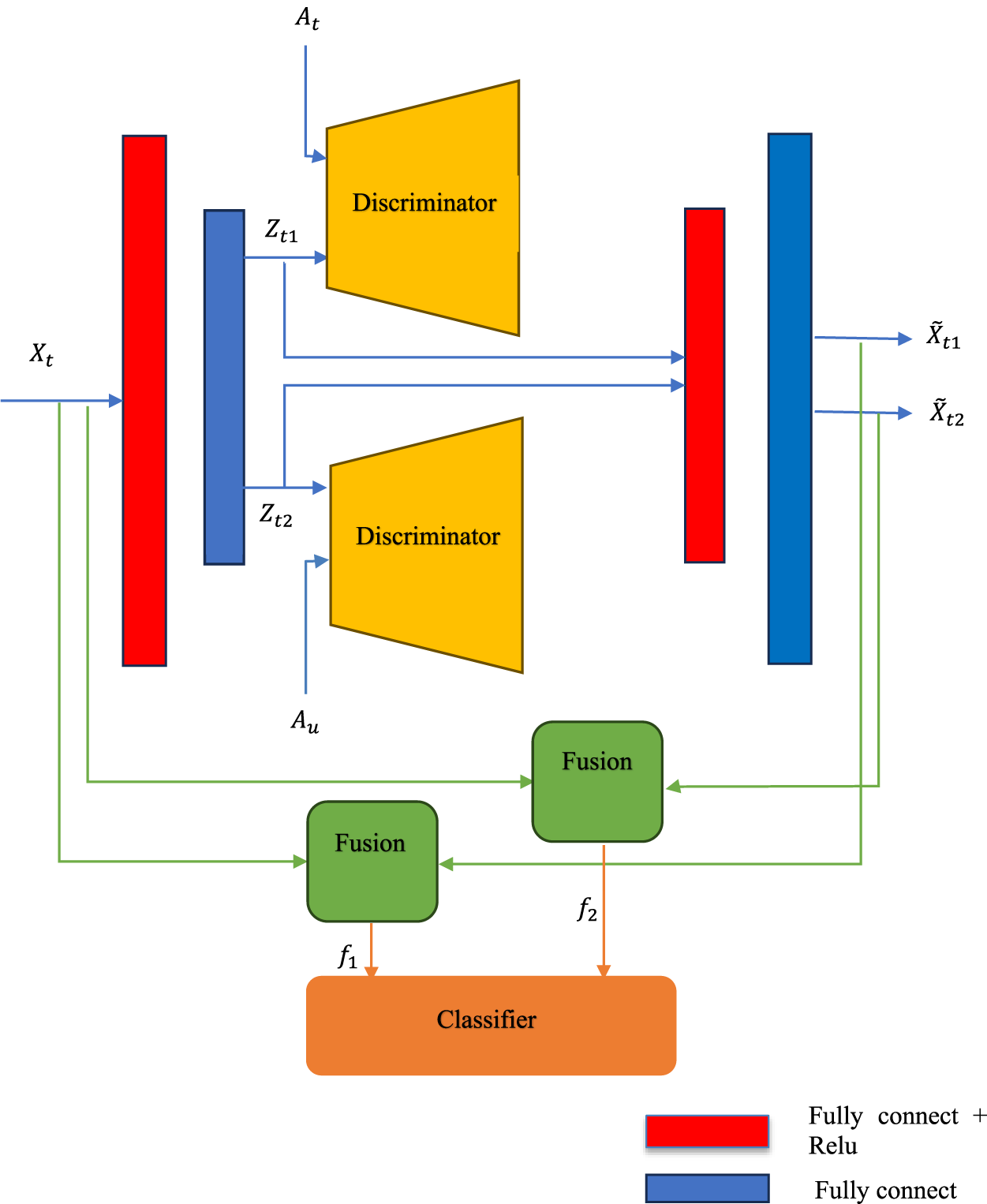
Figure 2: The proposed method

Semantic features and visual features belong to different feature spaces; mapping these two features to the same feature space and maintaining the consistency of these two features is an essential issue in zero-shot learning. Inspired by the literature [25], we use the latent space visual features to make the different modality features consistent.

In the literature [15], the authors used a discriminator to discriminate the different modality features. Different from the literature [15], we use two discriminators to enhance the consistency of the two modality features. We take one of the discriminators as an example, and its structure is shown in Fig. 3. Inspired by generative adversarial networks [26], a discriminator can be used in generative adversarial networks to distinguish whether the sample is a generated sample or a real sample. This approach can make the generated samples more similar to the real samples. In this paper, we regard the hidden space visual features obtained by using the encoder as generative samples and regard the semantic features as real samples so that the discriminator can make the hidden space visual features more similar to the semantic features and enhance the visual features consistent with the semantic features. Also, to reduce the domain shift problem and increase the information of the unseen class, a discriminator is used for the semantic features Au and the hidden spatial visual features.

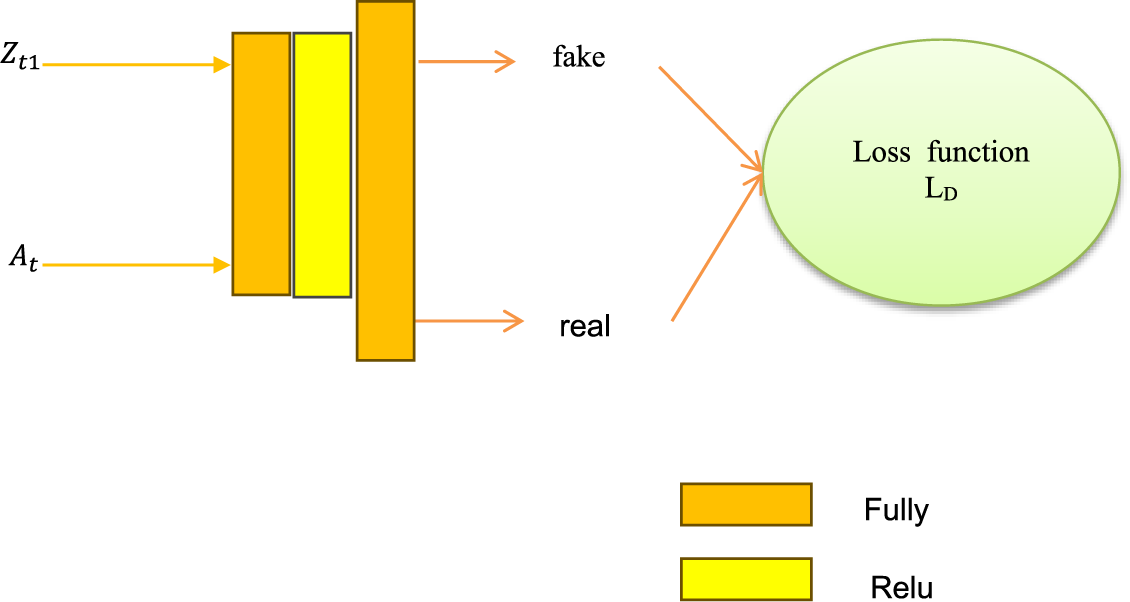
Figure 3: The structure of the discriminator

The other discriminator has the same structure as Fig. 3. Inspired by Wasserstein Generative Adversarial Nets (WGAN) [26], we write the loss function of the discriminator in the following form:

LD= EZt1∼Pg[D1(Zt1)]−EAt∼Pt[D1(At)]+λ1EZ˙1∼PZ1˙[(‖∇Z˙D1(Z˙1)‖2−1)2]+EZt2∼Pg[D2(Zt2)]−EAu∼Pu[D2(Au)]+λ2EZ˙2∼PZ2˙[(‖∇Z˙D2(Z˙2)‖2−1)2](1)

Here, λ1 and λ2 represents the coefficients. D1 and D2 represent the two discriminators, where D1 denotes the discriminator associated with Zt1 and At and D2 denotes the discriminator associated with Zt2 and Au. The subscript P represents the distribution of the data. In this paper, our calculation of Z˙1 is slightly different from that in the literature [26], we compute Z˙1 by Z˙1=δ∗Zt1+(1−δ)∗At and δ∼U(0,1). Z˙2 is computed as Z˙1. These two discriminators align semantic and visual features and add the information of unseen classes. The encoder in Fig. 1 can be seen as the generator and mean (•) represents the mean value. The loss function is shown in Eq. (2):

Lg=mean(−D1(Zt1)−D2(Zt2))(2)

The hidden visual features zt1 are passed through the decoder to get the new visual features x~t1, which need to be consistent with the original visual features, and this relationship can be written as:

Lr1=1n∑i=1n|x~t1−xt|(3)

Similarly, for the hidden spatial features zt2 to get the new visual features x~t2 through the decoder, the loss function concerning the original visual features is written as:

Lr2=1n∑i=1n|x~t2−Δx|(4)

Here, Δx=xt−x~t2. We first compute Δx, then we compute Eq. (4). We use Δx instead of xt because zt2 contains a portion of the information of the unseen class, and we want to reduce the compression of the knowledge of the unseen classes after the decoder. In the latent space, we also want the different modality features to be consistent with each other.

Ll1=1n∑i=1n|zt1−at|(5)

Ll2=1n∑i=1n|zt2−au|(6)

If only the features Xt are employed as input features to the classifier. The results will biased to the seen classes. So, before inputting the features into the classifier, feature fusion is used, as shown in Eqs. (7) and (8).

f1=μ1(Xt+X~t1)(7)

f2=μ2(Xt+X~t2)(8)

Here, μ1 and μ2 are coefficients. Feature fusion is equivalent to adding perturbations to the original visual features, which can compress the information about the seen classes and provide information about the unseen classes. The cross-entropy is used as the loss function in the classifier, yi represents the true label and yˇi represents the predicted label.

Lc=−12n∑i=12nyilog⁡(yˇi)(9)

The total loss function is:

L=Lr1+βLr2+Ll1+Ll2+Lc+Lg(10)

where β is the coefficient. The model proposed in this paper is optimized by alternating optimization method. The discriminator is firstly trained by Eq. (1), and then the other networks in the model are trained by Eq. (10).

4  Experiments

We validate our model on four datasets: Animals with Attribute 1 (AWA1) [27], Animals with Attribute 2 (AWA2) [28], Attribute Pascal and Yahoo (aPY) [29] and Caltech-UCSD Birds-200-2011 (CUB) [30]. The details of these four datasets are shown in Table 1.

In the proposed model, we use the RMSProp method to optimize the discriminator modules and the Adam method to optimize the other part of the proposed model. The learning rate is 0.001 for AWA1 and AWA2 datasets, and the learning rate is 0.006 for CUB and aPY datasets. The output of the first layer in the encoder contains 512 units, and the output of the first layer in the decoder contains 256 units. The output dimensions of the fully connected layer in the discriminator are 1024 and 256. We set μ1=0.5 and μ2=1 in our model. The visual features and semantic features are taken from the literature [28]. The dimension of the visual features is 2048. The complexity of the model are as follows: The flops for AWA1, AWA2, CUB and aPY are 4.86 M, 4.86, 6.77 M and 4.68 M, and the byte are 2.44 M, 2.44 M, 3.39 M, 2.35 M.

4.1 Results of GZSL

The proposed method is compared with other methods in GZSL settings. The evaluation method is taken from the literature [28]. We use 𝒞 to denote the average per-class top-1 accuracy and H to denote the harmonic mean. The subscripts s and u denote the seen classes and the unseen classes. The equations are as follows:

H=2×𝒞s×𝒞u𝒞s+𝒞u

The results of the proposed method are shown in Table 2. As seen from Table 2, the results of the proposed method on the AWA1 dataset are 2.2% lower than the best results. The method proposed in this paper achieves promising results on AWA2 and aPY datasets. Especially on the aPY dataset, the method in this paper outperforms the Spherical Zero-Shot Learning (SZSL) [24] method by 5.1%. The methods Semantic Autoencoder+Generic Plug-in Attribute Correction (SAE+GPAC) [23], SZSL [24], Transferable Contrastive Network (TCN) [21], and Modality Independent Adversarial Network (MIANet) [15] are considered the unseen semantic features in their models. Where SAE+GPAC, SZSL, and MIANet impose constraints on the semantic features, making the different classes of features more distinguishable. TCN proposed using the relationship of unseen class and seen class semantic features as the coefficients of the loss function. The method in this paper achieves better results than SAE+GPAC, SZSL, TCN, and MIANet these four methods on the AWA1, AWA2, and APY datasets, and the methods SZSL and TCN for the CUB dataset are better than the proposed method. In summary, the method in this paper gives good results on the AWA2 dataset and the APY dataset, and not as good as the other methods on the AWA1 dataset and the CUB dataset, especially on CUB dataset. This is because the CUB dataset is a fine-grained image dataset, although the method in this paper can provide features about unseen classes, it is not sufficiently discriminative between features of different classes, so it will lead to a decrease in classification results.

4.2 Parameters Influences

Figs. 4–7 show the effects of β in Eq. (10) on the generalized zero-shot classification results.

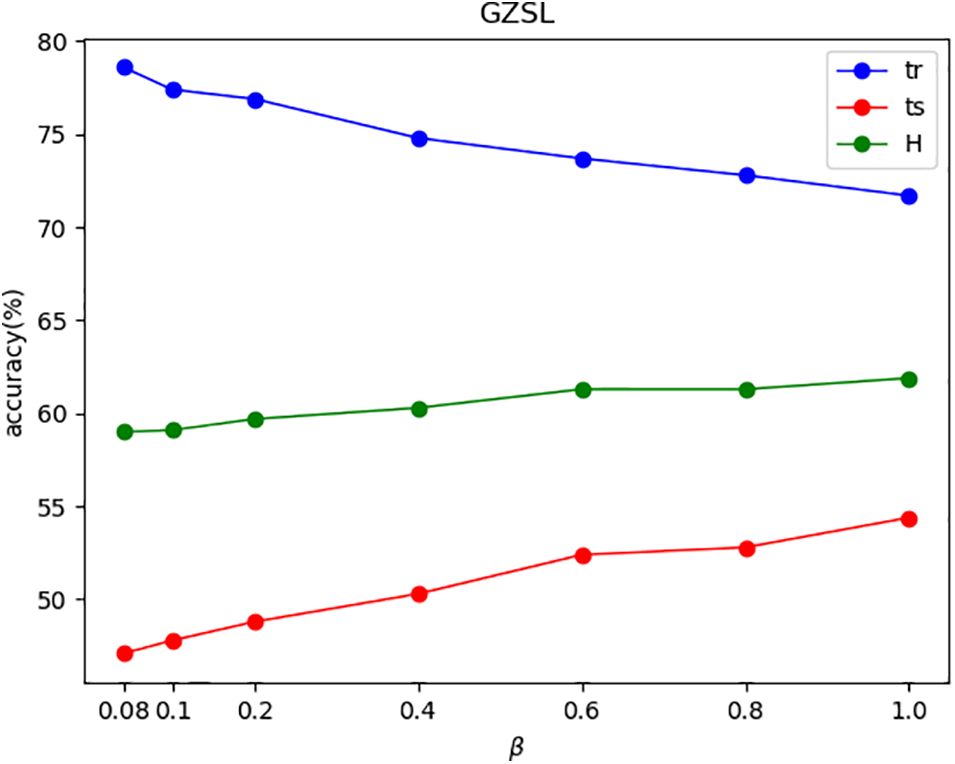
Figure 4: The effects of β on AWA1

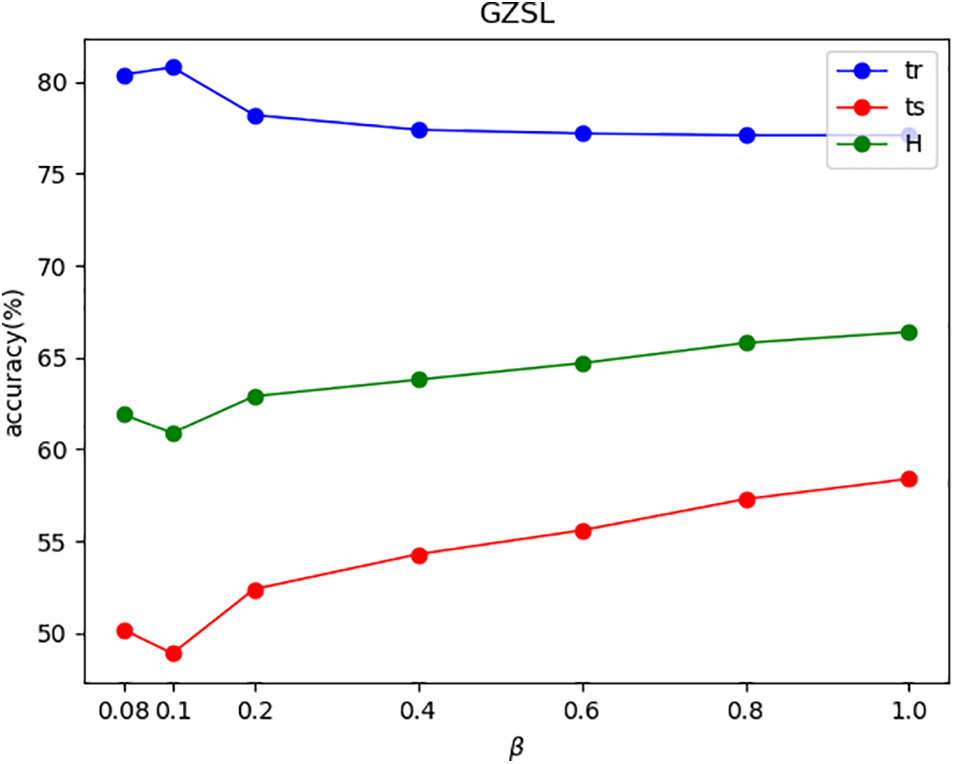
Figure 5: The effects of β on AWA2

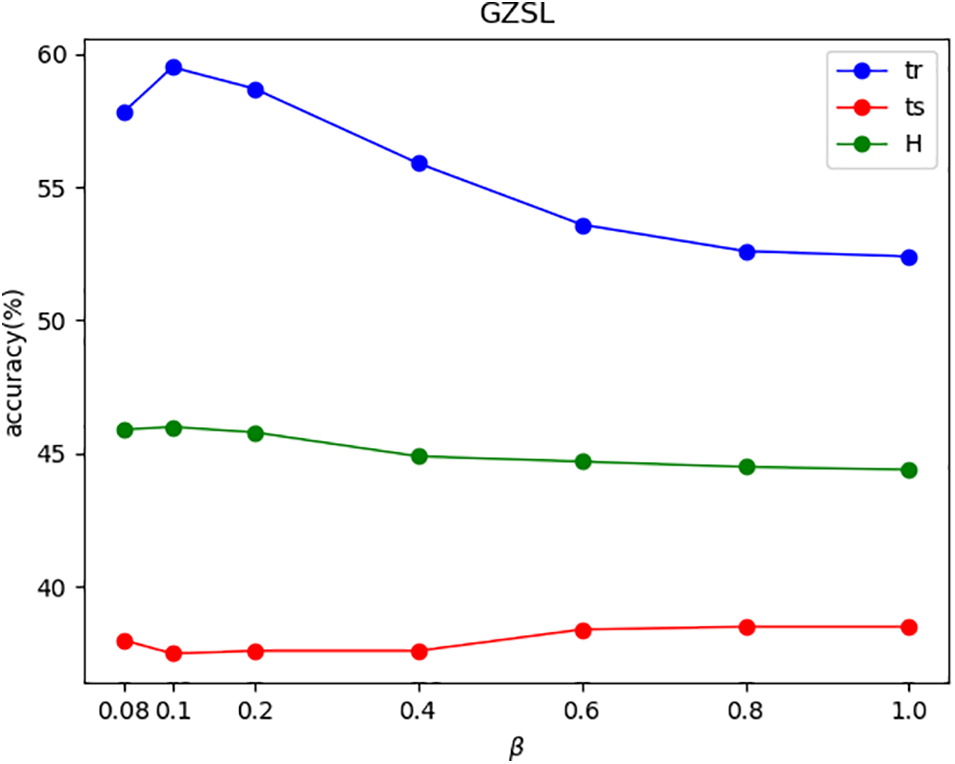
Figure 6: The effects of β on aPY

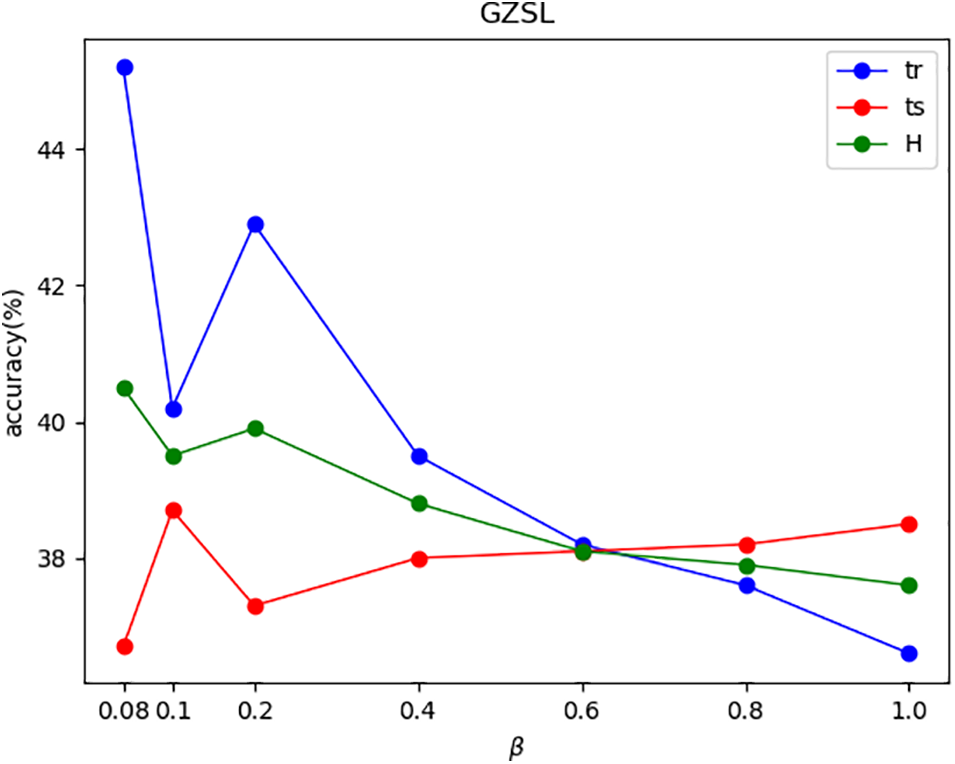
Figure 7: The effects of β on CUB

In Figs. 4–7, this paper uses ‘tr’ and ‘ts’ to denote the average per-class top-1 accuracy of the seen classes and the unseen classes, respectively. For the AWA1 and AWA2 datasets, as β increases, the accuracy is increased for the harmonic mean and unseen classes and decreased for the seen classes. For the aPY dataset, an increase in β has little effect on the harmonic mean, while the accuracy decreases for the seen classes and increases for the unseen classes. For the CUB dataset, accuracy increases for unseen class samples and decreases for seen class samples. In summary, as β increases, the accuracy of the unseen classes increases, while the accuracy of the seen classes decreases.

4.3 Ablation Experiments and tSNE

The results of the ablation experiments are shown in Table 3. The method without discriminator and feature fusion is denoted as the baseline. We use visual features as the input features f1 and f2 for the classifier in the baseline. We use ‘baseline+feature fusion’ to indicate that the model does not contain discriminators, f1 and f2 are calculated using Eqs. (7) and (8). ‘baseline+feature fusion+one discriminator’ denotes the method adds a discriminator related to semantic features of the seen classes.

Table 3 shows that for AWA1, AWA2, and CUB, the fusion of features in the three dataset models can drastically improve the harmonic mean. ‘baseline + feature fusion’ improves the accuracy of the seen classes compared to the baseline method, but does not reduce the accuracy of the unseen classes too much, which indicates that ‘baseline + feature fusion’ can improve the accuracy of the seen classes while still making the unseen class samples not massively biased toward the seen classes. ‘baseline+feature fusion’ can make the increase in both seen and unseen classes on aPY compared to the baseline method. From Table 3, it can be seen that when the discriminator is added, there is an increase in harmonic mean; this is because adding the discriminator not only adds information about the unseen class but also makes the features of the different modalities more consistent.

Figs. 8a and 8b show the tSNE for the AWA2 dataset. Fig. 8a shows the unseen class visual features in the AWA2 dataset, and Fig. 8b shows the visual features f2 obtained using feature fusion. Since the training set samples are used to obtain f2, the number of samples obtained for each class is different. The figure shows that the method proposed in this paper can provide a part of the distribution similar to the original sample features.

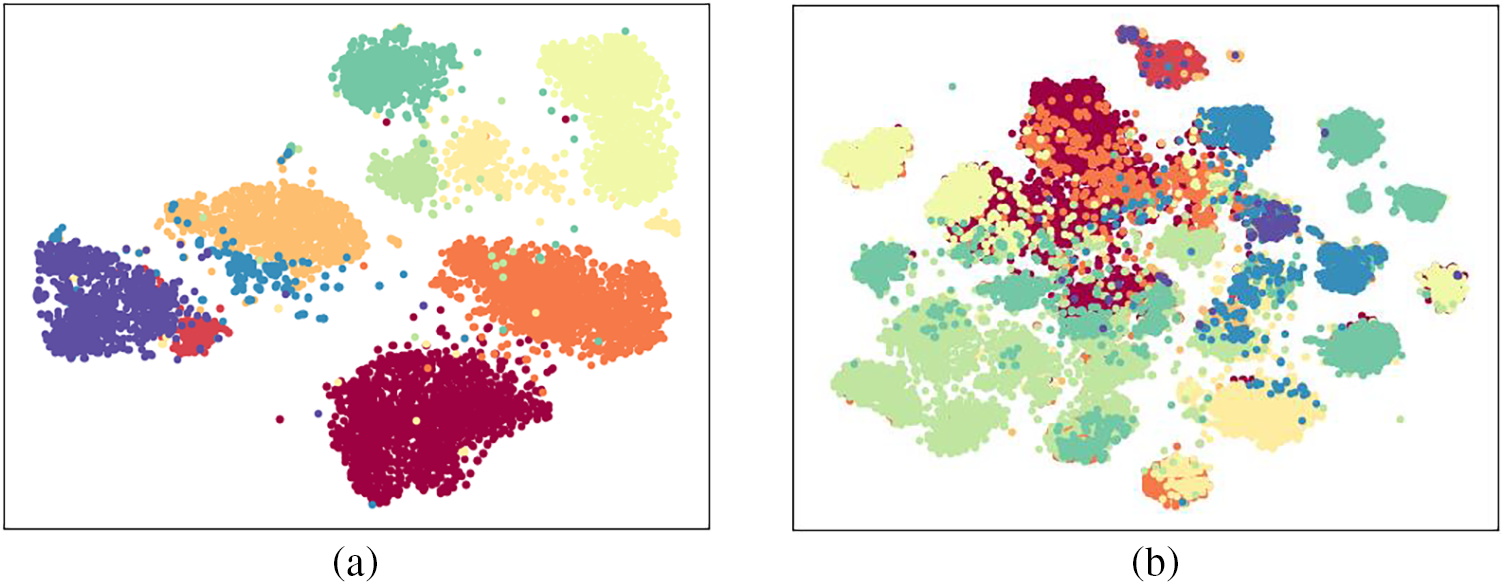
Figure 8: The tSNE of AWA2

4.4 The Influence of the Features ΔX

Fig. 9 shows the results of replacing ΔX in Eq. (4) with the original visual feature Xt. From Fig. 9, although good results can be obtained using the original visual features, the results are still low compared to the method in this paper.

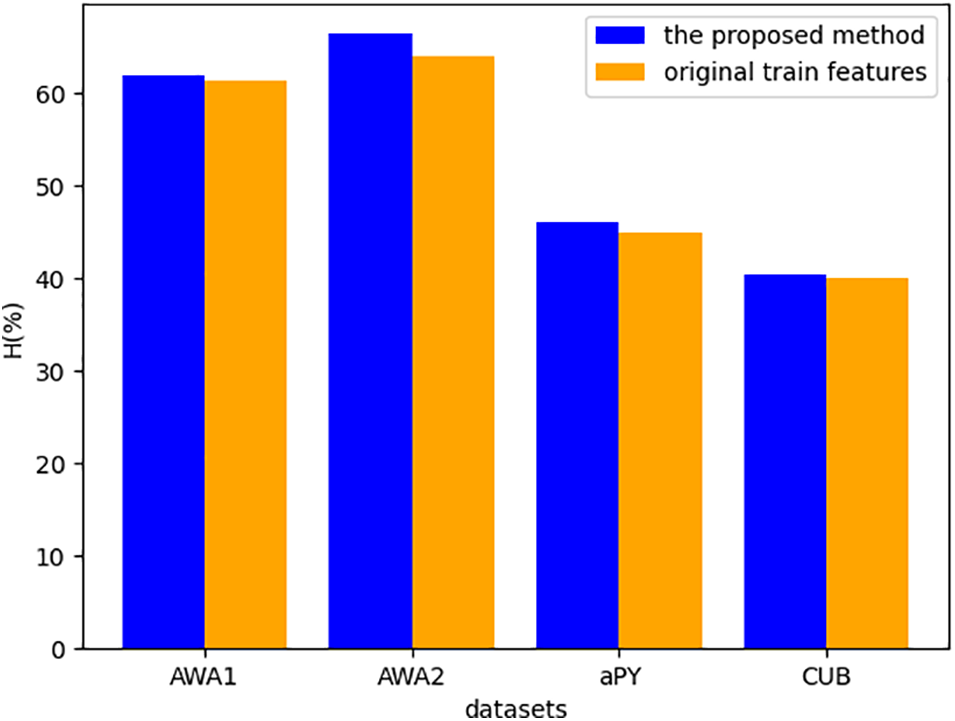
Figure 9: The harmonic mean of the original train features used in Eq. (4)

Fig. 10 shows the classification accuracy for each unseen class on the aPY dataset when replacing ΔX with the original feature Xt. From Fig. 9, the accuracy is less than the method proposed in this paper, except for very few classes where the accuracy increases when using the original features.

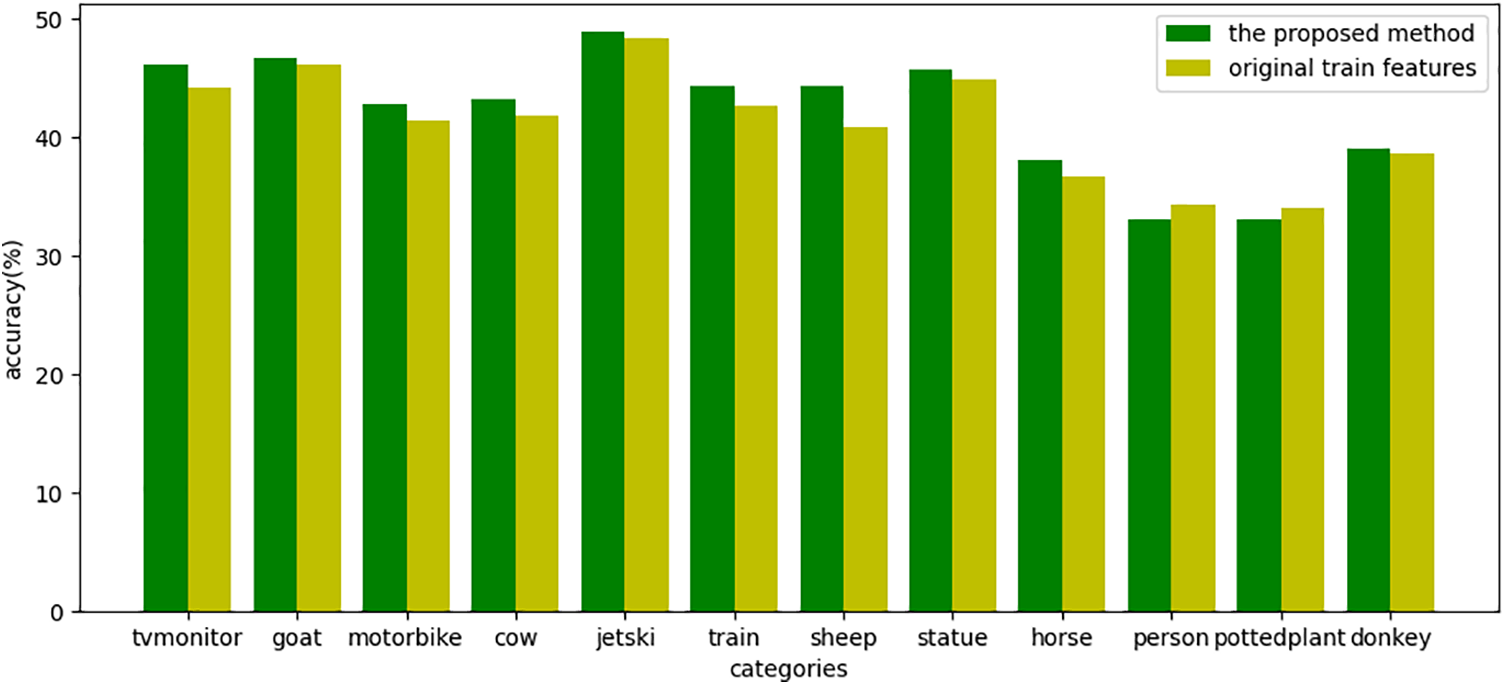
Figure 10: The accuracy of the unseen class samples of aPY

5  Conclusions

We propose a new model structure for the consistency problems of different modal features and domain shift problems in generalized zero-shot learning. Using a dual discriminator structure in the proposed model can lead to a better alignment of semantic and visual features, and this dual discriminator structure can provide part of the information about the unseen class. At the same time, this paper adopts a new feature fusion method to reduce the information about seen classes and provide information about unseen classes, so the model is not too biased towards seen classes in generalized zero-shot classification and improves the harmonic mean. We have experimented with our proposed model on four datasets, and the experimental results show the effectiveness of our approach, especially on the aPY dataset. We will further explore using an attention mechanism approach to extract more discriminative features, which will enable better alignment of features across modalities, and more discriminative features can improve the accuracy of zero-shot classification.

Acknowledgement: The authors sincerely appreciate the editors and reviewers for their valuable work.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study design and draft manuscript preparation: Tianshu Wei; reviewing and editing the manuscript: Jinjie Huang.

Availability of Data and Materials: The datasets used in the manuscript are public datasets. The datasets used in the manuscript are available from https://www.mpi-inf.mpg.de/departments/computer-vision-and-machine-learning/research/zero-shot-learning/zero-shot-learning-the-good-the-bad-and-the-ugly.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. G. Xu, Z. G. Zeng, C. Lian, and Z. G. Ding, “Semi-supervised low-rank semantics grouping for zero-shot learning,” IEEE Trans. on Image Process., vol. 30, pp. 2207–2219, 2021. doi: 10.1109/TIP.2021.3050677 [Google Scholar] [PubMed] [CrossRef]

2. Z. G. Ding, M. Shao, and Y. Fu, “Low-rank embedded ensemble semantic dictionary for zero-shot learning,” in Proc. CVPR, Honolulu, HI, USA, 2017, pp. 6005–6013. [Google Scholar]

3. M. Kampffmeyer, Y. B. Chen, X. D. Liang, H. Wang, Y. J. Zhang and E. P. Xing, “Rethinking knowledge graph propagation for zero-shot learning,” in Proc. CVPR, Long Beach, CA, USA, 2019, pp. 11479–11488. [Google Scholar]

4. C. W. Tang, X. Yang, J. C. Lv, and Z. N. He, “Zero-shot learning by mutual information estimation and maximization,” Knowl.-Based Syst., vol. 194, pp. 105490, 2020. [Google Scholar]

5. S. M. Chen et al., “TransZero++: Cross attribute-guided transformer for zero-shot learning,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 45, no. 11, pp. 12844–12861, 2023. doi: 10.1109/TPAMI.2022.3229526 [Google Scholar] [PubMed] [CrossRef]

6. Y. Liu, X. B. Gao, J. G. Han, L. Liu, and L. Shao, “Zero-shot learning via a specific rank-controlled semantic autoencoder,” Pattern Recognit., vol. 122, pp. 108237, 2022. [Google Scholar]

7. S. Li, L. Wang, S. Wang, D. Kong, and B. Yin, “Hierarchical coupled discriminative dictionary learning for zero-shot learning,” IEEE Trans. Circuits Syst. Video Technol., vol. 33, no. 9, pp. 4973–4984, 2023. doi: 10.1109/TCSVT.2023.3246475. [Google Scholar] [CrossRef]

8. J. Li, M. Jing, K. Lu, L. Zhu, and H. T. Shen, “Investigating the bilateral connections in generative zero-shot learning,” IEEE Trans. Cybern., vol. 52, no. 8, pp. 8167–8178, 2022. doi: 10.1109/TCYB.2021.3050803 [Google Scholar] [PubMed] [CrossRef]

9. B. R. Xu, Z. G. Zeng, C. Lian, and Z. M. Ding, “Generative mixup networks for zero-shot learning,” IEEE Trans. Neural Netw. Learning Syst., pp. 1–12, 2022. doi: 10.1109/TNNLS.2022.3142181 [Google Scholar] [PubMed] [CrossRef]

10. Y. Yang, X. Zhang, M. Yang, and C. Deng, “Adaptive bias-aware feature generation for generalized zero-shot learning,” IEEE Trans. Multimedia, vol. 25, pp. 280–290, 2023. doi: 10.1109/TMM.2021.3125134. [Google Scholar] [CrossRef]

11. Y. Li, Z. Liu, L. Yao, and X. Chang, “Attribute-modulated generative meta learning for zero-shot learning,” IEEE Trans. Multimedia, vol. 25, pp. 1600–1610, 2023. doi: 10.1109/TMM.2021.3139211. [Google Scholar] [CrossRef]

12. D. Huynh and E. Elhamifar, “Fine-grained generalized zero-shot learning via dense attribute-based attention,” in Proc. CVPR, Seattle, WA, USA, 2020, pp. 4482–4492. [Google Scholar]

13. W. J. Xu, Y. Q. Xian, J. N. Wang, B. Schiele, and Z. Akata, “Attribute prototype network for zero-shot learning,” in Proc. NeurIPS, Vancouver, Canada, 2020, pp. 21969–21980. [Google Scholar]

14. D. Cheng, G. Wang, N. Wang, D. Zhang, Q. Zhang and X. Gao, “Discriminative and robust attribute alignment for zero-shot learning,” IEEE Trans. Circuits Syst. Video Technol., vol. 33, no. 8, pp. 4244–4256, 2023. doi: 10.1109/TCSVT.2023.3243205. [Google Scholar] [CrossRef]

15. H. F. Zhang, Y. D. Wang, Y. Long, L. Z. Yang, and L. Shao, “Modality independent adversarial network for generalized zero-shot image classification,” Neural Netw., vol. 134, pp. 11–12, 2021 [Google Scholar] [PubMed]

16. S. T. Liu, J. J. Chen, L. M. Pan, C. W. Ngo, T. S. Chua, and Y. G. Jiang, “Hyperbolic visual embedding learning for zero-shot recognition,” in Proc. CVPR, Seattle, WA, USA, 2020, pp. 9270–9278. [Google Scholar]

17. B. N. Li, C. Y. Han, T. D. Guo, and T. Zhao, “Disentangled features with direct sum decomposition for zero shot learning,” Neurocomputing, vol. 426, pp. 216–226, 2021. [Google Scholar]

18. E. R. Kodirov, T. Xiang, and S. G. Gong, “Semantic autoencoder for zero-shot learning,” in Proc. CVPR, Honolulu, HI, USA, 2017, pp. 4447–4456. [Google Scholar]

19. Y. Liu, J. Li, Q. X. Gao, J. G. Han, and L. Shao, “Zero shot learning via low-rank embedded semantic autoencoder,” in Proc. IJCAI, Stockholm, Sweden, 2018, pp. 2490–2496. [Google Scholar]

20. Y. Q. Xian, T. Lorenz, B. Schiele, and Z. Akata, “Feature generating networks for zero-shot learning,” in Proc. CVPR, Salt Lake City, UT, USA, 2018, pp. 5542–5551. [Google Scholar]

21. H. J. Jiang, R. P. Wang, S. G. Shan, and X. L. Chen, “Transferable contrastive network for generalized zero-shot learning,” in Proc. ICCV, Seoul, Korea (South2019, pp. 9764–9773. [Google Scholar]

22. Y. D. Wang, H. F. Zhang, Z. Zhang, Y. Long, and L. Shao, “Learning discriminative domain-invariant prototypes for generalized zero shot learning,” Knowl.-Based Syst., vol. 196, pp. 105796, 2020. [Google Scholar]

23. H. F. Zhang, H. Y. Bai, Y. Long, L. Liu, and L. Shao, “A plug-in attribute correction module for generalized zero-shot learning,” Pattern Recognit., vol. 112, pp. 107767, 2021. [Google Scholar]

24. J. Y. Shen, Z. H. Xiao, X. T. Zhen, and L. Zhang, “Spherical zero-shot learning,” IEEE Trans. Circuits Syst. Video Technol., vol. 32, no. 2, pp. 634–645, 2022. doi: 10.1109/TCSVT.2021.3067067. [Google Scholar] [CrossRef]

25. W. P. Cao, Y. H. Wu, C. Chakraborty, D. C. Li, L. Zhao and S. K. Ghosh, “Sustainable and transferable traffic sign recognition for intelligent transportation systems,” IEEE Trans. Intell. Transport. Syst., vol. 24, no. 12, pp. 15784–15794, 2023. doi: 10.1109/TITS.2022.3215572. [Google Scholar] [CrossRef]

26. I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, and A. Courville, “Improved training of wasserstein GANs,” arXiv:1704.00028, 2017. [Google Scholar]

27. L. C. H, N. Hannes, and H. Stefan, “Learning to detect unseen object classes by between-class attribute transfer,” in Proc. CVPR, Miami, FL, USA, 2009, pp. 951–958. [Google Scholar]

28. Y. Xian, C. H. Lampert, B. Schiele, and Z. Akata, “Zero-shot learning a comprehensive evaluation of the good, the bad and the ugly,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 41, no. 9, pp. 2251–2265, 2019. doi: 10.1109/TPAMI.2018.2857768 [Google Scholar] [PubMed] [CrossRef]

29. A. Farhadi, I. Endres, D. Hoiem, and D. Forsyth, “Describing objects by their attributes,” in Proc. CVPR, Miami, FL, USA, 2009, pp. 1778–1785. [Google Scholar]

30. P. Welinder, S. Branson, T. Mita, C. Wah, and F. Schroff, “Caltech-ucsd birds 200,” Technical Report CNS-TR-2011-001, California Institute of Technology, 2010. [Google Scholar]

31. M. R. Vyas, H. Venkateswara, and S. Panchanathan, “Leveraging seen and unseen semantic relationships for generative zero-shot learning,” in Proc. ECCV, Glasgow, 2020, pp. 70–86. [Google Scholar]

32. H. F. Zhang, Y. Long, Y. Guan, and L. Shao, “Triple verification network for generalised zero-shot learning,” IEEE Trans. on Image Process., vol. 28, no. 1, pp. 506–517, 2019. doi: 10.1109/TIP.2018.2869696 [Google Scholar] [PubMed] [CrossRef]

33. R. Gao et al., “Visual-semantic aligned bidirectional network for zero-shot learning,” IEEE Trans. Multimedia., vol. 25, pp. 7670–7679, 2023. [Google Scholar]

34. Z. Ji, K. X. Chen, J. Y. Wang, Y. L. Yu, and H. A. Murthy, “Multi-modal generative adversarial network for zero-shot learning,” Knowl-Based Syst., vol. 197, no. 7, pp. 105874, 2020. doi: 10.1016/j.knosys.2020.105847. [Google Scholar] [CrossRef]

35. A. K. Pambala, T. Dutta, and S. Biswas, “Generative model with semantic embedding and integrated classifier for generalized zero-shot learning,” in Proc. WACV, Snowmass, CO, USA, 2020, pp. 1226–1235. [Google Scholar]

36. H. Zhang, Y. Long, L. Liu, and L. Shao, “Adversarial unseen visual feature synthesis for zero-shot learning,” Neurocomputing, vol. 329, pp. 12–20, 2019. [Google Scholar]

37. T. S. Wei, J. J. Huang, and C. Jin, “Zero-shot learning via visual-semantic aligned autoencoder,” Math. Biosci. Eng., vol. 20, no. 8, pp. 14081–14095, 2023. doi: 10.3934/mbe.2023629 [Google Scholar] [PubMed] [CrossRef]

38. Q. Yue, J. B. Cui, L. Bai, J. Q. Liang, and J. Y. Liang, “A zero-shot learning boosting framework via concept-constrained clustering,” Pattern Recognit., vol. 145, pp. 109937, 2024. [Google Scholar]

39. J. Sánchez and M. Molina, “Trading-off information modalities in zero-shot classification,” in Proc. WACV, Waikoloa, HI, USA, 2022, pp. 1677–1685. [Google Scholar]

40. C. Gautam, S. Parameswaran, A. Mishra, and S. Sundaram, “Tf-GCZSL: Task-free generalized continual zero-shot learning,” Neural Netw., vol. 155, pp. 487–497, 2022 [Google Scholar] [PubMed]