Blockchain-Based Key Management Scheme Using Rational Secret Sharing

1  Introduction

Key Escrow [1] refers to the storage of decryption keys in a key escrow system (also known as a key recovery system), and in some cases, authorizes third parties to access these keys, which is a key management mechanism for statutory escrow agency. Government and law enforcement agencies’ needs to access encrypted data and recover commercial data have made key escrow a popular research topic in the 1990s [2]. Key Escrow faces two challenges: the trust level of the key escrow agent and the ability to protect the keys [3]. It is easy for a single key escrow party to collaborate with illegal organizations to obtain confidential data, facing widespread user doubts. A single key escrow node also faces the risk of a single point of failure. Therefore, split key escrow has gradually become a new direction for the development of key escrow [4]. In this stage, Shamir [5] proposed partial key escrow for DES keys, Lenstra et al. [6] proposed a time-constrained key escrow system, and Micali et al. [7] proposed shared random functions and key escrow schemes. However, based on Shamir [8] and Blakley [9], independently proposed the concept of key dispersed management, using threshold secret sharing as the representative threshold cryptography as the theoretical basis, comprehensively considering the security and implementation difficulty of the scheme, studying threshold key escrow schemes has become the main trend of key split escrow. Therefore, the key to designing a threshold key escrow scheme that meets actual needs lies in studying and developing corresponding threshold secret sharing technology.

Shamir’s threshold secret sharing and other early-stage secret sharing schemes assumed that the secret distributor and participants were honest without considering deceptive behavior. In response, Chor et al. [10] proposed the concept of verifiable secret sharing (VSS), which added a verification algorithm to the traditional secret sharing scheme. However, this scheme required an interactive process, resulting in low efficiency. Bai et al. [11] proposed a verifiable quantum secret sharing scheme based on d-dimensional Greenberger-Horne-Zeilinger (GHZ) state and analyzed its security against three main quantum attacks: interception retransmission attack, entanglement measurement attack, and honest participant attack. Gentry et al. [12] proposed a non-interactive public verifiable secret sharing (PVSS) scheme for large-scale distributed networks, which can be extended to have hundreds or even thousands of participants to support secure computing in large-scale distributed systems. However, these VSS schemes only consider honest participants and suspected fraudulent participants, without considering the motivations and benefits of each participant. For large-scale institutions like governments or enterprises, key escrow participants are usually bound by political orders, business contracts, and other forms of compulsion, which do not need to consider the self-interested behavior of each participant in the threshold key escrow scheme. Whereas, for online distributed systems like blockchain that target a large number of network users, the traditional threshold key escrow scheme does not have such constraints, resulting in participants who do not upload or upload false key shares still being able to obtain reconstructed keys.

Halpern et al. [13] considered the selfish behavior of participants and introduced Game theory to secret sharing and secure multi-party computation. They proposed a rational cryptographic protocol represented by rational secret sharing and rational secure multi-party computation for the first time. However, traditional rational secret sharing schemes rely on synchronous communication environments and cannot be applied to distributed systems such as blockchains with asynchronous communication. Kol et al. [14] used cryptographic techniques such as oblivious transfer and secure multi-party computation to construct the first rational secret sharing scheme suitable for asynchronous communication. In addition, Zhang et al. [15] introduced rational cryptography into quantum secret sharing research and proposed a rational quantum secret sharing scheme based on GHZ states, which was implemented on the IBM quantum computer [16].

The wide application of blockchain and smart contracts in the Internet of Things has enabled the fulfillment of resource sharing and automated transactions without trusted centers [17]. The public key cryptography technology widely used in blockchain is highly related to the security of user private keys, user asset security, data security, and identity certification security. As there is no trusted third party in the blockchain system, individuals need to locally store their private keys. Once the device where the private key is stored is lost, data is damaged, or even hacked by hackers, it will lead to the loss or leakage of user data and assets. In this context, blockchain private key escrow solutions based on threshold key management technology have become a research hotspot for blockchain private key protection. However, the currently proposed key management schemes for blockchain private key recovery still adopt traditional VSS technology, without considering the rational self-interest behavior of the escrow users [18]; the successfully implemented rational secret sharing schemes on blockchain require the secret sharing participants to deliver deposits in advance [19]. These schemes do not meet the individual rational constraint in mechanism design, limiting the application and promotion of corresponding blockchain threshold key escrow design. The main contributions of this paper are as follows:

We proposed a threshold multi-key escrow management scheme that satisfied individual rational constraints and incentive compatibility: We first designed a reputation mechanism for participants during the key reconstruction phase with the process of uploading and verifying private key fragments and reporting. Then, according to the ratio of contribution to promote the cooperation and behavioral norms of blockchain users, we also proposed a benefit distribution mechanism that relied on a fair process of cooperative gaming.

We constructed the whole multi-key escrow and reconstruction process based on verifiable random functions (VRF) and analyzed and demonstrated the collusion resistance, security verification ability, incentive compatibility and individual rational constraints of the threshold key escrow scheme through utility function analysis. We also compared it with existing blockchain recoverable key management schemes.

We used the smart contracts to complete a multi-wallet key escrow simulation, demonstrating the ability of the scheme to manage wallet keys in Ethereum. We analyzed the performance and costs of the scheme, providing possibilities for achieving a distributed rational key management system for blockchain.

2  Related Work

2.1 Blockchain and Smart Contract

Nakamoto et al. [20] proposed Bitcoin, a virtual encrypted currency, and the blockchain transaction structure using Proof of Work and timestamp construction in 2008, which marked the birth of decentralized blockchain technology. Blockchain combines with cryptographic technology ensures traceability, immutability, non-repudiation, and non-counterfeiting of transactions, supporting data security sharing and large-scale collaborative computing, protecting user identity and confidential data privacy, and is suitable for high-privacy and secure distributed application scenarios. Traceability refers to the recording of transaction changes in a blockchain in chronological order, immutability and non-repudiation refer to the inability to modify and deny data written into a blockchain, and non-counterfeiting refers to the inability to forge transactions that can be verified by miners and the entire transaction change record. Blockchain uses hash functions, digital signatures, and distributed consensus fault tolerance to increase the difficulty and cost of attackers falsifying, forging, and denying data operations, enhancing data security.

Szabo proposed the smart contract, which is a computerized transaction protocol for executing contract terms [21]. In the context of blockchain, smart contracts serve as scripts on blockchain and are stored on the blockchain. As smart contracts are located on the blockchain, they have their unique addresses. We trigger their execution by sending transactions to their addresses. Subsequently, smart contracts will be executed independently and automatically on every node in the network according to the data contained in the triggered transaction. Smart contracts on blockchain possess uniqueness, transparency, predictability, and monitoring and tracking capabilities, and have fostered the concept of a decentralized autonomous organization, allowing blockchain to achieve general computing among users without a trusted central node’s supervision [17]. Raj et al. [22] proposed a blockchain smart contract scheme for supply chain management, which replaces the trust intermediary with smart contracts, shortens the payment process, reduces the communication cost, and improves the supply chain transaction efficiency.

2.2 Research on the Security of Blockchain Wallet and Threshold Key Escrow

Blockchain digital wallets provide users with a convenient way to manage private and public keys, while also enabling them to complete digital asset transfers and transactions, and record details of all transactions. The security of the wallet directly relates to the user’s asset security. The comparison of various blockchain key management schemes is shown in Table 1. The existing common wallet solution types include software wallets [23], hardware wallets [24], and custodial wallets [25], but they all have security risks in terms of centralized private key storage. To address these issues, decentralized secure threshold wallet schemes have emerged, which can split private keys into multiple parts and store them on different nodes, thereby achieving distributed storage and protection of private keys, while also allowing private keys to be restored. Therefore, this secure threshold wallet scheme is considered an effective protection plan.

A threshold secret sharing-based threshold signature wallet scheme such as [26] does not support the escrow and recovery of personal user wallet private keys, while a threshold wallet management scheme that meets the needs of personal key escrow and recovery, such as [18], is only applicable to consortium blockchain applications, which requires trusted central nodes and identity authentication mechanisms. In addition, the aforementioned threshold wallet schemes have not taken into account the rational self-interest behavior of participants, resulting in high costs and limited applicability, which cannot be satisfied to the safe escrow needs of public blockchain user wallet keys such as Ethereum. Therefore, designing a private key escrow smart contract based on rational secret sharing is beneficial for achieving the escrow and recovery of public blockchain user private keys in an environment without trusted nodes.

3  Preliminaries

3.1 Bilinear Mapping

Definition 1: Let G1 and G2 be the additive cyclic group and multiplicative cyclic group of a prime number p, respectively, let g be a generator of G. The mapping e:G1×G1→G2 is bilinear if it satisfies the following properties:

1) Bilinearity: For any m,n∈G1 and a,b∈Zp∗, exists e(ma,nb)=e(m,n)ab.

2) Non-degeneracy: e(g,g)≠1.

3) Computability: There exists an efficient algorithm to compute e(m,n) for any m,n∈G1.

Definition 2: Elliptic Curve Discrete Logarithm Problem (DCELP): Given an elliptic curve E defined over a finite field Fp, with a base point P∈E(Fq) of order n. Q∈E(Fq) where Q=IP,I∈n, it is difficult to compute I.

Definition 3: Computational Diffie-Hellman (CDH) Given aP,bP,cP∈G1, it is difficult to compute abP for any a,b∈ZP∗.

Definition 4: Bilinear Diffie-Hellman Problem Given aP,bP,cP∈G1, it is difficult to compute e(P,P)abc for any a,b,c∈ZP∗. This problem relies on the difficulty of the CDH problem in G1.

Definition 5: Decisional Bilinear Diffie-Hellman Inversion Assumption, also known as q-DBDHI problem. An adversary with polynomial time capability cannot distinguish between (g,gx,…,g(xq),e(g,g)1x) and (g,gx,…,g(xq),Γ) with a non-negligible advantage, where x∈ZP∗, Γ∈G2.

3.2 Game Theory Related Knowledge

3.2.1 Incentive Compatibility

Incentive compatibility refers to the consistency between individual incentive mechanisms and overall benefits in a game. It includes Bayesian incentive compatibility and dominant strategy incentive compatibility. It should be noted that Bayesian incentive compatibility is a weak concept in games, while dominant strategy incentive compatibility is a strong concept. If a game is dominant strategy incentive compatible, then it must be Bayesian incentive compatible.

In mechanism design, Bayesian incentive compatibility is considered a sufficient and necessary condition for participants to speak the truth. A game is Bayesian incentive compatible if and only if, for any player i, any possible private type θi, and any other players’ strategies σ−i, the following condition is satisfied:

∀θi,∀σi,∀σi′:Ui(σi,σ−i,θi)≥Ui(σi′,σ−i,θi)(1)

where Ui(σi,σ−i,θi) represents player i’s utility when their private type is θi, they choose strategy σi (the true strategy), and the other players choose strategies σ−i.

In a game, if each player adopts their dominant strategy regardless of the other players’ actions, the game is dominant strategy incentive compatible. Mathematically, a game is dominant strategy incentive compatible if and only if for any player i, any other player’s strategy σ−i, the following condition is satisfied:

∀σi,∀σi′:Ui(σi,σ−i)≥Ui(σi′,σ−i)(2)

where Ui(σi,σ−i) represents player i’s utility when all players adopt strategy σi,σ−i.

3.2.2 Individual Rationality

In game theory, individual rationality refers to each player choosing strategies that are beneficial to them in pursuit of their own maximum interests. This is also known as the assumption of rational participants. In mechanism design, individual rationality means designing a game mechanism to ensure that each participant has the motivation to participate and will not obtain a worse result due to participation.

Mathematically, individual rationality satisfies the following conditions:

For each participant i, individual rationality requires that their returns after participating in the mechanism are not less than their worst returns from leaving the mechanism, i.e.,

∀σi,∀σ−i:Ui(σi,σ−i)≥Ui(∅)(3)

where Ui(∅) represents the returns of participant i when they do not participate in the mechanism.

3.2.3 Fairness of Cooperative Game and Shapley Value Principle

Fairness is a concept to measure the justice of a game. In Game theory, fairness usually refers to whether a game satisfies some fair principles, such as the symmetry principle in a zero-sum game and the Shapley value principle in a cooperative game.

In a cooperative game, the Shapley value principle means that each player should get the corresponding reward for his contribution to the game. Specifically, the Shapley value refers to the average contribution of a player to all possible coalitions. If a player’s Shapley value is lower than other players, this situation is also unfair.

3.2.4 Rational Fairness

In Game Theory, rational fairness refers to the participants in a game mechanism pursuing their own interests (rationality) while also obtaining fair results. Rational fairness requires participants to consider not only their own interests but also the interests of other participants when choosing strategies, in order to achieve a fair balance.

Rational fairness should satisfy the following conditions:

For each participant, rational fairness requires that the chosen strategy is an optimal response, i.e.,

σi∗^∈BRi(s−i)(4)

3.2.5 Resisting Collusion Attack

In Game Theory, a Collusion Attack refers to participants secretly collaborating or cooperating to devise strategies for their own benefits while disregarding the interests of other participants. This collusion may distort the results of the game, sacrificing fairness and balance. Resisting Collusion Attack refers to a feature of strategic or mechanism design that aims to prevent participants from forming collusion or cooperation that could harm the fairness or balance of the game.

Reference [27] proposed a definition of a computable anti-collusion equilibrium: in a game Γ=({Ai}i=1n,{ui}i=1n), let T represent a collusion group and k be a secure parameter of a cryptographic protocol. Assuming that for each collusion group, the non-collusive strategy is aT, the collusive strategy is aT′, and the non-collusion group’s strategy is a−i, we call the strategic combination a=(a1,…,an)∈A a computable anti-collusion equilibrium if for Pi∈T, there exists a negligible function ε(k) such that the game remains in

ui(aT′(k),a−T(k))≤ui(aT(k),a−T(k))+ε(k)(5)

3.3 Verifiable Random Function

Verifiable Random Function (VRF) [28] is a random function with verification capabilities. It can generate an output and allow a verifier to verify that the output was generated from a specific input and key while maintaining the randomness and unpredictability of the output. Reference [29] proposed an efficient verifiable random function based on bilinear pairs. The scheme includes the following components:

a) Public-private key generation module Gen(1k): Input 1k, output SK=s,PK=gs.

b) Encryption module FSK(x): Input SK,x, output y=FSK(x)=e(g,g)1x+SK.

c) Evidence module πSK(x): Input SK,x, output π=πSK(x)=g1x+SK.

d) Verification module VPK(x,y,π): Determine whether y is the output corresponding to x, input (PK,x,y,π), verify whether e(g⋅pk,π)=e(g,g) and y=e(g,π) are both true, and output 1 if both are true, otherwise output 0.

4  Multi-Key Management Scheme Based on Rational Secret Sharing

Based on the anti-collusion rational secret sharing [27], and taking into account the practical situation of blockchain key escrow, the current and long-term benefits of secret-sharing participants, and the advantages of blockchain smart contracts, a multi-private key management scheme based on rational secret sharing is proposed as follows.

4.1 System Parameters

The parameters involved in the proposed scheme are shown in Table 2.

4.2 Key Generation Phase

This algorithm is executed by the system administrator to generate public key and private key of Pi. After executing this algorithm, the administrator will exit this program permanently. Especially, the setup algorithm inputs security parameter 1k and generates the public key pki and the private key ski by using Shamir’s (t, n)-threshold secret sharing scheme for Pi. Moreover, blockchain administrators use multiple servers provided by the blockchain platform to secretly obtain randomly generated two-dimensional point coordinates, reconstruct Lagrange polynomials, and generate private keys by substituting additional random values. Its purpose is to avoid the risk of a single point of failure during the user’s local private key generation process.

4.3 Key Escrow Negotiation Phase

As shown in Fig. 1, the key escrow user sets a threshold value t according to its own needs, determines the number of participants n to sign the key escrow agreement based on the active degree of the blockchain nodes and p encrypted keys s0,s1,…,sp−1, then negotiates the cost of the escrow contract M=M1+M2, determines the parameters of the geometric distribution λ based on the estimated benefits of the participants (see Section 6.3 for details) and generates a secure parameter r∗∈Z+ (Z+ is a positive integer set) based on this geometric distribution. The key escrow user learns the addresses of all participants and establishes secure channels with each participant. Send the private key ski(i=1,2,…,n) to the participant i through a secure channel and upload the public data to the smart contract: a) pki(i=1,2,…,n), b) M=M1+M2.

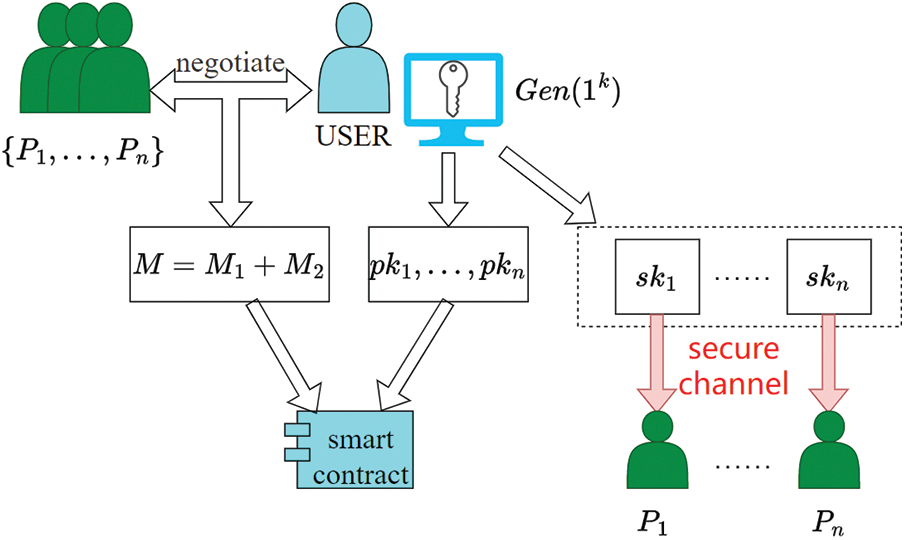
Figure 1: Key escrow negotiation process

4.4 Key Sharing Phase

Step 1: Key Escrow User uses the two-dimensional coordinate points (h(Add1||r∗),Fsk1(r∗)),(h(Add2||r∗),Fsk2(r∗)),…,(h(Addn||r∗),Fskn(r∗)) and (0,s0),(1,s1),…,(p−1,sp−1) determines a n+p−1 degree polynomial as follows:

G(x)=∑i=1nFski(r∗)∏j=1,j≠inx−h(Addj||r∗)h(Addi||r∗)−h(Addj||r∗)∏j=0p−1x−jh(Addi||r∗)−j+∑i=0p−1si∏j=0,j≠ip−1x−ji−j∏j=1nx−h(Addj||r∗)i−h(Addj||r∗)modq=a0r∗+a1r∗x+a2r∗x2+⋯an+p−1r∗xn+p−1(6)

Let V0r∗=s0⊕G(0),V1r∗=s1⊕G(1),…,Vp−1r∗=sp−1⊕G(p−1)

Step 2: To avoid duplicate numerical pairs causing failure during the key reconstruction phase, the key escrow user selects n+p−t smallest integers d1,d2,…,dn+p−t from [p,q−1]−{h(Addi||r)|i=1,2,…,n;r=1,2,…,r∗}.

Step 3: Upload public data to the smart contract: a) (d1,G(d1)),(d2,G(d2)),…,(dn+p−t,G(dn+p−t)), b) Vjr∗=sj⊕G(j)(j=0,1,…,p−1) and c) h(akr∗)(k=0,1,…,n+p−1).

Step 4: The key escrow user deletes ski(i=1,2,…,n), r∗, s0,s1,…,sp−1 and only retains the public information: pki(i=1,2,…,n), (d1,G(d1)),(d2,G(d2)),…,(dn+p−t,G(dn+p−t)), Vjr∗=sj⊕G(j)(j=0,1,…,p−1) and h(akr∗)(k=0,1,…,n+p−1).

The process of key sharing phase is shown in Fig. 2.

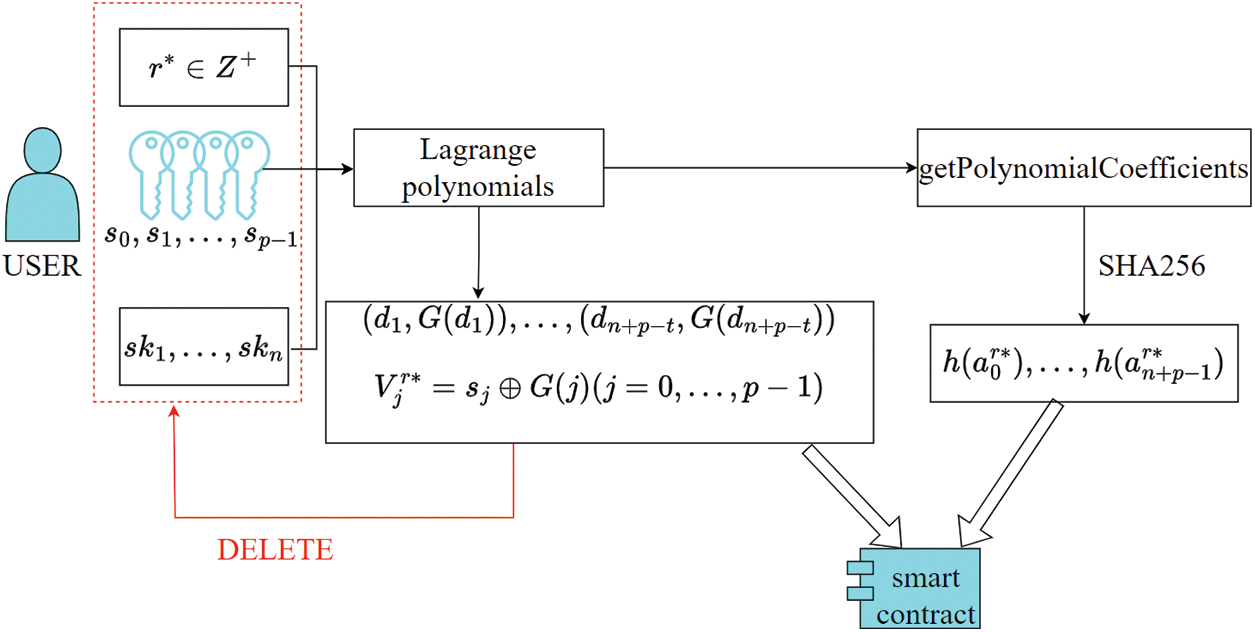
Figure 2: Key sharing process

4.5 Key Reconstruction Phase

Step 1: The contract indicates that round r(r=1,2,…,r∗) begins (the initial value r is 1), and i(i=1,2,…,mr,t≤mr≤n) participants must input yir=Fski(r)=e(g,g)1r+ski, πir=πski(x)=g1r+ski within the prescribed upload time T1 into the smart contract. Repeated uploads or yir,πir with a reputation value Rvi<0 are considered invalid inputs.

Step 2: During the verification time T2, all participants can make their own judgment about whether e(gr⋅pki,πir)=e(g,g) and yir=e(g,πir) both are valid or not. During this period, all participants can report anyone. If someone reports, the reported person will be marked as fl and sorted by order. For the same reported person, the reporter with the highest reputation value (or if the reputation values are the same, the one who reported earlier) will be marked as ld and proceed to Step 3. If no one reports, proceed to Step 4 directly.

Step 3: Performs automatic contract verification of the reported account in order of submission. If the verification result is 0, the reputation value of the reported account will be Rvfl−1, and the contribution value will be Cvld−1. At the same time, the reporter will be rewarded with a reputation value of Rvld+1 and a contribution value of Cvld+1. If the reporter ld has not uploaded yldr and πldr within T1, they can resubmit after the Step 3 contract automatic verification is completed and return to Step 2. If the verification result is 1, the reputation value of the reported account will remain unchanged, and the contribution value will be Cvfl+1. At the same time, the reporter will be penalized with a reputation value of Rvld−1 and a contribution value of Cvld−1.

Step 4: Within T3, the key escrow user calls the local resource to verify the remaining unreported participants one by one. If the participant i’s verification result is 0, the user will report feedback to the contract. After being verified by the contract, Cvi−1, mr−1. If the result is 1, it will continue to verify the participant i+1. Complete the verification of all participants and mr≥t, then proceed to Step 5.

Step 5: The key escrow user and participants use (h(Add1||r),Fsk1(r)),(h(Add2||r),Fsk2(r)),…,(h(Addmr||r),Fskmr(r)) and (d1,G(d1)),(d2,G(d2)),…,(dn+p−t,G(dn+p−t)) to reconstruct the following polynomial:

P(x)=∑u=1mrFsku(r)∏j=1,j≠umrx−h(Addj||r)h(Addu||r)−h(Addj||r)∏k=1n+p−mrx−dkh(Addu||r)−dk+∑i=1n+p−mrG(di)∏k=1,k≠in+p−mrx−dkdi−dk∏u=1mrx−h(Addu||r)di−h(Addu||r)modq=b0r+b1rx+b2rx2+⋯bn+p−1rxn+p−1,(7)

Then judge whether h(bkr)=h(akr∗)(k=0,1,…,n+p−1) is valid. If no one declares the reconstruction is correct (i.e., declares it to be invalid or remains silent), then proceed to Step 7. If at least the key escrow user declares the reconstruction is correct, proceed to Step 6.

Step 6: The contract automatically calculates and determines whether h(bkr)=h(akr∗)(k=0,1,…,n+p−1) is valid. If it is valid, the secrets si=P(i)⊕Vir∗(i=0,1,…,p−1) reconstruction are completed, the contract assigns each participant with the corresponding contribution value Ai=Cvi∑u=1nCvu⋅M1, and M2(r) is returned to the key escrow user, terminating the contract. If it is not valid, the invalid participants j will be executed Rvj+1 and proceed to Step 7.

Step 7: Check if M2(r) in the current contract is not less than the maximum cost L of the next round. If it is, proceed to Step 8; if not, notify the key escrow user to make up the payment (not less than L−M2(r)) within T5. If the payment is made promptly, proceed to Step 8. If not, the contract will be assigned to each participant with the corresponding contribution value Ai=Cvi∑u=1nCvu⋅M1, and M2(r) will be returned to the key escrow. The contract will be terminated.

Step 8: The contract executes r+1, and return to Step 1.

The process of the key reconstruction phase is shown in Fig. 3. The algorithm pseudocode mainly executed by the smart contract is shown in Fig. 4.

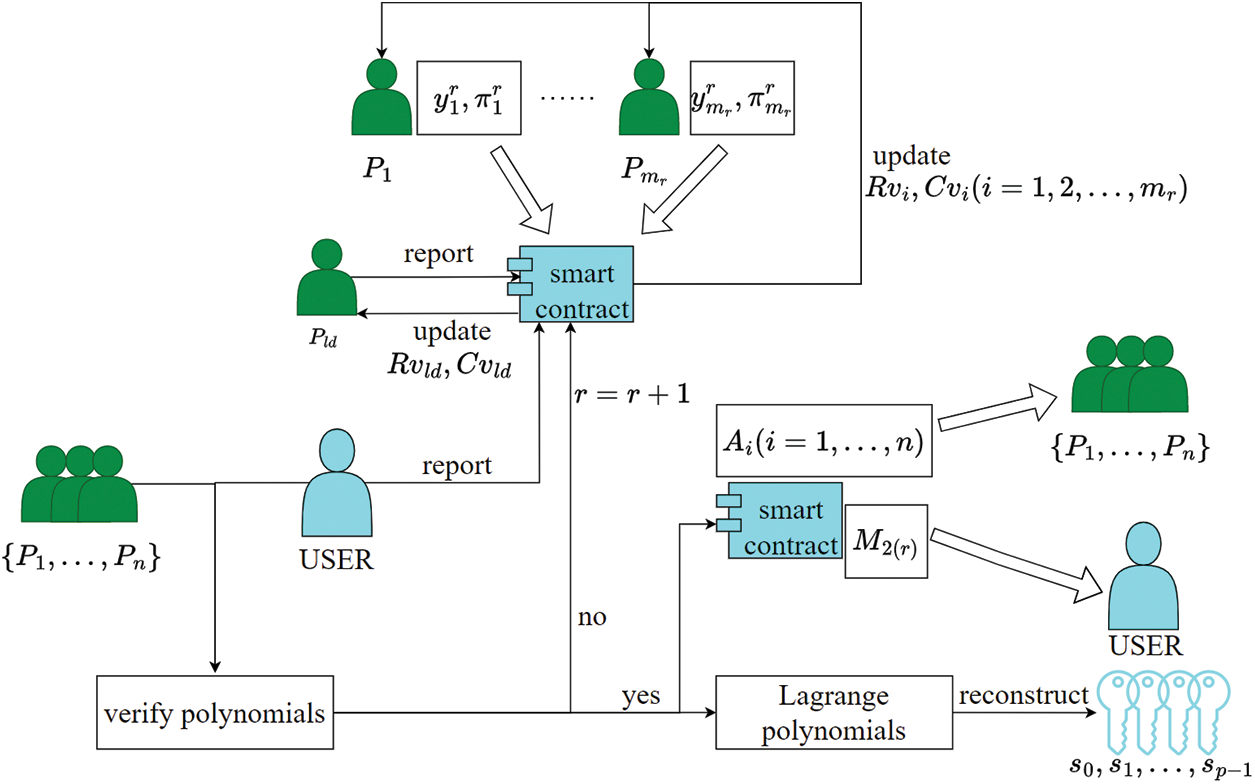
Figure 3: Key reconstruction process

Figure 4: Pseudocode for the main algorithms in the smart contract

5  Scheme Analysis

5.1 Correctness Analysis

Participants and smart contracts can verify the accuracy of the input yir=Fski(r)=e(g,g)1r+ski and πir=πski(x)=g1r+ski by checking whether e(gr⋅pki,πir)=e(g,g) and yir=e(g,πir) are both true.

Proof:

e(gr⋅pki,πir)=e(gr⋅gski,g1r+ski)=e(gr+ski,g1r+ski)=e(g,g)(r+ski)1r+ski=e(g,g)yir=e(g,g)1r+ski=e(g,g1r+ski)=e(g,πir)

5.2 Smart Contract Participant Utility Analysis

For Step 1, the contract setting does not allow participants to upload duplicate data to avoid “free-riding” behavior in a round of polynomial reconstruction, which would improperly increase the contribution value Cv and allow participants to obtain rewards that do not belong to them. Not allowing participants satisfied Rv<0 to upload data reflects punishment for malicious participants (those who often engage in dishonest behavior).

For Step 2 to Step 4, participants ld and participants fl can be viewed as the following extended game (a complete information dynamic game, which means participants know each other’s payoffs, the available actions, and the order in which moves are made):

Participant set N{ld,fl}, ld’s strategy space {‘‘report″,‘‘silence″}, fl’s strategy space {‘‘true″,‘‘false″}. The corresponding utility functions are:

{Uld(σld="report",σfl="false")={Cvld+1,Rvld+1}=aUld(σld="report",σfl="true")={Cvld−1,Rvld−1}=eUld(σld="silence",σfl="false")={Cvld,Rvld}=cUld(σld="silence",σfl="true")={Cvld,Rvld}=cUfl(σld="report",σfl="false")={Cvfl−1,Rvfl−1}=eUfl(σld="report",σfl="true")={Cvfl+1,Rvfl}=bUfl(σld="silence",σfl="false")={Cvfl−1,Rvfl}=dUfl(σld="silence",σfl="true")={Cvfl,Rvfl}=c

The game tree for two players is shown in Fig. 5 (a>b>c>d>e):

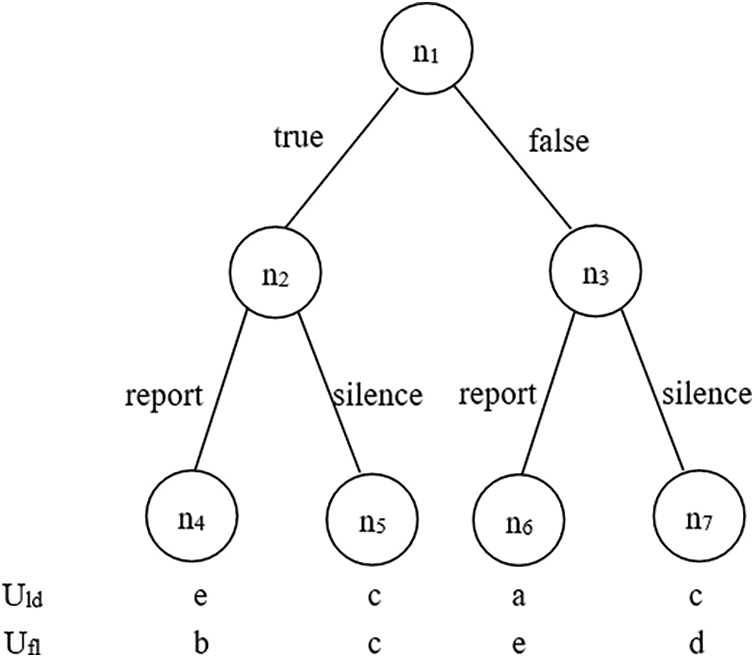
Figure 5: Participants’ game in key reconstruction phase

It is easy to find that the game has two optimal choices (true, silence) and (false, report) for participant ld. For the participant fl, is a strictly dominant strategy σfl="true", and from the perspective of individual rationality, the participant is more inclined to honestly upload their own data. When malicious participants upload false data, the contract can effectively use the reporting mechanism to punish malicious participants promptly. Ultimately, a unique pure strategy Nash equilibrium in the sequential game could be found: (σfl="true",σld="silence"), honestly uploading data in the data uploading stage and not making false reports in the verification stage.

For Step 5 to Step 8, there is actually no effective contribution value gain among participants, but only a reputation value reward is given to honest declaration behavior when the key escrow user declares deception to the contract. In principle, the key escrow user has no motivation to deceive, because the key escrow user needs to pay the contract verification overhead, and declaring success only increases the contract polynomial reconstruction overhead by 1 time when the polynomial is not reconstructed successfully. If the key escrow user does not declare reconstruction success in T4 when r=r∗, only the amount belonging to the user M2(r) will be consumed by the contract until it is not more than one round of the maximum contract overhead value L to stop.

For the entire key escrow protocol, the actual benefits for each participant are Ui=Ai=Cvi∑u=1nCvu⋅M1.

5.3 Analysis of Smart Contract Fairness

5.3.1 Fairness Analysis of Cooperative Game

In this key escrow contract scheme, the Shapley value of the participant i is Shvi=∑r=1r∗Cvir¯=∑r=1r∗(1⋅mrmr−1⋅mr−Cvirmr)mr∑r=1r∗mr=Cvi∑r=1r∗mr=Cvi∑u=1nCvu, which is proportional to its revenue Ai=Cvi∑u=1nCvu⋅M1, satisfying the fairness of the cooperative game.

5.3.2 Rational Fairness Analysis

In this scheme, everyone’s choice strategy σi∗^={"true",("false","report")}∈BRi(s−i) satisfies the requirement of rational fairness.

5.4 Mechanism Design Analysis

5.4.1 Fairness Analysis of Cooperative Game

In the key escrow contract scheme, ∀σi,∀σi′:Ui(σi=σi∗^,σ−i)≥Ui(σi′,σ−i), which means the scheme satisfies dominant-strategy incentive compatibility and also satisfies Bayesian incentive compatibility.

5.4.2 Personal Rational Analysis

In the key escrow contract scheme, it was found in the utility analysis in Section 5.2 that Ui=Ai=Cvi∑u=1nCvu⋅M1≥0=Ui{∅}, the condition for personal rationality in mechanism design is satisfied.

6  Security Analysis

6.1 Unforgeability of VRF

Proof: Assume there exists an algorithm A that can distinguish between a random element of G2 and y=FSK(x)=e(g,g)1x+SK with ε advantage (i.e., 12+ε probability of success). Then the advantage of the algorithm B constructed using this algorithm A to solve the DBDHI problem should be ε2 (i.e., 1+ε2 probability of successful solution). Given (g,gα,…,g(αq),Γ), B attempts to distinguish whether Γ is a random element of G2 or e(g,g)1α. If Γ is e(g,g)1α, output 0, otherwise output 1.

First, the challenger sets G1 and G2, determines the bilinear transformation e and generator g. Then, the challenger randomly selects ξ∈{0,1} without revealing it to B. If ξ=0, let Γ=e(g,g)1α; if ξ=1, then let Γ∈G2.

Initial phase: Simulate the algorithm B by running A, select a fake VRF value for some input x0, let χ=α−x0, define a function m(o)=∑j=0q−1cjoj, m′(o)=∑j=0q−2rjoj, calculate n=gm(χ), PK=nχ and SK=χ, and send the public key PK to the attacker A.

Phase 1: A ask for the VRF value of xi(xi≠x0), the oracle will return πSK(xi)=g1xi+χ and FSK(xi)=e(n,n)1xi+χ to A.

Challenge phase: A sends two equal-length values x0,x1 to B. B randomly select φ∈{0,1}, and generate πSK(xφ)=g1xφ+χ and FSK(xφ)=e(n,n)1xφ+χ.

Let Γ∗=Γ(r2)e(g,g)m(χ)2−r2α, if Γ=e(g,g)1α, then Γ∗=e(n,n)1α. B Send πφ,yφ,Γ∗ to A. When ξ=0, Γ and Γ∗ have the same distribution; when ξ=1, Γ and Γ∗ are both random numbers.

Phase 2: Repeat the process of Phase 1.

Guessing phase: A provides a guess value φ′. If φ′=φ, B outputs ξ′=0. If φ′≠φ, B outputs ξ′=1. When ξ=1, A obtains random number information with Pr[φ′≠φ|ξ=1]=12 and B outputs ξ′=1, Pr[ξ′=ξ|ξ=1]=12. When ξ=0, A obtains valid information with an advantage of ε, so Pr[φ′=φ|ξ=0]=12+ε, B outputs ξ′=0, Pr[ξ′=ξ|ξ=0]=12+ε. The probability of algorithm B cracking q-DBDHI is: Pr[ξ′=ξ]=Pr[ξ=0]Pr[ξ′=ξ|ξ=0]+Pr[ξ=1]Pr[ξ′=ξ|ξ=1]=1+ε2, i.e., the advantage of algorithm is ε2. However, there is currently no algorithm with an unignorable advantage in cracking q-DBDHI, so the advantage ε of the assumed algorithm A is negligible, i.e., the output value of VRF cannot be forged in the q-DBDHI problem. Therefore, using VRF for verification can detect the authenticity and correctness of the data to be verified.

6.2 Threshold Security: No More Than t−1 Participants Cannot Obtain Information about p Encrypted Keys

Public information (d1,G(d1)),…,(dn+p−t,G(dn+p−t)) consists of n+p−t numerical pairs, and no more than n+p−1 numerical pairs can be determined when no more than t−1 participants cooperate, making it impossible to determine a polynomial of n+p−1 degree as in Eq. (6) and obtain information about the corresponding p encrypted keys.

6.3 Resisting Collusion Attacks

Based on the threshold security analysis, any colluding party of the colluding group T⊂[n],|T|≤t−1 cannot determine whether the current round is the r∗ round through collusion. If the colluding party wants to obtain the encrypted keys information at this time, they can only guess, with βT the probability of guessing correctly, corresponding to the benefit Ui−; and 1−βT the probability of guessing incorrectly, corresponding to the benefit Ui+; the expected benefit of colluding party Pi for guessing is E(UiTguess)=βTUi++(1−βT)Ui−. Suppose the probability of attacking exactly at round r∗ is λT, and the benefit of attacking exactly at round r∗ is still Ui+, otherwise the benefit of colluding party Pi is E(UiTguess). Therefore, the expected benefit of colluding party Pi is E(UiT)=λTUi++(1−λT)E(UiTguess). If colluding members follow the protocol, the benefit of Pi at this time is Ui, so when Ui>E(UiT) (i.e., Ui>λTUi++(1−λT)E(UiTguess)), colluding members have no motivation to deviate from the protocol.

For this private key management protocol, the probability of guessing the plaintext of the private key of the blockchain private wallet is negligible, i.e., E(UiTguess) can be approximated to 0. This protocol only needs to ensure Ui>λTUi+. In the protocol, Ui=Ai=Cvi∑u=1nCvu⋅M1≥M1n, if the key escrow user is willing to pay no more than R to the colluding organization through signing a new smart contract for key shares trading when threatened by a collusion attack, then Ui+=R|T|<Rt. Therefore, λT<tM1nR, in the corresponding protocol, λ≤λT can meet the requirement of resisting collusion attacks.

7  Performance Analysis

7.1 Communication Cost

During key escrow agreement, the user uploads all public key data (512n bits), hash values of polynomial coefficients (256(n+p) bits), the XOR values of all keys (256p bits), and coordinates of n+p−t two-dimensional points (512(n+p−t) bits) to the blockchain. The total bits are 1280n+1024p−512t. For each round, each participant only needs to upload the encrypted information yir=Fski(r)=e(g,g)1r+ski and verification information πir=πski(x)=g1r+ski, which are 256 bits and 320 bits. Therefore, the communication overhead of each round of communication between participants and the smart contract is 576 bits. As a result, the total communication cost of our proposed scheme is 576∑1r∗mr+1280n+1024p−512t bits.

7.2 User Communication Overhead

As shown in Table 3, during the key distribution phase, whether it is Ogata’s scheme [30], Ra’s scheme [31], or the proposed scheme in this paper, it is necessary to transmit the corresponding key shares to n server/participant nodes through secure channels. When the server/participant nodes are honest, Ogata’s scheme [30] only needs to communicate and interact during the reconstruction phase without the verification stage of server information. Ra’s scheme [31] needs to communicate with each server through an interactive verification method and determine whether the corresponding node is malicious. When there are e malicious nodes among the server/participant nodes, the former cannot correctly reconstruct the corresponding escrow key, while the latter needs to communicate with these e malicious nodes for an additional round during the verification stage. For the proposed scheme in this paper, whether there are malicious nodes or not, in each round of key escrow user node verification, it only needs to obtain the verification information uploaded by each participant from the chain, that is, the communication overhead per round of verification is O(1), and the communication overhead of r∗ rounds of verification is O(r∗)=O(1λ). After r∗ rounds of iteration, the user reconstructs successfully locally and communicates with the smart contract deployed on the blockchain once, that is, the communication overhead of the reconstruction phase is O(1). However, for the proposed scheme, the overall communication complexity is O(n2) due to the participants broadcasting communication interactions during the reconstruction phase.

7.3 Feature Comparison

As shown in Table 4, the current password-protected secret sharing (PPSS)-based key recovery management schemes for blockchain can meet the key recovery needs of blockchain with semi-honest nodes, such as the consortium blockchain [30,31]. However, these schemes require interactive verification between users and servers and often require synchronous communication. At the same time, they do not consider the rational self-interested behavior of blockchain, and cannot realize key recovery in more blockchain application scenarios such as the public blockchain. Our scheme uses rational secret sharing and the non-interactive verification method Elliptic Curve VRF (ECVRF) to meet all the requirements in the table, thus realizing the key recovery needs of blockchain users in the asynchronous communication environment of the public blockchain.

7.4 Computational Efficiency Analysis

Based on the calculation efficiency analysis in Ra et al. [31] and the key distribution and reconstruction process proposed in the proposed scheme, we compare the computational complexity of Ogata’s scheme [30], Ra’s scheme [31], and the proposed scheme, as shown in Table 5.

The computational complexity of Shamir’s secret sharing is denoted as S, the time complexity of generating random numbers is denoted as k, the time complexity of performing one ECVRF execution is denoted as T, and the number of executions of the proposed scheme during secret reconstruction is denoted as r∗.

Typically, from the perspective of Byzantine fault tolerance, t∈(23n,n], E(r∗)=1λ≥1λT>nRtM1>nR23nM1=3R2M1. We consider the cost of the managed key service as M1, and the cost of the premium managed key service as R, and from a practical point of view, it should satisfy M1<R≤2M1, so E(r∗)=3 is more reasonable. The computational complexity of Shamir’s secret sharing is within 0.218 s [32], let r∗=3, and the following is the computational time overhead diagram:

As shown in Fig. 6, in the key distribution process, when the user only hosts one key, the computational time overhead of the proposed scheme is higher than Ogata’s scheme [30] and Ra’s scheme [31]. When the user hosts two keys at once, only in the case of n=2, the computational time overhead of the proposed scheme is the same as Ogata’s scheme [30], and in other cases, it is lower than Ogata’s scheme [30] and Ra’s scheme [31]. When the user hosts three keys at once, the computational time overhead of the proposed scheme is lower than Ogata’s scheme [30] and Ra’s scheme [31].

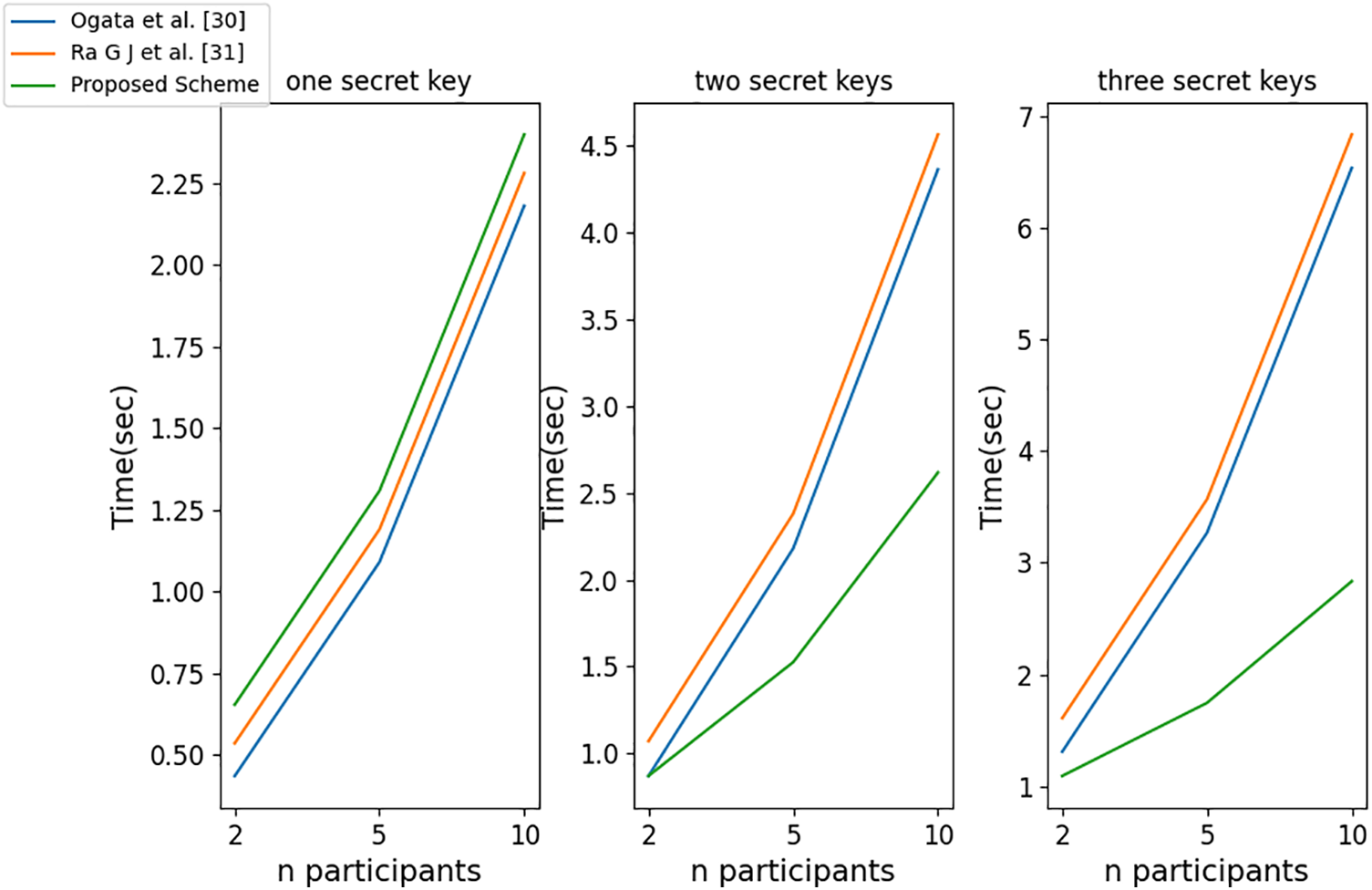
Figure 6: Computational efficiency comparison during distribution

As shown in Fig. 7, when the user only hosts one key in the key recovery process, the computational time overhead of the proposed scheme is higher than Ogata’s scheme [30] and Ra’s scheme [31]. When the user hosts five keys at once, in the case of n≥10, the computational time overhead of the proposed scheme is lower than Ogata’s scheme [30] and Ra’s scheme [31]. When the user hosts seven keys at once, in the case of n≥5, the computational time overhead of the proposed scheme is lower than Ogata’s scheme [30] and Ra’s scheme [31].

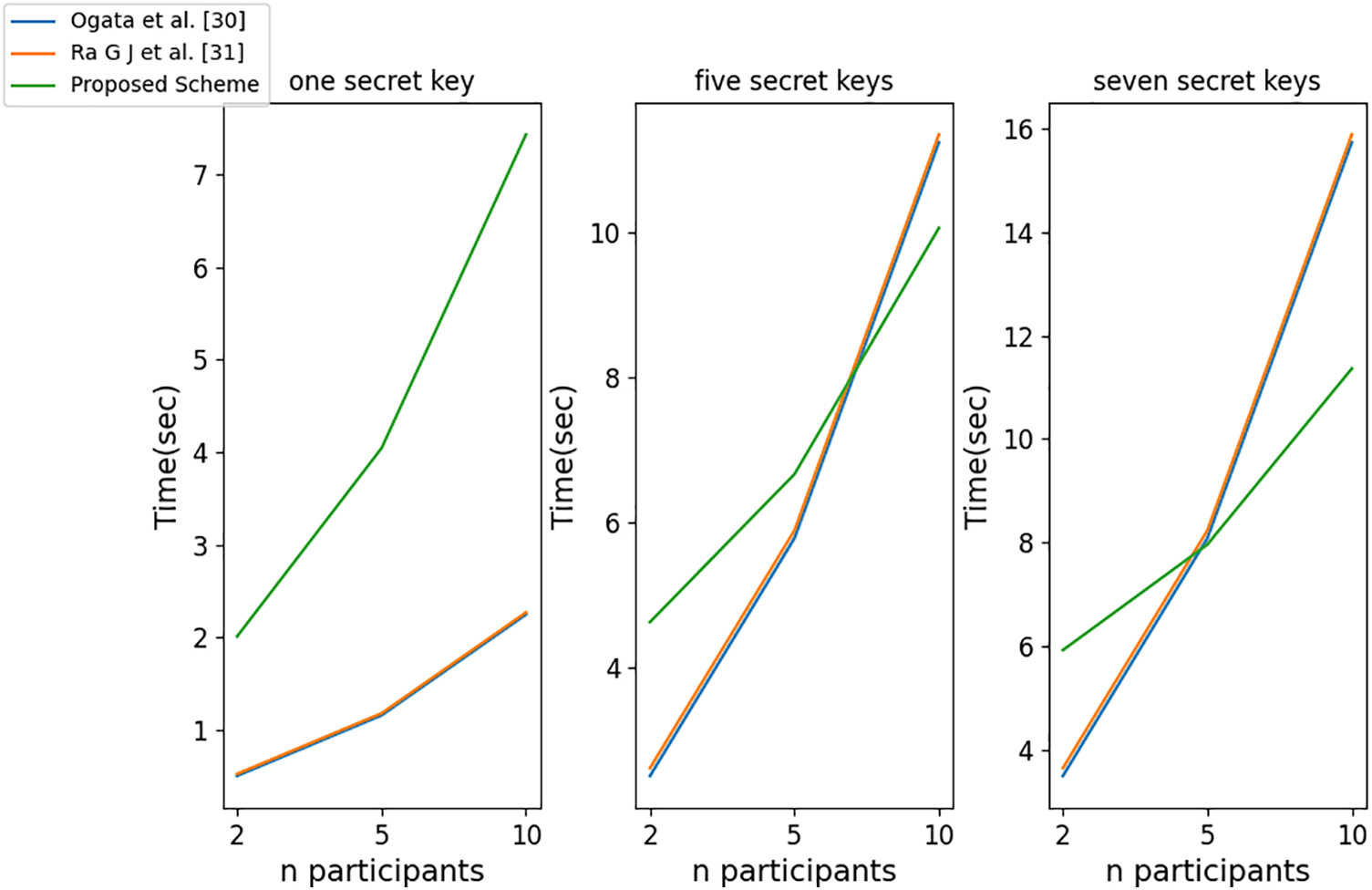
Figure 7: Computational efficiency comparison during recovery

We conducted computational cost simulations on a personal computer with a 12th Gen Intel (R) Core (TM) i7-12700H 2.70 GHz CPU and 16.0 GB RAM, using JavaScript language. The number of participants in the proposed scheme is set to be n=1000 and the number p of private keys that need to be escrowed is denoted as p=5. The computational cost for the negotiation and key sharing stage was 403881 ms, and the computational cost for the key reconstruction stage was 1248453 ms.

7.5 Ether Consumption

Table 6 shows the functions and corresponding Ether costs involved in the smart contract during the refactoring phase of the proposed scheme. However, according to the utility analysis in Section 5.2, participants will comply with the protocol and upload real data without false reporting. In principle, the contract will only execute a polynomial refactoring and hash value verification once, and will not execute the relevant functions of ECVRF (i.e., serial 2 and 3).

8  Conclusion

We proposed a blockchain private key management scheme based on rational secret sharing, which can achieve one-time escrow and recovery of multiple wallet private keys for blockchain private user. This scheme can be applied to the secure backup scenario of digital assets such as blockchain user wallets and encrypted data. The proposed scheme takes into account the self-interested behavior of participants and satisfies individual rational constraints and incentive compatibility. It promotes the cooperation and behavioral norms of blockchain users by designing a reputation mechanism and a revenue distribution mechanism based on contribution value proportion. In addition, the scheme also designed the whole process of multi-key escrow and reconstruction based on verifiable random functions and demonstrated the collusion resistance, security verification ability, communication overhead, computational overhead, incentive compatibility and individual rational constraints through participants’ utility function analysis. Finally, the scheme was simulated on Ethereum smart contracts to prove its feasibility on the public blockchain.

In the future work, in order to make the proposed scheme a long-term blockchain key management protocol, we will consider the evolutionary game of blockchain users, adjust the reputation incentive design in this scheme and improve the efficiency of blockchain private key escrow and recovery. In addition, we will consider extending the management of the blockchain user’s private key from the wallet to more application scenarios of blockchain key management.

Acknowledgement: I would like to express my deepest gratitude to all those who have supported and guided me throughout the course of this research.

Funding Statement: This work was supported in part by the State’s Key Project of Research and Development Plan under Grant 2022YFB2701400, in part by the National Natural Science Foundation of China under Grants 62272124 and 62361010, in part by the Science and Technology Planning Project of Guizhou Province under Grant [2020]5017, in part by the Research Project of Guizhou University for Talent Introduction under Grant [2020]61, in part by the Cultivation Project of Guizhou University under Grant [2019]56, in part by the Open Fund of Key Laboratory of Advanced Manufacturing Technology, Ministry of Education under Grant GZUAMT2021KF[01], the Science and Technology Program of Guizhou Province (No. [2023]371).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xingfan Zhao and Changgen Peng; supervision: Changgen Peng; data collection: Kun Niu; analysis and interpretation of results: Weijie Tan; draft manuscript preparation: Xingfan Zhao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: There is no available data and materials.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. E. Denning and D. K. Branstad, “A taxonomy for key escrow encryption systems,” Commun. ACM, vol. 39, no. 3, pp. 34–40, 1996. doi: 10.1145/227234.227239. [Google Scholar] [CrossRef]

2. H. Abelson et al., “The risks of key recovery, key escrow, and trusted third-party encryption,” World Wide Web J., vol. 2, no. 3, pp. 241–257, 1997. [Google Scholar]

3. C. Boyd, X. Boyen, C. Carr, and T. Haines, “Key recovery: Inert and public,” in Paradigms in Cryptology—Mycrypt 2016. Malicious and Exploratory Cryptology. Cham: Springer International Publishing, 2017, pp. 111–126. [Google Scholar]

4. M. Bellare and S. Goldwasser, “Verifiable partial key escrow,” in Proc. 4th ACM Conf. Comput. Commun. Secur., 1997, pp. 78–91. [Google Scholar]

5. A. Shamir, “Partial key escrow: A new approach to software key escrow,” in Key Escrow Conf., 1995. [Google Scholar]

6. A. K. Lenstra, P. Winkler, and Y. Yacobi, “A key escrow system with warrant bounds,” in Annual Int. Cryptol. Conf., Berlin, Heidelberg: Springer Berlin Heidelberg, 1995, pp. 197–207. [Google Scholar]

7. S. Micali and R. Sidney, “A simple method for generating and sharing pseudo-random functions, with applications to clipper-like key escrow systems,” in Annual Int. Cryptol. Conf., Berlin, Heidelberg: Springer Berlin Heidelberg, 1995, pp. 185–196. [Google Scholar]

8. A. Shamir, “How to share a secret,” Commun. ACM, vol. 22, no. 11, pp. 612–613, 1979. doi: 10.1145/359168.359176. [Google Scholar] [CrossRef]

9. G. R. Blakley, “Safeguarding cryptographic keys,” in Managing Requirements Knowl., Int. Workshop on, IEEE Comput. Soc., 1979, pp. 313. [Google Scholar]

10. B. Chor, S. Goldwasser, S. Micali, and B. Awerbuch, “Verifiable secret sharing and achieving simultaneity in the presence of faults,” in 26th Annual Symp. Foundations of Comput. Sci., Portland, OR, USA, 1985, pp. 383–395. [Google Scholar]

11. C. M. Bai, S. Zhang, and L. Liu, “Verifiable quantum secret sharing scheme using d-dimensional GHZ state,” Int. J. Theor. Phys., vol. 60, no. 10, pp. 3993–4005, 2021. doi: 10.1007/s10773-021-04955-1. [Google Scholar] [CrossRef]

12. C. Gentry, S. Halevi, and V. Lyubashevsky, “Practical non-interactive publicly verifiable secret sharing with thousands of parties,” in Annual Int. Conf. Theory Appl. Cryptographic Tech., 2022, pp. 458–487. [Google Scholar]

13. J. Halpern and V. Teague, “Rational secret sharing and multiparty computation,” in Proc. Thirty-Sixth Annual ACM Symp. Theory Comput., 2004, pp. 623–632. [Google Scholar]

14. G. Kol and M. Naor, “Cryptography and game theory: Designing protocols for exchanging information,” in Theory Cryptography Conf., Berlin, Heidelberg: Springer, 2008, pp. 320–339. [Google Scholar]

15. X. Zhang, L. Wang, S. Lin, N. Wang, and L. Hong, “Rational quantum secret sharing scheme based on GHZ state,” Quantum Inf. Process., vol. 22, no. 2, pp. 91, 2023. doi: 10.1007/s11128-022-03739-8. [Google Scholar] [CrossRef]

16. D. Joy, M. Sabir, B. K. Behera, and P. K. Panigrahi, “Implementation of quantum secret sharing and quantum binary voting protocol in the IBM quantum computer,” Quantum Inf. Process., vol. 19, no. 1, pp. 1–20, 2020. doi: 10.1007/s11128-019-2531-z. [Google Scholar] [CrossRef]

17. K. Christidis and M. Devetsikiotis, “Blockchains and smart contracts for the internet of things,” IEEE Access., vol. 4, pp. 2292–2303, 2016. doi: 10.1109/ACCESS.2016.2566339. [Google Scholar] [CrossRef]

18. G. Li, L. You, G. Hu, and L. Hu, “Recoverable private key scheme for consortium blockchain based on verifiable secret sharing,” KSII. Trans. Internet Inf. Syst. (TIIS), vol. 15, no. 8, pp. 2865–2878, 2021. [Google Scholar]

19. Z. Chen, Y. Tian, and C. Peng, “An incentive-compatible rational secret sharing scheme using blockchain and smart contract,” Sci. China Inf. Sci., vol. 64, no. 10, pp. 1–21, 2021. doi: 10.1007/s11432-019-2858-8. [Google Scholar] [CrossRef]

20. S. Nakamoto, “Bitcoin: A peer-to-peer electronic cash system,” White Paper, 2008. Accessed: Sep. 17, 2019. [Online]. Available: https://bitcoin.org/bitcoin.pdf [Google Scholar]

21. N. Szabo, “Smart contracts,” 1994. Accessed: Dec. 20, 2018. [Online]. Available: https://www.fon.hum.uva.nl/rob/Courses/InformationInSpeech/CDROM/Literature/LOTwinterschool2006/szabo.best.vwh.net/smart.contracts.html [Google Scholar]

22. P. V. R. P. Raj, S. K. Jauhar, M. Ramkumar, and S. Pratap, “Procurement, traceability and advance cash credit payment transactions in supply chain using blockchain smart contracts,” Comput. Ind. Eng., vol. 167, no. 8, pp. 108038, 2022. doi: 10.1016/j.cie.2022.108038. [Google Scholar] [CrossRef]

23. A. R. Thota, P. Upadhyay, S. Kulkarni, P. Selvam, and B. Viswanathan, “Software wallet based secure participation in Hyperledger Fabric networks,” in 2020 Int. Conf. Commun. Syst. Netw. (COMSNETS), 2020, pp. 1–6. [Google Scholar]

24. D. Park, M. Choi, G. Kim, D. Bae, H. Kim and S. Hong, “Stealing keys from hardware wallets: A single trace side-channel attack on elliptic curve scalar multiplication without profiling,” IEEE Access, vol. 11, pp. 44578–44589, 2023. [Google Scholar]

25. K. Chalkias, P. Chatzigiannis, and Y. Ji, “Broken proofs of solvency in blockchain custodial wallets and exchanges,” in Lecture Notes in Computer Science, Cham: Springer, vol. 13412, 2023. [Google Scholar]

26. R. Gennaro, S. Goldfeder, and A. Narayanan, “Threshold-optimal DSA/ECDSA signatures and an application to bitcoin wallet security,” in Appl. Cryptography Netw. Secur.: 14th Int. Conf.,Guildford, UK, Springer International Publishing, Jun. 2016, pp. 156–174. [Google Scholar]

27. E. Zhang, Q. Sun, and Y. Liu, “Collusion-free rational multi-secret sharing scheme,” Comput. Sci., vol. 42, no. 10, pp. 164–169, 2015. [Google Scholar]

28. S. Micali, M. Rabin, and S. Vadhan, “Verifiable random functions,” in 40th Annual Symp. Foundations Comput. Sci. (Cat. No. 99CB37039), New York, NY, USA, 1999, pp. 120–130. [Google Scholar]

29. Y. Dodis and A. Yampolskiy, “A verifiable random function with short proofs and keys,” in Int. Workshop Public Key Cryptography, Berlin, Heidelberg: Springer Berlin Heidelberg, 2005, pp. 416–431. [Google Scholar]

30. W. Ogata, “Improvement of IT-secure password-protected secret sharing,” in 30th Symp. Cryptography Inf. Secur. (SCIS 2013), 2013. [Google Scholar]

31. G. J. Ra, C. H. Roh, and I. Y. Lee, “A key recovery system based on password-protected secret sharing in a permissioned blockchain,” Comput.Mater. Conti., vol. 65, no. 1, pp. 153–170, 2020. doi: 10.32604/cmc.2020.011293. [Google Scholar] [CrossRef]

32. S. Sugianto, S. Suharjito, and N. Surantha, “Comparison of secret splitting, secret sharing and recursive threshold visual cryptography for security of handwritten images,” TELKOMNIKA. (Telecommun. Comput. Electron. Cont.), vol. 16, no. 1, pp. 323–333, 2018. doi: 10.12928/telkomnika.v16i1.6632. [Google Scholar] [CrossRef]