A Novel Insertion Solution for the Travelling Salesman Problem

1  Introduction

Various methods exist to solve the Travelling Salesman Problem (TSP), including exact solutions and heuristics [1]. Finding the shortest tour involves determining the optimal route through a set of cities, ensuring each city is visited exactly once before returning to the starting point [1–4]. This completed tour is known as the Hamiltonian Cycle. It is assumed that the cost of the distance between any pair of cities is predefined. The cost often relates to distance but may represent other notions, such as time or money. A Hamiltonian cycle, as depicted in Fig. 1, refers to a graph cycle that traverses all the graph’s vertices exactly once before returning to its starting vertex. The Travelling Salesman must traverse cities 1 to n in a Hamiltonian cycle, that is, start from city 1, traverse the remaining n−1 cities in a specified order and then connect back to the starting city, having touched each of the cities only once at a minimal cost.

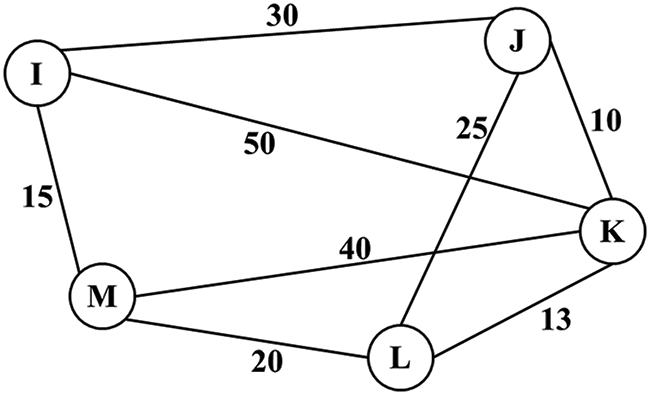
Figure 1: A Hamiltonian weighted graph

The TSP is simple to define, but the complexity can easily expand exponentially as the solution space increases; thus, it is classified as an NP-Hard problem [1].

Exact techniques involve the explicit enumeration of the solution space; they try out all possible permutations of the solution. Thus, they have a complexity of O(n!) [2–5]. Exact techniques such as Dijkstra or Bellman-Ford algorithms may be deployed to effectively solve TSPs with a small degree of search space [6]; others include Branch-and-Bound, Dynamic Programming Algorithms, Cutting Plane techniques and so on. Exact algorithms guarantee optimal solutions, at least hypothetically. However, the computational complexities of exact techniques are exponential [7]; thus, the time required to provide their solutions grows exponentially with its solution space [6–10]. Consequently, exact solutions are often impracticable and especially unsuitable for NP-hard problems with large solution space. For instance, the solution renowned as the best-performing exact technique is based on dynamic programming with a complexity of O(2nn2), thus making TSPs impracticable to solve with the exact approach as the search space expands [11]. These limitations of the precise method have driven the design, development, and deployment of heuristics.

Unlike precise methods [12–15], heuristics offer rough solutions while operating within a polynomial time limit. These methods are known for their reliance on probabilities and specific rules to solve problems [16–18]. For an iterative procedure, heuristics can be used when an optimal solution is guaranteed to obtain the solution quickly or make a decision within an exact process. In other words, using heuristics to solve the TSP and problems related to the TSP provides acceptable results that are not too far from the optimal yet computationally affordable.

There are different classifications of heuristics based on the atomicity of their solution procedures, such as Tour Construction, Improvement/Local Search Heuristics, and Compound Heuristics [19–21]. The Tour Construction heuristics are techniques that independently create solutions sequentially following predefined procedures within the problem space. These procedures outline the steps in the Initialization, Selection, and insertion stages. The focus of this study is on construction heuristics. Construction techniques generate reasonable approximate solutions for TSP and are equally central to the performance of the other classes of heuristics, such as improvement techniques, compound heuristics, and metaheuristics. Construction heuristics serve as a seed for the development of some heuristics and can be used to build initial solutions for high-performing techniques [22–25]. Construction heuristics generally generate better initial solutions in high-performing improvement methods/metaheuristics than random initial solutions, thereby enhancing the quality of solutions [26–29].

2  Related Works

Construction heuristic techniques have been widely utilized in addressing traditional combinatorial optimization challenges. Various methods, such as the Nearest Neighbour Heuristic (NNH), Nearest Insertion (NIH), Cheapest Insertion, Random Insertion, Addition heuristics, Savings Heuristics, and more are commonly used. Existing tour construction methods typically fall short by between 10–30% in terms of solution quality with a worst-case complexity of T(n)=O(n2). The Nearest Neighbour Heuristic, for instance, is fast, flexible, and simple to implement; it, however, solves the Travelling Salesman Problem using a greedy approach and suffers immensely from the “curse of dimensionality” phenomenon [30]. The Farthest Insertion, on the other hand, renowned as the best-performing lower-order complexity heuristic [31], suffers from a high upper bound of error with farther distance [32]. According to Huang et al. [32], the probability of attaining an optimal tour is higher if the distance can be reduced.

Some well-known constructive heuristic methods are described briefly in Table 1.

Recent research has highlighted the importance of using the Nearest Neighbor Heuristic in ways such as integrating it into methods [21–23] or utilizing it as an initial step in metaheuristics to create starting solutions [7,38]. While the Nearest Neighbor Heuristic is valued for its speed and simplicity, its strategy of selecting nodes with the lowest cost can lead to what is known as the “curse of dimensionality.” This means that outliers become apparent as the search space and nodes grow. The term “curse of dimensionality” is commonly used to explain how increasing dimensions result in a search space, causing data sparsity and outlier occurrences. Fischer et al. [39] described the Quadratic Traveling Salesman Problem (QTSP) as an expansion of the Traveling Salesman Problem (TSP). To solve the QTSP, they utilized a total of nine algorithms: Three exact algorithms (a polynomial transformation-based exact approach to a TSP, branch-and-bound algorithm, and branch-and-cut algorithm), seven approximate algorithms (Cheapest-Insertion Heuristic (CI), Nearest-Neighbour Heuristic (NN), Two-Directional Nearest-Neighbor Heuristic (2NN), Assignment-Patching Heuristic (AP), Nearest-Neighbour-Patching Heuristic (NNP), Two-Directional Nearest-Neighbour-Patching Heuristic (2NNP), and Greedy Heuristic (GR), and Nearest-Neighbour Heuristic (2NN) were utilized. Within around ten minutes, the branch-and-cut approach could tackle complicated real-world problems with as many as one hundred nodes in an efficient manner, successfully reaching optimality. Heuristics could handle the most complex cases in ten seconds or less, which was far faster than the running times of exact algorithms, which were acceptable. In terms of processing speed, the various iterations of the Nearest Neighbour algorithm worked well; nevertheless, when it came to the correctness of their solutions, they were not as good as the exact applications.

Lity et al. [22] modelled the product ordering process of the incremental Software Product Line (SPL) analysis as a Travelling Salesman Problem (TSP). The aim was to optimize product orders and improve the overall SPL analysis. Products were modelled as nodes in a graph, and the solution-space information defined edge weights between product nodes. Existing graph route-finding heuristics were used to obtain the path with minimal costs. The first heuristic deployed was the Nearest Neighbour heuristic. The nodes were analyzed according to their similarity, so the NNH path was built by adding the product (node) most similar to the last node. However, it was observed that the approximation quality was poor because it first greedily added all the similar nodes and later suffered the curse of dimensionality when not-so-similar nodes were to be added. To circumvent this, a lookup was introduced to examine the next node to be added to the computed path. Thereafter, two insertion heuristics, namely Nearest Insertion and Farthest Insertion, were deployed to insert the remaining product into the existing path created by the Nearest Neighbour Heuristic. The proposed method was simulated on a prototype and evaluated for applicability and performance; a significantly more optimized SPL process was reported.

In implementing the Iterated Local Search technique, Bernardino et al. [40] used a modified version of the Nearest Neighbor heuristic to obtain an initial answer. The Family Travelling Salesman Problem (FTSP), a famous version of the Travelling Salesman Problem (TSP), was the focus of their research efforts. The first thing they did was model the FTSP, aiming to traverse a certain number of nodes in each cluster to the lowest possible cost. After that, the FTSP sub tour was designed in both a non-compact form. Three compact models were created: The Single Commodity Flow model (SCF), the Family Commodity Flow model (FCF), and the Node Commodity Flow model (NCF), for the compact variations options such as the Connectivity Cuts (CC) model, Rounded Visits (RV) model and Rounded Family Visits (RFV) model were considered. These models were compared using experiments carried out in the C++ programming language. Implementing Iterative Local Search (ILS) in C++ aimed to establish limits for situations beyond what direct methods could handle. During the first phase of constructing the ILS, an initial solution was constructed using a modified version of the Nearest Neighbor heuristic. Subsequently, a local search was run to arrive at a local optimum. As a further step, they used a perturbation to break out of the local optimum, and finally, they applied removal criteria to harvest the accumulated excess nodes. A well-known research hypothesis that construction tour heuristics create excellent first solutions was verified by the International Land Survey (ILS) performance. Experiments were carried out on benchmark instances that were accessible to the general public, and the results of the experiments were recorded. Results showed that non-compact models did better than their counterpart compact ones.

In the study by Kitjacharoenchaia [41], the Nearest Neighbour and two other heuristics were used to build an initial solution for their proposed model. Motivated by the increasing adoption of drones to achieve fast and flexible delivery, they conducted a study to simulate a drone delivery system formulated as a multiple Travelling Salesman Problem (mTSP) to minimize time. They implemented Mixed Integer Programming (MIP) to solve the problem and proposed a new technique called the Adaptive Insertion Algorithm (ADI). The ADI was implemented in two phases. An initial solution on only truck tours was built using three heuristics (namely the Nearest Neighbour Heuristic, Genetic Algorithm, and Random Cluster/tour). The mTSP solution was generated from the initial tour in the second phase. The method was then experimented on a single truck, multiple trucks, and a single truck and drone system, and the solution was compared with the existing MIP solution. The system reported a promising, competitive performance. It could be deduced that solutions generated from the initial solution by heuristics, such as Nearest Neighbour, hold promising performances.

Víctor et al. [42] solved the Euclidean TSPs of small and large data sizes with an efficient heuristic that is based on the Girding Polygon, which does not take up much computer memory space and produces approximate results that are near-optimal. The computational performance of the proposed approximate heuristic was compared to that of NNH, which is another approximate heuristic. It was noticed that the proposed heuristic outperformed NNH with an average error of 16.89% while that of NN was 26.55%; it also had standard deviations of 0.05%, and NNH had 0.04%. Even though the proposed algorithm did not produce optimal solutions for the instances used, it gave an approximate solution significantly better than NNH’s.

Insertion heuristics starts from an arbitrary point to form a sub-tour or partial circuit. Nodes not already in the sub-tour are then inserted based on predefined criteria such that the increment to the total distance of the sub-tour is minimized [23,32]. Suppose that node x is to be added to the edge (xi,xj), and given the cost function c(xi,xj,x), then, c(xi,xj,x)=d(x,xi)+d(x,xj)−d(xi,xj). Each insertion technique method aims to add a node to an edge (that is, between two nodes) at a minimal cost. Given the sub-tour Ti, and given that x is the next node to be inserted, the insertion technique inserts x between xi∗ and xj∗ in Ti. Accordingly:

(xi∗,xj∗)=argmin(xixj)∈Ti c(xi,xj,x)(1)

Insertion techniques are desirable because of their speed, ease of implementation, quality of solutions, and the fact that they can be easily modified to handle complex constraints [43]. There are four generally known insertion techniques: Nearest Insertion, Cheapest Insertion, Random Insertion, and Farthest Insertion. Others include Priciest Insertion, quick insertion, and greatest angle insertion [36–44].

Insertion techniques can be used to get a good tour construction solution [45–47]; according to Rosenkrantz et al. [33], insertion techniques find O(logn)approximate solutions. Insertion techniques are also used as an initial solution for improvement heuristics and metaheuristics; insertion techniques have been proven to significantly improve the performance of 2-Opt methods when used as initial solutions [46]. Other researchers have presented new insertion techniques, either as a modification of state-of-the-art methods or as novel efforts.

Experimentally, the Farthest Insertion Heuristic has been known to outperform the Random Insertion, the Cheapest Insertion, and the Nearest Insertion in that order [33–47].

3  The Proposed HMIH Technique

The proposed technique is an insertion method referred to in this study as the Half Max Insertion Heuristic (HMIH). The motivation was to explore some strategies with the possibility of improved tour accuracy. The design of the HMIH was motivated by two observations in literature: One, the superior solution quality of insertion techniques based on the use of polygons as an initial tour [23–42] and secondly, the limitation of the FIH’s accuracy due to the distance between its initial circuits and the next node to be inserted. Huang et al. [32] argued that although FIH performs relatively well, the distance between its circuit and new nodes to be inserted impedes its accuracy.

Suppose that a new node x is to be inserted into a partial tour p_tour, the closer x is to the edge (xi,xj), the lesser the likelihood of it introducing error. Suppose that nodes x1 and x2 are to be inserted into the same edge (xi,xj) of the partial tour p_tour to produce partial tours p_tour1 and p_tour2, respectively. Suppose that cost function c(xi,xj,x1)<c(xi,xj,x2) and d(ptour1)≤d(ptour2), then the upper bounds of the error rate for the two tours are d(ptour1)d(ptour)=d(ptour)+c(xi,xj,x1)d(ptour) and d(ptour2)d(ptour)=d(ptour)+c(xi,xj,x2)d(ptour) such that d(ptour1)d(ptour)<d(ptour2)d(ptour). Thus, the performance of FIH still leaves much to be desired. If inserting the nearest nodes to the circuit leads to outliers and the performance of FIH is impeded by a longer distance, perhaps a half-max insertion routine may yield a better solution.

The insertion heuristics randomly pick one node from Q by init(Q) and create a partial circuit which is expanded with every iteration. The partial circuit is made up of a minimum polygon point u,v,w.

Let Ti represent the partial circuit across nodes of size i defined as Ti=(π1,π2,…,πi,π1). During the (i+1)th iteration, the insertion aims to add one node into the current circuit while minimizing the increment in the overall circuit distance. The objective is to determine how to select a node, x, from Q∖Ti and determine how to insert x into Ti to obtain Ti+1.

Consider an insertion of a node x(∉Ti) between u,v and w in Ti:

The method first determines the longest distance. dmax of any node from either of uorv and compute 12dmax. It then find a node w not in the sub tour whose distance from either u or v≈12dmax. Determine an edge (u,v) of the sub-tour to which the insertion of w gives the smallest increase of length, i.e., for which Δf=cux+cxv+cwx−cuvw is smallest. Insert x between u,v and w. This process is iterated until a Hamiltonian cycle is formed.

The procedure is as follows:

The HMIH searches require O(n) time; therefore, the time complexity of the algorithm is O(n2). The procedure is further depicted in the following flowchart in Fig. 2.

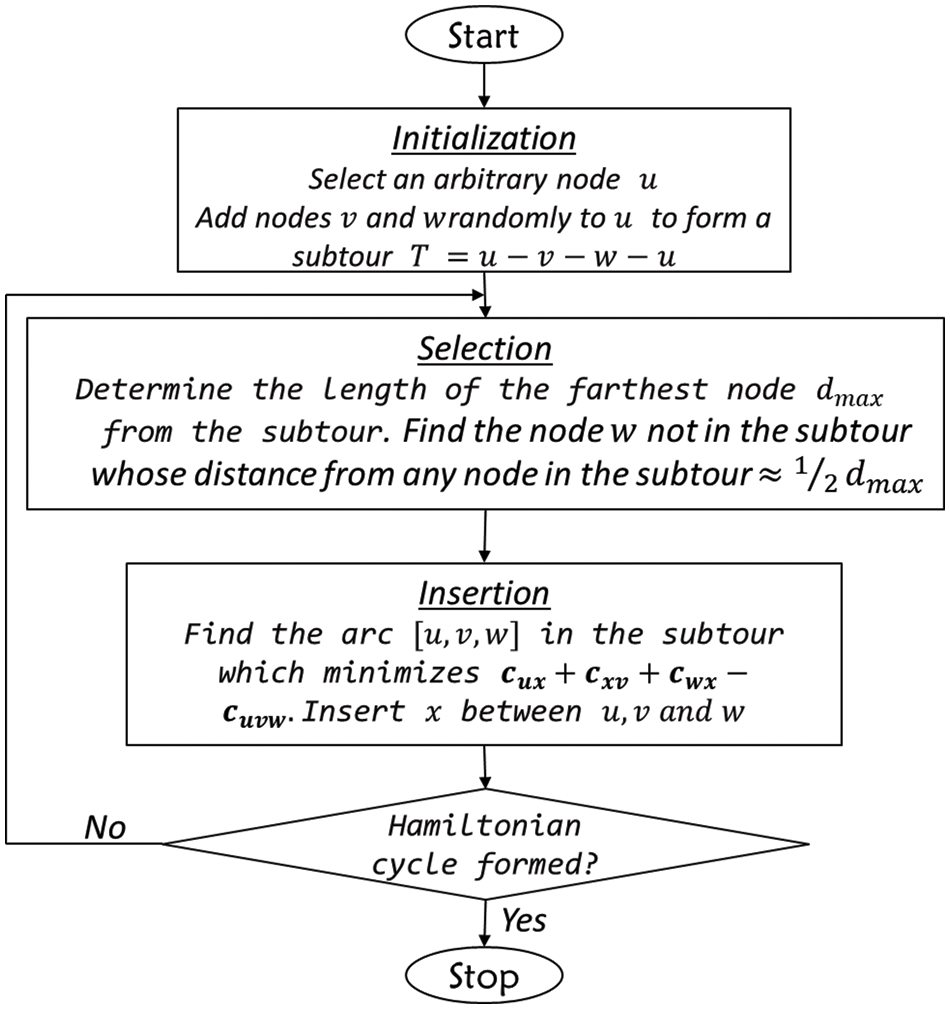
Figure 2: Flowchart of the half max insertion heuristic

In implementing the proposed technique, the JAVA programming language version 13.0.1. was used, while GNUplot 5.2 and patch-level eight were used to plot the path graph. The heuristic was implemented on Intel Pentium Core i7 3 GHz, Windows 10 (64 bit).

4  Experimental Results

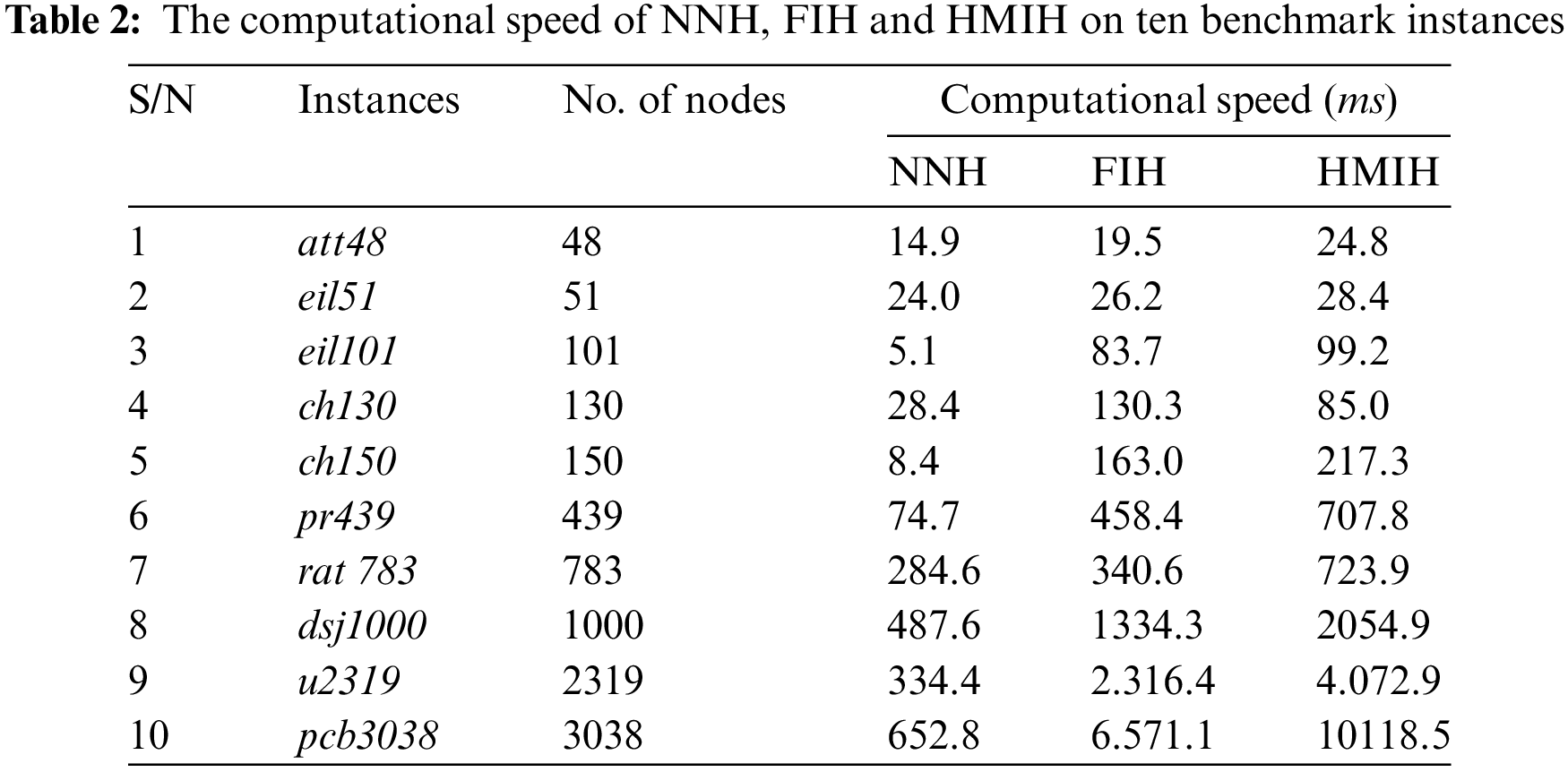
We experimented with the HMIH, together with two State-of-the-art heuristics (namely Nearest Neighbour Heuristic (NNH) and Farthest Insertion Heuristic (FIH)) on ten publicly available benchmark instances from TSPLIB made available by Heidelberg University on http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/. There were three groups of instances tested. Group one was instances whose nodes were less than 100. Group two: Instances whose nodes are more than 100 but less than 1000. Group three: Instances whose nodes are more than or equal to 1000. The implementation module generated three outputs. The first is the computation time in milliseconds (ms). Millisecond is one millionth of a second. Evidently, the accuracy of time is improved at that level of granularity. The second output is the tour cost, the distance taken to generate the tour. This is necessary for the performance evaluation of the heuristic. The third output is the tour path, the order in which the nodes join the tour. Table 2. shows the computational speed of the NNH, FIH and the proposed HMIH on the ten benchmark instances considered. Table 3 shows the tour cost of each of the three heuristics on the TSP instances.

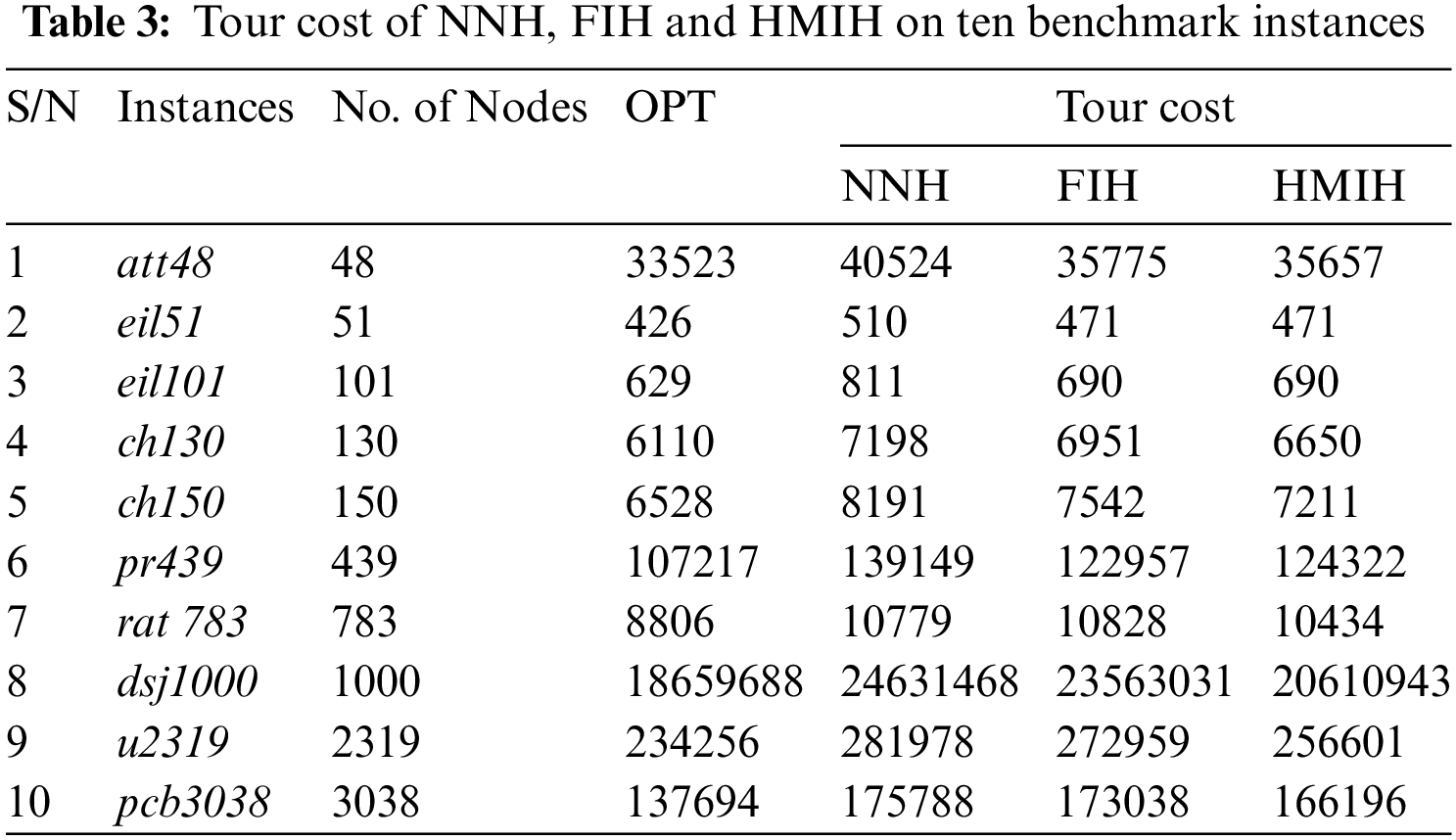
It is evident from Table 3 that the proposed HMIH has a shorter tour cost and is closer to the optimal tour cost in terms of solution quality than both FIH and NNH. FIH, however, compares more favourably with HMIH than NNH.

The FIH and HMIH tour graph for some benchmark instances is presented in Figs. 3–6. Fig. 3 displays the path graph of FIH and HMIH for the att48. Fig. 4 shows the path graph of FIH and HMIH for the eil51. Fig. 5 displays the path graph of FIH and HMIH for the eil101, and Fig. 6 displays the path graph of FIH and HMIH for the ch150.

Figure 3: Path graph of FIH and HMIH for att48

Figure 4: Path graph of FIH and HMIH for eil51

Figure 5: Path graph of FIH and HMIH for eil101

Figure 6: Path graph of FIH and HMIH for ch150

5  Non-Parametric Analysis of HMIH

Non-parametric analysis was conducted using Friedman’s test to validate the superior performance of the HMIH solutions for both NNH and FIH, which are classic tour construction heuristics. The test was conducted for all the ten instances considered in this study. The Friedman ranking was conducted based on the tour cost of the three algorithms, as presented in Table 3. The mean ranking for HMIH, NNH and FIH across all instances shown in Table 4 revealed a significant difference between the performance of HMIH and that of NNH and FIH.

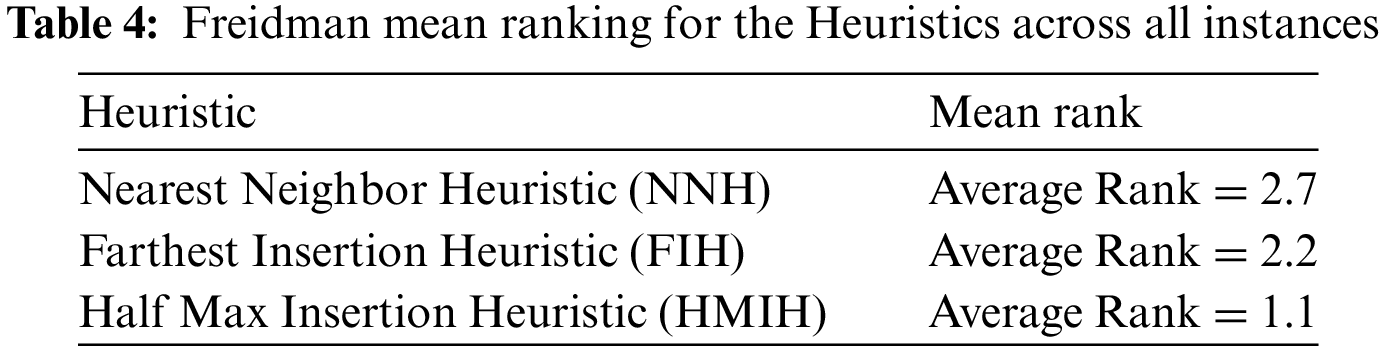
These rank scores indicate that, on average, the HMIH algorithm (with the least score) performed best, followed by FIH and NNH.

Given the rank, as presented in Table 4, Freidman’s test was then conducted using the following equation:

χ2=12n(k+1)(∑i=1kRi2−k(k+1)24)(2)

where:

n is the number of instances = 10

k is the number of TSP solutions, which in this case is 3

Ri is the sum of ranks for the i−th algorithm

The test was premised on the following hypothesis

- Null Hypothesis (H0): There is no significant difference among the algorithms.

- Alternative Hypothesis (H1): There is a significant difference among the algorithms.

Thus, Friedman’s test on the given data instances for the three TSP heuristics (NNH, FIH, HMIH) yielded a test statistic of approximately 15.37 and a p-value of about 0.00046. Since the p-value is less than 0.05, the null hypothesis that there is no significant difference in the performance of these algorithms is therefore rejected. This indicates that the HMIH performs significantly differently from the others.

Friedman’s analysis revealed that the HMIH technique exhibits a statistically significant superiority to NNH and FIH in performance.

6  Performance Evaluation and Discussion of Findings

Table 2 shows that the Nearest Neighbour Heuristic had the fastest computational speed, followed by the Farthest Insertion Heuristic and then the proposed HMI technique in all the instances. It should be noted that the proposed HMIH compared favourably with the FIH in this regard. This is consistent with literature findings that insertion techniques require more computational time than the NNH to complete tours [48–50]. Additionally, the increased computational time of the proposed HMIH can be attributed to the additional computation of the half-max insertion criteria. This is consistent with works by [47–49,51], which suggest that computational speed is affected by the insertion criteria computations.

The quality of the heuristic’s solution was assessed using the following factors:

Percentage Error (δ): the percentage error of the heuristics’ solution quality is the percentage deviation of the solution from the optimal tour solution. This is computed as solη−optopt×100%, where solη is the solution cost obtained by each heuristic, and opt is the optimal solution cost. This is equivalent to the performance ratio for suboptimal heuristics.

Quality impr. (Σ): this involves enhancing the solution quality of the HMI method with NNH and FIH. This is computed by E NNH/FIH−E HMIH, where E NNH/FIH is the error in percentage of the NNH or FIH and E HMIH is the error in the percentage of the HMIH.

Goodness Value (𝓰): this is also known as accuracy. This is the inverse of error and is computed as (1−solη−optopt)100%.

Table 5 displays the percentageerror,qualityimprandgoodnessvalue for all the heuristics on the ten benchmark instances.

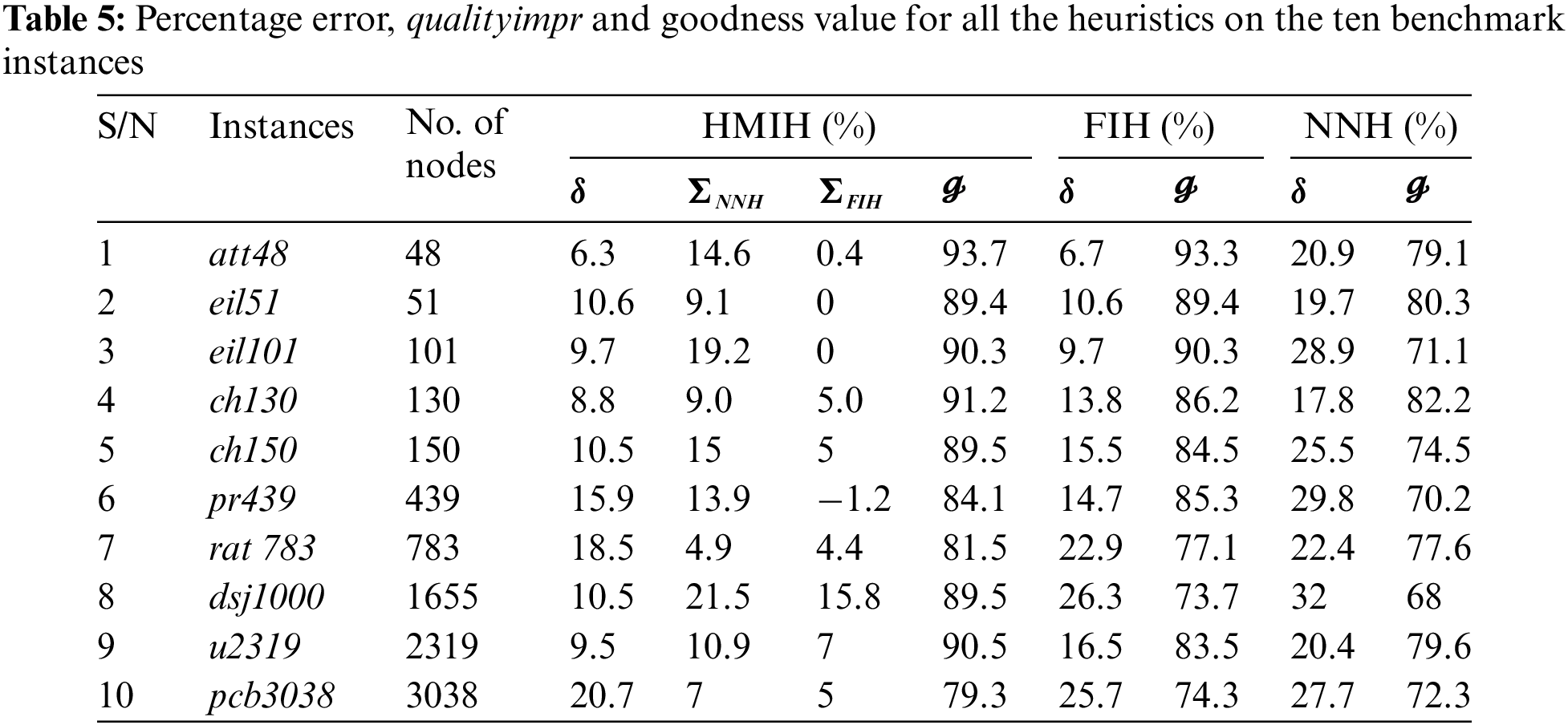
From Table 5, HMIH outperformed FIH in all the instances except pr439, eil51 and eil101. FIH outperformed HMIH for pr439, while FIH and HMIH had equal tour costs for eil51 and eil101. The quality of the NNH tour was, on average, 24.51% lower than the quality of the highest-quality trip. Regarding the examples that were considered, the FIH average performance was 16.24% of the Held-Karp lower limit. At its highest point, the Nearest Neighbour Heuristic attained a value of 32%, while its lowest point was 17.8%. At its highest point, the Farthest Insertion Heuristic achieved a value of 26.3%, while its lowest point was 6.7%. There is a correlation between these performances and the results that have been published in the literature about NNH and FIH [47–49]. Conversely, the performance of HMIH was 12.1% lower than the ideal tour duration. This was a significant difference. The HMIH that has been presented has a quality improvement of 4.14% points on average compared to the FIH. This chart, seen in Fig. 7, illustrates the percentage of departure that NNH, FIH, and HMIH have from the ideal tour length.

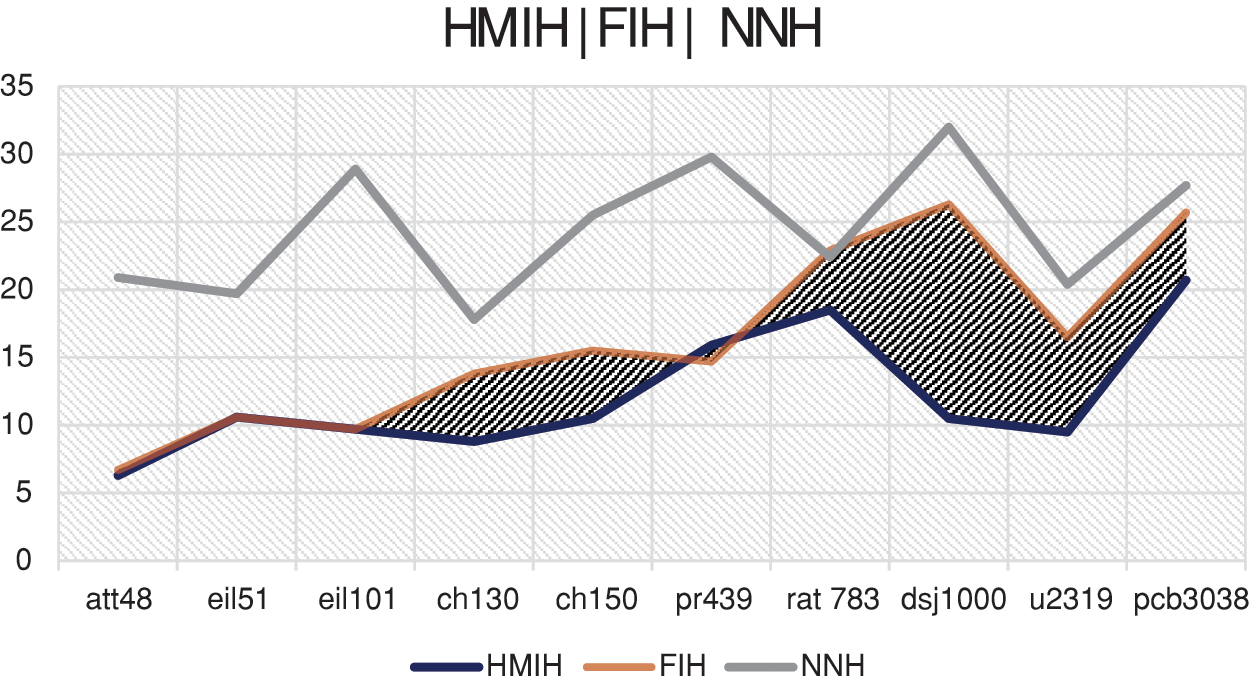
Figure 7: Percentage error of NNH, FIH and HMIH on the ten benchmark instances

The shaded area of the chart denotes the quality improvement of the HMIH over the FIH.

The proposed Half Max Insertion Heuristic consistently outperformed the Farthest Insertion. As seen by the shaded region of quality improvement in Fig. 7, the heuristic was applied throughout a broad spectrum of benchmark examples, and it had a statistical significance of up to sixteen percent at one point. A comparison was made between the proposed HMIH and the Farthest Insertion, which had an average goodness value of 81.7%, and the Nearest Neighbour Heuristic, which had an average goodness value of 74.5%. This means the proposed HMIH has a higher accuracy than FIH and NNH (see Fig. 8). It is worthy of note that the Farthest Insertion is considered the best-performing Insertion technique and among other lower-order complexity heuristics [31,47–50].

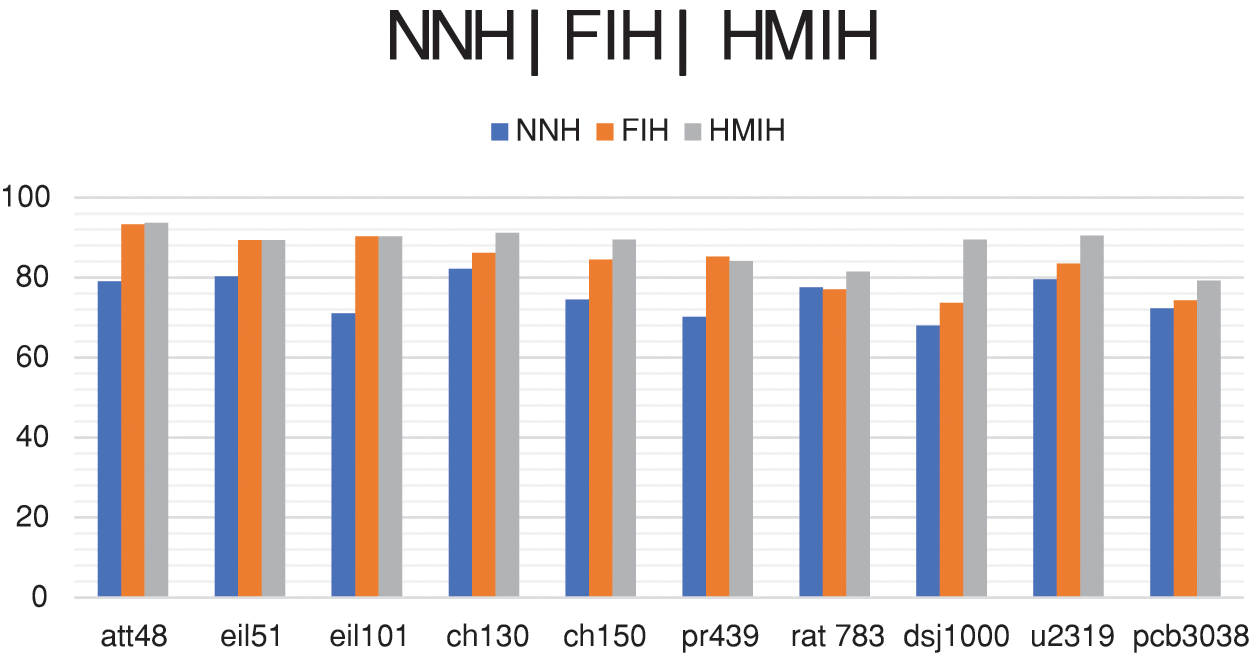
Figure 8: Measure of goodness value of HMIH, FIH and NNH

Additionally, while the Farthest Insertion is faster, the computation speed of the proposed HMIH is within the same range, and since the HMIH searches were conducted O(n) times, HMIH has the same complexity of O(n2) as the FIH and NNH. The computational speed performance of HMIH appears to follow a trend among lower-order complexity heuristics where the performing method tends to take longer computation time, perhaps owing to a more intricate process involved in getting better performance. Except for Random Insertion, which requires no computation effort to add new nodes, the better the performance, the longer the time of computation tends to be [47–52].

Acknowledgement: The authors gratefully acknowledge the support of the Landmark University Center for Research Innovation and Development (LUCRID) for access to research repositories, literary materials, useful insights from affiliate researchers and funding.

Funding Statement: This research is supported by the Centre of Excellence in Mobile and e-Services, the University of Zululand, Kwadlangezwa, South Africa.

Author Contributions: The authors confirm their contribution to the paper as follows: Study conception and design: E. O. Asani, A. E. Okeyinka; data collection: A. A. Adebiyi, E. O. Asani, and R. O. Ogundokun; methodology: A. E. Okeyinka, A. A. Adebiyi, and E. O. Asani; validation and visualization: E. O. Asani, R. O. Ogundokun, T. S. Adekunle, P. Mudali, and M. O. Adigun; analysis and interpretation of results: E. O. Asani, S. A. Ajagbe, T. S. Adekunle, P. Mudali, and M. O. Adigun; draft manuscript preparation: R. O. Ogundokun, E. O. Asani, S. A. Ajagbe. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data used for the implementation of this study is publicly available benchmark instances from TSPLIB made available by Heidelberg University on http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/tsp/.

Conflicts of Interest: The authors declare that there is no conflict of interest regarding the publication of this paper.

References

1. E. O. Asani, A. E. Okeyinka, and A. A. Adebiyi, “A construction tour technique for solving the travelling salesman problem based on convex hull and nearest neighbour heuristics,” presented at the 2020 Int. Conf. Math., Comput. Eng. Comput. Sci. (ICMCECS), Ayobo, Nigeria, 2020, pp. 1–4. doi: 10.1109/ICMCECS47690.2020.240847. [Google Scholar] [CrossRef]

2. H. A. Abdulkarim and I. F. Alshammari, “Comparison of algorithms for solving the traveling salesman problem,” Int. J. Eng. Adv. Technol., vol. 4, no. 4, pp. 76–78, 2015. [Google Scholar]

3. Z. Xiao et al., “Understanding private car aggregation effect via spatio-temporal analysis of trajectory data,” IEEE Trans. Cybern., vol. 53, no. 4, pp. 2346–2357, 2023. doi: 10.1109/TCYB.2021.3117705. [Google Scholar] [PubMed] [CrossRef]

4. Z. Xiao et al., “Predicting urban region heat via learning arrive-stay-leave behaviors of private cars,” IEEE Trans. Intell. Transport. Syst., vol. 24, no. 10, pp. 10843–10856, 2023. doi: 10.1109/TITS.2023.3276704. [Google Scholar] [CrossRef]

5. E. O. Asani, P. O. Ayegba, J. A. Ayoola, A. E. Okeyinka, and A. A. Adebiyi, “A preliminary study on the complexity of some heuristics for solving combinatorial optimization problems,” Int. J. Eng. Res. Technol., vol. 12, no. 10, pp. 1615–1620, 2019. [Google Scholar]

6. L. D. Giovanni, “Methods and models for combinatorial optimization: Heuristics for combinatorial optimization,” 2017. Accessed: Aug. 18, 2023. [Online]. Available: https://www.math.unipd.it/~luigi/courses/metmodoc1718/m02.meta.en.partial01.pdf [Google Scholar]

7. S. L. Smith and F. Imeson, “GLNS: An effective large neighborhood search heuristic for the generalized traveling salesman problem,” Comput. Oper. Res., vol. 87, no. 5, pp. 1–19, 2017. doi: 10.1016/j.cor.2017.05.010. [Google Scholar] [CrossRef]

8. R. Lin et al., “A machine learning study on superlattice electron blocking layer design for AlGaN deep ultraviolet light-emitting diodes using the stacked XGBoost/LightGBM algorithm,” J. Mater. Chem. C, vol. 10, no. 46, pp. 17602–17610, 2022. [Google Scholar]

9. R. Lin et al., “Low resistance asymmetric III-Nitride tunnel junctions designed by machine learning,” Nanomaterials, vol. 11, no. 10, pp. 2466, 2021. [Google Scholar] [PubMed]

10. L. Jiang, “A fast and accurate circle detection algorithm based on random sampling,” Future Gener. Comp. Syst., vol. 123, pp. 245–256, 2021. [Google Scholar]

11. M. Deudon, P. Cournut, A. Lacoste, Y. Adulyasak, and L. M. Rousseau, “Learning heuristics for the TSP by policy gradient,” in Integration of Constraint Programming, Artificial Intelligence, and Operations Research. Cham: Springer, Jun. 26–29, 2018, vol. 10848, pp. 170–181. [Google Scholar]

12. Y. Xie, X. Wang, Z. Shen, Y. Sheng, and G. Wu, “A two-stage estimation of distribution algorithm with heuristics for energy-aware cloud workflow scheduling,” IEEE Trans. Serv. Comput., vol. 16, no. 6, pp. 4183–4197, 2023. doi: 10.1109/TSC.2023.3311785. [Google Scholar] [CrossRef]

13. W. Zheng, S. Lu, Z. Cai, R. Wang, L. Wang and L. Yin, “PAL-BERT: An improved question answering model,” Comp. Model. Eng., vol. 139, no. 3, pp. 2729–2745. doi: 10.32604/cmes.2023.046692. [Google Scholar] [CrossRef]

14. Q. Li, H. Lin, X. Tan, and S. Du, “H∞ consensus for multiagent-based supply chain systems under switching topology and uncertain demands,” IEEE Trans. Syst. Man Cybern., Syst., vol. 50, no. 12, pp. 4905–4918, 2018. doi: 10.1109/TSMC.2018.2884510. [Google Scholar] [CrossRef]

15. H. Yang, X. Zhang, Z. Li, and J. Cui, “Region-Level traffic prediction based on temporal multi-spatial dependence graph convolutional network from GPS data,” Remote Sens., vol. 14, no. 2, pp. 303, 2022. doi: 10.3390/rs14020303. [Google Scholar] [CrossRef]

16. Q. Wang, Q. Jiang, Y. Yang, and J. Pan, “The burden of travel for care and its influencing factors in China: An inpatient-based study of travel time,” J. Transp. Health, vol. 25, pp. 101353, 2022. doi: 10.1016/j.jth.2022.101353. [Google Scholar] [CrossRef]

17. Y. Jiang, Y. Yang, Y. Xu, and E. Wang, “Spatial-temporal interval aware individual future trajectory prediction,” IEEE Trans. Knowl. Data Eng., vol. 1, pp. 1–14, 2023. doi: 10.1109/TKDE.2023.3332929. [Google Scholar] [CrossRef]

18. Y. Xu, E. Wang, Y. Yang, and H. Xiong, “GS-RS: A generative approach for alleviating cold start and filter bubbles in recommender systems,” IEEE Trans. Knowl. Data Eng., vol. 36, no. 2, pp. 668–681, 2024. doi: 10.1109/TKDE.2023.3290140. [Google Scholar] [CrossRef]

19. B. Cheng, M. Wang, S. Zhao, Z. Zhai, D. Zhu and J. Chen, “Situation-aware dynamic service coordination in an IoT environment,” IEEE/ACM Trans. Netw., vol. 25, no. 4, pp. 2082–2095, 2017. doi: 10.1109/TNET.2017.2705239. [Google Scholar] [CrossRef]

20. R. Marti and G. Reinelt, Heuristic Methods: The Linear Ordering Problem Exact and Heuristic Methods in Combinatorial Optimisation. Verlag Berlin Heidelberg: Springer, 2011, pp. 17–40. [Google Scholar]

21. M. Kyritsis, S. R. Gulliver, and E. Feredoes, “Human behaviour in the euclidean travelling salesperson problem: Computational modelling of heuristics and figural effects,” Cogn. Syst. Res., vol. 52, no. 10, pp. 387–399, 2018. doi: 10.1016/j.cogsys.2018.07.027. [Google Scholar] [CrossRef]

22. S. Lity, M. Al-Hajjaji, T. Thüm, and I. Schaefer, “Optimizing product orders using graph algorithms for improving incremental product-line analysis,” presented at the Proc. Eleventh Int. Workshop Variabl. Model. Softw.-Inten. Syst., 2017, pp. 60–67. doi: 10.1145/3023956.3023961. [Google Scholar] [CrossRef]

23. W. Huang and J. X. Yu, “Investigating TSP heuristics for location-based services,” Data Sci. Eng., vol. 2, no. 1, pp. 71–93, 2017. doi: 10.1007/s41019-016-0030-0. [Google Scholar] [CrossRef]

24. K. Ding, W. C. Choo, K. Y. Ng, and Q. Zhang, “Exploring changes in guest preferences for Airbnb accommodation with different levels of sharing and prices: Using structural topic model,” Front. Psychol., vol. 14, pp. 1120845, 2023. doi: 10.3389/fpsyg.2023.1120845. [Google Scholar] [PubMed] [CrossRef]

25. G. Kizilateş and F. Nuri̇yeva, “A new hybrid heuristic algorithm for solving TSP,” Anadolu Univ. J. Sci. Technol. B-Theoret. Sci., vol. 2, no. 2, pp. 143–148, 2015. [Google Scholar]

26. C. Wang, M. Lin, and Y. Zhong, “Swarm simulated annealing algorithm with knowledge-based sampling for travelling salesman problem,” Int. J. Intell. Syst. Technol. Appl., vol. 15, no. 2, pp. 74–94, 2016. doi: 10.1504/IJISTA.2016.076100. [Google Scholar] [CrossRef]

27. P. Vaishnav, N. Choudhary, and K. Jain, “Traveling salesman problem using genetic algorithm: A survey,” Int. J. of Scientif. Res. Comput. Sci., Eng. Infom. Technol., vol. 2, no. 3, pp. 105–108, 2017. [Google Scholar]

28. S. Neelima, N. Satyanarayana, and P. K. Murthy, “A comprehensive survey on variants in artificial bee colony,” Int. J. of Comput. Sci. Inform. Technol., vol. 7, no. 4, pp. 1684–1689, 2016. [Google Scholar]

29. Z. A. Ali, “Concentric tabu search algorithm for solving traveling salesman problem (Eastern Mediterranean University January-North Cyprus),” Master of Science in Computer Engineering thesis, 2016. Accessed: Feb. 13, 2020. [Online]. Available: http://i-rep.emu.edu.tr:8080/xmlui/handle/11129/2933 [Google Scholar]

30. G. H. Chen and D. Shah, “Explaining the success of nearest neighbor methods in prediction,” Found. Trends Mach. Learn., vol. 10, no. 5, pp. 337–588, 2018. doi: 10.1561/2200000064. [Google Scholar] [CrossRef]

31. Z. Ursani and D. W. Corne, “Introducing complexity curtailing techniques for the tour construction heuristics for the travelling salesperson problem,” J. Optim., vol. 2016, pp. 1–15, 2016. doi: 10.1155/2016/4786268. [Google Scholar] [CrossRef]

32. W. Huang, J. K. Yu, and Z. Shang, “A sketch-first approach for finding TSP,” in Databases Theory and Applications. Cham: Springer, 2016, vol. 9877 [Google Scholar]

33. D. J. Rosenkrantz, R. E. Stearns, and P. M. Lewis, “An analysis of several heuristics for the traveling salesman problem,” SIAM J. Comput., vol. 6, no. 3, pp. 563–581, 1977. doi: 10.1137/0206041. [Google Scholar] [CrossRef]

34. J. Fan, “The vehicle routing problem with simultaneous pickup and delivery based on customer satisfaction,” Procedia Eng., vol. 15, pp. 5284–5289, 2011. doi: 10.1016/j.proeng.2011.08.979. [Google Scholar] [CrossRef]

35. R. C. Cruz, T. C. B. Silva, M. J. F. Souza, V. N. Coelho, M. T. Mine and A. X. Martins, “GENVNS-TS-CL-PR: A heuristic approach for solving the vehicle routing problem with simultaneous pickup and delivery,” Elect. Notes Disc. Math., vol. 39, pp. 217–224, 2012. doi: 10.1016/j.endm.2012.10.029. [Google Scholar] [CrossRef]

36. M. Goetschalckx, “Single vehicle round-trip routing,” in Supply Chain Engineering. International Series in Operations Research & Management Science, vol. 161. Boston, MA: Springer, 2011. [Google Scholar]

37. S. P. Anbuudayasankar, K. Ganesh, and S. Mohapatra, “Survey of methodologies for TSP and VRP,” in Models for Practical Routing Problems in Logistics: Design and Practices. Cham: Springer, 2014, pp. 11–42. [Google Scholar]

38. G. Qiao, S. Huang, and O. Vorobjovas-Pinta, “Seeking tourism in a social context: An examination of Chinese rural migrant workers’ travel motivations and constraints,” Leisure Stud., vol. 103, no. 4, pp. 1–16, 2023. doi: 10.1080/02614367.2023.2249259. [Google Scholar] [CrossRef]

39. A. Fischer, F. Fischer, G. Jäger, J. Keilwagend, P. Molitor and L. Grosse, “Exact algorithms and heuristics for the Quadratic Traveling salesman problem with an application in bioinformatics,” Discrete Appl. Math., vol. 166, no. 1, pp. 97–114, 2014. doi: 10.1016/j.dam.2013.09.011. [Google Scholar] [CrossRef]

40. R. Bernardino and A. Paias, “Solving the family traveling salesman problem,” Eur. J. Oper. Res., vol. 267, no. 2, pp. 453–466, 2018. doi: 10.1016/j.ejor.2017.11.063. [Google Scholar] [CrossRef]

41. P. Kitjacharoenchaia, M. VentresHuangcaa, M. J. Mohammad, S. Leea, J. M. A. Tanchocoa and P. A. Brunesea, “Multiple traveling salesman problem with drones: Mathematical model and heuristic approach,” Comput. Ind. Eng., vol. 129, no. 1, pp. 14–30, 2019. doi: 10.1016/j.cie.2019.01.020. [Google Scholar] [CrossRef]

42. P. V. Víctor, A. H. José, M. S. José, and V. Nodari, “Simple constructive, insertion, and improvement heuristics based on the girding polygon for the euclidean traveling salesman problem,” Lect. Notes Comput. Sci., vol. 13, no. 5, pp. 1–30, 2020. doi: 10.3390/a13010005. [Google Scholar] [CrossRef]

43. R. Daamen and F. Phillipson, “Comparison of heuristic methods for the design of edge disjoint circuits,” Elsevier, Comput. Commun., vol. 61, pp. 90–102, 2015. doi: 10.1016/j.comcom.2015.01.001. [Google Scholar] [CrossRef]

44. E. O. Asani, A. E. Okeyinka, and A. A. Adebiyi, “A computation investigation of the impact of convex hull subtour on the nearest neighbour heuristic,” presented at the 2023 Int. Conf. Sci., Eng. Business Sust. Develop. Goals (SEB-SDG), Omu-Aran, Nigeria, vol. 1, 2023, pp. 1–7. doi: 10.1109/SEB-SDG57117.2023.10124469. [Google Scholar] [CrossRef]

45. M. Englert, H. Röglin, and B. Vöcking, “Worst case and probabilistic analysis of the 2-Opt algorithm for the TSP,” Algorithmica, vol. 68, no. 1, pp. 190–264, 2014. doi: 10.1007/s00453-013-9801-4. [Google Scholar] [CrossRef]

46. M. Jünger, G. Reinelt, and G. Rinaldi, “The traveling salesman problem,” Handbooks Operat. Res. Manag. Sci., vol. 7, pp. 225–330, 1995. doi: 10.1016/S0927-0507(05)80121-5. [Google Scholar] [CrossRef]

47. L. Babel, “New heuristic algorithms for the Dubins traveling salesman problem,” J. Heuristics, vol. 26, no. 4, pp. 503–530, 2020. doi: 10.1007/s10732-020-09440-2. [Google Scholar] [CrossRef]

48. G. Reinelt, “The traveling salesman: Computational solutions for TSP applications,” presented at the Lecture Note in Computer Science. Berlin Heidelberg New York, London: Springer Berlin, Heidelberg, vol. 840, 1994. [Google Scholar]

49. V. Ilin et al., “A hybrid genetic algorithm, list-based simulated annealing algorithm, and different heuristic algorithms for the travelling salesman problem,” Log. J. IGPL, vol. 31, no. 4, pp. 602–617, 2023. doi: 10.1093/jigpal/jzac028. [Google Scholar] [CrossRef]

50. D. Laha and J. N. D. Gupta, “A Hungarian penalty-based construction algorithm to minimize makespan and total flow time in no-wait flow shops,” Comput. Ind. Eng., vol. 98, pp. 373–383, 2016. doi: 10.1016/j.cie.2016.06.003. [Google Scholar] [CrossRef]

51. S. A. Ajagbe, M. O. Oyediran, A. Nayyar, J. A. Awokola, and J. F. Al-Amri, “P-acohoneybee: A novel load balancer for cloud computing using mathematical approach,” Comput. Mat. Contin., vol. 73, no. 1, pp. 1943–1959, 2022. doi: 10.32604/cmc.2022.028331. [Google Scholar] [CrossRef]

52. E. O. Asani, A. E. Okeyinka, and A. A. Adebiyi, “Performance evaluation of convex hull node-based heuristics for solving the travelling salesman problem,” in Lecture Notes in Networks and Systems, vol. 217. Singapore: Springer, 2021, pp. 665–673. [Google Scholar]