MIDNet: Deblurring Network for Material Microstructure Images

1  Introduction

In the era of advanced imaging technology, modern material scientists delve into the microscopic realm, exploring and analyzing intricate phenomena. Among the array of methodologies available, scanning electron microscopy (SEM) emerges as a powerful tool for characterizing materials, and uncovering their morphologies, crystal structures, and chemical compositions [1]. However, SEM images are susceptible to distortion, arising from instrument settings or operator inexperience, leading to blurred or defocused depictions that hinder research progress. When SEM images are blurry, the microstructural information of the material, such as crystal morphology, particle size, and pore structure, becomes less distinct, posing challenges to the accurate analysis of the material’s structural features. Additionally, the quantitative analysis of surface morphology, such as studying material texture and roughness, is also limited by the quality of SEM images. In the case of composite or multiphase materials, SEM images can reveal interface features between different phases. When the images are blurry, the interface structure may not be visible, thereby affecting the analysis and understanding of interface characteristics. SEM images are also employed for detecting defects in materials, such as cracks, voids, and particle non-uniformity. If the images are blurry, these defects may not be displayed, making defect detection and analysis difficult. The quest for effective deblurring techniques becomes paramount in ensuring the integrity of subsequent image analyses, particularly when grappling with suboptimal image quality. Our research is motivated by the imperative to investigate the paramount importance of this field, acknowledging the substantial adverse impact that blurry images can have on the further precise analysis of materials. Therefore, our study holds significant relevance in addressing this issue. We emphasize the pressing need for innovative deblurring solutions to address this issue effectively.

Traditional image restoration techniques often lean on deconvolution methods that presuppose specific blur kernels, thereby crafting filters like local linear, nonlinear, non-local self-similarity, and Bayesian image restoration filters [2,3]. However, their application in practical contexts remains challenging due to the prerequisite knowledge of blur kernels. The advent of deep learning revolutionizes image restoration, harnessing the prowess of deep neural networks to learn nonlinear mappings between degraded and sharp images, obviating the reliance on manually designed filters or blur kernels [4,5]. Deep learning methods excel in preserving finer details, such as texture, edges, and structures, during the image reconstruction process [6]. Furthermore, these methods demonstrate versatility in handling different levels of degradation and types of noise, allowing for image recovery across various scales [7]. Its application has further extended to microscopic systems for enhancing image quality, encompassing optical microscopy [8], electromagnetic imaging, and scanning electron microscopy [9].

While previous research has improved the quality of microscopic images, further investigation is warranted to explore the integration of deep learning for deblurring low-quality material microstructures. This inquiry begets key questions: (1) Can existing deblurring methods, which are applicable in real-world scenarios, be directly extended to address material data with blurred attributes using pre-trained weights? (2) Can retraining networks with material-specific blurry datasets lead to improvements in deblurring efficacy? (3) How can novel algorithms be developed to maximize their potential in enhancing the clarity of material microstructure images?

In pursuit of these goals, we present a deep learning-based approach that combines soft attention mechanisms with multifaceted loss functions, aiming to enhance image quality while preserving intricate details. Our methodology tackles the challenge of image blurring in SEM images, arising from inaccurate hardware calibration or automation glitches. With our approach, researchers can efficiently rectify subpar images, saving significant time and resources that would otherwise be required for re-scanning. This is particularly relevant for research projects that have limited budgets and require the rapid processing of numerous material samples within tight timeframes. In such circumstances, where image blurring continues to pose a recurring obstacle, our approach becomes especially crucial. In the dynamic field of high-throughput materials research, our innovation has the potential to enhance image quality and data fidelity, thereby accelerating the discovery and optimization of novel materials. In light of this, our approach emerges as a pivotal contribution, poised to catalyze diverse applications in the expanse of materials science research. The main contributions of this paper are as follows:

(1) We propose a Material Images Deblurring Network (MIDNet) that specifically sharpens blurred images of material microstructures and outperforms current SOTA deblurring networks.

(2) We introduce an attention mechanism that effectively mitigates the problem of inconsistent feature distributions by attending to the most informative features in both the encoder and decoder. This attention mechanism not only addresses the issue but also strengthens the interplay between components, enhancing overall performance.

(3) We propose a novel multi-loss function that enhances the supervisory signal, thereby preserving intricate details and texture features more effectively.

(4) Our MIDNet model’s superiority is thoroughly validated through rigorous experiments, both quantitatively and qualitatively. Through ablation experiments, we reveal the impact of different loss functions proposed in this paper on the model and demonstrate the effectiveness of constructing multi-loss functions.

2  Related Work

2.1 Image Deblurring

Several studies have combined computer science and materials science, with a particular emphasis on utilizing image processing methods for analyzing the microstructure images of materials. Varde [10] proposed a computational estimation method called AutoDomainMine, based on graph data mining. By integrating clustering and classification techniques, this method discovered knowledge from existing experimental data and utilized it for estimation. The main objective of this framework was to estimate the graphical results of experiments based on input conditions. Similar graph data mining methods can be employed for image deblurring tasks to analyze and extract patterns and features from image data to achieve image deblurring goals. Pan et al. [11] reviewed the evolution and impact of material microstructures during cutting processes, presenting a thermal-force-microstructure coupled modeling framework. They analyzed microstructural changes such as white layer formation, phase transformation, and dynamic recrystallization under different materials and cutting conditions, as well as the effects of these changes on cutting forces and surface integrity. Vibration of cutting tools or materials can cause motion in image acquisition devices (such as cameras) during the capturing process, resulting in image blurring. Therefore, studying the deblurring of material microstructures holds significant importance.

Many traditional image enhancement methods employ regularization and manually crafted prior images for blur kernel estimation [12]. Subsequent iterative optimization is used to gradually recover a clear image. However, this conventional approach involves intricate blur kernel estimation, leading to laborious sharpening, subpar real-time performance, and algorithmic limitations. To enhance the quality of image deblurring, many methods based on convolutional neural networks (CNN) have been proposed [13–15]. Chakrabarti [13] designed a neural network to generate a global blur kernel for non-blind deconvolution. Song et al. [14] proposed a method using a neural network for reliable detection of motion blur kernels to detect image forgeries. Wang et al. [15] proposed a network-based framework that learned to remove raindrops by learning motion blur kernels. Sun et al. [16] predicted the probability distribution of non-uniform motion blur using CNNs. However, most neural-network-based methods still rely on blur models to solve the blur kernel, limiting their performance.

In recent years, with the development of deep learning, a series of methods based on deep learning have been used for image deblurring [17,18]. Zhang et al. [19] proposed DMPHN, which is the first multi-scale network based on the multi-patch method for single-image deblurring. Chen et al. [20] proposed HINet, a deep image restoration network based on the HIN block. Fanous et al. [5] presented GANscan, a method for restoring sharp images from motion-blurred videos. The method was applied to reconstruct tissue sections under the microscope. Liang et al. [21] directly deblurred raw images using deep learning-based busy image-to-image blind-deblurring. DID-ANet [4] was designed specifically for single-image blur removal caused by camera misfocus. MedDeblur [18] was developed to remove blur in medical images due to patient movement or breathing. Xu et al. [22] proposed a deep-learning-based knowledge-enhanced image deblurring method for quality inspection in yarn production. Restormer [23] is an efficient transformer model that can be utilized for image restoration tasks at high resolutions. This model is effective for restoring high-resolution images. Chen et al. [7] found that nonlinear activation functions are not necessary and can be replaced or omitted, and developed NAFNet for both image denoising and deblurring. Due to the impressive performance of NAFNet in deblurring tasks, we are currently implementing modifications to its architecture.

2.2 Attention-Based Deblurring Model

In recent years, attention mechanisms have proven to be highly effective in various computer vision tasks [24,25]. As a result, attention-based methods have gradually been adopted for the task of image deblurring [26,27]. MSAN [28] is a convolutional neural network architecture based on attention that efficiently and effectively generalizes motion deblurring. D3-Net [26] can be used for deblurring, dehazing, and object detection, with the addition of a classification attention feature loss to improve deblurring and dehazing performance. Cui et al. [27] proposed a dual-domain attention mechanism that enhances feature expression in both spatial and frequency domains. Ma et al. [29] proposed an attention-based dehazing algorithm for deblurring to improve defect detection in inspection image pipelines. Shen et al. [30] introduced a supervised human-perception attention mechanism model, which performs exceptionally well in motion deblurring in an end-to-end manner. MALNET [31] is a lightweight network based on attention mechanisms, which also performs well in image deblurring. Zhang et al. [32] proposed an attention-based inter-frame compensation scheme for video deblurring. In this work, we also incorporate attention mechanisms into our image deblurring network to improve its deblurring capability.

3  Method

3.1 Architecture

The network structure of this paper is shown in Fig. 1. It follows a classical U-shape structure, which is an improvement from NAFNet [7]. The structure comprises an encoder and a decoder, both belonging to the MID-Block. An attention mechanism is introduced between the blocks to improve the image restoration quality of the network.

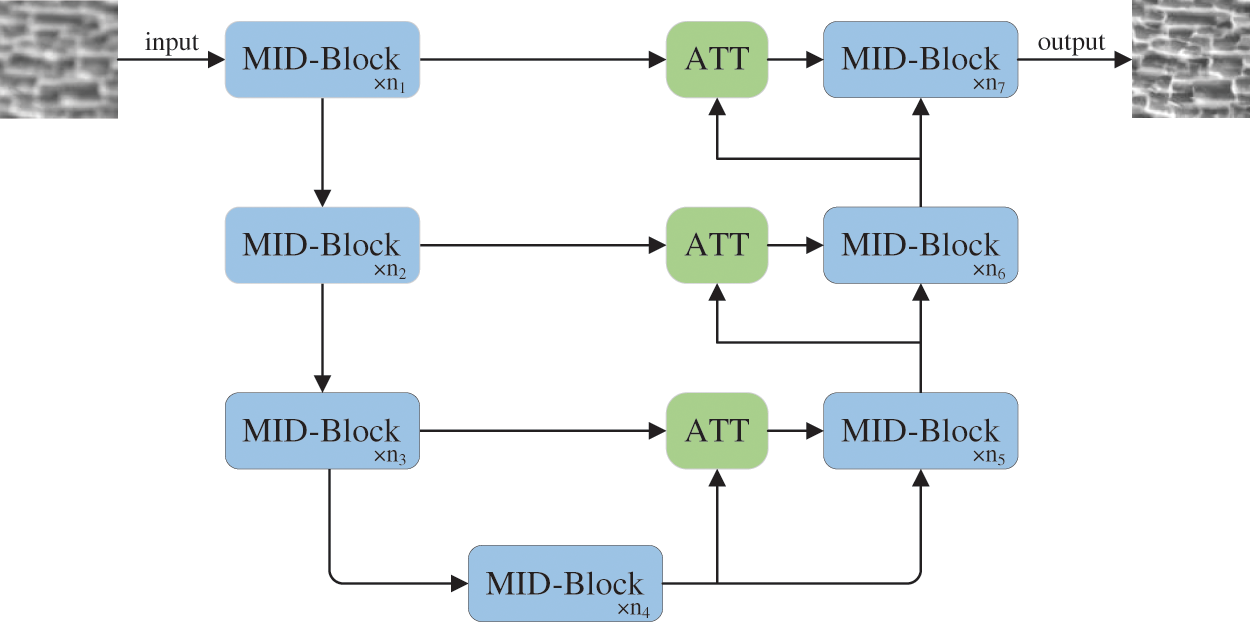
Figure 1: The MIDNet overview. The overall architecture of the network resembles a U-shape design, which is composed of MID-block and attention block

3.2 MID-Block

MID-Block is the basic building block of MIDNet. To avoid high complexity between blocks, MID-Block does not use any nonlinear activation functions such as ReLU, GELU, and Softmax. We construct a MID-Block using analogies with NAFNet blocks, as illustrated in Fig. 2.

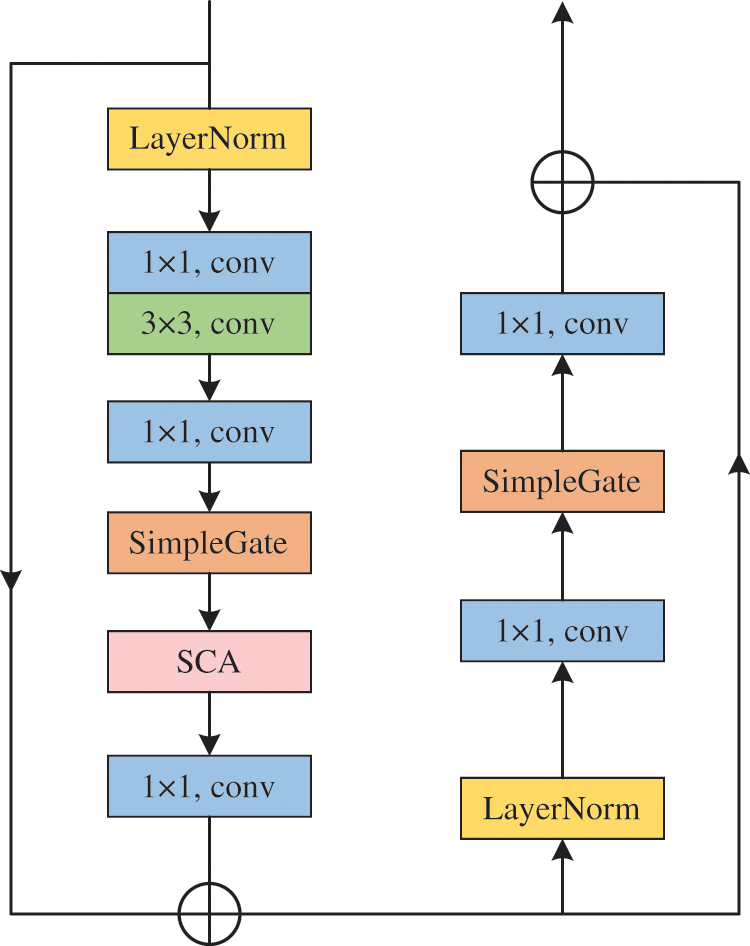
Figure 2: Architecture of MID-block

To stabilize the training process, the input is first passed through Layer Normalization. Next, the input undergoes convolution operations and is then processed by SimpleGate (SG) [7], which is a variant of Gated Linear Units (GLU) [33]. The GLU formula is as follows:

Gate(X,f,g,σ)=f(X)⊙σ(g(X))(1)

In Eq. (1), X represents the feature map, f and g function as linear transformers, σ represents a nonlinear activation function, such as Sigmoid, and ⊙ represents element-wise multiplication.

The GLU increases the intra-block complexity, which is not desirable. To remedy this issue, we reconsider the activation function in the block, specifically GELU [34], which is expressed as:

GELU(x)=xϕ(x)(2)

where ϕ represents the cumulative distribution function of the standard normal distribution. According to reference [34], it is suggested that the Gaussian Error Linear Unit (GELU) activation function can be effectively approximated and implemented by employing the following methodology:

0.5x(1+tanh[2/π(x+0.044715x3)])(3)

In Eqs. (1) and (2), GELU is a specific case of GLU, where the activation functions f and g are identity functions and the parameter σ is substituted with ϕ. The GLU incorporates nonlinearity and is not reliant on the parameter σ. Even in the absence of the parameter σ, the expression Gate(X)=f(X)⊙g(X) retains its nonlinearity. According to reference [7], we suggest a simple adjustment to GLU: Split the feature map into two parts along the channel dimension and multiply them. This could be done using a basic element-wise multiplication, which is represented by Eq. (4).

SimpleGate(X,Y)=X⊙Y(4)

In Eq. (4), X and Y represent feature maps of equal proportions.

The gating unit SG is a neural network component illustrated in Fig. 3, which is used in the processing of feature maps. It operates by splitting the feature map into two parts along the channel dimension, which is then multiplied to generate the final output. By splitting the feature map in this manner, SG can selectively emphasize or de-emphasize specific channels in the feature map, which can be useful for enhancing certain features or suppressing noise in the signal. This process is often referred to as channel-wise gating.

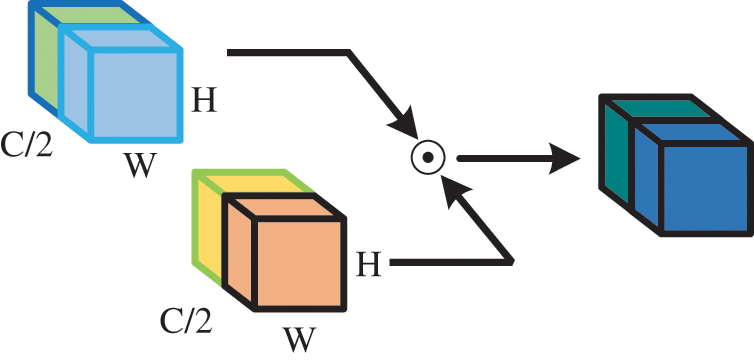
Figure 3: Simple gate as represented by Eq. (2). ⊙: Element-wise

Our novel approach introduces Simplified Channel Attention (SCA) [7], a new component that utilizes channel-wise attention to enhance relevant features in data. Compared to other approaches, SCA has a simpler structure which offers ease of implementation. Additionally, it adds minimal computational overhead to models, hence enhancing the efficiency of our approach. Please refer to Fig. 4 for an illustration of SCA.

Figure 4: Simplified channel attention (SCA). ∗: Channel-wise multiplication

SCA determines channel attention by computing the average of the feature map along the spatial dimensions and applying a fully connected layer to generate a channel-wise attention vector. This attention vector is then multiplied with the original feature map to selectively amplify important channels in the data while suppressing irrelevant or noisy channels.

Our experiments demonstrate that incorporating SCA into a standard convolutional neural network yields improved performance, highlighting the efficacy of enhancing feature representation using channel attention. SCA can be easily integrated into existing neural network architectures and represents a useful tool for improving the performance of deep learning models in a variety of applications.

SCA is derived from Channel Attention (CA) [35], which can be expressed by the Eq. (5).

CA(X)=X⊗σ(W2max(0,W1pool(X)))(5)

In Eq. (5), X denotes the feature map, pool denotes the global average pooling operation, σ denotes an activation function such as Sigmoid, W1, and W2 denote fully connected layers, and cross multiplication is the channel multiplication operation. By simplifying the Eq. (5), we can finally obtain SCA, as shown in Eq. (6).

SCA(X)=X⊗Wpool(X)(6)

3.3 Attention Mechanism

With the advancement of deep learning techniques, significant progress has been made in image restoration. The NAFNet model, in particular, has shown significant performance in various applications. However, a limitation of NAFNet is that the skip connections used for feature aggregation between the encoder and decoder have the potential to disrupt the feature distribution, resulting in inconsistencies between these components. Another shortcoming of NAFNet is that it only employs an intra-block attention mechanism and ignores attention-based skip connections.

To address these challenges, we introduce a soft attention mechanism to capture the latent relationship between the encoder and decoder more adaptively. We refer to the proposed soft attention mechanism as ATT. The architecture of the attention gate ATT is shown in Fig. 5. Specifically, the proposed attention gate ATT aggregates features from different blocks using a weighting scheme based on their relevance to the current image restoration task, instead of simple element-wise addition used in conventional skip connections. This allows the model to selectively focus on the most informative features while suppressing the irrelevant ones.

Figure 5: The architecture of ATT

Moreover, our attention mechanism enables us to incorporate attention-based skip connections, which further enhance the feature aggregation process. By attending to the most informative features in the encoder and decoder, the model can effectively alleviate issues related to feature distribution inconsistency and strengthen the correlation between these components. The formula of the soft attention mechanism can be expressed as follows:

Watt=ψT(σ1(WaTxa+WbTxb+bf))+bψ(7)

x^b=σ2(Watt)∗xb(8)

In Eqs. (7) and (8), σ1 and σ2 denote activation functions. The attention gate is represented by a set of parameters through mathematical formulas, including linear transformations Wa, Wb, ψ, and biases bf, bψ. The linear transformations are obtained by performing convolution operations on the input tensors. The output of the attention gate is the product of the input feature map and the attention coefficient.

3.4 Multi-Loss Function

The paper utilizes multi-loss functions, as shown in Eq. (9), which comprise the deblurring loss, edge loss, and FFT loss. The hyperparameters λ1 and λ2 are assigned the values of 0.05 and 0.01, respectively.

L=Ld+λ1Le+λ2Lf(9)

3.4.1 Deblurring Function

The deblurred image is compared with its ground truth in the spatial domain, using the standard l1 loss as shown in Eq. (10). We do not use l2 loss because it sometimes over-penalizes errors and leads to poor deblurring performance.

Ld=1N∑i=1n||xigt−MIDNet(xiblur)||1(10)

In Eq. (10), xigt denotes the ground truth of clear images, xiblur represents the output of the blurry image after passing through the MIDNet network proposed in this paper.

3.4.2 Edge Function

To restore the high-frequency details of the image, we introduce an edge loss function. It aims to focus on the gradient information of the image and enhance the edge texture features. The edge loss function of this paper is as follows:

Le(Ir,Igt)=||Δ(Ir)−Δ(Igt)||2+ε2(11)

In Eq. (11), Ir represents the reconstructed image, Igt represents the clear ground truth image and Δ denotes the Laplacian operator.

3.4.3 FFT Loss

The FFT loss is a type of loss function based on the Fourier transform that is used for image restoration tasks. It aims to penalize the discrepancy between the reconstructed image and the ground truth image in the frequency domain. The FFT loss is represented as follows:

Lf=1W×H∑i=1W∑j=1Hwi,j‖F(Ir)−F(Igt)⋅H‖2i,j(12)

In Eq. (12), the variables W and H refer to the width and height of the image being analyzed. The function F represents the Fourier transform of the image, which is a mathematical technique used to analyze its frequency components. Where wi,j represents the weight corresponding to the Fourier coefficient, and H represents the frequency response of the degradation function in the Fourier domain.

Specifically, the FFT loss can be calculated as the weighted sum of the squared Euclidean distance between the discrete Fourier transform coefficients of the reconstructed image and the ground truth image. The weight factors, which correspond to different Fourier coefficients, are used to emphasize the importance of different frequencies in the loss function, allowing it to focus more on the crucial parts of the reconstructed image spectrum. In the Fourier domain, high-frequency information such as edges and textures has a more significant impact on the visual quality of the reconstructed image. Therefore, incorporating the FFT loss can help the network better preserve these details, ultimately leading to an improvement in the image quality.

4  Experiments

4.1 Dataset

We utilize a dataset containing 120 paired images with both low and high quality to investigate material microstructure fuzziness. Specifically, low-quality images in this dataset are directly obtained from observations captured through the SEM rather than artificially blurred using blur kernels or algorithms. This approach replicates real-world scenarios more accurately while simultaneously presenting greater challenges for the process of deblurring. When low-quality images are captured in practice, operators take repeated images until high-quality ones are achieved. Consequently, we meticulously selected 120 matching low and high-quality images that met stringent criteria. All images are subsequently adjusted to 256 * 256 pixels. Several cropped images are displayed in Fig. 6. The dataset is randomly divided into a training set comprising 108 image pairs and a test set containing 12 image pairs.

Figure 6: A few sample images from our dataset. Column 1 shows the low-quality images, whereas Column 2 shows the high-quality images

4.2 Experiment Parameters

We optimize the model using Adam (β1 = 0.9, β2 = 0.999) for 200 K iterations with a cosine annealing schedule that decreases the learning rate from 10–3 to 10–7. We crop the images to a size of 256 * 256 pixels and apply rotation and flipping as data augmentation techniques. We employed the skip-init method to ensure stable training and implemented our code in the PyTorch framework. We evaluate our model using peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) metrics. All experiments are conducted on an NVIDIA Tesla V100 GPU.

4.3 Experiments on SOTA Algorithms

PSNR and SSIM are employed as quantitative evaluation metrics, with larger values indicating superior image quality. They are calculated according to Eqs. (13) and (14).

PSNR=10⋅log10⁡(MAX2MSE)(13)

SSIM(x,y)=(2μxμy+C1)(2σxy+C2)(μx2+μy2+C1)(σx2+σy2+C2)(14)

In Eq. (13), MAX represents the maximum pixel value of the image, typically 255 when each pixel is represented by an 8-bit binary. MSE (Mean Squared Error) is the mean squared error value between the blurred image and the clear image. In Eq. (14), x and y denote the original image and the deblurred image, respectively. μx and μy represent the mean pixel values of images x and y, σx and σy represent the standard deviations of pixel values in images x and y, and σxy is the covariance between the pixel values of the two images. C1 and C2 are constants introduced to prevent division by zero in the denominator.

To assess the generalizability of models trained on natural images to material microstructure fuzziness data, we conduct a series of relevant studies. Specifically, we employ pre-trained weights from the original papers of DMPHN, HINet, Restormer, and NAFNet methods to conduct inference on material blurry images. The deblurred images are displayed in Fig. 7, while the corresponding PSNR and SSIM values are summarized in Table 1.

Figure 7: Image deblurring performance on the material blurry dataset is evaluated using several SOTA algorithms with pre-trained weights

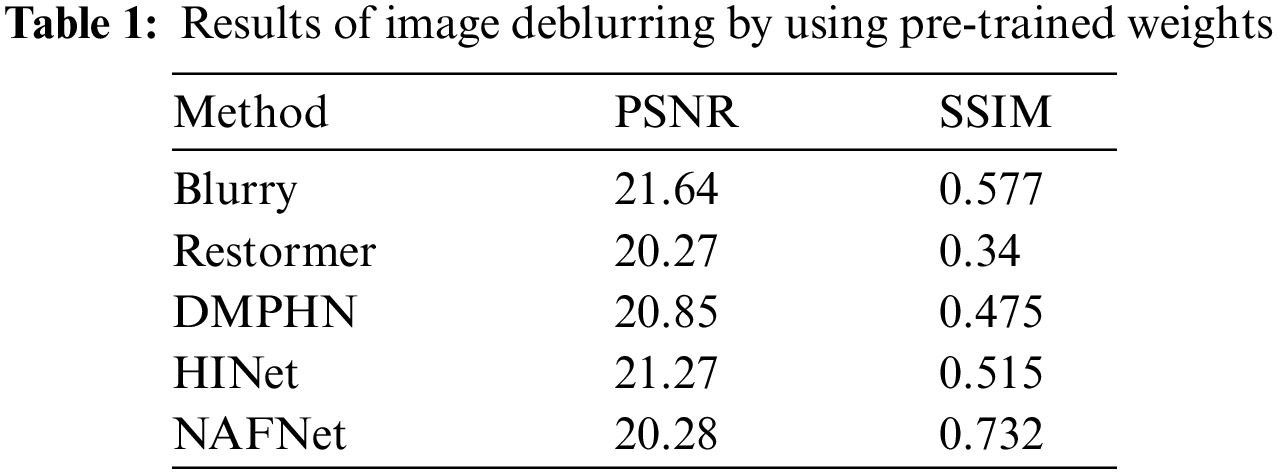
As observed in Fig. 7, these methods exhibit certain levels of processing applied to the blurry images. However, their ability to achieve satisfactory deblurring outcomes remains limited, with minimal improvement over the initial blurry images. By referring to Table 1, the PSNR and SSIM values of both the original blurry and clear images are provided in the input row. Notably, these methods yield relatively low PSNR and SSIM scores, with instances where deblurred images demonstrate worse performance compared to their initial states.

Interestingly, these methods have demonstrated proficiency on the GoPro dataset and have exhibited effective deblurring outcomes on real-world blurry images. Consequently, we postulate that their subpar performance on material images may be attributed to external factors rather than the inherent limitations of the methods themselves.

Upon meticulous scrutiny of the GoPro dataset, a notable distinction emerges in the PSNR values of its blurry images, which average approximately 23. In contrast, the blurry images originating from our material microstructure exhibit a lower PSNR value of approximately 21. Building upon these observations, a hypothesis arises: The relatively lower quality of material images, resulting in reduced information content, poses a heightened challenge for the deblurring process. Consequently, this challenge could potentially contribute to network degradation and the suboptimal performance observed.

Furthermore, an additional factor potentially influencing the subpar deblurring results is the unique visual characteristics inherent to material microstructures, setting them apart from real-world blurry images. This disparity in appearance might contribute to reduced reliability in the neural network’s performance when confronted with material microstructure fuzziness data. To address this challenge, we advocate for a proactive solution: Retraining and fine-tuning these methods using material blurry images. Our approach involves freezing the majority of the model layers and selectively unfreezing a small subset for training purposes. We apply data augmentation techniques, such as flip and rotate, to the dataset during the training process. Hyperparameters, including learning rate, batch size, and number of iterations, are adjusted based on the specific model to achieve optimal performance. Additionally, appropriate regularization strategies are employed to mitigate overfitting problems. Such an approach holds the promise of enhancing the network’s capability to effectively restore blurry images of materials. In line with this recommendation, we embarked on the process of retraining and fine-tuning these methods. To gauge the efficacy of this intervention, we present the deblurring outcomes in Fig. 8.

Figure 8: The outcomes of deblurring upon the retraining and fine-tuning of these methods with our blurry dataset

This study utilizes a dataset of material blurry images to conduct a detailed analysis of the deblurring capability of the original method compared to the retraining and fine-tuning methods. The outcomes of this comparison reveal a significant enhancement in deblurring quality for material images through retraining and fine-tuning, surpassing the performance of the no-training scenario and yielding satisfactory results. Notably, the process of retraining and fine-tuning contributes to the restoration of intricate features within material images, underscoring the pivotal role of material-specific data in optimizing deblurring effectiveness. These findings offer fresh insights into the efficacy of retraining and fine-tuning strategies in effectively addressing the intricate deblurring challenges posed by material images. Furthermore, they provide valuable guidance for the future development of more potent deblurring methodologies within the domain of material science and engineering. Importantly, this study also serves as a demonstration of the potential of deep learning techniques in enhancing the quality of visual data across a wide spectrum of scientific and industrial applications.

4.4 Comparative Experiment

4.4.1 Qualitative Results

We undertake a comparative evaluation of MIDNet alongside several SOTA deblurring methods that have undergone retraining and fine-tuning, as discussed in the previous section. The deblurring outcomes produced by each of these methods are depicted in Fig. 9. Within this array of tested approaches, Restormer’s results exhibit a residual blurriness accompanied by unclear edges, which implies a limited restorative impact. The HINet method, employing a patch-based testing strategy, manifests noticeable stripe artifacts, possibly attributed to boundary discontinuities. The DMPHN approach, although improved, still retains a degree of blurriness that hampers its ability to achieve significant image enhancement. The NAFNet method, while competent, sacrifices certain fine image details. In stark contrast, our proposed MIDNet method achieves a further elevation in image quality, facilitating the restoration of additional structural details without introducing any artifacts or related issues. By observing the image, we note that our method exhibits significantly clearer microstructural contours compared to other approaches, as indicated by the red arrow in Fig. 9. This enhanced clarity allows for a more accurate analysis of the material’s surface morphology and structural features based on these finer details.

Figure 9: Qualitative comparison of image deblurring methods on the dataset

The comparison between the original image and the deblurred image obtained through the model proposed in this study is illustrated in Fig. 10. In Fig. 10a, we present the original image, while Fig. 10b depicts the image after being processed by the model. Through visual observation, it is evident that the proposed model exhibits excellent deblurring performance. The outcomes of our study highlight the exceptional capabilities of MIDNet in effectively recovering intricate structures and details within material images. This showcases its potential as a promising solution for tackling intricate deblurring issues within the realm of materials science and engineering.

Figure 10: Comparison between original images and deblurred images

4.4.2 Quantitative Results

Table 2 outlines the quantitative findings of several deblurring techniques applied to material microstructure images. Our evaluation of image quality relies on two objective metrics: PSNR and SSIM, where higher values denote enhanced performance. Significant enhancements in PSNR are observed across HINet, Restormer, DMPHN, and NAFNet after the process of retraining and fine-tuning. The respective gains in PSNR are 7.89, 9.43, 10.13, and 13.53 dB. These compelling outcomes underscore the considerable potential of deep learning in addressing the intricate challenges associated with deblurring material microstructure images. This progress lays the foundation for practical applications within this domain.

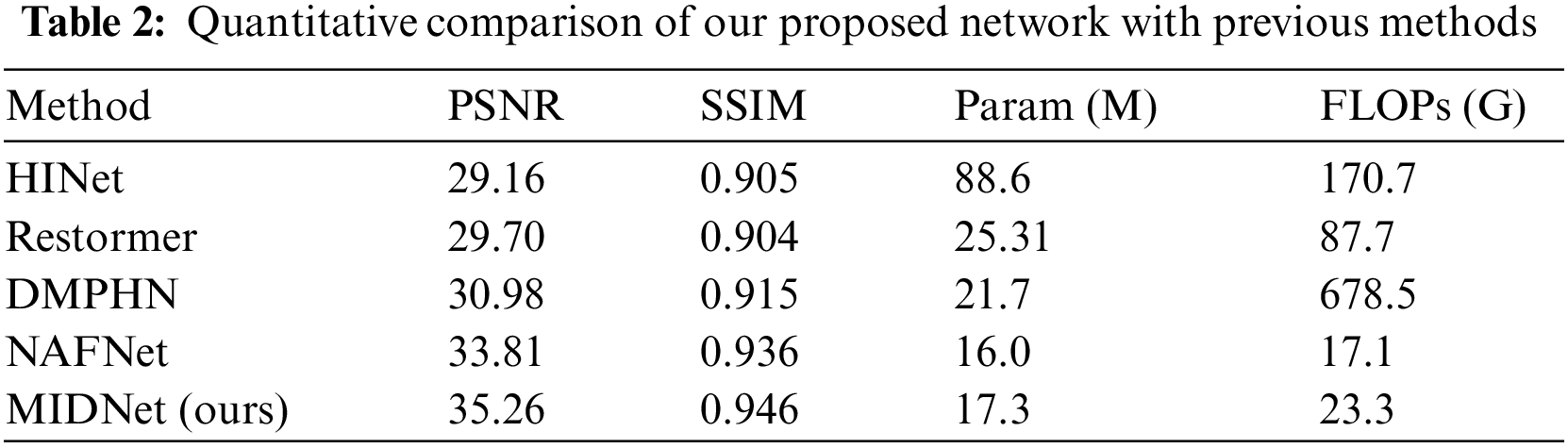
The insights provided by Table 2 highlight the substantial advancement brought forth by MIDNet, when compared with NAFNet, evaluated through both PSNR and SSIM metrics. Compared to NAFNet, MIDNet achieved an improvement of 1.45 dB in PSNR and 0.01 in SSIM. This indicates that our proposed method has an advantage in image deblurring. The efficacy of MIDNet in the deblurring task can be attributed to its integrative employment of an attention mechanism and a combination of diverse loss functions.

The attention mechanism significantly enhances the network’s ability to focus on pivotal features, leading to elevated deblurring performance. Our experiment results affirm that the simultaneous utilization of multiple loss functions empowers the network with enhanced image reconstruction supervision, consequently elevating image quality and augmenting fine detail preservation.

4.4.3 Ablation Experiment

To validate the efficacy of the newly introduced edge loss and FFT loss within the training process, we conduct ablation experiments. The outcomes of these experiments are meticulously presented in Table 3, showcasing the computed PSNR and SSIM values corresponding to each experimental configuration. The objective behind these ablation studies is to discern the impact and contribution of individual loss functions toward the process of image restoration. To achieve this, we train our model under different scenarios, each characterized by a distinct combination of loss functions. This systematic approach enables us to gain insights into the relative importance and effectiveness of each loss function in driving the enhancement of image quality.

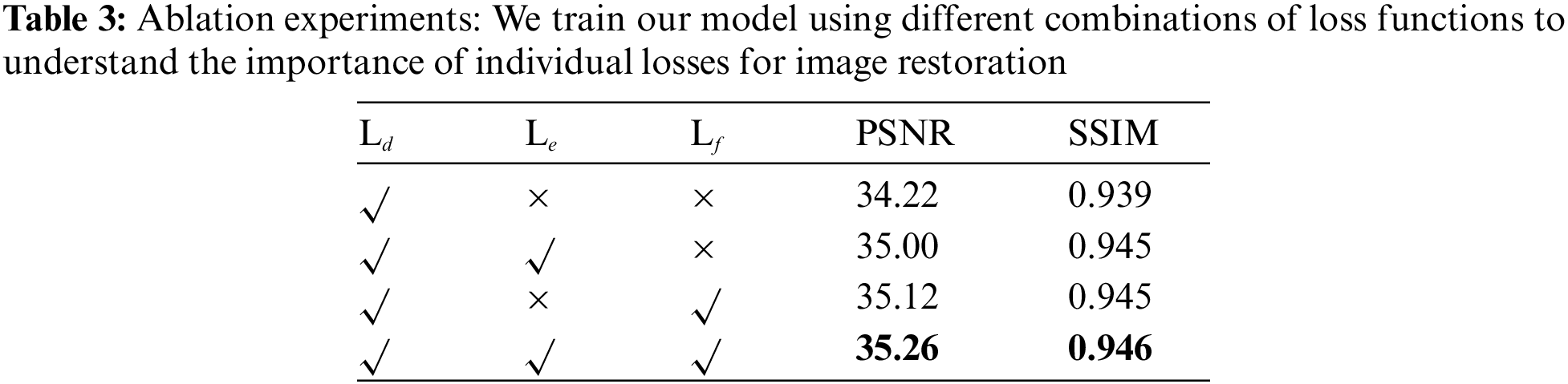
In this study, we undertake a series of ablation experiments with the intent of examining the impact of integrating various loss functions during the training phase. To maintain consistency, the Ld loss function, which plays a pivotal role in image restoration, is kept constant across all experiments. The outcomes of these ablation studies are summarized in Table 3. We observe that the inclusion of the Le loss function results in noticeable improvements in both PSNR and SSIM metrics. This suggests that the network effectively retains more intricate edge details through the utilization of this loss function. Furthermore, the inclusion of Lf loss further improves the image quality by providing more structural guidance to the network solution, as observed in row 3. It is worth noting that by combining all the loss functions during training, the network achieved its best performance. These findings highlight the importance of the proposed multi-loss functions in enhancing image restoration capabilities and offer valuable insights for the advancement of effective image restoration methods.

5  Conclusion and Future Work

In this study, we propose a method named MIDNet to address the issue of blurry images in material microstructures. MIDNet is an end-to-end deblurring network that enhances the clarity of blurry images in material microstructures by incorporating an attention mechanism and introducing multiple loss functions. Thorough qualitative and quantitative analysis indicates that MIDNet surpasses other approaches in terms of the quality of reconstructed images, marked by enhanced clarity and texture richness. Ablation experiments have also showcased the effectiveness of different loss functions within the network. Our work has the potential to encourage the extended use of deep learning within materials science and promote advancements in the mutually beneficial partnership between computer science and materials science.

The dataset utilized in this study comprises actual experimental material microstructural images. However, we acknowledge that the dataset size is relatively limited, which may potentially impact the accuracy of image deblurring when extrapolating our method to diverse materials. To address this limitation, our future research will emphasize the collection of SEM images encompassing a broader range of alloy materials, thereby expanding the dataset size. Through these endeavors, we aim to enhance the performance and adaptability of our model in the context of deblurring microstructural images across various materials. Our future work will be primarily focused on developing a video deblurring method that is specifically tailored to the demands of material science applications. Given the unique challenges posed by the complex and dynamic nature of material structures, a robust and effective video deblurring method would be of great value in enabling researchers to visualize and analyze material properties more accurately.

Acknowledgement: The authors especially acknowledge Prof. Liwu Jiang of National Center for Materials Service Safety.

Funding Statement: The current work was supported by the National Key R&D Program of China (Grant No. 2021YFA1601104), National Key R&D Program of China (Grant No. 2022YFA16038004), National Key R&D Program of China (Grant No. 2022YFA16038002) and National Science and Technology Major Project of China (No. J2019-VI-0004-0117).

Author Contributions: Study conception and design: J.X. Wang, H.Y. Yu and D.B. Sun; data collection: J.X. Wang, Z.Y. Li and P Shi; analysis and interpretation of result: J.X. Wang, P Shi. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Some dataset for the experiments uploaded to the author’s github repository: https://github.com/woshigui/MIDNet.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Reimer, “Scanning electron microscopy: Physics of image formation and microanalysis,” Meas. Sci. Technol., vol. 11, no. 12, pp. 1826–1826, 2000. doi: 10.1088/0957-0233/11/12/703. [Google Scholar] [CrossRef]

2. H. S. Kushwaha, S. Tanwar, K. Rathore, and S. Srivastava, “De-noising filters for TEM (transmission electron microscopy) image of nanomaterials,” in 2012 IEEE Conf. on Advanc. Comput. & Communicati. Technologi, Rohtak, Haryana, India, 2012, pp. 276–281. [Google Scholar]

3. R. S. Pantelic et al., “The discriminative bilateral filter: An enhanced denoising filter for electron microscopy data,” J. Struct. Biol., vol. 155, no. 3, pp. 395–408, 2006. doi: 10.1016/j.jsb.2006.03.030 [Google Scholar] [PubMed] [CrossRef]

4. H. Ma, S. Liu, Q. Liao, J. Zhang, and J. H. Xue, “Defocus image deblurring network with defocus map estimation as auxiliary task,” IEEE Trans. Image Process, vol. 31, no. 11, pp. 216–226, 2022. doi: 10.1109/TIP.2021.3127850 [Google Scholar] [PubMed] [CrossRef]

5. M. J. Fanous and G. Popescu, “GANscan: Continuous scanning microscopy using deep learning deblurring,” Light Sci. & Applicati., vol. 11, no. 1, pp. 265, 2022. doi: 10.1038/s41377-022-00952-z [Google Scholar] [PubMed] [CrossRef]

6. Z. Lian, H. Zhao, Q. Zhang, H. Wang, and E. Erdun, “Enhancement of biomass material characterization images using an improved U-Net,” Comput. Mater. Contin., vol. 72, no. 1, pp. 1515–1528, 2022. doi: 10.32604/cmc.2022.024779. [Google Scholar] [CrossRef]

7. L. Chen, X. Chu, X. Zhang, and J. Sun, “Simple baselines for image restoration,” in European Conf. on Comput. Vision, Tel Aviv, Israel, 2022, pp. 17–33. [Google Scholar]

8. C. Qiao et al., “Evaluation and development of deep neural networks for image super-resolution in optical microscopy,” Nat. Methods, vol. 18, no. 4, pp. 194–202, 2021. doi: 10.1038/s41592-020-01048-5 [Google Scholar] [PubMed] [CrossRef]

9. K. de Haan, Z. S. Ballard, Y. Rivenson, Y. Wu, and A. Ozcan, “Resolution enhancement in scanning electron microscopy using deep learning,” Sci. Rep., vol. 9, no. 1, pp. 12050, 2019. doi: 10.1038/s41598-019-48444-2 [Google Scholar] [PubMed] [CrossRef]

10. A. S. Varde, “Computational estimation by scientific data mining with classical methods to automate learning strategies of scientists,” ACM Transacti. on Knowledg. Discov. from Data (TKDD), vol. 16, no. 5, pp. 1–52, 2022. doi: 10.1145/3502736. [Google Scholar] [CrossRef]

11. Z. Pan, Y. Feng, and S. Y. Liang, “Material microstructure affected machining: A review,” Manuf. Rev., vol. 4, no. 5, pp. 5, 2017. doi: 10.1051/mfreview/2017004. [Google Scholar] [CrossRef]

12. A. Levin, Y. Weiss, F. Durand, and W. T. Freeman, “Understanding and evaluating blind deconvolution algorithms,” in 2009 IEEE Conf. on Comput. Vision and Pattern Recognit, Miami, FL, USA, 2009, pp. 1964–1971. [Google Scholar]

13. A. Chakrabarti, “A neural approach to blind motion deblurring,” in European Conf. on Comput. Vision, Amsterdam, The Netherlands, 2016, pp. 221–235. [Google Scholar]

14. C. Song et al., “Image forgery detection based on motion blur estimated using convolutional neural network,” IEEE Sens. J., vol. 19, no. 23, pp. 11601–11611, 2019. doi: 10.1109/JSEN.2019.2928480. [Google Scholar] [CrossRef]

15. Y. T. Wang et al., “Rain streaks removal for single image via kernel-guided convolutional neural network,” IEEE Trans. Neur. Net. Lear. Syst., vol. 32, no. 8, pp. 3664–3676, 2020. [Google Scholar]

16. J. Sun, W. Cao, Z. Xu, and J. Ponce, “Learning a convolutional neural network for non-uniform motion blur removal,” in 2015 IEEE Conf. on Comput. Vision and Pattern Recognit, Boston, MA, USA, 2015, pp. 769–777. [Google Scholar]

17. M. Chen, Y. Quan, Y. Xu, and H. Ji, “Self-supervised blind image deconvolution via deep generative ensemble learning,” IEEE Trans. Circ. Syst. Video Technol., vol. 33, no. 2, pp. 634–647, 2022. doi: 10.1109/TCSVT.2022.3207279. [Google Scholar] [CrossRef]

18. S. M. A. Sharif et al., “MedDeblur: Medical image deblurring with residual dense spatial-asymmetric attention,” Math., vol. 11, no. 1, pp. 115, 2022. doi: 10.3390/math11010115. [Google Scholar] [CrossRef]

19. H. Zhang, Y. Dai, H. Li, and P. Koniusz, “Deep stacked hierarchical multi-patch network for image deblurring,” in 2019 IEEE Conf. on Comput. Vision and Pattern Recognit, Long Beach, CA, USA, 2019, pp. 5978–5986. [Google Scholar]

20. L. Chen, X. Lu, J. Zhang, X. Chu, and C. Chen, “HINet: Half instance normalization network for image restoration,” in 2021 IEEE Conf. on Comput. Vision and Pattern Recognit, 2021, pp. 182–192. [Google Scholar]

21. C. H. Liang, Y. A. Chen, Y. C. Liu, and W. H. Hsu, “Raw image deblurring,” IEEE Trans. Multimedia, vol. 24, pp. 61–72, 2020. doi: 10.1109/TMM.2020.3045303. [Google Scholar] [CrossRef]

22. C. Xu, J. Wang, J. Tao, J. Zhang, and R. Y. Zhong, “A knowledge augmented image deblurring method with deep learning for in-situ quality detection of yarn production,” Int. J. Prod. Res., vol. 61, no. 13, pp. 4220–4236, 2023. doi: 10.1080/00207543.2021.2010827. [Google Scholar] [CrossRef]

23. S. W. Zamir et al., “Restormer: Efficient transformer for high-resolution image restoration,” in 2022 IEEE Conf. on Comput. Vision and Pattern Recognit, New Orleans, LA, USA, 2022, pp. 5728–5739. [Google Scholar]

24. M. Wang, Q. Li, Y. Gu, L. Fang, and X. X. Zhu, “SCAF-Net: Scene context attention-based fusion network for vehicle detection in aerial imagery,” IEEE Geosci. and Remote Sens. Letters, vol. 19, pp. 1–5, 2021. [Google Scholar]

25. H. Yang, L. Guo, X. Wu, and Y. Zhang, “Scale-aware attention-based multi-resolution representation for multi-person pose estimation,” Multimedia Syst., vol. 28, no. 1, pp. 57–67, 2022. doi: 10.1007/s00530-021-00795-5. [Google Scholar] [CrossRef]

26. J. Guo, H. Feng, H. Xu, W. Yu, and S. Shuzhi Ge, “D3-Net: Integrated multi-task convolutional neural network for water surface deblurring, dehazing and object detection,” Eng. Appl. Artif. Intel., vol. 117, no. 3641, pp. 105558, 2023. doi: 10.1016/j.engappai.2022.105558. [Google Scholar] [CrossRef]

27. Y. Cui, Y. Tao, W. Ren, and A. Knoll, “Dual-domain attention for image deblurring,” in 37th AAAI Conf. Arti. Intell., Washington DC, USA, 2023, vol. 37, no. 1, pp. 479–487. doi: 10.1609/aaai.v37i1.251223. [Google Scholar] [CrossRef]

28. C. Guo, X. Chen, Y. Chen, and C. Yu, “Multi-stage attentive network for motion deblurring via binary cross-entropy loss,” Entropy, vol. 24, no. 10, pp. 1414, 2022. doi: 10.3390/e24101414 [Google Scholar] [PubMed] [CrossRef]

29. D. Ma et al., “Automatic defogging, deblurring, and real-time segmentation system for sewer pipeline defects,” Automat. Constr., vol. 144, no. 2, pp. 104595, 2022. doi: 10.1016/j.autcon.2022.104595. [Google Scholar] [CrossRef]

30. Z. Shen et al., “Human-aware motion deblurring,” in 2019 IEEE Conf. on Comput. Vision and Pattern Recognit, Long Beach, CA, USA, 2019, pp. 5572–5581. [Google Scholar]

31. S. Wang and B. Liu, “Deep attention-based lightweight network for aerial image deblurring,” in Int. Conf. on Pattern Recognit, Montreal, Quebec, Canada, 2022, pp. 111–118. [Google Scholar]

32. X. Zhang, R. Jiang, T. Wang, P. Huang, and L. Zhao, “Attention-based interpolation network for video deblurring,” Neurocomputing, vol. 453, pp. 865–875, 2021. doi: 10.1016/j.neucom.2020.04.147. [Google Scholar] [CrossRef]

33. Y. N. Dauphin, A. Fan, M. Auli, and D. Grangier, “Language modeling with gated convolutional networks,” in Int. Conf. on Machine Learning, Sydney, NSW, Australia, 2017, pp. 933–941. [Google Scholar]

34. D. Hendrycks and K. Gimpel, “Gaussian error linear units (gelus),” arXiv preprint arXiv:1606.08415, 2016. [Google Scholar]

35. J. Hu, L. Shen, and G. Sun, “Squeeze-and-excitation networks,” in 2018 IEEE Conf. on Comput. Vision and Pattern Recognit, Salt Lake City, UT, USA, 2018, pp. 7132–7141. [Google Scholar]