An Innovative K-Anonymity Privacy-Preserving Algorithm to Improve Data Availability in the Context of Big Data

1  Introduction

With the rapid development of blockchain technology, it has offered Internet of Things (IoT) systems a more efficient and stable decentralized method for data storage and management. But at the same time, it has also raised a series of network security issues. For example, data privacy [1–3], validation techniques [4], and transmission reliability [5] are difficult to guarantee, which will lead to the leakage of user privacy. Nowadays, we generate a large amount of data every day, which contains great application value [6] but also implies sensitive information, such as location information [7–10] and transaction information [11]. Once this data is stolen by adversaries, it will possibly cause the leakage of user privacy. To solve the privacy security problems in networks in the context of blockchain and IoT integration, privacy-preserving algorithms are essential in addition to techniques such as authentication [8], distributed storage and computing [12–15], big data management [16,17], and anomaly detection [18]. The K-anonymity algorithm [19] is an effective privacy-preserving algorithm with lower time complexity compared with commonly used cryptographic algorithms such as homomorphic encryption [20]. In addition, compared to the commonly used differential privacy techniques, this algorithm does not need to add noise [21] to sensitive information, thus preserving the specific values of sensitive attributes for the subsequent statistical analysis process. The K-anonymity algorithm obtains less accurate datasets through steganography and generalization techniques so that at least K quasi-identified attributes in a certain sub-table have the same value, which in turn ensures that an adversary cannot use these quasi-identified attributes to link to a particular record [22]. By anonymizing the data with a K-anonymization algorithm before storing [23], publishing [24], or transmitting [25], the privacy of users can be secured to a certain extent. For example, by generalizing the age property in a data table from 25 to interval [20, 30], an adversary will not be able to guess the exact value of the age directly. However, the algorithm can lead to reduced usability of the data after generalization, which will be detrimental to the subsequent use of the data for statistical analysis [26] or forecasting. When the data owners get the data, they want to perform statistical analysis or prediction on this data. For example, they want to know the age distribution characteristics of the population in a certain region based on these data, but if the loss of information after generalization is too large, such as generalizing age from 50 to 100 [10], then the data owner will not be able to arrive at an accurate statistical analysis or prediction result based on these generalized values. Therefore, how to process the data with the K-anonymity algorithm to improve the usability of the data while safeguarding privacy is the main problem to be solved in this paper.

The K-anonymity algorithm consists of three processes: attribute classification, clustering, and generalization [27]. In clustering, the more similar the data in an equivalence class, the smaller the generalized interval or value, and the greater the availability of the generalized data [28]. Therefore, it is crucial to know how to perform equivalence class classification based on the similarity between tuples. The most common equivalence class partitioning method is the k-means clustering algorithm, which is a classical artificial intelligence algorithm. This algorithm guarantees that tuples belonging to the same equivalence class are as similar as possible by aggregating tuples that are close to each other to improve the usability of the data after generalization [29,30]. k-means clustering algorithm as an artificial intelligence [31] algorithm has the advantages of simplicity, speed, and low time complexity [32]. However, this clustering algorithm itself is unstable due to the randomness of the initial cluster center selection [33] and thus is not conducive to achieving a stable K-anonymity effect. To address the initial clustering selection problem of the k-means algorithm, Bhattacharya et al. explored the k-means++ algorithm and suggested that a better clustering effect can be achieved when the initial prime centers are as far away from each other as possible [34], however, the algorithm still suffers from randomness in the selection of the first prime center. The clustering algorithm in this paper is improved based on the above clustering algorithm, and the comparison of the improved effect is shown in Table 1.

Moreover, the greedy algorithm, as a common algorithm in the field of deep learning [35], is now also applied in K-anonymization algorithms to improve the usability of the data. Aghdam et al. applied a greedy algorithm in the K-anonymization algorithm to achieve high data utility [36]. Tang et al. proposed to achieve clustering and generalization of data by a greedy algorithm and binary classification as a way to fully exploit the value of data and safeguard user privacy [37]. Based on this, we apply the greedy algorithm in the K-anonymity algorithm to achieve lower information loss. The specific contributions are as follows:

1. We designed the information loss function for the K-anonymity algorithm. Based on the information quantity theory, we represent the information loss after the generalization of quasi-identified attributes, and also calculate the influence degree for each quasi-identified attribute on sensitive attributes, and set the weight value for each quasi-identified attribute according to the influence degree to improve the reasonableness of information loss assessment.

2. We improve the 2-means clustering algorithm. We designed a mean-center method to select the initial center of mass for clustering, which improves the effect of 2-means clustering and guarantees the stability of the clustering effect at the same time.

3. Based on the 2-means clustering algorithm and greedy algorithm, we propose an improved K-anonymity algorithm to reduce information loss while guaranteeing privacy. Finally, we experimentally demonstrate the effectiveness of the algorithm in improving the effect of 2-means clustering and reducing information loss.

The algorithm is innovative because it improves on the original algorithm by clustering the clusters to achieve more stable results and less loss of information. In addition, it introduces the amount of information to design the information loss function and uses the greedy algorithm to design the anonymization algorithm which again reduces the information loss. The overall structure block diagram of the algorithm in this paper is shown in Fig. 1.

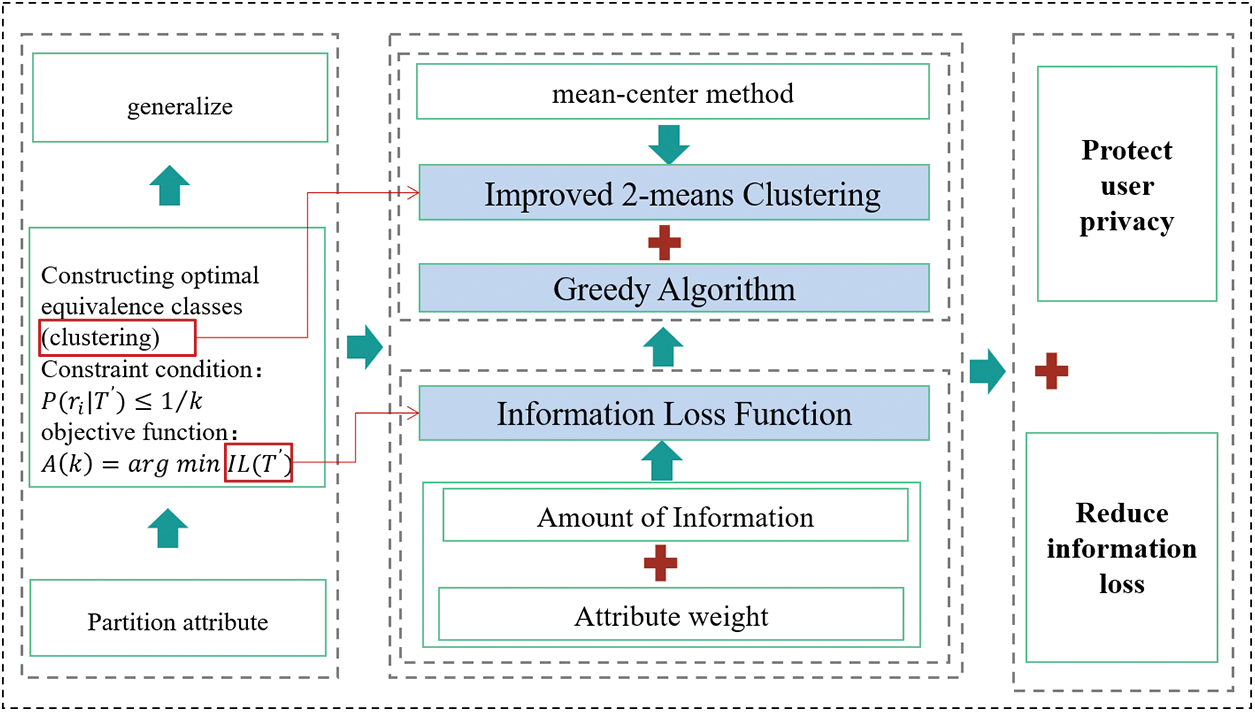
Figure 1: Block diagram of the overall structure of the algorithm

2  Basic Knowledge

This section will introduce the basics covered in this paper, including the introduction to the K-anonymity algorithm, the amount of information, and the k-means clustering algorithm.

2.1 K-Anonymity

The development of smart IoT [38] allows people and machines to be interconnected through the network, which also generates a huge amount of data that contains users’ privacy. K-anonymity algorithms [39] can solve the privacy leakage problem by ensuring that each record in the dataset cannot be distinguished from other K-1 individuals for sensitive attributes. Through generalization and steganography techniques, less accurate data is obtained such that there are at least K records for the same quasi-identifier, making it impossible for an observer to link records through the quasi-identifier [40]. K-anonymization algorithms are used in the context of big data [41] because of their low time complexity. Its processing process consists of attribute classification, clustering, and generalization. Attribute classification refers to the classification of attributes in a data table into identifying attributes, quasi-identifying attributes, and sensitive attributes. Identifying attributes are attributes that uniquely identify the user and are deleted directly for them. Sensitive attributes are attributes that the user does not want to be known by others, and they are not processed. The rest of the attributes are quasi-identifiable attributes, these attributes cannot be used alone to identify a user, such as age and gender. However, an adversary may infer sensitive information about a user based on some quasi-identifying attributes. For example, an adversary, with some background knowledge, may be able to locate a specific user based on information such as age, gender, and region of a record, so the quasi-identifiable attributes are generalized to protect the user’s privacy. Clustering refers to clustering tuples with high similarity into one class. Generalization refers to the generalization of attribute values of the same class.

2.2 Amount of Information

The amount of information [42] is the amount of information needed to select one event from N equally likely events. Shannon’s information theory applies probability to describe uncertainty. The smaller the probability of an event appearing, the more uncertainty there is, and the more information there is, and vice versa. After generalizing the data, the smaller the probability of an adversary inferring the true value through the generalized interval, the more information is indicated, but also the greater the loss of information. Therefore, we use the amount of information to measure the loss of information after the generalization of data tables. The Information volume of information x is denoted as:

l(x)=−log⁡P(x)(1)

where P(x) denotes the probability of occurrence of x. The log in the information quantity function of this paper is all taken to a base of 2.

2.3 k-means Clustering Algorithm

k-means clustering is a common algorithm in artificial intelligence and belongs to unsupervised machine learning algorithms. The algorithm has appeared in application scenarios such as the Internet of Things and cloud computing [43] and is used to solve clustering problems. The k-means clustering algorithm puts similar objects together according to some rules. Distance is a measure of similarity. The closer the distance of each object in a class, the better the clustering will be. In k-means clustering, k denotes the number of classes that need to be determined first before clustering. In this paper, we use binary classification for clustering, so k is 2. The steps of this algorithm are as follows [44]:

Step 1: Select the initialized k samples as the initial clustering centers notated as O=O1,O2,…,Ok;

Step 2: For each sample ri in the dataset, calculate its distance to each initial clustering center and assign it to the class corresponding to the clustering center with the smallest distance;

Step 3: For each class classi, recalculate the clustering center Oi;

Step 4: Repeat Step 2 and Step 3 above until the set number of iterations is reached or the clustering centers no longer change.

In this paper, we use binary classification for clustering, so k is 2.

3  Algorithm Design

In this section, we introduce the K-anonymity algorithm in this paper. Specifically, we introduce the designed information loss function and the 2-means artificial intelligence clustering algorithm. Finally, we apply the information loss function designed in this paper to the K-anonymity algorithm and construct the K-anonymity privacy-preserving algorithm in this paper based on two artificial intelligence algorithms, i.e., the greedy algorithm and the improved 2-means clustering algorithm. The parameters of this paper are defined in Table 2.

3.1 Information Loss Function Based on the Amount of Information

In this paper, we measure the information loss after generalization based on the amount of information. In addition, there are associations between attributes [45], and different quasi-identified attributes have different degrees of influence on sensitive attributes. In this section, we assign a weight to each quasi-identified attribute based on its influence on the sensitive attribute and introduce the weight into the information loss function. When generalizing the classified quasi-identified attributes, for numerical quasi-identifiers, the original data value is replaced by the minimum value field in the equivalence set. For example, generalize age 10 to interval [5, 15]. For Subtype quasi-identifiers, they are generalized to a minimum value that is larger than the original quasi-identifier value. For example, generalizing gender male as gender unknown.

For a numerical quasi-identification attribute, the amount of information loss for the tth numerical quasi-identification attribute value of a data table after a certain generalization is denoted as:

IL(Nt)={γt∑i=1n−log⁡(110x(stmax−stmin)+1)−log⁡(1|Rt|)=γtnlog⁡[10x(stmax−stmin)+1]log⁡(|Rt|),|Rt|>10,|Rt|=1(2)

where stmax denotes the maximum value under the tth numeric attribute in the generalized table, stmin denotes the minimum value under the tth numeric attribute in the generalized table, |stmax−stmin+1| denotes the number of values that can be taken for the tth numeric attribute in the generalized table, and |Rt| denotes the number of values contained in the total value field of the tth numeric attribute, |Rt|≥1. n is the number of records in this generalized data table. x=0,1,2,… symbolizes the step size of the value taken by the numeric attribute, if the value of the attribute takes a step size of 1, such as the age attribute, then x=0, if the step size is 0.1, then x=1.

For subtype quasi-identification attributes, assuming that the attribute weights are calculated in the order of numeric attributes first and subtype attributes second, and that there are m numeric attributes, the amount of information loss for the τth subtype quasi-identification attribute of a generalized data table is denoted as:

IL(Cτ)={γτ+m∑i=1n−log⁡(1leaf(Tτ))−log⁡(1leaf(TτR))=nγτ+mlog⁡(leaf(Tτ))log⁡(leaf(TτR)),leaf(TτR)>10,leaf(TτR)=1(3)

where leaf(Tτ) denotes the number of leaf nodes under the generalized value of the τth subtype attribute in this generalization table, and leaf(TτR) denotes the total number of leaf nodes in the classification tree where the τth subtype attribute is located, leaf(TτR)≥1. n is the number of records in the data table.

The amount of information lost in a particular generalized table after generalization is denoted as:

IL(DT ′)=∑t=1mIL(Nt)+∑τ=1nIL(Cτ)(4)

where γt, γτ+m represent the attribute weights, and assuming that the attribute weights are calculated in the order of numerical attributes first and subtype attributes second, we have:

∑t=1mγt+∑τ=1nγτ+m=1(5)

The total information loss after anonymization is equal to the sum of the information loss of each generalization table.

3.2 The 2-Means Improvement Algorithm Based on the Mean-Center Method

Before generalizing the data by a K-anonymization algorithm, to improve the usability of the anonymized data, the data with high similarity needs to be clustered into one class by a clustering algorithm. In this paper, an improved 2-means clustering algorithm is used for clustering. Next, we present the definition of the distance between data and tuples when applying the 2-means algorithm for clustering, and the mean-center method designed for initial center of mass selection.

3.2.1 Definition of Distance between Data and Tuples

(1) Distance between data

For a certain numerical quasi-identification attribute, let R be a finite numerical domain, and the distance between any values si,sj∈R in the tth numerical quasi-identification attribute is denoted as:

disN(si,sj)=γt|si−sj||smax−smin|(6)

where smax denotes the maximum value of the total value domain of the attribute and smin denotes the minimum value of the total value domain of the attribute.

For a subtype quasi-identification attribute, let TR be a classification tree R. Assuming that the attribute weights are calculated in the order of numerical attributes first and subtype attributes second and that there are m numerical attributes, the distance between any values si,sj∈R in the τth subtype quasi-identification attribute is denoted as:

disC(si,sj)=γτ+mleaf( ∧(si,sj))leaf(TR)(7)

where leaf( ∧(si,sj)) denotes the number of leaf nodes under the tree rooted by the smallest common ancestor of si and sj in the classification tree, and leaf(TR) denotes the total number of leaf nodes of the classification tree T.

(2) Distance between tuples

The distance between each data tuple is equal to the sum of the distances between each quasi-identified attribute in the tuple. Denote the tuple TU={N1,N2…Nm,C1,C2…Cn,S}, where N1,N2…Nm denotes m numerical quasi-identified attributes in a record, C1,C2…Cn denotes n sub-typed quasi-identified attributes in a record, and S is a sensitive attribute in a record, then the distance between tuple TUi and TUj in this scheme can be expressed as:

dis(TUi,TUj)=∑t=1mdistN(si,sj)+∑τ=1ndisτC(si,sj)(8)

3.2.2 Selection of the Center of Mass

To improve the clustering effect and ensure the stability of the clustering effect, we propose a mean-center method to select the initial center of mass for the 2-means algorithm. The algorithm is influenced by the idea of the farthest distance in the k-means++ algorithm. It aims to find the farthest point in the class and to avoid the problem of unstable effects caused by randomness. This section describes how to choose the initial center of mass and how to update the center of mass in this paper.

(1) Selection of the initial center of mass mean center method

In this paper, 2-means clustering is used for classification, and two initial centers of mass need to be selected for each clustering. In previous studies, the most common methods for selecting two centers of mass are the random selection method and the farthest distance method. The random selection method can affect the effect of clustering and make the clustering results unstable. The farthest distance method refers to choosing two points as far as possible from each other as the center of mass to make the clustering as effective as possible [46]. However, to fix two centers of mass, we need each node to be compared with other nodes, which have high time complexity. Based on this, we designed a mean center of mass method to select the initial center of mass. It can avoid the unstable clustering results and also make the selected initial center of mass as far as possible. The method is designed as shown in Algorithm 1.

When this scheme performs calculations on tuples, it refers to calculations on quasi-identifiers only. For numeric quasi-identifier attributes, the mean value of the tth numeric attribute in the data table can be expressed as:

mean(Nt)=∑i=1nsin(9)

where si denotes the value of the tth numeric attribute under the ith tuple and n is the number of tuples in the table.

For subtype quasi-identification attributes, direct averaging operations cannot be performed like numerical attributes. Therefore, in this paper, we design the mean value representation method for the quasi-identified attributes of subtypes by combining the property that the mean value is the smallest sum of squares of each number. Specifically, the mean value of the τth subtype attribute in the data table can be expressed as:

s=argmin∑i=1n(si−s)2(10)

mean(Cτ)=s(11)

where s and si are the values under a quasi-identified attribute in the equivalence class.

(2) Renewal of the center of mass

The k-means algorithm, after classification, for each class to re-select the clustering center and repeatedly iterate the clustering process until the required number of iterations is reached or the location of the clustering center no longer changes when the clustering ends [47]. In this process, we calculate the mean value of the data as the updated center of mass. The updated center of mass is denoted as:

O ′={mean(N1),mean(N2),…,mean(Nm),mean(C1),mean(C2),…,mean(Cn)}(12)

3.3 K-Anonymity Algorithm Based on Greedy Algorithm and Improved 2-Means Clustering

To make the K-anonymization algorithm improve the usability of the data while safeguarding user privacy, we use the greedy algorithm and 2-means clustering to cluster and generalize the dataset. The specific K-anonymization algorithm is designed as follows:

(1) Determination of identification attribute (La), quasi-identification attribute (QLa), and sensitive attribute (S)

We consider attributes that uniquely identify a user as quasi-identifying attributes and remove them directly. No processing is done for sensitive attributes. Other attributes, considered as quasi-identifying attributes, are generalized.

(2) Construct equivalence classes and generalize

In this paper, we construct an equivalence class that minimizes the loss of information under the condition of privacy protection. To guarantee the privacy of the data, based on the definition of the K-anonymity algorithm, the processed data table should satisfy the following equation:

P(ti|DT ′)≤1/K(13)

where ti denotes the ith record in the user data table and DT ′ denotes the data table after the clustering and generalization process. To achieve a certain goal, algorithms often need to satisfy a minimum threshold in their design. To guarantee that the amount of information loss is as small as possible, the algorithm should also satisfy the following equation:

K=arg minIL(DT ′)(14)

where IL(DT ′) indicates the degree of information loss in the data table DT ′ after the generalization process. Based on this, we classify the original data based on the improved 2-means algorithm and greedy algorithm. The overall algorithm flow is shown in Algorithm 2.

4  Simulation Experiments and Results

In this section, we mainly introduce the data set used for the experiments and the preprocessing process of the data, analyze the contribution of quasi-identified attributes, and verify that the 2-means algorithm designed in this paper can achieve better clustering results and the improved K-anonymity algorithm can better reduce information loss.

4.1 Experimental Data Set

This experiment uses the Adult dataset from the UCI machine learning repository, which contains partial U.S. Census data with over 30,000 records and is widely used in privacy protection and data mining research. The dataset has been de-identified with user identification attributes, and the remaining 15 attributes cover sub-type attributes and numerical attributes, such as age, job category, gender, etc. In addition, among these attributes, the attribute education-num corresponds to the attribute education, so only one attribute is kept in this paper for the experiments. Finally, we randomly selected 1000 data in the dataset, set income as a sensitive attribute, and set the remaining 13 attributes as quasi-identifying attributes for the simulation experiments in this paper.

4.2 Data Pre-processing

In this paper, the data was pre-processed before the experiments, including three processes data missing value processing, data standardization and normalization, and outlier processing.

4.2.1 Missing Value Handling

There are some missing values in the dataset, and before starting the experiment, this paper first deals with these missing values. For numerical attributes, the missing values are filled with the average of the data under the attribute. For the sub-type quasi-identified attribute, the missing values are filled with the plural of the values under the attribute, and then the complete experimental data set is obtained.

4.2.2 Data Standardization and Normalization

When clustering data using the k-means algorithm, the data needs to be standardized and normalized to achieve accurate clustering results. In this paper, the data are standardized using the Z-score [48]. Specifically, the data are processed by the following equation:

x ′=x−mean(x)Var(x)(15)

where mean(x) refers to the mean of x and Var(x) refers to the standard deviation of x. In addition, we use the maximum-minimum normalization to normalize the data. The formula is as follows:

x ′=x−xminxmax−xmin(16)

where xmax represents the maximum value of x in the data and xmin represents the minimum value of x in the data. After processing, the data values in the data set are in the interval [0,1].

4.2.3 Outlier Processing

Outliers [49] can affect the effectiveness of k-means clustering. We use the 3σ method to detect outliers in the data, which is based on the principle of 3σ of normal distribution to detect outlier points. If the data is in the interval [μ−3σ,μ+3σ], it is a normal point, and conversely, it is an outlier. Specifically, the following formula can be used to determine whether a point is an outlier.

d=x−μσ(17)

where μ refers to the mean of the data and σ refers to the standard deviation of the data. For outlier points existing in the data set, they are not taken into account in the process of calculating the mean value to select the initial center of mass.

4.3 Quasi-Identification Attribute Impact Degree Analysis

The weights of each attribute are taken into account when we design the information loss, and they represent the degree of influence of the quasi-identified attribute on the sensitive attribute. In the experiments, we use a machine learning [50] algorithm, namely logistic regression, to obtain the degree of influence of each quasi-identified attribute on the sensitive attribute according to the characteristics of the attributes, and the results are shown in Fig. 2. The algorithm can analyze the influence of the independent variables on the dependent variable. First, we construct a logistic regression model to obtain the coefficients of each independent variable in the model and then calculate the contribution of each quasi-identified attribute to the sensitive attribute based on the coefficients. Finally, the contribution degrees are processed so that the contribution degrees of each quasi-identified attribute are summed to 1, and the best combination of the weights of each quasi-identified attribute is obtained.

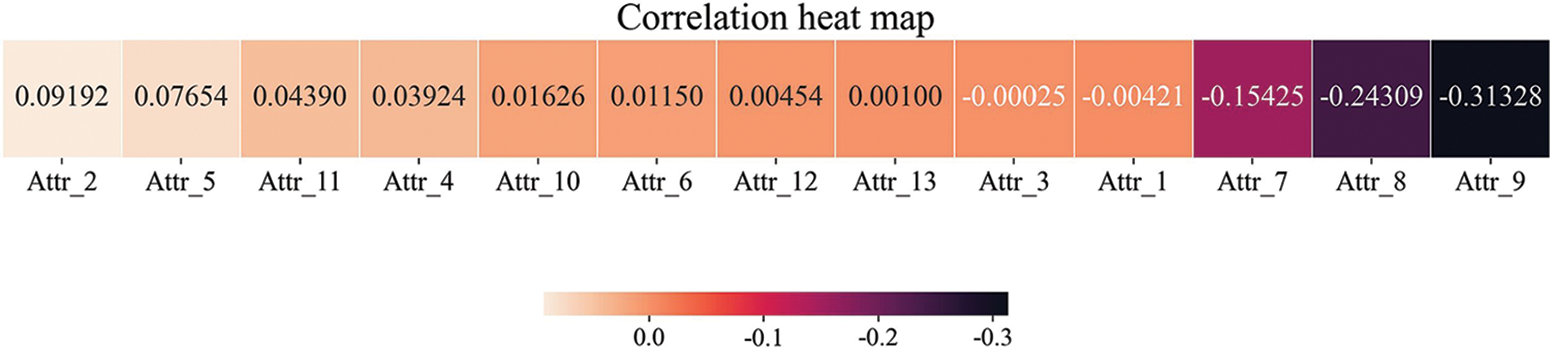
Figure 2: Degree of influence of each quasi-identified attribute on sensitive attributes

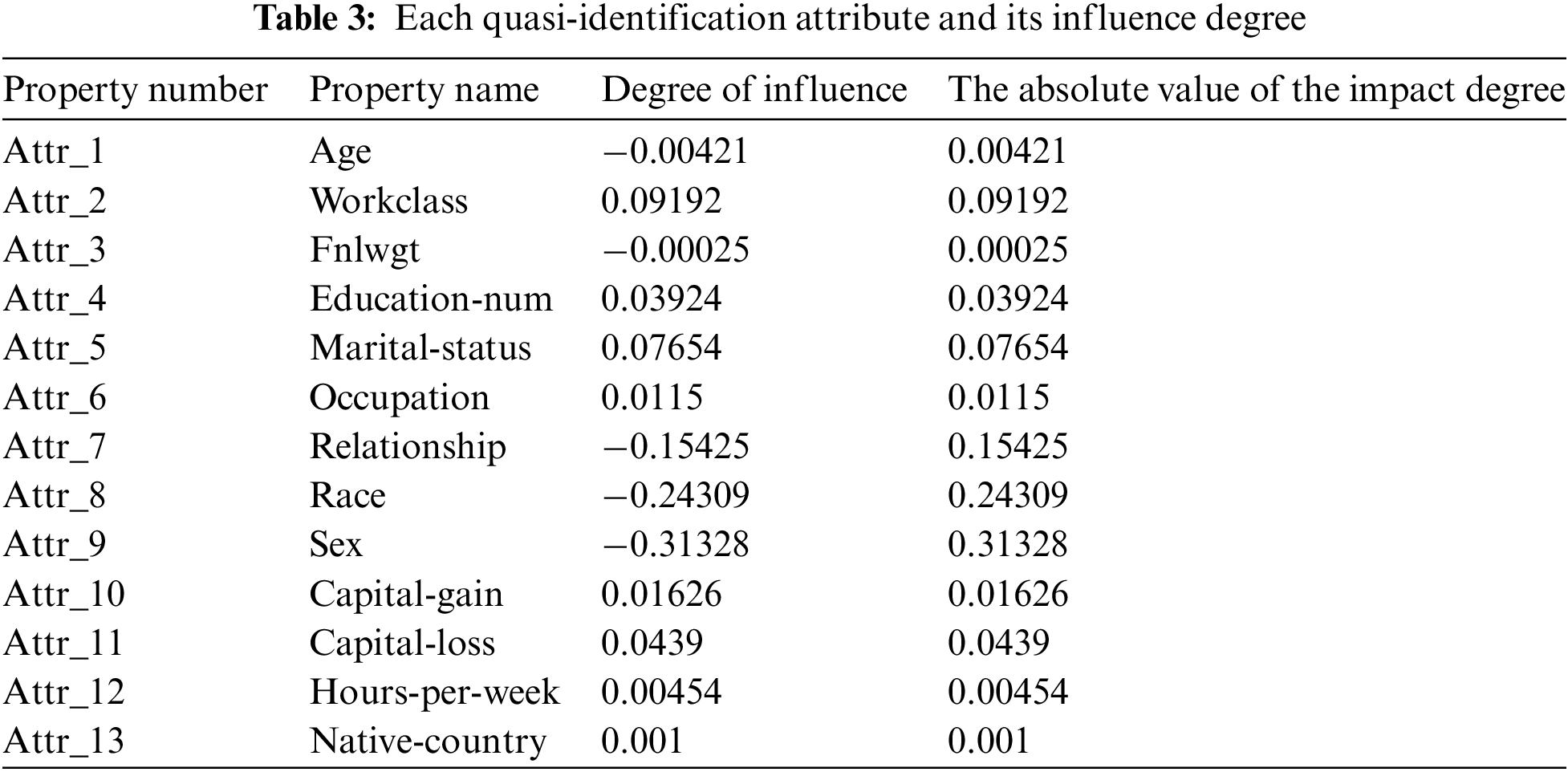
We use the absolute value of the influence degree as the weight value of each quasi-identified attribute. Table 3 shows the attribute name, influence degree, and absolute value of the influence degree corresponding to each attribute number.

4.4 2-Means Algorithm Improvement Effect

To verify the effect of 2-means algorithm improvement, simulation experiments are set up in this paper to compare the clustering effect of this scheme with the clustering effect of the randomized center of mass method. When measuring the clustering effect, we use the contour coefficient method, which is a clustering evaluation index used to evaluate the effect of data clustering. Its value ranges from [–1, 1], the higher the similarity of the data within a class and the lower the similarity of the data between classes, the larger the contour coefficient will be, which means the better the clustering effect. To enhance the accuracy of the experiment, 30 comparative experiments were conducted in this scheme, as shown in Fig. 3 for the comparison of the contour coefficients under 30 trials.

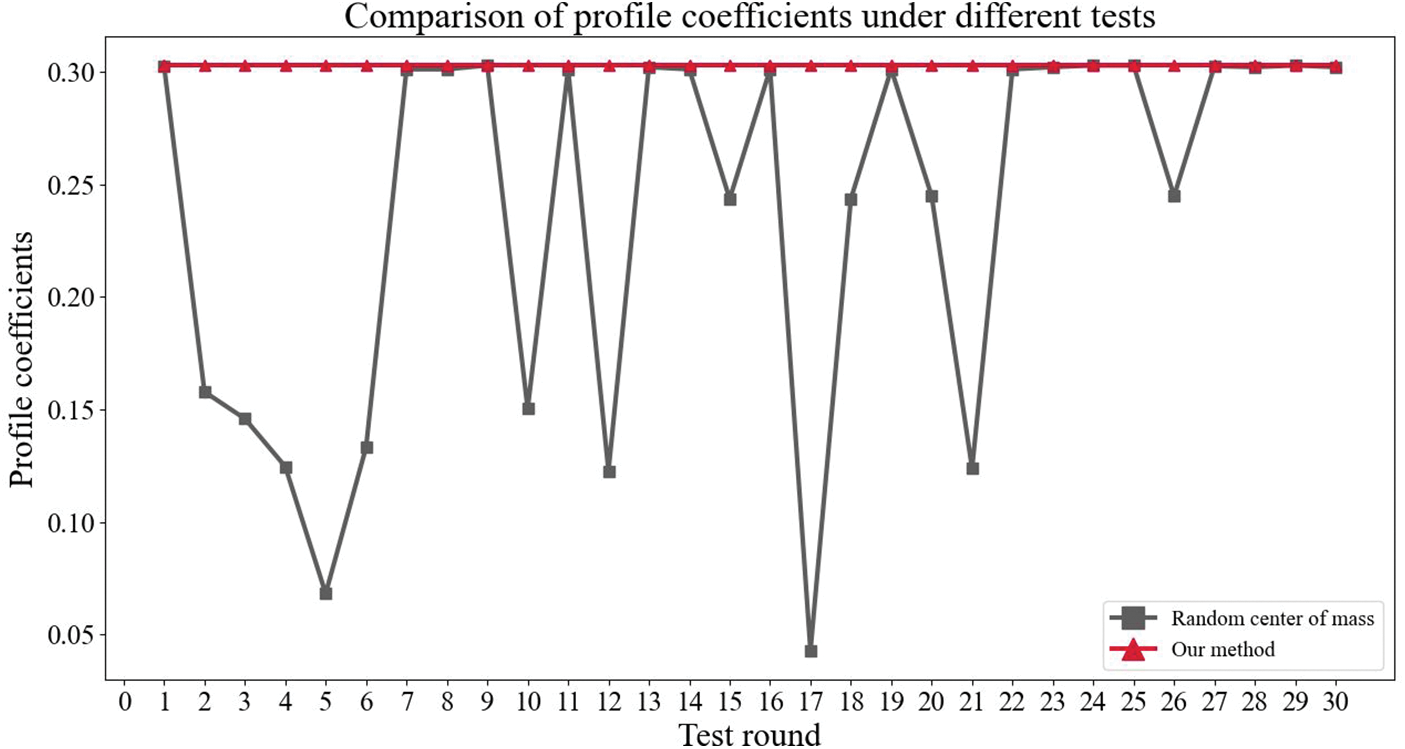
Figure 3: Comparison of profile coefficients under different tests

As can be seen from Fig. 3, in each experiment, the contour coefficients of the improved 2-means method in this paper are greater than or equal to the 2-means method under random prime selection. Therefore, it has been proved that our method has a better clustering effect. In addition, it can be seen that the improved 2-means method adopted in this scheme obtains a stable clustering effect because the center of mass is determined. That is, compared with the 2-means method under random center of mass selection, our method is both stable and improves the clustering effect.

To demonstrate the magnitude of the clustering effect improvement, we compare the average contour coefficients under a different number of experiments. In general, the more the number of experiments, the closer to the real situation, as can be seen from Fig. 4, our method has a greater improvement in the average contour coefficient when the number of experiments is 30. To show the improvement of the clustering effect more specifically, the average of the improvement rate of our algorithm under 30 experiments is calculated in this paper, and from the calculation results, the clustering effect of our algorithm has improved by 124.92% over the 2-means method under the random center of mass, which achieves a good improvement effect.

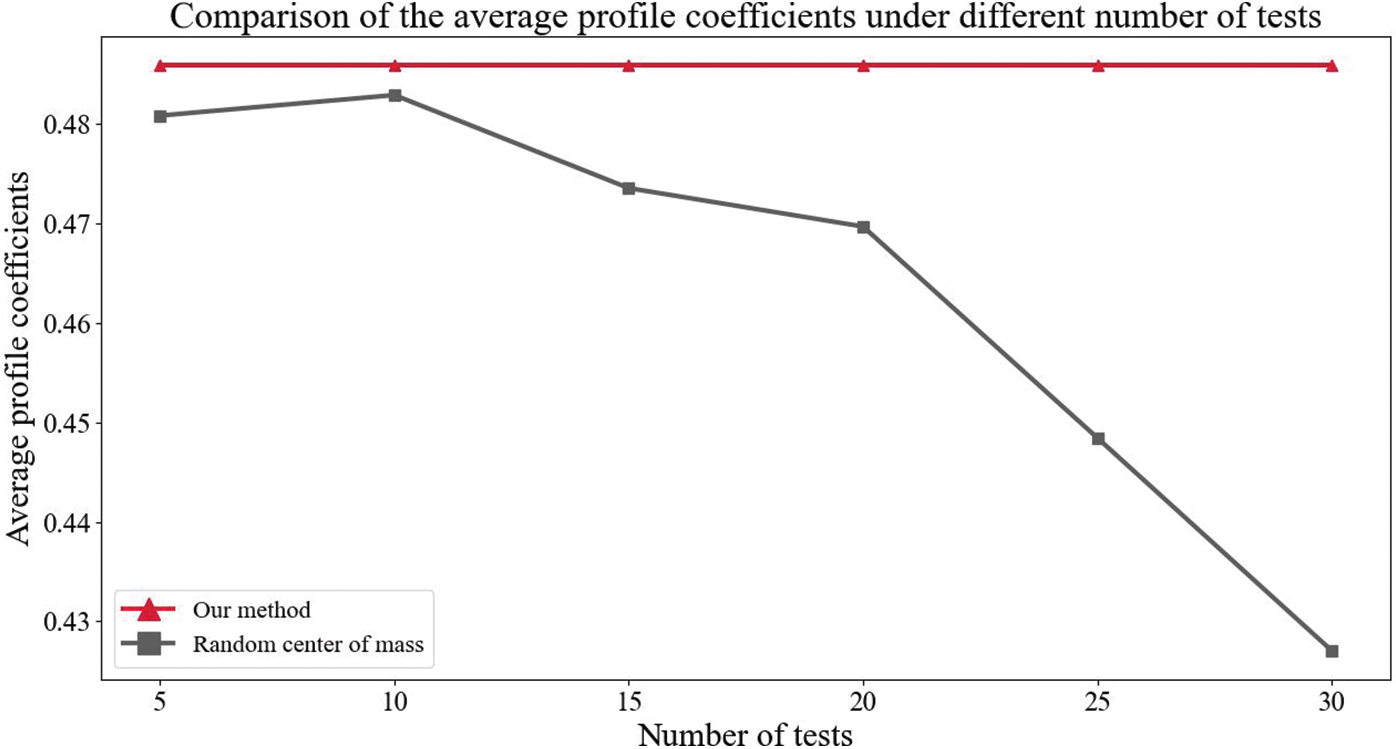
Figure 4: Comparison of the average profile coefficients under different number of tests

4.5 K-Anonymity Algorithm Improvement Effect

To verify the overall improvement of the K-anonymization algorithm in this scheme, simulation experiments are designed in this paper. First, we compared the information loss when using this scheme with the information loss from the direct generalization of the original data table. In addition, to verify the effect of the improvement of the 2-means algorithm on the degree of information loss of the whole K-anonymization algorithm, the degree of information loss using our method was compared with the degree of information loss using the randomized center of mass method.

(1) Overall information loss of K-anonymity algorithm

Fig. 5 shows the change of information loss with different K values. As the K value increases, the information loss of the data roughly shows an increasing trend. Because the larger the K value is, generally the more data in the generalization table, the longer the length of the generalized interval will be, and the information loss will be larger. In addition, it can be seen from Fig. 5 that using the method in this paper, the information loss is reduced, and the data availability is improved compared to the original.

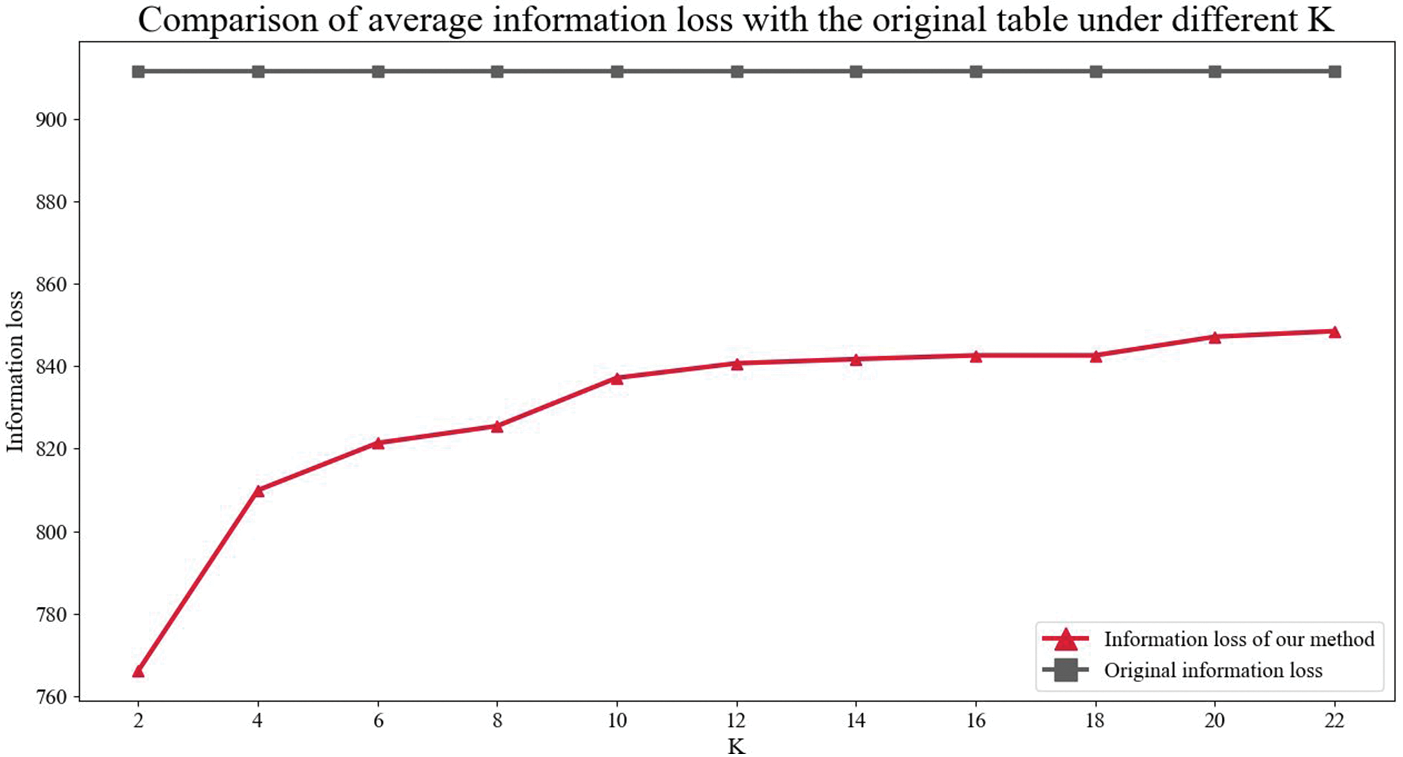
Figure 5: Comparison of average information loss with the original table under different K

(2) Comparison of information loss under different mass center selection methods

To verify the effectiveness of this paper’s mean-centered method in reducing the information loss of K-anonymity, we conducted 30 experiments to compare the information loss of K-anonymity with this paper’s method under the randomized center of mass method with different K and took the average of the 30 experiments as the final result. As shown in Fig. 6, the method of this paper achieves a better reduction of information loss at different K.

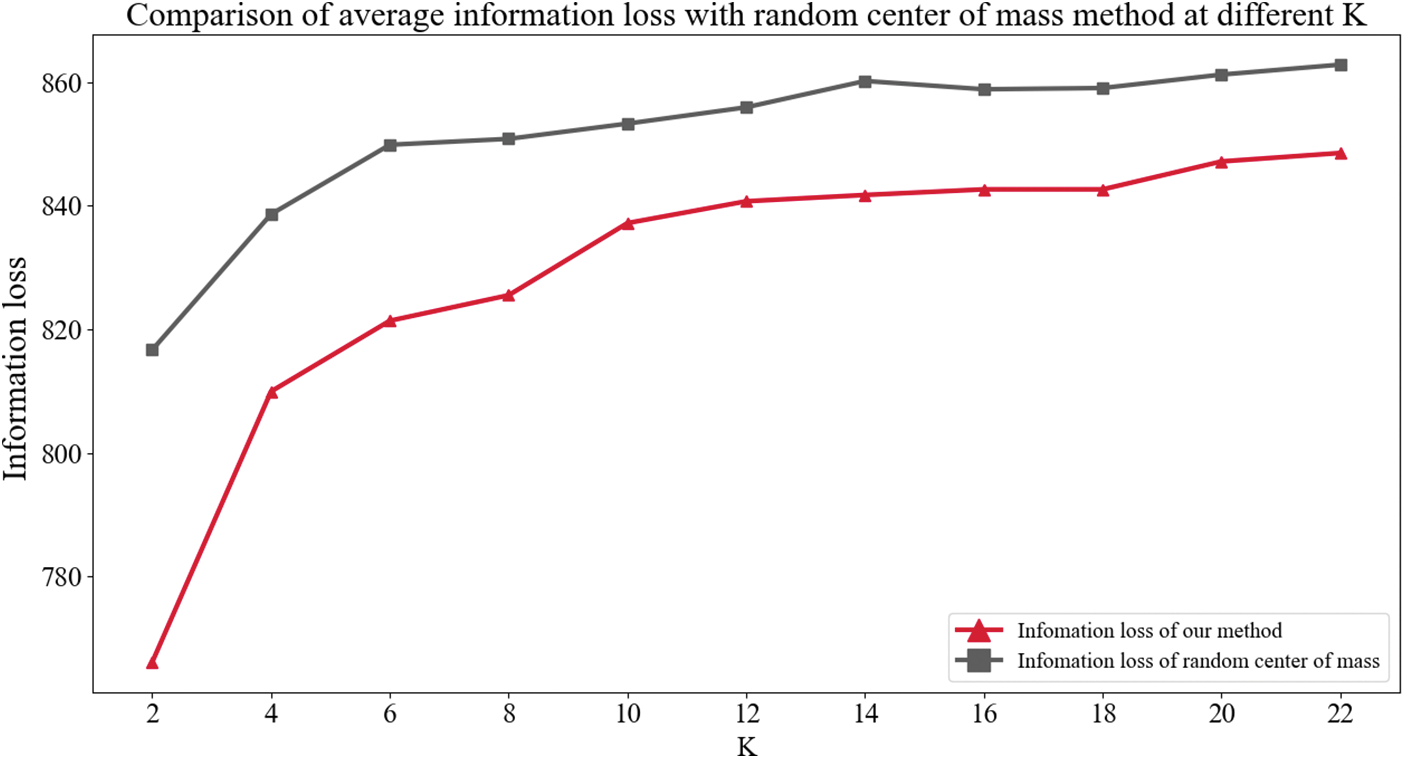
Figure 6: Comparison of average information loss with random center of mass method at different K

In addition, in this paper, K = 4, 8, 12, and 16 are uniformly chosen, and the comparison between the randomized center of mass method and our method in terms of information loss for 30 experiments at specific K values is plotted. As shown in Fig. 7, it can be seen that using the method in this paper can not only improve the information loss of the K-anonymity algorithm but also keep the information loss stable.

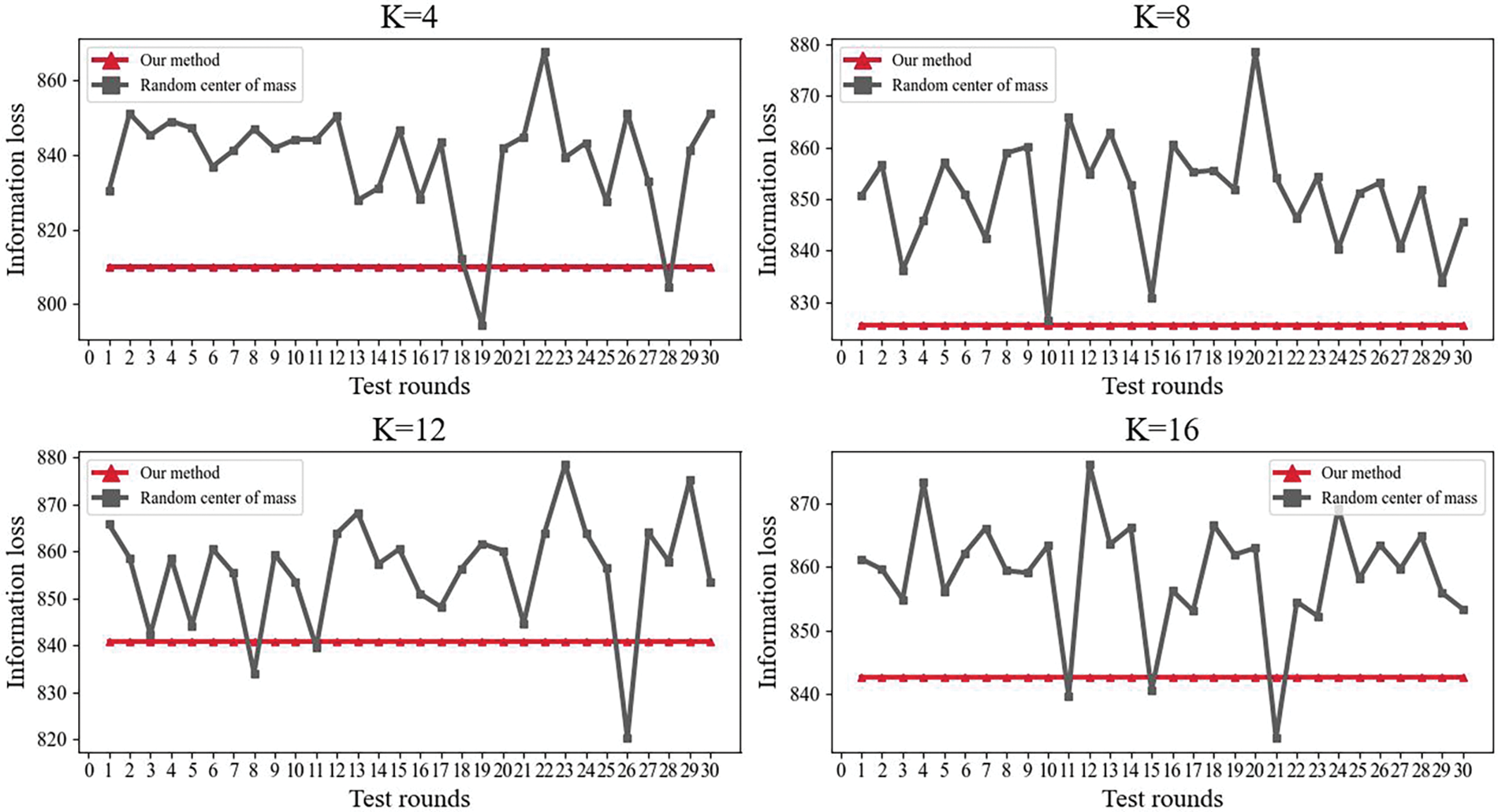
Figure 7: Comparison of information loss under different sub-experiments

5  Conclusion

We propose an improved K-anonymity algorithm to solve the problem of user privacy disclosure in the context of blockchain and IoT integration. This algorithm can improve the availability of data, and because of the improvement of the initial centroid selection method of the clustering algorithm, more stable results are achieved. In the future, privacy security issues in distributed storage and computing [51] can be considered, and combining the K-anonymization algorithm of this paper with distributed storage and techniques could solve privacy security issues in more scenarios. In addition, we use binary classification for clustering and design the initial center of mass selection algorithm only for the case of two initial centers of mass selection, which can be subsequently extended to solve the problem of the initial center of mass selection in multi-classification.

Acknowledgement: We sincerely thank the editors and reviewers for their comments on this paper.

Funding Statement: This research was supported by Foundation of National Natural Science Foundation of China (62202118), and Scientific and Technological Research Projects from Guizhou Education Department ([2023]003), and Guizhou Provincial Department of Science and Technology Hundred Levels of Innovative Talents Project (GCC[2023]018), and Top Technology Talent Project from Guizhou Education Department ([2022]073).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Linlin Yuan; data collection: Tiantian Zhang; analysis and interpretation of results: Yuling Chen; draft manuscript preparation: Yuxiang Yang, Huang Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: This paper uses the Adult dataset from the UCI machine learning repository, which contains partial U.S. Census data with over 30,000 records and is widely used in privacy protection and data mining research. These data were derived from the following resources available in the public domain: https://archive.ics.uci.edu/ml/datasets/Adult.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Liu, K. Qian, K. Wang, and L. He, “BCmaster: A compatible framework for comprehensively analyzing and monitoring blockchain systems in IoT,” IEEE Internet Things J., vol. 9, no. 22, pp. 22529–22546, 2022. doi: 10.1109/JIOT.2022.3182004. [Google Scholar] [CrossRef]

2. C. Zhang, C. Hu, T. Wu, L. Zhu, and X. Liu, “Achieving efficient and privacy-preserving neural network training and prediction in cloud environments,” IEEE Trans. Depend. Secur. Comput., vol. 20, no. 5, pp. 4245–4257, 2023. doi: 10.1109/TDSC.2022.3208706. [Google Scholar] [CrossRef]

3. C. Hu, C. Zhang, D. Lei, T. Wu, X. Liu and L. Zhu, “Achieving privacy-preserving and verifiable support vector machine training in the cloud,” IEEE Trans. Inf. Forensic. Secur., vol. 18, pp. 3476–3491, 2023. doi: 10.1109/TIFS.2023.3283104. [Google Scholar] [CrossRef]

4. M. Shen, Y. Deng, L. Zhu, X. Du, and N. Guizani, “Privacy-preserving image retrieval for medical IoT systems: A blockchain-based approach,” IEEE Netw., vol. 33, no. 5, pp. 27–33, 2019. doi: 10.1109/MNET.001.1800503. [Google Scholar] [CrossRef]

5. X. K. Zhou, X. Yang, J. H. Ma, and K. Wang, “Energy-efficient smart routing based on link correlation mining for wireless edge computing in IoT,” IEEE Internet Things J., vol. 9, no. 16, pp. 14988–14997, 2021. doi: 10.1109/JIOT.2021.3077937. [Google Scholar] [CrossRef]

6. Y. W. Liu et al., “Interaction-enhanced and time-aware graph convolutional network for successive point-of-interest recommendation in traveling enterprises,” IEEE Trans. Ind. Inf., vol. 19, no. 1, pp. 635–643, 2023. doi: 10.1109/TII.2022.3200067. [Google Scholar] [CrossRef]

7. Y. Chen, J. Sun, Y. Yang, T. Li, X. Niu and H. Zhou, “PSSPR: A source location privacy protection scheme based on sector phantom routing in WSNs,” Int. J. Intell. Syst., vol. 37, no. 2, pp. 1204–1221, 2022. doi: 10.1002/int.22666. [Google Scholar] [CrossRef]

8. C. Zhang et al., “POTA: Privacy-preserving online multi-task assignment with path planning,” IEEE Trans. Mob. Comput., pp. 1–13, 2023. [Google Scholar]

9. L. Qi, Y. Liu, Y. Zhang, X. Xu, M. Bilal and H. Song, “Privacy-aware point-of-interest category recommendation in internet of things,” IEEE Internet Things J., vol. 9, no. 21, pp. 21398–21408, 2022. doi: 10.1109/JIOT.2022.3181136. [Google Scholar] [CrossRef]

10. L. Qi et al., “A correlation graph based approach for personalized and compatible web APIs recommendation in mobile app development,” IEEE Trans. Knowl. Data Eng., vol. 35, no. 6, pp. 5444–5457, 2023. [Google Scholar]

11. F. Wang et al., “Identity authentication security management in mobile payment systems,” J. Glob. Inf. Manag., vol. 28, no. 1, pp. 189–203, 2020. doi: 10.4018/JGIM.2020010110. [Google Scholar] [CrossRef]

12. T. Li, Z. Wang, G. Yang, Y. Cui, Y. Chen and X. Yu, “Semi-selfish mining based on hidden markov decision process,” Int. J. Intell. Syst., vol. 36, no. 7, pp. 3596–3612, 2021. doi: 10.1002/int.22428. [Google Scholar] [CrossRef]

13. B. Zhao, J. Yuan, X. Liu, Y. Wu, H. H. Pang and R. H. Deng, “SOCI: A Toolkit for secure outsourced computation on integers,” IEEE Trans. Inf. Forensics Secur., vol. 17, pp. 3637–3648, 2022. doi: 10.1109/TIFS.2022.3211707. [Google Scholar] [CrossRef]

14. L. C. Stergiou, K. E. Psannis, and B. B. Gupta, “InFeMo: Flexible big data management through a federated cloud system,” ACM Trans. Internet Technol., vol. 22, no. 2, pp. 1–22, 2021. [Google Scholar]

15. A. P. Plageras, K. E. Psannis, C. Stergiou, H. Wang, and B. B. Gupta, “Efficient IoT-based sensor big data collection-processing and analysis in smart buildings,” Future Gener. Comput. Syst., vol. 82, no. 1, pp. 349–357, 2018. doi: 10.1016/j.future.2017.09.082. [Google Scholar] [CrossRef]

16. X. Xia, F. Chen, Q. He, J. Grundy, M. Abdelrazek and H. Jin, “Online collaborative data caching in edge computing,” IEEE Trans. Parallel Distrib. Syst., vol. 32, no. 2, pp. 281–294, 2020. doi: 10.1109/TPDS.2020.3016344. [Google Scholar] [CrossRef]

17. J. Wang, C. C. Han, X. F. Yu, Y. J. Ren, and R. S. Sherratt, “Distributed secure storage scheme based on sharding blockchain,” Comput. Mater. Contin., vol. 70, no. 3, pp. 4485–4502, 2022. doi: 10.32604/cmc.2022.020648. [Google Scholar] [CrossRef]

18. Z. Li et al., “A knowledge-driven anomaly detection framework for social production system,” IEEE Trans. Comput. Soc. Syst., pp. 1–14, 2022. [Google Scholar]

19. K. Stokes, “Reidentification and k-anonymity: A model for disclosure risk in graphs,” Soft Comput., vol. 16, no. 10, pp. 1657–1670, 2012. doi: 10.1007/s00500-012-0850-4. [Google Scholar] [CrossRef]

20. Y. L. Chen, S. Dong, T. Li, Y. L. Wang, and H. Y. Zhou, “Dynamic multi-key FHE in asymmetric key setting from LWE,” IEEE Trans. Inf. Forensic. Secur., vol. 16, pp. 5239–5249, 2021. doi: 10.1109/TIFS.2021.3127023. [Google Scholar] [CrossRef]

21. H. P. Dai et al., “Bloom filter with noisy coding framework for multi-set membership testing,” IEEE Trans. Knowl. Data Eng., vol. 35, no. 7, pp. 6710–6724, 2022. doi: 10.1109/TKDE.2022.3199646. [Google Scholar] [CrossRef]

22. L. Sweeney, “k-anonymity: A model for protecting privacy,” Int. J. Uncertain., Fuzz. Knowl.-Based Syst., vol. 10, no. 5, pp. 557–570, 2002. doi: 10.1142/S0218488502001648. [Google Scholar] [CrossRef]

23. Q. He et al., “EDIndex: Enabling fast data queries in edge storage systems,” in Proc. 46th Int. ACM SIGIR Conf. Res. Develop. Inf. Retr., Taipei, Taiwan, 2023, pp. 675–685. [Google Scholar]

24. J. Jayapradha, M. Prakash, Y. Alotaibi, O. I. Khalaf, and S. A. Alghamdi, “Heap bucketization anonymity— An efficient privacy-preserving data publishing model for multiple sensitive attributes,” IEEE Access, vol. 10, no. 9, pp. 28773–28791, 2022. doi: 10.1109/ACCESS.2022.3158312. [Google Scholar] [CrossRef]

25. F. Varghese and P. Sasikala, “A detailed review based on secure data transmission using cryptography and steganography,” Wirel. Pers. Commun., vol. 129, no. 4, pp. 2291–2318, 2023. doi: 10.1007/s11277-023-10183-z. [Google Scholar] [CrossRef]

26. S. Zhong, Z. Q. Yang, and T. T. Chen, “K-anonymous data collection,” Inf. Sci., vol. 179, no. 17, pp. 2948–2963, 2009. doi: 10.1016/j.ins.2009.05.004. [Google Scholar] [CrossRef]

27. K. Wang, W. Zhao, J. J. Cui, Y. P. Cui, and J. W. Hu, “A K-anonymous clustering algorithm based on the analytic hierarchy process,” J. Vis. Commun. Image Represent., vol. 59, no. 2, pp. 76–83, 2019. doi: 10.1016/j.jvcir.2018.12.052. [Google Scholar] [CrossRef]

28. Y. T. Liang and R. Samavi, “Optimization-based k-anonymity algorithms,” Comput. Secur., vol. 93, no. 8, pp. 101753, 2020. doi: 10.1016/j.cose.2020.101753. [Google Scholar] [CrossRef]

29. C. Y. Lin, “A reversible privacy-preserving clustering technique based on k-means algorithm,” Appl. Soft Comput., vol. 87, no. 6, pp. 105995, 2020. doi: 10.1016/j.asoc.2019.105995. [Google Scholar] [CrossRef]

30. F. Ashkouti, K. Khamforoosh, A. Sheikhahmadi, and H. Khamfroush, “DHkmeans-ldiversity: Distributed hierarchical K-means for satisfaction of the l-diversity privacy model using apache spark,” J. Supercomput., vol. 78, no. 2, pp. 2616–2650, 2022. doi: 10.1007/s11227-021-03958-3. [Google Scholar] [CrossRef]

31. Q. He et al., “Pyramid: Enabling hierarchical neural networks with edge computing,” in Proc. ACM Web Conf. 2022, Lyon, France, 2022, pp. 1860–1870. [Google Scholar]

32. A. Fahim, “K and starting means for k-means algorithm,” J. Comput. Sci., vol. 55, no. 1, pp. 101445, 2021. doi: 10.1016/j.jocs.2021.101445. [Google Scholar] [CrossRef]

33. M. Ahmed, R. Seraj, and S. M. S. Islam, “The k-means algorithm: A comprehensive survey and performance evaluation,” Electr., vol. 9, no. 8, pp. 1295, 2020. doi: 10.3390/electronics9081295. [Google Scholar] [CrossRef]

34. A. Bhattacharya, R. Jaiswal, and N. Ailon, “Tight lower bound instances for k-means++ in two dimensions,” Theor. Comput. Sci., vol. 634, no. 7, pp. 55–66, 2016. doi: 10.1016/j.tcs.2016.04.012. [Google Scholar] [CrossRef]

35. X. K. Zhou et al., “Edge-enabled two-stage scheduling based on deep reinforcement learning for internet of everything,” IEEE Internet Things J., vol. 10, no. 4, pp. 3295–3304, 2022. doi: 10.1109/JIOT.2022.3179231. [Google Scholar] [CrossRef]

36. M. S. Aghdam and N. Sonehara, “Achieving high data utility K-anonymization using similarity-based clustering model,” IEICE Trans. Inf. Syst., vol. 99, no. 8, pp. 2069–2078, 2016. [Google Scholar]

37. Z. Tang, W. Zhao, C. Wang, Z. Yang, Y. Xu and S. Cui, “A data desensitization algorithm for privacy protection electric power industry,” IOP Conf. Series: Mater. Sci. Eng., vol. 768, no. 5, pp. 052059, 2020. doi: 10.1088/1757-899X/768/5/052059. [Google Scholar] [CrossRef]

38. X. K. Zhou, X. S. Xu, W. Liang, Z. Zeng, and Z. Yan, “Deep-learning-enhanced multitarget detection for end-edge–cloud surveillance in smart IoT,” IEEE Internet Things J., vol. 8, no. 16, pp. 12588–12596, 2021. doi: 10.1109/JIOT.2021.3077449. [Google Scholar] [CrossRef]

39. S. B. Zhang, X. Li, Z. Y. Tan, T. Peng, and G. J. Wang, “A caching and spatial K-anonymity driven privacy enhancement scheme in continuous location-based services,” Future Gener. Comput. Syst., vol. 94, no. 5, pp. 40–50, 2019. doi: 10.1016/j.future.2018.10.053. [Google Scholar] [CrossRef]

40. A. Rodriguez-Hoyos, J. Estrada-Jiménez, D. Rebollo-Monedero, A. Mohamad-Mezher, and J. Forné, “The fast maximum distance to average vector (F-MDAVAn algorithm for k-anonymous microaggregation in big data,” Eng. Appl. Artif. Intell., vol. 90, no. 1, pp. 103531, 2020. doi: 10.1016/j.engappai.2020.103531. [Google Scholar] [CrossRef]

41. X. K. Zhou, W. Liang, K. Wang, and L. T. Yang, “Deep correlation mining based on hierarchical hybrid networks for heterogeneous big data recommendations,” IEEE Trans. Comput. Soc. Syst., vol. 8, no. 1, pp. 171–178, 2020. doi: 10.1109/TCSS.2020.2987846. [Google Scholar] [CrossRef]

42. K. R. Pilkiewicz et al., “Decoding collective communications using information theory tools,” J. Royal Soc. Interface, vol. 17, no. 164, pp. 20190563, 2020. doi: 10.1098/rsif.2019.0563. [Google Scholar] [PubMed] [CrossRef]

43. L. Yuan et al., “CSEdge: Enabling collaborative edge storage for multiaccess edge computing based on blockchain,” IEEE Trans. Parallel Distrib. Syst., vol. 33, no. 8, pp. 1873–1887, 2021. doi: 10.1109/TPDS.2021.3131680. [Google Scholar] [CrossRef]

44. P. Anitha and M. M. Patil, “RFM model for customer purchase behavior using K-means algorithm,” J. King Saud Univ.-Comput. Inf. Sci., vol. 34, no. 5, pp. 1785–1792, 2022. doi: 10.1016/j.jksuci.2019.12.011. [Google Scholar] [CrossRef]

45. L. Y. Qi, Y. H. Yang, X. K. Zhou, W. Rafique, and J. H. Ma, “Fast anomaly identification based on multiaspect data streams for intelligent intrusion detection toward secure industry 4. 0,” IEEE Trans. Ind. Inform., vol. 18, no. 9, pp. 6503–6511, 2021. doi: 10.1109/TII.2021.3139363. [Google Scholar] [CrossRef]

46. Q. Ren, H. Zhang, D. Zhang, X. Zhao, L. Yan and J. Rui, “A novel hybrid method of lithology identification based on k-means++ algorithm and fuzzy decision tree,” J. Pet. Sci. Eng., vol. 208, pp. 109681, 2022. doi: 10.1016/j.petrol.2021.109681. [Google Scholar] [CrossRef]

47. S. Kim, S. Cho, J. Y. Kim, and D. J. Kim, “Statistical assessment on student engagement in asynchronous online learning using the k-means clustering algorithm,” Sustain., vol. 15, no. 3, pp. 2049, 2023. doi: 10.3390/su15032049. [Google Scholar] [CrossRef]

48. B. Hafeez, X. P. Li, M. H. Kabir, and D. Tripe, “Measuring bank risk: Forward-looking z-score,” Int. Rev. Financial Anal., vol. 80, no. 3, pp. 102039, 2022. doi: 10.1016/j.irfa.2022.102039. [Google Scholar] [CrossRef]

49. H. Alimohammadi and S. N. Chen, “Performance evaluation of outlier detection techniques in production timeseries: A systematic review and meta-analysis,” Expert. Syst. App., vol. 191, pp. 116371, 2022. doi: 10.1016/j.eswa.2021.116371. [Google Scholar] [CrossRef]

50. Y. Wang, T. Li, M. Liu, C. Li, and H. Wang, “STSIIML: Study on token shuffling under incomplete information based on machine learning,” Int. J. Intell. Syst., vol. 37, no. 12, pp. 11078–11100, 2022. doi: 10.1002/int.23033. [Google Scholar] [CrossRef]

51. W. Liang, Y. Hu, X. Zhou, Y. Pan, I. Kevin and K. Wang, “Variational few-shot learning for microserviceoriented intrusion detection in distributed industrial IoT,” IEEE Trans. Ind. Inf., vol. 18, no. 8, pp. 5087–5095, 2021. doi: 10.1109/TII.2021.3116085. [Google Scholar] [CrossRef]