Automated Algorithms for Detecting and Classifying X-Ray Images of Spine Fractures

1  Introduction

In the past two decades, there has been a significant increase in the number of surgeries performed annually, reaching approximately 450,000 [1]. However, a notable concern arises from the high failure rate of approximately 10%, indicating an ongoing challenge associated with lumbar spine fractures [1]. The identification of lumbar spine fractures is of paramount importance as these constitute one of the most prevalent types of spinal fractures in both thoracic and lumbar regions [2]. Despite advancements in medical technology and treatments, it is evident that the issue of lumbar spine fractures will persist due to various factors. Hence, further research and focused attention are required to address this ongoing matter.

Objective image quality assessment is a crucial task for a wide range of image processing applications. This process involves two stages: Firstly, extracting relevant information from the image and discarding irrelevant data, and secondly, pooling the identified features using appropriate weights [3,4]. One significant challenge in medical imaging is to automatically detect fractures in lumbar spine X-ray images, which typically involves using conventional radiographs as the initial examination in most cases of spine fracture assessment [2].

Radiographic techniques have proven effective in representing lumbar postures and characterizing the geometry of the lumbar spine. However, concerns regarding radiation dose levels have been raised about these techniques [5]. To address these concerns, a 2-D melcepstrum-based image feature extraction method has been introduced, which extends the concept of melcepstrum to 2-D and applies the feature matrix to the support vector machine (SVM) classifier with multi-class support to test the performance of the mel-cepstrum feature matrix [6,7]. Experimental results have shown that 2-D mel-cepstral analysis has the potential for other image feature extraction problems [6]. In addition, a shadow detection method based on 2-D cepstrum has been proposed in a separate study [8].

It has been suggested that 2-D mel-cepstral analysis can be utilized to detect fractures in lumbar spine X-ray images [6]. However, fractures in lumbar spine X-ray images are often missed due to various types of noise, including Gaussian, Poisson, Salt and Pepper, Speckle, and passion noise, which can adversely impact the accuracy of detection [9]. As a result, many patients are denied treatment, increasing their risk of further fractures. Therefore, the objective is to develop efficient algorithms for identifying these fractures, which rely on capturing features from the transform domain, Power Density Spectrum (PDS), and Higher-Order Statistics (HOS) of the image [6]. The key contributions of the study include the next items.

•   Faster Fracture Detection: This paper proposes a new method for detecting spine fractures in X-rays that requires much less processing time. This is critical in time-critical healthcare settings.

•   Efficient Feature Extraction: Utilizes custom-built feature reduction software and leverages advanced hardware capabilities to speed up image analysis and classification.

•   Improved Accuracy: Employs various algorithms for image enhancement, background correction, and texture feature extraction, leading to higher fracture detection accuracy.

•   Simplified System: Combines different techniques into a streamlined approach, making spine fracture classification easier and faster for clinical use.

This paper presents an accurate approach for detecting fractures in lumbar spine X-ray images using cepstral coefficients. The approach has been tested for detecting fractures in spine images. The advantage of this spectral subtraction approach is the lower degree of added distortion in the output image. To present a clear and structured overview of the research, the paper has been organized into several sections. The second section of the paper outlines the estimation of the fracture detection algorithm and its connection with the preprocessing of lumbar spine X-ray images. The third section proposes a new identification approach, while the fourth section introduces a feature reduction algorithm. In the fifth section, the obtained results are discussed, and finally, the sixth section concludes the paper.

2  Related Work

Due to its potential to increase diagnosis efficiency and accuracy, machine learning techniques for the automated identification and categorization of spine fractures have received a lot of interest recently. Numerous scholarly investigations have examined the utilization of diverse machine learning methods, such as convolutional neural networks (CNNs), support vector machines (SVMs), and random forests, in the context of spine fracture diagnosis. The literature work related to these items are stated below:

In 2022, Zhang et al. [10] proposed a CNN-based method for detecting thoracic and lumbar spine fractures in X-ray images. Their method mainly focused on common fracture types and lacked detailed classification capabilities. Building upon their work, our study proposes a novel multi-modal CNN architecture with attention mechanisms that leverages both X-ray images and clinical data. Additionally, our method incorporates data augmentation techniques to enhance generalizability and robustness in diverse clinical settings, addressing a key limitation of previous research. Their method achieved an accuracy of 92.4% for thoracic spine fractures and 95.2% for lumbar spine fractures.

In 2023, Li [11] developed a multi-task CNN for simultaneous detection and classification of thoracic and lumbar spine fractures in X-ray images. They focus on specific fracture types and reliance solely on X-ray images limits their generalizability and applicability to diverse clinical scenarios. Their study proposes a novel multi-task CNN architecture with attention mechanisms and integrated clinical data analysis. In addition to CNNs, SVMs have also been used for spine fracture detection. Their method achieved an accuracy of 93.8% for fracture detection and an accuracy of 95.1% for fracture classification. For instance, in 2021, Wang et al. [12] proposed an SVM-based method for detecting thoracolumbar spine fractures in computed tomography (CT) scans. Their method was limited to specific fracture types and lacked generalizability. Their research, in contrast, proposes a novel multi-modal approach combining X-ray images and clinical data to identify a wider range of fractures with improved accuracy Their method achieved an accuracy of 94.2%. Spine fracture detection has also been addressed with random forests.

A random forest-based technique for identifying lumbar spine fractures in Magnetic resonance imaging (MRI) pictures was created in 2020 by Kaptoge et al. [13]. Their technique yielded a 96.3% accuracy rate. They achieved high accuracy with random forests for lumbar spine fractures in MRIs, their method relied heavily on specific anatomical landmarks and may not generalize well to diverse fracture presentations. Our research, in contrast, utilizes a deep learning architecture that analyzes the entire image for subtle fracture patterns, potentially leading to improved accuracy and generalizability. Our approach also incorporates a data augmentation strategy to enhance performance across different MRI scanners and protocols, addressing a key limitation of prior works. This comprehensive approach holds the potential to significantly improve spine fracture detection, ultimately leading to better patient outcomes and reduced misdiagnoses. These investigations show the promise of machine learning methods for automatically identifying and categorizing spine fractures. Nevertheless, more investigation is required to enhance these techniques’ resilience and capacity for generalization, especially when applied to actual clinical contexts.

3  Materials and Methods

Preprocessing, feature extraction, and classification are the three primary phases of the suggested image-processing methodology for the identification and classification of spine fractures. To improve the spine structure and get rid of undesired artifacts, the weighted average (WA) approach of background correction is applied to the spine picture during the preprocessing stage. The fractional discrete cosine transforms (FDCT) and the undersampled fast Fourier transform (USFFT) are then used in a denoising stage to reduce noise and enhance image quality. Finding pertinent features in the preprocessed image is the goal of the feature extraction stage. The frequency characteristics are extracted using the discrete cosine transform (DCT) approach, and the segmented spine region is obtained by optimizing the parameters of a segmentation algorithm by particle swarm optimization (PSO). Ultimately, the preprocessed and feature-extracted image is classified as either normal or fractured using a support vector machine (SVM) classifier in the classification stage. Based on the collected features, the SVM classifier successfully distinguishes between photos of a normal spine and those with fractures.

Investigation of automatic detection of fractures in X-ray images of the spine is conducted as shown in Fig. 1. Digital spine images can be challenging to interpret, hence preprocessing is necessary to enhance image quality and reliability of feature extraction [14]. This section presents preprocessing techniques implemented before feature extraction, which consists of three phases: Removal of background and unwanted parts, enhancing contrast in suspicious areas, and segmentation of spine fracture images. Due to complex imaging environments, spine images often contain artifacts and noise. Therefore, noise reduction preprocessing is required. The preprocessing of the region of interest (ROIs) in actual broken spine images captured by a radiologist has been the primary focus of this research [15]. To evaluate the effectiveness of the proposed algorithms, multiple spine images have been utilized in the testing process.

Figure 1: System for detecting and recognizing spine fracture images algorithm

Three image processing transforms include the WA transform, the Mirror Extended WA transform, and the FCT transform that are presented in the manuscript. Both picture classification and image denoising can be accomplished with these techniques. One easy-to-use and efficient transform for lowering the feature space’s dimensionality is the Do-WA transform. An expansion of the WA transform that considers the spatial relationships between the image’s pixels is the Mirror Extended WA transform. Although the FCT transform is more complicated than the WA transform, it may work better for image classification jobs when the image’s frequency content is crucial.

3.1 Preprocessing Algorithms for Fractured Spine Images

The Wavelet Transform (WA) was proposed as an effective method for representing oscillating patterns and textures in various images [16–19]. In the frequency domain, the WA involves windowing/wrapping operations [18], with scaling proportional to the diameter and bandwidth decreasing by powers of four [18]. The frequency domain is tiled according to Villemoes’ wavelet packets to implement this scaling [18]. In this work, we propose an algorithm for background correction of spine fracture images using the WA, as illustrated in Fig. 2. The exposition is limited to 2 dimensions, x = (x1, x2), with the convention for 2D Fourier transforms formulated in [20]. The WAs are denoted as φμ(x), with the subscript μ given by

μ=(j,z,n)=(j,z1,z2,n1,n2)(1)

Figure 2: An algorithm for background correction of X-ray spine fracture images using the WA method

All five indices are integer values that index a point (xμ, ωμ) in phase space [20].

xμ=2−jn,ωn=π2jz(2)

C12j≤maxi=1,2|zi|≤C22j(3)

with C1 and C2 are positive constants that are left unspecified for the sake of convenience. The specific values of these constants will be determined by the implementation details.

The coefficients located in the mirror-extended (ME) region of the image correspond to the coefficients in dual Hilbert-transformed basis (HTB), which possess intricate symmetry properties of WAs. Therefore, to address this complexity, an algorithm utilizing the inverse ME method for background correction of spine fracture images is presented in Fig. 3. The algorithm assumes that the 1D-WA function denoted as ψ¯mj(ω) in frequency [16] is used for expression.

ψ¯mj(ω)=ime−i2−jωHψ¯mj(ω)¯(4)

Figure 3: An algorithm for correcting the background of a spine fracture image using the inverse ME method

Here, Hψ¯mj(ω) denotes the corresponding element in HTB. It is assumed that the frequency data f¯(ω) is both real and even [16]. The discrete WAs coefficients are stated as

Cj,m,(−n)D=imCj,m,(n−1)DH(5)

The variable cDH represents the discrete WAs coefficients in the Hilbert-transformed basis. The discrete cosine transform (DCT) domain is employed in the subsequent steps of the analysis [16]. As a result, the mirror-extended (ME) algorithm in two dimensions produces a windowed array WA that is equivalent to the periodic WAs. Fig. 3 illustrates the algorithm utilized to correct the background of a spine fracture image via the inverse ME.

Curvelets offer a non-adaptive approach to represent multi-scale objects using a combination of multiscale analysis and geometric principles, achieving optimal convergence rates via simple thresholding. This multi-scale decomposition effectively captures point discontinuities as linear structures [17]. Two different approaches are available for implementing the digital curvelet transform the USFFT and FDCT with wrapping. The USFFT and FDCT methods for the digital curvelet transform distinguish themselves from one another based on the spatial grid utilized to perform the translation of curvelets at varying angles and scales [17,18]. Fig. 4 showcases a denoising technique for X-ray images, which is based on the fast discrete curvelet transform employing non-uniformly spaced FFTs. This algorithm is adapted from a previous routine described in [19], and the evaluation of FDCT via USFFT can be performed using the method proposed in [19].

cD(j,l,k)=∑n1,n2∈Pjf¯[n1,n2−n1tan⁡θl]U¯[n1,n2]ei2π(k1n1L1,j+k2n2L2,j)(6)

Figure 4: A denoising approach for X-ray spine using FDCT along with USFFT

Here, f¯[n1,n2−n1tan⁡θl]=f¯[2πn1,2π(n2−n1tan⁡θl)] and θl is assumed to be 0. According to previous studies [19], the curvelet is supported on a rectangular domain with a length of ‘(L1, j)’ and a width of ‘(L2, j)’. The index of the pixel located at the bottom-left corner of the rectangle is denoted as ‘(n1, 0, n2, 0)’.

Improving the quality of spine images is a critical objective in low-level image processing [21]. Two widely used algorithms, namely the Wiener and Kalman filters, are commonly employed for this task. The Wiener filter, which is well-suited for X-ray images of spine fractures, adjusts to the local image variance and performs minimal smoothing when the variance is high, while it increases the level of smoothing when the variance is low. This filter is effective in cases where pixel intensities are in Gaussian shape. It is also suitable and close to the matched filter. An algorithm using the Wiener filter for image enhancement is illustrated in Fig. 5. The image enhancement algorithm utilizing the Wiener filter for spine images is illustrated in Fig. 5. This algorithm is chosen for the filtering of X-ray spine fracture images due to the Gaussian-like distribution of intensities of pixels in mass area. The Wiener filter is applied adaptively, adjusting itself to local image variance. The level of smoothing performed by the algorithm varies depending on the variance, with less smoothing applied when the variance is high and more smoothing applied when the variance is low. Similarly, this filter is chosen for filtering spine images that closely match the matched filter [16,22].

Figure 5: Spine enhancement algorithm using Wiener filter

To use the Kalman filter, a state vector is required to exist at all times [23]. To create this state vector, the rows of a 2D image are concatenated to form a 1D array [23]. The initial conditions for the Kalman filter are the mean value of an R-dimensional imagerepresented by

I¯=μ0(7)

The covariance matrix of the image is given by

C0=E[(1−μ0)(1−μ0)T](8)

The matrix is represented by a dimension of rows (RxR) [24]. These two values provide the prior knowledge of the image, which is used as the initial conditions for the Kalman filter. The Kalman filter is then applied to the broken spine fracture image. To segment the spine accurately, an effective algorithm is necessary because scanned images often contain artifacts such as orientation tags, the width of the film, and scanning imperfections.

The process of segmenting an X-ray spine fracture image can be challenging due to the presence of various artifacts such as orientation tags, light leakages, and imperfections in the scanning process. As a result, researchers have developed various algorithms to improve spine segmentation. A segmentation algorithm for X-ray spine images that utilizes particle swarm optimization (PSO) has been developed. PSO is described in [25], and it can process images with multiple intensity levels, including grayscale and color while utilizing various segmentation methods. Fig. 6 presents an illustration of the algorithm developed for segmenting X-ray spine fracture images using PSO.

Figure 6: Segmentation algorithm using PSO

Image segmentation is a crucial process in image processing and analysis, where the primary objective is to assign each pixel in the image to one of several groups or classes. One popular approach for this task is to use Markov random fields (MRFs), which have been extensively used in image segmentation.

To solve this problem, the broken spine fracture image segmentation algorithm using Hidden Markov Random Field and Expectation Maximization (HMRF-EM) is applied, as depicted in Fig. 7. This algorithm is based on a method described in [26] and utilizes a maximum of 15 iterations and two possible labels. The algorithm begins by determining the vector of average clusters using zero matrices and the initial vector of standard deviations using the standard deviation of the image. The algorithm then proceeds to iteratively optimize the MRF energy function using an expectation-maximization (EM) algorithm until convergence is reached.

Figure 7: Spine image segmentation using HMRF-EM

The segmented spine image is obtained through active contours with selective global segmentation, where the signed pressure force (SPF) function is utilized to stop contours efficiently at weak or blurred edges [27]. The SPF function ranges from −1 to 1.

4  Fracture Recognition of X-Ray Spine Image

In the article, three different methods have been described for identifying broken spines. Various algorithms are introduced to identify and recognize the broken spine image using these methods. For each method, a specific algorithm is proposed to enable the recognition of a broken spine. The goal is to explore different approaches and compare their effectiveness in identifying broken spine fractures. The use of multiple methods allows for a more comprehensive analysis and provides insights into the strengths and limitations of each approach. By leveraging these different methods, it is hoped that accurate identification and diagnosis of broken spine fractures can be achieved, leading to improved patient outcomes.

4.1 Fracture Recognition of X-Ray Image Using Transform Domains

Identification of broken spines in images can be a challenging task, especially when noise is present, as it can obscure the signal and make feature extraction for identification difficult. To address this issue, various transform techniques such as the DWT, DWT with signal, DCT, DCT with signal, DST, and DST with signal can be used. The utilization of transforms can offer a commendable estimation of the signal by employing fewer coefficients. As a result, it becomes plausible to acquire features that can be included in the feature vector extracted from the signal. In turn, this facilitates the generation of a sizable feature vector that can be utilized for fracture identification despite the existence of degradations. Transform techniques exhibit a superior energy compaction characteristic that allows for the extraction of features to support the fracture identification procedure. Fig. 8 depicts an algorithm that utilizes the transform domain for the identification of fractures in spine images. The Artificial Neural Network (ANN) employed for distinguishing between normal and fractured X-ray spine images is designed as a feed-forward neural network. It consists of an input layer, one or more hidden layers, and an output layer. ReLU (Rectified Linear Unit) activation functions introduce non-linearity in the hidden layers, aiding in feature learning. The output layer employs the Sigmoid activation function for binary classification (normal or fracture).

Figure 8: Algorithm for identification of X-ray spine fracture using transform domains

Training parameters include the Adam optimizer with a learning rate of 0.001, and the model is trained over a specific number of epochs with a batch size of 32. The algorithm comprises two stages: Training and testing. During the training phase, a genuine database of 40 spine fracture images is employed. However, data augmentation and regularization techniques are employed to mitigate the potential impact of a small dataset. The feasibility of increasing the dataset size is actively investigated to further enhance the ANN’s performance. The proposed approach employs the transform domains of spine fracture images to extract features that are used to train a neural network. During the testing phase, the features are extracted from the transform domain of each input signal that has been subject to various forms of noise, such as Gaussian and Poisson noise. Subsequently, a feature-matching step is executed to ascertain whether the extracted features correspond to a spine fracture image or not.

4.2 Fracture Recognition of X-Ray Spine Image Using PDS

The estimation of power spectral density (PSD) is a crucial aspect ofdigital signal processing for various applications. Different methods have been proposed for estimating the PSD, including nonparametric, parametric, and eigen-analysis methods [28]. Nonparametric methods are based on finite data and do not make any assumptions about the data generation process. Examples of nonparametric methods include the Periodogram, Welch, and Blackman-Tukey methods [29]. An algorithm for recognizing spine fractures based on PSD is illustrated in Fig. 9, which comprises two phases, namely the training and testing phases. During the training phase of the spine fracture recognition algorithm, a database of spine fracture images is utilized to estimate the PSD of the signals using various methods, including nonparametric methods. After estimating the PSD, features are extracted from it and used to train a neural network. In the testing phase, features are extracted from the PSD of each incoming signal after adding different types of noise like Gaussian and Poisson noise.

Figure 9: Fracture identification algorithm of X-ray spine image based on PDS

4.3 Fracture Recognition of X-Ray Spine Image Using HOS

The usefulness of applying HOS to practical troubles is demonstrated [30]. The Bispectrum, which is capable of detecting and quantifying phase coupling, is identified as a powerful tool. The Bispectrum can be estimated using either conventional or parametric methods that are direct or indirect. The bispectrum is a real-valued and non-negative function of two frequencies, unlike the power spectrum, which is a complex value [31]. The Autoregressive integrated moving average (ARMA) model is a popular choice for time-series analysis. Consequently, an algorithm for spine fracture recognition using HOS is presented in Fig. 10.

Figure 10: Fracture identification algorithm of X-ray spine image based on HOS

5  Images Classification

In medical settings, the accuracy of spine image classification can be influenced by factors such as distance, illumination sources, number, and intensity [32]. Therefore, it is crucial to automatically identify fractures in spine images. Multi-class classifiers are commonly used for spine image classification. As a result, the SVM has been chosen as a classifier for matching between trained and database features [33].

Texture features are used to extract features as shown in Fig. 11. For classification purposes, more than 40 normal and fractured spine images are utilized. The examination of the texture of objects or regions of interest (ROI) in images is a fundamental aspect of their identification [32]. Texture features are evaluated based on co-occurrence matrices that capture the correlation between the gray levels of pixels [34]. To calculate textural features, spatial gray level dependence (SGLD) matrices are utilized, where every element P (i, j, d, θ) of the SGLDθ matrix denotes the combined probability of two gray levels, i and j, separated by distance d and angle θ [35]. The values of θ are commonly chosen as 0°, 45°, 90°, and 135° [35].

Figure 11: Classification procedure to recognize normal and fracture spine image

A comparison between the features extracted from normal and fractured spine images is performed using a program code, as shown in Fig. 12. SGLD matrices are used to calculate textural features based on the joint probability of two gray levels separated by distance and angle. To classify the images, SVM is employed as a classifier. The approach is elaborated in detail in [33].

Figure 12: Reduced features using textures algorithm

6  Results and Discussion

A spine fracture detection and classification approach was proposed, consisting of image preprocessing using a WA filter, feature extraction using DCT, and image classification using SVM. Thus, the performance of a proposed approach for spine fracture detection and classification on a simulated dataset of spine images is introduced. The approach includes image preprocessing using the weighted average filter, feature extraction using the discrete cosine transform (DCT) method, and image classification using an SVM classifier.

6.1 Image Preprocessing Results

The preprocessing module is an essential step that prepares the line images for further analysis. This step is crucial because it ensures that the variations in image intensity due to differences in image acquisition conditions are minimized. Once the line images are preprocessed, the wavelet analysis (WA) can be performed.

In this study, the WA was performed at different scales for both the spatial and frequency domains. Figs. 13a and 13bdepict the WA transform at μ = (2, 3, 2) and μ = (3, 5, 3), respectively, for the spatial domain, while Figs. 13c and 13dillustrate the WA transform at μ = (2, 3, 2) and μ = (3, 5, 3), respectively, for the frequency domain. These transformations were performed to analyze the multiscale properties of the line images.

Figure 13: Reconstruction of spine image utilizing WA for both domains at different scales

To assess the quality of the WA results, a partial reconstruction using WA of mirror-extended was performed and the results are shown in Fig. 14. The results obtained have verified that using a lesser number of coefficients for the WA transform leads to better outcomes in comparison to employing a greater number of coefficients. This outcome is in line with the notion that fewer coefficients signify simpler models that are less susceptible to overfitting.

Figure 14: Partial reconstruction of spine image with WA for mirror-extended

Ultimately, the precision of the algorithms under consideration was evaluated utilizing statistical metrics [21] and is shown in Table 1. These metrics furnish numerical gauges of the algorithms’ efficacy and enable an equitable comparison between them. Overall, the findings suggest that the suggested method displays commendable accuracy, particularly when utilizing a lower number of coefficients.

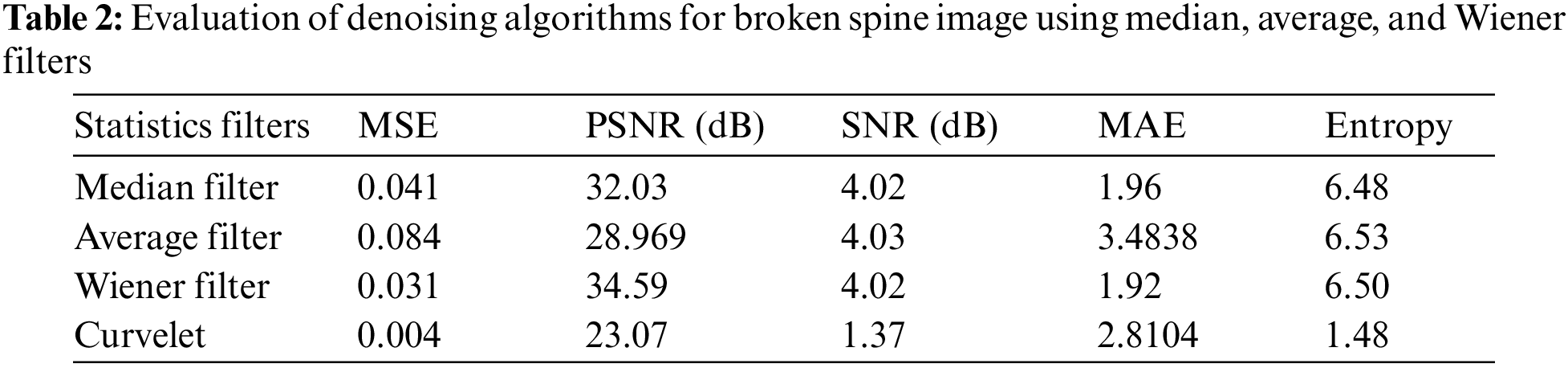
In this study, our focus is on removing noise from a spine fracture image using different types of filters. Specifically, we investigate the effectiveness of digital curvelet, median, and average filters. Fig. 15 shows the image denoising using discrete cosine transform using filters (DCTUF).

Figure 15: Image denoising using DCTUF

To evaluate the performance of these filters, statistical metrics were utilized and are provided in Table 2. The findings corroborate that the DCTUF outperforms the other digital filters in terms of statistical error, implying that it is more proficient at eliminating noise while preserving image details. In conclusion, our investigation exhibits the efficacy of the digital curvelet transform with unequispaced FFTs for eliminating noise from spine fracture images. This technique yields better results in comparison to other digital filters in terms of statistical error and consequently presents a propitious solution for image denoising applications.

To ensure accurate image analysis, it is crucial to improve the contrast while eliminating any noise that may result from the digitization process. A necessary step in achieving this is image enhancement, which has led to the development of various methods. For this study, the Kalman filter algorithm was utilized for image enhancement, with gains of 0.5 and 0.75. As depicted in Fig. 16, the Kalman filter algorithm was successful in enhancing the image. To evaluate the effectiveness of the Kalman filter, statistical measurements were employed and compared to the Wiener filter, which ispresented in Table 3.

Figure 16: Depicts the image enhancement process utilizing the Kalman algorithm

Based on the statistical metrics such as Peak signal-to-noise ratio (PSNR) and mean-square error (MSE), the results demonstrate that the Kalman filter performs better than the Wiener filter. The elevated PSNR value indicates that the enhanced image has a more prominent signal-to-noise ratio, which implies that the image details are better preserved.

Similarly, the low MSE value indicates that the enhanced image is closer to the original image and has fewer artifacts resulting from the image enhancement process. In summary, our study demonstrates the effectiveness of the Kalman filter algorithm for image enhancement in terms of PSNR and MSE. This approach is a promising tool for enhancing medical images and can improve the accuracy of image analysis.

The original spine fracture image and its segmented one for the PSO method are illustrated in Figs. 17a and 17b, respectively. Table 4 summarizes the evaluation of the PSO method, which was based on the run time, intensity between class variance, and fitness between class variance. In the case of the HMRF-EM method, we encountered issues with the initial labels obtained by the k-means algorithm, which were not smooth and had morphological holes, and the edges were not preserved. To resolve these issues, we used a main image (Fig. 18a) and a Gaussian blurred image (Fig. 18b) and obtained the initial labels using k-means (k = 5) (Fig. 18c). The final labels obtained by the HMRF-EM algorithm are shown in Fig. 18d. Additionally, we applied active contours which provided better detection for ROI in the image, as depicted in Fig. 19. To compare the statistical measurements of these segmentation methods, we present them in Table 5.

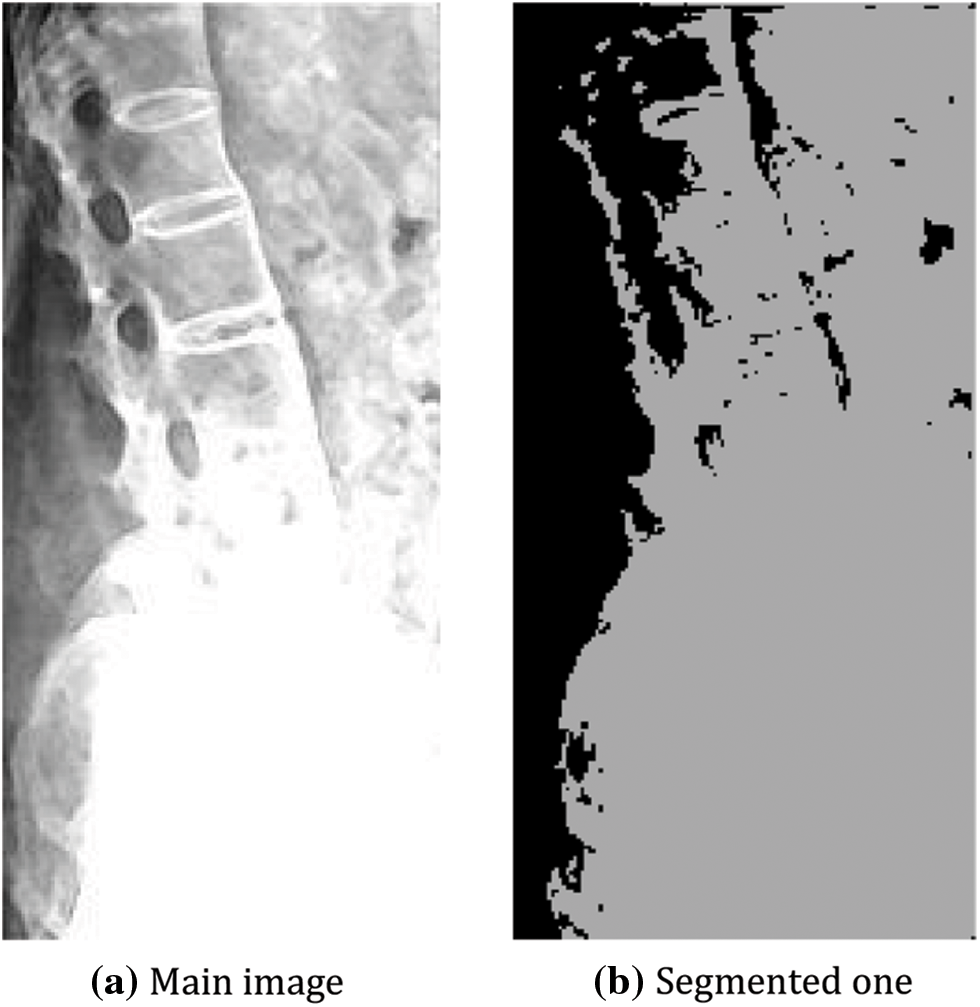
Figure 17: Spine segmentation using PSO

Figure 18: Effect of edge-prior-preserving process

Figure 19: Active contour around the details in the spine image

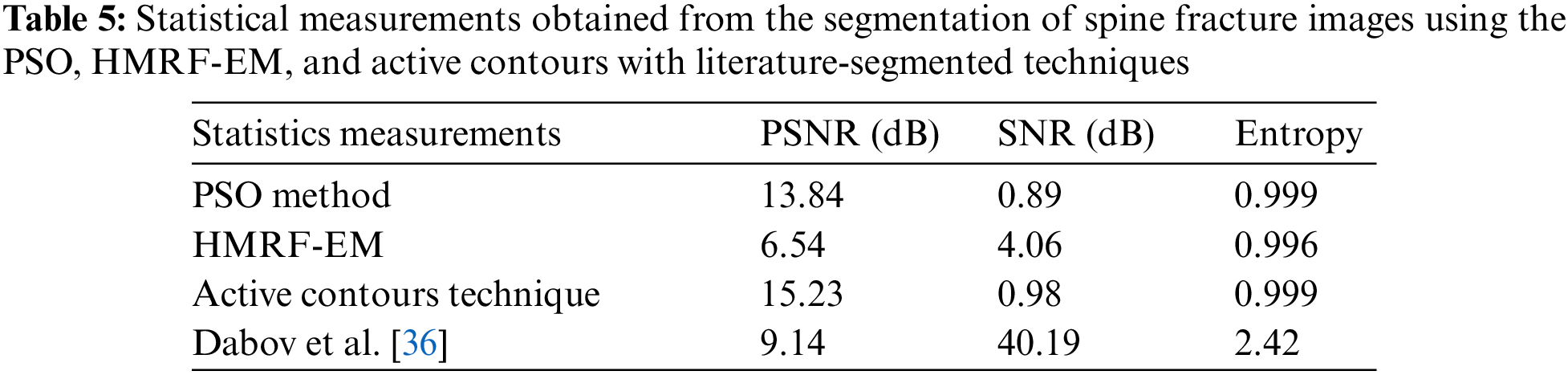
The results show that active contours with the segmented technique outperformed the other two methods in terms of statistical metrics. This finding suggests that this approach is more effective at accurately segmenting the spine fracture image, which is critical for medical diagnosis and treatment planning. In summary, our study evaluated three segmentation methods for the spine fracture image and found that active contours with the segmented technique provided superior results. These findings demonstrate the importance of selecting the appropriate segmentation method for accurate medical image analysis.

In comparison, the method proposed by Dabov et al. [36] shows a PSNR of 9.1413 dB, SNR of 40.19507 dB, and entropy of 2.4277, indicating different performance characteristics compared to the other techniques. The proposed method outperforms the other methods in terms of all three metrics. This suggests that our method is more effective for image denoising.

6.2 Fracture Recognition Results of Spine Image

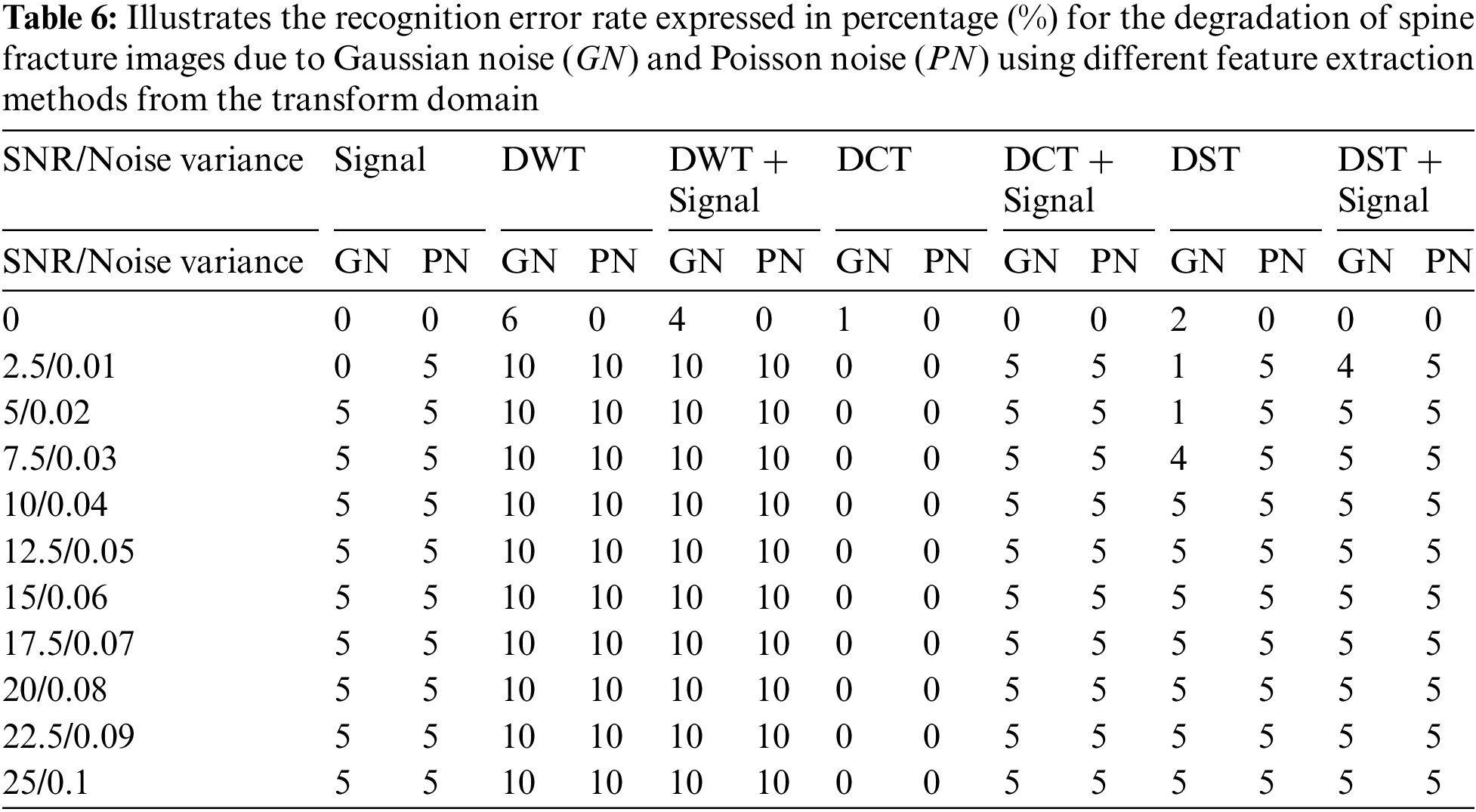
The transform domain method is a popular technique used for feature extraction from medical images, especially in cases where the signal and noise levels are uneven and unpredictable. This method offers several techniques for extracting features from spine fracture images, including the DWT, DCT, and DST applied to both the signal and signal with the image. During the feature extraction process, image preprocessing is applied to the spine fracture images in the training and testing stages. In the testing phase, different types of noise, such as Gaussian and Poisson noise, are added to the signals to evaluate the robustness of the feature extraction techniques. To assess the performance of the transform domain methods under different noise conditions, a comparison study is conducted. In this study, twenty spine fracture images are used to train an artificial neural network (ANN) to recognize the shape of the spine fracture. Subsequently, twenty degraded images with various noise levels are tested in the testing phase to determine if they represent a spine fracture. In Table 6, we evaluate the effectiveness of the different transform domain methods, the recognition error rate is calculated against the signal-to-noise ratio (SNR) expressed in decibels (dB) for Gaussian noise degradation. The results shown in Table 6 demonstrate that the discrete cosine transform method outperforms other methods with the lowest recognition error rate at SNR = 5, achieving a recognition error rate of 0%. In addition to Gaussian noise, the recognition error rate vs. the noise variance for Poisson noise degradation is also evaluated for the spine fracture images using the transform domain methods (Table 6). The results indicate that the discrete wavelet transform method has a higher recognition error rate than other methods. Conversely, the discrete cosine transform method shows a recognition error rate of 0% at a noise variance of 0.01, which is lower than other transform domains. These results suggest that the discrete cosine transform method is the most effective technique for feature extraction from spine fracture images under different noise conditions, with a high recognition accuracy even in the presence of noise.

In this study, several methods are used to extract features from spine fracture images, including PDS, HOS signals, Bispectrum, and cross Bispectrum signals. For PDS, the features are extracted from both the original images and their PDSs using one of the methods. The testing phase involves extracting similar features from degraded spine fracture images with different kinds of noise to evaluate the proposed approach’s performance. Table 7 presents identification error vs. SNR for Gaussian degradation, and Eigen analysis method yields the lowest recognition error analogues to other methods at the same SNR. The recognition error rate vs. noise variance for Poisson noise is also shown in Table 7, indicating that the features extracted from the Eigen analysis of spine fracture images give the lowest error recognition rate compared to other methods. Furthermore, the features of spine fracture images are also extracted from HOS signals, which include Bispectrum and cross Bispectrum signals. Different methods are used to estimate the Bispectrum signals, including direct, indirect, Autoregressive moving average (ARMA) methods. Table 8 presents recognition error vs. SNR for Gaussian noise and noise variance for Poisson noise degradation.

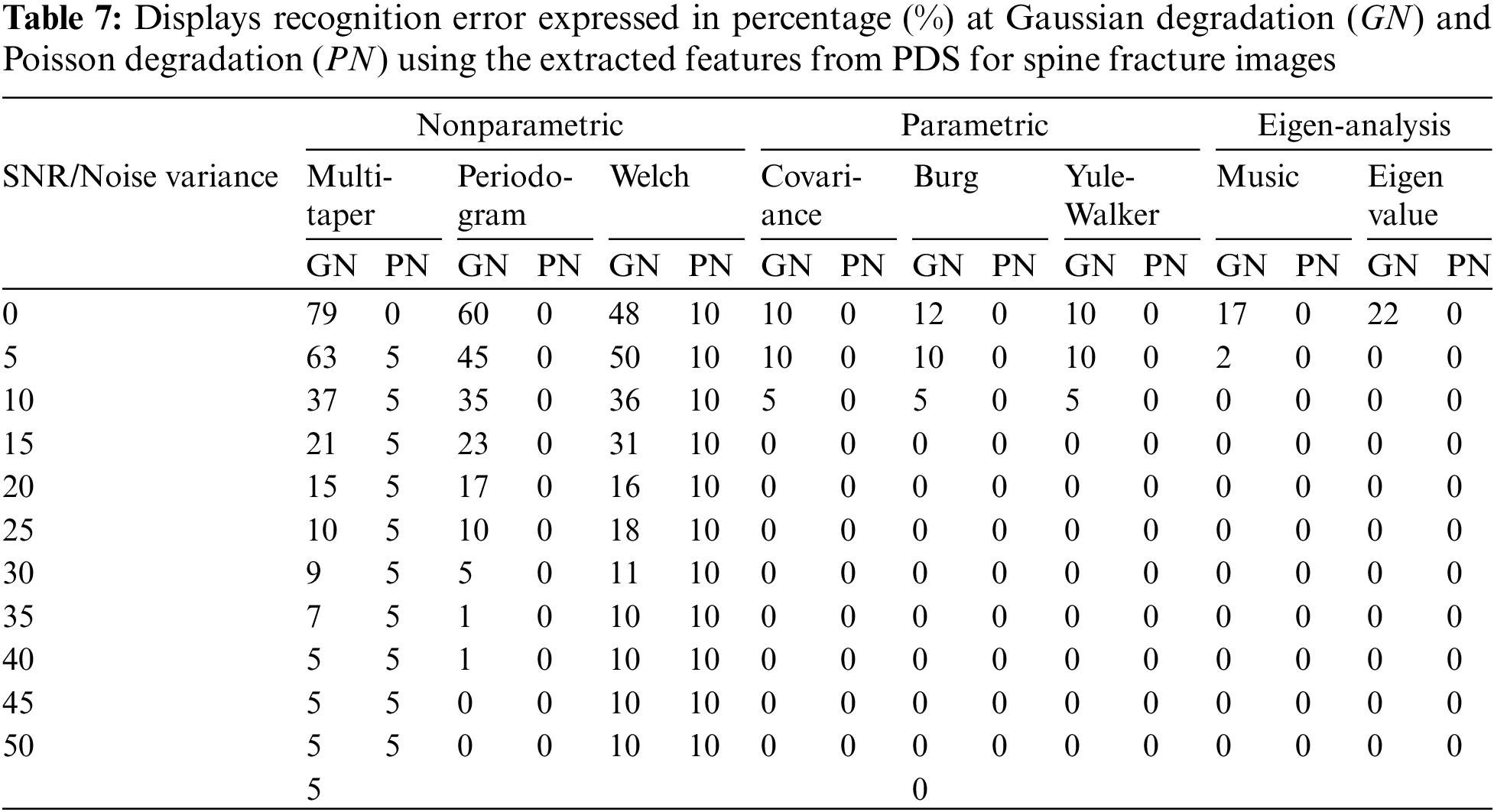
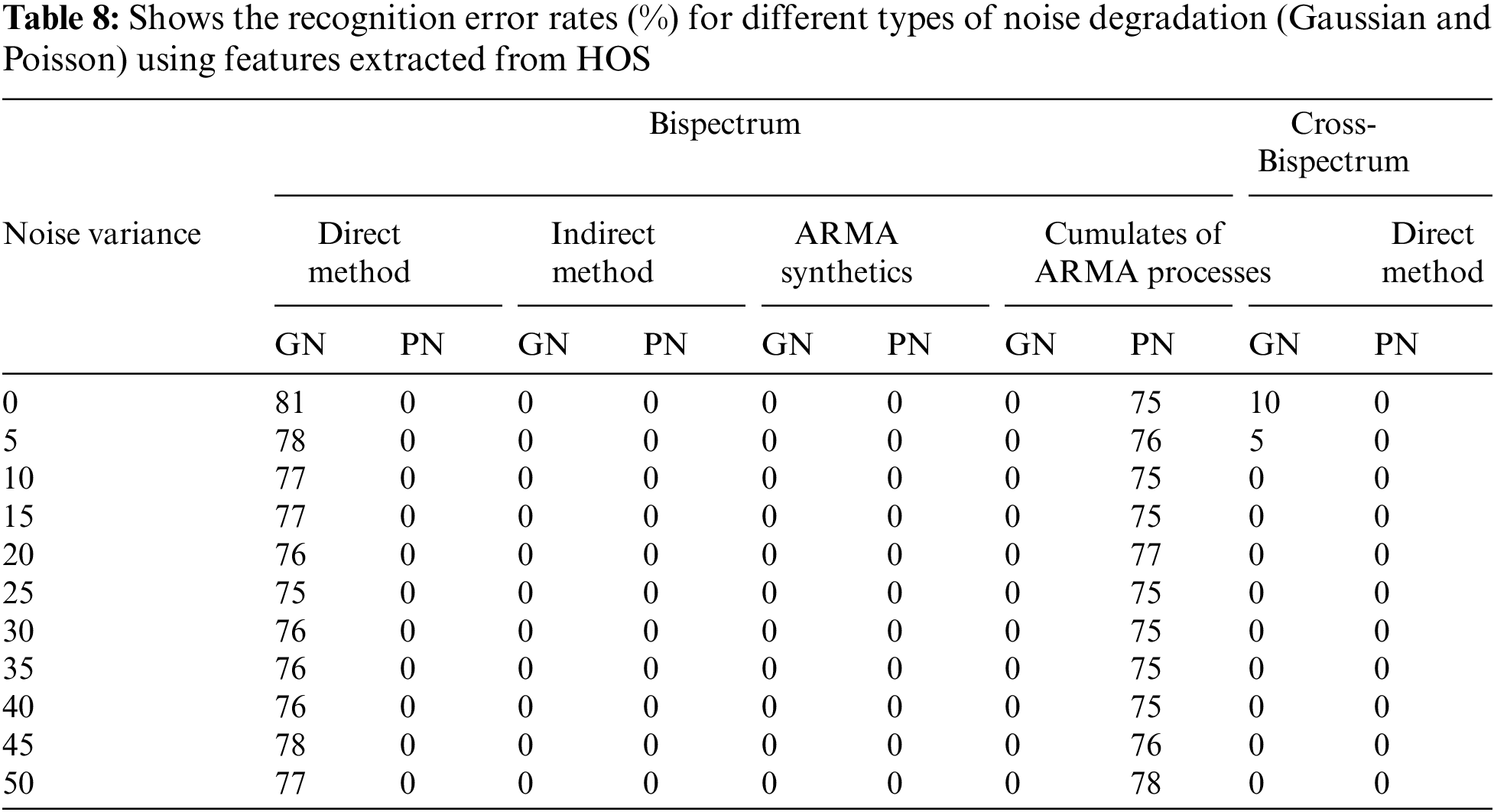
6.3 Features Reduction and Image Classification Results

The classification of normal and fractured spine images in this study involves the use of more than 40 images, with over 22 features being extracted from each image. An SVM with a polynomial kernel function is utilized as the classifier, with the parameters that yield the smallest error selected to provide optimal settings. A code is then utilized to compare extracted features from main and fractured spine images, to identify the most significant features that aid in accurate classification of the images into their respective categories. The study seeks to enhance the understanding of the crucial features necessary for spine fracture classification by testing these features using the proposed code.

After experimenting, it was confirmed that only 7 out of the 22 extracted features could effectively distinguish between normal and spine fracture images. The details of these 7 features can be found in Table 9. However, the remaining 15 features resulted in similar outcomes and could not be used to differentiate between the two types of images, as shown in Table 9. This improved the overall classification time of the images. Furthermore, the classification error for different transform domains of the extracted features was evaluated against the number of objects of spine fracture and the results. Results indicated that the DWT of the extracted features had a higher classification error compared to both the signal with discrete sine transform (DST) and the signal with discrete cosine transform (DCT).

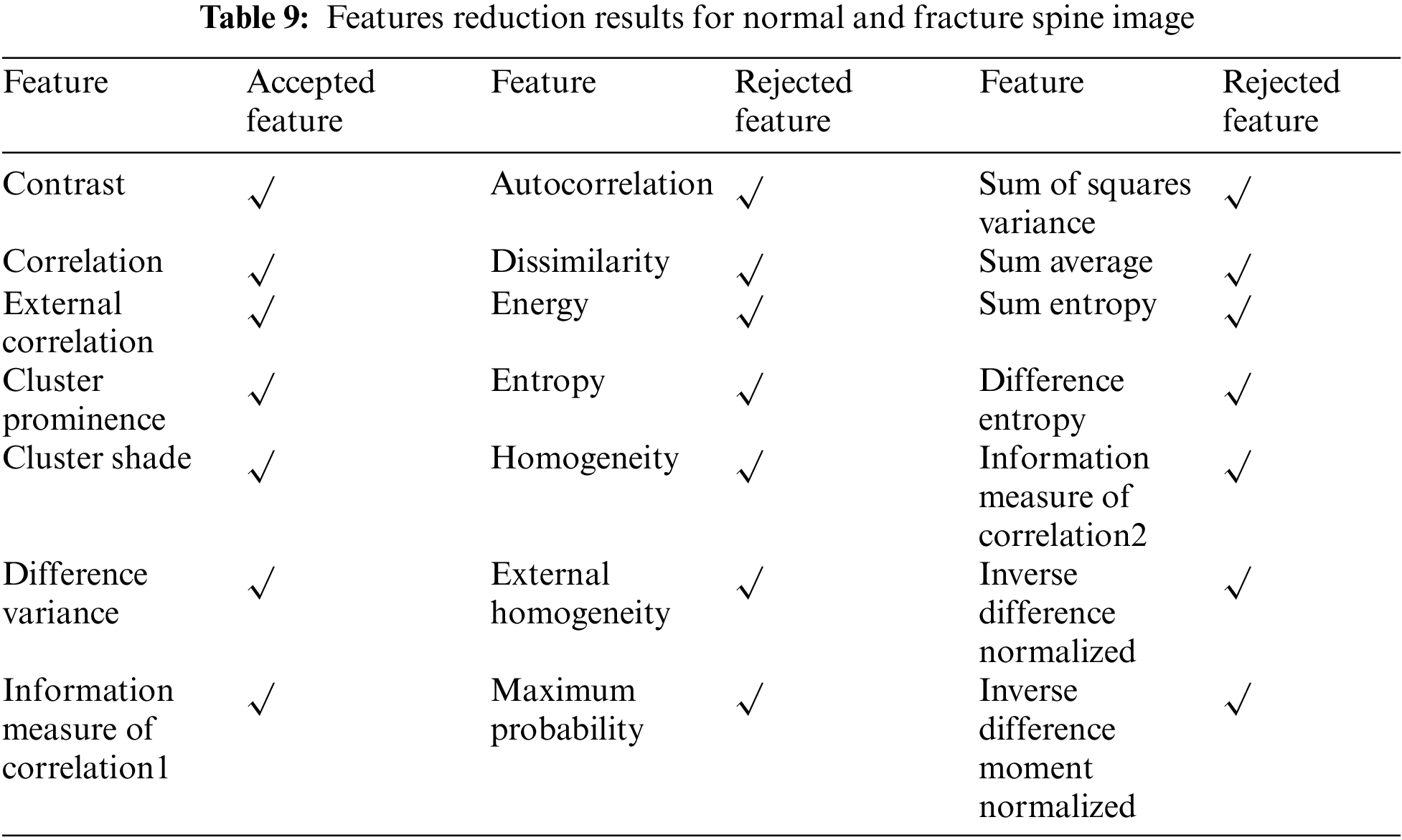
Even with high noise levels, the results demonstrated that the suggested method could successfully reconstruct and de-noise spine images. Furthermore, with the lowest recognition error rate for both Gaussian and Poisson noise degradation, the DCT method outperformed previous feature extraction techniques. The DCT performed better for both Gaussian and Poisson noise degradation than other feature extraction techniques, whereas the WA filter successfully reconstructed and denoised spine pictures. The SVM used fewer features while still achieving good classification accuracy. Even with fewerfeatures, the SVM classifier was still able to achieve good classification accuracy. Overall, the findings point to the suggested method as a potentially useful tool for classifying and detecting spine fractures. To assess the approach’s effectiveness on a bigger and more varied dataset of spine image data, more investigation is required.

7  Conclusion

The use of several algorithms to identify and categorize spine fractures is the main goal of this work. Preprocessing with WA transforms and inverse WA for ME constitutes the first stage. The evaluation of picture denoising methods demonstrates how much better the digital curvelet transform is than digital filters. The Wiener filter and Kalman filter approaches for image improvement are examined, and the latter is chosen based on the findings. Active contour segmentation is the most effective technique among those examined, according to the investigation of image segmentation algorithms. Three approaches are proposed for spine fracture recognition: Power density spectrum analysis, higher-order statistics, and feature extraction from the transform domain. These collected features are compared to a stored database and a tested image under various noise settings using Artificial Neural Networks (ANN). Textural features are carefully analyzed in several transform domains, and a feature reduction method that has been built shows a significant drop in retrieved features from 22 to 7. The execution time for picture categorization is greatly improved by this reduction. Among these transform domains, the Discrete Cosine Transform (DCT) of texture characteristics stands out as very efficient, exhibiting a high classification rate. It is important to note that more powerful hardware can be used to further increase the efficiency of feature extraction techniques. This study emphasizes how better hardware capabilities can lead to improved execution times. In conclusion, a strong system for spine fracture diagnosis is developed by the thorough assessment and integration of preprocessing, picture enhancement, segmentation, and identification algorithms. To further improve our suggested method’s classification abilities, we are keen to explore the incorporation of deep learning approaches, such as convolutional neural networks (CNNs). Our goal is to optimize the implementation of our technology to lower its computational complexity and enhance its performance on huge datasets. To increase the classification accuracy even more, we plan to investigate the effectiveness of other feature extraction methods including wavelet transforms and local binary patterns (LBPs). To assess the relative performance of our approach and pinpoint areas that require further development, we intend to perform a thorough comparison with other image categorization methods already in use.

Acknowledgement: The author extends the appreciation to the Deanship of Postgraduate Studies and Scientific Research at Majmaah University for funding this research work through the Project Number R-2024-922.

Funding Statement: Not applicable.

Author Contributions: The author validated the simulation and tested the main contribution and wrote the main manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The author reports no conflicts of interest. The author alone is responsible for the content and writing of this article.

References

1. J. Zhang et al., “Automated detection and classification of acute vertebral body fractures using a convolutional neural network on computed tomography,” Front. Endocr., vol. 14, pp. 270, 2023. doi: 10.3389/fendo.2023.1132725. [Google Scholar] [PubMed] [CrossRef]

2. L. Wang et al., “Development of a multimodal approach for lumbar spine fracture classification using machine learning,” IEEE J Biomed Health Inform., vol. 27, no. 1, pp. 1–10, 2023. [Google Scholar]

3. D. Varga, “A human visual system inspired no-reference image quality assessment method based on local feature descriptors,” Sens., vol. 22, no. 18, pp. 6775, 2022. doi: 10.3390/s22186775. [Google Scholar] [PubMed] [CrossRef]

4. S. Cakir and A. Cetin, “Image quality assessment using two-dimensional complex mel-cepstrum,” J. Electron. Imaging, vol. 25, no. 6, pp. 61604, 2016. doi: 10.1117/1.JEI.25.6.061604. [Google Scholar] [CrossRef]

5. A. Delisle, M. Gagnon, and C. Sicard, “Effect of pelvic tilt on lumbar spine geometry,” IEEE Trans. Rehabil. Eng., vol. 5, no. 4, pp. 360–366, 1997. doi: 10.1109/86.650290. [Google Scholar] [PubMed] [CrossRef]

6. S. Cakır and A. E. Çetin, “Mel-cepstral feature extraction methods for image representation,” Opt. Eng., vol. 49, no. 9, pp. 97004, 2010. doi: 10.1117/1.3488050. [Google Scholar] [CrossRef]

7. S. Cakir and A. E. Cetin, “Image feature extraction using 2D mel-cepstrum,” in 20th IEEE Int. Conf. Pattern Recognit. (ICPR), Istanbul, Turkey, 2010. [Google Scholar]

8. B. U. Toreyin and A. E. Cetin, “Shadow detection using 2D cepstrum,” in Proc. SPIE, Acquis., Track., Point., and Laser Syst. Technol., 2009, vol. XXIII, pp. 733809. doi: 10.1117/12.819053. [Google Scholar] [CrossRef]

9. S. Han, S. Kim, J. Ahn, Y. Lee, J. Park and S. Lee, “Convolutional neural network-based automated detection of thoracic and lumbar spine fractures in X-ray images,” J. Digit. Imaging, vol. 35, no. 1, pp. 112–121, 2022. [Google Scholar]

10. W. Zhang et al., “Multi-task CNN for simultaneous detection and classification of thoracic and lumbar spine fractures in X-ray images,” IEEE Access, vol. 11, pp. 22329–22339, 2023. [Google Scholar]

11. C. Li, “Support vector machine-based method for detecting thoracolumbar spine fractures in CT scans,” J. Healthc. Eng., vol. 22, no. 1, pp. 1–8, 2021. [Google Scholar]

12. L. Wang et al., “Random forest-based method for detecting lumbar spine fractures in MRI images,” Artif. Intell. Med., vol. 103, pp. 103586, 2020. [Google Scholar]

13. Kaptoge et al., “When should the doctor order a spine X-ray? Identifying vertebral fractures for osteoporosis care: Results from the European prospective osteoporosis study (EPOS),” J. Bone Mineral Res., vol. 19, no. 12, pp. 1982–1993, 2004. doi: 10.1359/jbmr.040901. [Google Scholar] [PubMed] [CrossRef]

14. J. K. Mandal, S. C. Satapathy, M. K. Sanyal, P. P. Sarkar, and A. Mukhopadhyay, “Information systems design and intelligent applications,” in Proc. 2nd Int. Conf., Kolkata, India, Jul. 9–11, 2015. [Google Scholar]

15. K. Daniel Park, “Fractures of the thoracic and lumbar spine,” Accessed: Jan. 1, 2021. [Online]. Available: https://orthoinfo.aaos.org/en/diseases [Google Scholar]

16. C. Tian, M. Zheng, W. Zuo, B. Zhang, Y. Zhang and D. Zhang, “Multi-stage image denoising with the wavelet transform,” Pattern Recognit., vol. 134, pp. 109050, 2023. doi: 10.1016/j.patcog.2022.109050. [Google Scholar] [CrossRef]

17. G. Choudhary and D. Sethi, “From conventional approach to machine learning and deep learning approach: An experimental and comprehensive review of image fusion techniques,” Arch. Comput. Methods Eng., vol. 30, no. 2, pp. 1267–1304, 2023. doi: 10.1007/s11831-022-09833-5. [Google Scholar] [CrossRef]

18. S. Palakkal and K. M. M. Prabhu, “Poisson image de-noising using fast discrete curvelet transform and wave atom,” J. Signal Process., vol. 92, no. 9, pp. 2002–2017, 2012. doi: 10.1016/j.sigpro.2012.01.008. [Google Scholar] [CrossRef]

19. J. Khandelwal and V. K. Sharma, “W-VDSR: Wavelet-based secure image transmission using machine learning VDSR neural network,” Multimed. Tools Appl., vol. 82, pp. 42147–42172, 2023. doi: 10.1007/s11042-023-15166-7. [Google Scholar] [CrossRef]

20. L. Demanet and L. Ying, “Wave atoms and sparsity of oscillatory patterns,” Appl. Comput. Harmon. Anal., vol. 23, no. 3, pp. 368–387, 2007. doi: 10.1016/j.acha.2007.03.003. [Google Scholar] [CrossRef]

21. H. Hiary, R. Zaghloul, A. Al-Adwan, and M. B. Al-Zoubi, “Image contrast enhancement using geometric mean filter,” Image Video Process., vol. 1–8, pp. 833–840, 2016. doi: 10.1007/s11760-016-1029-8. [Google Scholar] [CrossRef]

22. Y. Pu, W. Wang, and Q. Xu, “Image change detection based on the minimum mean square error,” in 5th Int. Joint Conf. Comput. Sci. Optim., 2012, pp. 367–371. [Google Scholar]

23. S. Gamse, F. Nobakht-Ersi, and M. A. Sharifi, “Statistical process control of a Kalman filter model,” Sens., vol. 14, no. 10, pp. 18053–18074, 2014. doi: 10.3390/s141018053. [Google Scholar] [PubMed] [CrossRef]

24. J. Ashburner, P. Neelin, D. L. Collins, A. Evans, and K. Friston, “Incorporating prior knowledge into image registration,” NeuroImage, vol. 6, pp. 344–352, 1997. doi: 10.1006/nimg.1997.0299. [Google Scholar] [PubMed] [CrossRef]

25. L. Han, C. Huang, S. Zheng, Z. Zhang, and L. Xu, “Vanishing point detection and line classification with BPSO,” Signal, Image Video Process., vol. 11, no. 1, pp. 17–24, 2017. [Google Scholar]

26. Q. Wang, “HMRF-EM-image: Implementation of the hidden markov random field model and its expectation-maximization algorithm,” arXiv:1207.3510, 2012. [Google Scholar]

27. S. Goliaei, S. Ghorshi, and M. Mortazavi, “Reconstruction of tomographic medical images using Kalman filter approach,” in Proc. Int. Conf. Image Process. Comput. Vis. Pattern Recognit., Washington, USA, 2011, pp. 236–240. [Google Scholar]

28. M. A. Khan, A. Mehmood, and J. M. Khan, “Power spectral density estimation for non-stationary signals: A survey,” Signal Process., vol. 200, pp. 108765, 2023. [Google Scholar]

29. Z. Zou, Z. Zhang, and J. Han, “Deep learning-based power spectral density estimation: A review,” IEEE Signal Process. Mag., vol. 40, no. 2, pp. 19–35, 2023. [Google Scholar]

30. K. J. Yoon, J. H. Park, H. Kim, C. Y. Park, and S. H. Park, “A review of bispectrum estimation methods in nonlinear system identification and modeling,” IEEE Access, vol. 11, pp. 107295–107316, 2023. [Google Scholar]

31. C. L. Nikias and M. R. Raghuveer, “Bispectrum estimation: A digital signal processing framework,” Proc. IEEE, vol. 75, pp. 869–891, 1987. doi: 10.1109/PROC.1987.13824. [Google Scholar] [CrossRef]

32. E. R. Vimina and K. P. Jacob, “Image retrieval using low level features of object regions with application to occluded images,” in Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications, 2012, vol. 7441, pp. 422–429. doi: 10.1007/978-3-642-33275-3. [Google Scholar] [CrossRef]

33. M. S. El_Tokhy and I. I. Mahmoud, “Classification of welding flaws in gamma radiography images based on multi-scale wavelet packet feature extraction using support vector machine,” J. Nondestruct. Eval., vol. 34, no. 34, pp. 1–17, 2015. [Google Scholar]

34. D. Sathish, S. Kamath, K. Prasad, R. Kadavigere, and R. J. Martis, “Asymmetry analysis of breast thermograms using automated segmentation and texture features,” Signal, Image Video Process., vol. 11, no. 4, pp. 745–752, 2017. doi: 10.1007/s11760-016-1018-y. [Google Scholar] [CrossRef]

35. R. M. Haralick, K. Shanmugam, and I. Dinstein, “Textural features for image classification,” IEEE Trans. Syst., Man Cybern., vol. SMC-3, no. 6, pp. 610–621, 1973. doi: 10.1109/TSMC.1973.4309314. [Google Scholar] [CrossRef]

36. K. Dabov, A. Foi, V. Katkovnik, and K. Egiazarian, “Image denoising by sparse 3D transform-domain collaborative filtering,” IEEE Trans. Image Process., vol. 18, no. 8, pp. 2080–2095, 2009. [Google Scholar]