Contrastive Consistency and Attentive Complementarity for Deep Multi-View Subspace Clustering

1  Introduction

The high-dimensional and complex big data create new challenges to traditional clustering methods, such as hierarchical clustering [1], density clustering [2], and fuzzy clustering [3]. In particular, the emergence of multi-view data has produced new requirements for clustering theory, models, and algorithms. Multi-view data are the different descriptions of the same object. Multi-view clustering (MVC) partitions the multi-view data by exploring consistent semantics with complementary information, which can improve clustering performance and the effectiveness of unsupervised data analysis [4,5]. Existing MVC can be roughly categorized as matrix factorization-based [6,7], graph-based [8,9], subspace-based [10,11], and kernel-based methods [12,13]. The multi-view subspace clustering (MVSC) methods have attracted more attention due to their easy implementation and outstanding performance [14,15]. MVSC methods are based on the self-expression property that each sample data can be a linear or affine representation by others in the same subspace. They learn the consensus self-expression to compute the affinity matrix of multi-view samples and then apply a spectral clustering algorithm to obtain clustering results. The traditional MVSC methods explore the intrinsic subspace self-expression by shallow model or linear embedding function. However, they can not be effectively applied in some nonlinear or complex scenarios attributed to their limited representation ability.

Recently, deep multi-view subspace clustering (DMVSC) methods have been proposed due to the powerful high-dimensional nonlinear representation ability [16,17]. DMVSC methods project the high-dimensional nonlinear data into low-dimensional latent features by deep model and then learn the consensus self-expression of multi-view data based on feature space. The consensus self-expression should reflect the consistent semantics and the complementarity across views. Most DMVSC methods learn the consensus self-expression by various fusion strategies at different stages, which can be divided into early fusion of the low-dimensional latent features and late fusion of the view-specific self-expressions, as shown in Fig. 1. In the early fusion, the latent features of all views are concatenated or directly used to learn shared self-expression for exploring consistent semantics by different diversity constraints. In the late fusion, the self-expression of each view is learned from view’s latent features individually and then fused to get the consensus self-expression across views for exploring the maximum complementarity. The fusion strategies contain average value, weighted sum, concatenating, and attention mechanism-guided fusion. However, view-private meaningless information or noise in view data may disturb the learning of consensus self-expression [18] and further result in the degeneration of clustering performance. For example, face images with different details can describe the same person, where the details can be different facial expressions, decorations, and illumination conditions. Therefore, to reduce the effect of view-private meaningless information or noise, an alignment strategy should be designed to satisfy the requirement of consistency across views in DMVSC methods.

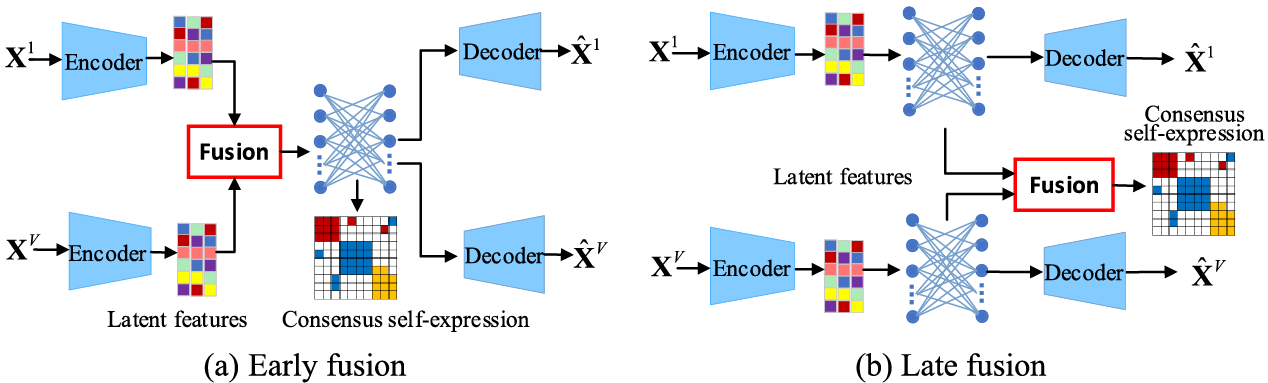
Figure 1: An illustration of fusion strategies in DMVSC methods

A novel framework of contrastive consistency and attentive complementarity (CCAC) for DMVSC is proposed to fully explore consistent semantics and complementary information across views by contrastive learning and attention mechanism, respectively. Specifically, we use an auto-encoder to obtain the low-dimensional latent features of each view. View-specific self-expression is learned from these features by a fully connected layer embedded into the auto-encoder. Subsequently, all the view-specific self-expressions are aligned by contrastive learning to avoid the effect of view-private meaningless information or noise. The aligned view-specific self-expressions are assigned adaptive weights by attention mechanism and then fused by convolution kernel to achieve consensus self-expression for computing affinity matrix. Finally, a spectral clustering algorithm is conducted on the affinity matrix to cluster multi-view data. The main contribution of our CCAC method can be summed up as follows:

•   We propose a contrastive alignment strategy based on multi-view self-expression space to avoid the effect of view-private meaningless information or noise on exploring consistent semantic information across views. Different from the previous contrastive alignment based on feature space in deep clustering, the contrastive alignment module is directly oriented to the clustering task, which can maximize the similarities of positive sample pairs while minimizing that of negative sample pairs.

•   Based on the aligned view-specific self-expression, we introduce an adaptive fusion strategy guided by the channel attention mechanism and convolution kernel to learn consensus self-expression of multi-view data, which can fully exploit the diverse complementary information across views for further boosting clustering performance.

•   Extensive experimental results on four benchmark datasets and one large-scale dataset verify the effectiveness and excellent clustering performance of CCAC over other state-of-the-art methods.

2  Related Work

2.1 Deep Multi-View Subspace Clustering

DMVSC has attracted more attention because of the outstanding performance and nonlinear application, which focuses on learning a high-quality consensus subspace self-expression based on deep learning. Inspired by the typical deep subspace clustering network [19], the unsupervised deep auto-encoder is widely used to learn latent low-dimensional features of multi-view data. Then, consensus self-expression is learned from the latent features. According to the strategy of learning consensus self-expression, existing DMVSC methods can be roughly divided into two categories, i.e., early fusion of the latent features and late fusion of the view-specific self-expressions.

In the first category, consensus self-expression is learned via a shared fully connected layer from the latent features with different diversity constraints. For example, different fusion functions, including sum, max-pooling, and concatenation, are proposed to combine the latent features of all the views for learning shared self-expression [20]. The t-SNE is used to supervise the latent features for learning shared self-expression by considering the inter-view and intra-view distributions [21]. The spectral clustering loss and classification loss are introduced and integrated into the deep auto-encoder network to supervise the shared self-expression learning while considering the impact of noise [22]. Hadanard product is proposed to constrain discrimination of low-dimensional latent features extracted by auto-encoder for learning shared self-expression with the global and local structure [16]. The view-specific latent features are weighted by the self-attention mechanism and fused to learn shared self-expression by a fully connected layer [23].

In the second category, multiple fully connected layers are inserted into the auto-encoder to learn self-expressions for multiple views, which are further fused to obtain consensus self-expression. For instance, view-specific self-expressions are learned with the diversity constraint of the Hilbert Schmidt Independence Criterion and aligned with common self-expression that is used for clustering [24]. All the view-specific self-expressions are fused to obtain the consensus self-expression by a fully connected layer [25]. In [17], the view-specific self-expressions are weighted by the channel attention mechanism and fused by the convolution kernel to learn consensus self-expression with maximum complementarity for precise clustering. Information bottleneck is extended to explore view-specific information in the latent feature space. After obtaining the view-specific self-expressions, the average is regarded as the final result for clustering [26].

In the above methods for DMVSC, the early fusion strategy pursues consistent semantics, and the late fusion strategy focuses on exploring complementary information. The DMVSC methods can achieve superior clustering performance compared with traditional MVSC methods. However, they suffer from the following limitations: 1) The view-private meaningless information or noise may interfere with the quality of consensus self-expression learning, which further leads to the degeneration of clustering performance; 2) They cannot fully explore consistent semantics and complementary information across views in a unified optimization framework.

2.2 Contrastive Learning

Contrastive learning is a self-supervised representation learning for mapping similar samples close and dissimilar samples far apart in the latent feature space. Thus, contrastive learning can maximize the similarities of positive sample pairs and minimize that of negative sample pairs [27]. It has been applied in existing deep MVC methods to explore consistency based on the latent feature space. The alignment of view-specific latent features based on contrastive learning has been demonstrated due to the excellent performance in deep multi-view clustering [18,28–30]. DMVSC methods based on contrastive learning have been proposed for learning consensus self-expression. For example, contrastive learning is used to obtain the common feature representation for self-expression learning [31]. The method can explore the consistency across views, which can not achieve the maximum complementarity to boost the clustering performance.

3  Proposed Method

To fully explore consistent semantics and complementary information across views, we propose a novel framework of contrastive consistency and attentive complementarity (CCAC) for DMVSC, which is implemented by a unified optimization network based on deep auto-encoder. The framework of our CCAC method is shown in Fig. 2. It consists of the view-specific self-expression learning, contrastive alignment, and adaptive fusion modules. In this paper, multi-view data denoted as {Xv∈RN×Dv}v=1V includes N samples of varying dimension Dv across V views.

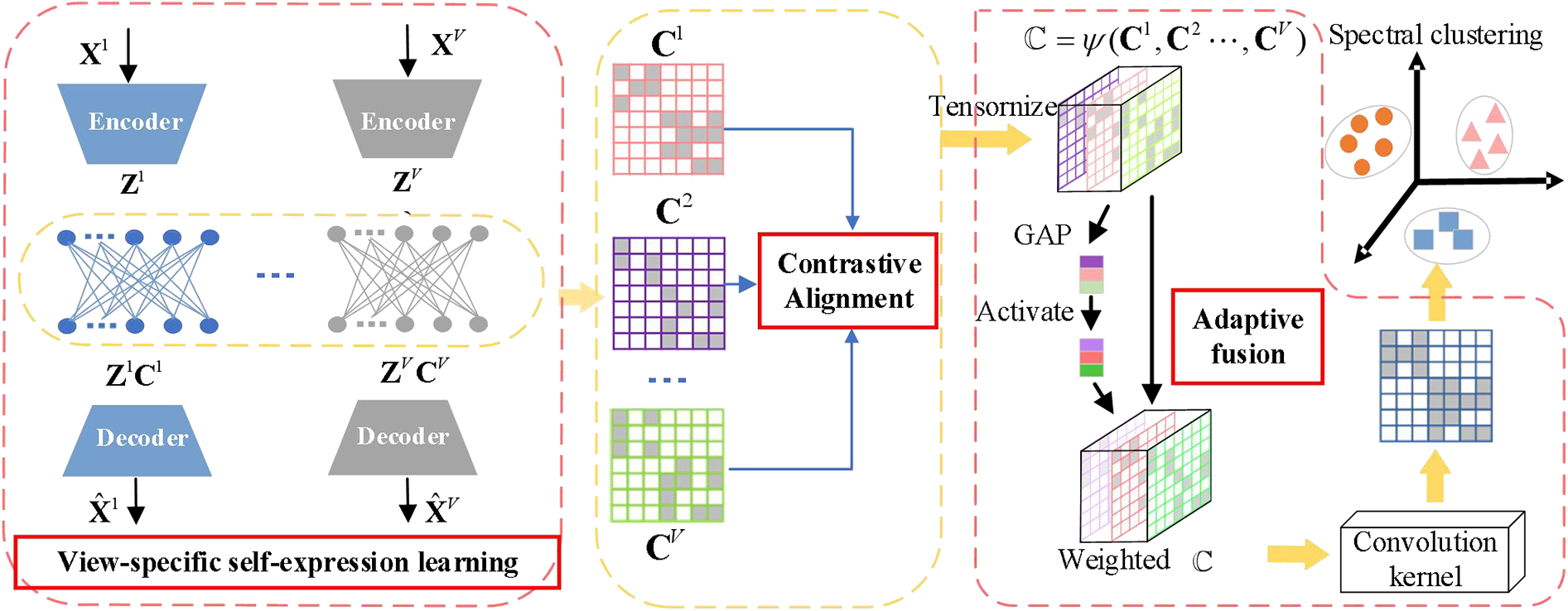
Figure 2: The framework of our proposed CCAC method mainly consists of three modules: 1) view-specific subspace self-expression learning module, which is constructed by multiple auto-encoders to extract deep latent features of multi-view data and from them to learn view-specific self-expression coefficient matrix by inserting a fully connected layer into each auto-encoder pair; 2) contrastive alignment module, which uses contrastive learning to align view-specific self-expression coefficient matrices of all views for achieving the consistency objective of multi-view data; and 3) adaptive fusion module, which comprehensively explores the complementary information of multi-view data by channel attentive mechanism guided fusion strategy

3.1 View-Specific Self-Expression Learning Module

The unlabeled multi-view data are usually represented by high-dimensional features accompanied by redundancy or random noise. As the unsupervised learning model for processing unlabeled data, auto-encoder is widely used to obtain the low-dimensional features with semantic information by filtering out the redundancy or random noise of original data. Therefore, we employ auto-encoder to map the original view data into the latent feature space by minimizing reconstruction loss. The auto-encoder is constructed by encoder and decoder with a symmetrical structure. Based on the latent feature space, existing DMVSC methods have two strategies to learn the consensus self-expression for clustering: 1) Early fusion. From the fusing latent features, the shared self-expression is learned by a fully connected layer embedding into the auto-encoder; 2) Late fusion. View-specific self-expressions are learned and then fused to obtain consensus self-expression. As analyzed above, the late fusion strategy learns diverse view-specific self-expressions for exploring complementary information, while the early fusion strategy only pursues consistency. Consequently, we adopt the late fusion strategy to learn the consensus self-expression.

Specifically, taking the individual view Xv as the input, an encoder Ev(Xv;Θev) is employed to learn the low-dimensional latent features Zv, i.e., Zv=Ev(Xv;Θev), where Θev is the network parameter of the encoder. We insert a fully connected layer without bias into the auto-encoder to obtain view-specific self-expression. The parameter of the linear fully connected layer is denoted as the self-expression coefficient matrix Cv∈RN×N, which depicts the similar relationship among the samples in the view data. Taking the ZvCv as the input, a decoder Dv(ZvCv;Θdv) having a symmetrical structure with the encoder is used to reconstruct data X^vwith the minimum error, i.e., X^v=Dv(ZvCv;Θdv), where Θdv is the network parameter of the decoder. Based on the self-expression property that one sample point can be expressed as a combination of others in the same view, the relationship should be reflected in the low-dimensional latent feature space, i.e., Zv=ZvCv. Therefore, the reconstruction error Xv−X^v and self-expression error Zv−ZvCv should be minimal to explore the self-expression relationship in the same view. For all the views, we can obtain the self-expression coefficient matrices {Cv}v=1V by optimizing the reconstruction error and self-expression error:

ℒ1=∑v=1V‖Xv−X^v‖F2+∑v=1V‖Zv−ZvCv‖F2+∑v=1V‖Cv‖F2,s.t.diag(Cv)=0(1)

where the last term is the regularization loss error to make Cv with block-diagonal structure by Frobenius norm for spectral clustering. The constraint diag(Cv)=0 can avoid the trivial solution for Cv, i.e., all the samples are partitioned into the same clusters.

3.2 Contrastive Alignment Module

Since the self-expression coefficient matrices {Cv}v=1V for all views obtained by Eq. (1) may receive interference with the view-private meaningless information or noise, which shifts the self-expression relationship that reflects consistent semantics across views, resulting in the degeneration of clustering performance. Recently, contrastive learning has been widely applied to pursue the consistent semantic objective in deep multi-view clustering methods [32–34]. They use contrastive learning to align the latent features of multiple views to explore consistent features. Different from the contrastive alignment based on the feature space, we use contrastive learning to align the {Cv}v=1V based on the self-expression space to achieve the consistency objective, with the following two considerations: 1) The self-expression coefficient matrices describe the similar relationship of samples in multiple views, which are direct for clustering task; 2) The consistent objective of self-expression coefficient matrices can boost exploring maximum complementary information across views.

Specifically, we select the view-specific self-expression coefficients of the same samples from different views as the positive pairs, and the self-expression coefficients of different samples from the same or different views as the negative pairs. For one sample in the self-expression coefficient matrix {civ}i,j=1,⋯,Nv=1,⋯,V, there are (V−1) positive sample pairs and V(N−1) negative sample pairs. The objective of contrastive learning based on self-expression is to maximize the similarities of positive sample pairs while minimizing that of negative sample pairs. In our method, the similarities between the view-specific self-expression coefficient matrices Cvand Cp are measured by cosine distance:

d(civ,cjp)=<civ,cjp>‖civ‖‖cjp‖,(2)

where <⋅,⋅> is the dot product operator. The loss function of contrastive loss between arbitrarily two view-specific self-expression coefficient matrices can be formulated as [18]:

ℓ(v,p)=−1N∑i=1Nlog⁡ed(civ,cip)/τ∑j=1N∑q=v,ped(civ,cjq)/τ−e1/τ,(3)

ℒ2=12∑v=1V∑p≠vℓ(v,p)(4)

Based on the view-specific self-expression contrastive loss across views, the self-expression coefficients of samples that belong to the same cluster will increase outstandingly, and oppositely, the coefficients of the samples in different classes will decrease. To this end, the consistent semantics across views can be mined, and the effect of view-private information or noise can be filtered out, which can boost clustering performance.

3.3 Adaptive Fusion Module

After aligning the self-expression coefficient matrices, they are fused to obtain the consensus self-expression with the complementary information across multiple views. Existing DMVSC methods adopt average, weighted sum, or concatenation strategies to fuse the self-expression coefficient matrices. However, they neglect the discriminative relationship among the self-expressions and the different contributions to consensus self-expression varying by each coefficient matrix. Inspired by the work in [35], we use the channel attention mechanism to weigh the multiple self-expression coefficient matrices according to their discriminative contribution. Then the weighted matrices are fused by convolution kernel to obtain the final self-expression coefficient matrix for spectral clustering.

Specifically, we stack the aligned {Cv}v=1V along the channel dimension as a three-order tensor 𝒞. The channel attention mechanism is employed on 𝒞 to explore the high-order relationships among {Cv}v=1V. The relationships of {Cv}v=1V are mapped to the weights to scale the self-expression tensor along the channel dimension. The channel attention mechanism network consists of one global average pooling (GAP) and two fully connected layers. The process is formulated as:

𝒞s=σ(θ2δ(θ11N×N∑i=1N∑j=1N𝒞(i,j)))⋅𝒞,(5)

where the formula 1N×N∑i=1N∑j=1N𝒞(i,j) is a descriptor with the global distribution of each channel in the self-expression tensor, which is implemented by GAP layer. θ1 and θ2 are the parameters of two fully connected lays without bias. The two fully connected layers δ(⋅) and σ(⋅), which can capture the dependencies among the self-expressions, are used to excite the descriptors into weight scalars to scale the tensor along the channel. The first layer is to reduce the dimensions, and oppositely, the second layer is for recovering the dimensions.

Subsequently, we use a convolution kernel k to fuse the scaled tensor 𝒞s for obtaining the consensus self-expression coefficient matrix C of multi-view data, which can achieve the maximum complementarity across views.

C=k∗𝒞s(6)

Finally, the consensus self-expression coefficient matrix C is used to calculate the affinity matrix of multi-view data for obtaining the final clustering results. Therefore, the Cshould be constrained by the block-diagonal structure. As in Eq. (1), we use the Frobenius norm to form the regularization loss on C.

ℒ3=‖C‖F2,     s.t.diag(C)=0(7)

3.4 Loss Objective and Optimization

In consequence, the loss functions of the three modules, including view-specific self-expression learning (ℒ1), contrastive alignment (ℒ2), and adaptive fusion (ℒ3), are integrated as the objective loss of our CCAC method, which is formulated as:

minCℒ=∑v=1V‖Xv−X^v‖F2⏟Reconstruction loss+λ1⋅(∑v=1V‖Zv−ZvCv‖F2⏟Self−expression loss+∑v=1V‖Cv‖F2+‖C‖F2⏟Regularization loss)−λ2⋅12N∑v=1V∑p≠v∑i=1Nloged(civ,cip)/τ∑j=1N∑q=v,ped(civ,cjq)/τ−e1/τ⏟Contrastive loss,     s.t.diag(Cv)=0,diag(C)=0,(8)

where λ1 and λ2 are the hyperparameters for balancing the consistency and complementarity across views.

Algorithm 1 gives the optimization process of CCAC, including the pre-training and fine-tuning stages. In the pre-training stage, we use the loss ∑v=1V‖Xv−X^v‖F2 to train the encoder and decoder for obtaining their initial parameters. In the fine-tuning stage, Eq. (8) is used to fine-tune the pre-trained encoder and decoder by embedding multiple self-expression learning layers for learning consensus self-expression C with contrastive alignment and adaptive fusion strategies. Finally, the affinity matrix is obtained by W=(|C|+|C|⊤)/2, and the clustering results are obtained by applying the spectral clustering algorithm on W.

4  Experiments

4.1 Experimental Setup

Datasets. We conduct experiments on four benchmark datasets: BBCSport1, Extended Yale B2, COIL203, UCI digits4, and one large-scale dataset: Caltech101-all5. BBCSport depicts 5 topical sports news of 544 samples by two publishers. Extended Yale B consists of 38 people faces and each face takes 64 images under different illumination. The top 10 classes of three feature views are selected in our experiments. COIL20 contains 20 object images of 1440 samples with three feature views. UCI digits dataset shows the handwritten digit images of 2000 samples with three different views. Caltech101-all is a large-scale dataset, which consists of 101 object categories images and a background class with 9144 image samples. Each image is extracted with five image features to form different views. The sample data in the five datasets are reshaped into vectors. Table 1 summarizes the details of the five datasets.

Comparison methods. Our CCAC method is compared with the state-of-the-art multi-view clustering methods, including LRR [2013, TPAMI] [36], DiMSC [2015, CVPR] [37], LTMSC [2015, ICCV] [38], AWP [2018, SIGKDD] [39], t-SVD-MSC [2018, IJCV] [40], ELTMSC [2019, TIP] [41], SCMV-3DT [2019, TNNLS] [42], LMSC [2020, TPAMI] [43], MCLES [2020, AAAI] [44], TRPCA [2020, TPAMI] [45], CDIMC-net [2020, IJCAI] [46], DMSC-UDL [2021, TMM] [16], SSSL-M [2022, TIP] [47], MDMVSC [2023, ESWA] [17], DeepMVC [2023, CVPR] [30], and ESCC [2023, TKDE] [48].

Implementation details. CCAC is implemented by PyTorch framework based on the code of DMSC-UDL, which is optimized by adaptive moment estimation optimizer. The encoder and decoder are constructed by a three-layer fully connected neural network with symmetrical structure. In the pre-training stage, the learning rate is set to 0.001 on five datasets. For the fine-tuning stage, it is set to 0.001 on BBCSport and COIL20, and 0.0001 on UCI digits, Extended Yale B, and Caltech101-all datasets. In the adaptive fusion module, the size of convolution kernel is set as k=3×3 to fuse the scaled view-specific self-expression tensor for obtaining the consensus self-expression on all datasets. The optimal hyperparameters λ1 and λ2 are selected by grid search strategy in a range of {0.01, 0.1, 1, 10, 100}. The temperature parameter τ is determined in a range of {0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0}. The detailed network structure and parameters are summarized in Table 2.

Evaluation metrics. Following the convention of clustering evaluation metrics [14,15], the six widely used performance metrics, including accuracy (ACC), normalized mutual information (NMI), adjusted rand index (ARI), F-score, precision, and recall, are used to fully evaluate the clustering performance and effectiveness of our CCAC method.

4.2 Experimental Comparative Result Analysis

Tables 3–7 give the comparative results with the 16 multi-view clustering methods on the five datasets in terms of the six evaluation metrics. The best performance results are highlighted in bold and the second in underline. To objectively exhibit the clustering performance of CCAC method, we perform experiments on large-scale Caltech101-all dataset 5 times and on other four datasets 30 times. The mean and standard deviation of clustering results are given in the tables.

From the tables, it can be observed that CCAC achieves better clustering performance than most state-of-the-art multi-view clustering methods. Specifically, the observations can be summarized as follows:

1.    The clustering results of our CCAC method exceed other comparison methods on BBCSport, COIL20, UCI digits, and Caltech101-all datasets. Especially, On the COIL20 dataset, CCAC is superior to the suboptimal method ETLMSC, improving the clustering results by 3.9%, 1.1%, 3.7%, 3.6%, 5.2%, and 1.7% in terms of ACC, NMI, ARI, F-score, precision, and recall metrics. The clustering results of CCAC on the Extended Yale B dataset are close to the optimal clustering performance. It is one of the two methods that can achieve more than 99% clustering performance.

2.    Compared with the deep MVC methods (SSSL-M, CDIMC-net, DeepMVC), our proposed CCAC method can obtain superior clustering results. CCAC integrates the advantages of deep learning and subspace learning to obtain a high-quality cross-view affinity matrix for clustering. Moreover, compared with the DMVSC methods (DMSC-UDL and MDMVSC), the CCAC method also performs well. For example, the clustering results of CCAC achieve above 98% on Extended Yale B, COIL20, and UCI digits datasets of all evaluation metrics. The outstanding clustering performance is attributed to the following observations. In DMSC-UDL, the Hadanard product is used to constrain discrimination of low-dimensional features to learn shared self-expression with the global and local structure. In MDMVSC, all the view-specific self-expressions are fused to obtain the consensus self-expression by channel attention mechanism and convolution kernel, which can explore the maximum complementarity of different views for precise clustering. However, it neglects the consistency across views for clustering. Compared with the two DMVSC methods, we use contrastive learning to align the view-specific self-expressions and channel attention mechanism to fuse the aligned self-expressions, respectively. Therefore, CCAC can comprehensively explore the consistency and complementarity across views to improve clustering performance.

3.    Our CCAC method can obtain the best clustering performance on large-scale Caltech101-all dataset among all methods. However, we can observe that the clustering results of all methods on this large-scale dataset are not as outstanding as other small-scale datasets. Moreover, the running time and memory space of CCAC and other subspace-based clustering methods increase with the number of multi-view data samples. It is because the subspace-based clustering methods learn the affinity matrix of multi-view and apply spectral clustering to obtain the final results, which need the running time of 𝒪(N3) and memory space of 𝒪(N2) at least. Therefore, we will optimize the CCAC method with learning-based anchors to improve efficiency and extend the application.

4.3 Model Analysis

Ablation studies. In this section, we perform ablation experiments to verify the effectiveness of contrastive alignment and adaptive fusion modules in CCAC. Taking the BBCSport dataset as an example, the clustering results of ablation experiments are given in Table 8. If the adaptive fusion module is not used, as in model A, we average the view-specific self-expression as consensus self-expression. Compared to B with A, contrastive alignment of the view-specific self-expressions can improve clustering performance by 6.3%, 4.4%, 4.8%, 6.6%, 2.9%, and 4.7% in terms of ACC, NMI, AR, F-score, precision, and recall. In model C, we use adaptive fusion instead of average values to further boost clustering performance. According to models C and A, we can observe that the adaptive fusion module plays the most important role in performance improvement of 12.1%, 21.4%, 20.1%, 18.2%, 13.9%, and 16.0%. From the clustering performance improvement comparison by contrastive alignment and adaptive fusion, we can observe that adaptive fusion outperforms contrastive alignment for enhancing performance. This can be attributed to the following reasons. Multi-view data are the different descriptions of the same object, including consistent and complementary information. In this paper, contrastive alignment aims to obtain consistent information, and adaptive fusion can fully mine the complementary information. Compared with consistent information, complementary information is the main reason for multi-view learning working and an important factor in improving the performance of multi-view clustering. When the two modules work together, the CCAC method achieves outstanding clustering results.

Parameter sensitivity analysis. There are two hyperparameters λ1 and λ2 in our CCAC method to balance the contribution of consistency and complementarity for multi-view clustering. The parameter sensitivity experiments are performed to evaluate the effect of hyperparameters in the range of {0.01, 0.1, 1, 10, 100}, which are implemented by the grid search strategy. The experimental results of NMI with respect to λ1 and λ2 on four datasets are shown in Fig. 3. It is observed that CCAC method is insensitive to the two hyperparameters within a certain range, especially hyperparameter λ2. The NMI metric decreases on BBCSport when λ1 is from 0.01 to 0.1. It is affected on Extended Yale B when λ1 is from 10 to 100. The NMI metric of CCAC on the UCI digits and COIL20 datasets always keeps stable with λ1 and λ2 in the range of {0.01, 0.1, 1, 10, 100}. It further verifies the parameter insensitivity and effectiveness of our CCAC method.

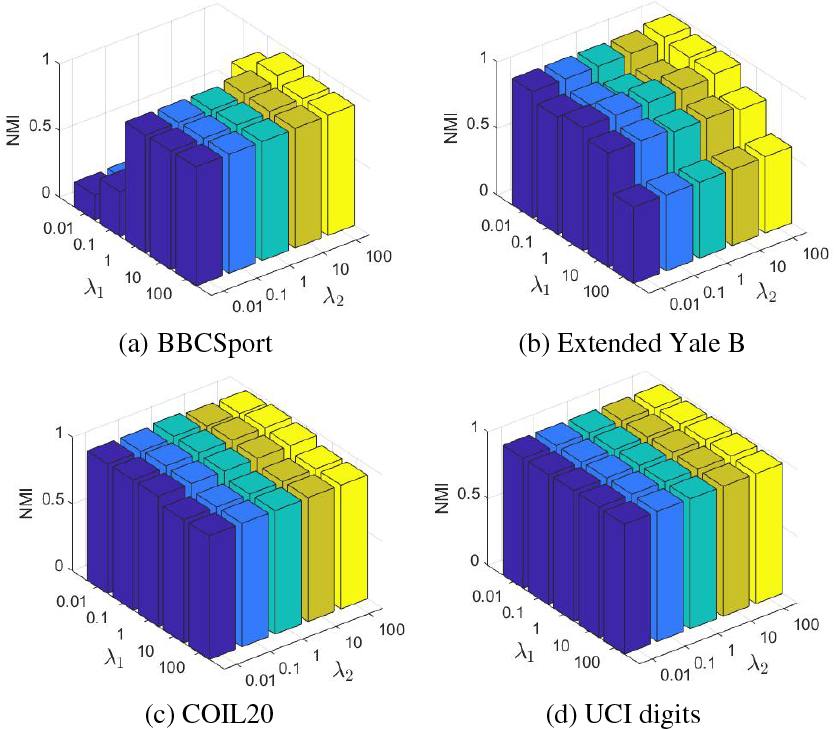
Figure 3: Parameter sensitivity analysis of λ1 and λ2 on the four datasets

Furthermore, the effect of temperature parameter τ in the contrastive alignment module on clustering performance is evaluated by experiments. Fig. 4 shows the parameter sensitivity results of ACC on the four datasets. We can observe that the clustering results of CCAC are insensitive to the choice of τ on BBCSport, COIL20, and UCI digits. There is a slight fluctuation of ACC on Extended Yale B, but the clustering performance is stable when the τ is from 0.3 to 0.6.

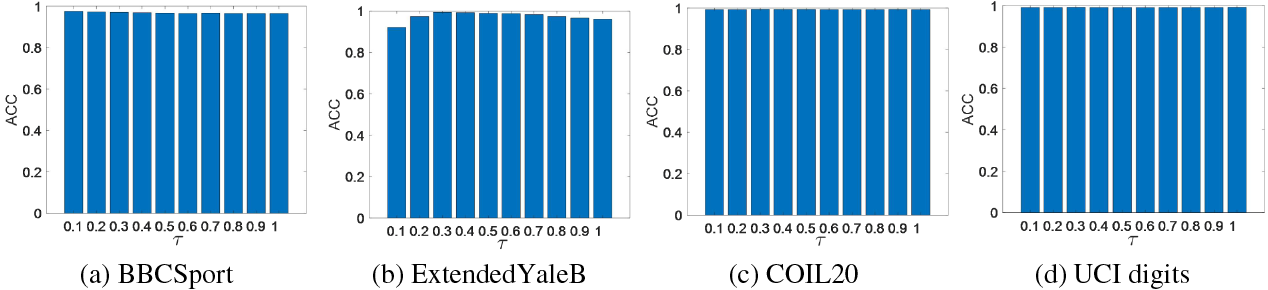
Figure 4: Parameter sensitivity analysis of temperature τ on the four datasets

Convergence analysis. We analyze the convergence of CCAC by plotting the changes of loss function logarithmic value and evaluation metrics with epoch on four datasets, as shown in Fig. 5. We can see the logarithmic value of loss monotonically descends until convergence, oppositely, the six clustering performance evaluation metrics increase rapidly and keep stable on the four datasets. For example, the convergence of CCAC on UCI digits is the fastest in the four datasets, which converges in 50 epochs with such stable clustering performance. Meanwhile, the clustering performance also increases at the highest rate on this dataset and remains stable over the epochs. CCAC on Extended Yale B shows the slowest convergence, and the clustering performance rises to the best values after 1600 epochs.

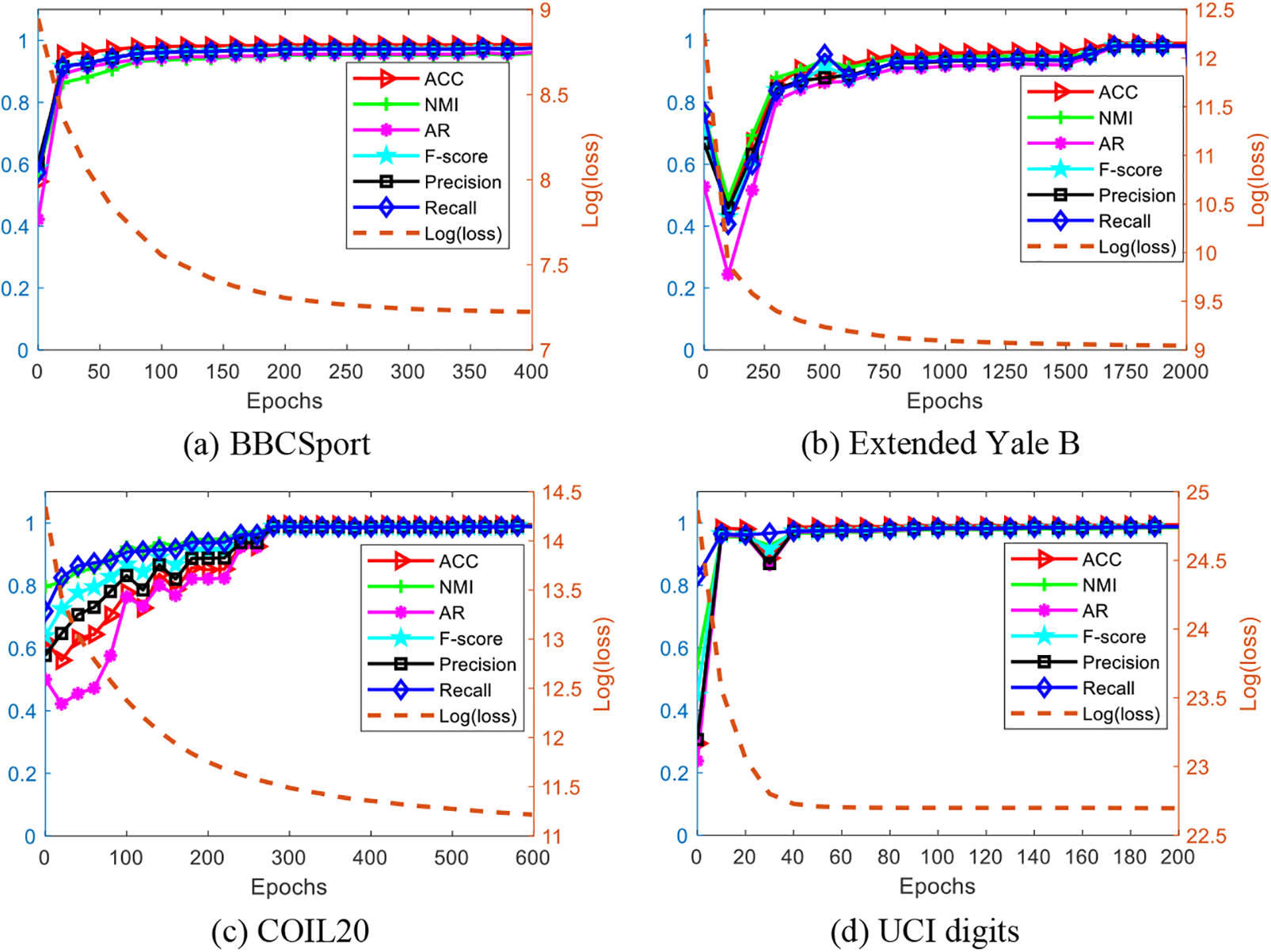
Figure 5: Convergence analysis on the four datasets

5  Conclusion

In this paper, we propose a novel framework of contrastive consistency and attentive complementarity for DMVSC. The auto-encoder is employed to learn the low-dimensional latent features of each view by reconstructing the original view data. Then, multiple self-expression learning layers are inserted into the auto-encoder to learn the view-specific self-expression. To fully explore the consistent semantics, all the view-specific self-expressions are aligned through contrastive learning to avoid the effect of view-private information. According to the diverse relationship, the aligned view-specific self-expressions are assigned adaptive weights and fused to obtain the consensus self-expression by channel attention mechanism and convolution operator, aiming at maximizing the complementarity of multiple views. Experimental results demonstrate the outstanding clustering performance and effectiveness of our method.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Jiao Wang: Methodology, Software, Validation, Writing—original draft. Bin Wu: Supervision, Methodology. Hongying Zhang: Investigation, Writing—review & editing.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

1http://mlg.ucd.ie/datasets/segment.html

2http://cvc.cs.yale.edu/cvc/projects/yalefacesB/yalefacesB.html

3https://www.cs.columbia.edu/CAVE/software/softlib/

4http://archive.ics.uci.edu/dataset/72/multiple+features

5https://data.caltech.edu/records/mzrjq-6wc02

References

1. C. K. Reddy and B. Vinzamuri, “A survey of partitional and hierarchical clustering algorithms,” in Data Clustering, Chapman and Hall/CRC, pp. 87–110, 2018. [Google Scholar]

2. R. J. Campello, P. Kröger, J. Sander and A. Zimek, “Density-based clustering,” Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, vol. 10, no. 2, pp. e1343, 2020. [Google Scholar]

3. S. Qaiyum, I. Aziz, M. H. Hasan, A. I. Khan and A. Almalawi, “Incremental interval type-2 fuzzy clustering of data streams using single pass method,” Sensors, vol. 20, no. 11, pp. 3210, 2020 [Google Scholar] [PubMed]

4. X. Jia, X. Jing, X. Zhu, S. Chen, B. Du et al., “Semi-supervised multi-view deep discriminant representation learning,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 7, pp. 2496–2509, 2021 [Google Scholar] [PubMed]

5. N. Mushtaq, A. Khan, F. Khan, M. Ali, M. M. Shahid et al., “Brain tumor segmentation using multi-view attention based ensemble network,” Computers, Materials & Continua, vol. 72, no. 3, pp. 5793–5804, 2022. [Google Scholar]

6. C. Zhang, S. Wang, J. Liu and S. Zhou, “Multi-view clustering via deep matrix factorization and partition alignment,” in Proc. of the 29th ACM Int. Conf. on Multimedia, Chengdu, China, pp. 4156–4164, 2021. [Google Scholar]

7. B. Li, Z. Shu, Y. Liu, C. Mao, S. Gao et al., “Multi-view clustering via label-embedded regularized NMF with dual-graph constraints,” Neurocomputing, vol. 551, pp. 126521, 2023. [Google Scholar]

8. H. Wang, Y. Yang and B. Liu, “GMC: Graph-based multi-view clustering,” IEEE Transactions on Knowledge and Data Engineering, vol. 32, no. 6, pp. 1116–1129, 2019. [Google Scholar]

9. Y. Du, G. Lu and G. Ji, “Robust and optimal neighborhood graph learning for multi-view clustering,” Information Sciences, vol. 631, pp. 429–448, 2023. [Google Scholar]

10. H. Li, Z. Ren, M. Mukherjee, Y. Huang, Q. Sun et al., “Robust energy preserving embedding for multi-view subspace clustering,” Knowledge-Based Systems, vol. 210, pp. 106489, 2020. [Google Scholar]

11. W. Guo, Z. Wang, Z. Chi, X. Xu, D. Li et al., “Scalable one-stage multi-view subspace clustering with dictionary learning,” Knowledge-Based Systems, vol. 259, pp. 110092, 2023. [Google Scholar]

12. Z. Ren, H. Li, C. Yang and Q. Sun, “Multiple kernel subspace clustering with local structural graph and low-rank consensus kernel learning,” Knowledge-Based Systems, vol. 188, pp. 105040, 2020. [Google Scholar]

13. Y. Zhao, W. Liang, J. Lu, X. Chen and N. Kong, “Trade-off between efficiency and effectiveness: A late fusion multi-view clustering algorithm,” Computers, Materials & Continua, vol. 66, no. 3, pp. 2709–2722, 2021. [Google Scholar]

14. X. Si, Q. Yin, X. Zhao and L. Yao, “Consistent and diverse multi-view subspace clustering with structure constraint,” Pattern Recognition, vol. 121, pp. 108196, 2022. [Google Scholar]

15. N. Zhao and J. Bu, “Robust multi-view subspace clustering based on consensus representation and orthogonal diversity,” Neural Networks, vol. 150, pp. 102–111, 2022 [Google Scholar] [PubMed]

16. Q. Wang, J. Cheng, Q. Gao, G. Zhao and L. Jiao, “Deep multi-view subspace clustering with unified and discriminative learning,” IEEE Transactions on Multimedia, vol. 23, pp. 3483–3493, 2021. [Google Scholar]

17. J. Wang, B. Wu, Z. Ren, H. Zhang and Y. Zhou, “Multi-scale deep multi-view subspace clustering with self-weighting fusion and structure preserving,” Expert Systems with Applications, vol. 213, pp. 119031, 2023. [Google Scholar]

18. J. Xu, H. Tang, Y. Ren, L. Peng, X. Zhu et al., “Multi-level feature learning for contrastive multi-view clustering,” in IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, pp. 16030–16039, 2022. [Google Scholar]

19. P. Ji, T. Zhang, H. Li, M. Salzmann and I. Reid, “Deep subspace clustering networks,” in Advances in Neural Information Processing Systems, Long Beach, CA, USA, vol. 30, 2017. [Google Scholar]

20. M. Abavisani and V. M. Patel, “Deep multimodal subspace clustering networks,” IEEE Journal of Selected Topics in Signal Processing, vol. 12, no. 6, pp. 1601–1614, 2018. [Google Scholar]

21. Q. Wang, W. Xia, Z. Tao, Q. Gao and X. Cao, “Deep self-supervised t-SNE for multi-modal subspace llustering,” in Proc. of the 29th ACM Int. Conf. on Multimedia, China, pp. 1748–1755, 2021. [Google Scholar]

22. X. Sun, M. Cheng, C. Min and L. Jing, “Self-supervised deep multi-view subspace clustering,” in Asian Conf. on Machine Learning, Nagoya, Japan, pp. 1001–1016, 2019. [Google Scholar]

23. R. Lu, J. Liu and X. Zuo, “Attentive multi-view deep subspace clustering net,” Neurocomputing, vol. 435, pp. 186–196, 2021. [Google Scholar]

24. P. Zhu, B. Hui, C. Zhang, D. Du, L. Wen et al., “Multi-view deep subspace clustering networks,” arXiv preprint arXiv:1908.01978, 2019. [Google Scholar]

25. B. Cui, H. Yu, L. Zong and Z. Cheng, “Self-guided deep multi-view subspace clustering network,” in IEEE Int. Conf. on Multimedia and Expo (ICME), Shenzhen, China, pp. 1–6, 2021. [Google Scholar]

26. S. Wang, C. Li, Y. Li, Y. Yuan and G. Wang, “Self-supervised information bottleneck for deep multi-view subspace clustering,” IEEE Transactions on Image Processing, vol. 32, pp. 1555–1567, 2023. [Google Scholar]

27. P. H. Le-Khac, G. Healy and A. F. Smeaton, “Contrastive representation learning: A framework and review,” IEEE Access, vol. 8, pp. 193907–193934, 2020. [Google Scholar]

28. Y. Tian, D. Krishnan and P. Isola, “Contrastive multiview coding,” in European Conf. Computer Vision (ECCV), Glasgow, UK, pp. 776–794, 2020. [Google Scholar]

29. D. J. Trosten, S. Løkse, R. Jenssen and M. Kampffmeyer, “Reconsidering representation alignment for multi-view clustering,” in IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, pp. 1255–1265, 2021. [Google Scholar]

30. T. Daniel, L. Sigurd, J. Robert and K. Michael, “On the effects of self-supervision and contrastive alignment in deep multi-view clustering,” in IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, pp. 23976–23985, 2023. [Google Scholar]

31. L. Cheng, Y. Chen and Z. Hua, “Deep contrastive multi-view subspace clustering,” in Int. Conf. on Neural Information Processing (ICONIP), New Delhi, India, pp. 692–704, 2022. [Google Scholar]

32. G. Ke, G. Chao, X. Wang, C. Xu, Y. Zhu et al., “A clustering-guided contrastive fusion for multi-view representation learning,” IEEE Transactions on Circuits and Systems for Video Technology, 2023. [Google Scholar]

33. W. Yan, Y. Zhang, C. Lv, C. Tang, G. Yue et al., “GCFAgg: Global and cross-view feature aggregation for multi-view clustering,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, pp. 19863–19872, 2023. [Google Scholar]

34. R. Lin, Y. Lin, Z. Lin, S. Du and S. Wang, “CCR-Net: Consistent contrastive representation network for multi-view clustering,” Information Sciences, vol. 637, pp. 118937, 2023. [Google Scholar]

35. J. Hu, L. Shen and G. Sun, “Squeeze-and-excitation networks,” in IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, pp. 7132–7141, 2018. [Google Scholar]

36. G. Liu, Z. Lin, S. Yan, J. Sun, Y. Yu et al., “Robust recovery of subspace structures by low-rank representation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, pp. 171–184, 2013 [Google Scholar] [PubMed]

37. X. Cao, C. Zhang, H. Fu, S. Liu and H. Zhang, “Diversity-induced multi-view subspace clustering,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, pp. 586–594, 2015. [Google Scholar]

38. C. Zhang, H. Fu, S. Liu, G. Liu and X. Cao, “Low-rank tensor constrained multiview subspace clustering,” in Proc. of the IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 1582–1590, 2015. [Google Scholar]

39. F. Nie, L. Tian and X. Li, “Multiview clustering via adaptively weighted procrustes,” in Proc. of the 24th ACM SIGKDD Int. Conf. on Knowledge Discovery & Data Mining, New York, NY, USA, pp. 2022–2030, 2018. [Google Scholar]

40. Y. Xie, D. Tao, W. Zhang and Y. Liu, “On unifying multi-view self-representations for clustering by tensor multi-rank minimization,” International Journal of Computer Vision, vol. 126, no. 11, pp. 1157–1179, 2018. [Google Scholar]

41. J. Wu, Z. Lin and H. Zha, “Essential tensor learning for multi-view spectral clustering,” IEEE Transactions on Image Processing, vol. 28, no. 12, pp. 5910–5922, 2019 [Google Scholar] [PubMed]

42. M. Yin, J. Gao, S. Xie and Y. Guo, “Multiview subspace clustering via tensorial t-product representation,” IEEE Transactions on Neural Networks Learning Systems, vol. 30, no. 3, pp. 851–864, 2019 [Google Scholar] [PubMed]

43. C. Zhang, H. Fu, Q. Hu, X. Cao, Y. Xie et al., “Generalized latent multi-view subspace clustering,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 1, pp. 86–99, 2020 [Google Scholar] [PubMed]

44. M. Chen, L. Huang, C. Wang and D. Huang, “Multi-view clustering in latent embedding space,” Proc. of the AAAI Conf. on Artificial Intelligence, vol. 34, no. 4, pp. 3513–3520, 2020. [Google Scholar]

45. C. Lu, J. Feng, Y. Chen, W. Liu, Z. Lin et al., “Tensor robust principal component analysis with a new tensor nuclear norm,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 4, pp. 925–938, 2020 [Google Scholar] [PubMed]

46. J. Wen, Z. Zhang, Y. Xu, B. Zhang, L. Fei et al., “CDIMC-net: Cognitive deep incomplete multi-view clustering network,” in Proc. of the Int. Joint Conf. on Artificial Intelligence, Yokohama, Japan, pp. 3230–3236, 2020. [Google Scholar]

47. Y. Qin, H. Wu, X. Zhang and G. Feng, “Semi-supervised structured subspace learning for multi-view clustering,” IEEE Transactions on Image Processing, vol. 31, pp. 1–14, 2022 [Google Scholar] [PubMed]

48. Y. Qin, N. Pu and H. Wu, “Elastic multi-view subspace clustering with pairwise and high-order correlations,” IEEE Transactions on Knowledge and Data Engineering, vol. 36, no. 2, pp. 556–568, 2024. [Google Scholar]