Hybrid Optimization Algorithm for Handwritten Document Enhancement

1  Introduction

Handwritten Documents may become blurry when viewed on electronic devices after capture, and their quality may deteriorate further with continuous dissemination, rendering them unreadable. Many manuscripts have been stored for decades, during which time they may have been affected by uneven lighting, humidity, and other factors, causing changes in handwriting. Consequently, enhancing the clarity or contrast of Handwritten Documents has become a problem that must be addressed in document image analysis.

In Optical Character Recognition (OCR) [1], preprocessing handwritten documents is a crucial step in the Optical Character process. Even the best text-recognition systems cannot accurately recognize blurry photographs of handwriting. The primary purpose of preprocessing is to reduce the noise and ensure the accuracy of the recognition system. Therefore, enhancing the contrast of Handwritten Documents is essential in the preprocessing stage. Well-known metaheuristic algorithms, PSO as Particle Swarm Optimization (PSO), Differential Evolution (DE), Cat Swarm Optimization (CSO), WOA (Whale optimization algorithm) [2], Artificial Bee Colony) [3], Grey Wolf Optimization) [4], and Ant Colony Optimization) [5], have been applied in various domains of image enhancement. The GOA is a Swarm Intelligence (SI) algorithm inspired by the foraging behavior of gannets [6], which can be used to solve continuous optimization problems and adapted for binary issues such as binarization. The WOA, on the other hand, is inspired by the hunting behavior of whales. Researchers have widely applied both algorithms to various optimization problems, including parameter optimization, knapsack problems [7], and scheduling issues across fields such as economics, engineering, and mathematics [8]. These algorithms are popular because of their simplicity of concept, concise code length, and minimal parameter-tuning requirements [9]. Additionally, the WOA has demonstrated superior performance to other well-known algorithms, such as DE, ABC, and PSO. In contrast, the GOA competes strongly (and even outperforms) the WOA in specific scenarios.

Existing methods often encounter several challenges when dealing with blurry Handwritten Documents. Traditional image enhancement methods such as histogram equalization and filters may not be effective in improving the clarity and contrast of Handwritten Documents. Conventional OCR systems may also encounter difficulties in processing blurry handwritten documents because they have difficulty accurately recognizing blurry handwritten text.

In addition, existing optimization algorithms may not be sufficiently practical for addressing the image enhancement problem. Some standard optimization algorithms, such as genetic algorithms, particle swarm optimization, and simulated annealing, have limitations. They may be affected by the choice of algorithm parameters, size of the search space, and convergence of the algorithm.

To overcome these problems, this study proposes an image-enhancement method based on a hybrid metaheuristic algorithm. This technique combines the Gannet Optimization Algorithm (GOA) and the Whale Optimization Algorithm (WOA) and introduces an adaptive parameter strategy. The performance and effectiveness of image enhancement can be improved by combining the advantages of GOA and WOA. Specifically, the proposed AIWGOA first utilizes the exploitation behavior of the GOA to generate a set of candidate solutions. The predation behavior of the WOA was then used to search for and optimize these candidate solutions to obtain the best enhancement results. Additionally, the AIWGOA enhances algorithm performance by introducing a parameter adaptive strategy, allowing for the adjustment of algorithm parameters based on the characteristics of the problem.

By combining the GOA and WOA and introducing the parameter adaptive strategy, the AIWGOA can overcome the problems faced by existing methods when dealing with ambiguous Handwritten Documents. This hybrid meta-inspired algorithm can enhance the clarity and contrast of images more effectively, thereby improving the accuracy and reliability of OCR systems in processing Handwritten Documents.

The AIWGOA can be applied to scanned Handwritten Documents for preprocessing to improve clarity and contrast. These preprocessed documents can then be recognized using an already-trained OCR system. Because the AIWGOA effectively enhances the clarity and contrast of Handwritten Documents, the OCR system can identify and transcribe handwritten text more accurately.

Metaheuristic algorithms are created by researchers, drawing inspiration from various sources, and can be broadly categorized into three classes. The first class consists of evolutionary algorithms, such as the highly cited GA (Genetic Algorithms) [10], as well as newer algorithms like COA, the Coati Optimization Algorithm (COA) [11], and firefly algorithm (FA) [12]. The second class includes swarm-based algorithms, such as the GOA (Gannet Optimization Algorithm), WOA (Whale Optimization Algorithm), COA (Cat Swarm Optimization), and QUATRE (Quasi-Affine Transform Evolutionary Algorithm) [13]. The third class comprises algorithms based on theories or physical phenomena, such as Simulated Annealing (SA) [14], sine cosine algorithms (SCA) [15], and PO (Political Optimizer) [16]. According to the No Free Lunch (NFL) theorem [17], no optimization algorithm can effectively solve all optimization problems. Therefore, researchers have strived to improve these algorithms by employing various optimization strategies.

The GOA and WOA can provide more stable performance and higher efficiency when exploring large search spaces. These two algorithms have been applied to optimize image problems and have demonstrated impressive performances. Evolutionary algorithms have also been used in other areas such as cost-driven service portfolio research and big data areas [18,19], with the increased research fervor in smart cities, there are also researchers who use evolutionary algorithms to deal with edge computing problems similar to click-through-rate prediction algorithms, and the use of evolutionary algorithms can be used to solve similar problems [20,21]. Furthermore, combining the GOA or WOA with other SI algorithms has shown better performance than the original algorithms, which inspired the development of the algorithm proposed in this paper. This study integrated whale-hunting behavior with gannet-foraging behavior to form a new computational formula, resulting in improved performance. Additionally, to the best of current knowledge, there have been no previous attempts to specifically combine the GOA and WOA for image enhancement. In this study, the AIWGOA combines the developmental behaviors of the GOA and WOA and utilizes parameter adaptive strategies, showing promising results in Handwritten Document Enhancement.

The remainder of this paper is organized into seven sections. Section 2 explains the concepts of image and document enhancement. Section 3 elaborates on the Gannet Optimization Algorithm (GOA) and relevant studies. The Whale Optimization Algorithm (WOA) and relevant studies are discussed in Section 4. Section 5 describes the proposed AIWGOA. The experimental results and analysis are presented in Section 6. Finally, Section 7 summarizes this study. The contributions of this study are as follows:

•   A hybrid strategy was used to combine the GOA and WOA, and a parameter-adaptive strategy was added to improve the performance of the algorithm.

•   The AIWGOA proposed in this paper uses CEC2013 to test the performance of the algorithm and compare it with the original GOA and well-known algorithms, such as WOA and PSO. The experiments prove that the AIWGOA has better performance.

•   The AIWGOA was applied to handwritten document image enhancement, and images enhanced by multiple algorithms were evaluated for metrics. These results indicate that the AIWGOA has several advantages.

2  Document Image Enhancement

Typically, Image Enhancement involves optimizing the visual appearance of an image and reducing the image noise for specific applications [22]. The objective of this study was to enhance images by reducing background noise while preserving text readability. In the spatial domain, to achieve the enhancement effect by controlling pixel values, the mapping function is defined by Eq. (1):

g(m,n)=T[f(m,n)](1)

Among them, f represents the original image, g represents the enhanced image, and T is the function applied to the original image. In the frequency domain, image enhancement is performed through three steps:

•   Compute the discrete Fourier transform of the original image.

•   Multiply the result from step 1 with a filter function.

•   Compute the inverse discrete Fourier transform to obtain the enhanced image.

Handwritten document enhancement based on Genetic Algorithms: Genetic Algorithms are widely used in optimization problems, including image processing. In Handwritten Document Enhancement, researchers use Genetic Algorithms to tune the parameters of image-enhancement algorithms to improve the clarity and contrast of Handwritten Documents. By optimizing the parameters of the image enhancement algorithm, genetic algorithms can enhance the readability of blurry handwritten documents.

Particle Swarm Optimization in Handwritten Document Enhancement: Particle Swarm Optimization is also used to address handwritten document enhancement problems. Researchers have applied Particle Swarm Optimization (PSO) to optimize the parameters in the Image Enhancement process to improve the quality of fuzzy Handwritten Documents. PSO can effectively enhance the clarity and contrast of Handwritten Documents by iteratively updating the positions of particles to find the best combination of parameters.

Evolutionary strategies for Handwritten Document preprocessing: Evolutionary methods are used to optimize the algorithms for preprocessing Handwritten Documents. Researchers have used an evolutionary approach to determine the best preprocessing parameters for enhancing the clarity and contrast of handwritten documents. Evolutionary strategies can help improve the readability of ambiguous handwritten documents by modeling the selection and mutation operations in the evolutionary process.

Owing to the rapid development of metaheuristic algorithms in recent years, an increasing number of evolutionary algorithms have been applied to image enhancement and have shown superior performance. The GOA and WOA, two of the best meta-heuristic algorithms, are also widely used. Inspired by researchers employing the Chicken Flock Algorithm for enhancing handwritten documents, this study explores other algorithms with proven efficacy for handwritten document enhancement. The experiments demonstrate that applying the GOA and WOA to handwritten document enhancement offers substantial advantages over other algorithms.

In these studies, evolutionary computational algorithms such as Genetic Algorithms, Particle Swarm Optimization, and evolutionary strategies are widely used for problems related to handwritten document enhancement. These algorithms can effectively improve the quality of handwritten fuzzy documents by optimizing the selection and tuning of the parameters in the image enhancement process, thereby improving their readability and recognizability.

3  Gannet Optimization Algorithm

Inspired by the real behavior of a gannet, Pan et al. [6] proposed a Gannet Optimization Algorithm (GOA) in 2022. The GOA combines the real behavior of gannets with mathematical principles and offers a method for solving complex engineering problems. Gannets are aquatic animals that live in groups and exhibit unique hunting behaviors. They can capture prey based on their location and perform U-shaped- and V-shaped dives to search for food.

Searching for prey: Gannets are clumsy on land and prefer to fly from the air to the water to search for prey. When they spot prey in the water, they assess the depth at which the prey is located. If the prey was in deeper waters, they used U-shaped dives to search for it. If the prey is in shallower water, they use V-shaped dives to search for it.

Capturing prey: After spotting prey through U-shaped or V-shaped dives, gannets must engage in capturing behavior. When the prey realizes that the gannets are chasing it, it attempts to escape into the water. They defined an energy function for the gannets; when the energy was sufficiently high, the gannets successfully captured the prey that escaped. However, if power is insufficient, the prey can escape.

Based on these two behaviors, a mathematical model was developed to drive the GOA towards promising space exploration and development continuously.

The GOA has been applied to various optimization domains in the literature. In literature, the GOA has been used for feature selection optimization. Reference [23] used the GOA to optimize train scheduling. In the literature, the GOA has been applied to maximize enterprise operational costs. The GOA is involved in the fitness function proposed in [24], which considers the entropy of sensitivity and specificity, classifier accuracy, and the proportion of selected features. This study improves the GOA using two strategies (parallel and compact), addressing the issue of early convergence that consumes high memory. Memory consumption is reduced through compactness (C), whereas parallelism avoids premature convergence (P). This paper discusses the problem of imbalanced train occupancy rates on railway train routes. A multi-objective Gannet Optimization Algorithm (MOGOA) was proposed [25,26]. MOGOA utilizes adaptive strategies and distance-based nondominated sorting algorithms to select advantageous gradients and optimize the train-scheduling problem. This study discusses the issues in managing and transporting traditional engine parts that may lead to increased transportation and management costs. The concept of a transportation center has been introduced, and an appropriate location can reduce transportation costs. The authors used the GOA to optimize the problem and selected the optimal transportation center hub utilizing the algorithm. However, currently, no literature has combined the GOA with other metaheuristic algorithms. This study aimed to optimize the GOA from this perspective.

4  Whale Optimization Algorithm

The Whale Optimization Algorithm (WOA) is a metaheuristic algorithm inspired by the feeding behavior of humpback whales. Humpback whales are fascinating because they exhibit a unique feeding behavior known as bubble-net feeding. To study this feeding behavior further, Mirjalili et al. used sensors for behavior detection and discovered two actions involved in bubble-net feeding: spiral and double spiral. The authors mathematically modeled the bubble-net feeding behavior.

Encircling prey: After locating the prey, humpback whales attempt to encircle it. Because the position of the optimal solution in the search space is unknown, the WOA considers the current best candidate solution as the prey location. In this manner, other whales try to update their positions to approach their prey. This behavior is defined by Eqs. (2) and (3):

D=|C∗X∗(t)−X(t)|(2)

X(t+1)=X∗(t)−A∗D(3)

where t denotes the current iteration count, X the position of the optimal candidate solution, A (Eq. (4)) and C (Eq. (5)) are coefficients ranging from 0 to 2: X∗ continuously updates each iteration.

A=2a∗r−a(4)

C=2∗r(5)

Among them, vector a gradually decreased from two to zero during the iteration process, whereas vector r was a random number ranging from zero to one.

4.1 Bubble Net Feeding Behavior

Shrinking encircling mechanism: The implementation of this behavior is straightforward, just by lowering the value of a as a result, the value of A will also decrease, allowing the search agent to be defined between the initial position and the current best position.

Spiral updating position: The spiral motion of a sperm whale, which is defined by Eq. (6):

X(t+1)=D∗ebl∗cos⁡(2πl)+X∗(t)(6)

where b is a constant for the logarithmic spiral and l is a random number ranging from −1 to 1.

Search for prey: When searching for prey, the author modified A. They used random values of A smaller than −1 or larger than 1 to cause the search agent to deviate from the optimal solution. Unlike the development phase, the updated search agent is randomly selected instead of the previous best position. When A is greater than 1, it allows for a global search using WOA (Whale Optimization Algorithm).

WOA (Whale Optimization Algorithm) starts with a set of random solutions. The search agent updates its position at each iteration based on a randomly selected search agent or the best solution. To achieve the goals of exploration and development, parameter a was gradually reduced from 2 to 0. When |A|> 1, a random search agent is selected, and when |A|< 1, the best solution is chosen to update the search agent’s position [27]. The WOA can flexibly switch between spiral and circular motion. Finally, when the termination condition was satisfied, the WOA stopped iterating.

5  Proposed Algorithm

This section introduces the Adaptive Inertia-weight Gannet Optimization Algorithm (AIGOA), which utilizes an adaptive strategy. Next, the inertia weight in the AGOA is discussed to optimize the algorithm. Subsequently, the AGOA is combined with inertia weight and the Whale Optimization Algorithm (WOA), culminating in the final improved algorithm, designated as the Adaptive Inertia Weight Whale Optimization Algorithm (AIWGOA).

The AIWGOA proposed in this study differs from the traditional GOA and WOA. The AIWGOA integrates the ideas of the GOA and WOA, namely, the gannet and the ideas of whale hunting and hunting prey. Theoretically, AIWGOA is no longer a single species but a combination of two species. Regarding algorithm implementation, part of the AIWGOA code is borrowed from the GOA and WOA codes, and the codes of the two algorithms are combined and modified to become harmonious. The AIWGOA can be viewed as a combination of the improved GOA and WOA with the addition of enhanced policies.

Advantages of handwritten document enhancement: The meta-heuristic algorithm is determined to find the optimal solution to the problem, and researchers can use handwritten document enhancement to make the document clear as the optimal solution. The ability of the AIWGOA to find the optimal solution and its convergence ability are better than those of the GOA and WOA (as can be seen from the experiment); therefore, the AIWGOA can improve the efficiency and speed of processing.

5.1 Inertia Weight

The inertia weight is a commonly used parameter in optimization algorithms to balance the tradeoff between local and global searches. In some metaheuristic algorithms, the inertial weight allows particles currently being searched to update their positions based on their previous velocities. When the inertial weight was high, the search particles had a more significant movement speed [28], which enhanced the global search capability. When the inertia weight is low, the search particles have a lower movement speed, which gives them an advantage in local search. For example, in PSO, the step size and movement direction of the ith particle are influenced by both velocity and position factors. Shi and Eberhart [29] proposed IWPSO, which optimizes PSO by adding an inertial weight before the velocity. In IWPSO, the inertia weight is defined by Eqs. (7) and (8):

Vi,G+1=ω∗Vi,G+2∗r1∗(Xfbi,G−Xi,G)+2∗r2∗(Xgb,G−Xi,G)(7)

Xi,G+1=Xi,G+Vi,G(8)

Among them, where Vi,G represents the velocity of the i-th particle in the G-th generation, ω represents the inertia weight, Xfbi,G represents the previous best position of the i-th particle [30], Xgb,G represents the global best position, and r1 and r2 are random numbers between 0 and 1. The inertia weight used in the proposed AIWGOA is defined by Eqs. (9) and (10):

ω=ωmax−(ωmax−ωmin)∗itergenmax(9)

V=ω∗l+c1+c2(10)

where ωmax and ωmin are preset values, iter represents the current iteration count, and genmax represents the maximum number of iterations. The defined inertia weight, ω, is introduced into the velocity calculation of the GOA. The velocity, vel, incorporates the concept of inertia weight, ω, and will change accordingly. l is a fixed value, c1 and c2 are variables used for parameter adaptation, which will be explained in the following context. Through experiments conducted on the CEC2013 test sets, it has been observed that incorporating the concept of inertia weight in GOA leads to a slight improvement.

5.2 Adaptive Inertia-Weight GOA (AIGOA)

Parameter adaptation is often employed as an optimization strategy to improve optimization algorithms [31]. Having fixed and constant parameter values in an algorithm often limits its capability [32]. By introducing parameter adaptation strategies, the parameter values in the optimization algorithm can be adjusted dynamically according to certain conditions, making it easier to handle various optimization problems. The main objective of parameter adaptation is to provide an algorithm with advantages in terms of application and performance. Different optimization problems may have other search spaces, and enhancing the robustness of the algorithm has become a goal for researchers. The global and local search capabilities of the algorithm are significantly improved when the parameters change from fixed to adaptive values. Parameter adaptation can be implemented based on heuristic rules, statistical analysis, or machine learning methods. The key is to choose an appropriate adaptive strategy and methodology based on problem characteristics and algorithm requirements. The parameter-adaptive strategy of AIGOA proposed in this study is defined by Eqs. (11) and (12):

c1=2.5−2∗itergenmax(11)

c2=0.5+2∗itergenmax(12)

where c1 and c2 are parameters that utilize an adaptive strategy, iter represents the current iteration count, genmax represents the maximum iteration count, c1 and c2 adaptively change with the iteration count, as defined by Eqs. (13) and (16) as follows:

bnd=⌊ps∗u⌋(13)

u=∑ibndbini(bnd)∑ibndbini(bnd)+∑ibndbinbnd+1(ps)(14)

u=⌈0.3,u⌉(15)

u=⌊0.7,u⌋(16)

When the global optimal value is greater than the fitness value of the current particle, the value of bin is set to 1; otherwise, it is set to 0, ps represents the number of particles in the population. This makes u an adaptive parameter and is restricted by two constraints to ensure it stays within bounds. In the original GOA algorithm, the capture behavior occurs only when the Captreabiit is more significant than a fixed number. However, in AGOA, the captured behavior occurs when the Captreabiit is greater than u, an adaptive parameter. Incorporating this adaptive parameter makes the algorithm more efficient and performs better.

5.3 Hybrid AIGOA and WOA

This section introduces the hybridization process of the AGOA and WOA. Although the GOA is a promising optimization algorithm with solid global search capabilities, its performance tends to decline in later iterations as it becomes trapped in local optima. Hybridization strategies are commonly employed in optimization algorithms to address this issue. Despite its tendency to converge to local optima in later iterations, the WOA can be refined and integrated with its advantages. By merging the bubble-net behavior of the WOA with that of the AGOA, the drawback above can be effectively addressed. The following section provides a detailed description of the hybridization steps. In AIGOA, the exploration phase is mainly defined by Eqs. (17) and (20), respectively:

u2=A∗(Xi(t)−Xr(t))(17)

MXi(t+1)=Xi(t)+u1+u2(18)

v2=B∗(Xi(t)−Xm(t))(19)

MXi(t+1)=Xi(t)+v1+v2(20)

where A and B are constants. If the value of ω is greater than 0.5, AIGOA uses Eq. (18) for exploration. If the value of ω is less than 0.5, AIGOA uses Eq. (20) for exploration.

In the AGOA, the main formula for the exploitation phase is defined by Eqs. (21) and (24) as follows:

delte=Captureability∗|Xi(t)−BestX|(21)

MXi(t+1)=t∗delta∗(Xi(t)−BestX)+Xi(t)(22)

P=levy(dim)(23)

MXi(t+1)=BestX−(BestX−Xi(t))∗P∗t(24)

In the original GOA, the value of u is 0.15. In AIGOA, u is a parameter used by the algorithm in the adaptive strategy. When the Captureability> u, AIGOA utilizes Eq. (22) for the exploitation. When the Captureability is less than u, AIGOA employs Eq. (24) for the exploitation. AIGOA replaces the initial value of 0.15 with u and has demonstrated an improved performance experimentally. Furthermore, it has been observed that when energy is insufficient, the use of the levy flight strategy is reasonable. However, the AIWGOA was further improved to achieve enhanced performance, which is discussed in the next section, introducing the hybrid algorithm. The GOA simulates the hunting and prey-searching behavior of gray wolves and searches for an optimal solution by adjusting the positions of the individual wolves. The WOA affects the calling and search behaviors of whales to find the optimal solution by changing the positions and velocities of individuals. The GOA and WOA can be combined to enhance the performance of the optimization algorithm further.

The hybrid algorithm combines the advantages of both the GOA and WOA by integrating their search strategies and parameter adjustment strategies with the aim of finding a better global optimal solution. In the hybrid algorithm, specific steps or methods for the GOA and WOA can be used selectively. For example, the GOA can be used for rapid searching in the initial stage, and the WOA can be used for more fine-grained searching in the further optimization stage. The hybrid algorithm can also be customized and adjusted according to the characteristics and requirements of the problem to achieve improved optimization results. By combining the GOA and the WOA, the advantages of both algorithms can be fully utilized to improve the search efficiency and quality of the optimization results. This hybrid approach provides a more flexible and robust method for solving optimization problems.

In summary, the execution process of AIWGOA is roughly as follows:

•   Initialize the population consisting of individuals, each of which represents a solution, according to the features of handwritten document enhancement and the optimization objective to be solved.

•   Calculate the individual fitness of each individual to calculate the individual, that is, the individual’s superiority or inferiority in the objective problem.

•   Using the combined formulation of the WOA and GOA, exploration and exploitation operations are performed on the individuals for which the fitness has been computed by combining the two algorithms to bring the individuals closer to the optimal solution in a continuous iteration.

•   The algorithm stops when the number of iterations reaches the maximum number of iterations or an optimal solution to the problem is found.

•   Output the optimal or near-optimal solution.

6  Experiments and Discussion

In this section, the effectiveness of the AIWGOA is validated by testing it on 28 benchmark functions from CEC2013 and comparing it with other algorithms, including GOA, WOA, PSO, DE, BOA, and AO. To provide a more intuitive representation of the test results, iteration curves of the algorithms were plotted using their fitness values. The first subsection evaluates the performance of the algorithm, and the second examines its performance in real-world applications.

6.1 Comparison of AIWGOA with Other Algorithms

This paper is divided into two sections: The first part introduces the parameter settings, and the second part presents and analyzes the experimental results.

6.1.1 Parameter Settings

The AIWGOA test was conducted using a computer equipped with Windows 11, Intel i5-13400 CPU, 16.0 GB RAM, and MATLAB R2021b. The parameters used for comparison are listed in Table 1.

6.1.2 Analysis of Test Results

To fairly compare the algorithm performances, each algorithm was set to a consistent number of iterations and population size. The CEC2013 test suite contains various types of functions, such as unimodal (Figs. 1–3), multimodal (Figs. 4–6), and composition (Figs. 7–9). Unimodal functions have unique global optimum values; multimodal functions have multiple local optimum values, and composition functions combine the unimodal and multimodal functions. The algorithm performance was evaluated by comparing the minimum values of the functions.

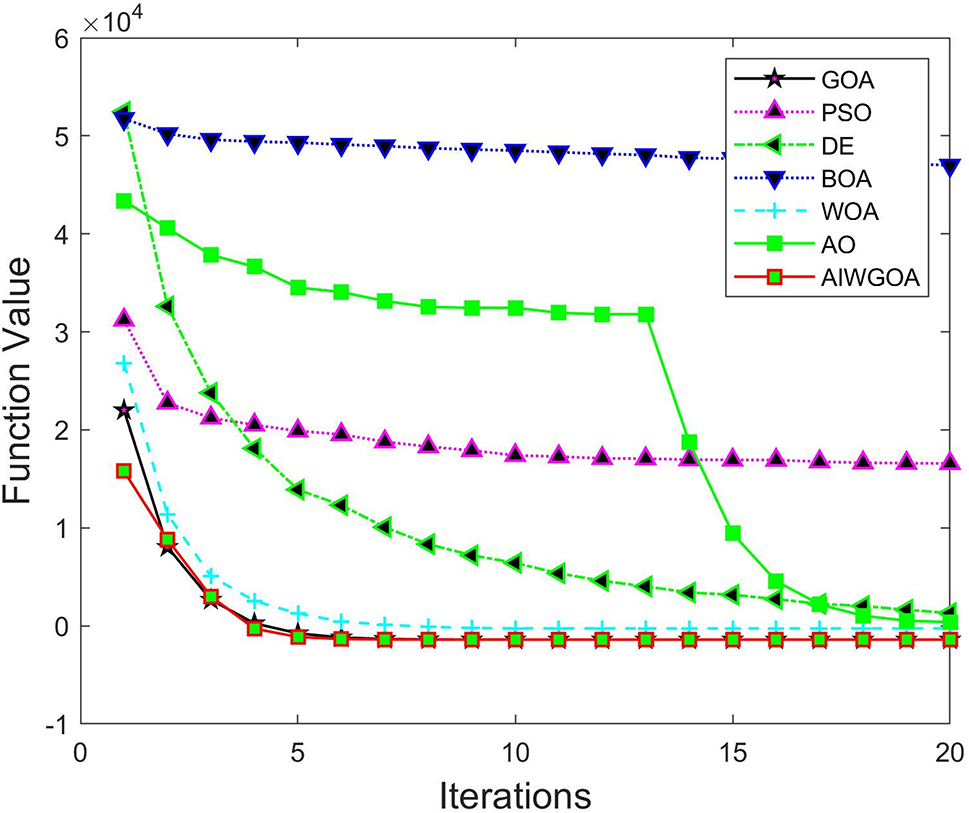
Figure 1: Single-peak function iteration curve (F1)

Figure 2: Single-peak function iteration curve (F2)

Figure 3: Single-peak function iteration curve (F3)

Figure 4: Multimode function iteration curve (F6)

Figure 5: Multimode function iteration curve (F7)

Figure 6: Multimode function iteration curve (F8)

Figure 7: Combinatorial function iteration curve (F21)

Figure 8: Combinatorial function iteration curve (F22)

Figure 9: Combinatorial function iteration curve (F23)

The algorithm was tested in three dimensions: 10-dimensional, 30-dimensional, and 50-dimensional. Tables 2–4 record the test results (mean and standard deviation) of all algorithms in these three dimensions. From the results in the table, it can be observed that the AIWGOA has advantages in all three dimensions and exhibits better performance in higher-dimensional problems. The values for the current winning function are in bold.

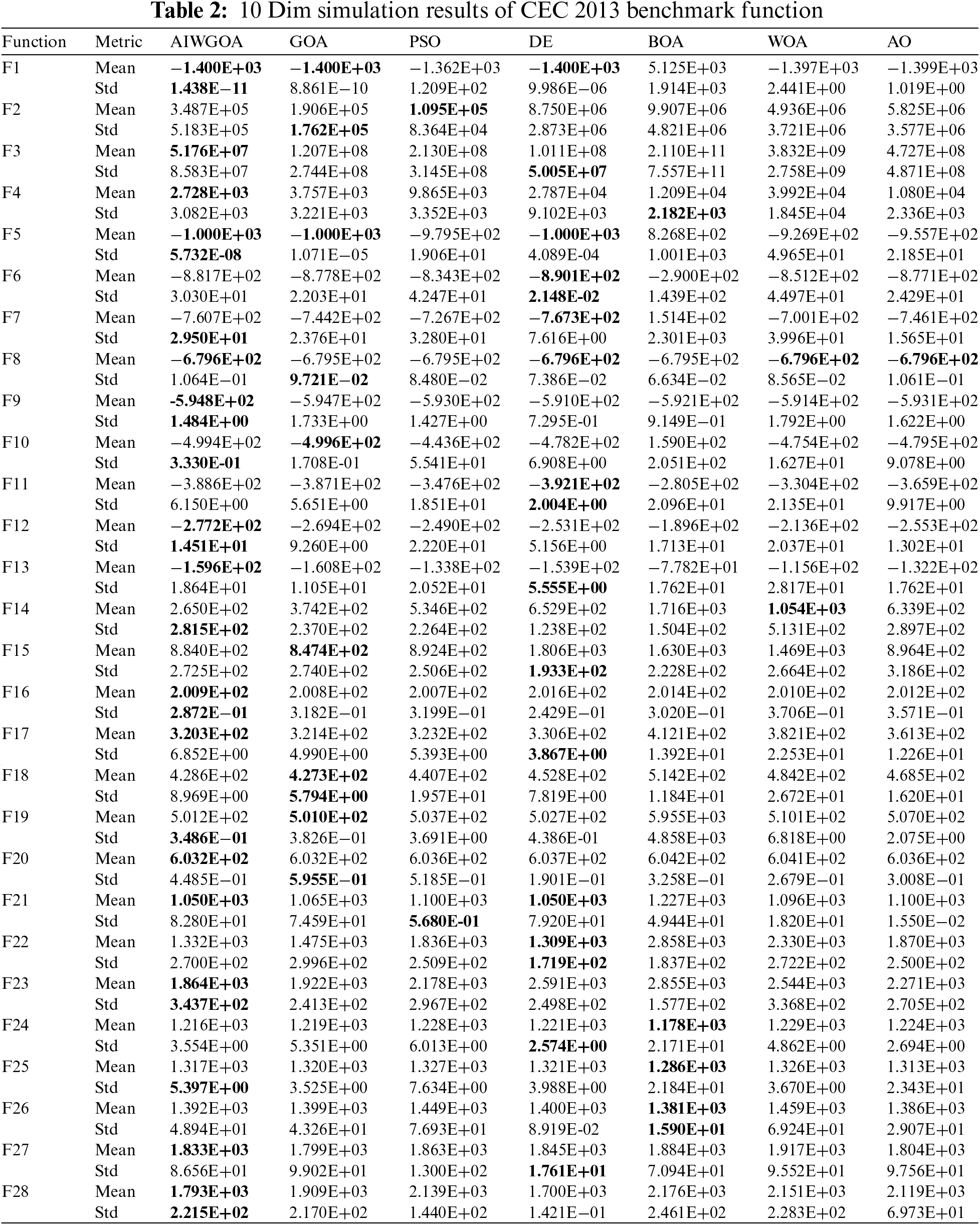
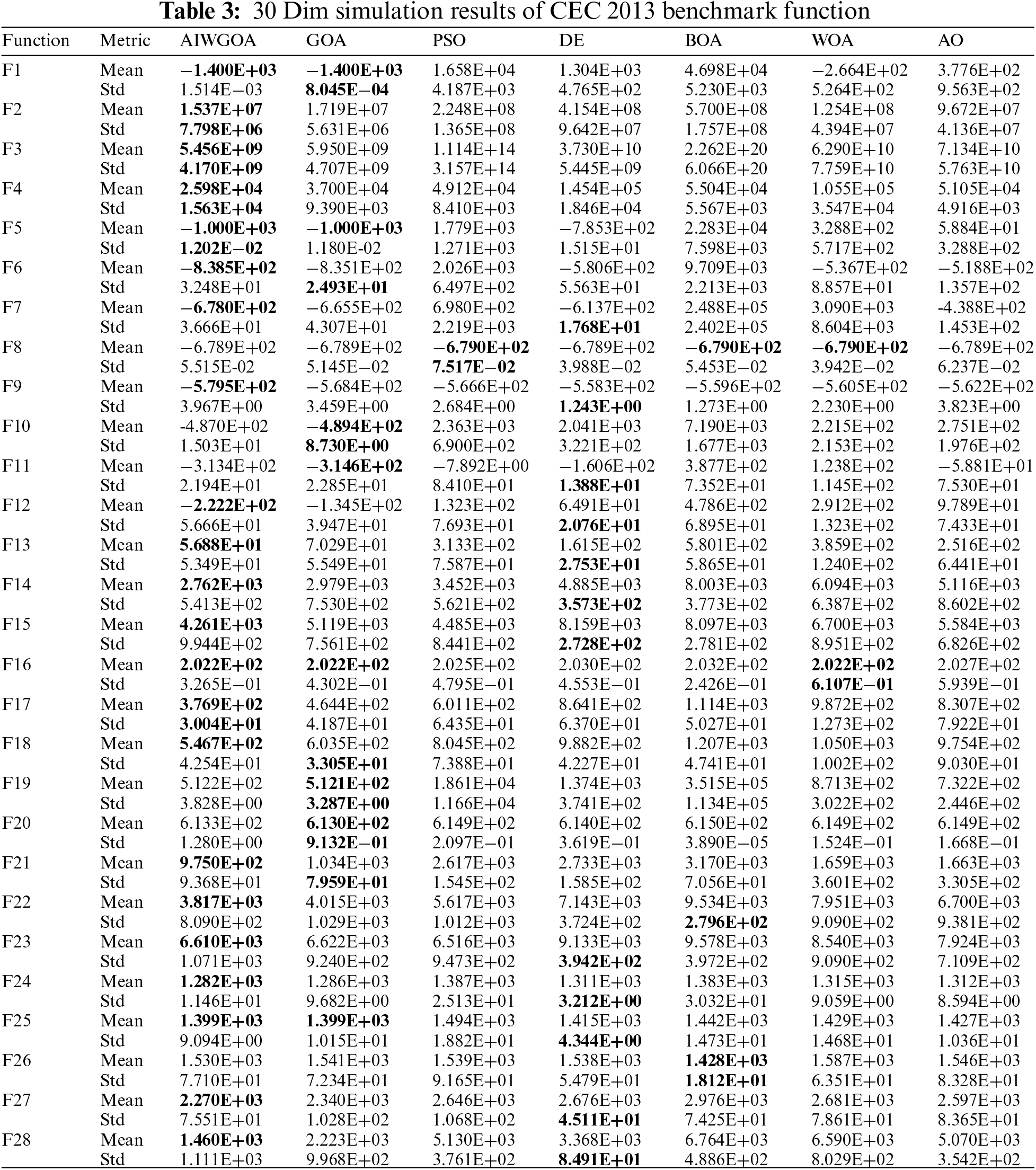
To compare the performance of the AIWGOA with that of other algorithms more intuitively, the convergence curve of the algorithm in the test function is presented in the text. The average iteration curves of all test algorithms on the 28 benchmark functions of CEC2013 are shown in Figs. 1–9 (list only 9), where the y-axis represents the average results of all test algorithms after running 30 iterations, and the x-axis represents the number of iterations of the algorithm. In these charts, a point is plotted every 50 iterations, with an average of 10 points. As can be seen from the statistics in Table 1, the AIWGOA shows a promising superiority. To avoid being too long, this paper only displays the iteration curve in a 30-dimensional case.

Figs. 1–3 show the iteration curves of a unimodal function. From this, it can be seen that the AIWGOA has a more important ability to find the optimal solution than the other algorithms because the original GOA algorithm itself can quickly find the optimal solution. The AIWGOA outperforms the GOA in several functions and all the different algorithms in the five functions. This indicates that the improved algorithm exhibits a promising performance.

Figs. 4–6 show the iteration curve of a multimodal function. Thus, it can be concluded that the AIWGOA can find the optimal solution from the start in several functions and is significantly ahead of the other algorithms. Although the AIWGOA does not outperform the other algorithms in the two functions, the difference is insignificant. In most algorithms, the AIWGOA significantly outperforms the other algorithms. While the original version of the GOA already has a strong performance, the AIWGOA surpasses it. The AIWGOA performs well on multimodal functions.

Figs. 7–9 show the iteration curve of a composite function. AIWGOA can generally win composite functions; however, it fails and converges prematurely in function F26. Although the convergence speed of the AIWGOA is not initially rapid in certain functions, it demonstrates good performance in subsequent stages.

The experimental results at CEC2013 show that the AIWGOA performs better in terms of performance and effectiveness than the other algorithms by measuring the mean and variance of the optimal solution. It also proves that the AIWGOA has better robustness, global search ability, and convergence performance, as well as excellent adaptability and efficiency in the corresponding optimization problems.

6.2 Comparing the Performance of Algorithms in Handwritten Document Enhancement

This section applies several metaheuristic algorithms to handwritten document enhancement, and several evaluation metrics are used to assess enhanced images [33]. The following will briefly introduce the evaluation metrics, demonstrate the enhancement effects, and present the experimental results.

6.2.1 Quality Measures

In this section, the evaluation of the images primarily considers entropy, variance, mean, and peak signal-to-noise ratio (PSNR) to quantify the experimental results [34]. The following provides a brief introduction.

Entropy is commonly used to measure the amount of information contained in images. In image processing, entropy can also be considered a measure of image complexity. The higher the amount of information in an image, the higher its entropy value; conversely, a lower entropy value indicates less information in the image. The entropy calculation is relatively simple: the frequency of occurrence of each pixel value in the image is obtained, the probabilities are calculated based on the frequency, and the values are then weighted and summed to determine the entropy value. Nowadays, an increasing number of researchers use entropy as a standard for evaluating image quality, where, in general, high entropy values indicate good image quality, and low entropy values indicate relatively poor image quality.

MSE (Mean Squared Error) calculates the difference between corresponding pixels in the original and enhanced images, squares the differences, and then takes the mean to obtain the final value. Therefore, a smaller MSE value indicates a minor difference between the two images, indicating better image quality for the enhanced image. In contrast, a greater MSE value indicates a more significant difference between the two images. The advantage of the MSE is its simplicity of calculation. However, it has a fatal flaw: the MSE value may not align with the quality of the image perceived by the human eye, even if the image appears visually pleasing. The MSE can be used in conjunction with the PSNR to provide a more comprehensive evaluation of image quality. The PSNR is introduced as follows.

PSNR (Peak Signal-to-Noise Ratio), similar to MSE, compares the enhanced image with the original image. PSNR first calculates the MSE between the two images, then takes the logarithmic value of the MSE and normalizes the error value to calculate the final PSNR value. Unlike MSE, a higher PSNR value indicates a minor difference and better image quality.

Although the PSNR is considered one of the most commonly used evaluation metrics, it still has limitations: a high PSNR value does not necessarily indicate a visually pleasing image. Therefore, it is recommended that multiple evaluation metrics be used for fair assessment.

6.2.2 Results and Discussion

The Entropy, MSE, and PSNR values of the enhanced images obtained using different algorithms are listed in Tables 5–8, indicating the heuristic algorithms used. Figs. 10–15 show the improved images, where the upper and lower images are the original and enhanced handwritten document images, respectively. The proposed algorithm exhibited good performance through evaluation indicators and visual observation, surpassing other algorithms.

Figure 10: Original image 1

Figure 11: Enhance image 1

Figure 12: Original image 2

Figure 13: Enhance image 2

Figure 14: Original image 3

Figure 15: Enhance image 3

In conclusion, the entropy values of all AIWGOA-enhanced images are better than those of the other algorithms (shown in bold), which shows that the three images enhanced by the AIWGOA have less randomness, and the quality of the images is better. The mean square error (MSE) was used as one of the measures; the larger its value, the more significant the gap between the image before and after enhancement. The MSE values of AIWGOA are smaller than the MSE values of the other algorithms. The experimental results show that the AIWGOA’s ability to enhance an image is better than that of the other algorithms. PSNR is widely used in image evaluation, and the PSNR value of the AIWGOA is slightly better than that of the different algorithms for all three images, which indicates that the enhanced image of the AIWGOA has a higher degree of similarity with the original image. By contrast, the PSNR values of the other algorithms were not satisfactory. Based on the three evaluation metrics, it can be concluded that the AIWGOA outperforms the original GOA and WOA for handwritten document enhancement applications with good results.

7  Conclusion

This study combines the GOA and WOA, introduces the concepts of inertial weight and parameter adaptation, and proposes a new hybrid algorithm. The combination of these two algorithms forms a comprehensive system with further performance improvements during the development and exploration phases. This combined algorithm can avoid falling into a locally optimal solution more effectively, has a faster convergence speed, and has better optimization capabilities than the two algorithms alone. In the CEC2013 test, the hybrid algorithm performed better than the GOA and WOA.

The AIWGOA has practical advantages when applied to Handwritten Document Enhancement. Handwritten Document Enhancement usually involves multiple operations, such as Denoising, Image Enhancement, and Edge Detection, and requires the adjustment of various parameters to optimize handwritten documents. The AIWGOA can effectively deal with multivariate optimization problems, search for the parameter space to find optimal combinations, and improve the enhancement effect of handwritten documents. In addition, handwritten documents often contain many nonlinear characteristics, such as irregular strokes and changing fonts and sizes. The AIWGOA is also suitable for solving nonlinear problems and can be adapted to specific problem domains to effectively address the complex nonlinear characteristics of handwritten document enhancement tasks.

Although evolutionary computation performs well, it still has some limitations; for example, evolutionary computation methods usually require a large amount of computational resources and time to search for the best solution for Image Enhancement. This computational complexity may become a limiting factor for large images or real-time Image Enhancement tasks, and the Evolutionary Computation may fall into a local optimum when searching the solution space, especially in high-dimensional image enhancement problems. This may result in the inability of the algorithm to achieve globally optimal enhancement. Evolutionary Computation Algorithms usually require the tuning of many parameters, including the crossover and mutation rates. Adjusting these parameters may require many experiments and optimizations, and it is sometimes difficult to determine the best combination of parameters. In future work, for insufficient performance, it will be possible to try to mix multiple algorithms and propose multiple mixing strategies. Although AIWGOA uses an adaptive parameter strategy, there are still several parameters that need to be set manually. In the future, an attempt could be made to reduce the number of manually set parameters further. In terms of application, in the future, experiments will be carried out on a large number of images to strengthen the algorithms and applications further.

Acknowledgement: The authors express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.

Funding Statement: The authors received no specific funding.

Author Contributions: Study conception and design, Shu-Chuan Chu and Xiaomeng Yang; data collection, Xiaomeng Yang; analysis and interpretation of results, Li Zhang; draft manuscript preparation, Václav Snášel and Jeng-Shyang Pan. All the authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The source code of the WOA can be found at http://www.alimirjalili.com/WOA.html. The source code for the GOA can be obtained from the corresponding author upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Mithe, S. Indalkar, and N. Divekar, “Optical character recognition,” Int. J. Recent. Technol. Eng., vol. 2, no. 1, pp. 72–75, 2013. [Google Scholar]

2. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 12, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

3. D. Karaboga and B. Akay, “A comparative study of artificial bee colony algorithm,” Appl. Math. Comput., vol. 214, no. 1, pp. 108–132, 2009. doi: 10.1016/j.amc.2009.03.090. [Google Scholar] [CrossRef]

4. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, 2014. doi: 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

5. M. Dorigo, M. Birattari, and T. Stutzle, “Ant colony optimization,” IEEE. Comput. Intell. Mag., vol. 1, no. 4, pp. 28–39, 2006. doi: 10.1109/MCI.2006.329691. [Google Scholar] [CrossRef]

6. J. S. Pan, L. G. Zhang, R. B. Wang, V. Snášel, and S. C. Chu, “Gannet optimization algorithm: A new metaheuristic algorithm for solving engineering optimization problems,” Math. Comput. Simul., vol. 202, no. 4, pp. 343–373, 2022. doi: 10.1016/j.matcom.2022.06.007. [Google Scholar] [CrossRef]

7. X. Xue, Y. Wang, and W. Hao, “Using MOEA/D for optimizing ontology alignments,” Soft. Comput., vol. 18, no. 8, pp. 1589–1601, 2014. doi: 10.1007/s00500-013-1165-9. [Google Scholar] [CrossRef]

8. X. Xue and Q. Huang, “Generative adversarial learning for optimizing ontology alignment,” Expert. Syst., vol. 40, no. 4, pp. e12936, 2023. doi: 10.1111/exsy.12936. [Google Scholar] [CrossRef]

9. H. Arora, N. K. Tiwari, B. Kumar, I. Harshwal, and G. Rathore, “Blockchain-based systems and applications,” Ann. Rom. Soc. Cell. Biol., vol. 25, no. 6, pp. 11768–11775, 2021. [Google Scholar]

10. S. Mirjalili, “Genetic algorithm,” Evol. Algorithms Neural Netw.: Theory Appl., vol. 780, pp. 43–55, 2019. doi: 10.1007/978-3-319-93025-1_4. [Google Scholar] [CrossRef]

11. M. Dehghani, Z. Montazeri, E. Trojovská, and P. Trojovský, “Coati optimization algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems,” Knowl.-Based Syst., vol. 259, no. 1, pp. 110011, 2023. doi: 10.1016/j.knosys.2022.110011. [Google Scholar] [CrossRef]

12. X. S. Yang and X. He, “Firefly algorithm: Recent advances and applications,” Int. J. Swarm. Intell., vol. 1, no. 1, pp. 36–50, 2013. doi: 10.1504/IJSI.2013.055801. [Google Scholar] [PubMed] [CrossRef]

13. Z. Meng, J. S. Pan, and H. Xu, “QUasi-Affine TRansformation Evolutionary (QUATRE) algorithm: A cooperative swarm based algorithm for global optimization,” Knowl.-Based Syst., vol. 109, no. 2, pp. 104–121, 2016. doi: 10.1016/j.knosys.2016.06.029. [Google Scholar] [CrossRef]

14. D. Bertsimas and J. Tsitsiklis, “Simulated annealing,” Stat. Sci., vol. 8, no. 1, pp. 10–15, 1993. doi: 10.1214/ss/1177011077. [Google Scholar] [CrossRef]

15. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowl.-Based Syst., vol. 96, no. 63, pp. 120–133, 2016. doi: 10.1016/j.knosys.2015.12.022. [Google Scholar] [CrossRef]

16. Q. Askari, I. Younas, and M. Saeed, “Political optimizer: A novel socio-inspired meta-heuristic for global optimization,” Knowl.-Based Syst., vol. 195, no. 5, pp. 105709, 2020. doi: 10.1016/j.knosys.2020.105709. [Google Scholar] [CrossRef]

17. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE. Trans. Evol. Comput., vol. 1, no. 1, pp. 67–82, 1997. doi: 10.1109/4235.585893. [Google Scholar] [CrossRef]

18. H. Gao, W. Huang, Y. Duan, X. Yang, and Q. Zou, “Research on cost-driven services composition in an uncertain environment,” J. Internet. Technol., vol. 20, no. 3, pp. 755–769, 2019. [Google Scholar]

19. J. Wang, Y. Yang, T. Wang, R. S. Sherratt, and J. Zhang, “Big data service architecture: A survey,” J. Internet. Technol., vol. 21, no. 2, pp. 393–405, 2020. [Google Scholar]

20. S. Chen, H. Wen, and J. Wu, “Artificial intelligence based traffic control for edge computing assisted vehicle networks,” J. Internet. Technol., vol. 23, no. 5, pp. 989–996, 2022. doi: 10.53106/160792642022092305007. [Google Scholar] [CrossRef]

21. Q. Yang, N. Li, S. Hu, H. Li, and J. Zhang, “Click-through rate prediction algorithm based on modeling of implicit high-order feature importance,” J. Internet. Technol., vol. 23, no. 5, pp. 1077–1086, 2022. doi: 10.53106/160792642022092305016. [Google Scholar] [CrossRef]

22. J. Sauvola and M. Pietikäinen, “Adaptive document image binarization,” Pattern. Recognit., vol. 33, no. 2, pp. 225–236, 2000. doi: 10.1016/S0031-3203(99)00055-2. [Google Scholar] [CrossRef]

23. M. L. Zhao, S. Q. Ni, Z. G. Du, X. Y. Wang, A. Q. Tian, and X. L. Ma, Multi-Objective Gannet Optimization Algorithm for Dynamic Passenger Flow Allocation in Train Operation Plan Optimization. IEEE Access, 2023. [Google Scholar]

24. M. H. Nadimi-Shahraki, S. Taghian, S. Mirjalili, and H. Faris, “MTDE: An effective multi-trial vector-based differential evolution algorithm and its applications for engineering design problems,” Appl. Soft. Comput., vol. 97, pp. 106761, 2020. doi: 10.1016/j.asoc.2020.106761. [Google Scholar] [CrossRef]

25. J. S. Pan, Q. Liang, S. C. Chu, K. K. Tseng, and J. Watada, “A multi-strategy surrogate-assisted competitive swarm optimizer for expensive optimization problems,” Appl. Soft. Comput., vol. 147, no. 2, pp. 110733, 2023. doi: 10.1016/j.asoc.2023.110733. [Google Scholar] [CrossRef]

26. Z. Xu, Y. Su, F. Yang, and M. Zhang, “A whale optimization algorithm with distributed collaboration and reverse learning ability,” Comput. Mater. Contin., vol. 75, no. 3, pp. 5965–5986, 2023. doi: 10.32604/cmc.2023.037611. [Google Scholar] [PubMed] [CrossRef]

27. K. M. Ong, P. Ong, and C. K. Sia, “A carnivorous plant algorithm for solving global optimization problems,” Appl. Soft. Comput., vol. 98, pp. 106833, 2021. doi: 10.1016/j.asoc.2020.106833. [Google Scholar] [CrossRef]

28. A. Lin, W. Sun, H. Yu, G. Wu, and H. Tang, “Global genetic learning particle swarm optimization with diversity enhancement by ring topology,” Swarm. Evol. Comput., vol. 44, pp. 571–583, 2019. doi: 10.1016/j.swevo.2018.07.002. [Google Scholar] [CrossRef]

29. Y. Shi and R. Eberhart, “A modified particle swarm optimizer,” in IEEE Int. Conf. on Evol. Comput. Proc., Anchorage, AK, USA, vol. 49, no. 12, pp. 60–73, 1998. doi: 10.1109/ICEC.1998.699146. [Google Scholar] [CrossRef]

30. X. F. Liu et al., “Historical and heuristic-based adaptive differential evolution,” IEEE Trans. Syst., Man, Cybern.: Syst., vol. 49, no. 12, pp. 2623–2635, 2018. doi: 10.1109/TSMC.2018.2855155. [Google Scholar] [CrossRef]

31. G. Xu et al., “Particle swarm optimization based on dimensional learning strategy,” Swarm. Evol. Comput., vol. 45, no. 1, pp. 33–51, 2019. doi: 10.1016/j.swevo.2018.12.009. [Google Scholar] [CrossRef]

32. M. R. Bonyadi and Z. Michalewicz, “Particle swarm optimization for single objective continuous space problems: A review,” Evol. Comput., vol. 25, no. 1, pp. 1–54, 2017. doi: 10.1162/EVCO_r_00180. [Google Scholar] [PubMed] [CrossRef]

33. S. Kang, B. K. Iwana, and S. Uchida, “Complex image processing with less data—Document image binarization by integrating multiple pre-trained U-Net modules,” Pattern. Recognit., vol. 109, no. 1, pp. 107577, 2021. doi: 10.1016/j.patcog.2020.107577. [Google Scholar] [CrossRef]

34. N. M. Kwok, Q. P. Ha, D. Liu, and G. Fang, “Contrast enhancement and intensity preservation for gray-level images using multiobjective particle swarm optimization,” IEEE. Trans. Autom. Sci. Eng., vol. 6, no. 1, pp. 145–155, 2008. doi: 10.1109/TASE.2008.917053. [Google Scholar] [CrossRef]