Applying an Improved Dung Beetle Optimizer Algorithm to Network Traffic Identification

1  Introduction

As an essential issue in network security, network traffic identification has received widespread attention. As the Internet develops rapidly, the scale and complexity of Internet traffic [1] continue to increase, and network attackers use increasingly complex and covert methods to carry out attacks. To effectively protect network security, quickly detecting and responding to these threats has become crucial. Network traffic identification is a critical technology that can identify traffic categories and detect potential threats and abnormal behaviors by analyzing the characteristic differences of traffic.

Traditional network traffic identification methods mainly rely on port numbers and protocol information to infer the application type of network traffic. However, with the diversification of network applications, port-based classification fails to meet practical application requirements. Deep Packet Inspection (DPI) methods have emerged to overcome the drawbacks of port number-based classification, which delves into the payload of data packets to understand the information contained therein. However, with the popularity of encrypted communications, DPI is usually unable to decrypt encrypted data packets, resulting in false positives or false negatives of encrypted traffic. Traditional traffic identification methods can no longer identify new applications and services accurately.

Due to advancements in machine learning technology, some researchers have applied it to traffic identification and achieved good results. For instance, Soysal et al. [2] proved that the machine learning algorithm solves the traditional method’s dependence on port numbers and can identify traffic categories like Peer to Peer (P2P). However, conventional machine learning methods demand the manual selection and extraction of features, which may result in loss of information or improperly selected features, thus affecting classification performance. How to select appropriate traffic features has become increasingly important. The deep learning model has powerful feature learning capabilities and addresses the deficiencies of traditional machine learning in manually selecting traffic features, but this also means that the process of model classification becomes completely uninterpretable. Metaheuristic optimization algorithms have been widely applied to effectively identify traffic features due to their self-organizing nature and adaptability. Our previous work [3–6] involved the integration of classical metaheuristic optimization algorithms for feature selection. However, traditional metaheuristic algorithms suffer from issues such as low searching efficiency and ineffective handling of high-dimensional problems.

The Dung Beetle Optimizer (DBO) is an emerging meta-heuristic algorithm presented by Xue et al. [7] in 2022. This algorithm, known for its simplicity and ease of implementation, has been successfully applied to various engineering design problems. However, achieving optimal solutions for specific optimization problems remains difficult. Although the DBO algorithm exhibits a strong capacity for global search and local exploration, it suffers from an unbalance between its global search and local exploitation capabilities. In the case of high-dimensional problems, the original DBO method tends to converge slowly and can become stuck in the local optimal solution.

To tackle the constraints of the DBO algorithm, address the challenges posed by high-dimensional traffic data, and achieve accurate identification of network traffic, this article introduces an Improved Dung Beetle Optimizer (IDBO) algorithm applied specifically to traffic identification. The IDBO algorithm rapidly identifies the optimal feature subset and employs the K-Nearest Neighbor (KNN) classification algorithm for feature classification to identify traffic types.

The following are this paper’s primary contributions:

(1) The sobol sequence is introduced for the initialization of the population. It ensures an even distribution of initial solutions, allowing the population to explore the area more thoroughly.

(2) The levy flight and golden sine strategy integration in the rolling dung beetle stage. This strategy reduces the impact of light intensity on the dung beetle’s rolling behavior, allowing it to have different motion trajectories during the rolling process and stay away from the local optimal solution.

(3) An adaptive weight factor ω is presented during the dung beetle stealing stage. It solves the trade-off problem between exploration and utilization in different iteration stages and increases the algorithm’s search efficiency.

(4) A new method for network traffic identification is presented. The method utilizes an IDBO algorithm to cope with the challenge of high dimensional data in network traffic identification and to improve the accuracy of network traffic identification.

The subsequent sections of this paper are structured as follows. Section 2 presents the related work. Section 3 introduces the mathematical preliminaries. Section 4 presents the network traffic identification method based on the IDBO algorithm. Section 5 provides the simulation experiment analysis. Section 6 summarizes the research results and future development directions of this article.

2  Related Work

With the continuous evolution of network technologies, DPI has emerged as the mainstream technique in traditional traffic identification methods. Sen et al. [8] and Moore et al. [9] proposed identification methods for deep packet inspection using application layer protocol feature fields in 2004 and 2005, respectively. Its identification accuracy surpasses that of the traffic identification method relying on port number. While traditional traffic identification techniques effectively handle non-encrypted traffic data, they encounter challenges when dealing with encrypted traffic identification.

To address the challenge of encrypted traffic, the academic community has increasingly favored the utilization of machine learning techniques with automated training deployment. Alshammari et al. [10] assessed the robustness of machine learning-based traffic classification, revealing improved classification performance using machine learning technology. Wang et al. [11] employed C4.5 to classify P2P traffic, describing the behavioral characteristics of applications. However, the effectiveness of machine learning in traffic classification largely hinges on manually selected data flow features by researchers, potentially leading to information loss. Selecting appropriate traffic characteristics is a pivotal step in traffic identification. Dong et al. [12] proposed a cost-sensitive Support Vector Machine (SVM) algorithm to address the imbalance issue in network traffic identification, which employs an active learning multi-class SVM algorithm, dynamically allocating weights to traffic types to resolve the imbalance problem, ultimately achieving enhanced classification performance. Additionally, the features of traffic flow are analyzed in [13–16]. The increase in traffic volume helps to reduce traffic congestion and greatly improves traffic safety. With the expansion of the Internet of Things (IoT), Wang et al. [17] proposed using an improved Convolutional Neural Network (CNN) to learn traffic characteristics for Distributed Denial of Service (DDoS) attack detection, which enhanced the accuracy of classification detection. Khan et al. [18] combined a Recurrent Neural Network (RNN) and a gated recursive unit to form a new intrusion detection model, using RNN to learn traffic characteristics to identify anomaly types. Although deep learning models can autonomously select features, their decision-making processes are difficult to explain.

Metaheuristic optimization algorithms imitate biological evolution and social behavior in nature and have strong self-adaptive characteristics. Qin et al. [19] presented using the enhanced Salp Swarm Algorithm (SSA) to automatically choose a feature subset appropriate for the classification algorithm to classify high-dimensional data. Safaldin et al. [20] presented an intrusion detection model using the gray wolf algorithm, finding the optimal intrusion detection performance by adding the number of wolves and improving the model’s overall performance through multi-objective functions.

However, the No Free Lunch theorem [21] proves that no metaheuristic algorithm is able to solve every optimization issue. Different application scenarios require the selection of different algorithms to be better applied in practice.

3  Mathematical Preliminaries

This section mainly introduces the DBO algorithm [7], which is derived from the social behaviors observed in populations of dung beetles in nature, categorizing these populations into rolling, breeding, small, and thief dung beetles. It executes global exploration and local exploitation based on the location update equations for each population subset.

3.1 Rolling Dung Beetles

Dung beetles tend to roll feces into a ball and transport it to a secure storage location. During the ball rolling, dung beetles employ celestial cues to guide their way around. The updated formula for the position is described below:

xi(t+1)=xi(t)+α×k×xi(t−1)+b×△x(1)

△x=|xi(t)−Xworst|(2)

where xi(t) represents the position information of the i th beetle during the t th cycle. α represents a natural coefficient, k is the deviation coefficient, b represents a constant in the range (0,1), Xworst denotes the worst position, and △x imitates changes in illumination. When encountering obstacles during the dung ball rolling process, dung beetles ascend onto the dung ball to perform a dancing behavior, determining their movement direction. The location update equation is described below:

xi(t+1)=xi(t)+tan⁡(θ)|xi(t)−xi(t−1)|(3)

where θ∈[0,π]. The position is not updated when θ=0, π/2 and π.

3.2 Breeding Dung Beetles

In the natural world, the female dung beetle rolls the dung ball to a secure and appropriate location for spawning, laying balls of eggs to reproduce their offspring. Dung beetle spawning is strictly confined within the spawning zone, and spawning occurs only when breeding dung beetles are within the safe area for spawning. The equation for updating locations is outlined below:

Xi(t+1)=X∗+b1×(Xi(t)−Lb∗)+b2×(Xi(t)−Ub∗)(4)

Lb∗=max(X∗×(1−R),Lb)(5)

Ub∗=min(X∗×(1+R),Ub)(6)

where Xi(t) is the position of breeding dung beetles, X∗ represents the current local optimal location, b1 and b2 are random vectors whose magnitude is 1×D, D is the dimensionality of the problem. Lb∗ and Ub∗ represent the spawning area’s lower and upper boundaries, respectively, R=1−t/Tmax and Tmax means the upper limit for the number of iteration, Lb and Ub denote the optimization problem’s lower and upper bounds, respectively.

3.3 Small Dung Beetles

Some mature dung beetles come out of underground to forage for food, and they are called small dung beetles. Their foraging activities are strictly confined within the ideal foraging region. The small dung beetles begin to forage when they are in the area. The formula for the updating of positions is described below:

xi(t+1)=xi(t)+C1×(xi(t)−Lbb)+C2×(xi(t)−Ubb)(7)

Lbb=max(Xb×(1−R),Lb)(8)

Ubb=min(Xb×(1+R),Ub)(9)

where Xb denotes the global optimal location, Lbb and Ubb denote the lower and upper boundaries of the foraging zone, respectively, xi(t) represents the location information of the i th small dung beetle during the t th iteration, C1 is a random number that follows a normal distribution, and C2 is a random vector belonging to (0,1).

3.4 Thief Dung Beetles

Certain dung beetles engage in the natural phenomenon of pilfering dung balls from fellow beetles. Thief dung beetles will engage in stealing behavior when they are in the vicinity of an optimal food source, and their positional update formula is described below:

xi(t+1)=Xb+S×g×(|xi(t)−X∗|+|xi(t)−Xb|)(10)

where xi(t) denotes the location of the i th thief dung beetle during the t th iteration, g denotes a random vector of size 1×D obeying a normal distribution, and S represents a constant.

4  Network Traffic Identification Based on IDBO Algorithm

This section is divided into two parts. The first part describes how to improve the DBO algorithm, and the second part introduces how to apply the IDBO algorithm to traffic identification.

4.1 Improvement Strategies of IDBO Algorithm

4.1.1 Sobol Sequence Strategy for Initialization Population

The DBO algorithm initializes its population using a random distribution method, resulting in an uneven distribution of individuals in the initial phase, thereby restricting the population’s search range. Sobol sequence [22], a deterministic and low-discrepancy sequence, is particularly suitable for generating random numbers in high-dimensional spaces. This study utilizes the Sobol sequence to initialize the DBO population, enhancing the diversity within the population. The expression for generating a population using the sobol sequence is described below:

xi=Lb+Sn×(Ub−Lb)(11)

where xi represents the population location, Lb and Ub are the search space’s lower and upper bounds, and Sn∈[0,1] is the random numbers produced by the sobol sequence.

Assume that in a two-dimensional space, the population number is N=500. The distribution of random sequence-generated populations and sobol sequence-generated populations in the range of [0,1] is shown in Fig. 1.

Figure 1: Comparison of Random Sequence and Sobol Sequence Distributions

From the comparison in Fig. 1, it is found that the sobol sequence has a more homogeneous population distribution and makes full use of the solution space, which increases the diversity of dung beetles in the search space.

4.1.2 Integration of Levy Flight and Golden Sine Strategy to Update Location of Rolling Dung Beetles

In the DBO algorithm, the ball-rolling behavior is easily affected by illumination and the global worst position, which in certain scenarios can limit the algorithm’s global search ability, potentially requiring more iterations to achieve the global optimal solution. This paper introduces the integration of levy flight and golden sine strategy in the rolling dung beetle stage, embedding it within the DBO algorithm. This integration aims to balance the algorithm’s global search and local exploration abilities, consequently enhancing the efficiency of global search.

Levy flight [23] is a random walk based on Levy distribution to generate step lengths, differing from conventional random walks where step lengths are typically represented by power-law distributions Levy(S)∼|S|−1−β(0<β<2), where S is the size of the step and Levy(S) is the probability when the step S is moved. Because of the complexity of the levy distribution, the Mantegna algorithm is commonly employed to simulate it.

S=θ|ω|1/β(12)

θ and ω follow a normal distribution.

θ∼N(0,σu2),ω∼N(0,σv2)(13)

σu={τ(1+β)sin⁡(πβ/2)2(β−1)/2τ[(1+β)/2]β}1/β,σv=1(14)

where τis the normal gamma function and β typically has a value of 1.5 [23].

The Golden Sine Algorithm (Gold-SA) is a novel metaheuristic algorithm proposed by Tanyildizi et al. [24] in 2017, exhibiting strong global search capabilities. It incorporates the golden ratio in the position update process to narrow down the solution space, enabling thorough exploration of local regions and thus balancing global and local search abilities. The updating formula for the golden sine is outlined below:

xi(t+1)=xi(t)|sin⁡(r1)|+r2sin⁡(r1)|c1xi(t−1)−c2xi(t)|(15)

c1=ah+b(1−h)(16)

c2=a(1−h)+bh(17)

where xi(t) represents the position information. r1 and r2 are random numbers in (0,2π) and (0,π), respectively. c1 and c2 are the coefficients that are obtained by introducing a golden section number, which is an irrational number with the formula h=(5−1)/2, a and b represent the initial values of the golden section coefficients, and a=−π, b=π [24].

The position update formula for embedding an integration of levy flight and golden sine strategy in a rolling dung beetle is described below:

xi(t+1)=Levy(S)xi(t)|sin⁡(r1)|+r2sin⁡(r1)|c1xi(t−1)−c2xi(t)|(18)

The integration of levy flight and golden sine strategy for ball-rolling behavior can offer several advantages. It aids in reducing the impact of light intensity on dung beetles’ rolling behavior, thereby enhancing algorithmic diversity and helping to avoid local optima. Simultaneously, it frees the dung beetles’ rolling behavior from the influence of the global worst position, somewhat expanding the search space, thereby enhancing the algorithm’s exploratory capabilities and facilitating the discovery of superior solutions.

4.1.3 Adaptive Weight Factor Strategy to Update Location of Thief Dung Beetles

The location update strategy of thief dung beetles usually relies on the information of surrounding dung beetles and the solution space, causing the algorithm to be overly sensitive to neighborhood information. If the neighborhood information is insufficient or misleading, it will affect the iteration speed of the algorithm. This paper introduces an adaptive weight factor update strategy in the thief dung beetle stage, which can automatically adjust the individual location according to the iteration count, thus enhancing the search and development performance of the dung beetle optimization algorithm, which can be achieved in “exploration” and “exploitation”. The balance between them speeds up the convergence performance of the algorithm. The adaptive weight factor ω [25] has the following mathematical expression:

ω=sin⁡(π×t2×Maxiteration+π)+1(19)

where t signifies the ongoing iteration count, Maxiteration denotes the upper limit for the number of iterations. After introducing an adaptive weight factor, the location update equation for the thief dung beetles is described below:

xi(t+1)=ω×(Xb+S×g×(|xi(t)−X∗|+|xi(t)−Xb|))(20)

where xi(t) denotes the location of the i th thief dung beetle during the t th iteration, g is a 1×D size random vector obeying a normal distribution, and S is a constant.

According to Eq. (20), it can be seen that the adaptive weight factor is maximum at the beginning of the search iteration, which can motivate the dung beetle to focus more on exploiting known solutions. As the iterations progress, the adaptive weight factor fluctuates up and down between 0 and 2, which can motivate the dung beetle to explore more to discover the possible global optimal solution and enhance the convergence speed.

Fig. 2 displays the flowchart of the IDBO algorithm.

Figure 2: Flowchart of IDBO algorithm

As shown in Fig. 2, the steps of the IDBO algorithm suggested in this paper are described below.

Step 1: Set the appropriate initial values for the population size N, the maximum number of iterations T, and other relevant parameters.

Step 2: Use sobol sequence Eq. (11) create the initial population in the search space, and calculate each dung beetle’s fitness value.

Step 3: The IDBO algorithm is used to update the individual location in the dung beetle population. If the individual dung beetle belongs to the rolling dung beetle, the position of the dung beetle is updated by Eq. (18) or Eq. (3); if the individual dung beetle belongs to the breeding dung beetle, the position of the dung beetle is updated by Eq. (4); if the individual dung beetle belongs to the small dung beetle, the position of the dung beetle is updated by Eq. (7); if the individual dung beetle belongs to the thief dung beetle, the position of the dung beetle is updated by Eq. (20).

Step 4: Calculate the fitness value of individual dung beetles after the position update by the fitness function Eq. (21). Compare these new fitness values with the previously found optimal fitness value and optimal position to determine whether the current population fitness and position need to be updated to obtain the optimal fitness value and optimal position.

Step 5: Judge whether the algorithm reaches the largest iteration count, if so, stop the iteration, and the global optimal location and fitness value are output; otherwise, jump to Step 3 for the next iteration of optimization.

4.2 Network Traffic Identification Process

The core of the proposed method for network traffic identification in this paper lies in utilizing the IDBO algorithm for feature selection, determining the feature subset that has the greatest information. Subsequently, this feature subset is utilized to train a KNN classifier for achieving accurate network traffic classification and identification. These two crucial components work in synergy to enhance the network traffic identification method’s accuracy and performance.

Fig. 3 illustrates the flowchart of network traffic identification based on the IDBO algorithm.

Figure 3: Flowchart of network traffic identification based on IDBO algorithm

As demonstrated in Fig. 3, the precise steps in the execution of the network traffic identification method based on the proposed IDBO algorithm are as follows:

Step 1: Preprocess the data, equalize the data stream sample set, and divide it into training and testing sets.

Step 2: Perform IDBO algorithm flow to find the global optimal solution.

Step 3: The optimal subset of features obtained in Step 2 is classified using the KNN algorithm. Evaluate the identification accuracy of the method based on various criteria, including the number of selected features, accuracy, fitness values, and other relevant indicators.

5  Experimental Simulation and Analysis

This section is divided into three sections. The first section describes the data selection and processing process of this article, the second section is the performance analysis of the IDBO algorithm, and the third section verifies its traffic identification effect on the CICIDS2017 dataset. The experimental environment used in this paper is a Windows 10 operating system with Intel (R) Core (TM) i7-8550U CPU @ 1.80 GHz and 12 GB of RAM. The simulation software is MATLAB.

5.1 Dataset Selection and Processing

The simulation experiments utilized the CICIDS2017 dataset to validate the performance of network traffic identification based on the IDBO algorithm proposed in this paper. This dataset contains 15 traffic categories, but the BENIGN traffic category is quite large, while the other traffic categories are relatively scarce.

In binary traffic identification, BENIGN denotes benign traffic, encoded as 0 using One-Hot, and the remaining 14 types denote abnormal traffic, coded as 1. To avoid the method bias towards one type of traffic during traffic identification, it is undersampled to balance the benign and abnormal traffic. The dataset was also preprocessed to remove dirty data, and all data were mapped between 0 and 1 using min-max normalization. From the processed data, 5000 pieces of data are randomly selected to form a new data sample.

In multi-classification traffic identification, the dataset was first preprocessed to eliminate the dirty data, and all data were mapped using min-max normalization between 0 and 1. Simultaneously, to balance the sample size of each category, a few categories with similar features and behaviors are merged to form a new category during preprocessing, while Infiltration and Heartbleed data with too few samples are ignored. The resulting seven categories are Benign, Botnet, Brute Force, DDoS, DoS, PortScan, and Web Attack, with 1000 randomly extracted data points from each category to form the dataset sample.

5.2 Performance Analysis of IDBO Algorithm

To validate the improved optimization capability of the IDBO algorithm proposed in this paper, a set of common optimization algorithms, such as Particle Swarm Optimization (PSO) [26], Grey Wolf Optimization (GWO) [27], Whale Optimization Algorithm (WOA) [28], and the original DBO algorithm, were chosen for comparative analysis against the IDBO algorithm in the simulation experiments. To keep the article from becoming too long, six different types of benchmark functions were chosen for the experimentation of the algorithms, namely unimodal test functions (f1; f2; f3) and multimodal test functions (f4; f5; f6). Table 1 shows the details of the test functions.

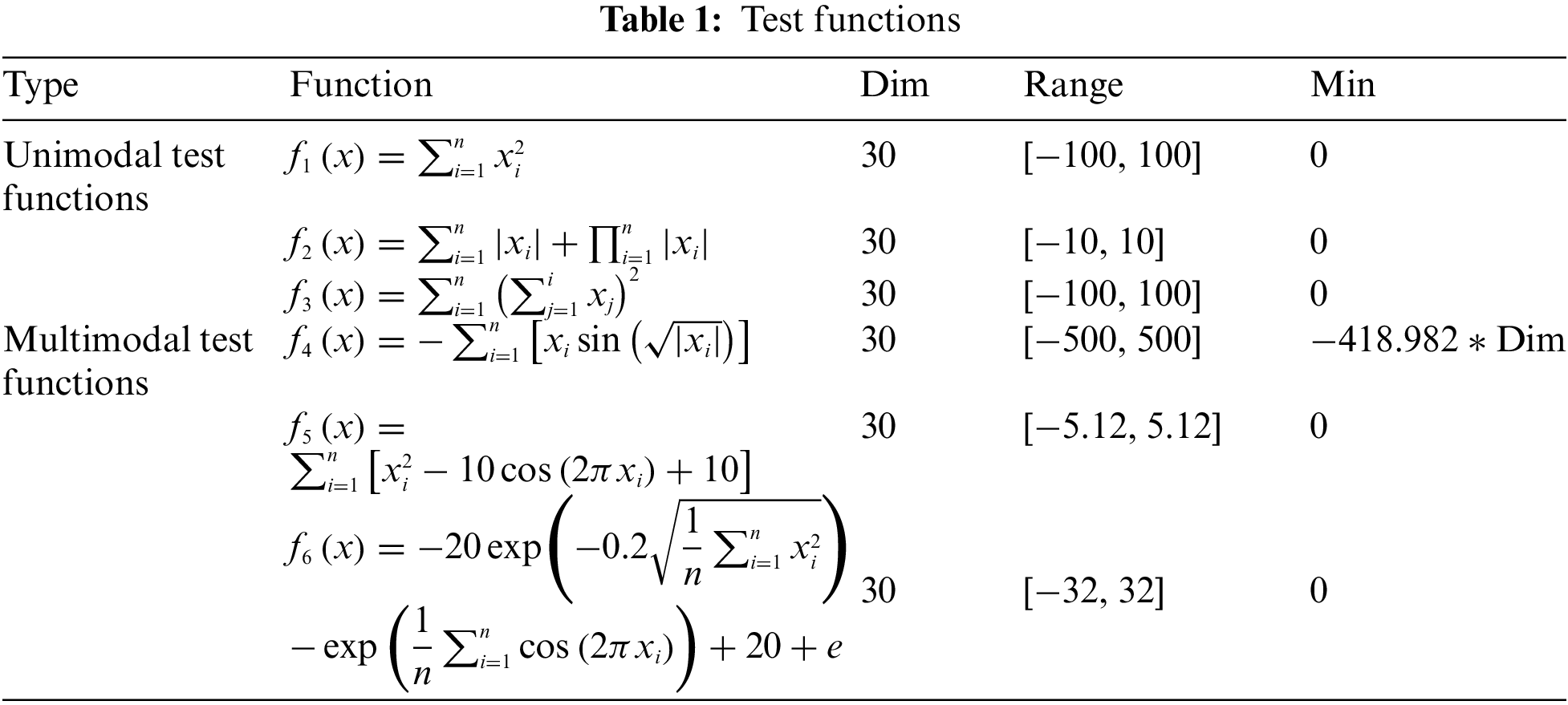
Considering that the algorithms have randomness, the above five algorithms were run independently and repeatedly 30 times. The mean and standard deviation of the 30 optimization results were computed and recorded in Table 2. Figs. 4 and 5 display the convergence curves for the five methods on benchmark functions.

Figure 4: Convergence curves for unimodal test functions

Figure 5: Convergence curves for multimodal test functions

The test results in Table 2 indicate that, compared to other algorithms, the IDBO algorithm exhibits smaller mean values and standard deviations for unimodal and multimodal functions. Although for f6, the IDBO algorithm’s mean value and standard deviation are equal, its convergence speed is faster, allowing it to find the global optimal more rapidly. Observing the convergence curves in Figs. 4 and 5, it is proven that the IDBO algorithm outperforms other algorithms. Its performance is superior, with higher convergence accuracy and speed when compared to the four different algorithms. Therefore, the IDBO algorithm, which is improved by the strategy presented in this research, has faster convergence during the iterative optimization search for different benchmark functions, and it has better stability and robustness than other algorithms.

5.3 Performance Analysis of Network Traffic Identification Based on IDBO Algorithm

5.3.1 Evaluation Function

In network traffic identification, the fitness function value reflects the effectiveness of the method’s identification. Its value is mainly related to the quantity of chosen features and identification accuracy. As a result, the fitness function in this work is designed as follows [4]:

F(i)=accuracy(i)1+η⋅n(i)(21)

where F(i) is the fitness value of the i th individual, accuracy(i) means identifying the correct ratio, n(i) is the quantity of chosen features, and η is the weighting coefficient, set to η=0.01 in this paper.

5.3.2 Network Traffic Identification Using the CICIDS2017 Dataset

To further evaluate the network traffic identification performance based on the IDBO algorithm, binary and multi-classification network traffic identification was conducted on the CICIDS2017 dataset. Given the high feature dimension and redundancy in the dataset, feature selection was performed. The preprocessed CICIDS2017 dataset was split into a training set (70%) for feature selection evaluation and a testing set (30%) for verifying the network traffic identification results. Various comparative algorithms were set with the same experimental parameters, including a population size (N) of 30, and a maximum number of iterations (T) of 50. The experiments were independently repeated 30 times to compare the accuracy, recall, precision, and F1 score for different traffic categories.

The experimental results for binary traffic identification are displayed in Table 3, and the comparison diagram of evaluation indicators for each category is shown in Fig. 6. The results of multi-classification network traffic identification experiments are introduced in Table 4 and Fig. 7.

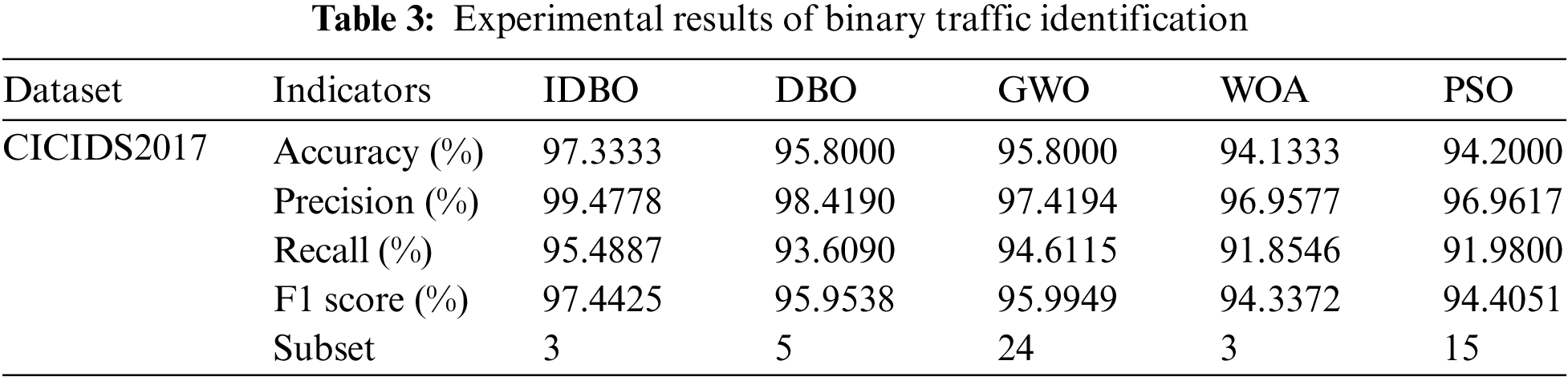
Figure 6: Comparison of each algorithm in binary classification

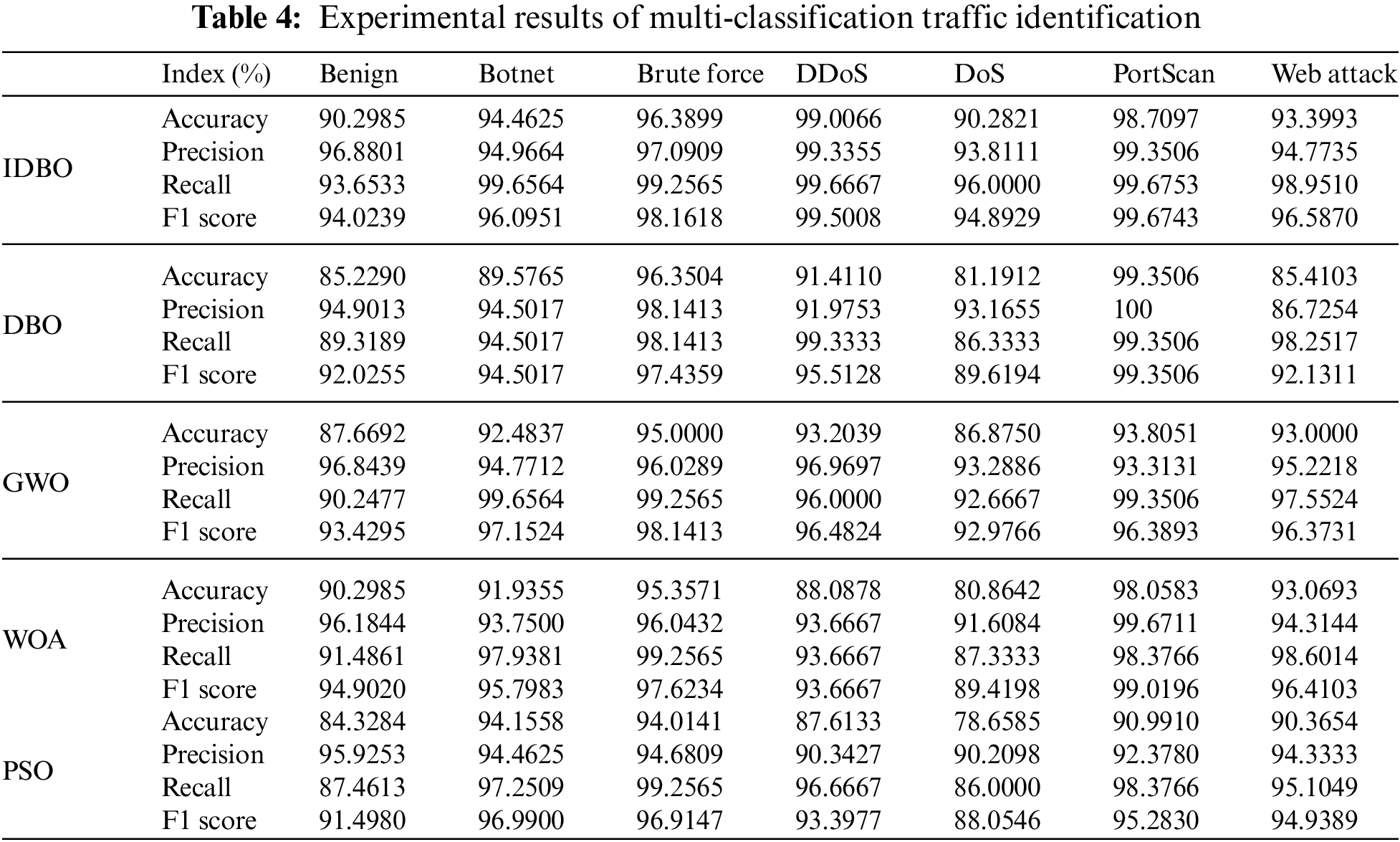
Figure 7: Comparison of each algorithm in multi-classification

According to the experimental results in Table 3 and the comparative chart of various category metrics in Fig. 6, in binary classification, the IDBO algorithm effectively reduces redundant features and exhibits higher accuracy, recall rate, precision, and F1 score across all categories compared to other algorithms. This suggests that the network traffic identification based on the IDBO algorithm generally makes correct classification decisions in most scenarios. It not only effectively distinguishes between BENIGN and abnormal traffic but also minimizes false positives and false negatives, thereby significantly enhancing traffic identification efficiency and ensuring the normal operation of the network.

It is evident from Table 4 that the network traffic identification method based on IDBO can identify different traffic categories with over 90% accuracy, precision, recall, and F1 score. As can be seen from Fig. 7, the recognition effect of the DDoS class and DoS class is the most obvious. The DDoS category accuracy rate increased by 5.80%, and the DoS category accuracy rate increased by 3.41%.

The experimental findings validate that the IDBO algorithm for network traffic identification proposed in this paper can overcome the issues of slow convergence and susceptibility to the local optimal solution that the original DBO algorithm faces when handling high-dimensional problems, thus enhancing data traffic identification efficiency.

6  Conclusion

A crucial component of network security and performance optimization is network traffic identification. To address the issue of the slow convergence speed of the original DBO algorithm which may trap in a local optimal solution in complex network traffic identification tasks, the IDBO algorithm is proposed. First, the population is initialized through the sobol sequence to enhance the global search ability of the algorithm. Secondly, the integration of levy flight and golden sine strategy is introduced to balance the algorithm’s global search and local exploration abilities. Finally, an adaptive weight factor enhances the convergence accuracy of the algorithm. The performance of the IDBO algorithm is verified through 6 different types of benchmark function tests. The results of the simulation on the CICIDS2017 dataset demonstrate that the IDBO algorithm can effectively reduce redundant features when handling high-dimensional problems. Compared with the original DBO, GWO, WOA, and PSO algorithms, it has a better convergence speed and solves the problem of traditional algorithms in traffic identification. However, this paper only uses the KNN classifier to evaluate the traffic identification effect. In the future, multiple classifiers can be compared to find the most suitable network traffic identification classifier for the IDBO algorithm.

Acknowledgement: We would like to take this opportunity to express our sincere gratitude to all the reviewers whose valuable insights greatly contributed to the completion of this manuscript.

Funding Statement: This work has been supported by the National Natural Science Foundation of China under Grant 61602162 and the Hubei Provincial Science and Technology Plan Project under Grant 2023BCB041.

Author Contributions: Study conception and design: Qinyue Wu, Hui Xu, and Mengran Liu; data collection: Qinyue Wu; analysis and interpretation of results: Qinyue Wu, Hui Xu; draft manuscript preparation: Qinyue Wu, Hui Xu, and Mengran Liu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The dataset used in this study is openly accessible and reliable. It can be obtained from the following website: https://www.unb.ca/cic/datasets/ids-2017.html.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Gui, Y. Cao, I. You, L. Ji, Y. Luo and Z. Luo, “A Survey of techniques for fine-grained web traffic identification and classification,” Math. Biosci. Eng., vol. 19, no. 3, pp. 2996–3021, 2022. doi: 10.3934/mbe.2022138. [Google Scholar] [PubMed] [CrossRef]

2. M. Soysal and E. G. Schmidt, “Machine learning algorithms for accurate flow-based network traffic classification: Evaluation and comparison,” Perform. Eval., vol. 67, no. 6, pp. 451–467, 2010. doi: 10.1016/j.peva.2010.01.001. [Google Scholar] [CrossRef]

3. H. Xu, K. Przystupa, C. Fang, A. Marciniak, O. Kochan and M. Beshley, “A combination strategy of feature selection based on an integrated optimization algorithm and weighted k-nearest neighbor to improve the performance of network intrusion detection,” Electron., vol. 9, no. 8, pp. 1206, 2020. doi: 10.3390/electronics9081206. [Google Scholar] [CrossRef]

4. H. Xu, Y. Lu, and Q. Guo, “Application of improved butterfly optimization algorithm combined with black widow optimization in feature selection of network intrusion detection,” Electron., vol. 11, no. 21, pp. 1206, 2022. doi: 10.3390/electronics11213531. [Google Scholar] [CrossRef]

5. H. Xu, X. Chai, and H. Liu, “A multi-controller placement strategy for hierarchical management of software-defined networking,” Symmetry, vol. 15, no. 8, pp. 1520, 2023. doi: 10.3390/sym15081520. [Google Scholar] [CrossRef]

6. H. Xu, Y. Hu, W. Cao, and L. Han, “An improved jump spider optimization for network traffic identification feature selection,” Comput. Mater. Contin., vol. 76, no. 3, pp. 3239–3255, 2023. doi: 10.32604/cmc.2023.039227. [Google Scholar] [PubMed] [CrossRef]

7. J. Xue and B. Shen, “Dung beetle optimizer: A new meta-heuristic algorithm for global optimization,” J. Supercomput., vol. 79, no. 7, pp. 7305–7336, 2023. doi: 10.1007/s11227-022-04959-6. [Google Scholar] [CrossRef]

8. S. Sen, O. Spatscheck, and D. Wang, “Accurate, scalable in-network identification of P2P traffic using application signatures,” in Proc. WWW04, New York, NY, USA, 2004, pp. 512–521. [Google Scholar]

9. A. W. Moore and K. Papagiannaki, “Toward the accurate identification of network applications,” in Proc. PAM, Boston, MA, USA, 2005, pp. 41–54. [Google Scholar]

10. R. Alshammari and A. N. Zincir-Heywood, “Machine learning based encrypted traffic classification: Identifying SSH and Skype,” in Proc. CISDA, Ottawa, ON, Canada, 2009, pp. 1–8. [Google Scholar]

11. D. Wang, L. Zhang, Z. Yuan, Y. Xue, and Y. Dong, “Characterizing application behaviors for classifying p2p traffic,” in Proc. ICNC, Honolulu, HI, USA, 2014, pp. 21–25. [Google Scholar]

12. S. Dong, “Multi class SVM algorithm with active learning for network traffic classification,” Expert Syst. Appl., vol. 176, pp. 114885, 2021. doi: 10.1016/j.eswa.2021.114885. [Google Scholar] [CrossRef]

13. J. Zeng, Y. Qian, F. Yin, L. Zhu, and D. Xu, “A multi-value cellular automata model for multi-lane traffic flow under lagrange coordinate,” Comput. Math. Organ. Theory, vol. 28, pp. 1–15, 2022. doi: 10.1007/s10588-021-09345-w. [Google Scholar] [CrossRef]

14. J. Zhang, Y. Qian, J. Zeng, X. Wei, and H. Li, “Hybrid characteristics of heterogeneous traffic flow mixed with electric vehicles considering the amplitude of acceleration and deceleration,” Physica A: Stat. Mech. Appl., vol. 614, pp. 128556, 2023. doi: 10.1016/j.physa.2023.128556. [Google Scholar] [CrossRef]

15. J. Zeng et al., “Expressway traffic flow under the combined bottleneck of accident and on-ramp in framework of Kerner’s three-phase traffic theory,” Physica A: Stat. Mech. Appl., vol. 574, no. 4, pp. 125918, 2021. doi: 10.1016/j.physa.2021.125918. [Google Scholar] [CrossRef]

16. X. Qin, Y. Qian, J. Zeng, and X. Wei, “Accessibility and economic connections between cities of the new western land-sea corridor in China—Enlightenments to the passageway strategy of Gansu province,” Sustain., vol. 14, no. 8, pp. 4445, 2022. doi: 10.3390/su14084445. [Google Scholar] [CrossRef]

17. J. Wang, Y. Liu, and H. Feng, “IFACNN: Efficient DDoS attack detection based on improved firefly algorithm to optimize convolutional neural networks,” Math. Biosci. Eng., vol. 19, no. 2, pp. 1280–1303, 2022. doi: 10.3934/mbe.2022059. [Google Scholar] [PubMed] [CrossRef]

18. N. W. Khan et al., “A hybrid deep learning-based intrusion detection system for IoT networks,” Math. Biosci. Eng., vol. 20, no. 8, pp. 13491–13520, 2023. doi: 10.3934/mbe.2023602. [Google Scholar] [PubMed] [CrossRef]

19. X. Qin, S. Zhang, D. Yin, D. Chen, and X. Dong, “Two-stage feature selection for classification of gene expression data based on an improved Salp Swarm Algorithm,” Math. Biosci. Eng., vol. 19, no. 12, pp. 13747–13781, 2022. doi: 10.3934/mbe.2022641. [Google Scholar] [PubMed] [CrossRef]

20. M. Safaldin, M. Otair, and L. Abualigah, “Improved binary gray wolf optimizer and SVM for intrusion detection system in wireless sensor networks,” J. Ambient Intell. Hum. Comput., vol. 12, pp. 1559–1576, 2021. doi: 10.1007/s12652-020-02228-z. [Google Scholar] [CrossRef]

21. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Trans. Evolut. Comput., vol. 1, no. 1, pp. 67–82, 1997. doi: 10.1109/4235.585893. [Google Scholar] [CrossRef]

22. S. Joe and F. Y. Kuo, “Remark on algorithm 659: Implementing Sobol’s quasirandom sequence generator,” ACM Trans. Math. Software, vol. 29, no. 1, pp. 49–57, 2003. doi: 10.1145/641876.641879. [Google Scholar] [CrossRef]

23. H. Haklı and H. Uğuz, “A novel particle swarm optimization algorithm with Levy flight,” Appl. Soft. Comput., vol. 23, pp. 333–345, 2014. doi: 10.1016/j.asoc.2014.06.034. [Google Scholar] [CrossRef]

24. E. Tanyildizi and G. Demir, “Golden sine algorithm: A novel math-inspired algorithm,” Adv. Electr. Comput. Eng., vol. 17, pp. 71–79, 2017. doi: 10.4316/aece. [Google Scholar] [CrossRef]

25. Q. Liu, M. Li, N. Cao, Z. Zhang, and G. Yang, “Improved harris combined with clustering algorithm for data traffic classification,” IEEE Access, vol. 10, pp. 72815–72824, 2022. doi: 10.1109/ACCESS.2022.3188866. [Google Scholar] [CrossRef]

26. D. Wang, D. Tan, and L. Liu, “Particle swarm optimization algorithm: An overview,” Soft Comput., vol. 22, pp. 387–408, 2018. doi: 10.1007/s00500-016-2474-6. [Google Scholar] [CrossRef]

27. E. Emary, H. M. Zawbaa, and A. E. Hassanien, “Binary grey wolf optimization approaches for feature selection,” Neurocomput., vol. 172, no. 1, pp. 371–381, 2016. doi: 10.1016/j.neucom.2015.06.083. [Google Scholar] [CrossRef]

28. F. S. Gharehchopogh and H. Gholizadeh, “A comprehensive survey: Whale optimization algorithm and its applications,” Swarm. Evol. Comput., vol. 48, pp. 1–24, 2019. doi: 10.1016/j.swevo.2019.03.004. [Google Scholar] [CrossRef]