Differentially Private Support Vector Machines with Knowledge Aggregation

1  Introduction

The rapid development of generative artificial intelligence and large language models (LLMs) is accelerating changes in our production and living habits [1,2]. As a subfield of artificial intelligence (AI), machine learning (ML) algorithms such as support vector machines and logistic regression can play important roles in text classification, sentiment analysis, information extraction, etc. [3]. However, the proliferation of data collection and training leads to increasing privacy concerns [4,5]. The adversary may snoop on users’ sensitive information through membership inference attacks, attribute inference attacks, or model inversion attacks [6,7], which leads to privacy breaches, identity theft, or other malicious activities.

Privacy-preserving machine learning (PPML) [4] addresses these concerns by allowing the training and inference processes to be performed without exposing the raw data. Support vector machine (SVM) [8] is one of the most elementary learning models. Therefore, there is a huge demand for studying privacy-preserving SVM algorithms. Differential privacy (DP) [9,10] is a rigorous privacy paradigm nowadays and is widely adopted in AI and ML. DP has a formal mathematical foundation and therefore prevents the disclosure of any information about the presence or absence of any individual from any statistical operations.

Several approaches have been proposed to train SVM models with differential privacy [11–13]. These methods typically add noise or perturbation to the training data or model parameters to limit the amount of information that can be learned about any individual data point. Due to the lack of dimensionality reduction considerations, both computation overhead and accuracy are restricted by the curse of dimensionality. Dwork et al. [14] first studied the problem of privacy-preserving principal component analysis (PCA) and proved the optimal bounds of DP-compliant PCA, which lays the foundation for applying PCA in PPML.

Hereafter, Huang et al. [15] leveraged the Laplace mechanism into PCA-SVM algorithms to achieve differential privacy protection. Sun et al. [16] proposed DPSVD which is a differentially private singular value decomposition (SVD) algorithm to provide privacy guarantees for SVM training. To sum end, these methods all consider achieving dimensionality reduction by using PCA, so the algorithms are usually divided into two stages: the PCA phase and the SVM phase. However, the DPPCA-SVM, PCA-DPSVM in [15], and DPSVD in [16] all apply differential privacy in only one stage of PCA or SVM, resulting in an insufficient degree of privacy protection. A strict differential privacy protection mechanism should satisfy that DP must be applied whenever the train data is accessed in the algorithm [10]. Therefore, a DP-compliant SVM training mechanism with dimensionality reduction should be further studied.

Besides, when considering distributed learning scenarios, a common challenge is that multiple parties often have unbalanced or small amounts of data, resulting in inaccurate model accuracy. Hopefully, federated learning [17,18] is proposed to solve this problem through federated averaging [19] (specifically, including model averaging [20,21] and gradient averaging [22,23]). The existing DP-based SVM training mechanisms almost focus on centralized settings and do not take federated learning into account. Some SVM training frameworks based on federated learning [24,25] are mainly based on encryption technology rather than differential privacy, resulting in high computational overhead. Intuitively, we can directly adopt model averaging to obtain global information in distributed training settings. However, this ignores the fact that different data owners have different contributions to the global model.

To this end, this paper studies a strict differentially private SVM algorithm with dimensionality reduction and knowledge aggregation, which aims to maintain high data utility while providing strong privacy protection. Furthermore, considering that data among participants may be small and uneven, this paper focuses on the collaborative training of a global machine learning model by multiple participants. Our main contributions are summarized as follows:

•   We propose FedDPDR-DPML, a federated machine learning framework incorporating dimensionality reduction and knowledge aggregation, which greatly improves data utility while providing strong privacy guarantees. FedDPDR-DPML enables multiple participants to collaboratively learn a global model based on weighted model averaging and then the server distributes the global model to each participant to improve local data utility.

•   We design a strict privacy-preserving machine learning mechanism DPDR-DPML which introduces DP in both the dimensionality reduction phase and SVM training phase to provide strict and strong privacy guarantees. Specifically, we leverage a DP-based principal component analysis (PCA) method to extract the key low-dimensional features from high-dimensional data, which reduces computation costs and improves model accuracy.

•   By leveraging the empirical risk minimization approximations, we train DP-compliant SVM classifiers by adding noise to the objective function itself, leading to better data utility.

•   We conduct extensive experiments on three high-dimensional datasets. The experimental results demonstrate that our mechanisms achieve high accuracy while ensuring strong privacyprotection.

The remainder of the paper is organized as follows. A literature review is provided in Section 2. Section 3 introduces preliminaries and research problems. We present our solution FedDPDR-DPML in Section 4. Section 5 shows the experimental results and Section 6 concludes the paper.

2  Related Work

Privacy-preserving machine learning (PPML) [4,26,27] enables data-driven decision-making and the development of intelligent systems while protecting individuals’ sensitive information. Since the introduction of differential privacy (DP) [9,10], DP-based PPML [28] has gained significant attention as a means to ensure privacy while training models on sensitive data. Support vector machine (SVM) [8,29] is a popular class of machine learning algorithm used for classification, regression, and outlier detection tasks. Differential privacy (DP) is widely adopted in SVM to provide privacy guarantees for sensitive data.

However, a serious challenge facing SVM model learning under DP is how to achieve a good trade-off between privacy and utility. To this end, Chaudhuri et al. [30] proposed to produce privacy-preserving approximations of classifiers learned via (regularized) empirical risk minimization (ERM). They also analyzed the accuracy of proposed mechanisms and the upper bound of the number of training samples, laying the foundation for subsequent research. Zhang et al. [11] first proposed a dual variable perturbation scheme for differentially private SVM classifier training, which improves prediction accuracy. Farokhi [12] introduced additive privacy-preserving noise when conducting DP-based SVM training, which is proved as the optimal privacy-preserving noise distribution. Besides, Chen et al. [13] focused on privacy-preserving multi-class SVM training on medical diagnosis, which can deal with both linearly separable data and nonlinear data. However, these works do not consider dimensionality reduction, which will lead to higher computational overhead and lower classification accuracy when directly applied to high-dimensional data.

To address this, Dwork et al. [14] first studied the problem of differential privacy-based principal component analysis (PCA) and proved the optimal bounds of DP-compliant PCA, which lays the foundation for applying PCA in DP-based SVM model learning. They proposed to perturb the matrix of covariance with Gaussian noise. In contrast, Jiang et al. [31] perturbed the matrix of covariance with Wishart noise, which was able to output a perturbed positive semi-definite matrix. Besides, Xu et al. [32] applied the Laplace mechanism to introduce perturbation and proposed the Laplace input perturbation and Laplace output perturbation. These studies focus on DP-based dimensionality reduction, which provides an important research foundation for DP-based SVM training with dimensionality reduction.

Therefore next, Huang et al. [15] proposed DPPCA-SVM and PCA-DPSVM for privacy-preserving SVM learning with dimensionality reduction, which perturbed the matrix of covariance with symmetric Laplace noise. However, the DPPCA-SVM and PCA-DPSVM mechanisms only apply differential privacy at one stage in PCA or SVM, resulting in an insufficient degree of privacy protection. It should be claimed that a strict differential privacy protection mechanism should satisfy that DP must be applied whenever the train data is accessed in the algorithm. Besides, Sun et al. [16] proposed DPSVD which uses singular value decomposition (SVD) to project the training instances into the low-dimensional singular subspace. They first added the noise to the raw data D and then obtained the singular values by applying SVD on the perturbed data D′. However, the original training dataset is accessed again when computing low-dimensional singular subspace, thus resulting in insufficient privacy protection.

Federated learning [17,18] is a distributed machine learning framework designed to allow dispersed participants to collaborate on machine learning without disclosing private data to other participants. Tavara et al. [33] used alternating direction method of multipliers to efficiently learn a global SVM model with differential privacy in a distributed manner. Moreover, Truex et al. [24] used an encryption-based federated learning framework to generate a new SVM model based on the received local parameters from different data parties. Meanwhile, they also discussed introducing Gaussian noise to the gradients to achieve differential privacy. However, the article does not consider dimensionality reduction and lacks clear derivation and proof. Xu et al. [25] also studied privacy-preserving federated learning over vertically partitioned data, which can be applied to SVM training. Like [24], Xu et al. also used secure gradient computation to compute the global model, but the difference is that it targets the vertical setting and uses encryption for privacy protection. These studies all achieve differential privacy by adding noise to gradients.

Furthermore, the above studies all adopt federated averaging [19] (including model averaging [21,22] and gradient averaging [22,23]) to obtain the global model parameters in many scenarios. However, the classical federated averaging schemes ignore the contribution degrees of different participants. Thus, this paper investigates and proposes to utilize a weighted model averaging mechanism for collaborative machine learning while satisfying strict differential privacy.

3  Preliminaries

3.1 System Model and Safety Model

The system model considered in this article is a distributed machine-learning scenario, which contains a central server and multiple participants. This paper considers that the central server obeys the semi-honest (honest but curious) adversary model. That is, the server adheres to the agreement but also tries to learn more from the received information than the output was unexpected. In addition, this paper assumes that the multiple participants adhere to the agreement but do not trust each other.

3.2 Differential Privacy

Differential privacy (DP) [9,10] is a strict privacy protection model that gives rigorous and quantified proof of privacy disclosure risk. Since differential privacy was proposed ten years ago, hundreds of papers based on differential privacy technology have been proposed in security, database, machine learning, and statistical computing applications.

Definition 3.1 ((ε,δ)-Differential Privacy ((ε,δ)-DP)). A randomized mechanism ℳ satisfies (ε,δ)-DP if and only if for any neighboring datasets D and D′, and for any possible output O⊆Range(ℳ), it holds

P[ℳ(D)∈O]≤eε⋅P[ℳ(D′)∈O]+δ,(1)

where P denotes probability.

(ε,δ)-DP is also called approximated DP. When δ=0, (ε,δ)-DP becomes ε-DP, that is, pure differential privacy. The neighboring datasets D and D′ are considered to be neighboring if they differ by a single record.

Differential privacy provides a mathematical guarantee of privacy by introducing controlled randomness (i.e., noise) into the data or results of computations. This paper adopts the Gaussian mechanism [10] to achieve differential privacy, which is defined as follows.

Theorem 3.1 (Gaussian Mechanism). The Gaussian mechanism achieves (ε,δ)-DP by adding Gaussian noise with standard deviation σ=2ln⁡(1.25/δ)⋅Δ/ε, where Δ is ℓ2-sensitivity and is computed as the maximal ℓ2-norm difference of two neighboring datasets D and D′.

3.3 Problem Formulation

Data model. Let N denote the number of participants. Each participant Pi(i={1,2,⋯,N})owns a local dataset Di={(xij,yij)∈𝒳×𝒴:j={1,2,⋯,n}} with n samples, where xij and yij in each sample (xij,yij) denote the data space and label set, respectively. As for binary classification in ML, the data space is 𝒳=Rd and the label set is 𝒴={−1,1}. That is, each xij=[xij1,xij2,⋯,xijd] is a d-dimensional vector, and each yij=−1 or yij=1. Besides, it assumes ‖xij‖2≤1 which facilitates the efficient calculation of sensitivity in the following [34,35]. For convenience, let Xi=[xi1;xi2;⋯;xin] denote the data space of dataset Di and let Yi=[yi1;yi2;⋯;yin] denote the label space of dataset Di. That is, Di=(Xi,Yi).

Empirical Risk Minimization (ERM). In this paper, we build machine learning models that are expressed as empirical risk minimization. We would like to train a predictor β:x→y. As for machine learning algorithms with empirical risk minimization, the predictor β minimizes the regularized empirical loss. For each participant Pi owning dataset Di, the ERM can be formulated as

ℱ(βi,Di)=1n∑j=1nℓ(βi;xij,yij)(2)

where ℓ(⋅) is the loss function, βi is a d-dimensional parameter vector.

Moreover, we further introduce structure risk on Eq. (2) as follows:

ℱ(βi,Di)=1n∑j=1nℓ(βi;xij,yij)+λ2‖βi‖22(3)

where λ>0 is a regularization parameter. Here, introducing regularization terms can effectively reduce the risk of overfitting.

Based on Eq. (3), we aim to compute a d-dimensional parameter vector βi∗ such that

βi∗=arg⁡minβiℱ(βi,Di)=arg⁡minβi[1n∑j=1nℓ(βi;xij,yij)+λ2‖βi‖22](4)

Problem Statement. For each participant Pi, we aim to privately train a machine learning model (i.e., private predictor β^i∗) based on ERM on the client side. For the service provider, we aim to privately aggregate all the local models of N participants and compute a global ML model β^Global∗ on the server side. Besides, we will also integrate dimensionality reduction into all training processes to improve model accuracy and reduce computing costs.

4  Our Solution

Insufficient data samples and high-dimensional features are some of the key factors restricting small data owners from training high-performance models. Therefore, this paper considers a scenario in which multiple participants collaborate to train a global machine learning model in a privacy-preserving way, which can improve accuracy while providing privacy guarantees. To this end, we propose a differential privacy-compliant federated machine learning framework with dimensionality reduction, called FedDPDR-DPML.

4.1 Overview of FedDPDR-DPML

The high-level overview of FedDPDR-DPML is shown in Fig. 1. The FedDPDR-DPML mainly includes two phases: the first phase aims to obtain the global low-dimensional features of high-dimensional data, and the second phase aims to obtain the global machine learning model. Specifically, the FedDPDR-DPML adopts three design rationales as follows. 1) To overcome the high-dimensional features of data, we conduct dimensionality reduction before training by using the principal component analysis (PCA) method, which can improve model accuracy and reduce computation overhead. 2) To provide strict privacy guarantees, we introduce differential privacy in both dimensionality reduction and machine learning. 3) To solve the challenges of unbalanced data size among data owners, we leverage weighted averaging for both dimensionality reduction and machine learning procedures to improve the model accuracy.

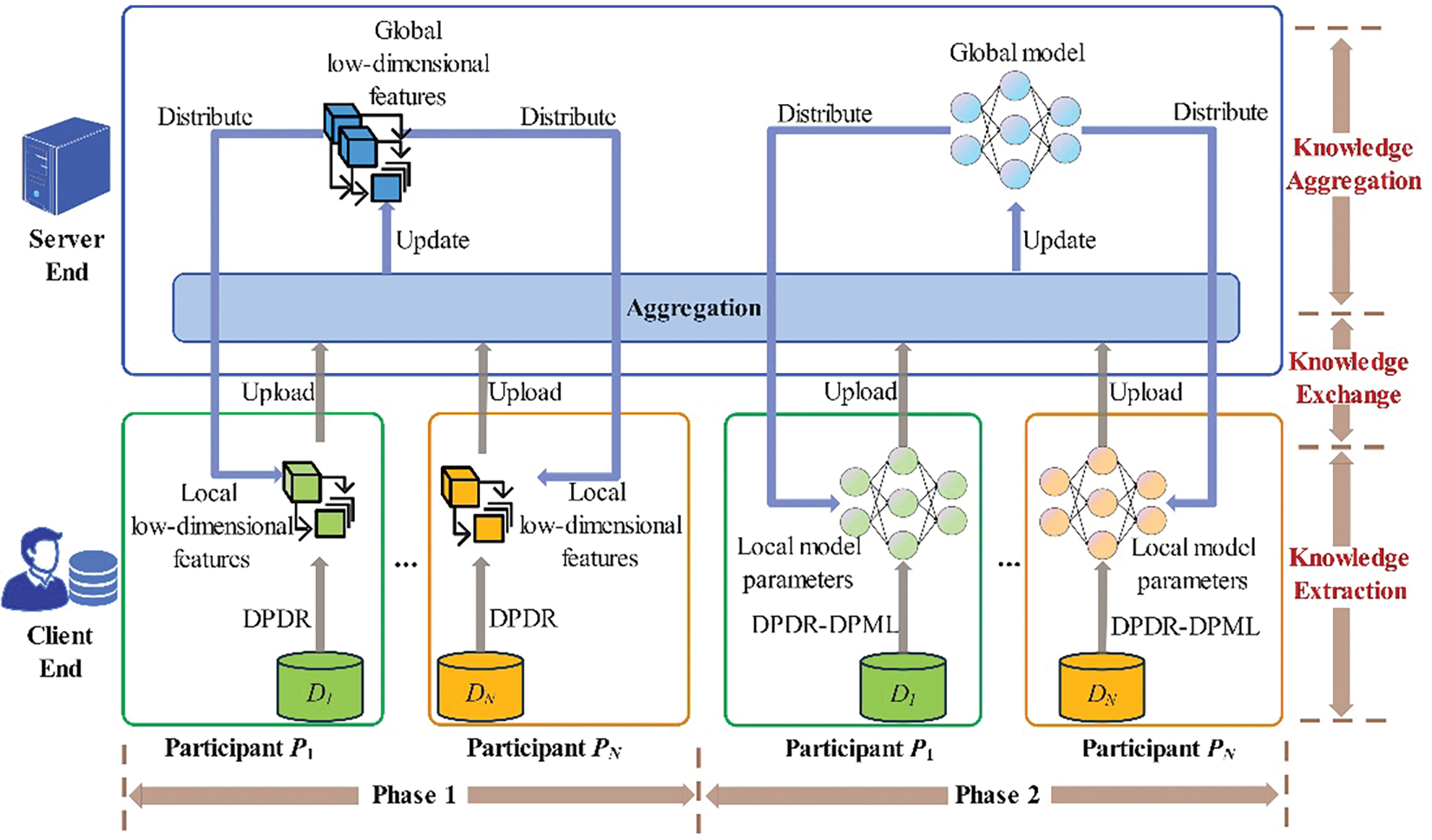
Figure 1: The framework of our FedDPDR-DPML mechanism

However, the traditional model averaging [20,21] method can improve the performance of participants who own a small amount of data, but will reduce the performance of participants who own a large amount of data. That is, participants with different amounts of data contribute differently to the global model. Therefore, we propose a weighted model averaging scheme that computes the global information through a weighted average method, in which the weight of each participant depends on the data size it possesses. Let ni be the data size of the participant Pi. Then, the weight of participant Pi is wi=ni/∑i=1Nni.

Algorithm 1 presents a high-level description of the proposed FedDPDR-DPML. The two phases are described in detail as follows:

•   In the first phase, each participant Pi locally employs a DP-compliant dimensionality reduction (DPDR) algorithm to generate private k-dimensional features U^ikand sends U^ik to the server. The server computes the weighted average of the private k-dimensional features as U^Globalk←1N∑i=1NwiU^ik and returns the global low-dimensional features U^Globalk to each participant. The DPDR satisfies (ε1,δ)-DP.

•   In the second phase, each participant Pi locally executes algorithm DPDR-DPML to get local ML model parameters β^i∗ and sends β^i∗ to the server. Next, the server computes the weighted average of the private ML predictor as β^Global∗←1N∑i=1Nwiβ^i∗ and returns the global machine-learning parameters β^Global∗ to each participant. In addition, as shown in the 5-th line, the raw dataset Di of each participant will be used when executing DPDR-DPML. To achieve privacy protection, the algorithm DPDR-DPML involves differential privacy again when training local ML models and satisfies ε2-DP.

4.2 DP-Compliant Dimensionality Reduction

We utilize principal component analysis (PCA) to achieve dimensionality reduction under DP. For d-dimensional dataset Di=(Xi,Yi) of participant Pi, the d×d covariance matrix is defined as

Mi=Xi⊤Xi=∑j=1nxij⊤xij.(5)

Thus, we can achieve DP-compliant PCA by applying the Gaussian mechanism to Mi. Then, the k-principle features of the original dataset are computed by choosing the top-k singular subspace of the noised covariance matrix based on singular value decomposition (SVD).

Algorithm 2 shows the pseudo-code of PCA-based dimensionality reduction while satisfying DP. We simply formalize Algorithm 2 as DPDR(Di,ε1,δ,k). Given dataset Di=(Xi,Yi) of each participant Pi, we add Gaussian noise to the covariance matrix to achieve DP. For the function f(Xi)=Xi⊤Xi, the sensitivity of f(Xi) is Δf=1, as shown in Lemma 4.1. Thus, the Gaussian noise matrix R1 is generated from 𝒩(0,2ln⁡(1.25/δ)Δf2/ε12) and is processed to be a symmetric matrix by each lower triangle entry copied from its upper triangle counterpart. Next, we apply SVD to the noisy covariance matrix M^i and thereby grab the top-k singular subspace of M^i, as shown in Lines 5–6. Then, U^ik is the private k-dimensional features of dataset Di.

Lemma 4.1. In Algorithm 2 (i.e., DPDR), for input dataset Di=(Xi,Yi), the sensitivity of function f(Xi)=Xi⊤Xi is at most one.

Proof. Let Xi′ denote the neighboring dataset of Xi. Assuming Xi′ and Xi differ in the t-th row. Then, based on the definition of DP, the sensitivity can be computed as

‖Mi−Mi′‖2=‖Xi⊤Xi−Xi′⊤Xi′‖2=‖[xit1xit1xit1xit2⋯xit1xitdxit2xit1xit2xit2⋯xit2xitd⋯⋯⋱⋯xitdxit1xitdxit2⋯xitdxitd]‖2=(xit1)2[(xit1)1+(xit2)2+⋯+(xitd)2]+⋯+(xitd)2[(xit1)1+(xit2)2+⋯+(xitd)2]=[(xit1)1+(xit2)2+⋯+(xitd)2]2=‖xit‖22≤1(6)

where the step of “≤” is achieved since ‖xij‖2≤1(j∈{1,2,⋯,n}).

4.3 DP-Compliant Machine Learning with Dimensionality Reduction

This part presents the DP-compliant machine learning with dimensionality reduction. As a representative, we consider building support vector machine (SVM) models from multiple participants. Specifically, the SVM model is trained based on empirical risk minimization. Moreover, the loss function of SVM is defined as ℓSVM(β,x,y)=max{0,1−yx⊤β}.

To improve model accuracy, we first apply dimensionality reduction on the original high-dimensional dataset. Besides, to achieve privacy protection, we perturb the objective function to produce the minimizer of the noisy objective function.

Algorithm 3 shows the pseudo-code of our proposed machine-learning training process under DP. We formalize Algorithm 3 as DPDR-DPML(Di,U^ik,ε2,λ,α). Given the dataset Di=(Xi,Yi) of participant Pi, we first project the data into k-dimensional space based on the private k-dimensional features U^ik. The U^ik can be obtained from Algorithm 2. Therefore, the input dataset for machine learning is D^ik=(X^ik,Yi). Next, we compute the privacy parameter which will be used to generate noise for objective function perturbation, as shown in Lines 3–9. The h is the Huber loss function parameter and is picked as h=0.5 for Huber SVM, a typical value [36].

Based on the privacy parameter p, the noise vector R2 can be drawn based on the probability density function α−1e−p2‖R2‖. Then, we can perturb the objective function as

ℱpriv(βi,D^ik)=ℱ(βi,D^ik)+1nR2⊤βi.(7)

At last, we can produce the minimizer of noisy ℱpriv(βi,D^ik) by

β^i∗=arg⁡minβi[ℱpriv(βi,D^ik)+θ2‖βi‖22],(8)

where β^i∗ is the optimal parameters of ℱpriv(βi,D^ik).

Based on Eq. (4) in Subsection 3.3, the minimizer of ℱpriv(βi,D^ik). is computed as

β^i∗=arg⁡minβi[ℱpriv(βi,D^ik)+θ2‖βi‖22]=arg⁡minβi[ℱ(βi,D^ik)+1nR2⊤βi+θ2‖βi‖22]=arg⁡minβi[1n∑j=1nℓ(βi;(x^ij)k,yij)+λ2‖βi‖22+1nR2⊤βi+θ2‖βi‖22](9)

where (x^ij)k denotes the private k-dimensional data space of x^ij.

4.4 Theoretical Analysis

4.4.1 Privacy Analysis

Theorem 4.1. Algorithm 2 (i.e., DPDR) satisfies (ε1,δ)-differential privacy.

Proof. As shown in the 4-th line of Algorithm 2, the Gaussian noise R1 is drawn from 𝒩(0,2ln⁡(1.25/δ)Δf2/ε12), that is, the deviation σ=2ln⁡(1.25/δ)⋅Δf/ε1, based on Theorem 3.1, Algorithm 2 (i.e., DPDR) satisfies (ε1,δ)-differential privacy.

Theorem 4.2. Algorithm 3 (i.e., DPDR-DPML) satisfies ε2-differential privacy.

Proof. The privacy guarantee of objective perturbation is shown in lines 3–10, which uses privacy parameter ε2. This can be proved to satisfy ε2-differential privacy by Theorem 9 in [30]. We omit the details due to space limitations.

Theorem 4.3. Algorithm 1 (i.e., FedDPDR-DPML) satisfies (ε,δ)-differential privacy, where ε=ε1+ε2.

Proof. As shown in Algorithm 1, FedDPDR-DPML sequentially executes DPDR(Xi,ε1,δ,k) and DPDR-DPML(Di,U^Globalk,ε2,λ,α). Thus, based on Theorem 4.1 and Theorem 4.2, Algorithm 1 (i.e., FedDPDR-DPML) satisfies (ε1+ε2,δ)-DP according to the sequential composition theorems [10].

4.4.2 Noise Scale Comparisons

Table 1 shows the comparisons between our proposed algorithms and other state-of-the-art mechanisms from different perspectives. At first, this paper considers a distributed scenario in which multiple participants jointly train a model, each of which has a different amount of data. In terms of privacy guarantees, our proposed FedDPDR-DPML insists that DP must be applied whenever the train data is accessed in an algorithm. Thus, compared to existing methods, FedDPDR-DPML involves noise addition in both the dimensionality reduction phase (i.e., PCA) and training phase (i.e., SVM), which provides strict and strong privacy protection.

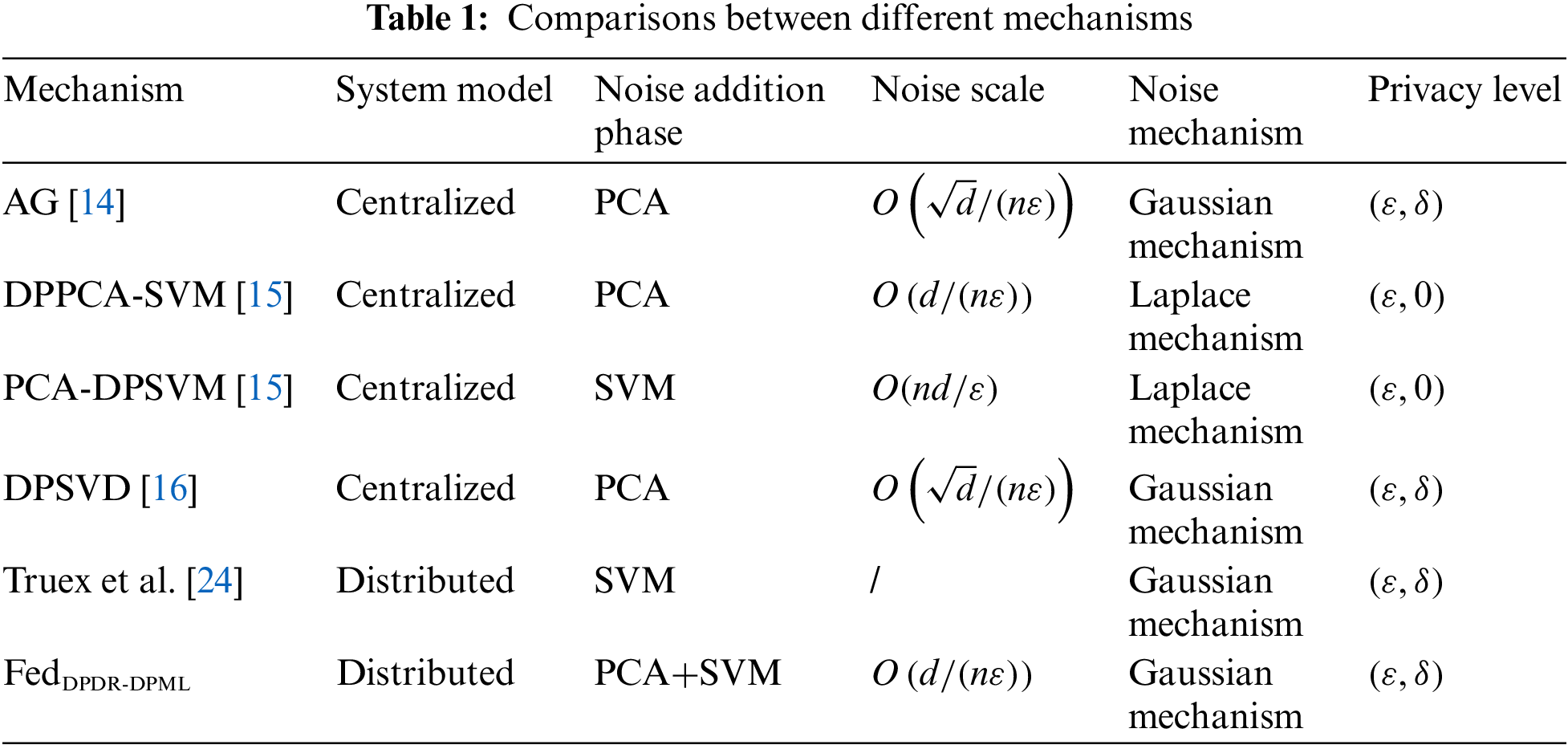
In addition, the noise scales of AG [14] and DPSVD [16] are both O(d/(nε)) since they only perturb the PCA procedure. DPPCA-SVM [15] and PCA-DPSVM [15] adopt the output perturbation in the noise addition phase, thus the noise scale is relatively large. Although our proposed FedDPDR-DPML introduces noise in both PCA and SVM phases, still maintains a small noise scale when compared to DPPCA-SVM and PCA-DPSVM. Besides, FedDPDR-DPML also has a relatively acceptable noise level compared to AG and DPSVD, while providing stronger privacy guarantees than AG and DPSVD.

5  Experiments

5.1 Experiment Setup

Dataset. As we know, image datasets usually have higher dimensions compared to general tabular data. Therefore, we select three image datasets with high dimensions and different characteristics to verify the performance of the mechanism proposed in this paper. MNIST and Fashion-MNIST share the same external characteristics, namely data size and dimension. But Fashion-MNIST is no longer the abstract number symbols, but more concrete clothing images. In contrast, the size of CIFAR-10 is similar to MNIST and Fashion-MNIST in magnitude, but the dimension of CIFAR-10 is much larger than the other two. The details of the three datasets (as shown in Table 2) are as follows.

•   MNIST dataset [37] consists of 60,000 training examples and 10,000 testing examples. Each example is a handwritten gray image with 28×28 pixels, associated with a label from 10 classes (i.e., numbers 0 to 9).

•   Fashion-MNIST [38] is a dataset of Zalando’s article images, which consists of a training set of 60,000 examples and a test set of 10,000 examples. Each example is a 28×28 gray-scale image, associated with a label from 10 classes (e.g., coat, dress, bag, etc.).

•   CIFAR-10 dataset [39] a computer vision dataset for universal object recognition, which consists of 50,000 training examples and 10,000 testing examples. Each example is a 32×32 color image, associated with a label from 10 classes (e.g., bird, cat, deer, etc.).

Competitors. Non-Priv conducts machine learning with dimensionality reduction but without privacy protection. DPML conducts machine learning under differential privacy protection but without dimensionality reduction. DPDR-DPML and FedDPDR-DPML are our proposed methods. As shown in Table 1, the existing mechanisms, such as AG [14], DPPCA-SVM [15], PCA-DPSVM [15], DPSVD [16], and Truex et al.’s method [24] all introduce perturbation to only one phase (i.e., PCA or SVM). In contrast, our proposed FedDPDR-DPML involves noise addition in both the dimensionality reduction phase (i.e., PCA) and training phase (i.e., SVM), which provides strict and strong privacy protection. Therefore, such existing mechanisms theoretically provide insufficient privacy protection, thus not comparable to our paper.

5.2 Experimental Results

This section presents our experimental results, including evaluations of accuracy and running time on SVM. By default, we set the parameters as ε=0.1, δ=10−4, k=20, N=5, n=104, and λ=0.01 in all experiments, where ε1=ε2=0.5ε are used for DP-compliant dimensionality reduction and DP-compliant machine learning, respectively. We will show the accuracy and run time of different methods varying from parameters ε,k,n.

5.2.1 Evaluation of Accuracy

We first validate the performance of dimensionality reduction on SVM classification varying from the target dimension k on three high-dimensional datasets, as shown in Fig. 2. We can see that the SVM classification accuracy of all mechanisms continuously increases with the dimension k increasing from 5 to 100 for all datasets. And, the accuracy does not change much when k is greater than 20. Therefore, we choose the target dimension as k=20 by default in the following experiments. Besides, it can be observed from three datasets that the accuracy of our proposed FedDPDR-DPML and DPDR-DPML is much better than that of DPML and is close to Non-Priv when k is large. This demonstrates that DPDR-DPML can improve accuracy when dealing with high-dimensional data and can ensure superior data utility while providing strong privacy protection. Besides, FedDPDR-DPML has the best accuracy on all datasets. It shows that knowledge aggregation can surely improve the data utility of machine learning.

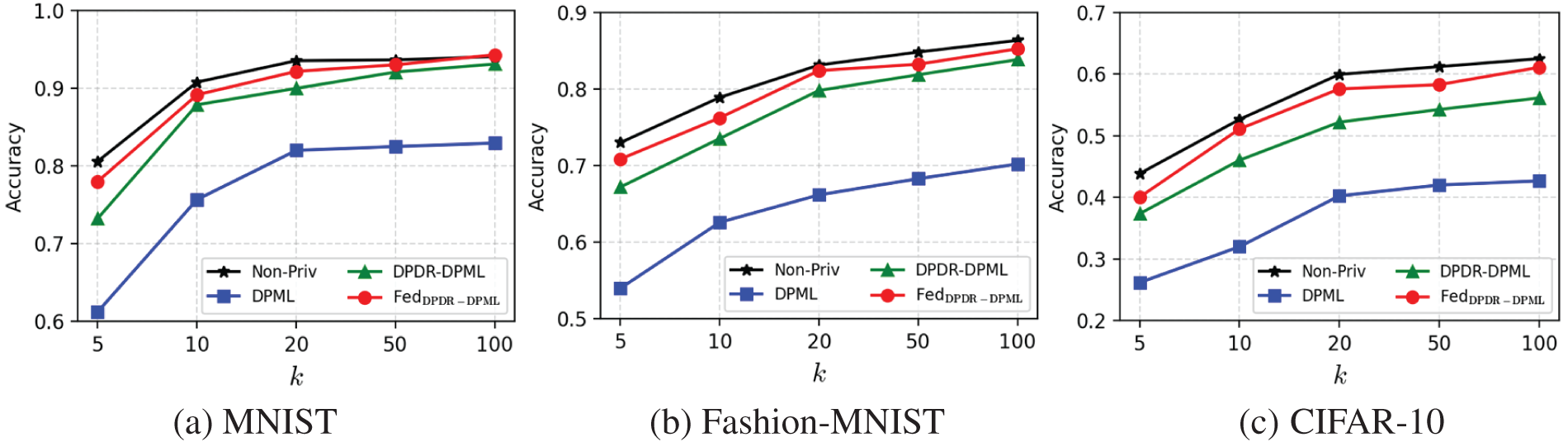
Figure 2: Accuracy vs. target dimension k on SVM classification (ε = 0.1, n = 10,000, N = 5)

As for the CIFAR-10 dataset that has much higher dimensions (i.e., d=3,072), we also utilize the histogram of oriented gradient (HOG) in the experiment to improve accuracy, where the HOG parameters are used as follows: cell size is 4 pixels, number of bins is 9, block size is 2 cell, sliding step is 4 pixels. Nonetheless, the accuracy is not very high compared to MNIST and Fashion-MNIST. Because the SVM used in this paper is a linear model (using hinge loss strategy), and no kernel function is introduced to build a nonlinear model, nor is a convolutional network used. In the follow-up, we will further study the privacy-preserving SVM under the nonlinear model and the convolutional network.

Moreover, Fig. 3 shows the high accuracy of our proposed mechanisms on three datasets with the privacy parameter ε varying from 0.01 to 2.0, where k=20,n=104,δ=10−4. Specifically, we consider ε∈{0.01,0.05,0.1,0.5,1.0,2.0}. It can be seen from the three figures in Fig. 3 that the accuracy of FedDPDR-DPML is much closer to Non-Priv which has no privacy protection. Thus, this demonstrates again that our proposed FedDPDR-DPML can achieve better accuracy in distributed training tasks while keeping strong privacy protection. What’s more, Fig. 3 shows that the accuracy of DPDR-DPML is much superior to DPSVM when applying the same level of privacy protection, which indicates DPDR-DPML holds better data utility while keeping the same privacy guarantees.

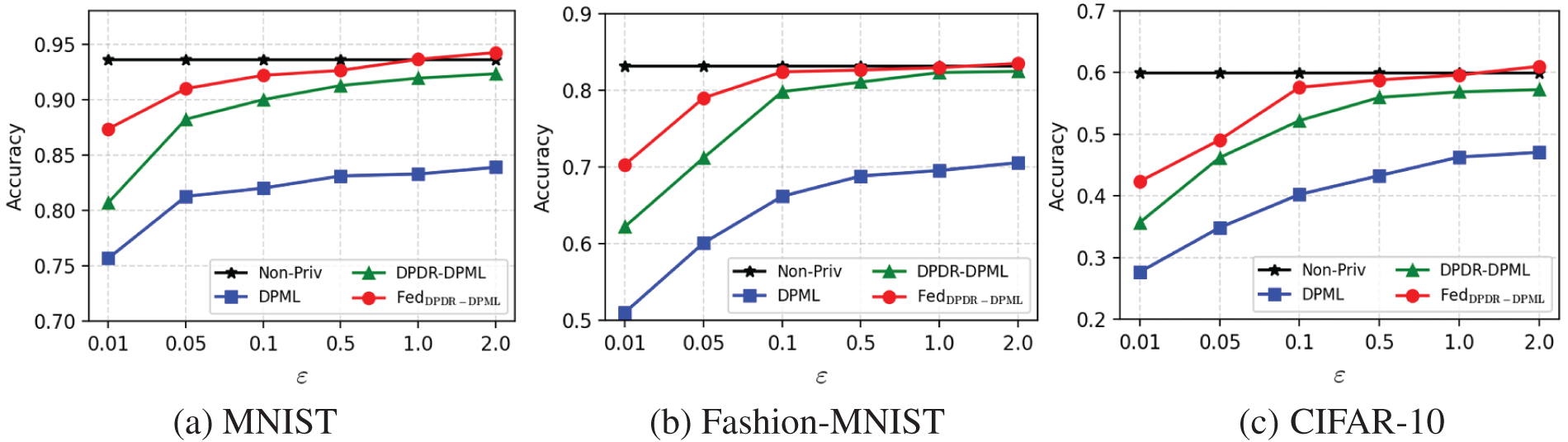
Figure 3: Accuracy vs. privacy parameter ε on SVM classification (k = 20, n = 10,000, N = 5)

Furthermore, Fig. 4 shows the comparisons of the impact of data size n on accuracy, where n is set as n={100,500,1000,5000,10000}. It can be seen from Fig. 4 that the accuracy of the three mechanisms will increase with the increase of data size for three datasets. With different data sizes, our proposed FedDPDR-DPML always outperforms DPML under the same privacy protection level. This is because FedDPDR-DPML involves the knowledge aggregation to learn the global information, thus leading to a better data utility. Besides, we can also observe that DPDR-DPML has a higher accuracy than DPML. This demonstrates that the DP-compliant dimensionality reduction in DPDR-DPML can surely extract the key feature of high-dimensional data, thus leading to a higher accuracy than DPML. This also demonstrates that FedDPDR-DPML can also improve the data utility in practice even when dealing with high-dimensional data.

Figure 4: Accuracy vs. data size n on SVM classification (ε = 0.1, k = 20, N = 5)

We also conduct experiments on uneven datasets to evaluate the performance of FedDPDR-DPML, as shown in Fig. 5. The number of participants is N=5. We used three sets of uneven data in the experiment, where the sizes of the three sets of uneven data are (0.05,0.1,0.5,1.0,2.0)×103, (0.1,0.5,1.0,5.0,10.0)×103, and (0.1,1.0,5.0,8.0,10.0)×103. That is, each set of uneven data contains five different data sizes, corresponding to the uneven data of five participants.

Figure 5: Accuracy vs. uneven data on SVM classification (ε = 0.1, k = 20, N = 5)

As we can see from Fig. 5, our proposed FedDPDR-DPML has a superior performance in dealing with uneven data. FedDPDR-DPML is almost guaranteed to be as accurate as the Non-Priv method, so it is more suitable for scenarios with imbalanced data. This is because FedDPDR-DPML can learn the global information of the training process through knowledge aggregation, thus performing well in handling imbalanced data. Compared to DPML and DPDR-DPML, our proposed FedDPDR-DPML will surely improve the data utility while providing strong privacy guarantees.

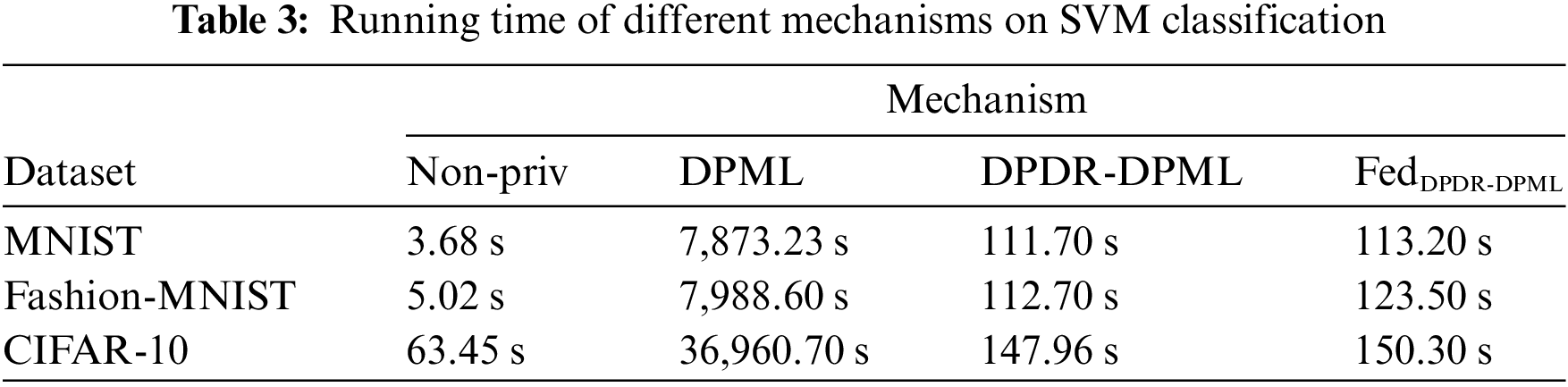
5.2.2 Evaluation of Running Time

We also compared the running time of different mechanisms on SVM, as shown in Table 3. Here, we set the data size as 10,000 and the target dimension as 20. It can be observed that the running time of Non-Priv, DPDR-DPML, and FedDPDR-DPML is much lower than DPML, especially when the dataset (i.e., CIFAR-10) is very large. This proves that privacy-preserving dimensionality reduction can surely improve the efficiency of SVM training while providing privacy protection. Besides, compared with Non-Priv and DPML, our proposed FedDPDR-DPML can maintain relatively excellent performance under the premise of providing strong privacy protection.

6  Conclusion

Support vector machine (SVM) training inevitably faces severe privacy leakage issues when dealing with sensitive or private high-dimensional data. Therefore, this paper proposes a differential privacy-compliant support vector machine algorithm called FedDPDR-DPML. Specifically, considering multi-party joint training with uneven data, FedDPDR-DPML is a distributed framework that incorporates dimensionality reduction and knowledge aggregation to obtain global learning information, which greatly improves the data utility while providing strong privacy guarantees. We conduct extensive experiments on three high-dimensional data with different characteristics. The experimental results show that our proposed algorithm can maintain good data utility while providing strong privacy guarantees.

Furthermore, the privacy paradigm and the framework of FedDPDR-DPML can be easily extended to other machine learning models, such as logistic regression, Bayesian classification, or decision trees. Based on FedDPDR-DPML, we will consider investigating distributed deep learning with differential privacy. Moreover, personalized, dynamic, and efficient privacy-preserving machine learning frameworks require further research in the future.

Acknowledgement: The authors wish to express their appreciation to the reviewers for their helpful suggestions which greatly improved the presentation of this paper.

Funding Statement: This work was supported in part by National Natural Science Foundation of China (Nos. 62102311, 62202377, 62272385), in part by Natural Science Basic Research Program of Shaanxi (Nos. 2022JQ-600, 2022JM-353, 2023-JC-QN-0327), in part by Shaanxi Distinguished Youth Project (No. 2022JC-47), in part by Scientific Research Program Funded by Shaanxi Provincial Education Department (No. 22JK0560), in part by Distinguished Youth Talents of Shaanxi Universities, and in part by Youth Innovation Team of Shaanxi Universities.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: T. Wang, Y. Zhang; validation: J. Liang, S. Wang; analysis and interpretation of results: T. Wang, Y. Zhang, S. Liu; draft manuscript preparation: T. Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The three data used in this study can be found in references [37, 38], and [39], respectively.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Kocon et al., “ChatGPT: Jack of all trades, master of none,” Inf. Fusion, vol. 99, pp. 101861, 2023. doi: 10.1016/j.inffus.2023.101861. [Google Scholar] [CrossRef]

2. T. Brown et al., “Language models are few-shot learners,” in Adv. Neural Inf. Proc. Syst. (NeurIPS), Dec. 2020, pp. 1877–1901. [Google Scholar]

3. N. Wu, F. Farokhi, D. Smith, and M. A. Kaafar, “The value of collaboration in convex machine learning with differential privacy,” in IEEE S&P, San Francisco, CA, USA, May 2020, pp. 304–317. [Google Scholar]

4. M. Al-Rubaie and J. M. Chang, “Privacy-preserving machine learning: Threats and solutions,” IEEE Secur. Privacy, vol. 17, no. 2, pp. 49–58, Mar. 2019. doi: 10.1109/MSEC.2018.2888775. [Google Scholar] [CrossRef]

5. H. C. Tanuwidjaja, R. Choi, S. Baek, and K. Kim, “Privacy-preserving deep learning on machine learning as a service-a comprehensive survey,” IEEE Access, vol. 8, pp. 167425–167447, Sep. 2020. doi: 10.1109/ACCESS.2020.3023084. [Google Scholar] [CrossRef]

6. M. Fredrikson, S. Jha, and T. Ristenpart, “Model inversion attacks that exploit confidence information and basic countermeasures,” in Proc. ACM SIGSAC Conf. on Comput. and Communica. Securi., Denver, USA, Oct. 2015, pp. 1322–1333. [Google Scholar]

7. X. Zhang, C. Chen, Y. Xie, X. Chen, J. Zhang and Y. Xiang, “A survey on privacy inference attacks and defenses in cloud-based deep neural network,” Comput. Stand. Interfaces, vol. 83, pp. 103672, Jan. 2023. doi: 10.1016/j.csi.2022.103672. [Google Scholar] [CrossRef]

8. V. Jakkula, “Tutorial on support vector machine (SVM),” Sch. EECS, Washington State Univ., 2006. [Google Scholar]

9. C. Dwork, “Differential privacy,” in Int. Conf. ICALP, Venice, Italy, Jul. 2006, pp. 1–12. [Google Scholar]

10. C. Dwork and A. Roth, “The algorithmic foundations of differential privacy,” Found. Trends® Theor. Comput. Sci., vol. 9, no. 3–4, pp. 211–407, Aug. 2014. doi: 10.1561/0400000042. [Google Scholar] [CrossRef]

11. Y. Zhang, Z. Hao, and S. Wang, “A differential privacy support vector machine classifier based on dual variable perturbation,” IEEE Access, vol. 7, pp. 98238–98251, Jul. 2019. doi: 10.1109/ACCESS.2019.2929680. [Google Scholar] [CrossRef]

12. F. Farokhi, “Privacy-preserving public release of datasets for support vector machine classification,” IEEE Trans. Big Data, vol. 7, no. 5, pp. 893–899, Jan. 2020. doi: 10.1109/TBDATA.2019.2963391. [Google Scholar] [CrossRef]

13. Y. Chen, Q. Mao, B. Wang, P. Duan, B. Zhang and Z. Hong, “Privacy-preserving multi-class support vector machine model on medical diagnosis,” IEEE J. Biomed. Health Inform., vol. 26, no. 7, pp. 3342–3353, Mar. 2022. doi: 10.1109/JBHI.2022.3157592. [Google Scholar] [PubMed] [CrossRef]

14. C. Dwork, K. Talwar, A. Thakurta, and L. Zhang, “Analyze gauss: Optimal bounds for privacy-preserving principal component analysis,” in Proc. ACM Symp. on Theory of Computi., New York, USA, May 2014, pp. 11–20. [Google Scholar]

15. Y. Huang, G. Yang, Y. Xu, and H. Zhou, “Differential privacy principal component analysis for support vector machines,” Secur. Commun. Netw., vol. 2021, pp. 1–12, Jul. 2021. doi: 10.1155/2021/5542283. [Google Scholar] [CrossRef]

16. Z. Sun, J. Yang, and X. Li, “Differentially private singular value decomposition for training support vector machines,” Comput. Intell. Neurosci., vol. 2022, pp. 1–11, Mar. 2022. doi: 10.1155/2022/2935975. [Google Scholar] [PubMed] [CrossRef]

17. P. Kairouz et al., “Advances and open problems in federated learning,” Found. Trends® Mach. Learn., vol. 14, no. 1–2, pp. 1–210, Jun. 2021. doi: 10.1561/2200000083. [Google Scholar] [CrossRef]

18. Y. Zhang, Y. Wu, T. Li, H. Zhou, and Y. Chen, “Vertical federated learning based on consortium blockchain for data sharing in mobile edge computing,” Comp. Model. Eng., vol. 137, no. 1, pp. 345–361, 2023. doi: 10.32604/cmes.2023.026920. [Google Scholar] [CrossRef]

19. B. McMahan, E. Moore, D. Ramage, S. Hampson, and B. A. Y Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Int. Conf. Artif. Intell. Stat. (AISTATS), Fort Lauderdale, USA, Apr. 2017, pp. 1273–1282. [Google Scholar]

20. H. Yu, S. Yang, and S. Zhu, “Parallel restarted SGD with faster convergence and less communication: Demystifying why model averaging works for deep learning,” in Proc. AAAI Conf. Artif. Intell., Honolulu, Hawaii, USA, Jan. 2019, pp. 5693–5700. [Google Scholar]

21. L. T. Phong and T. T. Phuong, “Privacy-preserving deep learning via weight transmission,” IEEE Trans. Inf. Forens. Secur., vol. 14, no. 11, pp. 3003–3015, Apr. 2019. doi: 10.1109/TIFS.2019.2911169. [Google Scholar] [CrossRef]

22. C. Yu et al., “Distributed learning over unreliable networks,” in Proc. Int. Conf. Mach. Learn. (ICML), Long Beach, California, USA, Jun. 2019, pp. 7202–7212. [Google Scholar]

23. Y. Zhao et al., “Local differential privacy-based federated learning for internet of things,” IEEE Internet Things J., vol. 8, no. 11, pp. 8836–8853, Nov. 2020. doi: 10.1109/JIOT.2020.3037194. [Google Scholar] [CrossRef]

24. S. Truex et al., “A hybrid approach to privacy-preserving federated learning,” in Proc. ACM Workshop Artif. Intell. Secur. (AISec), London, UK, Nov. 2019, pp. 1–11. [Google Scholar]

25. R. Xu, N. Baracaldo, Y. Zhou, A. Anwar, J. Joshi and H. Ludwig, “FedV: Privacy-preserving federated learning over vertically partitioned data,” in Proc. ACM Workshop Artif. Intell. Secur. (AISec), Korea, Nov. 2021, pp. 181–192. [Google Scholar]

26. T. Zhu, D. Ye, W. Wang, W. Zhou, and S. Y. Philip, “More than privacy: Applying differential privacy in key areas of artificial intelligence,” IEEE Trans. Knowl. Data Eng., vol. 34, no. 6, pp. 2824–2843, Aug. 2020. doi: 10.1109/TKDE.2020.3014246. [Google Scholar] [CrossRef]

27. N. Ponomareva et al., “How to DP-fy ML: A practical guide to machine learning with differential privacy,” J. Artif. Intell. Res., vol. 77, pp. 1113–1201, Jul. 2023. doi: 10.1613/jair.1.14649. [Google Scholar] [CrossRef]

28. Z. Ji, Z. C. Lipton, and C. Elkan, “Differential privacy and machine learning: A survey and review,” arXiv preprint arXiv:1412.7584, Dec. 2014. doi: 10.48550/arXiv.1412.7584. [Google Scholar] [CrossRef]

29. D. A. Pisner and D. M. Schnyer, “Support vector machine,” in Machine Learning, San Diego, USA, Academic Press, 2020, pp. 101–121. [Google Scholar]

30. K. Chaudhuri, C. Monteleoni, and A. D. Sarwate, “Differentially private empirical risk minimization,” J. Mach. Learn. Res., vol. 12, no. 3, pp. 1069–1109, Mar. 2011. [Google Scholar] [PubMed]

31. W. Jiang, C. Xie, and Z. Zhang, “Wishart mechanism for differentially private principal components analysis,” in Proc. AAAI Conf. Artif. Intell., Phoenix, Arizona, USA, Feb. 2016, pp. 1730–1736. [Google Scholar]

32. Y. Xu, G. Yang, and S. Bai, “Laplace input and output perturbation for differentially private principal components analysis,” Secur. Commun. Netw., vol. 2019, pp. 1–10, Nov. 2019. doi: 10.1155/2019/9169802. [Google Scholar] [CrossRef]

33. S. Tavara, A. Schliep, and D. Basu, “Federated learning of oligonucleotide drug molecule thermodynamics with differentially private ADMM-based SVM,” in ECML PKDD, Bilbao, Spain, Sep. 2021, pp. 459–467. [Google Scholar]

34. M. Abadi et al., “Deep learning with differential privacy,” in Proc. ACM SIGSAC Conf. on Comput. and Communica. Securi., Vienna, Austria, Oct. 2016, pp. 308–318. [Google Scholar]

35. M. Du, X. Yue, S. S. Chow, T. Wang, C. Huang and H. Sun, “DP-Forward: Fine-tuning and inference on language models with differential privacy in forward pass,” in Proc. ACM SIGSAC Conf. on Comput. and Communica. Securi., Copenhagen, Denmark, Nov. 2023, pp. 2665–2679. [Google Scholar]

36. O. Chapelle, “Training a support vector machine in the primal,” Neural. Comput., vol. 19, no. 5, pp. 1155–1178, May 2007. doi: 10.1162/neco.2007.19.5.1155. [Google Scholar] [PubMed] [CrossRef]

37. Y. LeCun, L. Bottou, Y. Bengio, and P. Haffner, “Gradient-based learning applied to document recognition,” in Proc. IEEE, vol. 86, no. 11, pp. 2278–2324, Nov. 1998. doi: 10.1109/5.726791. [Google Scholar] [CrossRef]

38. H. Xiao, K. Rasul, and R. Vollgraf, “Fashion-MNIST: A novel image dataset for benchmarking machine learning algorithms,” arXiv preprint arXiv:1708.07747, Sep. 2017. doi: 10.48550/arXiv.1708.07747. [Google Scholar] [CrossRef]

39. A. Krizhevsky and G. Hinton, “Learning multiple layers of features from tiny images,” in Technical Report (CIFAR), Toronto, Canada, University of Toronto, 2009, pp. 1–58. [Google Scholar]