RL and AHP-Based Multi-Timescale Multi-Clock Source Time Synchronization for Distribution Power Internet of Things

1  Introduction

Time synchronization (TS) is a key pillar of maintaining the secure and stable functioning of the distribution power Internet of Things (IoT), which enables all devices in the network to keep the same logical clock [1,2]. With the development of new power systems, massive intelligent devices, renewable energy devices, and other distributed devices are integrated to the distribution power IoT [3–6], resulting in an stringent requirement for TS. While distributed IoT devices can operate at the same time by receiving external high-precision time synchronization signals, such as satellite clock sources and ground clock sources [7,8], it is not economically feasible to equip all distributed IoT devices with expensive TS modules [9–11]. Deploying TS power IoT gateways can effectively reduce costs and improve TS accuracy. The power IoT gateway receives TS signals from multiple satellite clock sources and ground clock sources processes them, and performs high-accuracy TS for the distributed IoT devices within its communication range [12–14].

Multi-clock source time synchronization (MTS) has significant advantages compared with single-clock source TS. On the one hand, it ensures TS reliability in case a single clock source fails to function properly [15–17]. On the other hand, a comprehensive calculation method can be used to assign differentiated weight to each clock source, and the power IoT gateway can calculate a TS signal that reduces TS delay jitter and pulse phase difference [18]. However, MTS for the distribution power IoT still faces several challenges.

Firstly, the communication environment between the power IoT gateway and clock sources changes relatively slowly compared to the time synchronization signals. Hence, the multi-clock source selection and the clock source weight calculation are required to optimize at different timescales [19]. Multi-clock source selection requires optimization in the large timescale due to the high communication cost and delay of switching clock sources. In contrast, the pulse phase of the clock source changes rapidly due to factors such as temperature, pressure, and crystal oscillator operation state. It is necessary to optimize the clock source weight calculation in the small timescale [20,21]. Secondly, due to differences in the distance between the clock source and the power IoT gateway, as well as differences in the communication environment, the arrival time of TS signals varies. To ensure TS accuracy, simultaneous signal arrival should be achieved as much as possible to reduce TS delay jitter [22,23]. However, clock sources with low delay jitter may have significant pulse phase differences. Therefore, the minimization of TS delay jitter and pulse phase difference should be jointly considered.

Currently, there are several works exploring MTS for distribution power IoT [24,25]. In [26], Wang et al. proposed a precise point positioning time transfer approach via multi-satellites to minimize TS delays in distribution power IoT. However, this work does not consider the calculation of multi-clock source weight. Reinforcement learning (RL) allows the agent to learn the optimization decisions to maximize the expected cumulative reward by interacting with the environment. Therefore, RL provides a solution to adaptively optimize the TS based on the changing environmental conditions and communication costs. In [27], Destro et al. designed an RL-assisted TS method, using deep Q-learning networks and a limited set of predefined actions to learn the TS strategy and minimize the pulse phase difference between the multi-clock source and local clock source. However, this work neglected the joint optimization of delay jitter and pulse phase difference. In [28], Lu et al. proposed an RL-empowered smart route management mechanism to weigh multi-signals of synchronization, and feedback was provided through RL to eliminate the cumulative error of TS. However, this work did not optimize the multi-clock source selection and clock source weight calculation at different timescales.

The analytic hierarchy process (AHP) is widely leveraged in the functioning of distribution power IoT, which can be applied to solve the problem of MTS [29–31]. The primary concept of AHP involves breaking down a complicated decision problem into a hierarchical series of structures, and then transform them into a series of easy-to-handle comparison problems [32–34]. In cases where there are multiple constraints on the TS scheme, AHP can be used to find the optimal TS scheme by comparing the combined scores of different schemes. In [35], Wang et al. proposed a multi-source decision model using AHP to dynamically determine the priority of a multi-clock source. In [36], Fu et al. used AHP to establish an evaluation model for equipment microenvironment monitoring to achieve simultaneous real-time monitoring of multiple IoT devimultices. However, the AHP-based TS optimization algorithms mentioned above did not consider the fluctuation of pulse phase difference.

To solve the above problems, the RL and AHP-based multi-timescale MTS algorithm is designed. The multi-timescale MTS model for distribution power IoT is first constructed. Then, a minimization problem for the weighted summation of TS delay jitter standard deviation and average pulse phase difference is formulated. Finally, the RL and AHP-based multi-timescale MTS algorithm is proposed to optimize the multi-clock source selection in the large timescale and the clock source weight calculation in the small timescale. The contributions of this paper are elaborated below:

•   Minimization of synchronization delay jitter standard deviation and average pulse phase difference: The optimization goal is constructed as the weighted summation of TS delay jitter standard deviation and average pulse phase difference. It is solved by the proposed RL and AHP-based multi-timescale MTS algorithm. Specifically, the multi-clock source selection is optimized in the large timescale to reduce the synchronization delay jitter standard deviation and average pulse phase difference, and the clock source weight calculation is optimized in the small timescale to further reduce the average pulse phase difference.

•   Large-timescale multi-clock source selection optimization: In the large timescale, the multi-clock source selection problem is constructed as a multi-armed bandit (MAB) model. The proposed algorithm adopts Softmax to ensure the fast convergence while maintaining the diversity of multi-clock selection.

•   Small-timescale clock source weight calculation optimization: In the small timescale, the proposed algorithm employs the lower confidence bound-assisted AHP to solve the clock source weight calculation problem. Considering the fluctuation of pulse phase difference, the fixed value of the clock source score is replaced by a lower confidence bound to increase the evaluation precision for TS performances.

The organization of this work is arranged below. Section 2 introduces the multi-timescale MTS structure for distribution power IoT. Section 3 formulates the problem for improving the weighted summation of TS delay jitter standard deviation and average pulse phase difference. The proposed RL and AHP-based multi-timescale MTS algorithm is developed in Section 4. Section 5 provides the related simulations. Section 6 concludes this paper.

2  System Model

Fig. 1 shows the multi-timescale MTS structure for distribution power IoT, including a clock source layer, a gateway layer, and an IoT device layer. In the clock source layer, there are N clock sources. The set is represented as 𝒞={C1,C2,…,Cn,…,CN}. These clock sources consist of N1 satellite clock sources and N−N1 ground clock sources. The satellite clock source is represented as Cn, 1≤n≤N1, and the ground clock source is represented as Cn, N1+1≤n≤N. In the gateway layer, multiple TS signals collected from the clock sources are firstly analyzed by the power IoT gateway with a local clock source, and M clock sources with valid TS signals are selected. Then, the weighted summation of the selected clock source is calculated by the power IoT gateway to correct the time synchronization signal to achieve high-precision synchronization of the local clock source. In the device layer, the distributed IoT devices in the distribution power IoT are synchronized through the power IoT gateway with the local clock source.

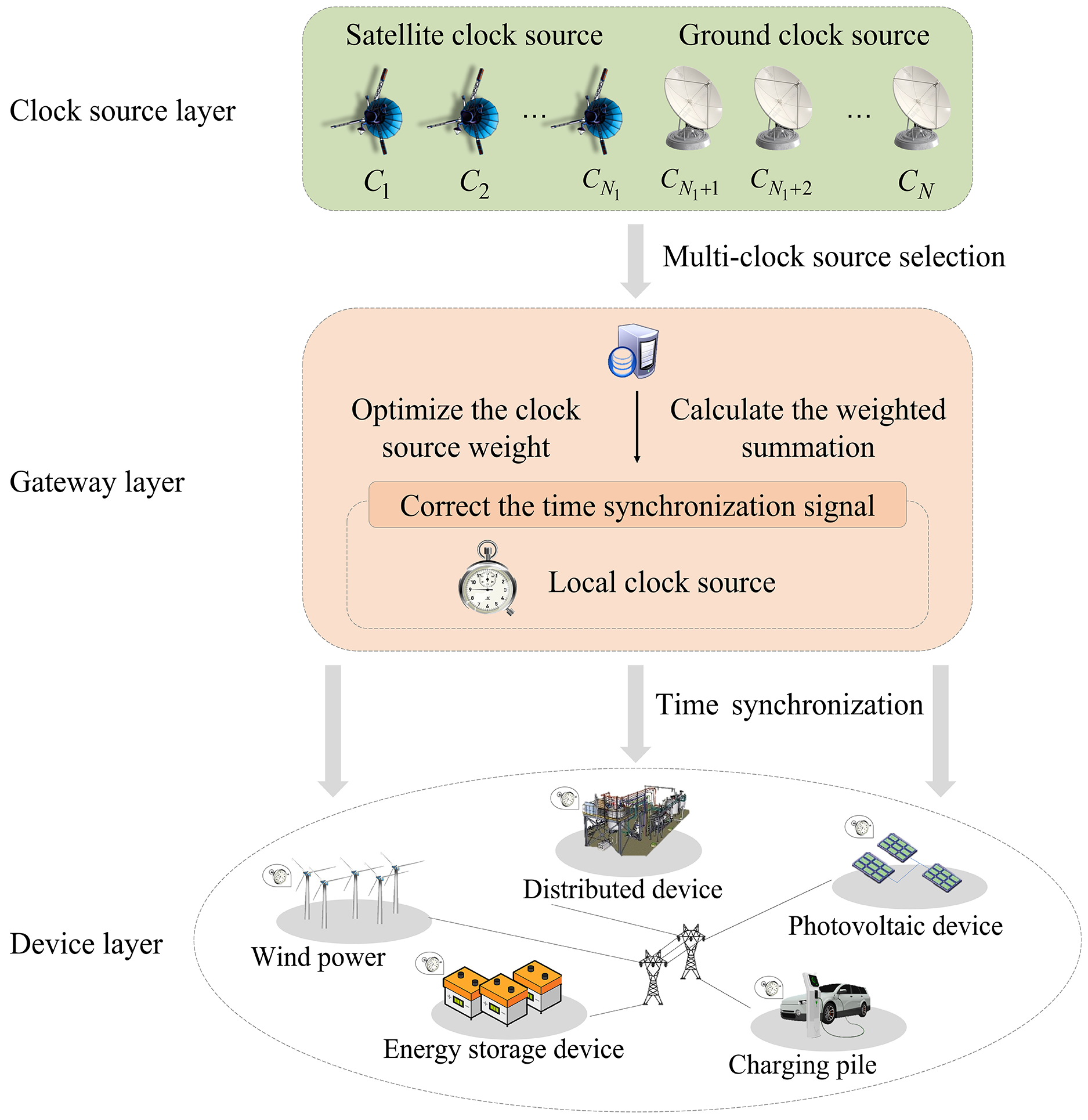
Figure 1: The multi-timescale MTS structure for distribution power IoT

Considering the high communication cost and delay of clock source switching, and the fast pulse phase change of the clock source, we model a multi-timescale process of TS. Considering I optimization periods, expressed as ℐ={1,2,…,i,…,I}. Each period is further divided into T time slots, expressed as 𝒯={1,2,…,t,…,T}. In the large timescale (period), the power IoT gateway selects M clock sources with low TS delay jitter and receives the TS signals. In the small timescale (time slot), the power IoT gateway calculates the weights of the valid selected clock sources based on the pulse phase difference and achieves the TS of the local clock source according to the weighted summation.

Denote the multi-clock source selection decision as xn(i), where xn(i)=1 represents the power IoT gateway selects the clock source Cn in the period i, and xn(i)=0 otherwise. In addition, considering that the power IoT gateway can only select M clock sources in the period i, the clock source selection decision must meet the constraint ∑n=1Nxn(i)=M. The TS delay jitter model and pulse phase difference model are introduced as follows.

2.1 Time Synchronization Delay Jitter Model

When clock source Cn sends TS signal to the gateway in the slot t of the period i, the transmission rate is given by

Rn(i,t)=Bnlog2⁡(1+Pnhn(i,t)σn2)(1)

Here, Bn represents the bandwidth of clock source Cn, Pn represents Cn’s transmission power, hn(i,t) represents the transmission gain between clock source Cn and power IoT gateway, and σn2 represents the Gaussian noise power.

Define the size of synchronization packet sent by Cn as Un(i,t). The TS delay from Cn to the power IoT gateway is given by

Dn(i,t)=Un(i,t)Rn(i,t)(2)

The range of TS delays of M selected clock sources is denoted as the TS delay jitter, i.e.,

ΔD(i,t)=max{xn(i)Dn(i,t),∀Cn∈𝒞}−min{xn(i)Dn(i,t),∀Cn∈𝒞}(3)

where max{xn(i)Dn(i,t),∀Cn∈𝒞} is the maximum TS delay, and min{xn(i)Dn(i,t),∀Cn∈𝒞} is the minimum TS delay.

The degree of TS delay jitter in the period i is measured by the standard deviation for all time slots within the period, which is expressed as

SD(i)=1T∑t=1T[ED(i)−ΔD(i,t)]2(4)

where ED(i) is the average TS delay jitter in the period i, i.e.,

ED(i)=1T∑t=1TΔD(i,t)(5)

A greater value of SD(i) reflects a larger fluctuation of TS delay. Therefore, SD(i) should be minimized through multi-clock source selection optimization.

2.2 Pulse Phase Difference Model

Define the pulse phase difference as the difference between Cn and the local clock source of power IoT gateway in the slot t of the period i, which is given by

Δpn(i,t)=τn(i,t)−τ0(i,t)(6)

where τn(i,t) and τ0(i,t) are the timestamps of the clock source Cn and the local clock source at the beginning of the slot t of the period i, respectively.

Define the weighted summation of the pulse phase differences of the selected clock sources as

Δp(i,t)=∑n=1Nxn(i)ωn(i,t)Δpn(i,t)(7)

where ωn(i,t) is the weight for the clock source Cn in the slot t of the period i. ωn(i,t) meets the constraint ∑n=1Nxn(i)ωn(i,t)=1.

The average pulse phase difference in the period i is expressed as

Ep(i)=1T∑t=1T|Δp(i,t)|(8)

A greater value of Ep(i) represents a larger average pulse phase difference and lower TS accuracy. Therefore, Ep(i) should be minimized through clock source weight calculation optimization.

3  Problem Formulation

Based on the above system model, we aim to improve the weighted summation of TS delay jitter standard deviation and average pulse phase difference by jointly optimizing the multi-clock source selection in the large timescale and the clock source weight calculation in the small timescale. The problem is modeled as

min{xn(i)},{ωn(i,t)}∑i=1I[SD(i)+VEp(i)]s.t.c1:xn(i)∈{0,1},∀Cn∈𝒞,∀i∈Ic2:∑n=1Nxn(i)=M,∀i∈Ic3:∑n=1Nxn(i)ωn(i,t)=1,∀i∈I,∀t∈T(9)

Here, V is the weight of the average pulse phase difference. c1 and c2 represent the constraints of M selected clock sources. c3 represents the constraint of clock source weight.

4  RL and AHP-Based Multi-Timescale MTS Algorithm

In this section, the RL and AHP-based multi-timescale MTS algorithm is designed to address the joint optimization problem of the multi-clock source selection in the large timescale and the clock source weight calculation in the small timescale, which is shown in Algorithm 1. Specifically, the proposed algorithm employs Softmax to address the large-timescale multi-clock source selection problem, and lower confidence bound-assisted AHP to address the small-timescale clock source weight calculation problem. Among them, the execution of the small-timescale lower confidence bound-assisted AHP requires multi-clock source selection result on the large timescale, and the weight calculation result of the multi-clock source on a small timescale will affect the reward of Softmax on a large timescale.

4.1 Large-Timescale Multi-Clock Source Selection Optimization Based on Softmax

The proposed optimization problem is non-convex and hard to be addressed by traditional convex optimization methods. MAB provides a powerful methodology to solve this kind of problem in an online fashion. In the MAB problem, the agent needs to make a decision among multiple choices, each of which corresponds to an “arm”. It can help us make optimal choices in large time scales to maximize the cumulative rewards. Q1-3: Therefore the multi-clock source selection problem is constructed as an MAB problem in the large timescale [37,38]. Softmax is adopted to ensure fast convergence while maintaining the diversity of multi-clock source selection. Compared with ϵ-greedy, Softmax not only guarantees fast convergence to the arm with high reward through the Boltzmann distribution but also preserves the diversity of arm selection [39,40]. According to MAB, the main elements are defined as follows.

•   Player: Denote the player as the power IoT gateway in the distribution network.

•   Arm: Denote the arm as the combination of M clock sources selected by the power IoT gateway from the total of N clock sources, i.e.,

K=N!M!(N−M)!(10)

Define the k-th clock source combination as Ak⊂𝒞, k=1,2,⋯,K

•   Action: Denote the action as the clock source combination selection decision, which is denoted as yk(i)∈{0,1}. When the power IoT gateway selects clock source combination Ak in the period i, set yk(i)=1, and set yk(i)=0 otherwise. The relationship between xn(i) and yk(i) is given by

xn(i)={1,yk(i)=1 and Cn∈Ak0,otherwise(11)

•   Reward: Denote the reward for selecting action yk(i) as the negative of the weighted summation of TS delay jitter standard deviation and average pulse phase difference, which is given by

rk(i)=−(SD(i)+VEp(i))(12)

The implementation process of large-timescale multi-clock source selection optimization contains three phases below.

Phase 1: Initialization

1. Initialize the temperature coefficient as λ>0. A larger value of λ represents that the arm with the higher average reward will be selected. When λ approaches 0, the arm with the lower average reward will be selected, and the power IoT gateway tends to explore. When λ approaches to positive infinity, and the arm with the higher average reward is selected, the power IoT gateway tends to exploit.

2. Define the times that the power IoT gateway selects Ak as Lk(i), and the corresponding average reward as r¯k(i). Initialize Lk(i)=0 and r¯k(i)=0, ∀Ak⊂𝒞.

3. Set the action yk(i)=0, ∀Ak∈𝒞.

Phase 2: Multi-clock source selection

1. According to the Boltzmann distribution, the probability of selecting Ak is estimated as

qk(i)=exp⁡[r¯k(i)λ]∑v=1Kexp⁡[r¯v(i)λ](13)

2. Calculate the cumulative distribution function as

Qk(i)=∑v=1kqv(i)(14)

3. Generate a random value q0∈[0,1]. If Qk−1(i)≤q0<Qk(i), the power IoT gateway selects Ak and sets yk(i)=1. Specially, if q0<Q1(i), the power IoT gateway selects A1 and sets y1(i)=1.

Phase 3: Large-timescale information updating

1. Perform the action yk(i), and get the reward rk(i) based on (12).

2. Update Lk(i) and r¯k(i) as

Lk(i)=Lk(i−1)+yk(i)(15)

r¯k(i)=r¯k(i−1)+yk(i)rk(i)−r¯k(i−1)Lk(i)(16)

4.2 Small-Timescale Clock Source Weight Calculation Optimization Based on Lower Confidence Bound-Assisted AHP

In the small timescale, the clock source weight calculation problem is solved by the lower confidence bound-assisted AHP. Traditional AHP uses the fixed clock source score to measure and quantify the empirical judgment, and a great value of clock source score represents large importance. However, due to the fluctuation of pulse phase difference, traditional AHP cannot achieve accurate evaluation for TS performances. Therefore, the lower confidence bound-assisted AHP is proposed in this section to address the above problem. By replacing the fixed clock source score with a lower confidence bound according to the average clock source weight and the number of times the clock source has been selected for TS, it can improve the evaluation accuracy for TS performances, optimize the clock source weight calculation, and reduce the pulse phase difference.

The hierarchical model of lower confidence bound-assisted AHP is shown in Fig. 2, which is described as follows:

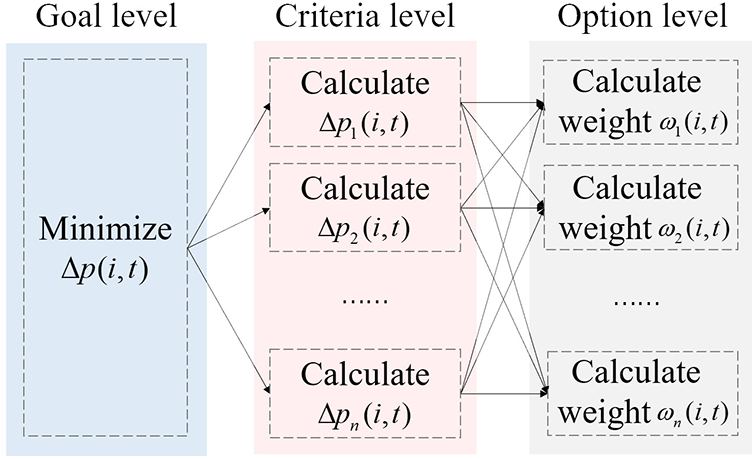
Figure 2: The hierarchical model of lower confidence bound-assisted AHP

•   Goal level: The goal is to improve the weighted summation of the pulse phase differences, which is denoted as Δp(i,t) and calculated by (7).

•   Criteria level: The optimization criteria is the pulse phase difference, which is denoted as Δpn(i,t).

•   Option level: The optimization option is the clock source weight, which is defined as ωn(i,t).

The implementation process of small-timescale clock source weight calculation optimization contains five phases, which are described as follows.

Phase 1: Initialization

1. Define the clock source score as ϕn(i,t) to measure the TS performance of Cn, and initialize ϕn(i,t)=0, ∀Cn∈𝒞.

2. Define the number of times that Cn participates in MTS up to the slot t of the period i as Hn(i,t), and define the corresponding average pulse phase difference as Δp¯n(i,t). Initialize Hn(i,t)=0, and Δp¯n(i,t)=0, ∀Cn∈𝒞.

3. Set ωn(i,t)=0, ∀Cn∈𝒞.

Phase 2: Validity check of the selected clock sources

1. Check the validity of the selected clock sources, which may be unavailable due to packet loss or abnormalities in the TS signal. Define the validity indicator variable as zn(i,t), where zn(i,t)=1 represents the selected clock source Cn is valid, and zn(i,t)=0 otherwise.

2. Calculate the number of valid selected clock sources, i.e.,

J(i,t)=∑n=1Nxn(i)zn(i,t)(17)

If there exists a valid selected clock source, i.e., J(i,t)>0, define the set of valid selected clock sources as 𝒞v(i,t), and perform the following process. Otherwise, stop the optimization process in the current slot and execute the validity check again in the next slot.

Phase 3: Judgment matrix construction

1. Calculate the pulse phase difference Δpn(i,t) based on (6) for the valid selected clock source Cn∈𝒞v(i,t).

2. Calculate the pulse phase score of the valid selected clock source Cn as

sn(i,t)=exp⁡(ϕn(i,t))|Δpn(i,t)|(18)

3. Construct the judgment matrix G(i,t)=(gnn ′(i,t))N×N, whose element gnn ′(i,t) is given by

gnn ′(i,t)={sn(i,t)sn ′(i,t),if Cn,Cn ′∈𝒞v(i,t)1,otherwise(19)

Here, Cn ′ is the n ′-th clock source in 𝒞v(i,t).

Phase 4: Weight calculation

1. Determine the geometric average for each element in the matrix G(i,t)’s rows as

ω^n(i,t)={[∏n ′=1Ngnn ′(i,t)]1J(i,t),if Cn∈𝒞v(i,t)0,otherwise(20)

2. Normalize ω^j(i,t), and get the weight of the valid selected clock source, i.e.,

ωn(i,t)=ω^n(i,t)∑n ′=1Nω^n ′(i,t)(21)

3. According to the optimized clock source weight ωn(i,t), calculate the weighted summation of the pulse phase differences based on (7), and realize the TS.

Phase 5: Small-timescale information updating

1. When 1≤t<T, update Hn(i,t) and Δp¯n(i,t) as

Hn(i,t+1)=∑u=1i−1∑v=1Txn(u)zn(u,v)+∑v=1txn(i)zn(i,v)(22)

Δp¯n(i,t+1)=1Hn(i,t+1)[∑u=1i−1∑v=1Txn(u)zn(u,v)|pn(u,v)|+∑v=1txn(i)zn(i,v)|pn(i,v)|](23)

When t=T, update Hn(i,t) and Δp¯n(i,t) as

Hn(i+1,1)=∑u=1i∑v=1Txn(u)zn(u,v)(24)

Δp¯n(i+1,1)=1Hn(i+1,1)∑u=1i∑v=1Txn(u)zn(u,v)|pn(u,v)|(25)

2. When 1≤t<T, update ϕn(i,t) as the lower confidence bound of the average pulse phase difference, which is given by

ϕn(i,t+1)=−Δp¯n(i,t+1)−θln⁡((i−1)T+t+1)Hn(i,t+1)(26)

When t=T, update ϕn(i,t) as

ϕn(i+1,1)=−Δp¯n(i+1,1)−θln⁡(iT+1)Hn(i+1,1)(27)

where θ is an adjustment coefficient.

5  Simulation Result

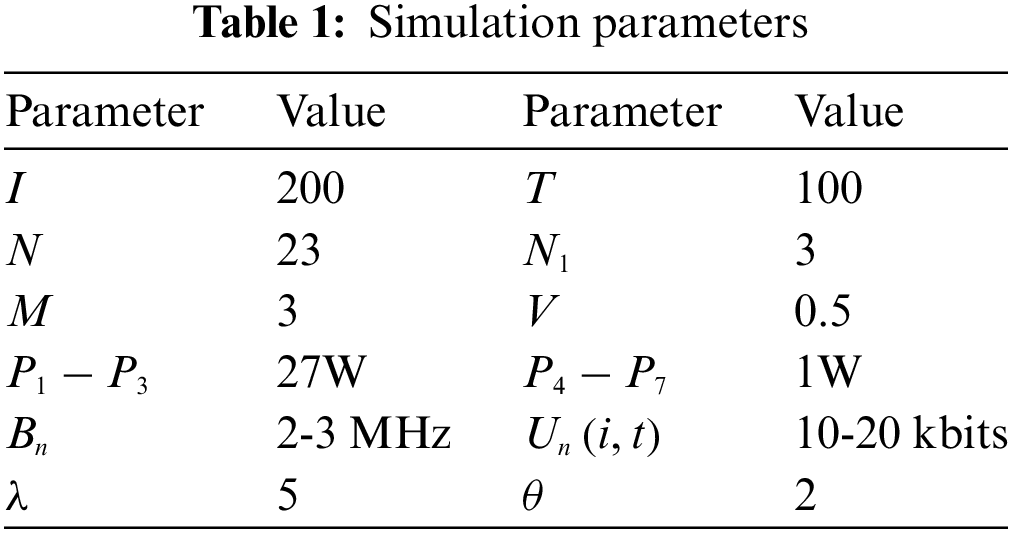
The TS scenario with a multi-clock source for distribution power IoT is considered for simulations, including three satellite clock sources and four ground clock sources. The power IoT gateway selects M=3 clock sources at each period. The related parameters [41,42] are introduced in Table 1.

We set two algorithms for comparison. The first one is the multiplex error compensation-assisted multi-clock source adaptive TS algorithm (MECTS) [43], which minimizes the pulse phase difference by analyzing the quality and validity of TS signals. MECTS sets the dynamic priority for multi-clock sources and corrects the TS signal with the maximum priority according to the quantization error of all valid clock sources. The second one is the RL-based multi-timescale MTS algorithm (RLMTS), which minimizes the TS delay and the pulse phase difference by optimizing the clock source selection based on RL in the large timescale and calculating the weighted summation of pulse phase difference according to the preset priority in the small timescale.

Fig. 3 demonstrates the weighted summation of TS delay jitter standard deviation and average pulse phase difference vs. period. Compared to MECTS and RLMTS, the proposed algorithm reduces the weighted summation by 54.26% and 35.71%. The proposed algorithm effectively reduces the weighted summation through the joint optimization of the multi-clock source selection in the large timescale and the clock source weight calculation in the small timescale. MECTS only minimizes the pulse phase difference by multiplexing error compensation, but cannot reduce the TS delay jitter. RLMTS minimizes weighted summation of TS delay and pulse phase difference based on RL and preset priority, but cannot reduce the TS delay jitter.

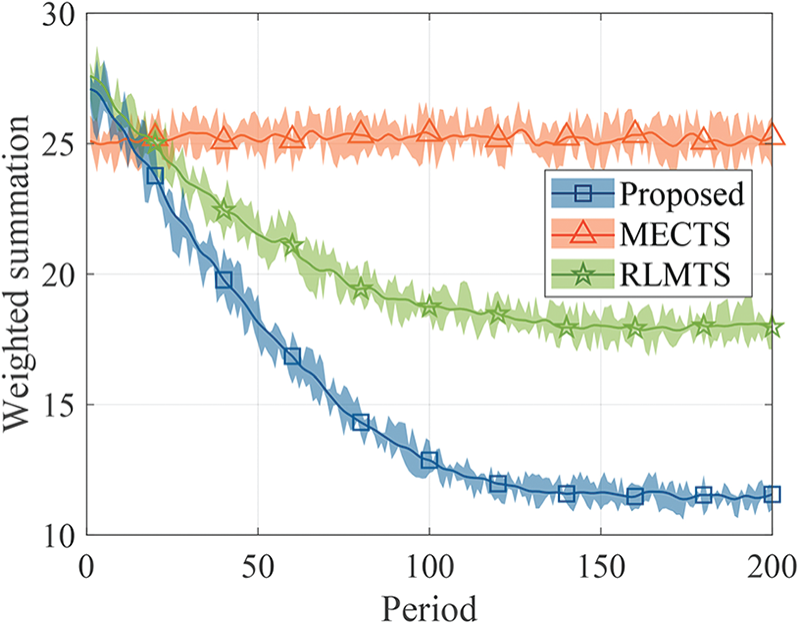
Figure 3: Weighted summation of TS delay jitter standard deviation and average pulse phase difference vs. period

Fig. 4 shows the TS delay jitter standard deviation and average pulse phase difference vs. V. With V increases from 0.1 to 1.1, the TS delay jitter standard deviation increases by 60.50%, and the average pulse phase difference decreases by 16.23%. The proposed algorithm is more biased towards optimizing the average pulse phase difference rather than the TS delay jitter standard deviation. By dynamically adjusting V, the proposed algorithm achieves the balance between TS delay jitter and average pulse phase difference to meet the differentiated TS requirements of distributed IoT devices.

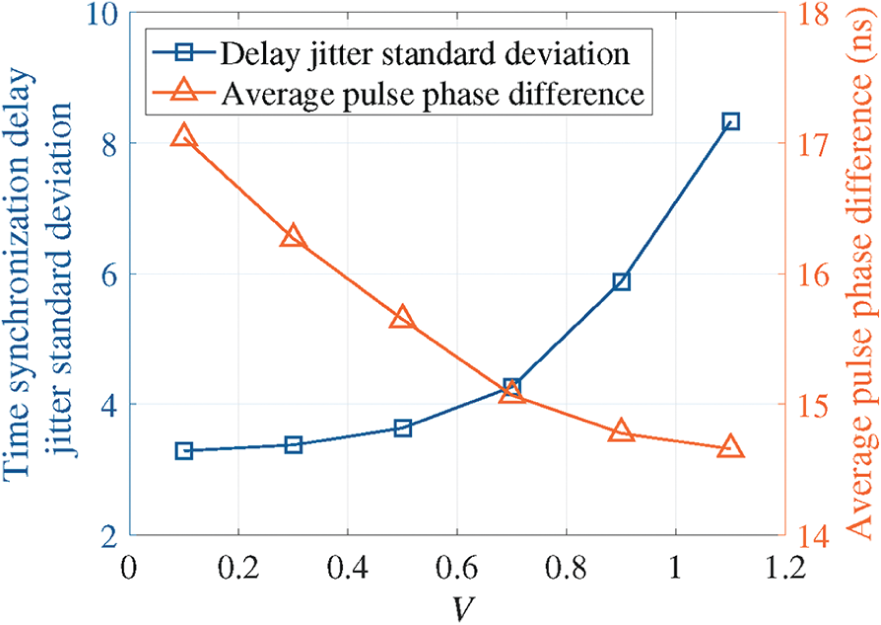
Figure 4: TS delay jitter standard deviation and average pulse phase difference vs. V

Figs. 5 and 6 show the TS delay jitter standard deviation and average pulse phase difference vs. period, respectively. Compared to MECTS and RLMTS, the proposed algorithm outperforms the standard deviation by 74.21% and 45.89% and respectively reduces the average pulse phase difference by 27.57% and 29.37%. In the large timescale, the proposed algorithm optimizes the multi-clock source selection based on Softmax, which not only guarantees fast convergence but also maintains the diversity for multi-clock source selection. The proposed algorithm can learn and find the multi-clock source selection with smaller TS delay jitter and pulse phase difference. In the small timescale, the proposed algorithm realizes the clock source weight calculation optimization based on lower confidence bound-assisted AHP. Replacing the fixed clock source score with a lower confidence bound according to the average clock source weight and the number of times the clock source participated in TS, improves the evaluation accuracy for TS performances. For periods less than 50 in Fig. 6, MECTS minimizes the pulse phase difference by dynamically adjusting the priority, so the pulse phase difference of MECTS is smaller. But MECTS cannot learn the multi-clock source selection with smaller synchronization delay jitter and pulse phase difference. RLMTS learns the multi-clock source selection to minimize synchronization delay and pulse phase difference, but cannot further reduce the pulse phase difference because the pulse phase difference is calculated based on the preset priority.

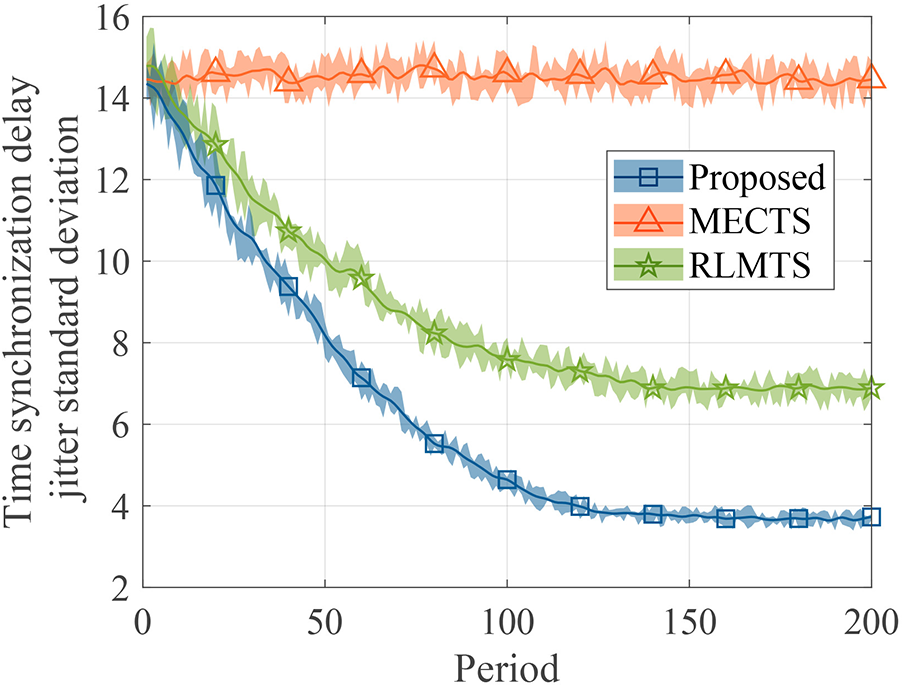
Figure 5: TS delay jitter standard deviation vs. period

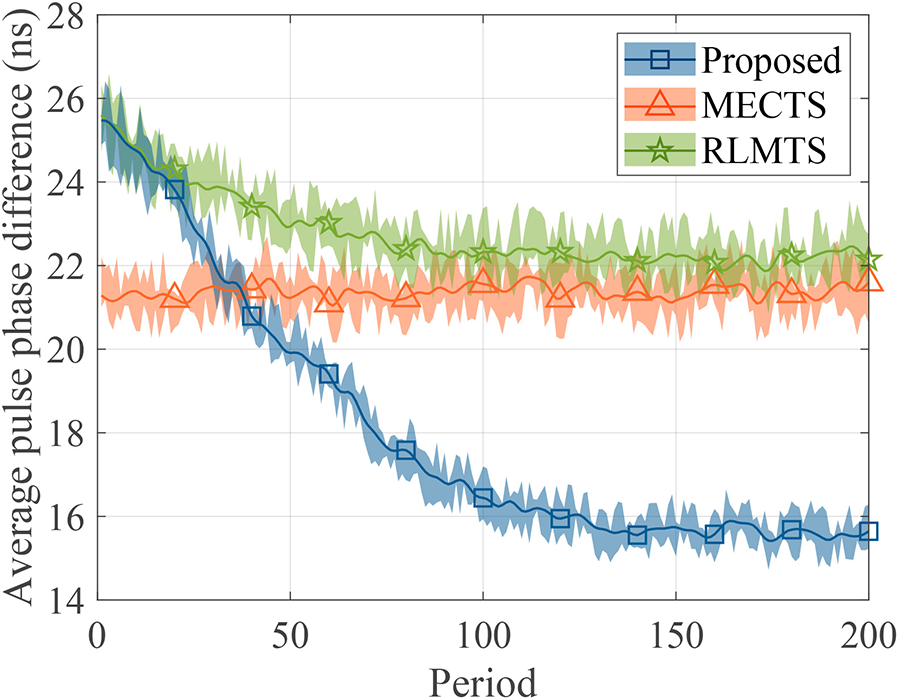
Figure 6: Average pulse phase difference vs. period

Fig. 7 shows the probability distribution and cumulative probability distribution of TS delay jitter for the proposed algorithm, MECTS, and RLMTS, respectively. The black solid line represents the cumulative probability distribution function curve. For the proposed algorithm, most of the time synchronous delay jitter, e.g., 80%, is less than 11.26 ms, while that of MECTS and RLMTS are 22.87 and 13.37 ms, respectively. Compared to MECTS and RLMTS, the proposed improves the TS delay jitter standard deviation for all I×T time slots by 42.52% and 11.44%. Through learning and optimizing the multi-clock source selection and improves its performance effectively, the proposed algorithm minimizes the TS delay jitter standard deviation. MECTS and RLMTS do not consider the optimization of TS delay jitter standard deviation, resulting in a large distribution range.

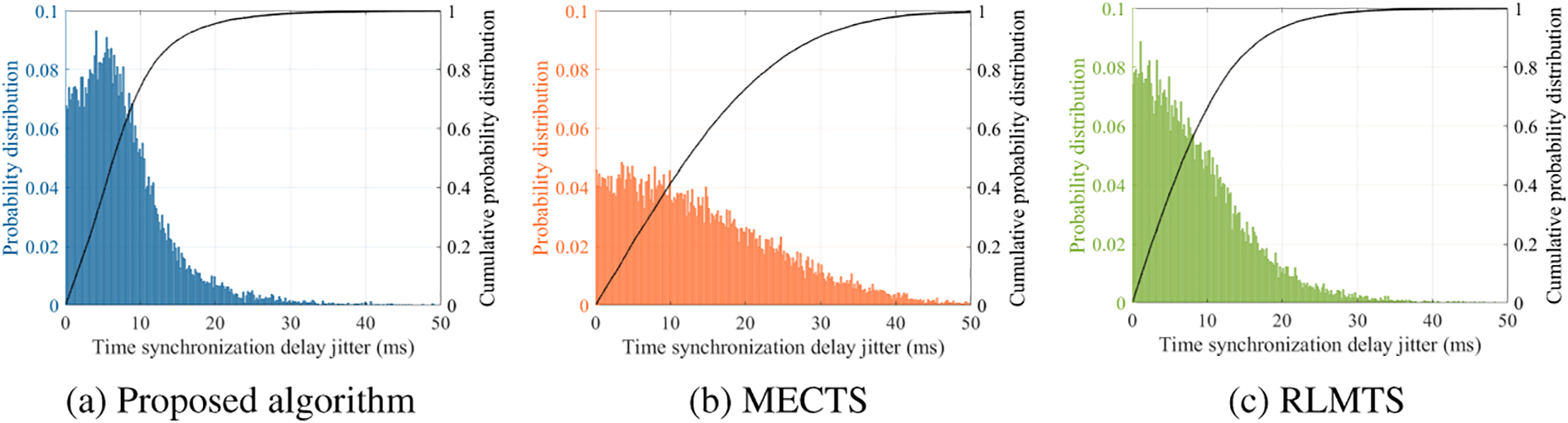
Figure 7: Probability distribution and cumulative probability distribution of pulse phase difference for the (a) Proposed algorithm, (b) MECTS, and (c) RLMTS

Fig. 8 shows the probability distribution and cumulative probability distribution of pulse phase difference for the proposed algorithm, MECTS, and RLMTS, respectively. For the proposed algorithm, most of the pulse phase difference, e.g., 80%, is less than 21.67 ns, while that of MECTS and RLMTS are 28.93 and 32.99 ns, respectively. Compared to MECTS and RLMTS, the proposed reduces the average pulse phase difference for all I×T time slots by 15.56% and 21.64%, respectively. The proposed algorithm minimizes the average pulse phase difference by learning the multi-clock source selection in the large timescale and optimizing the clock source weight calculation in the small timescale. MECTS cannot optimize the average pulse phase difference by learning, while RLMTS only calculates pulse phase differences based on the preset priority.

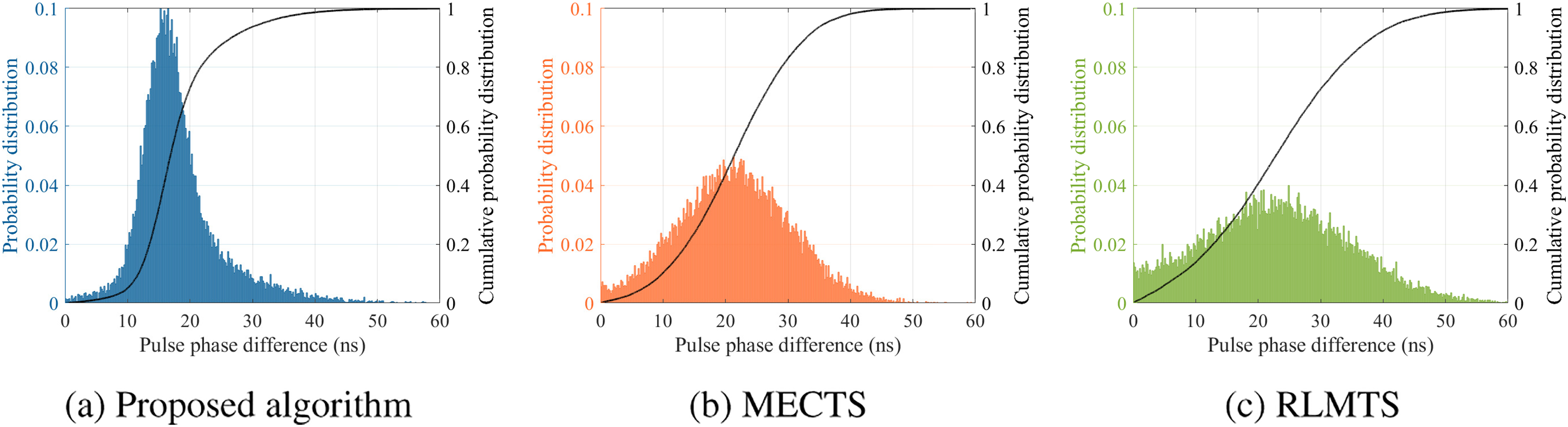
Figure 8: Probability distribution and cumulative probability distribution of pulse phase difference for the (a) Proposed algorithm, (b) MECTS, and (c) RLMTS

6  Conclusion

This work aims to solve a multi-timescale MTS problem for distribution power IoT. The RL and AHP-based multi-timescale MTS algorithm is designed to improved the weighted summation of TS delay jitter standard deviation and average pulse phase difference by the joint optimization of the multi-clock source selection in the large timescale and the clock source weight calculation in the small timescale. Compared to MECTS and RLMTS, the proposed algorithm improves the weighted summation by 54.26% and 35.71%. Future works will further focus on the high-precision TS problem between power IoT gateway and massive distributed IoT devices using power line communication.

Acknowledgement: The authors would like to express their gratitude to the Science and Technology Project of China Southern Power Grid Company Limited under Grant Number 036000KK52200058 (GDKJXM20202001) for supporting this study.

Funding Statement: This work was supported by Science and Technology Project of China Southern Power Grid Company Limited under Grant Number 036000KK52200058 (GDKJXM20202001).

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Jiangang Lu, Ruifeng Zhao, Zhiwen Yu; data collection: Jiangang Lu, Ruifeng Zhao, Zhiwen Yu, Yue Dai, Kaiwen Zeng; analysis and interpretation of results: Jiangang Lu, Ruifeng Zhao; draft manuscript preparation: Jiangang Lu, Yue Dai. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest.

References

1. Y. Zhang, R. Zhang, R. Wang, and H. Zhang, “The real-time framework of the push-to-talk (PTT) synchronization scheme for distributed SAR,” IEEE Geosci. Remote Sens. Lett., vol. 19, no. 1, pp. 1–5, 2022. doi: 10.1109/LGRS.2022.3173727. [Google Scholar] [CrossRef]

2. Z. Zhou et al., “DRL-assisted topology identification and time synchronization for PIoT-empowered distributed renewable resource dispatch,” IEEE Internet Things Mag., vol. 5, no. 2, pp. 13–19, 2022. doi: 10.1109/IOTM.006.2200032. [Google Scholar] [CrossRef]

3. J. Zuo, Y. Lu, H. Gao, R. Cao, Z. Guo and J. Feng, “Comprehensive information security evaluation model based on multi-level decomposition feedback for IoT,” Comput. Mater. Contin., vol. 65, no. 1, pp. 683–704, 2020. doi: 10.32604/cmc.2020.010793. [Google Scholar] [CrossRef]

4. F. Huang, Z. Liu, T. Wang, H. Zhang, and T. Yip, “The optimization study about fault self-healing restoration of power distribution network based on multi-agent technology,” Comput. Mater. Contin., vol. 65, no. 1, pp. 865–878, 2020. doi: 10.32604/cmc.2020.010724. [Google Scholar] [CrossRef]

5. M. Tariq, F. Naeem, M. Ali, and H. V. Poor, “Vulnerability assessment of 6G enabled smart grid cyber-physical systems,” IEEE Internet Things J., vol. 8, no. 7, pp. 5468–5475, 2021. doi: 10.1109/JIOT.2020.3042090. [Google Scholar] [CrossRef]

6. H. Liao et al., “Ultra-low AoI digital twin-assisted resource allocation for multi-mode power IoT in distribution grid energy management,” IEEE J. Sel. Areas Commun., vol. 41, no. 10, pp. 3122–3132, 2023. doi: 10.1109/JSAC.2023.3310101. [Google Scholar] [CrossRef]

7. R. Zhao, J. Lu, W. Guo, W. Zheng, and S. Li, “BP-LMS-based BDS-3 power system positioning method,” Global Energy Interconnect, vol. 5, no. 6, pp. 666–674, 2022. doi: 10.1016/j.gloei.2022.12.008. [Google Scholar] [CrossRef]

8. G. Zou, Y. Huang, W. Chen, L. Wu, and S. Wen, “Life-cycle cost model and evaluation system for power grid assets based on fuzzy membership degree,” Global Energy Interconnect, vol. 4, no. 4, pp. 434–440, 2021. doi: 10.1016/j.gloei.2021.09.006. [Google Scholar] [CrossRef]

9. H. Liao et al., “Adaptive learning-based delay-sensitive and secure edge-end collaboration for multi-mode low-carbon power IoT,” China Commun., vol. 19, no. 7, pp. 324–336, 2022. doi: 10.23919/JCC.2022.07.024. [Google Scholar] [CrossRef]

10. W. Liu, H. Yuan, and J. Ge, “Local-area nanosecond-accuracy time synchronization based on GPS L1 observations,” IET Radar Sonar Navig., vol. 13, no. 5, pp. 824–829, 2019. doi: 10.1049/iet-rsn.2018.5283. [Google Scholar] [CrossRef]

11. M. Tariq, M. Adnan, G. Srivastava, and H. V. Poor, “Instability detection and prevention in smart grids under asymmetric faults,” IEEE Trans. Ind. Appl., vol. 56, no. 4, pp. 4510–4520, 2020. doi: 10.1109/TIA.2020.2964594. [Google Scholar] [CrossRef]

12. T. Jia, Y. Ju, and J. Gu, “A dynamic timing enhanced DNN accelerator with compute-adaptive elastic clock chain technique,” IEEE J. Solid-State Circuits, vol. 56, no. 1, pp. 55–65, 2022. doi: 10.1109/JSSC.2020.3027953. [Google Scholar] [CrossRef]

13. X. Wang, M. Umehira, M. Akimoto, B. Han, and H. Zhou, “Green spectrum sharing framework in B5G era by exploiting crowdsensing,” IEEE Trans. Green Commun. Netw., vol. 7, no. 2, pp. 916–927, 2023. doi: 10.1109/TGCN.2022.3186282. [Google Scholar] [CrossRef]

14. M. Tariq and H. V. Poor, “Electricity theft detection and localization in microgrids,” IEEE Trans. Smart Grid, vol. 9, pp. 1920–1929, May. 2018. doi: 10.1109/TSG.2016.2602660. [Google Scholar] [CrossRef]

15. H. Zhou, X. Wang, M. Umehira, B. Han, and H. Zhou, “Energy efficient beamforming for small cell systems: A distributed learning and multicell coordination approach,” ACM Trans. Sen. Netw., 2023. doi: 10.1145/3617997. [Google Scholar] [CrossRef]

16. J. L. Gutiérrez-Rivas, F. Torres-González, E. Ros, and J. Díaz, “Enhancing white rabbit synchronization stability and scalability using P2P transparent and hybrid clocks,” IEEE Trans. Ind. Inf., vol. 17, no. 11, pp. 7316–7324, 2021. doi: 10.1109/TII.2021.3054365. [Google Scholar] [CrossRef]

17. V. G. Srivatsa, A. P. Chavan, and D. Mourya, “Design of low power & high performance multi source H-tree clock distribution network,” in 2020 IEEE VLSI Device Circuit and System (VLSI DCS), Institute of Electrical and Electronics Engineers Inc., USA, 2020, pp. 468–473. [Google Scholar]

18. Z. Li et al., “A novel calibration method for the master PTP clock in smart substations using new information sequence weighting and adaptive unscented Kalman particle filter algorithms (In Chinese),” Power Syst. Technol., vol. 46, no. 5, pp. 1662–1671, 2021. [Google Scholar]

19. W. B. Yang, K. N. Chang, and L. C. Yeh, “A programmable multiple frequencies clock generator with process and temperature compensation circuit for system on chip design,” IEEE Syst. J., vol. 16, no. 3, pp. 4222–4231, 2022. doi: 10.1109/JSYST.2021.3123051. [Google Scholar] [CrossRef]

20. N. M. Senevirathna, O. de Silva, G. K. I. Mann, and R. G. Gosine, “Asymptotic gradient clock synchronization in wireless sensor networks for UWB localization,” IEEE Sens. J., vol. 22, no. 24, pp. 24578–24592, 2022. doi: 10.1109/JSEN.2022.3213696. [Google Scholar] [CrossRef]

21. Z. Wang, Z. Zhou, H. Zhang, G. Zhang, H. Ding and A. Farouk, “AI-based cloud-edge-device collaboration in 6G space-air-ground integrated power IoT,” IEEE Wireless Commun., vol. 29, no. 1, pp. 16–23, 2022. doi: 10.1109/MWC.001.00254. [Google Scholar] [CrossRef]

22. Y. Zong, X. Dai, Z. Wei, M. Zou, W. Guo and Z. Gao, “Robust time synchronization for industrial Internet of Things by H∞ output feedback control,” IEEE Internet Things J., vol. 10, no. 3, pp. 2021–2030, 2023. doi: 10.1109/JIOT.2022.3144199. [Google Scholar] [CrossRef]

23. X. Xu, Z. Li, T. Yan, and E. Li, “A novel control approach for the fixed-time synchronization of the complex networks,” IEEE Trans. Circuits Syst. II Express Briefs, vol. 69, no. 6, pp. 2882–2886, 2022. doi: 10.1109/TCSII.2022.3150646. [Google Scholar] [CrossRef]

24. X. Li, Y. Li, X. Yun, J. Wu, H. Zheng and L. Li, “An efficient strategy for multi-GNSS real-time clock estimation based on the undifferenced method,” GPS Solut., vol. 27, no. 23, pp. 1–15, 2023. doi: 10.1007/s10291-022-01360-x. [Google Scholar] [CrossRef]

25. A. Mahmood, M. I. Ashraf, M. Gidlund, J. Torsner, and J. Sachs, “Time synchronization in 5G wireless edge: Requirements and solutions for critical-MTC,” IEEE Commun. Mag., vol. 57, no. 12, pp. 45–51, 2019. doi: 10.1109/MCOM.001.1900379. [Google Scholar] [CrossRef]

26. W. Wang et al., “Research on evaluation method of time transfer performance between ground stations in two-way satellite comparison network,” IEEE Access, vol. 9, pp. 14038–14047, 2021. doi: 10.1109/ACCESS.2021.3050749. [Google Scholar] [CrossRef]

27. A. Destro and G. Giorgi, “Reinforcement learning applied to network synchronization systems,” in IEEE Int. Symp. Measurements & Netw. (M&N), Padua, Italy, 2022, pp. 1–6. [Google Scholar]

28. J. Lu, R. Zhao, Z. Yu, Y. Dai, and K. Zeng, “Accurate time synchronization of power device based on multi-satellite clock sources,” in 4th Int. Acad. Exch. Conf. Sci. Technol. Innov. (IAECST), Guangzhou, China, 2022, pp. 669–672. [Google Scholar]

29. Y. Wang, C. Peng, and C. Feng, “Security assessment of coal mine power grid voltage based on an improved AHP-FCE,” Math. Probl. Eng., vol. 1, no. 1, pp. 1–12, 2022. [Google Scholar]

30. L. P. Raghav, R. S. Kumar, D. K. Raju, and A. R. Singh, “Analytic hierarchy process (AHP)–swarm intelligence based flexible demand response management of grid-connected microgrid,” Appl. Energy, vol. 306, no. 2, pp. 1–19, 2022. [Google Scholar]

31. F. Song and S. Tong, “Comprehensive evaluation of the transformer oil-paper insulation state based on RF-combination weighting and an improved TOPSIS method,” Glob. Energy Interconnect., vol. 5, no. 6, pp. 654–665, 2022. doi: 10.1016/j.gloei.2022.12.007. [Google Scholar] [CrossRef]

32. M. V. Carvalho Fagundes, A. C. Keler, E. O. Teles, S. A. B. V. Melo, and F. G. Mendonça Freires, “Multicriteria decision-making system for supplier selection considering risk: A computational fuzzy AHP-based approach,” IEEE Lat. Am. Trans., vol. 19, no. 9, pp. 1564–1572, 2021. doi: 10.1109/TLA.2021.9468610. [Google Scholar] [CrossRef]

33. D. Xu, K. Yu, L. Zhen, K. K. R. Choo, and M. Guizani, “Quantum learning on structured code with computing traps for secure URLLC in industrial IoT scenarios,” IEEE Internet Things J., vol. 10, no. 18, pp. 16516–16530, 2023. doi: 10.1109/JIOT.2023.3268608. [Google Scholar] [CrossRef]

34. Q. Ge, H. Qiao, C. Li, Q. Yang, and H. Jiang, “Real-time charging risk assessment for electric vehicles based on improved broad BP-AHP,” IEEE Trans. Ind. Electron., vol. 69, no. 9, pp. 9472–9482, 2022. doi: 10.1109/TIE.2021.3111591. [Google Scholar] [CrossRef]

35. H. Wang, R. Xiang, D. Zhang, L. Yang, and Y. Li, “Multi-source decision model of time synchronous device based on AHP,” J. Electr. Power Sci. Technol, vol. 31, no. 3, pp. 8–13, 2016. [Google Scholar]

36. Y. Fu, Y. Yuan, K. Chen, X. Lv, and B. Xie, “Research on intelligent monitoring of micro-environment in power communication rooms,” J. Front. Comput. Sci. Technol., vol. 10, pp. 481–485, 2016. [Google Scholar]

37. Y. D. Kim and S. Kim, “Network-aided intelligent traffic steering in 5G mobile networks,” Comput. Mater. Contin., vol. 65, no. 1, pp. 243–261, 2020. doi: 10.32604/cmc.2020.011253. [Google Scholar] [CrossRef]

38. F. Li, J. Zhang, E. Szczerbicki, J. Song, R. Li and R. Diao, “Deep learning-based intrusion system for vehicular ad hoc networks,” Comput. Mater. Contin., vol. 65, no. 1, pp. 653–681, 2020. doi: 10.32604/cmc.2020.011264. [Google Scholar] [CrossRef]

39. Z. Guo, K. Yu, N. Kumar, W. Wei, S. Mumtaz and M. Guizani, “Deep-distributed-learning-based POI recommendation under mobile-edge networks,” IEEE Internet Things J., vol. 10, no. 1, pp. 303–317, 2023. doi: 10.1109/JIOT.2022.3202628. [Google Scholar] [CrossRef]

40. Z. Guo et al., “Deep collaborative intelligence-driven traffic forecasting in green internet of vehicles,” IEEE Trans. Green Commun. Netw., vol. 7, no. 2, pp. 1023–1035, 2023. doi: 10.1109/TGCN.2022.3193849. [Google Scholar] [CrossRef]

41. H. Liao, Z. Zhou, X. Zhao, and Y. Wang, “Learning-based queue-aware task offloading and resource allocation for space-air–ground-integrated power IoT,” IEEE Internet Things J., vol. 8, no. 7, pp. 5250–5263, 2021. doi: 10.1109/JIOT.2021.3058236. [Google Scholar] [CrossRef]

42. J. Yang et al., “High-accuracy clock offsets estimation strategy of BDS-3 using multi-source observations,” Remote Sens., vol. 14, no. 18, pp. 4674–4681, 2022. doi: 10.3390/rs14184674. [Google Scholar] [CrossRef]

43. K. Zhang, Z. Deng, D. Zhang, X. Dend, J. Hu and Z. Qiu, “Research on multi-source adaptive time synchronization system for intelligent substation,” in 2011 Int. Conf. Adv. Power Syst. Autom. Protec., Beijing, China, 2011, pp. 2213–2217. [Google Scholar]