 Open Access
Open Access
ARTICLE
Chaotic Map-Based Authentication and Key Agreement Protocol with Low-Latency for Metasystem
1 School of Electronics & Information Engineering, Nanjing University of Information Science & Technology, Nanjing, 210044, China
2 Yancheng Polytechnic College, Yancheng, 224000, China
3 Jiangsu Province Engineering Research Center of Advanced Computing and Intelligent Services, School of Software, Nanjing University of Information Science and Technology, Nanjing, China
* Corresponding Author: Qi Liu. Email:
Computers, Materials & Continua 2024, 78(3), 4471-4488. https://doi.org/10.32604/cmc.2024.047669
Received 13 November 2023; Accepted 05 February 2024; Issue published 26 March 2024
Abstract
With the rapid advancement in exploring perceptual interactions and digital twins, metaverse technology has emerged to transcend the constraints of space-time and reality, facilitating remote AI-based collaboration. In this dynamic metasystem environment, frequent information exchanges necessitate robust security measures, with Authentication and Key Agreement (AKA) serving as the primary line of defense to ensure communication security. However, traditional AKA protocols fall short in meeting the low-latency requirements essential for synchronous interactions within the metaverse. To address this challenge and enable nearly latency-free interactions, a novel low-latency AKA protocol based on chaotic maps is proposed. This protocol not only ensures mutual authentication of entities within the metasystem but also generates secure session keys. The security of these session keys is rigorously validated through formal proofs, formal verification, and informal proofs. When confronted with the Dolev-Yao (DY) threat model, the session keys are formally demonstrated to be secure under the Real-or-Random (ROR) model. The proposed protocol is further validated through simulations conducted using VMware workstation compiled in HLPSL language and C language. The simulation results affirm the protocol’s effectiveness in resisting well-known attacks while achieving the desired low latency for optimal metaverse interactions.Keywords
With the arrival of 5G, the rapid development of artificial intelligence and cloud computing technology [1] has accelerated the realization of the metaverse. People can enter the virtual world and interact with others in the form of metaverse avatars [2] through virtual reality (VR) [3] headsets. This will change the organization and operation of existing societies by combining virtual reality. However, new challenges are also brought in protecting the privacy and security of the avatars. Different from the real world, the metaverse will not only face passive attacks and eavesdropping attacks but also more active attacks will be launched to gain the benefits of the virtual world. Therefore, preserving the security and privacy of the avatar [4] is a current issue that needs to be addressed urgently.
Identity verification is an essential part of either the real world or the metaverse. In the real world, authentication is also applied in multiple environments. Under the industrial IoT environment [5], the user and sensing device authenticate and negotiate a session key for communication. In the metaverse, users represent themselves virtually by creating avatars and can access a variety of services through these avatars. However, in the current metaverse environment, any user has the freedom to create any avatar as their virtual representative. This property provides an avenue for malicious users to create avatars and cause serious security issues during metaverse interactions. Therefore, it is essential to design an AKA protocol that allows users to securely access available services in the metaverse and remain safe against other security threats. In the metaverse, meta-users and virtual devices verify each other’s identity legitimacy and generate session key for communication transfer to protect the privacy of the users as well as the devices.
Although the metaverse can provide a variety of services, it is vulnerable to a variety of attacks that can threaten security. First, each communication in the metasystem may be maliciously attacked by an adversary. Attackers can illegally enter the virtual world of the meta-user or tamper with transmitted data by attacking the metasystem’s communication channels. In addition, performance is a significant aspect of the user experience, besides the security aspect. Ryu et al. [6] presented a mutual authentication scheme using Elliptic Curve Cryptography (ECC) to offer secure communication between users and servers as well as secure interactions between avatars and avatars of the platform. Thakur et al. [7] proposed a secure ECC-based authentication scheme utilizing a fuzzy extractor for more secure user-server and avatar-avatar interactions. However, the high computational cost of the above literature makes them unsuitable for deployment into the metaverse.
To solve the above problems, a chaotic mapping-based AKA protocol is proposed to protect the privacy of metaverse avatars, which can achieve secure communication between VR headset and tactile devices. Biometric of metaverse user is adopted as one of the authentication factors to improve the security of metaverse avatars which can resist malicious impersonation of the avatar. Further, user anonymity is achieved even if the tactile device is corrupted without any valid information. Finally, the proposed protocol is analyzed through experimental simulations and the experimental results show that it can be applied to privacy protection for metaverse avatars with better performance. The main contributions are summarized as follows:
1. User anonymity is considered to resist malicious attackers or corrupted tactile devices impersonating metaverse avatars when logging into a VR headset. To ensure the legitimacy of the avatar, the VR headset needs to verify the user’s identity and complete collaboration with the tactile device. It means multi-party authentication needs to be completed between the user, headset, and tactile device before entering the metaverse. Based on the semi-group attribute of the Chebyshev polynomial, the session key is established after multi-party authentication. Malicious attackers cannot obtain user information from VR device communication even if launching Man-in-the-middle (MITM), impersonation, and forgery attacks.
2. The security of the session key established between the VR headset and tactile devices has been formally proven under the ROR model. Additionally, informal proofs substantiate its resilience against both passive and active attacks. This paper adopts the robust DY threat model to define the capabilities of the adversary. Malicious attacker not only has access to information stored locally in sensor-based VR tactile devices through powerful analysis but also has absolute control over the information transmitted on the public channel. Without loss of generality, impersonation attacks on users, edge nodes, and tactile devices are analyzed in Section 5.1. The analysis results show that the proposed protocol can protect the security and privacy of metaverse avatars effectively despite strong attackers.
3. To further verify that the protocol can protect the privacy and security of the avatar effectively, security was further analyzed using the Automated Validation of Internet Security Protocols and Applications (AVISPA) tool. To provide a robust level of security for the proposed protocol, rigorous testing was performed using the AVISPA tool. This tool allowed us to simulate active attacks and thoroughly evaluate the protocol’s resistance to these attacks. The test results indicate that it provides efficient protection against replay and man-in-the-middle attacks. Based on the successful completion of these tests, it can be confidently asserted that the protocol is capable of withstanding a variety of active attacks and can offer a robust level of security for its intended use cases.
4. For security and performance, the proposed protocol is compared with related works and the result shows that the proposed protocol has better usability for Metasystem. The proposed protocol has undergone thorough analysis and comparison with other related works in terms of security and performance. The comparison results show that the proposed protocol has better usability, making it a more reliable and efficient means of authentication for secure communication in Metasystem. Overall, the comparison analysis highlights the strengths and advantages of the proposed protocol and confirms its potential as a leading solution in secure communication for Metasystem.
Although the exploration and development of metaverse is still in the infancy phase, some works on metaverse [8,9] have already been proposed. Additionally, several works [10–14] have discussed security and privacy issues in the metaverse. As relevant technologies are deeply explored, research on the metaverse has involved multiple areas. Park et al. [15] discussed the three components involved in the metaverse and review representative applications in the metaverse in terms of user interaction, and implementation. Wang et al. [2] analyzed what security threats the metaverse will face in terms of security and privacy.
However, the issue of security in the metaverse has been of considerable concern. Rafique et al. [16] found that virtual reality systems work by presenting interactive views on head-mounted displays. To make virtual reality systems more secure, they also propose possible countermeasures. O’Brolcháin et al. [17] focused on two core ethical issues that may exist in virtual reality and social networks, namely threats to privacy (information printing, physical privacy, associative privacy) and threats to autonomy (freedom, knowledge, authenticity). They also proposed some countermeasures to address the threats to privacy. Falchuk et al. [18] concentrated on the technological underpinnings that contribute to an increased level of privacy for VR participants while immersed in social VR in their article.
Authentication is the first line of defense against access by illegal meta-users in the metaverse, which protects the meta-user’s avatar [19] from unauthorized intrusion, therefore authentication is an integral part of the metaverse. Yang et al. [20] proposed a two-factor authentication framework based on chameleon signature and biometric authentication to suggest a secure meta-universe environment. In addition, the authentication framework is shown to guarantee the consistency and traceability of virtual identities after security analysis. Yu et al. [21] proposed a multi-server-based authentication key agreement to protect the user’s private information, which can achieve user untraceability. Although it reduced the communication and computation overheads compared to partially related works. However, it transmits 7 times, which cannot effectively guarantee the freshness of the message. Zheng et al. [22] proposed a three-party authentication key agreement based on chaotic mapping, considering the security needs of real applications, in which user anonymity is achieved.
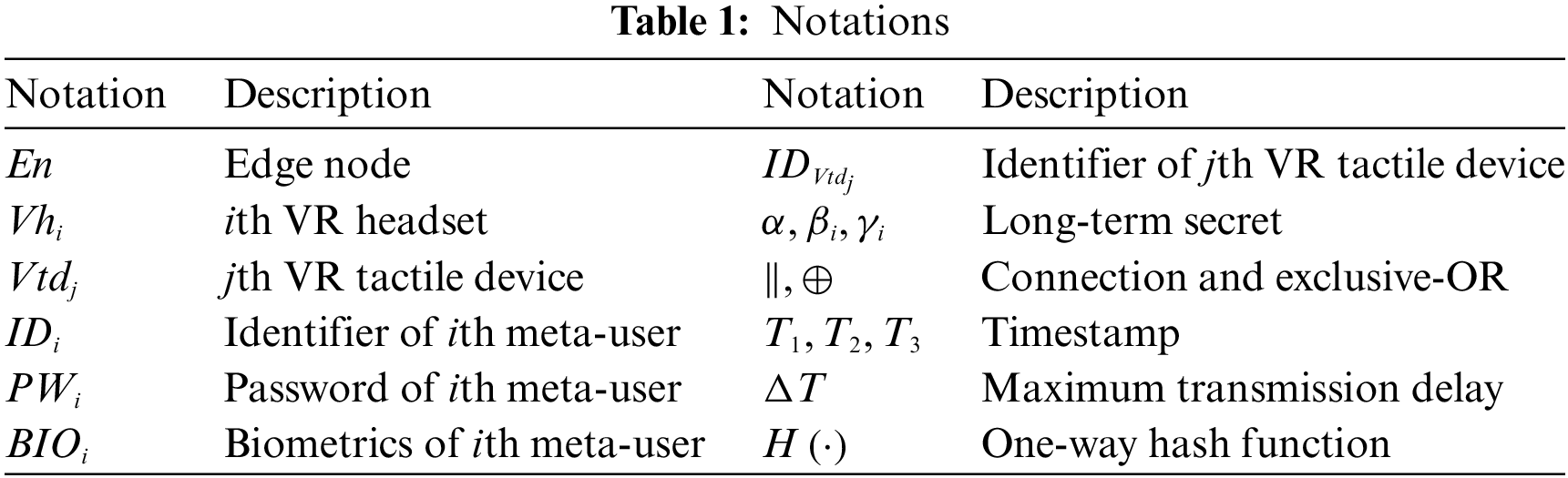
In this section, descriptions of the preliminaries are given and the notations are illustrated in Table 1.
Fuzzy extractor is widely accepted technique for extracting biometric characteristics. In this technique, it mainly contains generation and restoration functions. Now, we give the formal definitions of the two functions as follows:
Chebyshev chaotic-map is a chaotic mapping function for generating a pseudo-random sequence of numbers. The formal definitions of Chebyshev chaotic-map are given as follows:
Definition 1:
1. Recursiveness:
2. Semi-group:
Definition 2: Chaotic-map discrete logarithm (CMDL): For a given number
Suppose a scenario exists where a patient has a sudden illness that requires surgery. However, specialized surgical treatment is not available where the patient is located. The relevant experienced physician can access the metasystem through the terminal and operate on the patient through the sensory device. Under the above scenario, there are three entities in the proposed metasystem communication network as shown in Fig. 1. The detailed description of each entity is given as follows.

Figure 1: System model
Meta-user (
Edge node (
VR tactile device (
In this paper, the popular DY adversary model is adopted, in which a strong adversary
Information transmitted over public channels can be obtained by adversaries, and even more can be deleted and modified. Notably,
VR tactile devices in metasystem can be captured by
We prove session key security under the widely-used ROR model, which is applied in formal proofs of many authentication protocols. The detailed description of the ROR security model is provided and shown as follows:
Participants. For better identification, the
Acceptance. A participant
Partnering. Two participants
Freshness. If the session key between
There are four phases in our protocol. We will give the detailed construction of each phase in this section. Before adding an entity to the meta-system, initialization and entity registrations need to be completed. Then, the session key is generated between the meta-user and the device after verifying each other’s identities. The update of the authentication factor is additionally considered to prevent privacy breaches due to loss of passwords. The detailed construction of each stage is shown as follows.
First of all, En will start to initiate the metasystem and pre-deploy for VR tactile devices.
4.2 Offline-Registration Phase
Meta-user access to the metaverse via a VR headset means that the legitimate meta-user needs to complete meta-user registration to gain permission. As shown in Fig. 2, the offline registration phase for meta-users can be divided into the following 3 steps.
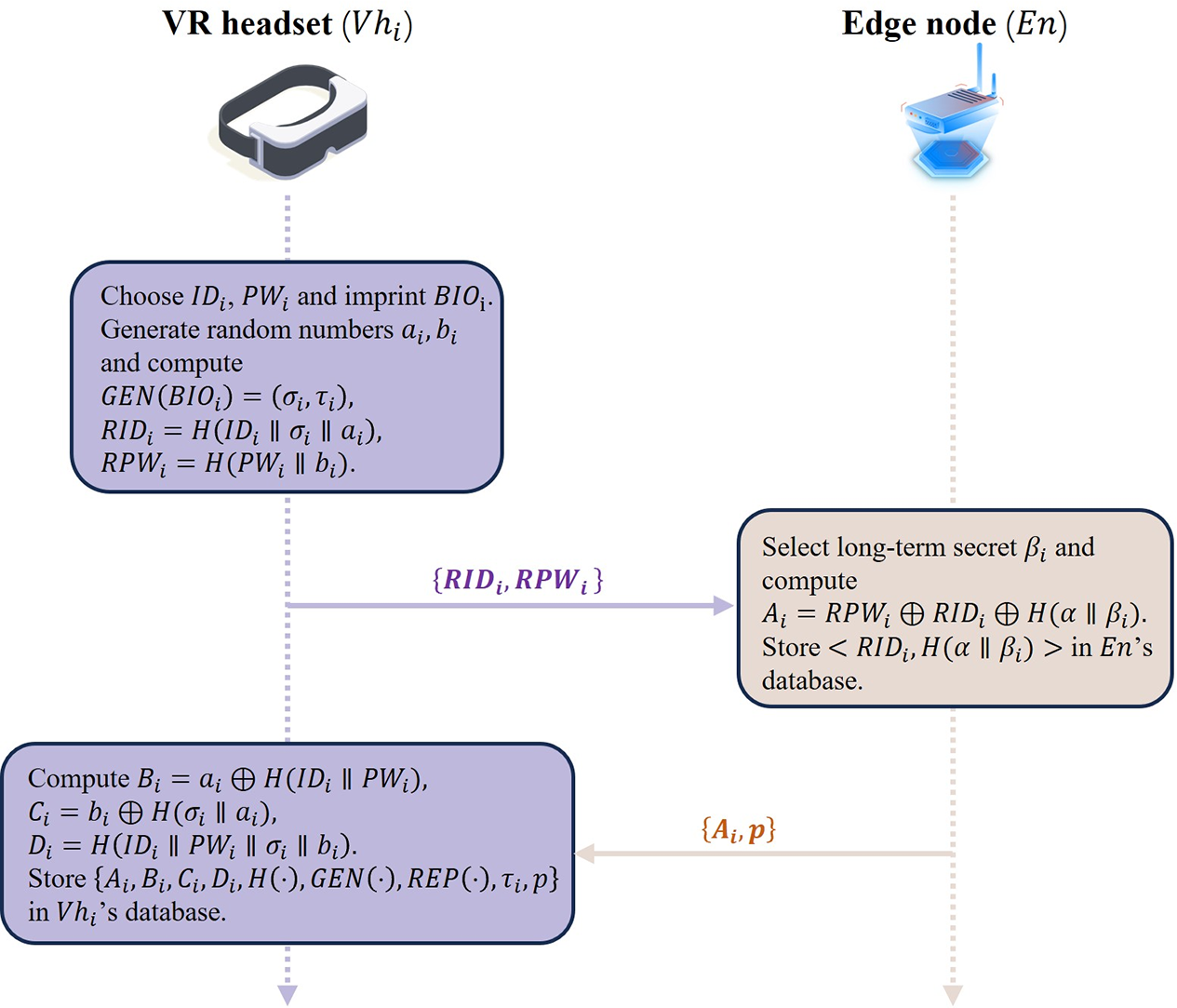
Figure 2: Meta-user registration
Step 1:
Step 2: After receiving the registration message from
Step 3:
4.3 Login and Authentication Phase
Once the meta-user wants to access the metaverse and collaborate with the VR tactile devices, a secure session key needs to be established between

Figure 3: Login and authentication
Step 1:
Step 2: If the above equation holds,
Step 3: En verifies whether
Step 4: If the above equation holds, En computes
Step 5:
Step 6: If the above equation holds,
Step 7:
Considering the practical needs of users who have lost their passwords or whose biometrics need to be updated, factors update is also designed. As shown in Fig. 4, the factors update phase can be divided into the following 3 steps.

Figure 4: Factors update
Step 1:
Step 2:
Step 3: Replace
In this section, formal and informal proofs are given to prove security. The detailed proofs are described as follows.
Assume that
Theorem 1: The advantage of
Proof. We prove Theorem 1 through five games, which are described in detail as follows.
The probabilities from
Through the trigonometric inequality, we can obtain the following equation:
Finally, Theorem 1 can be proved from the above equation and the final conclusion drawn.
Privileged-insider attack. In the meta-user registration phase,
Anonymity and untraceability. As shown in Section 4.3, information
Stolen headset attack. Assume the headset
Replay attack. Assume
MITM attack. Assume
Mutual authentication. In metasystem,
Meta-user impersonation attack. Assume
Edge node impersonation attack. Assume
Tactile device impersonation attack. Assume
Session key security. The session key
In this section, detailed performance analyses are described from theoretical side, tool simulation and experimental analysis.
6.1 Comparison of Security and Overhead
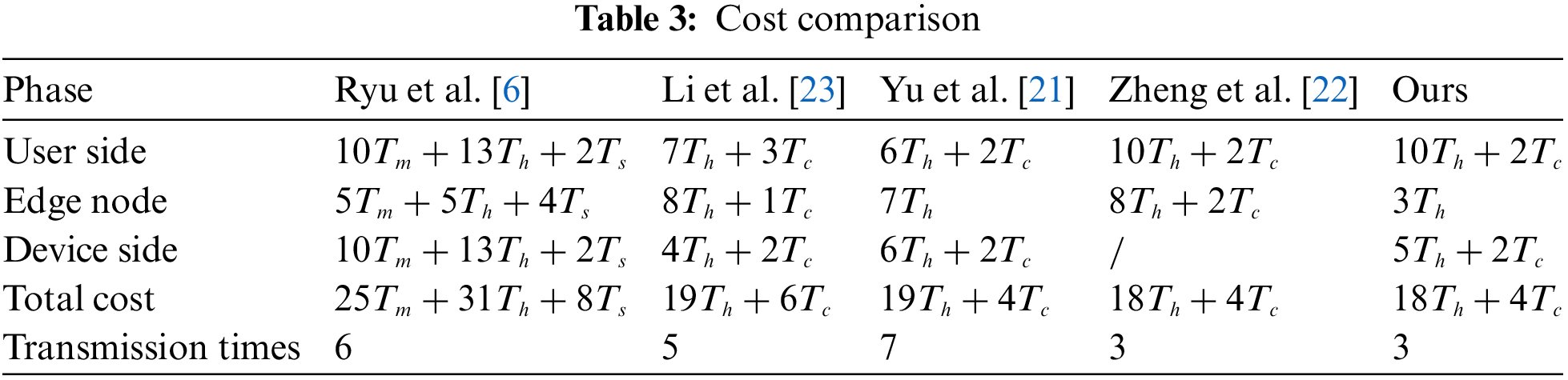
We will analyze the security and theoretical overheads compared to the associated metaverse authentication protocols, respectively. First, the security is compared and the results are presented in Table 2. Ryu et al. [6] proposed a blockchain-assisted authentication protocol for metasystem. In their protocol, elliptic curve is employed to provide secure communication between the user and the platform server as well as avatar security. However, it is not able to resist real-world impersonation attacks and ensure session key security. Li et al. [23] proposed a server-assisted authentication method using chaotic mapping. However, it is also impossible to resist an impersonation attack. Zheng et al. [22] proposed an efficient session key establishment method between users through chaotic mapping. However, it still has information leakage when facing MITM attacks. From Table 2, it is easy to find that just Yu et al. [21] and ours can satisfy the full security requirements.
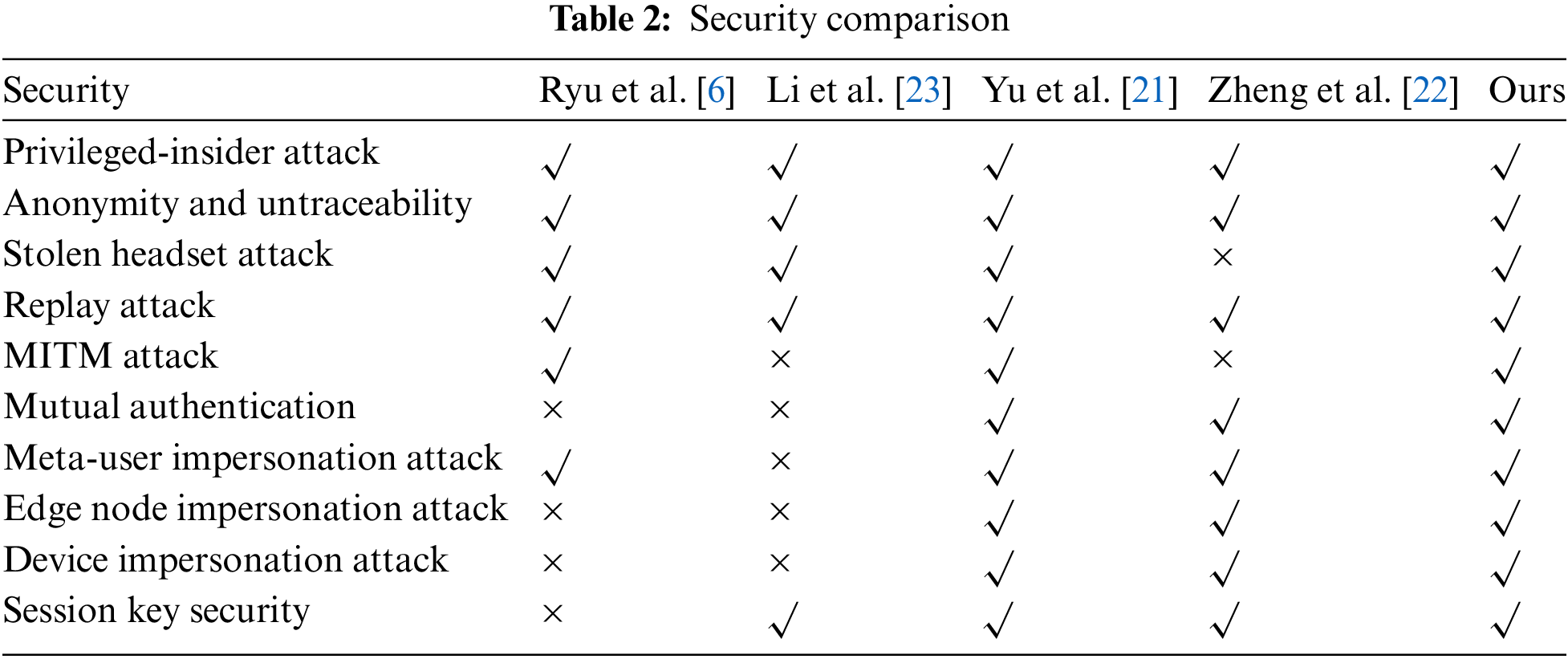
In terms of overhead, we compare and analyze the computation and communication overheads, respectively. From Table 3, We can find that our total cost is
In order to analyze whether the protocol is resistant to man-in-the-middle and replay attacks, the popular AVISPA tool is employed to verify security. AVISPA is a tool for proving network security protocols and applications, which is integrated into the SPAN virtual machine through a virtual box. Our protocol is compiled in the HLPSL language and the validation result is shown in Fig. 5.

Figure 5: Simulation result
To further compare the performance, the protocol was simulated with a VMware workstation at 2.7 GHz and 8 G RAM. We completed the experimental simulation using C based on PBC and GMP libraries. The computational and communication overhead results are shown in Figs. 6 and 7.

Figure 6: Computational overhead

Figure 7: Communication overhead
In [6], its runtime is 207.36 ms on the user side, 120 ms on the edge node side, 207.36 ms in the device side and transmission times is 6. Its total overhead is 534 milliseconds due to the high runtime of the power operation. In [23], its runtime is 53.54 ms in the user side, 19.66 ms in edge node side, 35.48 ms in the device side and transmission times is 5. In [21], its runtime is 36.12 ms in the user side, 2.24 ms in edge node side, 36.12 ms in the device side and transmission times are 7. In [22], its runtime is 37.4 ms in the user side, 36.76 ms in edge node side and transmission times is 7. Compared to the above protocol, our user-side runtime is 37.4 ms, node-side runtime is 0.96 ms and device-side runtime is 35.8 ms, which is the lowest total runtime. Importantly, we completed the session key establishment in the metasystem using only 3 rounds of transmission. This will reduce transmission delay and energy consumption in the metasystem.
In this paper, we proposed a chaotic map-based AKA protocol to secure the security of meta-users and avatars, which enables low-latency transmission of information in the metasystem. Considering the characteristics of the metasystem, meta-user biometrics are employed to strengthen session key security. Further, the functionality of updating passwords and biometrics through VR headsets by meta-users is considered. The security of the protocol is comprehensively analyzed through formal and formal security proofs. Finally, we simulated the performance of the protocol through theoretical analysis, tool simulation, and experimental simulation which shows that it can effectively resist MITM and replay attacks without additional overhead compared to other related protocols. In future work, we will take into account the frequent dynamic updates of devices in the metasystem. Improvement of secret values in the proposed scheme to reduce communication overhead and enhance security. Therefore, designing an authentication scheme without locally stored secret values is the first step in our future work.
Acknowledgement: Not applicable.
Funding Statement: This work has received funding from National Natural Science Foundation of China (No. 42275157).
Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Guojun Wang; data collection: Qi Liu; analysis and interpretation of results: Guojun Wang, Qi Liu; draft manuscript preparation: Guojun Wang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. M. E. M. Cayamcela and W. Lim, “Artificial intelligence in 5G technology: A survey,” in Proc. ICTC, Jeju, Korea, 2018, pp. 860–865. [Google Scholar]
2. Y. Wang et al., “A survey on metaverse: Fundamentals, security, and privacy,” IEEE Commun. Surv. Tutor., vol. 25, no. 1, pp. 319–352, 2022. [Google Scholar]
3. C. Anthes, R. J. García-Hernández, M. Wiedemann, and D. Kranzlmüller, “State of the art of virtual reality technology,” in 2016 IEEE Aerospace Conf., Big Sky, MT, USA, 2016, pp. 1–19. [Google Scholar]
4. R. D. Pietro and S. Cresci, “Metaverse: Security and privacy issues,” in Proc. TPS-ISA, Atlanta, GA, USA, 2021, pp. 281–288. [Google Scholar]
5. D. Liu, Y. Zhang, W. Wang, K. Dev, and S. A. Khowaja, “Flexible data integrity checking with original data recovery in IoT-enabled maritime transportation systems,” IEEE Trans. Intell. Transp., vol. 24, no. 2, pp. 2618–2629, 2023. [Google Scholar]
6. J. Ryu, S. Son, J. Lee, Y. Park, and Y. Park, “Design of secure mutual authentication scheme for metaverse environments using blockchain,” IEEE Access., vol. 10, pp. 98944–98958, 2022. [Google Scholar]
7. G. Thakur, P. Kumar, C. M. Chen, A. V. Vasilakos, Anchna and S. Prajapat, “A robust privacy-preserving ECC-based three-factor authentication scheme for metaverse environment,” Comput. Commun., vol. 211, pp. 271–285, 2023. [Google Scholar]
8. H. Ning et al., “A survey on the metaverse: The state-of-theart, technologies, applications, and challenges,” IEEE Internet Things, vol. 10, pp. 14671–14688, 2023. [Google Scholar]
9. N. A. Dahan, M. Al-Razgan, A. Al-Laith, M. A. Alsoufi, M. S. Al-Asaly and T. Alfakih, “Metaverse framework: A case study on e-learning environment (ELEM),” Electron., vol. 11, no. 10, pp. 1616, 2022. doi: 10.3390/electronics11101616. [Google Scholar] [CrossRef]
10. T. Zhang, J. Shen, C. F. Lai, S. Ji, and Y. Ren, “Multi-server assisted data sharing supporting secure deduplication for metaverse healthcare systems,” Future Gener. Comput. Syst., vol. 140, no. 1, pp. 299–310, 2023. doi: 10.1016/j.future.2022.10.031. [Google Scholar] [CrossRef]
11. S. Qamar, Z. Anwar, and M. Afzal, “A systematic threat analysis and defense strategies for the metaverse and extended reality systems,” Comput. Secur., vol. 128, no. 6, pp. 103127, 2023. doi: 10.1016/j.cose.2023.103127. [Google Scholar] [CrossRef]
12. J. D. N. Dionisio, W. G. B. Iii, and R. Gilbert, “3D virtual worlds and the metaverse: Current status and future possibilities,” ACM Comput. Surv., vol. 45, no. 3, pp. 1–38, 2013. doi: 10.1145/2480741.2480751. [Google Scholar] [CrossRef]
13. L. H. Lee et al., “All one needs to know about metaverse: A complete survey on technological singularity, virtual ecosystem, and research agenda,” arXiv preprint arXiv:2110.05352, 2021. [Google Scholar]
14. H. Yang, P. Vijayakumar, J. Shen, and B. B. Gupta, “A location-based privacy-preserving oblivious sharing scheme for indoor navigation,” Future Gener. Comp. Syst., vol. 137, no. 3, pp. 42–52, 2022. doi: 10.1016/j.future.2022.06.016. [Google Scholar] [CrossRef]
15. S. M. Park and Y. G. Kim, “A metaverse: Taxonomy, components, applications, and open challenges,” IEEE Access., vol. 10, pp. 4209–4251, 2022. doi: 10.1109/ACCESS.2021.3140175. [Google Scholar] [CrossRef]
16. M. U. Rafique and S. C. S. Cheung, “Tracking attacks on virtual reality systems,” IEEE Consum. Electron. Mag., vol. 9, no. 2, pp. 41–46, 2020. doi: 10.1109/MCE.2019.2953741. [Google Scholar] [CrossRef]
17. F. O’Brolcháin, T. Jacquemard, D. Monaghan, N. O’Connor, P. Novitzky and B. Gordijn, “The convergence of virtual reality and social networks: Threats to privacy and autonomy,” Sci. Eng. Ethics., vol. 22, no. 1, pp. 1–29, 2016. doi: 10.1007/s11948-014-9621-1. [Google Scholar] [PubMed] [CrossRef]
18. B. Falchuk, S. Loeb, and R. Neff, “The social metaverse: Battle for privacy,” IEEE Technol. Soc. Mag., vol. 37, no. 2, pp. 52–61, 2018. doi: 10.1109/MTS.2018.2826060. [Google Scholar] [CrossRef]
19. J. A. de Guzman, K. Thilakarathna, and A. Seneviratne, “Security and privacy approaches in mixed reality: A literature survey,” ACM Comput. Surv., vol. 52, no. 6, pp. 1–37, 2019. doi: 10.1145/3359626. [Google Scholar] [CrossRef]
20. K. Yang, Z. Zhang, Y. Tian, and J. Ma, “A secure authentication framework to guarantee the traceability of avatars in metaverse,” IEEE Trans. Inf. Foren. Secur., vol. 18, pp. 3817–3832, 2023. doi: 10.1109/TIFS.2023.3288689. [Google Scholar] [CrossRef]
21. Y. Yu, O. Taylor, R. Li, and B. Sunagawa, “An extended chaotic map-based authentication and key agreement scheme for multi-server environment,” Math., vol. 9, no. 8, pp. 798, 2021. doi: 10.3390/math9080798. [Google Scholar] [CrossRef]
22. Y. Zheng et al., “Design and analysis of a security-enhanced three-party authenticated key agreement protocol based on chaotic maps,” IEEE Access., vol. 8, pp. 66150–66162, 2020. doi: 10.1109/ACCESS.2020.2979251. [Google Scholar] [CrossRef]
23. X. Li et al., “A novel chaotic maps-based user authentication and key agreement protocol for multi-server environments with provable security,” Wirel. Pers. Commun., vol. 89, no. 2, pp. 569–597, 2016. doi: 10.1007/s11277-016-3293-x. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools