Falcon Optimization Algorithm-Based Energy Efficient Communication Protocol for Cluster-Based Vehicular Networks

1  Introduction

Over past several years, the increasing number of cars that are a part of global transportation systems has brought to light the essential function that Vehicular Ad Hoc Networks (VANETs) play in the development of intelligent transportation systems (ITS). Vehicular Ad Hoc Networks (VANETs) are essential for transforming transportation systems by facilitating direct communication between cars and infrastructure. This dynamic network enables the interchange of data and sharing of information, resulting in several enhancements in Improved Traffic Management, Increased Efficiency and Convenience, and Enhanced Safety [1]. The demand for driving experiences that are both more efficient and secure has drawn a significant amount of scholarly attention, notably in the field of VANET research. Collaborative driving and collision avoidance Imagine real-time speed, lane change, and blind area communication. VANETs help automobiles anticipate and respond to dangers in cooperative driving, lowering accidents. This study creates reliable data sharing, efficient communication protocols, and intelligent vehicle data interpretation and utilization algorithms. Traffic Optimization and Real-Time Management Vehicle congestion is widespread. VANETs deliver real-time traffic, accident, and road closure data, recommending a solution. Data can dynamically adjust traffic signals, suggest alternative routes, and charge congestion. This study includes traffic modeling, data analytics, and intelligent transportation systems design. Green Driving and Sustainability VANETs promote eco-friendly driving to lessen environmental effects. VANETs exchange fuel-efficient routes, real-time traffic, and electric car charging sites to help drivers minimize emissions and fuel use. Energy-efficient communication protocols, electric car infrastructure, and sustainable transportation are the focus of this research. Improved Safety and Emergency Response VANETs can improve road safety by warning drivers of threats, accidents, and medical emergencies. Sharing vehicle data helps drivers prepare for sudden stops, icy roads, and other risks. VANETs can route ambulances and rescue teams to accident scenes, speeding emergency response. This research examines reliable emergency communication protocols, first responder system integration, and emergency response coordination [2]. This demand has been brought about by the acceleration of urbanization. To improve safety, traffic efficiency, and communication dependability, virtual area networks (VANETs), which are characterized by dynamic topologies and high-speed node mobility, present a unique set of difficulties and opportunities [3]. Both intra-vehicular Vehicle-to-Infrastructure (V2I) and inter-vehicular Vehicle-to-Vehicle (V2V) transmissions are a part of the communication landscape that exists within VANETs. The electrical control units of vehicles serve as the infrastructure for these transmissions [4]. In contrast to Mobile Ad Hoc Networks (MANETs), Vehicle Ad Hoc Networks (VANETs) can establish predictable patterns along roadways, thereby taking advantage of the infrastructure's higher capacity for storage and processing [5]. In the core paradigm of a VANET, cars and various structures communicate with one another through Onboard Units (OBUs), Vehicle-to-Vehicle (V2V) connections, Road Side Units (RSUs), and Vehicle-to-Infrastructure (V2I) connections. This communication helps to ensure that the transportation system is both safe and efficient [6].

VANETs have been catapulted into a new era of efficient communication, which has enabled the delivery of both safety and non-safety information [7]. This has been made possible by the arrival of technologies such as cloud-edge computing, 5G, Software-Defined Networking (SDN), and the anticipated 6G. This ever-changing environment calls for the implementation of robust routing protocols to guarantee the transmission of data packets in real-time, which is essential for the success of VANETs [8]. The Cluster-Based Routing Protocol (CBRP) has emerged as one of the most extensively accepted protocols due to its effectiveness in unstable network topologies [9]. Routing protocols play an essential role in virtual area networks (VANETs). On the other hand, traditional clustering techniques frequently fail to meet the requirements for delivering Quality of Service (QoS) and maintaining network stability. Taking this into consideration, researchers have been looking for ways to improve existing protocols by experimenting with a wide variety of simulators and parameters to improve clustering algorithms in VANET topologies that are unpredictable [10]. As a means of catering to the ever-evolving requirements of virtual area networks (VANETs), this article presents the Falcon Optimization Algorithm-based Energy Efficient Communication Protocol for Cluster-based Routing (FOA-EECPCR) approach. To overcome the shortcomings of traditional clustering approaches, the FOA-EECPCR strategy makes use of the Falcon Optimization Algorithm for initial vehicle clustering. This technique incorporates fitness functions that take into account energy, distance, and trust level concerns. After that, the method of routing makes use of the Sparrow Search Algorithm (SSA), which is a fitness function that focuses on energy and distance factors. These optimization algorithms are being combined to improving the overall performance of VANETs. This will be accomplished by tackling the challenges that are posed by dynamic topologies and the requirement for real-time data transmission.

To put the FOA-EECPCR strategy into context, it is very necessary to investigate the present state of the art in VANETs as well as the optimization and routing protocols that are associated with them. Recent research has shed light on the connection between urbanization and the rapid expansion of virtual area networks (VANETs), highlighting the dynamic architecture of these networks as well as the importance of real-time data transfer. Cellular technologies such as voice over LTE (VoLTE) and long-term evolution (LTE), in conjunction with short-range wireless local area networks (WLAN), have played a crucial role in the utilization of VANET communication. Cluster-Based Routing Protocol, also known as CBRP, has been a focal point in VANET research because it is recognized for its overall performance in unstable network topologies. The requirement for increased Quality of Service (QoS) and network stability, on the other hand, has prompted researchers to investigate and change established protocols. The FOA-EECPCR technique is positioned within this ever-changing landscape, to improve the efficiency of routing and clustering algorithms. In addition to studies that are specific to VANETs, the incorporation of upcoming technologies such as cloud-edge computing and 5G has transformed communication paradigms in VANETs, making it possible to distribute both safety and non-safety information. A further demonstration of the dynamic character of this industry is provided by the envisioned 6G technology, which calls for routing protocols that are both adaptable and efficient.

Falcon optimization Algorithm and Sparrow Search Algorithm are two examples of optimization algorithms that are utilized in the FOA-EECPCR technique. These algorithms take their inspiration from the natural world to overcome the issues that are associated with dynamic topologies and real-time data transmission. The incorporation of fitness functions, which take into account energy, distance, and trust level concerns, demonstrates a comprehensive knowledge of the complex needs that are imposed by VANETs. Not only does the literature review position the FOA-EECPCR approach within the larger context of VANET research, but it also investigates recent developments and obstacles in the field. In conclusion, the literature review is a comprehensive report. The discussion highlights the necessity for communication protocols that are both adaptable and efficient, stressing the fact that VANETs are constantly evolving for better performance. This article presents a Falcon Optimization Algorithm-based Energy Efficient Communication Protocol for Cluster-based Routing (FOA-EECPCR) technique in VANETS. The FOA-EECPCR technique initially clusters the vehicles using FOA with fitness functions comprising energy, distance, and trust level. For the routing process, the sparrow search algorithm (SSA) is derived with a fitness function that encompasses two variables, namely, energy and distance. A series of experiments have been conducted to exhibit the enhanced performance of the FOA-EECPCR method.

2  Related Work

The article proposes Adaptive Neural Fuzzy Clustering (ANFC)-Quantum Glowworm Swarm Optimization-based Routing (QGSOR), a revolutionary VANET protocol [11]. To optimize VANET vehicle communication, the protocol leverages adaptive neural fuzzy clustering for cluster generation and CH selection. ANFC optimizes cluster construction using node degree, distance, and residual energy. Quantum Glowworm Swarm optimization optimizes routing for adaptive, efficient information delivery. The protocol promotes smooth automobile interaction to handle VANETs' dynamic nature. Literature evaluations must weigh the pros and downsides. Cluster assembly and CH selection efficiency improve communication and resource usage. Quantum swarm optimization and adaptive neural fuzzy clustering may be computationally and resource-intensive. These qualities are critical for judging the protocol's applicability and performance in real-world VANET applications, making the ANFC-QGSOR protocol a potential VANET communication protocol improvement. Bao et al. [12] provides CRBP-Clustering V2V Routing Based on PSO (Particle Swarm Optimization) in VANETs, an Efficient Clustering V2V Routing approach, using Particle Swarm Optimization (PSO) in Vehicular Ad Hoc Networks (VANETs) to improve V2V communication, using PSO and deliberately designating vehicle nodes with similar movement orientations enhances routing. Also labeled are cluster heads. The fitness function, encoding rules, and iteration rules for route particle velocity are carefully designed. Novel methods are also provided to improve routing inside and across clusters. Simulations using SUMO and NS3 show that maximal hops, number of nodes, and communication radius affect CRBP performance. Under ideal conditions, CRBP reduces latency by 47% and increases the packet delivery ratio (PDR) by 20%. This study shows how CRBP improves communication performance. It also acknowledges CRBP’s specific challenges and dependence on vital factors.

In [13], the researchers provide a revised approach for optimizing routes by grouping nodes, known as the modified optimal path algorithm. The proposed technique for stabilizing Vehicular Ad Hoc Networks (VANETs) involves utilizing mobility prediction to anticipate and account for their dynamic nature. The Location Aided Routing (LAR) protocol employs a dual-tier approach to minimize energy usage. This dual-level approach enhances the efficiency of LAR and minimizes energy consumption. The research tackles VANET challenges by employing a novel approach that involves predicting mobility, organizing clusters, and implementing a two-tier system architecture. Mobility prediction enhances route optimization, network stability, and energy-efficient routing through the use of a two-tier architecture. Nevertheless, the inclusion of mobility prediction and the implementation of the two-tier technique may introduce additional computing complexity and cost. Comprehending these components is crucial for evaluating the suitability and effectiveness of the proposed technique in VANETs, which makes it a potential path for vehicular communication routing protocols.

A novel routing protocol for Vehicular Ad Hoc Networks (VANETs) is suggested by integrating KMRP and K-Means algorithms inside a Continuous Hopfield Network architecture [14]. The objective is to enhance the efficiency of cluster and main Cluster Head (CH) selection by employing K-Means and Continuous Hopfield Network algorithms. To address the issue of arbitrary choices, the algorithm employs a systematic approach to determine input variables such as cluster count and primary CHs. Implementing this comprehensive approach can enhance VANET communication by optimizing cluster formation, selecting appropriate cluster heads, and optimizing routing. Integrating KMRP, K-Means, and Continuous Hopfield Network may lead to an increase in computational complexity. The assessment of these trade-offs is necessary to ascertain the feasibility and performance of the protocol in real-world VANET applications, hence establishing its potential value in the field. Reference [15] introduces a novel routing strategy for Vehicular Ad Hoc Networks (VANETs) that utilizes fuzzy logic and includes authentication capabilities. The proposed routing strategy consists of three stages: Authentication, clustering, and routing among Cluster Head (CH) nodes. Authentication involves a well-defined technique of efficiently grouping vehicles, which enhances the network's security. The technique emphasizes data flow by categorizing data packets as either regular or urgent. Efficient communication is essential for the rapid and secure transmission of data in VANETs. Fuzzy logic may be employed in this approach to make routing decisions, enhancing the network's adaptability to dynamic vehicular environments. Nevertheless, the use of fuzzy logic might lead to an escalation in computational burden and authentication latency. An exhaustive examination of these characteristics is important to evaluate the feasibility of the proposed approach in real-world VANET settings and include it in the growth of VANET routing protocols.

The article [16] presents GAACO, a system that combines Genetic Algorithm (GA) and Ant Colony Optimization (ACO) to optimize routing in VANETs. This innovative concept enhances routing algorithms for three specific VANET network traffic circumstances. Genetic algorithms (GA) are employed for dynamic optimization and adaptation to evolving traffic conditions, hence introducing a novel aspect to ant colony optimization (ACO). Implementing this hybrid approach can enhance the efficiency of network operations in the context of dynamic and unexpected vehicular communication by increasing the resilience and adaptability of routing decisions. Regrettably, the integration of GA may lead to an escalation of computational intricacy, perhaps impacting the ability to make real-time decisions in situations with a high volume of traffic. An evaluation of these trade-offs is necessary to establish the feasibility and effectiveness of the GAACO technique in different VANET traffic scenarios, which might potentially make it a valuable addition to VANET routing protocols. The Enhanced Cluster-Based Lifetime Protocol (ECBLTR) optimizes the average throughput and enhances the stability of routing networks in Vehicular Ad Hoc Networks [17]. The protocol assesses Cluster Heads (CH) based on factors such as concentration, residual energy, node degree, and local distance from the Base Station (BS) utilizing the Sugeno approach fuzzy inference system. ECBLTR enhances network performance and stability by optimizing the lifespan of clusters. The implementation of fuzzy logic in identifying Cluster Heads (CHs) enhances the decision-making process in VANETs, making it more informed and adaptable. Nevertheless, the utilization of the Sugeno approach might lead to an escalation in computational intricacy and pose challenges in the adjustment of fuzzy logic parameters. Comprehending these compromises is essential for assessing the practicality and effectiveness of ECBLTR in VANET applications, hence establishing it as a feasible cluster-based routing protocol [18]. The stability of VANET clusters is a significant concern. This article presents a novel clustering technique that utilizes the concept of average weight in geostationary coordinates (x,y) and drop density characteristics. The performance of Cluster Heads is affected by the frequent connection or disconnection of dynamic nodes in VANETs. The system employs a multi-objective framework to compute the mean value of crucial attributes, exclude cars with low mean values, and choose CHs based on the least Euclidean distance and social score across checkpoints. Quality of Service (QoS) characteristics are responsible for determining the social score, while the ADOV routing protocol is utilized for the transfer of data. The comparison study reveals that there is a 28.27% improvement in throughput, a 20.9% improvement in PDR (Packet Delivery Ratio), a 23.12% improvement in network lifespan, and a 27.48% improvement in energy use. The suggested methodology enhances network stability by extending the lifespan of cluster heads, which is a substantial improvement compared to existing VANET clustering methods.

3  Proposed Model

In this article, we have presented an energy-efficient communication protocol for VANET, named the FOA-EECPCR technique. The core objective of the FOA-EECPCR technique is to group the vehicles and determine the shortest route in the VANET. To accomplish this, the FOA-EECPCR technique involves FOA-based clustering and SSA-based routing. Fig. 1 implies the working process of the FOA-EECPCR approach.

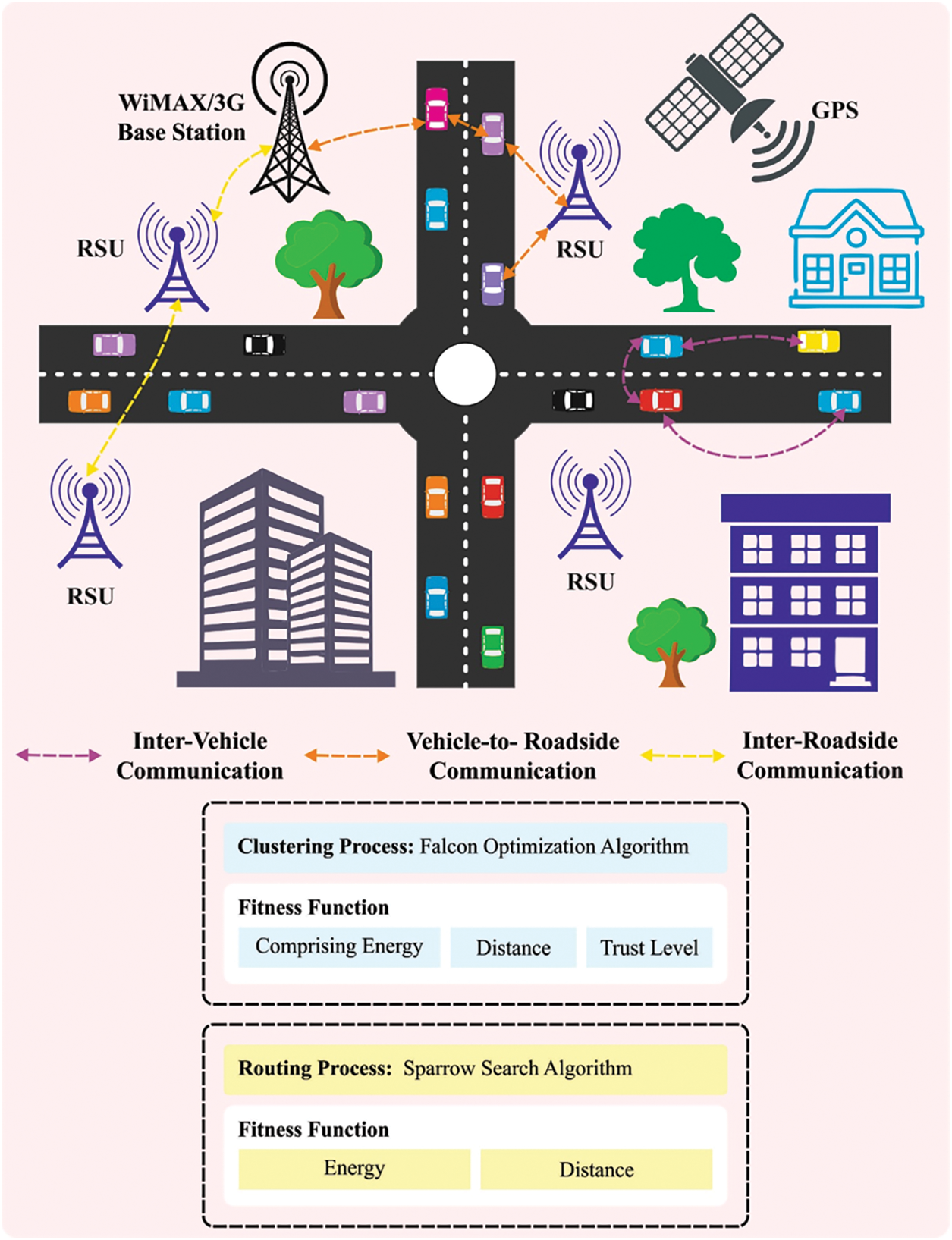
Figure 1: Working process of FOA-EECPCR approach

3.1 Design of Clustering Process

Primarily, the FOA-EECPCR technique designs the FOA for the CH selection and cluster construction process. While flying falcon approach their prey in different ways. The route is divided into a logarithmic curve and a straight segment. Initially, the falcon keeps its head straight while looking slantingly at the prey. Next, they fly towards the prey in their vision and dive when they become closer to it. Consequently, falcons primarily attain a movement that is split into three stages: The initial stage includes prey exploration; the next, which contains an enhancing look of the logarithmic curve; and the last which includes the dive itself that might result in effective outcomes, like picking prey. The falcon immediately changes its behavior rather depending on its previous experience; the five steps of a quick approach to adopting FOA are given in the following.

Step 1: Define the parameters of the optimization tasks like the social constant (sc), rate of (cc), cognitive rate, falcon number (NP), the limit of speed (Vmax), probability of dive (DP), following constant (fc), and the alertness probability (AP).

Step 2: Depending on the boundary condition where all falcon location is determined, allocate the velocity of falcons and the position of falcons in the D-dimensional space while considering the number of NP candidates in every D dimension. The velocities are generated at random between the Vmin and Vmax limitations that are given as follows:

Vmax=0.1∧∗ub(1)

Vmin=−Vmax(2)

where ub represents the upper bound of every dimension. Generate the pairing value (pAP, pDP) for all falcons at random for comparison with the dive probability and awareness.

Step 3: Discover the best (xbest) and global (gbest) positions by computing the fitness value. The selected position used for creating a new location depends on the logic that oversees the probabilities of awareness and the dive’s movement.

Step 4: Make a new location and reposition the falcon as needed. The falcon explores the pAP of the aware probability AP based on its experience, and if the AP is larger than the pAP, then the falcon avoids pursuing prey:

Xiter+1=Xiter+Viter+cc(Xbest,Xiter)+sc(gbest,Xiter)(3)

where Viter signifies the present velocity and Xiter signifies the falcon’s present position.

The probability of dive DP is compared with pDP if AP is lesser than pAP. If DP is lesser than pDP, then the Falcon chooses the target as the prey and completes the initial stage during hunting. The logarithmic spiral can be evaluated by Eq. (4):

X_(iter+1)=X_iter+|X_chosen−X_iter|exp(bt)cos(2πt)(4)

where b is a fixed number and considers the location of the logarithmic spiral that matches 1 and a random number within the interval (−1,1) which determines the falcon’s next precise position.

If AD is greater than pAP, the score function of the desired prey is compared to the scoring function of the falcon and follows the desired prey wherever it is better suited as a dive step:

Xiter+1=Xiter+Viter1+fc∗rand(Xchosen−xiter)(5)

In contrast, the falcon continues to fly around the optimum location:

Xiter+1=Xiter+Viter1+cc∧∗(rand)(Xbest,Xiter)(6)

Next, the new positions can be evaluated regarding location bounds and velocities. Then compute the new scoring function and update gbest and Xbest values.

Step 5: The assessment from Step 4 is reiterated till the iteration of the maximal number (itermax) is attained. Falcon GO, which demonstrates a DAG using arcs, tries, moves, addition, deletion, and reversal, goes to the newest solutions G1, G2, G3, and G4. G3 are selected meanwhile, it has the maximum score; then falcon continues to explore using a corresponding approach to arrive at G+3 as subsequent alternative. G+3 BDeu score was used when the G+3 BDeu score is greater than the G+1 BDeu score; then falcon will perform a similar operation. This process can be iterated while the repetition loop reaches its maximum length or the score of BDeu is fixed. Overall, the falcon should pick between additions, deletions, movement, and reversals.

The FOA technique gains a fitness function (FF) utilizing 3 input parameters distance to neighbors, energy for CH selection, and trust level [19].

Distance to a neighbor: It can be relevant to choose CH with lesser distance between adjacent nodes. During the intracluster transmission system, power utilization of sensor to CH communication. Once the neighboring node distance is minimalized, then the energy of the intracluster broadcast can be minimized correspondingly.

Objective 1: Minimizing

f1=∑j=1m⁡1lj(∑i=1lj⁡dis(CHj,si))(7)

Trust factor (TF): Primarily, every single node states that TF is 1. The TF value can be decreased with an anomalous forecast system, but the node procedure is an abnormal task and the nodes were termed as malicious nodes.

Objective 2: Maximizing

f2=∑j=1m1m(TFj)(8)

Energy: It is the energy count exhausted as CH to RE of CH. If the CH exploits a lesser energy process, the sensing, as well as broadcast procedure with greater RE was gathered at a lower energy ratio. Thus, with a lower energy ratio, CH selective grow is more possible.

Objective 3: Minimizing

f3=∑j=1mEc(CHj)ER(CHj)(9)

During the FOA system, it can be vital to use less the linear combination of objective functions. Therefore, the probable energy function of the FOA system was executed by:

Minimize Potiential energy function=α1⋅f1+α2⋅f2+α3⋅f3(10)

Here, α1 + α2 + α3 = 1, α2≥(α1 + α3). Also 0 < f1, f2, f3 < 1.

3.2 Process Involved in Route Selection

The SSA is a natural heuristic approach stimulated by the group socialization features and behaviors of sparrows foraging and avoiding predators. SSA has the advantage of stronger optimization ability, simple structure, easier implementation, few control parameters, and so on [20]. The SSA converges toward the present optimum solution to directly jump towards the locality of the present optimum solution; hence the SSA model is much better than particle swarm optimization, grey wolf optimization, and gravity search algorithms regarding robustness, accuracy, convergence speed and stability. In this work, sparrows are split into vigilant and discoverer followers. The sparrow location is corresponding to the solution. First population generation using randomly assigned sparrow pathways. The sparrows' positions are updated iteratively using the fitness function and social behaviors, which include exploring new routes and converging towards promising ones. After each iteration, choose the sparrow with the best match (shortest path). The position of each sparrow in the group can be denoted as X matrix as

X==(χ1,2…a1,d⋮…⋮xm,1…xm,d)(11)

In Eq. (11), d characterizes the dimension of the variable, and m signifies the number of sparrows. The fitness function respective to every sparrow can be denoted as F matrix:

F=(f([x1,1&…&x1,d])⋮f([xm,1&…&xm,d]))(12)

In Eq. (12), f([x_(i,1), ⋯ , x_(i,d)]) in line i signifies the fitness value of i-th sparrow. At all iterations, the position of the discoverer is upgraded as follows:

Xi,jt+1={xi,jt⋅exp⁡(−iα⋅N),if R2<STxi,jt+Q⋅L,if R2≥ST(13)

In Eq. (13), t signifies the existing amount of h iterations, and N characterizes the maximal amount of iterations. α refers to the random integer and α ∈ (0,1]. R2 and R2 ∈ [0,1] [0,1] denote the random numbers. ST signifies the safety threshold and ST ∈ [0.5,1.0]. Q denotes an arbitrary value subjected to a standard distribution, and L shows the row vector whose components were equivalent to one. The updating rules of the follower are shown below:

Xi,jt+1={Q⋅exp⁡(XWt−Xι,jti2),if i>n2xDBt+1+|Xi,jt−xDBt+1|⋅M′⋅L,if i≤n2(14)

In Eq. (14), XWt denotes the worst location of the t-th iteration, and xDBt+1 characterizes the location of the finder with the maximal fitness value at t+1iteration. M shows the 1 × d matrix, where the Process Involved in Route Selection is transposed. The flowchart of SSA has been illustrated in Fig. 2.

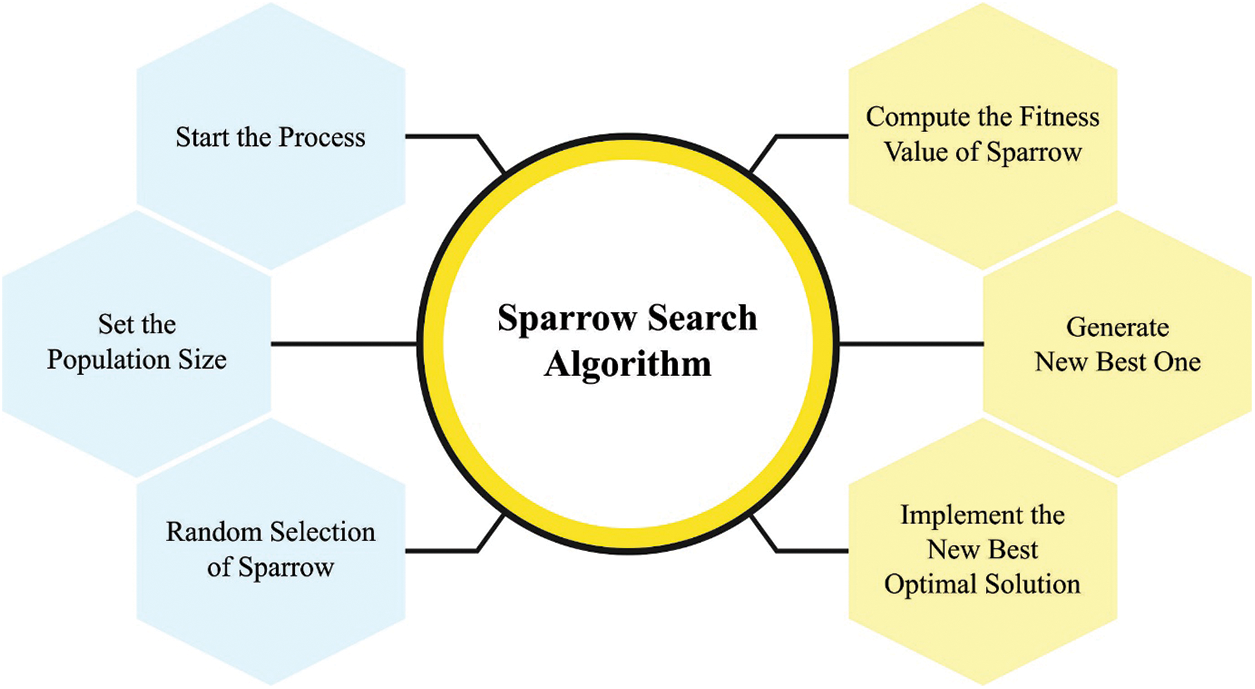
Figure 2: Flowchart of SSA

Algorithmic Parameter as follows:

Population Size (N): The number of sparrows in the population. A typical range is 10 to 50, but it can be adjusted based on the complexity of the problem.

Maximum Number of Iterations (T): The maximum number of iterations the algorithm will run. This is usually set to a high value to ensure convergence.

Control Parameters are as follows:

Number of Producers (NP): The proportion of sparrows that act as producers, typically set around 20% of the population.

Number of Scroungers (NS = N − NP): The proportion of sparrows that act as scroungers.

Number of Scouts (SD): A small number of sparrows assigned to scout for new areas, often set to 10% of the population.

Warning Threshold (ST): A value that determines when the sparrows sense danger and switch to vigilant behavior. A common value is 0.8.

Safety Threshold (SD): A value that determines when the sparrows move to a safe area. A common value is 0.6.

The optimal settings for SSA can vary depending on the specific problem being solved. It is often recommended to experiment with different parameter combinations to find the best configuration for your particular application. Adaptive parameter adjustment strategies can also be employed to dynamically adjust parameters during the optimization process.

The updating position of the vigilant is:

Xi,jt+1={xGBt+γ⋅|Xi,jt−xGBt|,if fi≠fBxGBt+k⋅(Xit′−xGBt|fi−fw|+ε),if fi=fB(15)

In Eq. (15), xtGB denotes the global optimum position at t-th iteration, γ indicates the control step size, and γ-N(O,1). k represents the random integer and k ∈ [−1,1], whereas ε shows the constant that rises to avoid the denominator from being 0. fB and fw denote the global optimum and worst sparrow fitness value, correspondingly. fi shows the fitness value of i-th sparrow.

In Fig. 2, the SSA model could adjust including the maximal number of iterations N, the number of sparrows n, and safety value ST. Furthermore, there exist upper and lower bounds of the independent parameter DL, the amount of discoverers PD, and the amount of vigilante SD. The d-dimension of the independent parameter is defined by the number of network layers and the input vector.

For defining the group of routes exploiting the SSA technique, the provided function has been executed for determining the successive hop to BS:

f(x)={i, for which|(i/k−X_(i_fj))|is minimum, ∀_i 1≤i≤k(16)

where, f(x): This represents the function you are defining, arg mini function is seeking the value of ii that minimizes the expression following it. i/k fraction where ii is divided by k. Xifj term involves the variable XX with subscripts if and j. It seems like a specific element in a matrix or array, but without more context, it is challenging to provide a precise interpretation. (i/k−X_(i_fj)) This is the absolute difference between the fraction ik and the value of Xifj.

The purpose is to determine a group of routes from CH to s applying an FF encompassing two variables like distance and energy. In the beginning, the RE of the Next-hop node can be introduced and nodes with maximal energy can be offered as relay nodes. For data broadcast, the source node transfers to the relay node, which transmits to BS with inter-CH. So, the node having superior RE can be offered as next-hop nodes. The f1 primary sub-objectives can be offered as:

f1=E_CH(17)

Euclidean distance is utilized to resolve the distance between CH to BS. The decrease in energy dissipation mostly depends on the communication distance. By exploiting a lesser distance, the energy can be preserved considerably. Once the distance can be higher, more count of energy can be utilized. Accordingly, the nodes with lesser distance can be preferred to relay nodes. Thus, the next sub-objectives utilizing distance f2 are written as:

f2=1∑i=1md is(CHi,NH)+d is(NH,BS)(18)

The aforementioned sub-objectives are supposed what FF is provided under, whereas α1 and α2 signify the weight assigned to every sub-objective.

Fitness=α1(f1)+α2(f2), where∑i=12αi=1αiε(0,1);(19)

4  Results and Discussion

In this section, the experimental validation of the FOA-EECPCR method is investigated in detail. Table 1 and Fig. 3 represent a comparative energy efficiency (EE) inspection of the FOA-EECPCR technique under several vehicles [21]. The results represent that the CBR and AODV-CV models attain lower values of EE. Simultaneously, the DACRS technique reaches moderate EE values. Although the EMCMHRLM model obtains a closer EE value, the FOA-EECPCR technique attains the maximum EE values. For example, with 50 vehicles, the FOA-EECPCR technique provides increasing EE of 10.92%, while the CBR, AODV-CV, DACRS, and EMCMHA LM models obtain reducing EE of 4.16%, 4.40%, 6.57%, and 8.26%, respectively.

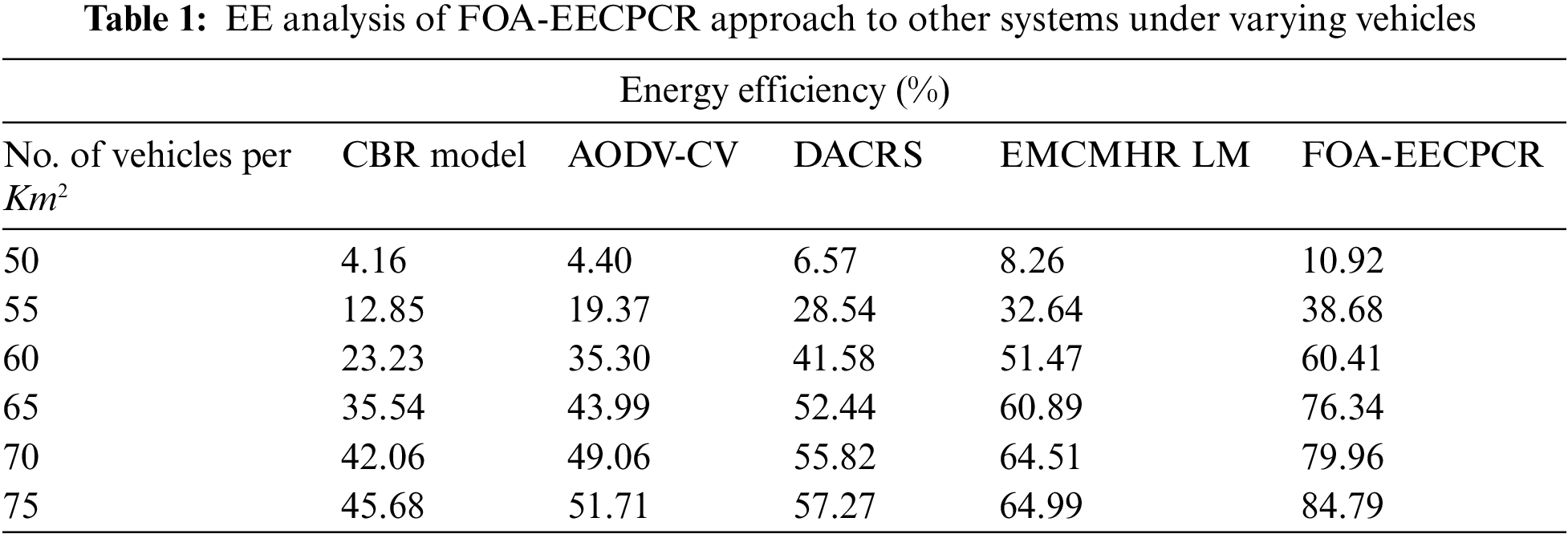
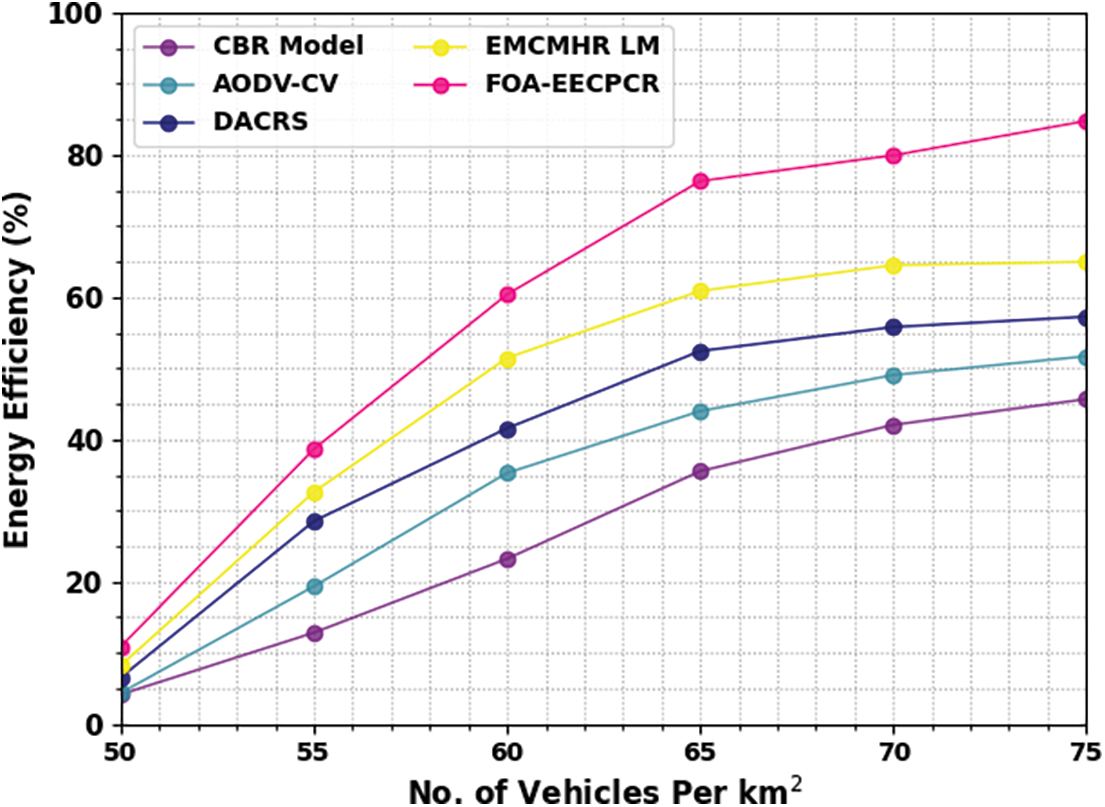
Figure 3: EE analysis of FOA-EECPCR algorithm under varying vehicles

FOA-EECPCR routes and clusters using SSA and FOA tuning parameters. Sensitivity studies improved energy efficiency, distance coverage, and trust. Multiple traffic scenarios tested protocol resilience. High-density traffic, rapid topological changes, and variable vehicle speeds were involved. Benchmark Protocols: The studies compared VANET benchmark protocols. We carefully compared FOA-EECPCR to other methods. Research approaches and algorithms are described in the methodology section. Data processing, analysis, and collecting are discussed. Some key elements are FOA-EECPCR clusters automobiles utilizing Falcon Optimization. Fitness functions—trust, energy, and distance—determine clusters. SSA Sparrow Search Algorithm routes utilizing distance and energy fitness functions. Energy and geographical coverage are optimized by routing. Simulations collected perimeter-specific energy, distance, and trust data. FOA-EECPCR effectiveness indicators were investigated using these data. Distance coverage, energy efficiency, and trust level adherence were FOA-EECPCR performance indicators. Being compared to benchmarks helps assess its efficacy.

Table 2 and Fig. 4 show a comparative packet delivery ratio (PDR) examination of the FOA-EECPCR method under several vehicles. The results represent that the CBR and AODV-CV methods attain lower values of PDR. Simultaneously, the DACRS system reaches moderate PDR values. Although the EMCMHRLM method obtains closer PDR values, the FOA-EECPCR technique obtains higher PDR values. For example, with 50 vehicles, the FOA-EECPCR method gives an increasing PDR of 67.27%, while the CBR, AODV-CV, DACRS, and EMCMHA LM methods obtain a reducing PDR of 42.52%, 48.09%, 53.21%, and 56.29%, respectively.

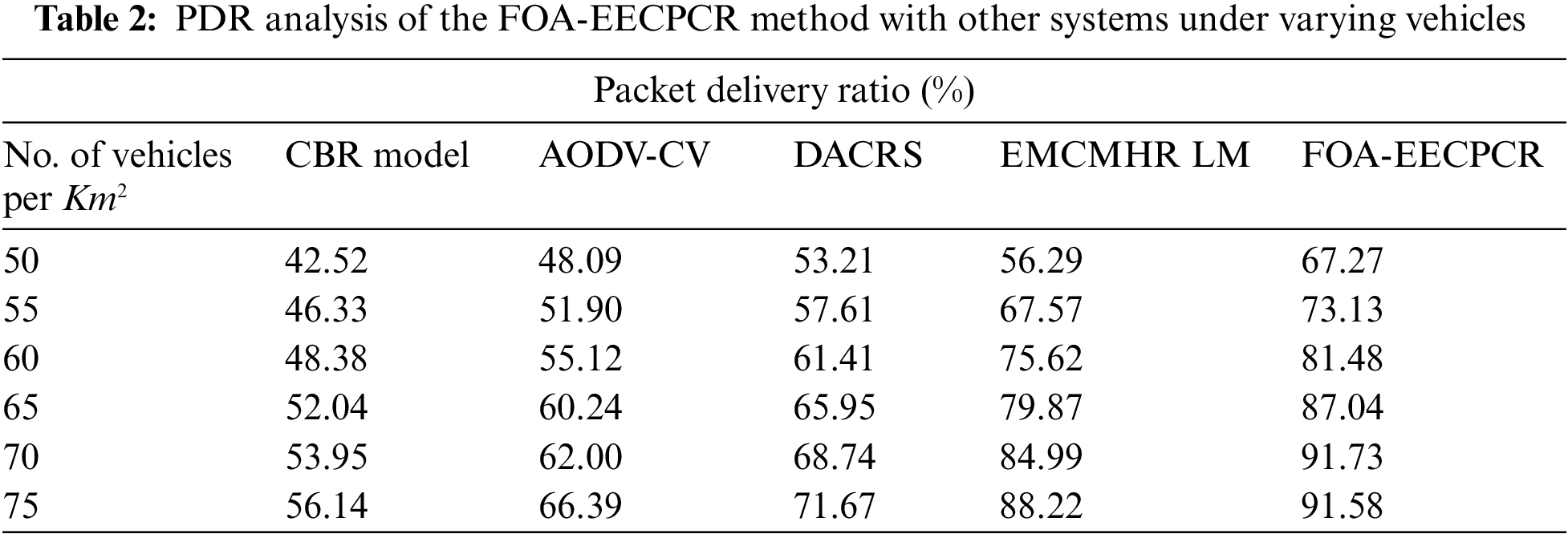
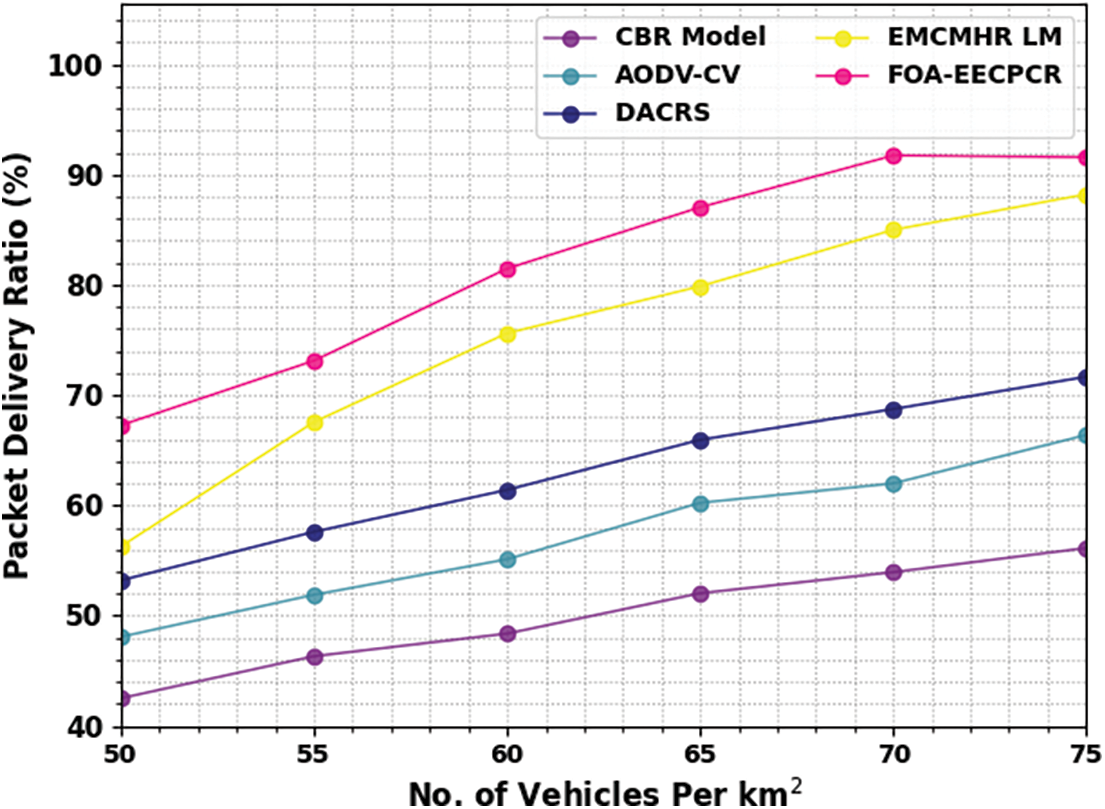
Figure 4: PDR analysis of FOA-EECPCR approach under varying vehicles

A comparative packet loss ratio (PLR) assessment of the FOA-EECPCR technique is studied under several vehicles in Table 3 and Fig. 5. The outcomes highlighted the PLR values of the FOA-EECPCR technique. For instance, with 50 vehicles, the FOA-EECPCR technique attains a decreasing PLR of 32.73%, while the CBR, AODV-CV, DACRS, and EMCMHA LM models provide increasing PLR of 57.48%, 51.91%, 46.79%, and 43.71%, respectively. At the same time, with 60 vehicles, the FOA-EECPCR method obtains decreasing PLR of 18.52%, while the CBR, AODV-CV, DACRS, and EMCMHA LM techniques provide increasing PLR of 51.62%, 44.88%, 38.59%, and 24.38%, correspondingly. Meanwhile, with 70 vehicles, the FOA-EECPCR method obtains decreasing PLR of 8.42%, while the CBR, AODV-CV, DACRS, and EMCMHA LM methods provide increasing PLR of 43.86%, 33.61%, 28.33%, and 11.78%, correspondingly.

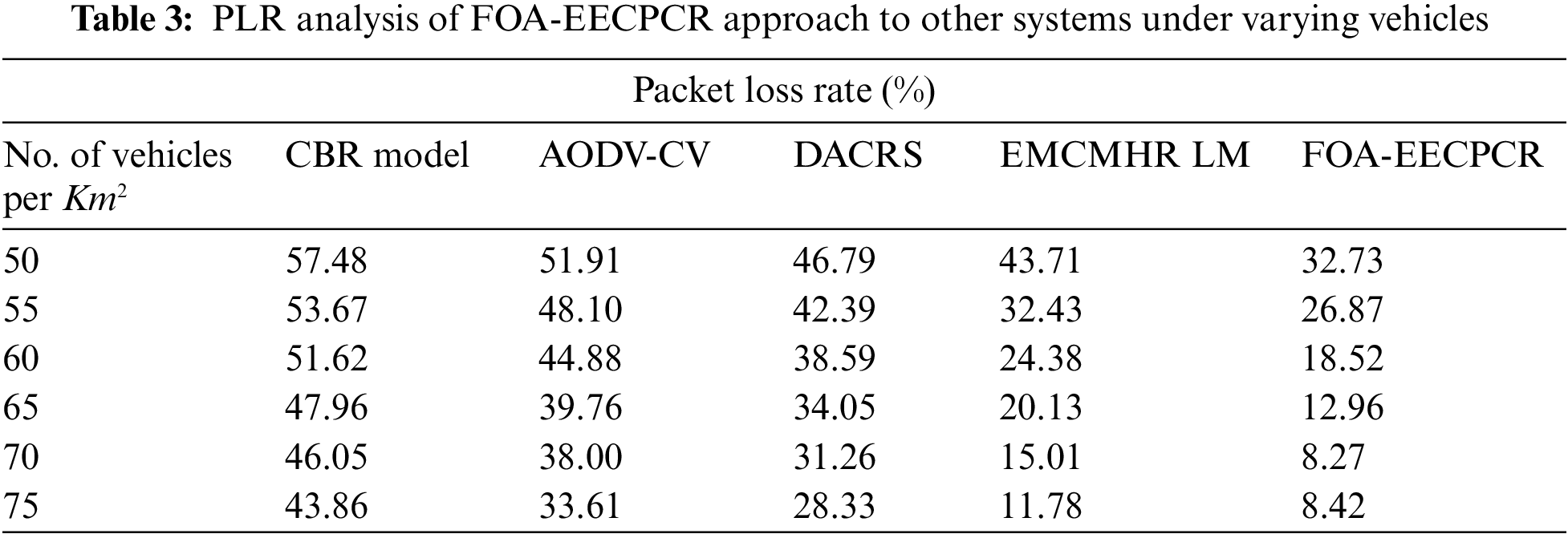
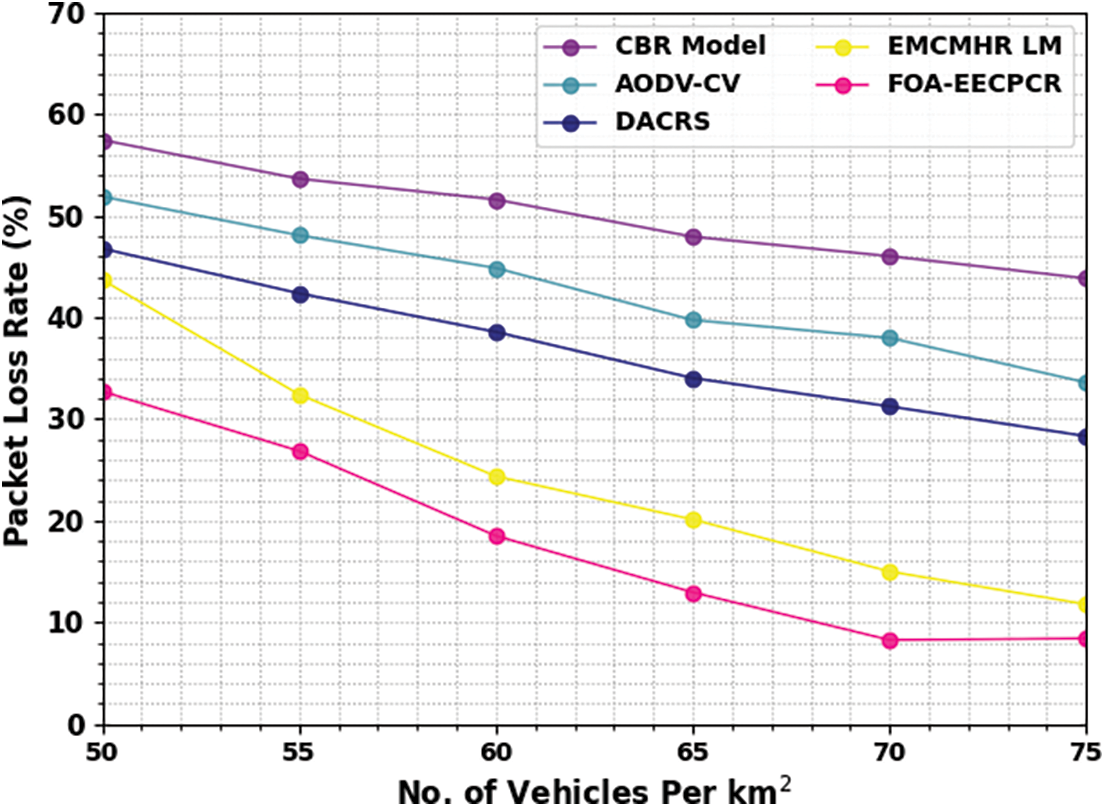
Figure 5: PLR analysis of FOA-EECPCR approach under varying vehicles

Table 4 and Fig. 6 represent a comparative throughput (THRO) examination of the FOA-EECPCR technique under several vehicles. The results represent that the CBR and AODV-CV methods attain lower values of THRO. Simultaneously, the DACRS method attains moderate THRO values. Although the EMCMHRLM method obtains closer THRO values, the FOA-EECPCR technique obtains maximum THRO values. For example, with 50 vehicles, the FOA-EECPCR method provides increasing THRO of 47.53 Kbps, while the CBR, AODV-CV, DACRS, and EMCMHA LM techniques obtain reducing THRO of 20.85, 26.19, 29.58, and 35.40 Kbps.

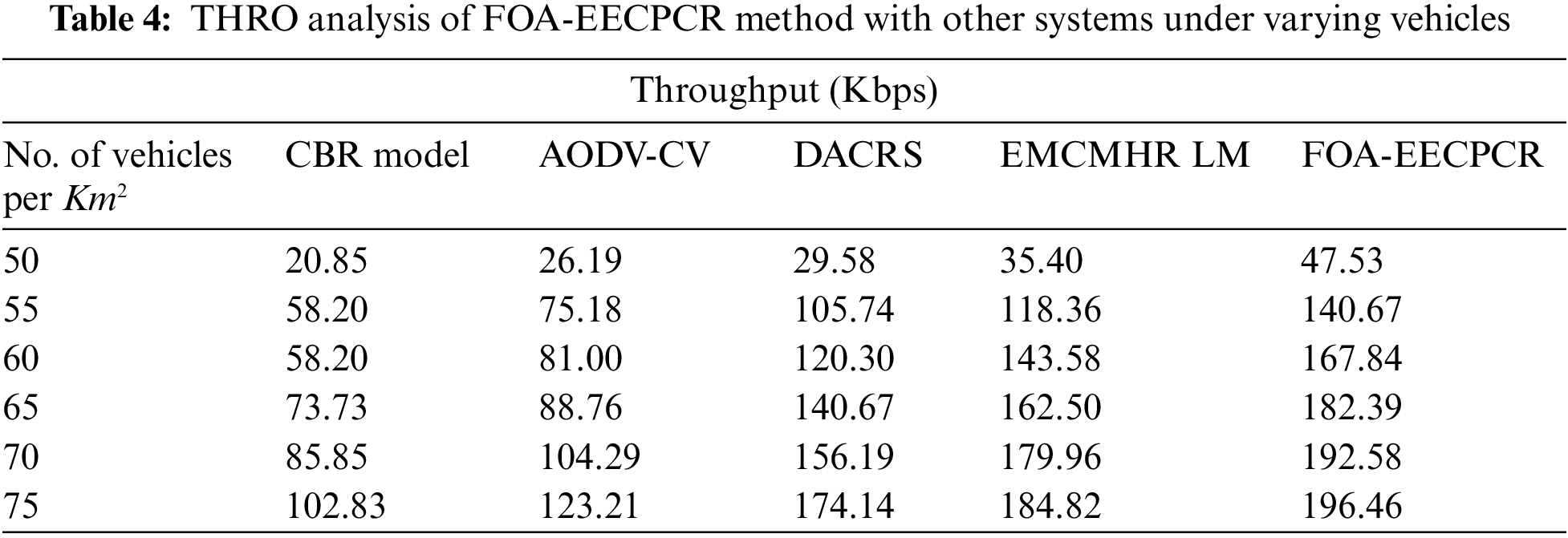
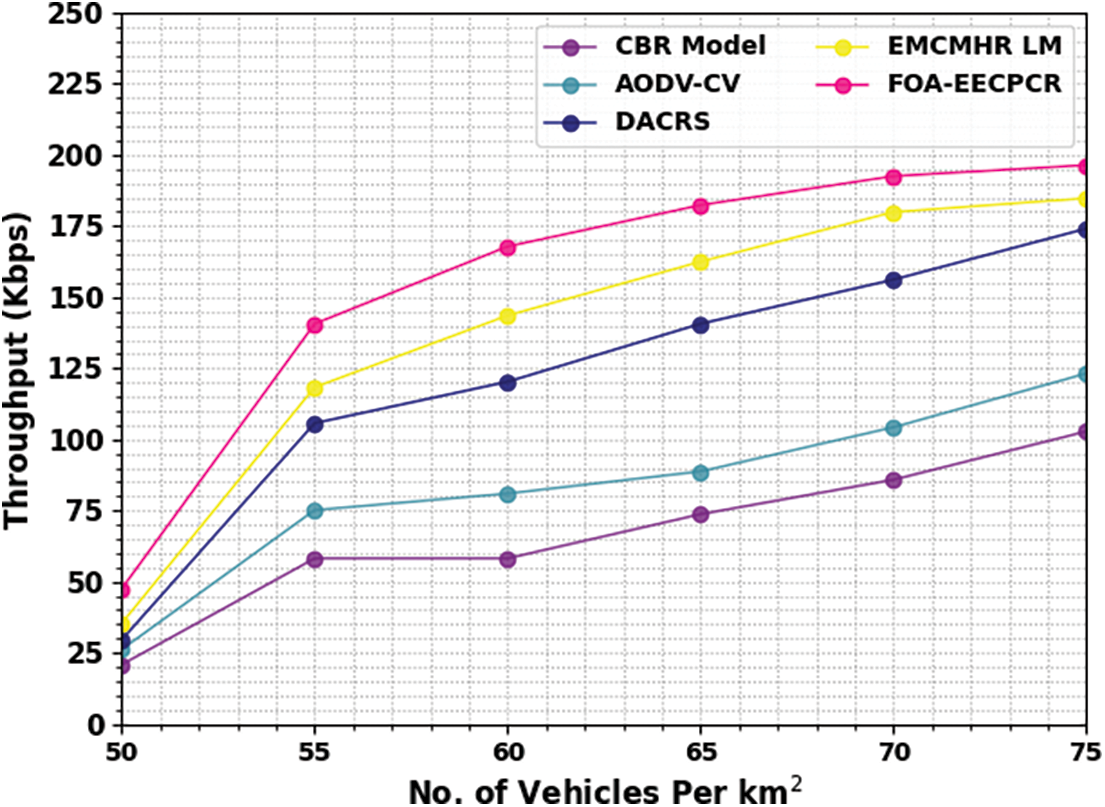
Figure 6: THRO analysis of FOA-EECPCR approach under varying vehicles

A comparative cluster overhead (COH) assessment of the FOA-EECPCR method is studied under several vehicles in Table 5 and Fig. 7. The figure highlights the COH values of the FOA-EECPCR method. For example, with 50 vehicles, the FOA-EECPCR method obtains decreasing COH of 3, while the CBR, AODV-CV, DACRS, and EMCMHA LM models provide increasing COH of 27, 22, 17, and 19, correspondingly. Simultaneously, with 60 vehicles, the FOA-EECPCR technique attains decreasing COH of 46, while the CBR, AODV-CV, DACRS, and EMCMHA LM methods provide increasing COH of 90, 83, 73, and 64, correspondingly. Meanwhile, with 70 vehicles, the FOA-EECPCR technique attains decreasing COH of 80, while the CBR, AODV-CV, DACRS, and EMCMHA LM methods provide increasing COH of 147, 145, 133, and 105, correspondingly.

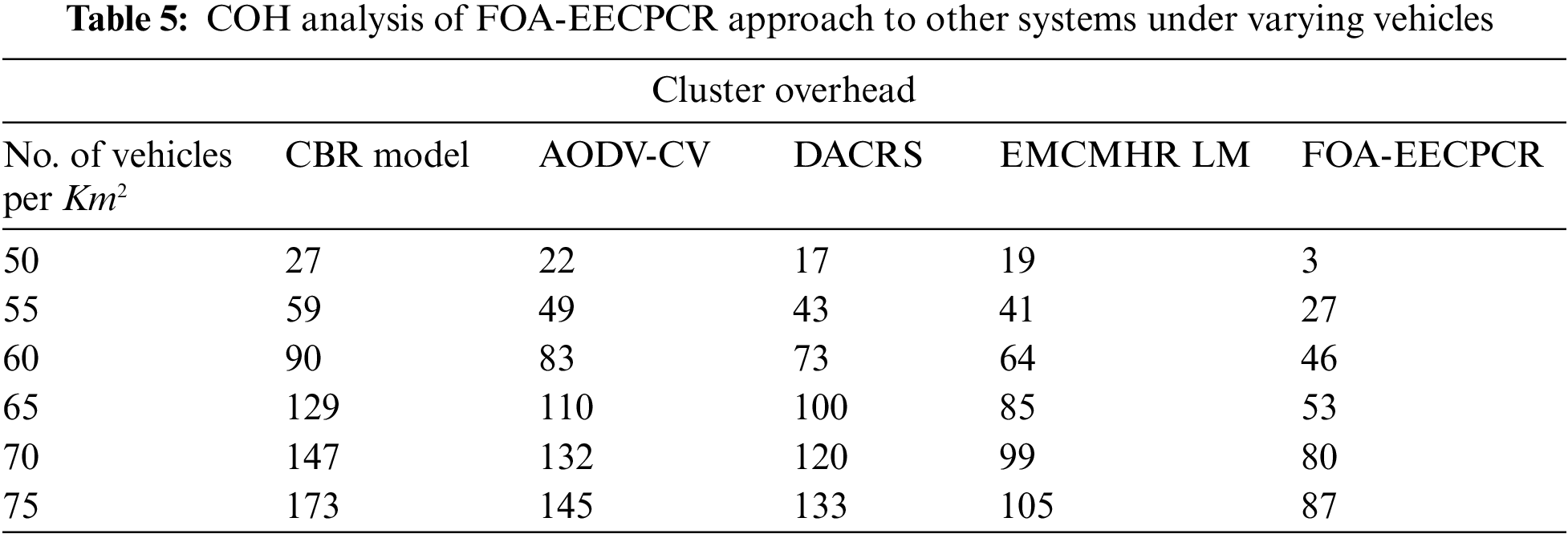
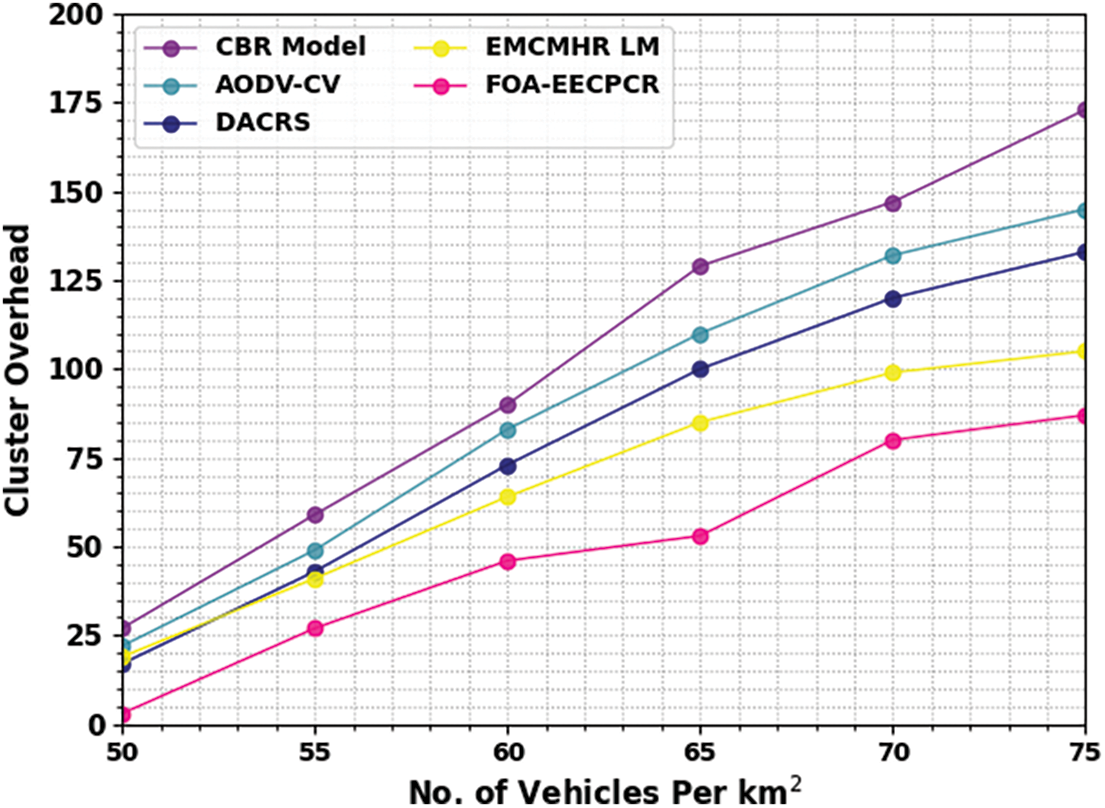
Figure 7: COH analysis of FOA-EECPCR approach under varying vehicles

Table 6 and Fig. 8 represent a comparative coverage (COV) inspection of the FOA-EECPCR technique under several vehicles. The results represent that the CBR and AODV-CV methods accomplish lower values of COV. Simultaneously, the DACRS method obtains moderate COV values. Although the EMCMHRLM model obtains a closer COV value, the FOA-EECPCR technique attains maximum COV values. For example, with 50 vehicles, the FOA-EECPCR method provides increasing COV of 34.99%, while the CBR, AODV-CV, DACRS, and EMCMHA LM models obtain reducing COV of 17.61%, 20.51%, 24.13%, and 28.23%, correspondingly.

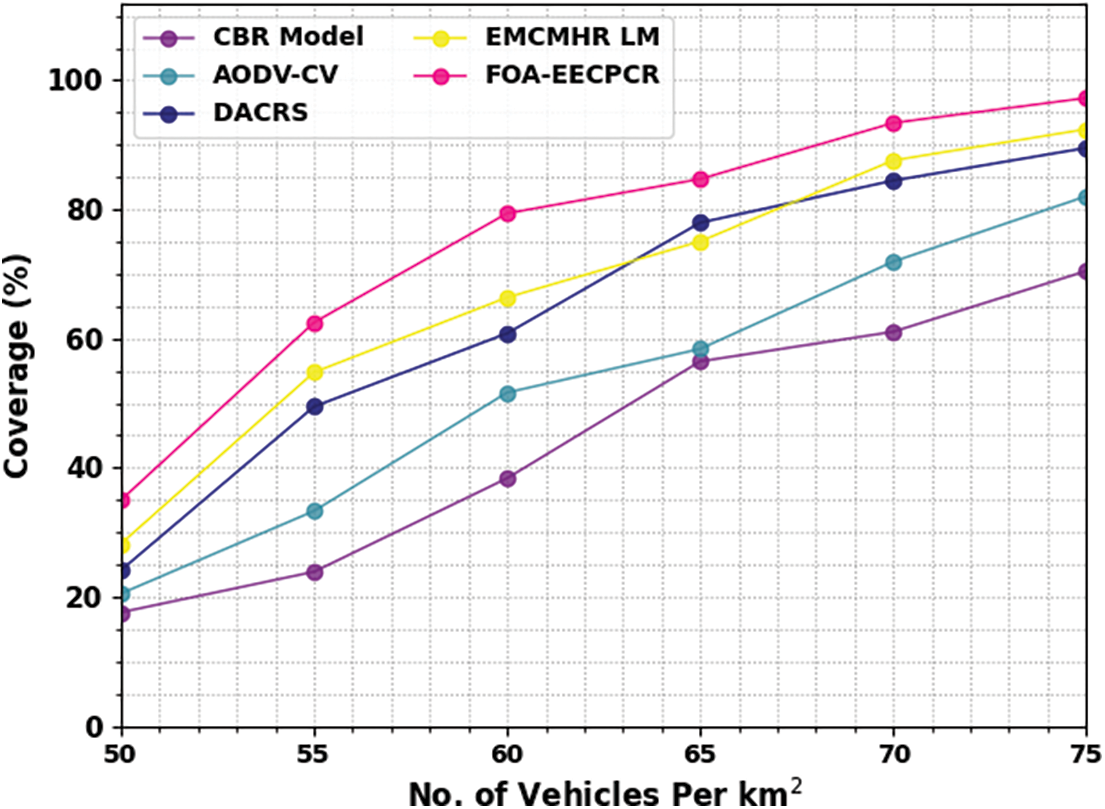
Figure 8: COV analysis of FOA-EECPCR approach under varying vehicles

A comparative end-to-end delay (ETED) assessment of the FOA-EECPCR method is studied under different vehicles in Table 7 and Fig. 9. The figure emphasizes the least ETED values of the FOA-EECPCR technique. For example, with 50 vehicles, the FOA-EECPCR method attains decreasing ETED of 11.06 s while the CBR, AODV-CV, DACRS, and EMCMHA LM models provide increasing ETED of 19.90, 18.20, 16.46, and 15.04 s, correspondingly.

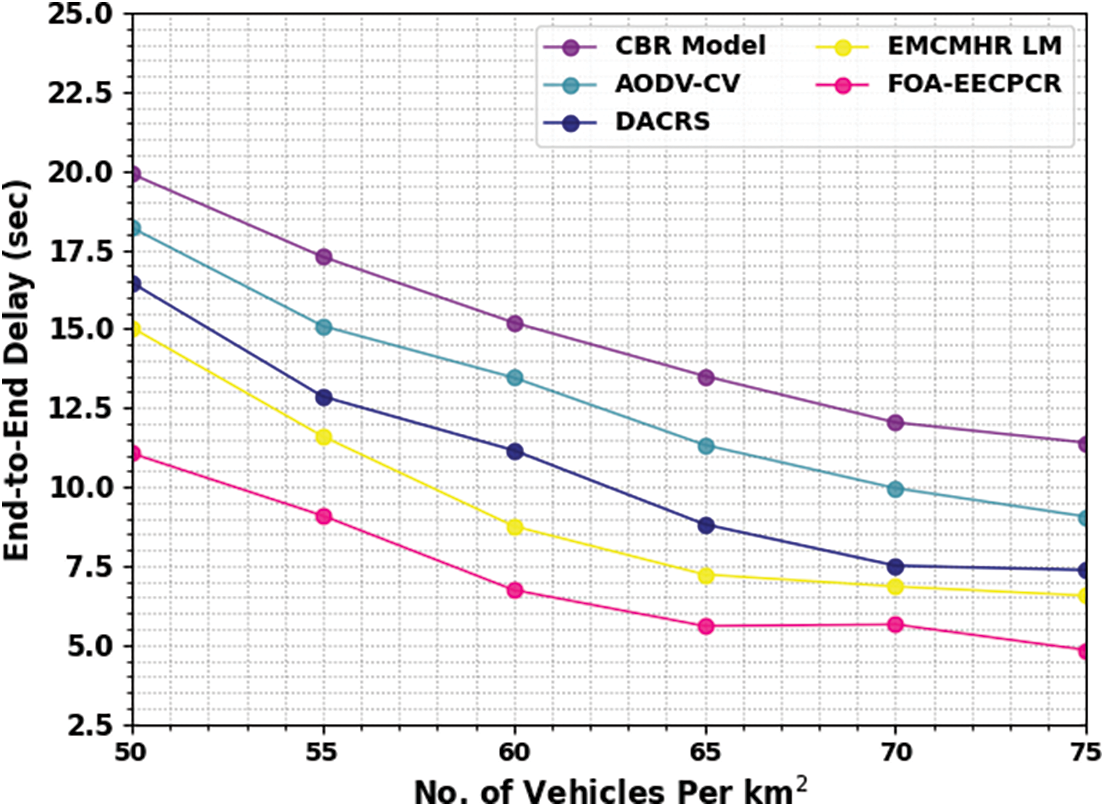
Figure 9: ETED analysis of FOA-EECPCR approach under varying vehicles

Simultaneously, with 60 vehicles, the FOA-EECPCR technique attains decreasing ETED of 6.74 s, whereas the CBR, AODV-CV, DACRS, and EMCMHA LM methods provide increasing ETED of 15.20, 13.46, 11.16, and 8.76 s, correspondingly. Meanwhile, with 70 vehicles, the FOA-EECPCR method attains a decreasing ETED of 5.65 s, while the CBR, AODV-CV, DACRS, and EMCMHA LM models provide increasing ETED of 12.04, 9.96, 7.51, and 6.85 s, respectively.

5  Conclusion

In this article, we have presented an energy-efficient communication protocol for VANET, named the FOA-EECPCR technique. The end goal of the FOA-EECPCR approach is to group the vehicles and determine the shortest route in the VANET. To accomplish this, the FOA-EECPCR technique initially clusters the vehicles using FOA with fitness functions comprising energy, distance, and trust level. For the routing process, the SSA is derived with a fitness function that encompasses two variables namely energy and distance. A wide range of experiments has been conducted to exhibit the enhanced performance of the FOA-EECPCR method. The experimental results demonstrate the enhanced performance of the FOA-EECPCR algorithm over other recent methods. The limitation of the Proposed solution is may not scale for VANETs with many automobiles. Network expansion may decrease efficiency. Practical Implementation Issues Test the approach with real-world traffic and cars. Consider hardware and deployment limits. For VANET security, the proposed protocol should be tested for malicious node injections, jamming, and surveillance. Data protection is crucial. Altered Dynamic Topology seems intriguing, but further study is needed to discover if it can withstand frequent and rapid network topology changes, especially from high-speed mobility. FOA-EECPCR energy model accuracy may impact routing protocol performance. Realism is important in energy models. In future, the presented FOA-EECPCR method will be extended to the design of data aggregation protocols. Fortify the security measures of the protocol by incorporating authentication, encryption, and intrusion detection systems to safeguard vehicular networks against a multitude of security risks.

Acknowledgement: The authors would like to express their gratitude to the Umm Al-Qura University, Sathyabama Institute of Science and Technology, Panimalar Engineering College, and Saveetha Institute of Medical and Technical Science.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, Y. A., and R. B.; methodology, S. R.; software, R. B.; validation, Y. A., S. R. and J. R.; formal analysis, Y. A.; investigation, S. R.; resources, Y. A.; data curation, J. R.; writing—original draft preparation, S. R.; writing—review and editing, Y. A.; visualization, Y. A.; supervision, R. B.; project administration, S. R.; funding acquisition, Y. A. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, Surendran Rajendran, upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. G. Husnain and S. Anwar, “An intelligent cluster optimization Algorithm-based on Whale Optimization Algorithm for VANETs (WOACNET),” PLoS One, vol. 16, no. 4, pp. 250–271, 2021. doi: 10.1371/journal.pone.0250271. [Google Scholar] [PubMed] [CrossRef]

2. K. Nagappan, S. Rajendran, and Y. Alotaibi, “Trust aware multi-objective metaheuristic optimization based secure route planning technique for cluster-based IIoT environment,” IEEE Access, vol. 10, pp. 112686–112694, 2022. doi: 10.1109/ACCESS.2022.3211971. [Google Scholar] [CrossRef]

3. C. J. Joshua, P. Jayachandran, A. Q. Md, A. K. Sivaraman, and K. F. Tee, “Clustering, routing, scheduling, and challenges in bio-inspired parameter tuning of vehicular ad hoc networks for environmental sustainability,” Sustainability, vol. 15, no. 6, pp. 47–67, 2023. doi: 10.3390/su15064767. [Google Scholar] [CrossRef]

4. D. Chandramohan, A. Dumka, and L. Jayakumar, “2M2C-R2ED: Multi-metric cooperative clustering based routing for energy efficient data dissemination in green-VANETs,” Technol. Econ. Smart Grids Sustain. Energy, vol. 5, no. 1, pp. 1–14, 2020. doi: 10.1007/s40866-020-00086-4. [Google Scholar] [CrossRef]

5. B. Iswarya and B. Radha, “Energy efficient clustering technique for VANET,” Adv. Parallel Comput. Tech. App., vol. 40, pp. 105, 2021. doi: 10.3233/APC210129. [Google Scholar] [CrossRef]

6. A. Nahar and D. Das, “MetaLearn Optimizing routing heuristics with a hybrid meta-learning approach in vehicular ad-hoc networks,” Ad Hoc Netw., vol. 138, no. 3, pp. 102996, 2023. doi: 10.1016/j.adhoc.2022.102996. [Google Scholar] [CrossRef]

7. N. N. Sulthana and M. Duraipandian, “EELCR: Energy efficient lifetime aware cluster based routing technique for wireless sensor networks using optimal clustering and compression,” Telecommun. Syst., vol. 85, no. 1, pp. 103–124, 2024. doi: 10.1007/s11235-023-01068-4. [Google Scholar] [CrossRef]

8. B. Kheradmand, A. Ghaffari, F. S. Gharehchopogh, and M. Masdari, “Cluster-based routing schema using harris hawks optimization in the vehicular Ad Hoc networks,” Wirel. Commun. Mob. Comput., vol. 9, no. 2, pp. 12–29, 2022. doi: 10.1155/2022/1606317. [Google Scholar] [CrossRef]

9. H. Fatemidokht and M. K. Rafsanjani, “QMM-VANET: An efficient clustering Algorithm-based on QoS and monitoring of malicious vehicles in vehicular ad hoc networks,” J. Syst. Softw., vol. 165, pp. 110561, 2020. doi: 10.1016/j.jss.2020.110561. [Google Scholar] [CrossRef]

10. N. Phull, P. Singh, M. Shabaz, and F. Sammy, “Performance enhancement of cluster-based ad hoc on-demand distance vector routing in vehicular Ad Hoc networks,” Sci. Program., vol. 1, no. 2, pp. 45–52, 2022. doi: 10.1155/2022/7423989. [Google Scholar] [CrossRef]

11. T. Thanarajan, Y. Alotaibi, S. Rajendran, and K. Nagappan, “Eye-tracking based autism spectrum disorder diagnosis using chaotic butterfly optimization with deep learning model,” Comput. Mater. Contin., vol. 76, no. 2, pp. 1995–2013, 2023. doi: 10.32604/cmc.2023.039644. [Google Scholar] [PubMed] [CrossRef]

12. X. Bao, H. J. Li, G. Q. Zhao, L. Chang, J. Zhou and Y. Li, “Efficient clustering V2V routing based on PSO in VANETs,” Measurement, vol. 152, no. 4, pp. 107306, 2020. doi: 10.1016/j.measurement.2019.107306. [Google Scholar] [CrossRef]

13. U. Agballa, A. Obiniyi, and B. Ayeni, “Design of an improved energy efficient routing protocol in VANET using a modified route-optimal path algorithm,” Int. J. Appl. Inf. Syst., vol. 12, pp. 18–37, 2019. doi: 10.5120/ijais2019451783. [Google Scholar] [PubMed] [CrossRef]

14. K. Kandali, L. Bennis, and H. Bennis, “A new hybrid routing protocol using a modified K-means clustering algorithm and continuous hopfield network for VANET,” IEEE Access, vol. 9, pp. 47169–47183, 2021. doi: 10.1109/ACCESS.2021.3068074. [Google Scholar] [CrossRef]

15. M. S. Azhdari, A. Barati, and H. Barati, “A cluster-based routing method with authentication capability in Vehicular ad hoc Networks (VANETs),” J. Parallel Distrib. Comput., vol. 169, no. 12, pp. 1–23, 2022. doi: 10.1016/j.jpdc.2022.06.009. [Google Scholar] [CrossRef]

16. G. D. Singh, S. Kumar, H. Alshazly, S. A. Idris, M. Verma and S. M. Mostafa, “A novel routing protocol for realistic traffic network scenarios in VANET,” Wirel. Commun. Mob. Comput., vol. 2, no. 5, pp. 1–12, 2021. doi: 10.1155/2021/7817249. [Google Scholar] [CrossRef]

17. A. Naeem et al., “Enhanced clustering based routing protocol in vehicular ad-hoc networks,” IET Electr. Syst. Transp., vol. 13, no. 1, pp. 12–39, 2023. doi: 10.1049/els2.12069. [Google Scholar] [CrossRef]

18. H. Qasim Awla, S. Wahhab Kareem, and A. Salih Mohammed, “A comparative evaluation of bayesian networks structure learning using falcon optimization algorithm,” Int. J. Interact. Multimed. Artifi. Intell., vol. 7, pp. 1–22, 2023. doi: 10.9781/ijimai.2023.01.004. [Google Scholar] [PubMed] [CrossRef]

19. T. Thanarajan, Y. Alotaibi, S. Rajendran, and K. Nagappan, “Improved wolf swarm optimization with deep-learning-based movement analysis and self-regulated human activity recognition,” AIMS Math., vol. 8, no. 5, pp. 12520–12539, 2023. doi: 10.3934/math.2023629. [Google Scholar] [CrossRef]

20. R. M. A. Latif, M. Jamil, J. He, and M. Farhan, “A novel authentication and communication protocol for urban traffic monitoring in VANETs based on cluster management,” Systems, vol. 11, no. 322, pp. 1–27, 2023. doi: 10.3390/systems11070322. [Google Scholar] [CrossRef]

21. P. Muthukrishnan and P. M. Kannan, “Metaheuristics-based clustering with routing technique for lifetime maximization in vehicular networks,” Comput. Mater. Contin., vol. 74, no. 1, pp. 1107–1122, 2023. doi: 10.32604/cmc.2023.031962. [Google Scholar] [PubMed] [CrossRef]