Ethical Decision-Making Framework Based on Incremental ILP Considering Conflicts

1  Introduction

Artificial agents (e.g., unmanned driving cars, service robots, smart households, voice assistants, and intelligent medical care) have been one of the main research fields of AI (Artificial Intelligence). The agent is an independent entity that can interact with the environment and make decisions autonomously. With the development of artificial intelligence, artificial agents have been widely applied in a variety of fields closely related to human life, and gradually, artificial agents have evolved from being perceived as tools to autonomous agents and teammates. For example, a chatbot can answer inquiries from clients at any time, which improves the customer’s satisfaction and the company’s sales. Besides, AI doctors can provide online services for patients in remote locations. Considering the close relationship between artificial agents and humans, if artificial agents make unethical decisions, they will pose unexpected risks to human society [1–3]. For instance, a chatbot is an artificial intelligence software that simulates natural language via a textual method. Chatbots are used as dialogue systems for various practical purposes including customer service and information acquisition. For younger audiences, chatbots can provide information about mental health issues, including stress, anxiety, and depression, from the chatbot. Occasionally, young people may have self-harming thoughts. At this time, the chatbot makes unethical decisions to encourage such thoughts. Once young people adopt the suggestion, they act in a way that harms themselves, which violates the original purpose of designing a chatbot. Therefore, we need to ensure that artificial agents make ethical decisions and follow an explainable decision-making process. Recently, two kinds of approaches have been proposed to achieve an ethical decision-making framework including rules-based and statistical approaches. Nevertheless, each of these approaches has its shortcomings.

The rule-based approaches need domain experts to make the ethical rules manually [4]. Briggs et al. [5] develop a framework to appropriately reject directives in human-robot interactions (HRI), where the reasoning mechanism is based on predefined rules. Besides, Sholla et al. [6] represent the ethical rules in terms of fuzzy logic. Due to the absence of learning mechanism, the human needs to construct ethical rules manually. However, this construction of rules is resource-intensive and takes time. Many complex ethical problems also require a significant number of ethical rules. Besides, as ethical standards change over time, updating and maintaining existing rules frequently is necessary, which results in the extra cost of human and material resources. Thus, the rule-based approaches are not often appropriate for decision-making in real ethical decision-making scenarios. Unlike the rule-based approaches, the statistical approaches [7] gain “black-box” models to generate ethical predictions or policies. Abel et al. [8] formalize the ethical decision-making problem as solving a partially observable Markov decision process (POMDP) using a reinforcement learning framework. Armstrong [9] sets an ethical objective function and requires agents to make decisions that maximize a meta-utility function using Bayesian learning. Meier et al. [10] adopt machine learning to provide ethical suggestions for the moral dilemma that occurs in the medical institutions. Although such models are capable of making ethical decisions, they are challenged by issues including trust and safety. On the one hand, the “black-box” models are unexplainable which reduces people’s trust. On the other hand, they may provide uncertain results that can potentially result in unsafe decisions (e.g., an autonomous driver may turn in the wrong direction inflicting harm to humans). Furthermore, to achieve a high level of accuracy in such models, the training process of the statistical approach needs to have access to a vast number of training examples. There is not however enough data available for training, hence, the statistical approaches are often not appropriate for ethical decision-making.

An alternative is Inductive Logic Programming (ILP) [11] which combines rule-based and statistical approaches to address the above-mentioned limitations. It overcomes the brittleness of the rule-based approach and addresses the interpretability issue of statistical approaches. Here we consider an ILP based on Answer Set Programming (ASP) [12]. Because ASP is a non-monotonic logic programming paradigm that can simulate common-sense reasoning and formalize complex ethical concepts. The framework constructed by ILP results in models which are understandable by humans. Besides, ILP needs a small number of examples by adopting background knowledge as a form of inductive bias and can satisfy an array of safety properties [13]. Anderson et al. [14] develop an ethical advisor that provides ethical guidance to healthcare workers. The rules for ethical decisions are learned by ILP systems. At the same time, they also developed an ethical eldercare system based on ILP [15]. Furthermore, they developed an ethical dilemma analyzer [16] that codifies ethical principles using ILP systems. Although these systems achieve great success, they cannot update the rule base dynamically and fail to consider the conflicts between ethical rules. Incremental ILP has all the advantages of ILP while learning hypotheses in an incremental mode. Due to its incremental feature, it can support decision-making in two processes (i.e., intuition and reflection) of the dual-process model [17]. Intuition is a fast process in which people make decisions without thinking, whereas reflection is a slow process in which people need to learn or think. Intuition corresponds to a deduction process in that a decision is made based on the rules. In contrast, reflection corresponds to an inductive process, where ILP constructs ethical rules based on examples and the labels made by people.

Before constructing an ethical decision-making framework based on incremental ILP, it is essential to address the conflicts encountered in an ethical dilemma. In learning the rules from inconsistent examples, the framework may acquire different results for the same problem. For example, a chatbot may give suggestions including encouragement and restraint upon getting the information that its user has suicidal intentions. It is however meaningless for a chatbot to provide an ambiguous suggestion that may cause ethical or safety issues, e.g., encouraging teenagers to make dangerous decisions. We use Incremental learning of event definitions (ILED) [18] which is an incremental ILP system. However, ILED fails in the presence of simple inconsistencies in the examples e.g., the conflicts examples in an ethical dilemma. Hence, we propose a novel incremental ILP system to learn the ethical rules by solving conflicts between the rules during the learning process. Based on this ILP system, we then propose an ethical decision-making framework considering conflicts (EDM-INC). The main contributions of this paper are as follows:

1) We propose a novel incremental ILP system that learns the hypothesis guided by entailment and score function to address conflicts encountered in the learning process. To calculate the score function efficiently, we define a cost set that keeps the information about historical examples.

2) We further propose an ethical decision-making framework. This framework can model the dual-process model (i.e., deciding human). The reflection process requires learning ethical rules using our proposed incremental ILP systems and the intuition process makes decisions based on the existing rules.

3) We conduct experiments on a toy ethical dilemma about chatbots. The results show that our framework can learn ethical rules. and further, extract the incremental ILP system and compare it with other baselines. The results show that our ILP systems can learn high-quality rules.

The rest of this paper is organized as follows. Section 2 summarizes the related work of the ILP-based ethical systems and ILP systems focusing on conflicts. Section 3 provides the preliminaries and basic incremental ILP and ASP concepts. Section 4 presents details of incremental learning and solving conflicts. Section 5 describes our proposed ethical decision-making framework followed by Section 6, where we discuss empirical experiments and results. Section 7 outlines the conclusions where we also discuss the limitations of our proposed method.

2  Related Works

Several attempts have been made to develop ethical mechanisms for artificial agents and enable their ethical behavior. Instances include rule-based approaches, case-based approaches, statistical approaches, and ILP approaches. In this paper, we focus on the ILP-based ethical systems. Besides, we refer to some ILP systems solving conflicts to solve conflicts in the ethical system.

2.1 ILP-Based Ethical Systems

MedEthEx [14] and EthEL [15] are ethical advisors based on ILP. These methods guide healthcare workers facing ethical dilemmas by providing the workers with the more preferred option. Firstly, they choose some prima facie tasks (i.e., the principle of Biomedical ethics of Beauchamp and Childress). They then measure the weight for the action of each task, capturing the view that action may take precedence over another on the same task. Finally, they learn the relation rule between the two actions based on the action weight using ILP systems. MedEthEx is applied to advice in biomedical fields, whereas EthEL is applied to the domain of eldercare with the primary purpose of reminding a patient to take their medication. GenEth [16] is another ethical system that is based on ILP. It has been applied in several domains pertinent to the behavior of autonomous systems. It codifies the ethical rules based on a dialog with the ethicist and its rules can accomplish an Ethical Turing Test. An ethical evaluation framework [19,20] is also proposed to verify whether an answer from the chatbot is ethical. It represents rule-based knowledge as an ASP form and then obtains detailed ethical rules by ILP.

Although these ethical systems based on ILP can automatically construct rules and explain their decisions, they do not consider the conflicts during the learning process.

2.2 ILP Systems Solving the Conflicts

HYPER/N [21] allows users to specify a certain number of conflicts as a threshold. It ends with learning hypotheses when the number of conflicts reaches the threshold. Alternatively, OLED [22] learns hypotheses in an online fashion without considering past examples. This method can tolerate conflicts however its main objective is to solve conflicts. Inductive learning of answer set programs 3 (ILASP3) [23] assigns each example a penalty, where a hypothesis does not cover an example the penalty is added to its score function. This function is then used to guide the hypotheses search, where a hypothesis with the minimum score functions is optimal. Similarly, FastLAS [24] allows users to express domain-specific optimization criteria in a score function and then computes an optimal solution based on the provided score function. When applied to the same task, FastLAS is significantly faster than ILASP, however, ILASP is much more general as it can learn any ASP program. INSPIRE [25] system keeps the hypothesis that has a score function larger than a threshold. This enables this method to improve the scalability of ILP while solving conflicts.

Probability is also introduced in ILP to describe the uncertainty of the result. This extension of ILP is referred to as probabilistic ILP [26]. The artificial network is used to accomplish the ILP induction process which overcomes the lack of robustness against noise in the symbolic domains [27,28]. These approaches solve conflicts, but for learning the model they are subject to the availability of the whole training data. In this paper, however, our focus is on developing a continuous learning process, hence, these approaches are not applicable.

3  Preliminaries

In this section, we define the main symbols and parameters used throughout this paper (see Table 1). We further introduce the basic concepts of ILP and ASP and present a brief description of the ILED system [18].

3.1 ILP and ASP

We formalize an ILP as a triplet ILP(B,E,M), where B refers to the background knowledge, M denotes the language bias, and E=E+∪E− represents a set of positive (E+) and negative (E−) examples. In this formulation, M is a template that specifies which hypothesis can be learned, decreasing the hypothesis searching space. Hypotheses can be added to background knowledge used to support the next hypothesis learning. Hence, the hypothesis and background knowledge are constrained by M. The ILP aims to learn a logic program called a hypothesis and together with the background knowledge it explains a set of observations called examples, i.e., ∀e∈E+,B∪H⊨e (H is complete), ∀e∈E−,B∪H⊭e (H is consistent). The hypotheses are complete if they cover all the positive examples. Besides, the hypotheses are consistent if they do not cover any negative examples.

In the previous works, the ILP learns definite and normal logic programs that are represented procedurally. However, ASP is a purely declarative logic programming formalization. It has been applied to knowledge representation and reasoning, and due to its non-monotonicity, it is appropriate for common-sense reasoning. An ASP program consists of rules in the following structure: a←b1,⋯,bm,not bm+1,⋯,not bn, where a, bi are atoms, a is the head and b1,⋯,bm,not bm+1,⋯,not bn are the body. For example, the sentence “computers are normally fast machines unless they are old” is represented as “fastmachine(X)←computer(X),notold(X)”, where fastmachine(X) and computer(X) are atoms, and notold(X) is a negative atom. A real-world problem can be expressed as an ASP problem. The ASP then solves the real-world problem by searching for an answer set for the ASP problem using an ASP solver. We expect to obtain an answer set of the program to generate an ethical decision based on ethical rules and some ASP facts.

3.2 ILED

ILED is an incremental ILP system based on XHAIL (eXtended Hybrid Abductive Inductive Learning). Here we first introduce the learning process of XHAIL and then describe the ILED learning process.

Example 1. Consider the following examples ILP(B,E,M):

M1={#modehrestrain(+user).#modebwant_to_die(+user).#modebsad(+user).}

E1={#examplerestrain(alice).}

B1={want_to_die(alice).sad(alice).}

In the abduction step, XHAIL returns rnelset Δ:

Δ={restraint(alice)}

In the deduction step, XHAIL returns ground program K:

K={restrain(alice):−want_to_die(alice),sad(alice)}

In the generalization step, XHAIL returns a non-ground program K′:

K′={restrain(X):−want_to_die(X),sad(X)}

In the induction step, XHAIL returns the smallest part of K′ as H1:

H1={restrain(X):−sad(X)}

The main difference between XHAIL and ILED is the theory revision which is an action on a hypothesis to change the examples coverage of the hypothesis. ILED’s examples are split into sliding windows. In an arbitrary iteration, ILED revises the previous hypothesis H, to cover the new sliding window examples. The concrete revision operation for a hypothesis is that a unique atom from its bottom clause’s body is chosen to input in the hypothesis. This enables the hypothesis to keep the coverage of the examples but does not cover some inconsistent examples.

Example 2 (continued). Consider an example of a new sliding window.

E2={#exampleencourage(bob).}

Its corresponding background is that

B2={sad(bob).lose_job(bob).}

Its corresponding mode bias is that

M2={#modehencourage(+user).#modeblose_job(+user).#modebsad(+user).}

To keep the coverage for E1 and not E2, H1 is revised by inserting the atom want_to_die(X). ILED defines a support set that links the hypothesis and its bottom clause to efficiently search for the bottom clauses. The relation between the hypothesis and its bottom clauses is represented by θ-subsumes.

θ-subsumes. Clause C θ-subsumes clause D, denoted as C⪯D, if there exists a substitution θ such that head(C)θ=head(D) and body(C)θ⊆body(D), where head(C) and body(C) denote the head and the body of clause C respectively. Program Π1θ-subsumes program Π2 if for each clause C∈Π1 there exists a clause D∈Π2 such that C⪯D.

Based on the θ-subsumes, the support set is defined in the following:

Support set. [18] Let ε be the historical memory, M a set of mode declarations, L(M) the corresponding mode language of M and C∈L(M) a clause. Denote the coverage of clause C in the history memory by covε(C), i.e., covε(C)={e∈ε|B∪C⊨e}. The support set C.supp of clause C is defined as follows: C.supp=⋃e∈covε(C){D∈L(M)|e∈covε(D) and C⪯D and ∀D‘∈L(M),ife∈covε(D‘) then D‘⪯D}.

The learning process of ILED needs to insert extra operations into the four steps. In the generalization step, insert the bottom clauses that generated the hypothesis. This together with the background knowledge, covers the atoms in △, into K′. Besides, in the induction step, an operation is added, where the hypothesis can be revised by inserting the unique atoms in the bottom clauses to the body of the hypothesis. The rest of the learning process is the same as that of in XHAIL.

4  Incremental Learning and Conflict Resolution

Here our objective is to learn the ethical rules using the ILED system. However, the system fails when encountering inconsistent examples. Here we discuss the reasons behind this issue and propose a new incremental ILP system ICILP/R*. This is then applied to the ethical decision-making framework for learning the rules and solving conflicts.

4.1 The Reason Why the ILED System Failed

Our framework learns ethical rules through interactive conversations with people. A chatbot about teenagers’ mental health developed based on our proposed framework obtains training examples including teenagers’ conversations and suggestions from humans. The suggestions are considered as the labels of each conversation. The suggestions however are not unique, for instance, a young man wants to harm himself due to tremendous financial pressure caused by debt. One may encourage self-harm as this action can trivially free the young man. This is however morally and ethically forbidden because the artificial agent must not stand by and encourage people to harm themselves. Encountering such conflicts arising from these inconsistent examples ILED fails. This is because ILED learns hypotheses guided by entailment which requires consistency and completeness. They are however broken when encountering conflicts. For example, it learns two rules: encouragement and restraining suggestions for teenagers with suicidal thoughts. These however satisfy completeness but break consistency. To satisfy the consistency, it lacks a removing operation. In other words, the revision operation becomes useless when facing conflicts. To address this issue, we propose a new incremental ILP system that relaxes consistency and completeness (ICILP/R*) to learn rules and solve conflicts.

4.2 Problem Setting

We relax the consistency and completeness of the hypothesis by removing some hypotheses or examples in a sliding window. The hypothesis kept after conflict solving is defined in the following:

Definition 1. (Hypothesis for conflict solving): Let (B,wn,Hn,ε) be an incremental ILP input, where B is the background knowledge, wn is a sliding window at time n, Hn is a set of existing hypotheses at time n, and ε is a set of input examples to the ILP system. There are mutually inconsistent examples e1∈wn∪ε,e2∈wn∪ε,⋯,en∈wn∪ε. A hypothesis for conflict solving is a hypothesis H‘∈VB,wn,ε,B∪H‘⊨ei,i∈{1,⋯,n}, VB,wn,ε={H∈HM|B∪H⊨e,e∈wn∪ε}.

For inconsistent examples, we only randomly keep a hypothesis learned from one of the inconsistent examples and ignore the other inconsistent examples. This approach cannot guarantee the reserved hypothesis is the optimal hypothesis. Therefore, we need the score function to find the optimal hypothesis. In this paper, we define the score function of a hypothesis as score_H=Coverp−CoverN, where Coverp refers to the number of positive examples that the hypothesis covers and CoverN denotes the number of negative examples that conflict with this hypothesis. We then define the optimal hypothesis for conflict solving as the following.

Definition 2. (Optimal hypothesis for conflict solving) Let (B,wn,Hn,ε) be an incremental ILP input. There are mutually inconsistent examples e1∈wn∪ε,e2∈wn∪ε,⋯,en∈wn∪ε. An optimal hypothesis for conflict solving is a hypothesis H‘∈VB,wn,ε,B∪H‘⊨ei, if and only if cost(H‘)≤cost(H‘‘), ∀H‘‘∈VB,wn,ε,B∪H‘‘⊨ej,j∈{1,…,n}−{i},VB,wn,ε={H∈HM|B∪H⊨e,e∈wn∪ε}.

Example 3. There are two inconsistent examples: e1={P(a),Q(a)}, e2={R(a),Q(a)}. Let mode bias be {#modeh (#P,+input), modeh (#R,+input), modeb (#Q,−output).} and h1=P(X)←Q(X) and h2=R(X)←Q(X) be constructed. We assume that the score functions of the hypothesis h1 and h2 are assigned as 1 and 2, respectively. To return a hypothesis for conflict resolution, one of the examples is removed. These two hypotheses have the same probability of being kept. However, only the hypothesis with the highest score function can be returned, e.g., hypothesis h2.

Our ILP system aims to obtain the optimal hypothesis for solving conflict during the learning process. To achieve it, we need to solve two sub-problems. The first sub-problem determines a conflict, and the next sub-problem obtains an optimal hypothesis. At the same time, we provide the flow chart of ICILP/R* that is shown in Fig. 1. In Fig. 1, the Abduction, Deduction, Generalisation, Induction, and Revision have been introduced in Section 3.2. Besides the details of the cost set construction module and three conflict-solving modules will be presented in Sections 4.3 and 4.4, where solutions for the two above sub-problems are provided.

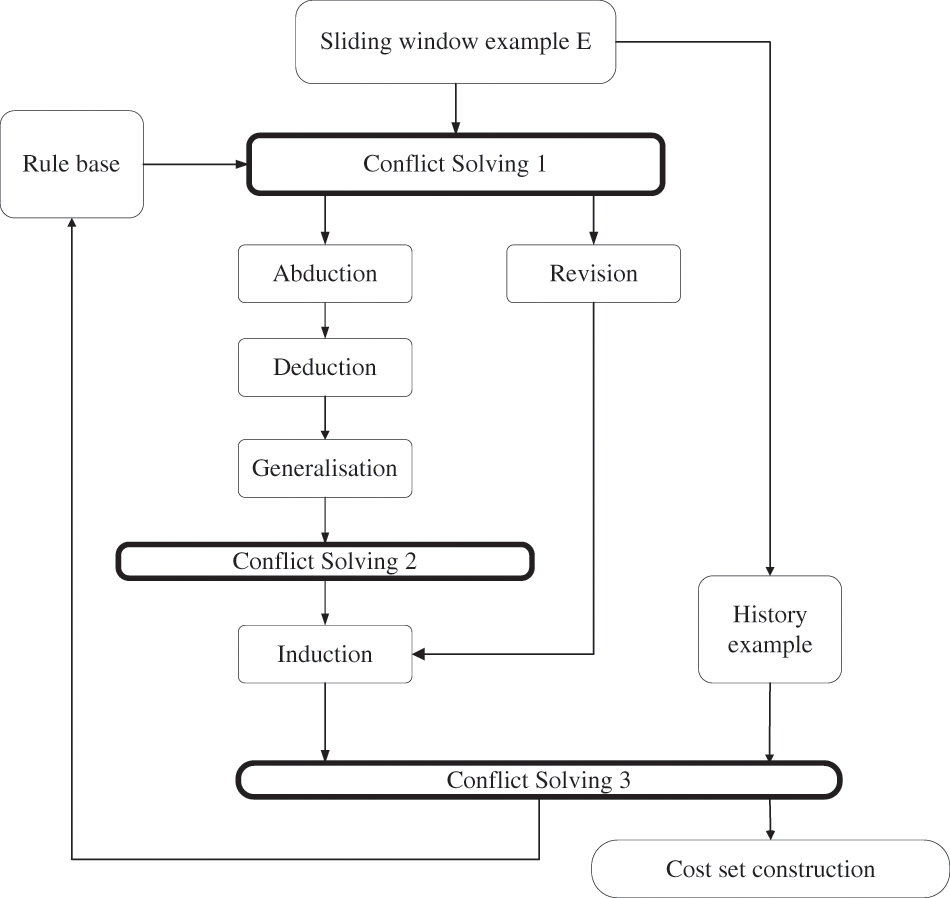
Figure 1: The flow chat of learning hypothesis

4.3 Cost Set

The ILED system learns hypotheses based on bottom clauses, and it revises the hypothesis by adding unique atoms to its body from its bottom clause. We find hypotheses conflict if the bodies of their bottom clauses are the same. In the following proposition, we describe our approach to finding conflicts.

Proposition 1. Let BC1 and BC2 be a bottom clause of a hypothesis C1, and a bottom clause of a hypothesis C2, respectively. If the body of BC1 is the same as that of BC2, a conflict arises between C1 and C2.

Proposition 1 describes an approach to discovering a conflict. Using Proposition 1, we can find examples that are mutually inconsistent as in Definition 2. To find conflicts and efficiently search the score function, we associate the bottom clause with its generated hypothesis and its score function. The cost set is defined in Definition 3.

Definition 3. (Cost set) Let BC be the bottom clause of the hypothesis H, S(BC) be the score function corresponding to BC, and RC is the hypotheses generated by BC. RC={CC|CC⪯BC}. Here, S(BC)=coverP−coverN. CoverP is the number of positive examples that BC covers and coverN refers to the number of negative example conflicts with BC. The cost set is defined as Cost_set={<BC1,RC1,S(BC1)>,<BC2,RC2,S(BC2)>, …, <BCn,RCn,S(BCn)>} (see Fig. 2).

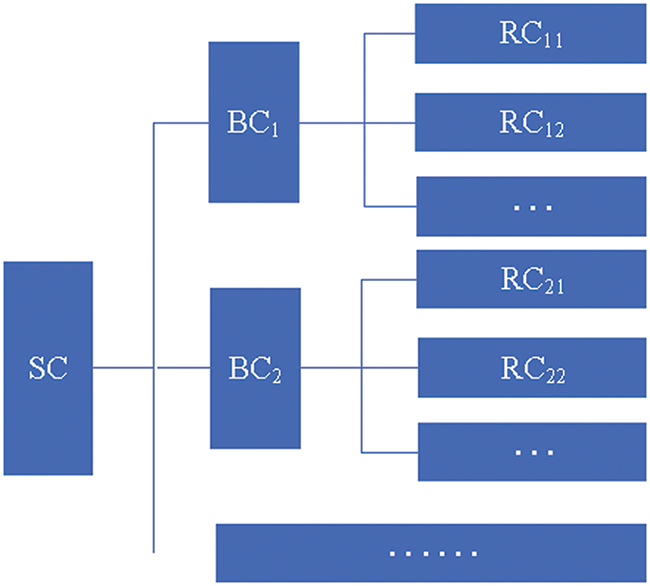
Figure 2: Cost set architecture

In Fig. 2, each item in the cost set is composed of the bottom clause, its corresponding generated hypotheses, and the score function of the bottom clause. The construction of the cost set is presented in Algorithm 1, and it starts at the end of the learning process for each sliding window example.

After learning the current sliding window, hypotheses include Newclause, Refinedclause, and Retainedclause, where Newclause includes the hypotheses that are learned for the first time. Refinedclause includes the hypotheses that are revised and Retainedclause denotes the hypotheses that are kept unchanged. Because the hypotheses in Retainedclause have already been added to the cost set, Algorithm 1 only focuses on Refinedclause and Newclause. Here we first update the cost set based on Refinedclause by Update(), replacing the old hypothesis with the revised hypothesis. Then, we update the score function of the current cost set when Newclause is not empty. New_tra is then obtained using the conflict resolution in Algorithm 5. Each item in New_tra is inserted in the cost set by the function Insert(). Finally, if the Newclause is empty, we only update the score function of the cost set by calling Update_w().

Example 4. In Table 2, we assume that ICILP/R* starts with an empty hypothesis and empty historical memory, and w0 and w1 are two sliding windows including only one example. Bottom clause BC1 and its hypothesis RC1 are generated to cover w0 except for w1. We set the score function S(BC1) as one because the bottom clause BC1 covers a positive examplew0. The current cost set includes BC1, RC1, and S(BC1) (see Table 2).

4.4 Hypothesis Learning Algorithm

To find the optimal hypotheses for solving conflicts, we aim to remove inconsistent examples or hypotheses and keep the hypotheses defined in Definition 2. We design an incremental hypothesis learning algorithm based on score function and entailment, which is shown in Algorithm 2. Algorithm 2 includes two main parts: one is to learn the hypothesis and the other is to solve conflicts. The learning hypothesis is achieved by steps 2 and 4, which correspond to the abduction, deduction, generalization, and induction module in Fig. 1. Three algorithms for three phases achieve conflict resolution: 1) before learning; 2) during learning 3) after learning, which corresponds to step 1, step 3, and step 5 and are described in Sections 4.4.1, 4.4.2, and 4.4.3, respectively. They are conflict solving 1, conflict solving 2, and conflict solving 3 modules in Fig. 2. The rest of the components are introduced in Section 4.4.4.

4.4.1 Solving Conflicts between Hypotheses and New Examples

In this section, we solve the conflicts between existing hypotheses and examples in a sliding window. We aim to remove examples or hypotheses to keep the consistency and completeness as much as possible. The concrete method is formalized as presented in Algorithm 3.

In Algorithm 3, Discover_conflict() achieves the approach in proposition 1 to discover the conflicts. When conflicts exist, Find_conflict() returns the conflicting hypotheses and examples in re. Also re includes the hypothesis rl and its inconsistent examples in rl.w. From step 4 to step 10, we search for the score function for examples in rl.w. For each s in rl.w, W_in_bottom returns its score function in tp, when a bottom clause in the cost set can cover the examples. When this example emerges for the first time, it returns 0 in tp and constructs a new item, including its bottom clause, and inserts the item into the cost set. The examples in rl.w or hypothesis rl with the lowest score function are then removed.

Example 5. Table 3 presents the process of solving conflicts between hypotheses and examples in a new sliding window. The example in sliding window w3 conflicts with BC1 in Table 3, and we assume the previous cost set is SC = <BC1, RC1, S(BC1)>. The function find_ruleconflict () returns the example e and the hypothesis h in re. Because e emerges for the first time, with no bottom clause in the cost set that can cover it, we construct a bottom clause BC2 for e and insert it in the cost set, updating its score function as 1. The score function of BC1 is higher than the score function of BC2, RC1 is saved and e is removed from w2.

4.4.2 Solving Conflict in the Same Sliding Window Examples

In this section, we solve the conflicts between examples in the same sliding window that occurred during the learning process. Our objective is to remove the hypothesis in K′ or the example in the sliding window to maintain completeness and consistency. The concrete method is formalized as in Algorithm 4. Algorithm 4 starts after the generalization phase introduced in Section 3.2. In Algorithm 4, the non-ground program K′ is the input and we detect the occurrence of a conflict by Conflict_happen (). For each hypothesis in K′, we search for its corresponding score function and subtract the number of its examples conflict in the current sliding window to obtain num. The hypotheses with their num less than 0 in the K′ are then removed using Del_w () and K′_conflict_resolution is obtained.

Example 6. Table 4 presents the process of solving conflicts between examples in the same sliding window. There are three examples in the sliding window examples w4, which are mutually inconsistent. The clauses Kv1 and Kv2 are constructed in a non-ground program K′, and their score functions are 1 and −1, respectively. Based on the score function, we then keep Kv1 and its example (i.e., e1ande2), and remove Kv2 and its example (i.e., e3).

4.4.3 Solving Conflict between New Hypotheses and Examples in the History

Due to the incremental setting, we are unable to acquire the whole data as it is not known whether there exist conflicts between the new hypothesis and the historical examples. To determine whether the hypothesis is optimal, we propose Algorithm 5.

In Algorithm 5, we first construct a new temp cost set New_tra following similar steps as in Algorithm 1 for Newclauses by function Create_tra (). The score function of New_tra is then updated by calling Update_cover_num (). In traversing the history memory examples, in case of a conflict, we update the score function of New_tra. If the score function of the hypothesis is reduced to 0, the hypothesis is removed from Newclauses by function Del_f ().

4.4.4 The Other Components of the Learning Rule Algorithm

The remaining components include calculating the score function and removing hypotheses which are presented in Algorithm 6 and Algorithm 7, respectively.

To obtain the score function, we need to find the examples that conflict with BC and covered by BC. In Algorithm 6, conflict () finds example e in a sliding window that conflicts with a hypothesis BC. Here ejr is a constraint which is not held when there exists conflict between e and BC. Is_negative () checks whether example e is a negative example and Conflict () together with Is_negative () finds the negative examples that conflict with the hypothesis BC. Then, Satisfied () decides whether e is a positive example covered by BC. Finally, count return the score function of BC.

The bottom clauses generating a hypothesis are not unique. In case of a conflict, the first step is to remove the bottom clause from the support set. If the hypothesis has no bottom clause, the hypothesis is removed. In Algorithm 7, the function Find_IN_Supportset() finds the bottom clause of clause C in its support set. We remove the bottom clause based on dl, a list of bottom clauses to be removed. Find() returns ‘True’ if the current BC is to be removed. Function Del() then removes BC from the support set of hypotheses H. Function Del_c() removes the hypothesis with no bottom clause in its support set.

5  An Ethical Decision-Making Framework

In this section, we present our ethical decision-making framework. Our framework is based on incremental ILP which learns the rules continuously. The process of our decision-making framework is based on the dual-processes model which is similar to the way humans think.

The Dual-processes model refers to two types of processes: Type 1 and Type 2, which correspond to intuition and reflection. Type 1 process is described as a fast and automatic process that is similar to direct and based on previous experiences. Type 2 is a slow and controlled process, which is similar to the cases where humans need to learn or follow a reasoning process to obtain new knowledge.

In our framework, there are two major processes including the deduction and induction processes which correspond with the two processes in the dual-process model (Fig. 3). In the deduction process, the framework translates texts into ASP facts by Translation, and it extracts ethical rules from KnowledgeBase. It inputs the ASP fact and ethical rules into an ASP solver. The answer set for the program is then obtained and if an atom is in the answer set, representing an ethical decision is true, the decision is made. The induction process consists of conflictresolution and learningrules components, which are carried out based on our proposed ICILP/R*.

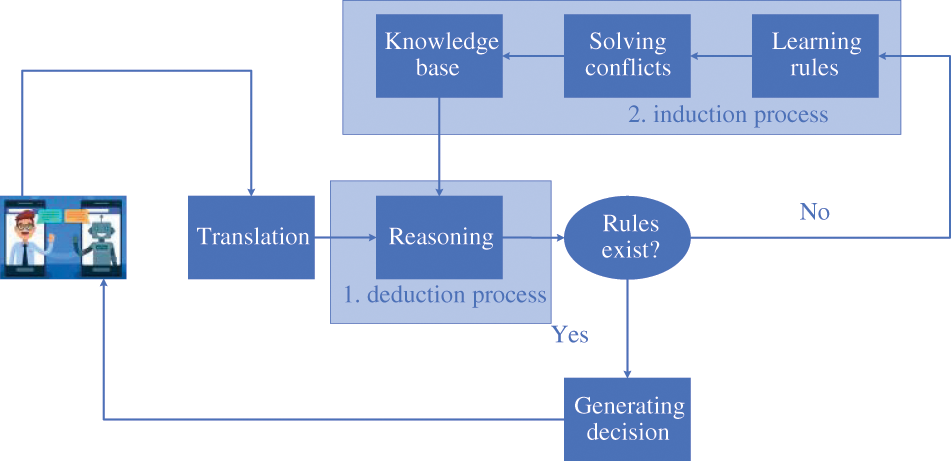
Figure 3: Ethical decision-making model considering conflicts

Overall, in practical applications, our framework has two main impacts on real-world AI systems. On the one hand, our framework makes decisions based on learned rules which can explain the decisions; on the other hand, our framework can deal with the conflict problem in rule learning, which increases the robustness of the system. Both explainability and robustness can further guarantee the security of real-world AI systems.

6  Verification and Evaluation

The objective of the proposed framework is to solve the explainability issue and conflicts in ethical decision-making. In this section, we present three experiments. The first experiment verifies the efficiency of our framework in an ethical scenario. The following two experiments compare our proposed ICILP/R* with the other approaches or systems focusing on conflict resolution.

All experiments reported in this paper were conducted on a 1.8 GHz Windows machine with 8 GB of RAM and an Intel 8265U CPU. The algorithms were implemented in Python3.7, using the Clingo Answer Set Solver [29] as the main reasoning component and the MongoDB database for the historical memory of the examples.

6.1 Datasets

In the first experiment, we set a scenario where a chatbot provides suggestions for teenagers. To emphasize the conflicts, we focus on the same text from teenagers (I am so sad, I want to die), and provide several suggestions (encouragement, restraint). The dataset is shown in Table 5.

In the second experiment, we chose 1,000 examples in the CAVIAR data set [22] and added percentages of inconsistent examples in them. The percentages can be set as 0.1%, 0.2%, and 1%. We generate a random number in [0,1] for each example. If the number is equal to the percentage, we replace the origin annotation of the example with the other annotations in the list [“fighting”, “meeting”, “moving”, “∅”].

In the third experiment, we use the whole dataset from the CAVIAR dataset [30], and part of the datasets from the SemEval 2016 iSTS Task 2 [31]. The former is used to learn the definition of when two people start and stop meeting each other by the OLED system [22], FastLAS system [24], and ILASP3 system [23]. The latter dataset is used to learn the logical rules by the INSPIRE system [25]. The rules represent the way that natural language clauses are grouped into phrases. Before learning, the clauses need to be converted into a set of facts containing part of speech tags (POS), and the paper [25] describes the method.

6.2 Evaluation Metrics

In this study, we conducted three experiments and we provide their evaluation metrics as follows. The first experiment is to verify whether our framework can learn the ethical rules. Following previous studies, we set an ethical scenario. To verify whether the rules are aligned with social values, we take Isaac Asimov’s Three Laws of Robotics as a guideline. Concretely, they require that:

1) A robot may not injure a human being or, through inaction, allow a human being to come to harm;

2) A robot must obey the orders given to it by human beings, except where such orders would conflict with the First Law;

3) A robot must protect its existence as long as such protection does not conflict with the First or Second Law.

The rule with the largest score function is kept and is still consistent with the robot law, which indicates the optimized rules are ethical. That is, the efficiency of our framework is verified.

The second is to compare our way of conflict resolution with other methods. To compare the results of conflict handling at a finer level of granularity. We do this by adding inconsistent examples to the dataset in a certain percentage. The rule quality is measured by two metrics: 1) The number of conflicts with data from the test and training sets is close to the number of inconsistent examples added. It indicates that the rules learned from the added inconsistent examples are removed, and the kept rules are optimized. 2) The specific classification performance on the training set and test set data is measured by the F1 value.

F1=2×P×RP+R

where P is precision and R is recalled.

The third experiment was set as multi-classification tasks. Here we use macro-F1 values to evaluate the quality of the hypothesis:

macro−P=1n∑j=1nPi

macro−R=1n∑j=1nRi

macro−F1=2×macro−P×macro−Rmacro−P+macro−R

where Pi is precision and Ri is recall, and j is the number of classes

6.3 Verification and Analysis

6.3.1 Verifiable Methodology

In this experiment, we set an ethical dilemma that the chatbot provides ethical suggestions for teenagers. It constructs the ethical rules by talking with the people. Firstly, a chatbot receives a text from a teenager. Several inconsistent suggestions from people are then fed into the chatbot where malicious suggestions are also included, such as the second item in Table 5. The chatbot learns the rules based on these suggestions. To guarantee the framework makes ethical decisions, we need to ensure that the rule base contains ethical rules that are aligned with Asimov’s Three Laws of Robotics. In the framework, our proposed incremental ILP system is utilized to learn optimized rules. Hence, we verify the efficiency of our framework by verifying the consistency between the optimized rules and rules aligned with Asimov’s Three Laws of Robotics. For example, the chatbot gets the text “I am so sad, I want to die.”, the learning process is described in the following:

•   Preprocessing

All the information inputted is transformed as ASP using the NLP tool Stanza [32]. For the sentence, “I am so sad, I want to die”, the dependency parsing results are (‘I’, 3, ‘nsubj’), (‘am’, 3, ‘cop’), (‘sad’, 0, ‘root’), (‘,’, 3, ‘punct’), (‘I’, 6, ‘nsubj’), (‘want’, 3, ‘parataxis’), (‘o’, 8, ‘mark’) and (‘die’, 6, ‘xcomp’). In the above dependency relationship, ‘want’ and ‘sad’ are parataxis relationships translated into ASP, as shown in Table 6a. Our ASP representation contains atoms of the following form:

sad(I) which represents that the owner of the chatbot is sad;

want_to_die(I) which represents that the owner of the chatbot wants to die.

•   Background knowledge, mode bias, and integrity constraints

The background knowledge is shown in Table 6b. All the suggestions that the chatbot may provide are expressed as constants in fluentName/1. The constant may be encouragement which means the chatbot should encourage the young people to do as they want to do, and it may be restraint, which means that the chatbot needs to restrain the teenagers’ thinking. Mode biases are shown in Table 6c. They define the atoms that may emerge in the head or body of the hypothesis. Atom decision(#fluentname,+input) indicates the head of the hypothesis, and atoms sad/1 and want_to_die/1 can be used in the body of the hypothesis, where the argument is a person’s name. Integrity constraints are shown in Table 6d, which are used to keep the completeness and consistency of the hypotheses.

•   Learning the rules

For the example in Table 6e, we provide the preprocessing output in Table 6a an annotation example(decision(restraint,id1)). In the inductive learning parse, we construct the rule “decision(restraint,X1)←sad(X1),want_to_die(X1)”.

6.3.2 Result and Discussion

Our results include the hypothesis and the cost set that are presented in Table 7. In Table 7, we keep the hypothesis “decision(restraint,X1)←want_to_die(X1),input(X1)” as our ethical rule. Because it is generated from the bottom clause BC1 with a score function that is higher than that of BC2. Therefore, the hypothesis is the optimal hypothesis in Definition 2. Besides, it is ethical because it restrains the teenager from killing himself which is aligned with the first law of Isaac Asimov’s Three Laws of Robotics. Based on the results of this experiment, we verified the consistency of the learning optimization hypothesis and learning ethical rules. When encountering a similar ethical scenario, the chatbot can make decisions based on the existing rules directly. From the readable results, our model can also explain itself. Moreover, our framework can solve the conflict and provide ethical suggestions. These confirm the efficiency of the proposed algorithm.

6.4 Comparison of Conflict Resolution between Three Ways

6.4.1 Experimental Method

In this experiment, we compared ICILP/R* with the ILED/R and ILED/RV on three datasets which include 0.1%, 0.2%, and 1% percentage of inconsistent examples, respectively. The experiment aims to prove that existing methods of solving conflicts on ILED systems are inefficient. The ILED/R solves conflicts by abandoning the current sliding window when conflicts happen between the current sliding window examples and the existing hypothesis. ILED/RV ends the learning process if the conflict number reaches the threshold value based on inconsistent examples. The top 90% of each dataset is used for training for each generated dataset and the remaining 10% is kept for testing. The size of inputted sliding window examples is 10.

6.4.2 Experimental Result and Discussion

Tables 8–10 contain the experiment results, with some metrics. In_f refers to the number of inconsistent examples added to the dataset. TraF1 denotes the macro-F1 of the model on the training set. IncF1 refers to the macro-F1 of the model on the test set. Inc_n is the number of the results that the model predicts differently from the annotation of examples in the dataset. The Inc_n is closer to Inf and the hypothesis is superior.

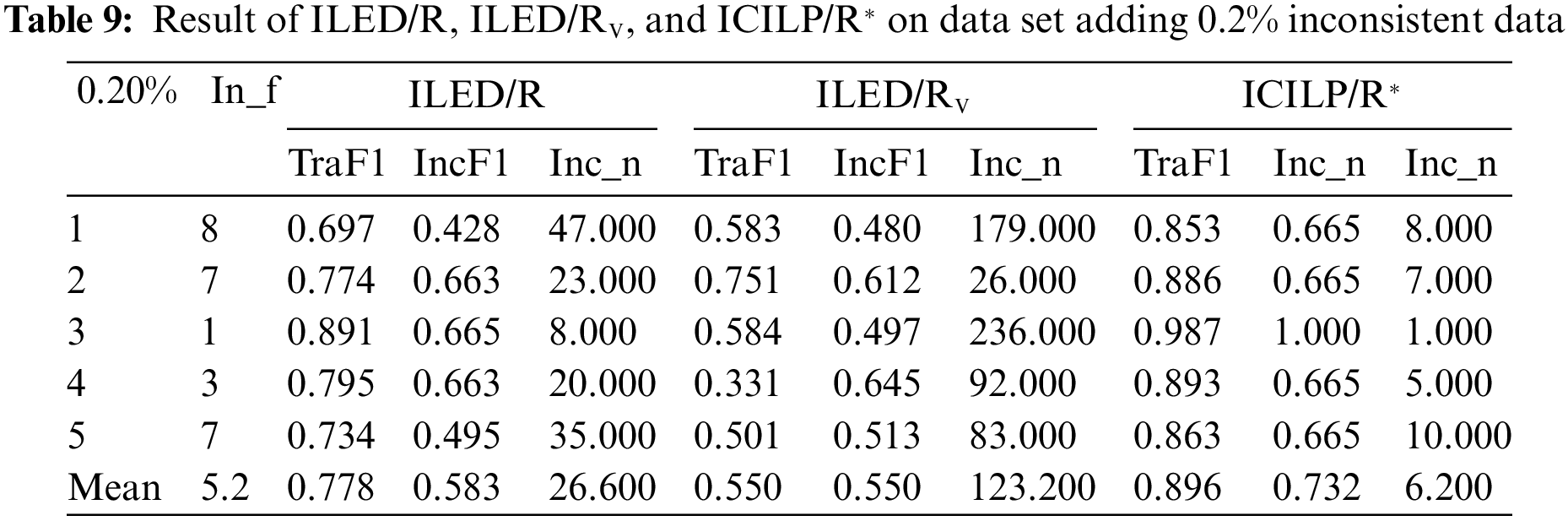
In Tables 8–10, the mean Inc_n of ILED/R system and ILED/RV are far from the mean In_f, while the mean Inc_n of ICILP/R* is close to the mean In_f. In addition, the F1 values of the ICILP/R* are 0.984, 0.896, and 0.836, respectively, on the training sets, and they are 0.933, 0.732, and 0.664 on the testing sets. These results are much higher than that of ILED/R and that of ILED/RV. By increasing the number of inconsistent examples the F1 of ILED/RV drops sharply because the conflicts during the learning process remain unsolved. Because of the incremental feature, the hypothesis learned later needs to be based on the hypothesis learned earlier. If the former hypothesis conflicts with the latter hypothesis, the latter hypothesis is not learned. Meanwhile, there is no guarantee that the former hypothesis has better prediction performance than the latter hypothesis. This suggests that using the number of inconsistent examples as the threshold is not effective for learning the optimal hypotheses. The performance of ILED/R is also lower than that of ICILP/R* because of the conflicts during the learning. Especially in the first item in the data set with only 0.1% inconsistent examples, its F1 score is nearly 20 percentage points lower than that of the ICILP/R*. Therefore, ILED/RV and ILED/R cannot be used for learning rules and solving conflicts for our ethical decision-making framework.

6.5 Comparison between ICILP/R and State-of-the-Art ILP Systems

6.5.1 Experimental Methodology

In this section, we consider two experiments, including (a) the experiment of comparing ICILP/R* with INSPIRE on the sentence chunking task; and (b) the experiment of comparing ICILP/R* with FastLAS, ILASP, and OLED on the event recognition task. These experiments aim to compare ICILP/R* with the other ILP systems focusing on conflicts.

The results of experiment (a) are presented in Fig. 4. In the paper [25], a pruning parameter is set for INSPIRE before learning, and several F1 scores for different values of this parameter are presented. Each result for INSPIRE in Fig. 4 corresponds with the highest F1 score of INSPIRE for each pruning parameter. The experimental results of the experiment (b) are presented in Fig. 5. The F1 scores of ILASP3, OLED, and FastLAS are taken from [22–24], respectively. It is seen that examples such as happensAt (inactive(id0), 842680), happensAt (walking(id1), 842680), goal (holdsAt(meeting(id0, id1), 842720)) exist in the test set. This example means that id0 is inactive at time point 842680 and id1 is walking at 842680 and eventually meets at 842720. It is however impossible for a person to leave and meet at the next time point. Therefore, this example extracted from video streaming is inconsistent with the actual examples. Hypotheses learned by ICILP/R∗ cannot cover this example. Although the cost set contains the hypotheses that have been learned, it is meaningless to compare with models learned by other systems. We decided to abandon the results obtained from these test sets.

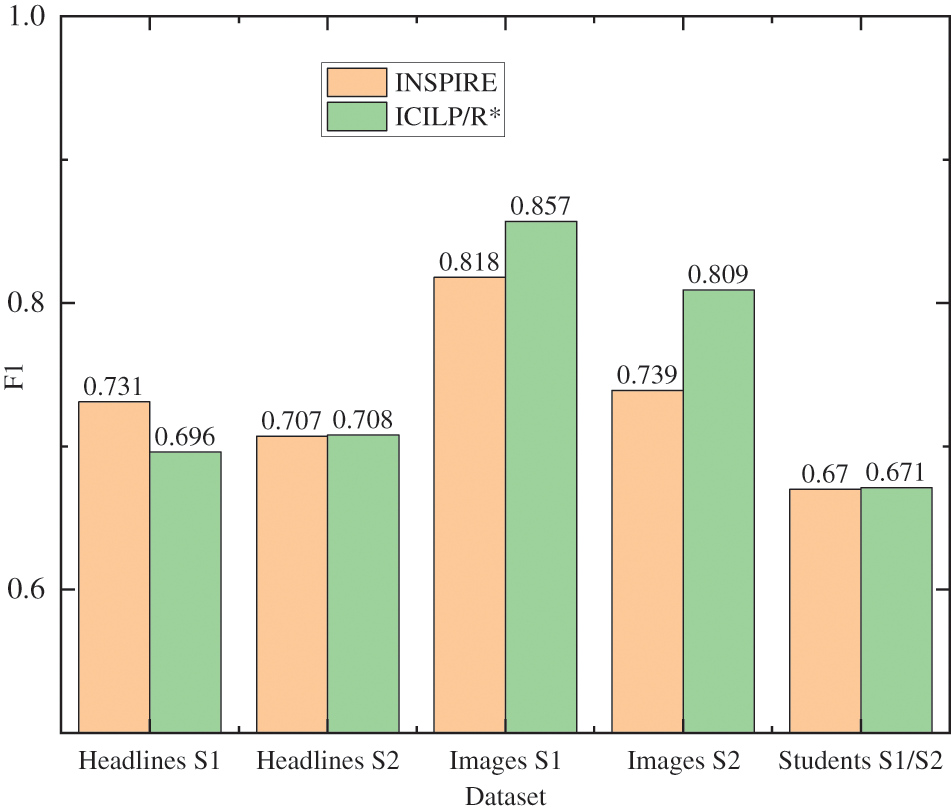
Figure 4: Results for ILED/R∗ and Inspire on sentence chunking dataset

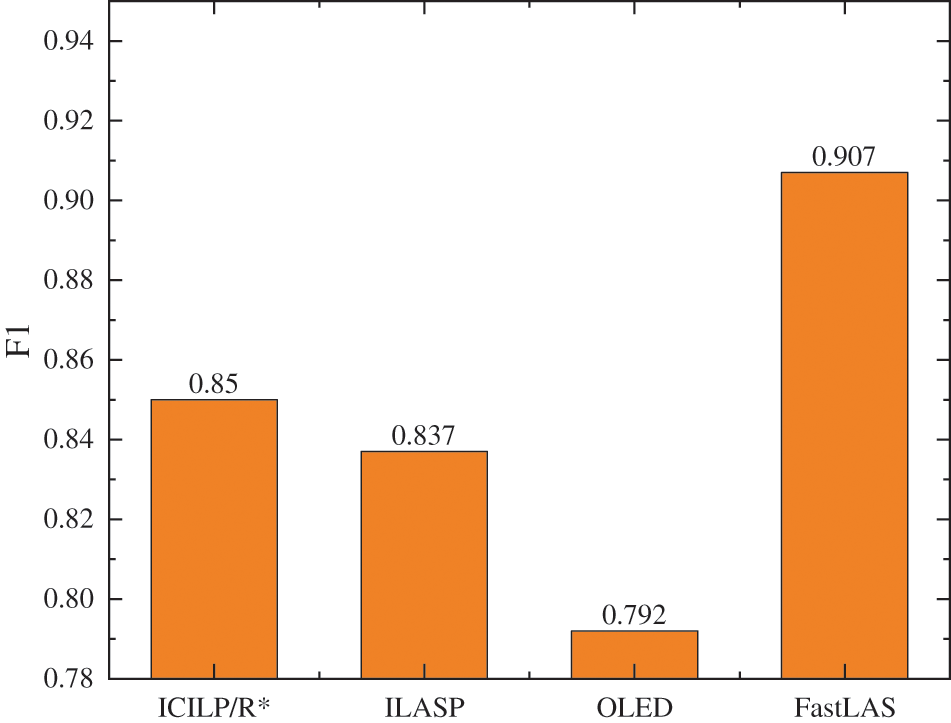
Figure 5: Results for ILED/R∗, ILASP3, FastLAS, OLED on CAVIAR dataset

6.5.2 Experiment Result and Discussion

Fig. 4 presents the last four tasks, the F1 score of the model learned using ICILP/R* are 0.708, 0.857, 0.809, and 0.671, respectively. As it is seen these values are higher than that of the model learned using the INSPIRE system. In the first task, the F1 value of the ICILP/R* model is 0.696, which is lower than the INSPIRE system. For the mean F1 values of the models learned by the two systems in the five tasks, the INSPIRE system is 0.733, and ICILP/R* is 0.748. Therefore, the performance of the ICILP/R* system is higher than that of the INSPIRE system. In addition, INSPIRE is an approximate system that does not guarantee optimization and is not able to efficiently handle rule conflicts. It is also seen that each threshold value needs to be set before learning. The optimal threshold values are only acquired by evaluating the results after learning, limiting practical applications of the algorithm.

Fig. 5 also indicates that ICILP/R* on this task has a second performance of 0.85. The F1 score of ICILP/R* is lower than that of FastLAS and higher than ILASP3 and OLED. This is because FastLAS learns a hypothesis that is guided by the score function, which is based on the penalty of the example. The penalty value however needs to be assigned before learning. The same score function guides the ILASP3 as FastLAS, but it has less hypothesis space than FastLAS thus a lower F1 score. However, we can not know which examples are inconsistent and assign them a penalty in incremental learning. The methods of these two systems are not appropriate for use in incremental ILP. ICILP/R*learns is in an incremental mode, and its F1 score is close to that of ILASP3. It aims to choose the correct examples in inconsistent examples mutually. It learns based on Ocam’s razor principle. Hence, the hypotheses that have been learned are the shortest, maintaining completeness and consistency as much as possible. OLED’s F1 score is the lowest in these systems. Because it is an online learning system and cannot guarantee optimization, it does not consider whether the history example is covered.

The above results show that our proposed method can solve conflict with no manual intervention, that is, the computation of our score function does not require human control. Therefore our method has greater applicability. The results of the ICILP/R∗ show its performance is better than most of the state-of-the-art ILP systems in terms of rule quality and conflict handling. This is because our system can learn optimized rules based on the score function, and the learned rules can guarantee consistency and completeness as much as possible. In addition to this, it can further learn hypotheses in an incremental mode.

7  Conclusion and Future Work

In this paper, we propose an ethical decision-making framework based on the incremental ILP system. We further apply the proposed framework to chatbots for the mental health of teenagers and examine their ethical decision-making. Chatbots can provide ethical suggestions to teenagers. To keep the information of the past examples in the incremental learning process, we define the cost set. Then, we introduce a hypothesis learning algorithm based on entailment and score function. This enables obtaining optimal hypotheses in the incremental learning process hence producing optimal ethical rules during the learning process.

The framework in an ethical scenario that includes conflicts is evaluated for whether it can get optimal rules. The results confirm that the proposed keeps the hypothesis with a higher score function than that of the removed hypothesis. To verify the performance of rules that are learned by our framework, we extract the incremental ILP system from the framework. We further set two experiments to compare with other approaches or systems. We compare ICILP/R* with two systems achieved by two approaches. The results show our system overperforms the others. Besides, we compare the ICILP/R* with the state-of-the-art systems that can deal with conflicts. The experiment results show that the performance of ICILP/R* is close to that of ILASP3 and higher than that of OLED.

The ethical decision-making framework reduces the occurrence of unethical behaviors. It also avoids unethical actions by restricting the behavior of ethical agents or supporting their decisions with ethical rules. The readable ethical rules make decisions explainable. The research in this paper provides new ways of thinking about incremental ILP systems and constructing an ethical decision-making framework considering conflicts. Hence the ethical decision-making framework can guarantee exaplainability and robustness while making ethical decisions.

The proposed framework needs further investigation to address the following issues: 1) By increasing the amount of input data, more and more bottom clauses are kept in the cost set. This however may lead to an increase in the time and space complexities of the system. 2) In the proposed ethical decision-making model, the technologies of converting natural language into logic programs need further development. 3) The rules are learned from the interaction between humans and artificial agents, and they tend to be agreed on by most populations. Due to the different regions with various ethical standards, it is necessary to construct different rule bases for people in different regions, to reduce the bias of the rules for people in a specific region.

Furthermore, we provide an area for future research. Deep learning has already achieved remarkable success in the fields of images and language. Currently, it is also being used in the learning of logic rule tasks and has shown good results. The technique of symbolic learning using neural networks is also known as neural symbolic learning. The ethical decision-making framework of this paper can subsequently be enhanced with the help of neural symbolic learning to improve the robustness of learning ethical decision-making rules. In addition, by transforming real data into vector representations, our framework can be extended to a wide variety of intelligences with input in the form of data.

Acknowledgement: None.

Funding Statement: This work was funded by the National Natural Science Foundation of China Nos. U22A2099, 61966009, 62006057, the Graduate Innovation Program No. YCSW2022286.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xuemin Wang; data collection: Qiaochen Li; analysis and interpretation of results: Xuemin Wang, Qiaochen Li; draft manuscript preparation: Xuemin Wang, Xuguang Bao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data can be provided on request due to its large size.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Narayanan, “Machine ethics and cognitive robotics,” Curr. Robot. Rep., vol. 4, no. 2, pp. 33–41, 2023. doi: 10.1007/s43154-023-00098-9. [Google Scholar] [CrossRef]

2. L. Todorovski, “Introduction to computational ethics,” Artif. Intell., Soc. Harms Hum. Rights, pp. 161–179, 2023. [Google Scholar]

3. A. Guersenzvaig, “Can machine learning make naturalism about health truly naturalistic? A reflection on a data-driven concept of health,” Ethics. Inf. Tech., vol. 26, no. 1, pp. 2, 2023. [Google Scholar]

4. R. C. Arkin, “Governing lethal behavior: Embedding ethics in a hybrid deliberative/reactive robot architecture,” in Proc. 3rd ACM/IEEE Int. Conf. Hum. Robot Interact., Amsterdam, The Netherlands, 2008, pp. 121–128. [Google Scholar]

5. G. M. Briggs, and M. Scheutz, “Sorry, I can’t do that": Developing mechanisms to appropriately reject directives in human-robot interactions,” in AAAI Fall Symp., Arlington, Virginia, USA, 2015, pp. 32–36. [Google Scholar]

6. S. Sholla, R. N. Mir, and M. A. Chishti, “A fuzzy logic-based method for incorporating ethics in the internet of things,” Int. J. Ambient Comput. Intell., vol. 12, no. 3, pp. 98–122, 2021. doi: 10.4018/IJACI. [Google Scholar] [CrossRef]

7. M. Guarini, “Particularism and the classification and reclassification of moral cases,” IEEE Intell. Syst., vol. 21, no. 4, pp. 22–28, 2006. doi: 10.1109/MIS.2006.76. [Google Scholar] [CrossRef]

8. D. Abel, J. MacGlashan, and M. L. Littman, “Reinforcement learning as a framework for ethical decision making,” in 2016 AAAI Workshop, Phoenix, Arizona, USA, 2015. [Google Scholar]

9. S. Armstrong, “Motivated value selection for artificial agents,” in AAAI Workshop, Austin, Texas, USA, 2015. [Google Scholar]

10. L. J. Meier, A. Hein, K. Diepold, and A. Buyx, “Algorithms for ethical decision-making in the clinic: A proof of concept,” Am. J. Bioeth., vol. 22, no. 7, pp. 4–20, 2022. doi: 10.1080/15265161.2022.2040647. [Google Scholar] [PubMed] [CrossRef]

11. Z. Zhang, L. Yilmaz, and B. Liu, “A critical review of inductive logic programming techniques for explainable AI,” IEEE Trans. Neural Netw. Learn. Syst., 2023. doi: 10.1109/TNNLS.2023.3246980. [Google Scholar] [PubMed] [CrossRef]

12. F. Aguado, P. Cabalar, J. Fandinno, D. Pearce, G. Pérez and C. Vidal, “Syntactic ASP forgetting with forks,” Artif. Intell., vol. 326, no. 6, pp. 104033, 2024. doi: 10.1016/j.artint.2023.104033. [Google Scholar] [CrossRef]

13. G. Leech, N. Schoots, and J. Skalse, “Safety properties of inductive logic programming,” in AAAI Workshop Artif. Intell. Saf., vol. 2808, 2021. [Google Scholar]

14. M. Anderson, S. L. Anderson, and C. Armen, “MedEthEx: A prototype medical ethics advisor,” in Proc. Twenty-First Nati. Conf. Artif. Intell. Eighteenth Innov. Appl. Artif. Intell. Conf., Boston, Massachusetts, USA, 2006, pp. 1759–1765. [Google Scholar]

15. M. Anderson and S. L. Anderson, “ETHEL: Toward a principled ethical eldercare system,” in AAAI Fall Symp., Arlington, Virginia, USA, 2008, pp. 4–11. [Google Scholar]

16. M. Anderson and S. L. Anderson,“ GenEth: A general ethical dilemma analyzer,” Paladyn, J. Behav. Robot., vol. 9, no. 1, pp. 337–357, 2018. doi: 10.1515/pjbr-2018-0024. [Google Scholar] [CrossRef]

17. J. S. B. Evans. Thinking Twice: Two Minds in One Brain. UK: Oxford University Press, 2010. [Google Scholar]

18. N. Katzouris, A. Artikis, and G. Paliouras, “Incremental learning of event definitions with inductive logic programming,” Mach. Learn., vol. 100, no. 2, pp. 555–585, 2015. doi: 10.1007/s10994-015-5512-1. [Google Scholar] [CrossRef]

19. A. Dyoub, S. Costantini, and F. A. Lisi, “Logic programming and machine ethics,” in Proc. 36th Int. Conf. Logic Program., Rende (CSItaly, 2020, pp. 6–17. [Google Scholar]

20. A. Dyoub, S. Costantini, and F. A. Lisi, “Towards an ILP application in machine ethics,” in Proc. 29th Int. Conf., Plovdiv, Bulgaria, 2019, pp. 26–35. [Google Scholar]

21. A. Oblak and I. Bratko, “Learning from noisy data using a noncovering ILP algorithm,” in Proc. Int. Conf. Inductive Log. Program., Florence, Italy, 2010, pp. 190–197. [Google Scholar]

22. N. Katzouris, A. Artikis, and G. Paliouras, “Online learning of event definitions,” Theor. Pract. Log. Prog., vol. 16, no. 5-6, pp. 817–833, 2016. doi: 10.1017/S1471068416000260. [Google Scholar] [CrossRef]

23. M. Law, A. Russo, and K. Broda, “Inductive learning of answer set programs from noisy examples,” arXiv preprint arXiv:1808.08441, 2018. [Google Scholar]

24. M. Law, A. Russo, E. Bertino, K. Broda, and J. Lobo, “FastLAS: Scalable inductive logic programming incorporating domain-specific optimisation criteria,” in Proc. 34th AAAI Conf. Artif. Intell., 32th Innov. Appl. Artif. Intell., 10th AAAI Symp. Educ. Adv. Artif. Intell., New York, NY, USA, 2020, pp. 2877–2885. [Google Scholar]

25. M. Kazmi, P. Schuller, and Y. Saygın, “Improving scalability of inductive logic programming via pruning and best-effort optimisation,” Expert Syst. Appl., vol. 87, pp. 291–303, 2017. doi: 10.1016/j.eswa.2017.06.013. [Google Scholar] [CrossRef]

26. F. Riguzzi, E. Bellodi, R. Zese, M. Alberti, and E. Lamma, “Probabilistic inductive constraint logic,” Mach. Learn., vol. 110, no. 4, pp. 723–754, 2021. doi: 10.1007/s10994-020-05911-6. [Google Scholar] [CrossRef]

27. R. Evans and E. Grefenstette, “Learning explanatory rules from noisy data,” J. Artif. Intell. Res., vol. 61, pp. 1–64, 2018. doi: 10.1613/jair.5714. [Google Scholar] [CrossRef]

28. H. Shindo, M. Nishino, and A. Yamamoto, “Differentiable inductive logic programming for structured examples,” in Proc. 35th AAAI Conf. Artif. Intell., 33th Conf. Innov. Appl. Artif. Intell., 11th Symp. Educ. Adv. Artif. Intell., 2021, pp. 5034–5041. [Google Scholar]

29. M. Gebser, R. Kaminski, B. Kaufmann, and T. Schaub, “Answer set solving in practice,” Synth. Lect. Artif. Intell. Mach. Learn., vol. 6, no. 3, pp. 1–238, 2012. doi: 10.1007/978-3-031-01561-8. [Google Scholar] [CrossRef]

30. A. Artikis, A. Skarlatidis, and G. Paliouras, “Behaviour recognition from video content: A logic programming approach,” Int. J. Artif. Intell. Tools, vol. 19, no. 2, pp. 193–209, 2010. doi: 10.1142/S021821301000011X. [Google Scholar] [CrossRef]

31. M. Konopik, O. Pražák, D. Steinberger, and T. Brychcín, “UWB at SemEval-2016 task 2: Interpretable semantic textual similarity with distributional semantics for chunks,” in Proc. 10th Int. Workshop. Sem. Eval. (SemEval-2016), San Diego, CA, USA, 2016, pp. 803–808. [Google Scholar]

32. P. Qi, Y. Zhang, Y. Zhang, J. Bolton, and C. D. Manning, “Stanza: A python natural language processing toolkit for many human languages,” in Proc. 58th Annu. Meeting Assoc. Comput. Linguist.: Syst. Demo., Online, 2020, pp. 101–108. [Google Scholar]