Data Secure Storage Mechanism for IIoT Based on Blockchain

1  Introduction

With the continued advancement of Internet of Things (IoT) technology in Industry 4.0, IoT has been widely used in industry and has spawned a new field—IIoT [1,2]. The IIoT can support enabling technology systems for smart manufacturing [3]. This technology makes use of the interconnection of various resources in industrial production, data interoperability and the interaction between heterogeneous systems to realize the flexible management and effective utilization of various resources in the industrial production environment [4,5]. The IIoT is in a stage of rapid development and has received extensive attention from government, industry, and academia [6]. However, as the number of devices grows, the IIoT generates a large amount of data. At the same time, big data generated by IIoT not only brings higher operation and management costs, but also puts forward higher requirements for the operability, privacy, security, and fault tolerance of IIoT [7]. To address these challenges, in recent years, many scholars have introduced blockchain technology into the IIoT. In recent years, many scholars have introduced blockchain technology into the IIoT. The main characteristics of the blockchain-based IIoT not only improve the data security of the IIoT system but also its operability [8,9]. Meanwhile, storing IIoT data in the blockchain can enhance fault tolerance [10]. The immutability of the blockchain also makes the stored IIoT data and event logs immutable and traceable to ensure data accountability.

In the traditional blockchain-based IIoT system, data is stored in the Merkle tree structure. The Merkle tree structure uses leaf node hash and intermediate node hash to form Merkle proof. The data is verified by Merkle proof in the Merkle tree structure. When verifying data availability, the required Merkle proof will also increase several times with the stored data. The increasing Merkle proof will bring a huge burden on the communication bandwidth of nodes, resulting in a certain degree of communication delay. If such communication delay is serious, the security and stability of IIoT will be threatened [11–13]. The emergence of Vector Commitment (VC) provides a new way to address the above problems. VC can reduce storage costs and communication overhead. The user only needs to store the commitment value and receive the value and proof of value as needed, rather than storing a vector of the stored value.

This paper focuses on the secure data storage of blockchain-based IIoT and constructs a verifiable secret sharing scheme for improving the data layer of traditional blockchain using an improved VC, namely Partition Vector Commitment (PVC). Compared with traditional VC, PVC greatly improves the time complexity of the commitment process, opening proof process, and query process.

The following are the contributions of this paper:

1.    First, this paper provides that the existing blockchain-based IIoT has some problems, such as low efficiency in data storage and data verification, and the proof size required for verification occupies too much communication bandwidth. To solve the above problems, this paper introduces VC to replace the traditional Merkle tree, thus reducing the memory and communication burden.

2.    Second, to improve the efficiency of data storage and verification, this paper proposes a new VC structure based on the traditional vector commitment structure: partition vector commitment. The Merkle tree storage mode in the blockchain data layer is replaced by PVC, speeding up the commitment, open proof, and query process without increasing the computing and communication burden on the client.

3.    Third, this paper uses PVC to construct a verifiable distributed storage scheme that effectively reduces the communication cost of blockchain-based IIoT while maximizing the use of storage resources, thereby improving its security, stability, and efficiency.

4.    Finally, this paper analyzes and compares the original blockchain-based IIoT scheme based on Merkle tree storage mode and other existing schemes. PVC reduces the time complexity of the commitment process of traditional VC from n to p+n/p (p is the number of groups), and the time complexity of the query process from n to n/p. The comparison results show that the new scheme has better communication bandwidth and good storage performance than other original schemes.

The remainder of this paper is organized as follows. Section 2 presents the related work on blockchain technology in IIoT and big data. Problems of IIoT data structure based on traditional blockchain are covered in Section 3. Section 4 proposes a data secure storage mechanism on blockchain for IIoT. Section 5 compares the proposed blockchain secure storage mechanism with other schemes. Finally, we conclude in Section 6.

2  Blockchain Technology in IIoT and Big Data

The IoT refers to the ability to send data over the network without the use of human-to-human or computer-to-computer communication [14]. The IoT has the effect of improving the need for information sharing, thereby enhancing people’s lives. Furthermore, IoT is considered to have wide-ranging benefits in applications such as agriculture, smart homes, healthcare, transportation, and the environment [15,16]. It is also considered that more effective monitoring and control can be achieved by reducing costs, thus having a significant impact on the industry [17]. In recent years, some scholars have introduced optimized machine learning into the IoT to make it more secure [18]. The use of the new feature selection metric CorrAU also makes IIoT more robust [19]. The IoT has propelled industries forward with tangible benefits, leading to the concept of the IIoT. In 2012, General Electric (GE) company released the first IIoT white paper [20,21]. It defines the core elements of the IIoT: linking the most core equipment, people and data in industrial production with the help of digitalization. It provides great efficiency and economic benefits in maintainability, reliability, scalability, and interoperability.

With the wide application of IIoT, the main components of IIoT, Cyber-physical Systems (CPS) and IoT devices, will generate a large number of data streams, thus generating big data [22,23]. The number of devices connected to IIoT is increasing and the data stored in third parties such as the cloud is increasing day by day. Therefore, it also faces challenges, such as data security and data leakage. The emergence of blockchain provides a new way of thinking about the problem of big data. Applying blockchain to big data generated by IIoT has the following advantages: ensuring data integrity, real-time data analysis, enhancing data sharing, and improving the quality of big data [24].

Recently, many scholars have introduced blockchain technology into IIoT to enhance fault tolerance, eliminate single points of failure, and greatly improve the security of big data [25]. Blockchain can provide more secure and reliable IIoT for enterprises and individuals. Blockchain is a special kind of database, in short, blockchain technology is a distributed ledger technology. The central concept behind blockchain technology is decentralization, which means that no trusted central organization is required to control or manage participating nodes. Instead, all participating nodes (or peer nodes) in blockchain networks maintain the same copy of their ledger [26]. Each node can verify the behavior of other entities in the network, as well as create and verify new transactions that will be recorded in the blockchain.

The decentralized architecture ensures robust and secure operation of the blockchain and enables many advantages (for example, tamper resistance and vulnerability to avoiding a single points of failure) [27]. The blockchain system consists of a Data Layer, Network Layer, Consensus Layer, Incentive Layer, Contract Layer and Application Layer from bottom to top. The basic architecture diagram of the blockchain is shown in Fig. 1. Furthermore, blockchain transactions are traceable and can only be viewed by authorized nodes [28]. This feature enables the IIoT data to be fair and open while protecting the privacy of users. The Merkle tree is used to store data in the distributed ledger in the traditional blockchain data layer. The Merkle tree structure places the final bottom-up Merkle root in the block header. When verifying data availability, Merkle proof is used to verify data in the traditional blockchain. Blockchain has received a lot of attention because of its characteristics such as immutability, traceability, and decentralization. The blockchain works as follows: first, a node generates transactions and broadcasts the transaction data to the entire network. The miner node packages the transactions collected over a while with a Merkle tree to generate a new block. The miner node performs a Proof-of-Work (PoW) on the generated new block. When the miner node completes the PoW, it immediately broadcasts this new block to the entire network. All nodes verify the new block and receive it if it passes the verification.

Figure 1: The basic architecture of blockchain

Overall, the distributed structure of blockchain is extremely suitable for IIoT. It can be used to build distributed trusted IIoT. Many features make blockchain unique, such as its decentralization, immutability, and traceability. These characteristics are very beneficial to the application of IIoT. Moreover, blockchain is built on a decentralized network, which reduces the installation and maintenance costs of centralized facilities such as data centers and reduces the cost of network equipment by distributing computing and storage requirements among all devices. In general, a decentralized communication model eliminates the single points of failure problem found in traditional centralized networks. By integrating a tamper-proof ledger, the decentralized model can achieve many of the characteristics required for the IIoT network (e.g., reliability and interoperability [29]). Fig. 2 shows the blockchain-based IIoT framework. The blockchain-based IIoT framework is mainly composed of four parts: Industrial Application Layer, Blockchain Composite Layer, Communication Layer, and Perception Layer [30]. The perception layer is mainly responsible for collecting data generated by devices in the IIoT, such as smart meters, surveillance cameras, and smart sensors. The communication layer is mainly responsible for using communication technology to transmit data of the IIoT, such as WSNs, WLAN, mobile networks, etc. The blockchain composite layer consists of five parts, which constitute the blockchain part of the blockchain-based IIoT. The industrial application layer mainly analyzes and integrates the collected data information and applies the data information to the manufacturing industry, smart grid, supply chain, etc.

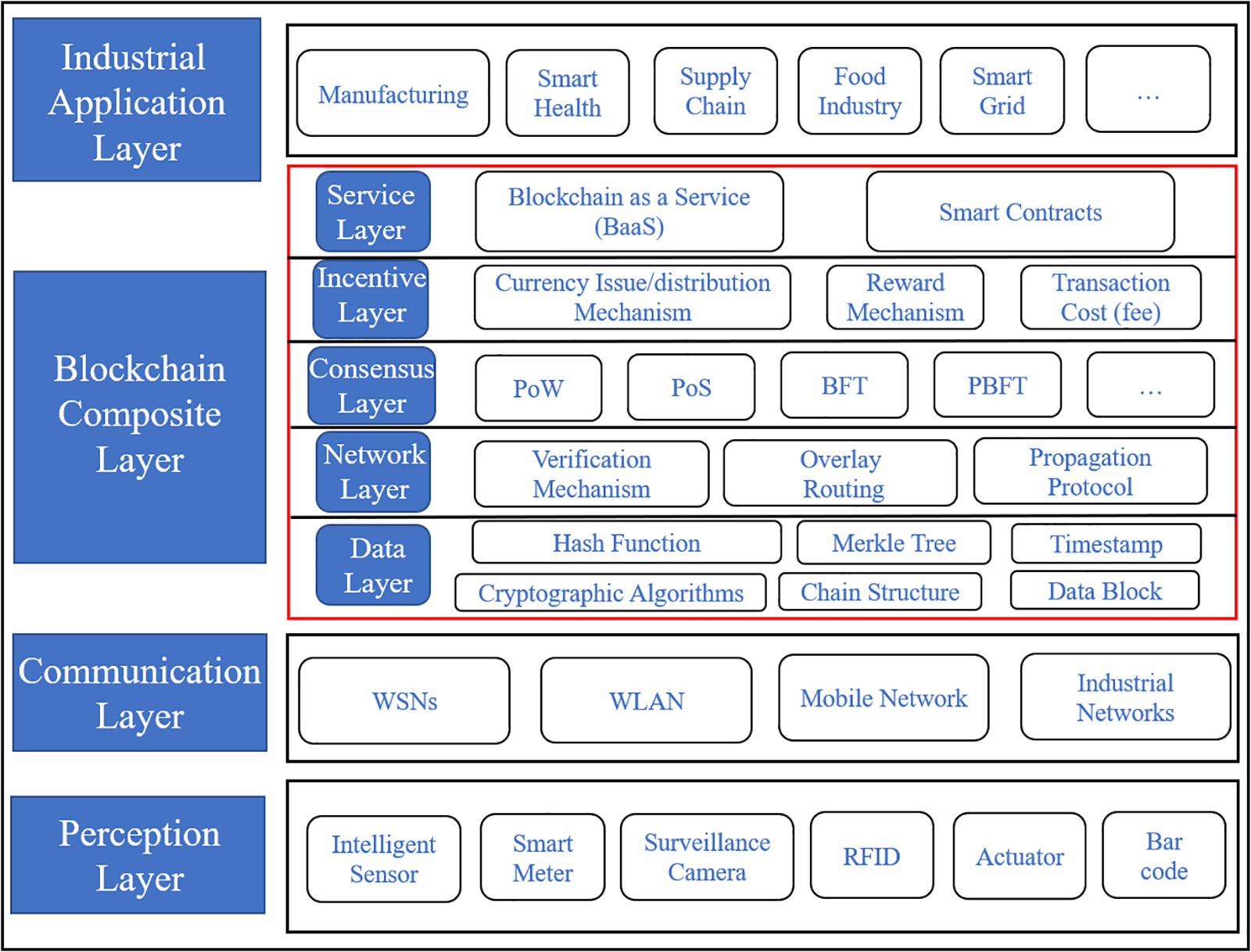
Figure 2: Blockchain-based IIoT framework

Blockchain will revolutionize IIoT and big data technology. On the one hand, in the IIoT, the decentralized nature of blockchain technology will play a key role between two untrusted devices to maintain information about the summary of their interactions, state and exchanged data [31]. On the other hand, blockchain can significantly reduce the current risks faced by users and save business process costs [32].

3  Problems Statement of IIoT Data Structure Based on Traditional Blockchain

3.1 Data Structure of Traditional Blockchain

The storage and verification of data in the traditional blockchain-based IIoT structure are completed through the Merkle tree. The Merkle tree is mainly used to encrypt data to be stored in the Distributed Ledger (DL). Fig. 3 depicts the Merkle tree structure (In Fig. 3, the hash value of the Merkel tree is Hash (E,F). Hash(Data1)−Hash(Data4) is the encrypted hash value of the Data1−Data4. Hash(Data2) and Hash (C,D) are Merkle proofs of Data1). The Merkle root of all transactions in the block is included in the block header on the blockchain to ensure that no transaction is tampered with [33]. The hash value of the leaf node and the hash value of the intermediate node of the transaction to be proved are required during data verification, and the Merkle root is then derived from the bottom up. By comparing the exported Merkle root with the Merkle root in the block, it is proven that the data is complete and has not been tampered with.

Figure 3: Blockchain-based Merkle tree data storage scheme

When verifying the stored data, Merkle proof is formed by the hash values of leaf nodes and intermediate nodes of transactions that need to be proved, and the availability of data is verified by Merkle proof [34]. If the number of nodes of the Merkle tree is k, then the query time complexity of the Merkle tree is O(log2k).

The main issue with the Merkle tree structure of the blockchain data layer is that it can only verify the availability of a single data point [35]. As more and more data are stored, the Merkle proof required to verify data availability will also increase logarithmically with the stored data. The increase of Merkle proof will put a great burden on the communication bandwidth of nodes, resulting in a certain degree of communication delay, which will seriously threaten the security and stability of IIoT [36]. Moreover, as the size of the Merkle proof increases, the time required for verification also increases rapidly, which leads to more power consumption. This phenomenon is not in line with the theme of the era of sustainable development. Therefore, it is necessary to improve the traditional blockchain storage scheme.

3.2 Solution

In traditional blockchain-based IIoT architecture, the Merkle tree verification process will place a significant amount of communication burden on nodes, potentially causing communication delays [37]. To better apply the blockchain to the IIoT, the Merkle tree in the traditional blockchain structure must be improved. There are two methods to improve the Merkle tree so far, one is based on the cryptographic accumulator scheme, and the other is based on the VC scheme. Although the accumulator can be operated in batches, reducing the storage space [38,39], there is no order of elements. In contrast, VC can open a commit value at a specified location, making it easier to index messages. In addition, the VC in the cryptographic commitment also has a constant size, which provides a new idea for solving the above problems.

VC is a type of cryptographic commitment. VC can commit a vector v of length n, and then open it at any position i ∈ [n], and prove that it is consistent with the initial commitment. The characteristic of VC is that the size of the commitment and the size of the opening at position i are independent of the vector length n, and the proof does not reveal which element is the commitment. VC is used to reduce storage costs in various applications, instead of storing the vector of data values. It can only store the commitment value and receive data values and their proofs as needed. VC allows applications to trade off storage (all values) against bandwidth (taken up by revealed values and proofs), which means that the size of commitments and opening proofs should be reduced [40].

Catalano et al. formalized the concept of VC, which first appeared in 2013 [41]. Its scheme is based on the CDH (Computational Diffie-Hellmen) assumption and the RSA problem. Dan et al. constructed VC using hidden-order groups, and their scheme is the first to allow aggregation of multiple proofs under certain conditions [42]. This scheme is also the first to have a constant size common parameter. Tomescu et al. constructed a VC scheme using polynomial commitments and Lagrangian polynomials. Using it in account-based stateless cryptocurrencies reduces the burden on nodes to store user balance states [43].

This paper applies VC to blockchain-based IIoT, which significantly improves the disadvantage of traditional Blockchain-based IIoT that uses the Merkle tree structure for storage. It can greatly reduce the communication loss of Blockchain-based IIoT, maximize the reasonable use of storage space, and ease the end-to-end communication burden. Although VC can greatly reduce the communication bandwidth of blockchain-based IIoT by replacing the Merkle tree, the storage structure of traditional blockchain, VC still has much room to improve the time complexity of the commitment process, opening proof process and query process. Therefore, based on the traditional VC structure, this paper proposes a new vector commitment structure-partition vector commitment (PVC). PVC significantly improves the efficiency of committed and open processes, greatly increasing the computing and communication needs of clients. In addition, PVC minimizes the size of the proof, thereby reducing the communication bandwidth burden on nodes. This reduction in proof size is not just a marginal improvement, but a significant enhancement that addresses a key bottleneck in blockchain technology. Therefore, PVC is suitable for building a data-secure storage mechanism for IIoT based on blockchain.

4  The Proposed Data Secure Storage Mechanism on Blockchain for IIoT

4.1 Data Storage Framework Based on PVC

Nowadays, the majority of smart factories are built using cloud-based manufacturing (CBM) [44]. Although this architecture can quickly share data with third parties to achieve resource configuration and management promptly [45,46], the centralized architecture is very fragile. Therefore, the introduction of a decentralized system is extremely necessary. The architecture of the blockchain is suitable for building IIoT, which can realize mutual supervision among decentralized nodes.

This section gives the specific system framework and basic components of the PVC-based IIoT system. The scheme combines blockchain technology with the IIoT system to accommodate the new requirements for secure data storage in IIoT.

Fig. 4 is the IIoT data storage system framework based on the blockchain proposed in this paper. There are two parts to this system: the IIoT network and the blockchain system.

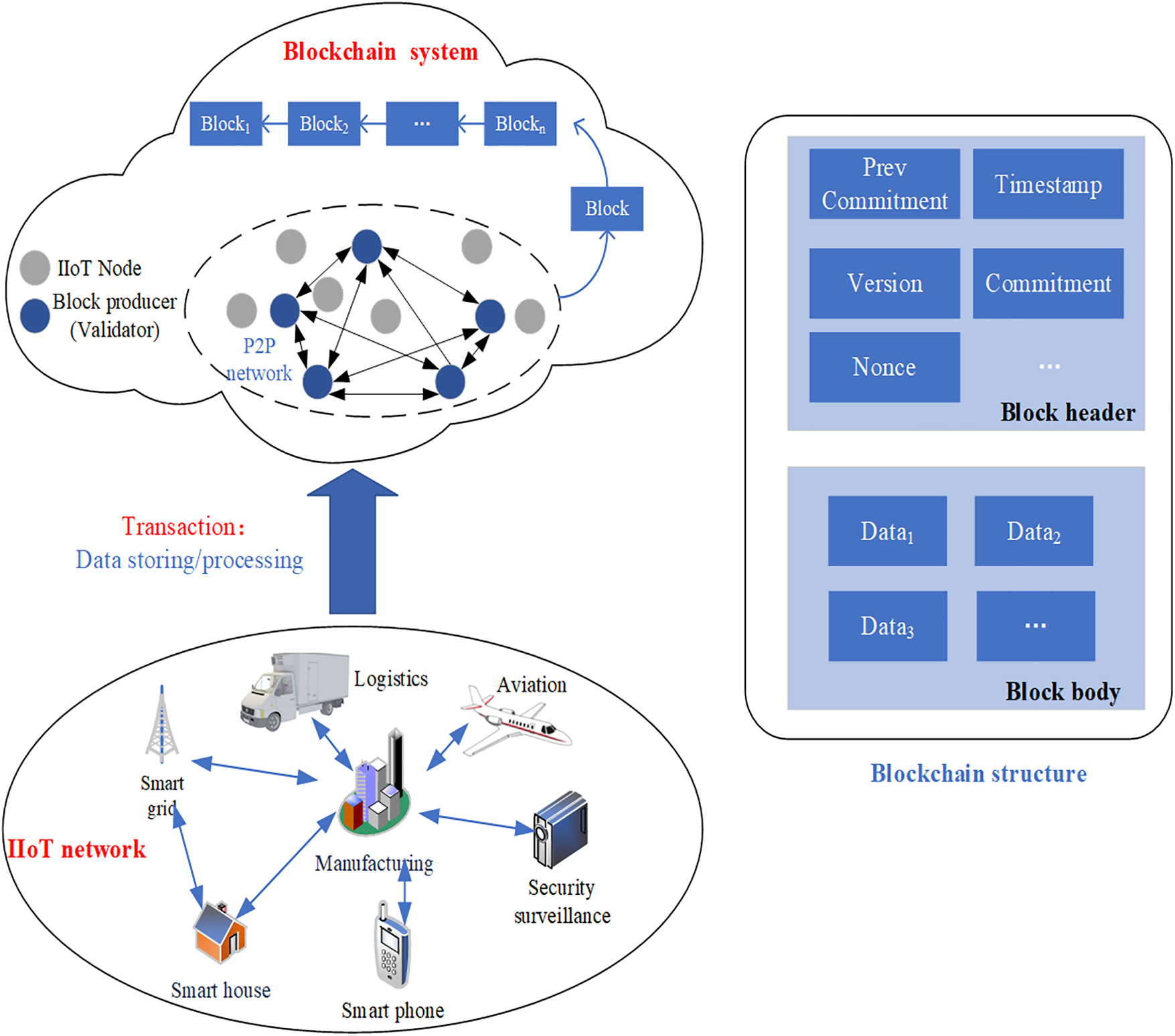
Figure 4: Data secure storage mechanism based on PVC

IIoT network: In the IIoT network, smart devices, such as IIoT nodes, collect surrounding information through sensors and assist in making decisions based on the collected or shared information. In the local IIoT network, blockchain-based IIoT leverages a security platform to secure raw data and send raw data into transactions. Local data sharing ensures the security and trustworthiness of transactions through the security platform. Smart devices create two types of transactions: data storage/processing and data sharing. These two kinds of transactions will be relayed to the blockchain system, which will store or retrieve data from the distributed ledger.

Blockchain system: After the IIoT network publishes transactions, the block producer in the peer-to-peer (P2P) network collects and verifies the transactions to generate blocks, and adds the generated blocks to the blockchain through a consensus mechanism. As well as, P2P networks are scalable, decentralized and robust. At the same time, blockchain is used to store data in the IIoT. In this paper, the Merkle tree used for storage in the data layer is replaced with a new PVC structure to reduce the size of the proof and reduce the burden of node communication bandwidth.

The flow of the data security storage mechanism proposed in this paper is shown in Fig. 5, and the specific contents are as follows:

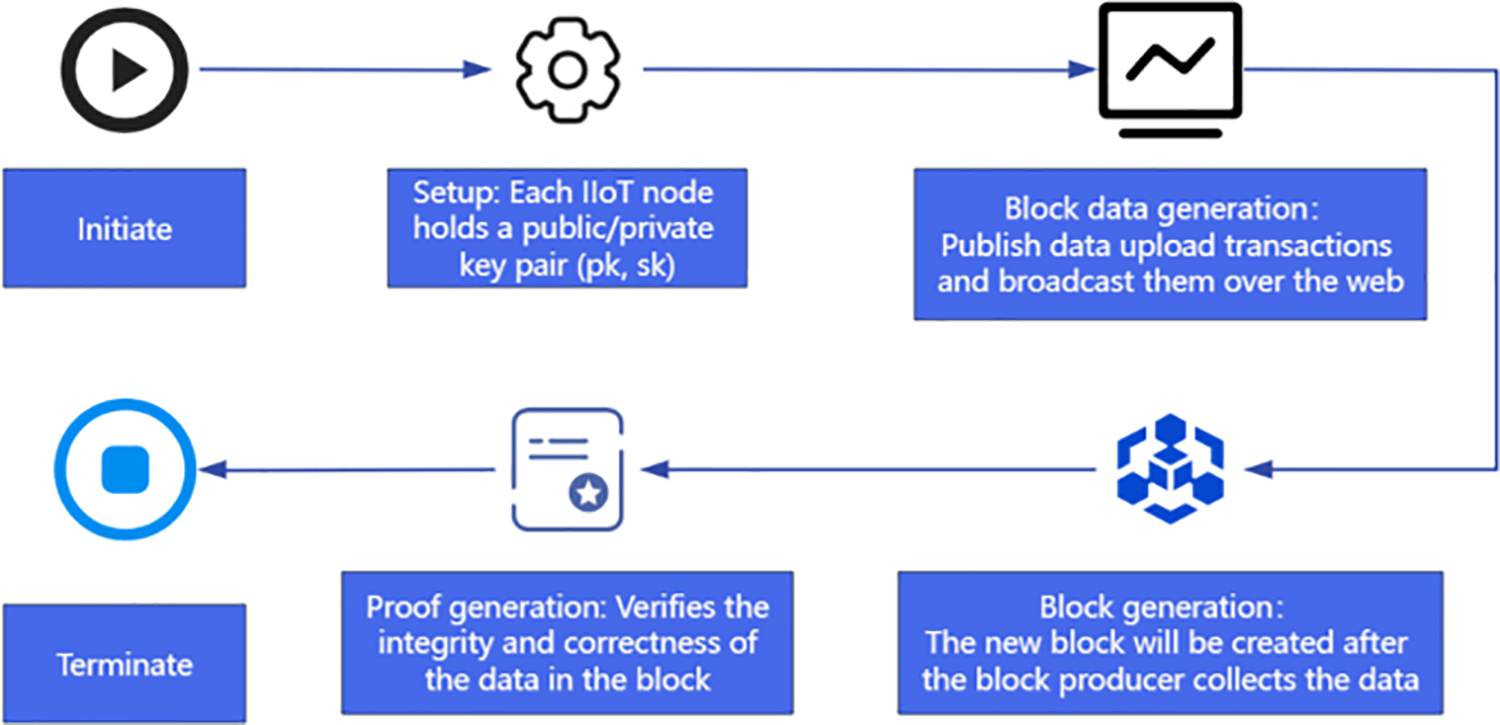
Figure 5: Flowchart of data security storage

Setup: Each IIoT node holds a public/secret key pair (pk, sk). The IIoT node uses the sk to sign the uploaded transaction data. Meanwhile, the pk is disclosed by IIoT node and shared by other nodes to verify whether the transaction data belongs to the IIoT node.

Block data generation: The IIoT node uploads data to the blockchain by publishing a data upload transaction Tx=[data,pk]. The IIoT nodes sign the transaction with the sk and broadcast it across the network, ensuring the integrity and provenance of the data uploaded to the blockchain.

Block generation: The timeline of block generation is shown in Fig. 6. The new block will be created after the block producer has collected data. When the block producer has collected enough data, the collected data is committed by the commit algorithm, and the commitment value is placed in the block header. The block header generates a random number based on the difficulty value. The first block to complete the random number search immediately broadcasts the block to the whole network. Other nodes in the network verify this block by checking the correctness of the promised value and the random number. Then the rest of the nodes verify that they have received the block by using it as the parent block to start finding the random number of the next block.

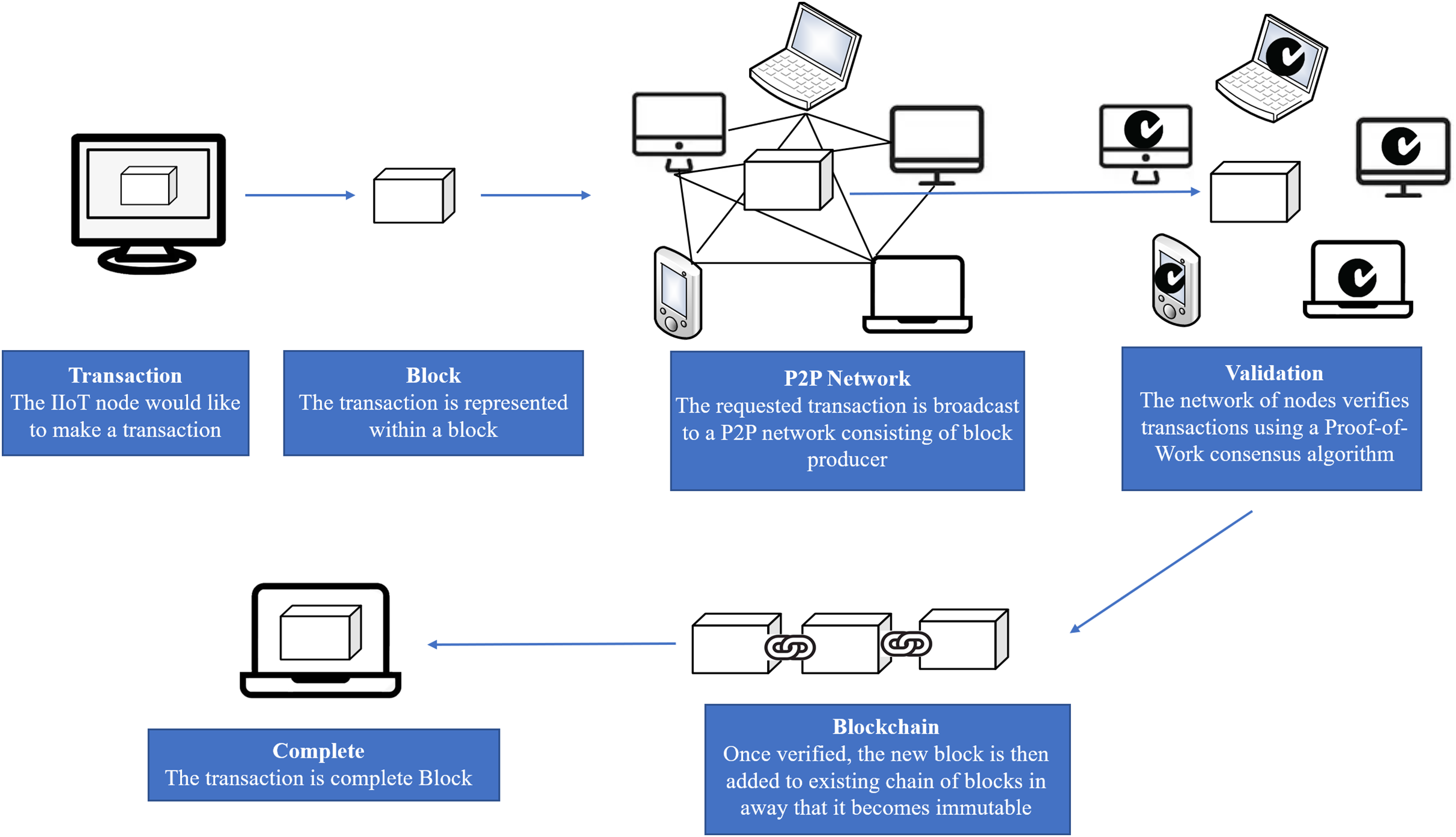
Figure 6: Timeline of block generation

Proof generation: To verify the integrity and correctness of the data in the block to the client, the block producer can generate the storage proof using the open algorithm. To verify the storage proof, the client can provide the node with the corresponding information and the storage proof generated by the open algorithm.

4.2 The Proposed Partitioned Vector Commitment

4.2.1 Preliminaries

Let G1, G2 be an additive cyclic group of order p, where p is a prime number. GT is a multiplicative cyclic group of the same order. Define e: G1 × G2 → GT as a bilinear mapping. Let integer a, b ∈ ZP∗, then the bilinear mapping satisfies the three properties listed below:

•   Bilinear: ∃e(Pa,Qb)=e(P,Q)ab for all P ∈ G1, Q ∈ G2, and a, b ∈ ZP*;

•   Non-degenerate: ∃e(P,Q)≠1 for all P ∈ G1, Q ∈ G2;

•   Computability: For all P ∈ G1, Q ∈ G2, there exists an efficient algorithm so that the result of e(P,Q) can be derived in polynomial time.

Definition 1. Square-CDH assumption. Let g be a generating element of the group 𝒢 and α∈Zp* be a random number. Then the probability of gα2 calculated from g,gα is negligible.

4.2.2 System Model

PVC in this paper is divided into two parts: Commitment and Update. The commitment part includes four algorithms: Setup algorithm, Commit algorithm, Open algorithm and Verify algorithm. The update part includes two algorithms: Update algorithm and Proofupdate algorithm.

−   Commitment part:

Setup: The committer executes the setup algorithm. It takes the size q of the committed vector (with q=poly(k)) and the security parameter k as input and outputs some public parameter pp.

−   Commit: The committer runs the commitment algorithm. The commitment algorithm takes pp and a sequence of q messages m1,…,mq as input. It returns the commitment value 𝒞 and the auxiliary information aux.

−   Open: The committer runs an open algorithm to generate a proof ψi that m is the i−th committed message. On inputting the pp, the message mi, a position i∈[q] and the aux, the open algorithm outputs a proof ψi.

−   Verify: Any client can run the verification algorithm. On input the pp, the open message m, the commitment 𝒞, the location i, and the proof ψi. If ψi is a valid proof that 𝒞 was created to a sequence (m1,…,mq), it returns 1; otherwise, it returns 0.

Update part:

−   Update: The update algorithm can update the commitment 𝒞 by changing the i-th message m to m′. On input the pp, the commitment 𝒞, the previous message m, the new message m′, and the location i, the update algorithm outputs the new commitment 𝒞 and the update message U.

−   Proofupdate: The proofupdate algorithm is run by any user holding a proofing ψj of a message at location j. On input the pp, the previous commitment 𝒞, the proofing ψj of some message at location j, the new message m at location i, and the U, the proofupdate algorithm outputs the updated commitment 𝒞′ and the updated proofing ψj′. In other words, the value U contains the necessary update information to calculate these values.

Definition 2. Correctness. When k∈N,q=poly(k), for all public parameters honestly generated by the Setup algorithm, if C is a commitment to the message m1,…,mq, and ψi is a proof at the location generated by the Open and ProofUpdate algorithms, the Verify algorithm passes with probability 1−ϵ(κ).

Definition 3. Position Binding. If for any probabilistic polynomial-time (PPT) adversary 𝒜, when the output (𝒞,m,m′,j,ψj,ψj′) satisfies:

Pr[Verify(𝒞,m,i,ψj)=1∧Verify(𝒞,m′,i,ψj′)=1∧m≠m′]=ϵ(κ)(1)

Definition 4. Conciseness. Vector commitment is concise if the security parameters contain a fixed polynomial poly(λ), such that the size of commitment 𝒞 and the open algorithm are all constrained by poly(λ).

4.2.3 Partition Vector Commitment

We use [q] to denote the set 1,…,q. [q∖i] denotes the elements in [q] other than i.

−   Setup(1k,q): First let G, GT be two bilinear groups of order p prime (p satisfying p∈poly(λ)) and satisfying e:G×G→GT. g∈G is a randomly generated element. Randomly choose z1,…,zq∈Zp.For all i∈[q], let ri=gzi.For all i,j∈[q] with i≠j, let ri,j=gzizj.This algorithm outputs the public parameters pp=(p,g,G,GT,{ri}i∈[q],{ri,j}i,j∈[q],i≠j).

−   Commit(m1,…,mq): Given a set of messages m1,…,mq and a common parameter pp, θ∈Zp is a number chosen randomly by the committer, the commitment algorithm outputs the commitment:

𝒞=gθ∏i∈[q]rimi=gθg∑i∈[q]mizi(2)

where the auxiliary information is aux=θ.

−   Open(m,i,j,aux): compute:For the j-th group in the [q] group, Λj is defined as follows:

Λj=∏k∈[q∖j]rk,jyk=(∏k∈[q∖j]rkyk)zj(3)

ψi←Λj(gzj∑ml∈Yj−{ei}ml)zj(4)

−   Verify(C,m,i,ψi): If the following equation holds:

e(𝒞rimi,ri)=e(ri,gθ)e(ψi,g)(5)

Then output 1, otherwise, output 0.

−   Update(C,m,m′,i): The algorithm is run by the original committer, which takes as input the old message m at position i and the updated message m′ and computes the updated commitment:

𝒞′=𝒞rim′−m(6)

Then outputs a new commitment 𝒞′ and an update message U.

Proofupdate(C,ψi,m′,i,U): The user holding an old proof can use U to compute updated commitment 𝒞′ and update proof at position j. If i=j, the proof holds. If i≠j, the updated commitment is: 𝒞′=𝒞rim′−m. The updated proof is:

ψi′=ψirj,im′−m(7)

4.2.4 Security Proof

The vector commitment is correct because the following equation holds:

e(𝒞rimi,ri)=e(gθ∏j∈[q]rjmjrimi,ri)=e(gθ,ri)e(∏j∈[q∖i]rjmj,gzi)=e(gθ,ri)e((∏j∈[q∖i]rjmj)zi)=e(ri,gθ)e(ψi,g)(8)

Frist, note that 𝒞 = gθ∏i∈[q]rimi and Λj=∏k∈[q∖j]rk,jyk=(∏k∈[q∖j]rkyk)zj, we have e(𝒞rimi,ri)=e(gθ∏j∈[q]rjmjrimi,ri). Second, due to ψi←Λj(gzj∑ml∈Yj−{ei}ml)zj, we have e(gθ,ri)e((∏j∈[q∖i]rjmj)zi)=e(ri,gθ)e(ψi,g). Hence, the output of the verification algorithm is always the value m.

Theorem 4.1. If the Square-CDH assumption holds, the proposed vector commitment scheme is secure.

Proof. Suppose there exists a PPT adversary 𝒜 that can produce two valid proofs for two different messages at the same location. Next, we will construct an algorithm E that takes g,gα as input to break the square CDH assumption (i.e., calculates gα2).

First, E randomly selects a number i∈[q] as the adversary’s query to break the position-bound index i. Then, E randomly selects zi∈Zp, for all j∈[q∖i], calculate rj=gzj, ri,j=(gα)zj, ri=gα, and ∀l,j∈[q∖i],l≠j:ri,j=gzizj.

The adversary then runs the Setup algorithm to obtain the public parameters pp, and outputs a set of (𝒞,m,m′,j,ψj,ψj′), where m≠m′, ψj,ψj′ can be correctly verified. When i≠j, the algorithm aborts the simulation. Otherwise, compute:

gα2=(ψi/ψi′)(m−m′)−1(9)

The correctness of the two proofs is verified below:

e(𝒞,ri)=e(rim,ri)e(ψi,g)=e(rim′,ri)e(ψi′,g)(10)

i.e.,

e(ri,ri)m−m′=e(ψi′ψi,g)(11)

Since ri=gα, this proves the correctness of the output of the algorithm E.

If the adversary succeeds with probability ϵ, then algorithm E can break the Square-CDH assumption with probability ϵ/q.

4.2.5 Performance Analysis

For the set S={m1,m2,…,mn}, first select an integer parameter p∈[1,n], divide the elements in the set S into p groups, each of which has n/p elements, and perform operations in groups, where the structure of the PVC is shown in Fig. 7.

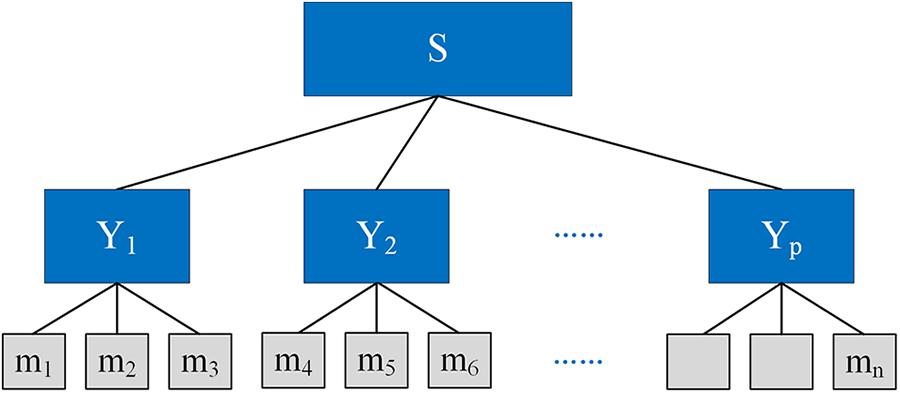
Figure 7: Data secure storage mechanism with PVC

Divide the set S into p groups, balance the number of elements in each group as much as possible, and keep the number of elements contained in each group consistent. There are about n/p elements in each group from Y1 to Yn. [p∖j] denotes the elements in [p] other than j. For the j-th group in the [p] group, Λj is defined as follows:

Λj=∏k∈[p∖j]rk,jyk=(∏k∈[p∖j]rkyk)zj(12)

where Λj is the cumulative product of the representatives of all elements outside the set Yj. When an update such as is performed in the set Yj, the data owner can compute the new value Yj in O(n/p) time complexity.

The overhead of maintaining each Yj is not significant and is determined by the number of elements in each cluster. We just need to ensure that each Yj has at least ⌈n/p⌉/2 and at most no more than 2⌈n/p⌉.

If the set Yj has too few elements, it is merged with the adjacent set Yj−1 or Yj+1. If merging Yj with an adjacent set Yj−1 or Yj+1 would result in element overflow, borrow some elements from the adjacent set so that the size of the set Yj is at least 3⌈n/p⌉/4. Similarly, if there are many elements in the set Yj, you need to divide the set Yj into two.

PVC’s partitioning strategy allows data to be balanced across different groups, not only optimizing processing efficiency, but also reducing the burden of data management and updating for a single partition. With this strategy, each partition can process its internal data independently, reducing the load on the overall system.

The above adjustment to the Partitioned vector commitment takes only O(n/p) time, and the value of n does not change significantly when performing insert and delete element operations. When there is a significant change in n, the priority queue can be checked when n is increased by insertion to see if the smallest set now needs some merging or borrowing to prevent it from becoming too small. Similarly, whenever n is reduced by deletion, the priority queue can be checked to see if the currently largest set must be split. Inductive arguments show that the method keeps the group size at O(n/p).

In practice, since Yj all expand or shrink at more or less the same rate, the overhead of keeping the size of Yj can generally be ignored. However, even if the set Yj updates are not uniform, all elements in Yj can be reallocated with O(min{p,n/p}) and the O(n) of this update is amortized to the last reallocated update set. This ensures high performance in dynamic data environments, and whenever data needs to be updated, the PVC structure can quickly calculate the change with only O(n/p) of required time complexity. The system’s efficient update processing capability is suitable for IIoT environments where data changes frequently.

The third-party storage organization receives the Λj values of all p groups Y at the time of update. Thus, the third-party storage organization can complete the update in O(p) time. Verify whether ei is in e by checking the ledger to determine whether Yj contains ei. Define that there are n/p elements in Y. Each element yi in Y represents the accumulation in the set elements. Then, compute:

ψi←Λj(gzj∑em∈Yj−{ei}ml)zj(13)

Therefore, the third-party repository can answer the query request in O(n/p) time.

The performance of PVC is shown in Table 1 below, which details the performance data of PVC solutions in terms of space use, submission, opening, updating, query, and verification, and quantifies the efficiency and effectiveness of PVC in various operational aspects.

5  Experimental Results and Analysis

5.1 Scheme Comparison

This section compares the proposed secure storage scheme with other schemes. As shown in Table 2.

As can be seen from the analysis in Table 2, other storage machine mechanisms have limitations in various aspects. In the Merkle tree scheme, only a single data set can be confirmed, and the Merkle proof provided with the sharp increase of transaction data also increases sharply. The size of the PVC and the size of the position i open are independent of the vector length n, which can circumvent the limitations of the Merkle tree. The PVC scheme reduces the O(n) required by other storage schemes in the commitment phase to O(p+n/p) and the query time to O(n/p). Aiming at the problem of low storage efficiency of the Merkle tree, the article [49] used an optimized cryptographic accumulator to improve it. Compared to the Merkle trees, the cryptographic accumulator is compact and can be used to prove membership while reducing storage overhead. While the CHKO scheme constructed by a cryptographic accumulator can be operated in batches and reduce storage space, there is no element order. PVC not only commits that the element is contained in the vector but also its position. In other words, PVC can prove on the full node whether an element exists at a certain position in the vector. The CF scheme constructed by traditional VC is superior to the Merkle tree scheme in all aspects, but VC still has a lot of room for improvement in the commitment process, the opening proof process, and the query process. The PVC constructed in this paper can improve the traditional VC problems.

This section compares the proposed scheme with other storage schemes. Based on the following comparisons, the PVC has comprehensive advantages in the time complexity of commitment, opening, and query.

5.2 Experimental Verification

In this section, we will evaluate the performance of the PVC scheme proposed in this paper compared to the vector commitment based on RSA [50]. We conducted experiments to verify the effectiveness of our scheme. The experiments were conducted on Amazon EC2’s MTA.4xlarge model, which is equipped with 64 GB of RAM and 16 virtual cores of AMD EPYC 7000 series processors with a core speed of 2.5 GHz. Fig. 8 shows the difference in authentication time for different key lengths. As can be seen from the figure, the verification time of PVC scheme is much lower than that of RSA-based hidden sequence scheme, and with the increase of key length, the verification time of PVC scheme remains at a low and stable level. In contrast, RSA-based schemes show a slight upward trend in validation time as the key length increases, indicating that they are less efficient when dealing with longer keys. This comparison shows that PVC schemes have obvious advantages in verification efficiency when the key length changes. In addition, the proof update algorithm for PVC shows logarithmic scale growth for vector size growth. In stark contrast, proof updating in RSA-based vector commitment systems is much more expensive because it uses a linear time algorithm. The algorithm needs to compute the product of prime numbers involving each vector position and perform modular exponentiation, which is computationally time-consuming.

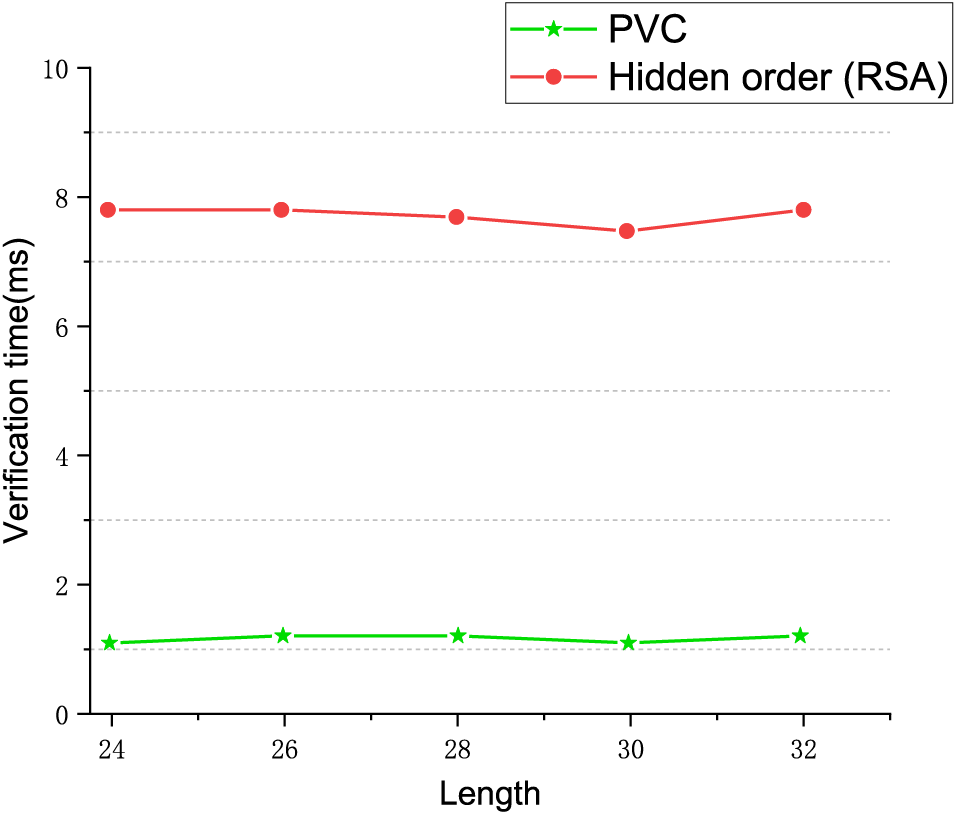
Figure 8: Verification time

Next, the PVC scheme proposed in this paper is compared with Merkle tree and CFGKN20 [51] commitment schemes. In the experimental setup phase, we set the size of each data block to 64 bits and ensure a security level of 128 bits. In addition, we adopted the BLS12-381 curve as a bilinear group scheme to evaluate the performance of various schemes with the same security level and data block size. When the transaction volume is set to 500, the experimental results of the block proof size are shown in Fig. 9, where the depth of the Merkle tree determines the size of the Merkle proof, which means that as the number of transactions contained in each block increases, the size of the proof required will also increase accordingly. As can be seen from the figure, compared with Merkle tree and CFGKN 13, PVC scheme has significantly smaller proof size and particularly significant advantages.

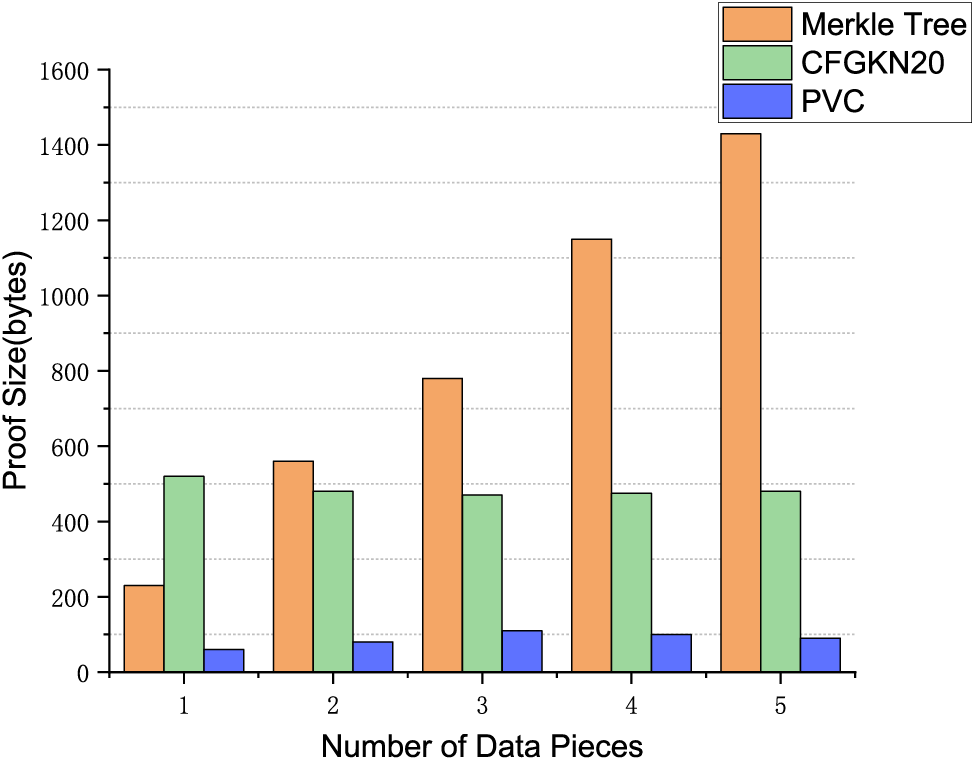
Figure 9: Proof size comparison

6  Conclusion

This paper first introduces the blockchain-based IIoT technology and then points out the problems of this traditional blockchain-based IIoT. To tackle the current issues, this paper improves the traditional VC structure and proposes a new vector commitment—PVC. It can optimize the Merkle tree, which stores data in traditional blockchain-based IIoT. Compared with other schemes, PVC significantly improves the time complexity in the process of commitment, opening proof, and query. In addition, the application of improved blockchain with PVC in IIoT can considerably reduce the scale of the required verification proof, thus reducing the bandwidth burden on nodes, and can enormously enhance the security, stability, and efficiency of blockchain-based IIoT. PVC reduces the time complexity of the commitment process of traditional VC from n to p+n/p (p is the number of groups), and the time complexity of the query process from n to n/p. Finally, compared with other schemes, our scheme has been found to effectively reduce communication consumption while improving communication efficiency.

The PVC proposed in this paper has good performance, and we will use PVC in more fields in future work. In recent years, the multilinear mapping proposed in cryptography has attracted the attention of the academic circle because of its powerful performance. In future work, we will use multilinear mapping to further optimize the performance of PVC.

Acknowledgement: We thank the reviewers and all people for their helpful comments and valuable efforts to improve the paper.

Funding Statement: This work was supported by China’s National Natural Science Foundation (Nos. 62072249, 62072056). This work is also funded by the National Science Foundation of Hunan Province (2020JJ2029).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Jin Wang, Guoshu Huang; data collection: R. Simon Sherratt; analysis and interpretation of results: Guoshu Huang, Ding Huang, Jia Ni; draft manuscript preparation: Jin Wang, R. Simon Sherratt. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. D. Rupasinghe, “Internet of things (IoT) embedded future supply chains for Industry 4.0: An assessment from an ERP-based fashion apparel and footwear industry,” J. Supply. Chain. Manag., vol. 6, no. 1, pp. 25–40, 2016. [Google Scholar]

2. H. Boyes, B. Hallaq, J. Cunningham, and T. Watson, “The industrial internet of things (IIoTAn analysis framework,” Comput. Ind., vol. 101, pp. 1–12, 2018. [Google Scholar]

3. A. Fu, X. Zhang, N. Xiong, Y. Gao, H. Wang and J. Zhang, “VFL: A verifiable federated learning with privacy-preserving for big data in industrial IoT,” IEEE Trans. Ind. Inform., vol. 18, no. 5, pp. 3316–3326, 2022. [Google Scholar]

4. K. Ashton, “That ‘internet of things’ thing,” Intell. Autom. Soft Comput., vol. 22, no. 7, pp. 97–114, 2009. [Google Scholar]

5. Y. J. Ren, Y. Leng, Y. P. Cheng, and J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Math. Biosci. Eng., vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar] [PubMed]

6. J. Q. Li, F. R. Yu, G. Deng, C. Luo, Z. Ming and Q. Yan, “Industrial Internet: A survey on the enabling technologies, applications, and challenges,” IEEE Commun. Surv. Tutor., vol. 19, no. 3, pp. 1504–1526, 2017. [Google Scholar]

7. R. Minerva, A. Biru, and D. Rotondi, “Towards a definition of the internet of things (IoT),” IEEE Internet Initiative, vol. 1, no. 1, pp. 1–86, 2015. [Google Scholar]

8. J. Qian, M. Zhu, Y. Zhao, and X. He, “Short-term wind speed prediction with a two-layer attention-based LSTM,” Comput. Syst. Sci. Eng., vol. 39, no. 2, pp. 197–209, 2021. [Google Scholar]

9. J. Sengupta, S. Ruj, and S. D. Bit, “A comprehensive survey on attacks, security issues and blockchain solutions for IoT and IIoT,” J. Netw. Comput. Appl., vol. 149, pp. 102481, 2020. [Google Scholar]

10. Y. Yao, N. Xiong, J. H. Park, M. Li, and J. Liu, “Privacy-preserving max/min query in two-tiered wireless sensor networks,” Comput. Math. Appl., vol. 65, no. 9, pp. 1318–1325, 2013. [Google Scholar]

11. K. He, J. Shi, C. Huang, and X. Hu, “Blockchain based data integrity verification for cloud storage with T-Merkle tree,” in Proc. ICA3PP, New York, NY, USA, 2020, pp. 65–80. [Google Scholar]

12. C. C. Han, G. J. Kim, O. Alfarraj, A. Tolba, and Y. J. Ren, “ZT-BDS: A secure blockchain-based zero-trust data storage scheme in 6G edge IoT,” J. Internet Technol., vol. 23, no. 2, pp. 289–295, 2022. [Google Scholar]

13. L. D. Xu, W. He, and S. Li, “Internet of things in industries: A survey,” IEEE Trans. Ind. Inform., vol. 10, no. 4, pp. 2233–2243, 2014. [Google Scholar]

14. M. Stoyanova, Y. Nikoloudakis, S. PanagIoTakis, E. Pallis, and E. K. Markakis, “A survey on the internet of things (IoT) forensics: Challenges, approaches, and open issues,” IEEE Commun. Surv. Tutor., vol. 22, no. 2, pp. 1191–1221, 2020. [Google Scholar]

15. J. Wang, C. C. Han, X. F. Yu, Y. J. Ren, and R. S. Sherratt, “Distributed secure storage scheme based on sharding blockchain,” Comput. Mater. Contin., vol. 70, no. 3, pp. 4485–4502, 2022. doi: 10.32604/CMC.2022.020648. [Google Scholar] [PubMed] [CrossRef]

16. M. A. Khan and K. Salah, “IoT security: Review, blockchain solutions, and open challenges,” Future Gener. Comput. Syst., vol. 82, pp. 395–411, 2018. [Google Scholar]

17. H. Ahmed, A. A. Ramadan, E. H. Elkordy, and A. A. Elngar, “Introduction to industrial internet of things (IIo-T),” in Industrial Internet of Things (IIT), 1st ed. Orlando, FL, USA: CRC Press, 2022, vol. 1, pp. 1–18. [Google Scholar]

18. M. Shafiq, Z. Tian, A. K. Bashir, X. Du, and M. Guizani, “IoT malicious traffic identification using wrapper-based feature selection mechanisms,” Comput. Secur., vol. 94, no. 4, pp. 101863, 2020. doi: 10.1016/j.cose.2020.101863. [Google Scholar] [CrossRef]

19. M. Shafiq, Z. Tian, A. K. Bashir, X. Du, and M. Guizani, “CorrAUC: A malicious Bot-IoT traffic detection method in IoT network using machine learning techniques,” IEEE Internet Things J., vol. 8, no. 5, pp. 3242–3254, 2021. doi: 10.1109/JIOT.2020.3002255. [Google Scholar] [CrossRef]

20. K. Prabhat et al., “PPSF: A privacy-preserving and secure framework using blockchain-based machine-learning for IoT-driven smart cities,” IEEE Trans. Netw. Sci. Eng., vol. 8, no. 3, pp. 2326–2341, 2021. doi: 10.1109/TNSE.2021.3089435. [Google Scholar] [CrossRef]

21. J. S. Park and J. H. Park, “Future trends of IoT, 5G mobile networks, and AI: Challenges, opportunities, and solutions,” J. Inf. Process. Syst., vol. 16, no. 4, pp. 743–749, 2020. [Google Scholar]

22. J. Lee, H. D. Ardakani, S. Yang, and B. Bagheri, “Industrial big data analytics and cyber-physical systems for future maintenance & service innovation,” in Proc. CIRP, vol. 38, pp. 3–7, 2015. doi: 10.1016/j.procir.2015.08.026. [Google Scholar] [CrossRef]

23. H. Alshammari, S. A. El-Ghany, and A. Shehab, “Big IoT healthcare data analytics framework based on fog and cloud computing,” J. Inf. Process. Syst., vol. 16, no. 6, pp. 1238–1249, 2020. [Google Scholar]

24. A. Deepa et al., “A survey on blockchain for big data: Approaches, opportunities, and future directions,” Future Gener. Comput. Syst., vol. 131, no. 2011, pp. 209–226, 2022. doi: 10.1016/j.future.2022.01.017. [Google Scholar] [CrossRef]

25. N. Teslya and I. Ryabchikov, “Blockchain platforms overview for industrial IoT purposes,” in Proc. FRUCT, Petrozavodsk, Kareliya Republits, Russia, 2018, pp. 250–256. [Google Scholar]

26. L. Bai, “Application and research of blockchain technology in industrial internet of things,” Cyberspace Secur., vol. 9, no. 9, pp. 87–91, 2018. [Google Scholar]

27. N. Kshetri, “Can blockchain strengthen the internet of things?,” IT Prof., vol. 19, no. 4, pp. 68–72, 2017. doi: 10.1109/MITP.2017.3051335. [Google Scholar] [CrossRef]

28. S. K. Singh, A. E. Azzaoui, T. W. Kim, Y. Pan, and J. H. Park, “Deepblockscheme: A deep learning-based blockchain driven scheme for secure smart city,” Human-Centric Comput. Inf. Sci., vol. 11, no. 12, pp. 1–13, 2021. [Google Scholar]

29. O. Novo, “Blockchain meets IoT: An architecture for scalable access management in IoT,” IEEE Internet Things J., vol. 5, no. 2, pp. 1184–1195, 2018. doi: 10.1109/JIOT.2018.2812239. [Google Scholar] [CrossRef]

30. Y. Yuan and F. Y. Wang, “Towards blockchain-based intelligent transportation systems,” in Proc. ITSC, Rio de Janeiro, Brazil, 2016, pp. 2663–2668. [Google Scholar]

31. K. Sharma and D. Jain, “Consensus algorithms in blockchain technology: A survey,” in Proc. ICCCNT, Kanpur, India, 2019, pp. 1–7. [Google Scholar]

32. A. Panarello, N. Tapas, G. Merlino, F. Longo, and A. Puliafito, “Blockchain and IoT integration: A systematic survey,” Sens., vol. 18, no. 8, pp. 1–37, 2018. doi: 10.3390/s18082575. [Google Scholar] [PubMed] [CrossRef]

33. H. Liu, X. Luo, H. Liu, and X. Xia, “Merkle tree: A fundamental component of blockchains,” in Proc. EIECS, Changchun, Jilin, China, 2021, pp. 556–561. [Google Scholar]

34. B. Liu, X. L. Yu, S. Chen, X. Xu, and L. Zhu, “Blockchain based data integrity service framework for IoT data,” in Proc. ICWS, Honolulu, HI, USA, 2017, pp. 468–475. [Google Scholar]

35. M. Yu, S. Sahraei, S. Li, S. Avestimehr, and S. Kannan, “Coded merkle tree: Solving data availability attacks in blockchains,” in Int. Conf. Financ. Cryptogr. Data Secur., Kota Kinabalu, Malaysia, 2020, pp. 114–134. [Google Scholar]

36. K. P. Yu, L. Tan, M. Aloqaily, H. Yang, and Y. Jararweh, “Blockchain-enhanced data sharing with traceable and direct revocation in IIoT,” IEEE Trans. Ind. Inform., vol. 17, no. 11, pp. 7669–7678, 2021. doi: 10.1109/TII.2021.3049141. [Google Scholar] [CrossRef]

37. S. Wang, L. Ouyang, Y. Yuan, X. Ni, X. Han and F. Y. Wang, “Blockchain-enabled smart contracts: Architecture, applications, and future trends,” IEEE Trans. Syst., Man, Cybernet.: Syst., vol. 49, no. 11, pp. 2266–2277, 2019. doi: 10.1109/TSMC.2019.2895123. [Google Scholar] [CrossRef]

38. A. Ozdemir, R. S. Wahby, B. Whitehat, and D. Boneh, “Scaling verifiable computation using efficient set accumulators,” in Proc. USENIX Security 20, Limoges, France, 2020, pp. 2075–2092. [Google Scholar]

39. Q. Yang and H. Wang, “Privacy-preserving transactive energy management for IoT-aided smart homes via blockchain,” IEEE Internet Things J., vol. 8, no. 14, pp. 11463–11475, 2021. doi: 10.1109/JIOT.2021.3051323. [Google Scholar] [CrossRef]

40. Y. J. Ren et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Gener. Comp. Syst., vol. 115, no. 2, pp. 304–313, 2021. doi: 10.1016/j.future.2020.09.019. [Google Scholar] [CrossRef]

41. D. Catalano and D. Fiore, “Vector commitments and their applications,” in Proc. PKC 2013, Nara, Japan, 2013, pp. 55–72. [Google Scholar]

42. B. Dan, B. Bünz, and B. Fisch, “Batching techniques for accumulators with applications to IOPs and stateless blockchains,” in Proc. CRYPTO 2019, Santa Barbara, CA, USA, 2019, pp. 561–686. [Google Scholar]

43. A. Tomescu, I. Abraham, V. Buterin, J. Drake, and D. Khovratovich, “Aggregatable subvector commitments for stateless cryptocurrencies,” in Proc. SCN 2020, Amalfi, Italy, 2020, pp. 45–64. [Google Scholar]

44. D. Wu, D. W. Rosen, L. Wang, and D. Schaefer, “Cloud-based design and manufacturing: A new paradigm in digital manufacturing and design innovation,” Comput. Aided Des., vol. 59, no. 4, pp. 1–14, 2015. doi: 10.1016/j.cad.2014.07.006. [Google Scholar] [CrossRef]

45. A. W. Colombo, T. Bangemann, S. Karnouskos, J. Delsing, and J. Lastra, “Industrial cloud-based cyber-physical systems,” The IMC-AESOP Approach, vol. 22, pp. 4–15, 2014. doi: 10.1007/978-3-319-05624-1. [Google Scholar] [CrossRef]

46. P. Kumar, R. Maddikunta, Q. V. Pham, B. Prabadevi, and M. Liyanage, “Industry 5.0: A survey on enabling technologies and potential applications,” J. Ind. Inf. Integr., vol. 26, no. 2, pp. 100257–100287, 2021. [Google Scholar]

47. P. Camacho, A. Hevia, M. Kiwi, and R. Opazo, “Strong accumulators from collision-resistant hashing,” in Proc. ICIS, Berlin, Heidelberg, Germany, 2008, pp. 471–486. [Google Scholar]

48. H. Liu, X. Luo, H. Liu, and X. Xia, “Merkle tree: A fundamental component of blockchains,” in Proc. EIECS, Changchun, China, 2021, pp. 556–561. [Google Scholar]

49. J. Wang, W. Chen, L. Wang, R. S. Sherratt, and A. Tolba, “Data secure storage mechanism of sensor networks based on blockchain,” Comput. Mater. Contin., vol. 65, no. 3, pp. 2365–2384, 2020. doi: 10.32604/cmc.2020.011567. [Google Scholar] [PubMed] [CrossRef]

50. D. Catalano and D. Fiore, “Vector commitments and their applications,” in 16th Int. Conf. Pract. Theory in Public-Key Cryptogr., Nara, Japan, 2013, pp. 55–72. [Google Scholar]

51. M. Campanelli, D. Fiore, N. Greco, D. Kolonelos, and L. Nizzardo, “Incrementally aggregatable vector commitments and applications to verifiable decentralized storage,” in 26th Int. Conf. Theory Appl. Cryptol. Inf. Secur., Daejeon, South Korea, 2020, pp. 3–35. [Google Scholar]