 Open Access
Open Access
ARTICLE
Multi-Branch High-Dimensional Guided Transformer-Based 3D Human Posture Estimation
1 School of Mechanical Engineering, Anhui University of Technology, Huainan, 232001, China
2 School of Artificial Intelligence, Anhui University of Technology, Huainan, 232001, China
3 Key Laboratory of Conveyance Equipment (East China Jiaotong University), Ministry of Education, Nanchang, 330013, China
* Corresponding Author: Xianhua Li. Email:
(This article belongs to the Special Issue: Recognition Tasks with Transformers)
Computers, Materials & Continua 2024, 78(3), 3551-3564. https://doi.org/10.32604/cmc.2024.047336
Received 02 November 2023; Accepted 16 January 2024; Issue published 26 March 2024
Abstract
The human pose paradigm is estimated using a transformer-based multi-branch multidimensional directed the three-dimensional (3D) method that takes into account self-occlusion, badly posedness, and a lack of depth data in the per-frame 3D posture estimation from two-dimensional (2D) mapping to 3D mapping. Firstly, by examining the relationship between the movements of different bones in the human body, four virtual skeletons are proposed to enhance the cyclic constraints of limb joints. Then, multiple parameters describing the skeleton are fused and projected into a high-dimensional space. Utilizing a multi-branch network, motion features between bones and overall motion features are extracted to mitigate the drift error in the estimation results. Furthermore, the estimated relative depth is projected into 3D space, and the error is calculated against real 3D data, forming a loss function along with the relative depth error. This article adopts the average joint pixel error as the primary performance metric. Compared to the benchmark approach, the estimation findings indicate an increase in average precision of 1.8 mm within the Human3.6M sample.Keywords
Using one single photograph to estimate the body’s three-dimensional (3D) position is crucial in interactions between humans and computers, augmented reality, and behavioral research. However, the uncertainty about two-dimensional (2D)-3D predictions, including self-occlusion and the absence of depth data, makes per-frame-based 3D pose estimation difficult.
Currently, there are two main categories of 3D estimation methods: direct approaches and 2-step methods. The direct method involves utilizing a singular frame picture as a source of information and directly estimating 3D position of the human body solely based on the image [1–4]. Although the direct method can obtain rich feature information from images, it is difficult for a single model to learn these features due to the lack of intermediate supervision and the impact of complex scenes and self-occlusion in images. The proposed approach involves a two-step methodology for the problem of 3D person estimation of poses. This methodology entails splitting the assignment into two distinct stages: the initial estimation of the 2D human pose within the provided image, and the subsequent estimation of the 2D human pose based on the obtained 2D posture. In their study, Martinez et al. [5] employed an entirely connected layer integrated by multi-layer remaining links to perform a regression of 3D posture based on 2D coordinates. Their findings demonstrate that the primary source of inaccuracy in 3D posture estimates stems from the accuracy of 2D estimations of pose. Furthermore, due to the advancement of 2D person key point estimation techniques, the two-step approach has gained significant popularity in contemporary 3D position estimation endeavors.
The main problem that the two-step method needs to solve is how to restore the depth information of each key point from the 2D pose to address this issue, Chen et al. [6] searched for the optimal 3D pose based on the nearest neighbor matching. Tekin et al. [7] used a 2D key point heat map as an intermediate representation to obtain richer spatial information. Moreno et al. [8] employed distance matrices that represented both 2D and 3D human postures. Additionally, the researchers converted the mapping from 2D to 3D to address the matrix regression issue. The enhancement of 3D pose estimate precision has been achieved through the utilization of feature extraction and subsequent fitting of the initial 2D pose. Nevertheless, the absence of any pre-existing knowledge to facilitate the convergence of networks ultimately results in an increased model complexity and challenges in achieving convergence.
The use of the relative level of important areas as a forecast target directly affects the accuracy of 3D posture estimation. The lack of homogeneity among devices used for collecting 3D person poses data results in notable variations in the 3D poses observed across different datasets, even when considering the global coordinate scheme. The utilization of the distance between key elements as a measurement objective is a highly effective approach to mitigating the influence of data disparities. However, the introduction of relative depth can lead to drift errors. The determination of the coordinates of smaller-scale key points is contingent upon the coordinates for upper-level crucial locations, and any inaccuracies with the higher-level connections will likewise impact the smaller-scale joints. The error of each level will gradually accumulate downwards, and the farther away from the root joint, the greater the accumulated drift error. To tackle the aforementioned concerns, this study presents a novel approach utilizing a transformer-based multi-branch structure to enhance the precision of 3D posture prediction. The network outlined in this paper has three distinct properties:
(1) Multi-parameter fusion of bones and projection towards higher dimensions combining the characteristics of self-attention mechanism networks, bone parameters are fused by quantitatively analyzing the motion of human joints in the 2D space, four virtual skeletons are constructed to reduce drift errors in limb pose estimation.
(2) Multi-scale feature fusion. Proposition of a multi-branch network to extract features of inter-skeletal and global motion by fusing motion features at different scales, the drift error caused by using relative depth as the prediction result is reduced.
(3) High dimensional projection guides model convergence. The acceleration of the algorithm’s convergence rate as well as improvements in network precision for estimation are achieved by mapping the estimated results into multidimensional and actual labeling for mistake calculation.
By projecting the estimation results onto high-dimensional and real labels for error calculation, the convergence speed of the model is accelerated while improving the estimation accuracy of the network.
2.1 Method Using Monocular Image
Along with the growth of deep neural networks that can learn better, like graph neural network (GNN), Transformer, which is a long short term (an LSTM) network, is being used for 3D pose estimation jobs. Combining what we already know about human anatomy with limits makes the model work better. Nie et al. [9] projected the dimensions of a person’s joints using 2D photographs of body parts and joint orientations. Zhou et al. [10] used all three connection temperature maps to show the corresponding depth data for the endpoints within each skeleton body part. Li et al. [11] suggested an innovative regression model that uses differential logarithm likelihood estimates to show how the network’s outcome is spread out. Wang et al. [12] combined the complex projection via supervised training. They projected the estimated 3D pose into 2D space and set a fixed bone length as the predicted goal. Wang et al. [13] came up with the idea for “virtual bones,” which adds new cyclic limits to the process of figuring out a person’s 3D pose. In the GNN algorithm learning, Zeng et al. [14] suggested a hop-aware layering channel compressing fusion layer that could successfully pull-out useful information from nearby nodes while blocking out noise. By adding a local linked network (LCN), Ci et al. [15] suggested a better graphic convolutional network that would clear up the confusion of 2D–3D. When people move, they have a link among the ligaments and tendons of their bodies. The self-attention system can learn how human bones rely on each other. Lutz et al. [16] effectively improved the performance of the self-attention mechanism network by introducing intermediate monitoring and residual connections between stacked encoders.
Due to issues such as self-occlusion, ill-posedness, and missing depth information in 2D-3D projection, the network is not only difficult to converge without prior knowledge but also has low performance. So it has become a trend to improve the learning performance of networks by introducing prior knowledge.
2.2 Method Based on Time Series
The duration series-based technique takes a set of frames consecutively as input and renders 3D human pose estimates more accurate and stable by adding time constancy. Liu et al. [17] utilized a multiple-scale framework for hollow inversion to improve the uniformity of time in temporally receptive fields. This allowed for over-time-dependent learning for tasks like estimating poses. In their study, Zheng et al. [18] reconstructed all the individual bone joints in every frame as well as the relationships among frames in terms of time. They then produced a precise 3D body pose for the center frame. The researchers, Li et al. [19] built multi-hypothesis-dependent connections and set up connections among hypothesis traits. They then combined several hypothesized traits and made the final 3D pose. Li et al. [20] aggregated local and global features into unidirectional representations by fusing features extracted from ordinary and step transformers. Wang et al. [21] improved the robustness of 3D sequence generation and key point motion recovery by integrating short-term and long-term motion information and introducing motion loss. Zhang et al. [22] acquired the knowledge regarding the spatiotemporal relationships with body joints across all global frames allowed for the estimation of human posture in three dimensions.
2.3 Method Based on Multiple Views
The utilization of multiple views has proven to be a successful approach to addressing the issue of lacking depth data during the process of projecting 3D objects onto a 2D plane. Brian et al. [23] learned 3D rotation and length between bones based on multi-view fusion layers, and reconstructed the skeleton through time-dependent joint rotation. Ma et al. [24] inspired by multimodal Transformers, proposed a 3D position encoder to guide the encoding of the corresponding relationships between pixels in different views. Shua et al. [25] proposed a unified framework consisting of feature extractors, multi-view fusion transformers, and time transformers, which can adaptively handle different views and video lengths without camera calibration.
The paper presents a suggested framework for 3D human posture estimation that relies upon the Transformer architecture and incorporates several branches to handle high-dimensional data. The construction of this framework is depicted in Fig. 1. It utilizes the estimation outcomes of pre-existing 2D detectors as its input. After preprocessing the 2D pose, the bone parameters are fused and projected to high-dimensional, and the fused parameters are input into two-branch networks for inter-bone and overall motion feature extraction. Branch 1 uses residual connections to avoid gradients in the deep network. Then, the extracted features are fused and connected to a fully connected network for bone relative depth estimation. Finally, the estimated relative depth is combined with the input real 2D bone length to guide the model convergence in a high-dimensional manner. The number of attention heads is configured as 8 to mitigate the computational complexity of attention calculations. The utilization of single-dimensional (1D) convolution is employed as a replacement for fully connected layers to achieve embeddings in higher dimensions. where
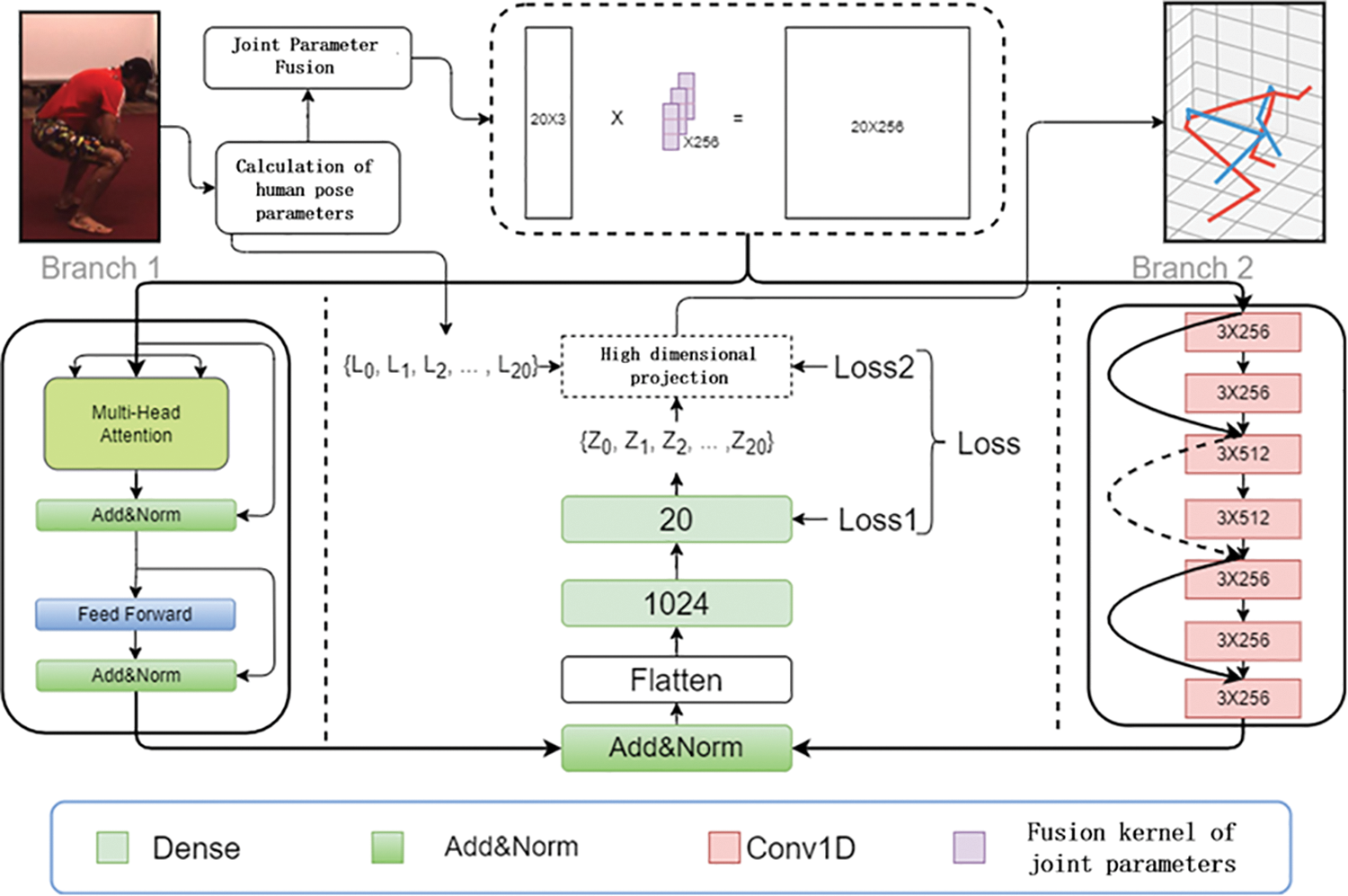
Figure 1: Overall network design
3.1 Determination and Preprocessing of Bones
Directly using 2D coordinates as input to the network will increase the convergence difficulty of the model. The human posture is described through directed encoding of bones, as shown in Fig. 2. This article takes the chest as the root coordinate, as indicated by the red dot in Fig. 2. By constructing joint vectors to reduce convergence difficulty, the preprocessing formulas are shown in Eqs. (2) and (3), the initial and final positions within the i-th skeleton are denoted as Jhi as well as Jei, respectively. The expression representing the i-th skeleton is [Vi, Mi]:
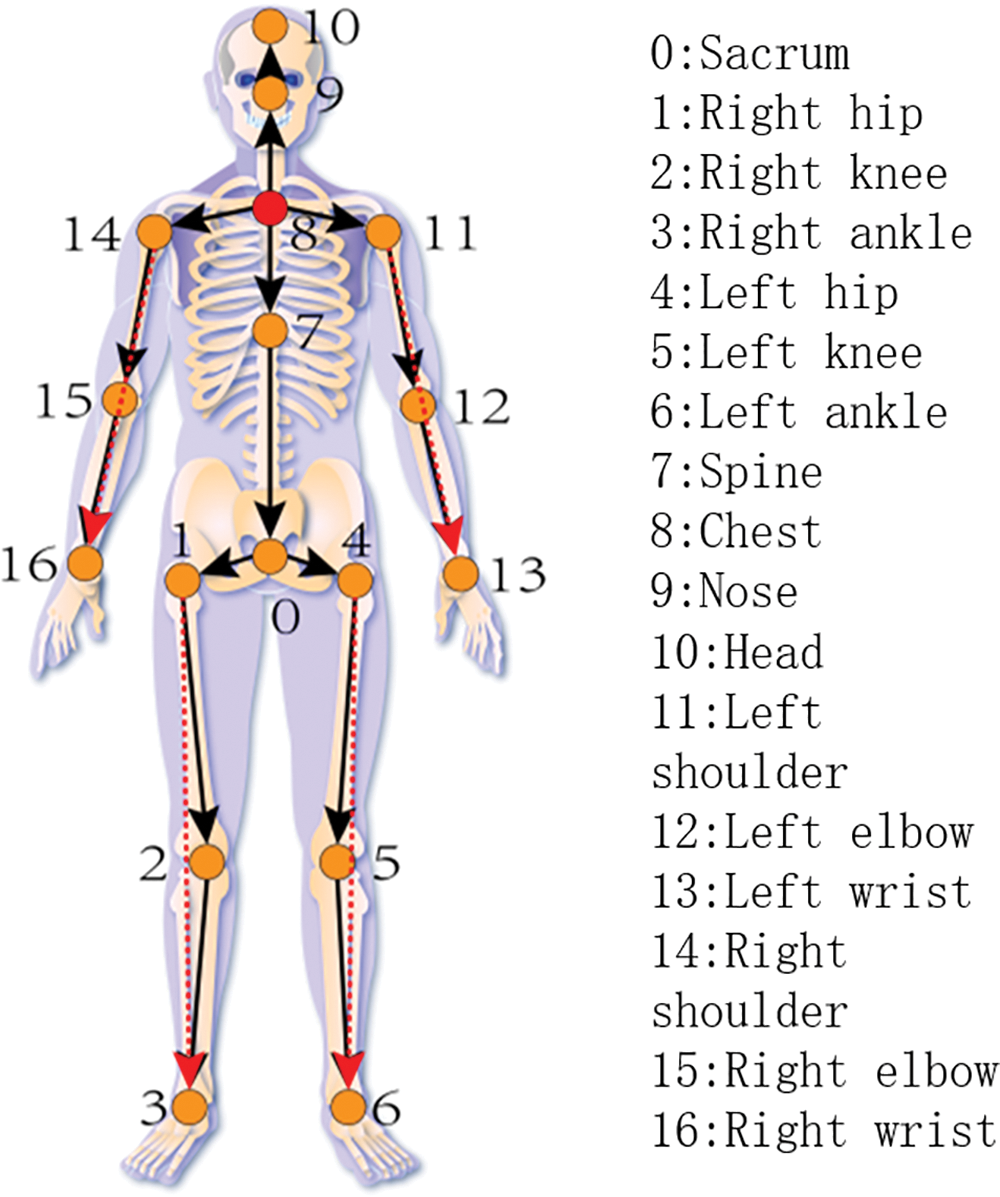
Figure 2: Directed encoding of human joints
To explore the response mechanism of human motion in 2D space, this article visualizes the motion of human bones in 2D space, as shown in Fig. 3. The color depth signifies the range of joint motion, with darker shades indicating a broader range of joint movement, while lighter shades denote a more limited range of joint motion. In terms of human anatomy, it is possible to say that a 2D unit vector represents each bone in the human body. Through the analysis of 300,000 samples, the range of motion of the human limbs is the largest. Moreover, due to the use of the relative depth of bones as the estimation result, the errors of the superior bones will accumulate in the subordinate bones, causing drift errors. The relative distance between the limbs and the root joint point is the farthest, and the cumulative drift error is also the largest, making it the most difficult to estimate human motion. Therefore, this article introduces four virtual bones to increase the cyclic constraints on human limbs and reduce drift errors. In the following illustration, the arms’ virtual bones are linked together using the red dotted line.
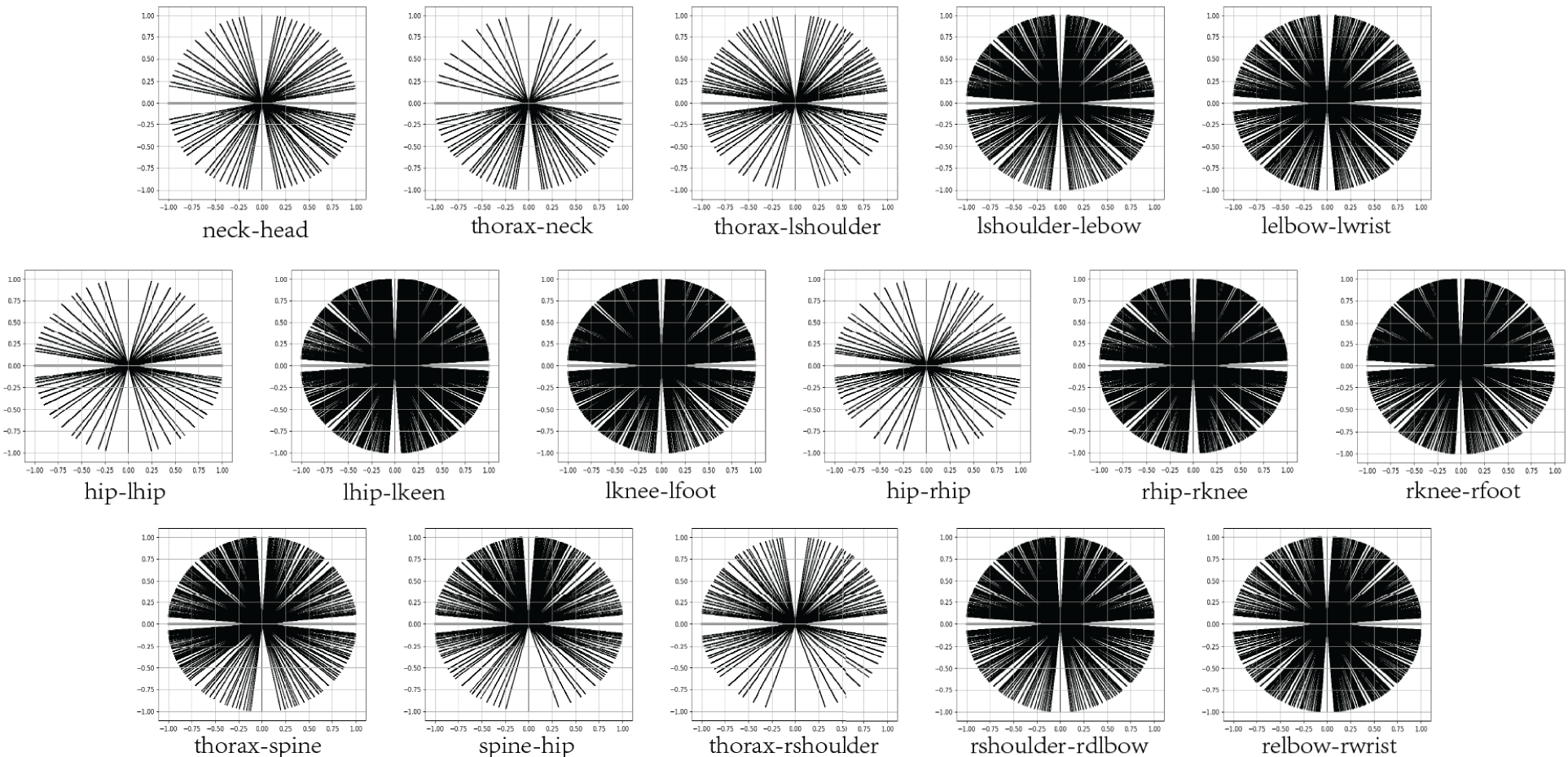
Figure 3: The movement of human skeletons in 2D space
After preprocessing bone parameters, each bone in the human body is represented by three parameters, with a total of 20 joints and 60 parameters. To resolve the issue of training bone dependency relationships from 60 parameters in networks based on self-attention mechanism, a joint parameter fusion algorithm was designed. The calculation formula is shown in (4), where Pj is the bone parameter matrix preprocessed by the method in 3.1, and the variable j represents the quantity of bones, whereas Wi is the fusion coefficient matrix for bone parameters and i is the number of weight matrices; Mj is the fused parameter matrix.
As shown in Fig. 4, the weight matrix slides in the column direction of the bone parameter matrix to obtain the fused bone parameter matrix in order to extract as many 2D pose features as possible, multiple W matrices will be created that can continuously update parameters with network training, achieving the encoding of bone parameters into high-dimensional space.
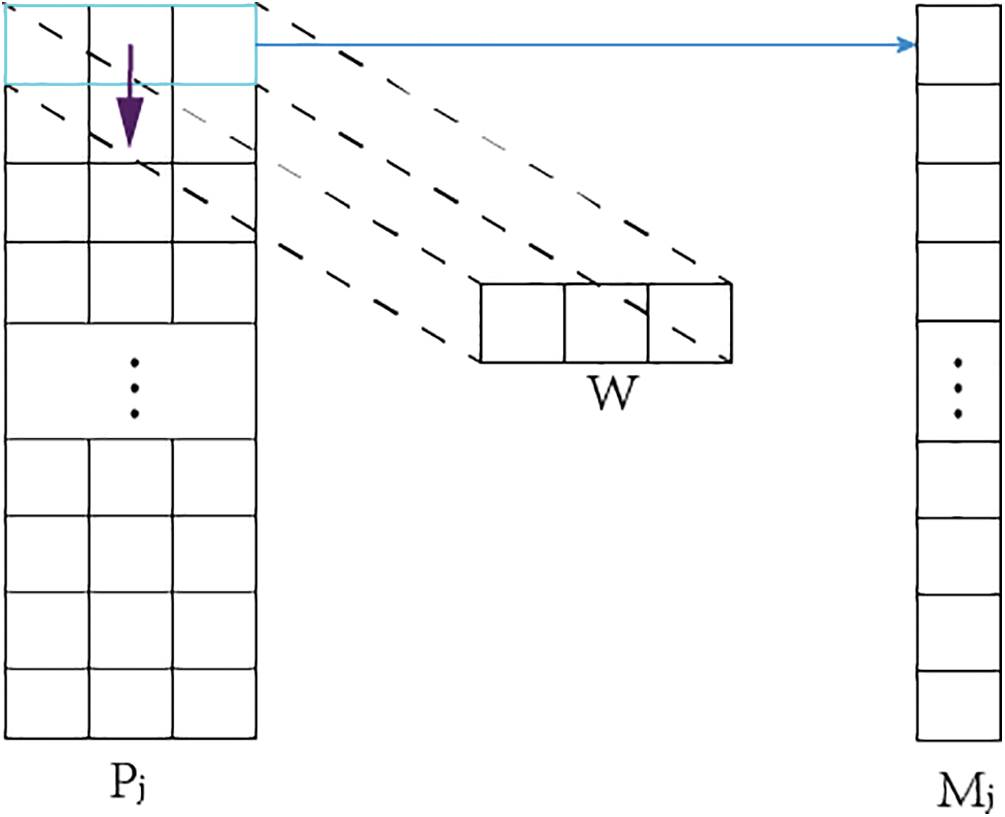
Figure 4: Bone parameter fusion
Branch 1 network adopts the encoding layer of Transformer [26], and through joint parameter fusion, a set of bones can be projected into higher dimensions to replace traditional Transformer’s word embedding operation, extending the input 2D pose parameters to the hidden dimensions of the network. In addition, the bone fusion matrix W only focuses on multiple parameters of a certain bone rather than multiple parameters of multiple bones, which avoids confusion of different bone features and achieves the extraction of features between different bones. The Branch 2 network is comprised of numerous 1D convolutional layers, each employing a convolutional kernel that has a desired quantity (3 kernels per layer), as shown in Fig. 1. Similarly, the fused bone parameters are used as inputs to the Branch 2 network, and the overall features of human movements are extracted by expanding the receptive field of the network through multi-layer convolution. Using residual connections to avoid gradient vanishing in deep networks, as shown in the schematic diagram of Branch 2 network in Fig. 1, the black curve represents the residual module. The dimensions of the upper and lower layers connected by black dashed lines are different. Here, the size of the residual block is filled with 0 to the same size as the end layer.
As shown in Fig. 5, C1 is the estimation result trained using the Branch 1 network; C2 is the estimation result trained using the Branch 2 network; All are the estimated results of using two branches to train simultaneously. The red skeleton represents the real data, and the blue skeleton represents the estimated results of each network. Obviously, the drift error of C1 is greater than that of C2. Experiments have shown that the features outputted by the network based on self-attention mechanism are concentrated between adjacent bones, and the description of the overall human motion features is insufficient. Hence, the integration of features at various scales has been observed to significantly enhance the efficacy of 3D estimation of pose networks, while concurrently mitigating systemic drift problems.
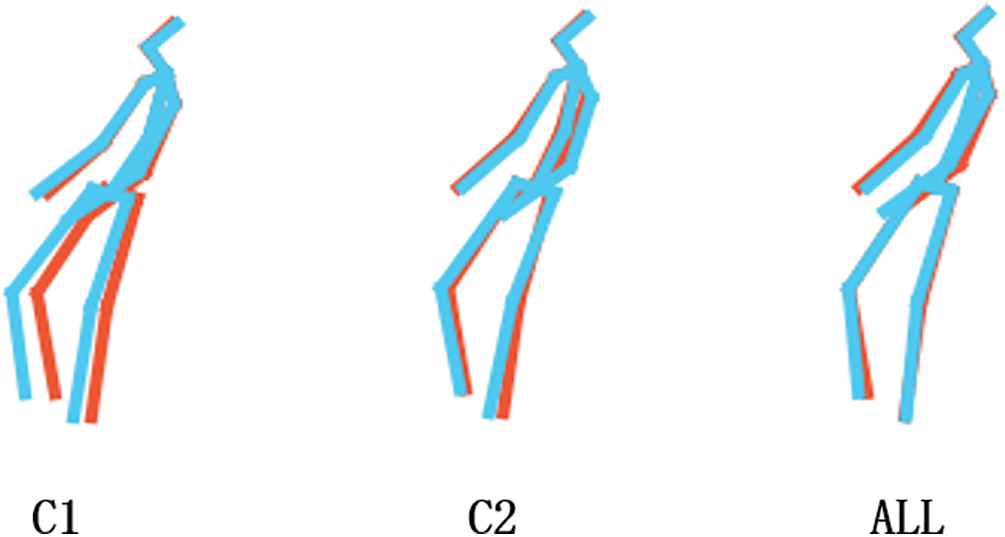
Figure 5: Estimation results of Branch 1, Branch 2, and overall network
This paper integrates the outcomes associated with network evaluation with the projections for the input information into a 3D space to facilitate the convergence of the network and improve the resilience of the 2D to 3D projection process. The final loss function will consist of two parts: the first part is the relative depth estimated by the network; the second part is a high-dimensional space projection. Let Zi be the relative depth of each bone estimated by the network, Li be the bone parameter matrix inputted into the network after preprocessing, Zi* be the actual relative depth of bones, Gi* be the actual length of bones in 3D space, n be the number of bones, and W be the weight, which is an empirical value of 0.3 The equation used to compute the entire coefficient of loss is:
This work utilizes the Human3.6M database [27], which is a commonly employed database for both training and assessing 3D estimation of human pose tasks. The system utilizes a motion capture device and a total of four cameras for gathering 3D posture data and matching images accordingly. The utilization of sensor calibration parameters facilitates the projection of 3D joint locations onto the 2D picture plane for every camera. The dataset comprises a collection of 3.6 million photos featuring seven individuals who are recognized as professional performers. These photographs capture a diverse range of 15 distinct actions. This paper follows the standard scheme, uses 1, 5, 6, 7, and 8 for training, and uses 9 and 11 for evaluation. The dataset processing refers to Dario [28] and other methods in the training process, only 1, 5, 6, 7, and 8 were used for training, without any additional datasets and data enhancement methods. The hardware platform for training is i7-12700 CPU, NVIDIA rtx3090ti GPU, and 32 G memory. The built model framework utilizes TensorFlow 2, employing the Adam optimizer with a learning rate set to 1 × 10−5. The number of items in each batch equals 512. The number of multiple heads in the attention mechanism network is 8, the embedded dimension is 256, and the hidden dimension is 1024.
4.1 Comparison with Advanced Methods
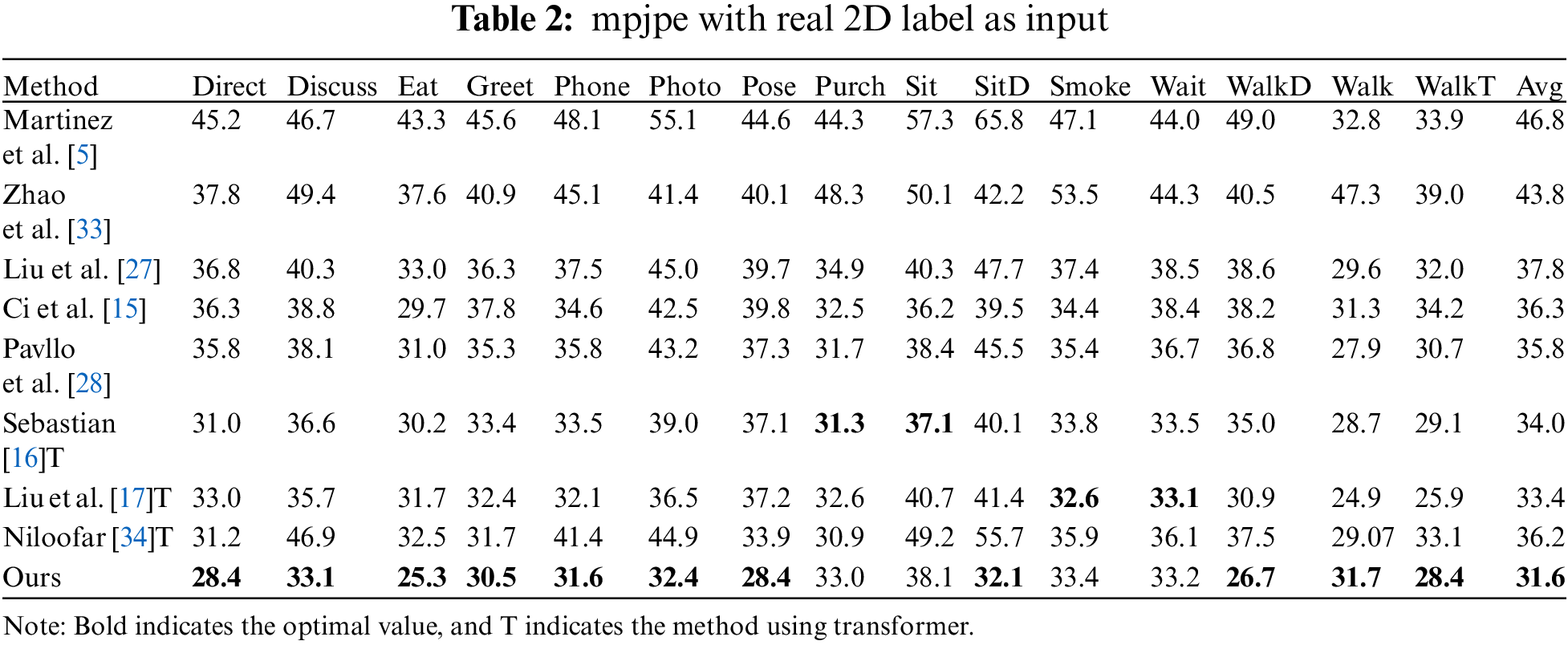
This work utilizes the mean per joint position error (mpjpe) for the evaluation metric, which is computed by measuring the discrepancy in millimeters among the actual value as well as the projected outcome after aligning with the base joint. Initially, the anticipated 2D position is utilized as a parameter to evaluate the network’s efficacy. The efficiency of the algorithm on the Human3.6M sample was evaluated using a cascaded pyramid network (CPN) [29], as indicated in Table 1. In comparison to the benchmark technique, joint precision, there is an observed enhancement in overall accuracy of around 1.4 mm. Additionally, the network’s efficacy is evaluated using the actual 2D position as its input, as demonstrated in Table 2. The best results in Tables 1 and 2 are shown in bold. The model in this paper has achieved the highest accuracy in most movements.
In this section, to demonstrate the precision improvement by a multi-branch network, experiments were conducted using C1, C2, and the entire network. C1 is a branch network using only the self-attention mechanism; C2 uses only deep convolution. All refers to the use of two branch networks. To eliminate errors produced by the 2D attitude detector, real 2D attitude is used as the input. All the experiments differ only in the network model, with consistent experimental platforms, node parameter processing, fusion, and loss parameters. The concluding investigational outcomes are presented in Table 3, with the greatest outcomes highlighted in bold. This indicates that the performance of the entire network is better than that of any single-branch network.

Because the relative depth of each bone is utilized as the forecasting consequence, the key positions, points at the end of the bone, are determined based on the starting point of the bone. Consequently, the error of the upper bone accumulates step by step to the next bone. To assess the impact of the system in this research on drift error suppression, the mpjpe of the model at 17 key points is obtained through tests of C1, C2, and All networks. The 17 key points are translated based on the chest key points. The final experimental results are presented in Table 4, with the worst result underlined. It can be observed from Table 4 that the estimation error of C1 in limb joints is significant, and the error increases as the distance from the root joint grows. The limb joints of the C2 branch also exhibit error accumulation, but correctness is notably enhanced when associated with C1. Ultimately, when the dual-branch network is trained, the drift error of the estimation result is reduced through the fusion of C1 features and C2 features. The estimation accuracy of the All network surpasses that of a single-branch network in all joints.

Finally, CPN and OpenPose [35] are used as 2D attitude estimators, which are visualized on Human3.6M and field datasets. As shown in Fig. 6, the visualization presents the prediction results of the Human3.6M dataset. CPN is utilized as the 2D detector for predicting the Human3.6M dataset. Fig. 7 displays the outcomes of single-person estimation using OpenPose as the frontend. Fig. 8 showcases the multi-person estimation results using OpenPose as the 2D detector.

Figure 6: Visualization of Human3.6M dataset prediction results

Figure 7: Single person estimation visualization

Figure 8: Visualization of multi person estimation
This study presents an innovative design for the 3D pose estimation, aiming to enhance the accuracy of estimation by leveraging the extraction of global as well as local motion information from the structure of a person. To address the issue of learning skeletal dependencies within the network, a joint parameter fusion algorithm is introduced, which leverages a multi-branch network for the extraction of both inter-skeletal and overall motion features. Specifically, branch C1 utilizes the encoding layers of a Transformer, while branch C2 employs convolutional layers; their combination through residual connections complements each other, thereby enhancing network performance. Ultimately, a high-dimensional guidance model is employed for convergence, incorporating relative depth and actual 2D skeletal lengths to construct a loss function aimed at improving the robustness of the 2D to 3D projection. The proposed approach is evaluated on the publicly available Human3.6M dataset, with an average joint pixel error of 48.7 when using CPN as the front-end network. The error using actual 2D coordinates as input is 31.6. Compared to the accuracies of the single-branch networks C1 and C2, it has improved by 6 and 1.4 mm, respectively. In comparison to state-of-the-art methods, the approach using 2D pose estimation as the front end has achieved a 1.4 mm improvement in accuracy. The method using actual 2D poses as input has demonstrated a 2.2 mm improvement in accuracy.
Acknowledgement: The author is very grateful to everyone who contributed to providing relevant information for this article.
Funding Statement: This work was supported by the Medical Special Cultivation Project of Anhui University of Science and Technology (Grant No. YZ2023H2B013), the Anhui Provincial Key Research and Development Project (Grant No. 2022i01020015) and the Open Project of Key Laboratory of Conveyance Equipment (East China Jiaotong University), Ministry of Education (KLCE2022-01).
Author Contributions: The authors confirm contribution to the paper as follows: investigation: X.H. Li, H.H. Yu, S.Y. Tian, F.T. Lin, U. Masood; data collection: X.H. Li, H.H. Yu, S.Y. Tian; analysis and interpretation of results: X.H. Li, H.H. Yu, S.Y. Tian; draft manuscript preparation: H.H. Yu, S.Y. Tian. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available on request from the authors. The data that support the findings of this study are available from the corresponding author, Xianhua Li, upon reasonable request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. Li and A. B. Chan, “3D human pose estimation from monocular images with deep convolutional neural network,” in Asian Conf. Comput. Vis., Singapore, 2014, pp. 332–347. [Google Scholar]
2. G. Pavlakos, X. Zhou, K. G. Derpanis, and K. Daniilidis, “Coarse-to-fine volumetric prediction for single-image 3D human pose,” in IEEE Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, 2017, pp. 1263–1272. [Google Scholar]
3. X. Sun, J. Shang, S. Liang, and Y. Wei, “Compositional human pose regression,” in IEEE Int. Conf. Comput., Venice, Italy, 2017, pp. 2621–2630. [Google Scholar]
4. X. Sun, B. Xiao, F. Y. Wei, S. Liang, and Y. C. Wei, “Integral human pose regression,” Comput. Res. Repository, vol. 11210, pp. 536–553, 2018. doi: 10.1007/978-3-030-01231-1. [Google Scholar] [CrossRef]
5. J. Martinez, R. Hossain, J. Romero, and J. J. Little, “A simple yet effective baseline for 3D human pose estimation,” in IEEE Int. Conf. Comput. Vis., 2017, pp. 2659–2668. [Google Scholar]
6. C. H. Chen and D. Ramanan, “3D human pose estimation = 2D pose estimation + matching,” in IEEE Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, 2017, pp. 5759–5767. [Google Scholar]
7. B. Tekin, P. Márquez-Neila, M. Salzmann, and P. Fua, “Learning to fuse 2D and 3D image cues for monocular body pose estimation,” in IEEE Int. Conf. Comput. Vis., Venice, Italy, 2017, pp. 3961–3970. [Google Scholar]
8. F. Moreno, “3D human pose estimation from a single image via distance matrix regression,” in IEEE Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, 2017, pp. 1561–1570. [Google Scholar]
9. B. X. Nie, P. Wei, and S. C. Zhu, “Monocular 3D human pose estimation by predicting depth on joints,” in IEEE Int. Conf. Comput. Vis., Venice, Italy, 2017, pp. 3467–3475. [Google Scholar]
10. K. Zhou, X. Han, N. Jiang, K. Jia, and J. Lu, “HEMlets pose: Learning part-centric heatmap triplets for accurate 3D human pose estimation,” in IEEE Int. Conf. Comput. Vis., Seoul, Korea (South2019, pp. 2344–2353. [Google Scholar]
11. J. Li et al., “Human pose regression with residual log-likelihood estimation,” in IEEE Int. Conf. Comput. Vis., 2021, pp. 11005–11014. [Google Scholar]
12. Z. H. Wang, R. M. Chen, M. X. Liu, G. F. Dong, and A. Basu, “SPGNet: Spatial projection guided 3D human pose estimation in low dimensional space,” in ICSM 2022: Smart Multimedia, pp. 41–55, 2022. [Google Scholar]
13. G. Wang, H. Zeng, Z. Wang, Z. Liu, and H. Wang, “Motion projection consistency-based 3-D human pose estimation with virtual bones from monocular videos,” IEEE Trans. Cogn. Develop. Syst., vol. 15, no. 2, pp. 784–793, 2023. doi: 10.1109/TCDS.2022.3185146. [Google Scholar] [CrossRef]
14. A. Zeng, X. Sun, L. Yang, N. Zhao, M. Liu and Q. Xu, “Learning skeletal graph neural networks for hard 3D pose estimation,” in IEEE Int. Conf. Comput. Vis., Montreal, QC, Canada, 2021, pp. 11416–11425. [Google Scholar]
15. H. Ci, C. Wang, X. Ma, and Y. Wang, “Optimizing network structure for 3D human pose estimation,” in IEEE Int. Conf. Comput. Vis., Seoul, Korea (South2019, pp. 2262–2271. [Google Scholar]
16. S. Lutz, R. Blythman, K. Ghosal, M. Moynihan, C. Simms and A. Smolic, “Jointformer: Single-frame lifting transformer with error prediction and refinement for 3D human pose estimation,” in Int. Conf. Pattern Recognit., 2022, pp. 1156–1163. [Google Scholar]
17. R. X. Liu et al., “Enhanced 3D human pose estimation from videos by using attention-based neural network with dilated convolutions,” Int. J. Comput. Vis., vol. 129, no. 5, pp. 1596–1615, 2021. doi: 10.1007/s11263-021-01436-0. [Google Scholar] [CrossRef]
18. C. Zheng, S. Zhu, M. Mendieta, T. Yang, C. Chen and Z. Ding, “3D human pose estimation with spatial and temporal transformers,” in IEEE Int. Conf. Comput. Vis., 2021, pp. 11636–11645. [Google Scholar]
19. W. Li, H. Liu, H. Tang, P. Wang, and L. V. Gool, “MHFormer: Multi-hypothesis transformer for 3D human pose estimation,” in IEEE Conf. Comput. Vis. Pattern Recognit., 2022, pp. 13137–13146. [Google Scholar]
20. W. Li, H. Liu, R. Ding, M. Liu, P. Wang and W. Yang, “Exploiting temporal contexts with strided transformer for 3D human pose estimation,” IEEE Trans. Multimed., vol. 25, pp. 1282–1293, 2022. doi: 10.1109/TMM.2022.3141231. [Google Scholar] [CrossRef]
21. J. Wang, S. Yan, Y. Xiong, and D. Li, “Motion guided 3D pose estimation from videos,” European Conf. Comput. Vis., vol. 12358, pp. 764–780, 2020. doi: 10.1007/978-3-030-58601-0. [Google Scholar] [CrossRef]
22. J. Zhang, Z. Tu, J. Yang, Y. Chen, and J. Yuan, “MixSTE: Seq2seq mixed spatio-temporal encoder for 3D human pose estimation in video,” in IEEE Conf. Comput. Vis. Pattern Recognit., 2022, pp. 13222–13232. [Google Scholar]
23. G. Brian, R. Sigal, A. Guy, G. Raja, and C. O. Daniel, “FLEX: Extrinsic parameters-free multi-view 3D human motion reconstruction,” in European Conf. Comput. Vis., 2022, pp. 176–196. [Google Scholar]
24. H. Y. Ma et al., “TransFusion: Cross-view fusion with transformer for 3D human pose estimation,” in British Mach. Vis. Conf., 2021. [Google Scholar]
25. H. Shuai, L. Wu, and Q. Liu, “Adaptive multi-view and temporal fusing transformer for 3D human pose estimation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 45, no. 4, pp. 4122–4135, 2022. doi: 10.1109/TPAMI.2022.3188716. [Google Scholar] [PubMed] [CrossRef]
26. A. Vaswani et al., “Attention is all you need,” in Conf. Neural Inf. Process Syst., 2017, pp. 5998–6008. [Google Scholar]
27. C. Ionescu, D. Papava, V. Olaru, and C. Sminchisescu, “Human3.6M: Large scale datasets and predictive methods for 3D human sensing in natural environments,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 36, no. 7, pp. 1325–1339, 2013. doi: 10.1109/TPAMI.2013.248. [Google Scholar] [PubMed] [CrossRef]
28. D. Pavllo, C. Feichtenhofer, D. Grangier, and M. Auli, “3D human pose estimation in video with temporal convolutions and semi-supervised training,” in IEEE Conf. Comput. Vis. Pattern Recognit., Long Beach, CA, USA, 2019, pp. 7745–7754. [Google Scholar]
29. Y. Chen, Z. Wang, Y. Peng, Z. Zhang, G. Yu and J. Sun, “Cascaded pyramid network for multi-person pose estimation,” in IEEE Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, 2018, pp. 7103–7112. [Google Scholar]
30. W. Yang, W. Ouyang, X. Wang, J. Ren, H. Li and X. Wang, “3D human pose estimation in the wild by adversarial learning,” in IEEE Conf. Comput. Vis. Pattern Recognit., Salt Lake City, UT, USA, 2018, pp. 5255–5264. [Google Scholar]
31. K. K. Liu, R. Q. Ding, Z. M. Zou, L. Wang, and W. Tang, “A comprehensive study of weight sharing in graph networks for 3D human pose estimation,” in European Conf. Comput. Vis., Glasgow, UK, 2020, pp. 318–334. [Google Scholar]
32. T. Xu and W. Takano, “Graph stacked hourglass networks for 3D human pose estimation,” in IEEE Conf. Comput. Vis. Pattern Recognit., 2021, pp. 16100–16109. [Google Scholar]
33. L. Zhao, X. Peng, Y. Tian, M. Kapadia, and D. N. Metaxas, “Semantic graph convolutional networks for 3D human pose regression,” in IEEE Conf. on Comput. Vis. Pattern Recognit., Long Beach, CA, USA, 2019, pp. 3420–3430. doi: 10.1109/CVPR.2019.00354. [Google Scholar] [CrossRef]
34. N. Azizi, H. Possegger, E. Rodol, and H. Bischof, “3D human pose estimation using möbius graph convolutional networks,” Comput. Vis.–ECCV 2022., vol. 13661, pp. 160–178, 2022. [Google Scholar]
35. Z. Cao, T. Simon, S. E. Wei, and Y. Sheikh, “Realtime multi-person 2D pose estimation using part affinity fields,” in IEEE Conf. Comput. Vis. Pattern Recognit., Honolulu, HI, USA, 2017, pp. 1302–1310. [Google Scholar]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF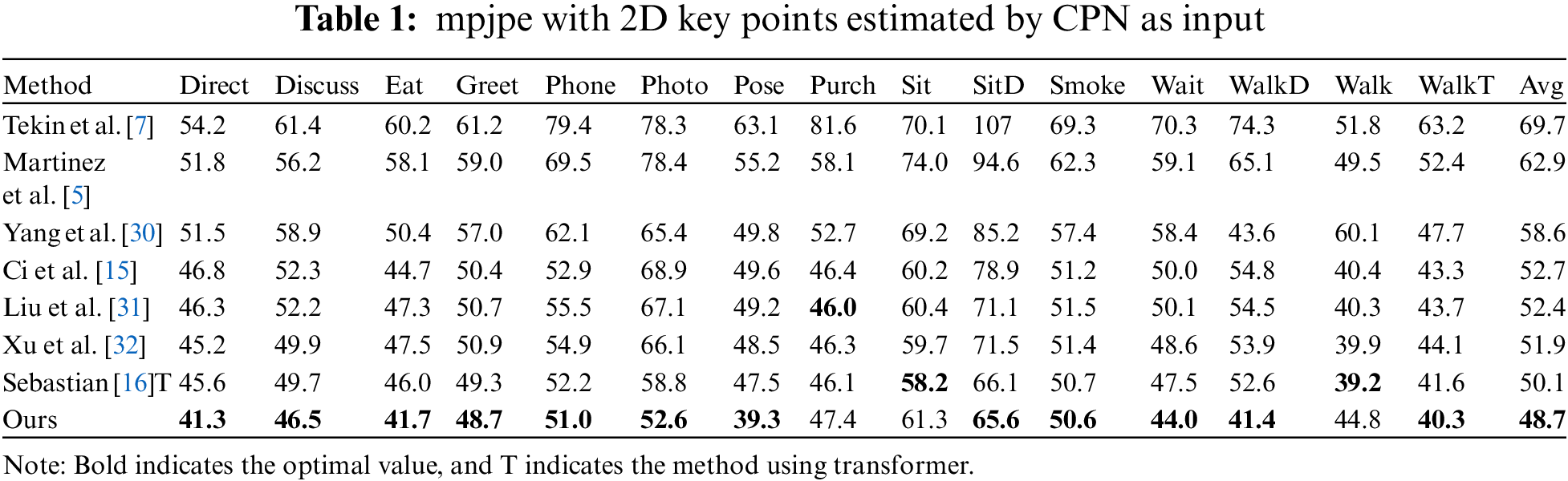
 Downloads
Downloads
 Citation Tools
Citation Tools