Path Planning for AUVs Based on Improved APF-AC Algorithm

1  Introduction

With the increase in ocean exploration activities and underwater development, Autonomous Underwater Vehicles (AUVs) have been widely used as automated equipment for underwater environment detection. In recent years, with the rapid development of AUV technology, the application scenarios of underwater robots have become increasingly diverse. The complex terrain, dim lighting, and hydrological conditions of the ocean all pose challenges to the widespread application of AUVs under existing technologies [1,2]. In complex marine environments, suitable path-planning algorithms are to enable AUVs to safely and effectively reach predetermined areas. Path-planning is also the research hotspot in the field of autonomous underwater robots, which is of great significance for improving the autonomy of AUVs [3].

With the deepening of research in the realm of AUVs, path-planning algorithms have become current research hotspots. Typical path planning algorithms for AUVs can be divided into three categories [4]: geometric modeling [5,6], virtual potential field [7,8], and artificial intelligence [9,10]. Recently, rapid-exploring random tree [11] has also received widespread attention due to its fast solving, as a type of extended geometric modeling. However, its generated path probability is not optimal. Although its improved algorithm [12] can obtain the optimal path, its solving speed has significantly decreased, and the smoothness of the path also can be improved. The ant colony algorithm has shown a wide range of application prospects due to its robustness and parallelism as a significant branch of artificial intelligence methods. Nevertheless, there are also lots of limitations such as unsmooth paths, falling into local optima easily, and low iteration efficiency. particle swarm optimization (PSO) [13] and genetic algorithm (GA) [14] also have similar problems [15]. In addition, some researchers have tried to use machine learning methods for path-planning [16], the difficulty is how to obtain sufficient and reliable samples, and its cost is much higher than that of other algorithms, but for dynamic complex environments, the path-planning method based on machine learning shows great potential [17]. To sum up, single traditional algorithms are difficult to carry out safe and efficient path-planning in complex underwater conditions [18,19]. Therefore, the research on fusion algorithms has the value that achieves the complementary advantages of different algorithms. Many researchers have improved the potential field and ant colony algorithm from different aspects for a single algorithm, mainly including the heuristic function [20], potential field function [21], initial pheromone distribution [22], and pheromone update strategy [23], etc. However, for AUVs, there are still problems such as insufficiently smooth paths and low execution efficiency.

By combining the efficient solving of artificial potential fields with the optimal solution ability of ant colony algorithms, to balance path smoothness, optimal solution, and iteration efficiency. Based on improving the artificial potential field and the ant colony algorithm, respectively, this paper proposes an improved artificial potential field ant colony (APF-AC) algorithm to address the issues that are present in traditional path planning methods. Comparative simulation experiments show that the improved algorithm has increased iteration speed and reduced path length. Meanwhile, based on the development prospects of AUVs and the existing experimental environment in the laboratory, this paper aims to enhance the existing product research by designing and assembling a multi-functional AUV for underwater observation and operation. The reliability of the improved APF-AC algorithm has been verified on this platform, and the prototype experimental data has improved in three indicators: time consumption, energy consumption, and avoiding dangerous navigation, showing higher algorithm efficiency and safety.

2  Structure

2.1 Principles of the Ant Colony Algorithm

The ant colony algorithm is a swarm intelligence algorithm formed by simulating the collective foraging behavior of ants in the real world. Ants will secrete pheromones in foraging and tend to choose the path with a high concentration of pheromones. Simultaneously, there will be more pheromones left on the shorter path, so there will be more ants choosing the shorter path. Ant colony system is composed of many ants, and according to the behavior characteristics of ants, it represents the positive feedback phenomenon based on pheromones [24]. In the process of foraging and exploring paths, the biological behavior of ants corresponds to two key steps of the ant colony algorithm: probability selection and pheromone update. Dorigo et al. [25,26] systematically proposed an intelligent optimization algorithm based on the ant colony for the first time in his doctoral dissertation. After that, many researchers made various improvements [27–29] to the algorithm and applied it to a wider range of fields [30–32], such as graph coloring, quadratic assignment, job sequencing, vehicle routing, job shop scheduling, network routing, large-scale IC design, etc. In recent years, Dorigo et al. have further developed ant colony optimization (ACO) as a universal optimization algorithm, and referred to all algorithms that comply with the ACO framework as “ant colony optimization algorithms”.

(1) The Transition Probability of the Ant Colony Algorithm

At the time t, the probability of ant k moving from node i to node j can be expressed as:

pijk(t)={[τij(t)]α[ηij(t)]β∑j∈allowedk⁡[τij(t)]α[ηij(t)]β,j∈allowedk0,otherwise(1)

In the above formula, α is the pheromone heuristic, and the larger α, the stronger the positive feedback performance of the population. β is the expectation heuristic, the larger β, the higher the greed of the group. Allowedk represents the set of nodes that the ant can arrive following, τij(t) is the pheromone content on the path (i,j) at time t, and ηij(t) is the expected degree from node i to node j at time t, and its expression is:

ηij=1/dij(2)

In the above formula, dij is the Euclidean distance from node i to node j.

(2) Pheromone Attenuation Mechanism

The residual amount of pheromone on the path of ants does not remain unchanged, but will gradually decrease with time, and the information transmission factors will gradually fade. This is like the memory characteristics of the animal brain, where old information is gradually forgotten. Every time the ants finish foraging, they update the pheromone on the path. The pheromone is updated as follows:

τij(t+1)=(1−ρ)τij(t)+Δτij(t)(3)

Δτij(t)=∑k=1mΔτijk(t)(4)

Among them, Δτij(t) is the pheromone increment on the iteration path (i,j), Δτijk(t) is the pheromone content released by ants on the iterative path (i,j), m is the total number of ants, and ρ is the pheromone attenuation coefficient (0<ρ<1).

However, it needs to be further explained that the ant colony algorithm will consume excessive computing power and time to eliminate bad paths due to the lack of pheromone at the initial stage of pathfinding, and the analysis of its algorithm complexity shows the above characteristics [33]; In addition, since the group accumulated a large number of pheromone on the suboptimal path in the later stage of pathfinding, the algorithm is more difficult to optimize the suboptimal path as the number of iterations increases, and the generated path may not optimal, or called fall into local optimization. For AUV applications, it is feasible to use the ant colony algorithm alone for path-planning without considering constraints such as energy consumption and task time. But considering practical applications, energy consumption and task time significantly increase is difficult to accept. It is particularly regrettable to use the ant colony algorithm alone to waste a large number of resources on unnecessary paths.

2.2 Principles of the Artificial Potential Field Algorithm

The artificial potential field Algorithm is an abstract description of obstacles and target points in the working environment of AUVs. The basic principle is to construct a potential field function to represent the overall impact of obstacles and target points on the motion of AUVs in their working environment [34,35]. The AUV achieves path planning by searching for directions with reduced potential energy and ultimately moves to the target point. The artificial potential field Algorithm needs to construct two potential field functions: attractive and repulsive potential fields. So all attractive potential fields and repulsive potential fields are superimposed to form the combined potential field at any location in the environment. The force acting on that point is the vector sum of the negative gradient values of the attractive potential field and repulsive potential field. Furthermore, the AUV moves toward the target point under the combined force.

Uatt(p)=0.5ζd2(P,G)(5)

Uatt(p) is the attractive potential function of the AUV, where ζ is the attractive coefficient and d(P,G) is the distance from the current position to the target point.

Fatt(p)=−ΔUatt(p)=ζd(P,G)n¯PG(6)

Fatt(p) is the attractive pull received by the AUV, which can be expressed by the negative gradient of the attractive potential function, and n¯PG is the unit vector pointing from the current position to the target point.

Urep(P)={0.5η{1d(P,Pobs)−1d0}2,d(P,Pobs)≤d00,d(P,Pobs)>d0(7)

Urep(p) is the repulsion potential function of the AUV, where η is the repulsion coefficient, d0 is the standard repulsion distance, d(P,Pobs) is the distance between the current position of the AUV and the obstacle, it is subject to repulsion when less than or equal to d0, and is not subject to repulsion when greater than d0.

Frep(P)=−ΔUrep(P)={η{1d(P,Pobs)−1d0}1d(P,Pobs)2n¯ob0,d(P,Pobs)>d0,d(P,Pobs)≤d0(8)

Frep(p) is the repulsive force received by the AUV, and ΔUrep(p) is the negative gradient of the repulsive potential function.

The artificial potential field is suitable for local path planning. Its use for local path planning mainly utilizes obstacle information detected by sensors carried by AUVs to avoid obstacles and ultimately achieve path planning. Since sensors can only detect obstacles within a certain range, the artificial potential field method can only consider the information of obstacles that the sensor can detect when planning paths. However, obstacles outside the sensor’s detection range cannot be considered. Therefore, using only the artificial potential field method for path planning is usually only applied locally [36]. Of course, the artificial potential field method can also be used for global path planning, but it is prone to deadlock in global planning. Due to local minima and unreachable goals, the artificial potential field method may not always plan a feasible global path. Although scholars have proposed improvements to address the above issues [37,38], they still perform not significantly compared to other global planning algorithms, so using artificial potential fields alone for global path planning does not have advantages.

2.3 Design of Improved APF-AC Algorithm

The ant colony algorithm has an excellent global search ability, but because the initial pheromone expression is unstable, it is prone to local optima problems, thus reducing the overall path generation quality [39]. In other ways, The artificial potential field has strong local planning ability, but due to the lack of randomness and the presence of local deadlocks, path generation cannot continue. Therefore, in complex underwater environments, it is laborious to plan a safe and optimal path solely through a single algorithm. For the path planning of AUVs in complex environments, this paper combines the ant colony algorithm with the artificial potential field algorithm and proposes an improved artificial potential field ant colony (APC-AC) algorithm. The ant colony is guided by the artificial potential field while applying randomness to the potential field to improve their respective problems.

Furthermore, the basic idea behind improving the algorithm is to complement the ant colony algorithm with the artificial potential field. The ant colony searches independently based on individual ability, and only exchanges information between the pheromone and the collective. The search process is changed from disorder to order without manual intervention, and the optimal solution is gradually obtained. The search process shows a strong ability for spontaneous organization and global search. At the same time, the ant search has low dependence on the selection of the initial route, reflecting strong adaptability and robustness, it can effectively solve the problem of planning task failure caused by local minima point generation and path oscillation under the influence of obstacles in the artificial potential field method; The artificial potential field algorithm has a simple and efficient operation logic, which can effectively utilize environmental information such as local obstacles and target positions to avoid ants entering deadlock paths. At the same time, under the guidance of potential field forces, it can effectively improve the search efficiency of the ant colony and accelerate convergence to the optimal path.

Furthermore, based on the above improvements, this paper further proposes three improvement schemes: the improved pheromone update strategy, the improved ant colony algorithm heuristic factor and the improved potential field function. On this basis, the artificial potential field algorithm and the ant colony algorithm are combined, also the APF-AC algorithm is proposed.

(1) Improve Pheromone Updating Strategy

When the traditional ant colony algorithm updates the pheromone, the ant colony will update the global pheromone of all the paths after the completion of a single iteration, which will cause the pheromone secreted by the poor path to weaken the guiding ability of the excellent path pheromone, which is not conducive to efficient selection in the next iteration. At the same time, the pheromone distribution on several suboptimal paths will reach a relatively uniform state, reducing the search efficiency of the ant colony algorithm.

This paper adds a reward and punishment mechanism for the local pheromone, distinguishes excellent paths from deadlock paths, and increases the utilization efficiency of the reliable pheromone. In one iteration, reward the ants who find the target point, such as formula (9), to enhance the pheromone concentration of the dominant local path; Punish lost ants who fail to find the target point, as shown in formula (10), to suppress the local pheromone concentration of the inferior path.

Δτij′(t+1)=Δτij′(t)+Ψ/lk(t)(9)

Δτij″(t+1)=Δτij″(t)−1/lm(t)(10)

In the above formula, lk(t) represents the path length information passed by the ant k at the time t, when the ant k has already found the target point; lm(t) represents the length information of the path that the ant passes through at any time, when the ant m is lost and has not reached the target point; Ψ is the pheromone reward parameter.

After local rewards and punishments are given to the pheromone, the optimized mathematical expression of the pheromone update is shown in formula (11).

τij(t+1)=(1−ρ)τij(t)+Δτij(t+1)+Δτij′(t)−Δτij″(t)(11)

By adding a local pheromone reward and punishment mechanism, the pheromone on the complete path of advantages is enhanced, and the pheromone on the incomplete path of disadvantages is reduced, so that the distribution of pheromone on different paths can be effectively distinguished. It is conducive to improving the utilization efficiency of ant pheromones in the next iteration and finding a path that is infinitely close to the optimal solution more efficiently. Using the optimized pheromone update strategy to improve the distribution of pheromone concentration can effectively reduce the number of times the algorithm wanders on the suboptimal path so that the algorithm planning efficiency can be further improved.

(2) Improving the Heuristic Factor of the Ant Colony Algorithm

In the conventional ant colony method, each path’s initial pheromone is the same, and it generates several different paths based on different heuristic information. The beginning trajectory established by the ant colony often leans towards the position approach to the target point, but it is far from the true optimal path. During this period, The ant colony algorithm performs similarly to greedy algorithms: seeks local optima in all steps, which often does not necessarily generate the optimal path in special conditions. Additionally, owing to the ant colony algorithm has mechanism of positive feedback, the results in even the initial wrong choice affect every subsequent iteration, which ultimately causes the ant colony to lose the bad orientation on the bad initial path.

This paper addresses this issue by employing the artificial potential field method to obtain the initial path and geometrical information between the AUV and the following node to comprehensively optimize the heuristic information, and use the new transfer probability to decide the selection of the next node. Considering that heuristic information mainly serves in the early stages of iteration, the first 30% of the iteration stage of the ant colony algorithm has the fastest convergence rate, and then enters a steady state, the dependence on heuristic information has also decreased. In the later stage of iteration, to prevent oscillations, the interference of heuristic information on ant colony search should be gradually suppressed. Therefore, the role of heuristic information will diminish with an increase in iteration times when the new heuristic function introduces the heuristic information-reducing coefficient. The improved heuristic function is shown in formula (12):

ηij(t)={[1−lij+Ljg∑s∈allowedk⁡lij+Ljg]e(NcmaxξNc−1),s∈allowedk0,otherwise(12)

In the above formula, lij is the distance from node i to node j, Ljg is the distance from the node j to the target point g obtained using the artificial potential field method, Ncmax and Nc are the maximum and current iterations, respectively. The attenuation function adopts an exponential form, similar to a forgetting curve, which can adaptively control the inflection point of the attenuation curve at the first 20%–30% of the iteration. As the iteration progresses, the Nc increases, the role of heuristic information fast decay. ξ is the decreasing coefficient of heuristic information and ξ>0. By setting ξ, the inflection point position can be adjusted, when ξ>1, the inflection point shifts to the right, and when ξ<1, the inflection point shifts to the left.

The utilization of paths derived from the aforementioned process in the heuristic function of the ant colony algorithm can mitigate local optimization issues arising from heuristic information with effect, thereby enhancing the search efficiency of the algorithm. This is attributed to the artificial potential field method has a straightforward model and high real-time capability.

(3) Improved Potential Field Function

The repulsion potential field function is a quadratic function of the reciprocal of the distance between the underwater vehicle and the obstacle. So on the one hand, when the distance from the obstacle is relatively close, the strong repulsive potential field will cause the AUV to move away from the obstacle, resulting in the AUV falling into a local optima and the overall path not being optimal. On the other hand, due to the significant variation in the intensity of the repulsive potential field, the speed of the AUV motor changes rapidly in a short time easy to causing the control system to oscillate. Therefore, this paper improves the repulsive force potential field function by changing the quadratic function with a faster change rate into an exponential function with a smaller change rate, to prevent the path from falling into local optima.The expression is shown in formula (13):

Urep′(P)={0.5ηe−d(P,Pobs)2,d(P,Pobs)≤d00,d(P,Pobs)>d0(13)

In addition, when there are many obstacles at the target location, because the repulsive effect of the obstacle is greater than the attractive effect of the target position, the AUV cannot reach the target position, that is, the target cannot be reached. To solve this problem, this paper introduces the repulsive potential field function influence factor ξ, and ξ=d(P,G)2, that is, the repulsive potential field function influence factor accounts for the square of the Euclidean distance from the underwater vehicle to the target point. The improved expression of the repulsive potential field function is shown in formula (14):

Urep″(P)=ξUrep′(P)={0.5ηd(P,G)2e−d(P,Pobs)2,d(P,Pobs)≤d00,d(P,Pobs)>d0(14)

After the improvement of the potential field function, the expression of the repulsion Fr′(P) of the AUV in the artificial force field is shown in formula (15), and the expression of the resultant force F′(P) in the artificial potential field is shown in formula (16). It can be seen from formula (15) that when the underwater vehicle is at the target position, that is, when the distance d(P,G) is zero, the repulsion of the underwater vehicle is zero, which solves the problem of the unreachable target.

Fr′(P)=−ΔUrep″(P)=ξUrep′(P)={ηd(P,G)2e−d(P,Pobs)2nOP,d(P,Pobs)≤d00,d(P,Pobs)>d0(15)

F′(P)=Fr′(P)+Fa(P)(16)

2.4 Algorithm Process and Analysis

STEP 1: Initialize various parameters. Select the starting point position S, target point position G, current iteration number Nc=0, set the maximum iteration number Ncmax, the number of ants m, pheromone heuristic factor α, expected heuristic factor β, heuristic information decline coefficient ξ, and various gains in the artificial potential field method.

STEP 2: Calculate initial heuristic information. According to formula (12), calculate the Euclidean distance between each path node and the endpoint to determine the initial heuristic information distribution.

STEP 3: Initial pheromone allocation. According to formula (11), the unbalanced allocation of the pheromone is carried out according to the starting and target points’ positions.

STEP 4: Calculate the resultant force of the potential field. Determine the distribution of obstacles at the selected node, calculate the magnitude and direction of the potential field resultant force on the node according to formula (16), and calculate the angle between the resultant force and each optional node.

STEP 5: Ants choose the next path. Place m ants at the starting point, each starting from the starting grid, calculate the potential field heuristic information of the combined force on each optional node, use the artificial potential field method to calculate the distance Ljg from the current node j to the target point g, obtain the probability distribution of the selected path according to formula (1), and then search for the next feasible node j+1 based on formulas (1) and (16), and must add the selected path point to the taboo table, Return to step 3 to calculate the potential field force of the current node, and cycle until the ant reaches the target point.

STEP 6: Partial update of pheromone. In one iteration, when an ant has finished searching the path, the last path node is matched with the destination. According to formula (9), pheromone rewards are given to the ants who have established a complete path, and pheromone punishment is given to the lost ants who have not established a complete path and are trapped in a deadlock according to formula (10). Then turn back to step 3 and start the search process for the next ant.

STEP 7: Update heuristic information. Create a distance matrix S to reserve the actual distance between the path node and the target point that each ant passes through, and realize the role of dynamically adjusting the heuristic information in the pathfinding process according to formula (12).

STEP 8: Global pheromone update. It is judged that all ants in this iteration have experienced a path search, and then the improved update function is used to determine the distribution of pheromone, and the global pheromone volatility coefficient is determined according to formula (3). The pheromone of the path of the best ant is updated according to formula (9), and the path of the worst ant is updated according to formula (10).

STEP 9: Output planning results. Determine whether the iteration has reached the maximum number of iterations. If all iterations are completed, the algorithm stops running and outputs the shortest path trajectory map, iteration convergence map, and shortest path length. If the iteration is not completed, clear the taboo table and return to the third step, with Nc=Nc+1, and cycle through step 3 until the number of cycles Nc=Ncmax is satisfied. Output the optimal path length until all iterations are completed before outputting the results.

Analyze the above process progressively, the time complexity T(n) and space complexity S(n) of the improved APF-AC algorithm are, respectively:

T(n)=O(Nc⋅n2⋅m)(17)

S(n)=O(n2)+O(m⋅n)(18)

It can be seen that its execution efficiency will not be worse than traditional algorithms. However, considering the large-scale map of the actual sea area leads to a sharp increase in calculation time and memory usage, this paper argues that zoning path planning or isometric scaling of the map is feasible, and we find that after several iterations, the pheromone matrix gradually appears as a sparse matrix, and it is also feasible to use sparsity for memory release.

The flowchart of the improved APF-AC algorithm is displayed in Fig. 1.

Figure 1: The flowchart of the improved APF-AC algorithm

2.5 Simulation and Result Analysis

To assess the feasibility and effectuality of the algorithm proposed in this paper, the improved APF-AC algorithm scheme is programmed to achieve path planning simulation experiments. Firstly, a simulation environment is constructed to optimize the combination of the introduced parameters and determine their values. Then, comparative experiments were conducted between APC-FC and traditional ant colony algorithms, and the algorithm in reference [40], in simple and complex environments. As a necessary explanation, the algorithm in reference [40] has been improved in the following four aspects. (1) Use non-uniform distribution in the initial pheromone. (2) Optimize pheromone update method. (3) Optimize the transfer probability with transfer factors. (4) Optimize with AUV motion characteristics. Based on the path planning results and relevant data, the superiority of the improved algorithm in achieving path planning and the effectiveness of the method improvement were verified.

The simulation experiment environment of the algorithm in this paper is: Matlab 2020a simulation environment is adopted, the computer configuration is Windows10 64 bit system, 8G RAM, CPU selected as Intel (R) Core (TM) i5-3230 M, and the main frequency is 2.60 GHz.

Parameter selection: In the computer simulation experiment of the traditional ant colony and improved APF-AC algorithm, parameter initialization has a notable impact on the algorithm results. After tuning, the parameter values selected in this paper are shown in Table 1.

2.5.1 Analysis of Simulation Results in the Simple Environment

In the grid map environment of a 20 × 20 simple environment model, compare the traditional ant colony algorithm with the improved algorithm for path planning, and set parameters for the simulation. The simulation results of the shortest path trajectory are shown in Fig. 2, where (a), (b), and (c) is the planning trajectory diagram of the traditional ant colony algorithm, the algorithm in References [40] and the improved APF-AC algorithm, respectively. The comparison of convergence curves is shown in Fig. 3.

Figure 2: Simulation results in a simple environment

Figure 3: The comparison of average convergence curves in a simple environment

To facilitate the comparison and improvement of the optimization performance of the APF-AC algorithm, multiple experiments were conducted and the relevant data were recorded as shown in Table 2.

From the comparison between Figs. 2 and 3, it can be demonstrated that in the 20 × 20 simple map model, all the three algorithm have obtained a complete path from the starting point to the endpoint, but their planned trajectory is different. It can also be demonstrated in Table 2 that the convergence speed of the improved algorithm has been significantly improved, and the number of iterations required for traditional ant colony algorithms to achieve stable convergence is much higher than the algorithm improved in this paper. Specifically, the number of lost ants decreased by 78.16% and 26.98%, the number of iterations decreased by 80.52% and 39.61%, the path length decreased by 1.57% and 0.63%, and the average time step consumption decreased by 28.48% and 18.05%. From the above figure, it can be expressed that the improved algorithm generates a smoother path and a greater distance from the obstacle. The former means that the speed control of the thruster is smoother, while the latter means that the possibility of accidental collision with the obstacle due to undercurrent is reduced, Therefore, it demonstrates higher safety both for driving devices and for the AUV itself.

2.5.2 Analysis of Simulation Results in the Complex Environment

With the scale of the environment changes, the robustness and adaptability of the improved algorithm in this paper are simulated and verified while increasing the complexity of the environment. Establish a 30 × 30 complex map environment model, and set parameters for the simulation. The shortest path trajectory planned is shown in Fig. 4, where (a), (b), and (c) is the planning trajectory diagram of the traditional ant colony algorithm, the algorithm in reference [40] and the improved APF-AC algorithm, respectively. The comparison of convergence curves is shown in Fig. 5.

Figure 4: Simulation results in a complex environment

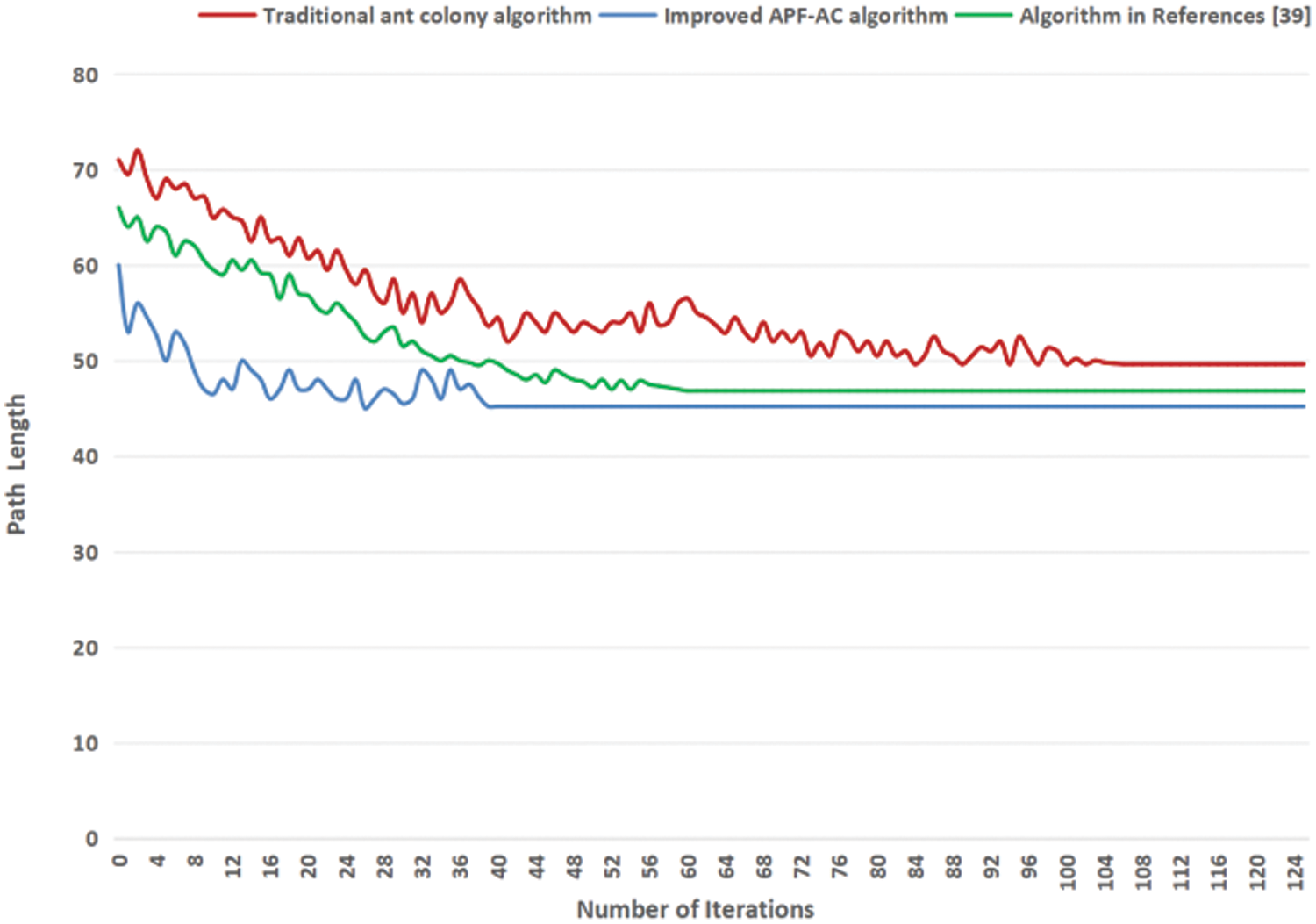
Figure 5: The comparison of average convergence curves in a complex environment

Record the relevant data after conducting multiple experiments in complex environments as shown in Table 3.

Analyzing the comparison results of Figs. 4 and 5, and Table 3, it can be concluded that at the map model of 30 × 30, the scale and complexity of the environment have increased, compared to simple scenarios, the iteration time and number of lost ants of the three algorithms have significantly increased. Traditional ant colony algorithms have significantly decreased their iteration and search efficiency due to the significant increase in iteration size. The improved algorithm has improved iteration efficiency and path length due to the introduction of artificial potential fields, and can still quickly converge to the optimal path in complex environments, Compared to the other two algorithms, the number of our algorithm-lost ants decreased by 87.81% and 33.97%, the iteration times are reduced by 61.2% and 33.65%, the average generated path length is reduced by 8.92% and 3.46%, and the time step consumption is reduced by 18.53% and 9.24%, respectively. Demonstrating good adaptability to the environment and having a certain degree of robustness. Meanwhile, it can be seen from the average number of lost ants that during the iterative evolution process of the traditional ant colony algorithm, there are always ants who can not find the target point because they are trapped in a deadlock path, which also reflects that the pheromone has low effective utilization of heuristic information, so improvements of the improved algorithm on pheromone are effective. Furthermore, according to Tables 2 and 3, the growth rate of lost ants in traditional algorithms and improved algorithms in simple and complex scenarios was significantly reduced, proving that the improved algorithm has a stronger path search ability in large-scale scenarios.

3  Experiment

3.1 Design of the AUV System

This paper designs a cable remote-controlled AUV, that can perform underwater movement, diving, floating, rotating, and robotic arm action functions through the handle operation instructions or pre-set instructions of onshore operators. The specific expected control function process is as follows: the onshore operator inputs the control instructions of the AUV into the ground station using a handle. The ground station converts the handle button information into signals that the AUV can process and transmits the control data to the controller of the AUV structure according to the corresponding communication agreement. The controller issues instructions based on the control information conveyed by the ground station, to realize the control of AUV thrusters, servo motors, cameras, and robotic arms. when implementing functions such as movement, observing, and grasping of the AUV, underwater information will be uploaded to the ground station, providing operators with an understanding of underwater information and the status of the AUV through the human-machine interface. By cooperating with the underwater control module, execution module, and observation module, the ability of the small vehicle to observe underwater operations is achieved.

Fig. 6 respectively shows the system diagram and overall appearance of the AUV.

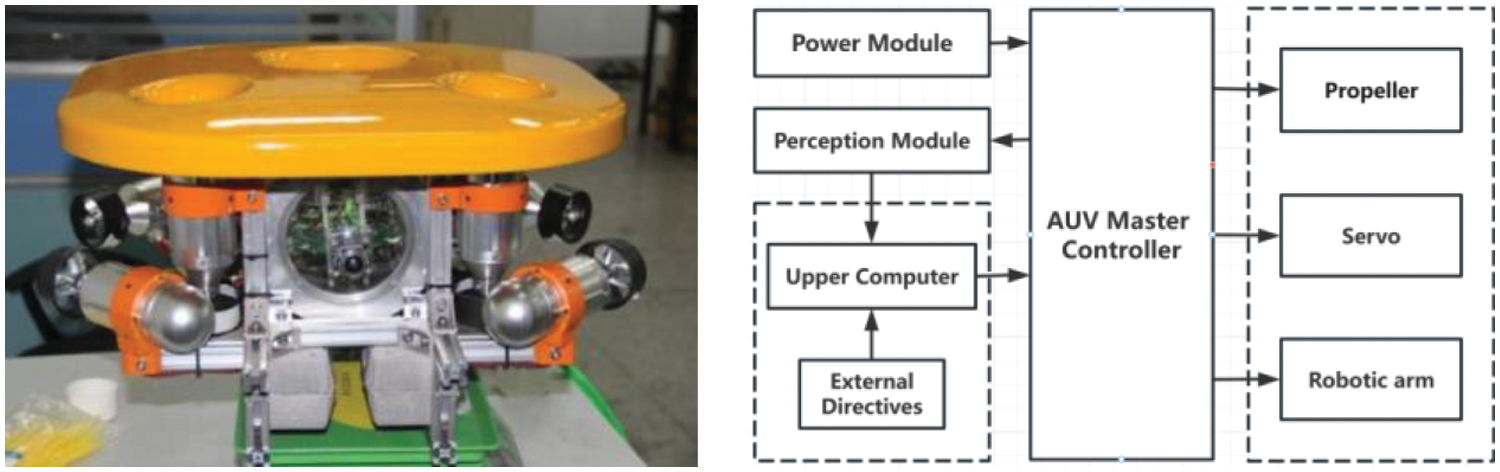
Figure 6: The system diagram and the overall appearance of the AUV

To enable the AUV to adapt to complex underwater environments, this paper adopts an active disturbance rejection controller to improve the robustness and stability of the system. ADRC can estimate and dynamically compensate for system disturbances, and treat all uncertainties acting on the controlled object as “unknown disturbances”, including system nonlinearity and coupling factors. Therefore, in the controller design process, each motion channel can be directly decoupled for control. Typically consists of ADRC has three parts: tracking differentiation (TD), extended state observer (ESO), and nonlinear state error feedback (NLSEF), while second-order linear ADRC is commonly used for attitude control of AUVs. Fig. 7 shows the system diagram of a typical second-order ADRC controller.

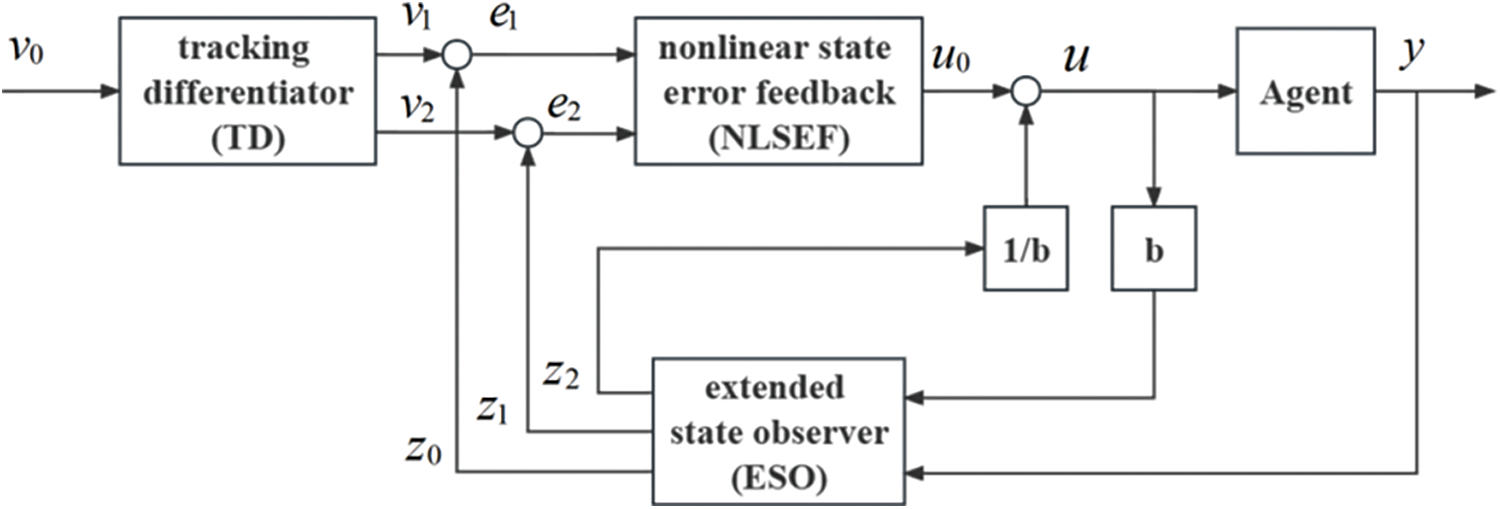
Figure 7: The controller structure diagram of the AUV

The design and functional parameters of the AUV are shown in Table 4.

3.2 Underwater Experiment

To test the reliability of the improved algorithm in practical scenarios, an experimental analysis will be conducted on the AUV in real underwater environments. The experimental design is as follows:

First, build a experimental scene and design four different specifications of virtual underwater obstacles to simulate complex underwater environments. Then, collecting the location and geometric shape of obstacles, the experimental scene is scaled proportionally. The environment and obstacles are dilated in MATLAB to obtain pre-collected global environmental information. Experimental requirements: The AUV searches for a feasible path from the starting point (red arrow point) to the target point (red star point) at low speeds of 0.8 m/s and high speeds of 1.5 m/s, respectively. The total task time, total power consumption, and number of accidental collisions are calculated, respectively. The experimental scene and process constructed are shown in Fig. 8.

Figure 8: AUV path planning experiment

In Fig. 8, from left to right are the generated path of a traditional ant colony, the algorithm in [40], the improved APF-AC algorithm, and the actual path of the Improved APF-AC algorithm in underwater experiments, respectively. In addition, the obstacles are marked in black, and the arrows indicate the approximate trajectory of the AUV. It can be seen that the AUV can complete the path planning task well in different scenarios. In addition, compared with traditional algorithms, the improved algorithm has made improvements in three aspects: average task time, average power consumption, and average number of dangerous navigation per task. The experimental results are shown in Table 5.

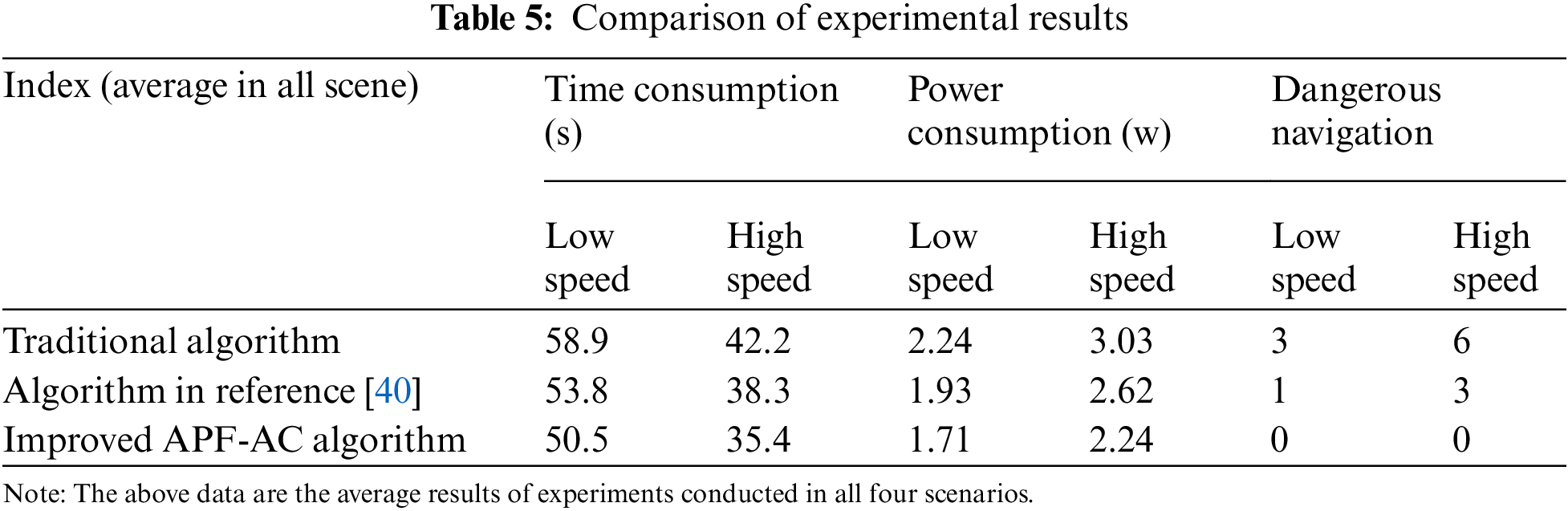
Comparing the generated path in Fig. 8 with the actual path, it should be further explained that: it can be seen that there is a certain deviation between the actual path of the AUV and the algorithm generation path, and the reasons for the deviation include external factors such as water flow and light and internal factors such as positioning and navigation, motor drive, mechanical structure error, etc., the above errors will be amplified when the underwater vehicle moves or rotates at high speed. Based on the above experimental phenomena, compared to traditional ant colony algorithms and algorithms in [40], the improved APF-AC algorithm reduces time consumption by 14.26% and 6.13% in low speed, 16.11% and 7.57% in high speed, and energy consumption by 23.66% and 11.4% in low speed, 26.07% and 14.5% in high speed, the average number of dangerous Navigation has been Significantly suppressed. It can be further inferred that the path generated by the traditional ant colony algorithm is low-safe since the AUV is too close to the obstacle. The path generated by the algorithm described in this article is smooth and farther away from obstacles, therefore it has higher safety. The above conclusion can be verified by underwater experiments and experimental data obtained from Table 5.

4  Conclusion

Based on the research and analysis of traditional path-planning algorithms, this paper proposes an improved APC-AC algorithm to address the drawbacks of traditional path-planning methods and improve the path-planning performance of algorithms. For improving the algorithm planning efficiency, a local pheromone reward and punishment mechanism have been used, and using the optimized pheromone update strategy to improve the distribution of pheromone concentration, the algorithm can effectively reduce the number of times wandering on the suboptimal path. Utilizing artificial potential field force factors to construct potential field force heuristic information, optimizing probability calculation methods, and effectively improving the low efficiency of ant colony search in the early stage of the algorithm; The repulsive force potential field function is improved by changing the quadratic function with a faster change rate into an exponential function with a smaller change rate to avoid the algorithm falling into local optima. In simple and complex simulation environments, the improved algorithm reduces the generated path length by about 1.57% and 8.92%, respectively, the iteration time has been reduced by approximately 28.5% and 15.5%, respectively.

Meanwhile, this paper considers the issue of internal and external disturbances affecting the safety of underwater operations in actual working scenarios of the AUV. This article designs four simulation environments with obvious differentiation and verifies the improved APF-AC algorithm on the AUV platform. The experimental and simulation results are consistent. In addition, the improved algorithm has improved task time and overall power consumption and has shown higher safety in actual experiments, which has a positive application value.

It should be pointed out that although the work done in this article is well adapted to the underwater environment under 2-D, static, and prior information conditions. The improved APF-AC algorithm is superior to the traditional algorithm in convergence. However, the computational complexity is the same as that of the traditional algorithm, so the efficiency advantage under the large map needs to be verified. The actual operating environment of AUVs may be 3-D, dynamic, and lacking prior information. Therefore, the future step is to improve the real-time dynamic path planning ability of AUVs in the aforementioned environment.

Acknowledgement: This paper grateful thanks to all reviewers for their selfless contributions to science, and to all editors for their outstanding work in improving the quality of the paper.

Funding Statement: This work is supported by Research Program supported by the National Natural Science Foundation of China (No. 62201249), the Jiangsu Agricultural Science and Technology Innovation Fund (No. CX(21)1007), the Open Project of the Zhejiang Provincial Key Laboratory of Crop Harvesting Equipment and Technology (Nos. 2021KY03, 2021KY04), University-Industry Collaborative Education Program (No. 201801166003) and the Postgraduate Research & Practice Innovation Program of Jiangsu Province (No. SJCX22_1042).

Author Contributions: Study conception and design: Guojun Chen, Danguo Cheng, Wei Chen; data collection: Tiezheng Guo; analysis and interpretation of results: Guojun Chen, Xue Yang; draft manuscript preparation: Guojun Chen, Danguo Cheng, Wei Chen.

Availability of Data and Materials:: The authors confirm that the data supporting the findings of this study are available within the paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Bogue, “Robots in the offshore oil and gas industries: A review of recent developments,” Ind. Robot.: Int. J. Rob. Res. Appl., vol. 47, no. 1, pp. 1–6, 2020. doi: 10.1108/IR-10-2019-0207. [Google Scholar] [CrossRef]

2. E. Zereik, M. Bibuli, N. Mišković, P. Ridao, and A. Pascoal, “Challenges and future trends in marine robotics,” Annu. Rev. Control., vol. 46, no. 4, pp. 350–368, 2018. doi: 10.1016/j.arcontrol.2018.10.002. [Google Scholar] [CrossRef]

3. Z. Zeng, L. Lian, K. Sammut, F. He, Y. Tang and A. Lammas, “A survey on path planning for persistent autonomy of autonomous underwater vehicles,” Ocean Eng., vol. 110, no. 3, pp. 303–315, 2015. doi: 10.1016/j.oceaneng.2015.10.007. [Google Scholar] [CrossRef]

4. C. Cheng, Q. Sha, B. He, and G. Li, “Path planning and obstacle avoidance for AUV: A review,” Ocean Eng., vol. 235, no. 7, pp. 1–18, 2021. doi: 10.1016/j.oceaneng.2021.109355. [Google Scholar] [CrossRef]

5. R. Yonetani, T. Taniai, M. Barekatain, M. Nishimura, and A. Kanezaki, “Path planning using neural A* search,” in Int. Conf. Mach. Learn., vol. 139, 2021, pp. 12029–12039. [Google Scholar]

6. L. Min, X. Hou, and J. Yang, “Surface optimal path planning using an extended Dijkstra algorithm,” IEEE Access, vol. 8, pp. 147827–147838, 2021. [Google Scholar]

7. O. Alparslan and C. Omer, “Real-Time indoor path planning using object detection for autonomous flying robots,” Intell. Autom. Soft Comput., vol. 36, no. 3, pp. 3355–3370, 2023. doi: 10.32604/iasc.2023.035689. [Google Scholar] [PubMed] [CrossRef]

8. S. M. Wang, M. C. Fang, and C. N. Hwang, “Vertical obstacle avoidance and navigation of autonomous underwater vehicles with H∞ controller and the artificial potential field method,” J. Navig., vol. 72, no. 1, pp. 207–228, 2019. doi: 10.1017/S0373463318000589. [Google Scholar] [CrossRef]

9. J. Ni, L. Wu, X. Fan, and S. X. Yang, “Bioinspired intelligent algorithm and its applications for mobile robot control: A survey,” Comput. Intel. Neurosc., vol. 2016, no. 1, pp. 1, 2016. [Google Scholar]

10. X. Cao, L. Chen, L. Guo, and W. Han, “AUV global security path planning based on a potential field bio-inspired neural network in underwater environment,” Intell. Autom. Soft Comput., vol. 27, no. 2, pp. 391–407, 2021. doi: 10.32604/iasc.2021.01002. [Google Scholar] [PubMed] [CrossRef]

11. T. Xu, Y. Xu, D. Wang, S. Chen, W. Zhang and L. Feng, “Path planning for autonomous articulated vehicle based on improved goal-directed rapid-exploring random tree,” Math. Probl. Eng., vol. 2020, pp. 1–14, 2020. doi: 10.1155/2020/7123164. [Google Scholar] [CrossRef]

12. I. Noreen, K. Amna, and H. Zulfiqar, “A comparison of RRT, RRT* and RRT*-smart path planning algorithms,” Int. J. Comput. Sci. Netw. Secur., vol. 16, no. 10, pp. 20–27, 2016. [Google Scholar]

13. X. Qi, H. Zhang, and Q. Rong, “Path planning based on improved particle swarm optimization for AUVs,” J. Coastal Res., vol. 111, no. SI, pp. 279–282, 2020. [Google Scholar]

14. S. Huang, J. Tian, L. Qiao, Q. Wang, and Y. Su, “Unmanned aerial vehicle path planning based on improved genetic algorithm,” J. Comput. Appl., vol. 41, no. 2, pp. 390, 2021. [Google Scholar]

15. C. O. Yinka-Banjo and U. H. Agwogie, “Swarm intelligence optimization techniques in mobile path planning–A review,” Int. J. Eng. Res. Afr., vol. 37, pp. 62–71, 2018. doi: 10.4028/www.scientific.net/JERA.37.62. [Google Scholar] [CrossRef]

16. T. Xu, S. Chen, D. Wang, T. Wu, Y. Xu and W. Zhang, “A novel path planning method for articulated road roller using support vector machine and longest accessible path with course correction.,” IEEE Access, vol. 7, pp. 182784–182795, 2019. doi: 10.1109/ACCESS.2019.2959346. [Google Scholar] [CrossRef]

17. S. Das and K. M. Sudhansu, “A Machine Learning approach for collision avoidance and path planning of mobile robot under dense and cluttered environments,” Comput. Electr. Eng., vol. 103, pp. 108376, 2022. [Google Scholar]

18. M. Seyedali, J. S. Dong, and A. Lewis, “Ant colony optimizer: Theory, literature review, and application in AUV path planning,” in Nature-Inspired Optimizers: Theories, Literature Reviews and Applications. Cham, Switzerland: Springer International Publishing, 2020, pp. 7–21. [Google Scholar]

19. F. Gul, I. Mir, L. Abualigah, P. Sumari, and A. Forestiero,“A consolidated review of path planning and optimization techniques: Technical perspectives and future directions,” Electronics, vol. 10, no. 18, pp. 1–38, 2021. [Google Scholar]

20. J. Zhang and X. Pan, “Path planning for mobile robots based on improved ant colony algorithm,” in Cogni. Comput.-ICCC 2022: 6th Int. Conf., Honolulu, HI, USA, Springer, 2023. [Google Scholar]

21. X. Fan, Y. Guo, H. Liu, B. Wei, and W. Lyu, “Improved artificial potential field method applied for AUV path planning,” Math. Probl. Eng., vol. 2020, no. 1, pp. 1–20, 2020. doi: 10.1155/2020/6523158. [Google Scholar] [CrossRef]

22. S. Zhang, J. Pu, and Y. Si, “An adaptive improved ant colony system based on population information entropy for path planning of mobile robot,” IEEE Access, vol. 9, pp. 24933–24945, 2021. doi: 10.1109/ACCESS.2021.3056651. [Google Scholar] [CrossRef]

23. Y. Zheng, Q. Luo, H. Wang, C. Wang, and X. Chen, “Path planning of mobile robot based on adaptive ant colony algorithm,” J. Intell. Fuzzy. Syst., vol. 39, no. 4, pp. 5329–5338, 2020. doi: 10.3233/JIFS-189018. [Google Scholar] [CrossRef]

24. O. Deepa and A. Senthilkumar, “Swarm intelligence from natural to artificial systems: Ant colony optimization,” Networks (Graph-Hoc), vol. 8, no. 1, pp. 9–17, 2016. [Google Scholar]

25. M. Dorigo and S. Thomas, Ant Colony Optimization: Overview and Recent Advances. Cham, Switzerland: Springer International Publishing, 2019. [Google Scholar]

26. M. Dorigo and S. Krzysztof, “An introduction to ant colony optimization,” in Handbook of Approximation Algorithms and Metaheuristics, Second ed. FL, USA: Chapman and Hall/CRC, 2018, pp. 395–408. [Google Scholar]

27. Q. Luo, H. Wang, Y. Zheng, and J. He, “Research on path planning of mobile robot based on improved ant colony algorithm,” Neural. Comput. Appl., vol. 32, no. 6, pp. 1555–1566, 2020. doi: 10.1007/s00521-019-04172-2. [Google Scholar] [CrossRef]

28. X. Dai, S. Long, Z. Zhang, and D. Gong, “Mobile robot path planning based on ant colony algorithm with A* heuristic method,” Front. Neurorobotics, vol. 13, pp. 1–9, 2019. doi: 10.3389/fnbot.2019.00015. [Google Scholar] [PubMed] [CrossRef]

29. G. Chen and L. Jie, “Mobile robot path planning using ant colony algorithm and improved potential field method,” Comput. Intel. Neurosc., vol. 2019, pp. 1–10, 2019. doi: 10.1155/2019/1932812. [Google Scholar] [PubMed] [CrossRef]

30. A. Qi et al., “Directional mutation and crossover boosted ant colony optimization with application to COVID-19 X-ray image segmentation,” Comput. Biol. Med., vol. 148, no. 3, pp. 1–19, 2022. doi: 10.1016/j.compbiomed.2022.105810. [Google Scholar] [PubMed] [CrossRef]

31. M. K. Hussein and H. M. Mohamed, “Efficient task offloading for IoT-based applications in fog computing using ant colony optimization,” IEEE Access, vol. 8, pp. 37191–37201, 2020. doi: 10.1109/ACCESS.2020.2975741. [Google Scholar] [CrossRef]

32. S. H. Huang, Y. H. Huang, C. A. Blazquez, and P. B. Germán, “Application of the ant colony optimization in the resolution of the bridge inspection routing problem,” Appl. Soft Comput., vol. 65, no. 3, pp. 443–461, 2018. doi: 10.1016/j.asoc.2018.01.034. [Google Scholar] [CrossRef]

33. C. Alberto, M. Dorigo, and V. Maniezzo, “An investigation of some properties of an “Ant Algorithm”,” Para. Prob. Solv. Nature, vol. 92, no. 1992, pp. 509–520, 1992. [Google Scholar]

34. C. W. Warren, “Global path planning using artificial potential fields,” in 1989 IEEE Int. Conf. Robot. Autom., Scottsdale, AZ, USA, IEEE Computer Society, 1989, pp. 316–321. [Google Scholar]

35. Y. Wang and S. C. Gregory, “A new potential field method for robot path planning,” in IEEE Int. Conf. Robot. Autom., San Francisco, CA, USA, vol. 2, 2000, pp. 977–982. [Google Scholar]

36. A. K. Kashyap and P. Anish, “Different nature-inspired techniques applied for motion planning of wheeled robot: A critical review,” Int. J. Robot. Autom., vol. 3, no. 2, pp. 1–10, 2018. [Google Scholar]

37. M. Guerra, D. Efimov, G. Zheng, and W. Perruquetti, “Avoiding local minima in the potential field method using input-to-state stability,” Control Eng. Pract., vol. 55, no. 5, pp. 174–184, 2016. doi: 10.1016/j.conengprac.2016.07.008. [Google Scholar] [CrossRef]

38. R. D. Puriyanto, W. Oyas, and I. C. Adha, “Improved artificial potential field algorithm based multi-local minimum solution,” Eng. Lett., vol. 29, no. 3, pp. 1277–1286, 2021. [Google Scholar]

39. S. Fidanova and S. Fidanova, “Ant colony optimization,” in Ant Colony Optimization and Applications, First ed. Honolulu, HI, USA: Springer, 2021, pp. 3–8. [Google Scholar]

40. J. Li and H. Wang, “Research on AUV path planning based on improved ant colony algorithm,” in 2020 IEEE Int. Conf. Mechatron. Autom., IEEE, 2020, pp. 1401–1406. [Google Scholar]