 Open Access
Open Access
ARTICLE
Computation Tree Logic Model Checking of Multi-Agent Systems Based on Fuzzy Epistemic Interpreted Systems
1 School of Computer Science and Engineering, North Minzu University, Yinchuan, 750000, China
2 School of Computer Science, FoSE, The University of Hull, Hull, UK
* Corresponding Author: Zhanyou Ma. Email:
Computers, Materials & Continua 2024, 78(3), 4129-4152. https://doi.org/10.32604/cmc.2024.047168
Received 27 October 2023; Accepted 05 February 2024; Issue published 26 March 2024
Abstract
Model checking is an automated formal verification method to verify whether epistemic multi-agent systems adhere to property specifications. Although there is an extensive literature on qualitative properties such as safety and liveness, there is still a lack of quantitative and uncertain property verifications for these systems. In uncertain environments, agents must make judicious decisions based on subjective epistemic. To verify epistemic and measurable properties in multi-agent systems, this paper extends fuzzy computation tree logic by introducing epistemic modalities and proposing a new Fuzzy Computation Tree Logic of Knowledge (FCTLK). We represent fuzzy multi-agent systems as distributed knowledge bases with fuzzy epistemic interpreted systems. In addition, we provide a transformation algorithm from fuzzy epistemic interpreted systems to fuzzy Kripke structures, as well as transformation rules from FCTLK formulas to Fuzzy Computation Tree Logic (FCTL) formulas. Accordingly, we transform the FCTLK model checking problem into the FCTL model checking. This enables the verification of FCTLK formulas by using the fuzzy model checking algorithm of FCTL without additional computational overheads. Finally, we present correctness proofs and complexity analyses of the proposed algorithms. Additionally, we further illustrate the practical application of our approach through an example of a train control system.Keywords
Model checking [1,2] is a formal method employed for the automatic verification of whether a model satisfies specific properties. This approach finds extensive application in multi-agent systems [3,4]. Property specifications for finite state systems are typically formalized using temporal logics like Computation Tree Logic (CTL) and Linear Temporal Logic (LTL) [5]. In contrast, multi-agent systems comprise interacting agents and place greater emphasis on the formalization of agents’ mental attitudes, such as knowledge, beliefs, and desires [6]. As a result, multi-agent system verification focuses on broadening the scope of classical model checking techniques by incorporating epistemic modalities that characterize agents’ knowledge and motivational attitudes.
Previous research has mainly demonstrated meta-logical outcomes across various temporal and epistemic combinations, with a particular emphasis on completeness and computational complexity. To enhance expressive capabilities, epistemic logic has undergone multi-directional expansion. In one research domain, scholars have adopted axiomatic approaches to extend temporal epistemic logic, with a focus on the meta-logical properties of the resultant logic, all without specific validation algorithms [7]. In another line of inquiry, a separate group of researchers have studied epistemic logic at the predicate level [8,9]. Recent years have seen a notable shift in research orientation towards the development of model checking techniques integrated with these formal languages, implying that researchers are moving away from traditional theorem-proving methods to the utilization of model checking methods for system verification. The knowledge in multi-agent systems has been widely modeled through the extension of temporal logic [10,11]. Despite the success of these methods in specifying and verifying multi-agent systems from different domains, current approaches overlook the uncertainty in multi-agent systems and tend to assume ideal behavior [12].
Real-world scenarios are uncertain, particularly when it comes to open systems that interact with complex environment. Uncertainties within such systems arise due to the ambiguity and limited knowledge of the environment. In such complex contexts, tools for uncertainty solving, such as probability theory [13] and fuzzy logic [14,15], become indispensable. Probability logic has been widely researched in epistemic multi-agent systems [16,17]. Epistemic itself is a complex and multifaceted concept involving numerous sources of uncertainty, including individual subjective judgments and emotions [18]. Since epistemic is often considered fuzzy, using precise probability logic for accurate description becomes nearly impossible. For instance, an individual’s perception of weather conditions could be described as ‘somewhat hot’ or ‘a bit cold,’ both expressions laden with ambiguity. It is difficult to represent such epistemic with precise probability values. Fuzzy logic is an approach for handling these situations, where fuzzy sets could be defined to capture the probabilistic uncertainty of epistemic. A fundamental model for tackling probabilistic uncertainty is by defining interpreted systems [18]. However, there is still a lack of sufficient exploration on how to effectively resolve fuzziness in epistemic multi-agent systems. Furthermore, there is currently a lack of logical language that can describe fuzzy epistemic attributes. This accentuates the importance of model checking in the context of fuzzy epistemic multi-agent systems and how to represent and verify quantified epistemic properties. Therefore, the purpose of this research is to address the verification issues of properties in fuzzy epistemic multi-agent systems.
The contributions of this paper can be divided into three major aspects: (i) the Fuzzy Computation Tree Logic of Knowledge (FCTLK) has been defined. This logical framework not only accommodates path fuzziness but also represents knowledge regarding quantification and uncertainty. Fuzzy Kripke structures (FKS) [19,20] have been combined with an interpreted system [18] for S5 epistemic logic to model fuzzy multi-agent systems. Fuzzy Kripke structures are widely applied in modeling systems with fuzziness. They serve as the formal model for Fuzzy Computation Tree Logic (FCTL); (ii) a method has been proposed to address epistemic property verification in fuzzy multi-agent systems. It employs an indirect fuzzy model checking algorithm that transforms the FCTLK model checking problem into the FCTL model checking. During this process, the fuzzy epistemic interpreted system (FEIS) is transformed into a Fuzzy Decision Process (FDP) [21] model. In addition, a scheduler is applied to eliminate the non-determinism of actions. Subsequently, the FDP model is transformed into an FKS model; (iii) the equivalence between the satisfiability of formulas in the FCTLK model and the FCTL model has been theoretically demonstrated using matrix synthesis operations. The algorithm time complexity analysis results show that formulas in FCTLK can be verified using the synthesis operations of fuzzy matrices without additional computational overheads. Furthermore, this computational process exhibits greater conciseness with improved readability.
As an automated formal verification technique, model checking has been widely employed for the verification of various critical properties, including security [22], fairness [23], and reachability [24]. In recent years, this technique has found extensive application in the verification of multi-agent systems. Skorupski [10] proposed an efficient model checking technique that reduces the problem of Computation Tree Logic of Knowledge (CTLK) model checking in multi-modal logic to the problem of model checking Action-Restricted CTL (ARCTL) [25]. In [11], Penczek et al. introduced group knowledge and applied verification techniques using bounded model checking to validate group knowledge attributes. However, this approach solely focuses on the absolute accuracy of properties in the model and ignores the influence of stochastic phenomena on the system. Additionally, it did not consider the relationships among the three types of group knowledge. In contrast, the work presented in this paper not only considers the uncertainty of the system but also extends the scope of the study from individual agents to the entire group.
Termine et al. [16] introduced an uncertain probabilistic interpreted system model for the modelling of epistemic multi-agent systems. They proposed an iterative process-based model checking algorithm to verify multi-agent systems with non-stationary characteristics. In [17], a different approach is employed to study the model checking problem of Probabilistic Epistemic Temporal Logic (PETL) logic and propose a symbolic model checking algorithm designed for in-memory schedulers. This algorithm simplifies the model checking problem into a mixed-integer nonlinear programming problem. It demonstrates particular advantages, especially in addressing cyclic aspects within the state space. Probability model checking primarily addresses model checking problems caused by uncertainty in stochastic processes to determine the accuracy of probabilistic systems under quantitative probability specifications.
While in fuzzy systems where data is uncertain, traditional probability logic might not always work effectively. Therefore, fuzzy logic has become a specialized tool for dealing with factual imprecision, particularly demonstrating excellent performance in situations where it is difficult to describe using precious true/false values. Many scholars have suggested a type of fuzzy epistemic logic that allows evaluating the robustness of knowledge without strictly relying on probability. They have chosen possible world models as semantic models, utilizing t-norms to tackle the ambiguity of logical connectors [26,27]. In this research, interpreted system were adopted as semantic models, and fuzzy interpretations of epistemic attributes were conducted within the framework of Zadeh’s fuzzy logic.
Li et al. [28] had previously proposed a model checking approach Generalized Possibilistic Computational Tree Logic (GPoCTL) based on Generalized Possibilistic Kripke Structures (GPKS), it overlooked non-deterministic choices in fuzzy systems. Addressing this gap, Li et al. [29] employed Possibility Decision Processes (PDPs), facilitating the modeling of unpredictability in fuzzy systems, and introduced Possibility Strategy Computational Tree Logic (PoSCTL) to handle attributes with non-deterministic choices, aiming to calculate the probability of model satisfaction. In a different approach, Pan et al. [30] suggested another model checking method based on FCTL with fuzzy Kripke structures. This method emphasis the actual values of attributes, addressing a distinct form of uncertainty caused by the vagueness in conceptual expansion. Consequently, this study proposes a simplified method for fuzzy model checking by transforming fuzzy-epistemic attributes into quantifiable ones that are easier to measure and analyze. This approach aims to facilitate the verification process of epistemic attributes in intricate, fuzzy multi-agent systems.
Furthermore, Fuzzy logic is widely used across various disciplines such as budget management [31], decision-making processes [32,33], and organizational management [34,35]. For instance, it has been integrated into TOPSIS method to better handle uncertain and complex decisions, enhancing the method’s effectiveness [32,33]. In budget management, El-Morsy [31] demonstrated the application of fuzzy logic in innovating zero-based budgeting (ZBB) within ambiguous environments. This approach involved the use of triangular fuzzy numbers to depict uncertain budget data, presenting an alternative method for those seeking more precise outcomes. In organizational management, Abolfazl et al. [35] applied the fuzzy Delphi method for eliciting expert opinions on requirements, which were then organized using Kano’s model and the Alpha-cut technique, with fuzzy AHP deployed for prioritizing them. The adaptability of fuzzy logic stems from its unique ability to quantify and manage ambiguity, making it a valuable tool in numerous fields.
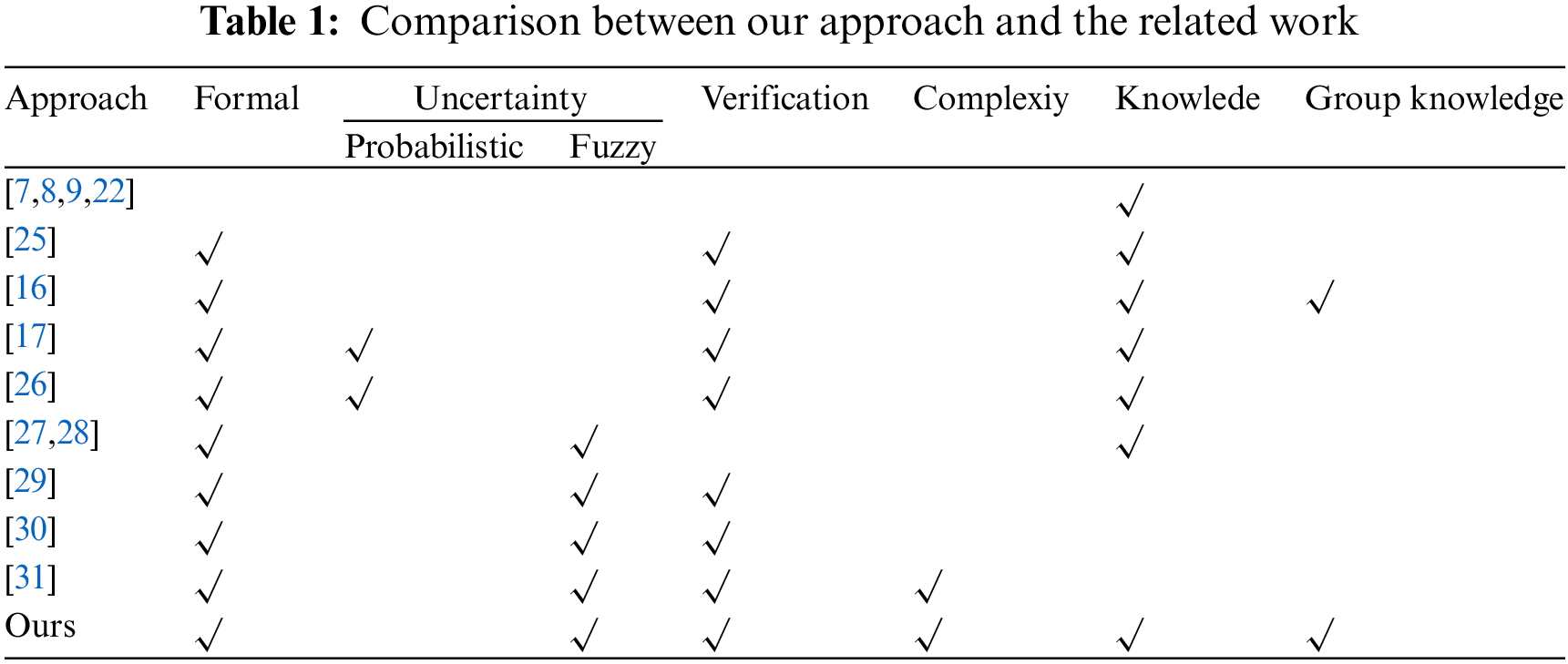
Table 1 provides an overview of the comparison between this study and previous research in terms of formalization, uncertainty, complexity analysis, knowledge, group knowledge, and verification. It highlights the limitations of earlier works [7–9,16,17,22,25–31] in addressing the validation issues of attributes in fuzzy epistemic multi-agent systems.
To model and validate fuzzy epistemic multi-agent systems, we offer essential knowledge, including fuzzy sets, fuzzy set operations, fuzzy matrix operations, and group epistemic accessibility relations.
Definition 1 ([36]). Let
Definition 2 ([36]). Let
Definition 3 ([37]). Let
Definition 4 ([38]). Group Epistemic Accessibility Relations.
(1)
(2)
(3)
The interpreted system is a framework used to model the interactions among multiple autonomous agents, with the aim of describing the temporal evolution process among these agents. The specific formal definition is as follows:
Definition 5([18]). An interpreted system (IS) is composed of n agents
(1) Each agent
(2)
(3)
(4)
(5)
Kripke structures are fundamental models commonly used in model checking. When conducting fuzzy model checking, we extend the concept of fuzzy Kripke structures, defined as follows:
Definition 6 ([19,20]) A fuzzy Kripke structure (FKS) is a tuple
(1)
(2)
(3)
(4)
(5)
3.3 Fuzzy Epistemic Interpreted System
We will integrate fuzzy Kripke structures with an interpreted system to construct a fuzzy epistemic interpreted system (FEIS) for modeling fuzzy epistemic multi-agent systems. The formal definition of the FEIS model is as follows:
Definition 7. FEIS is a six-tuple consisting of a set of n agents
(1)
(2)
(3)
(4)
The fuzzy transition function
Computation paths: If
Fuzzy measure: If
This function is referred to as a fuzzy measure on
For finite
For each
Let
Using the fuzzy matrix calculation form
The fuzzy matrix
Example 1. Fig. 1 represents a FEIS model containing two agents.
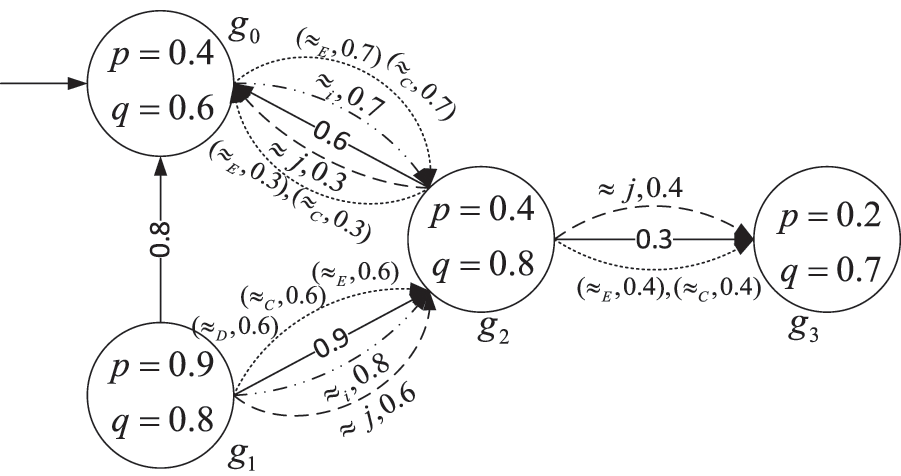
Figure 1: FEIS model M
Based on the epistemic accessibility relations of individual agents
The numerical values on the arrows in the diagram represent the possibility of a state transitioning to another state through epistemic accessibility relationships or joint actions. The resulting fuzzy transition function can be represented as a
4 Fuzzy Computation Tree Logic of Knowledge
To describe the specification of FEIS, we introduce FCTLK. Here we present the syntax of FCTLK and its semantic interpretation in FEIS.
Definition 8. (FCTLK syntax). Let
where
The following is the FCTLK path formula:
where
•
•
The following are the FCTLK social formula and epistemic formula:
•
Definition 9. (FCTLK semantics). Let
Given a fuzzy interpreted system model,
5 Model Checking FCTLK Based on FEIS
Given a fuzzy multi-agent system represented as a FEIS
During the process of model transformation, FEIS is converted into FDP. FDP is a formal model employed to depict the fuzzy and uncertain behaviors of a system, wherein there is at least one enabled action in each state. To address the issue of action uncertainty in FDP, the introduction of scheduler transforms FDP into FKS.
Before showing how to transform FEIS into an FDP, we recall the definition of the FDP model as follows:
Definition 10 ([21]). A fuzzy decision process (FDP) is a tuple
(1)
(2)
(3)
(4)
(5)
(6)
We say that action
It is evident from Definition 10 that the FDP model possesses a set of actions,
In addition, In the process of being transformed into FDP, the states, atomic propositions, and label functions remain unchanged. Algorithm 1 describes the specific process of transforming FEIS into FDP.

Example 2. Following the model transformation rules, we convert the FEIS model in Fig. 1 into the FDP model in Fig. 2.
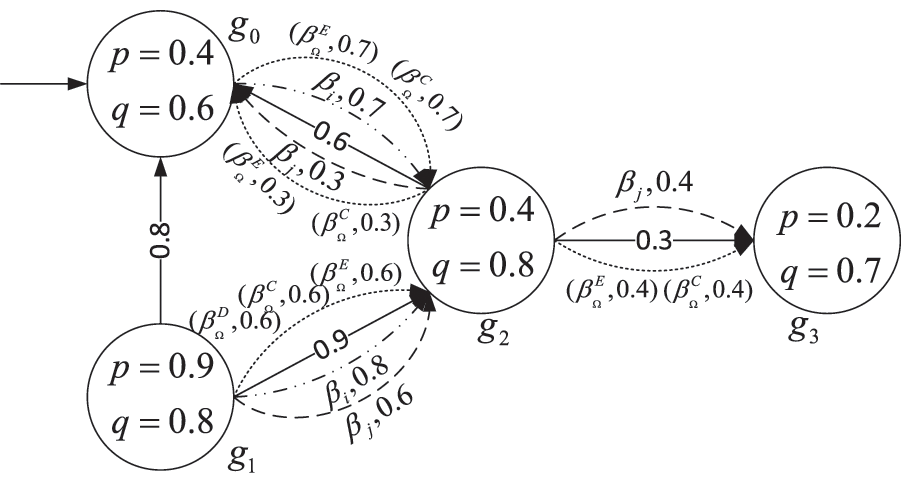
Figure 2: FDP model
The fuzzy transition matrix under group epistemic actions is as follows:
To address the uncertainty of actions in FDP. We defined five different schedulers to convert FDP to FKS. The specific definition of the scheduler functions is provided below.
Definition 11. Let
(1)
(2)
(3)
(4)
(5)
Under the scheduler
The FDP can be transformed into an action-determined FKS, with the transformation algorithm as follows:
Remark 1: As epistemic attributes are challenging to directly quantify and calculate, we utilize a conversion algorithm to transform fuzzy-epistemic attributes into computable quantitative attributes. Thereby transforming the model checking problem of FCTLK into the model checking problem of FCTL. Subsequently, it is essential to adapt the models and logical formulas describing system properties accordingly.

Example 3. For the FDP in Fig. 3, the scheduler functions are defined as
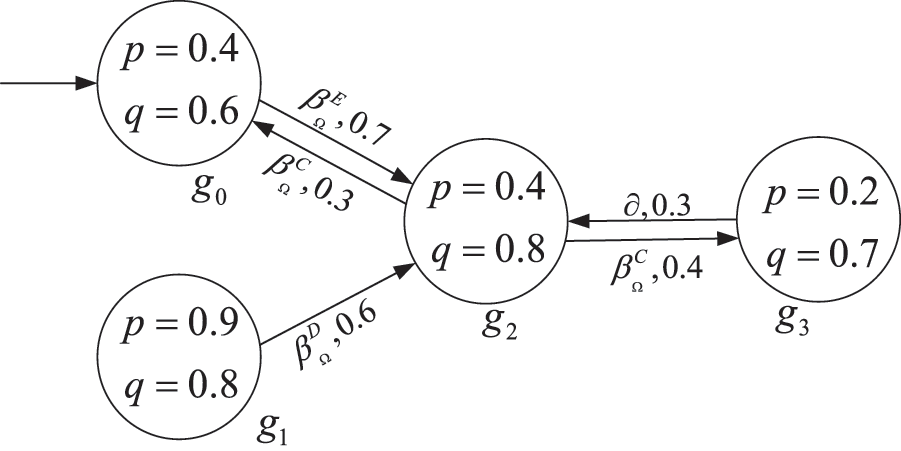
Figure 3: FKS model
This section presents proofs for the equivalence relationships among three epistemic formulas and simplifies FCTLK formulas through a scheduler function. Before the formula simplification, we briefly reviewed the syntax definition of FCTL logic [30].
The state formulas and path formulas are similar to FCTLK, excluding the knowledge operator. However, the FCTL logic we are transforming differs slightly from what is presented in the literature. We have introduced the fuzzy operator FM as a replacement for the path universal quantifier and path existential quantifier in FCTL.
Before simplifying the formulas, we can establish equivalence relationships between knowledge based on the semantics and epistemic accessibility relationship of the four knowledge types, and then prove them.
Theorem 1. Equivalence among epistemic logics:
Proof of the first equation in Theorem 1.
Consider a set of
Therefore, the calculation of
In conclusion, it can be concluded that
Proof of the second equation in Theorem 1.
The possibility value of epistemic formula
For finite
For each
Therefore, the calculation of
In conclusion, it can be concluded that
Proof of the third equation in Theorem 1.
It indicates that on all paths reached through group epistemic accessibility relationship
In conclusion, it can be concluded that
Hereafter, based on different scheduler functions
Theorem 2. Given the scheduler
Proof of Theorem 2.
When the scheduler function is
Theorem 3. Given the scheduler
When the scheduler functions are
Let
In the following, simplify the four epistemic formulas and express them in matrix form.
Proof of the first equation in Theorem 3.
Therefore, it can be proven that
Proof of the second equation in Theorem 3.
Therefore, it can be concluded that
Proof of the third equation in Theorem 3.
Therefore, it can be proven that
Proof of the fourth equation in Theorem 3.
Therefore, it can be proven that
Algorithm 3 describes the FCTL model checking algorithm based on the FKS model.

After model transformation and formula simplification, the model checking algorithm for FCTLK is converted into the model checking algorithm for FCTL, and Algorithm 3 is invoked for computation. The model checking algorithm for FCTLK based on the FEIS model is presented in Algorithm 4.

Example 4. Following the simplification rules of the formula, Next, we will provide the calculation of the possibility that everyone in the group knows content
6 Time Complexity of Model Checking FCTLK
In this section, we will analyze the time complexity of the fuzzy model checking algorithm proposed in Section five. The algorithm comprises the following three primary computational steps.
Lemma 1. The time complexity of the model transformation is linear concerning the size of the input model
Proof of Lemma 1. The problem of model transformation is tackled using a deterministic one-tape Turing machine (DTM) [40]. The DTM sequentially reads all the states, temporal transition relations, and epistemic accessibility relation within the input FEIS model, using distinct markers to signify these relations, and converting them into transition actions. The transformed states and actions are recorded onto an output tape. Through DTM’s examination, model transformation can be accomplished within polynomial time, demonstrating a linear relationship between the time complexity of transformation and the size of the input model.
Lemma 2. The translation from FCTLK formulae to FCTL formulae is linear in time in the size of the input formula
Proof of Lemma 2.
(1) We divide the FCTLK formula
(2) Apply the relevant reduction rule to the nth formula based on the form of its state sub-formula to generate an FCTL formula. This process involves straightforwardly applying the rules to each sub-formula, resulting in a constant time complexity, i.e.,
(3) Replace the nth sub-formula with the translated state formula. This step can also be executed in constant time.
(4) The preceding process is repeated until no more FCTLK sub-formulas exist in the formula.
(5) Therefore, since each sub-formula needs to be converted according to steps 2 and 3, the process needs to be iterated n times, where n is the number of sub-formulas. Since the number of sub-formulas is linearly related to the size of the formula, the time complexity of this step is
Theorem 4. A model checking algorithm exists for FCTLK formulae, which runs in time
Proof of Theorem 4.
For a given FKS model and FCTL formula, Pan et al. [30] determined that the time complexity of the model checking algorithm is
From Theorem 4, we know that the model checking problem exhibits a polynomial relationship with both the model size and formula length, indicating an upper bound of P. Through an investigation of [30], we discover that the FCTL model checking problem based on the FKS model is P-complete, suggesting a lower bound of P as well. In summary, the FCTLK model checking problem is P-complete.
The train control system consists of two trains, a controller, and a tunnel on a circular track. On the track, there are two trains moving clockwise and counterclockwise. The tunnel can only accommodate one train, and traffic lights are installed at both ends of the tunnel. These traffic lights can be either red or green. Each train carries a signal generator used to send signals to the controller when they approach the tunnel. The controller is responsible for receiving signals from both of two trains and controlling the traffic lights at both ends of the tunnel to ensure that the two trains never enter the tunnel simultaneously.
In the real world, controllers perceive their surrounding environment through sensors, but these sensors may be influenced by various interfering factors such as noise, errors, and communication delays. These factors introduce randomness and uncertainty, causing fluctuations and errors in sensor data, which in turn result in biases in the controller’s environmental perception and subsequently impact its decision-making process. Therefore, modeling with a fuzzy system can better capture the actual status of the trains, enabling the controller to make more flexible decisions and controls.
Let the set of agents be
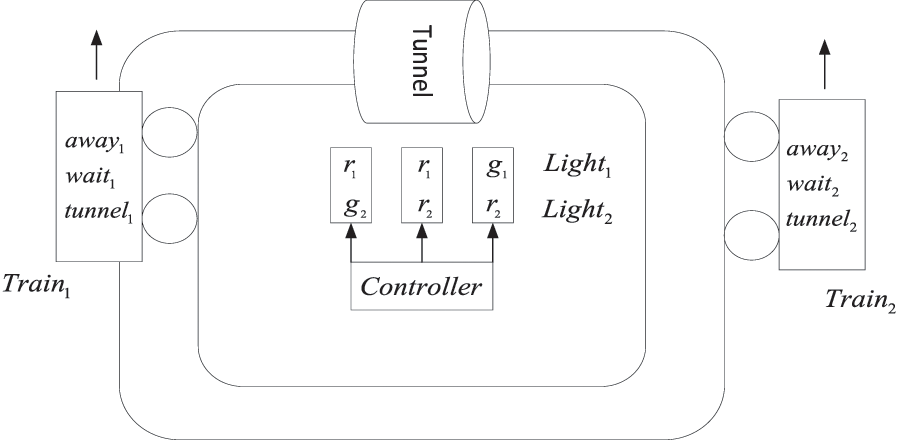
Figure 4: Train control system
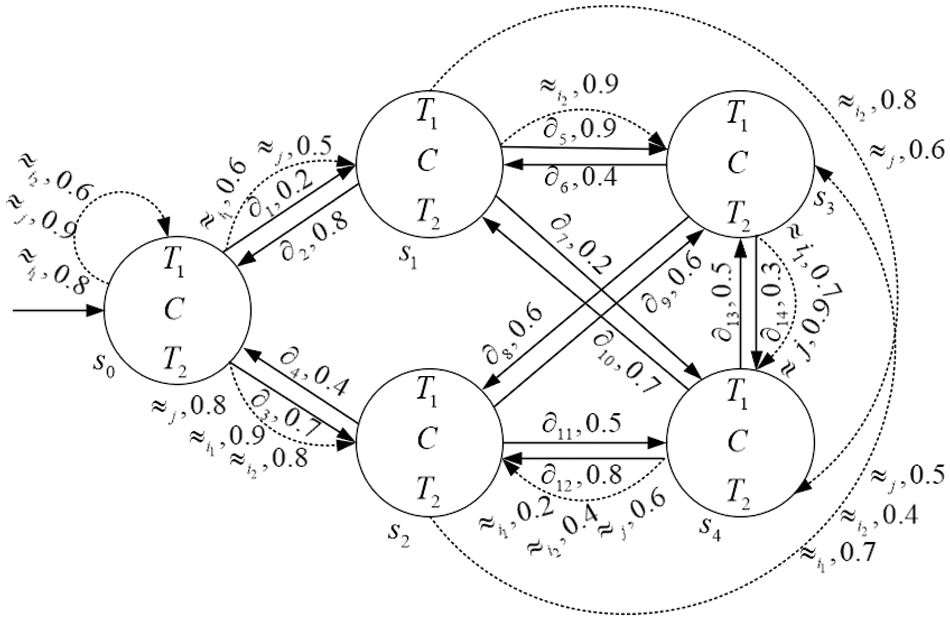
Figure 5: The FEIS model of the train control system
(1) The local state set of agents
(2)
(3) The initial state is
(4) The set of atomic propositions for agents
• The atomic propositions constituting “away” are
• The atomic propositions constituting “wait” are
• The atomic propositions constituting “tunnel” are
• The atomic propositions constituting “light1light2” are
(5) Joint actions are defined as
(6) The fuzzy values of atomic propositions under specific states are assumed as follows:
Because there is an epistemic accessibility relationship between states, the setting of fuzzy values needs to satisfy
(7) The arrowed lines in Fig. 5 represent fuzzy transitions. For example,
Remark 2. In this instance, the degree of satisfaction of atomic propositions and the possibility of transitions under specific states are both represented as fuzzy values subjectively acquired through expert experience.
According to the model transformation rules and the definition of group epistemic accessibility relationships, the FEIS model in Fig. 5 is transformed into the FDP model in Fig. 6, which includes group epistemic actions, as follows.
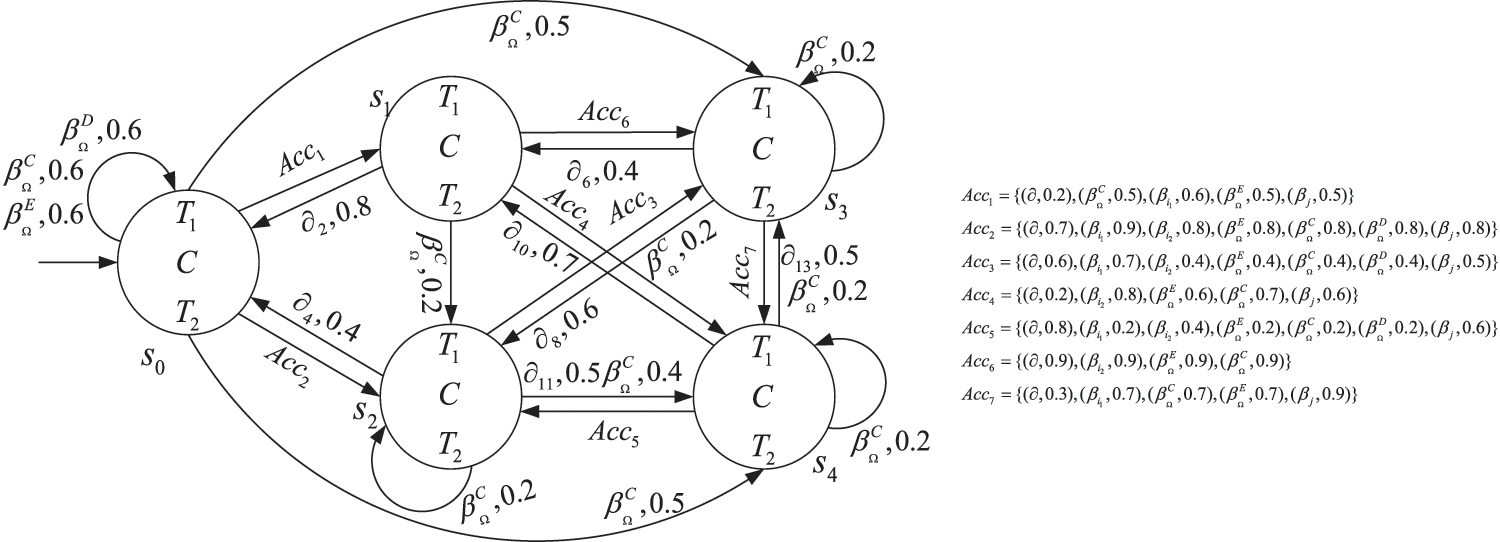
Figure 6: The FDP model of the train control system
This paper addresses the verification of attributes in fuzzy epistemic multi-agent systems using an indirect fuzzy model checking algorithm, which transforms the FCTLK model checking problem based on FEIS into the FCTL model checking problem based on FKS. It calculates the formulas of FCTLK through the synthesis operation of fuzzy matrices and proposes a polynomial-time fuzzy model-checking algorithm. An example of a train control system is presented as an illustration of the practical application of this algorithm.
In the future, we plan to explore the application of direct fuzzy model checking methods for verification. Simultaneously, we intend to utilize the decision framework of the FP-SVNSS method [41] and apply it to the verification of multi-agent systems based on fuzzy epistemic. The core idea of this method is to enrich the verification process through control processes, addressing the issue of fuzzy epistemic attributes influencing collaborative behavior among agents in multi-agent systems. In the application of the decision framework, we need to consider how to verify fuzzy factors in collaborative behavior to ensure the overall collaborative performance of the system.
Acknowledgement: We would like to thank the anonymous reviewers and editors for their suggestions. We would also like to thank for the support and help in scientific research offered by the Key Laboratory of Images & Graphics Intelligent Processing of State Ethnic Affairs Commission, North Minzu University (IGIPLab).
Funding Statement: The work is partially supported by Natural Science Foundation of Ningxia (Grant No. AAC03300), National Natural Science Foundation of China (Grant No. 61962001), Graduate Innovation Project of North Minzu University (Grant No. YCX23152).
Author Contributions: Conceptualization and Methodology, Z.M. and X.L.; Formal analysis, Y.G. and Z.L. All authors have read and agreed to the published version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. L. Ding, H. Wan, L. Hu, and Y. Chen, “Identifying counterexamples without variability in software product line model checking,” Comput. Mater. Contin., vol. 75, no. 2, pp. 2655–2670, 2023. [Google Scholar]
2. R. Jhala and R. Majumdar, “Software model checking,” ACM Comput. Surv. (CSUR), vol. 41, no. 4, pp. 1–54, 2009. doi: 10.1145/1592434.1592438. [Google Scholar] [CrossRef]
3. F. Huang, Z. Liu, T. Wang, H. Zhang, and T. Yip, “The optimization study about fault self-healing restoration of power distribution network based on multi-agent technology,” Comput. Mater. Contin., vol. 65, no. 1, pp. 865–878, 2020. [Google Scholar]
4. F. Belardinelli, A. Ferrando, and V. Malvone, “An abstraction-refinement framework for verifying strategic properties in multi-agent systems with imperfect information,” Artif. Intell., vol. 316, no. 5, pp. 103847, 2023. doi: 10.1016/j.artint.2022.103847. [Google Scholar] [CrossRef]
5. C. Baier and J. P. Katoen, Principles of Model Checking. Cambridge, MA, USA: MIT Press, 2008. [Google Scholar]
6. Y. Shoham and S. B. Cousins, “Logics of mental attitudes in AI: A very preliminary survey,” Foundations of Knowledge Representation and Reasoning, vol. 810, pp. 296–309, 2005. [Google Scholar]
7. V. D. Ron, “Axioms for knowledge and time in distributed systems with perfect recall,” in Proc. Ninth Annual IEEE Symp. on Logic in Computer Science, Paris, France, IEEE, 1994, pp. 448–457. [Google Scholar]
8. G. Lakemeyer, “Limited reasoning in first-order knowledge bases,” Artif. Intell., vol. 71, no. 2, pp. 213–255, 1994. doi: 10.1016/0004-3702(94)90044-2. [Google Scholar] [CrossRef]
9. G. M. Bodner, “Bodner constructivism: A theory of knowledge,” J. Chem. Educ., vol. 63, no. 10, pp. 837, 1986. [Google Scholar]
10. J. Skorupski, “Automatic verification of a knowledge base by using a multi-criteria group evaluation with application to security screening at an airport,” Knowl. Based Syst., vol. 85, no. 16, pp. 170–180, 2015. doi: 10.1016/j.knosys.2015.05.004. [Google Scholar] [CrossRef]
11. W. Penczek and A. Lomuscio, “Verifying epistemic properties of multi-agent systems via bounded model checking,” in Proc. Second Int. Joint Conf. on Auton. Agents and Multiagent Syst., Melbourne, Australia, 2003, pp. 209–216. [Google Scholar]
12. D. Xie, W. Xiong, L. Bu, and X. Li, “Deriving unbounded reachability proof of linear hybrid automata during bounded checking procedure,” IEEE Trans. Comput., vol. 66, no. 3, pp. 416–430, 2016. doi: 10.1109/TC.2016.2604308. [Google Scholar] [CrossRef]
13. G. B. Rossi, F. Crenna, and M. Berardengo, “Probability theory as a logic for modelling the measurement process,” Acta IMEKO, vol. 12, no. 2, pp. 1–5, 2023. doi: 10.21014/actaimeko.v12i2.1313. [Google Scholar] [CrossRef]
14. F. Pourpanah et al., “An improved fuzzy ARTMAP and Q-learning agent model for pattern classification,” Neurocomput., vol. 359, no. 10, pp. 139–152, 2019. doi: 10.1016/j.neucom.2019.06.002. [Google Scholar] [CrossRef]
15. A. K. Adak, M. K. Gunjan, and N. K. Agarwal, “Picture fuzzy semi-prime ideals,” J. Fuzzy Ext. Appl., vol. 4, no. 2, pp. 115–124, 2023. [Google Scholar]
16. A. Termine, A. Antonucci, G. Primiero, and A. Facchini, “Imprecise probabilistic model checking for stochastic multi-agent systems,” SN Comp. Sci., vol. 4, no. 5, pp. 443, 2023. doi: 10.1007/s42979-023-01817-x. [Google Scholar] [CrossRef]
17. C. Fu, A. Turrini, X. Huang, L. Song, Y. Feng and L. Zhang, “Model checking probabilistic epistemic logic for probabilistic multiagent systems,” in Proc. Twenty-Seventh Int. Joint Conf. on Artif. Intell., Stockholm Sweden, 2018, pp. 4757–4763. [Google Scholar]
18. F. Ronald and J. Y. Halpern, “Reasoning about knowledge and probability,” J. ACM, vol. 41, no. 2, pp. 340–367, 1994. doi: 10.1145/174652.174658. [Google Scholar] [CrossRef]
19. Y. H. Fan, Y. M. Li, and H. Y. Pan, “Computation tree logic model checking for nondeterminisitc fuzzy Kripke structure,” Acta Electon. Sin., vol. 46, no. 1, pp. 152–159, 2018 (In Chinese). [Google Scholar]
20. N. L. Anh, “Computing the fuzzy partition corresponding to the greatest fuzzy auto-bisimulation of a fuzzy graph-based structure under the Gödel semantics,” Inf. Sci., vol. 630, pp. 482–506, 2023. doi: 10.1016/j.ins.2023.02.029. [Google Scholar] [CrossRef]
21. Z. Ma, Z. Li, W. Li, Y. Gao, and X. Li, “Model checking fuzzy computation tree logic based on fuzzy decision processes with cost,” Entropy, vol. 24, no. 9, pp. 1183, 2022. doi: 10.3390/e24091183. [Google Scholar] [PubMed] [CrossRef]
22. P. Yannick and A. Subias, “Diagnosability of event patterns in safe labeled time Petri nets: A model-checking approach,” IEEE Trans. Autom. Sci. Eng., vol. 19, no. 2, pp. 1151–1162, 2021. [Google Scholar]
23. P. A. Abdulla, M. F. Atig, A. Godbole, S. Krishna, and M. Vahanwala, “Overcoming memory weakness with unified fairness,” arXiv:2305.17605, 2023. [Google Scholar]
24. Z. Ma, Y. Gao, Z. Li, X. Li, and Z. Liu, “Quantitative reachability analysis of generalized possibilistic decision processes,” J. Intell. Fuzzy Syst., vol. 44, no. 5, pp. 8357–8373, 2023. doi: 10.3233/JIFS-222803. [Google Scholar] [CrossRef]
25. A. Souri, A. M. Rahmani, N. J. Navimipour, and R. Rezaei, “Rezaei A symbolic model checking approach in formal verification of distributed systems,” Hum. Cent. Comput. Inf. Sci., vol. 9, no. 1, pp. 1–27, 2019. [Google Scholar]
26. B. Mário, A. Madeira, and M. A. Martins, “Graded epistemic logic with public announcement,” J. Log. Algebr. Methods Prog., vol. 125, pp. 100732, 2022. [Google Scholar]
27. H. Enhua, “Fuzzy epistemic logic,” Noesis XVIII, vol. 18, no. 1, pp. 19–32, 2017. [Google Scholar]
28. Y. M. Li and Z. Y. Ma, “Quantitative computation tree logic model checking based on generalized possibility measures,” IEEE Trans. Fuzzy Syst., vol. 23, no. 6, pp. 2034–2047, 2015. doi: 10.1109/TFUZZ.2015.2396537. [Google Scholar] [CrossRef]
29. Y. M. Li, W. Liu, J. Wang, X. Yu, and C. Li, “Model checking of possibilistic linear-time properties based on generalized possibilistic decision processes,” IEEE Trans. Fuzzy Syst., vol. 31, no. 10, pp. 3495–3506, 2023. doi: 10.1109/TFUZZ.2023.3260446. [Google Scholar] [CrossRef]
30. H. Y. Pan, Y. Li, Y. Cao, and Z. Ma, “Model checking fuzzy computation tree logic,” Fuzzy Sets Syst., vol. 262, no. 23, pp. 60–77, 2015. doi: 10.1016/j.fss.2014.07.008. [Google Scholar] [CrossRef]
31. S. A. El-Morsy, “Optimization of fuzzy zero-base budgeting,” Comput. Algorithms Num. Dimens., vol. 1, no. 4, pp. 147–154, 2022. [Google Scholar]
32. E. Elham, M. R. Fathi, and S. M. Sobhani, “A modification of technique for order preference by similarity to ideal solution (TOPSIS) through fuzzy similarity method (a numerical example of the personnel selection),” J. Appl. Res. Ind. Eng., vol. 10, no. 2, pp. 203–217, 2023. [Google Scholar]
33. B. Darko, D. Tesic, D. Marinkovic, and A. Milic, “Modeling of neuro-fuzzy system as a support in decision-making processes,” J. Mech. Eng., vol. 2, no. 1, pp. 222–234, 2021. doi: 10.31181/rme2001021222b. [Google Scholar] [CrossRef]
34. E. Ali, H. Mehrmanesh, and M. Mohammadi, “Identifying and prioritizing technology capability drivers in the supply chain using the fuzzy hierarchical analysis process (case study: Iran khodro and saipa automotive company),” Int. J. Res. Ind. Eng., vol. 12, no. 1, pp. 2783, 2023. [Google Scholar]
35. R. Abolfazl and M. Hemati, “Providing a hybrid fuzzy approach to explain managers’ mental paradigms to prioritize employee needs,” J. Fuzzy Ext. Appl., vol. 4, no. 3, pp. 155–172, 2023. [Google Scholar]
36. A. Z. Lotfi, “Fuzzy sets,” Inform. Comput., vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]
37. Y. G. Xue and Y. Deng, “Decision making under measure-based granular uncertainty with intuitionistic fuzzy sets,” Appl. Intell., vol. 51, no. 8, pp. 6224–6233, 2021. doi: 10.1007/s10489-021-02216-6. [Google Scholar] [PubMed] [CrossRef]
38. W. Wei, J. Bentahar, and A. B. Hamza, “Model checking epistemic-probabilistic logic using probabilistic interpreted systems,” Knowl. Based Syst., vol. 50, no. 9–10, pp. 279–295, 2013. doi: 10.1016/j.knosys.2013.06.017. [Google Scholar] [CrossRef]
39. V. Botti et al., “A temporal blackboard for a multi-agent environment,” Data Knowl. Eng., vol. 15, no. 3, pp. 189–211, 1995. doi: 10.1016/0169-023X(95)00007-F. [Google Scholar] [CrossRef]
40. B. Guillon, G. Pighizzini, L. Priginoiero, and D. Prusa, “Prusa weight-reducing turing machines,” Inf. Comput., vol. 292, no. 2, pp. 105030, 2023. doi: 10.1016/j.ic.2023.105030. [Google Scholar] [CrossRef]
41. M. Ihsan, M. Saeed, and A. U. Rahman, “Optimizing hard disk selection via a fuzzy parameterized single-valued neutrosophic soft set approach,” J. Oper. Strateg. Anal., vol. 1, no. 2, pp. 62–69, 2023. doi: 10.56578/josa010203. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2024 The Author(s). Published by Tech Science Press.
Copyright © 2024 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools