Material-SAM: Adapting SAM for Material XCT

1  Introduction

The structures such as phases, pores, cracks, and carbides in materials have a significant impact on their strength and properties. Therefore, the characterization of various structures plays a crucial role in the analysis of material performance. Traditional two-dimensional microscopy provides a 2D metallographic characterization of the material’s microstructure [1–4]. Although 2D characterization techniques establish a relationship between structure and material properties to some extent, they are limited in capturing complex three-dimensional features, which hinders accurate material analysis [4–8]. By employing X-ray computed tomography (XCT), we can visualize the internal microstructure of materials in three dimensions without damaging the material samples, thus obtaining a stereoscopic representation of features within the material.

To extract the regions of interest from the 2D slice images and achieve three-dimensional visualization, image segmentation is required. Traditional threshold-based segmentation methods rely on image grayscale values [9–12]. Although this process is fully automated, the segmentation outcome heavily depends on the selection of thresholds. This segmentation method fails when the target region and the background have similar grayscale values.

With the advancement of machine learning techniques, fully convolutional networks have shown promising applicability in image segmentation [13], and they have become the primary method for XCT image segmentation. Among them, U-Net is a representative network that has been widely used in the materials field [14,15]. However, like other deep learning methods, fully convolutional network segmentation methods require a large amount of data to train the network for a specific segmentation task. Since manual annotation is required for the dataset, using fully convolutional network segmentation methods still demands significant human effort. Moreover, deep learning methods are sensitive to the content of the dataset and often require multiple iterations of training and fine-tuning of the dataset to obtain satisfactory models. Additionally, using deep learning methods requires users to possess programming skills and knowledge of the corresponding models. Many related open-source codes lack user-friendly interactive systems, causing inconvenience for users.

Meta AI’s Segment Anything Model (SAM) [16] has become the state-of-the-art model in the field of image segmentation and marks the era of the foundation model in image segmentation. It has been trained on a massive dataset consisting of one billion masks and eleven million images, demonstrating its powerful capability for real-world object segmentation tasks. It also outperforms other models in zero-shot tasks, which leads us to consider applying it to the segmentation of material XCT images to overcome dataset limitations. However, SAM’s performance is not satisfactory in medical XCT segmentation tasks similar to material XCT segmentation [17–19]. Since SAM’s training dataset primarily comprises naturally captured images, its generalization ability to XCT images with blurry boundaries is relatively weak. Therefore, fine-tuning is required to adapt SAM to the task of material XCT image segmentation.

Traditional grayscale-based segmentation methods struggle to resist noise interference, especially in cases where materials exhibit similar grayscale values, making effective separation challenging. Most deep learning-based approaches face the issue of poor generalization and often require large annotated datasets for task-specific training. Particularly in the case of XCT images where data collection is challenging, deep learning methods may even surpass the overall data volume required for segmentation tasks. In contrast to the low robustness of traditional methods and the high data demands of deep learning, our approach can effectively distinguish between the background and phases in material XCT slice images without the need for additional training. Our method demonstrates excellent performance in accomplishing the segmentation tasks for the majority of material XCT slice images.

In this paper, we enhance XCT images by applying preprocessing techniques such as median filtering, histogram equalization, and gamma correction to highlight feature information. We apply SAM to the task of material XCT image segmentation and improve its performance by fine-tuning the model accordingly. By comparing the SAM, the U-Net model, and the fine-tuned Material-SAM, we evaluate the effectiveness of the fine-tuned model.

2  Literature Review

In the field of materials, the segmentation of XCT images is an important task that helps us understand the internal structure of materials and extract key features. Currently, there are various methods for XCT image segmentation, which can be mainly divided into two categories: traditional image processing-based methods and deep learning-based methods. However, each method inevitably has some limitations.

Traditional image processing methods usually rely on techniques such as statistical characteristics, edge detection, and threshold segmentation. These methods may perform well in certain cases, but their performance can be limited when dealing with complex textures, noise, or dense structures in XCT images. Moreover, traditional methods require manual selection and fine-tuning of parameters, which can be time-consuming and require expertise to achieve satisfactory segmentation results for different datasets and application scenarios.

Kim et al. [20] proposed a segmentation method based on the Gradient-based phase segmentation method for segmenting hydrating cement paste microstructures in XCT images. This method obtains the relationship curve between the segmentation threshold and the linear attenuation coefficient of pores in XCT images, identifies the gray value with the most dramatic change in the curve gradient, and performs segmentation based on this gray value. The method demonstrates good performance in pore segmentation tasks and can be extended to segmentation of other phases.

Compared to traditional methods, deep learning-based methods exhibit better flexibility and robustness in XCT image segmentation tasks. Deep learning models can automatically learn feature representations from XCT images and improve segmentation accuracy and efficiency through end-to-end learning using large-scale training data. Additionally, deep learning methods can further improve segmentation results through techniques such as data augmentation, transfer learning, and model fusion.

Stan et al. [21] used XCT images of Pb-74.4 wt%Sn samples and other datasets for three-channel restoration, denoising using Gaussian filtering, enhancing edge features using Canny edge detection, and training with the SegNet neural network with a learning rate of 0.01. The model achieved 99.7% accuracy on the dataset and demonstrated relatively excellent performance in other XCT image segmentation tasks. Helwing et al. [22] used deep learning methods to segment defects in fiber-reinforced polymers using the LeNet-5 convolutional neural network with a learning rate of 0.0001, achieving a dice coefficient greater than 0.749. Mahdaviara et al. [23] proposed the PoreSeg framework, which divided the model training into six modules to reduce coupling between steps. The entire framework involved preprocessing through filtering, feature extraction through convolution, and feature learning through bagging and boosting frameworks, demonstrating significant performance in multi-mineral segmentation.

Semantic segmentation, as a critical task in computer vision, has witnessed the emergence of highly effective network architectures. Fully Convolutional Network (FCN) [24], a pioneer in semantic segmentation, introduced end-to-end convolutional networks into the field by eliminating fully connected layers in the classifier, forming a fully convolutional network structure. Subsequently, U-Net [25] proposed a network that synthesizes FCN concepts by fusing deep and shallow network information, achieving a balance between overall and detail awareness. It significantly improved performance on limited datasets, particularly finding wide application in medical image segmentation. For instance, improvements by Jabbar et al. [26] achieved a Dice score of 0.92 in brain tumor segmentation, reducing training time from 2–3 days to 80–90 min. SegNet [27] shares a similar overall structure with U-Net, dividing the network into encoder and decoder parts, with the encoder utilizing the VGG16 network model. SegNet eliminates the need to store feature maps in the encoder, saving resources while effectively addressing segmentation coarseness issues. PSPNet [28] introduces a pyramid pooling module to aggregate background information, enabling the model to comprehend global contextual information. DeepLab v3 [29] removes the conditional random field used in v1 and v2, introducing the Multi-Grid strategy to address grid issues caused by hole convolution and improving Atrous Spatial Pyramid Pooling (ASPP). Fu et al. [30] proposed a novel Dual Attention Network (DANet) with a self-attention mechanism to enhance the discriminative capability of scene segmentation feature representation. This method significantly improves segmentation results by modeling rich contextual dependencies on local features.

As research into semantic segmentation deepens, models continue to evolve in depth and structure. However, due to the difficulty of obtaining medical image data and the diverse nature of medical segmentation tasks, U-Net and its improved networks remain mainstream. Material image segmentation faces challenges similar to medical images. Additionally, the random distribution of phases in materials makes segmentation more complex compared to organ segmentation in medical images. Current segmentation methods for material images primarily use traditional threshold segmentation methods, with most deep learning methods based on U-Net. However, these methods have strong dependencies on data quality, and poor model reusability. Therefore, material images require a simple segmentation method with minimal dependence on data.

The emergence of the Segment Anything model has ushered in the era of large models in the field of image segmentation, and its powerful generalization ability allows it to achieve zero-shot tasks in various domains. However, as the training set of the SAM model consists of natural images, it raises questions about its suitability for XCT image segmentation.

In [31], SAM was used for XCT image segmentation of multi-phase liver tumors. The article selected 1,552 multi-phase contrast-enhanced computed tomography images from 388 patients and evaluated the segmentation results using the Dice global score. Compared to the U-Net neural network frequently used in XCT image segmentation, SAM performed worse on images of various sizes. However, with an increase in the number of prompt points given to SAM, the segmentation performance of SAM also improved.

In [32], SAM was used for brain magnetic resonance images segmentation, and the segmentation results were compared with the Brain Extraction Tool (BET). Test datasets such as ATLAS [33] and white matter hyperintensities Challenge Segmentation [34] were selected. The Dice coefficient, IoU, Acc, Recall, and Prec were chosen as the evaluation parameters for segmentation results. It was found that SAM slightly outperformed BET in various datasets, indicating a promising future in medical segmentation.

In [35], to address the weak segmentation ability of SAM for weak boundary objects in XCT image segmentation, a model adjustment approach was proposed. This study froze the image encoder part and trained the image decoder using 33 segmentation tasks from a comprehensive dataset. During training, the unweighted sum of the Dice loss and cross-entropy loss was used, and the Adam optimizer was selected. On the test set, the adjusted model achieved an improvement of about 20 percentage points in the dice coefficient compared to the unadjusted model.

In [36], the adaptor technique from Natural Language Processing (NLP) was introduced to the SAM model to adapt it to XCT image segmentation tasks. This study inserted two adaptors in the image encoder and three adaptors in the image decoder of SAM, while partially freezing the original model. The study used approximately 1.35 million images for training and employed various self-supervised learning methods such as e-Mix, ShED, and MAE. The adjusted model showed better performance than models like U-Net in multiple XCT segmentation tasks.

In [37], MLP-based adaptor blocks were inserted at each layer of the image encoder in SAM, and datasets such as COD10K [38], CHAMELEON [39], CAMO [40], and ISTD [41] were selected for tasks such as camouflage object detection, shadow detection, and medical image segmentation. The AdamW optimizer was used with an initial learning rate of 2e-4. The trained SAM-adapter model achieved similarity (S-measure) scores of 0.896, 0.847, and 0.883 on the three datasets for camouflage object detection, reduced the balance error rate (BER) to 1.43 for shadow detection, and improved the dice coefficient to 0.850 for medical image segmentation.

For XCT image segmentation in materials, threshold segmentation methods are mainly used. However, when the grayscale variation is insufficient, this method may fail to produce satisfactory segmentation results. On the other hand, deep learning methods require a large amount of dataset and their generalization ability needs improvement. SAM has strong generalization ability, which enables it to perform well in zero-shot tasks, thereby simplifying the process of XCT image segmentation. In this study, SAM was improved and applied to the task of materials XCT image segmentation, overcoming these limitations. By comparing Material-SAM with other segmentation methods on the test dataset, the potential of Material-SAM as a novel feature segmentation approach in materials XCT image segmentation was validated.

3  Proposed Methodology

3.1 Datasets and Preprocessing

We utilized a dataset of nickel-based single crystal superalloy carbides [42] and successfully imaged their internal microstructure using a high-resolution and high-contrast Zeiss Xradia Versa 520 X-ray microscope. A total of 7,520 XCT slice images were obtained using a voltage of 150 kV and an output power of 10 W. Carbides exhibit a two-dimensional morphology primarily characterized by rod-like, plate-like, and mesh-like structures, with the possibility of some degree of fusion between them. In our experiments, we did not make explicit differentiations based on the morphology of carbides. In the image slices, carbides approximately occupy 20% of the total area, distributed uniformly throughout the interior of the specimen. To enhance the carbides in the images, we applied median filtering for noise reduction and performed histogram equalization and gamma correction algorithms to enhance the features in the XCT images, as shown in Fig. 1. Finally, we standardized the size of the dataset to 1024 × 1024. After an initial segmentation of the carbides in the images using a neural network, we performed manual adjustments to ensure the accuracy of the mask.

Figure 1: (a) XCT slice image of nickel-based single crystal high-temperature alloy carbide. (b) Image after median filtering. (c) Image after histogram equalization. (d) Image after gamma correction

To address the challenges of small contrast differences, blurred edges, and indistinct features between carbides and the matrix in XCT slice images, making them more amenable to extraction by convolutional neural networks, we employed the bilateral filtering method. This method, built upon Gaussian filtering, introduces pixel value weights to minimize noise and preserve grayscale gradients in the image. The filter is denoted as BF, with pixel value weights represented by Gr and spatial distance weights represented by Gs. The formula for the filter is as follows:

BF=1Wq∑p∈SGs(p)Gr(p)*Ip=1Wq∑p∈Sexp⁡(−||p−q||22σs2)exp⁡(−||Ip−Iq||22σs2)*Ip(1)

where Wq represents the weighted sum of each pixel value within the filtering window. Subsequently, the grayscale of each pixel in the image is adjusted by modifying the image’s histogram, enhancing the contrast of images with a limited dynamic range. The transformation formula is as follows:

T(sk)=∑j=0knjN(2)

where N is the total number of pixels in the image, and the value of the k-th grayscale level is denoted as sk. Subsequently, we further enhance the dynamic contrast of low grayscale value regions by applying gamma correction with a coefficient of 0.9, aiming to strengthen the image features.

3.2 SAM Analysis

SAM employs a transformer-based architecture [43], which has become prevalent in natural language processing and image segmentation in recent years. The model consists of an image encoder, prompt encoder, and mask decoder. The prompt encoder can accept four types of inputs: points, boxes, text, and masks, allowing users to interact and obtain the desired segmentation results. The mask decoder is designed to be lightweight and consists of two Transformer layers, one for dynamic mask prediction and the other for intersection over union score regression. The mask prediction head can generate three masks at a downscaled resolution of 1/4, corresponding to the whole, part, and subpart of the objects.

SAM supports three main segmentation modes: fully automatic segmentation of all content, bounding box mode, and point mode. In materials, carbides exist in various shapes and can appear in different regions of the sample. Fully automatic mode often fails to capture the details inside the sample and struggles with successful segmentation. Bounding box mode can only segment a small portion of the carbides, and when a bounding box is used to encompass the entire sample, SAM tends to segment the whole sample, which does not meet the segmentation requirements, as shown in Figs. 2a and 2b. On the other hand, when points are used as prompts, SAM tends to segment the internal details around the points, as shown in Fig. 2c. Therefore, during training, we use points as inputs to the prompt encoder.

Figure 2: (a) Mask obtained by selecting a portion of the carbides using the bounding box method. (b) Mask obtained by selecting all the carbides using the bounding box method. (c) Mask obtained using the point method

3.3 Evaluation Protocol

We adopted Dice Similarity Coefficient (DSC), Class Pixel Accuracy (CPA), Intersection over Union (IoU), and Pixel Accuracy (PA) as the evaluation metrics for our model. The Dice coefficient is a commonly used evaluation metric in semantic segmentation that directly reflects the effectiveness of the mask. It is calculated using the following Eq. (3). CPA reflects the accuracy of the model’s predictions with respect to the ground truth and is calculated using the Eq. (4). PA evaluates the model’s accuracy in predicting all pixels and is calculated using the Eq. (5). IoU is calculated as the ratio of the intersection to the union of the predicted results and the ground truth for a specific class, as computed using Eq. (6).

DSC=2× TP /(2× TP + FN + FP)(3)

CPA= TP /(TP + FP)(4)

PA=(TP + TN)/(TP + TN + FP + FN)(5)

IoU = TP /(TP + FP + FN)(6)

where True Positive (TP) represents the number of positive instances correctly predicted as positive, False Negative (FN) represents the number of positive instances incorrectly predicted as negative, False Positive (FP) represents the number of negative instances incorrectly predicted as positive, and True Negative (TN) represents the number of negative instances correctly predicted as negative. In this study, positive instances refer to carbides, while negative instances refer to the background.

4  Experiments and Results

4.1 Training of Mask Decoder

To meet the input requirements of the SAM network, we employed an eight-connectivity labeling method to process the ground truth map. This method effectively identifies connected regions of carbides in XCT images and selects the coordinates of the central pixel for each region as the optimal reference points, as illustrated in Fig. 3. In this study, we chose the coordinates of the central pixels for the three largest connected regions as inputs for the reference encoder. This approach provides effective cues required by the SAM network, contributing to a more accurate segmentation task.

Figure 3: (a) Division of different connected regions using eight-connected labeling method. (b) Prominent points corresponding to the three connected regions with the highest number of pixels

To adapt SAM for the segmentation of XCT images in materials, we performed fine-tuning. Among SAM’s three components, the image encoder has 632 million parameters. Due to the substantial data and computational resources required for modifying the image encoder, we decided to retain its structure, which achieved good results on a large dataset. Instead, we opted for transfer learning on SAM’s mask decoder to tailor it to the specific task of material image segmentation. During fine-tuning, we froze the image encoder and reference encoder, allowing only the gradient backpropagation for the mask decoder. We trained the mask decoder using target image data to enhance segmentation performance. To reduce computational expenses during training, we computed the image embeddings only once for each image in the dataset before training commenced. Subsequent training cycles avoided redundant embedding calculations. The generated reference points, after computation by the reference encoder, were inputted into the mask decoder along with the image embeddings. The architecture of fine-tuning is illustrated in Fig. 4. We calculated the loss functions for the three generated masks by the mask decoder and took their arithmetic average. This fine-tuning strategy helped the SAM network better adapt to the material image segmentation task while reducing computational burden.

Figure 4: Fine-tuning approach for Material-SAM: We freeze the image encoder and prompt encoder and only train the mask decoder

The dataset was divided into a training set and a test set in an 80% to 20% ratio. We used the image encoder of SAM-b to compute image embeddings for the preprocessed dataset. We employed the sum of Dice loss and cross-entropy loss as the training loss function, and utilized the Adam optimizer [44] with a learning rate of 1e-6. The batch size for training was set to 94.

4.2 Evaluation of Material-SAM

As mentioned earlier, in material image segmentation tasks, most researchers tend to adopt threshold segmentation methods to segment different phases within the specimen. Additionally, U-Net, a network that has demonstrated outstanding performance in the field of medical image segmentation, is currently widely applied in material image segmentation and has achieved significant results. To validate the performance of Material-SAM, we selected various methods for comparison, including threshold segmentation, the U-Net neural network, tansUnet, and other network architectures that have achieved important results in the field of semantic segmentation, such as FCN, SegNet, PSPNet, DANet, and EncNet. These networks utilized the same dataset as Material-SAM and employed a combination of BCELoss and DiceLoss as the loss functions, using the Adam optimizer for training. We set the learning rate to 0.01 and applied a 50% learning rate decay every ten epochs, with a total of 100 training epochs. Through this experimental setup, we aim to comprehensively assess the performance of Material-SAM in material image segmentation tasks relative to other methods. The evaluation results are shown in Table 1 and Fig. 5.

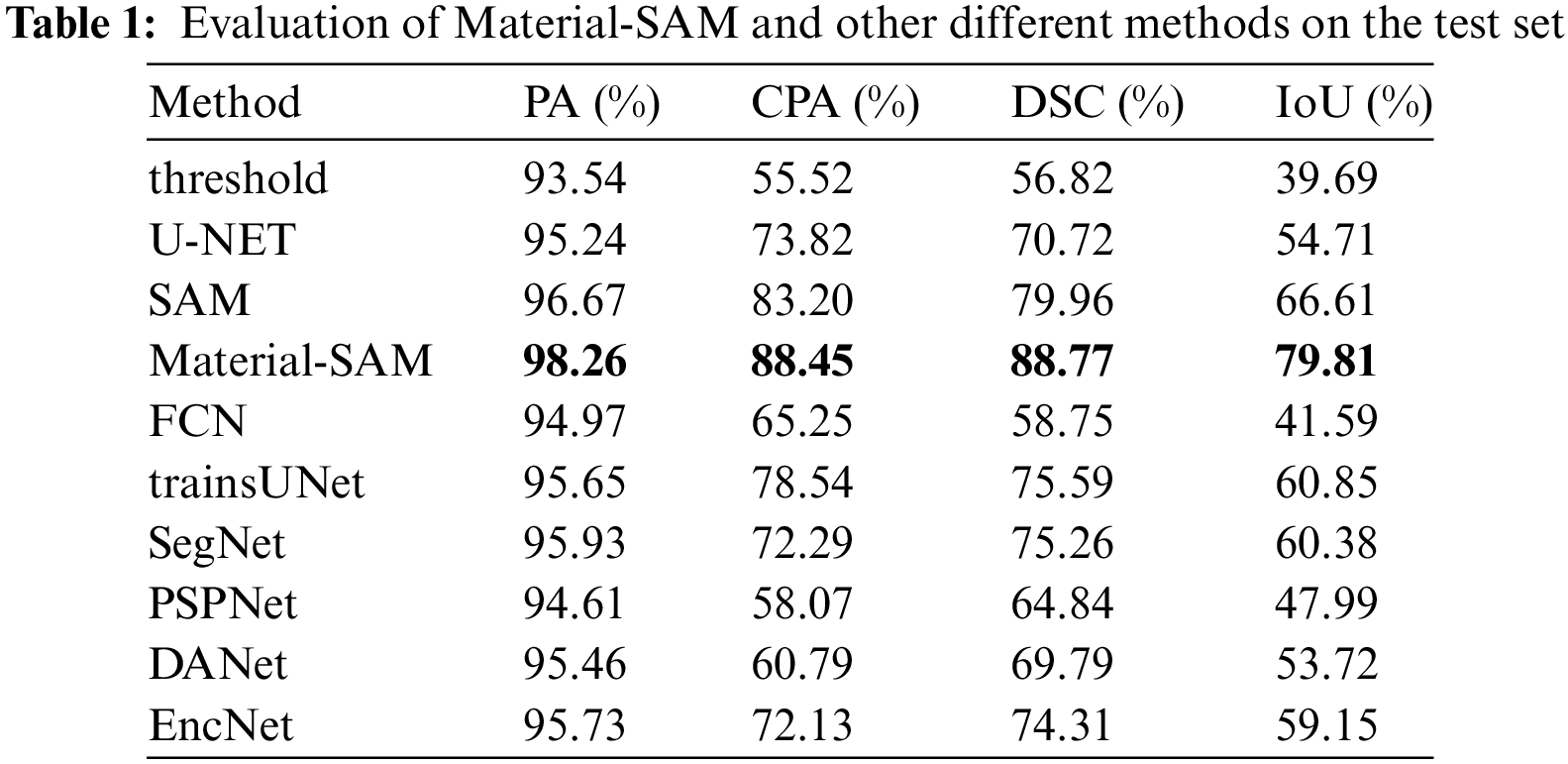
Figure 5: IoU, CPA and DSC of Material-SAM and other different methods on the test set

From the table, it can be observed that all methods achieved high values in terms of PA metric, successfully distinguishing most of the background. Among them, SAM achieved a PA of 96.67%, slightly higher than other methods, while the fine-tuned Material-SAM increased it to 98.26%. Our method improved the segmentation accuracy of SAM to some extent. The CPA of traditional thresholding segmentation methods was only 55.52%, as the thresholding approach failed in cases where there was a small threshold difference between carbides and some background regions. Although it was able to segment carbides, it also misclassified a significant amount of background as carbides. The CPA and DSC of the SAM method were 83.20% and 79.96%, respectively, higher than those of the other methods. The fine-tuned Material-SAM achieved scores of 88.45% and 88.77%, respectively. In summary, our method is capable of performing carbide segmentation in XCT images, and compared to the non-fine-tuned model, it improved the CPA by 5.25% and the DSC by 8.81%. In the task of segmenting the carbide in the slice diagram, Material-SAM performed better than the other nine methods.

The findings from the images are consistent with the results in Table 1. In the case of the thresholding segmentation results shown in Fig. 6, although the carbides were mostly segmented, the regions appeared to be fragmented. Additionally, numerous scattered segmented regions belonging to the background were observed, indicating poor overall segmentation performance due to the small threshold difference between carbides and the background. The segmentation result of U-Net shown in Fig. 6 generated a mask slightly larger than the ground truth mask, successfully detecting all carbide regions. However, it had false positive segmentations, such as an erroneous segmented region located at the sample edge in the upper left corner of the image, as well as cases where background regions were erroneously segmented in the left part of the image. Moreover, it exhibited poor segmentation capability for block-like carbide regions, such as the carbide region in the upper left corner of the image, where U-Net segmented based on rod-like features, resulting in hollow regions. In addition, the masks produced by most methods have a lot of noise. The segmentation result of SAM shown in Fig. 6 exhibited high segmentation accuracy, correctly distinguishing the background from carbides and showing good segmentation performance for large carbide regions. However, it was not sensitive enough to smaller regions and failed to segment the point-like carbides located in the lower part of the sample. Material-SAM inherited the advantages of SAM, demonstrating high background recognition capability without mistaking background regions as carbides, and it was more sensitive to small objects, successfully segmenting the point-like carbides in the lower part of the image. Although the segmentation performance was poorer for the carbide in the lower right corner, it could be improved by adjusting or increasing the prompt points.

Figure 6: Performance of Material-SAM and other different methods on test set

We utilized Avizo for three-dimensional visualization of the segmentation results, providing a more intuitive understanding of the impact of different segmentation methods on the quality of 3D reconstruction in practical analysis. From Fig. 7, it can be observed that the threshold-based segmentation results in a granular reconstruction, making it difficult to observe the morphology of carbides. On the other hand, the U-Net segmentation results contain significant redundancy, leading to potential interference. The 3D reconstruction models of other methods produced many fine particles, and showed obvious columnar shape. It can be found that these methods are easily affected by the noise in the image, and are too sensitive to the gray change of the edge of the image. The reconstruction results of SAM and Material-SAM effectively showcase the structural details of carbides in three dimensions.

Figure 7: 3D reconstruction of Material-SAM and other different methods

4.3 Prompt for SAM

In SAM, the input prompts play a crucial role in the mask generation process, and the number of prompt points has an impact on the segmentation performance. To investigate the relationship between the number of prompt points and the segmentation capability of SAM and validate the prompt point sensitivity of Material-SAM, we used different numbers of prompt points as inputs to the prompt encoder of the model, and evaluated the performance using PA, CPA, and DSC as evaluation metrics. The experimental results are shown in Table 2 and Fig. 8.

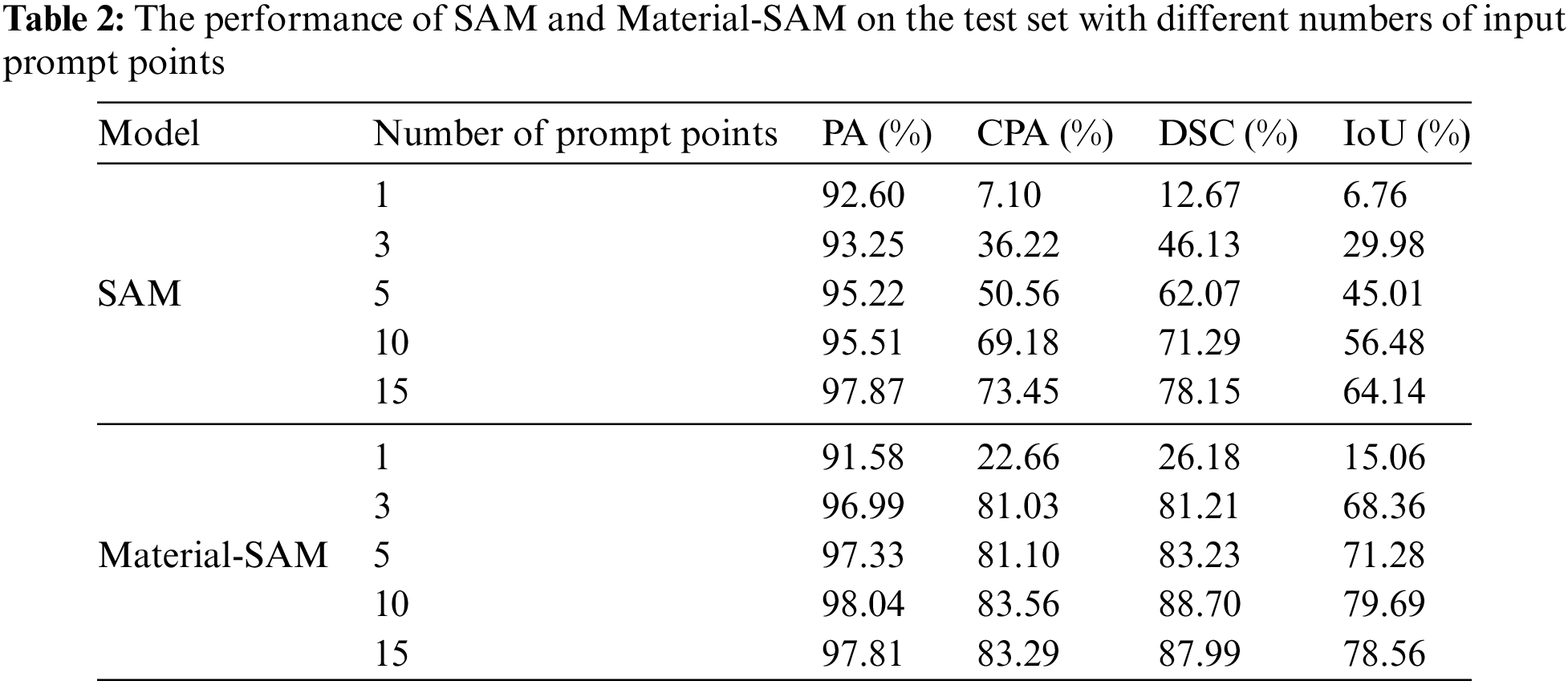
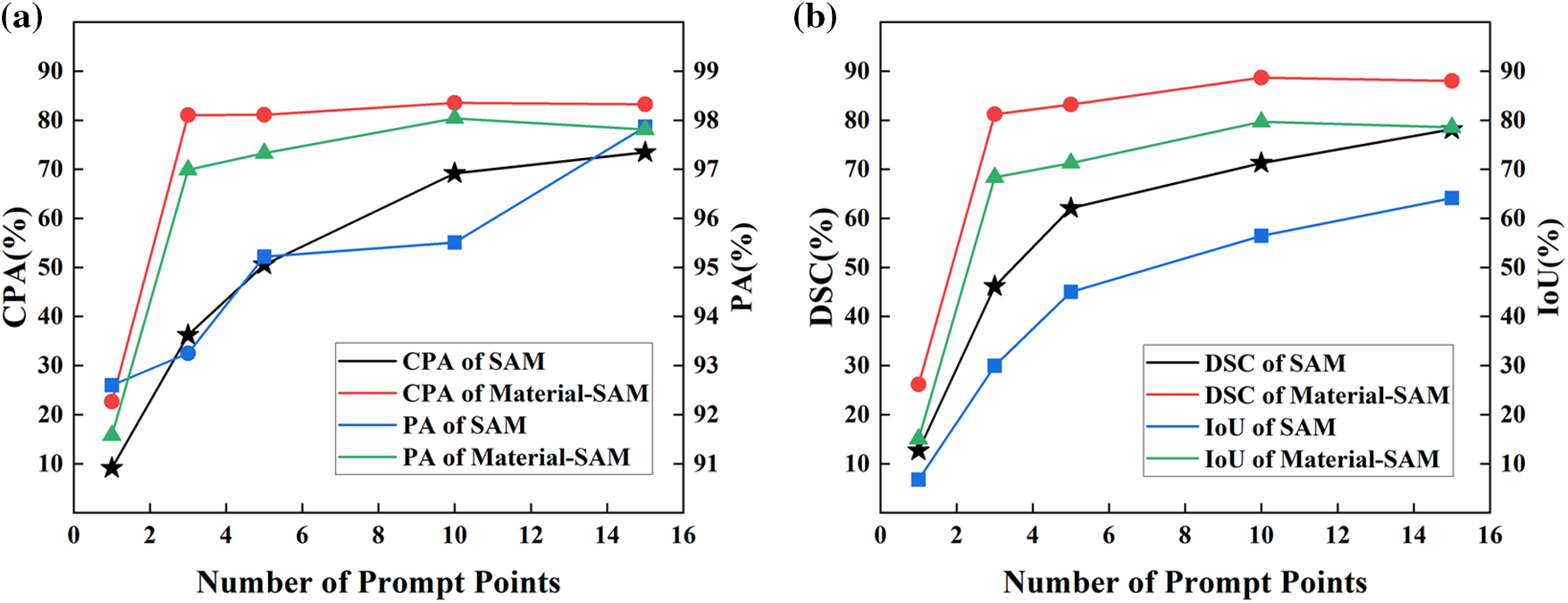
Figure 8: (a) PA, CPA, (b) DSC, IoU of SAM and Material-SAM with different numbers of input prompt points

From the data in the table, it can be observed that the segmentation performance of the SAM model improves with an increasing number of prompt points. When only one prompt point was used as input, the CPA and DSC were only 7.10% and 12.67%, respectively, which were insufficient for satisfactory segmentation. When the number of prompt points is increased to ten, SAM can segment the mask we expect. At this time, CPA and DSC are only 69.18% and 71.29%. It can be seen that SAM has a low sensitivity to features in XCT images and requires a significant number of prompt points to perform meaningful segmentation. On the other hand, Material-SAM achieved a CPA of 22.66% and DSC of 26.18% even with only one prompt point as input. With three prompt points, Material-SAM already achieved satisfactory segmentation performance, and the best performance was achieved with ten prompt points, resulting in a CPA of 83.56% and DSC of 88.70%. It is evident that Material-SAM can achieve significant segmentation results with fewer prompt points, overcoming the issue of SAM requiring a large number of prompt points for XCT image segmentation and reducing the complexity of the segmentation process. After inputting approximately ten prompt points, the performance of Material-SAM reached saturation, and further increasing the number of prompt points resulted in fluctuation in the segmentation performance.

In the process of segmenting a single slice image, it was clearly observed that SAM could only segment a small area when only one prompt point was used, while Material-SAM achieved a slightly larger segmented area. When three prompt points were used, SAM still exhibited a small segmentation range and produced low-quality generated masks, while Material-SAM could segment the carbides throughout the entire image, as shown in Fig. 9. It was not until 15 prompt points were used that SAM was able to complete the segmentation of the entire XCT image.

Figure 9: (a1–a5) The masks generated by SAM with different numbers of input prompt points. (b1–b5) The masks generated by Material-SAM with different input prompt points

4.4 Generalization Performance

Material-SAM is not only capable of carbide segmentation but also performs segmentation on other XCT images. To evaluate its generalization ability, we selected slice images from [45] that were not included in the training of Material-SAM. The resulting segmentation achieved a PA of 98.28%, CPA of 97.61%, DSC of 81.55%, and IoU of 68.95% reaching a high level of accuracy in pixel segmentation. The segmentation results are shown in Fig. 10.

Figure 10: (a–c) represent the ground truth images, and (d–f) represent the segmentation results of Material-SAM

Although there is a certain degree of redundancy in the segmentation of the target, the segmentation results of Material-SAM are very close to the ground truth, demonstrating its strong generalization ability in XCT image segmentation. Due to the fact that the image encoder of Material-SAM is constructed and trained based on SAM, it exhibits high sensitivity to changes in grayscale gradients. With appropriate reference points provided, Material-SAM can perform segmentation based on the grayscale values around these reference points, particularly excelling when there is a significant contrast between the grayscale values of the object to be segmented and the background.

We performed 3D reconstruction of the segmentation results and presented the results of two methods in Fig. 11. Overall, there is little difference between the results of these two methods, which confirms the excellent generalization performance of Material-SAM on XCT images and its capability to handle most material XCT image segmentation tasks.

Figure 11: 3D reconstruction results of (a) ground truth (b) Material-SAM segmentation

5  Conclusion

The emergence of SAM has introduced a new approach to the field of semantic segmentation, offering a powerful solution for various downstream tasks. Its strong generalization capability makes it possible to segment almost anything. However, SAM’s pretraining data primarily consists of natural images, which limits its performance in material XCT image segmentation. It struggles to accurately capture material features and requires a significant number of feature points to achieve satisfactory results.

To address this issue, this study constructed a dataset specifically for carbide segmentation in nickel-based single crystal superalloys. The dataset was adjusted using techniques such as median filtering, histogram equalization, and gamma correction to enhance the features. To overcome SAM’s limitations in material XCT image segmentation, we employed transfer learning to fine-tune SAM. Considering data requirements and computational costs, we froze the parameters of SAM’s image encoder and only trained the mask decoder. During training, we utilized eight-connected labeling to identify all carbide connected regions in the ground truth image and selected the coordinates of the center pixels from the three largest connected regions as input points for the prompt encoder.

To validate the internal validity of Material-SAM, we conducted two experiments comparing its performance with the original SAM model on our target task—material image segmentation. We used evaluation metrics such as PA, CPA, IoU, and DSC. In the first experiment, both models were tested using the same test set and identical reference point inputs. The results indicated that Material-SAM achieved an 8.81% improvement in DSC compared to SAM, demonstrating superior performance in material image segmentation and confirming the internal validity of our model optimization. Additionally, we compared Material-SAM with traditional segmentation methods such as threshold segmentation and state-of-the-art methods in semantic segmentation, including FCN, SegNet, PSPNet, DANet, and EncNet. The outcomes revealed that our approach outperformed other networks in various segmentation parameters for material image segmentation. In the second experiment, we tested Material-SAM and SAM using the same test set and analyzed the impact of the number of reference input points on segmentation performance. The results showed that Material-SAM required significantly fewer reference points than SAM to achieve optimal results, confirming that our model adjustments could reduce its reliance on reference points. Both experiments collectively validated the internal validity of our approach. To confirm the external validity of SAM-Material, we applied the model to another material, AZ91 magnesium alloy, segmenting corrosion pits in XCT slice images. The achieved DSC value for the segmentation result was 81.55%, and visually, it closely matched the ground truth map, demonstrating strong external validity of our model in material image segmentation tasks. This further confirmed that SAM-Material can be utilized as an excellent segmentation algorithm in material images.

This study presents a novel approach for material XCT image segmentation that achieves good results even with limited training data. It overcomes the limitations of traditional threshold segmentation, which relies on image grayscale values and often produces poor segmentation results. Moreover, it avoids the need for a large amount of training data and the computational costs associated with training neural networks. One limitation of Material-SAM is its reliance on manual input and adjustment of reference points. In large-scale segmentation tasks, this process may consume a considerable amount of time and human resources. Additionally, the segmentation results are influenced by the operator’s input of reference points, introducing a subjective element. This method is capable of segmenting only one type of object at a time. Moreover, when dealing with a large number of discrete objects for segmentation, a significant number of reference points may be required. If the grayscale difference between the segmentation target and the background is small, this method may struggle to accurately distinguish between the background and the segmentation target. These limitations need to be carefully considered in practical applications, especially when dealing with large-scale or complex scenarios. Future improvements could focus on enhancing automation to reduce manual intervention and improving adaptability to handle multiple object classes and grayscale-similar scenes. SAM provides a foundation for many downstream tasks, and there are still opportunities for further improvements and enhancements to enhance its performance in material XCT image segmentation.

Acknowledgement: The authors would like to thank the experimental support from the Analysis & Testing Center, Beijing Institute of Technology. We are grateful for the help from all members at the Integrated Computational Materials Engineering (ICME) Lab, Beijing Institute of Technology, China.

Funding Statement: This work was supported by the National Natural Science Foundation of China (Grant Number 52073030) and National Natural Science Foundation of China-Guangxi Joint Fund (U20A20276).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Xuelong Wu, Junsheng Wang; data collection: Chengpeng Xue, Yuling Lang, Decai Kong, Xiaoying Ma, Haibo Qiao; analysis and interpretation of results: Xuelong Wu, Zhongyao Li, Yisheng Miao; draft manuscript preparation: Xuelong Wu, Junsheng Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data available on request from the authors.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. J. Fan, D. L. McDowell, M. F. Horstemeyer, and K. Gall, “Cyclic plasticity at pores and inclusions in cast Al-Si alloys,” Eng. Fract. Mech., vol. 70, no. 10, pp. 1281–1302, 2003. doi: 10.1016/S0013-7944(02)00097-8. [Google Scholar] [CrossRef]

2. Y. X. Gao, J. Z. Yi, P. D. Lee, and T. C. Lindley, “A micro-cell model of the effect of microstructure and defects on fatigue resistance in cast aluminum alloys,” Acta. Mater., vol. 52, no. 19, pp. 5435–5449, 2004. doi: 10.1016/j.actamat.2004.07.035. [Google Scholar] [CrossRef]

3. M. Lamm and R. F. Singer, “The effect of casting conditions on the high-cycle fatigue properties of the single-crystal nickel-base superalloy PWA 1483,” Metall. Mater. Trans. A., vol. 38, no. 6, pp. 1177–1183, 2007. doi: 10.1007/s11661-007-9188-4. [Google Scholar] [CrossRef]

4. S. Steuer, P. Villechaise, T. M. Pollock, and J. Cormier, “Benefits of high gradient solidification for creep and low cycle fatigue of AM1 single crystal superalloy,” Materials Science and Engineering: A, vol. 645, pp. 109–115, 2015. doi: 10.1016/j.msea.2015.07.045. [Google Scholar] [CrossRef]

5. A. Cervellon, J. Cormier, F. Mauget, and Z. Hervier, “VHCF life evolution after microstructure degradation of a Ni-based single crystal superalloy,” Int. J. Fatigue., vol. 104, pp. 251–262, 2017. doi: 10.1016/j.ijfatigue.2017.07.021. [Google Scholar] [CrossRef]

6. Y. Liu et al., “Crack formation and microstructure-sensitive propagation in low cycle fatigue of a polycrystalline nickel-based superalloy with different heat treatments,” Int. J. Fatigue., vol. 108, no. 6, pp. 79–89, 2018. doi: 10.1016/j.ijfatigue.2017.10.012. [Google Scholar] [CrossRef]

7. R. Jiang et al., “Strain accumulation and fatigue crack initiation at pores and carbides in an SX superalloy at room temperature,” Int. J. Fatigue., vol. 114, pp. 22–33, 2018. doi: 10.1016/j.ijfatigue.2018.05.003. [Google Scholar] [CrossRef]

8. M. Šmíd, V. Horník, L. Kunz, K. Hrbáček, and P. Hutař, “High cycle fatigue data transferability of MAR-M 247 superalloy from separately cast specimens to real gas turbine blade,” Metals, vol. 10, no. 11, pp. 1460, 2020. doi: 10.3390/met10111460. [Google Scholar] [CrossRef]

9. D. F. Song et al., “3D Fe-rich phases evolution and its effects on the fracture behavior of Al-7.0 Si-1.2 Fe alloys by Mn neutralization,” Acta. Metall. Sin., vol. 35, no. 1, pp. 163–175, 2022. doi: 10.1007/s40195-021-01299-x. [Google Scholar] [CrossRef]

10. Y. Hou, J. Lux, P. Y. Mahieux, P. Turcry, and A. Aït-Mokhtar, “Evolution of microstructure and CO2 diffusion coefficient of compacted recycled aggregates during carbonation investigated by X-ray tomography,” Constr. Build. Mater., vol. 372, no. 5, pp. 130715, 2023. doi: 10.1016/j.conbuildmat.2023.130715. [Google Scholar] [CrossRef]

11. A. Tsamos, S. Evsevleev, R. Fioresi, F. Faglioni, and G. Bruno, “Synthetic data generation for automatic segmentation of X-ray computed tomography reconstructions of complex microstructures,” J. Imag., vol. 9, no. 2, pp. 22, 2023. doi: 10.3390/jimaging9020022. [Google Scholar] [PubMed] [CrossRef]

12. Y. Yang et al., “Stress sensitivity of fractured and vuggy carbonate: An X-ray computed tomography analysis,” J. Geophys. Res.: Solid Earth, vol. 125, no. 3, pp. 13, 2020. doi: 10.1029/2019JB018759. [Google Scholar] [CrossRef]

13. Z. Li et al., “Characterization of the convoluted 3D intermetallic phases in a recycled Al alloy by synchrotron X-ray tomography and machine learning,” Acta. Metall. Sin. (English Letters), vol. 35, no. 1, pp. 115–123, 2022. [Google Scholar]

14. K. Liu, J. Wang, B. Wang, P. Mao, Y. Yang and Y. Zhou, “In-situ X-ray tomography investigation of pore damage effects during a tensile test of a Ni-based single crystal superalloy,” Mater. Charact., vol. 177, pp. 111180, 2021. doi: 10.1016/j.matchar.2021.111180. [Google Scholar] [CrossRef]

15. K. Liu, J. Wang, B. Wang, P. Mao, Y. Yang and Y. Zhou, “Quantifying the influences of carbides and porosities on the fatigue crack evolution of a Ni-based single-crystal superalloy using X-ray tomography,” Acta. Metall. Sin. (English Letters), vol. 35, no. 1, pp. 133–145, 2022. doi: 10.1007/s40195-021-01273-7. [Google Scholar] [CrossRef]

16. A. Kirillov et al., “Segment anything,” arXiv preprint arXiv:2304.02643, 2023. [Google Scholar]

17. R. Deng et al., “Segment anything model (SAM) for digital pathology: Assess zero-shot segmentation on whole slide imaging,” arXiv preprint arXiv:2304.04155, 2023. [Google Scholar]

18. S. He, R. Bao, J. Li, P. E. Grant, and Y. Ou, “Accuracy of segment-anything model (SAM) in medical image segmentation tasks,” arXiv preprint arXiv:2304.09324, 2023. [Google Scholar]

19. D. Han, C. Zhang, and Y. Qiao, “Segment anything model (SAM) meets glass: Mirror and transparent objectscannot be easily detected,” arXiv preprint arXiv:2305.00278, 2023. [Google Scholar]

20. J. S. Kim, J. Suh, J. Pae, J. Moon, and T. S. Han, “Gradient-based phase segmentation method for characterization of hydrating cement paste microstructures obtained from X-ray micro-CT,” J. Build. Eng., vol. 46, pp. 103721, 2022. doi: 10.1016/j.jobe.2021.103721. [Google Scholar] [CrossRef]

21. T. Stan, Z. T. Thompson, and P. W. Voorhees, “Optimizing convolutional neural networks to perform semantic segmentation on large materials imaging datasets: X-ray tomography and serial sectioning,” Mater. Charact., vol. 160, pp. 110119, 2020. doi: 10.1016/j.matchar.2020.110119. [Google Scholar] [CrossRef]

22. R. Helwing, D. Hülsbusch, and F. Walther, “Deep learning method for analysis and segmentation of fatigue damage in X-ray computed tomography data for fiber-reinforced polymers,” Compos. Sci. Technol., vol. 230, pp. 109781, 2022. doi: 10.1016/j.compscitech.2022.109781. [Google Scholar] [CrossRef]

23. M. Mahdaviara, M. Sharifi, and Y. Rafiei, “PoreSeg: An unsupervised and interactive-based framework for automatic segmentation of X-ray tomography of porous materials,” Adv. Water. Resour., vol. 178, no. 6, pp. 104495, 2023. doi: 10.1016/j.advwatres.2023.104495. [Google Scholar] [CrossRef]

24. J. Long, E. Shelhamer, and T. Darrell, “Fully convolutional networks for semantic segmentation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Boston, Massachusetts, USA, 2015, pp. 3431–3440. [Google Scholar]

25. O. Ronneberger, P. Fischer, and T. Brox, “U-Net: Convolutional networks for biomedical image segmentation,” in Medical Image Comput. Computer-Assisted Intervention-MICCAI: 18th Int. Conf., Munich, Germany, 2015, pp. 234–241. [Google Scholar]

26. M. Jabbar, M. Siddiqui, F. Hussain, and S. Daud, “Brain tumor augmentation using the U-net architecture,” in Int. Conf. Front. Inf. Technol. (FIT), 2022, pp. 308–313. [Google Scholar]

27. V. Badrinarayanan, A. Kendall, and R. Cipolla, “SegNet: A deep convolutional encoder-decoder architecture for image segmentation,” IEEE Trans. Pattern Anal. Mach. Intell., vol. 39, no. 12, pp. 2481–2495, 2017. doi: 10.1109/TPAMI.2016.2644615. [Google Scholar] [PubMed] [CrossRef]

28. H. Zhao, J. Shi, X. Qi, X. Wang, and J. Jia, “Pyramid scene parsing network,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Venice, Italy, 2017, pp. 2881–2890. [Google Scholar]

29. L. C. Chen, G. Papandreou, F. Schroff, and H. Adam, “Rethinking atrous convolution for semantic image segmentation,” arXiv preprint arXiv:1706.05587, 2017. [Google Scholar]

30. J. Fu et al., “Dual attention network for scene segmentation,” in Proc. IEEE/CVF Conf. Comput Vis. Pattern Recognit., Long Beach, California, USA, 2019, pp. 3146–3154. [Google Scholar]

31. C. Hu and X. Li, “When SAM meets medical images: An investigation of segment anything model (SAM) on multi-phase liver tumor segmentation,” arXiv preprint arXiv:2304.08506, 2023. [Google Scholar]

32. S. Mohapatra, A. Gosai, and G. Schlaug, “Brain extraction comparing segment anything model (SAM) and FSL brain extraction tool,” arXiv preprint arXiv:2304.04738, 2023. [Google Scholar]

33. S. L. Liew et al., “A large, open source dataset of stroke anatomical brain images and manual lesion segmentations,” Sci. Data, vol. 5, no. 1, pp. 1–11, 2018. doi: 10.1038/sdata.2018.11. [Google Scholar] [PubMed] [CrossRef]

34. H. J. Kuijf et al., “Standardized assessment of automatic segmentation of white matter hyperintensities and results of the WMH segmentation challenge,” IEEE Trans. Med. Imag., vol. 38, no. 11, pp. 2556–2568, 2019. doi: 10.1109/TMI.2019.2905770. [Google Scholar] [PubMed] [CrossRef]

35. D. Cheng, Z. Qin, Z. Jiang, S. Zhang, Q. Lao and K. Li, “SAM on medical images: A comprehensive study on three prompt modes,” arXiv preprint arXiv:2305.00035, 2023. [Google Scholar]

36. J. Wu et al., “Medical SAM adapter: Adapting segment anything model for medical image segmentation,” arXiv preprint arXiv:2304.12620, 2023. [Google Scholar]

37. T. Chen et al., “SAM fails to segment anything?—SAM-Adapter: Adapting SAM in underperformed scenes: Camouflage, shadow, and more,” arXiv preprint arXiv:2304.09148, 2023. [Google Scholar]

38. D. P. Fan, G. P. Ji, G. Sun, M. M. Cheng, J. Shen and L. Shao, “Camouflaged object detection,” in Proc. IEEE/CVF Conf. Comput. Vis. Pattern Recognit., 2020, pp. 2777–2787. [Google Scholar]

39. P. Skurowski, H. Abdulameer, J. Błaszczyk, T. Depta, A. Kornacki and P. Kozieł, “Animal camouflage analysis: Chameleon database,” Katedra Grafiki Wizji Komputerowej I Systemów Cyfrowych, Politechnika Śląska, 2018. [Google Scholar]

40. T. N. Le, T. V. Nguyen, Z. Nie, M. T. Tran, and A. Sugimoto, “Anabranch network for camouflaged object segmentation,” Comput. Vis. Image Underst., vol. 184, no. 152, pp. 45–56, 2019. doi: 10.1016/j.cviu.2019.04.006. [Google Scholar] [CrossRef]

41. J. Wang, X. Li, and J. Yang, “Stacked conditional generative adversarial networks for jointly learning shadow detection and shadow removal,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit., Salt Lake City, Utah, USA, 2018, pp. 1788–1797. [Google Scholar]

42. K. Liu, J. Wang, Y. Yang, and Y. Zhou, “Effect of cooling rate on carbides in directionally solidified nickel-based single crystal superalloy: X-ray tomography and U-Net CNN quantification,” J. Alloys Compd., vol. 883, no. 2, pp. 160723, 2021. doi: 10.1016/j.jallcom.2021.160723. [Google Scholar] [CrossRef]

43. D. Jha et al., “Kvasir-SEG: A segmented polyp dataset,” in MultiMedia Modeling: 26th Int. Conf., MMM 2020, Springer International Publishing, Daejeon, South Korea, 2020, vol. 26, pp. 451–462. [Google Scholar]

44. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” arXiv preprint arXiv: 1412. 6980, 2014. [Google Scholar]

45. C. Zhang, C. Liu, X. Li, K. Liu, G. Tian and J. Wang, “Quantifying the influence of secondary phases on corrosion in multicomponent Mg alloys using X-ray computed microtomography,” Corros. Sci., vol. 195, no. 2, pp. 110010, 2022. doi: 10.1016/j.corsci.2021.110010. [Google Scholar] [CrossRef]